Der experimentelle Befund zur Längenkontraktion
BLOG: Quantenwelt

Die Längenkontraktion ist irgendwie das Stiefkind unter den relativistischen Effekten. Das mit Abstand beliebteste Gedankenexperiment der Relativitätstheorie ist das Zwillingsparadoxon. Es veranschaulicht die Zeitdilatation, die sich über den relativistischen Dopplereffekt gut verstehen und messen lässt. Die Längenkontraktion ist dagegen etwas sperriger. Sowohl was die Erklärung angeht als auch in Bezug auf mögliche Messungen.
Experimentelle Befunde
Während sich die vergangene Zeit mit geeigneten Uhren gut vermessen lässt, ist zurückgelegter Weg bei sehr hohen Geschwindigkeiten kaum registrierbar. Zumal in der Realität ohnehin keine Rakten verwendet werden, sondern Atome und Elementarteilchen. Ein Atom ist von sich aus ein schwingfähiges System, dessen Eigenfrequenz von außen kaum beeinflussbar ist. Deshalb ist der optische Dopplereffekt an Atomen leicht messbar. Einen Entfernungsmesser haben Atome dagegen nicht eingebaut. Das macht die Messung der Längenkontraktion bei solchen Experimenten schwierig.
Michelson Morley mit Äther
Längenkontraktion lässt sich aber aus den Ergebnissen des Michelson-Morley-Experiments herleiten. Versuchen wir sie zunächst mit der Lorentzschen Äthertheorie zu durchschauen. Diese ist älter als die Spezielle Relativitätstheorie. Aus ihr stammt der heute noch verwendete Sprachgebrauch.
Ende des 19. Jahrhunderts war der Gedanke etabliert, dass sich Licht in einem Medium, dem Äther ausbreitet. Aus Messungen der Aberration des Sternenlichts war bekannt, dass sich die Erde im Äther bewegen muss. Also versuchten Michelson und Morley diese Bewegung mit ihren Interferometer zu messen… und scheiterten. Im Rahmen der Messgenauigkeit war kein Ätherwind feststellbar.
Ein Michelson-Interferometer besteht aus zwei zueinander orthogonalen Armen an deren Ende je ein Spiegel sitzt. Es teilt einen Lichtstrahl in zwei Teile, die je einen der Arme durchlaufen und bringt die beiden Strahlen dann wieder zum Überlapp. Ist nun ein Arm parallel zur Bewegung durch den Äther und einer Senkrecht dazu angeordnet, so müsste sich durch die Bewegung ein Laufzeitunterschied bemerkbar machen. Das Licht soll sich ja relativ zum Äther immer mit derselben Geschwindigkeit \(c\) bewegen.
Der parallele Arm
Betrachten wir zunächst den Arm parallel zur Bewegung. Der Abstand vom Strahlteiler zum Spiegel sei \(L_p\). Das Licht bewegt sich im Äther mit \(c\). Gleichzeitig bewegen sich Strahlteiler und Spiegel mit \(v\) in dieselbe Richtung. Auf dem Hinweg läuft der Spiegel der Lichtwelle davon, so dass diese dem Spiegel nur mit der Rate \(c-v\) näher kommt. Auf dem Rückweg kommt der Strahlteiler dem Licht entgegen. Der Abstand verringert sich mit \(c+v\). Das Licht braucht für Hin- und Rückweg auf diesem Arm also die Zeit
\(\Delta t_p = \frac{L_p}{c-v}+\frac{L_p}{c+v}=\frac{2\cdot c\cdot L_p}{c^2-v^2}=\gamma^2\frac{2\cdot L_p}{c}\).
Da die Zeit im ruhenden Arm einfach \(\Delta t_{p,0}=\frac{2\cdot L_p}{c}\) wäre, ist die Licht-Laufzeit also hier zwei mal um den relativistischen Faktor \(\gamma\) verlangsamt.
Der senkrechte Arm
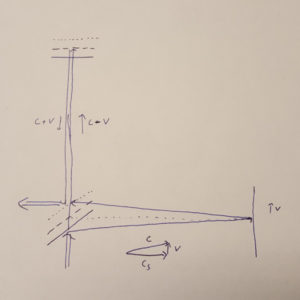
Im Arm senkrecht zur Bewegung, läuft das Licht schräg zwischen Strahlteiler und Spiegel mit der Ätherlichtgeschwindigkeit \(c\). Die auf die bewegte Verbindungslinie vom Spiegel zum Strahlteiler projizierte Lichtgeschwindigkeit berechnet sich über den Satz von Pythagoras zu
\(c_s=\sqrt{c^2-v^2}\).
Die Länge dieses Arms bezeichne ich mit \(L_s\). Damit ergibt sich für Hin- und Rückweg:
\(\Delta t_s = 2\cdot \frac{L_s}{c_s}=\frac{2\cdot L_s}{\sqrt{c^2-v^2}}=\gamma \frac{2\cdot L_s}{c}\).
Im Senkrecht zur Bewegung ausgerichteten Arm ist die Laufzeit also nur um den Faktor \(\gamma\) gegenüber dem ruhenden Arm verlängert.1
Laufzeiten vergleichen führt zu Zeitdilatation und Längenkontraktion
Zusammengefasst gibt es zwei Effekte: In einem gegen den Äther bewegten Interferometer müssten die Laufzeit in beiden Armen um den Faktor \(\gamma\) länger sein. Zusätzlich wäre die Laufzeit in dem Parallel zur Bewegung ausgerichteten Arm nochmal um den Faktor \(\gamma\) länger als im senkrechten Arm. Beide Effekte werden aber im Experiment nicht beobachtet .
Das lässt sich mit Zeitdilatation und Längenkontraktion erklären: Wenn alle physikalischen Effekte in einem gegen den Äther bewegten System um den Faktor \(\gamma\) langsamer ablaufen als im ruhenden System, merkt niemand etwas vom ersten Effekt. Wenn außerdem der Parallel zur Bewegung ausgerichtete Arm um den Faktor \(\gamma\) verkürzt ist, sind die Laufzeiten in beiden Armen wieder gleich.
Die Stärke eines Interferometers ist es, die Laufzeitunterschiede zwischen beiden Armen genau zu vermessen. Für absolute Laufzeiten ist es wenig empfindlich. Deshalb ist das Michelson Morley Experiment vor allem ein Beweis für die Längenkontraktion. Die Zeitdilatation kann durch den Dopplereffekt besser belegt werden.
Und nun ohne Äther
Die Ätherinterpretation der Längenkontraktion und Zeitdilatation hat einen entscheidenden Nachteil: Es gibt keinen plausiblen Mechanismus. Zwar ist beides denkbar: Mechanische Objekte werden über elektrische Kräfte zusammengehalten. Warum sollte das Medium, das elektromagnetische Wellen überträgt, nicht für eine Verkürzung von Objekten verantwortlich sein? Warum sollte eine Uhr, in der Schwingungen unter anderem elektrische Felder erzeugen, nicht durch Bewegung gegenüber dem Äther beeinflusst werden? Aber es gibt keinen Ansatz, der die exakte Größe des Effektes der Bewegung gegen den Äther erklären könnte.
Die Spezielle Relativitätstheorie dagegen erklärt die relativistischen Vorgänge durch Annahme einer bestimmten Symmetrie: In zwei zueinander bewegten Systemen werden Naturgesetze mit identischen Formeln berechnet, wenn man ihre Koordinaten über Lorentz-Transformationen ineinander überführen kann. Und aus der Lorentztransformation folgen direkt Zeitdilatation und Längenkontraktion.


Nur zur Erinnerung:
Ich habe immer noch keine Antwort auf meine Frage erhalten, warum ein Beobachter in einem angeblich kontrahiertes Raumschiff zwar nicht die Kontraktion des Raumschiffes wahrnehmen soll, aber die Kontraktion einer Distanz, die dieses Raumschiff durchfliegen wird, schon.
Rätsel über Rätsel bei der sRT. Aber zum Glück haben wir ja Koryphäen wie Sie und Herr Wappler und Herr Knoth und wie sie alle heißen, oder zumindest die Accounts …
Joachim Schulz schrieb (21. Dezember 2018):
> […] Ein Michelson-Interferometer besteht aus zwei zueinander orthogonalen Armen an deren Ende je ein Spiegel sitzt.
> […] Der parallele Arm Betrachten wir zunächst den [einen] Arm parallel zur Bewegung [der Erde im Äther]. Der Abstand vom Strahlteiler zum Spiegel sei \(L\).
> […] Der senkrechte Arm Im Arm senkrecht zur Bewegung […]
Stimmt es, dass (in gültigen Versuchen eines Michelson-Interferometers) der “Abstand vom Strahlteiler zum Spiegel” des einen Interferometer-Armes und des anderen Interferometer-Armes gleich sein soll, also gleichermaßen den Wert \(L\) haben soll ?
(Insbesondere einschließlich der Dicke von Spiegel-Substraten und von entsprechenden Kompensationsplättchen …)
Besteht diese Forderung insbesondere auch dann, falls das Interferometer im Verlaufe eines Versuches (in der durch die zueinander senkrechten Arme definierten Ebene) gedreht würde ?
@Frank Wappler
21. Dezember 2018 @ 13:45
Das Drehen des Aufbaus ist tatsächlich unverzichtbarer Bestandteil des Experiments. Und dann ist es unerheblich, ob die Arme tatsächlich gleich lang sind oder nicht. Wichtig ist, dass die Änderungen der Signallaufzeiten durch den hypothetischen Ätherwind sichtbar werden.
@Albrecht Storz
21. Dezember 2018 @ 13:41
Weil seine mitgeführten Maßstäbe derselben Längenkontraktion unterliegen wie das Raumschiff, während die Start und Ziel relativ zu ihm bewegt sind.
Joachim Schulz schrieb (21. Dezember 2018 @ 14:00):
> Das Drehen des Aufbaus ist tatsächlich unverzichtbarer Bestandteil des Experiments.
Das überrascht mich zwar nicht (schließlich habe ich durch meinen obigen Kommentar “das Drehen” ja überhaupt erst erwähnt) …
Trotzdem die (ziemlich “Sokratisch” gemeinte) Frage:
Warum ist “das Drehen des Aufbaus” überhaupt ein tatsächlich unverzichtbarer Bestandteil des Experiments ??
(Der obige SciLogs-Artikel kam ja offenbar ohne ausdrückliche Erwähnung dieses “Bestandteils” aus …)
> Und dann ist es unerheblich, ob die Arme tatsächlich gleich lang sind oder nicht.
Hmm …
Ist es denn (zunächst mal) für die im obigen SciLogs-Artikel gezeigte Argumentation unerheblich, ob die Arme tatsächlich gleich lang sind oder nicht ?
Immerhin taucht das selbe Symbol \(L\) dort offenbar in insgesamt drei anscheinend unterscheidbaren Zusammenhängen auf:
– ausdrücklich im Abschnitt “Der parallele Arm Betrachten wir zunächst den Arm parallel zur Bewegung. Der Abstand vom Strahlteiler zum Spiegel sei \(L\)“,
– aber auch in Formeln des Abschnitts “Der senkrechte Arm“, dort insbesondere im Ausdruck “\(2 \cdot \frac{L}{c_s}\)”,
– und (wiederum im Abschnitt “Der parallele Arm“) außerdem: “im ruhenden Arm einfach […] \(2 \cdot \frac{L}{c}\)“.
Falls es ausdrücklich unerheblich wäre, ob die (wie beschrieben identifizierten und offenbar unterscheidbar gedachten) Arme tatsächlich gleich lang sind oder nicht,
könnte und sollte deren jeweiliger “Abstand vom Strahlteiler zum Spiegel” (bzw. “Arm-Länge“) doch durch entsprechend
verschiedene Symbole ausgedrückt werden (nämlich um nicht deren vermeintliche Gleichheit zu unterstellen, die weder verlangt noch gewährleistet wäre); z.B.
– “Betrachten wir zunächst den Arm parallel zur Bewegung. Der Abstand vom Strahlteiler zum Spiegel sei \(L_p\)”,
– “Im Arm senkrecht zur Bewegung … \(2 \cdot \frac{L_s}{c_s}\)”, sowie
– “Im ruhenden Arm einfach […] \(2 \cdot \frac{L}{c}\)“.
Also, zur Ausnahme ganz sachlich:
Sie sagen also, der Beobachter auf dem Raumschiff müsste das Raumschiff mit anderen Standards messen als etwa die Flugdistanz?
Wie soll das gehen? Hat die Raumschiffbesatzung zu diesem Zweck mehrer, unterschiedliche Sätze von Standards dabei? Woher wissen die, welche Standards sie für welche Längenmessung einzusetzen haben?
Oder reden wir gar nicht von Messvorgängen? Ihre Aussage in Post 21. Dezember 2018 @ 13:41 erschließt sich mir in seiner vollen tiefsten Tiefe überhaupt nicht.
@Frank Wappler
Vielen Dank. Ich habe das entsprechend angepasst. Die Länge des ruhenden Arms soll natürlich gleich der Länge des bewegten sein.
Bei Michelson Morley stellt dich immer die Frage, wo taucht etwas auf und wo wird beobachtet.
Die Phasenverschiebungen tauchen in Lichtkegeln parallel zur Lichtausbreitungsachse auf, werden aber auf dem Screen senkrecht bzw. radial dazu beobachtet.
These: Davon ausgehend, dass selbst Laserlicht nicht bloß aus einer einzigen Welle, sondern aus mehreren sich kegelförmig ausbreitender besteht, ist die Summe der Phasenverschiebungen entlang der Lichtausbreitungsachse radial dazu nicht erkennbar.
Gestützt wird diese These z.B. von Martin Grusenick, selbst wenn er selber es auch nicht glaubt und statt dessen nach wie vor einen Äther bewiesen sehen will. Bei Michelson-Morley wurden, soweit ich weiß, nur die Achsen getauscht und nicht während der Messung kontinuierlich gedreht, wie bei Grusenick. Sowohl für die Ätherthese als auch für die RT-These hätte man auf dem Schirm bei kontinuierlicher Drehung zwischen 90° Winkeln die Phasenverschiebung zwischen den Armen erkennen können, aber wie Grusenick zeigt, tut sich da (horizontal) gar nichts.
Darüber hinaus ist gar nicht feststellbar, mit welcher Geschwindigkeit Licht auf dem senkrechten Arm unterwegs ist – es kann gemäß Reflektionsgesetz auch c-v sein, also alles zwischen c-v und sqrt(c²-v²). Die Schräge zwischen Strahlteiler (Start) und Spiegel (Ziel) ist jedenfalls eine projizierte Strecke und die Geschwindigkeit auf dieser deswegen auch nur eine projizierte Geschwindigkeit und als solche kaum messbar.
Ein Beweis für Längenkontraktion ist dies Alles deswegen immer noch nicht…
Zwei mit relativistischer Geschwindigkeit zueinander bewegte Objekte, die nichts von einander wissen, stellen für ihre jeweiligen Systeme (also unabhängig voneinander) Urmeter gemäß SI-Definition her. Was würden sie bei einer Begegnung feststellen, wenn die Objekte gegenüber dem Inertialraum mit unterschiedlichen Geschwindigkeiten unterwegs waren?
Joachim Schulz schrieb (21. Dezember 2018 @ 15:38):
> Vielen Dank. Ich habe das entsprechend angepasst.
Im obigen SciLogs-Artikel finde ich nun (was vorher sicherlich noch nicht da stand):
Relative Längenänderungen ?! …
Sind derartige Änderungen (oder zumindest die Denkbarkeit derartiger Änderungen) in den Symbolen bzw. Formeln des obigen SciLogs-Artikel (schon) erkennbar ausgedrückt ??
Außerdem steht dort (noch unverändert):
Müsste das anhand der vorgenommenen Anpassung, nämlich insbesondere der Unterscheidung zwischen \(L_p\) und \(L_s\), stattdessen nicht etwa heißen:
“… in dem parallel zur Bewegung ausgerichteten Arm nochmal um den Faktor \(\gamma \cdot \frac{L_p}{L_s}\) anders als im senkrechten Arm.”
?
Was endlich die Frage nahelegt, auf die ich (uns) hinzusteuern versuche:
Haben Michelson/Morley überhaupt den (reellen Verhältnis-)Wert “\(\frac{L_p}{L_s}\)” Versuchsabschnitt für Versuchsabschnitt gemessen ?
bzw.
Falls Michelson/Morley entsprechend der zitierten “Anmerkung 1.” (“einfach”) angenommen hätten, dass “\(\frac{L_p}{L_s}\) = 1”, wie hätten sie zumindest im Prinzip messen wollen, ob diese Annahme zutraf, oder in wie fern nicht (und den entsprechenden Beitrag zur “systematische Unsicherheit” ihrer Ergebnisse bewerten können) ? — Etwa durch den interferometrischen Vergleich von Pingdauern (alias “Signallaufzeiten“) ?? …
> Die Länge des ruhenden Arms soll natürlich gleich der Länge des bewegten sein.
Mag schon sein, dass das “natürlich so sein soll”. Aber, erneut:
Wurde das gemessen ?? (Und falls ja, wie?).
@A.S. 15:38 (Sie …) “… sagen also, der Beobachter auf dem Raumschiff müsste das Raumschiff mit anderen Standards messen als etwa die Flugdistanz?” Nein, ist keine Relativitätstheorie, nur Ihre falsche Meinung.
Der Beobachter mit seinem Meter ist zum Raumschiff !unbewegt, zur Distanz aber !bewegt, noch zwei!!
Das eigentlich interessante am Michelson ist, daß sich eigentlich nichts bewegt.
Deshalb kann es eigentlich keine Effekte geben, eigentlich ist nur das Nullresultat.
Die SRT ist konsistent und darf zwangsläufig eigentlich keinem 0-Ergebnis widersprechen.
Es ist ein (seltsames) didaktisches Dilemma *Audititakten* das mit SRT zu erklären.
@Senf:
Woher nimmst du denn diese Weisheit? Die einzige Formel, die passen würde, das es so aussieht es würde sich nichts bewegen selbst wenn sich ganz offensichtlich etwas bewegt, ist jene der Korpukel-Theorie:
\( T_H=\frac{D+vt}{c+v}+\frac{D-vt}{c-v}=\frac{2D}{c} \)
\( T_V=2\sqrt{\frac{D^2+(vt)^2}{c^2+v^2}}=\frac{2D}{c} \)
Als ich diese Weisheit vor Urzeiten im Netz präsentierte, hielt man es für falsch, ist aber der einzige Weg, bei dem sich sowohl bewegt als auch unbewegt nichts an
\( T=\frac{2D}{c} \)
ändert. Die SRT wäre demnach ein gesunder Mix aus Emmisions- und Äthertheorie. Nichts Halbes und nichts Ganzes, also vergiss es.
@Joachim
Das wäre jetzt so die klassische Erklärung, wie von Lorentz mit dem Aether gedacht. Wenngleich das alles in der LET schlüssig ist, wird es gelinde gesagt suboptimal, wenn man das einfach so für die SRT übernimmt, aus hinlänglich bekannten Gründen. Meines Erachtens geht es relativistisch viel einfacher, wenn man sich nicht so sehr an die LET-Interpretation klammert:
Bei einem im “ruhenden System” S bewegten Interferometer mit Armlänge \(L\) (proper length) ergibt sich parallel zur Bewgungsrichtung die Armlänge als \(L_p = \gamma L\) (Radar-Länge in S). Senkrecht zur Bewegungsrichtung ist hingegen die Armlänge \(L_s = L\) unverändert gleich der Ruhelänge.
Im parallelen Arm durchläuft dann ein Lichtsignal bei Hin- und Rückweg also eine Strecke \(2 L_p\) mit der Geschw. \(c\). Im senkrechten Arm durchläuft indessen ein Lichtsignal bei Hin- und Rückweg die Strecke \(2L_s\) mit der effektiven Geschw. \(c_s = c/\gamma\), wie oben im Artikel beschrieben. Für die Signal-Laufzeiten folgt dann
\[
\Delta t_p = \frac{2 L_p}{c} = \frac{2\gamma L}{c} = \frac{2L}{c/\gamma} = \frac{2L_s}{c_s} = \Delta t_s.
\]
Das erklärt das Michelson-Morley Nullresultat in S, ohne Aether und ohne Kontraktion. Im Ruhesystem des Interferometers ist der Fall ohnehin klar, da ist nichts mehr zu erklären.
@ all: spannendes Thema zu Verwirrung Michelson mit klassischen Vorstellungen
– man braucht keine Lorentz-Verkürzung “LV” als Notwehr von FitzGerald zur Ätherrettung
– man braucht keine Lorentz-Kontraktion LK im Sinne der Einstein’schen Definition
Die korrekte Interpretation “läuft” über die relativistische Hosenknopfaddition c=max,
also w=u⊕v<c mit w=c⊕v=c=max, bei Michelson ist u=c und v=0, deshalb ist Δt=0.
Wenn dagegen klassische Addition (ohne LV) w=c+v gelten würde, wären Interferenzstreifen da.
PS#22:55 (fast) alle Lehrbücher sündigen bei der Erklärung von Michelson mit dem Gamma-Faktor 😉
Chrys schrieb (21. Dezember 2018 @ 21:22):
> […] Interferometer mit Armlänge \(L\) (proper length) […]
Das im obigen SciLogs-Artikel betrachtete Interferometer besteht aber aus zwei verschiedenen (gegenüber einander senkrechten) Armen, deren Armlängen (selbstverständlich “proper length” — was denn sonst ?!?) nicht unbedingt gleich sind;
und deren Armlängen deshalb verschieden benannt sind; nämlich offenbar, spätestens seit Joachim Schulz den Artikel entsprechend “angepasst” hat (21. Dezember 2018 @ 15:38), als \(L_p\) und \(L_s\).
@Senf:
Und an der Logik aündigt man, wenn man ihn weglässt. Zwischen Vertikal und Horizontal bleibt definitiv ein zeitlicher Versatz von mindestens \( \frac{c}{\sqrt{c^2-v^2}} \). Alles Andere würde hier, wie gesagt, zur Emissions-Theorie führen – kann man also vergessen.
@Frank Wappler / 21. Dezember 2018 @ 23:34
Michelson & Morley (1887) verwendeten ein Instrument mit gleichen Armlängen. Und meines Wissens zumindest wurde das noch nirgendwo anderslautend behauptet.
@Chrys:
Stimmt auffallend… anders habe ich es auch noch nicht gehört… anders würden auch Berechnungen über unterschiedliche Laufzeiten keinen Sinn machen.
Was in diesem Zusammenhang noch interessant wäre, ist, ob man jemals versucht hat, die Arme per Microdchauben oder Ähnlichem auf derart unterschiedliche Längen zu bringen, das gar kein Zeitversatz und somit theoretisch auch kein Interferenzmuster entsteht.
Chrys schrieb (22. Dezember 2018 @ 06:52):
> Michelson & Morley (1887) verwendeten ein Instrument mit gleichen Armlängen.
Wie kommst Du denn darauf ?!?.
Und selbst falls Michelson & Morley (1887) nominell behauptet oder gewollt hätten, dass ihre jeweilige Interferometer-Versuchsanordnung “gleiche Armlängen” gehabt (bzw. sogar im Versuchsverlauf behalten) hätte —
wie hätten sie das denn überhaupt herausfinden und ggf. nachweisen wollen ??
Hatten Michelson & Morley überhaupt einen nachvollziehbaren Begriff davon, was mit “gleiche Längen (zwischen verschiedenen Paaren von Enden)” gemeint wäre ??
> Und meines Wissens zumindest wurde das noch nirgendwo anderslautend behauptet.
Dass manchen der Unterschied zwischen “behaupten” und “messen” nicht sofort auffällt … glaub ich sofort.
Man kann sich doch gar nicht gegen den “Äther” bewegen?
@Frank Wappler / 22. Dezember 2018 @ 07:41
H.A. Lorentz schreibt (meine Hervorhebung):
Ansonsten würde ich es gerne Hrn. Schulz überlassen, bei Bedarf die experimentelle Vorrichtung von Hrn. Michelson und Hrn. Morley kompetent zu expliciren.
Genauso kann man sich die Tatsache, daß ein Laser, auch dann noch funktioniert, wenn er um 90 Grad gedreht wird. Denn im Inertialsystem, in dem die Sonne ruht, würde ein längs der Bahnbewegung ausgerichteter Laser eine längere Laufzeit für das hin- und herlaufende Licht haben als ein quer zur Bewegungsrichtung ausgerichteter Laser. Daraus würde dann gefolgert werden, daß die Länge des längs der Bewegungsrichtung ausgerichteter Laser kleiner ist.
Noch mal zu dem hier:
in dem Video “überholen” sich die Phasen anscheinend recht schnell, bzw. entstehen aus der Mitte heraus immer Neue. Ein Interferenzmuster bleibt jedoch zu jeder Zeit sichtbar. Ist das nicht irgendwie ein Indiz dafür, dass das radiale Interferenzmuster auf dem Screen nicht viel über die achsialen Interferenzen aussagt?
Zitat Chrys: „H.A. Lorentz schreibt (meine Hervorhebung):
“Der Versuch wurde im Jahre 1881 von Hrn. Michelson ausgeführt. Sein Apparat, eine Art Interferentialrefractor, hatte zwei gleich lange, horizontale, zu einander senkrechte Arme P und Q, und von den beiden mit einander interferirenden Lichtbündeln ging das eine längs dem Arme P und das andere längs dem Arme Q hin und zurück. […] In Gemeinschaft mit Hrn. Morley hat dann später Hr. Michelson die Untersuchung wieder aufgenommen, wobei er, zur Erhöhung der Empfindlichkeit, jedes Lichtbündel durch einige Spiegel hin und her reflectiren liess. Dieser Kunstgriff gewährte denselben Vortheil, als wenn die Arme des früheren Apparates beträchtlich verlängert worden wären.“
.
Auch G.O. Mueller weist auf die Wiederholungen des Michelson-Experiments von 1887 mit einer verbesserten Meßanordnung und Methodologie hin, siehe: Der Michelson-Morley-Versuch 1881/87 soll die Nicht-Existenz des Äthers bewiesen haben
Vor allem Maurice Allais hat tiefgründig die Messreihen von Dayton C. Miller zu verschiedenen Jahreszeiten analysiert: Es würde ein Ätherwind der Größenordnung von 8 bis 16 km/s gemessen, siehe mit weiterführenden Links zu den Analysen von Maurice Allais: Das Michelson-Morley-Experiment hat kein Nullergebnis erzielt
@Alle
Ich versuche mal auf einige der Kommentare in einem Rutsch einzugehen. Einfach um die Diskussion wieder zu bündeln:
Ich habe diesen Text recht unvermittelt beendet als er auf die SRT kam. Das ist Absicht: Ich wollte mich hier auf das historische Experiment beschränken und motivieren, warm man noch immer von Längenkontraktion spricht, obwohl hier nichts kontrahiert. Das Erbe der Lorentzschen Äthertheorie. Eine relativistische Beschreibung habe ich mit für einen späteren Artikel vorgenommen.
Michelson und Morley (M&M) haben tatsächlich ein Interferometer mit gleichen Armlängen gebaut und in der Praxis wird es auch so gemacht. Aber es ist nicht wirklich notwendig, weil der damals gesuchte Ätherwind-Effekt ja darin bestehen soll, dass die Laufzeit in dem Arm, der in den “Wind” gedreht wird sich um den Gamma-Faktor verlängert und sich dann, wenn er wieder quer zum “Wind” steht, verkürzt. Und dieser Effekt ist davon unabhängig, was im anderen Arm passiert.
Herr Wappler würde vermutlich einwenden, dass es aufwendig wäre, ein Interferometer zu bauen, in dem beide Arme exakt gleich lang sind. Sie sind es in der Praxis eben nur fast.
Im M&M-Versuch werden beide Arme gedreht. Auch das hat pragmatische Gründe. Man könnte das Interferometer auch um einen Arm drehen, denn man dann als Referenz hat. Das ist aber aufwendiger. Oder man lässt das Interferometer wie es ist und überlässt es der Erde, es in den Wind zu drehen. Auch das wurde gemacht. Die Details des Experiments sind historisch interessant, aber für das Verständnis des Messprinzips unerheblich.
Bei M&M schwamm das Spektrometer auf Quecksilber. Das wurde unsere Sicherheitsabteilung heute nicht mehr zulassen 🙂
Ich habe den alten Markweger-Käse gelöscht. Und die Einlassungen von Herrn Storz, die mal wieder der SRT Aussagen unterstellen, die niemand je gemacht hat, auch.
@NvB 16:56 “Tatsächlich sind Geschwindigkeiten sowohl als auch.” wow aber auch 🙂
Die Lichtgeschwindigkeit LG=c=inv=const=max “erfüllt” diese Eigenschaften in einem wohldefinierten
Inertialsystem. Messungen und Randbedingungen müssen (überein)stimmen, sonst hast’e Trollerei.
Die generelle Richtungsunabhängigkeit der Lichtausbreitung wurde schon 50 J vor Einstein vermutet.
Die Versuche von Kohlrausch und Weber stützen das (skalare) Axiom der Konstanz direkt – so wath.
Die richtungsunabhängige Geschwindigkeit “c” erzwingt die Aufgabe “u+v” als Regel bei der “Zusammensetzung” von Geschwindigkeiten, weil ein Maximalelement die Regeln “u⊕v” bestimmt.
Das Michelson-Experiment kommt ohne LK aus und “bestimmt” nicht die SRT, richtige Mathe reicht.
@Senf:
Eben das glaube ich weniger. Die richtige Mathe zeigt nämlich, dass Laufzeitunterschiede auftreten müssen und diese nicht unbedingt einer Wellenlänge entsprechen. Also entweder sind die Verschiebungen im Femtometerbereich oder das radiale Interferenzmuster baut sich unabhängig von den achsial auftretenden Interferenzen auf, weswegen die radialen Interferenzen in Summe unverändert bleiben.
@NvB 17:49 hast’e schonmal aufgepaßt, daß das Interferenzmuster “radial” per Linse projeziert wird.
Wie beim Photoapparat mit Brennpunktstrahlen – hat mit Invarianz des Querabstandes nichts zu tun.
@Senf:
hast’e schon mal aufgepasst, dass das vollkommen egal ist, weil Lichtstrahlen inkl. Laserlicht ohnehin kegelförmig ist? Warum wohl wird bei Lasern entweder focusable oder der Fokus (Abstand) angegeben?
Chrys schrieb (22. Dezember 2018 @ 09:50):
> H.A. Lorentz schreibt (meine Hervorhebung):
> »Der Versuch wurde im Jahre 1881 von Hrn. Michelson ausgeführt. Sein Apparat, eine Art Interferentialrefractor, hatte zwei gleich lange, horizontale, zu einander senkrechte Arme […]«
Und wie will der genannte H.A. Lorentz zu seiner Beurteilung gekommen sein ?? …
Immerhin sind uns gewisse Beobachtungsdaten des Versuchs überliefert:
https://en.wikisource.org/wiki/File:On_the_Relative_Motion_of_the_Earth_and_the_Luminiferous_Ether_-_Fig_6.png
Vielleicht lässt sich ja daraus schließen, dass die beiden Arme im Versuchsverlauf (zumindest annähernd) von jeweils gleicher “Länge” geblieben wären ?
> Ansonsten würde ich es gerne Hrn. Schulz überlassen, bei Bedarf die experimentelle Vorrichtung von Hrn. Michelson und Hrn. Morley kompetent zu expliciren.
Einen wesentlichen Schritt dazu hat er durch sein o.g. “Anpassen” MBMN bereits unternommen.
@Joachim // 22. Dezember 2018 @ 17:27
»… obwohl hier nichts kontrahiert. «
„Hier“ im Michelson&Morley-Versuch oder generell im Kosmos?
Joachim Schulz schrieb (22. Dezember 2018 @ 17:27):
> […] Michelson und Morley (M&M) haben tatsächlich ein Interferometer mit gleichen Armlängen gebaut und in der Praxis wird es auch so gemacht.
Was wäre denn “in der Praxis zu machen” um zu gewährleisten und nachzuweisen, dass \(\left(\frac{L_p}{L_s}\right)\) (sofern das eben so gewünscht wäre) ??
Und haben Michelson/Morley das (guten Gewissens, so) gemacht ?
> Herr Wappler würde vermutlich einwenden, dass es aufwendig wäre, ein Interferometer zu bauen, in dem beide Arme exakt gleich lang sind. Sie sind es in der Praxis eben nur fast.
Der eventuelle Aufwand interessiert mich nur nebenbei. Ich möchte vielmehr zunächst konkret verstehen (und verstanden wissen), was zumindest im (Gedanken-experimentellen) Prinzip überhaupt “gemacht” werden soll, ohne Rücksicht auf damit eventuell verbundenen Aufwand.
(Falls von vornherein gar nicht nachvollziehbar wäre, was “gemacht” werden soll, dann bliebe das so auch bei beliebig großem Aufwand.)
Sofern “in der Praxis eben nur fast” Gleichheit der Armlängen gewährleistet und nachgewiesen werden soll, dann ist eben entsprechend konkret zu fragen, wie in den betreffenden Versuchen der bestimmte, endliche Wert einer positiven reellen Zahl \(\epsilon\) ermittelt werden soll (und von Michelson/Morley wohl ermittelt worden sein soll), für die galt:
\[ \mid \, \left(\frac{L_p}{L_s}\right) – 1 \, \mid \le \epsilon. \]
Sofern nicht gewährleistet werden soll und nachzuweisen wäre, dass die beiden Interferometerarme (durchwegs) gleiche “Länge(n)” gehabt hätten, bleibt die im obigen SciLogs-Artikel getroffene Unterscheidung in \(L_p\) und \(L_s\) offenbar relevant.
> […] Arm, der in den “Wind” gedreht wird […]
> […] dann, wenn er wieder quer zum “Wind” steht […]
Allmählich kommen wir wohl “auf den Dreh der Sache”:
Stimmt es also, dass (in gültigen Versuchen eines Michelson-Interferometers) ein Arm (bestehend insbesondere aus einem bestimmten Reflektor und dem Strahlteiler, als seinen beiden “Enden”), der (anfänglich) “quer zum “Wind” stand” und dessen “Armlängen“-Wert (dabei) deshalb als \(L_s\) bezeichnet wurde,
den “Armlängen“-Wert \(L_p\) haben soll, falls er (danach) “in den “Wind” gedreht” wurde;
usw. ?
Falls so: Wurde das von Michelson/Morley nachgewiesen ?
Spielen Sie etwa auf die 1881 mögliche Genauigkeit in der Maßhaltung an – so von wegen Maßtoleranzen und so?
Die Armlängen sind vollkommen uninteressant. Nimm mal die Mathematik von Wikipedia und berechne aus der Zeit des einen Arms, die Länge des zweiten, also so, dass die Laufzeiten in beiden Armen gleich sind. Dann bekommt man zwei unterschiedliche Armlängen. Tauscht man nun diese beiden Arme wieder aus, sind die Zeiten auch wieder unterschiedlich. Daraus folgt, dass in Ausbreitungsrichtung beim drehen der Achsen auf jedem Fall eine Phasenverschiebung stattfinden muss, was aber nie wirklich gemessen wurde.
@Jocelyne Lopez / 22. Dezember 2018 @ 17:21
Gemessen wird unausweichlich immer nur mit einer begrenzten Genauigkeit, und mit Hinblick auf die Signifikanz von Messresultaten hat man ja die auch `error bars’ eingeführt. Experimentell lässt sich also nur eine obere Grenze für die Geschwindigkeit eines hypothetischen “Aetherwindes” signifikant ermitteln. Dazu findet man bei Tipler & Llewellyn (Modern Physics, W.H. Freeman, 5th ed., 2008) folgende Bemerkung:
Und wenn diese Werte so stimmen, dann haben wir eben keinen signifkanten Hinweis auf das Vorhandensein eines Lichtaethers.
@Albrecht Storz
21. Dezember 2018 @ 13:41
”
“Ich habe immer noch keine Antwort auf meine Frage erhalten, warum ein Beobachter in einem angeblich kontrahiertes Raumschiff zwar nicht die Kontraktion des Raumschiffes wahrnehmen soll, aber die Kontraktion einer Distanz, die dieses Raumschiff durchfliegen wird, schon.”
Joachim Schulz
21. Dezember 2018 @ 14:08
weil seine mitgeführten Maßstäbe derselben Längenkontraktion unterliegen wie das Raumschiff, während die Start und Ziel relativ zu ihm bewegt sind.
”
Sie können kein Physiker sein, wenn Sie so etwas als Erklärung anbieten. Wenn es unterschiedliche Standards gibt (in verschiedenen Universen, in verschiedenen Inertialsystemen, …, wie und wo auch immer), so muss jeder Beobachter die Standards SEINES EIGENEN Systems anwenden, um für sich gültige Messungen durchzuführen, die Gegebenheiten in der Näher und in der Ferne für sich physikalisch korrekt zu erfassen. Von daher macht der Beobachter auf dem Raumschiff völlig korrekte Messungen mit SEINEN EIGENEN Maßstäben. Und wie Sie selber schreiben sind diese ja verkürzt gegenüber Maßstäben von “ruhenden” Beobachtern.
Nun behauptet der “ruhende” Beobachter, für den “bewegten” Beobachter seien Distanzen verkürzt. Der “bewegte” Beobachter misst mit seinen eigenen (verkürzten) Maßstäben nach, und stell fest, dass der Befund des “ruhenden” Beobachters falsch ist.
Wenn man verkürzte Strecken mit einem proportional verkürzten Maßstab misst, so kommt man zum selben numerischen Ergebnis, wie wenn man die unverkürzte Strecke mit dem unverkürzten Maßstab misst!
Herr Schulz, Sie sind nicht fähig konsistente physikalische Zusammenhänge zu formulieren.
Schon komisch Herr Schulz,
“Und die Einlassungen von Herrn Storz, die mal wieder der SRT Aussagen unterstellen, die niemand je gemacht hat, auch.”
Nach langer mühevoller Überzeugungsarbeit haben Sie und Ihre Kumpels (und nicht mal alle, Senf und so) es mühsam geschluckt, dass auf dem bewegten, “kontrahierten” Raumschiffs andere Standards vorliegen müssen (die natürlich die gleichen Namen haben wie immer; aber wenn jemand das Raumschiff verkürzt sieht, muss dessen Einheitsmeter offensichtlich länger sein als ein Beobachter, der das Raumschiff nicht verkürzt sieht).
Und nun kommen Sie mit solchen Behauptungen daher. Obwohl Sie offensichtlich eingeknickt sind. Und nun versuchen Sie das Desaster zu retten, indem Sie irgend welche kategorischen Unterscheidungen zwischen zu messenden Längen zu erfinden versuchen, warum die eine Länge so, die andere anders zu messen wäre.
Nein! Jede Länge ist im Prinzip genau so zu messen wie jede andere auch. Und jede Länge muss mit den Standards gemessen werden, die für den Betroffenen gültig sind.
Wenn man die Länge der Distanz von der Erde nach Proxima Centauri FÜR ein annähernd mit Lichtgeschwindigkeit fliegendes Raumschiff misst, so muss man diese Länge mit dem Einheitsmeter des Raumschiffes messen – und mit nichts sonst.
Und dann ergibt sich eine Distanz von 4,24 Lichtjahre, und eine Flugdauer von 4,24 Jahre. Egal was irgendwelche Relativisten auf der Erde zusammenmessen, zusammenrechnen und behaupten und erfinden und phantasieren.
Herr Storz, begreifen Sie nicht, daß es Grundsatz der Relativitätstheorie ist, alles mit gleichen Standards zu messen? Die Physik kann doch nichts dafür, daß die Natur es so eingerichtet hat, daß Messungen vom Standpunkt des Beobachters abhängig sind. Um die “Erscheinungen” korrekt zu untersuchen und zu erklären, muß man sich auf einen Referenzstandpunkt einigen, der für alle zum gleichen Ergebnis führt. Den Weg dahin nennt man Transformation (aber bitte in die richtige Richtung).
Die gesuchten Ergebnisse sind Invarianten (für alle überall gleich) – Einstein, Hilbert, Noether.
Trotzdem schöne Weihnachten zum Nachdenken – ein Tip von Dip
@Senf:
Das ist ja auch ein guter Vorsatz. Nur leider sind Meter, die man auf der ISS nach 31 Takten Lichtbewegung hat, kürzer als jene, die man nach 31 Takten auf der Erde hat. Eure Standards gehen da die Wupper runter, weil sich sogar Atomuhren wider Erwarten nicht an diese Standards halten.
Allen ein geruhsames Weihnachtfest.
@Joachim und Chrys
.
Ich hätte da nun mal von Euch beiden eine wirkliche klare unmissverständliche möglichst einfach gehaltene Aussage zum Garagen-Paradoxon.
.
Dazu noch mal das beschriebene Gedankenexperiment mit Zug und Bahnhof.
.
Im Bahnhof sind zwei synchronisierte Uhren im Abstand von 100 m aufgebaut und ein Zug mit einer Ruhelänge von 229,4 m fährt nun mit 0,9 c durch den Bahnhof.
.
Nach der SRT kann man nun Zuganfang und Zugende gleichzeitig mit einem Abstand von 100 m im Bahnhof messen. Heißt, der Zug passt mit seiner Ruhelänge von 229,4 m gleichzeitig zwischen zwei Lichtschranken mit einem Abstand von 100,001 m. (Ich gebe ein ganz klein wenig mehr dazu, damit es sauber passt)
.
Das ergibt sich so aus der SRT, der LT und durch die RdG.
.
Stimmt Ihr dem nun zu, oder widersprecht Ihr und wenn, warum.
.
Frohes Fest
@NvB.
.
.
Das ist nur eine Behauptung und die ist falsch.
.
Misst man auf der ISS mit Hilfe von Licht und einer Atomuhr die Strecke von einem Meter aus, ist diese im Vergleich genauso lang wie ein Meter mit Hilfe von Licht und einer Atomuhr auf der Erde ausgemessen.
.
Anders wäre es, wenn man Anstelle der Atomuhr (welche lokal in der ISS die SI-Sekunde richtig ausmisst) man die Koordinatenzeit von der Erde (über GPS oder so) nehmen würde und damit messen. Denn das ist eine Koordinatenzeit und gibt somit in der ISS dort lokal eben nicht mehr die Dauer der SI-Sekunde richtig wieder.
@Krüger:
Meine Behauptung ist richtig. Wenn sie falsch wäre, würde einem das Phänomen Zeitdilatation gar nicht auffallen. Uhrenvergleiche zeigen, dass nur eine Uhr langsamer ging, als eine andere, weswegen diese Uhren ganz sicher nicht wechselseitig langsamer gingen. Für den schnelleren Gang der Uhren auf der ISS gibt es einen Grund unddieser heisst mangelnde Gravitation. Meterenden, die lt. Definition mit solchen Uhren hergestellt werden, sind definitiv kürzer, als Meterenden, die unter den selben Voraussetungen auf der Erde hergestellt werden.
31 Takte dauern auf der Erde länger als auf der ISS – das gebietet die Logik.
@Joachim Schulz:
Im Übrigen habe ich bei Wikipedia einen “Kriegsentscheidenden” Satz gefunden:
Wellenlängen sind sozusagen zeitliche Ortsabstände und keine Anderen tauchen mMn in Minkowski-Diagrammen auf. Man könnte x also beliebig mit τ austauschen, oder nicht? Es sind ja nicht wirklich Längen fester physikalischer Körper, die sich da ändern, sondern tatsächlich nur zeitliche Abstände in welchen “Markierungen” auf diesen Körpern landen. Verstehen Sie, worauf ich hinaus will?
@Nicht von Bedeutung 25. Dezember 2018 @ 18:27
Dann sind wir wieder bei der stehenden Welle in einem Resonator. Mechanisch ändert sich der Resonator nicht aber aus der Länge der stehenden Welle berechnet man einen kürzeren Resonator.
Ja, NvB, ich verstehe. Ich denke noch etwas darüber nach, wie ich einen Artikel zur relativistischen Interpretation der Längenkontraktion aufziehe.
Deine Frage, Manuel, hat doch Herr Senf schon beantwortet: Ja, der Panzer passt in die Garage, aber er darf nicht anhalten. Nehmen wir an, A sei der Raum-Zeit-Punkt, also das Ereignis, zu dem die Spitze des Panzers gerade die hintere Tür passiert. B sei das Ereignis, an dem das Ende des Panzers die vordere Tür passiert. Es gibt nun drei Möglichkeien:
1) A liegt zeitartig vor B. Dann ist der Panzer für alle Beobachter länger als die Garage, der Panzer passt nie hinein.
2) B liegt zeitartig vor A. Dann ist der Panzer für alle Beobachter kürzer als die Garage, der Panzer passt immer hinein.
3) A und B liegen raumartig getrennt. Dann ist zwar die Reihenfolge der Ereigniss vom Beobachter abhängig, aber es kann kein Lichtsignal von A nach B oder von B nach A kommen.
P.S: Manuel: Antworte einfach nicht auf NvB. Das führt doch zu nichts.
Hallo NvB #25.12. 18:27 “Die Wellenlänge ist das räumliche Analogon zur zeitlichen Periodendauer.”
Da Deine angriffslüsternde Einlassung wie Wunder Weihnachten überstanden hat, wohl mal wieder die mißachtete Gleichzeitigkeit. Wenn Du ruhig bleibst und nicht zappelst stimmt’s so sogar, aber:
Die Wellenlänge setzt die Gleichzeitigkeit voraus, sie ist der Abstand gleicher Phasen zur gleichen Zeit, hängt damit von der Geschwindigkeit im Richtungssinne (so hat man das vor 100 Jahren gesagt) ab.
Nimm lieber eine stehende Welle, dann hast Du automatisch die Gleichzeitigkeit, mußt nicht suchen.
Die ist nämlich raumzeitlich verknotet, vielleicht lösen sich die ja bis Neujahr – guten Rutsch Dip.
@Herr Senf 26. Dezember 2018 @ 13:03
Das stimmt. Bei einer fortschreitenden Welle hat man wegen des Dopplereffekts und c=const auch die Relativität der Gleichzeitigkeit.
@Senf und Rudi Knoth:
Ihr tut gerade so, als hätten nur stehende Wellen Wellenlängen. Empfängt ein Empfänger, der an einer stehenden Welle vorbei fährt überhaupt noch eine stehende Welle? Nein, tut er natürlich nicht – wie sollte dies auch gehen. Ebenso empfängt ein Empfänger auch keine stehende Welle, wenn die Welle wandert und der Empfänger ruht – kommt nämlich aufs selbe raus. Wenn also etwas relativ ist, dann maximal stehende und wandernde Wellen.
Also nein Senf – ich vergesse hier keine RdG – ich mißachte sie absichtlich, weil nach wie vor überflüssig und das wird sie auch im nächsten Jahr noch sein – zumindest der Teil in welchem x-Achsen verdreht werden, was eher die Relativität der Gleichortigkeit betrifft, aber gut.
Darüber hinaus vergesst ihr die Logik. Schaut euch die Definition des Meters mal an. Wenn eine Sekunde andernorts länger dauert, als lokal, kann sie gleichzeitig lokal nicht länger dauern als andernorts – deswegen müssen Uhren hier, da und dort ja auch technisch verlangsamt werden. Wenn Uhren so funktionieren würden, wie Krüger das sagt, wäre dieser ganze Aufwand gar nicht nötig. Und schneller gehende Uhren ergeben nun mal per Definition technisch kürzere Meter.
Und wenn man so in Gedanken noch mal drüber nachdenkt, dann gelten 9192631770 Takte für 299792458 Meter und nicht bloß für 1 Meter. 1 Meter hingegen ließe sich dicht an dicht mit 13157894737 Kohlenstoff-Atomen nebeneinander realisieren, aber wenn euch Diamant zu teuer ist, dann nehmt halt 9009009009 Silizium-Atome und pfeifft auf das bisschen Genauigkeit bei Cäsium-Atomuhren. Und dann könnt ihr ja mal messen, wieviele Atome Licht nach einer Sekunde unterschiedlich gehender Uhren schafft.
@Manuel Krüger
Auch Lorentz kommt nicht deshalb zur kontrahierten Länge eines fahrenden Zuges, weil diese im System `Bahnhof’ unmttelbar festzustellen wäre. Vielmehr findet er im System `Zug’ zunächst eine (vermittels Lorentz Boost) um den Faktor γ gestreckte Länge des im Aether ruhend angenommenen Bahnhofs und begründet diese Streckung dann damit, dass die im fahrenden Zug mitgeführten Meterstäbe in Richtung der Bewegung wohl kürzer sein müssten als 1 Meter, wobei er den Meter als Längeneinheit durch im Aether ruhende Meterstäbe definiert. Um nun die Länge des fahrenden Zuges korrekt auszumessen, müsste das Zugpersonal die mitgeführten Meterstäbe um den Faktor γ verlängern, denn erst die wären dann wieder 1 Meter lang, womit logischerweise eine um 1/γ verkürzte Zuglänge ermittelt wird.
Die Meter-Definition von Lorentz ist allerdings weder mit dem spez. Relativitätsprinzip noch mit dem Minkowski-invarianten SI-Meter vereinbar. Für die SRT kann man also nicht so argumentieren wie für die LET; beide implizieren unterschiedliche Vorstellungen davon, wie der Meter als Längeneinheit zu definieren ist. Zwar kommen SRT und LET zum gleichen Wert für das vom fahrenden Zug aus beurteilte Verhältnis von Zuglänge zu Bahnhofslänge, doch ob dabei der Zug als verkürzt oder der Bahnhof als gestreckt zu gelten hat, hängt davon ab, auf welche Meter-Definition man sich bezieht, und hierin stimmen SRT und LET nicht überein.
Die mit einer Zug-Uhr ermittelte Radar-Länge des Bahnhofs kann beliebig gross sein, wenn der Zug schnell genug fáhrt, und nur auf diese Weise kann ein kurzer Bahnhof auch länger werden als ein langer Zug. Aber nur für die LET mit dem Lorentzschen Aether-Meter lässt sich dies zu einer Kontraktion des Zuges umdeuten. Für die SRT mit dem SI-Meter kontrahiert hier überhaupt nichts.
@Chrys:
Das ist doch genau der Unterschied Zugmeter zu Bahnhofsmeter, oder nicht. Hatte Krüger das nicht bereits als Unfug abgetan?
@NvB 18:08 “Das ist doch genau der Unterschied Zugmeter zu Bahnhofsmeter, …”
Nein, das ist der Unterschied zwischen Meßmethode LET und Meßmethode SRT. Vergiß nicht, daß Lorentz 1906 nachdem er die SRT “akzeptiert hat” die LET “nachgebessert” hat, aber mit Wirrwar.
@Senf:
Wie bitte? Du tust gerde so, als würde man in der LET mit Zoll und in der SRT mit Metern messen. Die Veränderung eines Maßnormals verändert sicher nicht die Meßmethode. Vergiss nicht, dass mich Theorien in der Regel gar nicht interessieren, sondern bloß die Logik. Und wenn die Logik nicht passt, dann passt auch die Theorie nicht. Und das Maßnormal würde durch unterschiedlich gehende Uhren verändert, wenn man es über Zeit definiert, wie es z.Zt. der Fall und demnach prompt unlogisch ist.
@Chrys
.
Das ist ja für Lorentz auch sehr schön, alles, aber für mich hier wenig von Belang.
.
.
.
Mir bekannt. Wobei auch nach der LET die Meter nicht unterschiedlich lang sein sollten, wenn sie in zwei zueinander bewegten Laboren ausgemessen werden.
.
.
.
Irgendwo dreht man sich mit Dir im Kreis. Die LK ist relativ und nicht absolut, so wie es auch mit der Geschwindigkeit ist. Ich habe nie behauptet, der Zug selber würde wo absolut zusammengedrückt.
.
.
Und wo wir gerade im Dialog sind, die Antwort von Dir steht noch aus, Joachim hat sie nun ja gegeben. Und was hältst Du von der Behauptung mit den unterschiedlich langen Meterstäben?
@Manuel Krüger / 26. Dezember 2018 @ 20:04
Erklärtermassen geht es Joachm Schulz in diesem Blogartikel doch auch gerade darum, zu »motivieren, war[u]m man noch immer von Längenkontraktion spricht, obwohl hier nichts kontrahiert. Das Erbe der Lorentzschen Äthertheorie.«
Eine Antwort auf die Frage, ob und wie ein langer Zug in einem kurzen Bahnhof passen kann, war im letzten Absatz durchaus schon enthalten. Die eigentlich heikle Frage ist aber die, ob und wie dabei für wen gegebenenfalls etwas kontrahiert.
In der Darstellung des Lokführers (nicht der des Bahnsteigwärters!) passt sein Zug der Länge \(L_Z\) in einen Bahnhof der Länge \(L_B < L_Z\) wenn
\[
\frac{L_Z\,[\text{m}]_{\text{SI}}}{\gamma L_B\,[\text{m}]_{\text{SI}}} = \frac{L_Z/\gamma\,[\text{m}]_{\text{LE}}}{L_B\,[\text{m}]_{\text{LE}}} < 1
\]
gilt, d.h., wenn der Zug nur hinreichend schnell fährt. Dabei ist wieder zwischen SI-Metern für die SRT und LE-Metern für die LET unterschieden. Kürzt man hier die Einheiten heraus, bleibt ein ambivalentes Längenverhältnis, bei dem sich noch gar nicht danach fragen lässt, ob da nun etwas kontrahiert oder nicht. Erst mit dem Bezug auf eine durch die besagten Einheiten festgelegte metrische Struktur lassen sich solche Fragen diskutieren.
Mit Hinblick auf diese Einheiten klärt sich dann aber auch, dass nur Lorentz mit dem LE-Meter den fahrenden Zug als kontrahiert deuten kann, wenn er dabei den Bahnhof als im Aether ruhend annimmt. In der SRT mit dem SI-Meter behält für den Lokführer auch der fahrende Zug seine invariante Länge \(L_Z\,[\text{m}]_{\text{SI}}\), und er misst die Länge des Bahnhofs gestreckt als \(\gamma L_B\,[\text{m}]_{\text{SI}}\), das ist gerade die mit einer Zug-Uhr ermittele Radar-Lánge des Bahnhofs.
Wie das in der Darstellung des Bahnsteigwärters aussieht, dazu sag’ ich jetzt erst mal nichts.
@Chrys:
Das klingt alles immernoch sehr verwirrend. Kann man nicht einfach sagen, dass tatsächlich gar nichts kontrahiert obwohl kontrahiert gemessen werden kann, wenn den Messungen (z.B. Radarmessung) Zeitdilatationen zugrunde liegen?
@Chrys
.
Und war er erfolgreich?
.
.
.
Da kommen wir nicht zusammen und die Aussage von Joachim war auch eine andere. Wie auch beim Garagen-Paradox befinden wir uns im Ruhesystem des Bahnhofs und messen dort die Länge des Zuges. Und dort ist der Zug lorentzkontrahiert, und passt in den Bahnhof, wenn er schnell genug bewegt ist. Und er ist im System des Bahnhofs bewegt.
.
Im Ruhesystem des Zuges bewegt er sich gar nicht, es ist also Unfug doch zu sagen, er muss nur schnell genug fahren. Dort ruht er einfach. Und in seinem System ist der Bahnhof bewegt und lorentzkontrahiert, da passt er also nie rein.
.
Mir unverständlich warum Du es immer verdrehst.
.
.
Die LET ist mir erstmal recht egal.
.
.
.
Das mit Lorentz ist klar, und ich finde es echt nicht interessant. Ja er postulierte einen Äther, ja er glaubte, da “staucht” sich real was, nur es kann dann nicht gemessen werden, weil sich eben alles gleich staucht. Du kannst es gerne noch ein paar mal “erklären”, wenn Du Freude daran hast, ich kann es Dir gerne immer wieder bestätigen.
.
Klar misst der Lokführer im Zug die Ruhelänge des Zuges, auch nun nicht wirklich was neues, kannst aber auch das gerne weiter wiederholen. Er misst aber nicht die Länge des Bahnhofs gestreckt, sondern kontrahiert. Es nennt sich nicht Lorentzkontraktion weil es eine Streckung ist.
.
.
.
Ich bin ja nun echt zu Tode betrübt. Wie gesagt, man nehme zwei Raumschiffe mit gleicher Ruhelänge und lasse sie aneinander vorbeifliegen, jedes misst das andere in seinem System bewegt und lorentzkontrahiert, nichts ist da mit einer Streckung.
@Chrys
.
Noch mal zu dem von Dir Geschriebenen, lesen wir mal auf Wikipedia:
.
Soll ich noch was hervorheben, oder geht es auch so? Und dort findet sich auch eine nette Grafik mit Erklärung. Das dort steht konträrer zu Deinen Behauptungen hier. Mir ist auch unklar, warum Du die Systeme tauschst, Du springst ins System des Zuges und willst Dich dort aber fahrend mit einer Geschwindigkeit gegeben sehen. Oder wie auch immer.
.
Warum bleibst Du nicht bei der üblichen Beschreibung?
.
.
Hier noch die Quelle: https://de.wikipedia.org/wiki/Lorentzkontraktion
.
Und in der Erläuterung wird genau das Beispiel mit Zug und Bahnhof erklärt, im Ruhesystem des Bahnhofs ist der Zug kontrahiert, er wird dort kürzer, als seine Ruhelänge ist, gemessen.
@Manuel Krüger / 27. Dezember 2018 @ 12:40
»Er [der Lokführer] misst aber nicht die Länge des Bahnhofs gestreckt, sondern kontrahiert.«
Nein, er misst die Länge des Bahnhofs um den Faktor γ gestreckt. Das folgt als unmittelbare Konsequenz aus der Konstanz der Lichtgeschwindigkeit nach letztlich der gleichen einfachen Rechnung, mit der auch die Relativität von Gleichzeitigkeit hergeleitet wird.
Und erst wenn das mit Überzeugung zugegeben wird, kann man damit anfangen, sinnvoll darüber nachzudenken, wie jemand wohl auf die Idee kommen kann, in dieser Streckung eine Kontraktion sehen zu wollen.
Noch ein Gedankenexperiment, um die “Längenkontraktion” zu erklären.
Angenommen die aufgehende oder untergehende Sonne scheint senkrecht über die Gleise auf den Bahnsteig während der Zug vorbeifährt. Dann ist klar, daß an beiden Enden des Bahnsteiges das Licht (die Wellenfront) gleichzeitig eintrifft. Damit ist die Länge des Zuges im Inertialsystem, in dem der Bahnsteig ruht, festgelegt. Wie sieht es im Inertialsystem des Zuges aus? Wegen der Aberration scheint die Sonne schräg von vorne. Daher kommt das vordere Ende der Wellenfront früher als das hintere am Bahnsteig an. Der Abstand zwischen vom vorderen Ende und vom hinteren Ende beschatten Teil des Bahnsteigs ist also kürzer als die Ruhelänge des Zuges.
@Chrys
.
.
Nein, er misst die Länge des Bahnhofs um den Faktor γ kontrahiert.
.
.
.
Das folgt als unmittelbare Konsequenz aus der Konstanz der Lichtgeschwindigkeit nach letztlich der gleichen einfachen Rechnung, mit der auch die Relativität von Gleichzeitigkeit hergeleitet wird.
.
.
.
Und nun? Ich sehe da auch keinen Sinn mit Dir den “Dialog” zuführen, Deine Aussagen steht diametral zu der Lehrmeinung und dem was man dazu auch auf Wikipedia lesen kann. Und das Du nun forderst, man sollte einfach Deine Behauptung mit Überzeugung zugeben ist gelinde gesagt befremdlich.
@Manuel, Joachim hat Michelson nach Lorentz erklärt, der Meterstab ist ein zeitloses Raumobjekt.
Chrys scheint sich an dieses Thema zu halten, bei Lorentz haben wir einen Längs-m und eine Quer-m.
Bei Einstein haben wir ein Raumzeit-Meter, jeder Punkt hat seine Zeit, er “dreht” und projeziert.
.
@Herr Senf
.
Was soll denn ein zeitloses Raumobjekt sein? Warum zeitlos und warum Raum? Wohin soll es denn nun führen, sprechen in Rätzeln?
.
Also ich schaue mir mal den Titel an, da heißt es:
.
Der experimentelle Befund zur Längenkontraktion
.
So was mit Experiment und was mit Längenkontraktion ist zu erwarten und zum Ende der Erklärung heißt es, nun ohne Äther und es geht direkt in die SRT.
.
Es wären doch mal klare Aussagen angebracht, so wie, also Leute die SRT ist schon richtig, aber alles was so im Netz und bei Wikipedia steht ist Müll, da kontrahiert gar nichts und wenn dann wird es eh gestreckt, aber auch nicht so wirklich, weil die LET eben nicht das Gelbe von Ei ist.
.
Was ist denn nun das Ziel hier, jeden versuchsweise zu verwirren, die mit der SRT soweit klar kommen, oder anderen die SRT näher zu bringen?
Zur Minkowski-Geometrie bewegter Stäbe
Ein in S mit der Geschwindigkeit \(v = c\beta\) in \(x\)-Richtung bewegter Stab sei in seinem Ruhesystem S’ dargestellt durch \(\{t’\vec{e}_{t’} + \xi\vec{e}_{x’}\mid t’ \in \mathbb{R}, 0 \le \xi \le L\}\). Mit \(c = 1\) gilt gemäss Lorentz Transf.
\[
\vec{e}_{t’} = \gamma\vec{e}_t + \gamma\beta\vec{e}_x,\quad
\vec{e}_{x’} = \gamma\vec{e}_x + \gamma\beta\vec{e}_t.
\]
Ein fester Parameterwert \(\xi\) markiert einen Punkt auf dem Stab, dessen Bewegung auf der \(x\)-Achse von S dargestellt ist durch die \(x\)-Komponente von
\[
t’\vec{e}_{t’} + \xi\vec{e}_{x’} = t'(\gamma\vec{e}_t + \gamma\beta\vec{e}_x) + \xi(\gamma\vec{e}_x + \gamma\beta\vec{e}_t) = (t + \xi\gamma\beta)\vec{e}_t + (t\beta + \gamma\xi)\vec{e}_x
\]
mit \(t = \gamma t’\), also durch den Ortsvektor
\[
\vec{x}_\xi(t) = (t\beta + \gamma\xi)\vec{e}_x.
\]
Bezeichnet \(\|\cdot\|_g\) die Minkowski-Norm, dann ist die Länge des bewegten Stabes gegeben durch
\[
-i\,\|\vec{x}_L(t)- \vec{x}_0(t)\|_g = \gamma L.
\]
Die Länge des in S bewegten Stabes ist demnach um den Faktor \(\gamma > 1\) grösser als seine Ruhelänge \(L\) in S’.
@Chrys
.
Das hast Du optisch wirklich schön geschrieben, aber ich bin kein Mathematiker und auch kein Physiker, ich habe nicht mal Abitur und bin Autodidakt, habe den Tipler nie ganz durchgearbeitet, ist ja auch eine Frage der Zeit. Bei Dir sehe ich da dann mal ein -i ist ja nett, aber ernsthaft, um das mal so eben nachzuvollziehen braucht man mindestens das Abitur, oder eben die mathematischen Kenntnisse die dort gegeben sind. Bin sicher, ich kenne viele mit Abi, die das dennoch nicht verstehen.
.
Also was soll das? Willst Du hier mit Deinen Fähigkeiten glänzen? Vermutlich nicht, wirst es nicht nötig haben, aber wenn Du damit wem was erklären wolltest, dann bist Du im Irrtum mit dem was Du da an mathematischen Kenntnissen unterstellst.
.
Ohne mich tiefer da einzuarbeiten kann ich damit nicht anfangen und ich glaube auch nicht, dass so etwas nötig ist um die Längenkontraktion im Rahmen der SRT verständlich zu beschreiben.
.
Es bleibt dabei, Deine Aussagen stehen diametral zu dem was Joachim bestätigt hat und was man auf Wikipedia über einen in einem Zug, mit diesem, bewegten Stab lesen kann. Wenn dessen Länge im Ruhesystem des Bahnhofs gemessen wird.
@Chrys
.
Noch mal, Du schreibst:
.
Auf Wikipedia steht hingegen:
.
https://de.wikipedia.org/wiki/Lorentzkontraktion#Erläuterung
.
Offensichtlich nicht das was Du so schreibst.
Schön, daß es die Gravitation gibt, wird morgen einiges geerdet haben 🙂
@Manuel
Die Lösung ist eigentlich ganz einfach: Die Längenkontraktion wird im Lorentz-Äther erst zu einer Kontraktion, indem man die Zeitdilatation quasi heraus destilliert, wie ich es im vorgehenden Artikel vorgemacht habe.
Dort wird die Zeit des unbewegten Äthersystems als Referenz genommen. Die Länge des bewegten Körpers ist der momentane räumliche Abstand zwischen Bug und Heck im Äthersystem. So ist er verkürzt. Die Relativität der Gleichzeitigkeit hat keine physikalische Konsequenz, man könnte sie auch weglassen. Dann sind wir bei der Selleri-Transformation.
In der SRT, darauf will Chrys hinaus, gibt es keinen Grundt, die Zeit eines Systems zu bevorzugen. Wir sollten die Eigenzeit jedes Objekts zur Referenz nehmen. Und nach dieser ergibt sich eben, dass Zeiten und Längen gleichermaßen gedehnt sind. Schöne Symmetrie, oder?
@Joachim Schulz:
Gute Idee, nur leider keine Symmetrie. Seien Sie mal so gut, stellen Meterendenden in zueinander bewegten Objekten nach Eigenzeit her, konservieren sie für den Rest der Bewegungen und prüfen dann die Längen, wenn die zueinander bewegten Objekte zusammengeführt sind. Meinen Sie etwa, nur die Uhren würden nach so einer Prozedur unterschiedliche “Zählerstände” haben? Wem will man denn so etwas weis machen? Vor Allem, wie und warum?
“Herr Wappler würde vermutlich einwenden, dass es aufwendig wäre, ein Interferometer zu bauen, in dem beide Arme exakt gleich lang sind.”
Das ist also das Niveau hier? Na, Danke!
Ein Tipp von mir: Man baut keine “exakt gleich langen Arme”. Man baut eine Feinverstellung in mindestens einen der Arme. Dann justiert man die Feinverstellung so, dass die gewünschte Interferenz (maximal konstruktiv oder maximal destruktiv) auftritt …
Hier scheint kein einziger Diskutant von Physik und insbesondere Experimentalphysik auch nur den leisesten Hauch einer Ahnung zu haben.
Zitat Joachim Schulz: “In der SRT, darauf will Chrys hinaus, gibt es keinen Grundt, die Zeit eines Systems zu bevorzugen. Wir sollten die Eigenzeit jedes Objekts zur Referenz nehmen. Und nach dieser ergibt sich eben, dass Zeiten und Längen gleichermaßen gedehnt sind. Schöne Symmetrie, oder?”
.
Ich sehe in der SRT gar keine “schöne Symmetrie“… Ganz im Gegenteil, sehe ich einen Symmetrie-Bruch.
Oder habe ich etwa übersehen, dass beim Zwillingsparadoxon der reisende Zwilling verkürzt zurückkommt?
@Jocelyne Lopez 29. Dezember 2018 @ 13:10
Sehr geehrte Frau Lopez:
Das haben Sie in der Tat. Im Zwillingsparadoxon wechselt der reisende Zwilling das Inertialsystem, in dem er ruht. Der andere Zwilling ruht während der ganzen Zeit im selben Inertialsystem.
Gruss
Rudi Knoth
@Joachim Schulz // 29. Dezember 2018 @ 08:47
»Wir sollten die Eigenzeit jedes Objekts zur Referenz nehmen. Und nach dieser ergibt sich eben, dass Zeiten und Längen gleichermaßen gedehnt sind.«
Aha. Wenn ich das recht verstehe kann man also sagen: Bei einer gegebenen Halbwertzeit von rund 2 Mikrosekunden im Vakuum kommt ein auf 0,9998 c beschleunigtes Myon dank der “Längendehnung” rund 33.000 m weit, bevor es im Mittel (also nach ca. 2 µs Eigenzeit) zerfällt. Richtig?
@Balanus 29. Dezember 2018 @ 17:33
So sieht es aus. Diese Aussage für die Strecke und die “Belegdauer” (Nach Wappler) gilt im Inertialsystem, in dem die Erde ruht.
@ Rudi Knoth:
Wo bleibt aber die Symmetrie des Relativitätsprinzips?
Man kann ja jeden Zwilling abwechselnd als bewegt oder als ruhend wählen.
@Jocelyne Lopez 29. Dezember 2018 @ 17:54
Nur den Wechsel von Hin- zu Rückflug kann der reisende Zwilling nicht in einem Inertialsystem ruhend durchführen.
Hat schon wer gemerkt, daß es kein Zwillingsparadoxon gibt, aber einen Zwillingseffekt. Das mit
dem “Paradoxon” benutzen nur “überbewußte Kritiker”, die so ihre Matheschwächen kaschieren.
Albrecht Storz
29. Dezember 2018 @ 13:07
Genau, dann ist der Unterschied der Armlängen ein ganzes oder halbes Vielfaches einer Wellenlänge. Exakt gleich sind sie bei maximaler positiver Interferenz höchstens zufällig.
Aber die Interferenzlänge ist ein Grund, warum die Armlängen in etwa gleich lang sein mussten: Michelson und Morley hatten schließlich noch keine Laser zur Verfügung.
@Joachim Schulz:
Also wenn bei wenig bis gar keinem monochromatischem Licht überhaupt ein Interferenzmuster zustande kommt, waren die Arme des Interferometers sicher nicht gleich lang.
@Joachim
Um die Bedeutung der Lorentz-Kontraktionsformel entspinnt sich schon in der LET historisch einige Verwirrung, die dann unversehens an die SRT vererbt wurde. In der LET impliziert die Hypothese der im Aether bewegungsbedingt verkürzten Meterstäbe zunächst, dass \(L_Z/\gamma\) die in LE-Metern gemessene Eigenlänge eines Zuges der (auf den absoluten Aether bezogenen) Ruhelänge \(L_Z\) ist. Das Zugpersonal würde mit Meterstäben und Uhren, die nach LE-Standard geeicht sind, \(L_Z/\gamma\) als Messwert für die “wahre” Zuglänge ermitteln. Zur Eichung müssten im fahrenden Zug die Meterstäbe gestreckt und die Uhren mit Hinblick auf die invariable Lichtgeschw. entsprechend verlangsamt werden.
Anscheinend hielt Lorentz dann aber die verkürzte Eigenlänge des fahrenden Zuges auch für seine Koordinatenlänge im Bezugsystem des (im Aether ruhenden) Bahnhofs. Denn J. Terrell (1959) verweist auf eine Vorlesung von Lorentz, wo der erklärte, bewegte Objekte sollten prinzipiell auch bei einer Momentaufnahme als verkürzt erkennbar sein. Wie Terrell, und unabhängig davon auch Penrose, gezeigt hat, lag Lorentz damit allerdings falsch — die Rechnung hat er offenbar ohne die relative Gleichzeitigkeit gemacht.
Die Bahnhof-gleichzeitig gemessene Länge des fahrenden Zuges ist eben nicht seine verkürzte Eigenlänge, sondern letztere muss Lorentz-transformiert werden, was erneut einen Faktor \(\gamma\) liefert und den Zug wieder auf die Länge \(L_Z\) bringt, weshalb die Lorentz-Kontraktion unsichtbar bleibt.
@Chrys:
Da kann man nur nochmal das Messbeispiel mit den zwei Lichtschranken bringen, denn sie transformiert ja “automatisch” über den Abstand der Lichtschranken und den gemessenen Zeiten:
L=100m
t1=848,7ns (ᒥLS B bis ᒣLS B)
t2=370,6ns (ᒥLS A bis ᒥLS B)
γ ergibt sich ja bereits aus t1/t2. Die Länge des Zuges ist somit \( L_Z=\frac{L \cdot t_1}{t_2}=L \cdot \gamma \)
Und das ist, wie gesagt, ein bewährtes Messverfahren – da kann man nichts machen.
@Chrys:
Naja, okay… der Gamma-Faktor ergibt sich hier ja auch nur, wenn die Zuglänge passend dazu gewählt wurde.
An die Geschwindigkeit kommt man mit \( v=\frac{L}{t_2} \) und an die Länge mit \( L_Z=v \cdot t_1 \)
Wäre der Zug nur 200m lang, würde t2 nur 741,3ns sein und 741,3/370,6 passt mal so gar nicht mehr zum Lorentz-Faktor von 0,9c. Trotzdem passt der Zug auch hier zu keiner Zeit in den Bahnsteig.
Korrektur:
t1 wäre natürlich 741,3ns nicht t2.
Herr Senf
29. Dezember 2018 @ 19:20
“Hat schon wer gemerkt, daß es kein Zwillingsparadoxon gibt, aber einen Zwillingseffekt. Das mit
dem “Paradoxon” benutzen nur “überbewußte Kritiker”,
”
Nicht mal wissen was ein Paradoxon ist – aber dafür Klappe ganz weit aufreißen …
@Joachim
.
.
Magst Du nicht mal Hartmut seine drei Fragen beantworten und ihm erklären, dass 1 m langer Stab auf der ISS hergestellt und dort ausgemessen, auf der Erde auch genau 1 m lang ist?
@Jocelyne Lopez
.
Man kann vor einem Berg stehen, die Augen zumachen und den Berg nicht sehen, bedeutet nicht, da ist kein Berg.
.
.
.
Das Relativitätsprinzips gilt nicht beim ZP, das ist für Inertialsysteme, das Ruhesystem des Reisenden ist aber über die Zeit nicht immer ein IS. Heißt, es treten Beschleunigungskräfte auf.
@NvB / 30. Dezember 2018 @ 10:57
Mal ganz ohne Rechnung. Wenn sich die Sache mit der langen Leiter in der kurzen Scheune wie hier skizziert verhielte, dann müsste die verkürzte Leiter auch verkürzt sichtbar und prinzipiell als Momentaufnahme so photographierbar sein. Nämlich mit einer Kamera, die mit gleichem Abstand von beiden Scheunentoren ruhend postiert ist und diese in simultan geschlossenem Zustand abbilden kann — mitsamt der komplett dazwischen befindlichen Leiter. Verträgt sich nur nicht sonderlich gut mit der Unsichtbarkeit nach Terrell und Penrose.
@Joachim
.
Schon klar, dass er da was “zaubert”, nur was ist nicht wirklich klar, so wie Du es nun auch bestätigst ist es eben nicht die SRT und passt so nicht. Wir erinnern uns, wir haben die LT nicht die ST und die RdG.
.
.
.
Gleichermaßen kontrahiert und ja schöne Symmetrie. 😀 Ach, eben nachgefragt, wo “wir” nun die Eigenzeit jedes Objektes als Referenz nehmen sollten, was ist dann aus den “zeitlosen” Objekten von Herrn Senf geworden?
@Senf:
Hast du schon gemerkt, dass man mit Mathematik allein nichts auf die Reihe bekommt? Du kannst keinen einzigen Rahmen rechtwinklig zusammenschweißen indem du die magische Formel “Pythagoras, Pythagoras, Pythagoras” sprichst. 😆
“Überbewusste Relativisten” kaschieren ihre Logik-Schwächen auch gerne mit Mathematik, wobei sie gerne vergessen, dass bei den aktuell geltenden Definitionen von Strecke und Zeit zu einer Eigenzeit auch eine Eigenlänge gehört, die sich genauso wenig ändert, wie ein festgesteller Gangunterschied bei Uhren.
Nicht die Lorentz-Transformation macht die Relativitätstheorie, die relativistische Addition ⊕ ist es.
Das hätten die Mathematiker ab 1860 erkennen müssen, lange bevor der Physiker Einstein es tat.
Minkowski hat es immerhin 1908 gemerkt, daß wir eine Menge mit Maximalelement “c” haben.
Mathematischen Operationen “+ – * :” haben sich dran zu halten, ⊕ “beseitigt” ∞der Fernwirkung.
Ich finde es sehr schade, dass eine solch schöne Diskussion so ausartet. Ein wenig verständlich ist es schon, dass man unsachlich wird wenn man aneinander vorbeiredet und man sich unverstanden fühlt. Aber man sollte doch versuchen sachlich zu bleiben.
Ich finde die Meinung von NvB schon gut nachvollziehbar. Ich glaube nicht, dass man aufgrund unterschiedlicher Ansichten zwei Lager im Sinne von “Relativisten” und “Kritiker” bilden sollte. Auch das führt nur zu Schubladendenken und wird einer sachlich geführten Diskussion nicht gerecht.
Ich glaube im Übrigen auch wie NvB, dass man nur mit Mathematik nicht weiterkommt. Der beste Lösungsweg ist immer eine Mischung aus Logik und Mystik, bzw. induktiver und deduktiver Denkweise. Keine von beiden ist in irgendeiner Weise mehr Wert als die andere.
Im Übrigen frage ich mich immer noch wo die ART bei der ganzen Diskussion bleibt?
@Jade
Mystik ist hier meines Erachtens fehl am Platz. Ein Wenig Mystik ist zwar gerade in der Weihnachtszeit nicht verkehrt, aber hier geht es letztlich um Mechanik, da ist alles ziemlich logisch und kausal.
Eine Mischung aus induktiver und deduktiver Denkweise wäre angebracht, wenn wir eine neue Theorie entwickeln wollten. Hier geht es aber nur um die Schilderung eines Experiments und seine Deutung anhand einer existierenden Theorie. Da muss nichts induziert oder deduziert werden. Die Theorie existiert und kann angewandt werden. Das ist ohne ein wenig Mathematik schlicht nicht möglich.
Die ART setzt auf die SRT auf, deshalb ist es sinnvoll, zunächst der Kern der Lorentz-Invarianz verstanden zu haben, bevor man sich zur ART aufmacht. Sonst sind wir wider unnötig früh bei der Mystik.
@Chrys
30. Dezember 2018 @ 10:07
Ich habe mir das Paper von Terrell jetzt man besorgt und werde zu gegebener Zeit darüber berichten. Jetzt schon kann ich sagen, dass es hier um einen weiteren Effekt geht, nämlich die Aberration der Wellenfronten geht. Die Längenkontraktion ist vorhanden, aber nicht sichtbar, wenn mit einer Kamera aufgenommen. Sehen Sie mal den letzten Satz des Abstacts:
“Even if methods of measuring distance, such as stereoscopic photography, are used, the Lorentz contraction will not be visible, although correction for the finite velocity of light will reveal it to be present.”
Wenn Laufzeiteffekte herausgerechnet werden, ist die Längenkontraktion doch wieder da.
@Herr Senf 31. Dezember 2018 @ 01:31
Diese Antwort kommt von mir leider etwas spät.
Dies ist nach meiner Meinung nicht richtig. Der einfachste Grund dafür ist, daß man auch mit der Transformation von Voigt diese Addition erhält. Der Faktor Gamma fällt nämlich bei der Division oder der Differentialquotientenbildung raus. Man könnte auch wie von mir den Dopplereffekt benutzen, um die SRT zu erklären.
@Joachim / 2. Januar 2019 @ 10:18
Minkowski-geometrisch stellt sich die Frage nach der Längenkontraktion etwa so: Gegeben seien zwei Inertialsysteme S und S’, wobei S’ relativ zu S in x-Richtung “geboosted” sei. Was soll dann unter der Länge des Einheitsvektors \(\vec{e}_{x’}\) von S’ längs der x-Achse von S verstanden werden?
Den Anschluss an die Physik hat man, wenn dieser Vektor als Modell eines in S bewegten Stabes gedeutet und die geometrisch zu definierende Länge des Vektors längs der x-Achse noch mit einer physikal. messbaren Länge des bewegten Stabes verknüpft wird.
Da x’- und x-Achse nicht parallel sind, erfordert die Antwort auf die genannte geometr. Fragestellung, dass der Vektor \(\vec{e}_{x’}\) irgendwie auf die x-Achse projiziert wird, und die gesuchte Länge des Vektors längs der x-Achse als die Länge des projizierten Vektors aufzufassen ist, der dann garantiert kein Einheitsvektor ist, sodass jedenfalls ein Effekt aufscheint. Eine solche Projektion ist aber nicht kanonisch gegeben; es bieten sich hier zwei Optionen an:
Entweder man projiziert orthogonal in S parallel zur t-Achse auf die x-Achse, dann hat der projizierte Vektor die Länge γ, was physikal. der mit einer S-Uhr ermittelten Radar-Länge des bewegten Stabes in SI-Metern entspricht.
Oder man projiziert schief in S parallel zur t’-Achse auf die x-Achse, dann hat der projizierte Vektor die Länge 1/γ, passend zur gängigen, von der LET inspirierten Vorstellung von Lorentz-Kontraktion. Unklar ist dabei noch, welche am bewegten Stab vorzunehmende physikal. Messoperation diesen Messwert in SI-Metern eigentlich liefern soll.
@Joachim Schulz:
Hier geht es mal wieder nur um die Schilderung einer existierenden Theorie, also mal wieder nur um die Verteidigung dieser Theorie. Das ist nach wie vor traurig. Den Beitrag, wie man zu etwas Neuem kommt, haben Sie ja letztendlich doch gelöscht, nachdem Sie ihn gestern noch stehen lassen haben. Die Längenkontraktion nach RT fällt nun mal komplett aus, wenn man zwischen (zeitlichen) Abständen (fester Gegenstände) und Längen fester Gegenstände unterscheidet. Ein Zug der Länge 229,4m wird nun mal nur mit dem Maßstab, der mit einer durch v=0,9c verlangsamten Uhr definiert wurde, 100m lang. Da ändert sich aber nicht die Länge des Zuges, sondern die Länge des Maßstabs – schauen Sie sich die Definitionen doch mal genau an.
Die Frage ist nun, warum eine solche Theorie, die prompt unlogisch ist, so vehement verteidigt wird.
BTW.: (Das passt zwar schon woanders wieder viel besser, aber) Mit den Definitionen von SI-Meter und SI-Sekunde gäbe es kein Problem, wenn man dazu schreibt, unter welchen Konditionen (Temperatur, Druck, Gravitationspotential und Geschwindigkeit) sie hegestellt werden müssen. Allerdings, hätte man dann auch gleichzeitig wieder ein Problem mit der Theorie, denn es wäre ja nicht mehr relativ.
Wie dem auch sei – man bekommt keine allgemein verständliche Lösung, wenn man davon ausgeht, dass alles, wie es ist, irgendwie verständlich sein muss, weil es anscheinend nicht anders funktioniert. Ich jedenfalls werde das Gefühl nicht los, dass man dank der Komplexität der Theorie, auf die Einfachsten Dinge gar nicht mehr kommt.
@Joachim Schulz:
Wo ist sie dann wieder da? 229,4m passen nun mal nicht in 100m, selbst wenn es die Mathematik hergibt – das sollte klar sein. Rechnen Sie an den korrekten Stellen mit “falsch” gehenden Uhren und die Längenkontraktion löst sich in Wohlgefallen auf, so einfach ist das.
@Chrys 2. Januar 2019 @ 10:18
Mir ist nicht ganz klar, inwiefern das jetzt eine Antwort auf meinen Beitrag von 10:18 sein soll. Dort geht es um das Paper von Terrell, nach dem eine fotografierte Kugel aufgrund der Aberration nicht abgeplattet sondern gedreht erscheint. Die Realität der Längenkontraktion stellt das nicht infrage.
Ein Einheitsvektor bleibt ein Einheitsvektor. Die Längenkontraktion beschreiben wir besser, indem wir uns den Stab aus Atomen vorstellt, die parallel zueinander eine gerade Bahn durch die Raumzeit durchlaufen. Diese Bahn sei Parallel zur Zeitachse von S. Der Stab ruht also in S. Die Frage ist nun: Welche Länge hat derselbe Stab in dem geboosteten Inertialsystem S’?
@Nicht von Bedeutung
2. Januar 2019 @ 14:58
Es wäre schön, wenn Sie meine Artikel nicht nur Kommentieren, sondern auch lesen würden. Gerade beim Michelson-Morley-Versuch lässt sich mit verstellten Uhren nichts erklären. Die Laufzeit des Arms, der parallel zur Bewegung ausgerichtet ist, verlängert sich klassisch um den Faktor \(\gamma^2\), die Laufzeit des senkrechten Arms nur um \(\gamma\). Mit einer falsch gehenden Uhr lässt sich das fehlen dieses Effekts im Experiment nicht erklären, denn das Experiment misst Laufzeitunterschiede.
@Joachim Schulz:
Ist ja auch nicht nötig und die LK auch nicht. Es genügt nämlich die ganz einfache Annahme, dass das radiale Interferenzmuster auf dem Screen mal so gar nichts mit der Interferenz parallel zur Lichtlaufstrecke zu tun hat. Man geht davon aus, dass sie zusammenhängen, nur wie kommt man darauf?
@Nicht von Bedeutung,
Das kann man an einem Michelson-Interferometer leicht verifizieren: Wenn Sie die Länge des einen Arms ein wenig verstellen, sehen Sie, wie sich die Ringe verstellen. Längen- und Abstandsmessung ist eines der wichtigsten Anwendungsgebiete von Interferometern.
@Joachim Schulz:
Kann man eben nicht – behaupte ich mal. Wenn man die Länge eines Arms verstellt, verstellt man nicht nur die parallele Interferenz, sondern auch die radiale. Die Fläche des veränderten Lichtkegels ändert sich dadurch ja auch relativ zur Fläche des unverstellten Lichtkegels. Das sich dadurch das radiale Interferenzmuster verändert, ist nur logisch.
Wenn sich also irgendwelche Längen ändern sollten, dann müsste sich das Interferenzmuster zumindest zwischen zwei 90°-Stellungen verändern, also schwingen, wenn es wie bei Martin Grusenick während des Betriebes gedreht wird. Nur leider passiert das nicht, weswegen die Vermutung naheliegt, dass die parallele Interferenz mal so rein gar nichts mit der radialen Interferenz zu tun hat. Ich würde es Ihnen ja aufzeichnen, wenn das nicht ewig zu Linienchaos führen würde (was allerdings tatsächlich nur mein Problem bleibt).
Hallo NvB 17:04 “Wenn man die Länge eines Arms verstellt, verstellt man nicht nur die parallele Interferenz, sondern auch die radiale.” kannste denen, die deine neue Physik nicht verstehen mal erklären,
was deine radiale Interferenz sein soll, vor allem bei parallelen Strahlen?
@Senf:
Vermutlich besser, als hier einer von euch Paradoxa der Relativitätstheorie aufklären kann.
Zunächst erstmal sind parallele EM-Wellen reine utopie – sogar Laser müssen noch fokussiert werden. EM-Wellen – unter anderem also auch Licht – breiten sich kegelförmig aus.
Solche Wellen ergeben Wellenfronten, wie etwa Tropfen auf einer Wasseroberfläche nur halt mit der Silhouette, wie man sie (eben) vom Doppelspalt her kennt und das entspricht dem radialen Interferenzmuster.
Bei der parallelen Interferenz jedoch verschieben sich die Phasen entlang der Lichtlaufrichtung, was aber vermutlich an der Interferenz an der Wellenfront nichts ändert – weil in Summe immer gleich. Erst wenn sich das Verhältnis der Kegellängen ändert, ändert sich vermutlich auch das radiale Interferenzmuster.
Hast du jetzt genug Linienchaos im Kopf? Naja, warum sollte es dir besser gehen, als mir?
@Nicht von Bedeutung
2. Januar 2019 @ 17:04
Selbst wenn es so wäre, zeigt das doch, dass das Interferometer für Längenänderungen empfindlich ist. Darauf kommt es hier an.
Mystik ist hier nur als Gegensatz zur Logik zur verstehen. Mystik im Sinne von Esoterik ist nicht gemeint.
@Joachim Schulz:
Ja, das zeigt es wohl. Und dass Längenänderungen zur Phasenverschiebungen im radialen Interferenzmuster führen. Da aber beim simplen Vertauschen oder Drehen der Achsen keine Phasenverschiebungen im Radialmuster erkennbar sind, kann man gut daraus schließen, dass eben keine Längenänderungen stattfinden und das für die parallelen Phasenverschiebungen entweder die Rechnungen falsch sind, was äußerst unwahrscheinlich ist, oder aber sich diese Verschiebungen nicht auf das radiale Muster auswirken, was immer wahrscheinlicher wird, je mehr man darüber nachdenkt.
@Joachim Schulz:
Im Übrigen müsste man dies ja ganz leicht emulieren können, wenn man die Spiegel an Mikroschrauben koppelt. Beim Drehen soll lt. Theorie der eine Arm länger und der Andere kürzer werden, also dreht man entsprechend die Mikroschrauben, statt das ganze Interferometer. Man braucht das gar nicht praktisch durchführen, um zu erkennen, was da passiert: Das Muster ändert sich – ganz anders also als bei der LK durch die Drehung des Interferometers und das wars dann mit der LK.
@Nicht von Bedeutung:
Nein, das wars dann mit dem klassischen Äther oder ihrer Initialraum-Theorie.
Sehen Sie, ich habe diesen Artikel ja (auch) für Sie geschrieben. Ihrer Initialraum-Theorie zufolge ist die Lichtgeschwindigkeit nur in einem Koordinatensystem konstant und isotrop, nämlich dem zum Fixsternhimmel unbewegten. Dann muss aber für ein auf der Erde Befindliches Interferometer mein Obiger Artikel gelten: Das Licht, das den parallel zum Initialraum bewegten Arm durchläuft, ist länger unterwegs als das, das quer läuft. Ob es nun direkt an den Weg liegt oder an die größeren Lichtkegel, wie sie annehmen, ist in diesem zusammenhang unwichtig. Entscheidend ist, dass ein Interferometer für diese Änderung empfänglich ist.
Nun lässt sich aber die Abhängigkeit der Laufzeiten und -wege von der Ausrichtung der Arme nicht in der vorhergesagten Größenordnung feststellen. Die Geschwindigkeit der Erde relativ zum Fixsternhimmel ist ja bekannt. Also ist entweder die Initialraum-Theorie falsch, oder Längen, die in Richtung der Bewegung orientiert sind, werden gestaucht.
Haben Sie eine bessere Idee?
Ich schon: Die Interpretation der SRT.
@Joachim Schulz:
Sie haben meine “Idee” schlicht nicht verstanden – den Unterschied zwischen Radial- und Parallel-Interferenz, wobei Parallel nicht so ganz passt, aber gut. Das radiale Muster (Kegelgrundfläche, Screen) ändert sich nur, wenn sich mindestens eine Länge der interferierenden Lichtkegel ändert. Alle Phasenverschiebungen, die bei gleichbleibenden Kegeln entlang der Lichtausbreitung (Parallelinterferenz) im restlichen Kegelvolumen stattfinden, beeinflussen die Radialinterferenz nicht, weil sie In Summe unverändert bleiben. Bei Michelson Morley wird nur die Radialinterferenz (auf dem Screen) betrachtet, die Interferenz entlang der Lichtlaufstrecke, wird gar nicht gemessen, das dürfte auch äußerst schwierig sein.
Es ist also egal, ob Sie mit LET oder SRT auf die Stauchung entlang der Bewegungsrichtung des Interferometers kommen, in beiden Fällen müsste das Muster, wenn man das Interferometer wie Grusenick parallel zur Erdoberfläche kontinuierlich dreht, zwischen zwei Extremen bei 90° hin und her wandern, weil sich die kontrahierten und nicht kontrahierten Arme abwechseln. Nur leider wandert auch da nichts, weswegen jede Theorie falsch sein dürfte, die grundsätzlich annimmt, Änderungen in den Parallelinterferenzen würden zwangsläufig Änderungen in den Radialinterferenzen bedeuten.
Ich denke mal, Sie fragen sich ebenso wie Herr Senf, was Radial- oder Parallelinterferenz überhaupt ist. Das ist nicht weiter verwunderlich, weil es offenbar Wortschöpfungen für eine vermutlich ganz neue Idee sind. Ich jedenfalls finde im Internet gar nichts darüber – ich wüsste auch nicht, wonach ich suchen sollte.
Hien mal eine stark vereinfachte Skizze – die roten und blauen Linien darin sollen nur den Verlauf von Spiralwellen andeuten, welcher normalerweise stets von der Kegelspitze ausgeht. Einzelne Spiralwellen sind dabei zylindrisch. Lässt sich das Linienchaos jetzt irgendwie besser denken?
@Joachim / 2. Januar 2019 @ 15:03
Okay, das war wohl zu sparsam formuliert, um verständlich zu sein. Und ich hatte den Stab ruhend in S’ angesetzt, also bewegt in S.
Ein in S bewegter Stab der oBdA normierten invarianten Länge 1 lässt sich (wieder mit \(c = 1\)) zur S-Zeit \(t \in \mathbb{R}\) vektoriell darstellen als
\[
t(\vec{e}_t + \beta\vec{e}_x) + \xi\vec{e}_{x’},\;0 \le \xi \le 1.
\]
Hier ist \(\vec{e}_{x’}\) der Richtungsvektor von einem Endpunkt des Stabes zum anderen, und nur die Endpunkte interessieren für Betrachtungen zur Stablänge. Der Term \(t(\vec{e}_t + \beta\vec{e}_x)\) beschreibt die durch \(t\) parametrisierte Weltlinie des Endpunktes \(\xi = 0\), und alle Fragen zur Länge des Richtungsvektors lassen sich dann auch am Fall \(t = 0\) erörten.
Geometrisch lässt sich die Frage nach Längenkontraktion somit auf das Problem einer Projektion des Richtungsvektors \(\vec{e}_{x’}\) auf die x-Achse reduzieren. Dafür kommen nur die beiden schon genannten Optionen sinnvoll in Betracht.
Physikalisch ist davon aber nur eine auf offenkundige Weise mit einer observablen und in SI-Metern messbaren Grösse verknüpft, die als “Länge des Stabes in S” bezeichnet werden kann, nämlich die mit einer S-Uhr ermittelte Radar-Länge des in S bewegten Stabes. Die relativist. Längenkontraktion ergibt sich dann schlicht als eine Proportion, als ein Verhältnis zweier messbarer Längen, genauso wie die Zeitdilatation sich als Verhältnis zweier messbarer Zeitdauern ergibt,
Als eine aus messbaren Grössen gebildete Proportion ist `Längenkontraktion’ selbst aber kein observables Phänomen, und es verwundert daher auch nicht, dass sie nicht photographierbar ist. Eine solche Erwartung mag vor dem Hintergrund der Aether-Hypothese vertretbar gewesen sein, für die SRT ist sie indessen eigentlich von vornherein völlig abwegig.
@Chrys 3. Januar 2019 @ 13:14
Allerdings ist zu bedenken, daß in Einsteins “Zur Elektrodynamik bewegter Körper” der Eindruck erweckt wurde, daß die Messung dann für eine Kugel einen Rotationsellipsoid ergibt. Der optische Effekt ist aber dann ein anderer. Die Kugel bleibt eine Kugel, die aber gedreht ist.
Sorry, Chrys, aber beim letzten Absatz kann ich nicht mitgehen. Was, wenn nicht eine “aus messbaren Grössen gebildete Proportion”, soll denn sonst ein observables Phänomen sein?
@Rudi Knoth
Terrell schreibt in seinem Paper, das Problem läge hauptsächlich in der sprachlichen Ungenauigkeit in Einsteins Paper. Was bedeutet beobachten? Die gleichzeitige Messung der Grenzfläche der bewegten Kugel ergibt sehr wohl einen Rotationsellipsoiden. Die Abbildung ergibt dagegen, aufgrund von Laufzeiteffekten, eine Kugel.
@Rudi Knoth:
Dass eine Messung eine abgeplattete Kugel ergibt, steht eigentlich sogar außer Frage. Ob eine Beobachtung das tut, ist Definitionssache.
@Albrecht Storz 3. Januar 2019 @ 14:44
Der Laufzeiteffekt, der die Kugel optisch wieder als Kugel erscheinen lässt, ist schon lange (vor über 40 Jahren in meinem Studium) bekannt. Die Messung misst den X-Abstand der beiden in Bewegungsrichtung entgegengesetzt liegenden Punkte.
@Rudi Knoth
Ja, die Veröffentlichung ist von 1959.
@Joachim / 3. Januar 2019 @ 13:46
Wenn man das Verhältnis zweier zuvor ermittelter Messwerte betrachtet, indem man daraus einen Quotienten bildet, dann ist das doch eine Rechenoperation und keine erneute Messoperation. Den Quotienten aus gemessenen Längen oder Zeitdauern kann man bilden, man kann es aber auch lassen. Penrose lässt es in The Road to Reality, wenn man davon absieht, dass er einen Abschnitt zur Nicht-Sichtbarkeit der FitzGerald-Lorentz Kontraktion bringt, die er ja unabhängig von Terrell und im selben Jahr demonstriert hatte. Ansonsten schert er sich bei seinen Ausführungen nicht um Zeitdilatation und Längenkontraktion, ohne dass er damit irgend etwas ausliesse, was man unbedingt über RT wissen müsste.
»Dass eine Messung eine abgeplattete Kugel ergibt, steht eigentlich sogar außer Frage.
Für Lorentz mit seinem Aether-Meter ist das ganz gewiss so. Doch welche auf SI-Meter bezogene Messoperation sollte dies denn als ein Messergebnis liefern?
Rudi Knoth
3. Januar 2019 @ 15:01
@Albrecht Storz 3. Januar 2019 @ 14:44
“Der Laufzeiteffekt, der die Kugel”
ich habe nichts von irgend einer Kugel geschrieben. Die Zensurorgien von Herr Schulz hier scheint doch einige Verwirrung zu stiften.
@Chrys
3. Januar 2019 @ 16:43
Wenn Sie als Messoperation nur direkte Messungen zulassen, dann geht das wohl nicht. Allerdings ist es dann nach Lorentz auch schwer. Sonst würden mir spontan zwei Möglichkeiten einfallen:
1) Fotographie und herausrechnen der Laufzeiteffekte.
2) Feststellen der Orte von Spitze und Ende zur Gleichenzeit und Messung des Abstands beider Punkte.
Bei 2) ist natürlich die Reihenfolge dieser Aktionen unwichtig. Manuel Krüger brachte die Möglichkeit einer Lichtschranke ins Spiel: Wir machen eine auf Rechnungen basierte Annahme über die Länge des Zuges, der Leiter, der Kugel. Wir installieren zwei Lichtschranken im erwarteten Abstand. Wir registrieren, ob die beiden Lichtschranken im Rahmen der Messgenauigkeit gleichzeitig ansprechen.
Beachten Sie, dass das SI Meter in jedem beliebigen IS realisiert werden kann. Nicht nur im Ruhesystem des zu messenden Objektes.
Joachim Schulz
4. Januar 2019 @ 09:20
“Herr Storz:
4. Januar 2019 @ 09:17
Es stört mich etwas, wenn Sie diesen Beitrag immer wieder hier einstellen, weil er die anderen laufenden Diskussionen stört. Soll ich einfach mal einen neuen Artikel erstellen, in dem ich diesen Beitrag zitiere und Stellung nehme?”
Tun Sie, was Sie nicht lassen können. Vor allem zensieren. Das Spielchen macht doch Spaß. Sie bekommen von mir extra immer wieder Post durch die Sie mich als bösen Störer darstellen können. Und ich bekomme viel Material für mein Buch. Ist doch bestens.
Ich sehe, Herr Storz, Sie fühlen Sich in der Rolle als Troll ganz wohl. Dann werde ich Sie in Zukunft nur noch ignorieren und Ihre Beiträge löschen.
@Storz:
Gerade die Ansicht, ich würde die SRT retten wollen, ist ja wohl hahnebüchener Unsinn, über den du mal gründlich nachdenken solltest. 😆
Mit ART ist btw. nicht “the art of entertainment” gemeint, falls du es noch nicht wusstest – aber du machst das t(r)oll, ich jedenfalls bin außerordentlich amüsiert. 😆
@Joachim Schulz:
Und wann und warum genau sollten die Lichtschranken so etwas tun? Sie tun es nicht, das ist der Punkt – 229,4m passen physikalisch nun mal nicht in 100m. Sie tun es auch an Bord des Zuges nicht – 100m passen physikalisch nun mal nicht in 43,6m.
@Nicht von Bedeutung
4. Januar 2019 @ 10:54
Natürlich passen 229,4m nicht in 100m. Die Frage ist ja, ob Bewegung die 229,4m auf 100m stauchen kann.
Aber Chris’ Frage wa ja viel weniger SRT bezogen. Nämlich nur, wie die Länge eines bewegten Objekts zu messen ist. Da könnte man auch einfach zwei Reflex-Lichtschranken (A und B) im Abstand von einem Meter nehmen. Jede Schranke registriert zwei Statusänderungen: (a) Zugspitze passiert Lichtschranke (Reflex an). (b) Zugende passiert Lichtschranke (Reflex aus).
Es sind also vier Ereignisse Aa, Ba, Ab, Bb.
Aus der Zeit, die die Spitze von Lichtschranke A nach Lichtschranke B braucht (Aa bis Ba), erhält man die Geschwindigkeit. Aus der Zeit, die der Zug braucht, um eine Lichtschranke komplett zu passieren (Aa bis Ab), lässt sich die Zuglänge bestimmen.
Mit der Zeit (Ab bis Bb) lässt sich verifizieren, dass die Zuggeschwindigkeit wirklich konstant ist und (Ba bis Bb) ist noch eine zweite Längenmessung.
Einverstanden?
@Joachim Schulz:
Nun eben diese Frage stellt sich mir jedenfalls nicht mehr und ich weiß nicht wirklich, wie es bei Chrys aussieht. Diese Stauchung ist mMn ganz allein die Interpretation der LET. Die Interpretation der SRT hingegen hängt mit der Definition von SI-Meter und SI-Sekunde, sowie dem Postulat der Konstanz der LG in jedem Inertialsystem zusammen, weswegen zu Eigenzeiten auch Eigenstrecken gehören. Denn definiert man eine Strecke über LG und Eigenzeit gemäß der SI-Definitionen, bekommt man eine Eigenstrecke. Bei 0.9c ist diese Eigenstrecke 2,294 mal so lang als die Eigenstrecke bei 0c.
Natürlich bin ich damit einverstanden, nur Herr Krüger war es bisher nicht. Das war ja genau das, was ich in der Automatisierungstechnik gelernt habe und was ich hier mitteilte (nur dass Ab in der Praxis weggelassen wird). MMn können Ba und Ab zu keiner Zeit gleichzeitig einteffen (zumindest sofern Strecke AB ungleich der zu messenden Länge ist) und ich bin mir ziemlich sicher, dass mir da jeder Konstrukteur von “Produktionsstraßen” der Welt zustimmt.
@NvB 11:48 die SRT ist von 1905, der SI-Meter ist Einsicht in die Notwendigkeit von 1983.
Dazwischen über die 78 Jahre hat sich die Urmeter-Physik nicht geändert, nur die Erkenntnisse.
@Senf:
Der SI-Meter iat dank der RT seit 1983 die falsche Einsicht – er wurde zugunsten der LoTra eingeführt. Seither erben Strecken zu den eigenen in Laboren kontrollierbaren Anfälligkeiten für Temperatur und Druck auch noch die in Laboren unkontrollierbaren Anfälligkeiten für Bewegung und Gravitation von Uhren. Das die LoTra nur wegen dieser Definitionen noch gültig ist und selbst Atomuhren bei weitem nicht so genau sind, wie angenommen, sind auch Erkenntnisse, die aber nach wie vor ignoriert werden.
Ich würde gar nicht wissen wollen, wie Einstein selbst zu seiner Ansicht gestanden hätte, nach welcher die LG gegenüber jedem Inertialsystem konstant sein soll, wenn er die Messungen ab 1973 der LG gegenüber dem Vakuum noch erlebt hätte.
(Den Beitrag von 12:56 bitte löschen, Danke)
@Nicht von Bedeutung 13:09
Die Diskussion über die Genauigkeit von Atomuhren gehört eigentlich dort hin. Deshalb hier nur so viel: Die Genauigkeit von Atomuhren ist sehr gut bekannt und wird ständig überwacht. Da gibt es keine Überraschungen.
Ich wundere mich, dass sie glauben, die Geschwindigkeit und das Gravitationspotential eines Labors sei schwierig zu kontrollieren. Die meisten Labore sind Ortsfest. Ihre Geschwindigkeitrelativ zum Fixsternhimmel ist damit gut zu ermitteln und das Gravitationspotential ist konstant und damit auch leicht zu messen.
Nachtrag: Die Lorentztransformation hat mit der Meter-Definition von 1983 nichts zu tun. Es ging einfach darum, eine höhere Langzeitstabilität und Reproduzierbarkeit zu erreichen.
@Joachim Schulz:
Zumindest gab es eine – 1971 bei H&K. Atomuhren seien unter allen Umständen genau, wäre, als wenn man behauptet, die LG sei im Wasser genauso schnell, wie im Vakuum. Atomuhren sind nun mal anfällig für Gravitation und Bewegung.
Na wunderbar. Dann sind Geschwindigkeiten also keineswegs relativ, sondern absolut, womit das RP auf den Brettern liegt und Gravitation lässt sich im Labor ebenso verändern, wie Druck und Temparaturen in Druckbehältern.
Die Langzeitstabilität bei Atomuhren ist nun mal nicht gegeben, denn die einzigen Strecken, die sich durch Bewegung und Gravitation ändern, sind Wellenlängen, welche das Pendant zur zeitlichen Periodendauer sind, wozu dummerweise auch jene Periodendauer gehört, mit welcher die SI-Sekunde definiert wird. Eine Atomuhr ist nur bei g=9,81m/s² und v=0c genau. Wäre es Anders, hätte man selbst bei H&K nichts gemessen. Ist das eine Erkenntnis, oder ist das keine?
Langzeitstabiler sind Atomanordnungen (z.B. Silizium oder Kohlenstoff) bei definiertem Druck und definierter Temperatur.
Das habe ich auch nicht gesagt. Die Definition des Meters fiel 1983 nur zu Gunsten dieser Transformation aus, was sich mMn jedoch als grober Fehler erweist, wenn man drüber nachdenkt – Uhren gehen nun mal nicht genau, Meter sind jedoch von dieser Genauigkeit abhängig.
@Joachim
.
Ja und ich würde das als eine direkte Längenmessung des Zuges im Ruhesystem S des Bahnhofs bezeichnen. Man könnte sogar dann gleichzeitig über diese ganze Strecke von 100 m eine Fotoplatte belichten oder einen CCD-Chip. Will sagen, man könnte den kontrahierten Zug theoretisch real kontrahiert fotografieren.
.
Ging auch um die direkte Messung, Hartmut hat ja mal länger an einer indirekten herumgenörgelt und deren die nötige Genauigkeit abgesprochen. Aufmal mag er nun die direkte Messung so wie beschrieben doch nicht mehr und will selber indirekt messen.
.
Nach Deiner Beschreibung der vier Ereignisse wären dann Aa, Ba gleichzeitig. Ich hatte mehrfach die Lichtschranken um 10 Millimeter weiter auseinander platziert, um den Zug wirklich vollständig zwischen beiden zu “fangen”. Heißt, beide Lichtschranken sind gleichzeitig nicht unterbrochen und der Zug befindet sich innerhalb.
.
Das dieses so möglich ist ergibt sich zwingend aus der SRT und wurde experimentell bestätigt, und das hat natürlich nichts mit der Definitionsmethode der SI-Sekunde und des SI-Meters zu tun.
.
Um es für Hartmut möglichst klar und unmissverständlich zu erklären, es werden am Bahnhof und im Zug Messstäbe von 1 m hergestellt und während der Fahrt getauscht.
.
Der vom Bahnhof ist im Zug gleichlang dem dort hergestellten und umgekehrt und im Zug wird die Zuglänge nun mit beiden dort mit 229,4 m gemessen. Und beide Messstäbe sind auch im Bahnhofssystem gleichlang und der Abstand zwischen beiden Lichtschranken wird dort mit beiden auf 100,01 m gemessen.
.
Das ist wichtig so noch mal explizit zu benennen, denn Hartmut behauptet ja weiterhin, die beiden Messstäbe hätten nach aktuellen Definitionen in beiden unterschiedlichen Systemen hergestellt und dann in einem verglichen unterschiedliche Längen. Also es gäbe da einen Zug-Meter und einen Bahnhofs-Meter und beide würden in demselben System zusammengebracht und verglichen unterschiedliche Längen haben.
.
An dem ist es eben nicht.
@NvB.
Warum sollten die Lichtschranken das nicht tun, weil Du es Dir nicht vorstellen kannst? Und wieder bist Du unpräzise, richtig hingegen ist, ein Zug mit einer Ruhelänge von 229,4 m denkt bei 0,9 c im Ruhesystem des Bahnhofs eine Länge von 100 m ab.
.
Ich hatte es eben noch mal präzisiert.
.
Es ist wichtig, dass man sich erstmal wirklich einig über die Aussagen der SRT wird und was die Definition des SI-Meters und der SI-Sekunde wirklich bedeuten und bedingen.
.
Es ist unabdingbar zu verstehen, dass die Länge des SI-Meters unabhängig vom System seiner Herstellung ist. Heißt, wird der aus dem Zug geworfen, nach seiner dortigen Herstellung auf Basis der SI-Sekunde, ist er gleichlang eines Meters welcher am Bahnhof hergestellt wurde, auf der Basis einer dortigen SI-Sekunde.
.
Darüber gibt es auch nichts ewig lang zu lamentieren und debattieren. Solange die Definition der SI-Sekunde und darauf aufbauen die des Meters nicht richtig verstanden ist, bringt es nichts groß weiter hier über die Längenkontraktion zu debattieren, denn dafür muss wohl ganz klar unmissverständlich Einigkeit darüber herrschen, was die Länge genau ist und wie sie gemessen und verglichen wird.
@Krüger:
Na und? Dazu stehe ich auch. Du bist es ja nicht, der in seinem Beruf andauernd Lichtschranken justieren darf bzw. durfte, weil die Genauigkeit es erforderte. Lichtschrankenmeßstrecken müssen nun mal, wegen ihrer Fehleranfälligkeit, weil indirekte Messung, kalibriert werden. Hast du ein Problem damit?
Joachim
.
Tut mir ja leid, aber auch Dir muss ich sagen, so formuliert ist es einfach nicht präzise. Bedenke, es werden hier zwei Längenmessungen verglichen und die sind von einem Objekt aber in unterschiedlichen Systemen gemessen und erstere ist dazu noch eine Ruhelänge, zweite hingegen nicht.
.
Auch bringt der Begriff “Stauchen” vermutlich schnell die alte Dame aufs Parkett. Präzise formuliert ist die Frage, ob ein Zug mit einer Ruhelänge von 229,4 m mit 0,9 c im Bahnhofssystem dort mit einer Länge von 100 m gemessen wird.
.
Und da haben wir mehrfach nun die klare Antwort, ja kann er und ja wird er.
@Krüger:
Das kannst du für so wichtig halten und explizit benennen, wie du willst, denn richtig ist, dass wenn Uhren Eigenzeiten messen und Strecken über die Anzeige von Uhren (1 Sekunde) definiert werden, es sich bei diesen Strecken zwangsläufig auch um Eigenlängen handelt, die, wenn man sie austauscht nicht zwangsläufig gleich lang sein können.
Der Schlüsselsatz ist dieser hier:
Die Langzeitstabilität bei Atomuhren ist nun mal nicht gegeben, denn die einzigen Strecken, die sich durch Bewegung und Gravitation ändern, sind Wellenlängen, welche das Pendant zur zeitlichen Periodendauer sind, wozu dummerweise auch jene Periodendauer gehört, mit welcher die SI-Sekunde definiert wird.
Verbunden mit der Frage, warum sich ausgerechnet jene Wellenlänge, die das Pendant zu jener Periodendauer darstellt, mit welcher die SI-Sekunde definiert wird, durch Bewegung und/oder Gravitation nicht verändert. Sie ändert sich und deswegen dauern SI-Sekunden mit fester Taktzahl (9192631770) nicht immer gleich lange.
Ein Zug mit der Ruhelänge 229,4m wird deswegen bei 0,9c im Bahnhofssystem aber immer noch nicht mit nur 100m gemessen, sondern nur im Zugsystem mit Eigenlängen des Zuges, welche durch Eigenzeiten des Zuges zustande kommen und das auch nur dann, wenn c=invariant pro Inertialsystem gilt. Wie präzise, muss ich eigentlich noch werden?
Manuel Krüger // 4. Januar 2019 @ 15:19
»Es ist unabdingbar zu verstehen, dass die Länge des SI-Meters unabhängig vom System seiner Herstellung ist. Heißt, wird der aus dem Zug geworfen, nach seiner dortigen Herstellung auf Basis der SI-Sekunde, ist er gleichlang eines Meters welcher am Bahnhof hergestellt wurde, auf der Basis einer dortigen SI-Sekunde.«
„Ein Meter ist definiert als die Länge der Strecke, die das Licht im Vakuum während der Dauer von 1/299 792 458 Sekunde zurücklegt.“ (Wiki)
Wie kann ein Meter, der in einem mit 0,9 c bewegten System hergestellt wird (etwa auf dem Weg zum Alpha-Centauri-System), die gleiche Länge aufweisen wie ein Meter, der zuhause auf der Erde hergestellt worden ist? Wenn die Uhr aus der Rakete geworfen wird, zeigt die ja auch nicht plötzlich die gleiche Zeit an wie die Weltraumbahnhofsuhr. (Oder etwa doch?)
@Joachim / 4. Januar 2019 @ 09:18
Für einen im Inertialsystem S geboosteten Stab lässt sich, etwas salopp formuliert*, folgendes feststellen:
1) Der Boost lässt die Minkowski Norm und somit die Eigenlänge (proper length, in SI Metern) des Stabes unverändert, denn ein Boost ist Minkowski-isometrisch.
2) Der geboostete Stab hat in S-Koordinaten eine t-Komponente, die umso grösser ist, je schneller sich der Stab in S bewegt. Je grösser aber die t-Komponente ist, desto grösser muss dann auch die x-Komponente sein, denn es gilt ja \(c^2t^2 – x^2 = -\text{(proper length)}^2 = \text{const.}\).
Dann stellt sich die Frage: Ist der Betrag der x-Komponente eine in SI-Metern messbare Länge?
Die Antwort wäre: Ja. Das ist c/2 mal die Dauer eines Lichtsignal Roundtrips zwischen den Stabenden, gemessen mit einer S-Uhr.
Dann hätten wir zwei in SI-Metern gemessene Längen. Und das Verhältnis von Eigenlänge zur x-Komponenten-Länge (projizierte Länge) ist gerade \(1:\gamma\).
Kommen wir erst mal bis hierhin überein?
*In dem Bemühen um einen erträglichen Kompromiss zwischen formaler Korrektheit und allgemeiner Vertändlichkeit.
@NvB.
[Von Joachim Schulz gekürzt]
@Balanus
.
Es gilt das Relativitätsprinzip, im Zug ist das Ruhesystem des Zuges nicht bewegt, es ist nur in einem anderen System, hier dem des Bahnhofs mit 0,9 c bewegt. Es ist relativ, das “bewegte” System hat beliebig viele Geschwindigkeit in beliebigen anderen Systemen.
.
Auch wenn es Hartmut nicht glauben will, ob ein System bewegt ist oder nicht und wenn wie schnell ist nur eine Frage der Definition eines anderen Systems.
.
.
.
Nicht die gleiche Zeit, aber sie geht dann gleich schnell. Noch immer scheint es hier ein Problem zu sein, eine gemessene Zeitdauer und die Geschwindigkeit mit der eine Uhr geht klar zu trennen.
.
Daher kommt auch öfter die falsche Behauptung, die LK wäre nachher weg, die ZD würde bleiben.
.
Das ist falsch, nach der Reise ist die zurückgelegte Strecke des dort auf der Reise bewegten Objektes kürzer, als die Entfernung zum Objekt vor der Reise im anderen System. Ja kann man sicher besser formulieren, aber es wurde schon ganz oft sauber erklärt und will ja nicht verstanden werden. Und ebenso ist die Dauer der Reise in beiden Systemen unterschiedlich.
@Krüger:
Das sind nur dann verschiedene Paar Schuhe, wenn man schizophren ist – der eine Teil des Verstandes ist der einen Meinung, der Andere Teil der anderen Meinung.
Manuel Krüger // 4. Januar 2019 @ 22:00
» Nicht die gleiche Zeit, aber…«
Kein aber. Wenn der Meterstab mittels einer Uhr hergestellt wird (durch eine Zeitdauer definiert ist), dann ist meinem Verständnis nach die Länge äquivalent zur Uhrzeit (man denke an die Strecke, die ein Uhrzeiger im Laufe der Zeit zurücklegt).
@Balanus 04.01. 23:28 Die Uhrzeiger legen in gleicher Zeit gleiche Strecke zurück, deshalb sind
die Meters immer gleich egal ob auf der Erde oder im Raumschiff mit 0,9c.
@Senf // 5. Januar 2019 @ 10:44
» …Uhrzeiger…in gleicher Zeit gleiche Strecke…«
Ja, gewiss, nur vergeht eben die Zeit, so habe ich es zumindest gelernt, bei 0,9 c relativ zum Ruhesystem langsamer.
@Senf:
Wahnsinnig witzig. Wenn der große Zeiger der einen Uhr warum auch immer mehr Zeit für eine Runde braucht als der große Zeiger einer anderen Uhr, geht die eine Uhr nun mal langsamer als die Andere. Wenn die Takte der einen Uhr warum auch immer zeitlich weiter auseinander liegen (Periodendauer) als die Takte einer anderen Uhr, hat die eine Uhr später 9192631770 Takte gezählt als die Andere. Die Periodendauer ist das zeitliche Pendant zur Wellenlänge und von dieser Wellenlänge hängt ab, wie lang ein damit definierter Meter wird. Im Klartext kommt bei den aktuellen Definitionen von SI-Meter und SI-Sekunde heraus, dass ein Meter rd. 30,6633 (9192631770/299792458) Periodendauern lang ist. Ändert sich warum auch immer die Periodendauer, ändert sich auch die Länge des Meters, es sei denn für Licht gilt c±v gegenüber Inertialsystemen.
@NvB.
.
Mal anders, Du sagst doch, Du kannst das alles ganz logisch “begründen”, dann mal ein paar einfache Fragen, geht so auch an Dich @Balanus oder @Storch.
.
Gehen wir mal von den beiden unterschiedlichen Postionen aus, einmal den der Physik, auch von mir vertreten und der von Hartmut.
.
Wir bauen uns zwei 1 SI-Meter-Messstäbe am Bahnhof, heißt wir messen dort mit der SI-Sekunde dort eben 1 m aus und erstellen zwei Messstäbe mit je einem SI-Meter am Bahnhof. Nennen wir mal Bahnhofsmeter.
.
Nun steht der Zug im Bahnhof, wir messen den mit einem der zwei Messstäbe aus.
.
Wir messen 229,4 SI-Bahnhofsmeter, eben die Ruhe- oder Eigenlänge des Zuges.
.
Soweit sollte doch Einigkeit herrschen.
.
Nun beschleunigt der Zug auf 0,9 c und fährt durch den Bahnhof, wir werfen einen der beiden SI-Bahnhofsmeter-Messstäbe durch das Fenster in den Zug.
.
Und nun wird damit im Zug noch mal die Länge des Zuges ausgemessen.
.
Die Frage ist, wie viele SI-Bahnhofsmeter hat nun der Zug, welche Länge wird man mit dem Messstab vom Bahnhof, der nun in den Zug gebracht wurde für den Zug im Zug messen?
.
Ich sage 229,4 SI-Bahnhofsmeter.
.
Und was sagst Du Hartmut? Und die Anderen?
@Chrys,
Sie machen meines Erachtens den Fehler, Koordinatentransformation und Beschleunigung zu vermischen. Ein Stab kann nicht geboostet werden, der Lorentz-Boost ist eine Koordinatentransformation. Er lässt die im Koordinatensystem befindlichen Objekte unverändert.
Zu 1)
Der Boost lässt die Minkowski Pseudonorm jedes beliebigen Vierervektors unverändert. Aber ein Stab ist nicht ein Vierervektor. Er ist ein Bündel von Weltlinien der einzelnen Atome, aus denen er besteht.
Wie Sie bereits schrieben, kommt es eigentlich nur auf zwei Punkte an: Die Spitze und das Ende. Diese Definieren die Länge.
Im 3D-Raum werden die Positionen von Spitze und Ende jeweils durch einen Ortsvektor repräsentiert. Dieser Ortsvektor wird in newtonscher Mechanik durch die Zeit parametrisiert, wie ich es in meinem Artikel Wie schnell wir durch die Zeit reisen dargestellt habe. Zu jeder Zeit haben Spitze und Ende einen Ort. Die Länge des Stabes ist die 3D-Norm des Differenzvektors zu einer gegebenen Zeit.
Gehen wir nun zur 4D-Raumzeit über, so sind Spitze und Ende des Stabes je durch eine Weltlinie definiert, die jede Zeitkoordinate \(t\) genau einmal durchläuft und über die Eigenzeit \(\tau\) parametrisiert ist. Da nun Spitze und Ende nicht mehr Punkte sondern eine Geraden sind, hängt der Abstand davon ab, welchen Punkt der Weltlinie man nimmt. Es hängt von der Definition der Gleichzeitigkeit ab. Die ist bekanntlich davon abhängig, in welchem Bewegungszustand sich das verwendete Koordinatensystem relativ zum Stab befindet.
Selbstverständlich kann man in der Minkowski-Metrik auch Analog zum Euklidischen Abstand zweier Geraden, einen extremalen Abstand definieren. Das ist dann die Eigenlänge des Stabes. Die Länge im Ruhesystem.
Noch dazu eben eine Antwort:
.
@NvB.
.
Unfug, es ist wie mit der Geschwindigkeit, die Geschwindigkeit eines Objektes im All kann im Ruhesystem der Erde eine andere sein, als im Ruhesystem eines Raumschiffes. Zwei unterschiedliche Systeme und somit zwei unterschiedliche Geschwindigkeiten.
.
Ebenso geht das mit anderen Größen, hier ist es eben die Länge. In der SRT ist die Länge nun mal nicht invariant sondern abhängig vom System in dem sie gemessen wird.
.
.
.
@Balanus
.
Und? Gerade das bestreite ich ja nicht. In jedem System haben wir den SI-Meter und die SI-Sekunde, bringt man hier zwei Messgeräte in einem System zusammen, messen die natürlich auch gleich.
.
Schon klassisch ist es so, Du sitzt im Auto und fährst von Berlin nach Hamburg. Dauert eine gewisse Zeit, die Frage ist nun aber, welche Entfernung hat das Auto in Deinem Ruhesystem für Dich in dieser Zeit zurückgelegt?
.
Eben genau 0 m, wenn Du nicht aus dem Fenster gefallen bist. Für wen im Ruhesystem Berlin schaut das anders aus. Dort hat das Auto die Entfernung Berlin Hamburg zurückgelegt.
.
Dennoch messt Ihr mit gleichen Messstäben, unterschiedliche Systeme, unterschiedliche Entfernungen. Klassisch ist hier eben nur die Zeitdauer gleich. In der SRT ist das eben dann anders.
@Krüger:
Natürlich sage ich auch 229,4 SI-Bahnhofsmeter, warum sollte ich etwas anderes sagen?
Allerdings sage ich auch, dass auch der bewegte Zug im Bahnhofssystem noch 229,4 SI-Bahnhofsmeter misst und deswegen nicht vollständig zwischen zwei Lichtschranken im Abstand von 100 SI-Bahnhofsmetern passt.
Nun stelle ich aber im bewegten Zug einen SI-Zugmeter her und stelle fest, dass dieser 2,294 mal länger ist, als der SI-Bahnhofsmeter, zumindest wenn sich Licht vom jedem Sitz- oder Stehplatz aus in alle Richtungen mit c ausbreitet. Mit einem solchen SI-Zugmeter ist der Zug nur noch 100 SI-Zugmeter lang. Werfe ich dieses Meßmittel nun durch ein Fenster auf den Bahnsteig, stelle ich auch dort fest, dass der SI-Zugmeter 2,294 mal so lang ist, wie der am Bahnsteig verbliebene SI-Bahnhofsmeter. Die Lichtschranken haben somit einen Abstand von 43,6 SI-Zugmetern.
Alles in Allem stellt man damit fest, dass die Lichtgeschwindigkeit im Zug eine Andere ist, wenn man sie mit SI-Bahnhofsmetern misst. Alles in Allem bleibt damit die gesamte Längenkontraktion an der veränderten Periodendauer (welche immer noch das zeitliche Pendant zur räumlichen Wellenlänge ist) hängen. Alles in Allem weiß man nun, wie man absolute Geschwindigkeiten messen kann, wenn man genau eine davon bereits gefunden und parametrisiert hat – man transformiert über unveränderliche Strecken statt über unveränderliche Zeiten.
Und was wolltest du mir sagen?
@NvB.
.
Warum ist erstmal egal, komme ich noch drauf, gut, sind wir uns ja auch dann bis dahin schon einige, mal sehen wann es kippt.
.
Dann stelle doch nun mal bitte im Zug einen SI-Meter her, auf Basis der SI-Sekunde dort im Zug. Also Atomuhr bauen, SI-Sekunde im Zug ausmessen, und den SI-Zug-Meter-Messstab bauen.
.
Nun messe mal mit diesem Messstab die Länge des Zuges aus. Ich sage, auch mit diesem wird man 229,4 SI-Bahnhofsmeter an Länge für den Zug im Zug messen.
.
Heißt, der so hergestellte Messstab ist gleichlang bei 1 m wie der vom Bahnhof.
.
Stimmst Du noch zu, oder siehst Du es dann hier anders?
.
Zum Rest später, auch ist ja bekannt, wie es richtig geht.
NvB.
.
Verzeihung, hatte ich übersehen, muss gleich was anderes machen und habe erst später wieder Zeit, also gut, dann hast Du die Antwort ja schon gegeben, mal sehen was bis nachher so von anderen hier dazu kommen wird, klar ist, ich stimme dem natürlich nicht zu. Und kannst ja schon mal grübeln, das gibt so einen fetten Widerspruch.
.
Also bis später, ich komme drauf zurück … 😀
@Krüger:
Es gibt da nur einen Widerspruch zur SRT, jedoch keinen zur Logik – da muss ich nicht drüber nachdenken.
Fakt ist nämlich, dass wenn eine Uhr langsamer geht als eine Andere, die Adndere definitiv schneller geht als die Eine und nichts mit Wechselseitigkeit, wie von der SRT gefordert, wofür man dann auch noch, warum auch immer, noch eine RdG beachten muss.
Im Gegensatz zur Aussage wurden nämlich stets unterschiedlich gehende Uhren gemessen, was bei wechselseitiger Gangveränderung jedoch gar nicht hätte auftreten dürfen.
Das Ganze löst sich schnell auf, wenn man geradlinig gleichförmige Bewegungen als das ansieht, was sie sind – der äußerst seltene Spezialfall (Wellenausbreitung) aller Bewegungen inkl. Beschleunigungen und dann wird einem schnell klar, wann und wo die SRT überhaupt gilt, nämlich gar niemals für massebehaftete Objekte (sprich Gegenstände). Kannst du ja mal drüber nachgrübeln.
@Joachim / 5. Januar 2019 @ 12:27
Die vektorielle Darstellung (im Minkowski-Diagramm mit c = 1) eines in S mit der Geschw. \(\beta\) bewegten Stabes durch einen entlang der Weltlinie \(w(t) := t(\vec{e}_t + \beta\vec{e}_x)\) parallel transportierten Richtungsvektor \(\vec{e}_{x’}\), der für einen beliebig fixierten Parameterwert \(t\) gerade der Differenzvektor zwischen den durch \(w(t)\) und \(w(t) + \vec{e}_{x’}\) repräsentierten Endpunkten des Stabes zur S-Zeit \(t\) ist, hatte ich eigentlich hier hinreichend geklärt zu haben gehofft. Oder ist daran noch irgendwas grundsätzlich unklar?
Mit diesen Bezeichnugen ist die (reelle) `proper length’ des Stabes dann der Imaginärteil der (für raumartige Vektoren imaginären) Minkowski Norm des Richtungsvektors, also
\[
\Im\|\vec{e}_{x’}\|_g = \Im\sqrt{g(\vec{e}_{x’},\vec{e}_{x’})} = 1.
\]
Und da die SI-Einheiten im relativist. Kontext als `proper units’ aufzufassen sind, lässt sich sagen, die Darstellung modelliert einen Stab der Länge 1 Meter.
In S hat der bewegte Stab resp. der ihn repräsentierende Richtungsvektor die Komponenten-Darstellung (und hier schreibe ich das oben noch normalisierte c mal explizit hin)
\[
\vec{e}_{x’} = \gamma\vec{e}_x + c^{-1}\gamma\beta\vec{e}_t.
\]
Die zuvor salopp hingeschlampte Formel für die Quadrate von t- und x-Komponente besagt dann präziser
\[
c^2\|c^{-1}\gamma\beta\vec{e}_t\|^2_g – \|\gamma\vec{e}_x\|^2_g = \gamma^2\beta^2 – \gamma^2 = -\text{(proper length)}^2 = -1.
\]
Die x-Komponente, \(\gamma\vec{e}_x\), ist vom Betrage her also umso grösser, je grösser die Geschw. \(\beta\) des Stabes in S ist. Und, wie schon gesagt, der Betrag der x-Komponente, \(\gamma\), ist eine in SI-Metern am bewegten Stab zu messende Länge, nämlich c/2 mal die mit einer S-Uhr gemessene Dauer eines Lichtsignal-Roundtrips zwischen den Stabenden.
Ist das so jetzt etwas deutlicher?
Erratum zu 5. Januar 2019 @ 16:36: Das \(c^2\) ganz vorn in der letzten abgesetzten Formel muss weg. Das kommt erst bei der Auswertung der Norm als Faktor hinzu.
@Chrys:
Also wenn es das bedeutet, was ich denke, versteh’ ich das, aber deutlicher ist es deswegen nicht gerade – behaupte ich mal.
Richtig deutlich werden Formeln nach Meinung einer meiner Ausbilder erst dann, wenn man sie in Worten ausdrücken kann, die auch für Laien verständlich sind. Vor Allem kann man auf die Art auch zeigen, ob und, wenn nicht ganz, wie weit man sie selbst verstanden hat. Das ist nicht böse gemeint, also nimms mit Humor.
Erratum #2 zu 5. Januar 2019 @ 16:36: In der schon nachkorrigierten Formel sollte zudem das erste Minus ein Plus sein. Insgesamt also
\[
\|c^{-1}\gamma\beta\vec{e}_t\|^2_g + \|\gamma\vec{e}_x\|^2_g = \ldots
\]
off topic: wollte nur kurz einen Begriff richtigstellen – weiter oben sollte es heißen: der Gegensatz von Logik ist Mythos, nicht Mystik. Eine weitere Begriffliche Spitzfindigkeit.
Zitat NvB: „Die Langzeitstabilität bei Atomuhren ist nun mal nicht gegeben, denn die einzigen Strecken, die sich durch Bewegung und Gravitation ändern, sind Wellenlängen, welche das Pendant zur zeitlichen Periodendauer sind, wozu dummerweise auch jene Periodendauer gehört, mit welcher die SI-Sekunde definiert wird. Eine Atomuhr ist nur bei g=9,81m/s² und v=0c genau. Wäre es Anders, hätte man selbst bei H&K nichts gemessen. Ist das eine Erkenntnis, oder ist das keine?“
.
Ich finde, das ist in der Tat eine klar formulierte Erkenntnis. 🙂
Die Länge einer SI-Sekunde wurde willkürlich, jedoch verbindlich, per internationaler Konvention einzig unter den Bedingungen g=9,81m/s² und v=0c festgesetzt, die in der Praxis von den weltweit 15 Primäruhren in Metrologie-Instituten konkret vorgegeben wird.
Eine Uhr, egal welcher Bauart, die die Dauer dieser konkret vorgegebenen SI-Sekunde nicht realisiert, geht per Konvention falsch: Seine Anzeigen sind ungültig und müssen als Fehlmessungen zwingend verworfen werden. Sonst handelt es sich um eine unzulässige Veränderung der Maßeinheit Sekunde.
Eine Atomuhr, die nicht die Dauer der Sekunde der Primäruhren anzeigt, geht falsch, die Messung ist ungültig und muss korrigiert werden.
Das gilt natürlich auch für alle anderen Uhren-Bauarten wie Pendeluhren, mechanische Uhren oder Quarzuhren, die jedoch wiederum nicht dadurch funktionieren, dass man Cäsium-Takten, Wellenlängen bzw. Periodedauer zählt.
Deshalb sehe ich die “Definition” der Sekunde selbst eigentlich als irrelevant. Einzig relevant ist die konkrete Realisierung der SI-Sekunde durch die ein für alle Mal ausgewählte Primäruhr / Primärühren in Metrologie-Instituten, die als einzig gültige Referenz gilt. Man hat zwar als erste Primäruhr eine Cäsium-Uhr gewählt, man hätte aber auch eine Pendeluhr, eine mechanische Uhr oder eine Quarzuhr wählen können, die Messungen wären genauso gültig und zulässig gewesen. Verstehen Sie, was ich meine, NvB?
@10:01 Eine “Primäruhr” ist eine Uhr, deren “Pendel” 9.192.631.770 mal pro Sekunde (133Cs) schwingt.
Jede Uhr, die das kann, ist als “Primäruhr” geeignet, das ist Physik und Definition “ohne Überwachung”.
Diese Physik wird genommen, um die internationale Atomzeit (Metrologie-Institute) zu vereinbaren.
Nur ist diese TAI-Sekunde keine Physik mehr, sondern Konvention und Anwendung als Sonnenersatz.
In der Physik interessiert die natürliche Zeit also “133Cs-bio”, nicht die “verarbeitete” TAI-Kunstzeit.
@Jocelyne Lopez:
Das Letzte nicht wirklich. Bei der Definition der Sekunde geht es ja auch sozusagen noch um eine weitere Genauigkeit im Sinne von Teilbarkeit. Wenn ein Pendelschwung 0,5 Sekunden dauert, könnte man nur in 0,5 Sekundenschritten Zeit messen. Deswgen wählt man dafür Cäsium-Uhren, weil man damit Zeit in 1/9192631770tel Sekunden einteilen kann.
Nur leider mißachtet man mMn die sich ändernde Periodendauer (Wellenlänge) durch Bewegung und Gravitation und außerdem wäre ein SI-Meter auf die Art nur etwa 31 Takte lang, wenn man einen Meter aber über den Kovalenzabstand von z.B. Silizium-Atomen definieren würde, wäre er etwa 9009009009 Kovalenzabstände lang, bei Kohlenstoff (Diamant) sogar noch mehr. Unter diesen Umständen wäre ein Uhrentakt bei g=9,81m/s² und v=0c etwa 293804106 Silizium-Kovalenzabstände lang, was mMn eine beachtliche Teilbarkeit für die Wellenlänge (Periodendauer) darstellt, die für die Definition der SI-Sekunde herangezogen wird. Ich bin mir sowas von sicher, dass sich diese Wellenlänge (Periodendauer) durch Gravitation und Bewegung ändert und wenn man es mit der Längenkontraktion immer noch derartig ernst meint, wie hier nachzulesen, dann sollte man damit doch bitte, bei genau dieser Wellenlänge (Periodendauer) beginnen.
@Jocelyne Lopez:
Nachtrag:
Die definition eines solchen Meters trifft jedoch auch nur unter gewissen Vorraussetzungen zu: z.B. 20°C und 1bar Luftdruck – und das kann im Gegensatz zu g=9,81m/s² und v=0c in jedem Labor erreicht werden.
Zitat NvB: “Bei der Definition der Sekunde geht es ja auch sozusagen noch um eine weitere Genauigkeit im Sinne von Teilbarkeit. Wenn ein Pendelschwung 0,5 Sekunden dauert, könnte man nur in 0,5 Sekundenschritten Zeit messen. ”
.
Ja, das leuchtet ein. Vielleicht hat man deshalb als Primäruhr eine Atom-Uhr gewählt, weil sie eben eine extrem feine Unterteilung der Maßeinheit Sekunde erlaubt, was für Hochgenauigkeitsmessungen wichtig ist. Die Unterteilung hat aber keinen Einfluß auf die per Konvention festgesetze Dauer der Sekunde, die auf jeden Fall von Uhren aller Bauarten zu realisieren ist. Ich kann mir vorstellen, dass moderne Hochgenauigkeit-Pendeluhren, -mechanische Uhren oder -Quarzuhren gar kein Problem haben, die SI-Sekunde genau zu realisieren – ich kenne allerdings nicht ihre Unterteilungsmöglichkeiten. So viel ich weiß, war die Vorgängerin der ersten Atom-Primäruhr (des britischen Physikers Louis Essen) in den 60-igen Jahren eine Hochgenauigkeitspendeluhr im britischen Metrologie-Institut in Greenwich, und ich kann mir ganz gut vorstellen, dass sie auch eine sehr feine Unterteilung der Sekunde erlaubte. Der Physiker Maurice Allais hat auch in den sechziger Jahren annerkannte Hochgenauigkeitsmessungen mit einer Pendeluhr in einem unterirdischen Labor bei Paris durchgeführt.
Der Vorteil der feinen Unterteilung der Atomuhren ist wohl leider geschwächt durch ihre Empfindlichkeit auf Bewegung (Quarzuhren sollen zum Beispiel gar nicht so empfindlich sein bei Bewegungen). Keine Uhr von keiner Bauart kann darüber hinaus von der Gravitation abgeschirmt werden.
.
Zitat NvB: “Nur leider mißachtet man mMn die sich ändernde Periodendauer (Wellenlänge) durch Bewegung und Gravitation“.
Ich glaube nicht, dass man diese Störungen in der Empirie missachtet, weil man eben Korrekturen vornimmt, wenn eine Atomuhr nicht die Periodedauer der konkret durch eine Primäruhr vorgegebenen SI-Sekunde ausweist: Messen ist vergleichen.
Es steht aber mit absoluter Sicherheit fest: Es gibt keine „ideale Uhr“, wie sich es Einstein geträumt hat. Jede Bauart von Uhren hat ihre “Macken”.
Und eins steht auch mit absoluter Sicherheit: Die Uhrenbauer und Metrologen tun pragmatisch alles, um die bestmöglichste Stabilität des Gangs der verschiedenen Bauarten gegen alle möglichen bekannten Störfaktoren zu gewährleisten, und sie arbeiten auch ständig zu diesem Zweck an der Entwicklung von neuen Bauarten. Das ist ihr Job und ich vertraue ihnen blind, dass sie ihren Job fantastisch tun. Sie haben Kenntnisse und Erfahrungswerte, sie testen das Verhalten ihrer Uhren im Labor unter verschiedenen Bedingungen soweit es möglich ist, es zu testen – sie können zum Beispiel nicht ihre Uhren auf Lichtgeschwindigkeit beschleunigen oder den Gang einer Uhr über 1 Million Jahren beobachten, klar, so etwas kann man nicht von ihnen verlangen.
Ich vertraue den Uhrenbauern und Metrologen absolut blind, dass sie alles tun und testen, um die Stabilität des Gangs ihrer Uhren bestmöglichst zu gewährleisten. Eins weiß ich aber auch mit absoluter Sicherheit von den Uhrenbauern und Metrologen: Sie haben sich nie darum gekümmert zu beobachten und zu testen wie sich eine Uhr verhält, wenn andere Uhren an sie vorbeirauschen. Das weiß ich mit Sicherheit: Uhrenbauer und Metrologen sind Techniker, keine Spinner. 😉
@Jocelyne Lopez:
Würde man es beachten, wäre eine Sekunde nicht das 9192631770-Fache einer (als fest angenommenen) Periodendauer sondern die Zeit, die Licht benötigt, um an 299792458*9009009009 Silizium-Atomen vorbeizukommen.
Und genau das können Uhrenbauer nicht, weil die Störfaktoren Bewegung und Gravitation heißen. Daraus folgt, dass eine Uhr falsch geht, sobald sie bewegt ist und/oder sobald sich das Gravitationspotential ändert, in welchem sie sich befindet. Das kann man höchstens mit Frequenzstabilisatoren ausgleichen, was aber auf Kosten der Teilbarkeit (also die geforderte Genauigkeit) geht. Die von Ihnen erwähnten 15 Uhren weltweit gehen ja nur deswegen so genau, weil sie (nahezu) identischen Bewegungen und (nahezu) identischen Gravitationspotentialen ausgesetzt sind.
@Jocelyne Lopez / 6. Januar 2019 @ 12:14
»Eins weiß ich aber auch mit absoluter Sicherheit von den Uhrenbauern und Metrologen: Sie haben sich nie darum gekümmert zu beobachten und zu testen wie sich eine Uhr verhält, wenn andere Uhren an sie vorbeirauschen.«
Die haben sich nicht nur darum gekümmert, die haben das sogar publiziert.
@Chrys:
Nur leider war da wieder nichts mit Wechselseitigkeit, wie von der SRT postuliert und trotzdem wurde nur die SRT bestätigt, nicht wahr?
Zitat Chrys: “Die haben sich nicht nur darum gekümmert, die haben das sogar publiziert: Optical Clocks and Relativity
.
Meine Fragen zu dieser Publikation aus dem Jahre 2010:
– Worum handelt es sich bei diesen „Optical Clocks“? Um Cäsium-Uhren? Oder um eine neue Generation von Uhren, die die Cäsium-Atomuhren ablösen sollte, wobei die PTB über solche Uhren 2016 aussagt, dass sie aufgrund der extrem hohen Empfindlichkeit immer noch nicht zuverlässig funktionieren? Siehe hier: „Ganz zuverlässig funktioniert die optische Uhr aus Braunschweig aber noch nicht. „Ein lautes Türenkallen reicht manchmal schon und der Laser kommt aus dem Lot“…
– Kann man die Abweichungen, die bei zwei relativ zueinander bewegten „Optische Uhren“ auftreten, auf das Relativitätstprinzip der SRT zurückführen? Oder auf technisch bedingte Störungen?
Nicht von Bedeutung // 6. Januar 2019 @ 11:07
»Nur leider mißachtet man mMn [bei der Atomuhr] die sich ändernde Periodendauer (Wellenlänge) durch Bewegung und Gravitation«
Das sehe ich völlig anders. Moderne Atomuhren arbeiten so exakt, dass man mit ihnen sogar nachweisen kann, dass der Verlauf der Zeit von Gravitation und Bewegung abhängt.
Und da Raum und Zeit gemäß der RT miteinander verknüpft sind, hängen auch alle räumliche Größen, die mittels Zeitspannen definiert sind, von Gravitation und Bewegung ab.
Das war zumindest bislang meine Auffassung. Inzwischen bin ich mir nicht mehr so sicher, ob die moderne Physik nicht schon weiter ist und solche (naiven?) Vorstellungen über den Zusammenhang von Raum und Zeit mittlerweile hinter sich gelassen hat.
@Balanus:
Ähhhmmmm… Ich würde das “exakt” (etwa so) in Anführungszeichen setzen. Unter exakt verstehe ich nämlich, dass eine Sekunde einer solchen Uhr unter allen Bedingungen genau solange dauert, wie sie definiert wurde. Wenn Gravitation und Bewegung die Dauer einer solchen Sekunde beeinflusst, ist eine solche Uhr für Gravitation und Bewegung störanfällig und Selbiges gilt für Strecken, die störanfällig für Druck und Temperatur sind.
Über die Logik, dass ein SI-Meter, der über eine bewegte Uhr definiert wird, länger wird, waren wir uns doch schon einig, oder nicht?
@Nicht von Bedeutung
6. Januar 2019 @ 13:46
Nun, der Punkt, den Balanus hier anspricht, ist dass wir von anderen Uhren vermuten, dass sie genau gleich beeinflusst werden. Nur können wir das nicht messen, weil die relativistischen Effekte in einer Größenordnung stattfinden, in der diese Uhren bereits durch andere Einflüsse ungenau sind.
@Joachim Schulz:
Woran erkennt man, dass Sie meine anderen Beiträge vermutlich noch gar nicht gelesen haben – z.B. jenen von 11:07 Uhr?
Darin taucht dieser Satz auf:
Bedeutet: Und wie das gemessen wird. Wann immer baugleiche Uhren unterschiedliche Gangraten aufweisen, misst man das. Nur beachten tut man es nicht, sonst würde längst \( \tau \cdot t=\tau’ \cdot t’ \) gelten.
An Alle: Bitte beenden Sie jetzt des Thema “Genauigkeit von Uhren”. Das passt unter einen anderen Beitrag. Hier geht es um die Längenkontraktion. Ja, das hängt miteinander zusammen, aber eben nur am Rande. Ich möchte gern konzentriert beim Thema bleiben.
(Keine Sorge, was bis hierher noch steht, bleibt. Sie können also ggf. drauf verlinken.)
@NvB.
.
Hier tobt ja wieder der Bär. Also ich mache mal eben ganz sachlich weiter, Du hast erklärt, der Zug-Meter wäre länger als der Bahnhofs-Meter im Zug und nur mit diesem könnte man die Ruhelänge des Zuges im Zug mit 229,4 m richtig ausmessen.
.
Gut, Du hast da also eine Methode um im Zug den Zug-Meter herzustellen, ich nenne diese mal die pohl’sche Methode.
.
Nun frage ich Dich, welcher von beiden Messstäben macht im Zug mehr Sinn, mit welchem misst man die Zuglänge im Zug denn nun richtig? Mit dem Bahnhofs-Meter oder mit dem den Du da im Zug hergestellt hast?
.
Und noch was, stell Dir vor, es gibt nun noch eine Methode die Länge des Bahnhofs-Meter im Zug herzustellen, nennen wie das mal die krügerische Methode.
.
Ich kann also im Zug die Länge des Bahnhofs-Meter herstellen und brauch da keinen mehr durchs Fenster geworfen. Damit kann ich dann den Zug im Zug mit 229,4 m sauber ausmessen. Cool, oder?
.
Also, wie schaut es aus, im Grunde braucht doch keiner diesen Zug-Meter oder?
@Balanus / 6. Januar 2019 @ 13:33
»Moderne Atomuhren arbeiten so exakt, dass man mit ihnen sogar nachweisen kann, dass der Verlauf der Zeit von Gravitation und Bewegung abhängt.«
Bei der Definition der SI-Einheiten wird davon ausgegengen, dass der “Verlauf der Zeit” gerade eben nicht von Gravitation und Bewegung abhängt.
Andernfalls müsste man die SI-Sekunde doch auch in Abhängigkeit von Bewegung und Gravitation definieren, wenn das ein Standard zur Vergleichbarkeit gemessener Zeitdauern werden soll. Was sich dann entsprechend an den SI-Meter vererbt.
Und müsste man in der GR davon ausgehen, dass der “Verlauf der Zeit” von der Gravitation abhängt, wäre es bereits unmöglich, eine relativistische Bewegungsgleichung für ein im Gravitationsfeld frei fallendes Testpartikel überhaupt hinzuschreiben, geschweige denn zu lösen.
@Krüger:
Mit dem Bahnofsmeter misst man im Zug und am Bahnhof 229,4m Zuglänge unabhängig davon, ob sich der Zug bewegt oder nicht.
Mit dem Zugmeter misst man im Zug und am Bahnhof 100m Zuglänge unabhängig davon, ob sich der Bahnhof bewegt oder nicht.
Die Länge der jeweiligen Meter hängt per Definition vom Gang der Uhren ab, welche bewegt langsamer gehen als ruhend. Wie du den Zugmeter bei 0,9c im Zug lt. Definition ebenso lang hinbekommst, wie den Bahnhofsmeter, musst du erst mal erklären – vergiss dabei aber möglichst nicht, die verlängerten Periodendauern, mit denen die SI-Sekunde definiert wurde. Kurz gesagt: Die krügerische Methode funktioniert nicht, jedenfalls nicht, wenn man den Zugmeter gemäß Definition im fahrenden Zug herstellt – den Bahnhofsmeter kopieren gilt nicht.
Meinst du richtig per Definition im Inertialsystem oder zweckmäßig richtig? Richtig per Definition misst man mit dem Zugmeter, aber zweckmäßig ist der Bahnhofsmeter. Daraus folgt, dass die Definitionen von SI-Meter und SI-Sekunde fatal falsch sind und das unabhängig davon, wie hoch die Teilbarkeit von 9192631770 ist.
Natürlich braucht den Zugmeter keiner. Längenkontraktion braucht aber auch keiner mehr, wenn man beachtet, dass die zeitlichen Abstände, welche das Pendant zur Wellenlänge bleiben, mit welcher die SI-Sekunde definiert wird, die erste Länge ist, die sich ändert, weswegen sich alle Meter, die gemäß Definition über LG und SI-Sekunde hergestellt wurden, ebenfalls ändern.
Du hattest mir einen Widerspruch in meiner Logik versprochen und alles, was dabei herum kam, war der offensichtlichste Widerspruch in der SRT. Herzlichen Glückwunsch.
@Chrys:
Und das bedeutet dann was? Nicht etwa, dass man mit der GR nicht mehr allzuviel anfangen kann? [ironie]Och… Tut mir das leid. Dann muss man sich für Gravitation ja auch noch eine andere “Ursache” als Raumzeitkrümmung einfallen lassen. Ui, das wird aber schwierig.[/ironie]
Die Entschuldigung, man hätte nichts Besseres, lasse ich nicht gelten, sofern man nichts Besseres zulässt.
Zitat Joachim Schulz: „An Alle: Bitte beenden Sie jetzt des Thema “Genauigkeit von Uhren”. Das passt unter einen anderen Beitrag. Hier geht es um die Längenkontraktion. Ja, das hängt miteinander zusammen, aber eben nur am Rande. Ich möchte gern konzentriert beim Thema bleiben.“
.
Die Messung der Längenkontraktion eines starren Stabes in der SRT wurde von Einstein selbst mit zwei verschiedenen Meßmethoden beschrieben:
1. Operation a): Mit einem starren Maßstab
Hier ist das Thema bzw. das Ergebnis der Messung nicht strittig: Man misst mit Anlegen eines starren Maßstabes immer die gleiche Länge des Stabes, egal ob der Stab im Raum ruht oder ob er sich im Raum bewegt. Es gibt keine materielle Veränderung eines im Raum bewegten Stabes: Sie haben es unmissverständlich bereits 2011 hier bei SciLogs ausgesagt, Ihr Kollege Markus Pössel ebenfalls bereits 2008.
Diese Meßmethode mit einem starren Maßstabes kann man also ruhig abschließen und abhacken, bei diesem Thema herrscht darüber bereits Konsens.
.
2. Operation b): Mit zwei Uhren
Hier ist das Thema immer noch strittig, denn manche Autoren und Kommentatoren sind der Meinung, dass die Messung der Länge eines im Raum bewegten Stabes mit zwei Uhren eine materielle Verkürzung des Stabes in Bewegungsrichtung nachweist. Dies wäre allerdings in Widerspruch zu der Meßmethode nach Operation a), worüber bereits Konsens besteht, denn ein und denselbe im Raum bewegten starren Stab kann nicht gleichzeitig materiell unverändert und materiell verändert sein.
Herr Schulz, könnten Sie hier bitte auch unmissverständlich Ihre eigene Position zu der Operation b) der Messung der Länge des im Raum bewegten Stabes mit zwei Uhren mitteilen? Das würde weitere Wiederholungen, Irrungen und Verwirrungen ausräumen:
a) Erfährt der im Raum bewegte Stab eine materielle Verkürzung in Bewegungsrichtung, wenn man ihn mit zwei Uhren misst?
Oder
b) Erfährt der im Raum bewegte Stab keine materielle Verkürzung in Bewegungsrichtung, wenn man ihn mit zwei Uhren misst?
@Chrys
5. Januar 2019 @ 16:36
Deutlich genug und noch immer dasselbe Problem: Sie gehen davon aus, die Länge des Zuges würde durch einen Vierer-Vektor repräsentiert und die Länge im bewegten Bezugssystem müsse eine Projektion dieses Vektors sein. Das ist aber nicht der Fall.
Es gibt beliebig viele Vektoren von Ende zu Spitze des Zuges, denn für jeden Zeitpunkt gibt es einen Vektor, der das Zugende bestimmt, und einen, der die Zugspitze bestimmt. Die Längenkontraktion erhält man, indem man die Punkte wählt an denen Zugende und Zugspitze nach den verwendeten Bezugssystem gleichzeitig sind. Der Abstand dieser Punkte ist die kontrahierte Länge. Die Zeitkomponente ist trivialer Weise Null.
Damit kommt man auf \(L/\gamma\).
Ihre Definition ist keine Länge des Stabes, denn die Pingdauer entlang eines bewegten Stabes ist, wie ich im obigen Artikel berechne um den Faktor \(\gamma^2\) länger als Länge pro Signalgeschwindigkeit.
Wozu brauch man eigentlich Uhren? Ich stelle mir die Messung so vor:
Senkrecht zu den Bahngleisen wird ein Lichtblitz in Richtung Bahnhof gesendet und mit einer Reihe von Detektoren am Bahnsteig registriert. Da die Wellenfront parallel zum Bahnsteig verläuft, ist also der Abstand zwischen in Bewegungsrichtung des Zuges letzten belichteten Detektor und dem wieder ersten belichteten Detektor die Länge des Zuges im Inertialsystem, in dem der Bahnsteig ruht. Im Inertialsystem, in dem der Zug ruht, ist aber die Wellenfront wegen der Aberration schrägt. Daher ist der Abstand zwischen dem letzten belichteten Detektor und dem ersten belichteten Detektor kleiner als die Ruhelänge des Zuges.
Zitat Rudi Knoth: “Daher ist der Abstand zwischen dem letzten belichteten Detektor und dem ersten belichteten Detektor kleiner als die Ruhelänge des Zuges.”
.
Auch an Sie, Herr Knoth, die Frage, die ich weiter oben Herrn Schulz gestellt habe:
Sind Sie der Meinung, dass mit dieser Messmethode nachgewiesen wird:
a) dass der fahrende Zug eine materielle Verkürzung seiner Ruhelänge erfahren hat?
oder
b) dass der fahrende Zug keine materielle Verkürzung seiner Ruhelänge erfahren hat?
@Krüger:
Noch langsamer! Ich gebe nicht einfach vor, ich stelle per Definition her und dies tue ich nach Definition im Zweifelsfalle auch ohne Kenntnis des Bahnhofmeters oder gar des Bahnhofssystems. Ich lasse also beispielsweise ein Rundeisen 31 Atomuhr-Takte lang vorschieben und säge dann an dieser Stelle ab. Das ist mein Meter. Das selbe mache ich bei verschiedenen Geschwindigkeiten in verschiedene Richtungen bei gleichbleibendem Gravitationspotential. Die Meter sammle ich und markiere sie, damit ich weiß, unter welchen Umständen sie hergestellt wurden. Bei meiner Methode gehe ich davon aus, dass Uhren durch Bewegung beeinflusst werden, deswegen habe ich die kürzesten Meter genau dann, wenn ich mich gegenüber dem Vakuum/Raum am wenigsten bewegt habe. Bei deiner Methode gehst du davon aus, dass Uhren eben nicht durch Bewegung beeinflusst werden, weswegen deine Meter alle gleich lang sind. Die Frage ist nun aber, wie du mit deiner Methode jemals unterschiedlich gemessene Uhrengänge erklären willst oder wie mit unterschiedlichen Uhrengängen gleich lange Meter gesägt werden sollten. So schwer kann das doch nicht sein, also warum zum Henker brauchst du solange? Vor Allem wofür brauchst du solange? Mir die SRT so beizubiegen, wie es dir gefällt, wird endlos lange dauern, denn es ist schlicht unmöglich – meine Übezeugung ist eine Andere – meine Blickwinkel sind Andere. Auf den Köpfen von Riesen genießt man mehr Weitsicht als bloß auf deren Schultern.
@NvB.
.
Du hast die Frage nicht beantwortet, kann der Zug-Meter nach Deiner Methode auch mal kürzer als der Bahnhofs-Meter sein? Oder ist der zwingend in Deiner “Physik” immer länger?
zu Chrys 16:27 “Bei der Definition der SI-Einheiten wird davon ausgegangen, dass der “Verlauf der Zeit” gerade eben nicht von Gravitation und Bewegung abhängt.”
Oi …, das ist jetzt eher ein Bärendienst für die Mißverständnisse der “Neuen Freunde der Physik”.
Die Definition der Sekunde ist 9.192.631.770 133Cs (absichtlich ohne Gravitation/ Bewegung), weil wir wissen, daß Druck, Temperatur und Schlaglöcher 133Cs nicht ändern, wenn dann geht die Uhr kaputt.
Damit wird (technisch) die Gleichberechtigung aller Beobachter garantiert, die sich auf die Verläßlichkeit ihrer (baugleichen) Armbanduhren verlassen müssen, die zeigen ihre Zeit also die der Beobachter an.
Physik beginnt beim Uhrenvergleich von Zeitdauern, zwei Uhren zeigen bei Bewegung Zwillingseffekt oder im Gravitationspotential die Höhendifferenz durch unterschiedlich Zeitanzeige. Alle Uhren gehen per Definition gleich rasch, die LG ist inv=const, damit haben alle den gleichen Meter 1m=0,…c*1s.
Es gibt keine materielle Verkürzung von Meternormalen und materielle Veränderungen von Uhren.
Was unterschiedlich ist, sind reale Meßwerte T und L, die müssen per Lorentztrafo auf “Normbedingung Bewegung gleich Null” T_o und L_o zurückgeführt werden, das macht “Operation b” bei (17:05) Einstein.
Gravitation ist Zeitdilatation, alles fällt nach unten, wo die Zeit langsamer läuft, alles will älter werden 🙂
@Jocelyne Lopez 6. Januar 2019 @ 17:45
Die Antwort ist eindeutig b. Der Zug hat keine materielle Verkürzung erfahren. Denn der zuletzt belichtete Detektor (Sensor) bewegt sich im Inertialsystem des Zuges zum zuerst wieder belichteten Detektor.
@Krüger:
Gehen Uhren nun unter Umständen unterschiedlich schnell oder nicht? Wenn ja, heißt das dann nicht, dass SI-Sekunden unter Umständen unterschiedlich lange dauern, oder nicht? Wird der SI-Meter über die Dauer einer SI-Sekunde definiert oder nicht? Uhren gehen unterschiedlich schnell und deswegen funktioniert deine Methode nicht. Der Bahnhofsmeter ist kürzer als der Zugmeter. Der Zugmeter kann nur dann kürzer sein, wenn sich der Bahnhof gegenüber dem Raum bewegt, in welchem sich Licht isotrop ausbreitet und nicht der Zug. In meiner Physik gibt es keinerlei Wechselseitigkeit, warum auch – die ist hochgradig irrational.
Und dein RP kannst du vergessen – zumindest das Galileische. Das ist hinfällig, nachdem die LG im und gegenüber dem Vakuum konstant gemessen wurde. Das Galileische RP galt für Objekte inkl. “Photonen” – das aktuelle RP gilt nur noch für Inertialsysteme und Inertialsysteme existieren für massebehaftete Objekte genau genommen gar nicht. Dagegen kannst du dich wehren, soviel du willst – das hat nur den selben Effekt, den es bei Flacherdlern hat, wenn sie sich gegen eine Erdkugel aussprechen. Leider braucht man für diese Erkenntnisse eine weitaus klarere Weitsicht und vor Allem eine breitsprigere Übersicht, als wie man sie von deinem schmalen Blickwinkel aus erreicht – daran ist nichts zu ändern. War das jetzt deutlich genug? War das wieder beleidigend oder verträgst du nur die bittere Wahrheit nicht?
Zitat Rudi Knoth: “Die Antwort ist eindeutig b. Der Zug hat keine materielle Verkürzung erfahren.”
.
Danke für die unmissverständliche Antwort. 🙂
Ich gehe stark davon aus, dass es auch die Auffassung von Herrn Schulz ist.
Das ist allerdings auch die Auffassung, die alle Kritiker vertreten.
Und somit haben wir also einen wichtigen Konsens für die Messung der Längenkontraktion erzielt. 🙂
Dies bedeutet, dass sowohl Längenkontraktion als auch ihr Pendant Zeitdilatation keine physikalische Relevanz in der Realität haben, in dem Sinne, dass es einzig physikalische Wechselwirkungen mit der Materie des Stabes bzw. des Zuges geben kann. Wechselwirkungen mit der Materie der bewegten Objekte werden dementsprechend nie am Ort und zum Zeitpunkt stattfinden können, die mit der Längenkontraktion und der Zeitdilatation berechnet werden.
@NvB 19:27 🙁 “Wenn ja, heißt das dann nicht, dass SI-Sekunden unter Umständen unterschiedlich lange dauern, oder nicht?” Wie denn, die SI-Sekunde ist 9.192.631.770 lang, wo ist da ein Unterschied ?!!11elf
@Senf:
Die SI-Sekunde ist 9192631770 PERIODENDAUERN lang!!11elf
Die Länge der PERIODENDAUERN ändern sich durch Gravitation und Bewegung 12drei45.
zu J.L. 19:47 “… keine materielle … Das ist allerdings auch die Auffassung, die alle Kritiker vertreten.”
Nein, daß ist Konsens aller Physiker, was die *Kritiker* seit über 100 Jahren nicht verstehen.
Und deshalb ist “… keine physikalische Relevanz in der Realität haben …” mal wieder auslegungsfalsch.
Jeder Beobachter sieht gleichberechtigt seine Realität, die hängt aber von seinem Standpunkt ab.
Diese unterschiedlichen Beobachterrealitäten (im Theater links oder rechts, vorne oder hinten sitzen) müssen abgeglichen werden, weil alle doch dasselbe Theaterstück gucken – die Bühne ist invariant.
@NvB 20:00 “Die Länge der PERIODENDAUERN ändern sich durch Gravitation und Bewegung 12drei45.”
Kannst Du mit Dir nicht vertrauten Physikern erklären, was für Mechatroniker eine Definition bedeutet.
Dort steht zwar Periodendauer, aber eben nicht wie lang sie sein muß, es gilt 9.192.631.770bio.
@Senf:
Deswegen steht bei der Definition auch nicht, wie lange eine Sekunde dauert. Deswegen steht bei der Definition des Meters auch nicht, wie lang er wird. Offebar sehen Physiker das anders und spielen sich deswegen als die Klügsten der Welt auf, oder wie seh ich das?
Das ist doch reinste Comedy. 😆
@Chrys // 6. Januar 2019 @ 16:27
» Bei der Definition der SI-Einheiten wird davon ausgegengen, dass der “Verlauf der Zeit” gerade eben nicht von Gravitation und Bewegung abhängt. «
Das ist gewiss vernünftig, dass man da von einer absoluten Zeit ausgeht. Man braucht ja eine feste (invariante?) Basis für seine Berechnungen und Transformationen. Aber wie auch schon Roger Penrose in Computerdenken (1991) schrieb:
»Man kann heute derart genaue Uhren („Atomuhren“) herstellen, daß diese Zeitdehnungseffekte sich mit Uhren, die in schnell und tief fliegenden Flugzeugen transportiert werden, direkt nachweisen lassen.« (HdA)
Wenn es diese „Zeitdehnungseffekte“ also realiter gibt, dann muss das doch auch Konsequenzen für Maßstäbe haben, die anhand einer bestimmten Zeitspanne hergestellt werden. Wenn nicht, wüsste ich gerne, warum nicht.
@Joachim / 6. Januar 2019 @ 17:06
Welchem Objekt, das in der Minkowski Geometrie einen Stab repräsentiert, soll denn bitte eine als die `proper length’ des Stabes erkennbare Invariante zugeschrieben werden, wenn nicht einem 4-Vektor?
Da ist nicht das Problem, denn auch eine verkürzte x-Komponente ist das Ergebnis einer Projektion. Das wird erhalten, indem man als Basis \(\{\vec{e}_{t’}, \vec{e}_x\}\) wählt, was (vorsichtshalber wieder mit c = 1) zur Komponenten-Darstellung
\[
\vec{e}_{x’} = \gamma^{-1}\vec{e}_x + \beta\vec{e}_{t’}
\]
führt, von der man den x-Anteil nimmt. Das ist dann eine schiefe Projektion auf die x-Achse. Das geometrische Prozedere ist in beiden Fällen dasselbe, nur die Art der Projektion macht den Unterschied aus.
Die Frage ist dann aber, bei welcher Messung mit Uhr und Licht \(1/\gamma\) als Ergebnis herauskommen soll. Die Konstanz der Lichtgeschw. impliziert, dass alle Längenmässung in der SR auf Zeitmessung mit anschliessender Konvertierung durch Multiplikation mit c zurückführbar ist. Und genau das liegt dann auch der Def. des SI-Meters (1983) zugrunde.
Jegliche mit Meterstab-Akrobatik vorgenommenen Längenmessungen, deren Ergebnis sich nicht ersichtlich aus einer konvertierten Zeitmessung ergibt, sind irrelevant. Und es passiert sehr leicht, dass man beim rechnerischen Hantieren mit Meterstäben die Übersicht verliert, mit welcher Meter-Definition man eigentlich gerade operiert und dann unversehens die Aether-Meter aus der LET wieder hereinbringt.
Und wenn man noch etwas weiter schaut, was verkürzt sich denn am “längenkontrahierten” Umfang einer rotierenden Kreisscheibe? Der kommt schliesslich als \(2\pi R\gamma\) und keineswegs verkürzt heraus.
@Balanus:
Mein Geheimtipp: Nie hat ein Mensch Kontrollmaße unter zeitlich gedehnten Bedingungen hergestellt, sondern konsequenterweise nur in Eichlaboren auf der Erde, wo g=9,81m/s² und v=0 gilt. Dass sich solche Kontrollmaße unter besagten Bedingungen verändern, ist deswegen noch nie aufgefallen. Außerdem unterscheiden sich die Uhrenanzeigen erst bei etwa 4422m/s=15919km/h (und g=9,81m/s²) um 1 Takt pro Sekunde – das heißt die bewegte Uhr zeigt erst nach 9192631771 Takten der unbewegten Uhr 9192631770 Takte an. Das heißt, Geschwindigkeits- und/oder Gravitationspotentialunterschiede müssen dann auch noch unheimlich hoch sein, bevor überhaupt etwas so glas klar auffällt, dass man unterschiedliche Meterenden bekommt.
@Balanus / 6. Januar 2019 @ 21:33
Im Original schreibt Penrose unmittelbar im Anschluss an Dein Zitat noch, »agreeing with the Minkowskian ‘distance’ measure s, and not with t!« Das s ist demnach ein Bogenlängen- oder Eigenzeit-Parameter der Uhren-Weltlinie, mit Bezug auf den aber gar kein `time-slowing’ auftreten kann. Da hat sich Sir Roger schon missverständlich artikuliert, aber inzwischen hat er ja auch gezeigt, dass er es besser kann. Was da gemessen wird, ist stets nur die Länge von Uhren-Weltlinien, und nicht die 4-Geschwindigkeit, mit der diese durchlaufen werden, denn die ist für alle überhaupt zulässigen Uhren gleich.
»Wenn es diese „Zeitdehnungseffekte“ also realiter gibt, dann muss das doch auch Konsequenzen für Maßstäbe haben, die anhand einer bestimmten Zeitspanne hergestellt werden. Wenn nicht, wüsste ich gerne, warum nicht.«
Die Eigenzeit ist eben nicht `dehnbar’, sondern ein invariantes Mass für Zeitdauer, und die SI-Sekunde ist expressis verbis als Einheit für Eigenzeit ausgewiesen. Die Dauer der SI-Sekunde also nicht variabel, weshalb der SI-Meter dann auch immer mit der gleichen Lánge herauskommt.
@Chrys:
Und mit einer Eigenzeit lassen sich nun mal nur Eigenstrecken herstellen. Eigenzeiten sind expressis verbis nicht gleichlang und das hat man gemessen. Das liegt daran, dass die Periodendauern, mit denen diese Eigenzeiten definiert wurden, unterschiedlich lang sind. Jene Periodendauern, die immernoch das zeitliche Pendant zu räumlichen Wellenlängen sind. Und wenn man es mit Längenkontraktion ernst meint, sollte man – expressis verdis – gerade diese Länge konsequenterweise nicht aus den Augen verlieren. Nur leider haben hier bisher alle SRT-Befürworter zugegeben, dass man diese Länge vollständig ignoriert, was mMn ein fataler Fehler ist. Da darf sich jetzt niemand mehr rausreden. Ist die Kritik jetzt angekommen?
@Chrys 6. Januar
Sie schütten das Kind mit dem Bade aus. Ich bin hier (fast) bei Nicht von Bedeutung: Wenn Sie nur Eigenzeiten und Eigenlängen zulassen, können Sie nichts über Beziehungen zwischen Objekten aussagen. Es gibt überhaupt keinen Grund, sich in der SRT auf die Betrachtung von Objekten in Ruhesystemen zu beschränken.
Jede Beschreibung in einem beliebigen Bezugssystem ist Äquivalent zu jeder anderen. Natürlich ist die Beschreibung der stationären Länge eines Stabes im Ruhesystem ein Vierer-Vektor mit dem Betrag der “proper Length” \(L\). Eine ebenso gültige Beschreibung desselben Stabes ist ein Vierer-Vektor der Länge \(L/\gamma(v)\) in einem Bezugssystem, in dem der Stab mit Geschwindigkeit \(v\) bewegt ist.
Ihre Fixierung auf Ruhelängen und -zeiten funktioniert überhaupt nur in den relativ langweiligen stationären Beispielen ohne Beschleunigungen und Wechselwirkungen. Sobald ein Objekte beschleunigt bewegt sind, werden Sie sie in Koordinaten beschreiben müssen, in denen sie nicht stationär sind. Oder Sie bekommen es mit sehr komplizierten Koordinatensystemen zu tun.
Die Definition des Meters bedeutet keinesfalls, dass Längen nicht mehr mit materiellen Maßstäben gemessen werden dürfen. Es ist lediglich eine Eichvorschrift für diese Art von Maßstäben.
@Joachim Schulz:
Wieso nur fast? Eichvorschriften werden vorzugsweise in Eichlaboren auf der Erde eingehalten und dort stellt man die Meßstäbe her, mit denen alles verifiziert wird. Ist doch klar, dass alle Meßstäbe von dort gleich lang sind, weil dort annähernd TAI-Sekunde=SI-Sekunde gilt. Kein Mensch würde Meßstäbe in 400km oder gar 21000km Höhe oder irgendwie wie und worin auch immer bewegt Meßstäbe herstellen. Idealisiert baugleiche Uhren sind dann auch von den Maßen her idealisiert baugleich und auf die Art, kommt nur noch eine einzige Länge dafür in Frage, wenn solche Uhren unter Umständen unterschiedlich ticken und man muss kein Genie sein, um darauf zu kommen, welche das ist. Es sind nicht die Maße der Uhren oder die Maße der Cäsium-Fontänen, sondern besagte Periodendauer.
Erst wenn die Definition der SI-Sekunde von der Definition des SI-Meters abhängig gemacht wird, statt umgekehrt, entspräche dies den aktuellen Eichvorschriften und dann darf auch besagte Periodendauer weiter ignoriert werden, weil sofort klar ist, das sie die einzige ist, die sich ändert, wenn Uhren unterschiedliche Gangraten aufweisen.
BTW.: Wie würde Ihnen \( \tau_{TAI}=\tau_{SI} \cdot t_{SI}=\tau_{n} \cdot t_{n} \) gefallen? Jetzt macht es doch Sinn, oder nicht? Wie dem auch sei – für mich bleibt es der Grund, an der SRT zu zweifeln und kein SRT-Befürworter hat bisher ein Argument dagegen.
Fazit: Der experimentelle Befund zur Längenkontraktion lautet, dass es keinerlei Längenkontraktion im Sinne der LET, der SRT oder überhaupt gibt.
Joachim Schulz schrieb (7. Januar 2019 @ 08:50):
> […] Betrachtung von Objekten […] Jede Beschreibung in einem beliebigen Bezugssystem ist Äquivalent zu jeder anderen.
(Zumindest sofern die geforderte “Betrachtung” überhaupt “in” dem jeweils beliebenden bestimmten Bezugssystem erfolgen kann; d.h. abgesehen von Inäquivalenz verschiedener bestimmter Bezugssysteme wegen ungleicher Rindler-Horizonte, u.Ä.)
Jede Beschreibung eines “Objektes in einem (anfänglich beliebig wählbaren, aber im Verlauf festgehaltenen/bestimmten) Bezugssystem” besteht aber aus den (eigentlichen) geometrischen (bzw., falls das in Betracht gezogene Bezugssystem nicht stationär wäre, geometrsch-kinematischen) Beziehungen der Mitglieder genau dieses gewählen und bestimmten Bezugssystems untereinander;
zusammen mit den Koinzidenz-Bestimmungen welche Mitglieder genau dieses gewählten und bestimmten Bezugssystems vom “betrachteten Objekt” in welcher Reihenfolge getroffen (und ggf. passiert) wurden,
und welche Pings (bzgl. welcher weiterer Mitglieder dieses Bezugssystems) von vorausgegangenen (Signal-, Treff- bzw. Passage-) Anzeigen des “betrachteten Objekts” jeweils dabei/koinzident wahrgenommen wurden.
> Natürlich ist die Beschreibung der stationären Länge eines Stabes im Ruhesystem
… d.h. in dessen Ruhesystem, sofern gemessen wurde bzw. vorausgesetzt/angenommen wird, dass (zumindest) die beiden relevanten Enden des betreffenden Stabes gegenüber einander (durchwegs, hinreichend) ruhten …
> […] “proper Length” \(L\) .
D.h. selbstverständlich dessen, eigentliche “Länge \(L\)”.
> Eine ebenso gültige Beschreibung desselben Stabes ist […] Länge \(L/γ(v)\) in einem Bezugssystem, in dem der Stab mit Geschwindigkeit \(v\) bewegt ist.
Beim Wert “\(L \, / , \sqrt{1 – \beta^2}\)” handelt es sich aber (i.A.) gerade nicht um die (selbstverständlich eigentliche) “Länge” des betreffenden Stabes, sondern um die (selbstverständlich eigentliche) Distanz zwischen (jeweils) zwei bestimmten, durch geeignete “Projektion” im Zusammen miteinander identifizierten Mitglieder des Intertialsystems, die die Geschwindigkeit (beider Enden) des Stabes als \(v \equiv \beta \, c\) ermittelten.
Dem Stab anstatt des “Längen”-Wertes \(L\) den Wert \(L \, / , \sqrt{1 – \beta^2}\) als “(selbstverständlich dessen) Länge” zuzuschreiben, wäre mutwillig improper und inkonsistent mit der jedenfalls (und insbesondere zur Ermittlung des zutreffenden Wertes \(\beta^2\)) erforderlichen oben beschriebenen Bestimmung von geometrisch(-kinematischen) Beziehungen von Mitgliedern jeweils eines bestimmten Bezugssystems untereinander.
@Joachim / 7. Januar 2019 @ 08:50
»Eine ebenso gültige Beschreibung desselben Stabes ist ein Vierer-Vektor der Länge L/γ(v) in einem Bezugssystem, in dem der Stab mit Geschwindigkeit v bewegt ist.«
Nein, die Länge eines den Stab repräsentierenden, raumartigen 4-Vektors ist der Imaginärteil der Minkowski-Norm dieses 4-Vektors, und das ist eine invariante Grösse bei jeglichem Wechsel des inertialen Bezugssystems. An dieser Eigenlänge des Stabes ändert sich in der SRT nichts durch relative Bewegung mit Geschw. v, weder geometrisch noch physikalisch. In der LET ist das anders, da wird der mit Geschw. v im Aether bewegte Stab um den Faktor 1/γ(v) verkürzt gedacht, denn Lorentz definiert keine invariante Eigenlänge, sondern eine, die mit wachsendem v schrumpft.
Ich bin nicht auf Ruhelänge fixiert, ich bin lediglich konsequent in der Verwendung von `proper length’, und das ist die einzig koordinaten-unabhängig definierte und somit physikal. relevante Länge, die sich dem Stab zuordnen lässt. Dem Ruhesystem des Stabes kommt dabei nur insofern eine spezielle Rolle zu, als dort die `proper length’ als ein physikal. Messwert herauskommt, mit Radar oder hier gerne auch mit Meterstab.
Das Prinzip bei der Längenmessung mit Meterstab ist und war schon immer, dass die Endpunkte eines Gegenstandes, dessen Länge gemessen werden soll, gleichzeitig(!) mit zwei Markierungen auf der Meterstab-Skala koinzidieren. Das geht aber nur, wenn Gegenstand und Meterstab relativ zueinander ruhen. Andernfalls ist die Forderung nach gleichzeitiger Koinzidenz nicht erfüllbar. Die Länge eines bewegten Gegenstandes lässt sich aber unter der Annahme des Lichtpostulats noch immer mit einer ruhenden Uhr durch die Dauer eines Lichtsignal-Roundtrips längs des Gegenstandes messen. Nur kommt dabei nicht seine Eigenlänge als Messwert heraus.
Apropos Beschleunigung. Nehmen wir mal an, ein 200 Meter langer, sehr schneller Zug, der auf 2 cm geschrumpft sein soll, fährt komplett in einen 100 Meter langen Bahnhof und bremst dann brutal so ab, dass er zum Stillstand kommt, noch bevor die Lok aus dem Bahnhof heraus ist. Der stehende Zug ist dann wieder 200 Meter lang. Kommt dann der schon im Bahnhof befindliche Wagon am Zugende beim Bremsen im Rückwärtsgang wieder aus der Bahnhofseinfahrt herausgeschossen?
@Chrys:
Der Meinung dürfte Herr Schulz aber auch sein, denn bei seinen Ausführungen über Michelson Morley kommt er auf Ähnliches: nicht grundsätzlich auf c/2*t, sondern auf L/γ quer und L/γ² längs zur Bewegungsachse – also einem bleibenden Unterschied von 1/γ, was der Faktor der LK sein soll.
Nur leider muss man lt. Rechnung davon ausgehen, dass sich die Phasen kontinuierlich zyklisch verschieben, wenn man das Interferometer kontinuierlich dreht und deswegen, müsste sich auch das Interferenzmuster am Screen kontinuierlich verändern und in jeweils 90° Schritten gleich und unverschoben aussehen, wenn tatsächlich LK vorläge (vgl. mit Interferometern mit mind. einem per Mikroschraube justierbaren Spiegel). Das geschieht aber nicht (Grusenick), also liegt auch keine LK vor. Fazit: die Phasenverschiebungen längs zu den Achsen ergeben in Summe stets das selbe Interferenzmuster radial zu den Achsen, vorausgesetzt, die Rechnungen stimmen.
Zitat Chrys: “Die Länge eines bewegten Gegenstandes lässt sich aber unter der Annahme des Lichtpostulats noch immer mit einer ruhenden Uhr durch die Dauer eines Lichtsignal-Roundtrips längs des Gegenstandes messen. Nur kommt dabei nicht seine Eigenlänge als Messwert heraus.”
.
Die Eigenlänge eines Stabes kommt doch mit einem Lichtsignal hin-und-zurück zwischen den zwei Enden des Stabes (mit einer Uhr am Ende A und einem Spiegel am Ende B) als Messwert heraus, vorausgesetzt man kennt genau die Geschwindigkeit des Lichtssignals und die Geschwindigkeit des Beobachters (Uhr). Oder nicht?
@Chrys:
Wohl kaum. Die sich verlängernden Waggone klatschen mit einer derartigen Wucht auf die nun wie eine Wand wirkende Lok, dass sich Crash-Gemetzel und Längenkontraktion egalisieren. Wussest du das nicht? 😆
So, nu aber wieder ernst.
@Nicht von Bedeutung
Das wäre auch meine Antwort: Wenn wir instantan alle Atome von 90% c auf 0 abbremsen könnten, käme dabei ein Zug heraus, dessen Atome um den Faktor \(\gamma(0,9\cdot c)\) gegenüber ihren Normalabstand gestaucht sind. Dass uns so ein Konstrukt um die Ohren fliegen würde, ist nicht lustig.
Nicht von Bedeutung
7. Januar 2019 @ 12:46
Das ist was passieren müsste, wenn keine Längenkontraktion vorläge. Die Längenkontraktion ist für das Null-resultat des M&M-Experiments verantwortlich.
@Jocelyne Lopez
7. Januar 2019 @ 12:50
Nur wenn der Stab ruht. Deshalb spricht man auch von Ruhelänge. Wenn der Stab in bewegt ist, kommt ein um \(\gamma^2\) zu großer Wert heraus.
@Joachim Schulz:
Veto. Die Enden des Armkreuzes des Interferometers würden sich ellipsenartig bewegen, wobei sich die Lage der Ellipse quer zur Bewegungsrichtung des Interferometers auf der Umlaufbahn nicht ändert. Bei einer Drehung um das Zentrum würde der kontrahierte Arm länger und der nicht kontrahierte Arm kürzer. Bei 45° schließlich wären beide idealisiert gleich lang. Kurz gesagt, die Längenverhältnisse wechseln sich kontinuierlich ab. Solche tatsächlichen Längenänderungen führen aber zu Änderungen des radialen Interferenzmusters, was man ganz leicht mit per Mikroschrauben verstellbaren Interferometern simulieren kann, in dem man beide Spiegel gleichmäßig hin und her in entgegengesetzte Richtungen dreht.
Man kann auch noch mal das vertikale Experiment von Herrn Grusenick zu Rate ziehen und sich fragen, ob dieser dubiose Sinusschwinger dort von einer gravitativen Rotverschiebung, der Stabilität des Interferometers oder substanzieller Längenkontraktion durch Schwerkraft kommt.
Aber dass die Nullresultate des M&M-Experiments von einer LK verursacht werden, halte ich jedenfalls für einen euphorischen Fehlschuss (ein Irrtum den man aus einer Euphorie heraus als Volltreffer identifiziert).
@Nicht von Bedeutung
Auch hier bringen Sie wieder historische Abläufe durcheinander. Michelson Morley war damals eher eine Enttäuschung, weil jeder mit einem positiven Ergebnis gerechnet hatte. Eben die von Ihnen angesprochene Sinus-förmige Abhängigkeit des Interferenzmusters von der Ausrichtung im Äther. Da war also niemand euphorisch. Das Ergebnis war komplett unerwartet.
@Joachim Schulz:
Natürlich sind es immer die “Laien”, die etwas durcheinander bringen und nie die, die etwas studiert haben. Hier aber Irren Sie, denn bei Michelson-Morley erwartete man die Phasenverschiebung nach einer 90°-Drehung und schon diese traf nicht ein, was unerwartet war. Dann kam die LK, mit welcher dieses erklärt wurde und dann erst kam Martin Grusenick, der meines Erachtens auch diese Erklärung zu Nichte machte, weil sich LKs bei kontinuierlicher Rotation nun mal kontinuierlich umkehren müssen, was aber auch nicht passiert.
Nicht von Bedeutung
7. Januar 2019 @ 14:37
Dann sind wir uns ja einig. Und wo war da mein Irrtum? Und wer soll hier was “aus einer Euphorie heraus als Volltreffer identifiziert” haben?
@Joachim Schulz:
Ich denke, wir sind uns nicht einig. Die Erklärung LK passt nur bei Drehungen um 90°, wobei der kontrahierte Arm auf Normallänge kommt und der normal lange Arm kontrahiert wird. Bei einer kontinuierlichen Rotation müsste man nun an schwingenden Interferenzmustern sehen können, wie sich Kontraktion und Normallänge stetig abwechseln. Passiert aber nicht – ergo keine Längenkontraktion. Die Erklärung LK für die Nullresultate des M&M-Experiments waren ein euphorischer Fehlschuss und nicht bloß ihr Irrtum. Was gibt es da denn nicht zu verstehen?
@Joachim Schulz:
Ergänzung (falls nötig):
Dass man es bei Rotationen nicht nur mit 90° Derhungen zu tun hat, sondern auch mit unendlich vielen Winkeln dazwischen auch, wissen Sie hoffentlich.
@Krüger:
Außerdem habe ich beschlossen, einem geistig unbewaffneten, bildungsresistenten, verbal inkompetenten, kognitiv subobtimierten, parasitären Heuchler, wie dir, nicht mehr zu antworten, und du tätest gut daran, meine Annahmen nicht ewig mit deinem haltlos schwachsinnigem Geseiere “verbessern” zu wollen. Denke mal dran, dass “Nebenexistenz” das einzige Wort ist, was in dem mir verpasseten Avatar auf deiner Selbstdarstellungsplattform auf mich zutrifft – der Rest mehr auf dich.
Solltest du dich nicht dran halten, gebe ich Herrn Schulz 24 Stunden, um deinen Müll zu entsorgen. Ansonsten gehe ich drauf ein und das wird sicher nicht freundlich.
@Nicht von Bedeutung
Mir war nicht klar, dass das ihr Problem ist. Bewegungen in einem beliebigen Winkel können in die Komponenten quer und längs zur Hauptachse zerlegt werden. Dadurch ergibt sich dann der Sinus-Zusammenhang.
Wenn man ein Michelson-Interferometer hochkant dreht, muss man natürlich mit der begrenzten Steifigkeit der Arme rechnen. Der nach oben gedrehte Arm wird unter der Schwerkraft biegen.
@NvB.
.
Du hast einfach keine sachlichen Argumente, hast es ja selber beschrieben. Klar suchst Du nun nach einem Auswege, warum ich Schuld sein soll, dass Du nicht antworten kannst. 😀
.
.
.
Drohungen sind immer gut, weißt doch wie schnell Dein Mist hier immer weg ist.
.
Mess erstmal eine Geschwindigkeit gegenüber dem Raum und/oder dem Vakuum … 😀
@Joachim Schulz:
An welches Problem dachten Sie denn? Was ergäbe sich dann aus diesem Sinus-Zusammenhang (ist doch mal ein schönes Wort)? Sagen wir Kontraktion Sinus und Normallänge Cosinus. Bei 45° ist beides gleich – die Arme also gleich lang und selbiges gilt für 135°, 225° und 315°. Dazwischen sins die Längen der Arme verschieden, nur das einmal der eine und 90° später der andere Arm länger bzw. resp. kürzer ist, was zu kontinuierlichen Schwingungen im Interferenzmuster führen sollte, was aber nun mal nicht passiert. Mache ich einen Denkfehler oder Sie (vertretend für alle, die Ihrer Meinung sind)?
Beim Hochkant-Interferometer kommen zu viele Faktoren zum Tragen, dass man gar nicht sagen kann, woher die Sinusschwingung genau kommt. Z.B. hängen die Enden des Arms parallel zur Erdoberfläche ja auch noch durch. Läge es aber am Durchbiegen der Arme oder an der Instabilität des Interferometers liegen, würde sich am oberen Ende ein plötzliches Umschwingen ergeben, was sich in einer plötzlichen Änderung des Interferenzmusters äußern würde. Das Interferenzmuster aber schwingt stets recht seicht und der Umschwung taucht bei 45° auf – die Spiegel stehen dann senkrecht und parallel zur Erdoberfläche. Darüber wurde in Foren schon angeregt diskutiert – auch über Frank G Pearce, der Herrn Grusenick zeigen wollte, dass es an seinem “Klapperkasten” lag, wo man aber deutlich sieht, dass das Muster auch bei ihm schwingt. Genug Offtopic.
Chrys schrieb (7. Januar 2019 @ 12:22):
> […] der Imaginärteil der Minkowski-Norm […]
Da eine Norm ganz allgemein eine Abbildung in die (nichtnegativen) reellen Zahlen (bzw. kommensurable Größen wie “Längen” oder “Dauern”) bezeichnet, also grundsätzlich keinen (von Null verschiedenen) Imaginärteil hat, bieten sich zur Beschreibung der geometrischen Beziehungen zwischen (Paaren von) Ereignissen stattdessen eher die (Verhältnisse von) Raumzeit-Intervallen \(s^2 : \mathcal E \times \mathcal E \rightarrow \mathbb R\) an.
> Das Prinzip bei der Längenmessung mit Meterstab ist und war schon immer, dass die Endpunkte eines Gegenstandes, dessen Länge gemessen werden soll, gleichzeitig(!) mit zwei Markierungen auf der Meterstab-Skala koinzidieren.
Da der Begriff der “Gleichzeitigkeit” erst seit ca. 100 Jahren überhaupt nachvollziehbar (als Messgröße definiert) ist,
bestand “das Prinzip bei der Längenmessung mit Meterstab” zumindest vorher wohl eher darin,
dass die Enden eines Gegenstandes, dessen Länge (als Distanz zwischen den beiden Enden) gemessen werden soll, dauerhaft/permanent mit zwei Markierungen auf der Meterstab-Skala koinzidieren (sollen).
(Wobei allerdings nicht nachvollziehbar ist, was damals überhaupt mit einem “Meterstab” gemeint gewesen wäre,
bzw. mit der Forderung oder Behauptung, dass zwei bestimmte Stabenden und/oder zwei bestimmte Markierungen “relativ zueinander geruht” hätten.)
> `proper length’ […] ist die einzig […] physikal. relevante Länge, die sich dem Stab zuordnen lässt.
Und (deshalb insbesondere wohl) einem “Meterstab“.
Das Ruhesystem zweier bestimmter Beteiligter spielt dann insofern eine besondere Rolle, als
– diese beiden gegenüber einander ruhen (sollen), und ihnen deshalb eine bestimmte Distanz voneinander zugeschrieben werden kann, und sie deshalb (auch) als Enden eines bestimmten Stabes gelten können, dem die Distanz der beiden voneinander als dessen Länge zugeschrieben werden kann, und
– dass die Distanz- bzw. Längenverhältnisse bzgl. weiterer Mitglieder des selben Ruhesystems unmittelbar aus Ping-(Koinzidenz-)Verhältnissen ermittelt werden können; während Distanz- bzw. Längenverhältnissen andernfalls durch die “(unilaterale) Einstein-Projektion” unter Berücksichtigung des in diesem Zusammenhang bekanntlich (gegenseitig) herleitbaren Faktors \(\sqrt{1 – \beta^2 }\) insbesondere für von Null verschiedene gegenseitig gleiche Werte \(\beta^2\) zu ermitteln sind.
p.s.
> Nehmen wir mal an, ein […] Zug […] bremst […] brutal so ab, dass er [bzgl. den Bestandteilen eines Bahnhofs] zum Stillstand kommt […]
Zu M&Ms Anordnung »revolving very slowly« (deren Fehlen im obigen SciLogs-Artikel mir auffiel) bestünde wohl allenfalls ein quantitativer Unterschied.
Zitat Chrys: „Die Länge eines bewegten Gegenstandes lässt sich aber unter der Annahme des Lichtpostulats noch immer mit einer ruhenden Uhr durch die Dauer eines Lichtsignal-Roundtrips längs des Gegenstandes messen. Nur kommt dabei nicht seine Eigenlänge als Messwert heraus.“
Zitat Jocelyne Lopez: „Die Eigenlänge eines Stabes kommt doch mit einem Lichtsignal hin-und-zurück zwischen den zwei Enden des Stabes (mit einer Uhr am Ende A und einem Spiegel am Ende B) als Messwert heraus”
Zitat Joachim Schulz: „Nur wenn der Stab ruht. Deshalb spricht man auch von Ruhelänge. Wenn der Stab in bewegt ist, kommt ein um γ2 zu großer Wert heraus.“
.
Ein zu großer Wert für die Länge des bewegten Stabes kommt heraus???
Es war doch immer seit 100 Jahren die Rede von einer Verkürzung der Länge des bewegten Stabes… 🙁
Was nun? Wir hatten uns doch dahingehend geeinigt, dass der Stab nie eine materielle Veränderung seiner Länge erfährt, egal ob er ruht oder ob er sich bewegt. Oder nicht? Sind Sie vielleicht seit 2011 einer anderen Meinung, Herr Schulz?
Wenn nicht, können wir nicht bei diesem Konsens bleiben und diese Diskussion als konstruktiv abgeschlossen ansehen? Das wäre ein Novum in den kontroversen Physik-Diskussionen bei SciLogs seit 11 Jahren – eigentlich etwas zum feiern. 🙂
Ich schließe mich voll umfänglich dem Fazit dieser Diskussion von NvB weiter oben:
Fazit: Der experimentelle Befund zur Längenkontraktion lautet, dass es keinerlei Längenkontraktion im Sinne der LET, der SRT oder überhaupt gibt.
@Jocelyne Lopez
.
Du willst Dir da nur was basteln, und dann wo in Deinem Blog verdreht erklären, Joachim hätte Dir ja nun endlich bestätigt und zugegeben, es gibt keine Längenkontraktion.
.
Das ist falsch, wie das Zitat von Hartmut. Es gibt selbstverständlich die Längen- oder besser Lorentzkontraktion. Nur bedeutet diese eben nicht, ein Körper wird physikalisch gestaucht.
.
.
@NvB.
.
Dein Zug-Meter müsste von der Richtung abhängen, in dem dieser gemessen wird. Heißt, in Fahrtrichtung müsste der eine andere Länge haben, als vertikal ausgemessen.
.
Dann hast Du erzählt, der Zug-Meter könnte kürzer sein, wenn der Bahnhof, also die Erde mit, sich gegenüber dem Raum mit einer Geschwindigkeit bewegen.
.
Da die Erde um die Sonne kreist, wird sich nur schwer auf dieser Bahn ein Punkt finden lassen, zu dem man dann ein “gegenüber” dem Raum, besser Äther, ruhendes System definieren könnte. Heißt, die Erde müsste sich demnach immer wo “gegenüber” dem Raum bewegen. Damit wäre auch auf dieser der Meter dann von der Ausrichtung in seiner Längen abhängig.
.
Das gilt so natürlich nur für Deine Meter, in der Physik besitzt der SI-Meter keine solche Abhängigkeiten und Einschränkungen.
zu J.L. 17:18 Wir “hatten uns doch dahingehend geeinigt, dass der Stab nie eine materielle Veränderung seiner Länge erfährt, …” Nein, hatten wir eigentlich nicht, Stab ist nicht (immer)= “seine Länge” 😉
Materiell gibt es keine Verkürzung nach FitzGerald (Lorentz-Äther), heißt nicht, daß seine Länge nicht kontrahiert (Einstein wie Lorentz), Länge ist eine Meßgröße, gilt auch für die Länge des Urmeters.
@Senf:
Mal wieder sowas von lustig… Rein zufällig soll die SRT auch für Zoll und Meilen gelten. Also es geht nicht um Meßgrößen, sondern um Meßartefakte.
Und bei Lorentz sollen sich Längen sehrwohl physikalisch verkürzen, nur in der SRT ist man sich nicht einig, wie LK überhaupt funktionieren soll – Hauptsache, sie bleibt im Gespräch. 😆
Vielleicht nochmal zur Erinnering eine Kurzfassung des obigen Artikels: Aus einfachen kinematischen Betrachtungen folgt, dass in einem bewegten Michelson-Interferometer die Lichtlaufzeit im Arm parallel zur Bewegung um den Faktor \(\gamma^2\) und im Arm senkrecht zur Bewegung um den Faktor \(\gamma\) verlängert ist.
Dass beides im mitbewegten System, also zum Beispiel auf der Erde, nicht beobachtet wird, kann erklärt werden, wenn man sowohl die Zeitdilatation als auch die Längenkontraktion als real begreift. Die Zeitdilatation wirkt auf beide Arme und erklärt den Faktor \(\gamma\), die Längenkontraktion gleicht den Laufzeit-Unterschied in beiden Armen gerade aus.
Da ein Interferometer für Unterschiede sehr empfindlich ist, beweist das Experiment von Michelson und Morley und seine Folgeexperimente im wesentlichen den Effekt der Längenkontraktion. Die Zeitdilatation lässt sich mit dem Dopplereffekt viel genauer vermessen.
@Joachim Schulz:
Sie reden wieder nur von senkrecht und parallel – ergo 90°. Dreht man das Interferometer ist das, was senkrecht war parallel und das was parallel war senkrecht. Bei jedem beliebigen Winkel dazwischen schwanken die Längen zwischen γ, γ² und zurück bzw. zwischen γ², γ und zurück. Dadurch wird eine Rotation sozusagen zu einer Ellipse, deren Lage sich im Gegensatz zum Winkel nicht verändert. Das Interferenzmuster müsste gemäß der nun schwankenden Kontraktionen zwischen zwei 90°-Stellungen ebenfalls schwanken, nur leider passiert das nicht. Ergo kontrahiert da nichts und ergo haben die Phasenverschiebungen “längs” der Arme nichts mit dem Interferenzmuster radial zu den Armen zu tun. Soll ich das aufzeichnen oder gar animieren, oder kommen Sie auch so dahinter?
Korrektur:
muss “Dreht man das Interferometer um 90°, ist das” heißen.
@Frank Wappler / 7. Januar 2019 @ 16:41
Das heisst auch dann noch Norm — bisweilen auch Lorentzian norm — wenn das innere Produkt nicht positiv definit ist, guckst Du hier. Bei den References dort ist Ratcliffe massgeblich. Der verwendet im übrigen auch imaginäre Norm und imaginäre Länge synonym, während ich hier vorsichtshalber die Längen raumartiger Vektoren reell und nur ihre Minkowski-Norm imaginär genommen habe. Man will schliesslich niemanden hier mehr als nötig überfordern. 🙂
Dein Spacetime-Link beschert noch die Animation eines bewegten Stabes, die ziemlich genau das illustriert, was ich Joachim Schulz mit einem parallel transportierten Richtungsvektor und wohl zweifelhaftem Erfolg nahezubringen versucht hatte.
Man sieht, was als die kontrahierte Länge eines in S bewegten Stabes von Einheitslänge gehandelt wird, ist nur der S-gleichzeitge Abstand zwischen den Weltlinien der Endpunkte des Stabes.
Wenn dieser Stab ein Zug und \(|OC| = 1/\gamma\) die Länge des Bahnhofs ist, dann sollte Gerüchten zufolge dieser Zug haargenau in den Bahnhof passen. Die Animation zeigt jedoch, dass vorne die Lok schon wieder aus dem Bahnhof hinaus ist, bevor hinten der letzte Wagon ganz hineingelangt ist.
@Chrys // 6. Januar 2019 @ 23:22
» Im Original schreibt Penrose unmittelbar im Anschluss an Dein Zitat noch, »agreeing with the Minkowskian ‘distance’ measure s, and not with t!« «
So steht’s auch in der deutschen Übersetzung: » –in Übereinstimmung mit dem Minkowskischen „Abstand“ s, aber nicht mit t! « . Aber das ist ja wohl klar, dass im Experiment das herauskommt, was die Minkowski-Geometrie „vorhersagt“.
„Abstand“ bedeutet bei Penrose ja soviel wie „erfahrene Zeit“ oder „Eigenzeit“.
Demnach wird die Uhr im Flugzeug zwischen den Ereignissen Abflug und Landung ein kürzeres Zeitintervall „erfahren“ als die baugleiche stationäre Uhr am Boden und somit auch entsprechend weniger SI-Sekunden anzeigen als ihr unbewegter Counterpart.
Wie kann das überhaupt sein? Was passiert da physikalisch in der Luft im kreisenden Flugzeug? Die Uhren funktionieren einwandfrei und zählen dennoch unterschiedlich viele SI-Sekunden zwischen den beiden aufeinander folgenden Ereignissen. Es ist, als wäre die Zeit beim Fliegen gedehnt, weshalb die Borduhr während des Fluges langsamer tickt als auf dem Boden (die Relativität von Gleichzeitigkeit spielt bei diesem Experiment hoffentlich keine Rolle…)
@all
Mir ist nach all den vielen Kommentaren immer noch nicht klar, wie man das in der Physik nun mehrheitlich sieht: Haben wir es hier mit realen Effekten und validen Messungen zu tun, oder handelt es sich bloß um irgendwelche „Messeffekte“, die erst nach entsprechenden Transformationen die realen Verhältnisse widerspiegeln?
Bislang bin ich davon ausgegangen, dass es in der Tat die besonderen Eigenschaften des Raum-Zeit-Gefüges sind, die zu diesen relativistischen Phänomenen führen. Mittlerweile kommt es mir so vor, als hätte man sich von dieser Vorstellung weitestgehend verabschiedet, als beruhten die merkwürdigen Messergebnisse (bei bewegten Systemen) allein auf der Konstanz der Grenzgeschwindigkeit. „Messeffekte“ halt…
Chrys schrieb (7. Januar 2019 @ 21:20):
> […] Ratcliffe […] verwendet im übrigen auch »imaginäre Norm«
LOL.
p.s.
> […] sollte […] dieser Zug haargenau in den Bahnhof passen.
Natürlich für eine geeignete, nachvollziehbare Definition von “haargenau in den Bahnhof passen”; nämlich:
dass die Anzeige des Bahnhofs-Ausfahrsignals von/bei Eintreffen der Zug-Lokomotive und die Anzeige des Bahnhof-Einfahrsignals von/bei Passage des Zug-Brems-Caboose-Wägelchens einander (“haargenau”) gleichzeitig waren.
> […] dass vorne die Lok schon wieder aus dem Bahnhof hinaus ist, bevor hinten der letzte Wagon ganz hineingelangt ist.
Natürlich betreffend die “umgekehrte Beziehung”, d.h. hinsichtlich der Anzeige der Lok bei Passage des Ausfahrtssignals vor der Anzeige der Caboose bei Passage des Einfahrtsignals.
Die (Koordinaten-frei definierte) Gleichzeitigkeits-Beziehung nach Einstein (1916/17) bzw. Comstock (1910) spielt bekanntlich auch beim Vergleich von Längen durch Einstein-Projektion (also Herleitung des Verhältniswertes \(\sqrt{1 – \beta^2}\)) eine wichtige Rolle …
@Chrys
Nochmal ein (vielleicht letzter) Klärungsversuch. Ein physikalischer Stab ist kein Vierervektor, der durch die Raumzeit fliegt. Er ist eine Menge von Atomen, die durch Weltlinien dargestellt werden können. Zum Beispiel in parametrisierter Form:
\(r_n(\lambda)\) mit \(0\leq n\leq N\), \(\lambda\in \mathbb{R}\)
Die \(r_n\) sind Vierer-Vektoren.
Nehmen wir an, das Atom der Spitze sei dargestellt durch \(r_0\), das des Endes durch \(r_N\). Der Parameter \(\lambda\) kann, muss aber nicht mit der Eigenzeit identisch sein.
Nun lassen sich die Vierervektoren in kartesischen Koordinaten darstellen. Im System \(S\) als \((t_n(\lambda),x_n(\lambda),y_n(\lambda),z_n(\lambda))\), im System \(S’\) als \((t’_n(\lambda),x’_n(\lambda),y’_n(\lambda),z’_n(\lambda))\). Wir nehmen an, dass diese Systeme inertial sind.
Da die Weltlinien jeden beliebigen Wert der Zeitachse durchlaufen (eine Besonderheit der Zeit- gegenüber den Ortskoordinaten), lässt sich das umparametrisieren zu \((t,x_n(t),y_n(t),z_n(t))\) und analog im gestrichenen System. Die Länge des Stabes im System \(S\) ist nun einfach der geometrische Abstand der Punkte \((x_0(t),y_0(t),z_0(t))\) und \((x_N(t),y_N(t),z_N(t))\) zu einer frei wählbaren Zeit \(t\). Im System \(S’\) wählt aufgrund der Relativität der Gleichzeitigkeit die Zeit \(t’\) ein anderes Vektorpaar \((x’_0(t’),y’_0(t’),z’_0(t’))\) und \((x’_N(t’),y’_N(t’),z’_N(t’))\) aus. Der Stab hat eine andere Länge.
Der Unterschied zwischen LET und SRT ist nun, dass in der LET ein Inertialsystem als absolut gesehen wird und nur der Darstellung in diesem System Realität zugesprochen wird. In der SRT sind dagegen alle Inertialsysteme gleichwertig.
Eine Theorie, die nur dem Ruhesystem Realität zuspricht, gibt es nur in der Phantasie einiger Relativitäts-Kritiker. Es wäre eine ziemlich zerstückelte Weltsicht.
Balanus
7. Januar 2019 @ 23:26
Das ist nach wie vor auch meine Auffassung. Wir haben es mit validen Messungen zu tun, wobei es manchmal auch für Physiker überraschend ist, was bei einer gegebenen Messung herauskommt.
Zum Glück ist es ja eben nicht so, dass ein physikalisches Zentralkomitee den Physikern sagt, wie sie etwas zu interpretieren haben. Gerade im Metaphysischen haben wir durchaus unterschiedliche Auffassungen.
[[von Joachim Schulz gelöscht]]
Frau Lopez,
Sie dürfen sich hier gerne mit kurzen Beiträgen an Diskussionen beteiligen, aber für Ihre größtenteils faktenfreien Belehrungen benutzen Sie bitte ihr eigenes Blog.
@ Joachim Schulz: “Sie dürfen sich hier gerne mit kurzen Beiträgen an Diskussionen beteiligen, aber für Ihre größtenteils faktenfreien Belehrungen benutzen Sie bitte ihr eigenes Blog.”
.
OK, für interessierte Teilnehmer siehe hier meinen soeben gelöschten Kommentar.
@Joachim Schulz:
Valide Messungen sind gut. Was sind valide Messungen? Nur das Ablesen einer Zahl, oder gehört da noch ein wenig mehr zu?
Wir spannen eine Federwaage auf 100N, messen die Länge und spannen das Ganze mit einer Kette zwischen zwei festen Orten, deren Abstand zwei mal dieser Länge entspricht. Auf dieser Federwaage lesen wir nun 100N ab und wissen, das Kette und Waage mit 100N gespannt sind. Nun ersetzten wir die Kette durch eine zweite baugleiche Federwaage, die also, wenn man sie auf Länge der Kette bringt, auch 100N anzeigt. 2x100N sind 200N. Messen wir jetzt 200N? Das ist doch der Betrag, den wir zusammen ablesen, oder nicht?
Da wir gerade so schön bei Spannung waren, nehmen wir nun zwei identische Widerstände und schließen sie in Reihe an 200mV. Einzeln über den Widerständen messen wir nur 100mV und kommen somit wieder auf die 200mV. Es ist also durchaus legitim, Messergebnisse z.B. zusammenzuzählen.
Nun wissen wir aber, dass zwischen den zwei Orten nur 100N wirken, womit das Messergebnis “falsch” wäre, ebenso wie wir wissen, dass die zusammengezählten Einzelspannungen die Spannung der Quelle liefern. Was fehlt denn nun zu dieser Erkenntnis? Nicht etwa eine Vorschrift, wie man Messungen zu interpretieren hat? Deswegen gelten auch bei Messungen von bewegten Strecken Vorschriften, die sagen, wie man damit umzugehen hat. Wenn man also bewegt eine Strecke kürzer misst, als sie ruhend ist, muss sie per Faktor korrigiert werden, damit die Messung valide ist.
Leider gibt es bisher keine Messvorschrift, die uns sagt, dass das Interferenzmuster radial zur Lichtlaufstrecke nichts mit Phasenverschiebungen entlang der Lichtlaufstrecke zu tun hat. Man geht davon aus, dass diese Interferenzen zusammenhängen und erwartet deswegen Änderungen im radialen Interferenzmuster bei Michelson Morley, welche aber niemals auftauchen, solange die Armlängen unverändert bleiben. Die radialen Interferenzmuster ändern sich auch bei rotierenden MM-Interferometern nicht, was aber in den Abschnitten zwischen senkrecht und parallel des einen und parallel und senkrecht anderen Arms passieren müsste, wenn man von Längenkontraktion ausgeht.
Fazit: Phasenverschiebungen parallel zur Lichtlaufstrecke beeinflussen das Interferenzmuster radial zur Lichtlaufstrecke nicht, solange die Lichtlaufstrecken unverändert lang bleiben.
Bitte, Nicht von Bedeutung,
wie oft sollen wir denn das “Nein, Doch, Nein, Doch”-Spiel noch spielen?
Die Änderungen bei rotierendem Interferometer müssten auftreten, wenn sich die Erde im Äther bewegt und keine Längenkontraktion diese Laufzeiteffekte ausgleicht. Dass Sie das nicht glauben, haben wir zur Kenntnis genommen. Ich werde jede weitere Wiederholung derselben Behauptung löschen.
1. Länge senkrechter Arm:
\( s_S=2L\gamma \)
2. Länge paralleler Arm:
\( s_P=L\gamma^2+\frac{L}{\gamma^2} \)
Für \( v=0 \) ergibt sich \( \gamma=1 \) und daraus \( s_S=s_P \) sowohl bei Drehungen in 90°-Schritten als auch bei kontinuierlicher Rotation. Die Annahme einer LK ist in keinem Falle nötig. Für \( v \neq 0 \) ergibt sich \( \gamma>1 \) und daraus \( s_S>s_P \). Bei Drehungen in 90°-Schritten wechseln sich die Arme theoretisch in den Längen ab und die starren Interferenzmuster könnten mit LK erklärt werden. Bei einer konstanten Rotation jedoch müsste sich, sofern LK eine gültige Erklärung ist, der Wechsel der Längen in wandernden Interferenzmustern äußern, was aber nicht geschieht. Ergo ist LK keine gültige Erklärung. Können Sie mir folgen?
@Joachim Schulz:
Wem sagen Sie das? Aber erstens habe ich bereits mit Worten versucht, hier etwas darzulegen und nicht bloß zu behaupten und zweitens sehen Physiker Hypothesen gerne mit einer Formel untermauert. Die Formel ist hier auch nicht wichtig, sondern mehr die eindeutige Aussage, die dahinter steht und im Beitrag auch erklärt wird:
Bei v=0 muss LK nicht angenommen werden und v≠0 schießt die LK in den Hades, wenn man das MMI rotieren lässt. Das ist keine Behauptung mehr, sondern eine bittere Erkenntnis, die Sie schlucken müssen. Wenn Sie es nicht glauben, dann führen Sie widerlegende Experimente durch und sagen Sie bescheid, wenn das schwierig wird.
@NvB.
.
Aus Deinen Beiträgen wird es keine neuen Erkenntnisse gegeben, zumindest nicht physikalischer Natur. Und warum ist es nun Joachims LK? Und warum damit durchkommen?
.
.
.
Nette Drohung, Du gibst nun vor, was Joachim hier löschen muss? Beiträge die Dich stören “könnten” sind zu löschen? Spannend … 😀
.
.
Hartmut, natürlich hast Du nur Behauptungen, wie die wo Du erklärst, die Lichtgeschwindigkeit wurde gegenüber dem Raum und/oder dem Vakuum gemessen.
.
Oder das mit Deinem Zug-Meter. Oder das mit den Federwaagen. Oder das Lustige mit Deinen radialen und parallelen Polarisationen. Dazu wird wohl nur noch der Kopf auf den Schreibtisch geschlagen.
.
Problem ist weiterhin, Du verstehst all die Dinge nicht mal im Ansatz, welche verstanden werden müssen, um das mit das mit dem Michelson-Morley-Experiment richtig verstehen zu können.
.
Hartmut, ernsthaft, Du glaubst wirklich von Dir, Du hast die “Erkenntnis” geliefert, die Lorentzkontraktion gibt es nicht, die SRT wäre also falsch? Dann bist Du ja wirklich mit Zarathustra fast auf Augenhöhe, auf diese Höhe willst Du je eh immer mit allen sein. Oder höher.
.
Und Joachim muss nun echt diese “bittere Erkenntnis” schlucken?
.
Und er soll nun für Dich Experimente dazu machen? Um Deinen Unfug zu widerlegen?
.
Zum Glück kenne ich Joachim und er hat ja Humor. 😀
Nicht von Bedeutung
8. Januar 2019 @ 13:27
Die Längenkontraktion wurde doch erst postuliert, weil man bei einem rotierenden Michelson-Interferometer nicht die periodische Änderung des Beugungsmusters fand, die aufgrund der oben berechneten Laufzeitunterschiede im “Ätherwind” zu erwarten war. Ihre Behauptung, gerade das Experiment, das erstmals durch Längenkontraktion erklärt wurde, würde diese wiederlegen, ist einfach albern und bräuchte schon etwas mehr Substanz, wenn ich sie ernst nehmen soll.
@Joachim Schulz:
Das ist falsch. Die Längenkontraktion wurde nicht für ein rorierendes MMI postuliert, sondern nur für ein in 90°-Winkeln gedrehtes. In 90°-Winkeln tauschen parallerer und senkrechter Arm nur die Plätze, nicht aber die Streckenverhältnisse, die auf diesen Strecken gelten. Daraus folgt, dass der zuvor längere Arm nun der kürzere ist und vice versa. Daraus folgt weiter, dass sich bei allen Winkeln dazwischen im Interferenzmuster zeigen muss, wie sich der kürzere Arm verlängert und der längere verkürzt. Passiert aber nicht – schauen Sie sich den Grusenick-Film noch mal an.
Fazit: Entweder das MMI ruht im Äther oder der Äther ist nicht vorhanden. In beiden Fällen wird eine LK nicht benötigt. Ein bewegtes MMI zeigt nicht bloß in 90°-Steps ein starres Interferenzmuster, sondern bei jedem anderen Winkel relativ zur Bewegung (im Äther oder im Vakuum) auch. Ergo fällt LK hier aus und das radiale Interferenzmuster ist von “parallelen” Phasenverschiebungen unabhängig.
Sie müssen mit dieser Substanz klar kommen, wenn ich Sie noch ernst nehmen soll.
Sie müssen mich nicht ernst nehmen. Aber bitte lesen Sie die Veröffentlichung von Michelson und Morley. Was glauben Sie denn, wie man zwei Arme tauschen soll, ohne sie zu drehen? Michelson und Morley haben ihr Interferometer auf Quecksilber schwimmend aufgebaut und die Interferenzmuster beobachtet, während sie das Gerät gedreht haben. Dabei haben sie überraschender Weise ein Null-Resultat bekommen. Das wurde dann durch Längenkontraktion erklärt.
Die Erde bewegt sich immer relativ zum Fixsternhimmel. Dieses System wurde damals als Ruhesystem des Äthers betrachtet. Eine ruhende Erde im Zentrum des Universums (v=0) war lange wiederlegt und die Interpretation, nach der es keinen Äther braucht, ist die SRT.
@Joachim Schulz:
Am Ende erzählen Sie mir auch noch, dass sowohl die Arme als auch die Wellenlängen des Lasers darin entsprechend mitkontrahieren, oder wie? Wo bleibt dann c=invariant? Sie wissen schon, dass man auf die Art dann auch bei der Formel der Korpuskel-Theorie hätte bleiben können?
Und wenn Michelson und Morley ihr Interferometer bereits haben rotieren lassen, wieso gibt es dann keine Rechnungen mit Zwischenwinkeln, sondern nur parallel und senkrecht?
Ob sich das Interferometer nun relativ zu einem Äther oder relativ zu sonstwas bewegt, ist vollkommen uninteressant. Fakt ist, dass man, sobald es sich bewegt, nach traditionellen Theorien außer Korpuskel-Theorie die LK benötigt, obgleich diese hochgradig irrational ist. Wobei… in der Äthertheorie wäre sie ja noch angebracht, weil der “Ätherdruck” die Strecken verformt, aber in der SRT? Nein, man kann die LK nicht ernst nehmen und eigentlich auch niemanden, der es tut.
@NvB 15:37 Man braucht in der SRT die LK nicht, um MM=0 zu erklären, es geht auch mit Mathe.
Aber die “Erklärung” soll doch erst noch kommen, greifen wir nicht vor, aber sonst ist die LK da.
@Senf:
Okay, für solche wirren Sätze reicht mein Verstand nun auch nicht aus. MM=0? Was soll das sein? Nullresultat bei v ungleich 0?
Es geht btw. nur mit Mathe und dabei kommt man darauf, dass sich einer der beiden Arme verkürzen muss, wenn KT nicht gilt, womit man auf LK kommt, weil sich das radiale Interferenzmuster bei v ungleich 0 wider Erwarten nicht ändert. Und welche Erklärung, die nicht schon im Blog-Beitrag steht, soll nun noch kommen?
@Joachim / 8. Januar 2019 @ 03:17
Zur raumzeitlichen Modellierung eines Stabes interessieren doch keine Atome, sondern nur diejenigen seiner Eigenschaften, die auch Einstein 1905 schon interessiert haben. In der Minkowski-Geometrie wird so ein idealisierter Stab dann tatsächlich repräsentiert durch einen raumartigen 4-Vektor. Damit lässt sich die Minkowski-invariante Eigenlänge des Stabes definieren, seine `proper length’, über die Minkowski-Norm dieses Vektors. Diese Grösse korrespondiert dann mit der Länge des Stabes in SI-Metern, denn die SI-Einheiten sind im relativist. Kontext als `proper units’ zu verstehen. Und ein inertialer Stab ändert seine physikal. messbare Länge ja nicht, wenn er etwa statt in seinem Ruhesystem S’ in einem relativ dazu bewegten Inertialsystem S dargestellt wird.
Mir ist schon völlig klar, welche Betrachtungen über die Endpunkte des in S bewegten Stabes suggerieren, dieser sei doch S-gleichzeitg zu jeder S-Zeit \(t\) dargestellt durch
\[
t(\vec{e}_t + \beta\vec{e}_x) + \gamma^{-1}\vec{e}_x \quad\text{anstatt}\quad t(\vec{e}_t + \beta\vec{e}_x) + \vec{e}_{x’}
\]
mit einem längenkontrahierten Richtungsvektor. Nur wird damit u.a. gerade die Eigenlänge mit dem Faktor \(1/\gamma\) verkürzt, d.h., man macht letztlich wieder genau das nach, was Lorentz in der LET vorgemacht hat. Da jedoch die Eigenlänge des Stabes in der SRT eine Invariante ist, muss sie in allen Bezugssytemen gleich sein. Wer also hier für die SRT mit der Stablänge so argumentiert wie Lorentz für die LET, macht garantiert etwas falsch.
Einen dringenden Klärungsbedarf hätte ich also unbedingt bei der Frage, wie denn die `proper length’ eines Stabes ohne den geometrischen Bezug auf einen 4-Vektor definiert sein soll?
@Balanus / 7. Januar 2019 @ 23:26
Ja, das s bei Penrose bezeichnet die Eigenzeit, wie sich aus dem vorhergehenden Kontext erschliessen lässt.
»Demnach wird die Uhr im Flugzeug zwischen den Ereignissen Abflug und Landung ein kürzeres Zeitintervall „erfahren“ als die baugleiche stationäre Uhr am Boden und somit auch entsprechend weniger SI-Sekunden anzeigen als ihr unbewegter Counterpart.«
Im Prinzip richtig, nur war’s beim Maryland-Experiment gerade umgekehrt, und die Uhr im Flugzeug hat die längere Zeitspanne zwischen Abflug und Landung gemessen als die am Boden verbliebene Uhr.
»Wie kann das überhaupt sein? Was passiert da physikalisch in der Luft im kreisenden Flugzeug?«
Mir scheint, Du suchst nach einer Ursache von der Art eines “Wirkmechanismus”, doch so etwas gibt es hier nicht. Indessen gibt es einen Grund für die festgestellte Differenz, nämlich die bezüglich der Raumzeit-Geometrie unterschiedliche Länge der zeitartigen Wege (Weltlinien), auf denen sich die beiden Uhren zwischen den Ereignissen Abflug und Landung durch die Raumzeit bewegt haben. Nicht etwa die “Gang-Geschwindigkeit” der Uhren macht den Unterschied aus, denn die ist für beide Uhren gleich. Einzig die jeweils zwischen Abflug und Landung absolvierte zeitartige Weglänge ist für die resultierende Zeitdifferenz massgeblich.
@Chrys:
Ach nein? Was macht den Mainstream in dieser Hinsicht so sicher? Warum wird das Postulat der LK nicht bei der Periodendauer, die immernoch das zeitliche Pendant einer räumlichen Wellenlänge ist und die zur Definition einer Zeitspanne herangezogen wird mit welcher widerum eine Länge definiert wird, nicht angewendet? Wieso ist die Dauer dieser Periodendauer “nachweislich” egal, wo es doch genau nur diese Wellenlänge ist, die per Definition alle anderen Strecken beeinflusst?
Die veränderte Wellenlänge/Periodendauer ändert die Gangrate der Uhren und das ist ein physikalischer Wirkmechanismus und obenfrein auch noch ein extrem logischer, der ganz ohne Raumzeit auskommt.
@NvB 17:04 “… dass sich einer der beiden Arme verkürzen muss, …”
bei MM ist die Lichtquelle mit dem Interferometer verbunden, also v=0 immer, Äther mit “v” ist nicht.
@NvB 20:53 “… wo es doch genau nur diese Wellenlänge ist, …”
Uhren messen aber keine Wellenlängen, insbesondere wenn keine Wellen da sind.
Balanus schrieb (7. Januar 2019 @ 23:26):
> […] „Abstand“ bedeutet bei Penrose ja soviel wie „erfahrene Zeit“ oder „Eigenzeit“.
Sicher nicht, denn unter “Abstand” wird üblicherweise ein Maß (einer gegebenen Menge) verstanden, und nicht etwa “diese betreffende Menge an sich”; und natürlich erst recht nicht “nur ein (mehr oder weniger bestimmtes) Element dieser Menge”, die sich durch Einsteins Setzung ergibt
Es geht auch bei Penrose also sicherlich eher jeweils um die Dauer der “erlebten Zeit” eines bestimmten Beteiligten; üblicherweise symbolisiert durch den Buchstaben “\(\tau\)” usw. …
> Demnach wird die Uhr im Flugzeug zwischen den Ereignissen Abflug und Landung ein kürzeres Zeitintervall „erfahren“
… hinsichtlich des Maryland-Experiments richtigerweise stattdessen: “längeres Zeitintervall „erfahren“ …
… bzw. “größere/längere Dauer erleben” …
> als die baugleiche stationäre Uhr am Boden
Die Ungleichheit der beiden beschriebenen Dauern ist dabei natürlich ganz unabhängig davon, ob die betreffenden Uhren dabei “baugleich” gewesen und geblieben wäre, bzw. ob die betreffenden Uhren dabei gleiche Gangraten gehabt und behalten hätten, oder in wie fern nicht.
> und somit auch entsprechend weniger [bzw. mehr] SI-Sekunden anzeigen als ihr unbewegter Counterpart.
Zunächst mal: reelle Anzeige-Werte “\(t\)” usw., deren Differenzen man ausrechnen und miteinander vergleichen kann, werden nicht schlicht “angezeigt“, sondern den Anzeigen (“Zeigerstellungen” u.Ä.) jeweils eines bestimmten Beteiligten/Anzeigenden zugeordnet.
Falls die Anzeigewert-Differenzen “\(\Delta t\)” der beiden Uhren das gleich Verhältnis aufwiesen, wie die beiden o.g. entsprechenden Dauern, dann ist daraus zu schließen/messen, dass diese beiden Uhren gleich (Durchschnitts-)Gangraten hatten.
(Um zu dieser Schlussfolgerung/Messergebnis zu gelangen, wäre natürlich zunächst erforderlich, den Verhältniswert der beiden o.g. Dauern an sich zu ermitteln.)
In wie fern Anzeigenwerte bzw. deren Differenzen darüberhinaus eventuell mit “SI-Sekunden” zu tun hätten, also mit Anzahlen von hfs-Übergangs-Periodendauern von “auf 0 K bezogenen, ungestörten” Cs_133-Atomen, sprengt das Thema “Relativitätsthheorie” allerdings bei Weitem …
> Was passiert da physikalisch in der Luft im kreisenden Flugzeug?
Was “passierte” ist die geometrisch-kinematische Beziehung zwischen den beiden Uhren im Versuchsverlauf: die “im Flugzeug” kreiste “wesentlich mehr” als die andere (“im Hangar”), und dabei außerdem wesentlich höher.
Und “wie kann es sein”, dass Gleichheit oder Ungleichheit der o.g. Dauern damit zusammenhängt? — Das ist durch (die Anwendung der) Messdefinition der RT begründet, was überhaupt mit “Dauer” als Messgröße gemeint ist, also insbesondere, wie die o.g. Dauern überhaupt miteinander verglichen werden sollen.
(Andere, frühere eventuelle Bestrebungen, “Dauer” als Messgröße zu definieren, sind ja schlicht gar nicht nachvollziehbar.)
Joachim Schulz schrieb (8. Januar 2019 @ 03:17):
> Ein physikalischer Stab ist […] eine Menge von Atomen
> […] das Atom der Spitze […] das des Endes […]
Diese Beschreibung mag konkret z.B. auf einen monoatomaren Draht zutreffen;
allgemein(er) ist ein physi(kali)scher Stab insbesondere durch zwei identifizierbare, unterscheidbare, voneinander getrennte materielle Beteiligte (seine beiden sogenannten “Enden” bzw. “Endpunkte”) bestimmt.
> Eine Theorie, die nur dem Ruhesystem Realität zuspricht […]
Aha! — diese beiden Enden eines bestimmten, in Betracht gezogenen Stabes, sollen offenbar:
– gegenüber einander ruhen (zumindest in gewisser Näherung, sofern sich diese geometrische Beziehung z.B. zwei bestimmten Atomen überhaupt zuschreiben lässt), und sie sollen
– gemeinsam zu einem bestimmten Inertialsystem gehören (zumindest in gewisser Näherung, sofern sich diese geometrische Beziehung z.B. zwei bestimmten Atomen überhaupt zuschreiben lässt), nämlich ihrem (gemeinsamen) Ruhesystem, und sie sollen
– weder gemeinsam noch einzeln zu irgendwelchen anderen Inertialsystemen gehören; denen (natürlich) ebenfalls dahingehend “Realität zuzuspechen” ist, dass deren jeweilige Mitglieder jedenfalls denkbar sind und ggf. sogar aufgefunden werden mögen.
> Die Länge des Stabes im System \(S\) ist nun einfach der geometrische Abstand der Punkte […]
Entweder handelt es sich bei diesen genannten (zwei) “Punkten im System \(S\)” ganz konkret um die beiden Endpunkte des betrachteten Stabes. Dann ist zwangsläufig das “System \(S\)” ganz konkret das (gemeinsame) Ruhesystem dieser beiden Enden, und “der geometrische Abstand” dieser beiden schlicht die (eigentliche) Länge des Stabes.
Oder es handelt sich bei den o.g. beiden “Punkten im System \(S\)” ansonsten eben ausdrücklich nicht um die beiden Endpunkte des betrachteten Stabes.
Dann ist es improper, den “geometrischen Abstand dieser beiden Punkte im System \(S\)” als “die Länge des betrachteten Stabes” anzusprechen;
sondern es handelt sich stattdessen um die Länge eines anderen Stabes, nämlich stattdessen des Stabes, dessen beide Enden konkret die o.g. beiden “Punkten im System \(S\)” sind.
(Ob die Länge des einen Stabes und die Länge des anderen Stabes gleich sind, oder ob diese beiden unterscheidbaren Längen ungleich sind, und welches reell-wertige Verhältnis sie zueinander haben, lässt sich bekanntlich messen.)
Herr Wappler,
auch für Sie gilt: Fassen Sie sich kurz und nehmen Sie zu dem Diskussionspunkt stellung, dem Sie widersprechen. Ständige Wiederholungen ihrer koordinatenfreien Physik langweilen mich. Ich werde sie in Zukunft löschen.
Nein, ein Stab, der aus Atomen besteht, ist nicht zwingend Monoatomar dünn. Und es gibt immer mindestens ein Atom an der Spitze und eins am Ende.
@Chrys
8. Januar 2019 @ 17:11
Das ist sehr einfach: Die ‘proper length’ des Stabes ist der extremale Abstand zwischen den Weltlinien \(r_0(\lambda)\) und \(r_N(\lambda)\). Da diese beiden Weltlinien für einen unbeschleunigten, stationären Stab Geraden sind, ist dieser Abstand wohl definiert und zeitlich konstant. Er ist identisch mit der Ping-Distanz zwischen diesen beiden Atomen.
Übrigens ist jeder Vierer-Abstand zwischen Endpunkten mit beliebig definierter Gleichzeitigkeit, \(|r_0(\lambda_1)\)-\(r_N(\lambda_2)|\), Lorentz-Invariant. Nicht nur die ‘proper-length’. Jeder hinreichend gut definierter Messwert ist invariant.
@Joachim Schulz:
Was ist? Entspricht v=0 beim MM-Experiment auch Ihren Vorstellungen? Dann wars das wohl mit experimentellem Befund der LK durch das MM-Experiment, denn bei v=0 wird keine LK benötigt. Ansonsten, wo ist mein Beitrag mit der entsprechenden Entgegnung gegenüber Senfs Aussage vom 8.1.2019 um 22:23? Wo ist Ihre Stellungnahme dazu?
Und seit wann gehören Wellenlängen bzw. Periodendauern nicht mehr zur Definition einer Sekunde? Uhren messen nun mal nicht, sie zählen und zwar Wellenlängen bzw. Periodendauern, die sehr wahrscheinlich unter gegebenen Umständen unterschiedlich lang sind bzw. unterschiedlich lange dauern. Wo also ist mein Beitrag mit der entsprechenden Entgegnung gegenüber Senfs Aussage vom 8.1.2019 um 22:23? Wo ist ihre Stellungnahme dazu?
Ach, Sie sehen keinen Unterschied zwischen meinem “Nein falsch” und Krügers? Nun, meine “Nein falsch” liefern Argumente und nicht bloß ein “das ist so, weil RT”.
Außerdem:
Funktioniert ja gar nicht, weil sich Strecken von Gegenständen nun mal nicht durch Bewegung physikalisch ändern. Wenn also eine Uhr durch Bewegung langsamer geht als eine Andere misst man damit allenfalls unterschiedlich lange dauernde Periodendauern bzw. unterschiedlich lange Wellenlängen und nur solche ändern sich, weil Doppler-Effekt. Aber die Einsicht gegenüber dieser Erkenntnis lässt vermutlich wohl noch ein Weilchen auf sich warten, obwohl man nicht mal Mathe dafür braucht. Echt unglaublich (und vor Allem äußerst ärgerlich).
@Nicht von Bedeutung
Die Definition der Sekunde ist hier nicht Thema.
v=0 relativ zu was?
Das ist der Punkt. Deshalb muss der Messwert invariant sein. Was wir messen darf nur vom Messprozess, nicht aber vom verwendeten Koordinatensystem abhängen.
Joachim Schulz schrieb (9. Januar 2019 @ 08:21):
> Herr Wappler, auch für Sie gilt: Fassen Sie sich kurz
… ich bedanke mich an dieser Stelle (trotzdem) gerne ausdrücklich für die Entsorgung meines Kommentarversuchs https://scilogs.spektrum.de/quantenwelt/der-experimentelle-befund-zur-laengenkontraktion/#comment-34816 den ich leider erst lange nach dem Absenden (im Anschluss an meine zugegebenermaßen nicht hinreichend gründlicher Nutzung der Kommentar-Vorschau) als fehlerhaft formatiert erkannte und erst etwa eine Stunde später durch https://scilogs.spektrum.de/quantenwelt/der-experimentelle-befund-zur-laengenkontraktion/#comment-34818 korrigierte …
> und nehmen Sie zu dem Diskussionspunkt stellung, dem Sie widersprechen.
Darum bemühe ich mich immer. Um aber eventuellen Zweifeln oder (impliziten) Nachfragen bezüglich des genannten Kommentars zu begegnen, ergänze ich gerne noch die (vermeintlich) “offensichtliche Pointe”, die ich oben (der Kürze halber) weggelassen hatte:
Joachim Schulz schrieb (8. Januar 2019 @ 03:17):
> […] Der Stab hat eine andere Länge.
Falls zwei Längen-Werte in Betracht stehen, die nicht gleich sind, sondern ungleich bzw. “einer anders als der andere”,
dann handelt es sich zwangsläufig um Längen-Werte verschiedener Stäbe;
es sei denn der Begriff “Länge” wäre nicht im Sinne einer nachvollziehbaren Messgröße gemeint, sondern improper.
> Ständige Wiederholungen ihrer koordinatenfreien Physik langweilen mich. Ich werde sie in Zukunft löschen.
Ich bleibe (trotzdem) einigermaßen gespannt, welche bzw. wessen Äußerungen hinsichtlich Physik nicht langweilen;
und setze dahingehend weiterhin auch gewisse Erwartungen in Chrys’ ggf. wiederholte Frage zu “`proper length’ eines Stabes ohne den geometrischen Bezug auf einen 4-Vektor“.
Falls meine Beiträge zur (selbstverständlich in erster Linie Koordinaten-freien) Physik in diesem SciLog aus Langeweile gelöscht werden sollten, bliebe (mir) ein SciLog zu finden, in dem (meine) Beiträge zur (selbstverständlich in erster Linie Koordinaten-freien) Physik hinreichend weniger langweilen …
p.s.
> Nein, ein Stab, der aus Atomen besteht, ist nicht zwingend Monoatomar dünn.
Warum “Nein” ??
Ich stimme der Aussage: “Ein Stab, der aus Atomen besteht, ist nicht zwingend monoatomar dünn. ” jedenfalls zu, finde sie völlig kompatibel zu den Aussagen meines obigen Kommentars, und bitte (wie immer) um konkrete Zitate, falls diesbezüglich irgendwelche Zweifel oder (ggf. implizite) Nachfragen bestehen.
> Und es gibt immer mindestens ein Atom an der Spitze und eins am Ende.
Dieser Auffassung entspräche (meines Erachtens) weniger die Formulierung (Joachim Schulz, 8. Januar 2019 @ 03:17; Betonung und Zitat-Auswahl FW): “das Atom der Spitze [… und] das des Endes“,
sondern eher die Formulierung: “ein Atom der Spitze [… und] eines des Endes”.
@Joachim Schulz:
Ist die Frage ernst gemeint? Relativ bzw. differenziert zum Licht natürlich. Wieso sonst der ganze Umstand mit c±v in den Rechnungen? Wie sonst sollte man auf die LK kommen? Das funktioniert bei v=0 nämlich gar nicht. Wussten Sie das nicht?
Messwerte von Strecken sind aber nun mal nicht invariant, wenn man Strecken per Lichtlaufzeiten, Radar oder sonstigem misst. Das liegt aber stets am Gang der eigenen Uhr – an der Eigenzeit. Über fest und von unabhängig definierte Strecken könnte man jedoch den Gang der eigenen Uhr ermitteln und die einzigen Strecken, die dann noch invariant gemessen werden, sind Wellenlängen – z.B. auch jene, die das Pendant… Mensch das kennen Sie doch schon, oder?
Herr Senf
23. Dezember 2018 @ 12:14
“Herr Storz, begreifen Sie nicht, daß es Grundsatz der Relativitätstheorie ist, alles mit gleichen Standards zu messen? Die Physik kann doch nichts dafür, daß die Natur es so eingerichtet hat, daß Messungen vom Standpunkt des Beobachters abhängig sind. Um die “Erscheinungen” korrekt zu untersuchen und zu erklären, muß man sich auf einen Referenzstandpunkt einigen, der für alle zum gleichen Ergebnis führt.”
Noch ein Versuch, da so etwas Inkonsistentes doch nicht stehen bleiben kann:
a) haben Sie endlich begriffen, dass wenn es Längenkontraktion gäbe, die Maßstäbe, Meterstäbe, Skalen des bewegten Beobachters, wie alle anderen Längen und Distanzen für den bewegten Beobachter auch, kontrahiert sein müssten (vom ruhenden Beobachter aus gesehen!)?
b) dass es dann keinen “Referenzstandpunkt” geben kann ist doch völlig klar: für den bewegten Beobachter müssen alle Längen und Distanzen mit dessen Maßstab gemessen werden. Sonst haben die Messungen für diesen keinerlei Relevanz.
c) Wenn es für einen Beobachter scheinbar kontrahierte Längen und Distanzen gäbe, gäbe es eben keinen Beobachter an einem “Referenzstandpunkt” dessen Messungen “für alle zum gleichen Ergebnis führt”.
d) Wenn es kontrahierte Längen und damit unterschiedliche Maßstäbe gäbe, müsste jede Messung für einen Beobachter mit dessen individuellem Maßstab durchgeführt werden (oder in dessen Maßstab umgerechnet werden) – sonst wäre die Messung für diesen Beobachter unsinnig.
Hier noch einmal die korrekte Vorgehensweise für solche Messungen, analog zu Messungen bei perspektivischer Verzerrung:
Man misst die Länge eines Einheitsmeters beim beobachteten Objekt (in der gleichen Entfernung) und korrigiert seine eigene Messung mit dem gewonnenen Proportionalitätsfaktor “Länge eigener Einheitsmeter / scheinbare Länge beobachteter Einheitsmeter”.
Wenn man die scheinbare Größe eines in der Ferne stehenden Menschen misst, und die scheinbare Länge eines Einheitsmeters dort, errechnet man unschwer die tatsächliche Größe des Menschen.
Analog ist bei bewegten Objekten zu verfahren. Dort ist nur eben ein mitbewegter Einheitsmeter zu vermessen.
@Joachim / 9. Januar 2019 @ 08:32
Ping-Distanz ist stets mit einer Koordinaten-Uhr zu messen, das Lichtsignal kann schliessliche keine Uhr auf den Roundtrip mitnehmen. Ping-Distanz zwischen den Stabenden ist die Radar-Lange des Stabes und hängt von der relativen Geschw. v zwischen Stab und Uhr ab. Das ist ganz gewiss keine Invariante.
»Übrigens ist jeder Vierer-Abstand zwischen Endpunkten mit beliebig definierter Gleichzeitigkeit, |r0(λ1)-rN(λ2)|, Lorentz-Invariant.«
Und zu je zwei raumartig getrennten Punkten \(P, Q\) in einem affinen Punktraum über dem Minkowskischen Vektorraum \(\mathbb{M} = (\mathbb{R}^{1,3},g)\) existiert auch ein Stab mit der Eigenschaft, dass der raumartige 4-Vektor \(Q – P = \vec{PQ} \in \mathbb{M}\) ein Differenzvektor zwischen den Endpunkten des Stabes ist. Der (reelle) Abstand zwischen \(P\) und \(Q\) ist gegeben durch
\[
|PQ| = \Im\,\|\vec{PQ}\|_g
\]
und folglich eine Minkowski-Invariante; sie ist die `proper length’ des durch \(P\) und \(Q\) charakterisierten* Stabes. Die Eigenlänge eines Stabes lässt sich insbesondere definieren, ohne dass man hierzu Koordinaten einführen müsste.
*Charakterisiert im betonten Unterschied zu repräsentiert, nur um allfälligen Missverständnissen vorzugreifen. Das Punktepaar beschreibt den Stab nur modulo einer parametrisierten Schar von Translationen des Punktraumes.
@Chrys
Nur eine Frage der Definition. Ich verstehe unter einer Ping-Distanz die halbe Roundtrip-Zeit eines Lichtstrahls zwischen den Punkten gemessen in Eigenzeit und geteilt durch Lichtgeschwindigkeit. Misst man das in Koordinatenzeit für bewegte Punkte, kommt kein Abstand heraus, sondern das, was ich in diesem Artikel gerechnet habe: \(\gamma^2 L\) für parallele, \(\gamma L\) für Senkrechte Bewegung. Den Laufzeiteffekt kann man aber selbstverständlich herauskorrigieren.
Ansonsten reden wir aneinander vorbei, weil ich unter einem Stab ein materielles Objekt verstehe, während sie Offenbar ein mathematisches Objekt in einem Vektorraum sehen. In meinen Augen ist ein Raumzeitpunkt ein Ereignis. Eine Punktmasse muss durch eine Weltlinie dargestellt werden und nicht durch einen einzelnen Vektor. Das ist im 3D-Raum anders. Da wird der Ort einer Punktmasse durch einen Vektor definiert.
@Chrys // 8. Januar 2019 @ 18:08
»Im Prinzip richtig, nur war’s beim Maryland-Experiment gerade umgekehrt, und die Uhr im Flugzeug hat die längere Zeitspanne zwischen Abflug und Landung gemessen als die am Boden verbliebene Uhr.«
Wegen der Gravitation, schon klar, aber mir ging es hier um die bewegte Uhr im Vergleich zur unbewegten (bei stets gleichem bzw. normalisiertem Gravitationspotential).
Und ich suche auch nicht nach einer Art „Wirkmechanismus“, sondern nach einer physikalischen Erklärung für das Ergebnis eines physikalischen Experiments, bei dem eine bestimmte „geometrisch-kinematische Beziehung“ (Wappler) zwischen zwei Uhren hergestellt wird (eine bewegt, eine unbewegt).
Es ist doch höchst erstaunlich, dass zwischen zwei Ereignissen gerade dann weniger Zeit vergeht, wenn man sich zwischenzeitlich schnell bewegt (und nicht in Ruhe abwartet).
Oder anders formuliert: ich frage nach dem Grund, warum die Raumzeit-Geometrie mit ihren ‚Weltlinien‘ gerade so und nicht anders aussieht.
Meine Vermutung wäre, dass es hierfür keinen besonderen Grund gibt, so wenig wie es einen besonderen Grund für die Grenzgeschwindigkeit der elektromagnetischen Strahlung gibt. Wir haben es hier schlicht und einfach mit fundamentalen Eigenschaften der „Natur“ (des Universums) zu tun, die sich eben auf die bekannte Weise beschreiben lassen.
Chrys schrieb (9. Januar 2019 @ 12:01):
> Ping-Distanz ist […] ganz gewiss keine Invariante.
Als einer, der schon von “(jemandes) Ping (bzgl. jemand anderem)” und von “(jemandes) Ping-Dauer (bzgl. jemand anderem)” und (sofern diese beiden Beteiligten gegenüber einander ruhten) von der (chronometrischen) Distanz dieser beiden voneinander als “c/2 Ping-Dauer” geschrieben hat, als Barriere-freies öffentliches Korrespondieren noch in Usenet-Gruppen möglich gewesen sein mag, möchte ich darauf hinweisen,
dass der “Ping”-Begriff historisch mit dem sogenannten “aktiven Sonar” verbunden ist und insbesondere bedeutet, dass dabei
– derjenige Beteiligte, der eine bestimmte Signalanzeige dargestellt hatte, und
– derjenige Beteiligte, der seine (allererste) Wahrnehmung des (allerersten) Echos eines bestimmten bzw. identifizierbaren anderen bzgl. dieser Signalanzeige anzeigte
ein-und-der-Selbe Beteiligte sein soll;
in diesem Bild: https://de.wikipedia.org/wiki/Datei:Sonar_Principle_DE.svg insbesondere als “Sender/Empfänger” bezeichnet.
p.s.
> […] Und zu je zwei raumartig getrennten Punkten \(P, Q\) in einem affinen Punktraum über dem Minkowskischen Vektorraum \(\mathbb M = (\mathbb R^{1, 3} , g) \) existiert auch ein Stab mit der Eigenschaft, dass der raumartige 4-Vektor \(Q – P = \vec{PQ} \in \mathbb M \) […]
Die Menge \(\mathbb R^{1, 3}\) tritt hier wohl in doppeltem Sinne einerseits als “Punkt“-Menge und andererseits als “4-Vektor“-Menge auf (?).
(Ich finde allerdings Fragen interessanter, die ganz ohne Bezug auf (einen oder mehrere) 4-Vektoren gestellt und beantwortet werden könnten. … &)
p.p.s.
> […] Das Punktepaar beschreibt den Stab nur modulo einer parametrisierten Schar von Translationen des Punktraumes.
Beschreibt jedes raumartig getrennte Punktepaar, das aus dem einen (anfänglich betrachteten) bestimmten Paar \(P, Q\) durch eine “Translation des Punktraumes” hervorginge, gleichmaßen den selben Stab “modulo einer parametrisierten Schar von Translationen des Punktraumes” ?
Oder bestehen diebezüglich eventuelle Ambiguitäten ?? …
p.p.p.s.
Joachim Schulz (9. Januar 2019 @ 08:32) erwähnte im selben Zusammhang den “extremalen Abstand zwischen den Weltlinien“, was übrigens durchaus (auch) ohne Bezug auf einen oder mehrere 4-Vektoren relevant und diskutabel sein mag.
Von “Extrema” ist wiederum (ausschließlich?) im Zusammenhang mit geordneten Mengen bzw. deren (ebenfalls geordneten) Teilmengen die Rede, wie zum (typischen) Beispiel der Menge der reellen Zahlen, \(\mathbb R\).
@Joachim / 9. Januar 2019 @ 12:32
»Ich verstehe unter einer Ping-Distanz die halbe Roundtrip-Zeit eines Lichtstrahls zwischen den Punkten gemessen in Eigenzeit …«
Wessen Eigenzeit?
In jedem Inertialsytem S wird schliesslich die S-Koordinatenzeit durch die Eigenzeit einer in S ruhenden Uhr etabliert. Die Roundtrip-Dauer wird also in jedem Fall als eine Messung von Eigenzeit ermittelt, egal ob der Stab in S bewegt ist oder nicht.
Der Kontext lässt jedoch vermuten, dass hier mit `Eigenzeit’ präziser die Koordinatenzeit des Ruhesystems S’ des Stabes (oder sonstigen zu vermessenden Gegenstandes) gemeint war? Dass in S’ die Eigenlänge dann gerade als Ergebnis einer Radar-Messung herauskommt und insofern dem Ruhesystem eine gesonderte Rolle zufällt, hatte ich am 7. Januar 2019 @ 12:22 ja bereits angemerkt — freilich nachdem mir, wie wir nicht ganz vergessen wollen, eine Fixierung auf Ruhelängen und -zeiten vorgeworfen worden war…
Zwar sind `Ruhelänge’ und `Eigenlänge’ quantitativ als numerische Werte gleich, doch die Begriffe sind qualitativ ganz unterschiedlich definiert. Denn `Ruhelänge’ enthält den Bezug auf ein spezielles Koordinatensystem, während `Eigenlänge’ völlig koordinatenfrei definierbar ist.
N.B. Die Roundtrip-Dauer wächst übrigens linear mit \(\gamma(v)\) als Funktion von \(v\), nicht quadratisch. Entsprechend wächst auch die Roundtrip-Dauer bei der rotierenden Kreisscheibe mit \(gamma(\omega R)\) als Funktion der Geschw. \(\omega R\) und nicht mit dem Quadrat.
Ist es nicht schön, wie sich hier die Allianzen ändern. Nun hat Herr Wappler, den ich sonst oft kaum verstehe, genau meinen Punkt getroffen: Ping-Distanz ist auch nach meinem Empfinden eine Distanz, die der Sender quasi mit Bordausstattung ermitteln kann. Er misst die Zeit, die ein Signal braucht um zum Messobjekt und zurück zu kommen und teilt sie durch Zwei (wegen zwei Wegen) und Lichtgeschwindigkeit. Die Zeit misst er selbstverständlich in Eigenzeit.
Die definition der “proper Length” über den “extremalen Abstand” der Weltlinien ist dazu äquivalent.
@Joachim Schulz:
Ja, herrlich. Nur eine Allianz ändert sich komischerweise nicht.
Wir sind genau jetzt bei dem Punkt, an denen nur noch zeitliche Abstände (Periodendauern) Strecke machen – sowohl bei der Laufzeit des Pings als auch in der Uhr, die nach einer gewissen Anzahl an Takten wiederholt pingt.
Dadurch ändert sich nun aber die Länge eines starren Körpers (idealisiert) immer noch nicht. 111pm bleiben 111pm (Kovalenzabstand von Silizium-Atomen).
An solchen Dingen wird man also fest machen können, wie weit die lokale Uhr durch Bewegung (und/oder Gravitation, aber die lasse ich mal kurz weg) beeinflusst wird, z.B. wenn man nach etwa 31 Takten mehr als 9009009009 Silizium-Atome in lokal zugeschnittenen “Metern” zählt.
In diesem Fall gilt auch nicht mehr (unbedingt) c/2, denn Wellen bewegen in dem Umfeld, in welchem man sich vermutlich gerade selbst bewegt, isotrop, also differenziert mit c±v und daraus folgt, dass Ping-Hin und Ping-Zurück unterschiedlich lange dauern.
Sind wir jetzt noch bei der LK oder schon bei der erarbeiteten Vermutung, dass man Dank der Isotropie des Lichts doch feststellen kann, ob man sich bewegt oder nicht?
Hier helfen weder Einstein noch Lorentz oder Minkowski weiter, sondern nur eiserne Logik.
Herr Storz 11:40 ” … Analog ist bei bewegten Objekten zu verfahren. Dort ist nur eben ein mitbewegter Einheitsmeter zu vermessen. …” Was reklamieren Sie denn? Nichts anderes sagen wir doch die ganze Zeit.
Die Frage ist aber, wie man zum Ergebnis kommt, wenn der Flieger den Einheitsmeter vergessen hat.
Dann müssen Sie ins bewegte System aus der Ferne mit Licht messen und mit LoTra umrechnen.
@Senf:
Dann muss man sich im Vakuum (1bar Luftdruck wäre größtenteils zu aufwändig) bei einer gewissen Temperatur einen Silizium-Kristall ziehen und diesen auf 9009009009 Atome in einer Reihe bringen. Diese Länge ist nämlich immer gleich und damit kann man dann auch messen, wie korrekt die eigene Atomuhr geht, weil man damit auch die Periodendauer messen kann, die man bisher vollkommen außer Acht ließ.
Aber flieg du nur ins bewegte System und rechne da um was du willst und wie du willst. Gute Reise und viel Spaß.
@NvB.
.
Also Deine Behauptung ist nun aufmal eine erarbeitete Vermutung? Wer neben Dir hat da was “erarbeitet”? Und nein das kann man nicht feststellen, weil es falsch ist. Bewegung ist relativ und nicht absolut.
.
.
.
Es ist egal, wie man den SI-Meter lokal herstellt, macht man es richtig, ist es der Bahnhofs-Meter nach der k-Methode, oben der normale SI-Meter.
.
Und für den gilt natürlich, die Anzahl der Atome ändert sich nicht, heißt, wenn man die am Bahnhof auszählt und auf 9009009009 Atome in einer Reihe für den SI-Meter bringt, dann ergibt das im Zug ebenso dort den SI-Meter.
.
In der Physik gibt es den pohl’schen Meter (Zug-Meter) nicht und erstellt man lokal die SI-Sekunde im Zug und misst damit den SI-Meter aus, eben die Strecke die Licht bei v = c für 1 m benötigt, dann ist das der SI-Meter, der Bahnhofs-Meter.
Chrys schrieb (9. Januar 2019 @ 15:11):
> Zwar sind `Ruhelänge’ und `Eigenlänge’ quantitativ als numerische Werte gleich,
Längen-(Mess-)Werte sind nicht “numerisch” bzw. reell-wertig (oder gar komplex-wertig …), sondern Dimensions-behaftet; nämlich:
“längliche Werte”Werte von “räumlicher Ausdehnung”. (Danke, Herr Prof. Graßmann; das wäre soweit alles.)Reell sind dagegen die (Mess-)Werte von Längen-Verhältnissen.
> doch die Begriffe sind qualitativ ganz unterschiedlich definiert. Denn `Ruhelänge’ enthält den Bezug auf ein spezielles Koordinatensystem, während `Eigenlänge’ völlig koordinatenfrei definierbar ist.
Diese (vermeintliche) begriffliche Unterschiedung finde ich dermaßen fremd und schockierend, dass, anstatt eine diesbezügliche Frage zu formulieren, ich im Moment lediglich auf Ockhams Klinge verweisen möchte; und natürlich auch darauf, dass “ein gesonderter [SciLog-]beitrag zur Frage von Koordinaten und koordinatenfreien Darstellungen“ vor mittlerweile über zwei Jahren zwar in Aussicht gestellt, aber noch immer nicht zur öffentlichen, Barriere-freien (und hoffentlich auch \(\LaTeX\)-unterstützten) Kommentierung gegeben wurde.
Die Vorstellung, dass Kommentatorfreund(-in?) Chrys in bewährter Manier noch irgendeine obskure Monographie aus dem Hut zaubern könnte, in der diese (vermeintliche) begriffliche Unterschiedung ebenfalls gemacht (wenn nicht gar begründet) würde, lässt mich sowohl schaudern als auch bangen …
(Als ob es nicht schon fürchterlich genug wäre, was ich erst jüngst feststellen musste: dass Ratcliffe den Begriff “Lorentzian distance” ganz anders auffasst als z.B. Beem/Ehrlich/Easley … &)
p.s.
> […] bei der rotierenden Kreisscheibe […]
… ist jedenfalls dies meine Vorgabe hinsichtlich sich eventuell anbahnender Alliancen, oder Mesalliancen.
p.p.s. — Anstelle eines (kanonisch URL-formatierten) Memos:
http://Das.Wesen.eines.Experten.besteht.darin–sich.an.Regeln.zu.halten–die.er.begreift.–Das.Wesen.eines.Physikers.besteht.darin–Regeln.aufzustellen–deren.Begreiflichkeit.zugleich.jedem.zugesichert.ist–und.jedem.zugestanden.werden.muss–der.in.der.Lage.ist–sich.wie.jeden.anderen.zu.fragen–welche.Regeln.aufgestellt.werden.sollten.
@NvB 17:00 “… Silizium-Kristall ziehen und diesen auf 9009009009 Atome in einer Reihe bringen.”
Dein privater Si-Meter ist 4,8918 9189(2) mal zu lang 🙂 es reichen 1841620626 Stück.
Kann man nur beantworten mit Empfehlung von Andre Maurois “Das Schwierigste am Diskutieren ist nicht, den eigenen Standpunkt zu verteidigen, sondern ihn zu kennen.” Anm: ” zu verstehen”
@Senf:
Das ist vollkommen uninteressant, solange er eine feste Länge hat. Eure Meter erfüllen diese Eigenschaft nicht, denn die sind etwa 30,6633 Takte lang und diese Takte variieren in ihren zeitlichen Abständen. Wie dem auch sei. 1841620626 sind immernoch mehr als etwa 31. Ich kenne meinen Standpunkt – du und Krüger verstehen ihn nur nicht, was auch irgendwie kein Wunder ist.
@Senf:
Im Übrigen… Welche Gruppe verteidigt ihren Standpunkt hier eigentlich? Sicher nicht die, die mit Argumenten, die ihr nicht im Geringsten versteht, angreift. 😉
Nu NvB 20:59 “sind etwa 30,6633 Takte lang und diese Takte variieren …” was sagt λ = c/f zu 9192631770?
@Joachim Schulz // 8. Januar 2019 @ 03:29
»Zum Glück ist es ja eben nicht so, dass ein physikalisches Zentralkomitee den Physikern sagt, wie sie etwas zu interpretieren haben. Gerade im Metaphysischen haben wir durchaus unterschiedliche Auffassungen.«
Ich wäre ja schon zufrieden, wenn unter Physikern wenigstens weitestgehend Einigkeit darüber bestünde, was (noch) zur Physik und was (schon) zur Metaphysik gehört.
Wenn man z. B. nicht entscheiden kann, ob die relativistische „Längenkontraktion“ als „Gegenstück“ zur relativistischen „Zeitdehnung“ ein reales Phänomen oder bloß eine Art Scheineffekt ist, dann sollte das entsprechend kommuniziert werden (vor allem in Lehrbüchern).
In der Biologie beispielsweise herrscht (nahezu) Einigkeit darüber, dass ein Evolutionsprozess stattfindet. Uneinigkeit mag bestehen über die jeweilige Bedeutung einzelner Einflussfaktoren. Metaphysisches jedenfalls kommt meines Wissens nicht vor bzw. ist nicht Teil des Fachgebiets Biologie—so wenig wie in der Physik, vermute ich mal.
Ansonsten: Danke für die Antwort! Schön zu wissen, dass man nicht vollends mit seiner (laienhaften) Auffassung danebenliegt… 🙂
@Senf:
Und wie du auf 1841620626 kommst, erklärst du sicher noch, nicht wahr?
Herr Senf
9. Januar 2019 @ 16:51
” Was reklamieren Sie denn? Nichts anderes sagen wir doch die ganze Zeit.
Die Frage ist aber, wie man zum Ergebnis kommt, wenn der Flieger den Einheitsmeter vergessen hat.”
So, sagt IHR das die ganze Zeit? Ach, das hatte ich gar nicht bemerkt. Also haben Sie jetzt endlich verstanden, dass der “bewegte Beobachter” einen kürzeren Einheitsmeter haben müsste als der “ruhende Beobachter”?
So, und jetzt messen Sie mal die angeblich kontrahierte Distanz (ZB zwischen Erde und Proxima Centauri für ein Raumschiff mit annähernd LG von 4,24 LJ auf 0,06 LJ) mit dem auf 1/70 Meter verkürzten Einheitsmeter des “bewegten Beobachters”.
Oh, da kommt aj 4,24 LJ raus. Na sowas aber auch!
Übrigens fliegt kein Raumschiff mit “vergessenem Einheitsmeter”. Der Einheitsmeter ist in fast jedes Messgerät auf irgend eine Art und Weise implementiert.
Was man hier endlich verstehen müsste ist die Tatsache, dass für jeden Beobachter nur Messungen mit seinem eigenen Einheitsmeter gelten können. Eine für einen Beobachter valide Messung muss die Meßgröße auf der Basis des Einheitsmeters des Beobachters ausdrücken. Alle anderen Angaben wären falsch.
@Senf:
Klar… λ=(c±v)/f triffts eher, aber egal. Und dann kommt irgendwo auch noch die Gravitation da rein und dann hast du die Formel für die Periodendauer, wie sie bei der definition der SI-Sekunde verwendet werden sollte.
Und bevor du die 1841620626 erklärst… Gitterparameter brauchen wir hier nicht, weil hier nicht dotiert werden muss. 😉
Nicht von Bedeutung schrieb (9. Januar 2019 @ 17:00):
> […] im Vakuum
… gemeint ist offenbar der sogenannte “umgangssprachliche Sinn”, insbesondere “Luftdruck gleich oder nahe 0 mbar” …
> (1bar Luftdruck wäre größtenteils zu aufwändig) bei einer gewissen Temperatur
… Oh! — diese Temperatur ?? (Oder eher “jene” ? …) …
> einen Silizium-Kristall ziehen und diesen auf 9009009009 Atome in einer Reihe bringen.
Na gut: reines Zählen sollte nachvollziehbar sein.
> Diese Länge ist nämlich immer gleich
Wohl kaum falls die betreffenden Silizium-Atome (einzeln und/oder im Zusammenhang) geeignet/relevant “gestört” wären; auch obwohl sie sich im “luftdruck-technischen Vakuum” befänden, und auch obwohl ihre “Temperatur” (der noch festzulegenden “Art”) hinreichend “gewiss” wäre bzw. bliebe.
Stattdessen können und sollten Versuch zu Versuch die Längen des betreffenden Kristalls mit den rein geometrischen Messmethoden der RT gemessen bzw. verglichen werden;
und falls gefunden würde, dass diese Werte durchwegs gleich waren, also der beschriebene Kristall konstant eine bestimmte Länge hatte und behielt,
dann ließe sich zumindest schlussfolgern, dass eventuelle relevante “Störungen” im Verlaufe dieser Versuche wahrscheinlich “effektiv konstant” geblieben wären.
Merke: Aus geometrisch-kinematischen Messwerten (sogenannten “constraints”) folgert man die wahrscheinlichsten Verteilungen von dynamischen Größen (“Massen”, “Ladungen”, “Potentialen”).
(Aus diesen so ermittelten wahrscheinlichsten Verteilungen von dynamischer Größen lassen sich zwar wiederum bestimmte Erwartungen errechnen, welche constraints in folgenden Versuchen wohl gefunden werden mögen;
die damit verbundene Mathematik nennt man gewisse Varianten der Variationsrechnung.
Aber das ist offensichtlich keine Garantie gegen eventuelle “Überraschungen” bzgl. der errechneten Erwartungen.
Gewissheit hinsichtlich geometrisch-kinematischer Beziehungen/constraints, wie z.B. zur “Länge” des Kristalls und deren eventueller Variabilität, lässt sich eben nur durch ausdrückliche Messung, Versuch für Versuch, gewinnen.)
Aber dennoch muss ich ein wenig zurück rudern… 111pm ist nur der Kovalenz-Radius und demnach wäre man für einen Kovalenz-Durchmesser mit 222pm dabei – damit käme man auf 4504504505, was aber immer noch mehr als 31 ist.
@Frank Wappler:
Auf jeden Fall aber eine “Garantie” gegen die Überraschung des satten Kreisbezugs, die man durch die augenblickliche Definition von SI-Meter und SI-Sekunde erlebt. Druck, Temperatur und mögl. auch noch Geschwindigkeit lassen sich wenigstens beeinflussen. Gravitation an diversen unterschiedlichen Orten beispielsweise jedoch (noch) nicht. Das ist der entscheidende Punkt – ganz egal welchen Gitterparameter man verwendet.
Herr Storz 21:31 “Also haben Sie jetzt endlich verstanden, dass der “bewegte Beobachter” einen kürzeren Einheitsmeter haben müsste als der “ruhende Beobachter”?” Nein, hat er nicht und müßte nicht haben.
Deswegen brauchen wir die LoTra – es war eben 5 vor 12 😉 vlt wird’s besser danach.
@Senf:
Okay, in dieser Hinsicht hast du wohl gewonnen. Irgendwie ist mir die Dichteanomalie von Silizium entfallen, aber was solls – Die höchste Dichte hat Silizium (ähnlich wie Wasser) in flüssiger Form. Der Druck und Temperatur stabilste Abstand zweier Silizium-Atome im kristallinen Verband ist dann wohl doch 543pm. Allerdings ist Silizium in flüssiger Form auch nicht unbedingt das, worauf es in elektronischen Bauteilen ankommt und von daher ist mir diese Anomalie auch nicht so geläufig.
Dennoch bleibt es dabei – mein Meter hat dadurch eine feste definierte Länge im Gegensatz zum SI-Meter, der seinerseits von der Periodendauer/Wellenlänge die in der Definition der SI-Sekunde verwendet wird.
Korrektur:
der seinerseits von der Periodendauer/Wellenlänge die in der Definition der SI-Sekunde verwendet wird, abhängig ist.
Herr Senf schrieb (9. Januar 2019 @ 20:17):
> […] mit Empfehlung von Andre Maurois “Das Schwierigste am Diskutieren ist nicht, den eigenen Standpunkt zu verteidigen, sondern ihn zu kennen.”
Von André Maurois ?? (– Computer sagt: »Nein.«) …
Trotzdem: Empfehlenswert! (Und unerwartet eloquent dazu.)
(Denjenigen, die sich weniger leicht den sprichwörtlichen “Bären aufbinden”, oder “Mustard abschneiden”, oder “Tangentialraum anhängen” lassen (wollen), bleibt doch wenigstens die Empfehlung, »gnothi seauton« zu recherchieren …)
Nicht von Bedeutung schrieb (9. Januar 2019 @ 21:56):
> […] die Überraschung des satten Kreisbezugs […]
Bevor ich (erneut) näher auf solche (doch ziemlich vorhersehbaren, wenn auch nicht unbedingt leicht durchschaubaren) “Definitionsverflechtungen” (“interdependencies”) eingehe (in einem späteren Kommentar, sofern auch das mir gestattet sein möge (Vielen Dank.)), möchte/muss ich zunächst von einer Stelle etwas zurückrudern:
Frank Wappler schrieb (9. Januar 2019 @ 21:33):
> Nicht von Bedeutung schrieb (9. Januar 2019 @ 17:00):
> > > […] einen Silizium-Kristall ziehen und diesen auf 9009009009 Atome in einer Reihe bringen.
> Na gut: reines Zählen sollte nachvollziehbar sein.
Dabei hatte ich (leider …) übersehen, dass es ja gar nicht nur um “reines Zählen” ging, sondern dabei außerdem um bestimmte geometrische Beziehungen zwischen den abzuzählenden Atomen; nämlich:
um die Forderung, jeweils “in eine Reihe” gebracht zu werden, bzw. so vorgefunden zu werden.
(Und womöglich sogar: mit bestimmten “Abständen” voneinander. …)
Wie wäre das denn überhaupt machbar, oder wenigstens vorstellbar, wenn man einen bestimmten Begriff von “Länge” und sogar einen bestimmten “Maßstab” nicht schon zur Verfügung hätte?,
also ausgerechnet genau das, was doch stattdessen überhaupt erst wie beschrieben “aus Silizium angefertigt” werden soll ?!?
(Die Frage ist zumindest teilweise rhetorisch gemeint, denn die RT stellt ja Messmethoden zur Verfügung, um diesem “Teufelskreis” zu entkommen.)
Anders/praktischer/suggestiver gefragt:
Wie könnte/sollte überhaupt herausgefunden werden, ob eine gegebene Anzahl von “Silizium-Atomen” “kristallin” wäre, und nicht stattdessen “amorph” (“flüssig”, “gasförmig”, …), wenn …
… ja — wenn man nicht schon vorher und von vornherein ein anderes geeinetes “Kristall” hätte bzw. anfertigen könnte bzw. (nur das ist letztlich wesentlich!) nachvollziehbar erkennen könnte ?!?
(Und da komme ich dann mit der RT wieder mal auf tetragonal-oktahedrale Ping-Koinzidenz-Gitter …)
Herr Senf
9. Januar 2019 @ 23:56
“Also haben Sie jetzt endlich verstanden, dass der “bewegte Beobachter” einen kürzeren Einheitsmeter haben müsste als der “ruhende Beobachter”?” Nein, hat er nicht und müßte nicht haben.
Deswegen brauchen wir die LoTra – es war eben 5 vor 12 😉 vlt wird’s besser danach.”
Entscheidens Sie sich endlich mal. Holen Sie sich evtl. Hilfe. Lassen Sie sich erklären. Denken Sie mal gerade aus!
Wenn ein “ruhender Beobachter” Strecken, Längen und Distanzen in Bezug auf einen “bewegten Beobachter” als kontrahiert sieht, muss er auch dessen Einheitsmeter kontrahiert sehen. Alles andere ist inkonsistent.
@Joachim / 9. Januar 2019 @ 15:38
Ich verstehe nicht, was an der unmissverständlichen Auskunft, »Die Roundtrip-Dauer für ein Lichtsignals längs des Stabes soll in im Ruhesystem des Stabes gemessen werden,« — sofern dies denn überhaupt gemeint war — eigentlich so schwierig sein soll. Je klarer man sich artikuliert, desto besser für alle Beteiligten.
Aber sei’s drum. Für klar und hilfreich halte ich jedenfalls noch diese animierte Darstellung eines bewegten Stabes im Minkowski-Diagramm. Wer da einen bewegten Stab erkennen kann, sollte auch imstande sein, sich diesen durch einen 4-Vektor repräsentiert zu denken. Womit dann die Frage nach der dem Stab zugeordneten `proper length’ geradezu trivial wird.
Etwas mehr raumzeitliches Nachdenken erfordert sicherlich die Frage, ob und in welchem Sinne der Stab zur Zeit \(t = 0\) in dem durch die Strecke \(OC\) der Länge \(1/\gamma\) markierten Abschnitt auf der x-Achse komplett enthalten ist. Aber auch hierbei scheint mit die Animation hilfreich, eine schlüssige Antwort zu finden.
Die Animation ist irreführend. Im Minkowskidiagramm ist die Zeit als Achse nach oben aufgetragen. Da zusätzlich etwas zu animieren, ist völlig unnötig. Der Stab ist nicht die dunkelblaue Linie, die da durchzieht, sondern das hellblaue statische Band.
@Frank Wappler:
Erlich gesagt, gar nicht. Aber bei der Sekunde hat man es nicht anders gemacht. Die Entwicklung ging ja von einem Urmeter aus, mit welchem man die LG ziemlich genau gemessen hat und dann kam die Annahme hinzu, dass Atomuhren zumindest in Erdnähe annähernd gleichmäßig laufen, während feste Gegenstände auf Umwelteinflüsse reagieren. Das gehört mMm aber alles in einen anderen Blog.
@Nicht von Bedeutung
10. Januar 2019 @ 10:11
Vielen Dank! Ja. Oder, wenn es speziell um Zeit und Uhren geht, in diesen.
Wir wollen ja, dass wir gute Gedanken später wiederfinden. Das geht am besten, wenn wir uns ans Thema halten.
Herr Senf
9. Januar 2019 @ 23:56
“Also haben Sie jetzt endlich verstanden, dass der “bewegte Beobachter” einen kürzeren Einheitsmeter haben müsste als der “ruhende Beobachter”?” Nein, hat er nicht und müßte nicht haben.”
Nun, ohne Zweifel verwirrend ist der Umstand, dass man “von einem Beobachter zum anderen Beobachter” blickt (und derjenige, diese Szenarien Betrachtende oft noch einen weiteren Beobachter darstellt, also eine Art geistiger Dreisprung). Dafür eine einheitliche, klare Sprechweise zu finden, wäre sehr förderlich.
Also: natürlich ist nur dann eine Kontraktion feststellbar (wenn überhaupt), wenn ein Beobachter den Meter eines anderen Beobachters mit seinem eigenen Meter vermisst.
Ganz analog zur Perspektive: wenn ich den Meter eines in der Ferne stehenden Menschen messe (mit einer Mess-Skala bzw. Maßstab in definiertem Abstand vor meinem Auge), so erscheint dieser Meter mir verkürzt (ich messe eine Scheinlänge), genau so, wie der Mensch in der Ferne mir kleiner erscheint als in der Nähe (Scheingröße). Allerdings sind wir an diesen Effekt so gewöhnt, und verstehen ihn als einen Scheineffekt, so dass wir das gar nicht mehr bewusst registrieren.
Wir erkennen intuitiv die Scheingröße als nicht der Tatsache entsprechend, das Gehirn “rechnet” uns die Scheingröße direkt um. Deshalb ist für uns ein Zwerg in der Ferne trotzdem ein Zwerg, ein Riese trotzdem ein Riese, und ein normal großer Mensch in der Fern trotzdem normal groß.
Also noch einmal ganz klar gesagt: die Lorentz-Kontraktion kann, wenn überhaupt beobachtbar, nur ein Scheineffekt sein, den ein Beobachter wahrnimmt, der einen anderen Beobachter beobachtet.
Und deshalb ist diese stellenweise geführte Diskussion um materielle/nicht materielle Verkürzung auch nicht zielführend. Es kann selbstverständlich nicht sein, dass jemand, nur weil sich jemand anderes relativ zu ihm bewegt, irgendwie verkürzen würde. Die sRT-Kontraktion kann nur einem Beobachter so scheinen.
Satz:
Es gibt keinen “Erleidenden” bei der Lorentz-Kontraktion.
@Joachim Schulz:
Sorry, wenn ich mich einmische, aber wie soll das verstanden werden? Wenn das blaue Band der Stab wäre, wären die blauen Linien dessen Durchmesser in S und S’ oder wie und in beiden Fällen sozusagen “zeitlich verkantet”?
Aber klar… Animieren ist irreführend. Die Gleichzeitigkeit von ct’ senkrecht zu ct’ anzudeuten wäre hilfreicher gewesen. Dann hätte man sofort gesehen, dass zwischen O und C in S’ Zeit vergeht und in S halt nicht. OB ist hier für eine Längenmessung nicht wichtig, denn diese Ereignisse sind in keinem der beiden Fälle S und S’ gleichzeitig.
Die Stablänge ist demnach in beiden Fällen OC und OB gibt es gar nicht, jedenfalls nicht als Messung. Wenn OB nun aber die Ruhelänge des Stabes sein soll, dann ist das Ruhesystem aber verdammt falsch eingezeichnet, nämlich bewegt und damit verzerrt also transformiert – womit wir btw. genau bei der Begründung meiner Interpretation der Zuglängen-Messung wären.
Korrektur:
Und deshalb ist diese stellenweise geführte Diskussion um materielle/nicht materielle Verkürzung auch nicht zielführend. Es kann selbstverständlich nicht sein, dass jemand, nur weil sich jemand anderes relativ zu ihm bewegt, irgendwie verkürzt werden würde. Die sRT-Kontraktion kann nur einem Beobachter so scheinen.
Satz:
Es gibt keinen “Erleidenden” bei der Lorentz-Kontraktion!
@Herr Storz 07:35 was ist los ? “Wenn ein “ruhender Beobachter” Strecken, Längen und Distanzen in Bezug auf einen “bewegten Beobachter” als kontrahiert sieht, muss er auch dessen Einheitsmeter kontrahiert sehen.”
Warum reklamieren Sie ständig dasselbe, was wir Ihnen schon die ganze Zeit beim Bewegten erzählen?
Der bewegte hat keinen Kürzeren, deswegen brauchen wir die LoTra, daß der Kürzere nicht kürzer ist.
Sie #10:56 wollen klare Worte, also dann selbst nicht “in Bezug auf einen “bewegten Beobachter”, sondern “von seinem Bezug aus gegenüber zu einem bewegten Beobachter” in Wappler-Sprech 😉
@Chrys @Joachim Schulz // Wikimedia-Animation
Na bitte, geht doch: Einer liefert die Animation, einer die passende Erklärung dazu. Und schon meint der eine oder andere, die Sache mit der Längenkontraktion halbwegs zu verstehen.
In etwa so:
@Chrys interpretiert die Sache anscheinend so, dass der bewegte Stab lediglich verkürzt erscheint, es handelt sich sozusagen um eine raumzeitliche Wahrnehmungsverzerrung.
Für @Joachim ist der bewegte Stab tatsächlich verkürzt, weil die gegebene raumzeitliche Struktur des Universums das so fordert (der Stab folgt sozusagen der Geometrie des Raums).
Joachim Schulz schrieb (10. Januar 2019 @ 08:33):
> Die Animation
Diese Animation, auf die Chrys in zwei Kommentaren (7. Januar 2019 @ 21:20, 10. Januar 2019 @ 07:48) hinwies, findet sich übrigens (wohl seit fast zwei Jahren) Wikipedia-Artikel “Spacetime”, Sektion “Time dilation and length contraction” ( https://en.wikipedia.org/wiki/Spacetime#Time_dilation_and_length_contraction ) als
> ist irreführend.
Vor allem ist diese Animation (hinsichtlich des Anliegens der Darstellung eines “rods”, also eines “Stabes”) meiner bescheidenen Meinung nach völlig unzureichend beschriftet, und deshalb nahezu unbrauchbar, denn:
Es sind darin ja nicht einmal (symbolische) Namen für die beiden Enden des betreffenden Stabes angegeben!
(Ganz zu schweigen von Namen anderer Beteiligter, die ebenfalls relevant sein dürften.)
Zumindest ersatzweise möchte ich diesen beiden Enden bestimmte Namen geben, sagen wir \(J\) und \(K\) damit im Folgenden überhaupt erst eindeutig benannt (und erst unter dieser Voraussetzung sinnvoll diskutiert) werden kann
– die Distanz dieser beiden Enden voneinander: \(JK\) als “Länge des Stabes”,
– bestimmte Ereignisse, an denen \(J\) teilgenommen hatte; z.B. das Koinzidenz-Ereignis des Treffens/Passierens von \(J\) und (jeweils mindestens einem weiteren geeigneten benannten Beteiligten) \(P\) als \(\varepsilon_{JP}\),
– bestimmte Ereignisse, an denen \(K\) teilgenommen hatte; z.B. das Koinzidenz-Ereignis des Treffens/Passierens von \(K\) und (jeweils mindestens einem weiteren geeigneten benannten Beteiligten) \(Q\) als \(\varepsilon_{KQ}\),
– bestimmte Anzeigen \(J\)s; z.B. \(J\)s Anzeige der Passage von \(P\), d.h. \(J\)s Anteil am Ereignis \(\varepsilon_{JP}\) als \(J_P\),
– bestimmte Anzeigen \(K\)s; z.B. \(K\)s Anzeige der Passage von \(Q\), d.h. \(K\)s Anteil am Ereignis \(\varepsilon_{KQ}\) als \(K_Q\).
> Im Minkowskidiagramm ist die Zeit als Achse nach oben aufgetragen.
Falls so: Wessen Zeit(-Verlauf) ??
> […] Der Stab ist […] das hellblaue statische Band.
Falls so, dann wären die beiden “seitlichen” Ränder dieses hellblauen Bandes wohl als die beiden o.g. Enden des Stabes anzusehen
Und ggf. entsprechend zu bezeichnen/beschriften: sagen wir
– der rot linierte Rand des hellblauen Bandes als \(J\)
(wobei ein Punkt dieses Randes in der gegebenen Animation außerdem als “O” beschriftet ist …), und
– der gegenüberliegende Rand des hellblauen Bandes als \(K\)
(auch dieser weist schon weitere Beschriftungen auf — wozu auch immer).
> nicht die dunkelblaue Linie, die da durchzieht
Jeweils eine einzelne solche dunkelblaue Linie (aus jeweils einem einzelnen “Schnappschuss” der Animation) wäre dann wohl eine Darstellung jeweils einer Menge von gleichzeitigen Anzeigen der Bestandteile des Stabes;
d.h. jeweils eine Gleichzeitigkeits-Projektion des gesamten Stabes.
(Worin manche, so wie Chrys, wohl auch jeweils “einen Stab zu erkennen” meinen;
bzw. im “Durchziehen” all dieser Gleichzeitigkeits-Projektionen des gesamten Stabes im Verlaufe der Animation “einen bewegten Stab zu erkennen” meinen.)
Aber:
Sind in einem Minkowski-Diagramm denn nicht stattdessen ganze Ereignisse gezeigt und ggf. markiert ??
Wäre es also nicht stattdessen denkbar (und vielleicht sogar so gemeint), dass das hellblaue statische Band nicht nur “den Stab” an sich darstellt, sondern die Menge von Ereignissen, an denen jeweils mindestens ein Bestandteil des Stabes teilgenommen hatte,
bzw. (sicherlich äquivalent), die Menge von Ereignissen, an denen jeweils genau ein Bestandteil des Stabes teilgenommen hatte
??
Jeweils eine dunkelblaue Linie wäre dann wohl die Darstellung einer sogenannten “line of simultaneity” (dieser Begriff findet sich zumindest mehrfach im genannten Wikipedia-Artikel), also jeweils die Darstellung einer gewissen Teilmenge von Ereignissen, an denen (alle) Bestandteile des Stabes teilgenommen hatten.
(Was manche allerdings nicht unbedingt davon abhalten müsste, in den dunkelblauen Linien “einen bewegten Stab zu erkennen” …)
> Da zusätzlich etwas zu animieren, ist völlig unnötig.
Mag sein.
Die ganze graphische Darstellung von Mengen von Anzeigen, oder aber von Mengen von (Koinzidenz-)Ereignissen, ist sicher nicht unbedingt nötig, wenn z.B. deren (verbale) Beschreibung im Zusammenhang doch ohnehin gegeben sein dürfte und richtig verstanden werden muss.
Eine graphische Darstellung kann aber als Gedächtnishilfe für umfangreiche Verbal-Beschreibungen dienen.
(Was wiederum mit der individuell ggf. verschieden ausgeprägten Fähigkeit bzw. Einbildung verbunden wäre, das jeweils eine im anderen erkennen bzw. rekonstituieren zu können.)
p.s. (Frank Wappler, 10. Januar 2019 @ 12:12):
Was ich in der Animation https://en.wikipedia.org/wiki/Spacetime#Time_dilation_and_length_contraction außerdem besonders vermisse,
und in einer brauchbar(er)en Animation außerdem dargestellt werden könnte,
ist die Darstellung von ausdrücklichen Ping-Beziehungen zwischen den Stabenden
(entweder “alle davon, im Durchziehen”, oder wenigstens einige oder zumindest eine ausgewählte).
Korrektur:
Upps, nu hab’ ich zwei Dinge verwechselt. Erstens die Zeit – der Beitrag hätte erst um 17:18 Uhr gepostet werden dürfen und zweitens habe ich die 9009009009 nicht verbessert – ich war ja inzwischen auch schon bei den von Senf vorgeschlagenen 1841620626.
Naja, wenn der Beitrag gelöscht wird, habe ich später ja noch mal Gelegenheit das zu verbessern. 😉
Nicht von Bedeutung
10. Januar 2019 @ 11:06
Das Minkowski-Diagramm ist im Wesentlichen in Weg-Zeit-Diagramm. Nach links ist die Position (leider nur eine Dimension) aufgetragen, nach oben die Zeit. Eine ruhende Punktmasse ist auf solch einem Diagramm eine Senkrechte gerade. Eine mit konstanter Geschwindigkeit bewegte Punktmasse ist eine schräge gerade. Je flacher je schneller. Ein beschleunigtes Punktteilchen ist eine Kurve. Da Punktmassen in der Physik weder aus dem Nichts entstehen noch einfach verschwinden oder sich verdoppeln, darf keine solche Kurve (Weltlinie genannt) in der Zeit zurück gehen. Im Ort (links-rechts) können sie aber durchaus oszillieren.
Mehrere Punktteilchen sind mehrere Linien auf solch einem Diagramm und ein in der Ortsachse ausgedehntes Objekt, wie dieser Stab ist ein Band. Ein waagerechter Schnitt durch dieses Diagramm zeigt die Konstellation zu einem bestimmten Zeitpunkt. Hier also die räumliche Ausdehnung (also Länge) des Stabes. Ein Senkrechter schnitt zeigt den Zeitverlauf in einem Punkt. Also wann dort eine Masse ist und wann nicht.
In einem Weg-Zeit-Diagramm bewegt sich also nichts. Eine Bewegung ist durch Veränderungen aufeinander folgender waagerechter Schnitte zu erkennen. Im Falle des Stabes, sieht man, dass der Stab sich mit fortlaufender Zeit immer weiter nach rechts verschiebt.
Das besondere am Minkowski-Diagramm im Vergleich zum klassischen Weg-Zeit-Diagramm ist nur, dass flache (>0°, 45°, <90°) Schnitte sind Zeitverläufe in anderen Ruhesystemen.
Daran erkennt man schön, dass die SRT erfüllt, was Herr Storz fordert: Die Änderung des Koordinatensystems ändert nichts an der physikalischen Situation. Es ist nur eine andere Sichtweise, ein anderer Schnitt durch das Geschehen.
@Joachim / 10. Januar 2019 @ 08:33
»Der Stab ist […] das hellblaue statische Band.«
Was wir schon deshalb verwerfen können, weil alle Punkte (oder meinetwegen Ereignisse) auf diesem statischen Band S-gleichzeitig (da auf der x-Achse) sind, wohingegen alle Punkte auf dem in S bewegten Stab mit dem Ruhesystem S’ stets S’-gleichzeitig (d.h. parallel zur x’-Achse) sind. Das ist ist schlicht die Relativität von Gleichzeitigkeit.
@Chrys
Nein, die Ereignisse sind eben nicht alle Gleichzeitig. Sie zeigen die Position des Stabes für alle Zeiten vom unteren bis zum oberen Bildrand.
@Joachim Schulz:
Die Widerlegung der LK durch rotierende Michelson-Morley-Interferometer, kann man ja noch mal deutlicher machen…
1. \( L_1=\sqrt{(L\gamma^2 \cdot cos \alpha)^2+(L\gamma \cdot sin \alpha)^2} \)
2. \( L_2=\sqrt{(L\gamma^2 \cdot cos \alpha)^2+(L\gamma \cdot sin \alpha)^2}) \)
Auf die Art alternieren die Längen \( L_1 \) und \( L_2 \) abwechselnd in Abhängigkeit von \( \alpha \) und in jeweils 90°-Schritten ist ein kompletter Alternierungszyklus vollzogen. Einverstanden?
Balanus schrieb (10. Januar 2019 @ 12:10):
> […]Chrys interpretiert die Sache anscheinend so, dass der bewegte Stab lediglich verkürzt erscheint, es handelt sich sozusagen um eine raumzeitliche Wahrnehmungsverzerrung.
> Für […]Joachim ist der bewegte Stab tatsächlich verkürzt, weil die gegebene raumzeitliche Struktur des Universums das so fordert (der Stab folgt sozusagen der Geometrie des Raums).
Mindestens eine weitere, von den beiden zitierten Interpretationen abweichende Auffassung bleibt (beinahe wie schon gewohnt) zu ergänzen:
dass zwei verschiedene Stäbe in Betracht stehen, die ungleich lang sind (und bleiben), die sich gegenüber einander geradlinig-gleichförmig bewegten, und deren geometrisch-kinematische Beziehung darüberhinaus als “Einstein-Projektion (der beiden Enden des längeren Stabes auf die beiden Enden des kürzeren Stabes)” bekannt ist. (Oder etwas genauer und bescheidener: zumindest einigen Fachleuten/Physikern unter diesem Namen bekannt sein dürfte.)
@Joachim Schulz:
Der Beitrag sollte doch wohl eher an Chrys gerichtet sein, oder nicht? Mir ist das längst klar. Ich schrieb ja bereits, dass die Animation irreführend ist – die zeigt eher den zeitlichen Verlauf des Stabes im bewegten System und das auch noch falsch, wenn man es genau nimmt, denn eigentlich hätte der waagerechte blaue Strich, der sich auf der x-Achse befindet animiert werden müssen. Der animierte blaue Strich existiert eigentlich gar nicht (höchstens ruhend im bewegten System) – dafür aber die “verdrehte” Gleichzeitigkeit senkrecht zur ct’-Achse, die jedoch fehlt ganz.
@Krüger:
Der animierte blaue Strich in Chrys’s Animation ist btw. sozusagen der pohl’sche SI-Meter.
@Joachim Schulz:
Korrektur:
Bei den Formeln oben muss \( L_1 \) gegenüber \( L_2 \) um 90° verdreht sein, was man entweder mit α+90° oder durch vertauschen von sin und cos bei einem von beiden erreicht. Verdammtes copy-paste.
@NvB 13:50 “… alternieren die Längen L1 und L2 … von α …” die Plusse “+” sind falsch.
@Frank Wappler / 10. Januar 2019 @ 12:12
»Vor allem ist diese Animation (hinsichtlich des Anliegens der Darstellung eines “rods”, also eines “Stabes”) meiner bescheidenen Meinung nach völlig unzureichend beschriftet, und deshalb nahezu unbrauchbar, …«
Hübsch wäre da jedenfalls noch eine animierte Uhr, die etwa auf der t-Achse als ihrer Weltlinie nach oben läuft und dabei den jeweils aktuellen t-Wert als ihre Eigenzeit anzeigt. Vielleicht würde so der eine oder andere Groschen über die Vorteile eines animierten Minkowski-Diagramms fallen.
Es sollte nach einigem Nachdenken einleuchten, dass es mit Lorentz Transf. und etwas linearer Algebra in diesem (1+1)-dim. Minkowski-Diagramm-Raum möglich sein muss, eine Formel zur Bestimmung der S-Zeit t anzugeben, bei welcher der rechte Endpunkt des bewegten Stabes den rechten Rand des durch die Strecke OC auf der x-Achse markierten Bereichs erreicht. Das ist einfacher, als es zunächst scheinen mag, und es läuft durchaus auf eine Koinzidenz-Bestimmung hinaus.
—
@Joachim / 10. Januar 2019 @ 13:19
»Nein, die Ereignisse sind eben nicht alle Gleichzeitig.«
Wer hier konsequent nur S-gleichzeitg und S’-gleichzeitig verwendet und sorgsam unterscheidet, ist klar im Vorteil. Markus Pössel wird das gewiss bestätigen können.
@Senf:
Begründung?
Hier ist meine, warum sie richtig sind.
Beide Arme haben ein gemeinsamen Startpunkt am Strahlteiler, die anderen Enden bewegen sich sozusagen auf dem Umfang einer Ellipse (in der LET auf einem Ellipsoid), von welcher die große Achse stets parallel zum Geschwindigkeitsvektor v verläuft – entsprechend die kleine Achse senkrecht dazu. Bei jedem Winkel ergibt sich die Länge eines Arms über Pythagoras, Sinus und Kosinus. Bei einer der Armlängen muss nur sin und cos vertauscht werden, das ist der einzige Fehler (mal abgesehen von der überflüssigen Klammer bei L2, von der ich ohnehin nicht weiß, wie sie dahinkommt). Also was soll das gezappel?
@Chrys
10. Januar 2019 @ 15:14
Selbstverständlich. Aber das hellblaue Band enthält alle Ereignisse, an denen ein Teil des Stabes teilnimmt. Sie sind weder in S’ noch in S alle gleichzeitig. Wir haben verstanden, dass der dunkelblaue Strich jeweils ein S’-gleichzeitiger Längsschnitt des Stabes zu einer bestimmten Koordinatenzeit t’ ist, und dass der mittelblaue Strich ein Längsschnitt des Stabes S-gleichzeitig bei t=0 ist. Dennoch wird der zeitliche Verlauf des Stabes, seine Realität sozusagen, durch das hellblaue Band dargestellt. Jedes hellblaue Ereignis koinzidiert mit einer Weltlinie des Stabes.
Und wieder Korrektur:
So gilt das für die Laufzeiten. Für die LK ist’s natürlich andersherum, damit die Laufzeiten wieder identisch werden.
Das ist aber auch ein Knoten im Kopf. 😀
@Chrys:
Herr Pössel würde eher bestätigen, dass die Gleichzeitigkeit für den animierten Stab noch gar nicht “hergestellt” wurde, weil dazu müsste ct’ senkrecht auf x’ stehen und ct und x entsprechend “verzerrt” (transformiert).
Nicht von Bedeutung schrieb (10. Januar 2019 @ 13:50, 14:54):
> […] kann man ja noch mal deutlicher machen …
Find ich auch:
\[ \left( \frac{L_2}{L_1} \right) = \sqrt{ \frac{ (\gamma \, \cdot \, \text{Tan}[ \, \alpha\, ])^2 + 1}{\gamma^2 + (\text{Tan}[ \, \alpha\, ])^2} }.\]
(Womit insbesondere noch mal deutlicher gemacht sein soll, wie egal hierbei irgendwelche “Maßeinheiten” sind.)
> Auf die Art alternieren die Längen \(L_1\) und \(L_2\) abwechselnd in Abhängigkeit von \(\alpha\) […]
Wie ist “\(\gamma\)” als Messgröße definiert?, d.h. Wie misst man (reelle Werte von) “\( \gamma \)” (zumindest im Prinzip) ??
Wie ist “\(\alpha\)” als Messgröße definiert?, d.h. Wie misst man (reelle Werte von) “\( \alpha \)” (zumindest im Prinzip) ?? …
Und nicht zu vergessen:
Zwischendurch fiel hier, im Zusammenhang mit “Michelson-Interferometer”, bisher genau einmal der Begriff
“Steifigkeit der Arme” …
Haben Michelson/Morley also durchwegs im Verlaufe ihrer Versuche gemessen, dass
\[ \left| \left( \frac{L_2}{L_1} \right) – 1 \right| \ll 1 \]
?
Und falls so: Wie haben sie das gemessen? (Etwa: interferometrisch ??)
Oder haben Michelson/Morley (“der Einfachheit halber”) angenommen, dass
\[ \left| \left( \frac{L_2}{L_1} \right) – 1 \right| \ll 1 \]
im Verlaufe ihrer Versuche durchwegs erfüllt gewesen wäre ?
Oder — haben die vielleicht “anstatt Silizium einfach Granit” gedacht ?
Falls so: Wie hätten sie zumindest im (gedanken-experimentellen) Prinzip messen wollen, ob diese Annahme zugetroffen hätte bzw. in wie fern nicht; um auf dieser Grundlage die systematische Abweichung ihrer Resultate hinsichtlich dieser speziellen Annahme abzuschätzen ? (Etwa: interferometrisch ?? …)
Herr Senf
10. Januar 2019 @ 11:43
“Warum reklamieren Sie ständig dasselbe, was wir Ihnen schon die ganze Zeit beim Bewegten erzählen?”
Sie wissen ja selbst nicht genau, was IHR die ganze Zeit erzählt habt! Mal schreiben Sie so, mal anders. Aber nie klar.
“Der bewegte hat keinen Kürzeren, deswegen brauchen wir die LoTra, daß der Kürzere nicht kürzer ist.”
Was soll der Unsinn? Der “ruhende Beobachter” misst einen Einheitsmeter beim “bewegten Beobachter” kontrahiert gegenüber seinem ruhenden Einheitsmeter. Was Sie da ob sagen wollen ist komplett unverständlich.
“Sie #10:56 wollen klare Worte, also dann selbst nicht “in Bezug auf einen “bewegten Beobachter”, sondern “von seinem Bezug aus gegenüber zu einem bewegten Beobachter” in Wappler-Sprech 😉”
Sie wollen meine Aussagen entstellen. Behalten Sie Ihren “Wappler-Sprech”. Sie geben so oder so auf keinem Fall meine Aussagen korrekt wieder.
@Frank Wappler:
Das ist Alles recht einfach…
1. Das Iterferometer (Zentrum) bewege sich entlang einer beliebigen Richtung (bei Michelson Morley Ost-West-Richtung) mit eine beliebigen Geschwindigkeit v.
2. Bei v=0 ist γ=1 und die Arme damit in jeder Position gleich lang. Ergo ändert sich das Interferenzmuster nicht und man muss auch keine Kontraktion annehmen.
3. Bei v≠0 ist γ>1 und die Arme eben nicht mehr gleich lang – der Arm quer zur Bewegungsrichtung muss weniger Laufzeit ausgleichen, als der Arm längs zur Bewegungsrichtung, weswegen Ersterer entsprechend länger ausfällt.
4. Bei einer Rotation des Interferometers wechseln sich die Armlängen in 90°-Schritten ab und deswegen muss man bei Winkeln 0°<α<90° davon ausgehen, dass sie sich kontinuierlich ändern, was zu einem wandernden Interferenzmuster führen müsste.
5. Martin Grusenick zeigte 2009, dass sich die Interferenzmuster zumindest bei einem horizontal rotierendem Interferometer nicht ändern.
6. Bei einem vertikal rodierendem Interferometer schlägt jedoch die Gravitation zu und deswegen wandert das Muster dort.
Ach ja…
7. Bei Michelson und Morley waren die Winkel zwischen 0° und 90° nie maßgeblich, sonst sähen die gängigen Formeln anders aus.
@Frank Wappler:
BTW.: Der “Trick” mit dem Tangens ist gut… nur was sagt er zu α=90°?
@NvB 17:18 “… 1. Das I?terferometer (Zentrum) bewege sich entlang einer beliebigen Richtung …”
Woher weiß das Interferometer oder Du, daß es sich bewegt, wenn Jalousien vor den Fenstern sind?
Wie bestimmst Du denn v≠0 und γ>1, wenn Du nicht siehst, gegenüber was was los ist, gleichförmige Bewegung ändert nichts an der physikalischen Beobachtung. MM sollte den Ätherwind bestimmen, der mit “v” durchs Interferometer geht, äquivalent MM bewegt sich mit v im (absoluten) Äther.
Es gab ein Nullresultat, also keinen Äther, damit ist v=0, was willst Du mit andern v’s gegen irgendwas?
Wenn viele MM’s rumtanzen mit beliebigen v’s, zeigen sie alle nichts an – Gleichwertigkeit nach Galilei.
Einstein hat das Michelson für seine SRT nicht gebraucht, schon gar nicht für die LK, wenn sowieso v=0.
Von daher gibt es für Michelson auch nichts nach SRT zu erklären, wo die Lampe festgeschraubt ist.
@Senf:
Ich weiß das Alles gar nicht. Ich weiß nur, dass bei v=0 auch keine LK benötigt wird. Klar soweit? MAW.: mit v=0 kann MM kein experimentum crucis sein.
Deswegen solltest du deine v=0-Idee lieber Herrn Schulz mitteilen, der nämlich in seinem Blog ganz klar v≠0 annimmt und deswegen auf seinen experimentellen Befund zur LK kommt. Klar soweit?
@Joachim / 10. Januar 2019 @ 15:29
»Dennoch wird der zeitliche Verlauf des Stabes, seine Realität sozusagen, durch das hellblaue Band dargestellt.«
Das hellblaue Band auf der x-Achse besteht überhaupt nur im flüchtigen Moment \(t = 0\). Dieses Band ist nur eine momentane Projektion des Stabes auf die x-Achse, die farblich hervorgehoben wurde, um die Lorentz Kontraktion zu demonstrieren, oder was man eben dafür hält. Wegen \(|OC| = 1/\gamma < 1\) ist diese Strecke ja kürzer als die Stablänge.
In seinem Ruhesystem S' liegt der Stab stets parallel zur x'-Achse. Alle seine Punkte behalten ihre x'-Koordinaten und laufen auf ihren Weltlinien parallel zur t'-Achse, that's all. Und daran ändert eine Lorentz Transf. zur Darstellung in den S-Koordinaten (t,x) natürlich absolut nichts. Ein wie auch immer in S projizierter Stab ist ein anderes Objekt als er Stab selbst, und in etwa so real wie sein Schatten.
Chrys schrieb (10. Januar 2019 @ 15:14):
> @Frank Wappler / 10. Januar 2019 @ 12:12
Ist also davon auszugehen, dass Du (auch) meinen insbesondere an Dich gerichteten Kommentar 9. Januar 2019 @ 18:14 (weiter oben auf dieser Seite) zur Kenntnis genommen hast,
und dass Deine Kapriole aus Kommentar 9. Januar 2019 @ 15:11, gegenüber der ich mich äußerst besorgt geäußert hatte, nämlich dass
“die Begriffe `Ruhelänge’ und `Eigenlänge’ […] qualitativ ganz unterschiedlich definiert” seien, vom Tisch ist; und zwar endgültig ?!?
p.s.
> [»zahlreiche zusammenpassende Minkowski-Diagramme& … zusammengefasst als durchgezogene Animation«] Hübsch wäre da jedenfalls noch eine animierte Uhr,
[ Kommentar-Teil zurückgestellt; der Kürze wegen — FW. ]
p.p.s. — Doch eigentlich das Hauptanliegen dieses Kommentars:
> Wer hier konsequent nur S-gleichzeitg und S’-gleichzeitig verwendet und sorgsam unterscheidet, ist klar im Vorteil.
Ganz recht: wer mit solchen Begriffen umgehen und sogar die (S)RT lehren wollte, sollte und müsste besondere Sorgfalt walten lassen und wiederum abverlangen.
Es gilt aber auch Murphy’s Law:
Was wiederum einen guten, hinreichenden Grund für Defensive Design darstellt:
Deshalb:
Wer konsequent nur gleichzeitig verwendet, ist im Vorteil.
Die ansonsten bestehenden Gleichwertigkeit der entsprechenden Formulierung dürfte ja mittlerweile geläufig sein; z.B.:
– “Das Passage-Ereignis mit Bahnhofs-Ausfahrsignal und Zug-Lok und das Passage-Ereignis mit Bahnhofs-Einfahrsignal und Zug-Caboose waren Bahnhofs-gleichzeitig.”
ist ansonsten gleichwertig zu
– “Die Anzeige des Bahnhofs-Ausfahrsignal bei Passage der Zug-Lok und die Anzeige des Bahnhofs-Einfahrsignal bei Passage der Zug-Caboose waren gleichzeitig.”
Chrys schrieb (10. Januar 2019 @ 23:43):
> Das hellblaue Band auf der x-Achse […]
In der betreffenden Animation
https://upload.wikimedia.org/wikipedia/commons/8/85/Animated_Spacetime_Diagram_-_Length_Contraction.gif
erkenne ich ein (“großes”) hellblaues Trapez, dass auf seiner linken Seite von einer roten Linie berandet ist;
und diese Fläche habe ich in meinem Kommentar 10. Januar 2019 @ 12:12 als “hellblaues Band” bezeichnet.
(Auch Joachim Schulz erwähnte schon in Kommentar 10. Januar 2019 @ 08:33 ein “hellblaues statisches Band“.)
Mittlerweile bezweifle ich aber, dass Du unter “dem hellblauen Band” das selbe graphische Element verstehst wie ich …
(Wäre es nicht schick, wenn derlei Animationen umfassender beschriftet wären … Insbesondere auch mit eigenen Namen für die genannte rote Linie, für alle anderen hellblauen Linien, die dazu parallel liegen, für die vertikale schwarze Linie, usw. usf. ?)
p.s.
Ich hatte und habe noch Einiges hinsichtlich Deines Kommentars 10. Januar 2019 @ 15:14 über diese Animation, deren eventuelle Aufhübschung, und dazu zu bemerken, was sich nach einigem Nachdenken auch allein mit etwas (bi-)linearer Algebra für (1+1)-dim. Beziehungen zwischen Stäben herleiten lässt.
(Wobei: dort habe ich ja auch Bildchens hingemalt; sogar ganze Serien …)
Aber das soll lieber noch warten, bis wir alle wirklich das selbe “hellblaue Band” anvisieren.
@Chrys 23:43
Auch ich meine mit dem hellblauen Band was Frank Wappler oben beschreibt. Die andere Linie haben ich gesten 15:29 als mittelblauen Strich bezeichnet.
Ja, es macht keinen Sinn hier weiterzudiskutieren, wenn man sich nicht einmal einig wird, worüber überhaupt gesprochen wird. Ehrlich gesagt sehe ich aber ohnehin nicht, dass wir hier zu neuen Erkenntnissen kommen. Unsere Sichtweisen sind doch sehr unterschiedlich.
@Joachim Schulz, Frank Wappler und Chrys:
Ihr seid euch wahrscheinlich nur nicht Einig, was Gleichzeitig ist und wo der Unterschied zu Gleichotig liegt.
Ich sage als “Laie” mal, dass Beides “hergestellt” werden muss und dass erreicht man, wenn man die ct-Achsen senkrecht auf die x-Achsen stellt, was in der Animation für S’ – also dem Bewegten System – nun mal nicht zutrifft. Da kann man 1000 mal versuchen – per Animation oder wie auch immer – Gleichzeitigkeit (und btw. auch Gleichortigkeit) im Bewegten System darzustellen, es wird einem nicht gelingen. Was auch immer der Ein oder Andere sagen mag, was ich an der SRT nicht verstanden haben soll – das hier gehört jedenfalls nicht dazu.
https://www.youtube.com/watch?v=wvvngeHEq2M&feature=youtu.be&t=479
(etwa 3 Minuten lang ansehen)
Daraus folgt: Animation Irreführend! Der Animierte Stab ruht in S’ nur leider erkennt man es nicht.
Und btw. auch wenn offtopic. Schaut euch ruhig auch mal an, was mit der Differenzgeschwindigkeit c-v passiert. Die wird nicht plötzlich c’+v’ oder vergleichbares?
Nicht von Bedeutung schrieb (10. Januar 2019 @ 17:18):
> Das ist Alles recht einfach…
Ich neige (auch hier) dazu zu widersprechen:
Es ist recht einfach, sich aus Allem Einiges herauszupicken, was recht einfach ist. …
Netter “Trick”, übrigens, den beiden \(L\)-Werten der beiden unterscheidbaren Interferometer-Arme die Indices “\(1\)” und “\(2\)” zu verpassen,
und nicht etwa von “\(L_p\)” und “\(L_s\)” zu schreiben wie im obigen SciLogs-Artikel (seit es dazu kam …).
Die Fragen, von denen ich finde, dass sie Michelson und Morley nur gestellt sondern endlich mal (von denen selbst, und/oder von jenen, die sich auf Michelson/Morley zu berufen versuchen) sorgsam beantwortet werden müssten, kann ich wohl nicht noch deutlicher stellen, als zuletzt wieder in meinem obigen Kommentar (10. Januar 2019 @ 16:47).
p.s.
Nicht von Bedeutung schrieb (10. Januar 2019 @ 17:32):
> BTW.: Der “Trick” mit dem Tangens ist gut…
Ja, das Zusammenfassen und das Umbenennen find ich auch gut. Das Kürzen fand ich aber fast noch besser.
> nur was sagt er zu α=90° ?
Regel von de l’Hospital.
Frank Wappler schrieb (11. Januar 2019 @ 11:48):
> Die Fragen, von denen ich finde, dass sie Michelson und Morley […]
Nochmal:
Meine wesentlichen Fragen zum Michelson-Morley-Experiment habe ich schon mehrfach gestellt;
zuletzt wieder in meinem obigen Kommentar (10. Januar 2019 @ 16:47).
(Und dass ich diese Frage noch deutlicher formulieren könnte, als sie dort gestellt sind, bezweifle ich.)
Solang diese Fragen nicht entweder schon von Michelson bzw. Morley selbst beantwortet worden sind, oder wenigstens von denen, die sich (immer noch) auf das Michelson-Morley-Experiment berufen, (immer noch) beantwortet werden können, werde ich mich beim Lehren der (S)RT jedenfalls nicht auf das Michelson-Morley-Experiment berufen.
@Frank Wappler / 11. Januar 2019 @ 03:07
Generell ist `proper length’ für raumartige Kurven (in Analogie zur `proper time’ für zeitartige Kurven) durch ein invariantes Intergral definiert, und zwar ohne jegliche Bezugnahme auf Koordinaten. Im Falle einer raumartigen Strecke im Minkowski Raum vereinfacht sich dieses Integral zur Minkowski-Norm des Differenzwektors zwischen den Endpunkten der Strecke.
Die `Ruhelänge’ einer raumartigen Strecke im Minkowski Raum wird hingegen definiert als eine Koordinatenlänge mit Bezug auf ein spezielles Koordinatensystem, und zwar ohne jegliche Bezugnahme auf geometrische Invarianten.
Ist jetzt klar, dass es sich dabei um zwei ganz unterschiedlich definierte Begriffe handelt? Die Feststellung, dass diese Grössen dann als numerische Werte gleich sind, ist eine anhand der Definitionen zu beweisende Aussage. Und als geometrisch definierte Konzeptee sind sie naturgemäss nicht a priori »Dimensions-behaftet«.
Gerade bei einer vergleichenden Betrachtung über die unterschiedlichen Interpretationen von SRT und LET ist undedingt davon abzuraten, irgendwelche Längenangaben voreilig mit der Einheit `Meter’ zu verzieren. Sonst verliert man rasch die Übersicht, welche der Definition von `Meter’ da gerade verwendet wird.
N.B. Der Faktor 1/γ für die `Längenkontraktion’ in der SRT lässt sich aus der Lorentz Transformation und einer Projektion (die insbesondere zeigt, dass damit keine “physikal.” Veränderung an einem modellierten Gegenstand einhergeht) praktisch in einer Zeile herleiten und begreifbar machen. Das mag gewiss auch viel komplizierter gehen, doch das interessiert mich nicht wirklich.
@Joachim / 11. Januar 2019 @ 07:48
Ich muss aufrichtig gestehen, dass ich im Traum nicht auf die Idee gekommen wäre, mit der Formulierung »Der Stab ist […] das hellblaue statische Band,« (vom 10. Januar 2019 @ 08:33) hätte dieses hellblaue Band gemeint sein können. Das wäre mir wohl allzu abenteuerlich erschienen, doch ich habe es tatsächlich nicht mal einen Moment in Erwägung gezogen.
Zumal diese Formulierung von jemandem kam, der erst kürzlich noch völlig korrekt konstatiert hat, dass alles, was sich zeitartig durch die Raumzeit bewegt, mit Lichtgeschindigkeit reist, und der sogar bei der idealisierten Modellierung von Stäben in Raumzeit-Diagrammen dazu geneigt ist, diese eher aus Atomen denn aus abstrakten Punkten konstituiert zu denken.
Die Beziehung zwischen einem im Minkowski Raum modellierten Stab zu diesem hellblauen Band ist vergleichbar mit der zwischen einer dort modellierten Uhr und ihrer zeitartigen Weltlinie. Doch diese Uhr und ihre Weltlinie sind auch im Modell unterscheidbare und unterschiedlich benannte Objekte. Mit einem modellierten Stab ist ganz entsprechend zu verfahren, und so wird’s normalereise ja auch überall gemacht.
@Chrys
11. Januar 2019 @ 12:50
Hm, und das, obwohl ich immer wieder von Weltlinien geschrieben habe.
@Frank Wappler:
Könnte evtl. daran liegen, dass bei einer Drehung um 90° \( L_P \) zu \( L_S \) und \( L_S \) zu \( L_P \) und beide auf dem Weg zwischen 0° und 90° ihre Rollen Grad für Grad tauschen.
Mich wundert bei dem Ganzen nur, warum keiner mit dem relativistischen Doppler-Effekt bei beliebigen Winkeln argumentiert, welcher ebenso wie ZD und LK zu MM gehört, ebenfalls angenommen wird und letztendlich das selbe ergibt, wie die MM-Formel der Emissionstheorie: \( L=\frac{ct}{2} \) in beiden Armen für beliebige Winkel. Genauer gesagt, nimmt man nur den rDE für die ZD an und kommt damit auf die LK. Ich hingegen nehme den rDE – also die ZD – an und komme zu dem Schluß, dass die Phasenverschiebungen längs der Lichtausbreitung bei unveränderten Lichtkegellängen das Inrerferenzmuster radial zur Lichtausbreitung nicht verändern, weil sie in Summe immer das Gleiche ergeben. Kein Mensch wird mir je erzählen können, dass diese Theorien nicht gleichwertig dind, bis eine von Beiden widerlegt wurde, wie auch immer das gehen soll.
@Frank Wappler:
Zu “Lopital” (Offtopic):
Das kannte ich zwar noch nicht, aber ein gewisser Herr Kannenberg mit Mathe-Diplom offensichtlich auch noch nicht. Jedenfalls würde es mich nicht wundern, wenn l’Hospital (was hoffentlich nicht absichtlich so krank klingt 😀 ) zu den Rechenregeln mit 0, ±∞ und NaN in der IEEE 754 führt und auf die Art diese “Axiome” auch außerhalb von Computer-Algebra anwendbar sind.
Außerdem weiß ich nun auch, warum ich diesen “Trick” nicht wirklich kannte (man hätte durch Freistellen selbst drauf kommen können, aber gut) – Es macht in Computerprogrammen manchmal gar keinen Sinn, Formeln vollständig zu vereinfachen, z.B. wen, wie hier, mit Fehlersignalen zu rechnen ist.
@Frank Wappler:
Sind sie das nicht schon? Hätten Michelson und Morley oder andere Experimentatoren außer Martin Grusenick dies je getan, sähen die für das MM-Experiment gängigen Formeln ganz anders aus – dann wäre nämlich der Winkel stets berücksichtigt und Teil der Formel, oder nicht?
@Chrys:
Nö, eben nicht. So werden Stäbe auf der Erde in Eichlaboren modelliert, die dann auf der ISS oder sonstwo bei gleichem Druck und gleicher Temperatur immer noch so lang sind, wie zuvor. Lässt man an solchen Stäben im Vakuum Licht vorbei laufen, während man dabei die Takte einer Uhr zählt, zeigt diese Uhr abhängig vom Gravitationspotential, in welchem sie sich befindet, und der Bewegung mit der sie Unterwegs ist, unterschiedliche Zählwerte an, womit sich die Länge des Meters per SI-Definition verändert hat, nicht jedoch physikalisch.
Leider kann ich Ihnen mit der Originalveröffentlichung von Michelson und Morley nicht helfen, weil die nicht frei zugänglich ist.
NvB.
.
Du behauptest das, nicht mehr, Deine Behauptung ist falsch, die Länge ändert sich nicht und auch nicht per SI-Definition.
.
Es bleibt dabei, Du behauptest die Lichtgeschwindigkeit ist nicht konstant sondern variable und systemabhängig und alleine daraus erwächst die nächste falsche Behauptung von Dir, der SI-Meter wäre nun auch veränderlich.
.
Deine Behauptungen sind experimentell widerlegt, ganz oft, über 100 Jahre. Belegen kannst Du natürlich nichts.
@Joachim / 11. Januar 2019 @ 12:55
Asche auf mein Haupt … doch bei jemandem, dem ich zutraue, enen Unterschied zwischen Uhr und ihrer Weltlinie zu machen, erwarte ich anscheinend reflexhaft auch, dass er ebenso zwischen einem Stab und seiner Weltlinienschar unterscheidet.
Und einen idealiserten Stab kann man sich hier schliesslich auch denken als eine einparametrige Schar S’-synchroner Uhren, die alle S’-simultan den gleichen t’-Wert anzeigen. In S, wo der Stab bewegt ist und auf einer Geraden \(\{t = \text{const.}\}\) nur S-synchrone Uhren anzutreffen sind, muss der Lorentz-transformierte Stab dann logischerweise in einer Schieflage erscheinen. Aber mehr steckt eben auch nicht dahinter.
@Krüger:
Dann hör auf zu faseln und liefere ein verdammtes Argument dafür, warum Uhren bei H&K unterschiedliche Gangraten aufwiesen, mit denen man sicher keinen SI-Meter hin bekommt, der zu einem auf der Erde hergestellten identisch ist und die Uhren in GPS-Satelliten verlangsamt werden müssen, damit dort die TAI-Sekunde gilt, weil man sonst auch mit diesen Uhren ganz sicher keinen SI-Meter hin bekommt, der zu einem auf der Erde hergestellten identisch ist. SI-Meter haben nur dann identische Längen, wenn man sie mit identischen Zeiten (TAI-Sekunde und nicht SI-Sekunde) oder mit identischen Gitterabständen herstellt. So… und was wurde nun experimentell widerlegt? Genau – die Behauptung, dass du Recht hast! 😆
@Chrys
11. Januar 2019 @ 14:37
Was denn für eine Schieflage? Sehen Sie sich mal die Mittelblaue Linie an. Sie wird von allen den Stab konstituierenden Weltlinien zur Zeit t=0 auf einer x-Länge \(L/\gamma\) geschnitten. Die Schieflage besteht ausschließlich darin, dass die Uhren unterschiedliche Zeiten anzeigen. Sie sind aber alle auf der x-Achse und nicht etwa in y- oder z- verkippt. Es handelt sich nicht um einen Schatten, die einzelnen Punkte (Atome) des Stabs sind wirklich da.
@Krüger:
Du bist nicht etwa McMurdo im Mahag?
Nun ein “praktischer” Beitrag zum Thema Längenkontraktion.
Diese Betrachtung hat Ähnlichkeiten mit dem Grabenparadoxon. Ich nenne es Schalterparadoxon.
Der Schalter besteht aus zwei Kontakten, deren Abstand gleich der Länge des Leiters (in Ruhe) ist. Dann ist wohl klar, daß durch diesen Schalter Strom fließt. Angenommen der Leiter bewegt sich mit großer Geschwindigkeit über die Kontakte. Dann stellt sich die Frage, ob irgendwann für kurze Zeit Strom fließt.
Im Inertialsystem, in dem die Kontakte ruhen, ist wohl klar, daß kein Strom fließt, weil zu keinem Zeitpunkt der Leiter beide Kontakte gleichzeitig berührt.
Im Inertialsystem, in dem der Leiter ruht, sieht die Lage zuerst anders aus. Da der Abstand der Kontakte kleiner als die Ruhelänge des Leiters. Trotzdem fliesst kein Strom, denn der Kontakt, der den Leiter zuerst berührte, bewegt sich so schnell, daß der Strom, der sich mit Lichtgeschwindigkeit vom anderen Kontakt fließt, das Ende des Leiters erreicht, wenn der erste Kontakt ausserhalb des Leiters ist.
Damit fließt also zu keinem Zeitpunkt Strom.
@Rudi Knoth
Ja, genau. Man kann das herunterbrechen auf: Gleichzeitigkeit ist relativ, Raumartigkeit nicht.
Zwei Ereignisse, die in einem Inertialsystem gleichzeitig sind und in einem anderen nicht, können einander nicht beeinflussen.
@Rudi Knoth:
Das ist eher ein theoretischer Beitrag zum Thema Längenkontraktion.
Denn ein Leiter, der, solange alles ruht, die beiden Kontakte verbindet, lässt nun mal Strom fließen und das tut er ganz sicher auch dann noch, wenn er sich mit irgendeiner Geschwindigkeit zwischen den Kontakten durch bewegt. Ist der Leiter von vorne herein kürzer, fließt eben niemals Strom.
@Joachim Schulz:
Das ist in meiner Theorie so, nur leider in der SRT nicht. Das erkennt man daran, dass es in der SRT in “Weg-Zeit”- bzw. Minkowski-Diagrammen zu einer ct’-Achse immer eine x’-Achse gehört, auf welche ich gut verzichten kann.
@Nicht von Bedeutung 11. Januar 2019 @ 16:23
Aber auch der Strom wie auch ein elektrisches Feld hat eine endliche Geschwindigkeit nämlich die Lichtgeschwindigkeit. Auch wenn im Inertialsystem des Leiters beide Kontakte des Leiters diesen berühren, fließt nicht automatisch Strom vom vorderen Kontakt zum hinteren Kontakt. Nur wenn der hintere Kontakt vom Strom erreicht ist, wird ein Stromfluss im Stromkreis registriert.
@Rudi Knoth:
Okay, das ist zwar korrekt, aber nicht Gegenstand einer Diskussion über Längenkontraktion.
@Rudi Knoth:
Nachschlag:
Außerdem gilt LG in dieser Beziehung nur für das el. Feld. Die Geschwindigkeit des Stromes im Leiter hängt meines Wissens auch von der Anzahl der Kovalenz-Elektronen (“freie Elektronen”) darin ab.
@Joachim / 11. Januar 2019 @ 14:45
In dem Moment, wo die S’-synchronen Uhren auf dem Stab alle den Wert t’ = 0 als ihre Eigenzeit anzeigen, liegt der Stab gerade genau auf der x’-Achse. Und dieser Sachverhalt besteht natürlich auch dann noch unverändert fort, wenn er in den S-Koordinaten (t,x) dargestellt wird. Die x’-Achse liegt aber in den S-Koordinaten offenkundig “schräg”, folglich liegt auch der sich zur S’-Zeit t’ = 0 darauf befindliche Stab “schräg” in der S-Darstellung.
Wenn sich dann die S’-synchronen Stab-Uhren entlang ihrer Weltlinien zeitartig bewegen und S’-gleichzeitig alle einen anderen gemeinsamen Wert \(T’ \neq 0\) anzeigen, dann befindet sich der Stab auf der zur x’-Achse parallelen Geraden \(\{t’ = T’\}\). Die in der S-Darstellung natürlich genauso “schrag” liegt wie die x’-Achse.
Es existiert schlicht keine Darstellung des bewegten Stabes in (t,x)-Koordinaten, bei welcher der Stab parallel zur x-Achse ausgerichtet wäre; das ist unvereinbar mit der die Relativität von Gleichzeitigkeit.
Insbesondere ist diese mittelblaue Line, also die Strecke \(OC\) auf der x-Achse in der Animation (Habe ich wenigstens das jetzt korrekt identifiziert?) in der Minkowski-Geometrie nicht der bewegte Stab, sondern nur eine momentane Projektion des Stabes auf die x-Achse.
@Chrys:
Langsam muss aber mal gut sein. Die “Gleichzeitigkeit” von S’ wurde noch gar nicht “hergestellt”, denn ct’ und x’ stehen nicht im rechten Winkel aufeinander. In der (immer noch irreführenden) Animation betrachten wir die “Gleichzeitigkeit” von S.
Existiert QC in S’ real, würde er in S als QB gemessen. Existiert QB in S real würde er in S’ als QC gemessen.
Chrys schrieb (11. Januar 2019 @ 12:37):
(… zunächst einmal vielen Dank für die prompte Reaktion auf meine dringliche Nachfrage …)
> Generell ist `proper length’ für raumartige Kurven (in Analogie zur `proper time’ für zeitartige Kurven) durch ein invariantes Intergral definiert, und zwar ohne jegliche Bezugnahme auf Koordinaten.
Tja … Ich setzte dem mal entgegen, woran ich (insbesondere im Zusammenhang mit “einem Stab”, von dem ja oben die Rede)
bei “Eigenlänge, und zwar ohne jegliche Bezugnahme auf Koordinaten” bzw. kurz “Länge” denke:
Weil wir uns ja offenbar hinsichtlich (des Weglassens) “jeglicher Bezugnahme auf Koordinaten” mehr oder weniger verständigt haben,
hatte ich mir eingebildet, dass “das, dann noch übrig blieb, notwendiger Weise übereinstimmend” sein müsste; jedenfalls sofern wir über Physik nachdenken.
— Pustekuchen!: Unsere Sichtweisen sind doch jedenfalls sehr unterschiedlich …
Nun denke ich mir bei “Integral” insbesondere Riemannsches Interal (wie insbesondere Dir schon aufgefallen sein mag),
weil:
der Gedanke an “Riemannsche Partialsumme” die Betrachtung von “zunächst mal nur einem einzelnen Term” dieser Summe nahelegt, und damit ein “(Sub-)Intervall (des Integrations-Parameters)”, also immerhin jeweils zwei unterscheibare Werte des Integrations-Parameters (als “Sub-Intervall-Grenzen”). Vgl. https://en.wikipedia.org/wiki/Riemann_integral#Partitions_of_an_interval
> Im Falle einer raumartigen Strecke im Minkowski Raum vereinfacht sich dieses Integral zur Minkowski-Norm des Differenzwektors zwischen den Endpunkten der Strecke.
(Das “w” lass ich mal so stehen. 🙂
Da haben wir jedenfalls auch “die zwei” relevanten, i.A. voneinander unterscheidbaren und (deshalb) voneinander getrennten … Entitäten, als “ein Ganzes”.
Allerdings tauchte in dieser Formulierung nun der “Minkowski Raum” auf, und die “Minkowski-Norm“.
Versteht sich das (immer noch) strengstens ohne jegliche Bezugnahme auf Koordinaten ?!?
Im Zweifelsfalls würde ich lieber von “flacher Raumzeit” sprechen, ohne jegliche Bezugnahme auf Koordinaten,
und bekanntlich den darin
gegebenenzumindest als reelle Verhältniswerte ermittelbaren Intervallen \(s^2 : \mathcal E \times \mathcal E \rightarrow \mathbb R\).Anhand der (Verhältnisse von) \(s^2\)-Werte lassen sich die Teilmengen (“Geraden”) herausfinden, deren Elemente Tripel-weise gegenüber einander “gerade” lagen (Heron/Cayley/Menger/Kockendorff lassen grüßen).
Die “Vorzeichen”-Frage klären wir durch Auffinden von Tripeln
\(x, y, z \in \mathcal E : \)
\(\left( \frac{s^2[ \, x, z \, ]}{s^2[ \, x, y \, ]} \right) = \left( \frac{s^2[ \, y, z \, ]}{s^2[ \, x, y \, ]} \right) = \left( \frac{s^2[ \, x,z \, ]}{s^2[ \, y, z \, ]} \right) = 1. \)
Diejenigen Geraden, die jeweils höchstens nur ein Element solcher (“Raum”-)Tripel enthalten, heißen “zeitartig” und (auch) “(einzeln) ruhend”.
Für (zwangsläufig) andere Tripel
\(a, e, z \in \mathcal E \) mit
\(\left( \frac{s^2[ \, a, e \, ]}{s^2[ \, a, z \, ]} \right) = \left( \frac{s^2[ \, e, z \, ]}{s^2[ \, a, z \, ]} \right) = 0\)
nennen wir \( \sqrt{ s^2[ \, a, z \, ] } \) die Ping-Dauer (bzgl. \(e\)) einer zeitartigen Geraden, die \(a\) und \(z\) enthielt.
Damit suchen wir die Geraden-Paare mit konstanten gegenseitigen Ping-Dauern.
Genau solche Paare heißen “gegenüber einander ruhend”.
Der jeweilige konstante Ping-Dauer-Wert eines solchen Geraden-Paares wird noch ergänzt mit dem konventionellen Faktor “½” und dem (ebenfalls von Null verschiedenen) “Symbol-Faktor c”, zur formalen Unterscheidung der dadurch erhaltenen Längen-Werte von “allen möglichen anderen Dauern”.
Fertig ist die (Eigen-)Länge eines (raumartigen) Stabes im Flachen, ausgedrückt durch \(s^2\)-Werte.
Soweit dieser (offensichtlich von mir vorgetragener) Versuch einer “gemeinsamen Sichtweise”.
(Ich müsste für mich, als Experimental-Physiker, erst noch (er)klären, wie die erforderlichen Werte \(s^2\) zunächst überhaupt ermittelt werden sollten.)
> Die `Ruhelänge’ einer raumartigen Strecke im Minkowski Raum wird hingegen definiert als eine Koordinatenlänge mit Bezug auf ein spezielles Koordinatensystem, und zwar ohne jegliche Bezugnahme auf geometrische Invarianten.
Wieso denn ausgerechnet dieser Name ?!?
Was hat ein bestimmter Koordinaten-Abstand zweier Koordinaten-Tupel mit “Ruhe (an sich)” bzw. “Ruhe gegenüber einander” zu tun ?? …
p.s.
> Der Faktor 1/γ für die `Längenkontraktion’ in der SRT lässt sich aus der Lorentz Transformation und einer Projektion
… einer Koordinaten(!)-Projektion ? …
> praktisch in einer Zeile herleiten und begreifbar machen.
Mag sein; sofern man beim Rechnen mit bzw. Transformieren von Koordinaten von “Begreifen” reden mag.
Der Faktor “\radic{1 – β^2 }” zum Vergleich der Längen verschiedener, gegenüber einander bewegter Stäbe, in der SRT, ohne jegliche Bezugnahme auf Koordinaten, lässt sich in ein paar Zeilen herleiten.
(Und mich erstaunt gelegentlich, wer sich alles dafür nicht zu interessieren scheint. …)
(Dass jeder dieser betreffenden Stäbe dabei insbesondere als ein Paar von Enden aufzufassen ist, die gegenüber einander ruhen, wird dabei vorausgesetzt und muss also schon im voraus begriffen worden sein.)
@Joachim 14:10 hilft das kostenlos weiter: MM von 1987 Am.Jour.ofScience
https://history.aip.org/exhibits/gap/PDF/michelson.pdf
@Senf:
Danke. Ist das das Original? Sieht jedenfalls ganz danach aus – zumindest nach einem, sofern es mehrere Veröffentlichungen gab.
Aber so richtig weiter hilft es nicht, weil daraus auch nicht hervor geht, ob man auch MMI-Stellungen zwischen 0° und 90° ausprobiert hat. Die einzigen Berechnungen mit Winkeln darin (relativ am Schluß), befassen sich mit der Teilreflektion am ruhenden bzw. bewegten Strahlteiler.
@Joachim
Noch etwas Raumzeit-Geometrie als Ergänzung zu meinem Kommentar vom 11. Januar 2019 @ 17:12. Der ÜbersichtlichkeIt halber wieder mit c = 1.
Die Schar der Weltlinien von S’-synchronen Uhren auf einem Stab, der in seinem Ruhesystem S’ zur S’-Zeit \(t’ = 0\) durch die Punkte \(\{\xi\vec{e}_{x’}\mid 0 \le \xi \le 1\}\) gegeben sei, ist bei Parametrisierung durch die gemeinsame (S’-synchronisierte) Eigenzeit \(s\) dieser Uhren dargestellt durch
\[
w_\xi(s) = s\vec{e}_{t’} + \xi\vec{e}_{x’} = \gamma(s + \xi\beta)\vec{e}_t + \gamma(s\beta + \xi)\vec{e}_x, \quad 0 \le \xi \le 1.
\]
Es ist daher gerechtfertigt, den Parameter \(s\) hier auch kurz als die Eigenzeit des Stabes zu bezeichnen. In S-Koordinaten \((t,x)\) lässt sich diese parametrisierte Weltlinien-Schar alternativ schreiben als
\[
w_\xi(s) = (t_\xi(s), x_\xi(s)) = (\gamma(s + \xi\beta), \gamma(s\beta + \xi)), \quad 0 \le \xi \le 1.
\]
Mit dem Verrinnen der Eigenzeit des Stabes ist auf der x-Achse also der linke sowie der rechte Endpunkt des Stabes gemäss \(x_0(s)\) sowie \(x_1(s)\) bewegt. Die Frage, ob der in S bewegte Stab in die durch \(0 \le x \le 1/\gamma\) auf der x-Achse abgesteckte Strecke passt, lässt sich dann offenbar auch so stellen: Existiert ein \(s\) mit der Eigenschaft, dass für den linken Endpunkt \(x_9(s) \ge 0\) und für den rechten Endpunkt \(x_1(s) \le 1/\gamma\) gilt?
@All:
Noch etwas Logik
Chrys schrieb (12. Januar 2019 @ 13:00):
> […] S-Koordinaten \((t,x)\) [… und S’-Koordinaten \((t^{\prime},x^{\prime})\) …]
> [… mit Koordinaten-Transformation:] \[s \, \vec e_{t^{\prime}} + \xi \, \vec e_{x^{\prime}} = \gamma \, (s + \beta \, \xi) \, \vec e_t + \gamma \, (\beta \, s + \xi) \, \vec e_x) \]
> […]
Dabei sollen \(\vec e_{t^{\prime}}\) und \(\vec e_{x^{\prime}}\) wohl Koordinaten-Basis-Vektoren darstellen, die bzgl. eines Koordinaten-Produktes (“\(( \_ \cdot \_) : \mathbb R^2 \times \mathbb R^2 \rightarrow \mathbb R \)”) gegenüber einander orthogonal und einzeln (in geeignetem Sinne) normal wären. Und ebenso wohl \(\vec e_{t}\) und \(\vec e_{x}\).
Für \(\xi := 0, s \neq 0 \) ergibt sich somit insbesondere:
\[((s \, \vec e_{t^{\prime}}) \cdot (s \, \vec e_{t^{\prime}})) = (((\gamma \, s \, \vec e_t) + (\gamma \, \beta \, s \, \vec e_x)) \cdot ((\gamma \, s \, \vec e_t) + (\gamma \, \beta \, s \, \vec e_x))), \]
\[ s^2 (\vec e_{t^{\prime}} \cdot \vec e_{t^{\prime}}) = \gamma^2 \, s^2 ((\vec e_t \cdot \vec e_t) + \beta^2 \, (\vec e_x \cdot \vec e_x)), \]
\[ \gamma^2 = \frac{(\vec e_{t^{\prime}} \cdot \vec e_{t^{\prime}})}{((\vec e_t \cdot \vec e_t) + \beta^2 \, (\vec e_x \cdot \vec e_x))}, \]
Und ebenso für \(s := 0, \xi \neq 0 \):
\[((\xi \, \vec e_{x^{\prime}}) \cdot (\xi \, \vec e_{x^{\prime}})) = (((\gamma \, \beta \, \xi \, \vec e_t) + (\gamma \, \xi \, \vec e_x)) \cdot ((\gamma \, \beta, \xi \, \vec e_t) + (\gamma \, \xi \, \vec e_x))), \]
\[ \xi^2 (\vec e_{x^{\prime}} \cdot \vec e_{x^{\prime}}) = \gamma^2 \, \xi^2 ((\beta^2 \, \vec e_t \cdot \vec e_t) + (\vec e_x \cdot \vec e_x)), \]
\[ \gamma^2 = \frac{(\vec e_{x^{\prime}} \cdot \vec e_{x^{\prime}})}{(\beta^2 \, (\vec e_t \cdot \vec e_t) + (\vec e_x \cdot \vec e_x))}. \]
Zusammen ergibt sich:
\[\frac{(\vec e_{x^{\prime}} \cdot \vec e_{x^{\prime}})}{(\vec e_{t^{\prime}} \cdot \vec e_{t^{\prime}})} = \frac{(\beta^2 \, (\vec e_t \cdot \vec e_t) + (\vec e_x \cdot \vec e_x))}{((\vec e_t \cdot \vec e_t) + \beta^2 \, (\vec e_x \cdot \vec e_x))} = \frac{\frac{(\vec e_x \cdot \vec e_x)}{(\vec e_t \cdot \vec e_t)} + \beta^2}{1 + \beta^2 \, \frac{(\vec e_x \cdot \vec e_x)}{(\vec e_t \cdot \vec e_t)}}.\]
Parameter \(\beta\) ist demnach in der oben angegebenen Koordinaten-Transformation nur dann ein unabhängiger Parameter, falls
\[ \frac{(\vec e_{x^{\prime}} \cdot \vec e_{x^{\prime}})}{(\vec e_{t^{\prime}} \cdot \vec e_{t^{\prime}})} \, \frac{(\vec e_x \cdot \vec e_x)}{(\vec e_t \cdot \vec e_t)} = 1 \]
und
\[ \frac{(\vec e_{x^{\prime}} \cdot \vec e_{x^{\prime}})}{(\vec e_{t^{\prime}} \cdot \vec e_{t^{\prime}})} = \frac{(\vec e_x \cdot \vec e_x)}{(\vec e_t \cdot \vec e_t)}; \]
und Parameter \(\gamma\) hängt von \(\beta\) und den (in geeignetem Sinne) normalen Koordinaten-Produkten der Koordinaten-Basis-Vektoren ab wie gezeigt. (Es erscheint daher irreführend, die obige Koordinaten-Transformation überhaupt unter Verwendung von “\(\gamma\)” als gesondertem Symbol auszudrücken.)
Sagenhaft, die Verwirrung hier. Ich greife mal einen Verweis auf Wiki auf:
https://de.wikipedia.org/wiki/Lorentzkontraktion
unter “Experimentelle Bestätigungen” steht da:
“Für den mitbewegten Beobachter ist die eigene Kontraktion folglich nicht existent.”
Was für ein verdrehter Satz. Da ist eine “eigene Kontraktion”, die aber für den irgendwie doch Kontrahierten irgendwie dann doch nicht existent wäre.
Geht es noch verdrehter?
Die Auflösung ist ganz einfach: der “Kontrahierte” ist eben nicht kontrahiert. Es scheint nur jemand anderem so. Stellen wir die ganz einfache Kinderfrage: “Wer hat nun recht?”
Ganz einfach: der, der eben nicht kontrahiert ist und daher auch kein Kontrahierter ist.
Ich versuche es noch einmal ganz einfach: nur weil wir jemanden in der Ferne perspektivisch verkleinert sehen, ist der deshalb trotzdem nicht kleiner.
Nur weil jemand den “mitbewegten Beobachter” kontrahiert sieht, ist dieser eben dennoch nicht kontrahiert.
Ist das tatsächlich so schwer, dass darüber seit Wochen hier disputiert werden muss?
@Frank Wappler:
Zur Info: Man kann seine Latex-Konstrukte auch online testen, bevor man sie hier abschickt, z.B. auf zahlen-kern.de.
Die Vorschau hier macht sowas ja leider nötig. Nix für Unkluk. 😀
@A.S. 17:27 Nur weil jemand den “mitbewegten Beobachter” kontrahiert sieht, ist dieser eben dennoch nicht kontrahiert. ___ Ist das tatsächlich so schwer, dass darüber seit Wochen hier disputiert werden muss?
Wer? außer Sie! wundert sich denn seit Wochen darüber – die es verstehen, denen ist es doch klar.
Herr Senf
14. Januar 2019 @ 19:35
”
@A.S. 17:27 “Nur weil jemand den “mitbewegten Beobachter” kontrahiert sieht, ist dieser eben dennoch nicht kontrahiert. ___ Ist das tatsächlich so schwer, dass darüber seit Wochen hier disputiert werden muss?”
Wer? außer Sie! wundert sich denn seit Wochen darüber – die es verstehen, denen ist es doch klar.
”
Na prima. Immerhin Herr Senf hat also verstanden, dass die angebliche Längenkontraktion nur eine scheinbare ist. Wie sieht es damit bei den anderen hier aus?
Und was ist mit den übrigen Mythen der sRT? Verstehen Sie auch, dass damit auch die angebliche Zeitdilatation eine scheinbare ist? Und die angebliche “Relativität der Gleichzeitigkeit” damit auch hinfällig wird?
So einfach können und wollen wir es uns nicht machen. Die Längenkontraktion ist Abhängig vom Bezugssystem, aber sie ist keine Illusion. Bewegte Körper sind tatsächlich verkürzt und wenn ich hier nicht ständig die Ausfälle zweier Lieblingsfeinde löschen müsste, hätte ich den Artikel zur relativisischen Sicht auf die Längenkontraktion wohl längst fertig.
Es gibt übrigens eine schöne Parallele in der klassischen Physik: Die kinetische Energie ist auch Bezugssystemabhängig und dennoch keine Illusion. Man könnte sich ja mit Chrys auf den Standpunkt stellen, es käme nur auf die jeweilige Sicht im Ruhesystem an. Dann gäbe es keine kinetische Energie. Man könnte aber auch keine Wechselwirkungen zueinander bewegter Körper betrachten.
Für das Verstehen von Stoßprozessen ist es unerlässlich, die Körper alle im selben Bezugssystem darzustellen. Und dann sind eben einige Objekte bewegt und haben damit kinetische Energie und sind relativistisch verkürzt. (Dass außerdem ihre Uhren unterschiedlich gehen und ihr natürliches Verständnis von Gleichzeitigkeit verschieden ist, spielt im mechanischen Stoß nicht wirklich eine Rolle.)
Natürlich können und wollen wir es uns “so einfach machen” wie notwendig und erforderlich, Herr Schulz.
Und wie Herr Senf jetzt richtig bemerkt hat: nichts ist kontrahiert. Die Längenkontraktion ist ein Scheineffekt, wie die “perspektivische Verkleinerung” oder der Dopplereffekt.
Solche Scheineffekte zeichnen sich dadurch aus, dass sie bei der Beobachtung entstehen – nicht am Beobachteten.
* die entfernte Person ist nicht kleiner – sie scheint einem Beobachter nur so
* der vorbei rasende Krankenwagen ändert nicht die Frequenz seines Martinshorns – es scheint dem Beobachter nur so
* bewegte Objekte sind nicht verkürzt – es scheint dem Beobachter nur so
All dies kann auch einfach nicht anders sein, weil ja auch keine Wirkungen auf die beobachteten Umstände erfolgen die “echte Effekt” bewirken könnten. Wenn sich A realtiv zu B bewegt, so kann dies auf B doch keine Auswirkungen haben. Wir müssten ja ständig Effekten gewärtig sein, weil sich im Weltall irgendwo der Bewegungszustand von irgend etwas ändert. Das ist aufgrund fehlender Kausalitätsbeziehung aber völlig unmöglich.
Die kinetische Energie halte ich für einen ungeeigneten Vergleich. Letzlich handelt es sich ja um die Masseträgheit die nur bei Wechselwirkung mit Massen mit Relativgeschwindigkeit zum Tragen kommt. Natürlich hängt die einem Objekt zugeschriebene kinetische Energie davon ab, welche Realtivgeschwindigkeit ich betrachte. Ein mir gegenüber ruhendes Objekt (Auto) hat für mich (relativ) keine kinetische Energie – wenn wir zusammen auf eine Wand fahren wird es trotzdem krachen.
Herr Schulz,
Sie suchen auf Teufel komm raus irgend welche Erklärungen, um Inkonsistenzen in der sRT wegerklären zu können. Lassen Sie doch einfach mal die Denkmöglichkeit zu, dass die sRT, so wie sie heute interpretiert wird, nicht ganz stimmt. Plötzlich wird vieles, was vorher schwierig und unverständlich war, einfach und klar.
Die Aufgabe ist, die richtigen Teile der sRT von den Fehlinterpretationen zu trennen. Natürlich müssen Scheineffekte wie Längenkontraktion oder Zeitdilatation zB bei Beschleunigern berücksichtigt werden. Schließlich wird dort von außen beobachtet.
Aber es gibt keine verschieden schnell alternde Zwillinge, es gibt keine durch Bewegung verkürzten Distanzen, es gibt keine zerrissene Raumzeit durch eine “Relativität der Gleichzeitigkeit” und ähnliche SF-Märchen.
@Albrecht Storz
15. Januar 2019 @ 10:55
Exakt dasselbe gilt für die Längenkontraktion auch.
Joachim Schulz
15. Januar 2019 @ 11:48
@Albrecht Storz
15. Januar 2019 @ 10:55
”
“Die kinetische Energie halte ich für einen ungeeigneten Vergleich. Letzlich handelt es sich ja um die Masseträgheit die nur bei Wechselwirkung mit Massen mit Relativgeschwindigkeit zum Tragen kommt.”
Exakt dasselbe gilt für die Längenkontraktion auch.
”
Worin sehen Sie die Wechselwirkung im Falle der Längenkontraktion? Die Beobachtung etwa?
Auch ich halte die kinetische Energie für einen ungeeigneten Vergleich, denn Energien gibt es in dieser Hinsicht nur eine. Strecken aber gibt es auf zweierlei Art und zwar physische Strecken bestehend aus Teilchen und objektive Strecken bestehend aus Wellen.
Was mich nun nur noch wundert, ist die Tatsache, dass man einmal physische Längenänderung annimmt, damit sich Frequenzen egalisieren, damit sich ihre Phasen nicht verschieben (Michelson Morley) und ein anderes mal, damit sich Frequenzen nicht egalisieren, damit Uhren unterschiedliche Taktraten aufweisen können (H&K, GPS). Ganz unabhängig von der Ahnung, die ich nicht habe, stimmt da etwas ganz und gar nicht.
@Nicht von Bedeutung
15. Januar 2019 @ 12:07
Zwei wesentliche Unterschiede:
1) Bei Michelson Morley messen wir in erster Linie die Längenkontraktion, bei Hafele Keating und GPS nur die Zeitdilatation. Das sind unterschiedliche Effekte.
2) Bei Michelson Morley findet der Vergleich innerhalb eines Inertialsystems statt, bei Hafele Keating und GPS werden Uhren in unterschiedlichen Bewegungszuständen miteinander verglichen.
@Joachim Schulz:
Und wie real waren Inertialsysteme doch gleich? Was solls – ich bleibe bei meiner Ahnung. Ist es möglich, dass Sie diese nicht haben können, weil Sie von etwas überzeugt sind, dass Sie irgendwo hörten?
Michelson bewegt im Inertialsystem, für alle Beobachter (mit v) dasselbe Interferenzbild.
Lp/(c⊕v) + Lp/c⊖v) – 2Ls/c =ΔT = 0 für beliebige v ohne LK und ZD, y steckt in den Operatoren.
@Frank Wappler / 14. Januar 2019 @ 17:25
Diese Transformation von (Minkowski-orthonormalen) Lorentz frames hatte ich bereits weiter oben (28. Dezember 2018 @ 07:44) als solche hier präsentiert und seither wiederholt verwendet.
»(Es erscheint daher irreführend, die obige Koordinaten-Transformation überhaupt unter Verwendung von “γ” als gesondertem Symbol auszudrücken.)«
Das Symbol γ erscheint mit der gleichen Bedeutung schon im Blogartikel und ist im gegebenen Kontext immerhin so geläufig, dass seit ca. 1905 so gut wie niemand mehr auf die Idee gekommen ist, seine Verwendung sei irreführend.
@Joachim / 15. Januar 2019 @ 08:31
Das magnetische Feld einer bewegten Ladung ist auch keine Illusion, doch es ist in der Lorentz-covarianten Beschreibung lediglich die systemabhängige Projektion einer Invarianten, die auch im Ruhesystem der Ladung vorhanden ist. Nicht viel anders ist es mit der projizierten Länge eines Stabes, die sich systemabhängig aus einer Invarianten ergibt, der `proper length’ des Stabes. Man darf nicht `Projektion’ mit `Illusion’ verwechseln. Aber man darf vor allem nicht die Projektion eines Gegenstandes auf einen raumartigen Schnitt mit dem Gegenstand selbst verwechseln.
Der Lorentz-kontrahierte Stab kommt aus der für die SRT völlig irrigen Vorstellung, der bewegte Stab müsse sich irgendwie raumartig entlang einer x-Achse bewegen. Lorentz hat so gedacht, und für die LET ist das in Ordnung. Doch für die SRT bewegt sich ein Stab stets zeitartig, auch in seinem Ruhesystem. Wenn das ignoriert wird, kann nur inkonsistentes Zeug herauskommen.
Und insbesondere braucht die SRT keine Lorentz Kontraktion zur Erklärung des Nullresultats von Michelson & Morley. Herr Senf hatte ja irgendwo schon darauf hingewiesen, dass sich das in der SRT praktisch als Trivialität ergibt. Dem kann ich mich eigentlich nur anschliessen.
@Senf:
Ja sicher steckt das in den Operatoren, das hat Herr Schulz oben ja schon geschrieben. Aber der letzte Term deiner Rechnung ist dennoch falsch, denn er führt zu γ²-1 und nicht zu γ²-γ, wenn ich das richtig überblicke. \( – \frac{2L_s}{\sqrt{c^2}-v^2} \) müsste da stehen.
Und gerade weil es nur in den Operatoren steckt, ist meine Theorie gegenüber der RT gleichberechtigt.
@Chrys:
Das ist genau der Punkt, weshalb auch in der RT eine tatsächliche Längenänderung der Arme stattfinden müsste – damit die verschobenen Phasen an den Spiegeln und am Screen verschwinden. Das kann man programmtechnisch simulieren.
Die tatsächliche Längenänderung der Arme wird erst durch meine Hypothese überflüssig – das kann ich leider noch nicht programmtechnisch simulieren, weil es zu unverständlichem Linienchaos führt.
Hallo NvB #14:50 und PS zu mir selbst #14:13
Die Irritation ist “c+v” bzw “c-v”, das ist klassisch addiert, aber die LG “setzt sich” mit keiner anderen Geschwindigkeit zusammen. Joachim schreibt nicht umsonst Lichtlaufzeit analog wie beim Sagnac L=c*t+v*t=(c+v)*t. (c+v) ist eine mathematische Klammerung, keine physikalische Geschwindigkeit!
Das (c²-v²) wäre aufgelöst (c+v)*(c-v), da geht’s dann verwirrend, SRT-Sprech ist (c⊕v)*(c⊖v)=c².
Selbstverständlich ist noch Ls=Lp=L=Eigenlänge, Ls ist eh querinvariant und Lp hier ohne LK.
Trivial kommt für Michelson für beliebige Beobachter-v relativistisch raus L/c + L/c -2L/c =0.
@Senf:
Natürlich, es sind Differenzgeschwindigkeiten, aber darum geht es nicht. Es ging um das 2Ls/c und das passt nicht.
\( t_P=\frac{L}{c+v}+\frac{L}{c-v}=\frac{2Lc}{c^2-v^2} \)
\( t_S=\frac{L}{\sqrt{c^2-v^2}}+\frac{L}{\sqrt{c^2-v^2}}=\frac{2L}{\sqrt{c^2-v^2}} \)
In beiden Fällen für v=0
\( t=\frac{2L}{c} \)
Von daher gilt \( \frac{t_P}{t}=\gamma^2 \), \( \frac{t_S}{t}=\gamma \) und folglich \( \frac{t_P}{t_S}=\gamma \). Oben steht es zwar etwas anders, aber das Ergebnis ist das selbe. Was du da mit deiner SRT-Sprech willst, erschließt sich mir beim besten Willen nicht. Das es sich dabei um die Multiplikation zweier relativistisch addierter Geschwindigkeiten handelt, ist klar und das bei v1=c dann “v2=0” gilt auch. Nur wie man damit auf die LK kommt nicht und das führt dann dazu, dass man sie, wie du, mitsamt v unter den Tisch fallen lässt, oder wie?
[OT]
…wobei mir auffällt… ist das relativistische Additionstheorem überhaupt zulässig für Differenzgeschwindigkeiten?
Wenn nur eine Geschwindigkeit c ist, kein Problem, aber sobald beide 1 sind, ergibt dies eine Division durch 0. Das Ergebnis einer solchen Addition ist doch ohnehin eine Relativgeschwindigkeit, oder nicht? Und aus einer Geschwindigkeit, die gegenüber jedem Inertialsystem invariant sein soll eine Relative zu machen, klingt ohnehin schon irrational – man könnte dann ja bei jedem c±v grundsätzlich c annehmen.
[/OT]
Hallo NvB #18:22 “… Nur wie man damit auf die LK kommt, nicht und das führt dann dazu, dass man sie, wie du, mitsamt v unter den Tisch fallen lässt, oder wie?” Ne, ist gewöhnungsbedürftig, ich kreisele 😉 schon.
Du brauchst keine LK, nur für den Lorentz-Äther, und v_rel≠0 spielt keine Rolle für’s Einstein-Ergebnis.
Eigentlich ist diese Diskussion verfrüht, ich wollte ja abwarten, bis Joachim seine Variante kommt.
In den meisten Büchern ist es nach SRT “didaktisch” falsch vorgeführt, vlt bringt Joachim die richtige.
Einstein selbst in etwa: für das MI-Ergebnis braucht’s nur das Relativitätsprinzip, Rechnen überflüssig.
@Senf:
Steht die nicht schon im letzten Absatz des Blogs? Und dann auch noch mit Link auf jenen Blog, in welchem alle meine Beiträge, in denen ich \( (\tau_{TAI}=)\tau_{SI} \cdot t_{SI}=\tau_n \cdot t_n \) erläuterte oder die LK vorgegriffen habe, verschwunden sind.
Also entweder es gibt ein v≠0 oder es gibt auch keine LK und ZD bzw. nach meiner Theorie nur “ZD” – ganz simpel.
“Na prima. Immerhin Herr Senf hat also verstanden, dass die angebliche Längenkontraktion nur eine scheinbare ist. Wie sieht es damit bei den anderen hier aus?”
Ich bin auch für scheinbar, das scheint aber insgesamt wohl ein Definitionsproblem (wie und wo messe ich) zu sein. Hab ich so auch bei Wikipedia gefunden. Wenn an der Außenhülle des Objekts gemessen wird, zB. ein Maßband angelegt wird, dürfte sich die Länge ja eigentlich nicht verändern.
Jade
16. Januar 2019 @ 08:36
”
“Na prima. Immerhin Herr Senf hat also verstanden, dass die angebliche Längenkontraktion nur eine scheinbare ist. Wie sieht es damit bei den anderen hier aus?”
Ich bin auch für scheinbar, das scheint aber insgesamt wohl ein Definitionsproblem (wie und wo messe ich) zu sein.
”
Wenn hier Definitionsprobleme auftreten, so wird hier nicht Physik und auch nicht Mathematik verhandelt. Sondern sonstwas.
Wo ist so ein Definitionsproblem zB bei der Messung der Größe eines Objektes in der Ferne? Es ist ganz klar, dass bei korrekter Messung die korrekte Größe heraus kommt. Ignoriert aber der Messende die Entfernung, kommt Mist heraus.
Wenn jemand etwas misst, was das gemessene Objekt gar nicht erleidet (oder darauf gar nicht zu trifft), so hat der Messende Mist gemessen. So einfach ist das.
Wenn jemandem eine ihm gegenüber bewegte Länge verkürzte misst, so muss er eben mit geeigneten Korrekturtermen die korrekte Länge ermitteln.
Aber genau hier liegt der Knackpunkt der sRT. Und deshalb werden sich alle mit aller Macht daraus heraus winden. Das beste Mittel erscheint dann immer, mit irgendwelchen Wahnsinns-Formeln um sich zu werfen. Anstatt die Frage sachlich und auf der einfachsten Ebene zu betrachten:
einem “ruhenden Beobachter” erscheint ein “bewegter Beobachter” verkürzt. Der “bewegte Beobachter” stellt aber eindeutig fest, dass er nicht verkürzt ist. Also ist der “ruhende Beobachter” bei der Messung einem Scheineffekt erlegen.
Fertig. Da kann man mit Kreuzprodukt, Tau, Omega, Delta, wunderbar anzuschauendem LaTex-Formeln oder sonstigem mathematischen Kram kommen. Der Sachverhalt bleibt trotzdem wie er ist.
Also sofern es noch eine (richtige) Erklärung dafür seitens Herrn Schulz geben sollte, dann kann es nur die Raumzeit selber betreffen und sich schlicht auf die Aussage beschränken, die Raumzeit verhielte sich halt so.
Womit wir dann wohl beim Thema seines nächsten Blogs sein dürften, für welchen er einst den von mir bei SciLogs eingeführten Begriff “verstofflichte Mathematik” verwenden wollte.
Aber ehrlich gesagt, gefällt mir meine Idee, physische Strecken (feste Gegenstände) und “objektive” Strecken (Wellenlängen) zu trennen, weitaus besser, als Raum und Zeit in einer nötigen Zusatzannahme (Raumzeit) zu verbinden. Zusatzannahmen sollten, wenn es nach einem sich rasierenden Ockham ginge, verworfen werden, sobald es einfachere Erklärungen gibt.
@Albrecht Storz 16. Januar 2019 @ 11:26
Genau das sieht Herr Wappler möglicherweise anders. Wenn die “richtige” Länge also im Ruhesystem bestimmt werden soll, dann wird die Längenkontraktion in Betracht gezogen. Wenn etwa ein Astronom das Spektrum einer fernen Galaxie anschaut, dann wird er die relativistische Formel für den Dopplereffekt benutzen, um die “Geschwindigkeit” dieser Galaxie zu bestimmen.
@Rudi Knoth:
Etwa auch anders als Herr Schulz, Chrys oder gar Sie? Das ist nämlich das, was mir hier auffällt… Jeder SRT-Befürworter (hier) sieht das Ein oder Andere anders. 😉
Und um das, was sie Anders sehen, zu verdeutlichen, werfen sie sich gegenseitig Formeln und Animationen zu, die mit realen Beobachtungen oder Logik kaum noch etwas zu tun haben können – über Logik muss man sich nämlich weiträumig einig sein, sonst ists keine Logik.
@Nicht von Bedeutung 16. Januar 2019 @ 15:09
Die Grundaussagen der SRT werden natürlich von allen SRT-Befürwortern akzeptiert. Unterschiede siehe ich in folgenden Aspekten:
1. Didaktik der SRT. Damit ist die Vermittlung gemeint. Das kann Dopplereffekt (Schulz und ich), Koordinatenfreie Darstellung (Wappler) oder Minkowski-Darstellung (Chris) sein.
2. Unterschiedliche Formulierungen
3. “Philosophische” Aspekte wie Falsifizierbarkeit etc.
@Rudi Knoth:
Schon klar… aber wieso taucht unter 3. nicht “Nicht von Bedeutung” auf? 😆
“Philosophische” Aspekte steht glücklicherweise nicht umsonst in Anführungszeichen. Man muss wissen, worauf sie Gründen. Worauf gründeten z.B. die einst “philosophischen” Aspekte eines gewissen Herrn Einstein? Nicht etwa auf “Education and Thinking” kurz auf Autodidaktik? Welcher Personengruppe hat wohl Einstein damals nur “Blödsinn” erzählt? 😉
Rudi Knoth
16. Januar 2019 @ 16:35
“Die Grundaussagen der SRT werden natürlich von allen SRT-Befürwortern akzeptiert.”
Das halte ich für einen frommen Wunsch.
– Gibt es eine physikalische Wirkung einer “Längenkontraktion”, außer als Scheineffekt für einen Beobachter auftretend?
– Gibt es eine physikalische Wirkung einer “Zeitdilatation”, außer als Scheineffekt für einen Beobachter auftretend?
…
Und nicht zu vergessen: die “Relativität der Gleichzeitigkeit” ist für uns Menschen, die wir mit den modernen Mitteln der Kommunikation (digitale Übertragung von Bilddaten, Zeitstempel, Berechnung von Laufzeiten, …) vertraut sind, völliger Unsinn.
@Albrecht Storz 17. Januar 2019 @ 07:24
Was die “Scheineffekte” Zeitdilatation und Längenkontraktion angeht, soe sind diese schon “Wirklichkeit”.
Bei der Zeitdilatation gibt es die bekannten kosmischen Myonen, die in grosser Zahl auf der Erde eintreffen, obwohl die Halbwertszeit 2 Mikrosekunden beträgt und die Strecke 10 Kilometer beträgt.
Für die Längenkontraktion gibt es bei Schwerionen Effekte, die mit der Längenkontraktion erklärt werden.
Was die Relativität der Gleichzeitigkeit angeht, so erklärt diese die seit langem bekannte astronomische Aberration bei der Annahme der Wellenatur des Lichtes. Die Erklärung über Laufzeiteffekte hat insoweit ein Problem, weil auch mit Wasser gefüllte Teleskope die gleiche Abweichung zeigen.
Ob Scheineffekt, Messeffekt oder Wirklichkeit ist natürlich immer auch eine Definitionsfrage. Natürlich man bei Kenntnis der Theorie von einer Messung der bewegten Länge auf die Ruhelänge zurückrechnen. Und die Ruhelänge als die wahre Länge zu bezeichnen ist durchaus nachvollziehbar. Ich wehre mich aber dagegen, die Längenkontraktion als Scheineffekt darzustellen, weil das leicht die Assoziation zu einem optischen Effekt weckt. Also als läge es an den Lichtlaufzeiten oder der Aberration, dass das Objekt kürzer scheint als es ist. Das Gegenteil ist der Fall. Die Längenkontraktion kommt heraus, wenn man die Laufzeiteffekte herausrechnet.
Rudi Knoth
17. Januar 2019 @ 08:32
“Was die “Scheineffekte” Zeitdilatation und Längenkontraktion angeht, soe sind diese schon “Wirklichkeit”. ”
Was ist dann wohl “Wirklichkeit” in Anführungszeichen? Typische Leer-Aussage von sRT-Vertretern.
Eine Kontraktion ohne Kontraktion ist nicht einmal “Wirklichkeit” in Anführungszeichen, sondern reiner Unfug.
“Für den mitbewegten Beobachter ist die eigene Kontraktion folglich nicht existent.”
Der Betroffene ist nicht betroffen? Der Kontrahierte nicht kontrahiert?
Das ist kein “Scheineffekt”, sondern ein Scheineffekt, und dieser Scheineffekt ist nicht “Wirklichkeit”, sondern Wirklichkeit.
Joachim Schulz
17. Januar 2019 @ 09:50
” Ich wehre mich aber dagegen, die Längenkontraktion als Scheineffekt darzustellen, weil das leicht die Assoziation zu einem optischen Effekt weckt.”
Hier missdeuten Sie das “schein” vom “Scheineffekt”. Auch der Doppler-Effekt ist ein Scheineffekt, obwohl er nichts mit Optik zu tun hat: es handelt sich ja idR (zumindest in der Mehrzahl der Erwähnungen) um ein akustisches Phänomen.
Außerdem frage ich mich, was Sie an Assoziationen stört. Geht es Ihnen mehr um Didaktik oder um Inhalte?
Und drittens ist die “Lägenkontraktion” natürlich ein Scheineffekt. Denn der Beobachter scheint eine Kontraktion zu beobachten wo tatsächliche keine ist. Es ist wie mit der Perspektive: ein entfernter Mensch scheint kleiner, ist es aber nicht. Ein Scheineffekt also.
Albrecht Storz
17. Januar 2019 @ 10:04
Der klassische Dopplereffekt ist ein Laufzeit-Effekt, wenn man die Laufzeiten herausrechnet, bleibt die Zeitdilatation übrig.
Da ist Ihnen ein “scheint” zuviel reingerutscht. Er beobachtet tatsächlich. Aber Sie irren sich: Der Beobachter sieht eine Kugel gedreht, erst nach Herausrechnen der Laufzeiten ergibt sich, dass die Kugel in Wahrheit in Bewegungsrichtung gestaucht ist. Auch hier: Laufzeiteffekt plus Längenkontraktion.
@Albrecht Storz 17. Januar 2019 @ 09:53
Mit dieser Wirklichkeit meine ich eine Wirklichkeit für den Beobachter gegenüber dem sich das Objekt bewegt. Wenn er etwa eine Längenmessung mit einer Lichtschranke vornimmt, wird er eine kürzere Längeals die Ruhelänge des Objektes messen. Für ihn ist also diese Länge wirklich. Ebenso wird er die Zeittakte einer Uhr, im Moment, in dem er diese senkrecht zur Bewegungsrichtung empfängt, langsamer als für einen Beobachter, der sich mit der Uhr bewegt messen.
Joachim Schulz
17. Januar 2019 @ 10:12
“Der klassische Dopplereffekt ist ein Laufzeit-Effekt, wenn man die Laufzeiten herausrechnet, bleibt die Zeitdilatation übrig.”
Ich spreche ganz konkret vom akustischen Doppler-Effekt. Also von dem, was die meisten Leute unter “Doppler-Effekt” verstehen. Deshalb auch an anderer Stelle mein Hinweis auf das Martinshorn, von dessen Klang auch die meisten Menschen den Doppler-Effekt kennen.
https://de.wikipedia.org/wiki/Doppler-Effekt
“Da ist Ihnen ein “scheint” zuviel reingerutscht.”
Nein. Der Beobachter scheint eine Kontraktion wahrzunehmen, die aber nicht der Fall ist. Deshalb spricht man auch davon, dass jemandem “etwas so und so erscheine”.
Gedrehte Kugel? Von mir aus.
Tatsache ist:
Ein relativ zu einem “ruhenden Beobachter” dagegen “bewegter Beobachter” erscheint dem “ruhenden Beobachter” kontrahiert. Der “bewegte Beobachter” kann aber objektiv feststellen, dass er nicht kontrahiert ist. Also scheint dem “ruhenden Beobachter” der “bewegte Beobachter” nur kontrahiert. Denn tatsächlich ist keine Kontraktion beim “bewegten Beobachter” der Fall. Ein Scheineffekt also.
Rudi Knoth
17. Januar 2019 @ 11:08
“Mit dieser Wirklichkeit meine ich eine Wirklichkeit für den Beobachter gegenüber dem sich das Objekt bewegt.”
Es erscheint mir in keinerlei Hinsicht zielführend, nun auch noch “verschiedene Wirklichkeiten” anzunehmen, nur um die sRT zu retten. Darauf lasse ich mich gewiss nicht ein.
Die Frage ob die SRT die Natur richtig beschreibt ist lange experimentell geklärt, ja sie tut es. Es gibt da unter den Physikern keine zwei Gruppen, die Relativisten und die Anderen die sich auf Augenhöhe gegenüber stehen. Auch SRT-Befürworter klingt so, als wäre es noch immer eine offene Geschmacksfrage.
.
Wenn sich nicht dreht und beschleunigt ist die SRT auch wirklich sehr einfach, von der Mathematik und generell.
.
Es gilt nur noch diese richtig zu verstehen, oder eben nicht.
@Joachim Schulz:
Ja genau. Eine Definitionsfrage. Bemessen wir die sich ändernden Strecken, die Doppler-Effekte auslösen über die Frequenzen, die man dort misst. Oops… Geht ja gar nicht… Es wurde nämlich bisher noch nicht eine einzige Wellenlänge definiert, geschweige denn eine Periodendauer. Aber kein Problem, denn wir kennen ja die Lichtgeschwindigkeit, also rechne man \( \lambda=\frac{c}{f}=ct \) in Lichtsekunden also \( \lambda=\frac{1}{f}=t \). Dummerweise kann man mit diesen Strecken kaum etwas messen, weil sie von der Zeit abhängen – nicht mal einen Doppler-Effekt, zumindest keinen, der noch symmetrisch ausfallen würde. Irgendwo hat man also mal eine feste Strecke festgelegt, von der nun auch angenommen wird, sie würde relativistischen Effekten unterliegen, was aber nicht der Fall ist. Oder woher kommen wohl die Probleme, die auftauchen, wenn man ruhende Strecken mit bewegten Uhren misst/bestimmt/herstellt? Es sind nicht die Naturgesetze, die Lorentz-Invariant sind, sondern Kristallgitterabstände, die überhaupt (bei stabilem Druck und stabiler Temperatur) invariant sind. Sagen Sie bloß nicht, diese Behauptung wäre unbelegt.
@Joachim Schulz:
Korrektur:
Wenn ich es mir recht überlege, muss es nach meiner Theorie folgerichtig \( \lambda=c\tau \) bzw. \( \lambda=\tau \) heißen. Noch ist das aber egal.
@Rudi Knoth / 17. Januar 2019 @ 11:08
»Wenn er [ein ruhender Beobachter] etwa eine Längenmessung mit einer Lichtschranke vornimmt, wird er eine kürzere Länge[]als die Ruhelänge des [für den Beobachter bewegten] Objektes messen.«
Darf ich gedanken-experimentell da nochmals auf den langen Zug im kurzen Bahnhof rekurrieren? Nennen wir hierzu dasjenige Ende des Bahnsteigs, wo der Zug in den Bahnhof hineinfährt, die Einfahrt, und das andere Ende, wo er wieder hinausfährt, die Ausfahrt. Es erfolge nun an Einfahrt und Ausfahrt `Bhf’-gleichzeitig jeweils ein Lichtblitz. Aus der Relativität von Gleichzeitigkeit folgt bekanntlich, dass sich diese beiden Lichtblitze `Zug’-ungleichzeitig ereignen. Doch welcher der beiden Lichtblitze ereignet sich dann im System `Zug’ eigentlich früher — der bei der Einfahrt oder der bei der Ausfahrt?
N.B. Gefragt ist dabei nicht nach visuellen Effekten für die Wahrnehmung des Lokführers, sondern allein danach, was die Lorentz Tranf. hierzu für die SRT aussagt.
@Chrys 17. Januar 2019 @ 14:09
Nach der LoTra wohl das Signal von Ausfahrt. Der Lokführer sieht zwar beim Passieren der Einfahrt das Signal sofort und das der Ausfahrt später, aber nach der Korrektur über den Abstand kommt das Signal der Ausfahrt “früher” an.
@Chrys:
Ging das Gedankenexperiment nicht noch ein wenig anders? War von dem Zug nicht bloß ein Punkt interessant, der sich mit einer gewissen Geschwindigkeit zwischen den beiden Blitzen bewegte und man klassisch und relativistisch berechnen musste, wann an diesem Punkt die Blitze im Zug gleichzeitig gesehen würden, wobei man bei beiden Rechnungen auf unterschiedliche Ergebnisse kommt? Wichtig, war dabei doch, dass es im Zug einen solchen Punkt gibt, dieser aber nicht mehr im Zentrum des Bahnhofs liegt, oder nicht?
Das ist eigentlich einfach zu verstehen: Im Ruhesystem Zug ist der Zug länger als der Bahnhof, also muss die Spitze die Ausfahrt früher erreichen als das Ende die Einfahrt.
@Joachim Schulz:
So einfach ist das eben nicht zu verstehen, jedenfalls nicht von meiner Warte aus. Von meiner Warte aus ist man in dieser Hinsicht nämlich nicht konsequent genug. Alles kreist um den Satz: “Ja, ein 229,4m langer Zug passt bei 0,9c in einen 100m langen Bahnhof, er darf nur nicht anhalten.”
Denn wenn er anhält, schießt der letzte Waggon aus der Einfahrt des Bahnhofs wieder hinaus, oder es geschehen Dinge, die Sie gar nicht lustig fanden.
Werfen wir noch mal den Bahnhofsmeter in den fahrenden Zug – er ändert seine Länge – warum auch immer – ja nicht. Wie lang wäre denn der Meter, wenn der Zug plötzlich anhält, und warum (der Meter verbleibt dabei natürlich im Zug)? Wäre er
a) länger als der ursprüngliche Bahnhofsmeter, wie beim Fall, in welchem der letzte Waggon aus der Einfahrt wieder hinausschießt? oder
b) genauso lang, wie der ursprüngliche Bahnhofsmeter, weil die LK eigentlich nie tatsächlich stattfand?
Was denn nun?
Joachim Schulz schrieb (17. Januar 2019 @ 09:50):
> […] Natürlich [kann] man bei Kenntnis der Theorie von einer Messung der bewegten Länge auf die Ruhelänge zurückrechnen. Und die Ruhelänge als die wahre Länge zu bezeichnen ist durchaus nachvollziehbar.
Ich empfehle (deshalb), auf die Erwähnung von jeglichen “un-wahren Längen” ganz zu verzichten.
Längenangaben lassen sich (stattdessen) jeweils dadurch ganz eindeutig machen, dass das betreffende Paar von gegenüber einander ruhenden Enden ausdrücklich genannt wird, um dessen Länge es dabei geht.
Zum Beispiel lassen sich dadurch
– die Länge einer bestimmten Garage (d.h. die Distanz zwischen Garagen-Tor unf Garagen-Rückwand),
– die Länge eines bestimmten Bahnhofs (d.h. die Distanz zwischen Einfahrt-Signal und Ausfahrt-Signal),
– die Länge eines bestimmten Zuges (d.h. die Distanze zwischen Lokomotiven-Spitze und Caboose-Bremswägelchen-Zugende) oder
– die Länge eines bestimmten Pfeils (d.h. zwischen der äußersten Pfeilspitze und dem äußersten Ende der Nocke)
bezeichnen und unterscheiden.
Und natürlich kann man in Anwendung der (S)RT, nämlich durch Anwendung der Einstein-Projektion, z.B. die Länge eines Bahnhofs und die Länge eines Zuges insbesondere auch dann miteinander vergleichen (also deren numerisches Verhältnis messen), falls sich diese beiden gegenüber einander gleichförmig bewegten.
> Ich wehre mich aber dagegen, die Längenkontraktion als Scheineffekt darzustellen […]
Ich auch. Aber mehr noch:
Ich wehre mich dagegen, die Längenkontraktion überhaupt als “Effekt” darzustellen.
Es handelt sich vielmehr um ein Messverfahren der SRT (zum Vergleichen der Längen von Gegenständen, die nicht gegenüber einander ruhten).
Nicht von Bedeutung
17. Januar 2019 @ 15:53
Er ist aber auch noch immer mit 0.9c unterwegs. Das heißt, er verlässt im Nullkommenichts den Zug durch die Rückwand. Wenn wir ihn dagegen im Zug abbremsen, wird er sich zwingend verformen. (Je nachdem, wo Sie die Bremskraft anlegen und wie zäh das Material ist.)
Nun ja, wenn man es schafft den Bahnhofsmeter schnell genug auf 0,9c zu beschleunigen ist er im Zug einen Zugmeter und damit SI Meter lang und damit aus Sicht des Bahnhofs kürzer oder?
Jetzt bremse ich ab so das der Zug zum Bahnhof ruht, dann ist er einen Bahnhofsmeter lang oder? Wenn ich am Bahnhof einen Vergleichsmeter habe der vorher genau so lang war wie der geworfene Meter sind die beiden dann jetzt auch wieder gleich lang. Obwohl die Längenkontraktion stattgefunden hat als ich ihn auf Zuggeschwindigkeit gebracht habe.
Frank Wappler
17. Januar 2019 @ 16:23
Sie machen es sich zu einfach. Es gibt nicht die Länge einer bestimmten Garage. Die Garage wird repräsentiert durch ein Bündel von Weltlinien der einzelnen Atome oder meinetwegen Punktmassen, aus denen sie besteht. Jede Weltlinie besteht aus einer unendlichen Schar von Raum-Zeit-Punkten (sogenannten Ereignissen). In zueinander bewegten Koordinatensystemen sind unterschiedliche Ereignisse von jeweils Tor und Rückseite gleichzeitig. Deshalb ist auch ihre räumliche Länge unterschiedlich. Die augenblickliche Länge einer Garage ist der raumartige Abstand des Ereignisses des Tors von dem Ereignis der Rückseite, das mit diesem im betrachteten System Gleichzeitig ist.
@Uli Schoppe
Genau. Wenn man es schafft, den Stab schnell aber sanft genug zu beschleunigen, ist er hinterher kürzer. Das geht übrigens indem man das hintere Ende stärker beschleunigt als das vordere. Rindler-Koordinaten sind das Stichwort.
@Joachim Schulz:
Also dass sich der Bahnhofsmeter durch die Zugrückwand umgehend wieder verabschiedet, war nie Teil des Gedankenexperiments und mit der plötzlichen Verformung (nicht zufällig auf die Länge eines Zug-Meters?) käme man ruhend im Zug nicht mehr auf die selbe Länge, mit der man den Zug ruhend am Bahnhof gemessen hat – das aber behauptete Herr Krüger. Wissen Sie, was eine Zwickmühle ist? In einer solchen befindet ihr euch gerade.
Nun mache ich es Ihnen mal einfach. Die Raumzeit wird in der RT wie ein neuer Hammer verwendet, der jedes Problem wie einen Nagel aussehen lässt. Tatsächlich aber hängen Raum und Zeit nur auf eine Art zusammen, nämlich über Periodendauern und Wellenlängen, was aber nicht der selbe Nagel wie Periodendauern und Kristallgitterabstände ist. Niemals war ein Paradigmenwechsel nötiger als hier.
@Joachim Schulz:
Okaaayyy… bei mir wurde der Zugmeter zwar länger, was aber kein Problem darstellt, weil er mit der Zug-Uhr hergestellt wurde, während Herr Schoppes Bahnhofs-Meter nur mit der Zug-Uhr nachgemessen wurde. Alles kein Problem. Nur, ähhh… Wieso ist meine Version falsch und Herrn Schoppes Version richtig? Warum waren wir uns uneins über die Längenänderung des SI-Meters, während Sie beim selben Thema mit Herrn Schoppe konform gehen? Wissen Sie jetzt, was eine Zwickmühle ist?
@Joachim Schulz:
…wobei mir grad noch auffällt, dass Herr Schoppes Version mit dem Resultat a) Endet – der letzte Wagon schießt beim Abbremsen des Zuges wieder aus der Bahnhofseinfahrt hinaus (oder es geschehen andere unlustige Dinge).
Mehr und mehr fühle ich mich in meinen Hypothesen bestätigt, auch wenn hier alle widersprechen.
@Rudi Knoth / 17. Januar 2019 @ 11:08
»Nach der LoTra wohl das Signal von Ausfahrt.«
Sicher?
Denken wir uns noch zwei jeweils an Ein- und Ausfahrt postierte Bhf-synchrone Uhren hinzu; die Lichtblitze sollen e.g. erfolgen, wenn beide Uhren `0′ anzeigen. Vom Zug aus beurteilt hat jedoch der Anzeigewert der Einfahrt-Uhr einen konstanten positiven Offset gegenüber dem der Ausfahrt-Uhr, d.h., die Einfahrt-Uhr geht gegenüber der Ausfahrt-Uhr vor — ganz egal, wo sich der Zug auf der Bahnstrecke befindet, und welche visuellen Eindrücke der Lokführer von den Anzeigen dieser Uhren haben mag.
Vom Zug aus beurteilt zeigt also in dem Moment, wo die Ausfahrt-Uhr `0′ anzeigt, die ihr vorauseilende Einfahrt-Uhr einen grösseren Wert an, und deren Anzeige `0′ ist dann bereits passé. Demnach ereignet sich im System `Zug’ der Lichtblitz an der Einfahrt früher als der an der Ausfahrt.
@Joachim Schulz:
Und dann auch noch dieses Wort “zäh”. Kristallgitterabstände… Kristalle sind mWn von Natur aus unheimlich zäh – vor Allem Silizium oder Diamant.
Ich nenne das mal Schachmatt oder verstehe ich mal wieder irgendwelche Grundlagen nicht?
Hallo Herr Wappler #16:23 “Ich wehre mich dagegen, die Längenkontraktion überhaupt als “Effekt” darzustellen. Es handelt sich vielmehr um ein Messverfahren der SRT (zum Vergleichen der Längen von Gegenständen, die nicht gegenüber einander ruhten).” Schön, daß Sie es wiederholt wiederholen.
Ich werfe ja auch immer ein, daß die LK ein metrologischer Effekt des synchronen Messens ist.
Der y-Faktor “gilt nicht” für das zu vermessende Objekt, er “gilt” für den messenden Beobachter.
Wenn wir ohne LK messen möchten, müßten wir eine Ungleichzeitigkeit wählen, dafür müßten wir aber vorher die Geschwindigkeit v_rel bestimmen. Die Meßmethode soll mal wer einem Physiker erklären 🙂
Für beliebige Beobachter ist die gleichzeitige Ankunft der Signale von beiden Meßenden eindeutig.
Nur müssen diese Beobachter mit ihrer Ungleichzeitigkeit gegeneinander klarkommen – eben Rechnen.
Aus dem Verhältnis L/Lo<1 kann/muß jeder "sein y" bestimmen und sein v_rel zum Objekt. Dem Objekt wird auch nicht weh getan, keiner verkürzt es, kein Äther – wie beim Zahnarzt, wenn der nur guckt.
@Senf:
Ähhhh… habe ich das nicht schon zur Genüge getan?
Dann stimmen also die Rechnungen für die Laufzeiten nicht, oder wie? Relativistische Geschwindigkeitsadditionen haben in denen nichts verloren, weil es um Differenzen von Geschwindigkeiten geht. Geht man davon aus, dass korrekt gerechnet wurde, bleiben nur tatsächliche LK oder meine Hypothese (längs und radial unabhängig) für starre Interferenzmuster übrig.
Es ist unglaublich, was hier läuft. 😆
@Chrys 17. Januar 2019 @ 17:27
Sorry, da lag ich wohl falsch. Nur wenn ich annehme, daß die Uhren gleichzeitig im Zug abgelesen werden, geht die Uhr am Ausgang vor. Sonst ist es nach der LoTra umgekehrt.
@Joachim
.
Wobei diese “Verformung” eben eine andere ist, als jene die der Bahnhofs-Meter im Bahnhofssystem erfährt, wenn er in den Zug geworfen wird und lorentzkontrahiert.
.
Denn bei dieser Kontraktion spielt das Material gar keine Rolle, alleine die Geschwindigkeit mit der sich der Meterstab dann im Ruhesystem bewegt ist entscheidend. Und wird er aus dem Zug wieder zurück auf den Bahnhof geworfen, dann “dehnt” er sich wieder auf die Länge des SI-Meters am Bahnhof aus.
.
Würde im Zug ein Meterstab nach der SI Definition hergestellt, und aus dem Fenster auf den Bahnhof geworfen, würde er sich auch entsprechend “ausdehnen”.
.
Das wirklich “spannende” dabei ist, dass aus dem Zug gemessen der sich nicht ausdehnt sondern kontrahiert.
Ich demonstrier das mal:
So wollte Krüger es mir “beibringen”.
Also ist seine Länge nun tatsächlich eine, die sich von der Länge des Bahnhofs-Meters unterscheidet, wie ich sagte?
Ach, es ist bloß eine andere Länge, als die, die sich von der Länge des Bahnhofs-Meters unterscheidet, wie ich sagte.
Ab hier ist’s nur noch Double-Talk, denn offenbar ist die tatsächliche LK selektiv. Wenn Kritiker sie erwähnen, dann wird sie geleugnet und wenn Kritiker sie leugnen, ist sie vorhanden, oder wie? Solche Manöver funktionieren bei kritischen Denkern nicht!
Chrys
17. Januar 2019 @ 14:09
Die Frage lässt sich gut am bereits oben verlinkten animierten Raumzeitdiagramm beantworten:
Es handelt sich um die Ereignisse O und C. O ist die Einfahrt des Zugendes und C die Ausfahrt der Zugspitze. Diese Ereignisse geschehen zur Zeit t=0. Im Zugsystem liegt C aber unterhalb der x’-Achse, also zu einer Zeit t'<0 Null. Die Ausfahrt geschieht im Zugsystem früher. Herr Knoth hatte sich nicht geirrt.
@Joachim Schulz:
Zugende an Einfahrt und Zugspitze an Ausfahrt finden in t (bei t=0) aber nun mal nicht Gleichzeitg statt. Das sieht man aber erst, wenn man den bewegten Zug ins Ruhe- und den Bahnhof entsprechend ins bewegte System transformiert. Dann kann man die Zuglänge (jetzt eine waagerechte Strecke) entlang des blauen Bandes (jetzt senkrecht verlaufend) animieren. C liegt dann immernoch unterhalb der (nun waagerechten) x’-Achse und daraus folgt dann die Meßreihenfolge am Bahnhof – ZS an Einfahrt, ZS an Ausfahrt, ZE an Einfahrt und ZE an Ausfahrt. Die Gleichzeitigkeislinien des Bahnhofs verlaufen nun alle parallel zur x’-Achse vor der Transformation. Auf einer dieser Linien dürfen Sie nun die beiden Blitze platzieren und schon ist das Ergebnis umgekehrt – Blitz an O geschieht aus Sicht des Zuges früher.
https://youtu.be/6KhMNqwM9wY?t=1025
@Rudi Knoth / 17. Januar 2019 @ 18:45
Das mit dem Clock Offset habe ich mir jetzt nochmals überlegt. Der Offset meint hier die im Zug ermittlete Zeitdauer zwischen zwei gleichen Anzeigen der beiden Bhf-Uhren, und ich hätte noch hinzufügen sollen, dass ich mich mit dem Vorzeichen beim Offset an dem Standard orientiere, wie er auch bei NTP verwendet wird. Dann ist aber die Uhr mit dem positiven Offset gegenüber der andern diejenige, die vom Zug aus beurteilt nachgeht. Ich schrieb es zuvor umgekehrt, das nehme ich zurück. Wie ich es jetzt sehe war Ihre Chronologie der Lichtblitze also schon richtig.
@Joachim Schulz:
Okay, Irrtum meinerseits. Die Gleichzeitigkeit ist ja unabhängig vom Winkel zur ct-Achse immer parallel zur x-Achse und die hat ja nun Gefälle und keine Steigung mehr. Also doch Blitz C zuerst.
@all:
Lassen Sie uns bitte bei der Lorentztransformation bleiben und und nicht durch akustischen Dopplereffekt oder triviale Laufzeiteffekte ablenken lassen.
Ich möchte mich auch bei Chrys entschuldigen, dass ich mich etwas ungeduldig gezeigt habe. Ich sehe immer noch eine Diskrepanz in unserer Sichtweise, aber ich bin sehr Dankbar für die Anregungen, die sicher in einen meiner nächsten Artikel eingehen werden.
Auch Herrn Wappler möchte ich für seine konstruktiven Beiträge danken.
Und er hat es wieder gemacht: andere Leute dürfen hier jeden Senf abgeben. Meine Kommentare werden weg gelöscht. Damit bleibt unbegründetes Gelaber stehen und Richtigstellungen werden in den Orkus verbannt. Bravo.
Gut, ich habe einfach immer noch nicht verstanden, dass dies ein Blog für pseudowissenschaftliches Geschwafel ist (“verschiedene Wirklichkeiten”, “Scheineffekte sind keine Scheineffekte”, “nicht-kontrahierte Kontraktionen”, Ereignisse werden mit deren Wahrnehmung verwechselt, Definitionen von Begriffen sind unerwünscht, …). Ich unterliege immer noch der Täuschung, dass hier auch nur ein Einziger an Logik, Argumenten, Physik, Wahrheit irgend ein Interesse hätte …
Herr Schulz,
damit Sie sich nicht aus der Verantwortung schleichen können:
im Folgenden wiederhole ich, was Sie wegzensiert haben, was aber ganz wesentliche zu der Diskussion über Scheineffekte, die eben insbesondere auch bei der Längenbestimmung (offensichtliches Thema dieses Blogs) eine Rolle spielen, beitragen könnte – wenn denn eine fundierte Diskussion erwünscht wäre.
Zitat aus meiner Post:
“Ein Scheineffekt zeichnet sich dadurch aus, dass er nicht durch den Beobachtungsgegenstand selbst, sondern durch Bedingungen bei der
Beobachtung des Beobachtungsgegenstandes verursacht ist.
[…]
Ein Scheineffekt ist ein Effekt, der nicht auf Gegebenheiten des Beobachtungsgegenstand selbst beruht, sondern auf Bedingungen bei der
Beobachtung. Damit zeichnen sich Scheineffekte dadurch aus, dass verschiedene Beobachter verschiedene Beobachtungen am selben
Beobachtungsgegenstand machen. Ziel von Wissenschaft und Physik ist es, aus den verschiedenen Beobachtungen verschiedener
Beobachtungen die Scheineffekte zu identifizieren und zu eliminieren, um eine objektive, für alle Beobachter gültige Aussage über den
Beobachtungsgegenstand machen zu können.”
Wenn Sie solche Beiträge wegzensieren, muss man als Leser und Schreiber in diesem Blog zum Urteil kommen, dass keine fundierte Diskussion, sondern vages Herumlavieren erwünscht ist. Beliebiges, freidrehendes “philosophieren” über “Scheineffekte” bleibt stehen, eine klare Unterscheidung zwischen den Begriffen “Effekt” und “Scheineffekt” wird von Ihnen gelöscht.
Was für ein Problem haben Sie mit klar definierten Begriffen?
Wann wird denn bei scilogs der neue KI-Spamfilter aktiviert?
Herr Senf schrieb (17. Januar 2019 @ 17:42):
> […] Ich werfe ja auch immer ein, daß die LK ein metrologischer Effekt des synchronen Messens ist.
Mir scheint die Bezeichnung als “Effekt” unpassend, weil bzw. sofern damit etwas gemeint ist, das nicht unbedingt von vornherein und zwangsläufig feststeht, sondern das beeindruckt bzw. beeindrucken soll, das erst durch die konkrete Anschauung bestimmt wird und mehr mit “experimentellem Befund” bzw. “experimentellem Test” zu tun hätte.
Deshalb bezeichne ich die (aus historischen Gründen so genannte) “Längenkontraktion” als Messoperation und als Konsequenz der dafür zu befolgenden Versuchsanordnung (“Einstein-Projektion”).
> Der y-Faktor
… gemeint ist sicherlich der (aus historischen Gründen so genannte) “Lorentz-Faktor √{ 1 – β^2 }”, bisweilen auch abgekürzt als “1/γ” (sofern es sich versteht, dass mit “β” dabei die reell-wertige, im Rahmen der RT definierte Messgröße gegenseitig-gleichförmiger Bewegung gemeint ist, und nicht etwa nur irgendein numerischer Parameter irgendeiner Koordinaten-Transformation) …
> “gilt nicht” für das zu vermessende Objekt, er “gilt” für den messenden Beobachter.
Die Einstein-Projektion (“vom Objekt auf das Bild”, also von zwei bestimmten identifizierbaren Enden des einen Stabes, auf die zwei bestimmten identifizierbaren Enden eines anderen Stabes; z.B. von der Lok und der Caboose eines Zuges auf die Ausfahr-Signalanlage und auf die Einfahr-Signalanlage eines Bahnhofs) ist nicht direkt umkehrbar, d.h. nicht zwischen genau diesen vier genannten Beteiligen umkehrbar.
(Wobei allerdings Einstein-Projektionen gegenseitig “zwischen geeigneten Mitgliedern der beiden betreffenden Systemen” möglich sind, z.B. von Ausfahr-Signalanlage und auf die Einfahr-Signalanlage des genannten Bahnhofs auf die Lok des genannten Zuges und einen geeigneten Zugteil zwischen dessen Lok und Caboose; d.h. es besteht zumindest “indirekte Umkehrbarkeit”.)
Für die Messung, also die Einhaltung der entsprechenden Versuchsanordnung, haben allerdings alle vier genannten Beteiligten (“Stabenden”) ihren jeweiligen Beitrag (des Sammelns und Bewertens von Beobachtungsdaten) zu leisten;
insbesondere zur Identifizierung eines Zugteil als “Mitte zwischen” Lok und Caboose und zur Identifizierung eines Bahnhofs-Bestandteils als “Mitte zwischen” Ausfahr-Signalanlage und Einfahr-Signalanlage; entsprechend der (nachvollziehbar Koordinaten-frei beschriebenen) Einsteinschen Versuchsanordnung.
Versuche, zwischen “zu vermessendem Objekt (bzw. dessen Bestandteilen)” und “messendem Beobachter” zu unterscheiden, erscheinen dabei irreführend und sind mit Ockhams Klinge zu beseitigen.
> […] Für beliebige Beobachter ist die gleichzeitige Ankunft der Signale von beiden Meßenden eindeutig.
Nicht “die gleichzeitige“, sondern die koinzidente Ankunft bzw. Wahrnehmung!
Bewertungen von Koinzidenz (oder ansonsten: Nicht-Koinzidenz, Separation) zu begreifen, und Koinzidenz von eigenen Wahrnehmungen zumindest im Prinzip zu beurteilen, ist in der RT jedem einzelnen Beteiligten selbstverständlich zugestanden.
Die Bewertung von Gleichzeitigkeit (oder ansonsten: Ungleichzeitigkeit) der Anzeigen verschiedener Beteiligter ist dagegen Gegenstand von Messung, deren Verfahren/Versuchanordnung/Messoperation erst festgelegt werden musste und von Einstein (Comstock, …) unter Anwendung des selbstverständlichen “Koinzidenz”-Begriffes konstruiert wurde.
> […] Aus dem Verhältnis L/Lo<1 kann/muß jeder "sein y" bestimmen und sein v_rel zum Objekt.
Umgekehrt:
Aus dem (gegenseitig gleich) ermittelten Wert β ist der Verhältniswert
L/Lo ≡ L_Bild / L_Objekt = √{ 1 – β^2 }” zu ermitteln.
Wie denn sonst? …
@Joachim / 17. Januar 2019 @ 20:29
Gehen wir doch mit den eher heuristischen Einsichten zum fahrenden Zug jetzt nochmals hinüber zu etwas rigoroseren Betrachtungen zum bewegten Stab. Dabei greife ich auf einige zuvor von mir sowie in der Animation verwendete Bezeichnungen zurück, was hoffentlich keine Schwierigkeiten bereitet.
Denken wir uns in S bei \(x = 0\) und \(x = 1/\gamma\) zwei S-synchrone Uhren \(u_O\) und \(u_C\) aufgestellt, die durch die Eigenzeit \(\tau := t_0(s) = \gamma s\) parametrisiert seien, wobei \(s\) wie zuvor die `Eigenzeit des Stabes’ bezeichnet. Die so parametrisierten Weltlinien dieser Uhren sind in S dargestellt durch
\[
u_O(\tau) := \tau\vec{e}_t = (\tau,0) \quad\text{und}\quad u_C(\tau) := \tau\vec{e}_t + \gamma^{-1}\vec{e}_x = (\tau,\gamma^{-1}).
\]
Es gilt dann \(u_O(0) = O\) und \(u_C(0) = C\) mit den der Animation entnommenen Benennungen. Und die Parametrisierung ist gerade so justiert, dass die Uhr \(u_O\) genau dann \(\tau = 0\) anzeigt, wenn das linke Stabende in S die Position \(x = 0\) hat.
Jetzt können wir uns fragen: Was zeigt die Uhr \(u_C\) in dem Moment an, wenn das rechte Stabende in S die Position \(x = 1/\gamma\) hat?
Das rechte Ende unseres Lorentz-transformierten Stabes von Einheitslänge bewegt sich in S gemäss \(w_1(s) = (t_1(s), x_1(s)) = (\gamma(s + \beta), \gamma(s\beta + 1))\) und die Gleichung \(x_1(s) = 1/\gamma\) hat die Lösung \(s = -\beta\). Folglich zeigt die Uhr \(u_C\) in dem Moment, wo das rechte Stabende in S die Position \(x = 1/\gamma\) hat, den Wert \(\tau = -\gamma\beta < 0\) an.
Das bedeutet aber, dass bei einer Zeitmessung mit S-synchronen Uhren das linke Stabende die Position \(x = 0\) erst dann erreicht, wenn das rechte Stabende die Position \(x = 1/\gamma\) schon längst passiert hat. (Und das liegt auch nicht an der speziellen Wahl \(\tau = \gamma s\), denn jede andere Eigenzeit-Parametrisierung dieser Uhren bewirkt nur eine Zeitverschiebung der Form \(\tau' = \tau + \tau_0\).)
Mit anderen Worten, zu keiner von S-Uhren angezeigten S-Zeit \(\tau\) befinden sich die Positionen der Stabenden auf der x-Achse beide zugleich in der Strecke \(OC\). Oder?
Frank Wappler schrieb (18. Januar 2019 @ 12:22):
> Die Einstein-Projektion (“vom Objekt auf das Bild” […] z.B. von der Lok und der Caboose eines Zuges auf die Ausfahr-Signalanlage und auf die Einfahr-Signalanlage eines Bahnhofs) ist nicht direkt umkehrbar […]
> (Wobei allerdings Einstein-Projektionen gegenseitig “zwischen geeigneten Mitgliedern der beiden betreffenden Systemen” möglich sind, z.B.
… auch …
> von Ausfahr-Signalanlage und
… Einfahr-Signalanlage des genannten Bahnhofs auf die Lok des genannten Zuges und auf einen geeigneten Zugteil zwischen dessen Lok und Caboose.)
@NvB.
.
Eigentlich hatte ich Dich damals gefragt, ob der Meterstab seine Länge ändert, wenn er in den Zug geworfen wird. Und Du hast erklärt, er würde seine Länge nicht ändern. Er hätte aber nicht die Länge Deines Zug-Meters sondern die des Bahnhofs-Meters.
.
Nun muss man schauen, in welchem System man die Länge angibt, Ruhesystem des Zuges oder des Bahnhofs. Bleibt man im Bahnhofssystem ändert der Meterstab natürlich seine Länge, er kontrahiert. Wechselt man mit in den Zug, also das Ruhesystem, ändert sich die Länge nicht, man hat immer einen SI-Meter langen Meterstab.
.
.
Also man erstellst drei Meterstäbe am Bahnhof, einer bleibt da, einen gibt man gleich mit in den Zug, der dann auf 0,9 c beschleunigt und den dritten wirft man dann durchs Fenster in den Zug. Alle beiden Meterstäbe im Zug sind gleichlang. Beide sind aber aus dem Ruhesystem des Bahnhofs gemessen kontrahiert, ebenso wie der Zug. Dadurch misst man im Zug mit beiden die Ruhelänge des Zuges von 229,4 m.
.
Nun erstellt man im Zug einen Meterstab auf Basis der SI-Sekunde im Zug, dieser Stab ist auch gleichlang mit den anderen beiden vorhandenen. Im Ruhesystem des Bahnhofs ist dieser auch kontrahiert. Wirft man nun diesen aus dem Zugfenster wird er ruhend am Bahnhof genauso lang sein, wie der dort verbliebene Meterstab.
.
Ein im System ruhender SI-Meterstab ist eben immer einen SI-Meter lang, wird dessen Länge in einem System gemessen, in dem dieser bewegt ist, ist diese Länge kontrahiert.
.
.
.
Nein, das passt alles und ist alles konsistent, Missverständnisse erstehen nur durch die umständlich extrem einfache Beschreibung, weil gewisse Grundlagen nicht bekannt sind.
.
Im Grunde ist es ganz einfach, ein “bewegtes” Objekt ist in Richtung der Bewegung lorentzkontrahiert. Und die Kontraktion ist relativ, es ist wie mit der Frequenz des Feuerwehrautos. Bleibt man ruhend zur Sirene ändert sich die Frequenz nicht, ist die Sirene zu einem bewegt, ändert sich diese. Wie dieselbe Sirene für unterschiedliche Beobachter unterschiedliche Frequenzen haben kann, kann ein Objekt unterschiedliche Längen haben, je nach Geschwindigkeit.
@Frank Wappler:
Was ist denn gegeben? L und Lo oder L und β? L und β, richtig? Oder besser gesagt L und v_rel, wobei sich aus Letzterem β ergibt. Gesucht ist also Lo.
Die Frage, die ich mir nun schon die ganze Zeit stelle, ist die, wie man beiderseitig auf identische v_rel kommen kann, denn eine Uhr geht schneller als die Andere und sofern sich bewegte Strecken nur scheinbar ändern, wenn man sie per Uhr bestimmt (siehe erwähntes Problem seitens Herr Schulz), kommen über abgezählte Gitterabstände unterschiedliche v_lokal dabei heraus und man wüsste, worin sich die LK begründet.
Also: Wenn man annimmt, dass nur Periodendauern proportional zu Wellenlängen relativistischen Effekten unterliegen, Gitterabstände jedoch nicht, wüsste man dann nicht auf Anhieb, wie schnell man sich relativ zum Licht bewegt? Auf die Art landet man btw. auch bei jenem Kreisbezug, den hier anscheinend sonst keiner sieht – Der SI-Meter wird an undefinierten Wellenlängen proportional zu den Periodendauern der SI-Sekunde bemessen, was ihn zu einer Eigenstrecke macht. Und nur, weil Gitterabstände keinen relaticistischen Effekten unterliegen, kann das überhaupt gemessen werden. Ist da was dran oder ist da was dran?
@Krüger:
Stimmt auffallend. Bei uns ging es um zueinander bewegt hergestellte Meter. Aber vermutlich ists ein Kreuz mit der “Verformung” – ich hatte nämlich auch gesagt, dass er genau dies nicht tut, weswegen er zu jeder Zeit genauso lang wie der Bahnhofs-Meter und kürzer als der Zug-Meter ist, weil die Uhr im Zug tatsächlich langsamer tickt, als die am Bahnhof. Gitterabstände unterliegen bei mir keinen relativistischen Effekten und das ist der Weg zum Kreisbezug bei der Definition von SI-Meter und SI-Sekunde, den ihr nicht seht. Mir geht es jetzt darum, ihn sichtbar zu machen.
@Nicht von Bedeutung 18. Januar 2019 @ 14:40
Eigentlich ist das gleiche v_rel die Annahme des Relativitätsprinzips. Denn sonst könnte man zwischen den Inertialsystem einen Unterschied feststellen.
Man würde aus der Resonanzbedingung aber messtechnisch folgern, daß die Gitterabstände verkleinert sind.
Warum ändern sich die Taktraten von Uhren, so dass man von Eigenzeit reden muss? Würden sich Resonanzgehäuse in ihrer Länge proportional zu Wellenlängen, welche widerum proportional zu Periodendauern sind, ändern würden unterschiedliche Taktraten gar niemals auffallen, weil sie ebenso “starr” wären, wie Interferenzmuster bei Michelson und Morley.
Fazit 1: Es ändert sich in Atomuhren nur eine “Strecke”, nämlich jene Wellenlänge, die proportional zur sich ändernden Periodendauer ist.
Daraus erwächst aber umgehend ein Problem bei Michelson und Morley. Denn wenn sich Gitterabstände nicht ändern, ändern sich auch Armlängen nicht, welche sich laut Rechnung aber ändern müssten, weil man anders die starren Interferenzmuster nicht erklären kann.
Oder etwa doch? Berechnet werden Laufzeiten und Phasenverschiebungen längs der Lichtbewegungsrichtung, betrachtet wird aber eine Frequenz radial zur Bewegungsrichtung. Wer sagt, dass Längsinterferenzen mit Radialinterferenzen auf die Art zusammenhängen, wie es angenommen wird?
@Storz
.
Kurz nur Sirene, nein es ist kein Scheineffekt, die Frequenz wird real höher gemessen, wenn die Sirene auf einen zu bewegt ist. Eine ruhende andere Sirene mit höherer Frequenz kann nicht unterschieden werden. Heißt, für den messenden zur Sirene bewegten Beobachter ist die Frequenz die er misst real höher und nicht nur scheinbar höher.
.
So ist es auch mit der Lorentzkontraktion. Der zum Objekt bewegte Beobachter mist ein andere, eben kontrahierte Länge. Der zum Objekt ruhende Beobachter misst weiter die Ruhelänge. Das ist schon alles.
@Rudi Knoth:
Wessen Relativitätsprinzip? Das von Galilei kann nicht mehr gemeint sein. Galilei konnte 1632 weder etwas von Inertialsystemen noch etwas von der Invarianz der Lichtgeschwindigkeit ahnen. Tatsächlich betrachtete Galilei nur stur materielle Objekte und EM-Wellen, Licht oder Dergleichen gehörte damals noch nicht dazu.
Heute gilt das Relativitätsprinzip, wenn man es genau nimmt, nur noch auf dem Papier für Inertialsysteme in welchen mindestens eine Geschwindigkeit gerade diesem Relativitätsprinzip widerspricht – die invariante Lichtgeschwindigkeit, welche nämlich gar nicht hätte festgestellt werden können.
Aber nur, wenn sich die Periodendauern/Wellenlängen nicht ändern würden – sonst “starre” Taktraten” gleichbedeutend mit “starren” Interferenzmustern.
Ich bin in der Lage, alles auf Wellenlängen und Periodendauern zu schieben – ihr nicht. 😉
@Krüger:
Sorry wenn ich mich einmische, Schall=Welle=Wellenlängen=Periodendauern=Frequenzen. Keine Gitterabstände.
NvB.
.
Ich schrieb: “Eigentlich hatte ich Dich damals gefragt, ob der Meterstab seine Länge ändert, wenn er in den Zug geworfen wird. Und Du hast erklärt, er würde seine Länge nicht ändern. Er hätte aber nicht die Länge Deines Zug-Meters sondern die des Bahnhofs-Meters.”
.
.
Wahnsinn, wir sind uns mal einig.
.
.
.
Nun ja, die Sirene selber ändert sich auch nicht, auch wenn man eine höhere Frequenz misst. Die Sendefrequenz ändert sich nicht, die “verformt” sich nicht. Und da ist dann dieses “tatsächlich langsamer” und das geht in Richtung “absolut”. Das wäre dann eine andere Sendefrequenz der Sirene. Also in der Analogie bleibend.
.
Basis sind immer die Aussagen der SRT und nicht persönliche Interpretationen, die Uhr im Zug ist im Bahnhofssystem bewegt und geht darum in diesem langsamer. Sie geht aber eben nicht tatsächlich so langsamer, wie eine ruhende Uhr die man langsamer laufen lässt.
.
Denn das ist wechselseitig, die am Bahnhof ruhende Uhr geht im Ruhesystem des Zuges ebenso langsamer.
.
.
.
Es geht um die SRT und die Lorentzkontraktion im Rahmen dieser, es geht nicht um Deine persönliche Physik. Ob bei Dir die Gitterabstände keinen relativistischen Effekten unterliegen ist darum egal. Wir sind im Rahmen der SRT und da kontrahieren auch Diamanten und Kristalle und alle eben gleich.
.
Und im Rahmen der SRT gibt es keinen Kreisbezug, es mag einen im Rahmen Deiner “These” geben, aber das ist dann Dein Problem und das Deiner “These”.
@NvB.
.
Deine Gleichheitszeichen sind einfach falsch, eine Welle ist nicht gleich einer Wellenlänge sondern hat eine und eine Dauer wird in Einheiten der Zeit gemessen, eine Frequenz nicht. Ich weiß aber was Du meinst. Ändert aber nichts, es geht erstmal da ja nur im die Analogie und um den “Scheineffekt”.
.
Ansonsten bleibt es dabei, alle materiellen Objekte kontrahieren im Rahmen der SRT. Du magst da gerne eine eigene “These” haben wo Kristalle dann eben nicht kontrahieren, dass hat aber nichts mit der SRT nun der LK hier als Thema zu tun. Das ist dann Deine eigene private Physik die Du im MAHAG oder bei Lopez vorstellen und erörtern kannst.
.
Und noch mal, wird im Zug der Meterstab auf Basis der SI-Sekunde dort hergestellt, dann hat er die Länge eines SI-Meters und damit im Zug gemessen ist der Zug 229,4 m lang. Kommen da bei Dir nur “100 m” raus, bewegst Du Dich nicht im Rahmen der SRT sondern Deiner eigenen “These”.
.
Das Problem ist weiterhin, Du nimmst Deine eigene Vorstellung als reale Basis und gehst von einem absoluten Raum aus und von absoluten Geschwindigkeiten, darum haust Du auch das RP raus. Die SRT hat aber das RP als Basis. Wenn Du da was änderst, kann es nicht mehr passen, das liegt aber nicht an der SRT, sondern an dem was Du da änderst.
@Frank Wappler:
Wenn die SRT nur eine Meßvorschrift ist, wie erklärt sich dann die Myon Lebensdauer beim Durchqueren der Athmosphäre? Also wenn die Strecke nicht tatsächlich verkürzt wäre?
@Krüger:
Da wäre ich mir nicht mehr so sicher, nur fallen relativistische Effekte noch nicht sonderlich ins Gewicht, selbst wenn man 70220m/s (Speedrecord by Helios 2) fliegt.
Mathematisch sind sie falsch aber das ändert nichts an der Message. Glaubst du etwa, ich mach mir die Mühe dafür extra das “entspricht” Zeichen aus der Zeichentabbelle zu angeln?
Natürlich. Ich bewege mich immer im Rahmen meiner eigenen These – ist das etwa falsch, wenn man alle Anderen verstanden hat und einem Diskrepanzen auffallen? Z.B. solche Diskrepanzen wie bei Herrn Schulz und Chrys, wie Herr Schulz sie erwähnte.
Das ist für dich und Andere, die in der RT festhängen ein Problem, nicht aber für die, die ernsthaft weiter kommen wollen. Leider kocht jeder der Letzteren ohnehin ein eigenes Süppchen und ich koche meines.
@Krüger:
Das wäre ja schön. Fakt ist, dass ich sie leider nirgendwo vorstellen kann, weil jeder überall sein eigenes Süppchen vorstellen oder Mainstream erlären will, weswegen dort überall die selbe unflätige “Funkdisziplin” herrscht. Deswegen finde ich es ja auch nicht sinnvoll, mir meine eigene Selbstdarstellungplattform aufzubauen, weil dort genau das selbe passieren würde.
@Krüger:
Für dich habe ich btw. noch eine These: Dir gelingt es nicht, meine Thesen mit der RT zu zerpflücken (da bist du nicht der Einzige) und das bringt dich auf die Palme.
@Uli Schoppe:
Das ist doch wirklich eine ganz einfache Übung: Myonen leben schlicht länger, weil Wechselwirkungen bei hohen Geschwindigkeiten langsamer wirken – Myonen halten deswegen länger zusammen. Tatsächlich hat ja auch noch nie ein Augenzeuge berichten können, was in so einem Myon vorgeht, weswegen LK gerade dort nur Theorie ist.
@U.S. 15:52 Wenn die SRT nur eine Meßvorschrift ist, wie erklärt sich dann die Myon Lebensdauer beim Durchqueren der Athmosphäre? Also wenn die Strecke nicht tatsächlich verkürzt wäre?
Einfach weil das Myon “schnell” ist, seine Ruhelebensdauer ist nur 2 μs, aber es fliegt mit 0,998c.
Durch die Zeitdilatation “bis zur Erde hin gesehen” sind das “im Myon” 30 μs, es schafft so 9 km.
@Herr Senf
Die Strecke müsste aber für den Beobachter auch kontrahiert sein oder? Das es gleichzeitig auch ZD gibt ist ja klar; mit der Aussage das sei nur wegen der ZD so wäre man aber recht nahe an NvB…
Und es kann sein das ich einen Knoten habe, aber wie funktioniert das über die ZD wenn die SRT doch nur eine Meßvorschrift wäre und nichts über die Wirklichkeit aussagt? 🙂
Nein, aus Sicht des Myons ist die Strecke verkürzt oder? 🙂
Sonst würde es ja in seiner Zeit die Strecke nicht schaffen…
@Uli Schoppe:
Ja, aus Sicht des Myons wäre die Strecke verkürzt. Aber wer nimmt erstens die Zeit und misst zweitens die Strecke im Ruhesystem des Myons?
Was wäre, wenn das Myon einen aus seiner Sicht 15km langen Stab vor sich herschiebt, der im Ruhesystem Erde verkürzt sein müsste? Er würde aus Sicht des Myons nicht etwa durch die Erde durch gehen und aus Sicht der Erde diese nicht mal erreichen?
Ruhend auf der Erde zerfallen 15 Myonen in der Zeit, in welcher das Bewegte lebt. Vom Yon aus vergeht jedoch die Erdzeit langsamer und die Myonen dort leben 15 mal länger. Vom bewegten Myon aus kann also gar nicht beobachtet werden, wie 15 Myonen auf der Erde zerfallen, denn dafür ist die Eigenzeit zu kurz.
Da stimmt doch etwas ganz und gar nicht, richtig?
@NvB
Also Du erwartest nicht das eine Person die Zeit im Inertrialsystem des Myons misst oder? Das Myon misst die Zeit und das Myon misst die Strecke. Sonst wäre es ja nicht sein Inertialsystem 🙂 In seiner Lebenszeit kann es halt nur eine bestimmte Strecke überwinden. In SEINER.
Mit dem 15km Stab willst Du mich linken oder? 😉 Was ist diese Entfernung für Dich? Ich nehme mal an die Entfernung im Inertialsystem Erde gemessen in der das Myon entsteht? Wir müssen uns erst mal einigen was wo gemessen wird. 🙂
@NvB
Die gemessene Strecke im Inertialsystem Erde ist im Inertialsystem Myon verkürzt. Da kann man nichts machen 😉
@Uli Schoppe:
Doch natürlich erwarte ich das. Macht nur keiner, weils nicht geht. Von daher bleiben diesbezügliche Annahmen der RT haltlose Behauptungen. Wen interessiert den das Bezugssystem “ruhendes Myon” wenn da keiner messen kann? Mich jedenfalls nicht.
Bist du ein (S)RT-Befürworter, dann ja – sonst eher nicht. Ich sage damit aus, dass “Jeder sieht die Uhr des Anderen (wechselseitig) langsamer gehen und Bewegte Strecken (wechselseitig) verkürzt.” tatsächlich gar nicht funktionieren kann. Myonen-Experimente bestätigen die SRT ebenso wenig, wie beispielsweise GPS und um das zu verstehen, muss man sein allgemein geläufiges Verständnis für die RdG at Acta legen.
@Uli Schoppe:
Kurz gesagt: I’m not impressed by relativity.
@NvB 18:34 “Ruhend auf der Erde zerfallen 15 Myonen in der Zeit, in welcher das Bewegte lebt.” aha,
bei Dir heißt das Logik? Die 15 Myonen zerfallen nicht hintereinander, sondern gleichzeitig in 2 μs.
@Senf:
Ja, das ist Logik. Wenn man alle 2 µs ein Myon erzeugt, zerfallen sie sicher nicht alle gleichzeitig – es sei denn, es gäbe in der RT etwas, was das möglich macht. 😉
Uli Schoppe schrieb (18. Januar 2019 @ 15:52):
> Wenn die SRT nur eine Meßvorschrift ist,
… die (S)RT ist eine Theorie. Also: bestehend
– aus (wenigen) axiomatischen/selbstverständlichen Begriffen (insbesondere: “identifizierbare materielle Punkte” und deren “Koinzdenzen“,
– aus daraus formulierten/konstruierten Messvorschriften, als Gedanken-experimentellen Definitionen von Messgrößen (z.B. von “gegenseitiger Ruhe”, “Gleichzeitigkeit”, “Dauer, betreffend Beteiligte, die gegenüber einander ruhten”, “Länge bzw. Distanz, betreffend Beteiligte, die gegenüber einander ruhten”, “Geschwindigkeit” usw., um in erster Linie die relevanten geometrisch-kinematischen Messgrößen zu nennen),
– aus Theoremen, d.h. logischen Konsequenzen dieser Definitionen im Zusammenhang (z.B. der Vergleich von Dauern zwischen Beteiligten, die nicht gegenüber einander ruhten, also “Zeit-Dilatation”; und der Vergleich von Längen zwischen Beteiligten, die nicht gegenüber einander ruhten, also “Längen-Kontraktion”) …
> wie erklärt sich dann die Myon Lebensdauer beim Durchqueren der Atmosphäre?
… Wie sich das Verhältnis der Lebensdauer eines Myons (das im Laufe seines Lebens die Atmosphäre durchquerte) und der Dauer der Atmosphäre (bzw. deren Bestandteile und weiteren diesbezüglich ruhenden Beteiligten, z.B. bestimmten Detektoren), von diesem Myon betroffen/besetzt/belegt gewesen zu sein, “erklärt” ?
Als Funktion des (Wertes des) (gegenseitigen) Geschwindigkeits-Parameters β?
Wie also der Verhältniswert “√( 1 – β^2 )” der genannten Dauern hergeleitet wird ? —
Das entsprechende Theorem ist (z.B.) dort skizziert.
(Womöglich produziert Joachim Schulz ja demnächst einen SciLogs-Artikel, zu dem diese Herleitung passenderweise als Kommentar beigefügt werden könnte.)
> Also wenn die Strecke nicht tatsächlich verkürzt wäre?
Da es (bei “der Längenkontraktion”) um den Verhältniswert der Längen zweier verschiedener “Strecken” (bzw. “Stäbe”) geht, sollten diese beiden unterscheidbaren “Strecken” bzw. deren jeweilige beide “Enden” zunächst ausdrücklich identifiziert und hier genannt sein. Es geht nämlich
– einerseits um “die Atmosphären-Strecke” (d.h. “die Reisestrecke des Myons”), bestehend zumindest symbolisch aus einem bestimmten Atmosphären-Atomkern als dem einen Ende (dem “Reise-Startblock”) und einem Detektor (“am Atmosphären-Boden”, also “auf der Erdoberfläche”) als dem “Reise-Zieltor”, und
– andererseits um eine bestimmte “Strecke des Myonen-Systems”, bestehend aus dem einen o.g. Myon (meinetwegen als “dem vorderen Ende”), und einem weiteren, gegenüber diesem Myon ruhenden, dem Myon beim “Durchqueren der Atmosphäre” nachfolgenden Beteiligten, meinetwegen einem bestimmten beeigneten Raumschiff, als “dem hinteren Ende”.
Falls diese zwei genannten Paare von Enden die Versuchsanordnung der Einstein-Projektion “der Atmosphären-Strecke” auf die “Myonen-Strecke” erfüllen,
d.h. konkret, falls die Anzeige des Myons bei Treffen/Passage des Boden-ständigen Detektors gleichzeitig zur Anzeige des Raumschiffs bei Treffen/Passage des Start-Atomkerns war,
dann ist die Länge der “Myonen-Strecke” das “√( 1 – β^2 )”-fache der Länge der “Atmosphären-Strecke”.
Von “Verkürzung” kann dabei doch gar keine Rede sein;
denn die betreffenden Längen der beiden beschriebenen, von verschiedenen Paaren von Enden bestimmten Strecken, waren und blieben doch schlicht so, ungleich, wie sie waren.
@Frank Wappler : OK, nehmen wir Stäbe. Der eine Stab entspricht dem Myon Stab, Der andere ist doppelt so lang wie der Atmosphären Stab. Da stellen wir nicht nur an den Enden einen Detektor auf sondern auch in der Mitte. In dem Moment wo der vordere Punkt den Detektor auf dem Mittelpunkt passiert beginnt der Myonen Stab abzubremsen und zwar so das in dem Moment wo das vordere Ende den Endpunkt des anderen Stabes erreicht beide Stäbe gegeneinander ruhen. Was passiert mit dem Myon Stab? Der wird doch länger?
@NvB.
.
Sag ich ja, unter den “Cranks” gibt es keine Einigkeit über die Behauptung die RT sei falsch hinaus.
.
.
.
These ist falsch, Du hast keine echte These im physikalischen Rahmen der Definition, sondern nur ein paar wilde Behauptungen voller Widersprüche und die ist so oder so zerpflückt, nur wirst Du das nie zugeben, so wie auch Zasada nie zugeben wird, da falsch zu liegen. Und Unwissenheit andere bringt mich nicht auf die Palme.
.
.
.
Nur eine Behauptung und die Frage ist dann, welche Geschwindigkeit soll es sein? Wie wird die gemessen? Bei Dir ist es doch eine absolute Geschwindigkeit gegenüber dem Raum, da müsste es dann Unterschiede geben, je nach dem wo sich die Erde wie bewegt.
.
Und Myonen sind Elementarteilchen, da hält nichts länger zusammen. Auch da brauchst Du dann zusätzliche Annahmen und stehst im Widerspruch zur QT. Warum der Faktor dann gleich auch noch Gamma sein sollte müsstest Du auch noch erklären, warum ist der nicht größer oder kleiner?
.
.
.
Muss man nicht, den langsamere Wechselwirkungen hat wohl auch noch nie ein Augenzeuge gesehen.
@Uli Schoppe
.
Du liest hier doch sicher länger mit, es ist nur ein neues altes Kaninchen, welches hier aus dem Hut gezogen wurde, die Tierchen rotieren. Dabei ist das mit den Myonen so oft richtig erklärt worden, immer wieder, als nächstes kommt dann wieder der angebliche Kreisbezug und so weiter und so fort.
@NvB.
.
Muss man nicht, man gibt auch in anderen Systemen Größen an, ohne in diesen direkt messen zu können. Im Ruhesystem von VY Canis Majoris bewegen sich geladene Teilchen mit der Geschwindigkeit 800–900 km/s von der Oberfläche weg.
.
.
.
Das sagst Du, behauptest Du, mehr nicht.
.
.
.
Die Myonen und deren Verhalten kann die SRT richtig vorhersagen und erklären, bei GPS wird mit der RT berechnet wie groß die ZD ist und dann werden mit diesen Werten die Uhren die Satelliten korrigiert. Die RT kann es richtig berechnen, das ist doch ein überzeugendes Argument. Kein “Kritiker” konnte bisher mit einer eigenen “These” diese Werte berechnen und keiner hat es bisher mal gezeigt.
@ Manuel Krüger 19. Januar 2019 @ 14:02
@Uli Schoppe
“Du liest hier doch sicher länger mit, es ist nur ein neues altes Kaninchen, welches hier aus dem Hut gezogen wurde, die Tierchen rotieren.”
Ich weiß, ich will ihn auch nicht zu sehr füttern. Wenn ich das Gefühl habe jemand meint die Verkürzung wäre das gleiche wie ein physisch hergestelltes Meter unter die 400t Presse hinten bei uns im Stahlbau zu legen (da verformt sich das beim Überschreiten der Knicklast ziemlich drastisch und die beiden Endpunkte von Frank liegen ziemlich dauerhaft deutlich näher aneinander als vorher 🙂 ) klinke ich mich aus. Wir sind hier nicht im Maschinenbau wo zB sich alle Objekte immer im gleichen Inertialsystem befinden.
@Krüger:
Sei doch einfach mal still. Wir kennen deine Ansicht. Ich behaupte nicht nur und das wprdest du erkennen, wenn du meine Argumente mal sacken lassen würdest – aber das ist ja zu viel verlangt.
Und Einigkeit, auf welche Weise eure heilige RT nun richtig sein soll, existiert unter euch (Du, Herr Schulz, Herr Knoth, Herr Wappler und Chys) auch nicht.
Ich kann das Verhalten von Myonen auch richtig vorhersagen und selbiges gilt für die beiden Arten der Zeitdilatation, für das Michelson Morley Experiment, für Sagnac, für die QM usw. usf. Nur bleiben bei mir Längenkontraktion, Raumzeitkrümmung, Dunkle Materie, Urknall und Dunkle Energie auf der Strecke. Ist aber Alles Nicht von Bedeutung, solange die RT ja so Gott verdammt Alles richtig beschreibt. Ich zweifle aber daran, dass du mit der RT die Dunkle Materie auch weg bekommst – ich bekomme das Alles durch simpelste Überlegungen weg, die du allesamt anzweifelst.
@Uli Schoppe:
Nun, so Dauerhaft ist das lt. RT aber nicht. Der Stab wird kürzer, wenn man ihn in den Zug hinein und wieder länger, wenn man ihn wieder hinaus wirft. Und weil das so ist, kann LK nur optisch “gemessen” werden, nicht aber, wenn man ein Metermaß anlegt.
Und Zeugen, die mit Myon-Air geflogen sind und Alles nachgemessen haben, gibt es nach wie vor nicht. 😀
@Krüger:
Also Beweis durch Behauptung. Aber gerade du verlangst für das eigentlich Offensichtliche (wie z.B. der erwähnte Kreisbezug bei SI-Meter und SI-Sekunde) immer Beweise. Du hast wohl ‘ne Meise, was? 😆
@NvB.
.
Wieso sollte ich, bist Du ja auch nicht und ich bin im Thema, Du nicht, Du bist gegen das Thema und willst Deine private Wasauchimmer predigen.
.
.
.
Hartmut, Du hast keine sachlichen Argumente und da muss man nichts sacken lassen, dass ist nur wieder ein Märchen, ein “Erklärung” und Behauptung für Dich, warum ich Dir nicht zustimme. Keiner mit Ahnung stimmt Dir zu, nach Deiner “Ausrede” scheint da dann wohl keiner was “sacken” zu lassen.
.
.
.
Wir sind uns in ganz vielem einig und oben steht eh Joachim als studierter Physiker der aktiv in dem Bereich arbeitet.
.
.
.
Quatsch, kannst Du nicht, rechne es doch vor.
.
.
.
Ja Dein Käse ist nicht von Bedeutung und warum sollte man über die RT die DM weg bekommen? Du bekommst die auch nicht weg, Du kennst ja nicht mal all die Dinge die Du dann ohne DM erklären und beschreiben müsstest.
.
.
.
Es gibt keinen Kreisbezug und kein Physik-Kundiger wird Dir da was zu bestätigen. Und Dein übliches Beleidigen war ja klar.
@Krüger:
Stimmt. Ich habe stichhaltige Argumente, ihr nicht – du hast nicht mal Argumente, geschweige denn sachliche, weswegen es sich um deinen Sch… nicht mehr um Argumente, sondern nur noch um Behauptungen handelt. Und das sind nicht mal deine Behauptungen, sonder jene eines gewissen A. Einstein. 😆
Kennst du überhaupt den Unterschied zwischen Einstein und mir? Bei mir gibt es weit mehr Begriffe, von denen ich überzeugt bin, dass sie standhalten werden.
Z.B. habe ich euch “Beweis durch Behauptung” per “Myonen-Experiment” nachgewiesen, während der Kreisbezug bei der Definition von SI-Meter und SI-Sekunde offensichtlich ist.
Mein Argument: Der SI-Meter hat eine Länge, die etwa 31 Wellenlängen entsprechen, die proportional zu etwa 31 Periodendauern sind. Was das in umgerechnet in Kristallgitterabständen ist, ist nicht definiert. Wenn man also bei der SI-Sekunde von Eigenzeit spricht, muss man beim SI-Meter von Eigenlänge sprechen – da führt kein Weg dran vorbei. Dass sich Kristallgitterabstände durch Bewegung ebenso verändern, wie Wellenlängen, ist nicht gegeben, denn wenn es so wäre, würde bei Atomuhren zu jeder Zeit die Resonanzbedingung erfüllt sein (vgl. mit Michelson Morley, wo dies wegen der LK der Fall sein soll) und unterschiedlich gehende Uhren könnten gar niemals festgestellt werden, was aber z.B. bei H&K der Fall war und tag täglich bei GPS noch der Fall ist. Du bist Schachmatt. Ende.
@Dumming Krüger:
Macht ja keinen Sinn bei dir. Das verstehst du ja eh’ nicht. 😆
Okay… Ein Nachtrag noch:
Der Kreisbezug äußert sich btw. auch noch in den Problemen, die e,s lt. Herrn Schulz, bei der Bestimmung (+Messung & Herstellung) ruhender Meter mit bewegten Uhren gibt. Einfach mal logisch denken, oder habt ihr das alle verlernt?
@Manuel Krüger 19. Januar 2019 @ 19:16
Und Herr Wappler ist auch in diesem Bereich tätig. Und die Unterschiede habe ich etwas früher erklärt. Es ist wohl eher die Frage, wie man die RT “laienhaft” ohne Formeln erklären kann.
Neben dem Privatkrieg hier, kann mir jemand erklären was mit meinem Myon Stab wirklich passiert? 🙂
@Rudi Knoth: Für die SRT reicht ja an Mathematik Mittelstufe 😉 Was hat sie für Konsequenzen, was sagt sie über die Realität?
@NvB: “Z.B. habe ich euch “Beweis durch Behauptung” per “Myonen-Experiment” nachgewiesen, während der Kreisbezug bei der Definition von SI-Meter und SI-Sekunde offensichtlich ist.” Hast Du nicht und offensichtlich ist nix. Und würdest Du Dein MAHAG Benehmen bitte im MAHAG lassen? Ich finde das unangenehm…
@Uli Schoppe:
Ich lasse mein Mahag-Benehmen bei den Leuten, bei denen es passt – beim Krüger z.B. Stell dich dazu und du wirst es erleben.
Wenn bei dem Kreisbezug auch für dich nix offensichtlich ist, dann versuche doch den Teil meiner Argumentation, der nicht schlüssig ist, zu entkräften. “Beweis durch Behauptung” bringt da gar nix.
Von welchem Myonenstab redest du eigentlich? Von dem, den ich hier eingeführt habe? All jene, die sich hier Physiker nennen, brauchst du kaum danach fragen, weil er ein Kritiker-Argument ist. Für die 15 nacheinander auf der Erde zerfallenden Myonen gilt das selbe – sie können weder mit, noch ohne RdG im Myonensystem gleichzeitig zerfallen.
@Rudi Knoth:
Bei manchen Personen sollte man sich nicht mehr fragen, wie man die RT “laienhaft” erklären kann, sondern eher, ob man sie überhaupt noch irgendwie erklären kann. Gerade mir muss man sie nämlich nicht mehr erklären und mit der Uneinigkeit unter euch Befürwortern, schafft das eh’ keiner, weil diese den Eindruck erweckt, es gäbe gar kein allgemeingültiges Verständnis der RT. Ein solches kann es aus meiner Sicht auch gar nicht geben, weil der Knackpunkt anscheinend tatsächlich nicht so offensichtlich ist, wie er mir vorkommt – aber er ist nun mal da. Nun ists wohl an mir, zu erklären, wo er auffällt und selbst das will keiner wissen. Und wenn ich es versuche, haut das Peer-Review dazwischen, wo jeder nur mit der nicht schlüssigen RT (dem Gegenstand der Verhandlung) dagegen argumentiert. Das ist doch krank.
Hauptsache hier ist jedem klar, was mir unangenehm ist. 😆
@Nicht von Bedeutung 20. Januar 2019 @ 12:51
Nun ja immerhin sind sich die Befürworter über die Postulate der SRT und den Aussagen wie dem Verhältnis von Längen und Zeitdauern etc zwischen sich gegeneinander bewegenden Beobachtern einig. Auch beim gerne diskutierten Zwillingsparadoxon gibt es über die “Paradoxie” Einigkeit. Nur wie dies “laienhaft” erklärt werden kann gibt es Unterschiede.
Und was haben die “Reviewer” so alles gesagt oder geschrieben? Und für welche Publikationen war dies denn?
@Rudi Knoth:
Sie können gerne versuchen, das einem zu erklären, der sieht, was sonst keiner sieht – das hat nur leider keinen Erfolg. Sagen Sie mir doch einfach (oder besser Herr Schulz) warum es ein Problem gibt, wenn man ruhende Strecken mit bewegten Uhren bestimmen will. Solange ich den Grund für das Problem kenne, während ihr alle euch erst einen aus den Fingern saugen müsst, weiß ich, dass ich richtig liege.
Die Reviewer sagen gar nichts. Bei Arxiv.org findet man nicht mal einen Endorsee. Die Einzigen, von denen jemals sachliche Resonanz (Rückfragen und/oder Meinungen) zu meinen PDFs kamen, sind Herr Schulz, Herr Manfred Pohl (weder verwandt noch verschwägert) und Herr David de Hilster – alles weder Reviewer noch Endorsees.
Dort werden NvB’s Autoritätsargumente zerlegt https://rationalwiki.org/wiki/Main_Page
Wer *renomierte* Einstein-Cranks sucht, die sind da schön versammelt neben allen anderen.
@Senf:
Wessen Argumente sind Autoritätsargumente und wessen Argumente sind kritisch durchdachte?
Mein “Kram” stimmt doch nur deswegen nicht, weil RT. 😆
Unangenehm finde ich z.B. die Tatsache, dass mir Hinz und Kunz erzählen will, wie Wissenschaft funktioniert – z.B. dass zu einer Hypothese auch Formeln und Experiment gehören. Und wenn man dann zur Hypothese Formeln liefert und auf bereits durchgeführte Experimente verweist, funktioniert Wissenschaft schon wieder ganz anders, nur weiß anscheinend kein Mensch mehr wie. Wissenschaft funktioniert nach meinem Dafürhalten jedenfalls nicht mit festhalten und predigen althergebrachter Ideen, schon gar nicht dann, wenn sie Hier da und dort zu unlösbaren Problemen führen, die als solche gar nicht erkannt werden, wenn man neue Ideen grundsätzlich ablehnt, weil sie keinem Konsenz entsprechen.
Alle vergöttern Einstein, nur keiner ist es. Alle vergöttern Einstein und nehmen sich deswegen damit zurück, klüger zu sein als er. Man denkt deswegen in letzter Konsequenz nicht weiter oder gar nach. Für mich existieren keine Götter, also entschuldigt bitte, dass ich auch vor eurem nicht halt mache.
@Nicht von Bedeutung 20. Januar 2019 @ 16:58
Nun mal halblang. Von einer “Vergötterung” von Einstein kann bei mir keine Rede sein. Seine Theorie ist ja keine “göttliche Eingebung” sondern eine Analyse des damaligen Standes der Experimentalphysik und aus diesem entwickelten Postulate aus der er seine Theorie entwickelte. Dafür wurden er und seine Theorie auch kritisiert.
Ihr Ansatz geht von Länge aus, die in allen Inertialsystem gleich sein sollen. Ebenso von Uhren, die auf geheimnisvolle Weise durch Bewegung oder Potentialunterschiede langsamer oder schneller gehen sollen. Nur gerade bei den Potentialunterschieden hat man ein Problem, weil die Gravitation und deren Kräfte nicht vom Potentialunterschied bestimmt wird. Etwa auf der ISS herrscht Schwerelosigkeit. Und damit keine Kraft. Im GPS-Satellit ist dies genauso. Wie soll denn dann das Cäsium-Atom wissen, daß es in der ISS oder im Satelliten befindet.
Nun gut, das war OT. Aber wenn jemand behauptet, seine Physik sei die bessere, dann stell ich mal meine Zweifel zur Diskussion.
@Rudi Knoth:
Was denken Sie wohl, wie das, von meinem Blickwinkel aus betrachtet, aussieht?
Was ist das für eine Frage? Aber seis drum. Je weniger Gravitation ein Cäsium-Atom beeinflusst, desto stärker beeinflussen die Kräfte zwischen Cäsium-Kern und seinen Elektronen die Energieniveaus des gesamten Atoms. Je mehr masse der Kern hat, desto höher ist die beeinflussende Kraft des Kerns und desto schneller bewegen sich wohl auch Elektronen um ihn herum. Vermutlich hat Rubidium nur deswegen eine niedrigere Frequenz als Cäsium, vermutlich liegt es aber auch nur an der unterschiedlichen Funktion der Taktgeber, aber wer weiß das schon. Wer will es überhaupt wissen? Von denen, die hier ständig mit argumentum ad verecundiam im Namen Einsteins argumentieren, jedenfalls keiner.
Wenn Sie das dürfen, darf ich das auch.
@Nicht von Bedeutung 20. Januar 2019 @ 17:53
Es ist doch eher die Ladung als die Masse. Die Gravitation ist wesentlich schwächer als die elektrische Anziehungskraft.
Aber jetzt schweifen wir doch ganz schön ab.
@Rudi Knoth:
BTW.: Woher weiß ein Myon, wie lange es lebt oder wie weit es fliegt?
@Rudi Knoth:
Nun, bei mir nicht. Bei mir ist Ladung eher eine Folge davon, wie sich Gravitation ausbreitet und was dabei alles passieren kann. Aber ja doch, wir schweifen ab.
Ich weiß ich nerve und halte Euch von den wirklich artikelbezogenen Dingen ab ^^. Was passiert denn nun meinem Stab? Frank ist ja der Antwort ausgewichen indem er sich auf Strecken zurückgezogen hat (Ist nicht persönlich, Du hast mir schon oft als armer verdummter Industriemechaniker mit Deiner Darstellung von Ereignissen weiter geholfen 🙂 ). Ich denke ja er verkürzt sich wirklich. Mal davon ab das mich Frank ja erst darauf gebracht hat mit seinem Beispiel…
@NvB 18:04 “BTW.: Woher weiß ein Myon, wie lange es lebt oder wie weit es fliegt?”
Das Myon muß gar nichts wissen, der Beobachter muß durchblicken. Wir haben doch langatmig genug erklärt, daß die Relativitätstheorie eine Invariantentheorie ist. Die Invarianten müssen in allen Bezugs-/ Koordinatensystemen logischerweise gleich sein. Invarianten sind die Physik, der Rest ist Messung.
Also auf Anfang: Ruhelebensdauer des Myons = 2μs Ruhelebensstrecke = 600 m = invariant.
Nun betrachten wir die Erscheinung “Entstehung Myon bis Detektion” im Erdsystem für 9 km Höhe.
Die Metrik (Ruhelebenstrecke)² = (Raumzeitstrecke)² = (Zeitstrecke)² – (Raumstrecke)² = (egal wo)²
Nun tanzen wir die Invarianzbetrachtung mit Grundschulanforderungen und mit Zahlen durch:
(6*10²m)² = (Zeitstrecke=?m)² – (9*10³m)² = inv, also (Zeitstrecke=?m)² = (9*10³m)² + (6*10²m)² größer.
(Zeitstrecke)² = 81*10^6 + 36*10^4 = 81,36*10^6 m² wobei (Zeit t in s) = (Zeitstrecke in m) / (LG in m/s)
Nun vollenden wir mit Rumwurzeln Zeitstrecke = 9,02*10³ m und LG = c =3*10^8 m, was ergibt für
Zeit t = 3*10^-5 s bzw 30*10^-6 = 30 μs, eine 15fache Zeitdilatation. Siehst’e iewo Längenkontraktion?
@Senf:
Das hast du gut erkannt. Ein Cäsium-Atom mus auch nichts wissen und Energieniveaus auch nicht. Es geht hier nur um eine Beobachtung und meine ist eben, dass die Periodendauer zwischen zwei speziellen Energieniveaus unter gegebenen Umständen unterschiedlich lange dauert, wodurch unterschiedlich lange Sekunden heraus kommen, wenn man die Taktraten von Uhren fixiert, was man dann Eigenzeit nennt woraus dann unterschiedliche Meter resultieren, wenn man Strecken an zu den speziellen Periodendauern proportionalen Wellenlängen bemisst, während sich Gitterabstände nicht ändern. Da kannst du noch millionenfach etwas mit Einstein oder was auch immer vorrechnen oder argumentieren – dein Argument bleibt dennoch das weitaus schwächere ad verucundiam im Namen Einsteins. Hast du das begriffen?
@Senf:
Tatsächlich sehe ich btw. nicht mal Myonen, sondern nur Energieniveaus, die gemessen werden. Und selbst wenn ich Myonen, so wie sie definiert sind, sehen würde, so sehe ich dann einen Wiederspruch darin, dass sie als Elementarteilchen zerfallen können sollen. Siehst’e irgendwo noch Logik in deiner Grunzschul-Invarianz-Physik? 😆
Nicht von Bedeutung
20. Januar 2019 @ 20:31
Oh, das ist interessant! Mit welcher Methode haben Sie das denn beobachtet und welche Genauigkeit haben Sie denn dabei erreicht? Wenn Sie damit eine Verletzung der Lorentzinvarianz nachweisen können, ist das eine Sensation. Entsprechend sorgfältig wird man Ihre Beobachtung natürlich zu reproduzieren versuchen müssen.
@Joachim Schulz:
Eigentlich sind es mehrere Methoden mit unterschiedlichen Genauigkeiten – Hafele und Keating, GPS, Maryland und weitere. Wenn Gitterabstände ebenso relativistischen Effekten unterlägen, wie Wellenlängen, wären die Frequenzen von Atomuhren ebenso starr wie die Interferenzmuster bei Michelson Morley und niemand würde jemals unterschiedlich gehende Uhren feststellen können. Nur leider stimmt diese These dann nicht mehr mit den Interpretationen der Nullresultate bei Michelson Morley überein, weil dazu die LK von Gitterabständen nötig ist, aber wer sagt denn, dass sich das beobachtete radiale Interferenzmuster entsprechend der Interferenzen entlang der Lichtlaufstrecken ändert, solange die Arme gleich lang bleiben?
Das funktioniert Alles – inkl. der Problematik, die existiert, wenn man ruhende Längen (Gitterabstände) mit bewegten Uhren (Wellenlängen/Periodendauern) misst.
Warum also sollte ich dies noch Leuten nachweisen, die sich (wie z.B. hier in diesem Blog) nur über Lorentzinvarianz einig sind, nicht aber darüber, wie sie sie Laien beibringen bzw. beweisen können.
Aber wenn Sie dennoch einen Beweis brauchen, dann überlegen Sie sich doch mal, mit was für einem Meter die Lichtgeschwingigkeit gemessen wurde bzw. überhaupt nur gemessen werden konnte.
@Herr Senf // 20. Januar 2019 @ 20:12
» Siehst’e iewo Längenkontraktion? «
Ich wurde zwar nicht gefragt, aber mir ist, als sähe ich da „iewo“ eine Längenkontraktion.
Das Myon kommt in 2 µs Eigenlebenszeit nur 600 m Ruhelebenstrecke weit, aber bis zur Erdoberfläche sind’s rund 20.000 m (im Ruhsystem des Myons). Ohne relativistische Kontraktion der Flugstrecke zur Erde käme das Myon kaum unten an, oder wie erklärt man sich das (als Myon-Mitreisender)?
@Balanus / 20. Januar 2019 @ 23:49
Das Myon legt nach eigener Einschätzung exakt null Meter durch den Raum, dafür aber eine Strecke \(c\Delta\tau\) auf seiner Lebens-Weltlinie durch die Zeit zurück. Von der Erde aus beschrieben bewegt es sich indessen mit einer Geschw. \(v\), und die Strecke auf der Lebens-Weltlinie hat in der erdbezogenen Darstellung dann eine zeitartige Komponente \(c\Delta t = \gamma c\Delta\tau\) sowie eine raumartige Komponente \(\Delta x = \gamma v\Delta\tau\), wobei \(\gamma = 1/\sqrt{1 – v^2/c^2}\).
Das ist alles, und da ist tatsächlich kein Bedarf an irgendwelcher Längenkontraktion.
@Balanus 20. Januar 2019 @ 23:49
Es ist wohl doch etwas anders, als Sie es darstellen. Das Myon hat in dem Inertialsystem, in dem es ruht, eine Lebensdauer von 2 µs . Die Strecke vom Entstehungsort bis zur Erdoberfläche beträgt im “Ruhesystem” der Erde 20.000? Meter. Die Zeit vom Enstehen des Myons bis zum Antreffen auf der Erde im Ruhesystem de Erde betragt also 66 µs. Wenn die Relativgeschwindigkeit des Myons gegenüber der Erde wegen des Relativitätsprinzips gleich sein soll, dann ist im Inertialsystem des Myons die Erdoberfläche zum Zeitpunkt der Entstehung nur 600 Meter entfernt. Denn sonst könnte die Erdoberfläche das Myon in der kurzen Zeit nicht erreichen.
@Nicht von Bedeutung:
Es wundert mich nicht, dass auf meine Nachfrage von Ihnen nur heiße Luft kommt. Hafele und Keating, GPS und Maryland-Experiment haben alle nicht das geringste mit der Gitterkonstante zu tun.
Chrys
21. Januar 2019 @ 07:43
Das Myon legt durchaus die Strecke vom Entstehungspunkt zum Detektor am Erdboden zurück. In welchem Bezugssystem das berechnet wird, ist dem Myon egal. Das Ruhesystem des Myons ist da genauso zulässig wie das der Erde.
@Joachim Schulz:
Natürlich ist das für Sie heiße Luft. Für euch scheint alles heiße Luft zu sein. Vermutlich baut ihr sogar Atomuhren aus heißer Luft. Natürlich sind in heißer Luft keine Gitterabstände erkenn bar. Mich wundert es also auch nicht, dass sie hier auch nur heiße Luft sehen. Als wenn Sie wüssten, wo Gitterabstände überall auftauchen – in Metallgehäusen von Atomuhren z.B. oder gar an jenen Stellen, an denen ziemlich genau 9192631770 Takte gezählt werden müssen, damit eine Azeige 1s anzeigt. Ganz sicher bestehen die nicht aus heißer Luft. Veralbern kann ich mich echt alleine.
@Joachim Schulz:
Nun, das ist aber Kritikern nicht egal – Kritiker bräuchten da nämlich nach wie vor einen Beweis aus dem Myonensystem, das da tatsächlich alles so gemessen wird, wie behauptet. Aber wenn Sie meinen Myonen ernster nehmen zu müssen, als Kritiker, warum erzählen Sie ihre RT-Geschichte dann nicht den Myonen? Bei heißer Luft waren wir ja schon.
Das Myon
Angeblich “sähe” das Myon eine verkürzte Entfernung bis zur Erdoberfläche, müsste als weniger weit fliegen wie wenn es langsamer wäre (“sRT-Längenkontration”).
Gleichzeitig würde aber für das Myon auch die Zeit langsamer ablaufen, was doch bedeutet, dass es in der Zeit eines dagegen ruhenden Beobachters weiter käme (“sRT-Zeitdilatation”) wie wenn sein Zeitablauf nicht dilatiert wäre.
Die beiden Effekte müssten sich addieren:
eine kürzere Distanz überwinden zu müssen, und dazu noch für einen Außenstehenden mehr Zeit bis zum Zerfall “zur Verfügung” zu haben würde im Endeffekt zu einer doppelt so langen Fluglänge führen.
Warum wird das nicht berücksichtigt? Warum wird immer entweder “Längenkontraktion” oder “Zeitdilatation” berücksichtigt, aber nicht beides?
Ich halte das Myonenexperiment für keinen Beweis für die sRT, da das Myon auch aufgrund der Energie, die durch die Beschleunigung zugeführt wurde, eine längere Lebensdauer haben könnte als ein unbeschleunigtes, quasi ruhendes Myon.
Es wird nämlich einfach angenommen, dass das beschleunigte Myon die gleiche Lebensdauer hätte wie ein unbeschleunigtes.
(Das das Myon nicht selbst beschleunigt wird, sondern sein Vorgängerteilchen, ist hierbei irrelevant. Das irgendwann beschleunigte Vorgängerteilchen überträgt natürlich seine Energie auf das sich in der Atmosphäre daraus bildende Myon.)
@Joachim / 21. Januar 2019 @ 08:50
»Das Ruhesystem des Myons ist da genauso zulässig wie das der Erde.«
Eben drum. Und das Ruhesystem des Myons wird `Ruhesystem des Myons’ genannt, weil das Myon dort nicht von Fleck kommt und einfach nur die Eigenzeit vergeht. Mit dem hyperbolischen Pythagoras,
\[
c^2(\Delta t)^2 – (\Delta x)^2 = c^2\gamma^2(\Delta\tau)^2 – v^2\gamma^2(\Delta\tau)^2 = c^2(1 -\beta^2)\gamma^2(\Delta\tau)^2 = c^2(\Delta\tau)^2,
\]
ist dann schon alles so einfach wie möglich erklärt, was es hier zu erklären gibt. Einfacher geht nicht.
@Albrecht Storz:
Das ist der Knackpunkt. Es wird allenfalls bewiesen, dass eine Rechnung theoretisch funktioniert. Nie aber sind Augenzeugen mit Myon-Air geflogen.
Aber anstatt den erforderlichen Beweis zu liefern, bauen Wissenschaftler lieber Atomuhren aus heißer Luft, um anschließend verkünden zu können, GPS, Maryland und all das hätte nichts mit Gitterabständen bzw. -konstanten zu tun.
Ich würde solch einen Zirkus jedenfalls nicht unter Wissenschaft einordnen, sondern klar unter Standup-Comedy.
@Albrecht Storz 21. Januar 2019 @ 12:20
Nein. Beides Längenkontraktion und Zeitdilatation beschreiben gleichermaßen die Tatsache, daß die Myonen mit einer Lebensdauer von 2 µs mit nahezu Lichtgeschwindigkeit eine Strecke von 10 Kilometern zurücklegen können.
@Rudi Knoth:
Aber die Tatsache, dass sich die Lebensdauer von Myonen durch Bewegung schlicht ändert, ist wohl zu einfach. Da muss die RT bemüht werden, damit sie ihre Existenzberechtigung behält. Also Leute, die Atomuhren aus jener heißen Luft bauen, die sie beim Myonen-Experiment produzieren, machen mir jedenfalls nichts mehr vor. Ich kann nur noch hoffen, dass das jetzt genauso verhöhnend rüber kommt, wie es gemeint ist. Ihr könnt eigentlich nur noch zugeben, dass ihr es vergeigt habt, statt weiterhin “Nein, Unfug, da hast du was falsch oder gar nicht verstanden” zu blöcken.
Rudi Knoth
“Nein. Beides Längenkontraktion und Zeitdilatation beschreiben gleichermaßen die Tatsache”
Ach so? Also wahlweise und beliebig? Oder mal so, mal so, nach bestimmten Regeln?
@Albrecht Storz:
Mal so, mal so, gerade wie man es braucht – keine Regeln, alles reine Interpretations- und Auslegungssache, je nach Verständnis der RT.
Man rechnet und rechnet und rechnet und rechnet sich nen Wolf. Bei Michelson Morley kommt man über dieses Gerechne z.B. darauf, dass eine tatsächliche LK in den Armen benötigt wird, damit eine Resonanzbedingung erfüllt bleibt, die starre Interferenzmuster erzeugt.
Bei Experimenten mit Atomuhren hingegen, darf diese Resonanzbedingung nicht erfüllt sein, damit eine Uhr auch mal schneller ticken kann, als die Andere, was z.B. bei H&K festgestellt wurde. Hier darf zur ZD also definitiv keine tatsächliche LK stattfinden.
Allerdings darf man auch der selben Meinung wie Herr Schulz sein, nach welcher sich wohl mehr die Resonanzkörper von Atomuhren verbiegen, als die gemessenen Wellenlängen bzw. Periodendauern, mit denen die SI-Sekunde definiert wird.
@Chrys // 21. Januar 2019 @ 07:43
Ok, wenn wir Herrn Senfs „Ruhelebensstrecke = 600 m“ beiseitelassen und aus Sicht des Myons keine Bewegung im Raum erfolgt (so war es eh von mir gemeint), dann rast eben der erdgebundene Myonendetektor dem Myon entgegen und überwindet dabei rechnerisch eine Strecke von weniger als 600 m. Das ist schon deutlich weniger als was Erdbewohner als Distanz zwischen Myonenentstehungsort und Detektor messen. Ergo: „Längenkontraktion“.
@Rudi Knoth // 21. Januar 2019 @ 08:04
» …dann ist im Inertialsystem des Myons die Erdoberfläche zum Zeitpunkt der Entstehung nur 600 Meter entfernt. «
Genau! Darin zeigt sich meinem Verständnis nach eben die „Längenkontraktion“, die von manchen bestritten bzw. als überflüssiges Konstrukt gesehen wird.
Uli Schoppe schrieb (19. Januar 2019 @ 09:45):
> OK, nehmen wir Stäbe.
Super! — Dann sollten wir vor allem die beiden Enden des jeweiligen Stabes ausdrücklich unterscheiden und geeignet verschieden benennen; z.B.
– die beiden (gegenüber einander ruhenden) Enden des einen Stabes: \(A\) und \(B\), und
– die beiden (gegenüber einander ruhenden) Enden des einen Stabes: \(P\) und \(Q\).
Und wir könnten die Zusammenhänge gern auch anhand des Einsteinschen Original-Beispiels “Bahndamm-und Zug” erörtern,
wobei
– der “Bahndamm-Stab” (bzw. der “Bahnhof-Stab”) ausdrücklich aus zwei gegenüber einander ruhenden “Stellen des Bahndamms” \(A\) und \(B\) bestehen soll (bzw. in den obigen “Bahnhof”-bezogenen Beispiel aus den gegenüber einander ruhenden “Ausfahr-Signal-Anlage” \(A\) und “Einfahr-Signal-Anlage” \(B\); und
– der “Zug-Stab” ausdrücklich aus zwei gegenüber einander ruhenden “Zug-Bestandteilen” \(P\) und \(Q\) bestehen soll,
anschaulich insbesondere aus “Lokomotive” (bzw. noch konkreter: deren “Spitze”) \(P\) und “Caboose” (bzw. deren extreme Schlusskante) \(Q\).
> Da stellen wir nicht nur an den Enden einen Detektor auf sondern auch in der Mitte.
Ganz prima!
Dann können wir nämlich die zum Verständnis der Versuchsanordnung (“Einstein-Projektion”) erforderlichen Feststellungen von Gleichzeitigkeit (bzw. von Ungleichzeitigkeit) ganz unmissverständlich und Koordinaten-frei behandeln.
Ganz wesentlich ist dabei die Einsicht, dass “die Mitte zwischen \(A\) und \(B\)” jemand anderes ist, als “die Mitte zwischen \(P\) und \(Q\)”;
sofern sich, wie in den bekannten Gedanken-Experimenten üblich, der Bahnhof \((A, B)\) und der Zug \((P,Q)\) sich gegenüber einander bewegen.
Und natürlich sollten wir diese beiden zusätzlichen Beteiligten ebenfalls ausdrücklich geeignet benennen:
– die “Mitte zwischen \(A\) und \(B\)” nennt man üblicher Weise \(M\) (vgl. Einsteins verlinkte Beschreibung); und
– die “Mitte zwischen \(P\) und \(Q\)” könnten wir \(N\) nennen.
Als Bestandteile des Bahnhofs sollen \(A\) und \(B\) und \(M\) gegenüber einander ruhen.
Als Bestandteile des Zugs sollen \(P\) und \(Q\) und \(N\) gegenüber einander ruhen.
Und insgesamt sollen sich \(A\) und \(B\) und \(M\) gegenüber \(P\) und \(Q\) und \(N\) gleichförmig bewegen,
und ebenso sollen sich \(P\) und \(Q\) und \(N\) gegenüber \(A\) und \(B\) und \(M\) gleichförmig bewegen.
(Was wiederum verdeutlicht, dass die beiden “Mitten” \(M\) und \(N\) verschiedene Beteiligte sind.)
> Der [eine Stab] ist doppelt so lang wie der [andere] Stab.
Damit ist das Ergebnis der Messung ausdrückt:
– falls \(A\) und \(B\) und \(M\) den Geschwindigkeits-Parameter von \(P\) und \(Q\) und \(N\) durchwegs als
\[\beta_{(AB)}[ \, P \, ] = \beta_{(AB)}[ \, N \, ] = \beta_{(AB)}[ \, Q \, ] = \frac{\sqrt 3}{2}\] ermittelten, und
– falls \(P\) und \(Q\) und \(N\) den Geschwindigkeits-Parameter von \(A\) und \(B\) und \(M\) durchwegs ebenfalls als
\[\beta_{(PQ)}[ \, A \, ] = \beta_{(PQ)}[ \, M \, ] = \beta_{(PQ)}[ \, B \, ] = \frac{\sqrt 3}{2}\] ermittelten,
– und falls \(M\) das Treffen von \(A\) und \(P\), d.h. das Koinzidenz-Ereignis \(\varepsilon_{AP}\), und das Treffen von \(B\) und \(Q\), d.h. das Koinzidenz-Ereignis \(\varepsilon_{BQ}\), koinzident wahrgenommen hatte,
(wozu man übrigens auch sagen kann, dass
“\(A\)s Anzeige der Passage von \(P\) und \(B\)s Anzeige der Passage von \(Q\) einander gleichzeitig waren”, bzw. dass
“Stab \((P, Q)\) auf Stab \((A, B)\) projiziert wurde”,
dann ist daraus der Wert des Längenverhältnisses dieser beiden Stäbe als \[\left( \frac{PQ}{AB} \right) := \sqrt{1 – \beta^2} = \sqrt{1 – \left(\frac{\sqrt 3}{2}\right)^2} = \sqrt{ 1 – \frac{3}{4} } = \sqrt{\frac{1}{4}} = \frac{1}{2}\]
zu schlussfolgern.
Und natürlich außerdem:
\[ \left( \frac{PN}{AM} \right) = \left( \frac{NQ}{MB} \right) = \left( \frac{PN}{MB} \right) = \left( \frac{NQ}{AM} \right) = \left( \frac{PQ}{AB} \right) = \frac{1}{2}.\]
Soweit die Betrachtung von durchwegs gegenseitig gleichförmiger Bewegung.
Nun die Variante(n) “mit Abbremsung”:
> In dem Moment [als sich \(P\) und \(M\) trafen bzw. passierten] beginnt der Stab [\(P, N, Q\)] abzubremsen und zwar so [, dass …]
Stellen wir uns am besten vor (nämlich um das obige Beispiel nicht zu verändern, sondern lediglich zu ergänzen), dass \(P\) und \(Q\) und \(N\) jeweils “Kamelle warfen”, konkret benannt z.B. \(J\) und \(K\) und … \(W\).
So, dass \(P\) und \(Q\) und \(N\) selbst genau wie im oben beschriebenen Versuch durchwegs in gleichförmiger Bewegung bzgl. \(A\) und \(B\) und \(M\) blieben;
aber die “Kamelle” “in Richtung von \(B\) zu \(A\)” entlangrollten und letztlich bzgl. \(A\) und \(B\) und \(M\) zur Ruhe kamen (liegen blieben).
Der Anfang der Versuchsanordnung lautet entsprechend offenbar:
“In dem Moment als \(P\) von \(M\) getroffen/passiert wurde und \(J\) abwarf, wurde auch \(W\) von \(N\) abgeworfen, und \(K\) von \(Q\) …”
> [… und zwar so,
dass] in dem Moment [als] das vordere Ende den Endpunkt des anderen Stabes erreicht beide Stäbe gegeneinander ruhen.
Im Sujet des Karneval-Umzugs ist die Versuchsanordnung demnach so fortzusetzen:
“… und zwar so,
dass in dem Moment, als \(J\) bei \(A\) austrudelte, alle drei Kamelle, \(J\) und \(K\) und \(W\), sowohl gegenüber einander ruhten, als auch gegenüber \(A\) und \(B\) und \(M\) ruhten.”
Offensichtlich bedarf nun die (zweimal benutzte) Phrase “in dem Moment als” besonderer Aufmerksamkeit, weil es dabei ja um (Vorgaben von Feststellungen hinsichtlich) Gleichzeitigkeit geht.
Variante 1:
Die Gleichzeitigkeits-Vorgabe bezieht sich in beiden Fällen auf die Anzeigen von \(A\) und \(B\) und \(M\).
Weil, wie oben beschrieben, “Stab \((P, Q)\) auf Stab \((A, B)\) projiziert wurde”, und weil \(N\) als “Mitte zwischen \(P\) und \(Q\)” identifiziert ist, und ebenso \(M\) als “Mitte zwischen \(A\) und \(B\)” identifiziert ist, gilt auch,
dass “Stab \((P, N)\) auf Stab \((M, B)\) projiziert wurde”.
D.h. \(M\)s Anzeige der Passage von \(P\) sowie des Abwerfens von \(J\) war gleichzeitig zu \(Q\)s Anzeige der Passage von \(N\) sowie des Abwerfens von \(W\).
Außerdem soll \(A\)s Anzeige des “Eintrudelns” von \(J\) gleichzeitig zu \(M\)s Anzeige des “Eintrudelns” von \(W\) sowie \(B\)s Anzeige des “Eintrudelns” von \(K\) gewesen sein.
Dazu würde passen, dass “die Kamelle” \(J\) und \(K\) (und \(W\)) alle gleichermaßen beschleunigt bzw. “abgebremst” wurden.
Außerdem, weil ja, wie bereits oben hergeleitet, nach wie vor gilt
\[ \left( \frac{PN}{AM} \right) = \frac{1}{2},\]
sagt man dazu auch, dass \(J\) und \(K\) (und \(W\)) dabei/dadurch/deshalb “zusammengestaucht” wurden.
Variante 2:
Die Gleichzeitigkeits-Vorgabe bezieht sich in beiden Fällen auf die Anzeigen von \(P\) und \(Q\) und \(N\).
Um die damit verbundenen detaillierten Beziehungen zu beschreiben, müssten noch etliche weitere Beteiligte benannt werden.
Die Schlussfolgerung kurzgefasst:
Auch dazu würde passen, dass “die Kamelle” \(J\) und \(K\) (und \(W\)) alle gleichermaßen beschleunigt bzw. abgebremst wurden;
man sagt dazu allerdings, dass \(J\) und \(K\) (und \(W\)) dabei/dadurch/deshalb “auseinandergedehnt” wurden.
(Insbesondere diese “Variante 2” ist auch als “Bellsches Raumschiffparadoxon” bekannt.)
Variante 3:
Die Gleichzeitigkeits-Vorgabe “in dem Moment als” bezieht sich hinsichtlich des “Abwerfens der Kamellen” auf die Anzeigen der “Werfer”, also von \(P\) und \(Q\) und \(N\),
aber hinsichtlich des “Austrudelns der Kamellen” auf die Anzeigen der “Fänger”, also von \(A\) und \(B\) und \(M\).
Dazu passt (wenn ich mir das recht überlege), dass \(J\) (geworfen von \(P\), gefangen von \(A\)) wesentlich sanfter abbremsen musste als \(K\) bzw. als \(W\).
Folglich wäre wohl zu sagen, dass \(J\) und \(K\) und \(W\) dabei/dadurch/deshalb “sogar noch stärker auseinandergezerrt” würden, als in “Variante 2” gefolgert.
(Eine weitere “Variante 4 des Karneval-Umzugs-Versuchs” ist denkbar, aber nicht sinnvoll.)
Frank Wappler schrieb (21. Januar 2019 @ 14:40):
> [… und falls] “Stab \((P, Q)\) auf Stab \((A, B)\) projiziert wurde”,
> dann ist daraus der Wert des Längenverhältnisses dieser beiden Stäbe als
Korrektur:
\[\left( \frac{AB}{PQ} \right) := \sqrt{1 – \beta^2} = \sqrt{1 – \left(\frac{\sqrt 3}{2}\right)^2} = \sqrt{ 1 – \frac{3}{4} } = \sqrt{\frac{1}{4}} = \frac{1}{2}\]
zu schlussfolgern.
Und natürlich außerdem:
\[ \left( \frac{AM}{PN} \right) = \left( \frac{MB}{NQ} \right) = \left( \frac{MB}{PN} \right) = \left( \frac{AM}{NQ} \right) = \left( \frac{AB}{PQ} \right) = \frac{1}{2}.\]
(Die obige Argumentation hinsichtlich verschiedener Varianten des “Karneval-Umzugs-Versuchs” und der entsprechenden “Längen-Verteilung von Karamelle(n)” besteht unverändert.)
Rudi Knoth
21. Januar 2019 @ 12:58
“daß die Myonen mit einer Lebensdauer von 2 µs mit nahezu Lichtgeschwindigkeit eine Strecke von 10 Kilometern zurücklegen können.”
Das ist wieder ein typisches Beispiel für “Relativitäts-Schludrigkeit”.
– Beträgt die Lebensdauer für das Myon oder für einen “dagegen ruhenden” Beobachter 2 Mikrosekunden? Wenn man den Bezug nicht angibt ist das einfach schludrig, egal ob das irgendwo schon steht oder nachgeschlagen werden kann.
– Offensichtlich handelt es sich um “10 km für den (dagegen ruhenden) Beobachter”. Aber auch dies gehört korrekter Weise angegeben. Es ist schlicht schludrig, immer wieder die Bezüge zu unterschlagen. Hat aber hier System.
Und zu Unterschlagen, dass kein Mensch weiß, ob ein beschleunigtes Myon auch eine durchschnittliche Lebensdauer von 2 Mikrosekunden wie das unbeschleunigte Myon besitzt, ist auch mindestens schludrig, wenn nicht noch schlimmeres.
@Albrecht Storz:
Natürlich ist das noch Schlimmeres. Ganz besonders dann, wenn man für eigentlich viel offensichtlichere Dinge, wie z.B. dem Kreisbezug bei der Definition von SI-Meter und SI-Sekunde Beweise einfordert, die man in Sachen Myonen-Experiment selbst nicht liefern kann. Das sich die Lebensdauer bewegter Myonen (falls sie denn überhaupt existieren) schlicht verlängert, ist für Relativisten nur sehr schwer zu begreifen – aber anscheinend hat genau nur der Recht, der die eindrucksvollste Mathematik – also solche, die kein Mensch mehr versteht, obwohl man es gerade Menschen beibiegen will – liefert. 😆
Fazit: Kritiker reden Stuss, weil Einstein. 😆
@Balanus / 21. Januar 2019 @ 14:23
Diese 600 Meter sind doch nur eine nichtrelativistische Vorhersage für die Länge der Strecke, die ein mit einer gewissen Geschw. v bewegtes Myon während seiner Lebensdauer von 2 μs schaffen kann. Diese Vorhersage ist observationell falsifiziert, und in einer relativist. Kalkulation kommen diese klass. 600 Meter überhaupt nirgendwo vor. Das ist keine kontrahierte, sondern gewissermassen schlicht eine falsifizierte Länge.
Rudi Knoth
21. Januar 2019 @ 12:58
“daß die Myonen mit einer Lebensdauer von 2 µs mit nahezu Lichtgeschwindigkeit eine Strecke von 10 Kilometern zurücklegen können.”
oder um es mal anders auszudrücken: dann müsste das Myon schneller als mit c unterwegs sein.
@Chrys:
Ich bin mir ziemlich sicher, dass das viele deiner Kollegen anders sehen, sonst würden sie darin nicht eine Bestätigung der RT sehen. “Nichtrelativistisch” kann hier gar nicht zutreffen, denn Relativitäts-Kritiker sehen diese Strecke ja nicht einmal. Kritiker sehen noch nicht einmal die 2µs Lebensdauer bei bewegten Myonen in irgendeiner Form. Das Ganze kann also, wenn überhaupt, nur in relativistischen Kalkulationen vorkommen und nirgendwo anders.
Aber gut, dass das Thema vom Tisch ist, dann kann man das Myonen-Experiment als Bestätigung für die RT ja ad Acta legen, oder nicht?
Hallo Balanus 14:23 “Ok, wenn wir Herrn Senfs „Ruhelebensstrecke = 600 m“ beiseitelassen …”
Die “Ruhelebensstrecke” ist keine Raumstrecke (in m), sondern eine Zeit (mit LG in m um/gerechnet).
Im relativistischen Raumzeitgefüge ist dieses Abstandsmaß RZ² = T² – L² ein invariantes Intervall für frei wählbare Koordinaten T;L, ähnlich Pythagoras, wo c²=a²+b²=inv=const erfüllt ist für verschiedene a;b.
Mach ich in RZ die Strecke L größer, muß auch T größer sein, also 2μs=600m für T=0 aber 15μs=9km.
Zur Veranschaulichung: nimm kariertes Papier X;Y , lege ein rechtwinkliges Dreieck 5²=4²+3² drauf.
Nun kann man dieses Dreieck drehen, die Eckpunkte für A;B;C werden ihre Koordinaten X;Y ändern, die Diagonale c bleibt als Abstand gleich, genauso kann man a und b ändern unter der Bedingung c=gleich.
@Albrecht Storz 21. Januar 2019 @ 14:03
Nun dies noch einmal genauer beschrieben:
Ruhesystem Erde:
Die Strecke, die das Myon zurücklegt, ist 10 Km lang. Bei einer gemessenen Geschwindigkeit von 300000 Km/s ergibt sich dann eine “Belegdauer” der Strecke von 33,3 µs. Die Lebensdauer des Myons im Inertialsystem, in dem es ruht, beträgt aber 2 µs. Damit haben wir eine Zeitdilatation.
Ruhesystem des Myons:
Die Lebensdauer des Myons beträgt darin 2 µs. Die Strecke im Ruhesystem der Erde aber 10 Km. Also ist die der Abstand der Erdoberfläche im Ruhesystem des Myons nur 600 m. Daher haben wir eine “Längenkontraktion”.
Pardon 17:51 anstelle “15μs=9km” muß natürlich hin”T=30μs=9km”, y-Faktor=15
@Herr Senf / 21. Januar 2019 @ 17:51
Ich glaub’, wir haben das gleiche gerechnet. Die “Ruhelebensstrecke” ist mein \(c\Delta\tau\), was mir aber bei meiner Entgegnung an Balanus nicht aufgefallen war. Hat sich jetzt geklärt, alles ok.
—
@NvB / 21. Januar 2019 @ 16:56
Doch, die schnellen Myonen bestätigen sehr schön die SRT Vorhersage. Nur braucht es dazu halt keine Längenkontraktion.
@Rudi Knoth:
Die Fakten noch mal genauer beschrieben:
1. Vorausetzung: Myonen existieren tatsächlich und sind keine Elementarteilchen dann…
2. Im Labor ruhend beobachtete Myonen haben eine durchschnittliche Lebensdauer von 2µs …
3. Myonen die beim Aufprall der kosmischen Strahlung auf die Erdatmosphäre entstehen, können in der nähe der Erdoberfläche noch gemessen werden, woraus folgt…
4. Myonen bewegen sich entweder mit ÜLG, auf der Erdoberfläche gemessene Myonen entstehen sehr viel später oder bewegte Myonen leben schlicht länger.
5. Keinesfalls aber kann irgend etwas, was aber von RT-Befürwortern oder Relativisten propagiert wird, im Ruhesystem eines bewegten Myons tatsächlich gemessen werden.
6. Daraus folgt, dass es unheimlich viele gültige Theorien über Myonen gibt und nicht bloß die Version der RT, die eine Längenkontraktion benötigt, die hier nicht mal funktioniert (15km-Stab im Ruhesystem des Myons auf die Erde gerichtet).
Es ist nach wie vor unglaublich, mit welchen Mitteln versucht wird, die RT in jedem Fall zu retten während Kritiker immer nur Blödsinn verbreiten sollen – das ist alles andere als wissenschaftlich.
Und Senfs Papier hilft da auch nur soweit, wie z.B. eine simple Weltraum-Simulation ala Elite oder Änliches. Würdet ihr freundlicherweise mal wieder erwachen und das nicht ewig von kritischen Denkern verlangen?
@Chrys:
Das Erste erzählst du besser einem Anderen und das zweite besser Herrn Knoth.
@NvB 19:21 “Würdet ihr freundlicherweise mal wieder erwachen und das nicht ewig von kritischen Denkern verlangen?” … 🙁 redet doch einer vom Erwachen, der noch nicht ausgeschlafen hat 🙂
Würdest Du mal langsam den Ausgang aus Deinem Kreisverkehr finden, mußt aber auf die Straße achten und Dich nicht ständig selbst mit der Verwechslung kleiner/größer besoffen reden 😉
@Senf:
Wer bitte redet sich denn hier gerade um Kopf und Kragen? 😆
Ihr Relativisten tut dies, indem ihr euch über eure phänomenale Längenkontraktion nicht einig werdet. 😆
Bestätigungen von irgendwelchen Theorien sehen jedenfalls anders aus – das hier ist und bleibt Hirnwichse vom Feinsten. 😆
@Chrys // 21. Januar 2019 @ 16:30
» Diese 600 Meter sind doch nur eine nichtrelativistische Vorhersage für die Länge der Strecke, die ein mit einer gewissen Geschw. v bewegtes Myon während seiner Lebensdauer von 2 μs schaffen kann. «
Diese 600 Meter waren aber nicht meinThema. Mir ging es nur darum, dass zwischen dem Ort der Myonentstehung und dem Ort der Myondetektion vom Erdbewohner rund 20.000 Meter gemessen werden, während man vom Ruhsystem des Myons aus im Moment der Myonentstehung den Myondetektor geschwindigkeitsbedingt in einer Entfernung von rund 400 Myon-Meter erblicken würde—statt der 20.000 Erd-Meter. Mit anderen Worten: Die 20.000 Meter schrumpfen allein aufgrund der Geschwindigkeit, mit der sich der Detektor dem ruhenden Myon nähert, auf etwa 1/50.
@Herr Senf // 21. Januar 2019 @ 17:51
» Die “Ruhelebensstrecke” ist keine Raumstrecke (in m), sondern eine Zeit (mit LG in m um/gerechnet). «
Sind das die besagten 600 Meter, die @Chrys oben erwähnt?
Ich bezweifle nicht, dass sich alles korrekt berechnen lässt und wir keine weiteren Annahmen brauchen als Eigenzeiten und Weltlinien (d.h., weder Zeitdilatation und Längenkontraktion). Aber mich beschäftigt vor allem, wieso wir überhaupt mit Eigenzeiten und Weltlinien rechnen müssen. Liegt es allein an der Tatsache, dass es für die elektromagnetische Strahlung eine Grenzgeschwindigkeit gibt, oder steckt doch mehr dahinter, ich denke da insbesondere an grundlegende Eigenschaften des Raumes bzw. der Raumzeit.
Balanus schrieb (21. Januar 2019 @ 14:23):
> der erdgebundene Myonendetektor […] rast […] dem Myon entgegen
Richtig; mit Geschwindigkeit \( \beta \, c und überwindet dabei rechnerisch eine Strecke von weniger als 600 m.
Nämlich die Strecke zwischen dem o.g. Myon als “dem Ende”,
und beginnend bei einem geeignet “vorausgeeilten” Beteiligten, leicht vorstellbar meinetwegen ein Neutrino, das gegenüber dem Myon ruhte, und dem der erdgebundene Myonendetektor ebenfalls mit Geschwindigkeit \( \beta \, c \) zunächst entgegenraste, und nach Treffen/Passage davonraste;
und außerdem dadurch bestimmt, dass die Anzeige dieses “vorausgeeilten” Beteiligten/Neutrinos bei Treffen/Passage des erdgebundenen Myonendetektors gleichzeitig zur Geburts-Anzeige des o.g. Myons war.
Und falls die Dauer des Myons von seiner Geburts-Anzeige bis zu seiner Anzeige bei Treffen/Passage des erdgebundenen Myonendetektors \(2 \, {\rm \mu s}\) sein sollte, wie hier offenbar angenommen wird, dann hat die Strecke zwischen Neutrino und Myon eine Länge von
\( \beta \, c \, 2 \, {\rm \mu s} = \beta \, 600 \, {\rm m} Das ist schon deutlich weniger als was Erdbewohner als Distanz zwischen Myonenentstehungsort und Detektor messen.
Auch richtig; nämlich um den Faktor \(\sqrt{1 – \beta^2}\) weniger.
> Ergo: „Längenkontraktion“.
Zwar ist nicht zu bestreiten, dass das Wort “Längenkontraktion” für den beschriebenen Sachverhalt, mit dem genannten Verhältnis der Längen zweier Strecken, historisch verwendet wurde.
Aber ist es etwa sinnvoll zu sagen, dass die längere dieser beiden Strecken deshalb kontrahiert sei ?? …
p.s.
Wegen Verwendung des “<“-Zeichens in einigen Formeln ist die SciLogs-Vorschau dieses Kommentars nicht so formatiert, wie ich meinen Kommentar wünsche. Diesen Kommentar trotzdem so abzusenden, stellt also einen weiteren Test der SciLogs-Kommentar-Vorschau dar, den ich mangels anderer SciLogs-Dokumentation gern als “Community-Service” auf mich nehme.
Balanus schrieb (21. Januar 2019 @ 14:23):
> der erdgebundene Myonendetektor […] rast […] dem Myon entgegen
Richtig; mit Geschwindigkeit \( \beta \, c\), also weniger als \(c\).
> und überwindet dabei rechnerisch eine Strecke von weniger als 600 m.
Nämlich die Strecke zwischen dem o.g. Myon als “dem Ende”,
und beginnend bei einem geeignet “vorausgeeilten” Beteiligten, leicht vorstellbar meinetwegen ein Neutrino, das gegenüber dem Myon ruhte, und dem der erdgebundene Myonendetektor ebenfalls mit Geschwindigkeit \( \beta \, c \) zunächst entgegenraste, und nach Treffen/Passage davonraste;
und außerdem dadurch bestimmt, dass die Anzeige dieses “vorausgeeilten” Beteiligten/Neutrinos bei Treffen/Passage des erdgebundenen Myonendetektors gleichzeitig zur Geburts-Anzeige des o.g. Myons war.
Und falls die Dauer des Myons von seiner Geburts-Anzeige bis zu seiner Anzeige bei Treffen/Passage des erdgebundenen Myonendetektors \(2 \, {\rm \mu s}\) sein sollte, wie hier offenbar angenommen wird, dann hat die Strecke zwischen Neutrino und Myon eine Länge von
\( \beta \, c \, 2 \, {\rm \mu s} = \beta \, 600 \, {\rm m}\), also weniger als \( 600 \, {\rm m}.\)
> Das ist schon deutlich weniger als was Erdbewohner als Distanz zwischen Myonenentstehungsort und Detektor messen.
Auch richtig; nämlich um den Faktor \(\sqrt{1 – \beta^2}\) weniger.
> Ergo: „Längenkontraktion“.
Zwar ist nicht zu bestreiten, dass das Wort “Längenkontraktion” für den beschriebenen Sachverhalt, mit dem genannten Verhältnis der Längen zweier Strecken, historisch verwendet wurde.
Aber ist es etwa sinnvoll zu sagen, dass die längere dieser beiden Strecken deshalb kontrahiert sei ?? …
p.s.
Resultat des in Kommentar 21. Januar 2019 @ 23:15 durchgeführten Test der SciLogs-Kommentar-Vorschau:
Verwendung des “<“-Zeichens in \(\LaTeX\)-Formeln führt zu Fehlformatierung, so wie in der SciLogs-Kommentar-Vorschau dargestellt.
Dann verwende einfach \\gt und \\lt in \LaTeX-Formeln
Mit jeweils nur einem Backslash.
Rudi Knoth
21. Januar 2019 @ 18:53
“Ruhesystem Erde:
Die Strecke, die das Myon zurücklegt, ist 10 Km lang. Bei einer gemessenen Geschwindigkeit von 300000 Km/s ergibt sich dann eine “Belegdauer” der Strecke von 33,3 µs. Die Lebensdauer des Myons im Inertialsystem, in dem es ruht, beträgt aber 2 µs. Damit haben wir eine Zeitdilatation.”
Das heißt, der “ruhende Beobachter” (im Ruhesystem Erde) beobachtet eine Myonenlebensdauer von 33,3 µs? Und was ist, wenn ein beschleunigtes Myon einfach so lange “lebt”, im Gegensatz zu einem unbeschleunigten, dass eben nur 2 µs “lebt”? D.h., damit ist überhaupt nichts bewiesen. Reine Akklamation ohne jeden Beweis. Das Myonenexperiment beweist höchstens, dass beschleunigte Myonen länger leben als unbeschleunigte Myonen. Aber wie oder warum lässt sich aus dem Experiment nicht ableiten.
“Ruhesystem des Myons:
Die Lebensdauer des Myons beträgt darin 2 µs. Die Strecke im Ruhesystem der Erde aber 10 Km. Also ist die der Abstand der Erdoberfläche im Ruhesystem des Myons nur 600 m. Daher haben wir eine “Längenkontraktion”.”
Das habe ich wohl schon ausreichen oft erklärt: wenn für einen “bewegten Beobachter” (oder ein Myon) irgend etwas verkürzt wäre, wäre auch sein Maßstab verkürzt (Anwendung der Lorentz-Kontraktion auf den bewegten Längenstandard). Mit dem verkürzten Maßstab wird aber die Distanz bis zur Erde mit exakt der selben Maßzahl ermittelt, wie “im Ruhesystem Erde” mit dem dort unverkürzten Maßstab.
Die “Beweisführung” beißt sich in den Schwanz. Der “Beweis” basiert auf unbegründeten Annahmen.
Rudi Knoth
21. Januar 2019 @ 18:53
Aber auf jeden Fall haben Sie hier mal ganz schön und eindeutig gezeigt, dass in der sRT Längenkontraktion und Zeitdilatation zwei untrennbare Seiten einer einzigen Medaille sein müssen. Denn selbst das wird ja immer wieder von “sRT-Verteidigern” bestritten. (Siehe hier zB “Chrys 21. Januar 2019 @ 19:05”.)
Ich begrüsse diesen Akt der Klärung durch eindeutige und definitive Aussagen in höchstem Maße. Vielen Dank Herr Knoth. Mehr davon 😉
@Nicht von Bedeutung 21. Januar 2019 @ 19:21
Myonen sind Elementarteilchen. Sie zerfallen zwar in Elektronen und Neutrinos, deren Ruhemassen aber kleiner als die des Myons sind.
Das stimmt.
Daraus folgt eine auf der Erde gemessen längere Lebensdauer.
In diesem Experiment im Labor wurden alle Möglichkeiten bis zur letzten ausgeschlossen.
Gibt es dann Gründe, warum die Myonen im Ruhesystem länger leben sollten?
@Albrecht Storz 22. Januar 2019 @ 07:10
Ich habe in meinem Post den Begriff “Längenkontraktion” absichtlich in Anführungszeichen gesetzt. Denn genaugenommen muß man sagen, daß im Ruhesystem des Myons die Erdoberfläche zum Zeitpunkt des Myons nur 600 Meter vom Entstehungsort des Myons entfernt ist. Was Chrys beschreibt, ist die Betrachtung aus dem Ruhesystem der Erde.
Im Prinzip ist dies dasselbe wie die Längenmessung mit einer Lichtschranke. Im Ruhesystem des Objektes wird eine Zeitdilatation der Lichtschranke gemessen und im Ruhesystem der Lichtschranke eine Längenkontraktion des Objektes.
Nicht von Bedeutung schrieb (22. Januar 2019 @ 00:17, 00:20):
> Dann verwende einfach \gt und \lt in \LaTeX-Formeln
Denkste ??
(Ich glaube mich zu erinnern, dass ich das vor ein paar Jahren schon mal in einem anderen SciLog ausprobiert habe, weil ich diese “\lt”- und “\gt”-Syntax auch aus “meiner \LaTeX-Umgebung bzw. -Sozialisation” gewohnt war. Die SciLogs-Kommentar-Dokumentation hat sich seitdem ja leider nicht verbessert …&)
Also probieren “wir” das doch (noch) mal hier aus:
“\( \beta^2 \lt 1 \)” wird dargestellt als: “\( \beta^2 \lt 1 \)”.
Die bekannte “Comprehensive \(\LaTeX\) Symbol List”, in der der Befehl “\lt” übrigens offenbar nicht auftaucht, enthält stattdessen den Befehl “\less” im Zusammenhang mit gewissen “Packages”.
Ob das wohl hier klappt ?:
“\( \beta^2 \less 1 \)” wird dargestellt als: “\( \beta^2 \less 1 \)”.
Nicht von Bedeutung schrieb (22. Januar 2019 @ 00:17, 00:20):
> Dann verwende einfach #92;gt und #92;lt in #92;LaTeX-Formeln
Denkste ??
(Ich glaube mich zu erinnern, dass ich das vor ein paar Jahren schon mal in einem anderen SciLog vergeblich ausprobiert habe, weil ich diese “#92;lt”- und “#92;gt”-Syntax auch aus “meiner #92;LaTeX-Umgebung bzw. -Sozialisation” gewohnt war. Die SciLogs-Kommentar-Dokumentation hat sich seitdem ja leider nicht verbessert …&)
Also probieren “wir” das doch (noch) mal hier aus:
“\( \beta^2 \lt 1 \)” wird dargestellt als: “\( \beta^2 \lt 1 \)”.
Die bekannte “Comprehensive \(\LaTeX\) Symbol List”, in der der Befehl “#92;lt” übrigens offenbar nicht auftaucht, enthält stattdessen den Befehl “#92;less” im Zusammenhang mit gewissen “Packages”.
Ob das wohl hier klappt ?:
“\( \beta^2 \less 1 \)” wird dargestellt als: “\( \beta^2 \less 1 \)”.
Nicht von Bedeutung schrieb (22. Januar 2019 @ 00:17, 00:20):
> Dann verwende einfach \gt und \lt in \LaTeX-Formeln
Denkste ??
(Ich glaube mich zu erinnern, dass ich das vor ein paar Jahren schon mal in einem anderen SciLog vergeblich ausprobiert habe, weil ich diese “\lt”- und “\gt”-Syntax auch aus “meiner \LaTeX-Umgebung bzw. -Sozialisation” gewohnt war. Die SciLogs-Kommentar-Dokumentation hat sich seitdem ja leider nicht verbessert …&)
Also probieren “wir” das doch (noch) mal hier aus:
“\( \beta^2 \lt 1 \)” wird dargestellt als: “\( \beta^2 \lt 1 \)”.
Die bekannte “Comprehensive \(\LaTeX\) Symbol List”, in der der Befehl “\lt” übrigens offenbar nicht auftaucht, enthält stattdessen den Befehl “\less” im Zusammenhang mit gewissen “Packages”.
Ob das wohl hier klappt ?:
“\( \beta^2 \less 1 \)” wird dargestellt als: “\( \beta^2 \less 1 \)”.
Frank Wappler // 21. Januar 2019 @ 23:21
» Zwar ist nicht zu bestreiten, dass das Wort “Längenkontraktion” für den beschriebenen Sachverhalt, mit dem genannten Verhältnis der Längen zweier Strecken, historisch verwendet wurde.«
Haben sich denn seitdem neue Erkenntnisse ergeben, die es nahelegen, dass der Begriff „Längenkontraktion“ die Sache nicht trifft (oder die Beobachtungen unzutreffend beschreibt)?
»Aber ist es etwa sinnvoll zu sagen, dass die längere dieser beiden Strecken deshalb kontrahiert sei ??«
Den meisten, die nicht Physik studiert haben, ist unmittelbar einsichtig, dass der Umstand, dass stets die gleiche Vakuumlichtgeschwindigkeit gemessen wird, egal, wie schnell man sich parallel zum Lichtstrahl bewegt, geradezu erzwingt, dass die Länge der Messstrecke nicht geschwindigkeitsunabhängig (konstant) sein kann.
Nun kann diese Einsicht dennoch auf einem grundlegenden Irrtum beruhen. Aber wenn das so ist, dann sollte dieser Irrtum doch leicht aufzuklären sein.
@Frank Wappler:
Also wenn ein MathJax-Demo nicht 100% kompatibel zum MathJax-Latex-Dialekt ist, was dann? Der Editor bei Zahlenkern, vllt.? Wenn ich MathJax verwende, erstelle ich bei Ersterem (wenn ich beim Antworten nicht gerade zu hibbelig bin) und poste dann hier per C+P. Das funktioniert prima und bisher ohne seltsame Überraschungen. Versuch:
\( Denkste \lt Wissen \)
@Rudi Knoth:
1. Elementarteilchen sind elementar und daraus folgt, dass Elementarteilchen nicht zerfallen.
2. Dann sind wir uns zumindest hier schon mal einig.
3. Bitte keine voreiligen Schnellschüsse, auch wenn das Ergebnis bereits fest steht. Voreilige Schnellschüsse sind nicht wissenschaftlich.
4. Netter Apparat. Hat man dort denn auch tatsächlich Myonen unter einem Mikroskop gesehen oder nur Myonen entsprechende Energieniveaus gemessen?
5. Wechselwirkungen breiten sich im und gegenüber dem Raum bzw. Vakuum mit c aus. Daraus folgt, dass für Teilchen, die sich ebenfalls im und gegenüber dem Raum/Vakuum mit v bewegen c±v für Wechselwirkungen. Wechselwirkungen, mit denen Einzelteilchen der (nicht elementaren) Myonen hier auseinander getrieben werden, wirken wechselseitig langsamer.
Fünftens bekommt nur deswegen kein Peer-Review, weil RT! Das ist nicht wissenschaftlich.
\( Wissen \gt Denkste \)
@All:
Wir können ja mal einen Silizium-Kristall von 10km Länge produzieren und ein Myon mit nahe LG dran vorbei fliegen lassen. An wievielen Silizium-Atomen wird das Myon wohl vorbei müssen, um die Erde zu erreichen?
Sagt einfach bescheid, wenn die bittere Wahrheit weh tut.
@Balanus:
Vielen, die nicht Physik studiert haben, ist aber auch klar, dass wenn die LG in oder gegenüber was auch immer konstant gemessen wurde, dies nicht für Objekte gelten kann, die sich parallel zum Licht bewegen. Es kann nicht gleichzeitig Lorentzsche Äther- und Newtonsche Korpuskel-Theorie gelten, das aber trifft genau auf die RT zu.
@ Nicht von Bedeutung // 22. Januar 2019 @ 13:05
»An wievielen Silizium-Atomen wird das Myon wohl vorbei müssen, um die Erde zu erreichen?«
Merkwürdige Frage. Wieso sollte sich die Zahl der Atome verringern, wenn vom Myon aus gesehen die Länge des Stabes erheblich weniger als 10 km beträgt?
@Balanus / 21. Januar 2019 @ 22:03
Die Überlegung, dass mit der von der Erd-Uhr gemessenen Zeit \(\Delta t\) sowie der von der Myon-Uhr gemessenen Zeit \(\Delta\tau\) und der dabei vom bewegten Myon scheinbar durchlaufenen Strecke \(\Delta x\) wegen der Beziehung
\[
\frac{\Delta x}{\Delta t} = v = \frac{\Delta x}{\gamma\Delta\tau} = \frac{\Delta x/\gamma}{\Delta\tau}
\]
die bewegte Erde dann im Myon-System wohl eine Strecke der kontrahierten Länge \(\Delta x/\gamma\) durchlaufen müsse, ist fúr die SRT falsch.
Im Erd-System verläuft die Verbindungslinie zwischen Erde und Myon parallel zur x-Richtung, im Myon-System hingegen ist das nicht mehr der Fall. Das Myon beurteilt den Abstand zur Erde entlang einer Verbindungslinie in x’-Richtung, die jedoch gegenüber der x-Achse des Erd-Systems durch Lorentz Transf. raumzeitlich `verdreht’ ist, und der vermeintlich kontrahierte Abstand \(\Delta x/\gamma\) ist nur das Ergebnis einer schiefen Projektion von der x’-Achse des Myon-Systems auf die x-Achse des Erd-Systems.
Die Betrachtung im Myon-System liefert nur, dass die bewegte Erde in genau der gleichen `proper time’-Zeitspanne zum Myon gelangt, die das mit betragsmässig gleicher Geschw. im Erd-System bewegte Myon für seinen Weg zur Erde benötigt. Das ist vollkommen symmetrisch. Was aber gar nicht sein könnte, wenn hierbei eine durch Kontraktion von Abständen bedingte Asymmetrie zwischen Myon-System und Erd-System bestünde.
@Balanus:
Vermutlich, weil sich die Gitterabstände nicht verringern. Schon mal versucht einen Diamanten zu komprimieren? Ich kenne Kristalle, die wehren sich übelst mit elektrischen Schlägen, wenn man es versucht.
Natürlich kann man die Gitterabstände anders beziffern, wenn man damit etwas beweisen will, aber bewiesen ist damit tatsächlich gar nichts.
Zählen wir also die Silizium-Atome und multiplizieren sie mit einem definierten Gitterabstand. Das ist meines Erachtens weitaus plausibler als einen Gitterabstand anhand einer langsamer gehenden Uhr zu definieren.
@NvB 13:25 “Es kann nicht gleichzeitig Lorentzsche Äther- und Newtonsche Korpuskel-Theorie gelten, das aber trifft genau auf die RT zu.” … ja dann, ist wohl für jedermann in letzter Konsequenz schlüssig, daß Korpuskular-Theo und Äther-Theo nicht stimmen. Nur die Spezielle Relativitätstheorie ist in sich widerspruchsfrei und auch empirisch belegt, kein Experiment konnte bisher Temposünder finden.
Das mathematische Pendant ist wegen c=inv=max=const der Hosenknopf, nicht die Kneifzange.
Chrys
22. Januar 2019 @ 14:51
Ich muss hier nochmal widersprechen: Die SRT postuliert eine Symmetrie der Naturgesetze. Das bedeutet nicht, dass nur symmetrische Situationen beschrieben werden können. Die Asymmetrie kommt hier daher, dass das Erde-Atmosphäre-System zueinander in Ruhe ist, während das Myon relativ zur Atmosphärenschicht, in der es entsteht, und Erdboden bewegt ist. Ganz analog zum Zwillingsparadoxon, in dem Erde und Zielplanet zueinander ruhen, während der Reisende bewegt ist.
Nach SRT sind die Betrachtungen in den Koordinatensystemen S und S’ äquivalent. In S ist der statische Abstand Atmosphärenschicht-Erdboden länger und die Zeit für das bewegte Myon geht langsamer. In S’ ist der bewegte Abstand verkürzt und die Lebenszeit des Myons ist seine Eigenzeit. Es gibt keine weitere Zeit unabhängig von t oder t’, die eine echte Gleichzeitigkeit definiert.
@NvB 12:19 “. Elementarteilchen sind elementar und daraus folgt, dass Elementarteilchen nicht zerfallen.”
Elementar heißt aber nicht “stabil”, anders zusammengesetzte quasistabile Neutronen, die frei sind.
#12:01 “… bisher ohne seltsame Überraschungen. Versuch: Denkste < Wissen" 🙂 stimmt 🙂
@Senf:
Zu Hosenknopf und Kneifzange:
Nur die Spezielle Relativitätstheorie ist in sich widerspruchsfrei und auch empirisch belegt, kein Experiment konnte bisher Temposünder finden.
@Senf:
Das ist doch Senf! Elementares ist gerade so stabil, dass es als Elementar durchgeht, oder wie? Was bedeutet Elementar, wenn es nicht “nicht teilbar” sein soll? Elementar: Besonders stabil, nämlich das stabilste überhaupt.
It’s not my intention telling whats right or telling whats wrong. It’s my intention guessing whats right and dumping the wrong. 😉
@Joachim Schulz:
Ein netter Versuch, der sich zunehmend als unbrauchbar erweist, was man daran erkennt, dass man es immer mit Asymmetrien zu tun hat.
@Joachim / 22. Januar 2019 @ 15:57
Die auf der x’-Achse des Myon-Systems dargestellte “Laufstrecke” der im Myon-System bewegten Erde hat exakt die gleiche Länge wie die auf der x-Achse des Erd-Systems dargestellte “Laufstrecke” des im Erd-System bewegten Myons. Das ergibt sich so aus der Transformation zwischen den beiden Inertialsystemen.
Eine Asymmetrie kommt da nur herein, wenn man im Myon-System beim Abstand noch immer entlang der x-Achse herumhampelt, so als wäre die gegenüber der x’-Achse irgendwie gesondert ausgezeichnet. Für Lorentz wäre das in der Tat gerechtfertigt, sofern er das Erd-System als das Aether-System auffasst. Damit schafft er eine Asymmetrie zwischen den beiden Inertialsystemen, die in der SRT jedoch unvereinbar mit dem spez. Rel.prinzip ist; hier existiert keine Rechtfertigung, die x-Achse eines Inertialsystems gegenüber der x’-Achse eines anderen irgendwie zu bevorzugen.
@NvB
.
.
Dass Du nachfragst ist prinzipiell erstmal gut, …
.
.
Dass Du selber Dir dann antwortest hingegen nicht, …
.
Nein das heißt es eben nicht. Es heißt mehr “nicht aus weiteren Teilchen zusammengesetzt”. Schau doch mal unter:
.
httpsx://de.wikipedia.org/wiki/Myon
httpsx://de.wikipedia.org/wiki/Elementarteilchen
.
Selbstverständlich ist das Myon ein Elementarteilchen und somit elementar und hat dennoch nur eine recht kurze Halbwertszeit. Nun willst Du auch noch in der Quantenphysik die Dinge beliebig umdefinieren und ändern, damit ist zu Deinem Unfug passt.
@Krüger:
Joachim hat hier verkündet, dass von mir nur heisse Luft kam, als ich von meinen Beobachtungen bei H&K, GPS und Maryland berichtete. Aber ich denke mal, inzwischen sehen Einige, die hier noch lesen, von wem die heisse Luft eigentlich kommt.
Hartmut, Du hast Dich in dem Zitat klar auf einen Beitrag und eine Aussage von Joachim bezogen, sei doch zumindest mal so mutig und stehe dazu, ging eben gar nicht um den Mist von Dir über Herrn Senf und mich.
.
Was willst Du denn hier?
.
Ums Thema geht es Dir nicht, denn das ist ja nicht, Kritik an der SRT, den Einheiten und die Ideen des Herrn Pohl.
.
Hast doch selber zugegeben, im MAHAG, den Foren für Kritik will auch keiner Deinen Mist und jeder kocht seine eigene Suppe. Hier bist Du noch mehr fehl am Platz.
.
Man stelle sich noch vier User wie Dich hier vor, jede mit einer eigenen Suppe und Hetze gegen die Physik.
@Krüger:
Und als Nachschlag: Joachim hat hier aber auch zu keiner Zeit beachtet, dass Atomuhren aus stabilen Gehäusen und noch weitaus stabileren Resonanzkörpern bestehen, durch welche Gitterabstände in diesen Experimenten überhaupt relevant werden.
Hartmut, dass ist nur wieder eine neue Nebelkerze, Du kommst immer mit was neuem an, wenn es eng für Dich wird. Wie Atomuhren funktionieren ist klar, aber nein, passt Dir nicht, musst alles wieder anders sein, die Einheiten ja auch nicht, Du zauberst immer wieder was aus dem Hut und auch im Kreise.
.
So wie mit dem “elementar”, Du hast einfach keine Ahnung, keinen Schimmer, machst aber den ober Klugscheißer. Du bist eine Lachnummer ohne Wissen und bist auch noch begriffsstutzig ohne Ende.
.
So und nun kotz Dich verbal aus, ich werde es wohl nicht mehr lesen, denn bis morgen hat Joachim sicher geputzt.
Balanus schrieb (22. Januar 2019 @ 12:00):
> Haben sich denn seitdem
… etwa seit H. A. Lorentz von
geschrieben hat …
> neue Erkenntnisse ergeben, die es nahelegen, dass der Begriff „Längenkontraktion“ die Sache nicht trifft (oder die Beobachtungen unzutreffend beschreibt)?
Ja, natürlich: die Aufstellung einer Theorie, nämlich der Relativitätstheorie, beginnend mit Einstein 1905, wie geometrisch-kinematische Beziehungen, wie z.B. “Länge eines Stabes” und deren eventuelle Änderung, bzw. “Längen“-Verhältnis, überhaupt nachvollziehbar (aufbauend allein auf dem “Koinzdenz“-Begriff) als Messgrößen definiert werden könnten.
> […] der Umstand, dass stets die gleiche Vakuumlichtgeschwindigkeit gemessen wird,
… beruht bekanntlich auf den Definitionen, im Rahmen der RT,
– der zugrundeliegenden Messgrößen (“gegenseitige Ruhe” zweier Beteiligter/Enden, “Distanz” zweier gegenüber einander ruhender Beteiligter/Enden, darauf aufbauend: “Geschwindigkeit” eines Austausches zwischen zwei gegenüber einander ruhended Beteiligten/Enden),
– der (zugrundeliegenden) Bedeutung des Signal-Austausches zwischen Beteiligten und der besonderen Beachtung von Signalfronten in den RT-Definitionen dieser Messgrößen, sowie
– der Auffassung von “Vakuumlichtgeschwindigkeit” als Signalfront-Geschwindigkeit.
> egal, wie schnell man sich parallel zum Lichtstrahl bewegt […]
In dieser Formulierung äußert sich eine Nachlässigkeit in der Zuschreibung von Messwerten von Messgrößen (hier offenbar: von Geschwindigkeit, und offenbar ohne zugrundegelegte Feststellung gegenseitiger Ruhe bestimmter Beteiligter/Enden, und ohne Zuschreibung einer konkreten Distanz zu einem solchen Paar), die auszutreiben einen Schwerpunkt des Studiums der (Experimental-)Physik bildet.
> Den meisten, die nicht Physik studiert haben, ist unmittelbar einsichtig, dass […] Nun kann diese Einsicht dennoch auf einem grundlegenden Irrtum beruhen. Aber wenn das so ist, dann sollte dieser Irrtum doch leicht aufzuklären sein.
Der betreffende Irrtum besteht konkret in einer Täuschung, und insbesondere Selbst-Täuschung. In Einsteins eindringlicher Formulierung:
.
@Frank Wappler // 22. Januar 2019 @ 23:25
Meine Frage…:
Haben sich denn seitdem neue Erkenntnisse ergeben, die es nahelegen, dass der Begriff „Längenkontraktion“ die Sache nicht trifft (oder die Beobachtungen unzutreffend beschreibt)?
…bezog sich selbstredend auf die relativistische Deutung oder Erklärung des Null-Ergebnisses des Michelson-Versuchs. Warum sonst hätte Joachim Schulz diesen Beitrag schreiben sollen?
Rudi Knoth schrieb (22. Januar 2019 @ 07:43):
> Denn genaugenommen muß man sagen, daß im Ruhesystem des Myons die Erdoberfläche zum Zeitpunkt des Myons nur 600 Meter vom Entstehungsort des Myons entfernt ist.
“zum Zeitpunkt des Myons” ?? …
Genaugenommen ist die Distanz zwischen dem o.g. Myon (“\(Q\)”) und einem ganz besonders ausgewählten weiteren (“vorauseilenden”) Mitglied des Myon-Ruhesystems (z.B. einem geeigneten Neutrino, “\(P\)”), nämlich dessen Anzeige bei Treffen/Passage des o.g. Erd-(Boden-)gebundenen Detektors (“\(B\)”) gleichzeitig zur Geburts-Anzeige des Myons war,
(nur) \( PQ \equiv \beta_{PQ}[ \, B \, ] \, c \, \tau Q[ \, \_ \text{Geburt}, \, \_ B \, ] \approx 600 \, {\rm m} \).
Und die Distanz zwischen dem Erd-(Boden-)gebundenen Detektor und einem ganz besonders ausgewählten weiteren (“vorauseilenden”) Mitglied des Detektor-Ruhesystems (z.B. einem geeigneten Stickstoff-Atomkerns, “\(A\)”), das nämlich am Geburts-Ereignis des betreffenden Myons, \(\varepsilon_{AQ}\), teilgenommen hatte, und dessen Anzeige \(A_Q\) in diesem Ereignis (deshalb) ganz wesentlich eher war als die Anzeige \(B_P\) des Erd-(Boden-)gebundenen Detektors bei Treffen/Passage des oben ausgewählten Neutrinos \(P\), ist (dagegen) \( AB \equiv \beta_{AB}[ \, Q \, ] \, c \, \tau A[ \, \_Q, \, \_ \text{gleichzeitig zu } B \_ Q \, ] \approx 10 \, {\rm km} \).
Die Geburts-Anzeige des Myons \(Q\) ist demnach auch die Anzeige des Myons bei Teilnahme am Ereignis \(\varepsilon_{AQ}\), also bei Treffen/Passage des Stickstoff-Atomkerns \(A\):
\[ Q_{\text{Geburt}} \equiv Q_A. \]
Dabei ist (natürlich)
\[ \beta_{PQ}[ \, B \, ] = \beta_{PQ}[ \, A \, ] = \beta_{AB}[ \, Q \, ] = \beta_{AB}[ \, P \, ] \equiv \beta, \approx 0,998 \]
und (dann offensichtlich)
\[ \left( \frac{PQ}{AB} \right) \equiv \left( \frac{\tau Q[ \, \_ \text{Geburt}, \, \_B \, ]}{\tau A[ \, \_Q, \, \_ \text{gleichzeitig zu } B\_Q \, ]} \right) \equiv \left( \frac{\tau Q[ \, \_ A, \, \_ B \, ]}{\tau A[ \, \_Q, \, \_ \text{gleichzeitig zu } B \_ Q \, ]} \right) \approx 0,06 \].
Mir scheint, das dürfte sowohl Albrecht Storz (23. Januar 2019 @ 10:59) als auch Chrys (22. Januar 2019 @ 18:36) … auffallen.
@Frank Wappler
Erst mal danke für Deine Ausführliche Ausführung 🙂 Ich habe das jetzt nur überflogen da mir unter dem ganzen Müll der hier reingekesselt wurde die Antwort leider durchgerutscht ist.
Ich schaue mir das nach der Arbeit mal in aller Ruhe an. Ich glaube aber ich weiß worauf Du raus willst. Scheint plausibel zu sein 🙂
@Frank Wappler / 23. Januar 2019 @ 12:25
Nehmen wir an, der Myon-Zerfall Z ereigne sich genau im Moment seines Zusammentreffens mit der Erde. Dann ist das Myon entstanden an dem Punkt P, der auf seiner Weltlinie 600 Meter vor Z liegt.* Und als es sich so begab, war die Erde an einem Punkt Q, der auf ihrer Weltlinie ebenfalls 600 Meter vor Z liegt.
Dann ist der Abstand des Myons bei seiner Entstehung von der Erde die Länge der raumartigen Strecke PQ. Dieser Abstand lässt sich in jedem beliebigen Inertialsystem bestimmen, und er kommt dabei auch immer mit dem gleichen Wert heraus. Und zwar mit welchem Wert?
*Wem nicht klar ist, was es mit den besagten 600 Metern auf sich hat, frage Herrn Senf.
@Chrys
24. Januar 2019 @ 00:13
Ich habe jetzt versucht, Ihnen kritisch zu antworten und dabei ist bei mir der Groschen gefallen. Tatsächlich haben Sie recht. Es gibt hier zwei eindeutige Ereignisse:
P: Das Myon entsteht.
Z: Das Myon zerfällt.
Der Raumzeitliche Abstand dieser beiden Ereignisse ist invariant. In diesem Fall geb ich Ihnen recht: Der längere Abstand, den der Erdhocker ermittelt, ist tatsächlich “nur” eine Projektion auf eine andere Gleichzeitigkeit.
Beim Garagenparadoxon bleibe ich bei meinem Standpunkt, denn da haben wir es nicht mit einzelnen Ereignissen, sondern mit Scharen von Weltlinien zu tun.
@Joachim Schulz // 24. Januar 2019 @ 08:15
» P: Das Myon entsteht.
Z: Das Myon zerfällt.
Der Raumzeitliche Abstand dieser beiden Ereignisse ist invariant. «
Dann bliebe für mich nur noch zu klären, inwiefern die „Kontraktion“ des Raumes in Bewegungsrichtung eine Asymmetrie zwischen Myon-System und Erd-System bedingen würde, wie @Chrys gemeint hat (22. Januar 2019 @ 14:51). Denn ich kann da keine Asymmetrie erkennen.
Irritierend fand ich auch @Frank Wapplers Bemerkung weiter oben (18. Januar 2019 @ 23:44). Er schreibt, dass es »(bei “der Längenkontraktion”) um den Verhältniswert der Längen zweier verschiedener “Strecken” (bzw. “Stäbe”)« ginge. Wohl wegen der Gedankenexperimente Zug/Bahnhof oder Leiter/Scheune.
Ich hätte aber gedacht, es ginge bei der „Längenkontraktion“ zuvörderst um den raumzeitlichen Abstand zwischen zwei Ereignissen: Je schneller sich ein Objekt von dem einen zum anderen Ereignis hin bewegt, desto kürzer ist (für das Objekt) die räumliche Distanz zwischen den beiden Ereignissen.
Wenn man denn Raum und Zeit gesondert betrachten will. Das muss man ja nicht, man kann ja auch bei der raumzeitlichen Weltlinie bleiben.
@Balanus
24. Januar 2019 @ 11:21
Wir können die Längenkontraktion in dieses Beispiel hineinbringen, wenn wir nicht (nur) den Abstand zwischen Ereignissen, sondern den zwischen Objekten betrachten.
Wir haben das Ereignis P, zu dem das Myon entsteht. Und wir haben den Detektor, in dem es zerfallen wird.
Im Ruhesystem des Myons gibt es nun ein Ereignis Q an dem nichts passiert, als dass sich dort der Detektor in dem Moment befindet, in dem das Myon entsteht. P ist im Ruhesystem des Myons gleichzeitig mit Q.
Weiter gibt es im Ruhesystem Erde ein Ereignis R an dem nicht weiter passiert, als dass sich dort der Detektor in dem Moment befindet, in dem das Myon entsteht. P ist im Ruhesystem der Erde gleichzeitig mit R.
Q und R sind nicht dasselbe Ereignis.
Die Entfernung PQ ist der Weg, den der Detektor im Ruhesystem des Myons während dessen Lebenszeit zurücklegt. Er hat dieselbe raumartige Länge, wie die zeitartige Länge PZ.
Die Entfernung PR ist der Weg, den das Myon im Erdsystem zurücklegt. Sie ist größer als PQ und das ist die Längenkontraktion. Sie ist eng mit der Relativität der Gleichzeitigkeit verbunden, denn diese besagt, dass Q und R nicht identische Raumzeit-Punkte sind.
Chrys schrieb (24. Januar 2019 @ 00:13):
> Nehmen wir an, der Myon-Zerfall Z ereigne sich genau im Moment seines
… “seines” — d.h. des in Betracht stehenden Myons (unter Fachleuten auch: \({\rm \mu}^{-}\)), das oben (23. Januar 2019 @ 12:25) auch kurz und symbolisch \(Q\) genannt wurde …
> Zusammentreffens mit der Erde.
Oben (21. Januar 2019 @ 14:23) wurde (wohl zur besseren Auflösung) ein “erdgebundener Myonendetektor” identifiziert, den ich (das Beste ist der Feind des Guten! ;) im Folgenden als “Erd-Boden-gebundenen Detektor \(B\)” bezeichnete.
Das obige Symbol “Z” soll also offenbar ein (Koinzidenz-)Ereignis bezeichnen, das ich (offensichtlich) \(\varepsilon_{BQ}\) nennen würde (auch wenn ich das in meinem obigen Kommentar 23. Januar 2019 @ 12:25 noch nicht ausdrücklich so getan hatte).
Zur vorgeschlagenen Annahme an sich:
dass der Anteil des Myons an genau diesem Ereignis nicht nur seine Anzeige des Treffens/Passierens des Erd-Boden-gebundenen Detektor \(B\) sein soll, sondern auch seine Zerfalls-Anzeige, hat den Vorteil, dass dadurch ganz selbstverständlich von der “Lebensdauer” dieses Myons die Rede sein kann; na gut (manche mögen sich z.B. an “OPERA” erinnern).
Der damit verbundene Nachteil besteht darin, dass für andere Fälle doch erst noch geeignete Terminologie vereinbart bzw. verstanden werden müsste.
> Dann ist das Myon entstanden an dem Punkt P
Mit “Punkt P” gemeint ist vermutlich wiederum ein bestimmtes Ereignis, das ich im obigen Kommentar schon ausdrücklich \(\varepsilon_{AQ}\) genannt hatte.
(Und nicht z.B. etwa nur der Anteil des Myons an diesem Ereignis, also dessen Anzeige \(Q_A\).)
Von (Koinzidenz-)Ereignissen als “Punkten” zu reden, ist allerdings Physikern (gegenüber) wenig sympathisch, weil denen eher die Auffassung von “Punkt” als
– “(bestimmter) materieller Punkt” bzw.
– “principal identifiable point”
geläufig sein mag;
also von bestimmten (unterscheidbaren, identifizierbaren) Beteiligten an Koinzidenz-Ereignissen.
> der auf seiner Weltlinie 600 Meter vor Z liegt.
Soweit ich verstehe, sind diese beiden Ereignisse aber zeitartig voneinander getrennt;
und der Wert ihrer “Lorentzschen Distanz” voneinander (d.h. der Wert des zeitartigen Abstands dieser beiden Ereignisse voneinander)
soll \(2 \times 10^{-6} \, {\rm s}\) betragen;
meinetwegen sogar genauer \(2,00 \times 10^{-6} \, {\rm s}\).
D.h. ausführlich (lieber schon hier oben, damit die Überraschung weiter unten nicht in einen Schock ausartet):
\[ \ell[ \, \varepsilon_{AQ}, \varepsilon_{BQ} \, ] = 2,00 \times 10^{-6} \, {\rm s}. \]
> * […]
Natürlich bezeichnet man \(2,00 \times 10^{-6} \, c \, {\rm s}\) auch als \(6,00 \times 10^{2} \, {\rm m}\).
Ein solcher Wert gehört aber zum Wertebereich von raumartigen Abständen zwischen entsprechend raumartig voneinander getrennten Ereignissen. (Wobei die allgemeine raumartige Entsprechung zur “Lorentzschen Distanz” im Sinne von Beem/Ehrlich/Easley noch zu vereinbaren wäre; ich schreibe diesbezüglich insgesamt von “chronometrischer Distanz \(\chi\)” jeweils zweier Ereignisse voneinander.)
> Und als es sich so begab, war die Erde an einem Punkt Q, der auf ihrer Weltlinie ebenfalls 600 Meter vor Z liegt.
Sofern hier also von einem bestimmten dritten Ereignis die Rede sein soll, an dem die Erde (und insbesondere der Erd-Boden-gebundenen Detektor \(B\)) teilgenommen haben soll, so gibt es zweifellos eines, das von “Ereignis Z ((\varepsilon_{BQ}\))” zeitartig getrennt ist und davon einen Abstand (\(\ell\)-Wert) von ebenfalls \(2,00 \times 10^{-6} \, {\rm s}\) hat.
Ist ein solches Ereignis hier irgendwie relevant, wo es doch um “Längenkontraktion” und um “(Einstein-)Projektion(en)” gehen soll ??
In meinem obigen Kommentar (23. Januar 2019 @ 12:25) hatte ich gerade deshalb (auch) ein ganz bestimmtes drittes Ereignis in Betracht gezogen, nämlich das Koinzidenz-Ereignis \(\varepsilon_{BP}\) des Treffens/Passierens des Erd-Boden-gebundenen Detektors \(B\) und eines geeigneten Beteiligten (“Neutrinos”) \(P\), der durchwegs gegenüber dem Myon \(Q\) ruhte, und dessen Anzeige der Passage, \(P_B\), gleichzeitig zur “Geburts”- bzw. “Entstehungs“-Anzeige des Myons \(Q_A\) war.
Diese beiden, durch die geforderte Gleichzeitigkeit des genannten Anzeigen/Anteile in Beziehung gesetzten Ereignisse \(\varepsilon_{BP}\) und \(\varepsilon_{AQ}\) sind (selbstverständlich) raumartig voneinander getrennt; und ihr Abstand beträgt (selbstverständlich) \[ \chi[ \, \varepsilon_{AQ}, \varepsilon_{BP} \, ] = 6,00 \times 10^{2} \, {\rm m} \equiv PQ. \]
Mir war allerdings bisher nicht in den Sinn gekommen (und ich hatte es demnach auch von niemand anderem vermutet), die Beziehung zwischen den beiden Ereignissen \(\varepsilon_{BP}\) und \(\varepsilon_{BQ}\) (Z) zu untersuchen.
Diese beiden Ereignisse sind offensichtlich zeitartig voneinander getrennt, denn \(B\) nahm ausdrücklich an beiden teil.
Was ist nun der Wert ihrer Lorentzschen Distanz \(\ell\) voneinander? (Wie bestimmt man den überhaupt? …) Ach ja (14. Juni 2018 @ 00:43, 07:54):
\[ \ell[ \, \varepsilon_{BP}, \varepsilon_{BQ} \, ] \equiv \tau B[ \, \_ P, \, \_ Q \, ] = \tau Q[ \, \_ A, \, \_ B \, ] \times \sqrt{ 1 – (\beta_{PQ}[ \, B \, ])^2 } = \]
\[ = \frac{PQ}{c \, \beta_{PQ}[ \, B \, ]} \times \sqrt{ 1 – (\beta_{PQ}[ \, B \, ])^2 } = \frac{PQ}{c \, \beta_{PQ}[ \, B \, ]} \times 0,06 \gtrsim 2,00 \times 10^{-6} \, {\rm s} \times 0,06 = \] \[ = 1.20 \times \times 10^{-6} \, {\rm s}. \]
Das o.g. Ereignis “Punkt Q” ist demnach nicht das von mir betrachtete Ereignis \(\varepsilon_{BP}\)
(und es erscheint mir deshalb hier nicht weiter relevant).
> Dann ist der Abstand des Myons bei seiner Entstehung von der Erde die Länge der raumartigen Strecke […]
Hinsichtlich der Beziehung zwischen (“kosmisch-atmosphärischem”) Myon und Erde (bzw. Erd-Boden-gebundenen Detektor) von “Abstand” zu sprechen ist absurd. Diese beiden stehen/ruhen nicht gegenüber einander, sondern sie bewegen sich gegenüber einander; ihre (einzeln bestimmbaren) Ping-Entfernungen gegenüber einander sind veränderlich.
Ein bestimmter Abstand voneinander ist dagegen dem Myon \(Q\) und dem Beteiligten (einem “vorauseilenden Neutrino”) \(P\) zuzuschreiben, die durchwegs gegenüber einander ruhen sollen; nämlich die Distanz (bzw. Länge der raumartigen Strecke)
\[ PQ \equiv \chi[ \, \varepsilon_{AQ}, \varepsilon_{BP} \, ] = 6,00 \times 10^{2} \, {\rm m}. \]
> Dieser Abstand lässt sich in jedem beliebigen Inertialsystem bestimmen, und er kommt dabei auch immer mit dem gleichen Wert heraus.
Die beiden konkreten Enden, denen dieser Abstandswert (bzw. Wert ihrer Distanz voneinander) zugeschrieben wird sind aber ganz ausdrücklich und ausschließlich das Myon \(Q\) und “das andere Ende” \(P\);
und diese beiden durchwegs gegenüber einander ruhenden, identifizierbaren materiellen Punkte bzw. Beteiligten gehören ausschließlich und gemeinsam zu ihrem eigenen Inertialsystem.
p.s.
Hinsichtlich “Längenkontraktion” etc. ist natürlich auch die Distanz \(AB\) von Interesse …
p.p.s.
Hinsichtlich des Kommentars von Joachim Schulz, 24. Januar 2019 @ 08:15:
Meine spontane Assoziation zu “Joachim Schulz ohne Koordinaten” betraf jemand (noch einigermaßen Bekannten) “ohne Mütze”.
Inzwischen scheint Herr Zensor Schulz subtiler vorgehen zu wollen. Halten Sie so etwas ernstlich für legitim. Oder einfach nur: “Der Zweck heiligt die Mittel!”
Diesen Beitrag von mir finde ich nicht mehr auf SciLogs:
>>>>
Rudi Knoth
21. Januar 2019 @ 18:53
“Ruhesystem Erde:
Die Strecke, die das Myon zurücklegt, ist 10 Km lang. Bei einer gemessenen Geschwindigkeit von 300000 Km/s ergibt sich dann eine
“Belegdauer” der Strecke von 33,3 μs. Die Lebensdauer des Myons im Inertialsystem, in dem es ruht, beträgt aber 2 μs. Damit haben wir
eine Zeitdilatation.”
Das heißt, der “ruhende Beobachter” (im Ruhesystem Erde) beobachtet eine Myonenlebensdauer von 33,3 μs? Und was ist, wenn ein beschleunigtes Myon einfach so lange “lebt”, im Gegensatz zu einem unbeschleunigten, dass eben nur 2 μs “lebt”? D.h., damit ist überhaupt nichts bewiesen. Reine Akklamation ohne jeden Beweis. Das Myonenexperiment beweist höchstens, dass beschleunigte Myonen länger leben als unbeschleunigte Myonen. Aber wie oder warum lässt sich aus dem Experiment nicht ableiten.
“Ruhesystem des Myons:
Die Lebensdauer des Myons beträgt darin 2 μs. Die Strecke im Ruhesystem der Erde aber 10 Km. Also ist die der Abstand der
Erdoberfläche im Ruhesystem des Myons nur 600 m. Daher haben wir eine “Längenkontraktion”.”
Das habe ich wohl schon ausreichen oft erklärt: wenn für einen “bewegten Beobachter” (oder ein Myon) irgend etwas verkürzt wäre, wäre auch sein Maßstab verkürzt (Anwendung der Lorentz-Kontraktion auf den bewegten Längenstandard). Mit dem verkürzten Maßstab wird aber die Distanz bis zur Erde mit exakt der selben Maßzahl ermittelt, wie “im Ruhesystem Erde” mit dem dort unverkürzten Maßstab.
Die “Beweisführung” beißt sich in den Schwanz. Der “Beweis” basiert auf unbegründeten Annahmen.
Frank Wappler schrieb (24. Januar 2019 @ 12:57):
> […] die Beziehung zwischen den beiden Ereignissen \(\varepsilon_{BP}\) und \(\varepsilon_{BQ}\) (Z) zu untersuchen.
> Diese beiden Ereignisse sind offensichtlich zeitartig voneinander getrennt, denn \(B\) nahm ausdrücklich an beiden teil.
Was ist nun der Wert ihrer Lorentzschen Distanz \(\ell\) voneinander? (Wie bestimmt man den überhaupt? …) Ach ja (14. Juni 2018 @ 00:43, 07:54):
\[ \ell[ \, \varepsilon_{BP}, \varepsilon_{BQ} \, ] \equiv \tau B[ \, \_ P, \, \_ Q \, ] = \tau Q[ \, \_ A, \, \_ B \, ] \times \sqrt{ 1 – (\beta_{PQ}[ \, B \, ])^2 } = \]
… an dieser Stelle ist nicht nur ein Formatierungsproblem aus dem obigen Kommentar zu umgehen, sondern auch ein Rechenfehler (in der letzten Zeile) zu korrigieren:
\[ = \frac{PQ}{c \, \beta_{PQ}[ \, B \, ]} \times \sqrt{ 1 – (\beta_{PQ}[ \, B \, ])^2 } = \frac{PQ}{c \, \beta_{PQ}[ \, B \, ]} \times 0,06 \approx 2,00 \times 10^{-6} \, {\rm s} \times 0,06 = \] \[ = 1,20 \times \times 10^{-7} \, {\rm s}. \]
Herr Schulz,
ich muss mein Urteil revidieren und bitte insofern um Entschuldigung. Der Kommentar von mir ist vielleicht doch noch da.
Aber zum einen bin ich durch leidvolle Erfahrungen hier geprägt, zum andere verhält sich Ihre Seite hier etwas merkwürdig gegenüber dem Browser, insbesondere mit der Refresh-Funktion scheint es nicht richtig mit Yandex zusammen zu spielen. Auch das ewige Formel-Parsingtools-Nachladen ist nicht gerade förderlich.
Balanus
24. Januar 2019 @ 11:21
“Irritierend fand ich auch @Frank Wapplers Bemerkung weiter oben (18. Januar 2019 @ 23:44). Er schreibt, dass es »(bei “der Längenkontraktion”) um den Verhältniswert der Längen zweier verschiedener “Strecken” (bzw. “Stäbe”)« ginge. ”
Herr Wappler betreibt “koordinatenfreie” sRT-Verteidigung. Dazu muss er Einheiten eliminieren. Deswegen betrachtet er Proportionen zwischen Strecken (wie wenn eine Maßangabe nicht die Proportion bezüglich eines Standards, im Falle von Längenmessungen also die Proportion zu einer Länge, der Einheitslänge, wäre, also auch wieder nur ein (Selbst-)Täuschungsmanöver). Letztlich läuft das auf die möglichst vollständige Beobachter-Eliminierung (bis auf einen) hinaus. Im Wappler-Kosmos ist nur noch Herr Wappler – alleine. Na, vielleicht ist Herr Knoth noch manchmal bei ihm. In einer passend herausgesuchten Knoth-Wirklichkeit 😉
“Ich hätte aber gedacht, es ginge bei der „Längenkontraktion“ zuvörderst um den raumzeitlichen Abstand zwischen zwei Ereignissen: Je schneller sich ein Objekt von dem einen zum anderen Ereignis hin bewegt, desto kürzer ist (für das Objekt) die räumliche Distanz zwischen den beiden Ereignissen.”
Keine Ahnung, wie sich ein Objekt von einem Ereignis zu einem anderen Ereignis bewegen soll. Normalerweise bewegen sich Objekte von Ort zu Ort. Ereignisse warten selten, bis sich etwas zu ihnen hin bewegt hat …
Wenn man das Eintreffen an einem Ort als Ereignis sehen will, kann man das freilich. Aber dennoch ist die Formulierung äußerst seltsam.
@Joachm
Nochmals erläuternd zum bewegten Stab. Da habe ich zunächst nur den Stab von Einheitslänge mit synchronisierten Uhren ausgestattet, was nur in seinem Ruhesystem S’ vorgenommen werden kann, und wie es Einstein verschiedentlich auch schon gemacht hat, wobei ich mir insbesondere bei jedem Punkt \(\xi\) des Stabes eine solche Uhr denke, nicht nur bei den Endpunkten. Weiters wird noch durch einen Lorentz Boost die Darstellung des uhrentragenden Stabes in S erhalten. Die S-Koordinaten \((t_\xi(s), x_\xi(s))\) geben dann zeiträumlich an, wo in der S-Darstellung sich die Uhr bei \(\xi\) just in dem Moment befindet, wenn sie die S’-Systemzeit \(s\) anzeigt.
Da die Stab-Uhren wegen des Boosts nicht S-synchron gehen, ist der Stab in der S-Darstellung nicht parallel zur x-Achse von S ausgerichtet. Soll nun eine S-gleichzeitige “Länge des Stabes in S” parallel zur x-Richtung bestimmt werden, kommt man um ein Projektion des Stabes auf die x-Achse nicht herum. Die Strecke \(OC\) bei der Animation ist eine solche Projektion, und man sieht dabei auch, wie das erst im eigenzeitlichen Verlauf von \(s\) — oder eben von \(\tau = \gamma s\) — von rechts nach links sukzessive konstituiert wird.
Mit Ausnahme von \(\xi = 0\) präsentiert die Strecke \(OC\) die durch \(\xi \in [0,1]\) unterschiedenen Punkte des Stabes in S eben nicht durch die Positionen \(x_\xi(0)\), die sie gemäss der Lorentz Transf. zu der von S-synchronen Uhren angezeigten S-Systemzeit \(\tau = 0\) haben, sondern durch die Positionen \(x_\xi(-\xi\beta)\), die sie jeweils zur angezeigten S-Systemzeit \(\tau = \tau(\xi) = -\xi\gamma\beta\) hatten.
Das hat dann aber die Konsequenz, dass in S zwischen dem Moment, wo sich das rechte Stabende \(\xi = 1\) bei der Position von \(C\) befindet, noch die Zeitspanne \(\gamma\beta \gt 0\) verrinnt, bis dass das linke Stabende \(\xi = 0\) die Position von \(O\) erreicht. Das rechte Stabende ist dann natürlich mit dem Zeitfluss schon weiter nach rechts gewandert.
@Albrecht Storz 24. Januar 2019 @ 13:53
Da haben Sie Herrn Wappler aber falsch verstanden. Für ihn gibt es eine Menge von “Beteiligten” in einem Szenario. Man kann diese auch als Beobachter bezeichnen aber in dem Sinne, daß sie Beobachtungen an ihrem Ort machen un keine Messungen zu entfernten Objekten durchführen.
@Joachim Schulz:
Raumartige Abstände (Wellenlängen) sind nun mal zu zeitartigen Abständen (Periodendauern) proportional.
Und auf beiden wird auch noch die selbe Anzahl an Kristallelementen (Myonenstab) gezählt, wie hier schon festgestellt wurde. Der Abstand der Kristallelemente hängt nun natürlich auch von der Myon-Eigenzeit ab, nicht wahr?
Eigentlich wüsste man ja nun genau, was eine Myonenuhr (sofern es denn mal eine geben mag) für einen Blödsinn anzeigt, wenn man die Abstände der Kristallelemente zuvor definiert hätte.
Raum- und zeitartige Abstände sind nun mal nicht in festen Gitterabständen zu bemessen und man könnte ja auch keine nicht vorhandene Symmetrie mehr forcieren, wenn man es täte.
@Frank Wappler / 24. Januar 2019 @ 12:57
Von Dir hätte ich eigentlich erwartet, dass Du als erstes überhaupt einen Deiner Beteiligten, wie sonst üblich, “in die Mitte” setzt, wo allfällige Lichtblitze von Myon und Erde stets gleichzeitig gesehen würden. Das erschiene mir hier gar keine so schlechte Idee; diesem Mittelmann wäre zumindest unmittelbar ersichtlich, dass P und Q raumartig separiert sind, wie er auch insgesamt eine sehr symmetrische Sicht von Myon und Erde hat. Warum fehlt der ausgerechnet hier, wenn er sonst schon praktisch überall beteiligt ist? Oder habe ich den übersehen?
Ungeachtet eines anscheinend weitgehend fehlenden terminologischen Einvernehmens über grundlegende Dinge wie `Anzeige’, `Eigenzeit’. oder sogar `Lorentzian distance’, scheint sich aber doch eine Gemeinsamkeit abzuzeichnen, nämlich die Einschätzung, dass sich in der SRT der Kontraktions-Faktor 1/γ lediglich als Proprtionalität aus einem Verhältnis zwischen gewissen Längen ergibt, und nicht irgendwie anders. Immerhin etwas.
Chrys schrieb (24. Januar 2019 @ 17:51):
> Von Dir hätte ich eigentlich erwartet, dass Du als erstes überhaupt einen Deiner Beteiligten, wie sonst üblich, “in die Mitte” setzt,
In etlichen meiner obigen Kommentare habe den Begriff und Messungen von Gleichzeitigkeit benutzt (und meistens auch hervorgehoben, damit er ja nicht übersehen würde). Dabei beziehe ich mich (das kann ich wohl nicht oft genug versuchen mitzuteilen) auf Einsteins Koordinaten-freie Definition von “Gleichzeitigkeit” (1916/17), in der der Begriff eines bestimmten Beteiligten als “Mitte zwischen” zwei anderen, voneinander getrennten, gegenüber einander ruhenden Beteiligten wesentlich ist; vgl.
und (wie immer) verbunden mit Anerkennung der (“komplimentären”) Definition von Comstock (1910)
https://en.wikisource.org/wiki/The_Principle_of_Relativity_(Comstock)#the_point_midway_between_A_and_B
und der relevanten Koordinaten-freien Versuchsanordnungen (Betrachtung von Pings, Forderung von Transitivität) die sich schon bei Einstein 1905 finden.
> wo allfällige Lichtblitze von Myon und Erde stets gleichzeitig gesehen würden.
Zu dieser Formulierung möchte ich dreierlei bemerken:
1. Die Beurteilung, die jedem einzelnen Beteiligten hinsichtlich bestimmter von ihm gesammelten Wahrnehmungen zumindest im Prinzip zugestanden werden kann/soll, ist die Beurteilung von deren Koinzidenz (bzw. Nicht-Koinzidenz).
Dass das Wort “Koinzidenz” in Einsteins o.g. Definition von Gleichzeitigkeit offenbar nicht auftaucht, finde ich eine gewaltige “Eselei”. (Immerhin hat Einstein den “Koinzidenz”-Begriff ja bekanntlich schon 1916 an entscheidender Stelle benutzt …)
2. Das Wort “allfällig” gehört nicht zu meinem aktiven Wortschatz; und ich begegne diesem Wort so gut wie nie, außer gelegentlich in Deinen Kommentaren … Meine Vorstellung der hier diskutierten Gedanken-Experimente geht jedenfalls dahin, dass die Beteiligten (“Myon/em>”, “Erde/em>”, usw.) durchwegs irgendwelche “Lichtblitze” darstellen, dass sie durchwegs irgendwelche anderen Beteiligten treffen/passieren, und durchwegs irgendwelche Anzeigen (also Anteile an Koinzidenz-Ereignissen) haben, die wiederum “stets und ständig” von (so gut wie) jedem anderen wahrgenommen werden,
also “stets und ständig” auch irgendeine Anzeige des Myons und irgendeine Anzeige “der Erde” von (so gut wie) jedem anderen koinzident wahrgenommen werden.
Die bloße konzidente Wahrnehmung ist also an sich gar nicht besonders/wesentlich/relevant, sondern es kommt außerdem darauf an, dass der Wahrnehmende erkennen und unterscheiden kann, um welche, besonders ausgezeichneten “Lichtblitze“ es sich jeweils handelte.
(Daher die Bedeutung der Wahrnehmung von “Pings”, verbunden mit der Annahme bzw. dem Zugeständnis, dass der jeweilige Wahrnehmende sich die eigenen Anzeigen merken könnte, und Anzeigen bzw. “Lichtblitze” von identifizierbaren anderen Beteiligten zumindest als Echos/Reflexions-Anzeigen bzgl. bestimmter eigener Signal-Anzeigen wiedererkennen und unterscheiden könnte. Sonst könnte man sich ja “einfach” mit Robb zufriedengeben … &)
Es kommt also jedenfalls darauf an, die relevanten “Lichtblitze” konkreter zu identifizieren; nämlich insbesondere dadurch, wer am jeweiligen Ereignis außerdem teilgenommen hatte; z.B.:
– das Ereignis \(\varepsilon_{BQ}\) (“Punkt Z“) dadurch zu identifizieren, dass daran sowohl das Myon \(Q\) als auch der Erd-Boden-gebundene Detektor \(B\) teilgenommen hatte, bzw.
– das Ereignis \(\varepsilon_{AQ}\) (“Punkt P“) dadurch zu identifizieren, dass daran sowohl das Myon \(Q\) als auch ein bestimmter “Atmosphären-Atomkern \(A\)” teilgenommen hatte.
3. Myon und “Erde” (besser: Erd-Boden-gebundener Detektor) sollen doch gar nicht gegenüber einander ruhen, sondern sich gegenüber einander bewegen! Jemanden als “Mitte zwischen Myon und Erd-Boden-gebundenem Detektor” zu bezeichnen wäre jedenfalls nicht im Sinne des Begriffs aus Einsteins o.g. Gleichzeitigkeits-Definition!
Gemeint ist stattdessen wohl jemand,
– der seine Pings bzgl. dem Myon und Erd-Boden-gebundenem Detektor durchwegs koinzident wahrnahm, und
– bzgl. dem das Myon zwei aufeinanderfolgende Pings koinzident mit einem Ping bzgl. des Erd-Boden-gebundenen Detektors wahrnahm, und
– bzgl. dem der Erd-Boden-gebundene Detektor zwei aufeinanderfolgende Pings koinzident mit einem Ping bzgl. des Myons wahrnahm.
(Zur Definition von “Mitte” im Sinne Einsteins gehört eben außerdem die Forderung, dass die beiden “Enden” gegenüber einander ruhen; und das ist doch etwas komplizierter, Stichwort: tetrahedral-octahedral honeycomb-Ping-Koinzidenz-Gitter)
> Das [“Mittelmann”] erschiene mir hier gar keine so schlechte Idee;
… hat aber keine für mich ersichtliche Relevanz zur Herleitung der Einstein-Projektions-Beziehungen.
> eine Gemeinsamkeit abzuzeichnen, nämlich die Einschätzung, dass sich in der SRT der Kontraktions-Faktor 1/γ [als √{ 1 – β^2 }] lediglich als Proprtionalität aus einem Verhältnis zwischen gewissen Längen ergibt,
Ja: nämlich das Verhältnis zwischen den Längen zweier gewisser verschiedener Stäbe, also zweier verschiedener Paare von gegenüber einander ruhenden Enden.
> und nicht irgendwie anders.
Und zwar konkret und insbesondere: nicht etwa zwei verschiedene Längen-Werte ein-und-des-selben Stabes, also nur eines bestimmten Paares gegenüber einander ruhenden Enden.
> Immerhin etwas.
Und meines Erachtens tatsächlich etwas Wichtiges;
etwas, worüber sich andere (trotz aller Anstrengungen) offenbar immer noch unklar bzw. uneinig sind;
etwas, das sich doch mitzuteilen und gemeinsam zu vertreten lohnt.
Joachim Schulz schrieb (17. Januar 2019 @ 16:39; ich habe diesen Kommentar erst vor Kurzem bemerkt -FW):
> Es gibt nicht die Länge einer bestimmten Garage. […]
Das finde ich eine absurde und schockierende Aussage! …
(… zumindest sofern sich eine Garage in den bekannten Gedanken-Experimenten schlicht als ein Paar von gegenüber einander ruhenden Enden vorstellen lassen soll; namentlich: “Garagen-Eingangs-Tor” und “Garagen-Rückwand”.)
> Die augenblickliche Länge einer Garage ist der raumartige Abstand des Ereignisses des Tors von dem Ereignis der Rückseite, das mit diesem im betrachteten System Gleichzeitig ist.
Dem ist entgegenzusetzen:
Der raumartige Abstand zwischen zwei (raumartige voneinander getrennten) Ereignissen, wovon das Garagentor an dem einen und die Garagen-Rückseite an dem anderen Ereignis teilgenommen hatte (natürlich jeweils zusammen mit zahlreichen weiteren vorstellbaren und ggf. sogar auffindbaren Beteiligten, wie z.B. Lokomotiven, Raketenspitzen, Stabspitzen, Pfeilspitzen bzw. Caboose-Wägelchen, Raketentriebwerken, Stabenden oder Pfeilnocken usw.),
ist die Länge eines bestimmten Stabes, also eines bestimmten Paares gegenüber einander ruhender Enden, von denen eines ebenfalls an dem einen o.g. Ereignis teilgenommen hatte, und das andere ebenfalls an dem anderen Ereignis teilgenommen hatte,
und deren Anzeigen (“Zeiger-Positionen”, “Lichtblitze” …), also deren jeweilige Anteile an den genannten zwei Ereignissen gleichzeitig im Sinne der Einsteinschen Definition (1916/17) waren.
Chrys
24. Januar 2019 @ 14:01
Ich habe noch immer Schwierigkeiten mit deiner Darstellung, nach der die Synchronisation von Uhren Einfluss auf die Realität hat. Ich stimme nicht mir der Aussage überein, die Uhren auf dem in S’ ruhenden Stab können nur in S’ synchron gehen. Klar ist das eine Art natürlichste Wahl, aber jede andere Synchronisation ist ebenfalls erlaubt, denn die Relativitätstheorie ist eine klassische Theorie in dem Sinne, dass Welchselwirkungen stets lokal sind. Es hat also auf einen Vorgang am Raumzeitpunkt P keinen Einfluss, was an irgendeinen anderen raumartig entfernten Raumzeitpunkt Q passiert. Insbesondere ist es also auch egal, was der Zeiger eine Uhr in Q zeigt, wenn der Zeiger in P t=0 zeigt.
Manuel Krüger
18. Januar 2019 @ 15:14
“Kurz nur Sirene, nein es ist kein Scheineffekt, die Frequenz wird real höher gemessen, …”
Herr Schulz, es ist nicht hinnehmbar, dass Sie so etwas stehen lassen, meine Erklärungen dazu aber löschen.
Nochmal: Wenn man keine klaren Begriffe hat, kann man beliebig rumschwurbeln. Das ist Antiwissenschaft. Daher muss der Begriff “Scheineffekt” ganz klar so verstanden werden, wie er auch bei geschulten Menschen gemeint ist, nämlich dass dieser Effekt (der Scheineffekt) nicht das Beobachtete (zB das Martinshorn) betrifft, und daher dem Beobachter eine Frequenzänderung, hier des Martinshorns, nur so erscheint.
Natürlich wird die Frequenz real höher gemessen. Wie kann man diese Selbstverständlichkeit auch nur anzweifeln. Dennoch könnenn wir klar zwischen Scheineffekten (Gegenstand in der Ferne scheint kleiner, Frequenz des Martinshorns scheint verändert, …) und echten Effekten (Gegenstand in der Ferne ist real kleiner als erwartet, die Frequenz des Martinshorns wird tatsächlich geändert, …) unterscheiden.
Wer das ableugnet oder verwirrt ist Antiaufklärer und will Leute verdummen.
@Albrecht Storz:
Ich hätte drei Ratschläge für Sie, die die Wahrscheinlichkeit erhöhen, dass ich einen Beitrag von Ihnen stehen lasse:
1) Versuchen Sie ohne Beleidigungen auszukommen.
2) Bleiben Sie beim Thema.
3) Verkaufen Sie uns nicht für dumm. Selbstverständlichkeiten sind langweilig.
@Joachim Schulz:
Ich fürchte, ich muss da für Herrn Storz mal eine Lanze brechen, was Ratschlag 3 angeht. Können Sie sich vorstellen, wie viele Kritiker sich bereits für dumm verkauft fühlen, wenn diese ach so langweiligen Selbstverständlichkeiten eurerseits übersehen und dann nicht mal akzeptiert werden, wenn man darauf hinweist? Das ist doch das Problem hier – Sie postulieren Symmetrie, wo keine ist und einen Kreisbezug, der hingegen ganz offensichtlich da ist, sehen Sie hingegen nicht. Dabei würde dieser weitgehend aus der Erklärungsnot, welche aus eurer Uneinigkeit bezüglich der Längenkontraktion hervor geht, heraus helfen. Sagen Sie hier, das funktioniert nicht, oder meinen Sie die RT funktioniert nur ohne diesen Kreisbezug?
@Nicht von Bedeutung
Unter uns: Herr Storz hat sogar recht: Natürlich ist der klassische akustische Dopplereffekt ein Scheineffekt. Das Martinshorn des sich nähernden RKWs ist nicht wirklich schneller. Rechnet man Laufzeiteffekte heraus, so sieht man, dass die Sirene nicht wirklich höher klingt. Im relativistischen Dopplereffekt und hier bei der Längenkontraktion bleibt jedoch ein realer Effekt zurück, wenn man die Laufzeiten berücksichtigt. Und in dem Sinne sind diese Effekte eben keine Scheineffekte.
Dass es schwer ist, mit Chrys einig zu werden, verblüfft mich tatsächlich. Bei Frank Wappler bin ich dagegen nicht erstaunt. Er verteidigt eine koordinatenfreie Physik. Die Relativitätstheorie ist aber nicht koordinatenfrei sondern invariant. Dieselben Formeln gelten in jedem Inertialsystem, wenn man mit ART rechnet sogar in jedem beliebigen Koordinatensystem. Und das ist die Symmetrie, die ich behaupte. Dass jedes Beispiel symmetrisch ist, ist eine unsinnige Forderung. Die Existenz von Materie erzeugt immer Asymmetrie.
@Joachim Schulz:
Die SRT fordert diese Symmetrie mit ihrer Wechselseitigkeit – weil alles eben relativ sein muss, was es (dank der Materie, die bereits ART ist) aber nicht ist.
Und Invarianz? Wo bitte haben wir die denn? Eher in einem Kristallgitter (z.B. Silizium) oder eher auf dem räumlichen Abstand zwischen Atomkern und Kovalenz-Elektron (z.B. Cäsium)?
Am Ende bleibt nur ein Inertialsystem übrig und in diesem ruht alles oder bewegt sich relativ zueinander. Und wenn es in diesem Inertialsystem eine konstante Geschwindigkeit geben soll, dann kann diese nicht gegenüber dazu bewegten Objekten konstant gemessen werden. Ebensowenig, wie nach einer Transformation aus einer Geschwindigkeit c eine Geschwindigkeit c±v (oder umgekehrt) werden kann.
Solange die ART nicht an etwas Anderem scheitert, würde ich ja vorschlagen, dass man beides (SRT und ART) nur noch zusammen betrachtet, ansonsten bliebe von der RT nur noch der Lorentz-Faktor übrig, den man auch in einer ganz anderen Transformation verwenden kann außer der Lorentz-Transformation – z.B. eine, die ganz ohne Lorentz-Kontraktion auskommt, weil sich eben nur “Wellenlängen” proportional zu “Periodendauern” dynamisch verändern.
Wer mir jetzt noch erzählt, dass z.B. ich nur Unsinn von mir gebe, der hat das Relativitätsprinzip ganz sicher verpazt.
Hallo Joachim @14:03 “Die Relativitätstheorie ist aber nicht koordinatenfrei sondern invariant.”
Hilf mir auf die Sprünge: die Trafo t′ = γ*(t−v*r/ c²) sind Formelzeichen, wo sind da die Koordinaten?
Wir nehmen den Abstand von Ereignissen, der ist unabhäng von Koordinaten, die sind “Rechenhilfe”.
Als ich noch am Anfang war, hab ich mal gehört, jede Theorie muß koordinatenfrei formulierbar sein,
sonst stimmt was mit ihr nicht. Weiß jetzt nicht ob das mit meinem Gedächtnis stimmt.
Grüße Dip
@Senf:
Im Ursprung! Die Koordinaten (t’, x’, y’, z’), die ein Beobachter einem Ereignis zuschreibt, hängen nur dann mit den Koordinaten (t, x, y, z) für das selbe Ereignis eines anderen Beobachters zusammen, wenn sie zum Zeitpunkt t’=t=0 ubereinstimmen. (Quelle: Wikipedia)
Die LoTra ist eine Koordinatentransformation und solche können sicher nicht koordinatenfrei sein, sonst machen sie ja keinen Sinn.
@Senf:
Und ich habe mal gehört, dass eine Theorie Bezugssystemfrei formuliert sein muss, sonst macht sie keinen Sinn. Das bedeutet, dass man den Ursprung des Bezugssystems beliebig bestimmen darf, nicht aber, dass man für Bezugssysteme plötzlich keine Koordinaten mehr benötigt.
Joachim Schulz
25. Januar 2019 @ 13:22
Herr Schulz,
wenn Sie falsche Behauptungen stehen lassen, muss ich widersprechen. Auch wenn es sich bei der Richtigstellung um Selbstverständlichkeiten handelt. Oder lassen Sie Unsinn stehen, weil der zwangsläufig eben nicht selbstverständlich ist und daher nicht Ihrem Punkt 3) widerspricht? Was wäre das für eine Verkehrung der Vernunft.
Joachim Schulz
25. Januar 2019 @ 14:03
” Im relativistischen Dopplereffekt und hier bei der Längenkontraktion bleibt jedoch ein realer Effekt zurück, wenn man die Laufzeiten berücksichtigt. Und in dem Sinne sind diese Effekte eben keine Scheineffekte.”
Genau diese Diskussion haben Sie sabotiert, indem Sie Unsinn stehen gelassen haben und deren Richtigstellung gelöscht haben, weil “Selbstverständlichkeit” hier unstatthaft sei! Wie soll in so einer Umgebung vernünftig diskutiert werden?
“Längenkontraktion” ist definitiv ein Scheineffekt, denn der Betroffene (Besatzung eines Raumschiffes, angenommener Mitreisender beim Myon, …) nimmt diesen Effekt an sich nicht wahr. Der Effekt tritt bei der Beobachtung auf, nicht am Beobachteten selbst. Also Schein-Effekt.
Niemand kann ernsthaft auf dem Standpunkt stehen, dass jemand der bewegt ist, deswegen kontrahieren würde, so lange Einigkeit darüber herrscht, dass Bewegung relativ ist! Es gibt keinen bewegten versus unbewegten Beobachter! Es gibt keine reale Längenkontraktion! Es gibt höchstens beobachtete Längenkontraktion, Schein-Längenkontraktion! Alles andere wäre widersprüchlich, unphysikalisch, alogisch!
Albrecht Storz
25. Januar 2019 @ 17:11
Ich habe auch gar keine Lust, diese Diskussion mit Ihnen zu führen. Mein SIWOTI-Syndrom hält sich hier in engen Grenzen. Diskutieren Sie das doch bei Frau Lopez. Ich habe sicher keine Intension, das zu verhindern oder gar zu sabotieren.
Herr Senf
25. Januar 2019 @ 15:07
Naja, hier sind offensichtlich t’,t und r Koordinaten. Es stimmt schon, dass Abstände und überhaupt alle Messgrößen Koordinaten unabhängig sind. Dennoch sind Koordinaten in konkreten physikalischen Fragestellungen unverzichtbar. Ich hatte dazus 2012 mal was geschrieben:
Ein Loblied auf Koordinaten
Joachim Schulz
25. Januar 2019 @ 18:06
“Ich habe auch gar keine Lust, diese Diskussion mit Ihnen zu führen.”
Ich mit Ihnen auch nicht. Aber Sie verbreiten mit Ihrere Seite hier antiwissenschaftlichen Unsinn, zB. dass es keine Schein-Effekte gäbe, wobei diese Behauptung auf dem offensichtlichen Unverständnis beruht, dass die Unterscheidung zwischen “Effekt” und “Schein-Effekt” natürlich auf der Frage beruht, was genau denn beobachtet werden soll.
Ist es Ziel dieser Seite, Unsinn unwidersprochen in die Welt setzen zu lassen? Hat diese Seite einen antiwissenschaftlichen, antiaufklärerischen Anspruch? Entscheiden Sie sich mal!
Die angebliche Längenkontraktion ist ein offensichtlicher Schein-Effekt, da er nicht dem Beobachtungsgegenstand zugehört, sondern durch die Beobachtung erst auftritt.
Kein Mensch kann ernsthaft behaupten, das Martinshorn würde durch die relative Bewegung des Beobachters seine Frequenz ändern, oder ein Objekt würde durch die realtive Geschwindigkeit eines Beobachters kontrahieren.
Albrecht Storz
26. Januar 2019 @ 10:21
Das behauptet auch kein Mensch. Ihre Kritik basiert auf sogenannte Strohmannargumente. Sie unterstellen der SRT Aussagen, die nirgends gemacht werden. Das liegt daran, dass Sie die SRT nicht im Ansatz verstanden haben. Und deshalb wiederhole ich meine Aufforderung:
Formulieren Sie ihre Fragen mit angemessener Bescheidenheit.
@Albrecht Storz:
Wie wäre es denn mal mit etwas Diplomatie?
@Joachim Schulz:
Ich erinnere mich dunkel daran, das wir beim relativistischen Doppler-Effekt keine Längenkontraktion benötigten.
Bei Atomuhren kann man unterschiedliche Gangraten auf unterschiedliche nicht näher definierte Periodendauern schieben, die vermutlich durch Gravitation und Bewegung beeinflusst werden (wegen der Massen von Atomkern und Elektronen).
Vom Myonen-Experiment braucht man gar nicht sprechen, denn es gibt dafür keinen Beweis, solange nicht einer mal mit Myon-Air fliegt.
Bleibt also nur Michelson Morley als einzige Hürde, wo noch tatsächliche Längenkontraktion benötigt wird.
Dazu mal folgende Analogie. Ich pumpe rot und blau gefärbtes Wasser gleichverteilt durch in einem Kreis angeordnete Röhrchen (parallele Interferenz) und richte den Gesamtstrahl auf klares Wasser (radiale Interferenz), wo sich sofort magenta gefärbtes Wasser als Resultat zeigt. Analog zum Michelson Morley Interferometer drehe ich nun eine Vorrichtung, die dafür sorgt, dass die Farben in den Röhrchen wechseln, was aber am Resultat nichts ändert. Und nun die Preisfrage, warum dies bei Licht anders sein sollte. Wenn ich wüsste, wie man das parallele Interferenzmuster beim Licht sichtbar machen kann, würde ich es tun.
Ja, der Dopplereffekt kommt ohne Längenkontraktion aus. Aber da Längenkontraktion und Zeitdilatation zwei Seiten derselben Medaille sind, müssen sie in gleicher Weise real sein.
Ich werde mich jetzt wirklich mal daran machen müssen, die Längenkontraktion aus Relativistischer Sicht zu erläutern.
@Joachim Schulz:
Finden Sie nicht, dass wenn man es schafft, all diese Längenkontraktionen auf Wellenlängen (proportional zu Periodendauern) abzuwälzen, man komplett aus dem Schneider ist? Wenn das geht, warum sollte man es anders machen, bzw. gar anders machen wollen? Nur weil ein Herr Krüger nicht begreifen will, dass es geht? Wen interessiert den noch eine Hand voll Relativisten, wenn die Wissenschaft weiter geht? Die Flacherdler hat man doch auch abgehängt.
@Joachim / 25. Januar 2019 @ 09:32
Synchronisierung ist zugegbenermassen vieldeutig, und ich hätte sagen sollen, dass ich hier speziell und ausschliesslich die Einstein-Poincaré Sychronisierung im Sinn habe, mit Hinblick auf ihre Bedeutung für die Definition und Beurteilung von Gleichzeitigkeit in der SRT.
Für die raumzeitliche Beschreibung eines inertialen Stabes im Minkowski Diagramm reicht es nicht hin, nur eine raumartig zusammenhängende Menge von Punkten \(\xi\) anzugeben, denn es ist einzubeziehen, dass alle diese Punkte sich entlang ihrer durch Eigenzeit parametrisierten Weltlinien bewegen, wobei der raumartige Zusammenhang des Stabes strukturell erhalten bleibt. Am einfachsten lässt sich ein Stab (oBdA von Einheitslänge) in seinem Ruhesystem S’ modellieren, also dargestellt in S’-Koordinaten durch die Schar von Weltlinien
\[
w_\xi(s) = (t’_\xi(s),x’_\xi(s)) = (s,\xi), \quad 0 \le \xi \le 1.
\]
Die 4-Geschw. ist \(\dot{w}_\xi(s) = (1,0) =\vec{e}_{t’}\), deren Betrag, wie gefordert, gleich der normalisierten Lichtgeschw. 1 ist. Dann ist die Koordinatenfunktion \(t’_\xi\) aber nichts anderes als die Anzeigefunktion einer Uhr mit der Weltlinie \(w_\xi\). Und für eine beliebig gegebene S’-Zeit \(s_0\) lässt sich durch
\[
\text{Stab zur S’-Zeit}\,s_0 = \{w_\xi(s) \mid t’_\xi(s) = s_0, 0 \le \xi \le 1\}.
\]
der Stab als raumartig zusammenhängende Struktur in der Raumzeit auffinden anhand der S’-synchronen Anzeige von Uhren, die sich an seinen verschiedenen Punkten \(\xi\) befinden.
Die transformierte Darstellung der Stab-Weltlinien in S-Koordinaten kann ich mit den verwendeten Bezeichnungen dann auch schreiben als
\[
w_\xi(s) = (t_\xi(s),x_\xi(s)) = (\gamma(t’_\xi(s) + x’_\xi(s)\beta),\gamma(t’_\xi(s)\beta + x’_\xi(s))), \quad 0 \le \xi \le 1,
\]
was offensichtlich erhalten wird durch Transformation mit dem ordinären Boost
\[
t = \gamma(t’ + \beta x’), \quad x = \gamma(x’ + \beta t’).
\]
Führt man nun \(\tau = \gamma s\) als Zeitparameter ein, so lassen sich damit S-synchrone Uhren \(u_x(\tau) = (\tau,x), x \in \mathbb{R}\), definieren, deren Anzeige \(\tau\) die S-Zeit, oder in Einsteins Formulierung von 1905,`die Zeit des ruhenden Systems’ S bestimmt. Zu einem beliebigen Anzeigewert \(\tau\) findet man den Stab in der S-Darstellung als die raumartig zusammenhängende Punktmenge
\[
\text{Stab zur S-Zeit}\,\tau = \{w_\xi(s) \mid t’_\xi(s) = \gamma^{-1}\tau, 0 \le \xi \le 1\}.
\]
Die Animation lässt sich somit als eine durch \(\tau\) parametrisierte Darstellung des Stabes zur S-Zeit \(\tau\) im zeitlichen Verlauf interpretieren.
Dann befinden sich aber zu keinem je von S-Uhren angezeigten Wert \(\tau\) die x-Komponenten \(x_0(\gamma^{-1}\tau)\) und \(x_1(\gamma^{-1}\tau)\) der beiden Stabenden innerhalb der Strecke \(OC\) auf der x-Achse von S.
Gänzlich irreal erscheint mir doch die Vorstellung, man könne sich bei eingefrorener Zeitkoordinate \(t = 0\) hinsetzen und abwarten, wie die Punkte des Stabes im Verlaufe des mysteriöserweise dann doch nicht eingefrorenen Zeitflusses die x-Achse passieren, um sie dort festzuhalten und die so konstruierte Strecke \(OC\) schlussendlich als den kontrahierten Stab zur Zeit \(t = 0\) zu präsentieren.