Längenkontraktion im Weg-Zeit-Diagramm
Beim Versuch, physikalische Vorgänge zu erklären, sind Bilder oft problematisch. Sie lösen manchmal Assoziationen aus, die der Autor oder die Autorin nicht beabsichtigt oder auch nur vorhergesehen hat. Insbesondere ist es schwierig, Bewegungen als Bild darzustellen. Eine dynamische Situation wird durch ein stehendes Bild nur unzureichend dargestellt, denn jegliche Information über die Bewegung fehlt.
Sehen wir eine Momentaufnahme zweier Autos kurz vor einem Unfall, so können wir nicht einschätzen, wie ernst die Lage ist. Die Geschwindigkeit ist entscheidend dafür, wie groß die zerstörerische Kraft des anstehenden Zusammenstoß ist. Sie kann uns außerdem einen Hinweis geben, ob es noch denkbar ist den Zusammenstoß durch Bremsen oder Ausweichen zu verhindern.
Standbilder in der Speziellen Relativitätstheorie
Noch kritischer sind Standbilder in der Speziellen Relativitätsthoerie. Dort sind Geschwindigkeiten vergleichbar mit der Lichtgeschwindigkeit. Dadurch können sich die Positionen der Objekte in der Laufzeit des Lichtes deutlich ändern. Eine Skizze der momentanen Situation ist nicht identisch zu einem optisch aufgenommenen Bild derselben Situation.
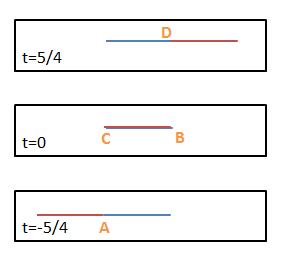
Links im Bild sehen Sie drei Skizzen einer Szene, wie Albert Einstein sie in seinem Artikel Zur Elektrodynamik bewegter Körper beschreibt: Ein Zug, hier als rote Linie dargestellt erreicht im unteren Bild den blau dargestellten Bahnhof. Bahnhof und Zug sind gleich lang.
Im mittleren Bild erreicht die Zugspitze die Ausfahrt des Bahnhofs und gleichzeitig erreicht das Zugende die Einfahrt. Im oberen Bild verlässt das Zugende schließlich den Bahnhof.
Jedes dieser Bilder für sich hat die beiden genannten Nachteile: Erstens zeigen sie keine Bewegung und zweitens sind sie keine Fotos sondern Skizzen. Sie beschreiben also nicht was man sieht, sondern was gerade ist. Die orangen Buchstaben bezeichnen die vier relevanten Ereignisse:
- Zugspitze erreicht Einfahrt
- Zugspitze erreicht Ausfahrt
- Zugende erreicht Einfahrt
- Zugende erreicht Ausfahrt
Dieses Beispiel ist im wesentlichen identisch zu den bereits früher besprochenen Beispielen, das Garagen Paradoxon und das Panzer Paradoxon.
Von Standbildern zum Weg-Zeit-Diagramm
Etwas besser als drei Standbilder ist diese Darstellung schon, weil ich Zeiten dran geschrieben habe: Der Zug bewegt sich mit 80% der Lichtgeschwindigkeit. Die Zeiten sind hier nicht in Sekunden angegeben, sondern in der Einheit Bahnhofslänge durch Lichtgeschwindigkeit. Der Zeitabstand t=1 ist also die Zeit, die Licht braucht um von einem Bahnhofsende zum anderen zu kommen. Vom unteren zum mittleren und vom mittleren zum oberen Bild vergehen je 5/4 Zeiteinheiten. Das ist der Kehrwert von 80%.
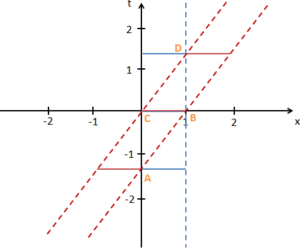
Die Darstellung in drei Standbildern lässt sich leicht zu einem Weg-Zeit-Diagramm erweitern. So lassen sich in einem Bild diese drei Zeitschritte, aber auch alle Zeiten davor, dazwischen und danach darstellen. Sie sehen das Weg-Zeit-Diagramm rechts im Bild.1
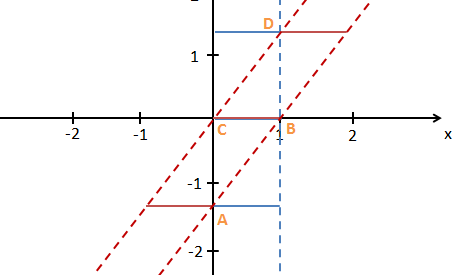
Zu den je drei blauen und roten Linien kommt das schwarze Koordinatenkreuz. Horizontal stellt es räumliche und vertikal zeitliche Abstände, also Dauern dar. Außerdem habe ich durch blaue gestrichelte Linien die Enden des Bahnhofs zu allen Zeiten markiert. Die roten gestrichelten Linien zeigen die Position von Zugspitze und Zugende zu jeder Zeit. Solche Linien, die die Bewegung eines Objektes beschreiben, nennt man Weltlinien.
Schräge, gerade Weltlinien, wie die beiden rot gestrichelten des Zuges, beschreiben eine Bewegung mit konstanter Geschwindigkeit. Je flacher desto schneller. Vertikale Linien, wie die blau gestrichelten des Bahnhofs, beschreiben ruhende Objekte. Weltlinien sind immer steiler als 45°, denn 45°-Linien haben Lichtgeschwindigkeit und das kann kein Objekt erreichen.
Horizontale Linien, bezeichnen räumliche Abstände gleichzeitig stattfindender Ereignisse. Jede horizontale Linie, die die blauen gestrichelten Linien verbindet, beschreibt den Bahnhof zu einer bestimmten Zeit. Jede horizontale Linie zwischen den roten gestrichelten Linien stellt die momentane Position des Zugs dar. So können wir im Weg-Zeit-Diagramm in Ruhe alle Aspekte von Bewegungen studieren.
Lorentztransformation und Längenkontraktion
Wie in einem früheren Artikel beschrieben, ergibt sich der Effekt der Längenkontraktion direkt aus der Lorentztransformation. Mal sehen, was passiert, denn wir das Weg-Zeit-Diagramm mit der Geschwindigkeit v=4/5 (also 80% Lichtgeschwindigkeit) transformieren…
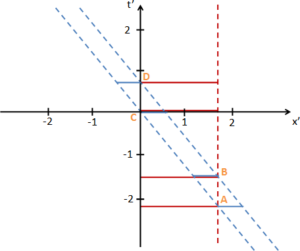
Das Ergebnis ist links im Bild dargestellt: Die Transformation ist genau so gewählt, dass die roten gestrichelten Linien senkrecht und die blauen schräg sind. Der Zug ruht also und der Bahnhof bewegt sich mit 4/5 Lichtgeschwindigkeit. Wir haben ein Ruhesystem des Zuges gewählt.
Bevor ich auf die Längenkontraktion zurück komme, möchte ich noch zwei weitere Effekte aufzeigen, die sich aus der Lorentztransformation ergeben:
Die Ereignisse B und C sind nicht mehr gleichzeitig. Die Spitze des Zuges lässt die Ausfahrt des Bahnhof zurück, bevor das Zugende an der Einfahrt ist. Das ist die Relativität der Gleichzeitigkeit. Zu Logikbrüchen kann das nicht führen, weil die Ereignisse B und C raumartig getrennt sind: Eine in B erzeugte, sich lichtschnell ausbreitende Wirkung kann C nicht erreichen.
Die jetzt am selben Ort geschehenden Ereignisse A und B und C und D passieren mit kürzerem Zeitabstand. Das ist die Zeitdilatation: Der Zug misst für den Durchgang des Bahnhofs eine kürzere Zeit als der Bahnhof für den Durchgang des Zuges.
Die Längenkontraktion ist zu allen vier eingetragenen Zeiten offensichtlich: Bei Transformation in das Ruhesystem des Zuges wird dieser länger. Der Bahnhof, der in diesem System bewegt ist, wird kürzer. Wichtig ist hier, dass es keine physische Verformung von Zug oder Bahnhof gibt. Es ist ja lediglich eine transformation zwischen verschiedenen Koordinaten, die denselben Vorgang beschreiben.
Real oder Täuschung
Die Änderung der Zuglänge ist trotzdem real. Es handelt sich nicht um eine Täuschung aufgrund von Lichtlaufzeiten. Die Längenkontraktion ist untrennbar mit der Relativität der Gleichzeitigkeit verbunden. Im Bahnhofssystem ist die Zuglänge der Abstand der Ereignisse C und B, die hier gleichzeitig sind. Im Zugsystem ist es der Abstand zweier Ereignisse, die aus Sicht der Zuges gleichzeitig sind.
In der Relativitätstheorie sind diese beiden Koordinatensysteme gleichwertig. In jedem gelten dieselben Naturgesetze. Jedes kann die Situation mit gleicher Berechtigung beschreiben. Deshalb kann man nicht eine Zuglänge realer nennen als die andere. Es sind einfach unterschiedliche Schnitte durch das Raum-Zeit-Diagramm.
Das Minkowski-Diagramm
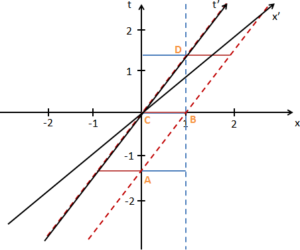 Zu guter letzt zeige ich rechts im Bild das sogenannte Minkowski-Diagramm zum hier behandelten Fall. Es entsteht einfach dadurch, dass man in das erste Weg-Zeit-Diagramm die x’- und t’-Achse des zweiten einzeichnet. Mit ein bisschen Übung lassen sich dann die Orte und Zeiten von Ereignissen in beiden Koordinatensystemen ablesen.
Zu guter letzt zeige ich rechts im Bild das sogenannte Minkowski-Diagramm zum hier behandelten Fall. Es entsteht einfach dadurch, dass man in das erste Weg-Zeit-Diagramm die x’- und t’-Achse des zweiten einzeichnet. Mit ein bisschen Übung lassen sich dann die Orte und Zeiten von Ereignissen in beiden Koordinatensystemen ablesen.


Aufgrund der angespannten Diskussionskultur bei Themen zur Relativitätstheorie bleibt der Kommentarbereich geschlossen. Ich freue mich trotzdem über Fragen und Anregungen. Bitte nutzen Sie dazu die sozialen Medien oder E-Mail.