Eine Bewegung zu viel
Animationen können ein wertvolles Mittel sein, um Vorgänge verständlich zu machen. Manchmal verwirren sie aber mehr als sie helfen. Dafür habe ich ein Beispiel in der englischsprachigen Wikipedia gefunden.
Wie ich im letzten Beitrag gezeigt habe, sind Weg-Zeit-Diagramme ein Instrument, Bewegungen statisch darzustellen. Die Zeit wird nach oben aufgetragen, momentane Position der Objekte ergeben sich als horizontale Schnitte durch das Diagramm.
Minkowski-Diagramm eines bewegten Stabes
Unter einem meiner letzten Artikel zur Längenkontraktion haben wir eine Animation eines Minkowski-Diagramms diskutiert.
Unten sehen Sie diese Animation, direkt eingebettet aus Wikimedia Commons. Sie stellt die Bewegung eines Stabes mit einer Geschwindigkeit von etwa 50% Lichtgeschwindigkeit dar.
Urheber: Stigmatella aurantiaca [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0)], from Wikimedia Commons
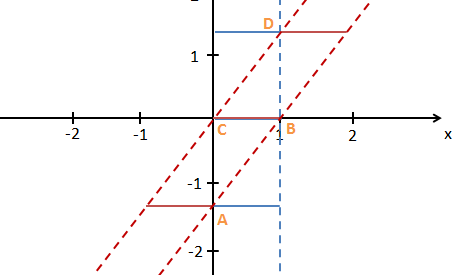
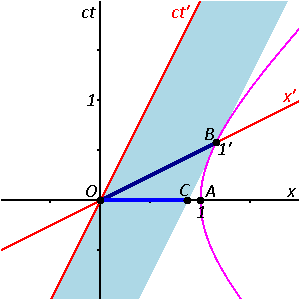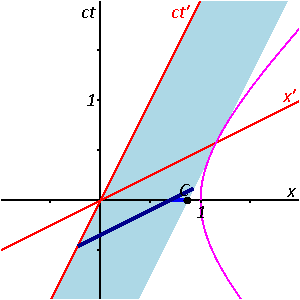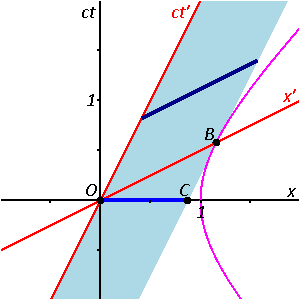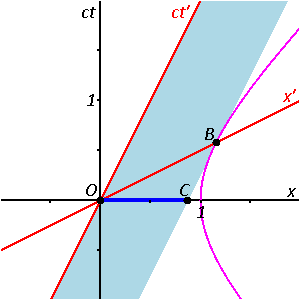
Das hellblaue Band , das links von einer roten Linie begrenzt ist und sich rechts an die pinke Hyperbel schmiegt beschreibt für jede beliebige Zeit, wo sich der Stab gerade befindet.
Das schwarze Koordinatenkreuz stellt nach oben die Zeit ct und nach rechts eine Ortskoordinate x dar.1 Die roten Linien sind die Achsen im Ruhesystem des Stabes. Sie gehen durch Lorentztransformation aus den schwarzen Achsen hervor. Diese Koordinaten-Achsen ct’ und x’ machen das Raum-Zeit-Diagramm zu einem Minkowski-Diagramm.
Die pinke Hyperbel ist eine Linie identischen Raumzeit-Abstands zum Nullpunkt 0 der Koordinatensysteme. Das ist vielleicht das spannendste in dieser Grafik: Abstände in der Raumzeit werden nicht durch den Satz von Pytagoras, sondern durch s²=x²-ct² gebildet. Punkte gleichen Abstands von einem Punkt bilden deshalb keinen Kreis, sondern eine Hyperbel. Alle Punkte auf dieser Linie haben den Abstand s=1 vom Nullpunkt.
Verwirrende Animation
Soweit zu den statischen Elementen des Bildes, kommen wir jetzt zu den bewegten Elementen:
Durch das hellblaue Band zieht von unten nach oben eine dunkelblaue Linie. Sie ist parallel zur roten x’-Achse. Das bedeutet, dass sie Punkte markiert, die in dem Koordinatensystem gleichzeitig sind, in dem der Stab ruht.
Die dunkelblaue Linie hält zweimal kurz an. Zunächst, wenn die rechte Spitze die schwarze x-Achse trifft. Dort erscheint dann die Markierung des Ereignisses C. Dann, wenn sie als ganzes die rote x’-Achse trifft. Dabei werden der Nullpunkt mit O und ein weiteres Ereignis mit B markiert. Während die dunkelblaue Linie durch die schwarze x-Achse durchläuft, färbt sie den berührten Punkt dieser Achse Mittelblau.
Es entsteht somit eine mittelblaue Line, die den Stab zur Zeit t=0 markiert. Am Schluss gibt es nochmal ein Standbild mit der mittelblauen Linie auf der x-Achse und der dunkelblauen auf der x’-Achse.
Das Standbild sagt schon alles
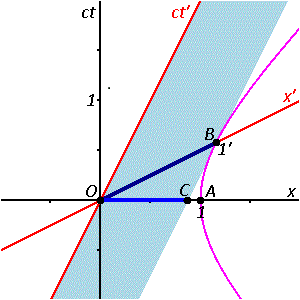
Rechts sehen Sie dieses Standbild noch einmal. Und es zeigt auch ohne Bewegung alles was es zu beschreiben gibt:
Das hellblaue Band beschreibt zu jeder Zeit ct die Ausdehnung des Stabes in der Achse x. Wenn Sie sich den Stab aus Atomen zusammengesetzt sehen, wird jedes Atom durch eine Weltlinie innerhalb dieses Band beschrieben.
Der mittelblaue Querschnitt zwischen den Punken O und C schneidet die Weltlinien aller Atome dieses Stabes. Ebenso schneidet der dunkelblaue Querschnitt zwischen den Punkten O und B alle Weltlinien. Sowohl OC als auch OB messen also die Länge des gesamten Stabes. Nur eben mit anderen Definitionen von Gleichzeitigkeit. Da B und C nicht derselbe Punkt sind, ist es auch nicht überraschend, dass zwei unterschiedliche Längen herauskommen. Beide Längen sind invariante Abstände zwischen zwei Raumzeit-Punkten, zwischen raumartig getrennten Ereignissen.
Keine übergeordnete Zeit
Animieren wir nun den dunkelblauen Stab, so zeigen wir nacheinander verschiedene Gleichzeitigkeiten in ct’. Das dürfen wie zweifellos tun. Man kann in diesem Bild beliebig viele mittelblaue und dunkelblaue Linien einzeichnen, die den Stab zu anderen Zeiten ct oder ct’ darstellen. Wir können auch beliebige andere Perspektiven wählen. Die Kernaussage der Relativitätstheorie ist, dass jede Darstellung von Gleichzeitigkeiten gleichwertig ist. Es gibt keine absolute Gleichzeitigkeit.
Die Animation kann aber leicht so gelesen werden, als gäbe es eine übergeordnete Zeit, die den mittelblauen Schnitt durch das Raum-Zeit-Diagramm erst erzeugt. Als sei die durch die dunkelblaue Linie dargestellte Gleichzeitigkeit der eigentliche, wirklich existierende Stab. Als würde die mittelblaue nur durch Durchlaufen der dunklen Line erzeugt.
Jeder Punkt der mittelblauen Line stellt aber genau eine Momentaufnahme eines Atoms des Stabes dar. Und daran ändert sich nichts. Zur Zeit t=0 befindet sich zwischen den Punkten O und C je ein Teil des Stabes. Das wird durch das statische Bild vollständig beschrieben. Es ist nicht so, dass der dunkelblaue Stab dort erstmal durchlaufen muss um diese Tatsache zu erzeugen.


Möchten Sie einen Kommentar loswerden?
Bitte bleiben Sie nett, halten sich kurz und ans Thema.
Kommentarregeln
Was ich (Laie) nicht so recht verstehe ist die Aussage: Es gibt keine absolute Gleichzeitigkeit.
Bei http://www.relativitätsprinzip.info/relative-gleichzeitigkeit.html heißt es: Ereignis A geschieht gleichzeitig mit Ereignis B und kann weder Ursache noch Wirkung von B sein (*und umgekehrt* müsste man vll. noch ergänzen). Das ist doch aber absolut gleichzeitig – “oder”? Jedenfalls kann ich mir vorstellen dass zwei Ereignisse absolut gleichzeitig passieren.
Auch die Variante Ereignis A ist raumartig von Ereignis B getrennt und kann weder Ursache noch Wirkung von B sein besagt doch im Grunde dasselbe – “oder”? Und selbst wenn sie nur (z. B.) 1 Meter voneinander entfernt sind – und natürlich von SEHR kurzer Dauer sind – können sie sich doch nicht gegenseitig beeinflussen …
Hallo Axel Krüger,
Ich habe den Link mal korrigiert. Es geht mit Umlaut, dann muss aber das xn-- am Anfang weg.
Der Unterschied zwischen gleichzeitig und raumartig ist, dass Gleichzeitigkeit transitiv ist. Wenn Ereignis A mit Ereignis B gleichzeitig ist und B mit C, dann sind auch A und C gleichzeitig. Für Raumartigkeit gilt das nicht. Es gibt Ereignisse A und C, die hintereinander geschehen und dennoch beide zu einem entfernten Ereignis B raumartig sind.
Raumartig getrennte Ereignisse sind in einem aber nicht in allen Bezugssystemen gleichzeitig.
Müsste das nicht wie folgt heißen?
s²=x²-(ct)²
Dann könnte man auch als “Koordinate” verwenden:
τ := ict , mit i = √(-1)
Dann müsste formal der Satz des Pythagoras gelten:
s²=x² + τ²
Müsste das nicht wie folgt heißen? s²=x²-(ct)²
Korrekt wäre ±s²=x²-(ct)², die Hyperbel hat zwei Äste +t und -t.
Joachim Schulz schrieb (12. Februar 2019):
> […] Es gibt keine absolute Gleichzeitigkeit.
In Einsteins Darstellung (gedanken-experimenteller Definition der Feststellung) von Gleichzeitigkeit geht es um
– zwei identifizierbare, bestimmte, voneinander getrennte, gegenüber einander ruhende Beteiligte (\(A\) und \(B\), konkret vorgestellt als “zwei weit voneinander entfernte Stellen unseres Bahndammes“,
– die jeweils den Einschlag eines Blitzes erlebten und anzeigten,
– und die einen bestimmten dritten Beteiligten (\(M\)) als “in die Mitte der Strecke gestellt” identifizieren,
– der die beiden Blitzanzeigen \(A\)s bzw. \(B\)s zusammen (koinzident) wahrnahm.
Was davon wäre nicht “absolut bestimmt” ?? —
Wären Bestandteile eines Bahndammes etwa mit Bestandteilen eines Zuges zu verwechseln, der auf diesem Bahndamm entlangfuhr ?
Wäre die Mitte zwischen zwei bestimmten, voneinander getrennten, gegenüber einander ruhenden Bestandteilen eines Bahndammes etwa mit der Mitte zwischen zwei bestimmten, voneinander getrennten, gegenüber einander ruhenden Bestandteilen eines Zuges zu verwechseln, der auf diesem Bahndamm entlangfuhr ?
Wäre etwa anzuzweifeln, dass \(M\) beurteilen könnte, ob er \(A\)s Blitzanzeige und \(B\)s Blitzanzeige zusammen (koinzident) wahrgenommen hatte, oder nicht, falls außerdem ein Zug an \(M\) vorbeifuhr ? …
Nun, Herr Wappler,
Gleichzeitigkeit gibt es ja nicht nur an einem Bahnsteig. Ich beziehe mich hier auf die allgemeine Definition von Gleichzeitigkeit. Die Existiert auch, wenn gerade kein Blitz eingeschlagen hat.
Hallo Herr Schulz,
das (1) Wenn Ereignis A mit Ereignis B gleichzeitig ist und B mit C, dann sind auch A und C gleichzeitig verstehe ich.
Das (2) Es gibt Ereignisse A und C, die hintereinander geschehen und dennoch beide zu einem entfernten Ereignis B raumartig sind hingegen nicht so recht.
https://de.wikipedia.org/wiki/Lichtkegel#/media/File:World_line-de.svg
Es gibt ja die Begriffe zeitartig, lichtartig und raumartig. Zeitartig ist innerhalb des Vergangenheits- und Zukunftslichtkegels. Lichtartig ist genau auf den beiden Diagonalen und raumartig außerhalb der beiden Lichtkegel. Bezogen auf (“zumindest”) die/eine Gegenwarts-Hyperfläche ist raumartig absolut gleichzeitig, weil Ereignisse dort sich nicht beeinflussen können, da Wirkungen (od. was auch immer) sich eben nur mit maximal Lichtgeschwindigkeit fortpflanzen können. Dass das (die abs. Gleichzeitigkeit) wiederum schwer zu beweisen/messen ist, sei zugegeben – eben da sich Informationen/Wirkungen nur mit maximal Lg. fortpflanzen können. Die Aussage aber dass es absolute Gleichzeitigkeit gibt (an verschiedenen Punkten des Raumes auf der/einer Hyperfläche) kommt mir deswegen trotzdem nicht falsch vor.
Transitiv (siehe 1) ist die Übertragung eines Verhältnisses (Gleichzeitigkeit z.B.) zwischen zwei Ereignissen auf weitere damit zusammenhängende Ereignisse (eben ihre Gleichzeitigkeit).
(2) Ereignisse A und C, die hintereinander geschehen. D.h. sie sind nicht gleichzeitig. Was aber meint, dass sie dennoch beide zu einem entfernten Ereignis B raumartig sind?
Alles was auf der/einer Gegenwarts-Hyperfläche passiert (die sich ja auch in den raumartigen Bereich erstreckt) ist absolut gleichzeitig. Ist es das (diese Gegenwarts-Hyperfläche) was Sie mit _einem_ bei Raumartig getrennte Ereignisse sind in einem aber nicht in allen Bezugssystemen gleichzeitig meinen (Sie sagen zwar nicht abs. gleichzeitig, aber macht das einen Unterschied)?
Der Zusatz in meinem ersten Kommentar Und selbst wenn sie nur (z. B.) 1 Meter voneinander entfernt sind – und natürlich von SEHR kurzer Dauer sind – können sie sich doch nicht gegenseitig beeinflussen kam mir später nicht mehr so gut/”intelligent” vor. Mir fiel eine Explosion ein. Da kann der “Knall“ (die Ursache) durchaus SEHR kurz sein, aber die Druckwelle (Wirkung) noch lange anhalten.
Zu dem Thema Raumzeit könnte man noch einiges sagen (“philosophieren“) .. 😉 ..
Joachim Schulz schrieb (13. Februar 2019 @ 14:51):
> Gleichzeitigkeit gibt es ja nicht nur an einem Bahnsteig. Ich beziehe mich hier auf die allgemeine Definition von Gleichzeitigkeit.
Soll damit etwa bestritten werden, dass die im Einsteinschen Gedankenexperiment erwähnten zwei weit voneinander entfernten Stellen A und B unseres Bahndammes beispielhaft für ganz allgemeine Paare von gegenüber einander ruhenden Beteiligten stehen ??
> Die Existiert auch, wenn gerade kein Blitz eingeschlagen hat.
Soll damit etwa bestritten werden, dass die im Einsteinschen Gedankenexperiment erwähnten Blitz-Einschlags-Anzeigen von A bzw. von B beispielhaft für ganz allgemeine wahrnehmbare und erkennbare Anzeigen (von Paaren der o.g. Beteiligten) stehen, deren Gleichzeitigkeit oder Ungleichzeitigkeit zu messen wäre ??
Erschöpft sich der Versuch, die aus dem obigen SciLogs-Beitrag zitierte Behauptung “Es gibt keine absolute Gleichzeitigkeit.” zu rechtfertigen, etwa in solchen Finten ? …
Axel Krüger schrieb (13. Februar 2019 @ 17:47):
> [Die Aussage] »Wenn Ereignis A mit Ereignis B gleichzeitig ist und B mit C, dann sind auch A und C gleichzeitig« verstehe ich.
Dann liegt offenbar ein Missverständnis vor, denn der Einsteinsche Begriff (einschl. gedanken-experimenteller Definition der Feststellung) von Gleichzeitigkeit ist gar nicht auf ganze Ereignisse anwendbar, sondern (nur) auf die Anteile, die bestimmte geeignete (gegenüber einander ruhende) Beteiligte an gewissen Ereignissen haben, d.h. auf deren individuelle Anzeigen (von “Blitzeinschlägen”, “Zeigerstellungen”, “Treffen/Passieren” anderer Beteiligter, usw. usf.).
Die Transitivität von Gleichzeitigkeits-Beziehungen besteht darin, dass
– falls eine bestimmte Anzeige des Beteiligten A (nennen wir sie Anzeige A_J) und eine bestimmte Anzeige des Beteiligten B (nennen wir sie Anzeige B_K) gleichzeitig waren, und
– falls Anzeige B_K und eine bestimmte Anzeige des Beteiligten C (nennen wir sie Anzeige C_Q) gleichzeitig waren,
dann ist auch garantiert, dass Anzeige A_J und Anzeige C_Q gleichzeitig waren.
Eng damit zusammen hängt übrigens die Transitivität von gegenseitiger Ruhe:
– falls A und B gegenüber einander ruhten, und
– falls B und C gegenüber einander ruhten,
dann ist auch garantiert, dass A und C gegenüber einander ruhten.
Im Übrigen ist es empfehlenswert und üblich, individuelle Beteiligte mit einfachen Großbuchstaben zu benennen, also z.B. A, B, usw.;
Ereignisse dagegen (zur Unterscheidung) durch Aufzählung derjenigen Beteiligten zu benennen, die daran gemeinsam teilgenommen hatten, also z.B. Ereignis ε_(AJ), Ereignis ε_(BK), usw.
> [Die Aussage] »Es gibt Ereignisse […], die hintereinander geschehen und dennoch beide zu einem entfernten Ereignis […] raumartig sind« [verstehe ich] hingegen nicht so recht.
Zumindest lässt sich das obige Beispiel zur Illustration dieser Aussage ausbauen:
Die beiden Ereignisse ε_(AJ) und ε_(CQ) sollen raumartig voneinander getrennt gewesen sein,
ein weiteres Ereignis ε_(CP) ist vorstellbar, an dem der Beteiligte C ebenfalls teilgenommen hatte, und das deshalb von Ereignis ε_(CP) zeitartig getrennt war,
aber so, dass ε_(AJ) und ε_(CP) raumartig voneinander getrennt waren.
@Joachim
»Das hellblaue Band […] beschreibt für jede beliebige Zeit, wo sich der Stab gerade befindet.«
Wo sich der Stab zu einer gegebenen Zeit gerade befindet, lässt sich aus dem hellblauen Band nicht ersehen. Schon zur Beurteilung, wo sich sich ein einzelnes punkthaftes Partikel zu einer bestimmten Zeit gerade auf seiner Weltlinie befindet, reicht es ja nicht hin, diese Weltlinie nur als unstrukturierte Punktmenge zu kennen.
Eine raumzeitl. Beschreibung des Stabes wird jedenfalls erhalten durch die Lösung einer Bewegungsgl. zu einer Anfangsbedingung, die sich am einfachsten im Ruhesystem des Stabes formulieren lässt. Durch die Wahl der Anfangsbed. ist die Lösung eindeutig bestimmt, und sie lässt sich vermittels Lorentz Boost dann auch in beliebig anderen Inertialsystemen darstellen, wo die Bewegung des Stabes, die in seinem Ruhesystem eine rein zeitartige ist, eine raumartige Komponente hat.
Wenn wir also sagen wollen, wo sich der Stab zu einer gewissen Zeit gerade befindet, dann müssen wir das mit Bezug auf eine solche Lösung tun, denn erst die liefert in eindeutiger Weise die dazu erforderliche Auskunft. Die Animation ist nun nichts anderes els die visuelle Veranschaulichung einer derartigen Lösung in ihrem (eigen-)zeitlichen Verlauf, und daran ist letztlich doch überhaupt nichts verwirrend. Die entsprechende Lösung in analytischer Form mit c=1 hatte ich ja wiederholt schon hingeschrieben; die Anfangsbed. für s=0 lässt sich daraus wieder rekonstruieren.
Die Animation zeigt insbesondere korrekt, wie die mittelblaue Linie geometrisch konstruiert wird, indem die einzelnen Punkte des Stabes die Strecke OC auf der x-Achse infolge seiner raumzeitl. Bewegung sukzessive passieren. Aus der Lösung der Bewegungsgl. lässt sich exakt berechnen, wie lange es im System S mit den Koordinaten (t,x) dauert, bis die mittelblaue Line vom rechten bis zum linken Endpunkt entstanden ist. Und diese positive Zeitspanne ist im Prinzip auch experimentell messbar mit S-synchronen Uhren, die an den Positionen x=0 und x=1/γ aufgestellt sind.
Die mittelblaue Linie ist folglich keinesfalls eine Momentaufnahme des Stabes zu irgendeiner Zeit. Das wird aber nicht ersichtlich, wenn man immer nur statische Bildchen betrachtet, in denen die raumzeitliche Bewegung des Stabes gar nicht wiedergegeben wird. Es sind gerade die Standbilder, die hier verwirren können, weil sie etwas unterschlagen und vor lauter Koordinaten sogar leicht den physikal. Hintergrund vergessen lassen, nämlich die relativist. Beschreibung der freien Fallbewegung eines inertialen Stabes.
@Chrys,
nein, Sie führen hier eine zweite Zeit ein, eine Art Metazeit, die eine Bewegung der Bewegung beschreibt.
Im Weg-Zeit-Diagramm ist die Zeit in eine Dimension (hier noch oben) bereits bedacht. Eine zweiter Zeitdimension ist unphysikalisch.
Der Kern der Relativität (übrigens nicht erst seit 1905) ist, dass derselbe Vorgang unterschiedlich beschrieben werden kann. Ein 1 Längeneinheiten langer ruhender Stab ist äquivalent zu einem 3/5 Längeneinheiten langen, 80% lichtschnellen Stab.
Die Bewegung wird durch die Anfangsbedingungen eindeutig beschrieben. Ob Sie diese bei t=0 oder t’=0 oder bei irgend einem anderen zeitartigen Schnitt durch die Raumzeit festlegen, ist Jacke wie Hose. Es darf keine rolle Spielen, welche Namen Sie den Raumzeit-Punkten geben.
@Axel Krüger
Sehen Sie sich mal in der oben beschriebenen Grafik die Ereignisse C und B an. Die passieren beide hintereinander an der Spitze des Zuges. In Koordinaten (x,t) ist C gleichzeitig mit O. In Koordinaten (x’,t’), also den mit dem Zug mitbewegten Koordinaten, ist B gleichzeitig mit O. Das meint “Gleichzeitigkeit ist relativ”.
Die Ereignisse C und B dagegen geschehen in jedem beliebigen Inertialsystem nacheinander an der Zugspitze. Sie sind in keinem Fall gleichzeitig, weil sie zeitartig getrennt sind.
@Frank Wappler
Sie betreiben Physik wie Literaturwissenschaft. Sie leiten aus ihren eigentümlichen Interpretationen von Einsteins Artikeln andere Bedeutungen für die Fachbegriffe her als in der Physik üblich. Das können Sie machen, Sie dürfen sich dann aber nicht wundern, wenn Sie nicht verstanden werden.
@ Frank Wappler – heute – 10:41
Zu Ihrem Link auf den Einstein-Aufsatz möchte ich meine Bemerkung v. vorgestern wiederholen, dass (die abs. Gleichzeitigkeit) wiederum schwer zu beweisen/messen ist. I.S.v. dass man um etwas für zutreffend (“wahr“) zu halten es auch (empirisch) beweisen/verifizieren (z.B. messen, “sehen“) muss/sollte – und möglichst _viel_ messen/verifizieren (von _vielen_ Menschen gesehen/verifiziert). Trotzdem wiederhole ich meine (unverfizierte?) Ansicht, dass es absolute Gleichzeitigkeit gibt (an verschiedenen Punkten des Raumes auf der/einer Hyperfläche) .. Ich hätte übrigens besser Gegenwarts-Hyperfläche schreiben sollen.
Ihr Beispiel Die beiden Ereignisse ε_(AJ) und ε_(CQ) sollen raumartig voneinander getrennt gewesen sein, ein weiteres Ereignis ε_(CP) ist vorstellbar, an dem der Beteiligte C ebenfalls teilgenommen hatte, und das deshalb von Ereignis ε_(CP) zeitartig getrennt war, aber so, dass ε_(AJ) und ε_(CP) raumartig voneinander getrennt waren bezieht sich offenbar auf/ist eine andere Variante von Herrn Schulzes Aussage (v. 12.2.) dass es Ereignisse A und C gibt, die hintereinander geschehen und dennoch beide zu einem entfernten Ereignis B raumartig sind. So recht verstehe ich aber auch das (Ihr Bsp.) noch nicht (mit *der Beteiligte C* meinen Sie den aus CQ?). Schulzes A und C entsprechen Ihren CQ und CP. AJ und CP sind raumartig getrennt – ebenso wie AJ und CQ. Zu Schulzes B sehe ich (im Augenblick) kein Analogon bei Ihnen.
Mein Schwerpunktgedanke ist halt, dass es (“absolute“) Gleichzeitigkeit gibt. Hintergrund ist z.B. die Idee/Assoziation, dass die Gegenwarts-Hyperfläche zeitlich SEHR kurz ist (“Planck-Zeit“), räumlich jedoch SEHR groß – um nicht zu sagen unendlich .. 😉 ..
Axel Krüger schrieb (14. Februar 2019 @ 17:28):
> Mein Schwerpunktgedanke […] Hyperfläche
Oh, na gut: “raumartige Hyperflächen” — jeweils eine Menge von Ereignissen, die alle (paarweise) gegenüber einander raumartig voneinander getrennt waren,
und die (im Flachen) durch Verhältnisse von “Raumzeit-Intervall”-Werten s^2 bzw. (allgemeiner, d.h. insbesondere im Krummen) z.B. durch Verhältnisse von Werten der “Syngeschen Weltfunktion” σ^2 oder (noch allgemeiner) durch Verhältnisse von Werten “chronometrischer Distanz” χ noch genauer beschrieben werden können.
Eine gegebene “raumartige Hyperfläche” kann dabei entweder “hyper-eben” sein, d.h.
– jeweils drei Ereignisse gegenüber einander (“Kerzen”-)gerade sein, bzw.
– jeweils vier Ereignisse gegenüber einander (“Tisch”-)eben sein, bzw.
– jeweils fünf Ereignisse gegenüber einander (“Euklidisch”) flach sein,
oder, ansonsten, nicht.
Wobei es für jeweils ein Ereignis recht offensichtlich zahlreiche verschiedene “hyper-ebene Hyperflächen” gibt, zu denen es gehört. (Im einfachsten Falle also: verschiedene raumartige Geraden “durch” jeweils einen Raumzeit-Punkt.)
Es dürfte auch Transitivität hinsichtlich der gemeinsamen Mitgliedschaft von je zwei Ereignisse in jeweils einer bestimmten “hyper-ebenen Hyperfläche” gelten (soweit ich das richtig überblicke).
> […] Gegenwarts-Hyperfläche
Bezüglich jeweils einer bestimmten “hyper-ebenen Hyperfläche” (im einfachsten Falle also: bezüglich jeder raumartigen Geraden) lässt sich in jedem ihrer Punkte/Ereignisse eine eindeutig bestimmte zeitartige Gerade als “zeitartige Normale” finden.
Und von jeder zeitartigen Kurve, die einen bestimmten Punkt einer bestimmten “hyper-ebenen Hyperfläche” enthielt, ließe sich wiederum feststellen, ob sie die entsprechende “zeitartige Normale” in diesem Punkt “(nur) berührte”, oder “schnitt”.
Zu jedem Punkt einer (“Knick-freien”) zeitartigen Kurve lässt sich demnach eine eindeutige “hyper-ebene Hyperfläche” bestimmen — meinetwegen die (eindeutige) “Gegenwarts-Hyperfläche” dieser Kurve, bzgl. dieses Punktes.
Aber: ich finde es (trotzdem) problematisch bis falsch, in diesem Zusammenhang von “Gleichzeitigkeit” zu sprechen …
Joachim Schulz schrieb (14. Februar 2019 @ 16:49):
> Sehen Sie sich mal in der oben beschriebenen Grafik die Ereignisse C und B an. Die passieren beide hintereinander an der Spitze des Zuges.
Im obigen SciLogs-Artikel war zwar von einem “Stab” die Rede, und von dessen “rechter Spitze“.
Da dieser identifizierbare materielle Punkt (Beteiligte) offenbar bedeutsam sein soll, wäre es dem Verständnis gewiss förderlich, diesen in einer Grafik, in der er dargestellt ist, auch ausdrücklich zu benennen (vorzugsweise mit einfachen Großbuchstaben, wie es Einstein bekanntlich vorgemacht hat);
und besonders relevante Ereignisse, an denen er teilgenommen hatte, so zu benennen, dass an deren Namen ablesbar ist, dass er daran teilgenommen hatte, und wer daran jeweils außerdem teilgenommen hatte.
> In Koordinaten (x,t) ist [Ereignis] C gleichzeitig mit [Ereignis] O. […]
Das Wort “gleichzeitig” in diesem Satz entspricht jedenfalls nicht dem Sinn von Gleichzeitigkeit in Einsteins Definition (1916/17),
da dort weder ein Zusammenhang mit Koordinaten hergestellt wird, noch Gleichzeitigkeit Paaren von ganzen Ereignissen zugeschrieben wird (sondern lediglich den “Blitzeinschlags”-Anzeigen bestimmter Beteiligter).
p.s.
Joachim Schulz schrieb (14. Februar 2019 @ 16:59):
> Sie betreiben Physik wie Literaturwissenschaft. […]
Vor allem: wie SciLogs-Blogging.
@Joachim / 14. Februar 2019 @ 16:40
Der Zeitparameter bei einer Bewegungsgl. für zeitartige Bewegung* in der Raumzeit ist grundsätzlich die von mitbewegten Uhren angezeigte Eigenzeit. Eigenzeit — und nicht etwa Koordinatenzeit — ist das für die raumzeitliche Bewegung “materieller” Objekte einzig relevante Konzept von Zeit. Bei der zughörigen Bewegungsgl. wird schliesslich nicht nach einer Koordinatenzeit t abgeleitet, stattdessen enthält die in Koordinaten ausformulierte Bewegungsgl. hier Ableitungen d²t/ds² der Koordinatenzeit t nach der Eigenzeit s.
Die Animation veranschaulicht durch ihren zeitlichen Ablauf einfach nur die durch Eigenzeit parametrisierte Bewegung des Stabes in der Raumzeit. Da ist keine »Bewegung zu viel«, denn ein Standbild der Raumzeit bei eingefrorener Eigenzeit drückt noch überhaupt keine Bewegung aus. Eine auf den Holzweg führende gedankliche Weichenstellung passiert meines Erachtens hier:
»Im Weg-Zeit-Diagramm ist die Zeit in eine Dimension (hier noch oben) bereits bedacht. Eine zweiter Zeitdimension ist unphysikalisch.«
Ein Raumzeit-Diagramm ist eben kein Raum-Zeit-Diagramm oder Weg-Zeit-Diagramm. Beim Raum-Zeit-Diagramm ist der als x-Achse dargestellte `Raum’ der Konfigurationsraum, wo sich etwas bewegt, wenn die auf der t-Achse abgetragene `Zeit’ vergeht. Im Raumzeit-Diagramm ist hingegen die als (t,x)-Ebene dargestellte Raumzeit selbst der Konfigurationsraum, wo sich etwas bewegt, wenn die auf gar keiner Achse abgetragen Eigenzeit vergeht.
*Hier im betonten Unterschied zu lichtartiger Bewegung, die mangels Eigenzeit einen Sonderfall darstellt.
Chrys schrieb (15. Februar 2019 @ 15:32):
> Eigenzeit s […] ist das für die raumzeitliche Bewegung “materieller” Objekte einzig relevante Konzept von Zeit.
> […] Ableitungen d²t/ds² der Koordinatenzeit t nach der Eigenzeit s.
Ich weise erneut auf Einsteins grundlegende Setzung des “Zeit“-Begriffes in der Relativitätstheorie hin:
Bezüglich “Stellung(en) des kleinen Zeigers einer Uhr” bzw. bezüglich den (unterscheidbaren) Anzeigen eines (identifizierbaren) materiellen Objektes/Beteiligten lassen sich keine Ableitungen bilden, geschweige denn auswerten,
weil eine Differenz, die im Nenner eines Ausdruckes auftritt, dessen Grenzwert als (Wert der) Ableitung bezeichnet wird, für “Stellung(en) des kleinen Zeigers einer Uhr” überhaupt nicht definiert ist.
“Stellung(en) des kleinen Zeigers einer Uhr” bzw. die “Anzeigen” eines bestimmten Beteiligten A stellen an sich keinen Vektorraum dar, sondern lediglich eine (geordnete) Menge 𝒜.
Weiterhin, falls
s : 𝒜 → ℝ
eine gute reelle Parametrisierung der Anzeigenmenge 𝒜 eines bestimmten Beteiligten A sein soll, d.h. so dass für je drei verschiedene seiner Anzeigen, A_J, A_K, A_Q ∈ 𝒜 erfüllt ist:
(s[ A_K ] – s[ A_J ]) =
(s[ A_Q ] – s[ A_J ]) * (τA[ _J, _K ] / τA[ _J, _Q ]),
wobei (τA[ _J, _K ] / τA[ _J, _Q ]) das reell-wertige Verhältnis der entsprechenden Dauern As bezeichnet,
dann ist p : 𝒜 → ℝ
mit p[ A_X ] ↦ s[ A_X ] * K
für alle Anzeigen A_X ∈ 𝒜 und für irgendwelche (nicht mal unbedings relle, und nicht mal unbedingt von Null verschiedene) Konstanten K
ebenfalls eine gute Parametrisierung der Anzeigenmenge 𝒜 dieses bestimmten Beteiligten A.
(Die Bezeichnung dieser Konstante als “K” soll dabei selbstverständlich an deren Auftauchen bei Gourgoulhon, “Probeseiten”, eq. (2.11) erinnern. Sofern bezüglich irgendeiner solchen guten Parametriesierung p der Anzeigenmenge 𝒜 dieses bestimmten Beteiligten A Ableitungen “gebildet” und ausgewertet werden sollen, wäre allerdings ausdrücklich zu fordern, dass K von Null verschieden ist, und dass die Parametrisierung s schon von vornherein verschiedenen Anzeigen As ungleiche relle Zahlenwerte zugeordnet hat.)
“Eigenzeit s” ist demnach offenbar nicht “das einzige“ für die raumzeitliche Bewegung eines bestimmten “materiellen” Objektes relevante “Konzept von Zeit“,
sondern (lediglich) irgendein (rell-wertiger) Repräsentant der Äquivalenzklasse von guten Parametrisierungen der Zeiten/Anzeigen dieses Beteiligten.
Darüberhinaus soll und muss die in Betracht gezogene “Koordinatenzeit t” ja eine ganz außerordentlich erlesene Art der Koordinaten-Bestreuselung der Anzeigenmenge 𝒜 sein, damit die o.g. Ableitungen überhaupt existieren.
p.s.
> […] Unterschied zu lichtartiger Bewegung, die mangels Eigenzeit einen Sonderfall darstellt.
Es erscheint in diesem Sonderfall schon von vornherein problematisch bis falsch überhaupt von “Bewegung” zu sprechen, weil bzw. sofern dem Austausch von Signalen dadurch ein bestimmter “Weg (der Signalfront)” zugeschrieben würde.
p.p.s.
Im Übrigen bin ich der Meinung, dass man nicht “Länge des Zuges” sagen soll, wenn man “Länge des Bahnsteigs” meint.
@ Joachim Schulz – vorgestern – 16:49
Sehen Sie sich mal in der oben beschriebenen Grafik die Ereignisse C und B an. Die passieren beide hintereinander an der Spitze des Zuges. *Hintereinander* meint hier an verschiedenen Orten (C bei C, B bei A). Und zur gleichen Zeit – möchte man meinen (da A zeitgleich mit C liegt). Müsste A aber nicht da eingezeichnet sein wo B ist und von dort eine waagerechte Linie auf die ct’ Achse führen? Andererseits kann man es sich aber auch so vorstellen, dass die Zugspitze bereits am Ortspunkt 1‘ ist – zum Zeitpunkt (ungf.) 0.6 auf der ct‘ Achse [“eigtl.“ auch der ct-Achse (riskante Aussage von mir); aber ct und x sowie ct‘ und x‘ sind eben verschiedene Koordinaten- bzw. Bezugssysteme] – während das (sich noch nicht in Bewegung gesetzt habende) Zugende sich noch am Orts- u. Zeitpunkt 0 befindet. O→C ist der stehende Zug (Standbild, “Blitzlichtaufnahme“) – alle Atome an unterschiedlichen Orten zur gleichen Zeit. Bei O→B ist das Ende/sind die letzten Atome (0) des Zuges (noch) am gleichen Ort zur gleichen Zeit, während B = die Atome der Zugspitze bereits losgefahren, also an einem anderen Ort zu einer anderen Zeit sind.
Sollte es (im Blogtext) bei Während die dunkelblaue Linie durch die schwarze x-Achse durchläuft, färbt sie den berührten Punkt dieser Achse Mittelblau nicht besser heißen: … färbt sie die berührten Punkte …? Bei Da B und C nicht derselbe Punkt sind, ist es auch nicht überraschend, dass zwei unterschiedliche Längen herauskommen. Beide Längen sind invariante (ax ?) Abstände zwischen zwei Raumzeit-Punkten klingen *unterschiedliche Längen* und *beide Längen sind invariante Abstände* für mich paradox (invariant als unveränderlich verstanden). Meinen Sie vll. *_jeweils_ beide Längen sind invariante Abstände* (jeweils = O→C und O→B)? Oder meinen Sie mit invariant C→A (was aber dann nur _eine_ Länge wäre)?
Das (Blogtext) Die Animation kann aber leicht so gelesen werden, als gäbe es eine übergeordnete Zeit, die den mittelblauen Schnitt durch das Raum-Zeit-Diagramm erst erzeugt. Als sei die durch die dunkelblaue Linie dargestellte Gleichzeitigkeit der eigentliche, wirklich existierende Stab. Als würde die mittelblaue nur durch Durchlaufen der dunklen Line erzeugt verstehe ich nicht so recht. Das Jeder Punkt der mittelblauen Line stellt aber genau eine Momentaufnahme eines Atoms des Stabes dar. Und daran ändert sich nichts. Zur Zeit t=0 befindet sich zwischen den Punkten O und C je ein Teil des Stabes entspricht meiner obigen Bem.: *O→C ist der stehende Zug (Standbild, “Blitzlichtaufnahme“) – alle Atome an unterschiedlichen Orten zur gleichen Zeit*.
Ich wiederhole nochmal dass ich der Meinung bin, dass es (absolute) Gleichzeitigkeit gibt (wobei abs. G. nicht mit abs. Zeit zu verwechseln ist). Ich sage aber ja auch, dass zum Beweis (nach-) gemessen werden sollte. Was jedoch wiederum aufgrund der begrenzten Licht- bzw. Informations-/Messdatenübertragungszeit schwierig ist. Absolute Zeit war (ist – insf.) wie Sie in https://scilogs.spektrum.de/quantenwelt/einsteins-blinddarm-der-kern-der-relativit-tstheorie/ (richtig) schreiben, nur Metaphysik.
Jedenfalls ein Thema mit vielen (komplizierten) Aspekten, Standpunkten/Ansichten, “Bezugssystemen“ – und unterschiedlichem Fachwissen.
Gibt es eine (absolute) Realität? .. 😉 ..
@Frank Wappler / 16. Februar 2019 @ 05:12
»Ich weise erneut auf Einsteins grundlegende Setzung des “Zeit“-Begriffes in der Relativitätstheorie hin: … dass ich an Stelle von “Zeit” die “Stellung des kleinen Zeigers meiner Uhr” setze.«
“We make this concept of time more concrete by assuming the existence of standard clocks, which may be carried by material particles, and the ticking of which provides a measure of proper time. Since this is the only time of basic importance in relativity, we shall drop the adjective proper and refer to it simply as time. […] Later we may have occasion to refer to coordinate time; there should be no confusion.”
—John L. Synge (1960)
Chrys schrieb (16. Februar 2019 @ 16:38):
> »We make this concept of time more concrete by assuming the existence of standard clocks […]« —John L. Synge (1960)
Diese Eselei ist nicht nur “nice” zurückzuweisen, sondern “kategorisch”:
Wenn ich könnte, würde ich ja eine andere Animation erstellen und zwar eine, bei der man sieht, was bei einer Transformation vorgeht – also das Verzerren der Achsen – und dann noch eine, bei welcher man sieht, wie man überhaupt feststellen kann, warum Uhren unterschiedlich gehen. Für unterschiedlich gehende Uhren ist es nämlich erforderlich, dass sich die Referenzstrecke auf welcher eine Frequenz gemessen wird im Gegensatz zu Wellenlängen und Periodendauern nicht ändert. Alternativ könnte man natürlich auch behaupten, dass sich statt der Wellenlängen und Periodendauern der zu messenden Frequenz diese Referenzlänge ändert, aber das wäre eher unwahrscheinlich, würde ich sagen. Fakt für mich ist jedenfalls, dass midestens eine der beiden Strecken (Wellenlänge oder Referenzstrecke) der sRT nicht gehorcht und Uhren nur deswegen “relativistischen Effekten” unterliegen. Ansonsten gäbe es hier nicht viel mehr zu sagen, als in den Themen zuvor – der Hinweis auf den Kreisbezug also, der hier nach wie vor nicht gesehen werden will.
Vielen Dank für die interessanten Beiträge und Anmerkungen. Mein Beitrag zum Thema steht in diesem Artikel und den älteren Artikeln, auf die ich explizit oder implizit aufbaue. Haben Sie deshalb Verständnis, dass ich auf einzelne Einwände nur dann eingehen werde, wenn sie mir neu erscheinen.
Ich habe sie aber zur Kenntnis genommen und werde ggf. in zukünftigen Artikeln darauf zurückkommen.
Meiner Ansicht nach kann man die Längenkontraktion in einem Epstein-Diagramm anschaulicher als in einem Minkowski-Diagramm darstellen, weil die Koordinatensysteme beider Bezugssysteme jeweils rechtwinklig sind.
Eine Animation halte ich für didaktisch sinnvoll, auch wenn sie redundant zur grafischen Darstellung der Zeit ist, weil man sich dann den Zeitablauf besser vorstellen kann.
@Anonym 2019:
Am besten finde ich solche Animationen, in welchen eine Lichtquelle und eine zu dieser bewegte Leinwand dargestellt werden. Im Ruhesystem der Leinwand bewegt sich das Licht gegenüber der Quelle dann mit c±v und im Ruhesystem der Quelle bewegt es sich plötzlich gegenüber der Leinwand mit c±v und kein Mensch weiß wirklich, wie dieses Phänomen in der Realität funktionieren soll.
Ich möchte noch einmal auf die Kommentarregeln hinweisen:
Bitte bleiben Sie beim Thema. Es geht hier um die didaktischen Schwierigkeiten, die entstehen, wenn man ein Raum-Zeit-Diagramm zu animiert.
Und ich möchte noch einmal darauf hinweisen, dass Herr Schulz hier ein drakonisches Zensur-Regime führt das jeglichem wissenschaftlichen Geist Hohn spricht.
Dies hier ist eine Gebetsplattform für “Relativitätsgläubige” und “Wissenschaftskriegern” von “relativ-kritisch” und ähnlichen Honeypot – sonst nichts.
Bitte lesen Sie schnell .. ist gleich wieder weg. 🙁
@NvB 11:05 dies ist ein “Hobbyblog” mit einer “Hobbydiskussion” für Physikinteressierte.
Wenn Du so eine dolle Konifere bist, reich doch Deine Trollerei ganz einfach zur Prüfung ein.
Erledigt sich in ein paar Wochen, deswegen mußt Du nicht jahrelang das Internet belästigen.
Und: warum? gehst Du Leuten auf den Keks, die die Miß-Phantastereien nicht hören wollen.
@Senf:
Warum hälst du nicht einfach deinen unflätigen Mund?
Das erledigt sich nämlich überhaupt nicht, weil es gegen die RT und den Urknall geht und deswegen kaum ein Peer-Rewiew schafft, aber selbst davon weißt du nichts.
Weil ihr dummschwätzenden Relativisten mir auf den Keks geht mit eurer arroganten Besserwisserei und hilflosem Herumgelabere, wenns ans Eingemachte geht.
@Nicht von Bedeutung
21. März 2019 @ 17:05
Es zwingt Sie doch niemand, dieses Blog zu lesen, wenn es Ihnen so “auf den Keks geht”. Ich habe kein Problem damit, dass sich nicht jeder für die Relativitätstheorie interessiert.
@Joachim Schulz:
Das ist nicht ganz korrekt. Immerhin stehe ich unter dem selben Zwang, wie Sie. Sie müssen Ihr RT-Wissen auch imer zum Besten geben und dabei kläglich an einfachsten physikalischen Zusammenhängen scheitern, wie jeder Relativist. Flacherdler haben btw. auch kein Problem damit, wenn sich Leute nicht mehr für eine flache Erde interessieren, aber trotzdem gehen sie anderen auf den Keks -ist das nicht komisch? Auf keiner physikalische Platform findet tatsächlich eine gemäßigte Diskussion zwischen Relativisten und ihren Kritikern statt, was auch nicht schlimm ist. Aber haben Sie auch die Beteiligungen an Physikforen und Blogs im Auge? Ach ja, ich vergas – Ihr Forum haben Sie ja aus Zeitgründen auch geschlossen und ich denke mal, der zweite Grund war, dass auch da die Beteiligung nicht besonders hoch war. Das ist ja auch kein Wunder, wenn man sich in solchen Gefilden immer nur selbst beweihräuchert und sich dabei in die Tasche lügt.