Gravitationswellendetektoren: wie sie funktionieren (GW Teil 2)
BLOG: RELATIV EINFACH

Gravitationswellendetektoren sind in aller Munde. Dass es am 11. Februar mehrere Pressekonferenzen zum Thema aktueller Stand der Gravitationswellenforschung gibt, ist mittlerweile offiziell. Dass es darum gehen wird, den ersten direkten Nachweis solcher Wellen zu verkünden, ist höchstwahrscheinlich. Für all diejenigen, die sich auf den Donnerstag und auf eine nobelpreisträchtige Bekanntmachung freuen, hier nochmal ein Crashkurs Gravitationswellen.
In Was sind eigentlich Gravitationswellen? hatte ich gezeigt, wie Gravitationswellen auf eine einfache Teilchenanordnung wirken. Mein Beispiel war ein Kreis frei im All schwebender Teilchen; läuft eine Gravitationswelle senkrecht von hinten durch das Bild auf den Betrachter zu, ändern sich die Teilchenabstände wie in dieser Animation dargestellt:
Das Ausmaß der Verformung ist dabei freilich extrem übertrieben. Eine realistische Welle würde selbst den riesigen Abstand von der Erde zur Sonne lediglich um eine Strecke verlängern bzw. verkürzen, die kleiner ist als der Durchmesser eines Wasserstoffatoms.
Wie kann man so etwas nachweisen?
Die ersten Versuche, solche winzigen Verzerrungen nachzuweisen, gehen auf Joseph Weber in den 1960er Jahren zurück. Rhythmische Abstandsänderungen sollten auch Festkörper (wo die Gravitationswelle gegen die den Körper zusammenhaltenden Kräfte “anarbeiten” muss) in winzige Schwingungen versetzen. Weber war sogar der Meinung, diesen Nachweis geliefert und Gravitationswellen gemessen zu haben. Die Physiker, die seine Experimente in verbesserten Versionen nachbauten und Webers Daten prüften, kamen allerdings zu dem Schluss, dass das nicht stimmen konnte. Weber starb im Jahre 2000, durchaus verbittert ob der fehlenden Anerkennung dessen, was er nach wie vor für seine Entdeckung hielt.
Zu jenem Zeitpunkt hatten die Physiker allerdings längst begonnen, ein anderes Nachweiskonzept zu verfolgen. Den ersten Teil davon kann man verstehen, wenn man sich nicht nur anschaut, wie eine Gravitationswelle auf nebeneinander im Raum schwebende Teilchen wirkt, sondern wenn man Licht von einem dieser Testteilchen zum anderen schickt und nachschaut, wie eine Gravitationswelle solch ein System beeinflusst.
Gravitationswellen wirken auf Lichtpulse
Hier ist die grundlegende Anordnung, zunächst noch ohne Gravitationswelle: Lichtteilchen, vereinfacht durch rote Kreise dargestellt, laufen von einem Sender (rechts) zu einem Empfänger (links). Jedesmal, wenn ein Lichtteilchen ankommt, blinkt die Leuchte am Empfänger auf:  Da die Teilchen in ganz regelmäßigen Zeitabständen abgeschickt werden, treffen sie beim Empfänger auch ganz regelmäßig ein, und der Blink-Rhythmus bleibt immer derselbe.
Da die Teilchen in ganz regelmäßigen Zeitabständen abgeschickt werden, treffen sie beim Empfänger auch ganz regelmäßig ein, und der Blink-Rhythmus bleibt immer derselbe.
Jetzt schicken wir eine Gravitationswelle von hinten nach vorne durch diese Anordnung. Unsere Kamera halten wir dabei immer auf den Empfänger gerichtet; der bleibt im Bild, wo er ist, und alle anderen Abstände ändern sich entsprechend dem Einfluss der Gravitationswelle:  Dabei ändert sich wiederum der Abstand der zwei frei fliegenden Teilchen, nämlich der Abstand des Senders vom Empfänger. Ganz analog dazu, als ob wir in der Animation oben jetzt nur noch den Mittelpunkt (hier: Empfänger) und das Teilchen im Kreis ganz rechts (hier: Sender) betrachten würden.
Dabei ändert sich wiederum der Abstand der zwei frei fliegenden Teilchen, nämlich der Abstand des Senders vom Empfänger. Ganz analog dazu, als ob wir in der Animation oben jetzt nur noch den Mittelpunkt (hier: Empfänger) und das Teilchen im Kreis ganz rechts (hier: Sender) betrachten würden.
Auch die Abstände hintereinander laufender Lichtteilchen ändern sich, und das hat sichtbare Folgen: Beim Empfänger blinkt die Leuchte abwechselnd etwas schneller und etwas langsamer. An diesem wechselnden Muster kann man den Einfluss der Gravitationswelle nachweisen.
Solche Effekte sind Grundlage der Pulsar-Timing-Methode, wie sie z.B. die Kollegen vom Max-Planck-Institut für Radioastronomie verfolgen. Dabei nutzt man aus, dass wir von sogenannten Pulsaren (rotierende, Radiowellen aussendende Neutronensterne) Radiopulse empfangen, deren Regelmäßigkeit es mit den besten irdischen Atomuhren aufnehmen kann. Die Änderungen der Ankunftszeiten sind dabei aber extrem gering – einige Dutzend Milliardstel Sekunden über ein halbes Jahr hinweg – und bislang ist es noch nicht gelungen, auf diese Weise Gravitationswellen nachzuweisen.
Um Gravitationswellen hier auf der Erde nachzuweisen, reicht unser Gedankenexperiment noch nicht ganz. Aber wir sind auf dem richtigen Wege.
Interferometrische Gravitationswellendetektoren
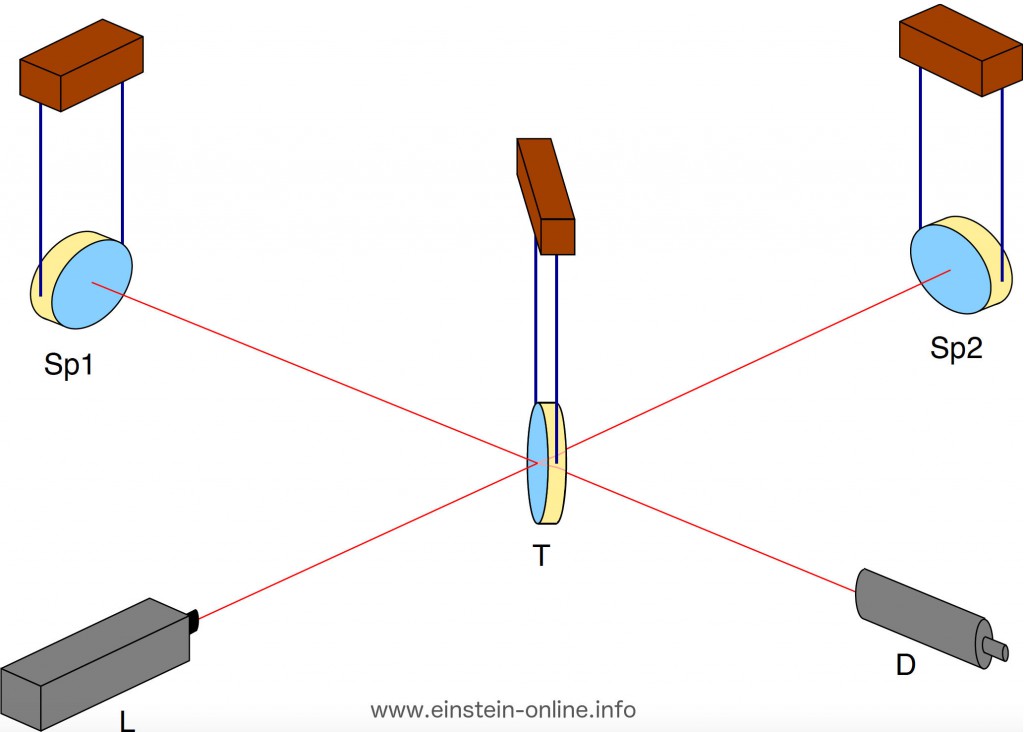
Verändern wir die einfache Situation wie folgt. Hier ist die grundlegende Anordnung für diejenige Sorte von Gravitationswellendetektoren, zu der auch der US-amerikanische LIGO gehört, perspektivisch dargestellt:
Von der Lichtquelle L aus laufen die Lichtpulse zu einer Art Weiche T, dem Strahlteiler. Die Hälfte der dort ankommenden Pulse läuft geradeaus weiter zum Spiegel Sp2. Die andere Hälfte wird um 90 Grad abgelenkt und läuft zum Spiege Sp1. Nach einer bestimmten Laufstrecke treffen die Pulse auf einen der Spiegel, werden dort reflektiert und wieder zum Strahlteiler zurückgeworfen.
Auch von den aus Richtung Sp1 (oder Sp2) bei T ankommenden Pulsen wird eigentlich nur die Hälfte zum Lichtdetektor D geleitet, die andere Hälfte zurück zur Lichtquelle L. Wir ignorieren diese zweite Strahlteilung, weil sie für das Grundprinzip keine Rolle spielt, und tun so, als würden all von Sp1 oder Sp2 bei T ankommenden Pulse direkt zum Lichtdetektor D gelenkt.
(Um Verwirrung zu vermeiden bezeichne ich D als “Lichtdetektor”; wenn ich von “Detektor” ohne Zusatz rede, ist die gesamte Anordnung gemeint, inklusive Lichtquelle, Spiegeln und allem Drumherum.)
Spiegel und Strahlteiler betrachten wir als freie Teilchen, deren Abstände von der Gravitationswelle beeinflusst werden. Der Lauf der Lichtpulse wird, ähnlich wie oben, natürlich auch beeinflusst.
Das ganze ist eine Variation eines sogenannten Michelson-Interferometers. Warum wir jetzt zwei Lichtbahnen haben und das Licht am Ende wieder zusammenführen wird weiter unten noch deutlich.
In wirklichen Detektoren sind die Abstände zwischen Strahlteiler und Spiegeln sehr groß – bei den größten heutigen Detektoren im Kilometerbereich – während Lichtquelle und Detektor recht nahe am Strahlteiler sitzen. Wichtig wird der Einfluss der Gravitationswelle daher zwischen T und Sp1 bzw. Sp2. Diese Laufstrecken, T–Sp1 bzw. T–Sp2 nennt man die Arme des interferometrischen Detektors.
Lichtpulse im Detektor
Schauen wir uns jetzt an, wie Lichtpulse durch solch einen Detektor laufen. Hier ist eine Momentaufnahme der schematischen Darstellung, die dann im Anschluss als Animation kommt, hier erstmal noch ganz ohne Lichtpulse: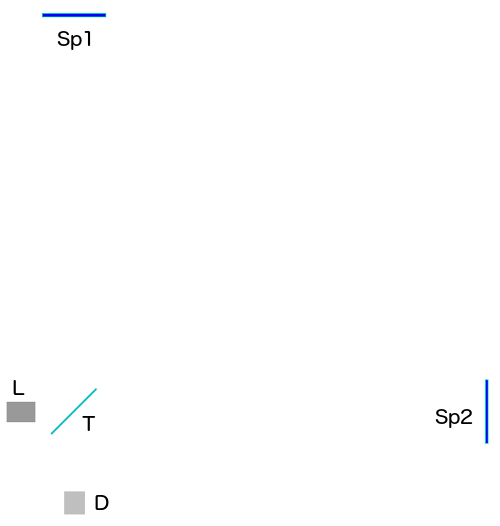 Der diagonale Strich T links unten ist der Strahlteiler, der jeweils nur die Hälfte der auftreffenden Teilchen durchlässt und die andere Hälfte reflektiert. Die dunkelblauen Striche Sp1 oben und Sp2 rechts sind die beiden Spiegel am Ende der Arme. Der graue Kasten L links ist die Lichtquelle, der graue Kasten D unten ist der Lichtdetektor.
Der diagonale Strich T links unten ist der Strahlteiler, der jeweils nur die Hälfte der auftreffenden Teilchen durchlässt und die andere Hälfte reflektiert. Die dunkelblauen Striche Sp1 oben und Sp2 rechts sind die beiden Spiegel am Ende der Arme. Der graue Kasten L links ist die Lichtquelle, der graue Kasten D unten ist der Lichtdetektor.
Jetzt lasse ich Lichtteilchen durch die Anordnung laufen, zunächst noch ohne Gravitationswelle. Damit man die Pulse unterscheiden kann, die zum oberen und zum rechten Spiegel gelaufen sind, habe ich sie unterschiedlich eingefärbt, rot und grün. (In Wirklichkeit läuft durch beide Arme die gleiche Art von Licht!) Ein zweiter Kunstgriff: Damit die Pulse auf dem Hin- und Rückweg nicht übereinander laufen (unübersichtlich!) habe ich sie künstlich etwas versetzt. Im senkrechten Arm beispielsweise laufen die Pulse auf dem Hinweg links, auf dem Rückweg rechts. Das ist in Wirklichkeit natürlich nicht so.
Hier ist die Animation: 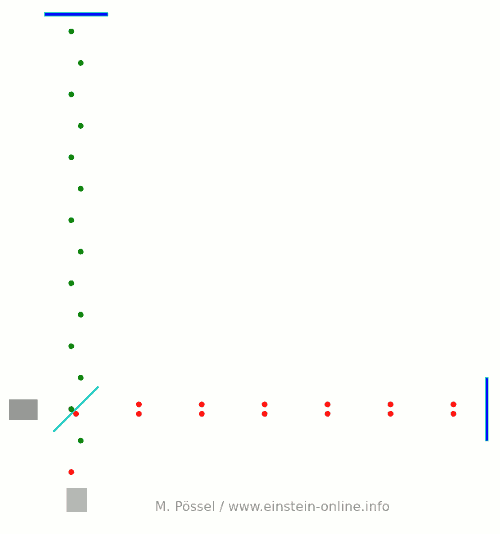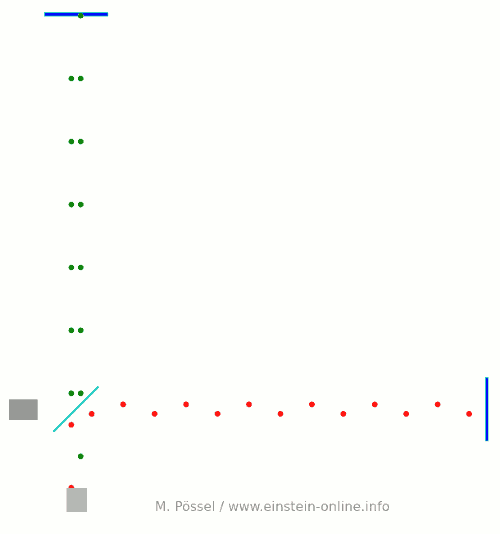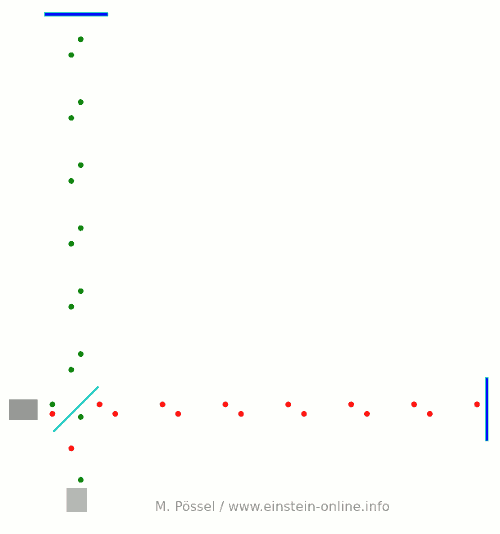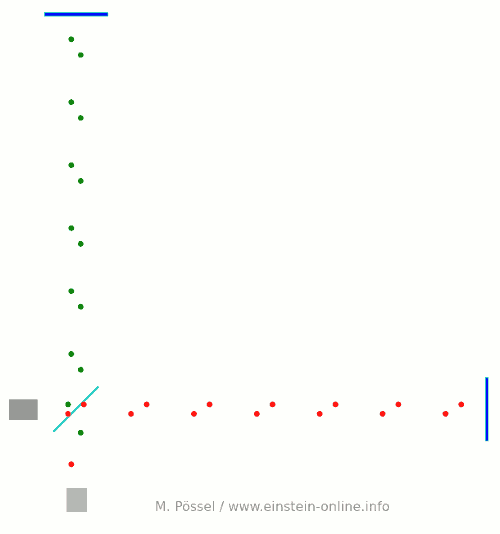 An der Lichtquelle laufen die Pulse gleichzeitig los. Aber die Länge des waagerechten Arms ist ein ganz kleines bisschen größer, so dass die roten Lichtpunkte etwas länger brauchen, um beim Detektor anzukommen. Die Längendifferenz ist gerade so gewählt, dass die roten und grünen Lichtpunkte unten am Detektor gerade abwechselnd eintreffen, rot, grün, rot, jeweils mit gleichem Abstand.
An der Lichtquelle laufen die Pulse gleichzeitig los. Aber die Länge des waagerechten Arms ist ein ganz kleines bisschen größer, so dass die roten Lichtpunkte etwas länger brauchen, um beim Detektor anzukommen. Die Längendifferenz ist gerade so gewählt, dass die roten und grünen Lichtpunkte unten am Detektor gerade abwechselnd eintreffen, rot, grün, rot, jeweils mit gleichem Abstand.
In diesem Diagramm sind die Ankunftszeiten der roten (waagerechter Arm) und grünen (senkrechter Arm) Punkte aufgetragen:
Auf der x-Achse ist dabei die Zeit aufgetragen (Zeiteinheit ist “Nummer des Einzelbildes der Animation”). Dass in dieser Konfiguration die Pulse jeweils abwechselnd ankommen, in gleichem zeitlichen Abstand voneinander, wird nachher noch wichtig.
…und jetzt mit Gravitationswelle
Jetzt lassen wir eine Gravitationswelle durch den Detektor laufen, wieder von hinten nach vorne, senkrecht zum Bild, auf den Beobachter zu. Was dabei passiert, zeigt die folgende Animation: 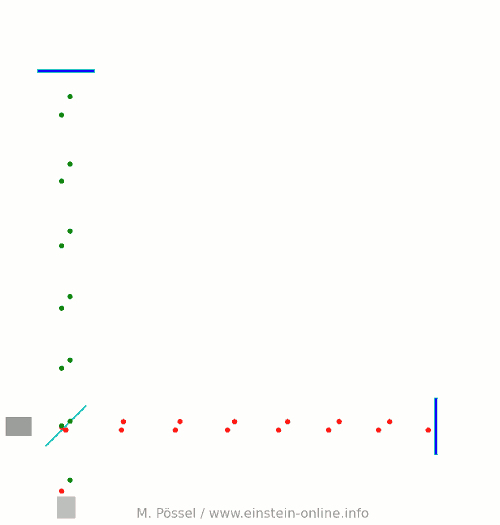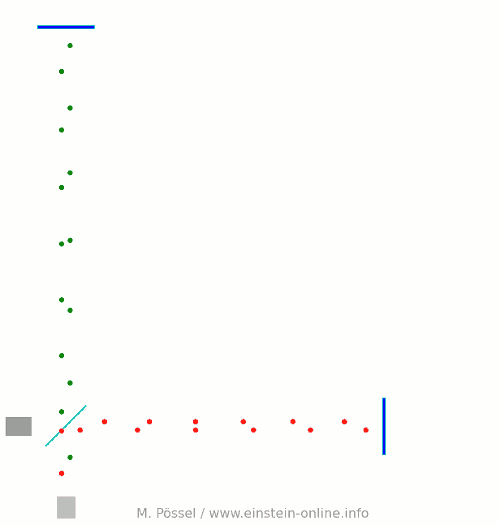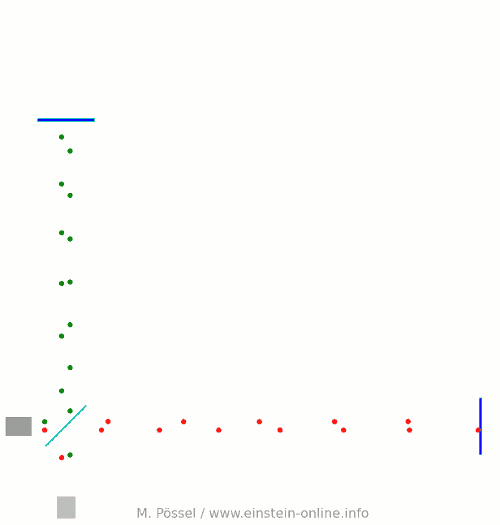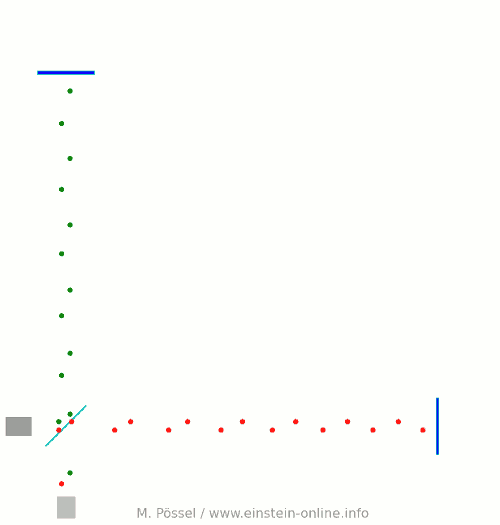
Entscheidend ist wieder, was beim Lichtdetektor ankommt. Dort kommen die grünen und roten Lichtpunkte – die den einen bzw. anderen Arm durchlaufen haben – manchmal gleichzeitig an, manchmal gegeneinander versetzt. Zur Erinnerung: Ohne Gravitationswellen waren die grünen und roten Lichtpunkte nur versetzt angekommen, immer schön abwechselnd.
Die Gravitationswelle verändert also, was da geschieht. Zum einen, weil sich die Armlänge ändert und damit die Laufzeiten der Pulse in jedem Arm, zum anderen, weil sich auch der Abstand aufeinanderfolgender Pulse durch die Gravitationswelle ändert (genau letzteres passiert übrigens auch bei der kosmischen Rotverschiebung).
[Nachtrag 12.5.16: Um sich ändernde Abstände in einer Animation darzustellen, muss ich wieder – willkürlich – einen Bezugspunkt wählen, dessen Position sich im Bild nicht verändert. Ich habe den Strahlteiler gewählt. Jede andere Wahl wäre aber physikalisch genau so gültig. Strenggenommen verändern sich auch die Abstände zwischen Detektor und Strahlteiler, und zwischen Laser und Strahlteiler. Da dieser Effekt bei wirklichen Detektoren sehr klein ist und keine Rolle spielt, habe ich diese Änderung in meiner Animation vernachlässigt.]
Hier ist das entsprechende Ankunftszeit-Diagramm für die grünen und roten Pulse:  Ungefähr da, wo ich den lila Pfeil eingemalt habe, kommen die Pulse so gut wie gleichzeitig an. Das war ohne Gravitationswelle nicht der Fall.
Ungefähr da, wo ich den lila Pfeil eingemalt habe, kommen die Pulse so gut wie gleichzeitig an. Das war ohne Gravitationswelle nicht der Fall.
Interferenz
Wenn Sie möchten, können Sie diesen Abschnitt überspringen und durch die Aussage ersetzen “…und diese unterschiedlichen Licht-Ankunftszeiten können die Forscher mithilfe der Welleneigenschaften von Licht nachweisen”. Dann springen Sie bitte direkt zur Zusammenfassung “Und jetzt tausendmal komplizierter”.
Wenn Sie verstehen wollen, wie das mit den Wellen funktioniert: hier kommt noch das letzte Puzzlestück.
Ich habe zwar mit Lichtteilchen argumentiert, weil das einfacher zu veranschaulichen ist. Licht hat aber (auch) Welleneigenschaften, mit Wellenbergen und Wellentälern (des elektrischen bzw. des magnetischen Felds), die aufeinander folgen. Die obigen Animationen kann auch so lesen, als würden sie den Durchgang von Lichtwellen durch das Interferometer zeigen. Man kann sich z.B. vorstellen, dass grüne bzw. rote Punkte jeweils anzeigen, wo diese Lichtwellen ihre Maxima (Wellenberg) haben.
Allerdings reagieren Wellen etwas anders als Teilchen wenn es darum geht, sie z.B. an einem Strahlteiler zusammenzuführen (zu “überlagern”). Die Kombination zweier Teilchen ist “doppelt soviel Teilchen wie vorher”. Die Kombination zweier Wellen kann eine stärkere Welle sein, aber auch – gar keine Welle. Oder eine komplizierte Welle.
Hier ist ein Beispiel für das, was passiert, wenn die unterschiedlichen Wellen vor dem Lichtdetektor wieder zusammengeführt (“überlagert”) werden. In meinem ersten Beispiel kommen grüne und rote Punkte jeweils gleichzeitig an, Wellenberg trifft auf Wellenberg und Wellental auf Wellental. (Das hatten wir in keiner der beiden Animationen, aber es ist ein mögliches Resultat.)
Die entsprechenden Lichtpunkte habe ich über jeden der im nächsten Diagramm eingezeichneten Wellenberge gesetzt, nur zur Veranschaulichung. Die senkrecht gepunkteten Linien zeigen zur Orientierung an, wo sich die Wellenberge der grünen Welle befinden: Das Ergebnis ist im unteren Feld gezeigt, nämlich die Summe der beiden Wellen zu jedem Zeitpunkt, als blaue Linie. Die blaue Linie schwingt noch deutlich mehr als die Einzelwellen. Das Ergebnis ist helles Licht, “konstruktive Interferenz”, mehr Licht als in jeder der Einzelwellen: 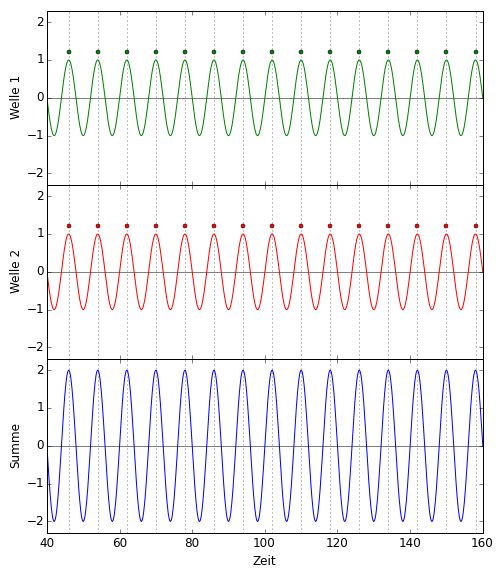 Bei unserem Detektor oben war es ohne Gravitationswelle aber genau anders. Dass grüne und rote Lichtpunkte am Detektor ohne Gravitationswelle versetzt ankommen, heißt nämlich, dass die Wellenberge des einen Lichtanteils gerade auf die Wellentäler des anderen treffen und umgekehrt. Das Ergebnis ist fast komplette Auslöschung, “destruktive Interferenz”, und damit nur sehr schwaches oder gar kein Licht am Detektor. Hier ist diese Situation dargestellt, die untere blaue Linie ist wieder die Summe der beiden Wellen darüber:
Bei unserem Detektor oben war es ohne Gravitationswelle aber genau anders. Dass grüne und rote Lichtpunkte am Detektor ohne Gravitationswelle versetzt ankommen, heißt nämlich, dass die Wellenberge des einen Lichtanteils gerade auf die Wellentäler des anderen treffen und umgekehrt. Das Ergebnis ist fast komplette Auslöschung, “destruktive Interferenz”, und damit nur sehr schwaches oder gar kein Licht am Detektor. Hier ist diese Situation dargestellt, die untere blaue Linie ist wieder die Summe der beiden Wellen darüber: 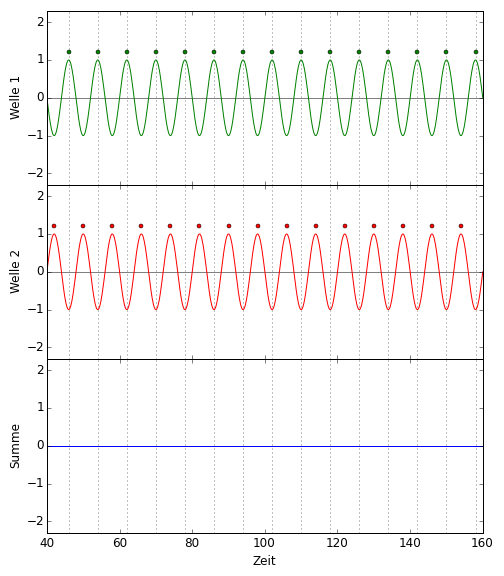 Die untere blaue Linie bleibt bei Null. Ohne Gravitationswelle kommt am Lichtdetektor offenbar gar kein Licht an. (Das ist bei wirklichen Detektoren fast, aber nicht ganz so.)
Die untere blaue Linie bleibt bei Null. Ohne Gravitationswelle kommt am Lichtdetektor offenbar gar kein Licht an. (Das ist bei wirklichen Detektoren fast, aber nicht ganz so.)
In der zweiten Animation dagegen, wo die Gravitationswelle durch den Detektor läuft, sieht das mit den Wellen so aus: 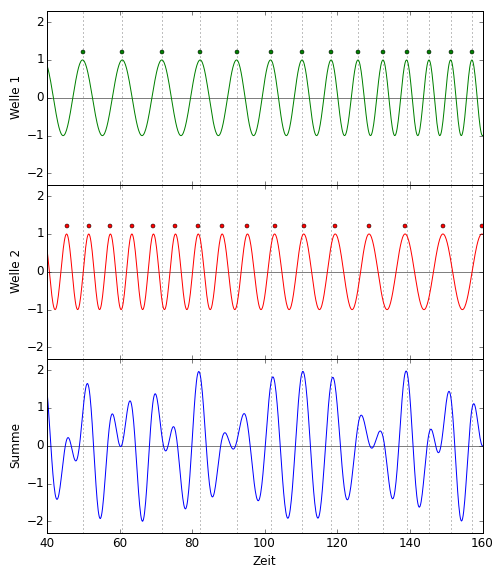 Beim Durchgang der Gravitationswelle zeigt sich am Lichtdetektor auf einmal ein Signal! Das ist, zumindest in stark vereinfachter Version, das Messprinzip der interferometrischen Gravitationswellendetektoren, um die es in der aktuellen Diskussion geht.
Beim Durchgang der Gravitationswelle zeigt sich am Lichtdetektor auf einmal ein Signal! Das ist, zumindest in stark vereinfachter Version, das Messprinzip der interferometrischen Gravitationswellendetektoren, um die es in der aktuellen Diskussion geht.
Und jetzt tausendmal komplizierter
Wirkliche Detektoren sind ungleich komplizierter. Wie schon erwähnt sind die Effekte einer Gravitationswelle sehr klein. Und, bislang noch nicht erwähnt: Es gibt eine Vielzahl von Störeffekten, die Gravitationswellen überlagern oder nachmachen können.
Wie hängt man die Spiegel so auf, dass sie (zumindest für bestimmte Gravitationswellen) wie frei im Raum schwebende Testteilchen von der Gravitationswelle beeinflusst werden? Wie verhindert man, dass seismische Störungen, vorbeifahrende Autos und ähnliches die Spiegel verschieben (und zwar sowohl durch die Übertragung mechanischer Schwingungen als auch durch die Gravitationswirkung der beteiligten Materie)? Was ist mit Fluktuationen des Laserlichts im Detektor?
Die Kollegen Gravitationswellenjäger machen sich extrem viel Mühe, all diese Effekte auszugleichen: Mit Detektoren, in denen des Laserlicht gleich vielfach hin und herläuft, mit Rückkopplungskreisen, Spiegelaufhängung und vielem mehr. Informationen dazu gibt es auf den Seiten der entsprechenden Kollaborationen, z.B. LIGO oder GEO 600:
Seiten der LIGO Scientific Collaboration
Weitere Informationen zu verschiedenen Aspekten von Gravitationswellen gibt es hier auf Einstein Online:
Einstein Online: Vertiefungsthemen Gravitationswellen
Derzeit die besten Nachweischancen haben die LIGO-Detektoren in den USA mit 4 Kilometern Armlänge, um die es am Donnerstag in der Pressekonferenz gehen wird. Ein ganz entscheidender Beitrag zu der Technologie, die dazu führt, dass jetzt realistische Nachweischancen bestehen, kommt übrigens aus Deutschland, von den Kollegen vom Max-Planck-Institut für Gravitationsphysik.
Soviel zum Nachweisprinzip. Ein direkter Nachweis wäre natürlich zunächst einmal interessant, weil damit eine weitere Vorhersage der Allgemeinen Relativitätstheorie direkt bestätigt wird. Aber es kommt noch besser: Gravitationswellen könnten ein ganz neues Fenster zur Astronomie eröffnen. (In meinem Buch zum Thema hatte ich das “Einstein-Fenster” genannt.) Darum wird es im nächsten Teil gehen: Gravitationswellenquellen (GW Teil 3).


Markus Pössel schrieb (9. Februar 2016):
> […] An der Lichtquelle laufen die Pulse [koinzident] los. Aber die Länge des waagerechten Arms ist ein ganz kleines bisschen größer, so dass die roten Lichtpunkte etwas länger brauchen, um beim Detektor anzukommen. Die Längendifferenz ist gerade so gewählt, dass die roten und grünen Lichtpunkte unten am Detektor gerade abwechselnd eintreffen, rot, grün, rot, jeweils mit gleichem Abstand.
Ist diese Bedingung wirklich ein Bestandteil der Versuchsanordnung, so dass Versuche wirklich als “ungültig” verworfen würden, falls diese Bedingung nicht erfüllt wäre?
Oder könnten Versuche trotzdem als “gültig” befunden und berücksichtigt werden, obwohl Pulse von verschiedenen Armen so gut wie koinzident beim (Koinzidenz-)Detektor ankamen?
(Falls so, dann ist die zitierte Beschreibung offenbar nur imaginär bzw. zu einfach formuliert, um die wirkliche Versuchsanordnung verständlich zu machen.)
Ungültig nicht, allerdings würde die Empfindlichkeit nicht ausreichen. Interferometrische Detektoren werden in der Tat nahe kompletter destruktiver Interferenz betrieben; soviel Licht im Detektor zu behalten wie möglich ist Teil der Messstrategie. Die Gründe liegen allerdings bei den Störquellen, auf die ich hier nicht genauer eingehe, nicht beim grundlegenden Messprinzip.
Markus Pössel schrieb (10. Februar 2016 6:11):
> Ungültig nicht, allerdings würde die Empfindlichkeit nicht ausreichen.
“Empfindlichkeit” … ist ein interessanter, wichtiger Begriff …
Er setzt voraus, zwischen den Begriffen „Eingangsgröße“ („Messgröße“, „physikalische Größe“) und „Ausgangsgröße“ („Anzeige“, „Bewertung“) zu unterscheiden.
Mich interessiert dabei ganz vorrangig die (Charakterisierung der) „Eingangsgröße“;
insbesondere: welche Zustände der Beteiligten („Bestandteile des Messgerätes, entsprechend des zugrundegelegten Messprinzips“) sind Eigenzustände (des dem zugrundegelegten Messprinzip entsprechenden Messoperators) der Eingangsgröße, so dass man entsprechend (Versuch für Versuch) sagen könnte, dass jeweils ein bestimmter (Eigen-)Wert der Eingangsgröße „vorlag“.
(Auf dieser Basis ließen sich dann auch eventuelle Zusammenhänge zur Ausgangsgröße analysieren, also die entsprechende Empfindlichkeit der gegebenen Gerätschaften charakterisieren.)
Meine obige Frage nach „Gültigkeit oder Ungültigkeit“ ist also im Sinne von „Eigenzustand der Eingangsgröße – Ja oder Nein?“ gemeint.
Und worauf ich damit hinauswill ist (selbstverständlich) die nachgeordnete Frage:
Sind
(1) „der Durchlauf einer Gravitationswelle durch die gegebenen Beteiligten (d.h. periodisch veränderte Krümmung der Region, in der die Beteiligten enthalten waren)“ und
(2) „das (bloße) Wackeln der Beteiligten gegenüber einander (in einer Region mit praktisch konstanter Krümmung“)
überhaupt orthogonale Eigenzustände der Eingangsgröße,
oder (nur) Mischungen davon
?
> Interferometrische Detektoren werden in der Tat nahe kompletter destruktiver Interferenz betrieben; soviel Licht im Detektor zu behalten wie möglich ist Teil der Messstrategie.
Steht es also im Widerspruch zur erklärten Messstrategie, wenn auch solche Versuche zur Analyse in Betracht gezogen würden, in denen Licht (wegen „konstruktiver Interferenz“) „aus dem Detektor drang“ und (deswegen) von bestimmten Photodioden abgefangen wurde?
Oder ist die Messstrategie anders/besser/genauer zu erklären?
Markus Pössel schrieb (10. Februar 2016 6:11):
> Ungültig nicht, allerdings würde die Empfindlichkeit nicht ausreichen.
“Empfindlichkeit” … ist ein interessanter, wichtiger Begriff …
Er setzt voraus, zwischen den Begriffen „Eingangsgröße“ („Messgröße“, „physikalische Größe“) und „Ausgangsgröße“ („Anzeige“, „Bewertung“) zu unterscheiden.
Mich interessiert dabei ganz vorrangig die (Charakterisierung der) „Eingangsgröße“;
insbesondere: welche Zustände der Beteiligten („Bestandteile des Messgerätes, entsprechend des zugrundegelegten Messprinzips“) sind Eigenzustände (des dem zugrundegelegten Messprinzip entsprechenden Messoperators) der Eingangsgröße, so dass man entsprechend (Versuch für Versuch) sagen könnte, dass jeweils ein bestimmter (Eigen-)Wert der Eingangsgröße „vorlag“.
(Auf dieser Basis ließen sich dann auch eventuelle Zusammenhänge zur Ausgangsgröße analysieren, also die entsprechende Empfindlichkeit der gegebenen Gerätschaften charakterisieren.)
Meine obige Frage nach „Gültigkeit oder Ungültigkeit“ ist also im Sinne von „Eigenzustand der Eingangsgröße – Ja oder Nein?“ gemeint.
Und worauf ich damit hinauswill ist (selbstverständlich) die nachgeordnete Frage:
Sind
(1) „der Durchlauf einer Gravitationswelle durch die gegebenen Beteiligten (d.h. periodisch veränderte Krümmung der Region, in der die Beteiligten enthalten waren)“ und
(2) „das (bloße) Wackeln der Beteiligten gegenüber einander (in einer Region mit praktisch konstanter Krümmung“)
überhaupt orthogonale Eigenzustände der Eingangsgröße,
oder (nur) Mischungen davon
?
> Interferometrische Detektoren werden in der Tat nahe kompletter destruktiver Interferenz betrieben; soviel Licht im Detektor zu behalten wie möglich ist Teil der Messstrategie.
Steht es also im Widerspruch zur erklärten Messstrategie, wenn auch solche Versuche zur Analyse in Betracht gezogen würden, in denen Licht (wegen „konstruktiver Interferenz“) „aus dem Detektor drang“ und (deswegen) von bestimmten Photodioden abgefangen wurde?
Oder ist die Messstrategie anders/besser/genauer zu erklären?
Hallo Herr Pössel,
schönen Dank für den Artikel, auch wenn ich als Laie zugeben muß (frei nach Monty Python) “mah brain hurts..” (und nein, Gravitationswellen werden nicht erzeugt “by smashing two bricks together”^^)
Grundlegende Frage zur Empfindlichkeit:
da das Detektorsystem ja nur zweidimensional mit zwei senkrecht zueinander stehenden Detektorstrecken ist, müsste doch eine konzeptbedingte “Blindheit” entlang der Winkelhalbierenden die Folge sein. Dies dürfte wohl ebenso der Fall sein wenn die Quelle vorrangig “über/unter” der Detektorebene liegt/lag. Wenn man jetzt noch eine winkelabhängige Blindheit (Nachweisgrenze/Rauschen) ab einem gewissen Winkel zugrundelegt bleibt ja nicht mehr viel an detektierbaren Richtungen über (Kudos, wenn es trotzdem geklappt haben sollte!).
Ist diese Empfindlichkeitscharakteristik irgendwo einsehbar/grafisch dargestellt?
(müßte ja irgendwas in der Art einer Sigma-Dual-Doppelkeule sein^^ – wobei die Keuligkeit/Kegeligkeit der Armebenen diskutierbar wäre)
Genau! Um Quellen zu lokalisieren zu können, benötigt man dementsprechend mehrere Detektoren. Erst durch den Vergleich der Messungen kann man erscliessen, aus welcher Richtung die Welle gekommen ist, und das durch die richtungsabhängige Empfindlichkeit.
“Wenn man jetzt noch eine winkelabhängige Blindheit […] zugrundelegt bleibt ja nicht mehr viel an detektierbaren Richtungen über.”
Hilfreich könnte hier der Umstand sein, dass sich die Erde dreht, und mit ihr die Messapparatur.
Nachdem ich gelernt habe, dass die beobachtete Verschmelzung von Schwarzen Löchern im Bruchteil einer Sekunde stattgefunden hat – was mich baff zurücklässt – möchte ich meinen Beitrag hiermit relativieren. In solch kurzen Zeiträumen kann die Erdrotation wohl kaum dazu beitragen, die Richtung zu bestimmen, aus der ein Signal kommt – Zirp.
Grundsätzliches zur Messmethode, welche die Existenz der Gravitationswelle belegen soll (publiziert bevor die Konferenzen zur möglichen Entdeckung der Gravitationswellen heute stattfinden J)
Für einen Beobachter, der sich innerhalb eines (zyklisch) gekrümmten Raumes befindet, bedeutet die (Wellenartige-) Raumkrümmung nicht etwa, dass die Abstände zwischen den Punkten seiner Umgebung zyklisch varieren – diese Veränderung findet aus seiner Sicht garantiert nicht statt, denn die Gravitation (und somit die Gravitationswelle) krümmt die Raumzeit mitsamt sich darin befindlichen Abständen, Bezugspunkten und Maßstäben.
Die weit verbreitete Meinung, dass die Überschreitung des Ereignishorizontes eines schwarzen Lochs katastrophale Konsequenzen für den Reisenden und seinen Raumschiff bedeuten würde (weil die “Gezeitenkräfte” des Schwarzen Lochs sie zerreißen würden), beruht auf der falschen Annahme, dass das Wesen der Raumzeit verschieden vom Wesen der darin Reisenden und ihres Instrumentariums wäre. In Wirklichkeit besteht kein Unterschied zwischen der Raumzeit selbst und den materiellen Strukturen, deren Konsistenz uns extrem stabil erscheint, weil sie u.a. zu dem gehören, was wir “das erfahrbare Selbst” nennen (was deshalb nicht die Raumzeit, sondern das “Ich” oder, als Werkzeug / Raumschiff, die Verlängerung des “Ichs” ist)
Wenn also die Gravitationswelle bestimmte Regionen der Raumzeit samt ihren Strukturen krümmt, dann unterliegt dieser Verformung absolut alles, was innerhalb dieser Regionen existiert, auch die sich darin befindliche Messapparatur, auch die Detektoren, auch die Abstände zwischen den Spiegeln und Reflektoren, ja, selbst das Licht, dessen Impulse als Referenz der Messung dienen (dass die Bahnen der Lichtstrahlen durch die Wirkung der Gravitation gekrümmt werden…etc. etc.)
Einer Messung der Gravitationswelle in der vorgestellten Form fehlt, soweit ich das beurteilen kann, der (relativ zur Messanordnung) ruhende Bezugspunkt, anhand dessen, sich die Veränderung innerhalb der Messanordnung, bezogen auf den Maßstab der Messung, überhaupt feststellen ließe.
Deshalb befürchte ich:
Wenn heute ein Effekt vorgestellt wird, der mit der Existenz der Gravitationswellen in Verbindung gebracht wird, dann wird es etwas sein, das nichts mit der Wirkung der Gravitationswelle zu tun hat.
11.02.2016
(ich nenne dies “Gran Sasso – Effekt”. Beim Gran Sasso Experiment ging es, soweit ich mich ohne Internet erinnern kann, darum, die Geschwindigkeit der Neutrinos zu messen. Zur Bestimmung des Abstandes zwischen dem Sende- und dem Empfangsort wurde GPS-System verwendet. Die erfolgte Messung ergab, dass sich die gesendeten Neutrinos mit der Hyper-Lichtgeschwindigkeit fortbewegten. Nach der anfänglichen Euphorie erklärte man die Ergebnisse des Experiments für ungültig (Rechenfehler)
Meiner Meinung nach beruhte der Fehler darin, dass man den Abstand zwischen dem Sender und dem Empfänger mithilfe des GPS-Systems bestimmte (der bei der Bestimmung der Abstände zwischen zwei Orten die Erdkrümmung selbstverständlich berücksichtigt) und nicht bedachte, dass Neutrinos auf ihren Wegen den geradlinigen Bahnen folgen und imstande sind, sich ungehindert durch die Erdkruste fortzubewegen. Die physikalischen Eigenschaften der Neutrinos bestimmten, dass der Weg, den sie tatsächlich bewältigten erheblich kürzer war, als der per GPS errechnete Abstand zwischen den Orten, an denen sie jeweils gesendet und empfangen wurden.)
Nö, da sagt Einsteins Theorie etwas ganz anderes. Erstens gibt es einen Unterschied zwischen Festkörpern und frei fliegenden Teilchen (ist z.B. auch bei der kosmischen Expansion so). Festkörper werden durch eine durchgehende Gravitationswelle kaum beeinflusst (Konkurrenz zwischen den formgebenden Kräften und der winzigen Beschleunigung aufgrund der Gravitationswelle), frei fliegende Teilchen maximal. Auch aus solchen Differenzen könnte man einen Nachweis ableiten.
Außerdem gibt es einen Einfluss auf Licht. Das zeigt ja gerade meine Animation oben, die in dieser Hinsicht keine vereinfachte Veranschaulichung ist, sondern wirkliche Lichtbahnen in der betreffenden Raumzeit wiedergibt (einfache lineare TT-Welle). Und der messbare Effekt findet ja gerade am Ort des Detektors statt: Man vergleiche Eintreffzeiten mithilfe einer Uhr (oder, wenn das messtechnisch nicht möglich ist, durch Interferometrie). Das sind die von Herrn Wappler zu recht so geliebten Koinzidenzen, hier zwischen Uhrentakt und Eintreffen der Teilchen; sobald man etwas darauf zurückgeführt hat, kann es keine Missverständnisse mehr geben, was real ist und was möglicherweise nur auf eine bestimmte Koordinatenbeschreibung zurückgeht.
Nö ist gut, doch dann wäre die Gravitation nicht eine universell wirkende Kraft….(Ursache: Schwerkraft, Effekt: Raumkrümmung / Ursache: Raumkrümmung, Effekt: Schwerkraft?))
Meine Vermutung ist, dass die Wirkung der Gravitation sich generell (universell) auf Raumzeit (und darin enthaltene Materie) erstrecken muss.
Wir operieren zunächst mit Modellen, nicht mit den objektiv existierenden Strukturen. Wir können uns anhand der Modelle vorstellen, wie die wirklichen Strukturen sich im Raum verhalten; wie sie beeinflussen und wie sie beeinflusst werden. Ich denke mir folgendes: alle bisher für wahr gehaltenen Modelle erwiesen sich als falsch, warum sollten ausgerechnet die heutigen wahr sein?
Um 16:30 Uhr wissen wir mehr, vielleicht. Sehr gute Artikel. Ich nehme viel mit und warte gespannt darauf, was Du um 17 Uhr zu sagen hast. Danke
PS:
“Und der messbare Effekt findet ja gerade am Ort des Detektors statt”
Der Ort des Detektors ist aber kein abgeschirmter, kein spezieller, oder?
Die Animation erweckt den Eindruck, die freischwebenden Teilchen, welche sich der Wellenbewegung unterordnen (somit die Welle an sich), sich um den starren Mittelpunkt bewegen…In Wirklichkeit muss auch der “Mittelpunkt” der “Bewegung” ein Bestandteil der universell wirkenden Wellenbewegung sein (die Geometrie der Welle, welche die Raumzeit krümmt muss mindestens 4-dimensional sein. Die Welle selbst breitet sich gleichmäßig omnidirektional aus. Die “ruhende” Mitte dieser Bewegung müsste sich dort befinden, wo die Quelle der Gravitationsstörung liegt.). Es ist 15:10 Uhr.
“Nö” ist in diesem Falle aber richtig. Kann man bei Gravitationswellen auch recht einfach einsehen: dass es weder Wirkungen in Zeit- noch in Ausbreitungsrichtung gibt, ist gerade Ausdruck der Transversalität der Wellen (wie auch vom Elektromagnetismus bekannt). Gravitation allgemein beeinflusst Zeit (Newton’sche Gravitation ist in den üblichen Koordinaten ein reiner Zeitdehnungseffekt), Gravitationswellen nicht.
Zur Bewegung: Der “messbare Effekt” ist, wie die Lichtpulse dort ankommen – so habe ich meinen Detektor aufgebaut! Dass ich meine Kamera auf diesen Punkt gerichtet habe ist willkürlich (aber praktisch). Von absoluter Bewegung oder Ruhe kann man in diesem Rahmen ja sowieso nicht sinnvoll reden. Aber eben z.B. darüber, wie eine Gravitationswelle Lichtpulse (eigentlich: Wellen) durcheinanderbringt, die nach vorgeschriebener Flugbahn zu vorgegebenen, möglichst frei aufgehängten Spiegeln an einem Detektor ankommen. Und da ist die Aussage: Im Prinzip so wie hier in der Animation gezeigt.
Maciej Zasada schrieb (11. Februar 2016 8:01):
> Gravitation (und somit die Gravitationswelle) krümmt die Raumzeit mitsamt sich darin befindlichen Abständen, Bezugspunkten und Maßstäben. […]
> Wenn also die Gravitationswelle bestimmte Regionen der Raumzeit samt ihren Strukturen krümmt, dann unterliegt dieser Verformung absolut alles, was innerhalb dieser Regionen existiert, auch die sich darin befindliche Messapparatur, auch die Detektoren, auch die Abstände zwischen den Spiegeln und Reflektoren […]
An diesen Formulierungen an sich, so wie sie sind, kann ich (bei allem Bemühen) wirklich nichts aussetzen.
Und trotzdem gibt es da noch eine gewisse Feinheit, die in den zitierten Formulierungen nicht ausdrücklich erwähnt wird; die aber wichtig ist und damit zu tun hat, wie „sich die Veränderung innerhalb der Messanordnung, bezogen auf den Maßstab der Messung, überhaupt feststellen ließe.“:
Man kann „Krümmung“ (bzw. ansonsten „das Fehlen von Krümmung“) nicht jeweils nur einem einzigen Paar von (unterscheidbaren, materiellen) Beteiligten und (ggf.) deren lediglich einem Abstandswert zuschreiben.
Sondern „Krümmung“ (bzw. ansonsten „das Fehlen von Krümmung“) charakterisiert mindestens drei (oder noch viel mehr; „n“) Beteiligte und (ggf.) deren zahlreiche, d.h. „n (n – 1)/2“ paarweise Abstände untereinander im Zusammenhang.
– Drei Beteiligte („Kimme, Korn, Bullseye“) können entweder gegenüber einander gerade gewesen/gelegen sein (oder ansonsten halt nicht, sondern ggf. durch einen bestimmten Krümmungsradius beschrieben werden);
– Vier Beteiligte („die Enden/Füße der vier Beine eines Tisches“) können entweder gegenüber einander eben gewesen/gelegen sein (oder ansonsten halt nicht, sondern ggf. durch einen bestimmten Radius der „mittleren bzw. Gauss“-Krümmung beschrieben werden);
– Fünf Beteiligte (wie man sie von Synges „five point curvature detector“ her kennt) können entweder gegenüber einander flach gewesen/gelegen sein (oder ansonsten halt nicht, sondern ggf. durch einen bestimmten Radius der „mittleren bzw. Riemann“-Krümmung beschrieben werden).
(Usw.; aber für diese Diskussion reicht das wohl.)
Die genannten Krümmungsradien lassen sich (natürlich) aus den „n (n – 1)/2“ paarweisen Abständen der Beteiligten untereinander berechnen;
dabei spielt insbesondere „Herons Formel“ bzw. deren Verallgemeinerung(en), die „Cayley-Menger-Determinante“ bzw. (letztlich) die „Gram-Determinante“ die entscheidende Rolle.
(Und MBMN sollte man jedem von MTW einzeln dafür in den jeweiligen Hintern treten, dass sie diese Bezeichnungen in ihrer „Box 13.2: The Metric Distilled From Distances“ verschwiegen haben. &)
Wenn sich also die Krümmung (in) einer bestimmten Region (zyklisch) ändert, dann ändern sich die Abstandsverhältnisse zwischen den hinreichend vielen, einzeln unterscheidbaren Bestandteilen der in der Region denkbaren (oder eventuell sogar auffindbaren) „materiellen Struktur“.
Und das kommt in den (bisher) in diesem SciLog gezeigten „Animationen von Gravitationswellen“ dieses SciLogs leider nicht recht zur Geltung.
Und, schlimmer: in der LIGO-Versuchsanordnung leider auch nicht.
p.s.
> Beim Gran Sasso Experiment ging es, soweit ich mich ohne Internet erinnern kann, darum, die Geschwindigkeit der Neutrinos zu messen.
Darum ging es unter anderem; richtig.
> Die erfolgte Messung ergab, dass sich die gesendeten Neutrinos mit der Hyper-Lichtgeschwindigkeit fortbewegten.
Das war zumindest der Stand, der bis ca. März 2012 von den maßgeblichen Experimentatoren mit ziemlich gutem Gewissen erreicht und vertreten wurde.
> Nach der anfänglichen Euphorie erklärte man die Ergebnisse des Experiments für ungültig
Richtig; im Sommer 2012.
> (Rechenfehler)
Nein: Man fand (vor allem) einen Hardware/Instrumentierungs/Verkabelungs-Fehler;
der dazu geführt hatte, dass die Dauer der CNGS-Strecke (bestehend insbesondere aus der CERN-Neutrino-Quelle und dem OPERA-Detektor im LNGS), während diese jeweils von einem Neutrino-Bunch bereist wurde, systematisch unterschätzt wurde.
> Meiner Meinung nach beruhte der Fehler darin, dass man den Abstand zwischen dem Sender und dem Empfänger mithilfe des GPS-Systems bestimmte (der bei der Bestimmung der Abstände zwischen zwei Orten die Erdkrümmung selbstverständlich berücksichtigt) und nicht bedachte, dass Neutrinos auf ihren Wegen den geradlinigen Bahnen folgen und imstande sind, sich ungehindert durch die Erdkruste fortzubewegen.
Bevor sich die Sache mehr oder weniger aufklärte, hatte auch ich so etwas (ähnliches) für denkbar gehalten:
Es ging darum, ca. 18 m des (vermeintlichen) Abstands zwischen Quelle und Detektor „irgendwie wegzuargumentieren“; und das käme z.B. hin, wenn der Höhenunterschied zwischen Quelle und Detektor nicht ganz korrekt berücksichtigt worden wäre.
Aber darin lag „das Problem“ natürlich nicht, denn, wie in den detaillierten „cngs baseline geodesy“-Reports dokumentiert ist, wurde der GPS-basierte Abstand „korrekt 3-dimensional“ behandelt und ausgewertet.
Aber dennoch lag der besagten Messung ein entscheidender Denkfehler zugrunde, den die maßgeblichen Experimentatoren (und viele andere) offenbar geschluckt hätten, wenn der berühmte „cable glitch“ unentdeckt geblieben wäre; nämlich:
Die Messung des Abstands (bzw. der Distanz) zwischen zwei Beteiligten (wie z.B. der Quelle und dem Detektor) beruht im Rahmen der RT definitionsgemäß auf der Berücksichtigung der Fronten jeglicher Signale, die zwischen Quelle und Detektor (hin als auch her) ausgetauscht wurden; also insbesondere auch auf der Berücksichtigung des Neutrino-Bunch-Signals an sich, sofern dieses die Front des Signals darstellte, durch das der Detektor zuerst davon erfahren hätte, dass der betreffende Neutrino-Bunch erzeugt und von der Quelle losgeschickt worden war.
Nicht umsonst bedeutet „c_0“ in der RT ja ganz grundsätzlich und wesentlich die Signal-Frontgeschwindigkeit;
ganz unabhängig davon, ob diese Front oder auch das Signal insgesamt dabei „elektro-magnetisch“ oder eher „elektro-schwach“ oder „stark“ oder „gravitativ/inertial“ charakterisiert würde.
Also entweder bildete der betreffende Neutrino-Bunch selbst die Front dieses Signals, oder ansonsten, entsprechend der Definition von „Signalfront“, er erreichte den Detektor erst nach der entsprechenden Signalfront (und falls so, dann folglich mit Geschwindigkeitswert kleiner als „die Signal-Frontgeschwindigkeit, c_0“).
Der Denk- bzw. Rechenfehler in den bekannten Neutrino-Geschwindigkeits-Veröffentlichungen liegt nach wie vor darin, dass diese zwangsläufige Grenzgeschwindigkeit, c_0, nicht ausdrücklich als solche in den Berechnungen des systematischen Vertrauensbereiches der Messwerte eingesetzt wird (Stichwort: „Feldman-Cousins“).
Der Nachweis ist geglückt.
Jetzt bleibt die spannende Frage: Wer bekommt den Nobelpreis?
Idee/ Methodik/ Rechnungen 1962: Gertsenshtein (*1926), Einstein meinte noch, geht nicht
Realisierbarkeit/ technische Finessen 1972: Weiss, die Empfindlichkeit hat’s gebracht
Theorie/ laufende “mathematische Begleitung”: Thorne für die vorhergesagten Signalformen
sind mögliche für max 3, aber stellvertretend für ganz viele
Herr Senf schrieb (12. Februar 2016 12:38):
> [Wer bekommt den Nobelpreis?]
> Idee/ Methodik/ Rechnungen 1962: Gertsenshtein (*1926)
Sehr gut!, denn demnach wäre ein weiterer Nobelpreis beruhend auf der Idee (?), Methodik (?), Theorie (!) von Synge (und natürlich vorrangig Einstein) immer noch zu haben.
> Realisierbarkeit/ technische Finessen 1972: Weiss […]
(Herzlichen Glückwunsch!)
> […] Thorne für die vorhergesagten Signalformen
… also für das zugrundegelegte Modell.
Jetzt bleibt die spannende Frage:
Was wird die genaue Bezeichnung dessen sein, wofür der in Rede stehende Nobelpreis ggf. vermutlich an Gertsenshtein, Weiss und Thorne verliehen würde?
(Etwa: Für die „Erste Beobachtung des Verschmelzens von Schwarzen Löchern“ ??)
.
p.s. – Ein‘ Kleks (Senf) hab ich noch:
https://de.wikipedia.org/w/index.php?search=Planck-Kraft&title=Spezial%3ASuche&go=Artikel
Ich habe eine Frage zur Korrelation der Meßdaten der LIGO-Detektoren.
Essentiell scheint ja zu sein das man zwei LIGO Detektoren hat deren Meßdaten im Nachhinein so korreliert werden das man das eigentliche Signal ermitteln kann, das SNR inkrementiert, verifiziert usw.
Ist folgendes denkbar?
Man kann heutztage LASER so aufbauen das deren Photonen quantenverschränkt arbeiten. So habe ich zumindesten andere Informationen im WEB verstanden. Wäre es nicht denkbar das man auch so die LASER der LIGO Detektoren arbeiten ließe und somit die Korrelation auf direktem optischen Wege realisieren kann?
Gruß hagen
Das dürfte bestimmte Messungen nur noch komplizierter machen, und ich sehe den Vorteil davon ehrlich gesagt nicht. Außerdem geht es nicht nur um die Korrelation.
Hallo Herr Pössel
Die Darstellung der beiden sich auslöschenden Wellen aus den beiden Armen in der Abbildung oben ist soweit verständlich. Nun habe ich gelesen, dass es sich beim verwendeten Laser um einen Infrarot-Laser handelt. Damit würde die Wellenlänge des Lichtes in der Grössenordnung von 1 E-6 m – also etwa 1 Mikrometer – liegen. Die Verkürzung/Verlängerung der Arme durch die Gravitationswellen soll jedoch bei 1 E-18 m liegen (1 Attometer). Das käme dann einer Verschiebung der Wellenphase um lediglich ein Billionstel (E-12) der Wellenlänge des Infarotlichts. Die Verschiebung von der (theoretisch, so weit überhaupt möglich) vollständigen Auslöschung der beiden Wellen wäre also extrem klein, nahezu Null. Kann so etwas überhaupt gemessen werden?
Hallo Herr Pössel,
das war ja nun ein Paukenschlag für die Gravitationswellen-Forschung.
Leider sind aus meiner Sicht wichtige Dinge nicht besprochen:
1. kein Nachweis der GW150914 an allen anderen GW-Detektoren
So erfolgreich wie dieser Nachweis für LIGO in Livingston und und Hanford dargestellt wird, so niederschmetternd muss er für alle anderen GW-Detektoren doch sein.
Ein so bedeutsames Ereignis wird wahrscheinlich nicht sehr häufig registrierbar sein und wenn es dann von den übrigen GW-Detektoren nicht mitgeschrieben wurde, werden diese auch in Zukunft keine ähnlichen und schwächere Signale jemals registrieren. Natürlich unterscheiden sich die bislang aufgebauten Detektoren im empfindlichen Frequenzbereich. Jedoch ist die kalkulierte Verschmelzung von Schwarzen Löchern mit einem Durchlaufen eines breiten Frequenzbandes beginnend bei sehr tiefen Frequenzen verbunden. Es bestand also gute Chance so eine einmalige Gelegenheit mitzuschreiben; hat man aber nicht. Man könnte also gut auf diese nicht ansprechenden Detektoren verzichten!
2. die Signale von Hanford und Livingston
In Hanford wurden die Signale ca. 7ms früher registriert als in Livingston. Dies entspricht in etwa der Zeit, die ein Signal mit Lichtgeschwindigkeit zur Bewältigung der räumliche Distanz der beiden Messorte benötigt. Das ist soweit denkbar. Anhand der Kurvenformen lassen sich die wichtigen Kenngrößen für M1, M2 und r aus der “Kosta Kotta”-Formel berechnen und so lange angleichen, bis die gemessene Kurvenform nahezu deckungsgleich wird.
Legt man jedoch die beiden Messsignale von Livingston und Hanford mit entsprechender zeitlicher Verschiebung von 7ms übereinander, so wird deutlich, dass das zu erst ankommende Signal in Hanford in seiner Amplitude mehrmals und deutlich jenes in Livingston überragt. In der Diskussion fehlt nun der Hinweis darauf, wie es beim Fortschreiten der GW von Hanford nach Livingston zu dieser Abschwächung kommen kann. Wäre dies aus dem Vorhandensein der Materie (“Erde”) zwischen den beiden Messorten zu erklären, ist mit höchster Wahrscheinlichkeit die errechnete Distanz zur Quelle der GW von 1,3 Milliarden Lj mit einer wesentlich höheren Abschwächungsrate für h zu kalkulieren.
3. keine Registrierungen von Strahlungsausbrüchen am 14.9.2015
Die wichtigste Eigenschaft von Schwarzen Löchern ist ihr fehlendes Aussenden von Lichtquanten jeglicher Form. Auf diesen Umstand wurde auch in einer Darstellung von Prof. Dr. Bruce Allen nochmals verwiesen.
Jedoch:
In aller Regel besitzen sie Akkretionsscheiben und sind von hieraus abstürzender Materie auf den Ereignishorizont durch Aussendung hochenergetischer Strahlung auffindbar (z.B. M87). Der fehlende Nachweis von Strahlungsausbrüchen am 14.9.2015 kann deshalb nur dadurch begründbar sein, dass
a) keines der beiden Schwarzen Löcher bzw. das lange Zeit zuvor existierende Doppelsystem eine Akkretionsscheibe besaß
oder
b) die Verschmelzung der beiden Schwarzen Löcher keine Auswirkung auf die Akkretionsscheibe(n) hatte
oder
c) es keine Veränderungen, die zum plötzlichen Aussenden von hochenergetischer Strahlung führen würde, gab.
4. Ihr Beitrag “Gravitationswellendetektoren: wie sie funktionieren (GW Teil 2)” vom 9.2.2016
Gravitationswellen wirken auf Lichtimpulse
Die von Ihnen gewählte grafische Darstellung mit dem Aussenden von Lichtimpulsen ist aus der Sicht des 3-dimensionalen Raumes verständlich. Auch der Hinweis auf den veränderlichen räumlichen Abstand der Lichtimpulse beim Durchgang von Gravitationswellen ist im 3-dimensionalen ok.
Es war jedoch Einsteins großer Verdienst, die Einheit von Raum und Zeit in einer 4-dimensionalen Wirklichkeit zu finden. Und genau das fehlt in Ihrer Darstellung! Denn neben der räumlichen Abstandsänderung werden auch die zeitlichen Abstände (gemäß der ART in entgegengesetztem Sinn) mit dem Durchgang von Gravitationswellen beeinflusst. Der Taktgeber für die Aussendung der Lichtimpulse ist also nicht konstant. Im Ergebnis dessen wird der Nachweis mit dieser Art von Detektor nicht gelingen.
Übrigens kannte Einstein die Empfindlichkeit von Michelson-Interferometern und hätte bestimmt schon zu seiner Zeit derartige Experimente vorgeschlagen, wenn er damit von der Möglichkeit des Nachweises der Gravitationswellen überzeugt wäre. Hat er aber nicht!
Zu 1: Advanced Virgo war zu dem Zeitpunkt noch dabei, fertiggestellt zu werden. Vermutlich sind die Kollegen dort in der Tat enttäuscht gewesen. Aber wenn der Detektor mit voller Empfindlichkeit läuft, sollte er entsprechende Signale ebenfalls nachweisen können. Zumal die bei der betreffenden Empfindlichkeit ja offenbar nicht so selten sind.
GEO600 war zwar in Betrieb, aber nicht im Beobachtungsbetrieb, und nicht empfindlich genug. Die dortigen Kollegen waren aber garantiert nicht enttäuscht. Advanced LIGO beruht ja weitgehend auf der bei GEO600 entwickelten Technologie, die Rollenverteilung mit GEO600 als Technologietester und aLIGO als eigentlichem Beobachtungsdetektor war seit langem so geplant und die Kollegen sind alle Mitglieder der LIGO Scientific Collaboration und als solche an der Entdeckung beteiligt.
Ein kleines Problem beim jetzigen Nachweis war, dass man mit nur zwei Detektoren keine gute Lokalisierung und auch keine vollständige Charakterisierung der Welle vornehmen kann. Dazu braucht man am besten vier Detektoren in entsprechender relativer Orientierung zueinander. Advanced VIRGO, KAGRA und am besten auch LIGO India werden auf alle Fälle gebraucht werden und bringen ja zum Teil auch etwas unterschiedliche Fähigkeiten mit (Advanced VIRGO und KAGRA kommen zu etwas tieferen Frequenzen). Ohne gute Lokalisierung kann man ja insbesondere keine
zu 2: Sie vergessen, dass da noch die Orientierung des Detektors eingerechnet werden muss. Je nach Orientierung des Detektors und Polarisation der Welle spricht der Detektor unterschiedlich empfindlich an (bei ungünstigster relativer Orientierung). Die unterschiedlichen Nachweisstärken gehen als wichtige Information bei der Abschätzung ein, wo am Himmel das Ereignis stattgefunden hat. (Auch wenn man mit zwei Detektoren dabei leider nur einen recht großen möglichen Bereich bekommt.)
zu 3: Aktive stellare Schwarze Löcher haben typischerweise einen nichtkompakten Begleiter, von dem sie Material für die Akkretionsscheibe abziehen. Das wäre bei einem doppelten Schwarzen Loch schon eine eher ungewöhnliche Situation. Wobei: Wer weiss, was wir jetzt dank Gravitationswellen noch über solche Schwarzen Löcher lernen. Beim jetzigen Kenntnisstand ist der Umstand, dass bei dieser Art von Ereignis kein optisches Gegenstück erwartet und auch keines sicher nachgewiesen wurde (bei FERMI gab es ja offenbar doch einen Kandidaten) nichts überraschendes. Interessanter wird es auch da, wenn man genügend Detektoren für eine gute Lokalisierung hat und dann ganz gezielt nachbeobachten kann. Und wenn die erste Neutronensternverschmelzung nachgewiesen wird, wo man im Ggs. zu doppelten Schwarzen Löchern gute Gründe hat, optische und andere Phänomene zu erwarten.
zu 4: Gravitationswellen sind, genau wie elektromagnetische Wellen, transversal. Dass es daher in einem der Situation angepassten Koordinatensystem keinen Effekt in Zeitrichtung und keinen in Beobachtungsrichtung gibt, ist daher keine Überraschung. Meine Animation bildet genau das ab, was die Metrik für solch eine Situation sagt – mit künstlich überhöhter Amplitude, aber ansonsten genau das, was die Formeln kodieren.
Zu Einstein: Der hatte, siehe die in Teil I verlinkten Artikel, erst einmal Probleme zu erkennen, ob Gravitationswellen ein Koordinatenartefakt sind oder nicht. Ob er, wenn er Gravitationswellen ernster genommen hätte, auch die prinzipielle Nachweismöglichkeit via Interferometer erdacht hätte, kann man nicht sagen. Wer welche Ideen hat ist nicht wirklich vorhersehbar. Und mit dem, was damals technisch möglich war, hätte der Nachweis ja auch tatsächlich nicht gelingen können.
Guten Tag
Was berechtigt Sie zu dem Postulat:zu 4: “Gravitationswellen sind, genau wie elektromagnetische Wellen, transversal” jede EW hat bekanntlich auch den longitudinalen Anteil (Prof. K.Meyl)
Meyl und Müller liest man nicht, ist alles Quatsch, was die “bekanntlich” schreiben.
Schon hat man eine ganz einfache Antwort, warum transversal richtig ist.
Selbst wenn alle Voraussetzungen für eine erfolgreiche Messung ideal gegeben sind, nämlich
1) Exakte Amplitudengleichheit der beiden interferierenden Teilstrahlen
2) Unterdrückung des Falschlichts um einen Faktor 10^(-24) gegenüber dem Primärlicht
3) Exakte Konstanz der Lichtleistung um schwankenden Strahldruck auf die Spiegel zu vermeiden
erhebt sich noch immer ein Empfindlichkeitsproblem. Wenn sich ein Spiegel um 1/1000 eines Protonenradius verschoben hat, wie behauptet, ergibt sich eine Phasenverschiebung von 2pi 10^(-18) m / 10^(-6) m = 2pi 10^(-12). Bei destruktiver Interferenz hellt sich die Amplitude im Dunkelfeld um diesen Faktor mal die Amplitude im Hellfeld (konstruktive Interferenz) auf. Somit ist die zu messende Intensität 36×10^(-24) mal die zirkulierende Lichtleistung von 100 kW im Interferometer. Rechnet man diese Leistung in den zugehörigen Photonenfluss dN/dt = Lichtleistung/(h f) um, so erhält man gerade mal 20 Photonen/Sekunde, also für den “Verschmelzungsvorgang” etwa 4 Photonen. Zu dem veröffentlichten Signal mit einem angeblichen Signal/Rauschverhältnis von ca. 20 gehört aber ein ungleich höherer Fluss von infraroten Photonen. Es gibt nur einen plausiblen Schluss:
Das veröffentlichte Signal entstammt einer rechnerischen Simulation, aber keiner realen Messung.
Dr. Engelhardt,
hatte ich Ihnen doch eben auf relativ-kritisch erklärt, daß Sie sich ungefähr um einen Faktor 5.000 vertan haben. Wollen wir zur Abwechslung hier jetzt weitermachen?
Grüße Senf
Zitat Markus Pössel: „Und nein, bei einer Sache, die man in jedem Lehrbuch zum Thema findet, wäre es ziemlich unhöflich, sich stattdessen an die AEI-Direktoren zu wenden. Das wäre das Analogon zu der Schüler-Email “bitte machen Sie meine Hausaufgaben für mich”.“
————
Da ich auch an der Hinterfragung des LIGO-Experiments sehr interessiert bin, erlaube ich mir hier eine kurze Anmerkung:
In jedem Lehrbuch wird die HYPOTHESE Relativitätstheorie dargelegt. Es handelt sich wohlbemerkt um eine Hypothese! Hier wird jedoch von Dr. Engelhardt nicht die theoretischen Grundlagen dieser Hypothese hinterfragt, die er als Physiker bestens kennt, sondern die experimentelle Bestätigung dieser Hypothese durch das LIGO-Experiment. Das ist etwas ganz Anderes, ich hoffe, das Sie es erkennen können, und das findet man eben nicht in jedem Lehrbuch: Wie hat das LIGO-Experiment es geschafft, diese Hypothese messtechnisch zu bestätigen?
Die meßtechnischen Fragen sind dementsprechend von essentieller Bedeutung in der Experimentalphysik, die einzig maßgeblich ist zur Bestätigung von Hypothesen. Ich finde es also mitnichten „unhöflich“, dass man das AEI darum bittet, offene Fragen über dieses Experiment zu klären, das ist hier sogar seine prädestinierte „Hausaufgabe“. Ihr Analogon zur Schüler-Email finde ich hier völlig unpassend – sogar vielleicht unhöflich gegenüber Dr. Engelhardt.
Mit freundlichen Grüßen
Jocelyne Lopez
Wenn Sie hier schon quer in eine Diskussion hineinspringen, dann seien Sie bitte so höflich, vorher zu lesen, worauf sich eine Antwort eigentlich bezieht. In diesem konkreten Falle auf Herrn Engelhardts Frage vom 17. Mai nach “der mathematischen Formulierung der Wellengleichung für das Gravitationsfeld sowie einer Lösung für die homogene Gleichung weit weg von der Quelle”, wie aus der Anordnung von Frage und Antwort ja auch eindeutig ersichtlich ist.
Das ist reiner Lehrbuchstoff, und Ihre Aussage, es ginge bei meiner Antwort und der vorangehenden Frage von Herrn Engelhardt, konkret um LIGO-Messtechnik, ist schlicht falsch. Wir sind noch bei den Voraussetzungen der Messung, also bei dem, was die ART über Gravitationswellen allgemein sagt.
Herr Pössel:
Ob nach der Befindlichkeit des Teilnehmers Manuel Krüger „Engelhardt bedient zu sein scheint“ ist ein erneuter unsachlicher und hetzender Einwurf dieses notorischen Stalkers in der Diskussion – sowie übrigens in früheren Diskussionen in Ihrem Blog. Sie hätten schon genug Anläße, diesen Ihre „Hilfsmoderator“ längst zu sperren, auch aus Ihrer Blog-Reihe „Einstein verstehen“, anstatt diese Drohung gegenüber Herrn Engelhardt und mir auszusprechen.
Ich bitte Sie ausdrücklich, die unsachlichen und herabsetzenden ad hominem Einwürfe dieses Teilnehmers konsequent zu moderieren, er ist nicht zu belehren und wird sein Verhalten nicht ändern, er kann es auch nicht, das ist eine langjährige Zwangshandlung.
Ihre äußerst lasche Moderation halte ich für unvertretbar und unzumutbar, vor allem jetzt, wo Dr. Engelhardt und ich angekündigt haben, dass wir uns von Ihrer Blog-Diskussion, die sich quasi vom Anfang an im Kreise dreht, sinnvolller Weise fern halten wollen.
Jocelyne Lopez
Herr Senf,
Sie haben meine obige Rechnung nicht widerlegt. Berechnen Sie erst mal die destruktive Interferenz und dann die Aufhellung durch die angenommene Phasenverschiebung. Es wird beim Amplitudenfaktor von 2 pi 10^(-12) bleiben.
Grüße,
Wolfgang Engelhardt
Nicht nur die Direktoren des Einstein-Instituts sind unfähig, die Intensität im Dunkelfeld eines Michelson-Interferometers auszurechnen, wenn die Phasenverschiebung zwischen den interferierenden Wellen 2 pi 10^(-12) beträgt. Auch die 84 Mitarbeiter, die ihre Namen auf die LIGO-Veröffentlichung setzen ließen, können es nicht und Herr Pössel schafft es hier auch nicht. Lieber akzeptiert man es, des wissenschaftlichen Betrugs geziehen zu werden, als dass man mal fünf Minuten nachdenkt.
Immerhin bemerkt Herr Pössel im Anschluss an seine Kinderzeichnung, in der er vorführt, dass sin (alpha) + sin ( – alpha) = 0 ist, dass sich die Strahlen “fast” auslöschen. Wie ist es genau, Herr Pössel? Als Theoretiker, der vermutlich noch nie in einem Labor gestanden hat, sind Ihnen die Realitäten eines Interferometers offenbar ein böhmisches Dorf. Darum gehen Sie den Betrügern von LIGO genauso auf den Leim, wie unbedarfte Max-Planck-Direktoren (http://www.kritik-relativitaetstheorie.de/Anhaenge/Anfrage%20LIGO-Experiment.pdf). Versuchen sie doch mal, etwas Experimentalphysik nachzuholen, indem Sie dieses Papier studieren: https://www.researchgate.net/publication/273333158_Phase_and_frequency_shift_in_a_Michelson_interferometer
Investieren Sie doch mal etwas von der Energie, die Sie hier in krude Beleidigungen investieren, in eine Diskussion zur Sache!
Es gab als Reaktion auf die Kommentare, die Sie unter den verschiedenen Gravitationswellenbeiträgen auf diesem Blog hinterlassen haben, eine ganze Reihe aus meiner Sicht schlüssige Einwände, z.B. der Kommentar zur Längenunterschiedsmessung von Herrn Wappler. Daraufhin folgte von Ihnen regelmäßig: Schweigen im Walde.
Sehr geehrter Herr Pössel,
ich hoffe nicht, dass ich Sie in irgendeiner Form beleidigt habe, denn das war keineswegs meine Absicht. Im Duden findet man für “unbedarft”: ahnungslos, arglos, blauäugig, einfältig, gutgläubig, gutmütig, leichtgläubig, naiv … Menschen, die auf einen offensichtlichen Betrug hereinfallen, darf man wohl so nennen, ohne sie zu beleidigen. Es kommt eben darauf an, wie raffiniert der Betrüger vorgeht.
Seit dem 14. April bemühe ich mich im Nachgang zur Anfrage von Frau Lopez (http://www.kritik-relativitaetstheorie.de/Anhaenge/Anfrage%20LIGO-Experiment.pdf) vom Einstein-Institut eine sachliche Aufklärung über die messtechnischen Voraussetzungen des LIGO-Experiments zu erhalten. Leider sind drei der dortigen Direktoren nicht imstande, meine einfachen Fragen zu beantworten, obwohl sie als co-Autoren bei der LIGO-Veröffentlichung verantwortlich zeichnen.
Wenn sich dann herausstellt, dass das veröffentlichte Signal gar nicht durch die wenigen Photonen erzeugt werden kann, die durch die Verschiebung eines Spiegels um ein Tausendstel eines Protonenradius zu erwarten sind, und die Autoren dem auch gar nicht widersprechen, dann geben sie damit zu, dass sie einem Betrug aufgesessen sind, so dass man sie mit Recht “unbedarft” nennen darf.
Es macht keinen Sinn, in diesem Blog über die Stichhaltigkeit der LIGO-Messungen zu diskutieren, solange das mitverantwortliche Einstein-Institut sich weigert, konkrete Angaben zur Messtechnik zu machen. Eine Eichkurve – Spiegelverschiebung vs. Strahlungsdruck auf die Spiegel – liegt nicht vor, so dass das Messergebnis völlig in der Luft hängt. Unbegreiflich, dass das Einstein-Institut seinen Namen für diese lückenhafte Veröffentlichung, die man als Betrug klassifizieren muss, hergegeben hat.
PS: Soweit ich weiß, ist Herr Wappler kein Mitglied des Einstein-Instituts und war an den Messungen nicht beteiligt. Er kann daher keine sachdienlichen Angaben zur Messtechnik machen.
Das hört sich für mich nicht so an, als ob es Ihnen um die Sache ginge. Wenn Herr Wappler oder andere Kommentatoren Ihnen in den Blogkommentatoren erklären, was an Ihren Argumenten (auf denen ja ihre vorschnellen und aus meiner Sicht sachlich unbegründeten Betrugsvorwürfe beruhen) falsch ist, warum weigern Sie sich, das zur Kenntnis zu nehmen oder auch nur in Betracht zu ziehen?
Sehr sonderbar.
Der researchgate-Murks wurde doch schon komplett zerlegt 🙂
Warum werden Kommentare von mir nicht mehr veröffentlicht, obwohl ich sieben – 6 = 1 ausrechnen kann?
Wenigstens Algebra klappt noch 😉
Nun klappt es doch! Sie können obige Frage wieder löschen.
Herr Pössel!
Geh zum Schmied und nicht zum Schmiedl. Herr Wappler konnte auf meine sachlich begründeten Argumente gar nicht antworten, weil er sich nach dem 12. Februar hier nicht mehr gemeldet hat, und ich erst am 19. April meine Fragen und Argumente, auf die das Einstein Institut nicht antworten wollte, hier eingestellt habe. Auch Herr Senf und Sie selbst konnten nichts zur Beantwortung meiner Fragen nach Gleichheit und Konstanz der Lichtleistung in beiden Armen, sowie Unterdrückung des unvermeidlichen Falschlichts beitragen.
Ihre Motivforschung geht völlig daneben und beweist nur, dass Ihnen die Sache, von der Sie offenbar nichts verstehen, völlig gleichgültig ist. Für einen Physiker, der sein Leben lang sich bemüht hat, der physikalischen Wahrheit auf den Grund zu gehen, ist es unerträglich mit anzusehen, wie Betrüger in Amerika durch unseriöse, marktschreierische marketing Shows die seröse Physik kaputt machen. Es ist einfach nur traurig, dass ein deutsches Max-Planck-Institut diesen Betrug indirekt unterstützt, indem seine Direktoren sich als co-Autoren einschreiben lassen, aber offensichtliche Fragen, die das Messprinzip betreffen, nicht beantworten können.
Ich hoffe nicht, dass an Ihrem Max-Planck-Institut eine ähnliche Ignoranz auf dem eigenen Fachgebiet vorherrscht. Niemand macht Ihnen einen Vorwurf daraus, dass Sie von Interferometrie nicht mehr als das primitivste Grundwissen beherrschen. Doch so viel Urteilskraft sollten Sie schon haben, dass Sie die notwendigen praktischen Grundvoraussetzungen für dieses Experiment quantitativ abschätzen können.
Selbst wenn Sie das nie gelernt haben, sollten Sie sich wenigstens darüber wundern, wie man mit konventionellen Mitteln die bis dahin unerreichte relative Mößbauer-Genauigkeit um einen Faktor eine Million übertreffen konnte. Natürlich muss man in einem solchen Fall dokumentieren, wie man mit Hilfe von 10(-7) W zusätzlicher Laserleistung die Spiegel um die Distanz von ein Tausendstel Protonenradius innerhalb 200 ms verrückt hat, und das mit einem s/n Verhältnis von 20 nachweisen kann. In der Tat ist es “sonderbar”, dass dieser Nachweis nicht vorliegt. Eigentlich ist nichts leichter als das, denn man muss auf kein singuläres Ereignis warten, sondern bewegt kontrolliert die Spiegel mit Strahlungsdruck. Warum dokumentiert man nicht dieses selbstverständliche Vorexperiment?
Sie wissen, dass die PTB nach dreijährigem Widerstand schließlich einräumen musste, nicht gewusst zu haben, ob überhaupt der Sagnac-Effekt in der Uhrensynchronisation beim Neutrino-Experiment berücksichtigt worden war. Wollen Sie, dass einem Max-Planck-Institut eine ähnliche Blamage widerfährt? Oder wollen Sie lieber daran arbeiten, dass in der Physik seriöse Standards, die man früher jedenfalls schon im Praktikum gelernt hat, aufrecht erhalten bleiben?
Mannomann. Wieder nur wildes Herumgeschimpfe, Betrugsgeraune, aber immer noch keine Antworten auf die Einwände gegen ihre ursprünglichen Argumente hier. Aber mir vorwerfen nicht an der Sache interessiert zu sein. Schon klar.
Wenn Sie bei Ihrer Anfrage an das Albert-Einstein-Institut in ähnlich sympathieheischendem Duktus formuliert haben, wundert mich nicht, wenn Sie von den Kollegen ignoriert worden sind. Was für Sie dann natürlich der klare Beweis gewesen sein dürfte, dass die Kollegen Ihre Fragen gar nicht beantworten *können*. Und so dreht sich das Karussell weiter.
Sorry, aber das führt zu nichts. Ich werde mir sicher irgendwann noch einmal genauer anschauen, ob und wie man mit Größenordnungsbetrachtungen reproduzieren kann, was die GEO600- und LIGO-Rauschkurven zeigen, und wieweit das Signal darüber liegt. Aber große Priorität haben diese Überlegungen bei mir derzeit nicht.
Erfreulicherweise hat meine scharfe Kritik Sie endlich zu der Einsicht gebracht, dass Größenordnungsbetrachtungen notwendig sind, um die Glaubwürdigkeit völlig unwahrscheinlicher “Ergebnisse” beurteilen zu können. Diese Hausaufgabe hätten Sie schon längst erledigen können, statt die Öffentlichkeit mit Trivialitäten wie sin (omega t) – sin (omega t) = 0 abzuspeisen.
Dem Einstein-Institut steht eine seriöse Prüfung des LIGO-Resultats noch bevor. Niemand hat dort offenbar eine Eichkurve “Spiegelauslenkung – Strahlungsdruck” eingefordert, obwohl deren Veröffentlichung unabdingbare Voraussetzung zum Nachweis der millionenfachen Verbesserung bisher erreichter relativer Genauigkeit ist.
Wenn ich geschrieben habe, dass die dortigen MPG-Direktoren meine Fragen nicht beantworten “können”, so ist das schmeichelhaft, denn ich müsste sie sonst schlecht erzogene Menschen nennen, die noch nicht mal den Eingang einer höflichen und sachlichen Anfrage bestätigen (http://www.kritik-relativitaetstheorie.de/Anhaenge/Anfrage%20LIGO-Experiment.pdf). Immerhin hat Herr Nicolai versichert, dass er von der Sache nichts verstehe, aber auch den Anstand besessen, sich nicht als co-Autor eintragen zu lassen. Doch was ist mit den “Experten”? Sie schweigen…
Leider nicht erstaunlich, aber trotzdem durchaus unverschämt ist die Selbstverständlichkeit, mit der Sie wahrheitswidrig behaupten, es sei Ihre Kritik gewesen, die mich bewogen hätte, die Beschäftigung mit Größenordnungsbetrachtungen auf meine To-Do-Liste zu setzen.
Dass Sie mit derartigen Fehlschüssen, gepaart mit durchaus scharfem Ton, unvorteilhaften Annahmen über Ihre potenziellen Gesprächspartner und – siehe die von Ihnen ja nach wie vor ignorierten Antworten auf Ihre Kommentare hier – physikalischen Fragwürdigkeiten bei vermutlich so gut wie allen mit dem Thema befassten Physikern schnell den Eindruck hervorrufen, dass ein Eingehen auf Ihre Fragen nichts bringen dürfte, liegt auf der Hand. Man muss ja glücklicherweise nicht über jedes Stöckchen springen, was einem hingehalten wird.
Für die Leser dieses Blogs dürfte unsere Diskussion hier auch herzlich wenig bringen. Brechen wir sie bitte an dieser Stelle ab. Auf die kritischen Stellungnahmen zu Ihren Kommentaren hier in meinem Blog dürfen Sie natürlich gerne eingehen; das wäre jetzt eine gute Gelegenheit.
Wodurch Sie inspiriert wurden, meine Größenordnungsabschätzungen auf Ihre To-Do-Liste zu setzen, ist unerheblich. Doch es ist erfreulich, wenn Sie zwei Monate nach Bekanntgabe der “Messung” vom 14.9.15 endlich versprechen, jene 5-10 Minuten aufzuwenden, um meine Abschätzungen, welche das veröffentlichte Ergebnis des LIGO-Experiments als Betrug entlarven, nachvollziehen zu wollen. Schon einmal hat ein Herr Neyrat am 13. Februar ähnlich wie ich gefragt, aber auch er hat keine tragfähige Antwort bekommen. Höchste Zeit also, wenn Sie sich jetzt dem Problem widmen.
Es gab keine inhaltlich-quantitative Reaktion auf meinen Kommentar vom 19. April. Wozu hätte ich also Stellung nehmen sollen? Lediglich ein Herr Senf behauptete, ich hätte mich um einen Faktor 5000 vertan, ohne das zu beweisen. Meine Nachfrage, wie er die Aufhellung des Dunkelfelds berechnet, hat er nicht beantwortet. Diese Frage hätten auch nur die Autoren des LIGO-Reports exakt und substantiell beantworten können, doch ihre Repräsentanten schweigen obstinat. Selbst wenn man jenen Faktor 5000 unbesehen akzeptiert, bräuchte man eine Photodiode zum Nachweis des Lichts im Dunkelfeld, die einen Dunkelstrom nicht größer als 1/1000 Picoampere hat. Eine solche Diode ist mir jedenfalls nicht bekannt.
Wenn Sie quantitative physikalische Diskussionen als “Springen über hingehaltene Stöckchen” empfinden, dann offenbart dies eine wissenschaftliche Auffassung von Physik, die mir fremd ist. Rudolf Mößbauer hat mir als seinem ersten Kandidaten in München noch in der Prüfung eingeschärft, dass qualitatives Reden in der Physik fruchtlos bleibt, wenn es nicht durch ständiges, zumindest halb-quantitatives Denken begleitet wird. Diese Vorgehensweise scheint aber weder Ihnen noch den Direktoren am Einstein-Institut vertraut zu sein, denn sonst würden sie nicht auf einen plumpen Betrug hereinfallen, bei dem eine Simulation als Messergebnis verkauft wird.
Ich denke, dass es für Leser dieses Forums, falls sie an der physikalischen Wahrheit interessiert sind, durchaus nützlich sein kann, sich quantitative Gedanken über angebliche Messresultate zu machen. Mit Spannung erwarte ich, ob Ihre quantitative Abschätzung zum interferometrischen Nachweis einer Spiegelverschiebung von 10^(-18) m sich von der meinigen wesentlich unterscheidet. Wenn Sie damit nicht weiterkommen, können Sie ja versuchen, sich beim Einstein-Institut Rat und Auskunft, insbesondere über die bisher noch nicht veröffentlichte Eichkurve zu holen. Falls man Sie einer Antwort würdigt, wäre es gut, wenn Sie deren Inhalt an dieser Stelle mitteilten.
“Stöcken springen” wäre, jetzt auf jede der vielen Verzerrungen, kleinen Ungenauigkeiten etc. in Ihrem letzten Kommentar einzugehen.
Bleiben wir doch stattdessen bei der Sache selbst. Stellung nehmen könnten Sie z.B. zu der recht ausführlichen schon erwähnten Überschlagsrechnung von Frank Wappler. Oder zu den kritischen Rückfragen zu Ihren Kommentaren hier. Z.B. warum Sie hier aus einer dimensionslosen Amplitude von 10-21 relativer Längenänderung eine Verschiebung von 10-21 m machen und damit in Ihrer Rechnung mal eben so eine gehörige Anzahl von Zehnerpotenzen einfach unter den Tisch fallen lassen. Oder wo Ihre Behauptung mit dem angeblich exponentiellen Abfall kommt. Wie sieht’s aus?
Eine Spiegelverschiebung von 10^(-18) m wurde von LIGO behauptet. Bezogen auf eine Messstrecke von 1000 m ergibt dies eine relative Messgenauigkeit von 10^(-21), welche jene des Mössbauereffekts um 6 Größenordnungen übertrifft. Sie wird auch in diversen LIGO-Papieren erwähnt und wurde von Speicher (NZZ) um den Faktor 100 000 hochskaliert. Dieses Beispiel hat Frau Lopez bewogen, beim Einstein-Institut nachzufragen, aber man hat sie für dumm hingestellt, weil sie glaube, die Messstrecke sei 400 000 km gewesen. Mein Sohn hat diese Messgenauigkeit auf ein Haar von 10 Mikron angewandt und landete beim nächsten Fixstern in 4 Lichtjahren Entfernung. Kein vernünftiger Mensch kann glauben, dass man eine so winzige Spiegelverschiebung in Relation zu 4 Lichtjahren messen kann, doch von LIGO wird frech behauptet es ginge.
Als Physiker hat man in Kenntnis von Naturgesetzen die Möglichkeit zu prüfen, ob die Behauptungen von LIGO wenigstens den Anschein von Glaubwürdigkeit haben. Daher habe ich ebenso wie Herr Neyrat überlegt, dass eine Phasenverschiebung von 2 pi 10^(-18) m / 10(-6) m = 2 pi 10(-12) (Neodymlaser) interferometrisch zu messen wäre. Bei exakter Amplitudengleichheit der interferierenden Strahlen wird das Dunkelfeld aufgehellt, so dass eine Intensität von 36×10^(-24) x 100 kW nachgewiesen werden muss. Das ergibt einen Photonenfluss von 20/s oder 4 Photonen für den “merger”. Über die Berechnung der “Dunkelheit” in einem Interferenzmuster können Sie in meinem Papier https://www.researchgate.net/publication/273333158_Phase_and_frequency_shift_in_a_Michelson_interferometer z.B. Formel (4) nachlesen.
Das einmalig “gemessene” Signal besteht nicht aus 4 spikes, kann deshalb auch keine Messung sein, sondern bestenfalls eine Simulation oder ein “hoax” wie die Amerikaner sagen. Um eine solche Abschätzung zu machen, muss man nicht besonders gescheit sein, sondern nur über ein ausreichendes Maß an Grundwissen verfügen, sowie den selbstverständlichen kritischen Geist eines Wissenschaftlers besitzen. Beides scheint den Herrschaften vom Einstein Institut zu fehlen.
OK, Schritt für Schritt.
Als erstes: Das Licht ist in LIGO ja nun einmal nicht wie in einem einfachen Interferometer einmal hin, einmal zurück unterwegs, sondern deutlich länger. Bei GEO600 ist das einfach (mehrfaches Hin- und Herlaufen); bei LIGO als Fabry-Perot-Interferometer kommt noch etwas Statistik hinzu.
In dem Kommentar von Herrn Wappler, auf den ich Sie wiederholt hingewiesen habe aber auf den Sie aus mir unerfindlichen Gründen bislang nicht eingehen wollten, ist auf die LIGO-Caltech-Webseite verlinkt, wo als effektive Länge aufgrund des Fabry-Perot-Aufbaus 1120 Kilometer angegeben sind. Um also mal mit dem einfachsten Fehler anzufangen: Warum ignorieren Sie diesen Faktor in Ihrer Rechnung völlig?
Bleibt noch zu ergänzen:
1) Was verstehen Sie unter einer “dimensionslosen Amplitude”? Bei mir kommt dieser Begriff nicht vor.
2) Ich habe niemals von einer Verschiebung von 10^(-21) m gesprochen, sondern nur LIGO mit 10^(-18) m ( = 1/1000 Protonenradius) zitiert.
3) Von “exponentiellem Abfall” habe ich auch nicht gesprochen. Ich weiß nicht, was Sie damit meinen.
4) Herr Wappler hat zu meinem Kommentar vom 19. April keine Stellung genommen. Es gab keine kritische Rückfrage, wenn Sie von Herrn Senfs unbegründeter Behauptung absehen.
Sorry, da hatte ich Sie mit Herrn Marquardt durcheinandergebracht, der hier eine ähnliche Argumentation vorgebracht hat. Ich bitte um Entschuldigung.
Aber der Kommentar von Herrn Wappler (zu Herrn Marquardt, nicht zu Ihnen) ist für Ihre Argumentation durchaus relevant, da es genau um die Art von Größenordnungsabschätzung geht, die Sie vornehmen möchten: https://scilogs.spektrum.de/relativ-einfach/gravitationswellen-warum-die-aufregung/#comment-22812
Markus Pössel schrieb (30. April 2016 23:53):
> Sorry, da hatte ich Sie mit Herrn Marquardt durcheinandergebracht, der hier eine ähnliche Argumentation vorgebracht hat. Ich bitte um Entschuldigung. Aber der Kommentar von Herrn Wappler (zu Herrn Marquardt, nicht zu Ihnen) ist […]
Vielen Dank für die Richtigstellung. (Auch mir selbst war zwischenzeitlich leider entfallen, dass ich damals auf einen Kommentar von Siegfried Marquardt geantwortet hatte, und nicht auf einen von Dr. Wolfgang Engelhardt; sonst hätte ich mich vielleicht im April zu einer entsprechenden Wiederholung aufgerafft.)
Allerdings möchte ich nicht unerwähnt lassen, dass ich auch für einige meiner eigenen Kommentare in diesem SciLog eine erkennbare Kenntnisnahme (wenn nicht sogar eine Beantwortung) vermisse;
im gegebenen Zusammenhang z.B. darauf:
https://scilogs.spektrum.de/relativ-einfach/gravitationswellenquellen-gw-teil-3/#comment-22761
Gut, dass Sie sich nun mehr der realistischen Problemstellung widmen. Man kann die Sache auch von hinten aufziehen und annehmen, dass der Dunkelstrom der Photodiode das Begrenzende sei. Falschlicht und Amplitudendifferenz der interferierenden Strahlen sollen völlig vernachlässigbar sein, was nicht realistisch ist, wozu allerdings vom Einstein-Institut keine Angaben gemacht werden.
Nehmen wir einen Dunkelstrom von 1 Picoampere an, dann musste das Signal bei s/n = 20 etwa 2×10(-11) A betragen. Dies entspricht bei einer spektralen Empfindlichkeit von 0.5 A/W einer Lichtleistung von 4×10(-11) W oder einem Faktor von 4×10^(-16) im Vergleich zur Gesamtleistung von 100 kW. Die Wurzel daraus ergibt 2×10^(-8) Amplitudenverhältnis zwischen Dunkel- und Hellfeld, entsprechend einer Verschiebung von d = 3×10(-15) m, was 3000 mal größer ist als ein Tausendstel Protonenradius. Auch wenn man das Licht 250 mal hin und her laufen lässt, fehlt immer noch eine Größenordnung.
Lassen Sie mich noch eine weitere Anmerkung machen: Nehmen wir mal eine Frequenz für die Gravitationswelle von 300 Hz an, so hat sie eine Wellenlänge von 1000 km wenn sie sich mit Lichtgeschwindigkeit ausbreitet. Bei einem Abstand von 4.5 km zwischen Strahlteiler und Spiegel werden beide in etwa gleicher Weise von der Welle bewegt, d.h. der Abstand ändert sich nicht. Mit d = 0 gibt es interferometrisch jedoch nichts zu messen.
Ich habe keine große Lust, mit diesen halbquantitativen Spekulationen fortzufahren, wo doch im Einstein-Institut alle nötigen Informationen vorliegen müssen. Insbesondere eine Veröffentlichung der Eichkurve – nämlich gemessene Verschiebung als Funktion des Strahlungsdrucks auf den Spiegel – würde Klarheit schaffen, so dass man nicht mehr über Dunkelstrom, Falschlicht, Amplitudengleichheit rätselraten müsste. Leider mauert das Institut und erhöht damit nicht die Glaubwürdigkeit der Messung.
Vielleicht gelingt es Ihnen, die relevanten Informationen, die das Institut bisher geheimhält, aus den Kollegen herauszukitzeln. Ich habe mein Möglichstes getan, aber leider auch vom Vereinsvorsitzenden Stratmann, weder eine Antwort noch Unterstützung für mein Anliegen erfahren. Irgendwann wird der Betrug, dem das Institut aufgesessen ist, auffliegen, aber dann ist es zu spät, um die Blamage noch zu verhindern.
Zitat “… Anmerkung machen: Nehmen wir mal eine Frequenz für die Gravitationswelle von 300 Hz an, so hat sie eine Wellenlänge von 1000 km wenn sie sich mit Lichtgeschwindigkeit ausbreitet. Bei einem Abstand von 4.5 km zwischen Strahlteiler und Spiegel werden beide in etwa gleicher Weise von der Welle bewegt, d.h. der Abstand ändert sich nicht. Mit d = 0 gibt es interferometrisch jedoch nichts zu messen.”
Dr. Engelhardt, jetzt aber:
wir haben einen Quadrupol – 2 senkrechte Arme mit gegenläufigen Amplituden.
Die Armlängen werden “verglichen” per Interferenz, da ist kein d=0, es wackelt.
Zitat “… Ich habe keine große Lust, mit diesen halbquantitativen Spekulationen fortzufahren, wo doch im Einstein-Institut alle nötigen Informationen vorliegen müssen.”
Dr. Engelhardt, und
diese “halbquantitativen Spekulationen” sind aber alle nur Ihre eigenen.
Wir “anderen” kennen die Informationen aus der veröffentlichten Literatur
und müssen nicht dem Einstein-Institut zur Nachhilfe auf den Keks gehen.
Wir haben rechtzeitig vorher verstanden wie Gravitationswellen laufen.
Wie sonderbar, dass Sie gerade dann die Lust an Größenordnungs-Abschätzungen verlieren, als sich zeigt, dass diese, sobald man Ihre Missverständnisse zum Detektionsprinzip herausrechnet, für LIGO recht gute Ergebnisse erbringen.
Mit einer effektiven Armlänge von 1120 km dank Fabry-Perot (siehe die verlinkte LIGO-Seite) bin ich bei einer relativen Längenänderung von 1e-21 schon bei einer Armlängenänderung von 1e-15 Metern, und damit bereits in der Größenordnung von dem, was Sie selbst als interferometrisch nachweisbar angeben. Ändert das Ihre Einschätzung? Und wenn nicht, warum nicht?
Auf den grundlegenden Irrtum, beide Endspiegel würden ” in etwa gleicher Weise von der Welle bewegt” ist Herr Senf ja schon eingegangen – Gravitationswellen sind Quadrupolstrahlung. Interessanter wird es bei noch größeren Armlängen; da bekommt man dann tatsächlich eine Verminderung der Empfindlichkeit, wenn die Schwingungszeit der Welle gerade der mittleren Licht-Verweildauer im Detektor entspricht. Nicht, weil die Spiegel dann “in etwa gleicher Weise von der Welle bewegt” werden, sondern weil der Einfluss auf das im Detektor befindliche Licht (analog zur kosmischen Rotverschiebung) sich unter diesen Verhältnissen gerade weghebt. Das begrenzt Detektoren wie eLISA. (Diesen Effekt zu modellieren war Ziel meiner erwähnten angefangenen einfachen Modellbetrachtungen – und eben derjenige Teil, der mehr als 5 bis 10 Minuten benötigt und den ich sobald ich Zeit habe noch weiterverfolgen werde. Die Animationen im Blogbeitrag oben stammen aus diesen früheren Überlegungen.)
Die Daten, anhand derer man die Empfindlichkeit der Messungen beurteilen kann, sind selbstverständlich in der Fachliteratur zugänglich. Mit nur etwas Googlen sollten Sie die Tests des DC-Auslesemechanismus für Advanced LIGO finden, die Rauschkurven, die auf tatsächlichen Messungen beruhen, die Testsignale durch gezielte Spiegelauslenkung und wie sie bei den Photodetektoren ankamen, und vieles mehr. Wissenschaftlich gesehen ist das alles vollständig dokumentiert. Die einzige Lücke gibt es zwischen der dort standardmäßig verwendeten Fourierdarstellung (mit power spectral density bzw. spectral energy) und dem für die allgemeine Öffentlichkeit sehr viel einfacher verständlichen Ortsbild (Verschiebung der Spiegel und entsprechender Phasenunterschied). Da eine Brücke zu schlagen ist für physikdidaktisch interessierte Menschen wie mich interessant, aber man kann es den Forschern nicht vorwerfen, wenn sie diesen für ihre Forschung eher nebensächlichen Aspekt nicht noch selbst mit abdecken.
Wie sollte sich meine Einschätzung ändern? Meine Fragen an das Einstein-Institut sind noch immer nicht beantwortet. Auch der geschäftsführende Direktor ist unfähig, die relevanten Informationen dem veröffentlichten Material zu entnehmen. Er selbst sei kein Experte in Laserphysik, in diesem Sinn also “Laie”, für den die Publikationen “nicht immer in verständlicher Form” geschrieben seien. Überraschenderweise kann er auch keinen Experten in seinem Haus benennen. Meine direkte Anfrage bei Herrn Danzmann konnte oder wollte dieser nicht beantworten, so wenig wie die beiden anderen Direktoren, die in der Autorenliste aufgeführt sind.
Es ist daher zu begrüßen, dass Sie nunmehr als “physikdidaktisch interessierter Mensch” eine “Brücke” über die “Lücke” schlagen wollen, welche darin besteht, dass das Messsignal, nämlich der “strain” zwischen beiden Interferometerarmen, als Funktion der Zeit präsentiert wird, während ein ebenso großer strain, der durch kontrollierbaren Strahlungsdruck in ähnlicher Wellenform erzeugt wird, dem Leser als Funktion der Zeit vorenthalten wird. Mir ist es trotz Googelns nicht gelungen, ein solches Eichsignal zu finden. Umso mehr bin ich auf Ihre Eichsignale als Funktion der Zeit gespannt, die Sie den einschlägigen Publikationen angeblich entnehmen können. Auch Herr Nicolai und die Direktoren am Einstein-Institut werden sich freuen, wenn Sie ihnen Ihre Signale schicken und so die “Lücke” schließen.
Es wird sich dann zeigen, ob das Dunkelfeld hinreichend “dunkel” war, weil die Amplituden der interferierenden Strahlen reproduzierbar exakt gleich eingestellt und das Falschlicht total unterdrückt werden konnte. Man wird auch sehen, ob der stets vorhandene Lichtdruck auf die Spiegel, welcher 12 Größenordnungen größer als der “Eichdruck” ist, hinreichend stabil war, so dass durch Schwankungen keine vergleichsweise winzige Spiegelauslenkungen hervorgerufen werden konnten. Natürlich benötigt man zum Zeitpunkt des “Ereignisses” oder kurz danach nicht nur eine, sondern viele kontrollierte Spiegelauslenkungen, um die Reproduzierbarkeit der Apparatur zu testen. Leider geht ja das nicht mit einer einzigen Spiegelverschiebung am 14.9.2015.
Auf den Nebenschauplatz, ob eine Gravitationswelle den Abstand zwischen Strahlteiler und Spiegel überhaupt zu ändern vermag, möchte ich zu gegebenem Zeitpunkt eingehen. Noch immer stehe ich nämlich auf dem Standpunkt, dass es gar keinen Nachweis einer Welle gibt, weil die behauptete relative Genauigkeit des Systems von 10^(-21) nicht durch Veröffentlichung einer relevanten Eichkurve nachgewiesen wurde.
Wenn Sie als Grund zur Skepsis und kritischen Nachfrage bestimmte Rechnungen durchführen und sich jetzt aufgrund des von Ihnen vergessenen Faktors 1000 herausstellt, dass die LIGO-Behauptungen im Gegenteil im Lichte solcher Rechnungen durchaus plausibel sind, könnte man naiv denken, dass Sie Ihre Meinung entsprechen anpassen.
Dass Sie die Korrektur schlicht übergehen, dieser offenbar nicht den geringsten Einfluss auf Ihre Einschätzung zuschreiben und munter mit der nächsten Frage weitermachen, zeigt aber doch schon ziemlich deutlich, wie wenig es Ihnen hier um die eigentliche Sache ging. Genau diese Sorte von Verhalten war es damals ja auch, die mich veranlasste, die Korrespondenz mit Frau Lopez abzubrechen. Wenn starke Gegenargumente oder das Aufzeigen von Unstimmigkeiten schlicht ignoriert werden, dann ist klar: hier geht es nicht um sachliche Diskussion, und jeder Versuch sachlich zu diskutieren ist von vornherein zum Scheitern verurteilt.
Vor diesem Hintergrund kann ich gut verstehen, dass sich die Potsdamer und Hannoveraner Kollegen auf diese Sorte von unfruchtbarem Austausch gar nicht erst einlassen.
Ihre “relevante Eichkurve” ist jedenfalls eine Nebelkerze. In Fourierdarstellung sind diese Kurven schließlich allgemein zugänglich. Und die Frage nach den Fluktuationen des Strahlungsdrucks wird durch jene Kurven auch direkt beantwortet. Wenn Ihnen die Sache wichtig ist, sollten Sie sich – wie es ja auch von jedem Wissenschaftler erwartet wird, der in der wissenschaftlichen Diskussion mitreden möchte – schlicht in die entsprechenden Konventionen und Konzepte einarbeiten.
Falls Sie das nicht verstanden haben sollten, noch einmal: Ich gehe zum Schmied und nicht zum Schmiedl, in diesem Fall zum Einstein-Institut. Keine einzige meiner Fragen wurde von dort befriedigend beantwortet. Der geschäftsführende Direktor selbst sah sich außerstande, die angefragten Informationen der Fachliteratur zu entnehmen und gemäß dem, was Sie hier schreiben, gelingt es Ihnen auch nicht. Es ist mir völlig unerfindlich, warum Sie die Veröffentlichung von LIGO verteidigen, mit der Sie selbst ja gar nichts zu tun haben.
Es ist bedauerlich, dass Direktoren des Einstein-Instituts darauf hereingefallen sind und sogar ihren Namen auf das Papier gesetzt haben. Es gelingt nun einmal nicht, den Nachweis zu führen, dass man einen “strain” von 10^(-21) gemessen hat, indem man in gleicher Weise die kontrollierte Spiegelauslenkung als Funktion der Zeit demonstriert. Solange dies nicht geschieht, muss das einmalige Signal als eine betrügerische Irreführung der Öffentlichkeit eingestuft werden, denn es wird nicht plausibel gemacht, dass die Amplituden der interferierenden Strahlen auf 10^(-12) genau gleich waren, dass das Falschlicht um 24 Größenordnungen unterdrückt werden konnte, dass die Laserleistung von 100 kW auf 10^(-12) genau über lange Perioden konstant gehalten werden konnte.
Inzwischen habe ich Kenntnis vom Datenblatt der verwendeten Dioden erhalten: http://www.excelitas.com/Lists/Photodiodes%20and%20Phototransistors/DispForm.aspx?ID=135. Der Dunkelstrom ist 25 nA, das gemessene Signal also mindestens 5×10^(-7) A entsprechend einer Lichtleistung von 5×10^(-12) W, bzw. einer Phasendifferenz von 2×10^(-6). Dazu gehört eine Spiegelverschiebung von 3×10^(-13) m und nicht 10^(-18) m. Es fehlen mindestens 5 Größenordnungen, die auch durch einen Faktor 1000 nicht wettgemacht werden können. Und all dies unter Beibehaltung der drei Grundvoraussetzungen, deren Einhaltung das AEI nicht zu bestätigen vermag! Es ist kein Wunder, dass das AEI betreten schweigt. Cum tacent clamant, pflegte Cicero in einem solchen Fall zu sagen.
Auch Sie sind in Ihrem Versuch gescheitert, eine “Brücke” über die “Lücke” zu schlagen, denn Sie konnten offenbar kein Eichsignal als Funktion der Zeit aus den veröffentlichten Daten extrahieren. Ihre unbewiesenen Behauptungen stehen auf derselben Stufe wie die unbewiesene Behauptung von LIGO, eine Gravitationswelle während der Testphase der Apparatur am 14.9.2015 gemessen zu haben.
Tatsächlich, LIGO used off-the-shelf Excelitas C30665GH InGaAs PIN Photodiodes.
Wellenlänge des Hochleistungslasers ist 1064 nm, die Quantenausbeute macht’s.
Was soll Dunkelstrom, man ist bis zur Grenze des Quantenrauschens gegangen.
Die Gravitationswelle wurde doch unabhängig an zwei Detektoren gemessen,
wurden die etwa gleichzeitig beschummelt nach Ihrer unmaßgeblichen Meinung?
Sie gehen aber mit ziemlich unrealistischen Ansprüchen zum Schmied und verlangen, der solle doch bitte alles fallen lassen und für Sie unter stundenlangem persönlichen Einsatz häppchenweise die Fachliteratur aufarbeiten. Sich zu wundern, warum die Kollegen da abwinken, zeugt schon von einigem Realitätsverlust.
Ich betrachte meine Antworten übrigens gar nicht als Versuch, die Brücke zu schlagen. Das würde deutlich mehr Aufwand erfordern, als ich derzeit leisten kann.
Einen elementaren Denkfehler machen Sie aber ganz offensichtlich, nämlich die Frequenzabhängigkeit zu vernachlässigen. LIGO behauptet ja nirgends, in jedem Frequenzbereich eine GW mit Amplitude 1e-21 nachzuweisen – wenn Sie mal einen Blick in die entsprechenden Artikel werfen, werden Sie schnell entsprechende Rauschkurven sehen. Insofern hängt auch der Einfluss des Dunkelstroms von dessen Frequenzspektrum ab (und dürfte in den entsprechenden Kurven auch unter Elektronikrauschen oder noch feiner aufgeschlüsselt verzeichnet sein)..
Soviel ich weiß, wurden mehrfach fake-Signale eingespeist, um die Auswerteverfahren zu überprüfen. Möglicherweise war das nach fünf Monaten veröffentlichte Signal ein solches fake-Signal. Warum brauchte man so lange, um seine angebliche “Echtheit” zu erkennen? Es sah doch schon am 15.9.2015 so “überzeugend” aus wie jetzt, oder?
Das Signal muss auf jeden Fall 20 mal größer als der Dunkelstrom gewesen sein, sonst hätte man nicht von einem s/n von 24 sprechen können. Dazu gehört eine Spiegelverschiebung, welche die behauptete um 5 Größenordnungen übertrifft. Warum äußert sich das AEI nicht zu diesen Fakten? Herr Nicolai ist nach eigenem Eingeständnis ahnungslos, aber warum haben die co-Autoren nicht längst die zum veröffentlichten Signal zugehörige Eichkurve ins Internet gestellt, um alle Zweifel zu zerstreuen? Erhalten sie diese Information auch nicht von den Amerikanern und sind auf Treu und Glauben angewiesen, so wie Herr Nicolai, Herr Pössel und die gesamte Öffentlichkeit?
Ich gebe gerne zu, dass meine Meinung “unmaßgeblich” ist, weil sie auf halb-quantitativen wissenschaftlichen Spekulationen beruht. Aber warum schweigen die “maßgeblichen” Leute im AEI? Ich kann nur wiederholen: Cum tacent clamant.
Ihnen kann man’s wirklich nicht recht machen. Bei den überlichtschnellen Neutrinos beschwerten Sie sich, warum sich die entsprechenden Forscher nicht zusammensetzten, alle Unsicherheiten abklärten und erst dann an die Öffentlichkeit gingen, wenn sie ein belastbares Ergebnis vorzuweisen hätten. Jetzt, wo es die LIGO-Mitglieder genau so gemacht haben, alle Störeinflüsse in ihrem ja in der Tat komplexen Detektor monatelang überprüft und das Ergebnis erst dann der Öffentlichkeit präsentiert haben, als es in einer Fachzeitschrift mit Peer Review angenommen war, meckern Sie über die Verzögerung.
Ihr Geraune über das angebliche Schweigen des AEI ist und bleibt absurd. Ja, sorry, da hat offenbar niemand die Lust, mit Ihnen stundenlang einen geführten Spaziergang durch die Fachliteratur zu unternehmen. Das ändert nichts daran, dass die LIGO-Wissenschaftler in der Fachliteratur alle Störquellen, Gegenmaßnahmen, Auswertungen etc. umfangreich dokumentiert haben. Auch die Rauschkurven sind da, aber eben in der fouriertransformierten Form.
Jetzt läuft das Theater hier jedenfalls lang genug; insbesondere, da Sie diesen Kommentarbereich hier offenbar nur als Verkündigungsorgan sehen, aber offenbar nicht gewillt sind, aus den Hinweisen auf Ihre Fehlschlüsse auch mal Konsequenzen zu ziehen – wie es für eine echte inhaltliche Diskussion notwendig wäre – ziehe ich an dieser Stelle die Bremse.
[Absurder und unkonstruktiver Kommentar von W. Engelhardt gelöscht. MP]
[Weiterer Kommentar von W. Engelhardt, der die Antworten nach wie vor ignoriert, ebenfalls gelöscht – wie angekündigt. MP]
Wie berechtigt meine Forderung nach interner Überprüfung im Falle des Neutrinoexperiments war, können Sie daran ersehen, dass die PTB schließlich einräumen musste, gar nicht zu wissen, unter welchen Annahmen die Uhrensynchronisation erfolgte (http://kritik-relativitaetstheorie.de/Anhaenge/Ablehnung-Auskuenfte-CERN-Neutrinoexperiment-o.pdf). Dies hätte man gleich ermitteln können und nicht erst 3 Jahre auf eine Klageandrohung durch Frau Lopez warten müssen. Will das AEI etwa auch so lange warten, bis endlich die Unhaltbarkeit der jetzigen „Entdeckung“ zugegeben werden muss?
Sie belehren mich mit den Worten: „Ihre “relevante Eichkurve” ist jedenfalls eine Nebelkerze. In Fourierdarstellung sind diese Kurven schließlich allgemein zugänglich. Und die Frage nach den Fluktuationen des Strahlungsdrucks wird durch jene Kurven auch direkt beantwortet. Wenn Ihnen die Sache wichtig ist, sollten Sie sich – wie es ja auch von jedem Wissenschaftler erwartet wird, der in der wissenschaftlichen Diskussion mitreden möchte – schlicht in die entsprechenden Konventionen und Konzepte einarbeiten.“ Gelten diese Worte nicht umso mehr für den geschäftsführenden Direktor des Einstein-Instituts, dem es offenbar auch nicht gelingt, sich „in die entsprechenden Konventionen und Konzepte einzuarbeiten“, obwohl ihm die Sache doch hoffentlich „wichtig“ ist?
Solange Sie eine Eichkurve (Spiegelverschiebung vs. kontrollierter Strahlungsdruck) eine „Nebelkerze“ nennen, die Sie selbst nicht aus den veröffentlichten Daten extrahieren können, und die auch Sie nicht von den beteiligten Forschern am AEI erhalten, werden Sie Ihrer selbst gewählten Aufgabe nicht gerecht, nämlich komplizierte physikalische Sachverhalte einer breiteren Öffentlichkeit zugänglich zu machen. Im Gegenteil: Immer deutlicher wird für jedermann, dass es gar keine „Entdeckung von Gravitationswellen“ gegeben hat, denn der schlüssige experimentelle Beweis kann nicht präsentiert werden. Meine Bemühungen um eine rationale Diskussion der veröffentlichten Messergebnisse sollten Sie mit inhaltlichen Beiträgen bereichern und sie nicht als „Theater“ abwerten. Sie setzen sich sonst dem Verdacht aus, ebenfalls dem Betrug zum Opfer gefallen zu sein.
Schließlich legen alle vernünftigen physikalischen Abschätzungen nahe, dass die Empfindlichkeit der Apparatur um Größenordnungen zu gering war, um einen relativen strain von 10^(-21) nachzuweisen. Und weiterhin ist nicht einzusehen, wie es bei einer Wellenlänge von 2000 km überhaupt zu einer relativen Verschiebung zwischen Strahlteiler und Spiegel kommen soll. Ihre Animation https://scilogs.spektrum.de/relativ-einfach/wp-content/blogs.dir/210/files/int-working-gw.gif beruht ja gerade auf der Annahme, dass sich die Spiegel relativ zum Strahlteiler bewegen, was aber bei Phasengleichheit an Spiegel und Strahlteiler eben nicht der Fall ist. Warum präsentieren Sie diese irreführende Animation in Ihrem Blog? Oder haben Sie aus c = lambda f niemals die Wellenlänge der angeblichen Gravitationswelle ausgerechnet?
Die von Ihnen geforderte Eichkurve ist solange eine Nebelkerze, wie sie dazu dient, zu behaupten, LIGO hätte die zur Beurteilung erforderlichen Daten nicht offengelegt. Wie schon mehrmals gesagt: Die frequenzabhängigen Rauschkurven, die zeigen, dass die Messung im Nachweisbereich der Detektoren liegt, sind veröffentlicht. Dass Sie diesen Umstand nach wie vor ignorieren und behaupten, die zur Untermauerung des experimentalen Nachweises nötigen Daten lägen nicht vor, zeigt ziemlich deutlich, wer hier Theater spielt.
Dass Sie einmal mehr behaupten, “alle vernünftigen physikalischen Abschätzungen [legten] nahe, dass die Empfindlichkeit der Apparatur um Größenordnungen zu gering war” ist von beeindruckender Vergesslichkeit oder aber von einiger Dreistigkeit. Schon vergessen? Ihre eigene Abschätzung hier zeigt, wenn man den von Ihnen vergessenen Faktor 1000 miteinbezieht, dass die Empfindlichkeit sehr wohl ausreicht. Und ihre andere Abschätzung hier in den Kommentaren hier kommt zu einem falschen Ergebnis, weil Sie die Frequenzabhängigkeit ignorieren – darauf hatte ich Sie hier hingewiesen.
Dass Sie diese konkrete Kritik und diese Korrekturen konsequent ignorieren, dürfte so ziemlich das Paradebeispiel sein für jemanden, der nicht an sachlicher Diskussion interessiert ist und blind in die einmal gewählte Richtung weiterprescht, was auch immer da an Sachinformationen kommen mag.
Auch auf Ihren Fehlschluss mit der Bedeutung der Wellenlänge, den Sie ja bereits hier zum besten gegeben hatten, waren ja bereits die Korrekturen gefolgt: Es geht um Quadrupolstrahlung. Und um transversale Wellen: In meinem Haupttext steht dementsprechend mehrmals, dass die Gravitationswellen bei den Animationen von hinten nach vorne durch das Bild laufen, auf den Betrachter zu. Die läuft definitiv nicht in Richtung der Arme! Auch das ignorieren Sie und wiederholen ihren Fehlschluss erneut.
Insofern wiederhole ich mich jetzt auch: Da Sie diesen Kommentarbereich hier offenbar nur als Verkündigungsorgan sehen, aber offenbar nicht gewillt sind, aus den Hinweisen auf Ihre Fehlschlüsse auch mal Konsequenzen zu ziehen oder auch nur darauf einzugehen – wie es für eine echte inhaltliche Diskussion notwendig wäre – ziehe ich an dieser Stelle die Bremse.
Und tschüss!
Dr. Engelhardt, welch seltsames geometrisches Vorstellungsvermögen?
die “Endspiegel” sind seismisch entkoppelt und aufgehängt, werden mitgenommen.
Laser und Strahlteiler sind festgenagelt, Endspiegel werden relativ dazu bewegt.
Wo haben Sie eigentlich Ihr s/n = 20 her, ich hab ein anderes s/n gelesen.
Hoppla, kaum lösche ich dann doch einmal eine der unbelehrbaren E-Mails von Herrn Engelhardt und schon war offenbar doch ein Missverständnis von allgemeinerem Interesse darin.
Erstens: Der Strahlteiler ist (sieht man auch im Bild oben) ebenfalls frei aufgehängt und seismisch entkoppelt, und benimmt sich wie ein freies Teilchen.
Bei der Darstellung der Abstandsänderungen in einer Animation muss man sich entscheiden, welches Teilchen man als Bezugspunkt nimmt relativ zu dem dann die Abstandsänderungen gezeigt werden. (Das ist die gleiche Situation und die gleiche Wahlfreiheit, wie wenn man die kosmische Expansion in einer Animation darstellt.)
Vielleicht finden wir ja einen Kompromiss, Herr Engelhardt. Ich habe keine Probleme mit einer Sachdiskussion, aber keine Lust auf einen unfruchtbaren und frustrierenden Diskussionsverlauf, wie ich ihn in Diskussionen mit unorthodoxen Kritikern beschrieben hatte.
Ich bin gerne bereit, mit Ihnen weiterzudiskutieren, wenn wir uns auf folgenden Rahmen einigen können:
Wir behandeln nur jeweils eine Frage zur Zeit – Sie können dabei gerne auswählen, womit wir beginnen. (Grund: Diskussionen, in denen viel parallel läuft, sind unübersichtlich und bringen den Lesern hier zuwenig Mehrwert.)
Wir bemühen uns beide jeweils um möglichst kurze Antworten (ein Dialog ist übersichtlicher als eine Abfolge langer Texte, aus der sich die Leser mühsam die Querverbindungen zusammensuchen müssen).
Wir lassen Meta-Aussagen (ich zur Unbelehrbarkeit bestimmter Arten von Kritiker, Sie zu diversen Betrugsvorwürfen etc.) bei unserer Sachdiskussion außen vor und konzentrieren uns auf die Physik.
Wie sieht’s aus?
Herr Senf,
das “combined” s/n Verhältnis von 24 finden Sie auf S. 3 oben der Phys. Rev. Lett. LIGO-Veröffentlichung vom 12.2.2016.
Herr Pössel,
wie Sie wissen, habe ich zuerst 3 Fragen an das Einstein Institut gerichtet:
1) Falschlicht?
2) Gleichheit der interferierenden Strahlen?
3) Konstanz der Laserleistung?
Nachdem ich Kenntnis von der verwendeten Photodiode erhalten habe, weiß ich, dass 5 Größenordnungen an Genauigkeit fehlen, um auf 10^(-18) m Spiegelverschiebung zu schließen. Daher eine weitere Frage:
4) Wie werden diese 5 Größenordnungen überbrückt?
Eine Eichkurve könnte alle diese Fragen gleichzeitig beantworten. In der unveröffentlichten Ref. 63 des LIGO Phys. Rev. Lett. Papiers wird die Eichmethode beschrieben, aber keine Eichkurve (kontrollierter Strahldruck – gemessene Verschiebung als Funktion der Zeit) mitgeteilt. Sie behaupten, diese Information wäre vorhanden. Deshalb meine Frage:
5) Aus welcher Figur des “calibration papers” kann man die Eichkurve extrahieren?
Nach Besichtigung Ihrer Animation muss ich feststellen, dass die Gravitationswelle zwar die Endspiegel zu bewegen vermag, nicht aber den Strahlteiler. Eine Relativbewegung zwischen Spiegel und Strahlteiler ist nur möglich, wenn die Welle unterschiedliche Phase beim Auftreffen auf diese Objekte hat. Bei 2000 km Wellenlänge und 4 km Messstrecke ist das aber praktisch nicht der Fall. Deshalb meine Frage:
6) Nach welchem Mechanismus bewegt eine Gravitationswelle zwei Spiegel unterschiedlich, wenn ihr Abstand klein gegen die Wellenlänge ist, die Spiegel also gleichsinnig mit praktisch gleicher Phase schwingen?
In welcher Reihenfolge möchten Sie sich diesen Fragen nacheinander und einzeln widmen? In der Hoffnung, nicht wieder “gelöscht” zu werden, sehe ich Ihrer Antwort mit Interesse entgegen. “So sieht’s aus.”
Herr Engelhardt: Das sieht doch gut aus!
Ich beginne mit Frage 6). Die passende Illustration zur Antwort finden Sie in Was sind Gravitationswellen? im Abschnitt “Was tut sich da?” – der dort animierte Teilchenkreis zeigt den Effekt einer Gravitationswelle die von hinten nach vorne, senkrecht zur Bildebene auf den Betrachter zu läuft.
Daraus folgt insbesondere, dass die Gravitationswelle sogar ganz ohne Betrachtungen der Wellenlänge per Definition an jedem der dargestellten Orte, in jedem Schnappschuss der Animation, die gleiche Phase hat.
Die Wirkung einer Gravitationswelle (Quadrupolverformung) ist nämlich gerade, dass sie Abstandsänderungen in der Ebene senkrecht zu ihrer Ausbreitungsrichtung hervorruft. In dem hier dargestellten vereinfachten, linearisierten Fall werden in der Phase φ alle Abstände in der Bildebene in y-Richtung um den Faktor 1 + A sin(φ) verändert, und alle Abstände in x-Richtung um den Faktor 1 – A sin(φ) verändert.
Genau diese Abstandsänderung versucht man, mit interferometrischen Detektoren nachzuweisen. Wie das funktioniert, ist im Haupttext dieses Blogbeitrags hier dargestellt.
Markus Pössel schrieb (12. Mai 2016 9:48):
> Quadrupolverformung […]
> In dem hier dargestellten vereinfachten, linearisierten Fall werden in der Phase φ alle Abstände in der Bildebene in y-Richtung um den Faktor 1 + A sin(φ) verändert, und alle Abstände in x-Richtung um den Faktor 1 – A sin(φ) verändert.
Offenbar lassen sich zumindest gewisse Paare von Beteiligten durch „Abstands“-Werte charakterisieren. (Wenn auch vermutlich nicht durchwegs alle, beliebige Paare; was damit zu tun haben dürfte, dass im Wort „Abstand“ der Wortstamm „stehen“ steckt, und im allgemeinen eher Werte der „Lorentzian distance“ eine Rolle spielen.)
Ziehen wir nun mal geeignete gegenüber einander stehende (starre) Beteiligte in Betracht, deren Abstandsverhältnisse untereinander möglichst genau der „Quadrupolverformung in der Bildebene“ bei einem bestimmten (geeigneten) Wert der „Phase φ“ entspräche.
Darunter gäbe es sicherlich z.B. drei Beteiligte (U, X, Y) so dass z.B.
a[ U, X ] / a[ U, Y ] = (1 – A Sin[ φ] ) / (1 + A Sin[ φ] )
und so dass (ebenfalls der Einfachheit halber)
– U und X „ in x-Richtung“ zueinander standen, und
– U und Y „ in y-Richtung“.
Dann liegen einige Fragen nahe, deren Beantwortung ich (auch) sachdienlich fände:
1. Welchen Wert hätte dann das Abstandsverhältnis
a[ X, Y ] / a[ U, Y ]
?
2. Ließen sich darunter zwei weitere Beteiligte (P, Q) finden, deren Abstandsverhältnisse
a[ U, P ] / a[ U, X ] = 1 + A Sin[ φ ]
und
a[ X, P ] / a[ U, X ] = A Sin[ φ ]
bzw.
a[ U, Q ] / a[ U, Y ] = 1 – A Sin[ φ ]
und
a[ Q, Y ] / a[ U, Y ] = A Sin[ φ ]
erfüllen?
3. Ließen sich darunter drei weitere Beteiligte (H, J, K) finden, deren Abstandsverhältnisse
a[ U, H ] / a[ U, P ] = a[ H, P ] / a[ U, P ] = 1/2,
a[ U, J ] / a[ U, Q ] = a[ J, Q ] / a[ U, Q ] = 1/2,
bzw.
a[ P, K ] / a[ P, Q ] = a[ K, Q ] / a[ P, Q ] = ½
erfüllen?
4. Welche Werte hätten dann die Abstandsverhältnisse
a[ U, H ] / a[ U, P ],
a[ U, J ] / a[ U, P ], bzw.
a[ U, K ] / a[ U, P ]
?
Markus Pössel schrieb (12. Mai 2016 9:48):
> Quadrupolverformung […]
> In dem hier dargestellten vereinfachten, linearisierten Fall werden in der Phase φ alle Abstände in der Bildebene in y-Richtung um den Faktor 1 + A sin(φ) verändert, und alle Abstände in x-Richtung um den Faktor 1 – A sin(φ) verändert.
Offenbar lassen sich zumindest gewisse Paare von Beteiligten durch „Abstands“-Werte charakterisieren. (Wenn auch vermutlich nicht durchwegs alle, beliebige Paare; was damit zu tun haben dürfte, dass im Wort „Abstand“ der Wortstamm „stehen“ steckt, und im allgemeinen eher Werte der „Lorentzian distance“ eine Rolle spielen.)
Ziehen wir nun mal geeignete gegenüber einander stehende (starre) Beteiligte in Betracht, deren Abstandsverhältnisse untereinander möglichst genau der „Quadrupolverformung in der Bildebene“ bei einem bestimmten (geeigneten) Wert der „Phase φ“ entspräche.
Darunter gäbe es sicherlich z.B. drei Beteiligte (U, X, Y) so dass z.B.
a[ U, X ] / a[ U, Y ] = (1 – A Sin[ φ] ) / (1 + A Sin[ φ] )
und so dass (ebenfalls der Einfachheit halber)
– U und X „ in x-Richtung“ zueinander standen, und
– U und Y „ in y-Richtung“.
Dann liegen einige Fragen nahe, deren Beantwortung ich (auch) sachdienlich fände:
1. Welchen Wert hätte dann das Abstandsverhältnis
a[ X, Y ] / a[ U, Y ]
?
2. Ließen sich darunter zwei weitere Beteiligte (P, Q) finden, deren Abstandsverhältnisse
a[ U, P ] / a[ U, X ] = 1 + A Sin[ φ ]
und
a[ X, P ] / a[ U, X ] = A Sin[ φ ]
bzw.
a[ U, Q ] / a[ U, Y ] = 1 – A Sin[ φ ]
und
a[ Q, Y ] / a[ U, Y ] = A Sin[ φ ]
erfüllen?
3. Ließen sich darunter drei weitere Beteiligte (H, J, K) finden, deren Abstandsverhältnisse
a[ U, H ] / a[ U, P ] = a[ H, P ] / a[ U, P ] = 1/2,
a[ U, J ] / a[ U, Q ] = a[ J, Q ] / a[ U, Q ] = 1/2,
bzw.
a[ P, K ] / a[ P, Q ] = a[ K, Q ] / a[ P, Q ] = 1/2
erfüllen?
4. Welche Werte hätten dann die Abstandsverhältnisse
a[ U, K ] / a[ U, P ],
a[ J, K ] / a[ U, P ], bzw.
a[ H, K ] / a[ U, P ]
?
Markus Pössel schrieb (11. Mai 2016 13:46):
> Der Strahlteiler ist […] ebenfalls frei aufgehängt und seismisch entkoppelt
… d.h. ähnlich wie die „beiden Endspiegel“ …
> und benimmt sich wie ein freies Teilchen.
Sicherlich nicht bei ansonsten „ungestörten Herumhängen“; d.h. sofern man unter „freien“ Teilchen bzw. Beteiligten diejenigen versteht, deren Dauer jeweils von ihrer Anzeige des Besuchs eines bestimmten Ereignisses bis zu ihrer Anzeige des Besuchs eines anderen bestimmten Ereignisses das Maximum der entsprechenden Dauern aller Teilchen bzw. Beteiligten war, die ebenfalls an den beiden jeweils betrachteten Ereignissen teilgenommen hatten.
(Nicht weniger zweifelhaft erscheint, dass Strahlteiler und/oder Endspiegel „frei“ gewesen wären, während sie gegenüber einander „wackelten“.)
“Freies Teilchen” im gleichen Sinne wie bei den Endspiegeln: Näherungsweise und bezüglich des für die Messung interessanten Frequenzbandes. (Bei niedrigen Frequenzen nutzt die Pendelaufhängung natürlich so gut wie nichts: Ein Pendel, dessen Auslenkungspunkt man ganz langsam hin und her bewegt, bewegt sich mit.)
Markus Pössel schrieb (12. Mai 2016 11:11):
> “Freies Teilchen” […] Näherungsweise
Zur Abschätzung der Näherung (im Vergleich zu eigentlicher, genauer Freiheit] ist sicherlich die Größe
Pingdauer * Aufhängungsbeschleunigung / c =~=
2 * 4 km / (300 000 km / s) * 9,8 m / s^2 / (300 000 km / s) =~=
10^(-12)
relevant.
Deren Wert ist zwar deutlich kleiner als z.B. 10^0 = 1,
aber auch deutlich verschieden von 0
(und beinhaltet auch keine Parameter, durch deren geeignete Variation „man sich (beliebig) weiter an 0 annähern“ könnte).
> und bezüglich des für die Messung interessanten Frequenzbandes.
Das bezieht sich wohl (nur) auf „relative, laterale Freiheit“ (wofür es sicherlich auch einen gebräuchlicheren „technischen“ Begriff gibt, der mir momentan aber leider entfällt); in Unterscheidung zu „eigentlicher Freiheit“ (im Sinne der RT, wie oben beschrieben).
Im Übrigen wäre natürlich (auch) interessant zu erfahren, in wie fern (oder nah) die eine oder andere Art der Freiheit bestand, als die Spiegel besonders auffällig gegenüber einander wackelten.
Herr Pössel,
ich komme auf meine Frage 6) zurück, da ich Ihre Antwort nicht verstehen kann. Nehmen wir an, es ist keine GW vorhanden, dann befinden sich die beiden Endspiegel eines Interferometer-Arms, die den Fabry-Pérot Resonator bilden, und der Strahlteiler in relativer Ruhe zueinander und auch in Ruhe relativ zur Erdoberfläche. Errichten wir ein Koordinatensystem auf der Erde, dessen x-Achse mit einem Arm des Interferometers zusammenfällt, dessen z-Achse senkrecht zur Erdoberfläche gerichtet ist, dessen y-Achse parallel zum anderen Arm gerichtet ist, und dessen Ursprung weit weg vom Kreuzungspunkt der beiden Arme auf der x-Achse liegt.
Nun werde das Interferometer von einer Gravitationswelle erfasst, die mit Lichtgeschwindigkeit darüber hinweg läuft. Gemäß Ihrer Animation beginnt der Endspiegel auf der x-Achse (ein “freies Teilchen”) mit A sin (f t) zu schwingen, wobei f eine Audiofrequenz von ungefähr 100 Hz ist. Nach Newton muss auf den Spiegel eine Kraft K wirken, die gegeben ist durch K = – A M f^2 sin (f t).
Meine konkrete Frage: Warum wirkt keine Kraft sowohl auf den Strahlteiler, der in Ihrer Darstellung stehen bleibt, obwohl er doch auch ein “freies Teilchen” ist, als auch auf den zweiten Resonatorspiegel, der ebenfalls stehen bleiben muss (von Ihnen nicht eingezeichnet), weil sonst der Vervielfachungseffekt bei mehreren (300?) Lichtdurchläufen nicht funktionieren würde. Mutatis mutandis gilt das gleiche für den zweiten Arm.
Nach meiner Vorstellung befinden sich angesichts der riesigen Wellenlänge von 2000 km alle optischen Elemente nahezu auf einem „Punkt“, d.h. es herrscht zu jedem Zeitpunkt dort die gleiche Phase. Die Elemente schwingen gleichsinnig, so dass keine Abstandsänderungen zwischen den Spiegeln auftreten. Dabei ist es unerheblich, ob die Welle transversal oder longitudinal ist. Bei einer em-Welle, die von München bis Moskau reicht, wird man mit Empfängern im Stadtgebiet von Regensburg keine nennenswerten Unterschiede messen können.
Überträgt man die Situation auf eine Schallwelle von 100 Hz, die eine Wellenlänge von etwa 3 m besitzt, so wird man an 2 Punkten, die 6 mm voneinander entfernt sind, kaum messbare Unterschiede im Schwingungsverhalten feststellen können. Winzige Mikrophone, so nahe nebeneinander aufgestellt, würden praktisch identische, synchrone Signale liefern. Nichts Anderes erwarte ich von den GW, die auch keine relativen Abstandsänderungen, sondern nur gleichsinnige Verschiebungen bei so geringen Abständen relativ zur Wellenlänge hervorrufen können.
Ich fange mal mit ihren letzten beiden Absätzen an. Die Wellenlänge spielt bei einer (so gut wie) ebenen Welle für die Feststellung der Phase nur dann eine Rolle, wenn wir Orte betrachten, die in Ausbreitungsrichtung der Welle voneinander entfernt liegen.
Beispiel: Bei 2 m Wellenlänge hat eine Wellen an zwei Orten, die in Ausbreitungsrichtung 1 m auseinanderliegen, maximal unterschiedliche Phasen. Bei derselben Wellenlänge hat die Welle an zwei Orten, die in Ausbreitungsrichtung nur 1 mm auseinanderliegen, so gut wie dieselbe Phase – so verstehe ich ihr Argument.
Wir reden aber, wie in meiner letzten Antwort geschrieben, sowieso über Orte, die in derselben Ebene liegen, und die Ebene wiederum liegt senkrecht zur Ausbreitungsrichtung. Damit spielt die Wellenlänge an dieser Stelle überhaupt keine Rolle (weder für elektromagnetische noch für Schall- noch für Gravitations- noch für sonstige Wellen).
Dass Sie mit der Wellenlänge argumentieren, ist insofern an dieser Stelle falsch.
(Die Frage, was denn nun an Orten gleicher Phase beim Durchgang einer Gravitationswelle passiert, können Sie aber selbstverständlich stellen, und ich gehe auch gerne darauf ein, sobald wir uns geeinigt haben, dass die Wellenlänge an dieser Stelle zu einem festen Zeitpunkt rein geometrisch erst einmal keine Rolle spielt.)
Warum werden die Kommentare nicht nach Datum und Uhrzeit geordnet?
Gute Frage. Ich gebe sie mal an die Technik weiter…
Herr Pössel,
wenn die Verbindungslinie von zwei Punkten parallel zur Wellenfront einer ebenen Welle, also senkrecht zum Ausbreitungsvektor liegt, so herrscht an diesen Punkten per definitionem zu jedem Zeitpunkt die gleiche Phase. Was immer diese Welle an diesen Punkten tut, es verläuft exakt synchron.
Man kann aber nicht davon ausgehen, dass der Wellenvektor der GW zufällig senkrecht auf der Verbindungslinie der beiden Punkte steht. Im Allgemeinen wird er einen Winkel zwischen 0 und 90 Grad einschließen, so dass eine Phasendifferenz an den beiden Punkten auftritt. Diese ist am größten, wenn der Wellenvektor parallel zur Verbindungslinie gerichtet ist.
Wenn nun der Abstand der beiden Punkte klein gegenüber der Wellenlänge ist, so ist die Phasendifferenz entsprechend klein. Ohne also irgend etwas über den Winkel zwischen Wellenvektor und Verbindungslinie der beiden Punkte zu wissen, kann man mit Sicherheit sagen, dass praktisch gleiche Phase an den beiden Punkten herrscht, wenn ihr Verhältnis “Abstand zu Wellenlänge” 4 km / 2000 km beträgt, wie im vorliegenden Fall.
Die beiden “freien Teilchen” Endspiegel und Strahlteiler werden unter den gegebenen Umständen praktisch in gleichsinniger Weise von der Welle zum Schwingen gebracht, so dass es keinen Grund für eine Abstandsänderung gibt. Ohne eine solche gibt es aber auch keine Phasenänderung, die mit einem Michelson-Interferometer nachgewiesen werden könnte.
Bleibt noch zu ergänzen, dass die Fabry-Pérot Anordnung keinen Verstärkungseffekt bringt, solange die Resonanzspiegel nicht gegeneinander schwingen. Dies ist aber unter den gegebenen Umständen nicht der Fall: Auch die beiden Endspiegel in jedem Arm schwingen (praktisch) synchron und gleichsinnig.
Das LIGO-Observatorium hat offenbar nur eine Chance, wenn es sehr starke GW´s im Frequenzbereich von 100 kHz finden kann, die dann allerdings nicht von der Verschmelzung zweier SL´s herrühren dürften.
Dr. Engelhardt,
der Beam-Splitter steht im Winkel von 45° zu den Fabry-Perots.
Und jetzt viel Klick ……
Ob der mitschwingen kann oder festgenagelt ist, spielt keine Rolle!
Ganz genau: Bei Punkten in derselben Ebene parallel zur Wellenfront hat die Welle per Definition dieselbe Phase. Betrachten wir doch erstmal diesen besonders einfachen Fall (entsprechend dem, was ich in meinen Animationen dargestellt habe).
Einsteins Allgemeine Relativitätstheorie liefert eine geometrische Beschreibung der Newton’schen Gravitation und einiger neuer Effekte. Grundlegende Größe der Theorie ist dabei die Metrik, also salopp gesprochen das mathematische Objekt, das es erlaubt, aus Koordinatendifferenzen Abstände (im Raum, in der Zeit, allgemeiner in der Raumzeit) zu berechnen.
Die einfachsten Gravitationswellen (lineare Näherung) wirken durch Quadrupol-Abstandsänderungen in denjenigen Ebenen, die senkrecht zur Ausbreitungsrichtung der Welle stehen (transversale Wellen). Das bekommt man direkt aus der Theorie heraus: Im steten Wechsel Abstandsstreckungen um einen gemeinsamen Faktor in einer Richtung senkrecht zur Ausbreitungsrichtung, Abstandsstauchungen um einen gemeinsamen Faktor in der Richtung senkrecht zur ersten Richtung und zur Ausbreitungsrichtung der Welle. Freie Teilchen machen diese Abstandsänderungen direkt mit – daher ist es so wichtig, Strahlteiler, Endspiegel und innere Fabry-Perot-Spiegel so aufzuhängen, dass sie zumindest senkrecht zur Erdoberfläche, in der Ebene des “L” der Detektorarme frei beweglich sind.
Diese Abstandsänderungen sind das, was man direkt aus der Theorie herausbekommt. Man kann dann für eine Newton-nähere Anschauung oder für eine bildliche Darstellung wie in meinen Blogbeiträgen versuchen, diese Abstandsänderungen darzustellen, indem man (willkürlich) eines der freien Teilchen als Bezugspunkt deklariert und Abstandsänderungen relativ zu diesem Teilchen kartiert bzw. in Animationen darstellt. Aber auch die Beschleunigungen der anderen Teilchen relativ zum Bezugsteilchen werden dann per Definition so wirken, dass sie die für Gravitationswellen charakteristischen Abstandsänderungen herbeiführen. ”
Ihre Behauptung, bei gleicher Phase würden Endspiegel und Strahlteiler “praktisch in gleichsinniger Weise von der Welle zum Schwingen gebracht” ist daher schlicht falsch. Gleiche Phase” heißt für eine Gravitationswelle eben nicht “gleiche Beschleunigungen der betrachteten Teilchen” sondern “gleiches Muster der Abstandsänderungen”. Und genau dieses Muster soll ein Detektor wie LIGO nachweisen.
Herr Senf,
Sie täuschen sich. Eine Phasenänderung kann nur gemessen werden, wenn sich die Armlängen relativ zueinander ändern. Die Armlänge ist definiert als Abstand zwischen Mitte Strahlteiler und Endspiegel. Schwingen Endspiegel und Strahlteiler gleichsinnig synchron, dann gibt es keine Abstandsänderung und auch keine Phasenänderung.
Bitte informieren Sie sich über die Funktionsweise des Michelson-Interferometers in den einschlägigen Fachbüchern (z.B. Pohl, Optik) oder in diesem Papier: https://www.researchgate.net/publication/273333158_Phase_and_frequency_shift_in_a_Michelson_interferometer. Man muss Ihnen zugute halten, dass die designer des fake-Signals sich auch nicht auskannten, sonst hätten sie nämlich ein Signal höherer Frequenz gewählt, dessen Wellenlänge vergleichbar mit den Abmessungen des Interferometers ist.
Das mach ich aber erst, wenn Sie sich mit dem Quadrupol einig geworden sind 😉
Researchgate druckt auch allen Quatsch ungeprüft ab … langweilig
Herr Pössel,
ich zitiere Sie: “Ganz genau: Bei Punkten in derselben Ebene parallel zur Wellenfront hat die Welle per Definition dieselbe Phase.” Die Wechselwirkung dieser Welle mit “Masseteilchen” führt offenbar zu einer Oszillation der Spiegel, welche senkrecht zur Ausbreitungsrichtung der ebenen Welle erfolgt. Da in der Ebene konstanter Phase, die sich bei ebenen Wellen per definitionem bis ins Unendliche erstreckt, überall zu jedem Zeitpunkt gleiche Verhältnisse vorliegen, vollführen alle dort befindlichen Teilchen synchron die gleiche Oszillation, nicht nur ein einziges, willkürlich herausgegriffenes Masseteilchen. Somit schwingen alle Spiegel, welche sich in der Ebene gleicher Gravitationswellen-Phase befinden, gleichsinnig synchron. Ihr Abstand bleibt daher konstant und es tritt kein Effekt beim elektromagnetischen Phasenvergleich im Michelson-Interferometer auf.
Würden zwei Spiegel gegenläufig schwingen, so wie Sie das gezeichnet haben, dann befänden sie sich notwendig nicht in der Ebene konstanter Gravitationswellen-Phase im Gegensatz zu Ihrer Voraussetzung.
Herr Senf,
wenn Sie nicht lernen wollen, wie ein Michelson-Interferometer funktioniert, können Sie hier schwerlich mit-diskutieren.
Ihre Argumentation wäre dann stimmig, wenn die definierende Größe einer Gravitationswelle eine Kraft oder eine Beschleunigung wäre (wie beim elektromagnetischen Feld).
Dann könnte man in der Tat schließen: Gleiche Phase, gleiche Wirkung auf Testteilchen in einer Ebene senkrecht zur Ausbreitungsrichtung; gleiche Wirkung, gleichsinnig synchrones Schwingen, also keine relative Abstandsänderung.
Aber wie in meinem letzten Kommentar schon geschrieben: Die definierende Größe einer Gravitationswelle sind stattdessen systematische Abstandsänderungen (mit Quadrupolcharakter).
Deswegen ist ihre Argumentation falsch – sie unterstellt den Gravitationswellen Eigenschaften, die diese Wellen in Einsteins Theorie gar nicht haben.
P.S.: Nicht-chronologische Kommentare und Ihren Namen im letzten Kommentar habe ich in Ordnung gebracht (und lösche jetzt Ihren nunmehr obsoleten Meta-Kommentar dazu).
Im Lexikon der Physik von Spektrum http://www.spektrum.de/lexikon/physik/gravitationswellen/6101lese ich:
“Gravitationswellen sind transversal und besitzen zwei Polarisationsfreiheitsgrade, sie verändern also temporär die Metrik der Raumzeit und sind in der Lage, Massen senkrecht zur Ausbreitungsrichtung zu beschleunigen, was prinzipiell ihren Nachweis ermöglicht.”
Sie bestätigen, dass diese Wellen “eben” bei uns ankommen, d.h. ebene Flächen konstanter Phase haben, senkrecht zu denen sich die Wellen mit Lichtgeschwindigkeit ausbreiten. Nach obigem Zitat sind diese Wellen in der Lage, Massen senkrecht zur Ausbreitungsrichtung zu beschleunigen. Wenn sie dies an einem Spiegel bewirken, wie Sie es gezeichnet haben, dann können sie es gewiss auch an anderen Massen vollbringen, welche in einer Phasenebene liegen, weil per definitionem kein Punkt vor einem anderen in der Phasenebene (Wellenfront) ausgezeichnet ist.
In Ihrer Animation beschleunigt aber die Gravitationswelle, deren k-Vektor in z-Richtung zeigt, nur die Masse des äußeren Endspiegels, während sie die Masse des zweiten inneren Resonator-Spiegels, sowie die Masse des Strahlteilers nicht beschleunigt. Wenn dies so wäre, würde sich ein Widerspruch ergeben, denn die Massen “zweiter Endspiegel und Strahlteiler” könnten sich nicht auf einer Phasenfläche befinden, was Sie jedoch annehmen.
Für die Detektion der Wellen mittels Michelson-Interferometer ist es unerlässlich, dass die Spiegel unterschiedlich beschleunigt werden, denn nur so ergeben sich Abstandsänderungen, welche den elektrodynamischen Phasenvergleich durch unterschiedliche Bewegung der Spiegel ermöglichen. Die Gravitationswellen müssten also die unmögliche Eigenschaft haben, Massen, die auf einer Gravitations-Phasenfläche liegen, unterschiedlich zu beschleunigen.
Eine ebene Welle wird beschrieben durch A cos (k z – omega t), wobei die Amplitude eine Vektorkomponente sein kann, die senkrecht auf dem k-Vektor steht, und unabhängig von den Koordinaten ist. Wählt man die Phasenebene z = 0, so muss die Wirkung auf alle dort befindlichen Massen die gleiche sein, nämlich eine Oszillation mit der Frequenz omega. Bitte geben Sie eine Formel an, welche einerseits Ihren Satz: „Die definierende Größe einer Gravitationswelle sind stattdessen systematische Abstandsänderungen“ mathematisch präzisiert, andererseits die Wechselwirkung dieser Welle mit einer Spiegelmasse beschreibt. Ohne eine präzise Modellierung der Spiegelbewegung als Funktion der Amplitude A, der Frequenz omega und des Wellenvektors k kommen wir hier nicht weiter.
Herr Pössel,
bezüglich der mathematischen Formulierung der Wellengleichung für das Gravitationsfeld sowie einer Lösung für die homogene Gleichung weit weg von der Quelle könnten Sie sich vielleicht an das Einstein-Institut wenden, wo Sie mal gearbeitet haben. Mir geben die dortigen Direktoren leider keine Auskunft.
Inzwischen könnten Sie sich vielleicht Frage # 4) widmen: Wie schafft es LIGO, fünf Größenordnungen zu überbrücken, die zwischen dem gemessenen und veröffentlichten Signal, sowie der angeblichen Spiegelverschiebung von 10^(-18)m liegen?
Natürlich wäre auch diese Frage relativ leicht zu beantworten, wenn endlich die Eichkurve offen gelegt würde, doch da hoffen wir wohl vergeblich, wenn nicht mal Prof. Nicolai diese Information dem “Calibration” paper entnehmen kann. Nicht zu reden von den anderen “Experten” wie Prof. Danzmann, der es eigentlich wissen müsste, aber schweigt…
Bitte respektieren die Regeln, unter denen ich die Diskussion fortsetzen wollte. Eine Frage zur Zeit, und möglichst kurz formulierte Beiträge. Und nein, bei einer Sache, die man in jedem Lehrbuch zum Thema findet, wäre es ziemlich unhöflich, sich stattdessen an die AEI-Direktoren zu wenden. Das wäre das Analogon zu der Schüler-Email “bitte machen Sie meine Hausaufgaben für mich”. Antwort auf Ihre letzte Frage oben folgt voraussichtlich morgen.
Hallo Herr Possel,
mein Kommentar von soeben an Sie vom 18. Mai wird in der Diskussion unter dem Datum 19. April veröffentlicht:
https://scilogs.spektrum.de/relativ-einfach/gravitationswellendetektoren-wie-sie-funktionieren-gw-teil-2/#comment-23112
Könnten Sie bitte meinen Kommentar chronologisch richtig anordnen? Die Diskussion ist sonst wegen diesem technischen Fehler kaum lesbar. Vielen Dank!
mfg
Jocelyne Lopez
Ihr Kommentar wurde oben eingereiht, weil Sie ihn explizit als Antwort auf einen anderen Kommentar geschrieben hatten (mit Klick auf das Link “Antworten”). So entsteht ein (durchaus lesbarer) “Thread”. Es handelt sich keineswegs um einen technischen Fehler, sondern um eine im Internet durchaus übliche Art und Weise, Kommentare und andere Beiträge anzuordnen.
Hallo Herr Pössel,
ich habe heute nie auf einen Beitrag von Dr. Engelhardt oder ´”Herr Senf” vom 19. April geklickt, warum sollte ich das? Aber sei’s drum, die Technik hat ihre Mysterien – auch in Ihrem Blog, nicht nur bei LIGO. 😉
Darf ich fragen was Sie inhaltlich zu meinem heutigen Kommentar sagen?
mfg
Jocelyne Lopez
Keine Ahnung warum Sie irgendetwas tun. Mysterien hat ja oft nicht die Technik selbst, sondern der (zum Teil unbedarfte Umgang) mit derselben. Müssen wir hier aber nicht klären.
Apropos: Sie können ja gerne fragen, was ich zu Ihrem Kommentar sagen. Sie können es aber auch wie alle anderen machen und einfach meine Antwort lesen, die direkt unter dem betreffenden Kommentar steht.
Moin Herr Pössel,
es ehrt Sie ja hier mit den Beiden in den Dialog zu gehen, jedoch ist es recht sicher fruchtlos, beide sind wie gewohnt uneinsichtig und nicht wirklich an Physik interessiert, geht primär nur darum Krawall zu machen und eine echte Diskussion mit den Personen die wirklich interessiert sind zu stören.
Erkennt man schon an der “geschrieenen” Behauptung die Relativitätstheorie sei nur eine Hypothese, reine Provokation, hier gar nicht Gegenstand der Diskussion. Kann man richtig stellen, dann gibt es dazu die übliche endlose Debatte, übergeht man es, könnten andere Leser den Unfug für richtig halten.
Ich sehe die Diskussion durch die Beiden hier gestört, beide zeigen sich auch seit Jahren unbelehrbar und hetzten wo immer möglich gegen Physiker. Der völlig haltlose Vorwurf des Betruges hier von Engelhardt zeigt dieses recht deutlich. Es sollte einen Weg geben, hier die Diskussion im angenehmen sachlichem Klima zu führen. Wer ans AEI Fragen via Mails stellt oder nicht und ob er Antworten bekommt oder nicht, und ob da wer vom AEI hätte antworten sollen oder müssen, oder nicht, … – hier in der Diskussion alles nicht Thema.
Wer damit ein Problem hat, kann ja klagen … 😀
Mit freundlichem Grüßen
Manuel Krüger
Warten wir doch mal ab. Zumindest Herr Engelhardt hat sich ja (einigermaßen) auf eine auf die Sachthemen begrenzte Diskussion eingelassen, da sehe ich derzeit keinen akuten Abbruchgrund.
Frau Lopez benimmt sich in der Tat nicht sehr konstruktiv (kaum überraschend, meinen früheren Erfahrungen nach); wenn das so weiter geht, werde ich ihre weiteren Kommentare in der Tat nicht mehr freischalten.
Herr Pössel,
Ich bin nicht in der Lage hier in Ihrem Sinne „konstruktiv“ zu wirken: Ich bin ja lediglich eine naturwissenschaftlich interessierte Bürgerin und dabei nicht fachlich qualifiziert – was allerdings sogar Prof. Herrmann Nicolai als Geschäftsführender Direktor am AEI für sich selbst beim Thema LIGO auch offen zugibt: Er sei ja mit der Lasertechnik nicht betraut und empfahl mir am 05.04.16 als interessierte Laiin u.a. Ihren Blog, um meine Fragen beantworten zu lassen, siehe seine Antwort: http://www.kritik-relativitaetstheorie.de/Anhaenge/Anfrage%20LIGO-Experiment.pdf
Dementsprechend bin ich hier weder „quer“ eingestiegen, sondern aus Empfehlung von Prof. Nicolai, noch gibt es Anlaß, mich hier ob meine kleine Anmerkung zu sperren. Für mich und für die Öffentlichkeit ist nun mal die Relativitätstheorie lediglich eine Hypothese, die man seit Jahrzehnten extrem aufwendig versucht, experimentell zu bestätigen. Wozu hätte man sonst so ein teures Experiment wie LIGO angestellt, wenn die Theorie schon experimentell bestätigt worden wäre? Wieso wurde die Entdeckung von Gravitationswellen nach den Vorhersagen der Theorie als „Sensation“ in den Massenmedien gefeiert, wenn die Theorie schon bestätigt worden wäre?
Ich sehe nicht, dass ich hier diese lange Diskussion über Gravitationswellen störe und dass ich mich in die Gefahr begehe, gesperrt zu werden, nur weil ich nicht „konstruktiv“ in Ihrem Sinne zur der gefeierten „Sensation“ der Bestätigung der Relativitätstheorie durch das LIGO-Experiment beteilige, sondern vordergründig an seine fachliche Hinterfragung interessiert bin. Ist eine fachliche Hinterfragung etwa nicht konstruktiv? Der Meinung bin ich nicht und das würde auch die Standards guter wissenschaftlicher Praxi gründlich widersprechen.
Mfg
Jocelyne Lopez
Ihre Zweifel an der Relativitätstheorie bringen Sie doch schon seit Jahren vor, immer mit denselben kindischen Behauptungen. Es hat wohl psychologische Gründe, wenn Laien meinen, eine längst etablierte und vielfach bestätigte Theorie der Physik mit einfachsten Mitteln anzweifeln oder widerlegen zu können. Das LIGO-Experiment dient bekanntlich dem Nachweis der vorhergesagten Gravitationswellen, nicht der Relativitätstheorie selber. Wenn die Gravitationswellen noch nicht nachgewiesen werden können, folgt daraus keine Widerlegung der Relativitätstheorie. Sie befinden sich auf der falschen Hochzeit!
Moin Herr Pössel,
Lopez schrieb: “Für mich und für die Öffentlichkeit ist nun mal die Relativitätstheorie lediglich eine Hypothese, …”
Normal wäre wohl: “Für die Öffentlichkeit und für mich …”, aber egal, die Frau kann nur für sich sprechen und nicht für die Öffentlichkeit (auch wenn sie anderes glaubt) und die RT ist nun mal für die Öffentlichkeit eine Theorie, wie es alleine auch schon der Name zeigt. Was die Allgemeinheit unter einer Theorie und einer Hypothese versteht ist zumindest im wissenschaftlichen Bereich wirklich klar verständlich formuliert und kann im Internet jederzeit nachgelesen werden.
Es ist das alte Spiel, hier wird Krawall gemacht und dann später sich im eigenen Blog darüber echauffiert und abwertend und polemisch ausgelassen.
Leider teile ich auch Ihre Sichtweise zu Engelhardt nicht, im Blog
http://www.relativ-kritisch.net/blog/kritiker/wolfgang-engelhardt-unsinn-michelson-interferometer
läuft schon viele Monate eine endlose Debatte, in der Engelhardt auch stetig Betrugsvorwürfe zelebriert und sich in jeder Weise in vielen einfachen physikalischen Dingen uneinsichtig zeigt, Aussagen anderer ignoriert und sinnentstellt wiedergibt, und lange bekannte Grundlagen bestreitet und ignoriert.
Es ist eben immer das alte Murmeltierspielchen, Verstanden und Begriffen wurde bisher gar nichts.
Ich lasse mich aber gerne überraschen, wollte auch nur kurz ein Feedback als Leser hier geben, einer der am eigentlichem Thema und Ihren Erklärungen interessiert ist und eben nicht am üblichen und bekannten Geplärre gewisser “Kritiker” …
Mit freundlichen Grüßen
Manuel Krüger
…und schon hat die Meta-Diskussion darüber, was Hypothese, Öffentlichkeit etc. ist, wie man mit Kritikern umgeht und wie nicht, die Fachdiskussion zu den Gravitationswellen mengenmäßig zumindest für heute wieder überflügelt.
Das ist in der Tat kein Mehrwert für die Leser hier. Und mir ist vergleichsweise egal, wie Herr Engelhardt sich auf anderen Blogs benimmt – hier hat er sich, soweit ich sehen kann, zumindest in diesem Diskussionsstrang (derzeit: Wirkung einfacher Gravitationswellen) auf die Physik beschränkt.
Ich werde jetzt nicht über die diversen hingehaltenen Meta-Stöckchen springen, sondern alles, was außerhalb des erwähnten Diskussionsstranges kommt, löschen.
Hier meine nächste Antwort auf die Frage von Herrn Engelhardt nach der Form der Gleichungen (hier), die die Wirkung von Gravitationswellen beschreiben.
Betrachten wir eine Ebene senkrecht zur Ausbreitungsrichtung der Gravitationswelle; konkret: die x-y-Ebene, während z die Ausbreitungsrichtung der Welle ist.
Wir wählen die üblichen kartesischen Koordinaten und betrachten nur Teilchen, die sich relativ zu unserem Koordinatensystem nicht bewegen, also in der von uns betrachteten Ebene konstante x- und y-Koordinatenwerte haben. Unser System möge, solange keine Gravitationswelle hindurchgeht, ein Inertialsystem sein. Insbesondere seien diejenigen Teilchen, die in unserer Ebene ruhen und deren Verhalten unter Einfluss der Gravitationswelle wir betrachten wollen, freie Teilchen.
Dann gilt bei Durchgang der (einfachen, linearen, geeignet ausgerichteten) Gravitationswelle, dass sich die x- und y-Koordinaten eines solchen freien Teilchens, dargestellt im üblichen abstandstreuen kartesischen Koordinatensystem, mit der Zeit wie folgt ändern:
x = x_0 [ 1+ 1/2 h(t) ]
und
y = y_0 [ 1 – 1/2 h(t) ]
wobei h(t) = A sin(ω t) ist und x_0 und y_0 die Koordinatenwerte für die Teilchen vor Durchgang der Gravitationswelle sind.
Ein paar Anmerkungen:
(1) Die Ausdrücke für die Koordinatenänderungen sind bereits linearisiert, d.h. Terme der Ordnung A^2 und höher werden vernachlässigt.
(2) Aus der Theorie folgen nicht direkt diese Koordinatenänderungen, sondern es folgen Abstandsänderungen, nämlich Änderungen der Metrik. Konkret ist der Abstand Δ l zweier Punkte, deren Koordinaten sich in dem gewählten System vor Durchgang der Gravitationswelle um Δ x_0 und Δ y_0 unterscheiden
Δ l^2 = [ 1 + h(t) ] Δ x_0^2 + [ 1 – h(t) ] Δ y_0^2.
Wählt man eines der freien Teilchen als Raumnullpunkt, kann man die Abstandsänderungen in die oben genannten Koordinatenänderungen umschreiben.
(3) Im Gegensatz zu vorher habe ich meine Konvention zur Amplitude A angepasst: was in meinen früheren Kommentaren A war ist jetzt A/2.
(4) Aus diesen Ausdrücken sollte Herr Wappler die von ihm gesuchten Verhältnisse ausrechnen können – zumindest bis hin zu Termen linear in A.
(5) Wer meine hier genannten Ausdrücke mit der Literatur vergleicht: Was dort x-y-Koordinaten heißt sind meist das, was ich hier x_0 und y_0 nennen. Abstandstreue Koordinaten werden dort üblicherweise gar nicht eingeführt.
Markus Pössel schrieb (18. Mai 2016 15:50):
> […] Konkret ist der Abstand […] zweier Punkte,
… sicherlich je zweier (geeigneter) “materieller/substantieller Punkte”, alias “principal identifiable points” oder “identifizierbarer Beteiligter” oder “Teilchen” …
> deren Koordinaten sich in dem gewählten System vor Durchgang der Gravitationswelle um Δ x_0 und Δ y_0 unterscheiden [, gleich der Wurzel aus … ]
> [ 1 + h(t) ] Δ x_0^2 + [ 1 – h(t) ] Δ y_0^2.
Es erscheint (mir) stets sehr bedenklich, wenn Werte “Abstand” (oder “Abstände” ?) genannt werden, die (hier explizit wegen h) i.A. nicht konstant sondern ununterbrochen veränderlich sind.
(Ähnlich bedenklich erscheint mir z.B., den Abstand zwischen zwei bestimmten Eisenbahnschwellen als Abstand zwischen Spitze und Ende eines darüberfahrenden Zuges zu interpretieren.)
> (4) Aus diesen Ausdrücken sollte Herr Wappler die von ihm gesuchten Verhältnisse ausrechnen können
Ja (danke für diesen Ausdruck der Kenntnisnahme); in meinem entsprechenden vorausgegangenen Kommentar (17. Mai 2016 13:03) hatte ich ja mehr oder weniger deutlich darum gebeten und mich darauf eingelassen, zumindest für solche Berechnungen die entsprechenden Formelwerte als Abstandswerte zu interpretieren.
Mit einiger Überraschung habe ich nun festgestellt: das ist leider gar nicht so interessant und sachdienlich, wie ich erwartet hatte.
Konkret: der “Abstand” zwischen U und J bleibt stets (d.h. für jeden Wert der “Phase φ” bzw. für jeden Wert des Koordinaten-Parameters t) gleich dem “Abstand” zwischen U und K.
Und sogar noch umfassender (um nicht zu schreiben “schlimmer”):
die entsprechenden Cayley-Menger-Determinanten verschwinden für beliebige vier Punkte (d.h. vier “x, y” – Koordinatenpaare);
sowohl für “Abstände” entsprechend dem zitierten Ausdruck, als auch für gewisse Varianten, die naheliegen, wenn man sich z.B. MTW chap. 35 näher anschaut (was gestern abend erstmal gemacht habe).
Die Werte der Abstands-Verhältnisse, nach denen ich gefragt hatte, sind also offenbar nicht geeignet, um die fraglich “Quadrupolverformung” nachzuweisen oder wenigstens zu veranschaulichen;
und die Flächen “gleicher Phase” (“senkrecht zur Richtung der Wellenausbreitung“) sind tatsächlich Ebenen (sofern die Formelwerte entsprechend als Abstände interpretiert werden).
Aber:
Das beeinträchtigt erstens nicht unbedingt die Opertionalisierung (in Anwendung des Syngeschen “Five point curvature detectors”, die ich u.a. hier skizziert hatte;
denn diese Anordnungen von je fünf Beteiligten haben nicht nur Ausdehnung in jeweils einer “Fläche gleicher Phase”, sondern auch “in Wellen-Ausbreitungsrichtung” und (jeder einzelne Beteiligte) auch “zeitlich”.
Mich würde folglich interessieren, ob und wie sich der zitierte “Abstands“-Ausdruck entsprechend verallgemeinern ließe; so dass insbesondere auch “Abstands“-Werte zwischen “Punkten ungleicher Phase” zu ermitteln wären.
(Die einzelnen “Punkte” verstünden sich dabei wohl anders als oben, eher als einzelne Anzeigen der Beteiligten; oder, falls das eindeutig ist, als einzelne Ereignisse.)
Mehr noch interessiert mich allerdings, das Thema von vornherein koordinaten-frei zu behandeln; am besten (im Sinne Einsteins) strikt basierend auf Feststellungen von Koinzidenzen (bzw. Reihenfolge, bzw. Identitäten).
Und zweitens besteht trotzdem unverändert das Problem nachvollziehbar (d.h. basierend auf Feststellungen von Koinzidenzen, Reihenfolge, Identitäten) zu definieren, welche Beteiligten als “frei” gelten sollen (bzw. relevante Varianten, etwa als “frei senkrecht zur Wellen-Ausbreitungsrichtung“); insbesondere auch in Versuchen, während denen sie gegenüber einander wackelten.
Frank Wappler schrieb (19. Mai 2016 5:58):
> Konkret: der “Abstand” zwischen U und J bleibt stets (d.h. für jeden Wert der “Phase φ” bzw. für jeden Wert des Koordinaten-Parameters t) gleich dem “Abstand” zwischen U und K.
Berichtigung:
Hier liegt leider der selbe Bennenungsfehler vor, wie in der Version meines Kommentars vom 17. Mai, die ich nachträglich korrigieren musste. Das Vergleich von Interesse (im Sinne Alexandrovscher Vergleichsdreiecke) wäre stattdessen von “Abstand” zwischen H und K und “Abstand” zwischen J und K
(gewesen; aber diese erwiesen sich als durchwegs gleich).
@Frank Wappler / 19. Mai 2016 5:58
»Markus Pössel schrieb (18. Mai 2016 15:50):
> […] Konkret ist der Abstand […] zweier Punkte,«
Als Abstandskonzept beziehen sich die GW-Sucher auf “proper distance”, vielleicht verhilft das hier noch zur Klärung:
Aufmuth, P., & Danzmann, K. (2005). Gravitational wave detectors. New J. Phys., 7(1), 202. DOI: 10.1088/1367-2630/7/1/202
Falls erforderlich lässt sich weiteres dazu in dem Übersichtsartikel von Flanagan & Hughes finden (Referenz [2] bei Aufmuth & Danzmann).
Doch egal wie proper die “proper distance” auch sein mag, das ist nicht messbar und kann immer nur im theoret. Rahmen berechnet werden. Mir scheint, die Diskussion hier entsteht nicht zuletzt aus dem vermittelten Eindruck, bei LIGO werde tatsächlich interferometrisch eine SI-kompatible Abstandsmessung vorgenommen. So ist das aber nicht.
Und es ist ganz grundsätzlich ja auch nicht so, dass die Vorhersage einer bestimmten Theorie von Gravitationsstrahlung unter kontrollierten Bedingungen der Observation bei LIGO nachvollziehbar getestet worden wäre, sondern es wurde zu einem spektakulären Wow!-Signal ungewisser Herkunft unter der Prämisse der Gültigkeit jener Theorie ein passendes Event konstruiert, woraufhin man schliesslich mit erheblichem Getöse einen “direkten Nachweis von GWs” erbracht zu haben beansprucht. Was sollen wir daraus nun schliessen?
Chrys schrieb (20. Mai 2016 17:07):
> Als Abstandskonzept beziehen sich die GW-Sucher auf “proper distance” […]
Hoffentlich nachvollziehbarer und Modell-unabhängiger als (nur irgendwelche) Koordinaten …
> dem vermittelten Eindruck, bei LIGO werde tatsächlich interferometrisch eine SI-kompatible Abstandsmessung vorgenommen. So ist das aber nicht.
Sofern ich am Auftreten eines solchen Eindrucks (hier) für nicht ganz schuldlos gehalten werden sollte, gestehe ich unumwunden zu, dass ich mich gern mit chronometrischen Beschreibungen beschäftige (“Dauern”, insbesondere “Pingdauern”, …, “Lorentzian distances”), weil diese noch am ehesten damit in Zusammenhang zu bringen scheinen, worum es eigentlich geht (oder gehen sollte): Beschreibungen, die ausschließlich auf Feststellungen von Koinzidenz (Reihenfolge von Wahrnehmungen, Identität von Beteiligten) hinauslaufen.
(Ein Zusammenhang ergibt sich konkret so: Falls jemand eine bestimmte Signalanzeige dargestellt hatte, und im Folgenden feststellte, bestimmte entsprechende Pingechos von bestimmten anderen Beteiligten koinzident wahrgenommen zu haben, dann war dessen Dauer von Signalanzeige bis zur Wahrnehmungsanzeige des einen Pingechos zwangsläufig gleich zu dessen Dauer von Signalanzeige bis zur Wahrnehmungsanzeige des anderen Pingechos.)
Zweitens erhebt sich (für mich, wieder mal) die Frage, in wie fern “SI-Kompatibilität” überhaupt fragliche sein könnte bzw. die SI-Meter-Definition überhaupt einschränkend sei (sofern sie nachvollziehbar ist). Schließlich wird darin offenbar nicht gefordert, dass zwei “Enden”, deren “Meter-Abstand voneinander” zu ermitteln wäre, gegenüber einander “ruhend” sein sollten.
Drittens sind für jede Messgröße ja ggf. die “prinzipielle definite Messoperation” von verschiedentlichen “praktischen Erhebungsoperationen” zu unterscheiden; wobei erstere immer festzulegen ist, um für letztere Betrachtungen zu deren “systematischen Unsicherheiten” anstellen zu können.
> […] Vorhersage einer bestimmten Theorie
Theorien, also Systeme von selbstverständlichen Begriffen, Definitionen (von Messgrößen), die unter Benutzung dieser Begriffe formuliert werden, sowie den sich daraus ergebenden Zusammenhängen (Theoremen), enthalten keine Vorhersagen zu bestimmten Messwerten.
Das unterscheidet Theorien von Modellen.
@Frank Wappler / 21. Mai 2016 9:15
»Sofern ich am Auftreten eines solchen Eindrucks (hier) für nicht ganz schuldlos gehalten werden sollte, …«
Es lag wiederum keinesfalls in meiner Absicht, den Eindruck einer Schuldzuweisung zu vermitteln. Der besagte Eindruck von Abstandsmessung ist kaum zu vermeiden, wenn gemessenene LIGO-Interferenzmuster mit Hinblick auf die GW-Theorie gedeutet werden als “relative Abstandsänderung” 2·ΔL/L, was gerade der gesuchte ‘wave strain’ ist. Man könnte ja meinen, hier seien eigentlich die Grössen ΔL resp. L mit dem Interferometer gemessen worden. Doch sind das gar keine Mess-, sondern reine Rechengrössen, die, wie gesehen, im Sinne von “proper distance” interpretiert werden. Und die müssen zu diesem Zweck auch überhaupt nicht metrologisch messbar sein, denn messtechnisch interessiert offenbar ausschliesslich deren Quotient.
»Theorien … enthalten keine Vorhersagen zu bestimmten Messwerten.«
Ja, quantitative Vorhersagen zu Messwerten. “Vorhersagen” lassen sich jedoch grundsätzlich auch verstehen als qualitative Aussagen zu gewissen Eigenschaften, die dann allen auf einer bestimmten Theorie basierten Modellen gemeinsam sind. So sagt e.g. die Superstring Theorie die Existenz von Superpartners bekannter Partikel voraus, oder die LQG sagt voraus, dass die Lichtgeschw. in vacuo von der Frequenz des Lichtes abhängt. Prinzipiell falsifizierbar wären allerdings nur Modelle, wo dann so etwas auch quantitativ konkretisiert würde. (Okay, diese Beispiele sind vielleicht etwas blöd, aber das fiel mir nur gerade so ein, und es geht ja ums Prinzip.)
Soweit ich sehen kann, ist die Diskussion mit Herrn Engelhardt zum jetzigen Zeitpunkt noch elementarer. Derzeit geht es noch um konzeptuelle Probleme damit, was die Wirkung einer Gravitationswelle eigentlich ist, am Beispiel der freien Teilchen, die das typische Quadrupolmuster bilden.
Zurm strain: Nein, was gemessen wird ist nicht direkt der Strain, sondern schon etwas, das mit ΔL zusammenhängt. Sonst würde man ja durch möglichst großes L auch keine Vorteile bekommen. Im einfachsten Fall (Verweildauer des Lichts im Detektor klein gegen Schwingungszeit der Gravitationswelle) geht es dabei tatsächlich um eine interferometrische Längenmessung. Schaut man genauer hin bzw. hat längere Verweildauern, wird die direkte Wellenlängenverschiebung für das Licht wichtiger (wie in der Animation oben auch richtig dargestellt ist).
Chrys schrieb (21. Mai 2016 14:34):
> […] Rechengrössen […] im Sinne von “proper distance” interpretiert werden
> […] messtechnisch interessiert offenbar ausschliesslich deren Quotient.
Als Messwerte bedeutsam sind letztlich stets reelle Zahlenwerte (wie man sie z.B. als Quotienten von Werten gewisser kommensurater „Rechengrößen“ ausdrücken würde); oder Boolesche Werte. Entsprechend sind auch (nur) solche Operatoren als Messoperatoren in Betracht, die reelle oder Boolesche Eigenwerte haben (die ggf. als Messwerte erhalten werden können).
Falls anstelle von definitiven Messoperatoren aber gewisse andere („praktischere“) Erhebungsoperatoren auf gegebene Beobachtungsdaten angewandt werden, dann lassen sich Messunsicherheiten (der Letzteren hinsichtlich des Ersteren) diskutieren.
> “Vorhersagen” lassen sich jedoch grundsätzlich auch verstehen als qualitative Aussagen zu gewissen Eigenschaften, die dann allen auf einer bestimmten Theorie basierten Modellen gemeinsam sind.
Aber eben gerade nicht im Sinne von „echten, experimentell prüfbaren Vorhersagen“, die eben auch die Möglichkeit einschließen, „auf das falsche Pferd gewettet“ zu haben.
> So sagt e.g. die Superstring Theorie die Existenz von Superpartners bekannter Partikel voraus
„Die Superstring Theorie“ dürfte demnach einen (hoffentlich nachvollziehbaren) Messoperator enthalten (oder vielleicht auch verschiedene Varianten „der Superstring Theorie“ verschiedene entsprechende Messoperatoren), um zu ermitteln, ob in jeweils einem Versuch Beteiligte („Partikel“) vorlagen, die gegenüber einander „Superpartner“ sind, oder nicht.
Jeder solche Messoperator sollte ganz unabhängig davon anwendbar sein und bleiben, was in eventuell vorausgegangenen Versuchen diesbezüglich schon gefunden worden wäre; insbesondere auch, falls (bisher) keine solchen Partnerschaften feststellbar gewesen wären.
> die LQG sagt voraus, dass die Lichtgeschw. in vacuo von der Frequenz des Lichtes abhängt.
Das verdeutlicht vor allem, dass der Messgröße, die im genannten Zusammenhang mit „LQG“ als „Geschw. In vacuo“ bezeichnet wird, offenbar nicht (wie im Rahmen der (S)RT) die chronometrische Distanzdefinition bzgl. der Signal-Front zugrundeliegt.
(Welche Distanzdefinition stattdessen im Rahmen „der LQG“ zugrundegelegt wird, falls überhaupt irgendeine nachvollziehbare, bliebe zu untersuchen.)
Im Allgemeinen stimmt natürlich, dass der (Eigen-)Wertebereich eines Messoperators mehr als nur ein Element enthält. Das lässt sich allerdings durch Inspektion des jeweiligen Messoperators an sich herausfinden; nicht erst in Auswertung tatsächlicher experimenteller Beobachtungsdaten.
> Okay, diese Beispiele sind vielleicht etwas blöd, aber das fiel mir nur gerade so ein […]
Es sollte nicht überraschen, dass sich keine gescheiten Beispiele für einen Messoperator (bzw. eine Theorie, in deren Rahmen er definiert wurde) finden lassen, dessen durch Anwendung auf gegebene Beobachtungsdaten erhaltene Ergebniswerte die Schlussfolgerung zuließen, dass diese Ergebniswerte falsch wären, oder dass sich dieser Messoperator nicht anwenden ließe, bzw. dass dieser Messoperator (samt zugrundeliegender Theorie) als experimentell falsifiziert zu verwerfen wäre. Denn das wäre schon aus Prinzip Unfug. (Die gelegentlich – nein: leider noch allzu häufig – anzutreffende Behauptung des Gegenteils bezeugt lediglich mangelhaftes Verständnis von Messung.)
@Markus Pössel / 21. Mai 2016 21:41
Konkret gemessen werden soll ja eine Phasenverschiebung Δφ nach dem Durchlaufen der Teilstrahlen in x- und y-Richtung, was ja auch oben als Animation zutreffend wiedergegeben wird. Das Design der Interferometer-Armlänge wird dabei massgeblich mitbestimmt durch das GW-Frequenzbereich, im welchem man Effekte zu finden hofft. Die für den Messvorgang eigentlich interessante Frage ist aber doch die, in welcher Grössenordnung die dabei erwartete Phasenverschiebung liegt. Dazu verweise ich mal auf M. Maggiore (Gravitational Waves, Vol. 1, OUP, 2008), insbes. Ch. 9. Der kalkuliert da überschlägig bei einer Laser-Wellenlänge von 1μm und einer Armlänge von 4km incl. Fabry-Perot einen Wert von Δφ ∼ 10^{−8}rad.
Und rechnerisch entspricht das einem ΔL ∼ 2×10^{−18}m. Was aber durchaus nicht heisst, dass dieses ΔL tatsächlich im Sinne einer SI-kompatiblen Abstandsmessung ermittelt worden wäre. Da wage ich mal die Vorhersage, dass der Herr Engelhardt das letztlich auch nicht schlucken wird, falls man ihm das so serviert.
Was soll den bitte eine “SI-kompatible Abstandsmessung” sein? Und worin unterscheidet sie sich von einer, allgemein, Abstandsmessung?
Eine Abstandsmessung, das ist ja auch ein wesentlicher Punkt im Haupttext, ist der Gravitationswellennachweis nur näherungsweise (im Grenzfall, dass die Verweildauer des Lichts im Interferometer klein ist gegen die Schwingungszeit der Welle). Was da wirklich vor sich geht zeigt ja gerade die obige Animation.
@Markus Pössel
»Was soll den bitte eine “SI-kompatible Abstandsmessung” sein?«
Gemeint ist eine Abstandsmessung, deren Ergebnis in SI-Metern (1983) ausgewiesen werden kann. Mit anderen Worten, eine Messung, deren Wert über die Ermittlung von Lichtlaufzeit bestimmt wird (also ‘radar’) oder in diesem Sinne interpretierbar ist.
Es ist zu beachten, dass eine Beziehung zwischen ‘radar distance’ und ‘proper distance’ wie in der SR, wo gewöhnlich letztere aus ersterer erhalten wird, in nicht-statischen Raumzeiten wie einer GW nicht generell gilt. Denn wo nicht garantiert ist, dass ein Radarsignal bei seinem Roundtrip für den Hinweg die gleiche Zeit benötigt wie für den Rückweg, wird rasch klar, dass diese Abstandskonzepte durchaus unterschiedlich sind.
»Was da wirklich vor sich geht zeigt ja gerade die obige Animation.«
Die Animation zeigt uns einen Sachverhalt aus der Sicht eines Beobachters in einem statischen Hintergrundraum, der dort gewisse zeitlich variierende x- und y-Koordinatenwerte registriert. Der LIGO-Beobachter wird jedoch mitbewegt und hat keinerlei Zugriff auf die Hintergrundmetrik. In den mitbewegten Koordinaten sind die LIGO-Armlängen dann sogar konstant, und was von LIGO überhaupt interferometrisch gemessen werden kann, ist eine Phasenverschiebung beim gesplitteten Lichtstrahl. Aus diesem Wert, sofern man denn etwas gemessen zu haben meint, wird dann gemäss Formelsammlung der ‘wave strain’ berechnet, wobei die Gültigkeit der GW-Theorie als Annahme vorausgesetzt und u.a. die der Theorie entnommene Grösse ‘proper distance’ im Zuge der Berechnung verwendet wird.
Es wäre mit Herrn Engelhardt sinnvollerweise zunächst die Frage zu klären, ob er Messungen einer Phasenverschiebung der Ordnung von 10^{−8}rad bei LIGO für plausibel hält, denn das ist das einzige, was dabei tatsächlich als Messwert behauptet werden kann. Der Weg vom phase shift bis zum wave strain ist theorieabhängige Rechnerei, und ihm dies zu explizieren erübrigt sich dann möglicherweise ohnehin.
Dass dessen ungeachtet hinsichtlich GW150914 noch etliche andere offene Fragen bleiben, wäre eine andere Baustelle, aber man kann und soll ja nicht alles zugleich machen.
Ein ergänzender Vorschlag wäre noch, sich diese Animation einmal in mitbewegten Koordinaten vorzustellen. Die physikal. Gegebenheiten dahinter blieben dieselben, speziell die am Detektor auftretende Phasenverschiebung. Lediglich die Darstellung wäre eine andere. Doch würde damit nun die Sicht eines in der GW befindlichen Beobachters eingenommen, dessen Meterstäbe dem Rhythmus der GW folgen.
In der mitbewegten Darstellung erscheinen die Spiegel nicht mehr bewegt, und das Vorhandensein der GW manifestiert sich in einer zeitlich variierenden Lichtgeschw., deren jeweiliger Wert in x- und y-Richtung wiederum aus den entsprechenden Koeffizienten der Metrik zu bestimmen ist, woraus die Phasenverschiebung am Detektor resultiert.
Dieses mitbewegte Bild vermittelt dann nicht länger den Eindruck, die Welle würde Objekte im Raume irgendwie herumschieben, und es ginge darum, deren Abstände zu messen. »Entscheidend ist wieder, was beim Lichtdetektor ankommt,« heisst es oben im Blogbeitrag. Und das stimmt, genau darum geht es.
Chrys schrieb (26. Mai 2016 17:26):
> [… dass] Meterstäbe dem Rhythmus der GW folgen. […]
Bezieht sich die SI-Definition dessen, was mit “Meterstab” gemeint ist, etwa nicht auf ein Paar von Enden, die gegenüber einander chronometrisch starr waren; also deren gegenseitige Pingdauern jeweils konstant blieben?
Bezieht sich die SI-Definition dessen, was mit “Meterstab” gemeint ist, etwa nicht auf ein Paar von Enden, die gegenseitig gleiche chronometrische Entfernung voneinander hatten; also deren gegenseitige Pingdauern gleich war
(nämlich: 2 / 299’792’458 Sekunden)?
Bezieht sich die SI-Definition dessen, was mit “Meterstab” gemeint ist, etwa nicht auf ein Paar von Enden, die frei waren; deren Pingdauer also maximal war, verglichen mit den Pingdauern denkbarer anderer Beteiligter, die jeweils am selben Ereignis teilnahmen, zu dem die Signalanzeige gehörte, sowie am selben Ereignis, zu dem die Anzeige der Wahrnehmung des Pingechos gehörte?
(Naja, offenbar noch nicht in der momentan vorhandenen Formulierung …)
@Frank Wappler
Mit “Meterstab” ist schlicht das gemeint, was Einstein 1916 in seinem Büchlein mit diesem Wort gemeint hat, wo man beispielsweise lesen kann: “Hierauf wird der Abstand dieser Punkte A und B durch wiederholtes Abtragen des Meterstabes längs des Bahndammes gemessen.“
Chrys schrieb (27. Mai 2016 8:53):
> Mit “Meterstab” ist schlicht das gemeint, was Einstein 1916 in seinem Büchlein mit diesem Wort gemeint hat […]
Dass mit der schlichten Nennung des selben Wortes der selbe Begriff und überhaupt etwas Bestimmtes gemeint wäre, ergibt sich (insbesondere für Physiker, allerdings auch für Nichtphysiker) erst durch einvernehmliche Berufung auf die selbe bestimmte nachvollziehbare Definition, wodurch die Methode an die Hand gegeben ist, im konkreten Fall herauszufinden, ob der Begriff zutrifft, oder nicht.
(Wie man dem besagten Büchlein ebenfalls entnehmen kann.)
D.h. hier um experimentell zu entscheiden, ob zwei betrachtete Beteiligte die beiden Enden des selben einen „Meterstabes“ waren; da ein solcher Befund ja offenbar nicht unbedingt/definitiv für alle beliebigen Paare von Beteiligten in allen Versuchen zu konstatieren sein muss.
Nach einiger Zeit des Nachdenkens hätte Einstein vermutlich eine geeignete Definition vorschlagen können; (insbesondere eine, die auf Feststellung von Koinzidenzen hinausläuft, wie Einstein an anderer Stelle ebenfalls 1916 forderte). Nicht auszuschließen, dass Einstein gerade mit einem Vorschlag äquivalent zur SI-Definition (einschl. der 27. Mai 2016 0:01 genannten Konkretisierungen) sehr zufrieden gewesen wäre. Leider scheint aber nicht überliefert, dass sich Einstein für solches Nachdenken Zeit genommen oder gar eine konkrete Definition selbst vorgeschlagen hätte.
OK, jetzt weiß ich, was Sie meinen. Da das SI im Namen zu führen, halte ich aber für ziemlich irreführend – die Einheiten sind ja nun wirklich austauschbar, und proper distance ist es egal, ob man sie in Fuß oder in Metern misst.
Dass “Der LIGO-Beobachter […] mitbewegt” wird, halte ich für keine sinnvolle Beschreibung. LIGO selbst ist nun mal eine komplizierte Kombination von Festkörpern, die durch die Gravitationswellen noch deutlich weniger beeinflusst wird als Strahlteiler und Spiegel. Letztere sind ja gerade so aufgehängt, dass sie in die Bewegungsrichtungen, auf die es bei der Messung ankommt, so nah wie möglich am Verhalten freier Teilchen sind. Insofern ist die Außenansicht, die die Animation zeigt, näherungsweise auch die Sicht eines “LIGO-Beobachters”.
Letztlich kommt es, klar, nur darauf an, was am Photodetektor registriert wird.
Mitbewegte Koordinaten kann man (wie unendlich viele andere Koordinaten) natürlich wählen, aber ich sehe momentan nicht, wie diese Wahl das Verständnis dessen fördern würde, was da vor sich geht. Die abstandstreuen Koordinaten haben zumindest den Vorteil, dass sie direkt Abstandsänderungen zeigen (sowohl der freien Detektorkomponenten als auch der Lichtwellenlängen).
@Markus Pössel
»OK, jetzt weiß ich, was Sie meinen.«
Da habe ich leider genau den gegenteiligen Eindruck. Von verschiedenen Längeneinheiten habe ich doch nirgends geredet, sondern von der Verschiedenheit zweier Abstandskonzepte. Das SI definiert ja nicht einfach eine Einheit ‘Meter’ für eine als selbstverständlich anzunehmende Idee von Abstand, sondern spezifiziert dabei insbesondere eine Vorgehensweise, nach der mit Bezug auf diese Einheit zu messen ist — nämlich grundsätzlich über die Ermittlung von Lichtlaufzeit, was zum Konzept von Radarabstand führt (resp. “Pingdauer”, um Herrn Wappler vorzugreifen). Die “proper distance” hat mit Lichtlaufzeit per definitionem nichts zu tun und lässt sich i.a. auch nicht durch Radarabstand ausdrücken, was etwa anhand der kosmolog. FLRW Modelle auch leicht einzusehen ist.
»Dass “Der LIGO-Beobachter […] mitbewegt” wird, halte ich für keine sinnvolle Beschreibung.«
Eine GW ist eine nicht-statische Raumzeit, und jeder Beobachter sitzt mit seinen Meterstäben dann unweigerlich mitbewegt in dieser Raumzeit, ganz speziell das komplette LIGO Equipment. Eine andere Möglichkeit zur Plazierung von Beobachtern existiert da überhaupt nicht. Die obigen Animationen zeigen nun einen statischen Hintergrund, die “Zeichenebene”, in welchem dann scheinbar irgendwelche Dinge von der GW herumgeschoben werden, wobei sich deren Koordinatenwerte in der Darstellung gemäss den Koeffizienten der Metrik ändern. Das ist jedoch gerade nicht das, was da vor sich geht, denn die GW bewegt Koordinatenorte, wobei die zugehörigen Koordinatenwerte — und folglich Koordinatenabstände — unverändert bleiben; vgl. dazu Flanagan & Hughes, Sec. 3. Der Unterschied zwischen im Raume bewegten Dingen und einer nicht-statischen Metrik wird durch obige Animationen jedoch weder begreifbar, noch wird er dabei überhaupt herausgestellt.
»Letztlich kommt es, klar, nur darauf an, was am Photodetektor registriert wird.«
Ja, und warum sagt das dann keiner dem Herrn Engelhardt? Stattdessen wird der Eindruck gepflegt, es werde bei LIGO eine metrolog. Abstandsmessung von wackelnden Spiegeln vorgenommen, und das könne man jetzt neuerdings bis zu einer Auflösung von 10^{−18}m tun. Natürlich kann man das nicht, damit hat er doch völlig recht.
P.S. zu 29. Mai 2016 22:26
Wenn ich es recht bedenke, ist das auch schon wieder Unsinn, wenn ich schreibe, die GW “bewege Koordinatenorte”. Was sich tatsächlich geometrisch sinnvoll sagen lässt ist, eine GW-Metrik verändert das intrinsische Abstandsmass zwischen raumartig getrennten Punkten von fixem Koordinatenabstand, ohne dass sich damit eine eigentliche Bewegung dieser Punkte verbinden liesse. Auch das Wort ‘mitbewegt’ ist hier letztlich eine gängige façon der parler, die nicht wortgetreu zu deuten ist.
Chrys schrieb (29. Mai 2016 22:26):
> Abstandskonzepte. Das SI […] definiert ja nicht einfach eine Einheit ‘Meter’ […] sondern spezifiziert dabei insbesondere eine Vorgehensweise
Dimensionsbehaftete Werte sind grundsätzlich unabhängig von der Wahl irgendwelcher Einheiten,
und regelrechte Messwerte sind sowieso nur reelle Zahlen (z.B. Werte von Abstandsverhältnissen), oder Boolesche Werte.
Sofern ein bestimmtes System durch einen bestimmten dimensionsbehafteten Wert charakterisiert ist (also z.B. durch „den Abstand seiner beiden Enden voneinander“), symbolisiert die Dimensionsangabe nicht mehr und nicht weniger, als welche Vorgehensweise in dieser Hinsicht für einen Vergleich mit anderen kommensuraten Systemen anzuwenden ist.
> nämlich grundsätzlich über die Ermittlung von Lichtlaufzeit
(Wer Einsteins Festlegung versteht und würdigt, dass „ich an Stelle der „Zeit“ die „Stellung des kleinen Zeigers meiner Uhr“ setze“, wird in Zusammenhängen, wo stattdessen „Dauer“ gemeint ist, nicht das Wort „Zeit“ einsetzten.)
> was zum Konzept von Radarabstand führt
(Wieso eigentlich, konkret?? Was ist überhaupt mit „Lichtlauf“ im Sinne der SI-Definition gemeint?)
> resp. “Pingdauer”
(Im Falle durchgängig variabler Pingdauerverhältnisse von „Abständen“ zu sprechen, wäre allerdings bestenfalls ungenau und irreführend; schließlich hat das Wort „Abstand“ mit „stehen“ zu tun. Sogar falls die Pingdauern zweier Beteiligter gegenüber einander jeweils konstant aber ungleich wären, würde man diese genaugenommen allenfalls “Quasiabstände“ nennen.)
> Die “proper distance” […] lässt sich i.a. auch nicht durch Radarabstand ausdrücken
(Und etwa auch nicht mal durch Pingdauern?? Das erschiene allerdings als Hürde auf dem Wege, alle zeiträumlichen Konstatierungen auf Feststellungen von Koinzidenzen hinauslaufen zu lassen.)
> Die obigen Animationen […]
… illustrieren offenbar Beteiligte, deren Pingdauern untereinander (i.A.) variable Verhältnisse haben.
(Was natürlich auch eng mit der Variabilität des tatsächlich durch den Photodetektor gefundenen Interferenzsignals verbunden ist; und natürlich völlig unabhängig davon, ob und welche Koordinaten auf die Beteiligten gestreußelt würden.)
> Der Unterschied zwischen im Raume bewegten Dingen und einer nicht-statischen Metrik wird durch obige Animationen jedoch weder begreifbar, noch wird er dabei überhaupt herausgestellt.
Ganz recht (sofern sich „Metrik“ hier als koordinatenfreie Beschreibung von Geometrie versteht):
Darauf hatte ich übrigens schon in meinem ersten Kommentar (9. Februar 2016 16:49) zum SciLogs-Beitrag „Was sind eigentlich Gravitationswellen? (GW Teil 1)“ (8. Februar 2016) hingewiesen und im Folgenden (11. Februar 2016 14:01) Vorschläge zur Verbesserung der Darstellung gemacht.
@Frank Wappler / 30. Mai 2016 11:07
Die Kosmologen bemühen gemeinhin proper distance als Abstandsmass zur Beschreibung ihrer expandierenden Universen, und zwei Punkte im Universum (“Galaxien”) können dann bekanntlich mit superluminaler Geschw. rezedieren. Das heisst zum einen, dass variierende proper distance nicht notwendig einer “regulären” Bewegung von Dingen im Raume zu entsprechen hat, und zum anderen, dass ein luminales Ping-Signal den Roundtrip von einer Galaxis zu einer anderen, weit entfernten, und wieder zurück nicht zwangsläufig in endlicher Zeit (Dauer) bewältigen können muss, obwohl die proper distance zwischen je zwei Galaxien stets einen endlichen Wert hat, was die Verschiedenheit dieser Abstandskonzepte verdeutlicht.
Chrys schrieb (30. Mai 2016 14:23):
> […] dass variierende proper distance nicht notwendig einer “regulären” Bewegung von Dingen im Raume zu entsprechen hat
> […] die proper distance zwischen je zwei Galaxien stets einen endlichen Wert hat, was die Verschiedenheit dieser Abstandskonzepte verdeutlicht.
Die offenbare Verschiedenheit (zwischen der genannten „proper distance“ und “regulärer” chronometrischer Abstandsbestimmung) beweist ja nicht, dass man Werte der einen Größe nicht durch Werte der anderen ausdrücken oder damit überhaupt nicht in Zusammenhang bringen könnte.
(Schließlich lässt sich ja z.B. auch „hyperbolic motion in a flat region“ dadurch ausdrücken, dass Koinzidenzen mit geeigneten Beteiligten beschrieben werden, zwischen denen reguläre chronometrische Beziehungen messbar sind.)
Zur Definition und eventuellen Feststellung der erforderlichen chronometrischen Beziehungen mögen natürlich nicht unbedingt bestimmte Galaxien selbst in Betracht kommen, sondern stattdessen eben geeignete andere gedachte oder sogar auffindbare Beteiligte, die von den fraglichen Galaxien passiert wurden.
Den Kosmologen sei ja gern zugestanden, allerlei Modelle zu entwerfen und diese oder jene modell-abhängige Größe aufzustellen; aber nachvollziehbar sollten sie schließlich sein, und das heißt (spätestens seit Einstein, 1916) auf Feststellungen von Koinzidenz hinauslaufen.
Zugegeben, erst *jetzt* weiß ich, worauf Sie hinauswollen, halte es aber nach wie vor für sehr missverständlich. Bei SI geht es ganz klar um die Einheitendefinition, nicht um Abstandsdefinitionen – deutlich wird das in den Umsetzungsanweisungen, in denen viel zur Realisierung des SI-Meters steht, aber meines Wissens nach nichts zu Radarmessungen etc. Warum nicht gleich von Radarkoordinaten reden, wenn das gemeint ist?
Zu Abstandsänderungen: Aber selbstverständlich kann man durch geeignete, möglichst starre Anordnungen, wie sie die LIGO-Anlagen darstellen, den Einfluss der veränderlichen Raummetrik weitgehend unterdrücken. Genau so wie bei der kosmischen Expansion ja auch nicht Atome, Galaxien und sonstige stark genug gebundene Systeme mit expandieren. Insofern: Doch, das in meiner Animation gewählte System ist durchaus in guter Näherung das eines äußeren LIGO-Beobachters.
Zu den LIGO-Messungen vs. Radarabstände: In der üblichen kurzer-Arm-Näherung sind es sogar in guter Näherung Radarabstände, die sich da ändern. Erst bei ganz langen Distanzen wie bei LISA wird die Frequenzverschiebung entscheidend. In meiner Animation sind beide Effekte eingearbeitet; die macht die kurzer-Arm-Näherung extra nicht. Zum grundlegenden Verständnis, was so eine Gravitationswelle mit einem interferometrischen Detektor macht, ist diese Näherung aber ein durchaus guter erster Schritt.
Herr Pössel,
ganz so, wie Sie das Problem beschreiben, kann die Sache nicht sein. Wenn beispielsweise für einen Endspiegel gilt:
x(t)=x0 [1 + A/2 sin(ω t)]
dann können wir die Beschleunigung dieses Spiegels ausrechnen:
dx/dt = x0 A/2 ω cos(ω t)
Da wir frei in der Wahl des Ursprungs sein müssen, ergeben sich für sehr große x0 beliebig große Beschleunigungen, zu deren Nachweis man kein 4 km langes Interferometer bräuchte. Man denkt sich einfach den Ursprung auf dem nächsten Fixstern gelegen und kann dann jede Masse unter dem Mikroskop um 10 Mikron schwingen sehen.
Zudem hängt nach Ihrer Formel die durch die ebene Gravitationswelle erzeugte Auslenkung vom Ort x0 ab: Δ(t) = x0 A/2 sin(ω t), d.h. auf der x-Achse kann keine räumlich konstante Phase der GW herrschen, was aber nach Voraussetzung der Fall sein soll.
Weiterhin haben Sie keine linearisierte Wellengleichung für das gestörte Gravitationsfeld und keine Lösung derselben angegeben. Damit hängt die Größe h(t) völlig in der Luft, weil Sie nicht angeben, wie das wandernde Gravitationsfeld mit einer Masse wechselwirkt.
Entsprechend dem Spektrum-Lexikon-Zitat führt eine Gravitationswelle zu einer Beschleunigung von Massen, die wohl der Gravitation analog sein muss: d(m v)/dt = m grad U(t). Das bedeutet: Endspiegel und Strahlteiler werden unabhängig von ihrer Masse in gleicher Weise beschleunigt, weil die Masse heraus fällt und die Phase der ebenen Welle an beiden Orten per definitionem die gleiche ist.
(PS: Morgen muss ich für einige Tage ins KH und werde deshalb in diesem Austausch pausieren.)
Hallo Herr Engelhardt, doch: das ist die richtige Beschreibung.
Zu Ihrem ersten Einwand: Nein, denn nachweisen können Sie nur relative Beschleunigungen (bzw. allgemeiner: Abstandsänderungen). Unter dem Mikroskop würden Sie Ihre Testmasse nur schwingen sehen, wenn sie relativ zum Mikroskop, zur Unterlage etc. beschleunigt würde. Die Abstandsänderung relativ zu einem fernen Fixstern macht aber auch die Erde als näherungsweise frei fallendes Teilchen mit. Das lässt Ihr Einwand zu unrecht außer acht.
Zur Phase: Sie gehen immer noch davon aus, dass gleiche Phase etwas mit gleicher Beschleunigung zu tun haben muss. Das ist bei einer Gravitationswelle aber explizit nicht so, wie Sie den Gleichungen ja auch entnehmen können. Gleiche Phase heißt in diesem Zusammenhang gleicher Wert für h(t). Nicht mehr und nicht weniger. Sie übertragen hier unzulässig Eigenschaften anderer Wellen auf die Gravitationswellen.
Zur linearisierten Gleichung: Ich hatte in der Tat nur die Lösung in einer Ebene hingeschrieben; wenn Sie das Argument im Sinus ergänzen, sin[ω (t-z/c)], sehen Sie direkt, wie sich die Welle fortpflanzt. Und wie die homogene Wellengleichung aussieht (Wellenoperator angewandt auf den kleinen Zusatzterm der Metrik ergibt Null).
Zum Spektrumzitat: Nein, die Beschleunigung ist ausdrücklich nicht analog zur herkömmlichen Gravitation, und das betreffende Zitat behauptet auch nichts dergleichen. Die Beschleunigungen, um die es geht, sind die relativen Beschleunigungen, die man aus den von mir angegebenen Formeln berechnen kann. Insofern geht Ihre Argumentation hier von falschen Voraussetzungen aus.
Die Wirkung auf Massen – zumindest auf freie Teilchen, und auf Gebilde wie Spiegel und Strahlteiler, die künstlich so aufgehängt sind, dass sie sich zumindest in einer Richtung fast frei bewegen – ergibt sich aus den Gleichungen, die ich angab: Die abstandstreuen Koordinaten von freien Teilchen, und damit auch die Abstände zwischen ihnen, ändern sich genau so wie in meiner letzten Mail beschrieben. Das ist die gesamte Wirkung der einfachen Gravitationswelle auf (freie) Massen.
Gravitationswellen äußern sich in Abstandsänderungen, Veränderungen der Metrik. Welche relativen Beschleunigungen sich daraus ergeben, kann man nach Wahl eines Nullpunkts ableiten. Das habe ich explizit in meiner letzten Mail getan. Wie sich die Abstände von Strahlteiler (Nullpunkt) und Endspiegeln bzw. inneren Fabry-Perot-Spiegeln ändern, die sämtlich so aufgehängt sind, dass sie sich in einer Richtung frei bewegen können, können Sie aus diesen Formeln ablesen.
(P.S.: Ich wünsche gute Besserung bzgl. des Krankenhausaufenthalts.)
Herr Pössel,
vielen Dank für die Besserungswünsche! Die Untersuchungen im KH haben mich etwas beruhigt.
Sie haben eine Größe G = (x02-x01)(1+A sin (kz-ωt)) definiert, welche wohl die Lösung der ebenen Wellengleichung c^2 (@^2 G) / @z^2 = (@^2 G) / @t^2 sein soll, aber nicht die Komponente eines Gravitationsfeldes darstellen soll. G besteht aus einem festen Abstand x02-x01 sowie einem propagierenden Anteil (x02-x01) A sin (kz-ωt), dessen Phase sich mit der Geschwindigkeit ω/k = c bewegt. Es bleibt offen, wie sich die dimensionslose Zahl A durch physikalische Größen ausdrückt. Weiterhin haben Sie keine Gleichung angegeben, welche die Wechselwirkung der Größe G mit einem Massenpunkt beschreibt. Die Wechselwirkung kann ja nicht von der zufälligen Wahl von zwei Punkten abhängen, sondern muss irgendwie z.B. durch den Kollaps von zwei SL bestimmt sein. Es wäre also weiterhin zu klären, welche physikalische Bedeutung dem Abstand x02-x01 zukommt und warum er bei LIGO und GEO600 unterschiedlich gewählt wird.
Nachdem im demonstrierten Beispiel von LIGO die Gravitationswelle von einem sehr entfernten Punkt ausging und sich isotrop mit c ausbreitete, müsste man in Ihrem Beispiel die Koordinate x0 durch x0 = R phi ersetzen und den Abstand durch x02-x01 = R (phi2-phi1). In diesem Fall wäre die Welle nicht axial-symmetrisch, d.h. man müsste bei irgendeinem Winkel phi eine Diskontinuität fordern, für die es nach meiner Meinung keinen plausiblen Grund gibt, zumal man keinen bestimmten Winkel angeben kann, wo die Welle unstetig wird.
Es bleiben also grundlegende Fragen offen: Welche physikalische Größe G(z,t) = A R (phi2-phi1) sin(kz-ωt) breitet sich als Gravitationswelle mit Lichtgeschwindigkeit aus? (Was ist A?) Nach welchem Gesetz wirkt sie auf einen Massenpunkt, wenn sie auf einen solchen trifft?
Zur Wellengleichung: Ja, das ist die betreffende Gleichung. Obacht: Die Größe ist nicht das übliche (Newton’sche) Gravitationsfeld, aber gelegentlich werden die betreffenden h_munu auch als verallgemeinertes Gravitationspotenzial bezeichnet. Wenn Sie fragen, welche physikalische Größe das sei: es sind kleine Korrekturen zum Raumanteil des metrischen Tensors.
Die Wechselwirkung mit Massen habe ich im letzten Kommentar zumindest für den einfachsten Fall angegeben, siehe den Absatz dort der mit “Die Wirkung auf Mason” beginnt. Und doch: Die Wirkung gilt für freie Teilchen in beliebigen Punkten. Wie die Gravitationswelle ursprübglich zustande kam, steckt nur noch im A und im omega, bzw. allgemeiner in einem komplizierter zeitabhängigem h(t). Das muss uns hier aber nicht kümmern, da alles im wesentlichen linear ist – sobald Sie verstehen, wie eine einfache sinusförmige Gravitationswelle wirkt, können Sie durch Überlagerung die Wirkung komplizierterer Wellen beschreiben. Ganz analog zum Elektromagnetismus, wo man sich bei einfachen Sinus-EM-Wellen und deren Wirkung ja auch erstmal keine Gedanken über die Erzeugung machen muss, wenn man die Wirkung einer Antenne verstehen will. Diese grundlegende Frage sollte also nicht mehr offen sein.
Und nein, man muss die Koordinate keineswegs durch R phi ersetzen. Was da an Abstandsabhängkeit da gewesen sein mag ist alles schon in der Größe kodiert, die A am Ort des Detektors hat.
Wie gesagt: Bei EM-Wellen geht man genau so vor und betrachtet als erstes die Wirkung einer ebenen Welle auf die Dipol- oder andere Antenne. Darüber, dass die ebene Welle in Wirklichkeit ein Ausschnitt aus einer großen Kugelwelle ist, muss man sich erst danach Gedanken machen. Dieselbe Trennung sollten wir auch hier vornehmen.
Markus Pössel schrieb (22. Mai 2016 21:45):
> h_munu […] welche physikalische Größe das sei: es sind kleine Korrekturen zum Raumanteil des metrischen Tensors.
Allmählich dürfte sich also die Beschäftigung damit anbahnen, wie „metrischer Tensor“ (bzw. dessen „Anteile“) als Messgröße(n) definiert sein sollen.
Oder, falls das immer noch als „Vorgriff“ gilt, dann zumindest vorbereitenden physikalisch-geometrische Messgrößen wie z.B. die Bewertung, welche Beteiligten, die koinzident waren, dabei (paarweise) „tangential“ gewesen wären, und welche nicht.
Es mag sich sogar als immer noch wesentlich einfacher erweisen, zunächst diese Messgrößen aus Bestimmungen von Koinzidenzen (usw.) zu konstruieren, als die hier schon mehrfach vorausgesetzten und hinterfragten Konstatierungen, welche Beteiligten als „freie Teilchen“ gelten sollten, und welche nicht.
@Frank Wappler: da wir her nicht im Rahmen der Serie “Einstein verstehen” sind, ist das mit Vorgriffen weniger problematisch. Trotzdem sollte das Niveau der Diskussion nicht zu hoch werden.
Zu Ihrer Fünfpunkt-Definition: Ich vermute, dass Sie damit weiterkämen, wenn Sie Ereignisse zu mindestens drei unterschiedlichen Zeitpunkten und räumlich so verteilt betrachteten, dass Sie die Quadrupol-Eigenschaft der Wellen einfangen.
Markus Pössel schrieb (24. Mai 2016 20:37):
> […] sollte das Niveau der Diskussion nicht zu hoch werden.
(Na, bloß nicht! ;)
Allerdings hoffentlich hoch genug, um (vor allem) sich selbst nicht gewissen allzu naheliegenden Täuschungen hinzugeben und entsprechende Enttäuschungen (nicht zuletzt bei anderen) zu riskieren.
(Und zur Sicherheit sei das konkretisiert: gemeint ist insbesondere der leichtfertigen Einsatz von Begriffen wie „freie Teilchen“ und „Beschleunigungen“, ohne Gedanken an nachvollziehbare Methoden zur Ermittlung was dahingehend zugetroffen haben mag, und erst recht ohne darauf basierende Betrachtungen zur eventuellen Inkompatibilität der entsprechenden Messgrößen.)
> Zu Ihrer Fünfpunkt-Definition: Ich vermute, dass Sie damit weiterkämen, wenn
Zumindest mag ja interessant sein, ob und wie „meine“ (letztmalig wohl von J. L. Synge 1960 im Buch „Relativity. The General Theory“ mehr oder weniger eigenständig entworfene) Methode zur Definition bzw. Messung von „Krümmung“ mit eventuellen anderen zusammenhängt.
> Ereignisse zu mindestens drei unterschiedlichen Zeitpunkten und räumlich so verteilt betrachteten, dass Sie die Quadrupol-Eigenschaft der Wellen einfangen.
Dass Versuch für Versuch hinreichend entsprechende Ereignisse in Betracht stehen,
sollte offensichtlich sein (nämlich für jeden einzelnen der je fünf Beteiligten jeweils mindestens eine Signalanzeige, die einzelnen Reflexionsanzeigen der vier anderen, eine Anzeige, in der mindestens drei dieser Reflexionsanzeigen wiederum koinzident wahrgenommen wurde, und ggf. sogar noch eine weitere Wahrnehmungsanzeige der „Reflexion von der diagonal gegenüberliegenden Tetraederspitze“, und entsprechend verschiedene Ereignisse, die diese Anzeigen enthielten).
Was dann??
Lässt sich die per 18. Mai 2016 15:50 eingeführte (Rechen-)Größe „h“ z.B. durch Werte der „Lorentzschen Distanzen“ zwischen den betrachteten Ereignissen ausdrücken?
Ließe sich ggf. insbesondere nachweisen, dass der Wert damit ermittelte „h“ ungleich Null ist;
Dass also die Beteiligten nicht „einfach (im Flachen) vor sich hinwackelten“?
Frank Wappler schrieb (25. Mai 2016 13:04):
> Ließe sich ggf. insbesondere nachweisen, dass der Wert damit ermittelte „h“ ungleich Null ist;
—(ist zu ersetzen mit)—>
Ließe sich ggf. insbesondere nachweisen, dass der damit ermittelte Wert (von) „h“ ungleich Null ist;
> Dass also die Beteiligten nicht „einfach (im Flachen) vor sich hinwackelten“?
—(ist zu ergänzen bzw. zu verallgemeinern als)—>
Dass also die Beteiligten nicht „einfach (im Flachen bzw. zumindest im Statischen) vor sich hinwackelten“?
Was da passiert, entspricht auf alle Fälle der aus meiner Sicht anschaulichsten Definition von Krümmung, wie sie Baez und Bunn in ihrer Elementarisierung der Einstein-Gleichungen beschreiben.
Sprich: Wir haben einen Ring von Testteilchen, wir haben eindeutige Gezeitenkräfte, und die Quadrupolnatur zeigt, dass da keine lokale Masse-Energiequelle im Spiel ist. (Ricci-Tensor verschwindet, Weyl-Tensor nicht.)
Markus Pössel schrieb (29. Mai 2016 13:29):
> Wir haben einen Ring von Testteilchen […]
Zum sicherlich *zigsten Male:
Durch welches nachvollziehbare, also auf Feststellungen von Koinzidenzen (bzw. Identitäten von Beteiligten) hinauslaufende Messverfahren, soll der Begriff „Testteilchen“ hier definiert sein??
Falls (sicherlich *zigsten Male) gar nicht, dann bleibt In Anlehnung an Planck immerhin zu hoffen, dass die Vertreter solcher Newtonscher Anmaßung demnächst aussterben, weil die heranwachsende Generation von vornherein damit vertraut gemacht werden kann, wie zu messen ist, ob ein Beteiligter „Testteilchen“ bzw. „frei“ war, oder nicht.
[Quote] “Es bleiben also grundlegende Fragen offen:
1. Welche physikalische Größe … breitet sich als Gravitationswelle mit Lichtgeschwindigkeit aus? .
2. … Nach welchem Gesetz wirkt sie auf einen Massenpunkt, wenn sie auf einen solchen trifft?” [/Quote]
zu 1. der physikalische Abstand in x-y zweier Teilchen auf Geodäten ändert sich abhängig von z bzw. t, aber das Koordinatenintervall bleibt konstant. Der meßbare phys Abstand wird durch das Linienelement bestimmt, man muß für die Entfernung das Eigenzeitintervall mit der Lichtgeschwindigkeit multiplizieren. Das geht aber nur im momentanen Ruheraum des Beobachters, also infinitesimal, weil allgemein Entfernungen von der Weltlinie abhängen.
Dr. Engelhardt, damit sind wir wieder bei den “physikalischen Fremdwörtern”, die Sie seit Wochen auf /relativ kritisch/ “negieren”, aber ohne die geht nichts zu erklären.
Das Problem ist Ihr Verständnis von Bezugssystemen, die Diskussion wird unendlich.
zu 2. Die “frei fallenden” Spiegel bleiben auf den Geodäten – das ist das Gesetz.
Ihr Bezugssystem mit Nullpunkt im Strahlteiler ist “steif” wie auch die Meter zum Messen, es sieht im x-y-Bezug so aus, daß die Spiegel beschleunigt werden – Scheinkraft.
HerrPössel,
ich möchte Ihre Bereitwilligkeit, das LIGO-Experiment zu erklären, nicht überstrapazieren. Offenbar sind auch Sie nicht in der Lage, die propagierende Größe G=(x02-x01) A sin (kz-ω t) in eine Kraft zu übersetzen, welche Strahlteiler und Endspiegel beim Eintreffen der Gravitationswelle relativ zueinander beschleunigt. Im Sinne der im Spektrum-Lexikon beschriebenen Beschleunigung einer Masse wäre dazu eine Kraft von 3×10^(-11) m kg/s^2 nötig, wenn man die veröffentlichten Daten 10^(-18) m, 40 kg, 150 Hz zugrunde legt. Ich verzichte auf weitere Erklärungen und „glaube“, dass man eine Spiegelauslenkung von 10^(-18) m gemessen hat.
Um die Messung zu eichen, musste man diese Kraft von 3×10^(-11) m kg/s^2 per Strahlungsdruck auf die Endspiegel ausüben, während gleichzeitig eine ca. 10^(12) mal größere Kraft aufgrund der zirkulierenden Lichtleistung auf die Spiegel einwirkte. Sie haben geschrieben, dass die Eichkurve im „Calibration-paper“ vorliege, allerdings hat Prof. Nicolai eingeräumt, dass sie nicht leicht zu entnehmen sei. Bitte geben Sie einen Hinweis, welche Rechnungen man mit welchen Daten anstellen muss, damit man aus den 10 noch nicht veröffentlichten Figuren in arXiv:1602.03845v1 [gr-qc] 11 Feb 2016 die Eichkurve konstruieren kann. Ich sehe mich wie Prof. Nicolai außerstande, diese Aufgabe zu bewältigen und vermute, dass es den anderen Lesern hier ähnlich ergeht.
Dr. Engelhardt,
der Strahlungsdruck wirkt “einseitig”, wackelt nicht – die Stabilität ist dokumentiert.
Die wackelnde Gravitationswelle überlagert als Differenzmessung – Empfindlichkeit.
Solange es da offenkundig noch Fehlvorstellungen gibt, möchte ich die Frage noch nicht abhaken; erfahrungsgemäß gibt es sonst später Probleme.
Also noch einmal in leicht variierten Worten: Die Allgemeine Relativitätstheorie sagt direkt voraus, wie sich die Metrik bei Durchgang einer (einfachen, linearisierten) Gravitationswelle verändert. Das ist, was sich direkt aus der Theorie ergibt. In den Koordinaten, in denen die oben hingeschriebenen Abstandsveränderungen angegeben sind, entsprechen diese Abstandsveränderungen genau denjenigen Abstandsänderungen, wie sie zwischen freien, vor Durchgang der Gravitationswelle im betreffenden Bezugssystem ruhenden Teilchen auftreten.
Wie solche Teilchen relativ zueinander beschleunigt werden, können Sie direkt aus den angegebenen Abstandsänderungen ablesen. Alle Information dazu ist vorhanden.
Spiegel und Strahlteiler kann man näherungsweise für die zum Nachweis nötigen Bewegungen als solche freien Teilchen auffassen. Aus den von mir angegebenen Formeln können Sie daher direkt schließen, wie sich die Abstände von Spiegel und Strahlteiler unter Einfluss der Gravitationswelle verändern.
Wenn Sie als Hilfsgrößen Kräfte einführen möchten, dann können Sie deren Größe – genau so wie man es bei Trägheitskräften ganz allgemein tut – aus den durch die angegebenen Beschleunigungen berechnen. Die Kräfte müssen eben genau so groß sein, dass sie die betreffenden Beschleunigungen gemäß F=ma hervorrufen. Wie gesagt: das läuft genau so wie bei den Trägheitskräften.
Insofern: Im Gegensatz zu Ihrem Behauptungen sind alle nötigen Informationen sowohl zu den Abstandsänderungen von Strahlteiler, Spiegeln etc. als auch zu etwaigen Hilfskräften vorhanden. Wenn daran noch etwas unklar ist, wäre mir wichtig zu verstehen, wo genau die Unklarheit liegt.
Herr Senf,
die erste Frage hat Herr Pössel insoweit beantwortet, als eine Größe G sich mit Lichtgeschwindigkeit gemäß einer homogenen, linearen Wellengleichung ausbreitet. Er konnte allerdings nicht präzise angeben, was die Amplitude (x02-x01) A physikalisch bedeutet. Insbesondere ist nicht klar geworden, welche Auslenkung ein Massenpunkt beim Eintreffen dieser Welle erfährt.
Über die Physik des Michelson-Interferometers, das auf der Erdoberfläche relativ zu seinen Beobachtern ruht, gibt es keine Zweifel: Die Endspiegel müssen sich relativ zum Strahlteiler bewegen, damit sich das Dunkelfeld der destruktiven Interferenz aufhellen kann. (Wahlweise kann man natürlich auch den Strahlteiler relativ zum Endspiegel bewegen, ein Verfahren, das allerdings im Längenkomparator nicht angewandt wird.) Das entsprechende Diodensignal wurde quantitativ veröffentlicht (24 mal Dunkelstrom von 25 nA, der durch Rauschen verursacht wird). Daraus kann man eine Spiegelverschiebung von 3×10^(-13) m errechnen. Wie die 5 Größenordnungen zur behaupteten Spiegelverschiebung von 10^(-18) m überbrückt wurden, ist bisher ein Geheimnis, das vom Einstein-Institut nicht enthüllt wurde.
Dr. Engelhardt,
der Massepunkt = Spiegel “erfährt keine Auslenkung”, er bleibt auf der Geodäten.
Wir “sehen” aber eine Auslenkung, weil unsere Maßstäbe starr sind, folgen nicht der Metrik.
Das Ding ist extra so konstruiert, daß die Spiegel der Metrik folgen können, schließlich hat man nach den vorhergesagten “Störungen” der Metrik per direkter Messung gesucht.
Dazu, wie die Wirkung auf Massenpunkte aussieht, siehe meine letzte Antwort.
Bitte machen Sie, solange es offenbar noch Missverständnisse auszuräumen gibt, keine Nebendiskussionen auf, und bitte halten Sie sich auch mit der Polemik wieder zurück. Das waren, wie Sie erinnern, beides Voraussetzungen von meiner Seite aus, um diese Diskussion fortzuführen. Ohne guten Willen von beiden Seiten geht es nicht – ich bitte Sie da um Ihre Kooperation.
Herr Pössel,
das Ergebnis habe ich ja verstanden: LIGO behauptet, eine Abstandsänderung von 10^(-18) m bezogen auf 4 km Armlänge bei einer Frequenz von typisch 150 Hz in der Ebene z=0 gemessen zu haben. Somit ergibt sich das Produkt in G=(x02-x01) A sin (kz-ω t) zu (x02-x01) A=10^(-18) m oder A=10^(-18)/4000 . Wie dieser Wert aus der Verschmelzung von zwei Schwarzen Löchern von ca. 30 Sonnenmassen in 1.3 Milliarden Lichtjahren Entfernung auszurechnen ist, haben Sie nicht vorgerechnet, und ich habe auf eine nähere Erklärung verzichtet.
Vielmehr bin ich genau den von Ihnen vorgeschlagenen Weg gegangen und habe aus der gemessenen Beschleunigung mit F=ma die zugehörige Kraft ermittelt. Sie ergab sich zu 3×10^(-11) m kg/s^2. Zur Eichung des Systems hat man diese Kraft per Strahlungsdruck auf die Spiegel ausgeübt. Ich frage danach, wo dies dokumentiert ist, Sie sagen, diese Information läge vor. Die “Unklarheit” besteht also genau darin, dass ich die Information über die “Hilfskräfte” im Calibration-paper nicht finden kann.
OK, also nur zur Sicherheit: Wie eine Gravitationswelle mit gegebenem A (die Größe hatte ich in der Tat nicht abgeleitet, war auch nicht Gegenstand der ursprünglichen Frage gewesen) auf ruhende freie Teilchen wirkt und warum es dabei zu relativen Beschleunigungen z.B. von Strahlteiler und Spiegel kommt (und nicht zu so gut wie synchronen Beschleunigungen) ist jetzt geklärt, Ihre Frage 6) aus Ihrer initialen Frageliste demnach zu Ihrer Zufriedenheit beantwortet?
Herr Pössel,
es ist schon verwunderlich, dass unterschiedliche Kräfte auf die Spiegel wirken, je nachdem wo man den Koordinatennullpunkt hinlegt. Sie haben ihn in Ihrer Animation in den Strahlteiler gelegt (x01=0),so dass dieser keine Kraft erfährt, sondern nur der Endspiegel bei x02. Man hätte es auch anders machen können: Am Endspiegel gilt x02=0 und am Strahlteiler -x01. In diesem Fall wirkt auf den Endspiegel keine Kraft, wohl aber auf den Strahlteiler. Natürlich hätte man den Nullpunkt auch zwischen Strahlteiler und Endspiegel legen können. Dann wirkt auf beide Spiegel eine Kraft, allerdings in verschiedene Richtungen. Meine Vorstellung von Physik wird dadurch stark strapaziert, aber das mag mit der Unanschaulichkeit der Raumkrümmung zusammenhängen. Ich will nun glauben, dass es so sei wie Sie sagen. Gehen wir also weiter zur Eichkurve, auf welcher der experimentelle Nachweis der Existenz von Gravitationswellen ruht.
Genau genommen möchte man zwei Kurven sehen: 1) den Strahlungsdruck als Funktion der Zeit, 2) die Spiegelauslenkung als Funktion der Zeit, die durch diesen Strahlungsdruck hervorgerufen wurde. Sicher hat man zumindest nachträglich der Auslenkung im Wesentlichen denselben zeitlichen Verlauf gegeben, den man am 14.9.15 beobachtet hat, indem man den Strahlungsdruck entsprechend kontrolliert hat. Natürlich könnte man auch die Auslenkung als Funktion des Strahlungsdrucks auftragen, was ich als “Eichkurve” bezeichnet habe. Ich bin gespannt, wie Sie diese Informationen aus den Figuren im Calibration paper herausholen.
“Verwunderlich” ist natürlich sehr subjektiv. Ich finde im Gegenteil recht schön, wie sich selbst mit den üblichen Konzepten und Hilfsvorstellungen, die man bei populärwissenschaftlichen Darstellungen der Allgemeinen Relativitätstheorie nutzt, qualitativ verstehen kann, was da vorgeht. Die Relativität von Beschleunigungen ist ja typischerweise eine der ersten Eigenschaften, die diskutiert wird, wenn man von der Speziellen zur Allgemeinen Relativitätstheorie übergeht; hier wird sie wichtig. Und mit fortgeschritten-populärwissenschaftlichem Wissensstand (einfache Geometrie-Analogie, Gezeitenkräfte, Zusammenlaufen von Weltlinien in An- und Abwesenheit von Quellen) kann man ja durchaus auch ein paar weitere Eigenschaften der Gravitationswellen (insbes. die Quadrupolnatur) verstehen. Sprich: Dass die (zugegebenermaßen vereinfachten!) Bilder hier so stimmig zusammenspielen ist für mich per Definition Anschaulichkeit. Aber klar: Es ist, wenig überraschend, anders als in der klassischen Physik.
Zur Eichkurve: Ich bin etwas überrascht, dass Sie die aus meiner Sicht physikalisch naheliegenderen Fragen zur Nachweisplausibilität, nämlich die Frage der Stärke der verschiedenen Störeinflüsse, überspringen und jetzt zu einem eher technischen Thema übergehen, nämlich der Kalibration des Auslesesystems. (Zentral dafür, dass jetzt der Nachweis gelungen ist, dürften schließlich die Rauschkurven sein, die zeigen, wieweit es den Physikern gelungen ist, die diversen Störeinflüsse so zu vermindern, dass der Nachweis möglich wurde.)
Für diejenigen, die hier einfach nur mitlesen: Eine der Vereinfachungen in meinem Haupttext oben ist die Aussage, dass der interferometrische Detektor frei auf die durchlaufende Gravitationswelle reagiert und die Auswirkungen der Gravitationswelle auf das am Photodetektor einfallende Licht ausgelesen wird, um die Gravitationswelle nachzuweisen. In Wirklichkeit ist die technische Umsetzung komplizierter: Das am Photodetektor ausgelesene Signal wird als Input für einen Kontrollschaltkreis verwendet, der den Armlängenunterschied durch Verschiebung eines der Spiegel weitgehend direkt wieder ausgleicht. Dazu erzeugt der Kontrollschaltkreis elektrostatische Abstoßung zwischen dem betreffenden Spiegel und einer dahinter hängend angebrachten (und wie der Spiegel als Mehrfach-Pendel isolierten) Reaktionsmasse.
Um die Wirkung der Gravitationswelle zu sehen, muss man daher sowohl das Signal am Photodetektor aufzeichnen als auch berücksichtigen, welche aktiven Änderungen der Kontrollkreis wann hervorgerufen hat.
Dazu wiederum muss man ein gutes Modell dafür haben, wie der Kontrollkreis auf das Gesamtsystem wirkt. Dafür muss man Modellparameter bestimmen und die Güte des Modells testen. Das ist die Kalibration, auf die sich die Frage von Herrn Engelhardt bezieht. Sie wird in diesem Artikel (eines der vielen Abbott et al. 2016) direkt für den ersten Gravitationswellennachweis beschrieben; im Einsatz war sie aber auch schon für die vorangehende LIGO-Konfiguration, siehe diesen Artikel (Goetz et al. 2009a).
Die Kalibration erfolgt über eine zusätzliche kleine Quelle von Strahlungsdruck, nämlich die “photon calibrators”: Schwache Laser, deren Licht am zu untersuchenden Spiegel reflektiert und deren Laserleistung anschließend mit einem geeichten Detektor gemessen wird. Die Wirkung dieses Laserlichts (Strahlungsdruck) lässt sich direkt berechnen.
Dann (vgl. Goetz 2009a, Abschnitt 4) werden der elektrostatische Aktuator und der Photonen-Kalibrator gleichzeitig mit fast derselben Frequenz laufen gelassen – beim Photonen-Kalibrator mit einer kleinen, sinusförmigen Modulation der Laserleistung. Das gleichzeitige Laufen bewirkt, dass zeitabhängige Störeinflüsse auf beide Systeme im wesentlichen gleich sind. Anhand des kleinen Frequenzunterschieds (0,1 Hz) lässt sich trotzdem gut auseinanderhalten, welches System welche Wirkung hat. Die Wirkung des Photonen-Kalibrators ist, wie gesagt, direkt berechenbar. Aus dem Vergleich mit dem elektrostatischen Aktuators ergibt sich dann auch dessen Wirkung.
Die Kurven, die sich daraus ergeben, sind in Abb. 5 und 6 im oben zitierten Paper Abbott et al. 2016 zu sehen. Die Unsicherheit, die sich aus der Streuung der Messpunkte um die daraus bestimmten Parameterwerte ergibt, wird später neben vielen anderen Faktoren in den Gesamt-Messfehler des LIGO-Nachweises einbezogen.
Alle Gravitationswellendetektoren haben eine deutlich frequenzabhängige Empfindlichkeit und insbesondere eine stark frequenzabhängige Rauschkurve. Für die Auswertung macht man daher immer eine Fourieranalyse und benötigt dementsprechend auch die Aktuatorfunktion A(f) in Fourier-Form, sprich: als Funktion der Frequenz. In dieser Form, nämlich moduliert mit konstanter Frequenz, wurde die Aktuatorfunktion denn auch mithilfe des Photon-Kalibrators gemessen. Genau diese Messung wurde benötigt, genau diese Messung wurde durchgeführt. Und genau die Ergebnisse dieser Messung finden Sie an der angegebenen Stelle in dem genannten Artikel.
“Natürlich könnte man auch die Auslenkung als Funktion des Strahlungsdrucks auftragen, was ich als “Eichkurve” bezeichnet habe. Ich bin gespannt, wie Sie diese Informationen aus den Figuren im Calibration paper herausholen”
Dr. Engelhardt,
denken Sie einfach mal an den Luftballon, alles wird gleich klar:
drücken, loslassen, drücken, loslassen, usw. … Graviwelle hin und her
manchmal ist Physik ganz anschaulich – Quadrupol – invariant: Oberfläche=const.
Herr Senf schrieb (26. Mai 2016 1:57):
> denken Sie einfach mal an den Luftballon, alles wird gleich klar:
drücken, loslassen, drücken, loslassen, usw. […]
Ja sicher ist es kinderleicht sich Dinge vorzustellen (und vielleicht ggf. sogar aufzufinden), deren Bestandteile quadrupolartig gegenüber einander wackelten; insbesondere im interferometrischen Sinne.
Aber um so weniger berechtigt erscheint es doch, allein aus dem (interferometrisch ermittelten) quadrupolartigen Wackeln von Bestandteilen eines gewissen Dings den Schluss zu ziehen, dass die (ebenfalls im chronometrisch-interferometrischen Sinne definierte ) Krümmung der Region, in der diese Bestandteile enthalten waren, sich dabei quadrupolartig wiederholt verändert hätte.
Überzeugender wäre, die Krümmung der betreffenden Region definitionsgemäß an sich zu messen (und dabei ggf. festzustellen, ob und wie diese sich veränderte).
Herr Wappler,
noch einfacher ist es doch, die Eichkurve zu veröffentlichen, die man gemäß dem Text im Calibration Papier als Formel (10) aufgenommen hat, dann allerdings in Fig. 2 nur “schematisch”, nicht als Messung zeigt. Durch die Veröffentlichung dieser Daten könnten viele offene Fragen, die ich nun noch einmal an Bruce Allen anlässlich seines Vortrags im IPP gerichtet habe (http://www.kritik-relativitaetstheorie.de/Anhaenge/LIGO-Experiment-Engelhardt-an-Bruce_Allen_27_05_16.pdf), beantwortet werden.
Herr Senf,
anlässlich der LIGO-Veröffentlichung denke ich nicht nur an Luftballons, sondern viel mehr noch an Seifenblasen, die nicht sehr haltbar sind und ziemlich schnell zerplatzen. Freilich denke ich auch an mein physikalisches Grundwissen und werde schwindlig, wenn jemand so nebenbei behauptet, er habe mit konventionellen Mitteln eine relative Genauigkeit erzielt, die jene des Mößbauer-Effekts um den Faktor eine Million übertrifft. Den Wahrheitsgehalt dieser Behauptung hätte ich gerne zweifelsfrei dokumentiert gesehen, aber ich werde mit einer Schemazeichnung des experimentellen Aufbaus der Eichmessung abgespeist.
Dr. Wolfgang Engelhardt schrieb (27. Mai 2016 14:13):
> Herr Wappler, […]
Herr Dr. Engelhardt, ich bitte um Verständnis, dass ich mit Ihnen hier keine direkte Diskussion führen möchte, bis Ihre Diskussion mit Markus Pössel als abgeschlossen gelten kann.
(Dass ich dabei gelegentlich die direkte Diskussion mit Herrn Pössel suche, sei mir auch gestattet, sofern er den Anspruch verfolgt, allgemeinverständliche Antworten auf Ihre konkreten Fragen finden zu können;
und meine Korrespondenz mit anderen Kommentatoren beeinträchtigt Ihre und Herrn Pössels Aufmerksamkeit füreinander hoffentlich auch nicht. Ich freue mich jedenfalls, wenn meine Kommentare gelesen werden; vielleicht sind sie ja trotzdem hilfreich, auch wenn Sie darauf vorerst bitte nicht mehr direkt reagieren würden.)
Engelhardt, ob ihnen, in Anbetracht ihres offenkundig mangelnden physikalisches Grundwissen, nun schwindelig wird, oder nicht und ob sie irgendeinen Wahrheitsgehalt anzweifeln oder nicht, ist alleine ihre persönliche Angelegenheit und hat hier sachlich in keiner Weise was mit dem Thema zu tun, das sind keine Argumente, sie zweifeln ja auch schon am Wahrheitsgehalt der Relativitätstheorie selber.
Bleiben sie einfach beim Thema und vor allem sachlich und verschonen sie die Leser bitte mit ihren ganz persönlichen Problemen und Befindlichkeiten.
Herr Pössel,
ich versuche, so sachlich wie möglich zu bleiben und warte noch immer auf die Daten zur Eichkurve.
Im Papier “Calibration of the Advanced LIGO detectors for the discovery of the binary black-hole merger GW150914”, das zeitgleich mit der Publikation in Phys. Rev. Lett. im Internet “geposted” wurde: arXiv:1602.03845v1 [gr-qc] 11 Feb 2016 finde ich im Abschnitt IV, wo die Eichung per Strahlungsdruck beschrieben wird, den Satz:
„Power modulation is accomplished via an acousto-optic modulator that is part of an optical follower servo that ensures that the power modulation follows the requested waveform [14].”
Und weiter unten:
“The laser power modulation induces a modulated displacement of the test mass that is given by [12]:
x^(PC)_T ( f ) =2P( f )/c s( f ) cos θ [1 + (M_T / I_T) \vec a . \vec b)] (10)
This modulated displacement is shown schematically on the left of Fig. 2.”
Die Unterschrift dieser Figur lautet:
“FIG. 2. Block diagram of the differential arm length feedback control servo. The sensing function, digital filter function, and actuation function combine to form the open loop transfer function G( f ) = A( f ) D( f ) C( f ). The signal x^(PC)_T is described in section IV.”
Es werden keine Daten mitgeteilt, wo etwa die gleiche oder eine ähnliche Wellenform und Amplitude wie GW150914 durch Strahlungsdruck erzeugt und gleichzeitig interferometrisch gemessen wurde. Somit existiert keine Dokumentation der Eignung des Apparats für den Nachweis einer Spiegelverschiebung von 10^(-18) m. Ohne einen solchen Nachweis kann man jedoch nicht von der experimentellen „Entdeckung von Gravitationswellen“ sprechen. Sehen Sie das anders?
Wie in meinem letzten Kommentar geschrieben:
Bei dem von Ihnen angegebenen Paper bezieht sich “Kalibration” auf die Kalibration des elektrostatischen Aktuatorsystems mithilfe eines Hilfslasers. Die Kalibrationskurven für diesen Kalibrationsvorgang sind, wie ebenfalls dort geschrieben, im betreffenden Paper die Abbildungen 5 und 6.
Mein Eindruck ist, dass in Ihrer Nachfrage (mindestens) zwei Dinge durcheinandergehen. Bitte sagen Sie mir, um welche der zwei folgenden Fragen es Ihnen geht:
Geht es Ihnen (A) um das, was bei den Detektorenbetreibern Hardware-Injektionen heißt, also darum, wie mithilfe der elektrostatischen Aktuatoren künstliche Spiegelverschiebungen im Detektor erzeugt und unter realisitischen Bedingungen ausgelesen, sprich: wie künstliche Gravitationswellensignale im Detektor simuliert werden?
Damit hat das genannte Kalibrations-Paper und hat die Auslenkung durch Strahlungsdruck dann nicht direkt etwas zu tun.
Oder geht es Ihnen (B) um die spezifische Kalibration der elektrostatischen Aktuatoren mithilfe des kleinen zusätzlichen Lasers, der einen wohldefinierten Strahlungsdruck erzeugt? Zu dieser Frage habe ich in meinem letzten Kommentar ja schon eine Antwort geliefert; wenn Ihnen bei dieser Antwort etwas fehlt, sagen Sie mir bitte direkt, was.
Was in arXiv:1602.03845v1 mit Kalibration gemeint ist, hatte ich in diesem Kommentar beschrieben; dort hatte ich dasselbe Paper (eines der vielen) Abbott et al. 2016 genannt. Die Kalibrationskurven sind, wie dort beschrieben, als Abb. 5 und 6 in dem betreffenden Paper enthalten.
Aus meiner Sicht scheint das Problem aber vielmehr zu sein, dass Sie zwei unterschiedliche Kalibrationsvorgänge vermischen:
(1) Mit den elektrostatischen Aktuatoren hat man eine “ähnliche Wellenform und Amplitude wie GW150914 […] erzeugt und gleichzeitig interferometrisch gemessen” (das sind die sogenannten hardware injections), aber eben nicht “durch Strahlungsdruck”.
(2) Mit Strahlungsdruck hat man die elektrostatischen Aktuatoren kalibriert (darum, und nur darum, geht es in arXiv:1602.03845v1 alias Referenz [63]).
Sie vermischen diese beiden ganz unterschiedlichen Kalibrationsvorgänge; daher meine Frage: Welchen davon möchten Sie diskutieren? Ich vermute stark, dass Sie die Kalibrationskurve zu (1) sehen wollen; in Ihren Nachfragen reden Sie aber andauernd von (2).
Herr Pössel,
leider funktioniert die chronologische Einordnung der Kommentare noch immer nicht, so dass ich Ihren Kommentar vom 29.5., 16h59, der vor Herrn Senfs Kommentar vom 26.5., 1h57, eingeordnet wurde, zunächst übersehen habe.
Sie beziehen sich offenbar auf einen unveröffentlichten internen Report von LIGO (https://dcc.ligo.org/public/0122/P1500248/010/P1500248_EarlyaLIGOCalUncertainty.pdf), der noch kein peer review Verfahren durchlaufen hat. Im offiziellen “Entdeckungspapier” in Phys. Rev. Lett. wird das ebenfalls unveröffentlichte Papier arXiv:1602.03845v1 [gr-qc] 11 Feb 2016 als Ref. [63] zitiert. Schon aus dem Titel kann man erkennen, dass selbstverständlich die Notwendigkeit einer Eichung der Detektoren als integraler Bestandteil der Entdeckung anerkannt wird. Ohne Eichung hätte der claim, Gravitationswellen nachgewiesen zu haben, den Status einer bloßen Behauptung.
Gemäß Figur 1 des Phys. Rev. Lett. Papiers wurde ein relativer strain von 10^(-21) als Funktion der Zeit während etwa 150 ms gemessen. Er entspricht einer oszillierenden Spiegelauslenkung von 10^(-18) m. Genau diese Spiegelauslenkung kann mit gleicher Frequenz auch durch Strahlungsdruck erzeugt werden, wie in Ref. [63] beschrieben, jedoch nicht veröffentlicht wurde. Nirgendwo, auch nicht in Figur 5 und 6, wird dokumentiert, wie der applizierte Strahlungsdruck eine Spiegelauslenkung erzeugt, die vergleichbar wäre mit jener durch die Gravitationswelle bewirkten. Es ist von den Experimentatoren nicht zuviel verlangt, diese Information, die ja zugegebenermaßen während der Eichmessung gewonnen wurde, zum Beleg ihrer angeblichen Entdeckung dem Leser mitzuteilen. Nachdem dies nicht geschehen ist und noch nicht mal das Eichpapier Ref. 63 ordnungsgemäß veröffentlicht wurde, muss man die “Entdeckung” als vorläufig, bzw. als nicht vorhanden bezeichnen. Zu viele sensationelle „Entdeckungen“ mussten in der Vergangenheit revidiert werden. Im vorliegenden Fall wird dies aller Wahrscheinlichkeit nach auch geschehen, denn man hat noch nicht einmal den Versuch gemacht, die behauptete relative Genauigkeit, die alles Bisherige millionenfach übertrifft, auf solide Weise experimentell zu untermauern.
Ich habe denb Eindruck, dass die Animation mit ein Paar kleinen Tricks arbeitet, und deshalb die Sache nicht richtig darstellt:
1. Die Längen der beiden Schenkel ändern sich in der Laufzeit des Lichts durch das Interferometer doch viel weniger als hier dargestellt. Sind sie in dieser Zeit nicht praktisch konstant?
2. Die beiden Schenkel verlängern bzw. verkürzen sich um einen anderen Faktor als die Wellenlängen bzw. Punkt-Abstände.
Ich denke, wenn sich die Wellenlängen genau so verändern würden wie die Schenkellängen, dann passen immer gleich viele Wellen bzw. Punkte auf die Schenkellängen. Deshalb würden sie dann am Detektor auch wieder mit dem gleichen Phasenunterschied ankommen, wie ohne GW. Richtig?
Nö, Tricks sind da nicht im Spiel.
Klar sind die Parameter so gewählt, dass die Animation möglichst anschaulich wird: Riesige Amplitude, Verhältnis Teilchenabstand/Armlänge sehr viel größer als in Wirklichkeit, ganzzahliges Verhältnis von Teilchenreisezeit und Schwingungsdauer der Welle, damit sich das ganze in vertretbarer Einzelbildanzahl periodisch wiederholt.
Ob die Längenänderungen durch die Gravitationswelle während der Lichtlaufzeit konstant sind, hängt natürlich von der Armlänge ab. Bei LIGO ist es in guter Näherung so. Bei LISA nicht. Die Animation zeigt den allgemeinen Fall, in dem die Näherung nicht gemacht wurde.
Wie sich die Lichtteilchen (die man als Wellenberg-Marker betrachten kann) ausbreiten, ist in der Animation nicht vereinfacht, sondern direkt aus der geomtrischen Beschreibung der Welle abgeleitet (Aufintegration von Null-Geodäten, wie es sich aus der Metrik ergibt). Da ist nichts vereinfacht.
Und warum die Argumentation “Wellenlängen dehnen sich genau so wie Armlängen, also keine Phasenänderung” falsch ist, zeigt die Animation doch sehr schön: Zum einen durch die Laufzeitunterschiede (dominiert bei LIGO), zum anderen dadurch, dass man mit Wellen unterschiedlicher Wellenlänge eben prinzipiell keine komplett destruktive Interferenz machen kann.
Drei Sachen sind mir nach wie vor unklar:
1. Wieso werden die Wellenlängen nicht im jeweils gleichen Verhältnis gestaucht bzw. gestreckt, wie die entsprechenden Schenkel des Interferometers? Ich dachte dafür wäre die GW verantwortlich und die ist doch zur gleichen Zeit am gleichen Ort gleich.
2. Wieso ist für die Interferenz die Lichtlaufzeit entscheidend? Ich dachte, es wäre die Phasenbeziehung. (Wenn die Laufzeit entscheidend wäre gäbe es keine Interferenz am Doppelspalt oder Gitter, wenn man das Licht schräg einstrahlt.
3. Wieso sollen die Wellenlängen auf dem Wegstück vom halbdurchlässigen Spiegel zum Detektor nicht gleich sein?
@Markus Pössel / 30. Mai 2016 22:17
Mit einer Entgegnung setze ich mal hier mal separat an; da scheint mir doch noch etwas mehr Klärungsbedarf zu bestehen, als ich eigentlich angenommen hatte.
»Aber selbstverständlich kann man durch geeignete, möglichst starre Anordnungen, wie sie die LIGO-Anlagen darstellen, den Einfluss der veränderlichen Raummetrik weitgehend unterdrücken.«
Sei nochmals in Erinnerung gebracht, eine GW ist nicht daran feststzusellen, dass sie Dinge wie Testmassen oder Spiegel im Raume bewegt, vielmehr ist dabei — populär gesprochen — “der Raum selbst bewegt”. Eine GW deformiert nicht die Anordnung der LIGO-Instrumente, die bleibt in der darstellenden Koordinatengeometrie einer Karte völlig unverändert, was dann allerdings in den Animationen überhaupt nicht ersichtlich wird. Starrheit ist hier ein deplaziertes Argument, und die Aufhängung der LIGO-Spiegel hat auch absolut nicht den Grund, dass sie so von einer GW besser herumgeschubst werden können, denn eine GW schubst nichts herum. Können wir uns darauf einigen?
Es ist dann noch erforderlich, der populären Sprechweise, dass “der Raum selbst bewegt” sei, eine nachvollziehbare Bedeutung zu geben, denn das ist zunächst nur ein sinnfreies Geschwafel. “In essence,” schreiben Flanagan & Hughes, “the coordinates move with the waves,” was natürlich derselbe Unsinn ist, den ich weiter oben schon hereingebracht und dann wieder zurückgenommen hatte, denn das bleibt letztlich nur ein Ausdruck von Hilflosigkeit bei dem Versuch, eine Intuition von Bewegung hier noch irgendwie einzubinden. Tatsächlich ist es jedoch so, dass die innere Geometrie der Raumes sich zeitabhängig ändert, und dadurch bedingt das geometrische Mass gewisser intrinsischer Grössen wie der “proper distance” zwischen stationären Punkten variiert. Letztere ändert sich tatsächlich in einer GW, aber nicht, weil diese Punkte bewegt würden, sondern weil hier die durch das Pseudo-Skalarprodukt g gegebene Massbestimmung dynamisch ist. Das wird jedoch durch die Animationen nicht dargestellt.
Das Wörtchen ‘selbstverständlich’ sollte man im übrigen besser generell aus seinem wissenschaftl. Vokabular streichen. Und gerade bei GWs ist doch überhaupt nichts selbstverständlich.
Sorry, aber: nein, das stimmt hinten und vorne nicht.
Die Situation ist genau wie bei der kosmischen Expansion (und die Metrik zur Beschreibung ist ja auch sehr ähnlich), und hie wie dort gilt: Wenn man wissen will, wie gebundene Systeme reagieren, gibt einem ein lokales soweit-wie-möglich-Inertialsystem die richtigen Antworten. Details stehen z.B. in Giulini 2013. In diesem lokalen System macht sich die differentielle Beschleunigung durch die Gravitationswellen in Konkurrenz mit den Bindungskräften bemerkbar.
Bei solchen (und anderen) Fragen führt das Bild vom “Raum selbst, der sich ausdehnt” (oder staucht) zu falschen Vorstellungen.
Chrys schrieb (31. Mai 2016 18:20):
> Eine GW deformiert nicht die Anordnung der LIGO-Instrumente
Es wurde aber doch experimentell festgestellt, dass sich die interferometrisch (bzw. deshalb auch implizit chronometrisch) zwischen drei wesentlichen LIGO-Bestandteilen definierte “Form” tatsächlich veränderte.
(Ob diese Veränderung allerdings mit der “Passage einer GW” einherging, oder stattdessen z.B. einem “Wackeln im Statischen”, ist anhand dieser Deformation allein nicht entscheidbar.)
> Starrheit ist hier ein deplaziertes Argument
Wenn hinreichend viele (n) geeignete Beteiligte in Betracht gezogen werden (also i.A. fünf; bei geeigneter Anordnung reichen auch nur vier),
und darunter
(n + 1) (n – 2) / 2 = (n (n – 1) / 2) – 1
Paare, d.h. alle Paare bis auf eines, gegenüber einander (chronometrisch-interferometrisch) starr angeordnet waren und blieben, dann lässt sich aus der eventuellen Deformation des übrigen Paares (in Bezug auf die “starre Form” der (n + 1) (n – 2) / 2 anderen Paare) messen, ob die Region, in der alle Beteiligten enthalten waren, veränderlich gekrümmt war, oder statisch.
(Dieses Argument lässt sich zugegebener Maßen nicht unmittelbar auf die vorliegende LIGO-Anordnung anwenden, und darin liegt ja LIGOs Schwäche; aber doch hoffentlich auf gewisse Ausbaustufen von LISA.)
> […] die durch das Pseudo-Skalarprodukt g gegebene Massbestimmung
Sofern Werte des Pseudo-Skalarprodukts g mit (koordinaten-freier) Maßbestimmung zu tun haben, handelt es sich nicht um von vornherein gegebene Werte, sondern um Werte, die gesucht sind und die sich ggf. aus gemessenen geometrischen Beziehungen ermitteln lassen.
@Markus Pössel / 1. Juni 2016 9:59
»Sorry, aber: nein, das stimmt hinten und vorne nicht.«
So, meinen Sie? Na, dann würde ich doch vorschlagen, dass Sie zunächst einmal Ihre animierte Kreistanzgruppe freier Teilchen mit der Theorie in Einklang bringen.
Da Sie sich und uns die Bewegung freier Teichen in Ihrer linearen Sinus-GW als das erklären wollen, was die Animation ganz zuoberst im Blogtext zeigt, können Sie sicherlich auch diese Bewegungsform aus der zugehörigen Geodätengl. herleiten? Allerdings, wer diese Gleichung inspiziert, kann rasch darauf kommen, dass Ihre animierten freien Teilchen nur auf Koordinatenwellen schaukeln.
Ich fürchte, es sind Ihre Bildchen und deren Deutung, wo hinten und vorne etwas nicht stimmt.
Meine Bilder und Animationen geben genau das wieder, was die (zeitabhängige) Metrik einfacher Gravitationswellenlösungen für die Eigenentfernungen (sprich: räumliche Entfernung zweier Punkte, mithilfe der Metrik bestimmt zu einem konstanten Zeitpunkt).
Und nein, das sind keine reinen Koordinateneffekte. Das sieht man ja schon daran, dass sich die Messgröße (Phasenvergleich der beiden Licht-Teilwellen am Strahlteiler) ändert. Reine Koordinatenänderungen können keine physikalischen Effekte erzeugen.
Insofern: Meine Bilder/Animationen und deren Deutung geben recht treu wieder, was aus der (linearisierten) Metrik folgt.
Wenn Ihre vereinfachten Beschreibungen, was eine Gravitationswelle ist und kann, dem widerspricht, sind diese vereinfachten Beschreibungen eben falsch.
@Frank Wappler / 1. Juni 2016 10:31
»Es wurde aber doch experimentell festgestellt, dass sich die interferometrisch (bzw. deshalb auch implizit chronometrisch) zwischen drei wesentlichen LIGO-Bestandteilen definierte “Form” tatsächlich veränderte.«
Eine GW deformiert nichts in dem Sinne, dass Punkte im Raume, die ohne GW stationär sind, auch in der GW stationär bleiben. Denkt man sich also die Elemente eines Michelson Interferometers repräsentiert durch solche stationären Punkte, dann verändert eine GW nichts daran. Davon unbenommen liesse sich das Vorhandensein einer GW mit dem Interferometer rein theoretisch durch eine gemessene Phasenverschiebung feststellen.
Naturgemäss lässt das alles nur im Rahmen von Einsteins linearisrter Theorie sagen, wo GWs als kleine Störungen betrachtet werden können. Sind diese Störungen zu gross, kollabiert auch die ganze geometrische Interpretation.
Chrys schrieb (2. Juni 2016 10:14):
> Eine GW deformiert nichts in dem Sinne, dass Punkte im Raume, die ohne GW stationär sind, auch in der GW stationär bleiben.
Für welche nachvollziehbare, auf Feststellungen von Koinzidenz (Nicht-Koinzidenz, Identität, …) hinauslaufende Definition des (vermeintlichen) Begriffs “stationär” denn ?!?
Die betreffenden Beteiligten (wesentliche Bestandteile von Interferometern) sollen m Laufe eines jeden gültigen Versuchs doch gewiss unterscheidbar bleiben, und sich sicherlich nicht treffen.
Ist die Erfüllung dieser Bedingungen hinreichend, um jeden einzelnen Beteiligten dabei “stationär” zu nennen, und deren Gesamtheit (im Vergleich mehrerer Versuche) als “in diesem Sinne undeformiert“?
Allein für sich reichen diese genannten Bedingungen ja offenbar nicht zur Definition bzw. zum Nachweise eventueller GW. Sie mögen in jedem Fall gefordert werden; und wir beschäftigen uns mit Interessanterem:
> Davon unbenommen liesse sich das Vorhandensein einer GW mit dem Interferometer rein theoretisch durch eine gemessene Phasenverschiebung feststellen.
Eben.
(Allerdings nicht mit irgendeinem Interferometer, sondern nur unter bestimmten Bedingungen; Stichwort: Synge.
Und um die Bemerkung “rein theoretisch” nicht unkommentiert durchgehen zu lassen:
Natürlich beschäftigen wir uns hier mit Gedankenexperimenten, um Begriffe zu definieren und die Auswahl und Bewertung tatsächlicher Beobachtungsdaten nachvollziehbar zu machen.)
> [ … nur sofern] GWs als kleine Störungen betrachtet werden können. Sind diese Störungen zu gross, kollabiert auch die ganze geometrische Interpretation.
Das begriffliche Fundament der RT erscheint jedenfalls erforderlich, um eventuelle “Störungen” überhaupt zu quantifizieren.
Was ist damit gemeint, “dass Punkte im Raume, die ohne GW stationär sind, auch in der GW stationär bleiben”? Richtig ist, dass die mitbewegten Koordinatenwerte gleichbleiben – das ist gerade die Definition mitbewegter Koordinaten. Und es heißt (siehe kosmische Expansion) noch lange nicht, dass die Abstände zwischen solchen gleich bleiben.
Wie gesagt, die Abstände, gemessen zu einem konstanten Zeitpunkt t (bestimmt mithilfe von Uhren, die vor Durchgang der Welle in üblicherweise synchronisiert waren), ändern sich. Das lässt sich direkt aus der Metrik ablesen.
@Markus Pössel, Frank Wappler / “stationär” etc.
Dazu möchte ich jetzt gerne einfach nur nochmals auf die schon genannte Literatur verweisen, nämlich die Übersicht von Flanagan & Hughes, Sec. 2-3, sowie, en détail, Maggiore, Gravitational Waves, Ch. 1.
Die Bewegung freier Teilchen in einer GW wird von der Geodätengl. beschrieben, wobei jedoch speziell darauf zu achten ist, dass man tatsächlich den TT Anteil erwischt und keine koordinatenbedingten Artefakte mitschleppt.
@ Chrys
Wenn ich mich kurz als Physiklaie naiv einmischen darf.
Die “animierte Kreistanzgruppe freier Teilchen” von Herrn Pössel sieht der Abbildung (Fig. 1.1, Seite 26) sehr ähnlich, die ich in dem von Dir empfohlenen Maggiore, Gravitational Waves, Ch. 1 gefunden habe.
Der Autor gibt dazu auch eine Kraft an, mit der die Testmassen im Raum bewegt werden, beim Durchlauf der Gravitationswelle und aus Sicht eines Eperimentators.
So ganz falsch scheint mir die Animation und deren Interpretation also nicht zu sein. Dass man das alles auch anders beschreiben kann, bleibt unbenommen.
Chrys schrieb (2. Juni 2016 15:16):
> […] “stationär” etc.
> Dazu möchte ich jetzt gerne einfach nur nochmals auf die schon genannte Literatur verweisen, nämlich die Übersicht von Flanagan & Hughes, Sec. 2-3, sowie, en détail, Maggiore, Gravitational Waves, Ch. 1.
Das Wort “stationär” (das in diese Diskussion durch Kommentare 31. Mai 2016 18:20 bzw. 2. Juni 2016 10:14 eingeführt und anschließend in Frage gestellt wurde) bzw. das (sprachlich sicherlich) entsprechende “stationary” tritt in “Flanagan & Hughes (The basics of gravitational wave theory)” nur ein einziges Mal, offenbar in einem anderen, nachrangigen Zusammenhang auftritt (und in “Maggiore, Gravitational Waves, Ch. 1? … wer weiß).
> Die Bewegung freier Teilchen in einer GW
Dazu möchte ich (nochmals) feststellen:
1. Das Wort “Bewegung” erscheint hier möglicher Weise missverständlich; vielleicht geht es ja eher um geometrische Beziehungen (und insbesondere um Pingdauern) von “freien” Beteiligten untereinander.
2. Die Animationen im obigen SciLogs-Artikel mögen diese geometrische Beziehungen (variable Pingdauern!, und damit verbundene variable Koinzidenz- bzw. interferometrische Feststellungen) gut veranschaulichen; aber: Es lässt sich nicht erkennen, dass die identifizierbaren Beteiligten an sich und einzeln “frei” wären. (Diese Forderung wurde wird stattdessen ausdrücklich hinzugefügt.)
3. Es erscheint (deshalb) zweifelhaft, dass die in den Animationen veranschaulichten geometrischen Beziehungen spezifisch/ausschließlich auf “freie Teilchen in einer GW” zutreffen.
> wird von der Geodätengl. beschrieben […]
… was die Frage nahelegt, ob und wie die Größen, die in einer solchen “Geodätengl.” auftreten, überhaupt als Messgrößen definiert sind, so dass deren Bewertung auf Feststellungen von Koinzidenz hinausläuft.
Ich verstehe nicht, was Sie wollen. Was Flanagan und Hughes (2005) im Abschnitt 3 schreiben und beschreiben, ist doch genau das, was meine Animation zeigt und wie meine Animation berechnet wurde!
Mit Gleichung (3.4) zeigen Flanagan/Hughes, dass für mitbewegten Koordinaten konstante Koordinatenwerte geodätischer Bewegung entsprechen. Etwas später sagen sie explizit “In fact the GWs cause the proper separation between two freely falling particles to oscillate, even if the coordinate separation is constant.” Genau diese schwingenden proper separations zeigt meine Animation. Das dafür eingeführte, in x- und y-Richtung vom Nullpunkt gemessen aus abstandstreue Koordinatensystem meiner Animation ist gerade der proper reference frame, den die beiden auf S. 14 beschreiben. (3.13) mit einfacher Sinusfunktion ist die in der Animation dargestellte Abstandsänderung der Spiegel vom Strahlteiler in meiner Animation.
Ich bin dann noch einen Schritt weitergegangen und habe für meine Animation noch die lichtartigen Geodäten berechnet, um die Bewegung von Lichtteilchen darstellen zu können. Das haben Flanagan und Hughes, soweit ich sehen kann, nicht gemacht. Aber in den Bereichen, zu denen sich die beiden äußern, sind meine Animation und die von Flanagan/Hughes referierte Theorie komplett im Einklang.
@Markus Pössel / 3. Juni 2016 22:04
Die Animationen lassen sich beziehen auf das, was Maggiore den Proper Detector Frame nennt. Doch hier ist die Raumzeit flach, auch mit Störung durch eine GW, und eine Beschleunigung der Testmassen erfolgt dann durch eine Gravitationskraft, denn Gravitation ist hier nicht geometrisiert.
Im TT Frame wird hingegen eine lineare GW durch einen gekrümmten Lorentzschen Raum dargestellt, hierbei ist Gravitation dann geometrisiert. Die Beziehung zwischen Proper Detector Frame und TT Frame ist aber keineswegs eine schlichte Koord.-Transfomation, denn dabei bliebe ja die Krümmung invariant.
Betrachten wir nun im TT Frame zwei fixierte Punkte P, Q, auf der x- oder y-Achse, deren Koordinatenabstand L betrage. Dann ist die proper distance zwischen P und Q zur Zeit t die geodätische Länge der Strecke PQ bezogen auf die GW-Metrik, wobei t = const. gesetzt ist. Da die GW-Metrik g nicht statisch ist, variiert dieser Wert in Abhängigkeit von der Zeit t. Doch er variiert, weil sich die durch g gegebene Massbestimmung ändert, und nicht, weil eine Form von Bewegung der Punkte P und Q damit zu assoziieren wäre. Und auf diesem Wege gelangt man schliesslich auch zur verlangten relativen Änderung ΔL/L bei einem, wohlgemerkt, festen Koordinatenabstand L.
Ein physikal. Vorgang von Abstandsmessung ist damit nicht verbunden, und wenn das ΔL rechnerisch in der Grössenordnung von 10^{−18} herauskommt, ist da kein Konflikt mit den metrolog. Grenzen der Genauigkeit von Abstandsmessungen. Denn gemessen werden kann in diesem Kontext allein eine interferometr. Phasenverschiebung Δφ, auf deren Grundlage dann der wave strain kalkuliert wird.
Ich habe keinen Zugriff auf Maggiore, aber bei dem Koordinatensystem, was meinen Animationen zugrundeliegt und auch bei Flanagan/Hughes genutzt wird ist die Raumzeit nur lokal am Nullpunkt des Koordinatensystems flach (das ist schlicht der Umstand, dass man sein Bezugssystem immer so wählen kann, dass der Nullpunkt im freien Fall ist und die Christoffel-Symbole dort verschwinden).
(Raumzeit-)Krümmung gibt es da (wenn auch nur in linearer Näherung) sehr wohl – die systematischen Abstandsänderungen, die in diesem System sichtbar werden, bewirken exakt das, woran sich Krümmung per Definition erkennen lässt (Geodäten werden differenziell aufeinander zugebogen).
Und sowohl bei Flanagan/Hughes, bei mir und ich würde wetten auch bei Maggiore ist der Übergang vom einen zum anderen System selbstverständlich eine Koordinatentransformation (was denn auch sonst?), und ja: Krümmung ist in beiden Koordinatensystemen vorhanden, und ja: auch in diesem Koordinatensystem ist Gravitation geometrisiert (und es gibt eine entsprechende Metrik – die schreiben Flanagan/Hughes ja auch hin!).
Ob mit einer Abstandsänderung eine “Bewegung” zu “assoziieren” ist, ist eine sehr vage Formulierung. Fakt ist doch, dass Bewegung in einer Theorie, die beliebige Koordinatendefinitionen zulässt, kein eindeutiger Begriff mehr ist. Dass kein “physikalischer Vorgang von Abstandsmessungen” vorliegen soll, ist ähnlich unscharf. Physikalische Abstände (im Gegensatz zu den für sich genommen bedeutungslosen Koordinatenabständen) sind das, was man aus der Metrik ableiten kann, und das was prinzipiell als Abstand messbar ist. Und das sind genau die Abstände (proper distances), und Abstandsänderungen, die meine Animation wiedergibt.
Markus Pössel schrieb (5. Juni 2016 21:39):
> Abstandsänderungen […] woran sich Krümmung per Definition erkennen lässt (Geodäten werden differenziell aufeinander zugebogen).
Um diesen Zusammenhang als Definition einzusetzen, müssten sich ja „Geodäten erkennen“ bzw. definieren lassen, bevor und ohne dass „Krümmung“ schon ermittelt worden wäre.
(Sicherlich lässt sich eine Definition von „Krümmung“ stattdessen unmittelbar durch selbstverständliche Begriffe ausdrücken, also insbesondere aus Bestimmungen von Koinzidenzen;
und sicherlich lassen sich auch Zusammenhänge zwischen „Krümmung“ und Pingdauern formulieren, für die der Begriff „Geodäte“ nicht erforderlich ist.)
@Markus Pössel / 5. Juni 2016 21:39
»Ich habe keinen Zugriff auf Maggiore, …«
Das lässt sich ändern, denn dankenswerterweise hat Joker ja entdeckt, dass OUP uns das Ch. 1 gratis spendiert. [Download ‘Sample Material’]
»… aber bei dem Koordinatensystem, was meinen Animationen zugrundeliegt …«
Wenden Sie Ihre Koord.transf. doch einfach mal auf Ihr Beispiel mit der Sinus-GW und schauen, was passiert. Die GW-Metrik ist dabei als g = η + h gegeben, und Ihre Transformation lässt dann einfach das h verschwinden. Sie landen so in einem flachen Minkowski Raum, wo Ihre Kreistanzgruppe Quadrupolka tanzt, wie Sie es haben wollten, nur ist das dann halt kein geodätischer Tanz. Doch das ist nichts anderes als die Darstellung in Maggiores Proper Detector Frame (und nein, Flanagan & Hughes zaubern die Störung da nicht weg).
Ihre Transformation hat sozusagen Risiken und Nebenwirkungen, indem sie Krümmung in Kraft verwandelt. Oder anders gewendet, sie erlaubt Ihnen, linearisierte Gravitation als ein masseloses Spin-2 Feld über einer flachen Raumzeit darzustellen. That’s not a bug, that’s a feature! Sie gelangen so ja gerade zu eben jenem Feld, das man schon seit langem erfolglos nach dem Vorbild des EM-Feldes zu quantisieren versucht.
Zu den Risiken sei bemerkt, dass Ihre Sinus-GW als ein Feld dann auch eine physikal. Kraft zu entfalten scheint, wohingegen sie im Lichte der nichtlinearen geometr. Theorie noch immer als unphysikalisch zu gelten hat, indem sie ein Vakuum repräsentiert, das nicht Ricci-flach ist.
»Fakt ist doch, dass Bewegung in einer Theorie, die beliebige Koordinatendefinitionen zulässt, kein eindeutiger Begriff mehr ist.«
Sie verkennen irgendwie, dass wir mit den linearen GWs schliesslich in Einsteins linearisierter GR sind, die keine covariante Theorie ist, und hier hat es bevorzugte Frames. Der TT Frame ist genau diejenige adaptierte Darstellung, die den (physikal. einzig relevanten) TT Anteil ohne darstellungsbedingte Artefakte zeigt. Für geodätische Bewegung in einer linearen GW lässt sich so tatsächlich konstatieren, dass sie beschleunigungsfrei ist, in einem absoluten Sinne.
@Markus Pössel
Mir dämmert inzwischen, dass sich gewisse Schwierigkeiten der Verständigung wohl aus dem Physiker-Dialekt ergeben, indem ‘gedesic deviation’ dort ‘tidal force’ genannt wird. Wenn ein Physiker Kraft sagt, denkt er gewöhnlich auch Beschleunigung hinzu und hat dann wenig Hemmungen, auch geodätische Bewegung in einer linearen GW infolge von Gezeitenkraft zu beschleunigen. Obwohl das natürlich zum Oxymoron wird; entweder Geodäte oder Kraft, man kann nicht alles zugleich haben.
Insofern die Animationen darauf abzielen, eine lineare GW als den Effekt einer Gezeitenkraft zu veranschaulichen, ist festzustellen, dass diese Darstellungen auf eine flache Raumzeit zu beziehen sind, wo die Beschleunigung der Testmassen durch ein Feld erfolgt. Und Herrn Wapplers Frage, in welchem Sinne die betrachteten Testmassen als “frei” anzusehen sind, hat mithin einige Berechtigung. Da bekanntlich für den Physiker der Begriff erst dann existiert, wenn die Möglichkeit gegeben ist, im konkreten Falle herauszufinden, ob der Begriff zutrifft oder nicht, scheinen mir hinsichtlich des “freien Teilchens” jedenfalls noch gewisse begriffliche Unklarheiten zu bestehen.
Dass Verständigungsschwierigkeiten bestehen, sehe ich ganz genau so. Ich habe mir jetzt das Maggiore-Kapitel durchgelesen und sehe da wieder keine Widersprüche zu dem, was ich behauptet oder in der Animation umgesetzt habe, und wieder einiges, was mir Ihren Behauptungen zu widersprechen scheint.
Zu Ihrem letzten Kommentar: Die Animation weiß nichts von Gezeitenkräften, sondern zeigt lediglich Abstandsänderungen (proper distances) zwischen Teilchen, wie sie sich direkt aus der einfachen Metrik ergeben. Die Darstellung nutzt aus, dass der Raum (bzw. die Ebene), um die es geht, in der Tat näherungsweise flach ist. Die Raumzeit, die hier gezeigt wird, ist es nicht; dafür sind die differenziellen Abstandsänderungen (geodesic deviation) ja gerade ein Ausdruck.
Was meinen Sie mit “entweder Geodäte oder Kraft, man kann nicht alles zugleich haben”?
Zu den freien Teilchen und Herrn Wappler: Da unterschätzen Sie, denke ich, die Physiker. Es ist ja nicht so, dass man in der Physik in jeder Situation jeden Teilaspekt eines Modells einzeln isolieren könnte. Geodätische Bewegung ist zunächst mal ein geometrisches Konzept; dass ich für bestimmte Körper, z.B. die LPF-Testmassen, postuliere, ihre Bewegung sei geodätisch ist ein Modell; ob das Modell ein gutes Modell ist, zeigt sich zum einen durch Konsistenzchecks, zum anderen daran, ob die aus dem Modell abgeleiteten beobachtbaren Konsequenzen tatsächlich beobachtet werden. Im Falle der LPF-Testmassen wäre der Konsistenzcheck, dass auf die Testmassen tatsächlich keine merklichen elektrische Kräfte, magnetischen Kräfte, Druckkräfte z.B. durch einfallende Teilchen wirken; stellt man fest, dass doch solche Kräfte wirken, dann wäre das ein Widerspruch zur Annahme der geodätischen Bewegung. Die wichtigste Vorhersage ist im Falle von LPF wohl die relative Abstandsänderung der beiden Testmassen, und die scheint sich ja auch so zu verhalten, wie vorhergesagt.
Markus Pössel schrieb (8. Juni 2016 17:04):
> Geodätische Bewegung ist zunächst mal ein geometrisches Konzept
Gut;
denn sicherlich laufen geometrische Konzepte direkter und zuverlässiger auf Feststellungen von Koinzidenz hinaus, als Konzepte der Dynamik (die z.B. erst per Variationsrechnung aus geometrischen Messwerten nachvollziehbar sind).
> dass ich für bestimmte Körper, z.B. die LPF-Testmassen, postuliere, ihre Bewegung sei geodätisch ist ein Modell
Ein experimentell überprüfbares Modell, ganz recht.
> Die wichtigste Vorhersage ist im Falle von LPF wohl die relative Abstandsänderung der beiden Testmassen, und die scheint sich ja auch so zu verhalten, wie vorhergesagt.
Diese Vorhersage ist weder hinreichend noch notwendig für die Richtigkeit bzw. hinsichtlich der Überpfüfung des oben vorgeschlagenen Modells:
Falls sich die Entfernung der beiden LISA-Pathfinder-Testmassen voneinander sich im betreffenden Versuch nicht wesentlich verändert hätte, dann folgt daraus keineswegs, dass sie sich einzeln geodätisch bewegt hätten;
sie hätten sich stattdessen z.B. geeignet (d.h. zueinander starr, in einer geeigneten Region) hyperbolisch beschleunigt bewegen können.
Und falls sich die Entfernung der beiden Testmassen voneinander sich im betreffenden Versuch wesentlich verändert hätte, dann folgt daraus keineswegs, dass sie sich nicht einzeln geodätisch bewegt hätten;
sondern das kommt auf weitere (geometrische) Bedingungen an, die über das genannte Modell hinausgehen, insbesondere die Krümmung der Region, in der der Versuch stattfand.
> Es ist ja nicht so, dass man in der Physik in jeder Situation jeden Teilaspekt eines Modells einzeln isolieren könnte.
Seit und sofern die Physiker sich ausdrücklich auf bestimmte, nachvollziehbare Messoperatoren beziehen,
– um Versuch für Versuch aus gegebenen Beobachtungsdaten Messwerte zu gewinnen, und
– um Modelle und Erwartungen hinsichtlich bestimmter Messwerte aufzustellen,
können sie zumindest kompetent beurteilen, welche Annahmen/Forderungen/Erwartungen überhaupt als Teilaspekte eines bestimmten, prüfbaren Modells miteinander kompatibel sind.
@Markus Pössel / 8. Juni 2016 17:04
»Die Animation weiß nichts von Gezeitenkräften, …«
Am 29. Mai 2016 13:29 haben Sie doch selber Herrn Wappler die in den Animationen vermittelte Bewegung von Testmassen durch den Hinweis auf Gezeitenkräfte zu explizieren versucht. Das ist ja nicht falsch, doch wenn man das so macht, wird damit halt die Bewegung von Testmassen in einem Gravitationsfeld bei zugleich flacher Metrik beschrieben.
Im Prinzip haben Sie zwei Möglichkeiten, das Verhalten von Testmassen mit Bezug auf eine lineare GW zu darzustellen, und zwar entweder als geodätische (d.i. kräftefreie) Bewegung in dem durch die GW-Metrik gegebenen Lorentzschen Raum, oder als Bewegung in einem masselosen Spin-2 Feld über einer flachen Raumzeit. Dabei entspricht ersteres der Darstellung im TT Frame, letzteres der im Proper Detector Frame. Beides ist zulässig, doch sollte in Zweifelsfällen auch nachvollziehbar sein, welche Darstellung gemeint ist.
Versteht man Ihre Animationen bezogen auf den Proper Detector Frame, dann sieht das okay aus. Doch bei Herrn Wappler (und nicht nur bei ihm) war das so jedenfalls zunächst nicht angekommen — er fragt ja u.a. nach Krümmung — und man sollte ihn darauf hinweisen, dass die lineare GW hierbei überhaupt nicht als Krümmung, sondern als ein Kraftfeld im Minkowski Raum zu deuten ist.
Chrys schrieb (9. Juni 2016 13:30):
> zwei Möglichkeiten, das Verhalten von Testmassen mit Bezug auf eine lineare GW zu darzustellen […]
Um meine diesbezüglichen Ansichten nochmals zu dokumentieren, und von mehr oder weniger abwegigen Interpretationen abzugrenzen:
Soweit ich verstehe, schließt die Beschreibung dessen, was durch die erste Animation des obigen SciLogs-Artikels abgebildet sein soll, Folgendes ein:
(1): 33 Beteiligte deren Pingdauerverhältnisse (von je dreien) untereinander sich periodisch änderten und wiederholten,
(2): dass diese Pingdauerverhältnisse nahezu denen gleichen, die von (ggf. anderen) 33 Beteiligten zu finden wären, die sich in einer ganz flachen Region so bewegen, dass „32 Beteiligte gleichmäßig verteilt kreisförmig quadrupolmäßig oszillierten und der 33-ste ununterbrochen im Zentrum dieser Anordnung blieb“,
(3): wobei (trotzdem) für jeden einzelnen dessen Dauer von seiner Teilnahme an einem bestimmten Ereignis bis zu seiner Teilnahme an einem bestimmten anderen Ereignis gleich der Lorentzschen Distanz dieser beiden Ereignisse voneinander (also dem Supremum aller Reisedauern von denkbaren Teilnehmern an diesen beiden Ereignissen) ist.
Ich habe auch die Vermutung, dass eine (3+1-dimensionale) Region, die solch eine Anordnung von 33 Beteiligten enthält, nicht flach ist (also nicht mit unbeschränkt feinen Ping-Koinzidenz-Gittern gefüllt werden kann).
Dagegen erfüllt das, was durch die erste Animation des obigen SciLogs-Artikels tatsächlich dargestellt ist, ausdrücklich lediglich Punkte (1) und (2) der Beschreibung. Es wird kein Anspruch darauf erhoben, dass Punkt (3) durch die Abbildung an sich erfüllt und in der Abbildung an sich erkennbar und anschaulich gemacht wäre, sondern die entsprechende Beschreibung muss ausdrücklich hinzugefügt werden.
> […] Hinweis auf Gezeitenkräfte […]
Der mag ja nicht ganz falsch gewesen sein, kam/käme bei mir aber ganz schlecht an, weil Dynamik sicherlich nicht als verständlich gelten kann, bevor Geometrie/Kinematik verstanden worden ist.
Aber immerhin lassen sich ja z.B. auch Beteiligte in Betracht ziehen, die gegenüber „dem im Zentrum“ ununterbrochen starr gewesen wären (also konstante Pingdauern gefunden hätten) und auf die Punkt (3) der Beschreibung (folglich) ausdrücklich nicht zuträfe …
> […] dass die lineare GW hierbei [in den Animationen] überhaupt nicht als Krümmung, sondern als ein Kraftfeld im Minkowski Raum zu deuten ist.
Dem entspräche wohl eine Beschreibung, in der Punkt (3) durch einen geeigneten anderen Punkt (3*) ersetzt würde (der natürlich ebenfalls als eine Forderung an bestimmte Dauern auszudrücken wäre). Zusammen mit Forderungen (1) und (2) erscheinen (mir) diese beiden allerdings experimentell unterscheidbar …
@Frank Wappler / 9. Juni 2016 16:44
Die 33 Beteiligten in der ersten Animation des obigen SciLogs-Artikels bewegen sich in einer “ganz flachen Region”. Und ihre wechselseitigen Pingdauerverhältnisse sind dabei exakt dieselben wie die der so plazierten 33 Beteiligten im nicht-statisch gekrümmten GW-Raum.
Es ist zu überdies zu betonen, dass jeder der 33 Beteiligten von sich behaupten kann, in Ruhe zu sein, denn keiner von denen registriert bei sich selbst eine beschleunigende Kraft.
Chrys schrieb (9. Juni 2016 23:52):
> Die 33 Beteiligten in der ersten Animation des obigen SciLogs-Artikels bewegen sich in einer “ganz flachen Region”.
(Eigentlich wollte ich mich nicht auf die genauen Umstände festlegen, unter denen diese Animation auf dem einen oder anderen Bildschirm ablaufen mag. Aber dieses Haar muss wohl nicht unbedingt noch gespalten werden; also meinetwegen: ja.)
> Und ihre wechselseitigen Pingdauerverhältnisse sind dabei exakt dieselben wie die der so plazierten 33 Beteiligten im nicht-statisch gekrümmten GW-Raum.
Ja, so verstehe ich das auch. Diese „Platzierung/Anordnung“ entspricht der Beschreibung (im SciLog-Artikel und im obigen Kommentar zusammengefasst in drei Punkten).
Die als Animation vorliegende Abbildung ist also der Beschreibung in bestimmter Hinsicht untreu., nämlich betreffend Punkt (3).
(Aber hinsichtlich des interferometrischen Messverfahrens sind die Animationen bestimmt sehr treu gemeint; natürlich abgesehen von der „extremen Übertreibung der Amplituden, im Dienste der Anschaulichkeit.
Daher die Schlussfolgerung, dass dieses interferometrische Messverfahren allein auch nicht geeignet ist, zwischen “Wackeltanz im Flachen” und „Dahindriften im nicht-statisch Gekrümmten“ zu unterscheiden.)
> Es ist zu überdies zu betonen, dass jeder der 33 Beteiligten von sich behaupten kann, in Ruhe zu sein, denn keiner von denen registriert bei sich selbst eine beschleunigende Kraft.
Das ist sicherlich mit der Beschreibung gemeint, auch wenn das nicht unbedingt durch die Animation abgebildet und anschaulich ist. (Mein Interesse liegt nun vor allem darin, ob und wie das eventuelle „Registrieren einer beschleunigende Kraft , bzw. ansonsten deren Fehlen“ auf Feststellungen von Koinzidenz hinausläuft … Damit zusammenhängend bereite ich auch eine Antwort auf Markus Pössels Kommentar 8. Juni 2016 17:04 vor. Ich möchte aber noch etwas Anstrengung investieren, damit sie nicht zu lang wird.)
@Frank Wappler / No-hair theorem?
»Aber dieses Haar muss wohl nicht unbedingt noch gespalten werden; also meinetwegen: ja.«
Nur um nicht missverständlich zu sein, Haare will ich auch nicht unbedingt spalten, und mir geht’s mehr um flat space und weniger um flat screen.
Die Pösselsche Transformation der Beispiel Sinus-GW sieht ja lediglich neue “propere” Koordinaten auf der x- und der y-Achse vor, bei t und z bleibt alles wie gehabt. D.h. konkreter etwa für x,
√{1 + A sin(ωt − kz)} dx → dx’,
sowie mutatis mutandis für y. Das alles dann einfach in die GW-Metrik eingesetzt, und zack — die Welt ist flach!
Chrys schrieb (10. Juni 2016 14:16):
> neue “propere” Koordinaten
Also nicht (nur) irgendwie dahergestreußelte reelle Zahlenpaare (bzw. allgemeiner: n-Tupel) wie z.B. hier dargestellt,
sondern ausdrücklich „proper“ in Bezug auf … (was wohl?) … bestimmte Verhältnisse von Pingdauern bzw. (sogar) bestimmte Ping-Koinzidenz-Gitter?
> auf der x- und der y-Achse vor, bei t und z bleibt alles wie gehabt. […] und zack — die Welt ist flach!
Ich hatte ja oben (19. Mai 2016 5:58) schon beschrieben, dass ich (mal so zum Spaß) die Ausdrücke, die Markus Pössel 18. Mai 2016 15:50 als „Abstände &Delta l“ angegeben hatte, in Cayley-Menger-Determinante eingesetzt und (zu meiner ziemlichen Überraschung) ganz exakt Null herausbekommen hatte.
Wie, bitteschön, wären denn entsprechende … ähm … Entfernungen zwischen Ereignissen auszudrücken, deren hier offenbar als festgesetzt zu betrachtende Koordinaten-Namen sich (i.A.) in allen vier Werten unterscheidet?
p.s.
Mir ist gerade das Licht aufgegangen (und das sicherlich nicht von ganz alleine), dass die Nachvollziehbarkeits-Forderung, die ich in meinen Kommentaren stets Einstein zugeschrieben habe (dass „alle unsere zeiträumlichen Konstatierungen stets auf die Bestimmung zeiträumlicher Koinzidenzen hinauslaufen“, insbesondere auch was die Beurteilung der eventuellen „Freiheit“ von Beteiligten angeht), mit dem Begriff „conformal equivalence“ verbunden ist (bzw. sich dadurch von weniger nachvollziehbaren Ansätzen abgrenzt).
Dadurch wird (mir) nun natürlich offensichtlich, dass es dazu schon wesentliche Arbeiten gibt (wenn auch mehr oder weniger seltsamer Weise nicht vorrangig von Einstein); und (wie nicht anders erwartet) folgt eine (die?) entsprechende Dynamik ziemlich selbstverständlich. (Meine ausstehende Antwort auf 8. Juni 2016 17:04 beschleunigt das aber leider nicht …)
@Frank Wappler / 10. Juni 2016 15:28
Im Grunde wird da gar keine Koordinatentransformation im eigentlichen Sinne definiert, sondern eine spezielle Abbildung zwischen einer linearen GW und dem Minkowski Raum, wobei — plakativ gesprochen — unbewegte Beteiligte im nicht-statischen und gekrümmten Raum zu bewegten Beteiligten im statischen und flachen Raum gemacht werden, und zwar dergestalt, dass deren wechselseitige Pingdauerverhältnisse invariant bleiben. Das “proper” war nur eine Anspielung darauf, dass im TT Frame diese Abbildung vermittels der “proper length”-Funktion von Koordinaten gegeben ist.
Die Beteiligten können also anhand der von ihnen festgestellten Pingdauern nicht zwischen den beiden Szenarien unterscheiden. Das sind observationell gleichwertige Beschreibungen, sofern die Beteiligten sich noch eine adäquate Gezeitenkraft als Erklärung für ihr Herumwackeln in Flachen hinzumodellieren.
Chrys schrieb (11. Juni 2016 0:11):
> Im Grunde wird da gar keine Koordinatentransformation im eigentlichen Sinne definiert, […]
Naja, wie Markus Pössel die obigen Animationen begründet, kann er wohl am besten selbst darlegen; aber ich denke der Begriff “Abbildung” trifft jedenfalls zu.
> sondern eine spezielle Abbildung zwischen einer linearen GW und dem Minkowski Raum, […] dergestalt, dass deren wechselseitige Pingdauerverhältnisse invariant bleiben.
Ganz sicher was die Pingdauerverhältnisse des einen abgebildeten Beteiligten “im Zentrum des Rings” bzgl. denen “im Ring” angeht;
denn das illustriert/veranschaulicht ja direkt das interferometrische LIGO-Verfahren.
Betreffend die Beteiligten “im Ring” untereinander (bzw. auch gegenüber “dem im Zentrum”) und auch in (hypothetischer) Betrachtung weiterer “Ringe” mit anderen, insbesondere größeren Radien bin ich mir aber gar nicht so sicher, dass auch deren “im nicht-statisch Gekrümmten” ermittelte Pingdauerverhältnisse exakt “ins Flache” abgebildet werden könnten. (Ganz im Gegenteil; vgl. meinen Illustrationsvorschlag.)
> Die Beteiligten können also anhand der von ihnen festgestellten Pingdauern nicht zwischen den beiden Szenarien unterscheiden.
Diese Schlussfolgerung geht mir (meinen Vorurteilen! &) also entschieden zu weit, sofern die Beziehungen zwischen hinreichend viele geeigneten Beteiligte in Betracht gezogen werden (nach Synge sollten ca. fünf allgemein gewählte ausreichen). Und sofern sogar mehr oder weniger raum-füllende Anordnungen von Beteiligten betrachtet werden (sog. “Kongruenzen“), dann sollten allein alle Feststellungen jedes dieser Beteiligten hinsichtlich Koinzidenz (bzw. Nicht-Koinzidenz) zur Unterscheidung ausreichen.
> gleichwertige Beschreibungen, sofern die Beteiligten sich noch eine adäquate Gezeitenkraft als Erklärung für ihr Herumwackeln in Flachen hinzumodellieren.
(Um mit diesem Gedanken so glückseelig zu werden, wie es Einstein offenbar eine Weile war, wären aber eben gleichwertige Beschreibungen hinsichtlich der wohlbekannten zeit-räumlichen Konstatierungen erforderlich.)
> “proper length”-Funktion von Koordinaten
(Ich musste nochmals darüber nachdenken und mich erinnern, warum ich mich entschlossen hatte, mit der “proper length”-Funktion nichts anzufangen, und mich stattdessen auf die “Lorentzian distance”-Funktion zurückzuziehen, sofern es um verallgemeinert-metrische Bewertungen geht. Das sollte mich aber nicht davon abhalten, demnächst, mal so zum Spaß, geeignete Werte dieser gegebenen “proper length”-Funktion in entsprechende Cayley-Menger-Determinanten oder sogar Kokkendorff-Gram-Determinanten einzusetzen.)
Zum Thema Koordinatentransformation: Jein.
Was ich bei meiner Vorbereitung gemacht habe und was Maggiore mit seinem proper detector frame auch macht, ist selbstverständlich eine Koordinatentransformation, da sind wir uns hoffentlich einig.
Zumindest ich bilde nirgends in den Minkowski-Raum ab. Ich bilde zwar auf eine ebene Fläche ab (das geht, weil ja keine signifikanten Raumkrümmungs-Anteile dabei sind), aber die gemischten Komponenten des Krümmungstensors sind ja gerade das, was in der Animation für die differenzielle Beschleunigung zwischen den dargestellten Teilchen sorgt. Die verbliebene Raumzeit-Krümmung steckt in der Art und Weise, wie sich die Teilchen relativ zueinander bewegen. Und bei der Bewegung der Lichtteilchen sieht man sofort, dass man nicht im Minkowski-Raum mit seinen einfachen Gesetzen der Lichtausbreitung ist.
Welche Interpretation dahintersteht (nach wie vor geometrisch, oder vereinfachte Beschreibung in einem gedachten Newton’schen Rahmen, die zumindest für die Nicht-Lichtteilchen richtige Ergebnisse liefert) kann man der Animation nicht ansehen. Die relativen Abstandsänderungen (proper distances) sind in beiden Fällen gleich.
Die erwähnte “spezielle Abbildung”, von der Sie reden, geht damit deutlich darüber hinaus, was die Animation tatsächlich darstellt. Ob man zum Kräftebild übergeht oder nicht ist zusätzliche Interpretation. Die Abläufe, die in der Animation dargestellt werden, erhält man so oder so.
“[O]bservationell gleichwerti[g]”? Oberflächlich meinetwegen, wenn man mal von den Problemen mit der Lichtausbreitung absieht. Aber ohne ein vernünftiges Modell dahinter, wie diese speziellen Gezeitenkräfte zustandekommen, gibt es keinen Grund, hinter der Gezeitenkraft-Deutung mehr zu vermuten als tatsächlich dahintersteckt: Man kann in der Allgemeinen Relativitätstheorie immer lokal flache Bezugssysteme einführen. Und in der ART gibt es Gravitationswellen mit bestimmten Eigenschaften.
@Markus Pössel / 11. Juni 2016 11:02
Recht offensichtlich unterscheiden Sie nicht sorgsam zwischen dem Minkowskischen Raum (M,η) und dem GW-Raum (M,g) mit g = η + h, die ja beide über demselben Punktraum modelliert sind, dem Euklidischen 4-Raum M. Mit der Angabe einer formalen Transformation (t,x,y,z) = Φ(t’,x’,y’,z’) von M ist jedoch noch kein Wort darüber gesagt, was das hinsichtlich der Geometrie, die einzig durch die jeweilige Metrik bestimmt wird, überhaupt bedeuten soll. Ob damit ein Kartenwechsel von (M,g) gemeint ist (d.i. eine Koord.transf. im eigentlichen Sinne) oder eine Abbildung Φ:(M,η) → (M,g) zwischen zwei geometrisch verschiedenen Räumen, wird nur erkennbar, wenn der Bezug zur Metrik deutlich gemacht wird. Tatsächlich ist der Übergang vom Proper Detector Frame zum TT Frame bei Maggiore gerade eine Abbildung der letztgenannten Art. Denn im Proper Detector Frame ist die Welt flach, und das will er auch so haben, weil nämlich die feldtheoretische Interpretation der linearisierten Gravitation, auf der die ganze GW-Theorie dann im weiteren aufbaut, zwingend einen flachen Hintergrund erfordert.
»Zumindest ich bilde nirgends in den Minkowski-Raum ab.«
Für Ihre Beispiel-GW wäre die Transformation (t,x,y,z) = Φ(t’,x’,y’,z’) gegeben durch
t = t’
x = x’/√{1 + A sin(ωt’ − kz’)}
y = y’/√{1 − A sin(ωt’ − kz’)}
z = z’
Dann schreiben Sie sich dich bitte die transformierte GW-Metrik in den gestrichenen Koordinaten einmal hin, damit erst hätten Sie einen Kartenwechsel, eine Isometrie des GW-Raumes. Wegen der dabei anfallenden partiellen Ableitungen ∂x/∂t’ und ∂x/∂z’ sowie ∂y/∂t’ und ∂y/∂z’ stimmt dann jedoch leider diese Animation nicht mehr, denn die erhalten Sie in der gezeigten Form nur, wenn Sie diese Terme geflissentlich unter den Tisch fallen lassen resp. gleich null setzen. Und damit haben Sie sich wohl doch auf den Minkowskischen Raum bezogen, Sie haben es nur nicht gemerkt.
Nee, sorry, Sie geben schlicht nicht richtig wieder was Maggiore da macht und schreibt. Der proper detector frame ist auch bei Maggiore (wie bei mir auch) ein üblicher Koordinatenwechsel.
Und die Welt im proper detector frame ist eben nicht flach. Siehe die Definition des Begriffs “proper detector frame” bei Maggiore, S. 20: “The frame where the metric has the form (1.88) is called the proper detector frame.” Und (1.88) ist ganz klar keine Minkowski-Metrik, sondern enthält Krümmungsterme. Und die Metrik (1.88) ergibt sich über eine stinknormale Koordinatentransformation.
Flach wird die Raumzeit in dieser Metrik nur, wenn man höhere Terme vernachlässigt. Das ist beim Übergang in frei fallende Bezugssysteme immer so.
@Markus Pössel / 11. Juni 2016 20:02
Bei einer linearen GW hat es keine Terme höherer Ordnung, da ist nichts zu vernachlässigen. Solche Terme treten auf in Fällen, wo h nur näherungsweise eine Lösung der linearisierten Feldgl. repräsentiert, und speziell für Ihre lineare Beispiel-GW trifft das schliesslich nicht zu.
Diese Terme höherer Ordnung sind feldtheoretisch zu verstehen als Ausdruck einer nichtlinearen Selbstwechselwirkung jenes masselosen Spin-2 Feldes, das, um überhaupt definiert zu werden, eine flache Hintergrundmetrik erfordert. Erzähle ich Ihnen denn damit etwas Neues?
Hier sind zwei Entwicklungen im Spiel: Einmal für die linearisierte Gravitation (Entwicklung in h), zum anderen, wie immer beim Übergang in ein frei fallendes System, eine Taylorentwicklung in den Koordinatenwerten rund um den Nullpunkt des Systems.
Und für letztere Taylorentwicklung zeigt Maggiore S. 20 (1.88) die höheren Terme (in den Koordinaten), an denen man die Abweichung von der flachen Metrik sieht.
@Markus Pössel, Frank Wappler
Die Idee beim Übergang vom TT Frame zum Proper Detector Frame besteht doch darin, die im TT Frame verwendeten geometr. “Massstäbe” dt, dx, dy, dz, zu ersetzen durch solche, mit denen geometr. (Pseudo-)Abstände im “properen” Abstandsmass ausgedrückt werden. Motiviert durch die Heuristik, dass ein Detector mit eben solchen “Massstäben” misst und auch schon damit gemessen hat, bevor überhaupt eine GW präsent war. Der besagte Übergang meint also die Einführung veränderter geometr. “Massstäbe”, und für die lineare Beispiel-GW bedeutet das konkret die Ersetzung
dt’ ← dt
dx’ ← √{1 + A sin(ωt − kz)} dx
dy’ ← √{1 − A sin(ωt − kz)} dy
dz’ ← dz
Setzt man nun die gestrichenen “Masstäbe” in den Ausdruck für die GW-Metrik ein, dann heisst das anschaulich, dass jetzt diese zur Skalierung verwendet werden, wodurch die Darstellung der geometr. Gegebenheiten entsprechend verzerrt wird. Speziell wird die Beispiel-GW hierdurch in einem flachen Minkowski Hintergrund dargestellt, denn man erhält dabei
c²(dt’)² − (dx’)² − (dy’)² − (dz’)² = η.
Und wenn dem Physiker dies leichthin unter “Koordinatentransformation” durchgeht, darf es auch nicht verwundern, wenn Herr Wappler sich wundert, dass plötzlich alles so flach aussieht.
Eine lineare GW ist durch den TT Anteil bereits vollständig charakterisiert, und es ist alles gesagt. I.a. ist der TT Anteil jedoch nur die (lokale) lineare Approximation an h, und man hat zusätzliche nichtlineare Anteile, die jedoch lokal von mindestens quadratischer Ordnung verschwinden. Das muss uns hier allerdings nicht bekümmern, diese Anteile sind im Beispiel nicht vorhanden, und danach hat schliesslich die ganze Zeit auch noch kein Hahn gekräht.
Chrys schrieb (13. Juni 2016 17:05):
> […] nicht verwundern, wenn Herr Wappler sich wundert, dass plötzlich alles so flach aussieht.
Anstatt “flach aussehen” halte ich aber ggf. “messbar flach sein” für wesentlich;
was nachvollziehbar auf Feststellungen von Koinzidenz hinausläuft (schmatisch z.B. als raumfüllendes [tetrahedral-oktahedrales](https://en.wikipedia.org/wiki/Tetrahedral-octahedral_honeycomb) Ping-Koinzidenz-Gitter von geeigneten Beteiligten),
und, das möchte ich als Physiker nochmals betonen, was völlig unabhängig von irgendwelchen Koordinatenzuordnungen ist.
Und anstatt dass “plötzlich alles” derart messbar flach gewesen wäre, würde ich (nur) erwarten, dass das mehr oder weniger auf die Abbildungen zutrifft, die im obigen SciLogs-Artikel bzw. im entsprechenden “Teil 1” gezeigt wurden; aber sicherlich nicht auf Systeme mit tatsächlichen Gravitationswellen, die ggf. abgebildet wären.
(Verwunderliches bleibt (mir) auch ansonsten noch genug …)
@Chrys:
Wie gesagt, zwei Arten von Nichtlinearität! Und in den zwar in h linearen, aber in den x^i quadratischen Termen steckt nach der Koordinatentransformation (!) die Information über die Gravitationswelle.
Genau aus diesen in x^i quadratischen Termen bekommt ja auch Maggiore zwischen Gl. (1.90) und (1.95) die Wirkung der Gravitationswelle im neuen System heraus.
Insofern: Dass die Metrik nach der Koordinatentransformation selbstverständlich weiterhin nicht flach ist, ist hier ganz entscheidend.
Was man da noch an zusätzlichen Interpretationen aufhängen möchte, ist dann wieder optional. Aber wenn man sich allein an die geometrische Beschreibung hält, bekommt man durch die Koordinatentransformation die richtigen Abstandsänderungen heraus, und kann diese Abstandsänderungen wie in meiner Animation bildlich darstellen.
Mehr habe ich nicht gemacht, weniger aber auch nicht: Eine Darstellungen der Abstandsänderungen (proper distance mit der TT-Zeitkoordinate) durch eine Gravitationswelle. Was haben Sie daran denn nun auszusetzen?
Markus Pössel schrieb (14. Juni 2016 10:12):
> [Dass ein System von identifizierbaren, voneinander getrennten Beteiligten mit] Gravitationswelle […] weiterhin nicht flach ist, ist hier ganz entscheidend.
> [… deren] Abstandsänderungen wie in meiner Animation bildlich darstellen.
> Was haben Sie daran denn nun auszusetzen?
Nachdem Chris, dem oder der die zitierte Frage insbesondere galt, darauf geantwortet hat (zuverlässig, wie gewohnt),
und da ich mit den darin (wie leider fast schon gewohnt) aufkommenden Koordinatenmauscheleien nichts anfangen mag, insbesondere weil diese nicht (für mich) erkennbar mit “Maßstäben” in dem (für Phyisker relevanten) Sinne zu tun haben, dass deren Endenpaare gegenüber einander chromonetrisch-starr (oder mehrere Endenpaare gegenüber einander Ping-Koinzidenz-starr) gewesen wären,
möchte auch ich die zitierte Frage hiermit beantworten:
Erstens habe ich (immer noch) die Formlität auszusetzen, dass veränderliche Größen als “Abstände” bezeichnet werden. Man beziehe sich besser aus (ggf. variable) “Pingdauern” (bzw. wenigstens, wie Maggiore p. 19 ziemlich unbeholfen formuliert, “the time taken by light to make a round trip“); oder wenigstens (ggf. variable) “Entfernungen”.
Zweitens und wesentlicher habe ich (immer noch) auszusetzen, dass die laut obigem Zitat entscheidende Sache (“Krümmung”, _nicht_ “Flachheit”), in den bildlichen Darstellungen nicht (für mich) erkennbar und zwangsläufig ist.
Die Kekskrümel, die auf meinem Bildschirm so herumrutschen, dass sie den (jeweils) 33 Punkten der Animationen folgen –
– bilden die (allein deshalb) ein System, dass wie gewünscht _nicht_ flach ist?
bzw.
– sind die (allein deshalb, alle) “frei/inertial”?
Wenn nicht, dann ist das ein Mangel der Abbildungen in den betreffenden SciLogs-Artikeln (und vermeintlich weniger mangelhafte habe ich schon vorgeschlagen).
p.s.
Wer orthographische Fehler in SciLogs-Kommentaren findet, darf sich der (nicht zuletzt dadurch stets dringender werdenden) Bitte nach Implementierung einer Kommentarvorschau oder (ja-was-denn-noch-alles-!?) einer evtl. zeitnahen nachträglichen Editier- oder Löschmöglichkeit anschließen.
@Markus Pössel / 14. Juni 2016 10:12
»Mehr habe ich nicht gemacht, weniger aber auch nicht: Eine Darstellungen der Abstandsänderungen (proper distance mit der TT-Zeitkoordinate) durch eine Gravitationswelle. Was haben Sie daran denn nun auszusetzen?«
Sie wollen für Ihre Darstellungen einen Frame, der proper time auf der t’-Achse sowie proper length auf den x’-, y’-, und z’-Achsen darstellt. Wenn noch keine GW da ist, haben Sie einen solchen mit dem rest frame Ihres im Minkowski Vakuum frei fallenden Detectors aus dem Beispiel. Und dieser Detector Frame soll dann auch verwendet werden, um die Effekte der Beispiel-GW zu illustrieren.
Für die Beispiel-GW werden im TT Frame in t- und z-Richtung schon propere Werte genau wie im Detector Frame dargestellt, und nur in x- und y-Richtung ist tatsächlich etwas zu justieren. Diese “Justierung” ist das, was ich oben (13. Juni 2016 17:05) mit den “←”-Relationen formuliert habe. Man beachte, dass eine Integration eines jeden dieser Ausdrücke über ein Intervall auf der jeweils zugehörigen Achse dessen properes Längenmass liefert.
Nun meinen Sie, dass sich diese “Justierung” durch eine Koord.transf. zwischen Detector Frame und TT Frame bewerkstelligen lässt, von der Art, wie ich es oben (11. Juni 2016 18:37) mit Φ angegeben hatte. Dieses Φ etabliert x’ und y’ als neue ‘proper length’-Koordinaten für x und y im TT Frame, alles andere bleibt dort unverändert. Allerdings werden dabei auch die Differentiale der Koord.funktionen (und damit schliesslich der metrische Tensor) unter Φ covariant transformiert, was man explizit durch die Jacobische von Φ erhält. Wenn jetzt wirklich alles “proper justiert” wäre, müssten sich aus der so erhaltenen linearen Transformation durch Invertieren gerade die “←”-Relationen ergeben, nur mit einem “=”-Zeichen anstelle des Pfeils. Doch das klappt nicht.
Sie haben zwar für feste Werte von t und z jeweils eine 1-dim. Koord.transf. in x- und in y-Richtung auf ‘proper length’-Koordinaten x’ und y’, können das aber nicht covariant zu einer 4-dim. Transf. vom TT Frame in den Detector Frame fortsetzen. Diesen Übergang zwischen den Frames kriegen Sie nur hin, indem Sie die Covarianz ignorieren und faktisch eine Reskalierung der x- und y-Achsen auf properes Längenmass vornehmen, wobei dann jedoch auch die Metrik des TT Frames in die des Detector Frames verzerrt wird — und die war von Beginn an η.
Mit Ihrem Beispiel-Szenario von Sinuswelle und frei fallendem Detektor kommen Sie beim Proper Detector Frame über Maggiores Gl. (1.86) nicht hinaus. Und nichtlineare Bedingungen etwa für räumlich regionale Beschränkungen sind im Beispiel auch keine eingebaut. Mit dem Bezug auf diesen Detector Frame haben Sie dann für die Darstellungen eben Koordinaten gewählt, “so that even in the presence of GWs, the metric is flat.”
P.S. Die eigentliche Pointe hätte ich noch nachzutragen: Die oben (11. Juni 2016 18:37) angegebenen Formeln für Φ sagen allein noch nichts darüber aus, ob damit eine Transformation des (t,x,y,x)-Raumes oder eine durch die (t,z)-Ebene parametrisierte Familie linearer Transformationen der (x,y)-Ebene dargestellt werden soll. Bei der letztgenannten Deutung wird die Geometrie des totalen 4-Raumes nicht erhalten, und in genau diesem Sinne ist der Übergang zwischen TT Frame und Proper Detector Frame zu interpretieren.
Doch wenn man das nun alles schlicht und “selbstverständlich” als Koordinatentransformation feilbietet, schickt man u.a. Herrn Wappler nur auf den Holzweg.
Chrys schrieb (15. Juni 2016 9:07):
> […] nachzutragen: Die oben (11. Juni 2016 18:37) angegebenen Formeln für Φ sagen allein noch nichts darüber aus, ob damit eine Transformation des (t,x,y,x)-Raumes oder eine durch die (t,z)-Ebene parametrisierte Familie linearer Transformationen der (x,y)-Ebene dargestellt werden soll.
Es ist ja üblich, von der Gesamtheit reell-wertiger Quadrupel als „(mathematischem) Raum (ℝ^4)“ zu sprechen.
Von der Gesamtheit reell-wertiger Paare als „Ebene“ zu sprechen, kann allerdings als Unterstellung geometrischer Ebenheit (d.h. Flachheit einer Fläche) missverstanden werden;
was sich vermeiden lässt, indem man diese Menge schlicht ebenfalls als „(mathematischen) Raum (ℝ^2)“ anspricht;
bzw. im Zusammenhang als „einen Unterraum (ℝ^2) des Raumes ℝ^4“.
(Im Kommentar hat Markus Pössel allerdings auch Andeutungen zu geometrischen Beziehungen gemacht, aus denen sich eventuell die Ebenheit des mit (x,y) parametrisierten Unterraumes schließen lässt, und die sich allein durch irgendeine eins-zu-eins Umbennenung von Punkten natürlich nicht ändern würde.)
> Bei der letztgenannten Deutung wird die Geometrie des totalen 4-Raumes nicht erhalten
Das unterstellt, dass eine bestimmte „Geometrie des totalen 4-Raumes“ überhaupt gegeben wäre; und insbesondere von Markus Pössel schon angegeben worden wäre. Welche sollte das denn sein??
> Doch wenn man das nun alles schlicht und “selbstverständlich” als Koordinatentransformation feilbietet, schickt man u.a. Herrn Wappler nur auf den Holzweg.
Der Holzweg beginnt leider schon da, wo Koordinaten anstatt geometrischer Beziehungen feilgeboten werden.
(Obligatorische Pointe: Dem anzuhängen hieße, sich als Physiker (allerdings auch als Nichtphysiker!) einer Täuschung hinzugeben …)
Chrys schrieb (15. Juni 2016 9:07):
> […] nachzutragen: Die oben (11. Juni 2016 18:37) angegebenen Formeln für Φ sagen allein noch nichts darüber aus, ob damit eine Transformation des (t,x,y,x)-Raumes oder eine durch die (t,z)-Ebene parametrisierte Familie linearer Transformationen der (x,y)-Ebene dargestellt werden soll.
Es ist ja üblich, von der Gesamtheit reell-wertiger Quadrupel als „(mathematischem) Raum (ℝ^4)“ zu sprechen.
Von der Gesamtheit reell-wertiger Paare als „Ebene“ zu sprechen, kann allerdings als Unterstellung geometrischer Ebenheit (d.h. Flachheit einer Fläche) missverstanden werden;
was sich vermeiden lässt, indem man diese Menge schlicht ebenfalls als „(mathematischen) Raum (ℝ^2)“ anspricht;
bzw. im Zusammenhang als „einen Unterraum (ℝ^2) des Raumes ℝ^4“.
(Im Kommentar vom 18. Mai 2016 15:50 hat Markus Pössel allerdings auch Andeutungen zu geometrischen Beziehungen gemacht, aus denen sich eventuell die Ebenheit des mit (x,y) parametrisierten Unterraumes schließen lässt, und die sich allein durch irgendeine eins-zu-eins Umbennenung von Punkten natürlich nicht ändern würde.)
> Bei der letztgenannten Deutung wird die Geometrie des totalen 4-Raumes nicht erhalten
Das unterstellt, dass eine bestimmte „Geometrie des totalen 4-Raumes“ überhaupt gegeben wäre; und insbesondere von Markus Pössel schon angegeben worden wäre. Welche sollte das denn sein??
> Doch wenn man das nun alles schlicht und “selbstverständlich” als Koordinatentransformation feilbietet, schickt man u.a. Herrn Wappler nur auf den Holzweg.
Der Holzweg beginnt leider schon da, wo Koordinaten anstatt geometrischer Beziehungen feilgeboten werden.
(Obligatorische Pointe: Dem anzuhängen hieße, sich als Physiker (allerdings auch als Nichtphysiker!) einer Täuschung hinzugeben …)
Noch einmal: Woraus lesen Sie ab, dass meine Metrik in der Animation die Minkowski-Metrik sein soll?
Dass die geodätische Bewegung (gewonnen aus der direkten Transformation der geodätischen Bewegung im TT-System) nicht linear ist, zeigt doch im Gegenteil, dass dem nicht so ist, und die Lichtfortpflanzung ist auch ganz un-Minkowskisch.
Auch Ihre Einwände, warum das, was Maggiore vorrechnet und ich genauso nachbilde, keine Koordinatentransformation sein soll, kann ich weiterhin nicht nachvollziehen. Sie hatten da z.B. mit partiellen Ableitungen nach z argumentiert, aber wenn man genauer hinschaut ergeben sich daraus nur quadratische Terme in h, die man wie alle solchen Terme vernachlässigen kann.
@Markus Pössel / 15. Juni 2016 15:48
»Woraus lesen Sie ab, dass meine Metrik in der Animation die Minkowski-Metrik sein soll?«
Indem Sie die proper time vom TT Frame beibehalten sowie ‘proper distance’-Koordinaten für x und y einführen wollen, haben Sie 3 von 4 Koeffizientten der tranformierten GW-Metrik bereits verraten. Diese muss dann in den neuen (t’,x’,y,z’)-Koordinaten die Form
g’ = c²(dt’)² − (dx’)² − (dy’)² − ???(dz’)²
haben. Zudem wandern in den animierten 3D-Impressionen die Wellenfonten offenbar gleichförmig mit einer konstanten Geschw. in z’-Richtung, die für die Beispiel-GW naturgemäss gleich der Lichtgeschw. in vacuo ist. Damit ist jedenfalls ??? = const., und g’ ist flach. Und wenn z’ auch noch proper ist, was sich oBdA arrangieren lässt, gilt auch g’ = η.
Ich rätsele im Moment, in welcher Sprache ich mich Ihnen verständlich machen kann. Wenn Ihnen das alles noch immer nicht einleuchtet, dann schreiben Sie doch die Koord.transformation einfach mal hin, die Ihnen dabei vorschwebt, vielleicht hilft das weiter.
Ich behalte die Koordinatenzeit als Koordinatenzeit bei. Und ich nutze später aus, dass diese Zeitkoordinate für die Uhr im Raumnullpunkt (also dort, wo die Phasenvergleiche etc. stattfinden, nämlich effektiv beim Strahlteiler) die Eigenzeit misst. (Dass sie weiterhin auch die Eigenzeit der im neuen System bewegten Testteilchen misst, kann man dazu sagen, es bringt aber soweit ich sehen kann keinen soooo großen Erkenntnisgewinn.)
Aber ich mache vorab keine Aussage über den metrischen Koeffizienten g_00.
Stattdessen bekomme ich genau wie bei Maggiore (1.87) plus dort darauf folgende Vereinfachungen (nur der g_00-Term trägt bei) heraus, dass die wichtigen differenziellen Beschleunigungen nach der Transformation im g_00 stecken.
Genauer gesagt: “bekäme”, denn ich komme zum gleichen Ergebnis auf einfachere Art und Weise: Ich schreibe die entsprechenden Geodäten im TT-Frame hin (konstante Orte bzw. beim Licht etwas komplizierter) und transformiere dann die Bahnen ins neue System. Kovarianz ist ja gerade so definiert, dass dieses Vorgehen dasselbe Ergebnis liefert wie Matrix-Transformation von g.
Da liegt aus meiner Sicht der Knackpunkt: Sie behaupten fälschlicherweise, ich würde g_00 inklusive höherer Terme in den x^i gleich 1 setzen. Ich setze es bis O(1) gleich eins (wie immer beim Übergang in lokal flache Systeme), aber nicht darüber hinaus.
So richtig verstehe ich den Streit um die “relativ-einfach”-Animation zwar nicht,
habe aber einen dritten Autor, der vielleicht schlichten könnte:
Akhmedov http://arxiv.org/pdf/1601.04996.pdf
dort Lec.IX S.71 ab F.(215) “Minkowskian”
@Markus Pössel / 16. Juni 2016 13:23
Dass Maggiore da proper time verwendet, sehen Sie doch an (1.86). (Und was motiviert wohl das “proper” bei “proper detector frame”?) Bezogen auf Ihre Beispiel-GW ist die Beziehung zwischen diesem Proper Frame und dem TT Frame gerade durch die obige Abb. Φ gegeben, und das, wohlgemerkt, als Abbildung eines flachen in einen gekrümmen Raum. Damit lässt sich die GW nun im Proper Frame darstellen, und es erweist sich, die benimmt sich dort, im Flachen, gerade so, wie es in Ihren Visualisierungen erscheint. Das kann doch nicht so schwer zu begreifen sein.
Und anschliessend, nachdem Sie diese flache Darstellung Ihrer Beispiel-GW haben, können Sie ja immer noch danach fragen, ob dabei vielleicht irgendwelche nichtliearen Anteile höherer Ordnung vorliegen, hinsichtlich derer Korrekturen in Betracht zu ziehen wären, womit Sie dann zu (1.87) vorrücken könnten. Das ist für Ihr pure-TT Beispiel freilich nicht der Fall.
@Chrys In Ihrem letzten Kommentar reiht sich aus meiner Sicht wieder eine falsche Aussage an die nächste (und ja, “Das kann doch nicht so schwer zu begreifen sein” kann ich postwendend zurückgeben).
(1.86) ist nichts anderes als (1.87). Aus der Transformation erhält man (1.87); erst wenn man alles jenseits linearer Terme wegwirft landet man bei der Minkowski-Metrik (1.86), zu der Maggiore dann ja auch extra schreibt “if we restrict our attention to a sufficiently small region of space”.
Damit hat man die Gravitationswelle dann aber gleich mit weggeworfen. Sprich: Wenn meine Metrik tatsächlich Minkowski wäre, dann würde sich auch gleich Licht mit konstanter Geschwindigkeit bewegen, und Geodäten wären nicht mehr relativ zueinander beschleunigt. Setzt man das um, sähe die Animation völlig anders aus.
Aber man kann ja auch die quadratischen Terme in x^i mitnehmen – mache ich für meine Animation so, macht Maggiore für seine Ableitung der relativen Beschleunigung von Geodäten so. Dann (und erst dann) hat man die Wirkung der Gravitationswelle wieder mit drin (periodische relative Beschleunigung der in TT-Koordinaten ruhenden Teilchen), und dann und erst dann kommt man auf meine Animation. (Alternativ kann man auch dann, und erst dann, ob der Gezeitenkräfte eine künstliche Newtonsche-Kraft-Deutung einführen; muss man aber nicht. Habe ich auch nicht.)
Dass Ihre Aussage, für mein “pure-TT Beispiel” gäbe es “freilich” keine Korrekturen wie in (1.87) falsch ist, können Sie auch direkt bei Maggiore nachlesen. Mein h(t) ist proportional zu sin(omega t). Dass dessen zweite Ableitung nach der Zeit nicht verschwindet, liegt auf der Hand. Damit ist aber auch der gemischte Zeit-Raum-Riemann-Term, den Maggiore bei (1.94) hinschreibt, ungleich Null. Und der wiederum liefert in (1.87) den x^i x^j – Term für den Koeffizienten g_00 (wie in meiner letzten Antwort an Sie schon gesagt). Dieser höhere Term in g_00 enthält die Wirkung der Gravitationswelle. (Und der Umstand, dass er in g_00 und nur dort wichtig wird, erlaubt die optionale alternative Deutung als künstliche Newton-artige Kraft.)
@Markus Pössel / 16. Juni 2016 19:33
Vor ein paar Tagen hatte ich Sie gefragt, ob ich Ihnen mit der feldtheoret. Deutung der linearisierten Theorie etwas Neues erzähle. Auch wenn Sie mir keine Antwort darauf gegeben haben, kann ich mir jetzt gewiss sein, dass Sie das in der Tat nicht kennen. Daher sehen Sie auch nicht, dass diese Abb. vom Flachen ins Gekrümmte gerade die Verbindung schafft zwischen der feldtheoretischen Beschreibung, die unbedingt einen flachen Hintergrund erfordert, und der geometrischen. Mit Ihren Visualisieerungen sind Sie allerdings dann doch in Flache gerutscht, ohne es zu merken. Sie wähnen sich dabei jedoch irrtümlich noch immer im Gekrümmten und verstehen dann auch nicht, warum Herr Wappler keine Krümmung in Verbindung mit Ihren Bildern finden kann. Er kann da keine finden, weil da gar keine ist. Das Herumwackeln von Testmassen ist hier als Bewegung in einem Gravitationsfeld und nicht geodätisch zu denken, in Analogie zur Bewegung von Testladungen in einem EM-Feld.
Im weiteren meinen Sie offensichtlich, die Bewegung Ihrer Testmassen linear (oder auch von höherer Ordnung) im Ortsraum approximieren zu müssen, aber das ist ein Irrtum. Bei der Linearisierung geht es indessen um eine lokale lineare Approximation von Feldern, in einem Funktionenraum. Dabei liefert der TT Anteil eines Feldes h eine lokale lineare Näherung an h, und der TT Anteil ist linear im selben Sinne, wie ein EM-Feld linear ist, nämlich indem er eine lineare Wellengleichung löst. Wenn ein h wie das aus Ihrem Beispiel schon linear ist, also nur aus dem TT Anteil besteht, dann fällt es mit seiner linearen Approximation zusammen, und nichtlineare Terme höherer Ordnung hat es da keine.
Chrys schrieb (17. Juni 2016 11:13):
> […] warum Herr Wappler keine Krümmung in Verbindung mit Ihren Bildern finden kann
Das ist zwar entscheidend übertrieben –
mein Standpunkt war und bleibt, dass Markus Pössels in Frage stehende Animationen, die ja zumindest die Pingdauern (u.Ä.) des „Teilchens im Zentrum“ getreu abbilden (sollen), mich (oder auch jeden anderen) aber nicht dazu zwingen, darin eine Region/Anordnung mit Krümmung zu erkennen.
Die entsprechenden Hinweise/Forderungen (etwa, dass alle gezeigten 33 Teilchen „frei“ zu sein hätten, und nicht z.B. nur die „auffallend geraden 5“) müssen und wurden (durch Herrn Pössel) eben immer nur zusätzlich gegeben.
(Die Konsequenz dieses meines Standpunktes für LIGO an sich mag man sich denken.)
– aber trotzdem gut erkannt (und ich hatte mich ja weiter oben zum Zwecke der Diskussion unter uns ja doch darauf eingelassen „die Animationen strikt flach anzusehen“).
> […] feldtheoretische Beschreibung, die unbedingt einen flachen Hintergrund erfordert
In dieser Hinsicht kann und möchte ich allerdings keinesfalls mitreden; doch vielleicht/hoffentlich/wenn man auf bisherige Erfahrungen vertrauen darf gibt’s ja noch was Interessantes dazu zu lesen …
@Chrys Ich verkneife mir mal, zu allem etwas zu sagen, was ich in Ihrer letzten Antwort korrigierenswert finde, sondern gehe in den Schritt-für-Schritt-Modus über. Anders kommen wir hier, glaube ich, nicht weiter.
Angenommen, Sie bekommen eine Animation gezeigt wie meinen periodisch deformierten Teilchenkreis, und Sie bekommen die Zusatzinformation (!), dass sich alle dort dargestellten Teilchen geodätisch bewegen und dass die räumlichen Abstände in der Animation “proper distance” entsprechen.
Können Sie aus der Animation auf das Vorliegen oder die Abwesenheit von Raumzeitkrümmung schließen? Wenn ja, mit welchem Ergebnis?
@Markus Pössel / 17. Juni 2016 15:53
Die Zusatzinformation verstehe ich dann dahingehend, dass der Darstellung eine Koord.transf. (Isometrie) des TT Frames zugrundeliegt. Die Krümmung der Raumzeit wird durch eine Isometrie nicht verändert, die Darstellung bezieht sich folglich dann auf eine gekrümmte Raumzeit.
Die (x,y)-Ebene ist in dieser Darstellung allerdings zu jedem Zeitpunkt flach, d.h., die Gauss Krümmung verschwindet.
Denke ich mir noch an festen Orten dieser (x,y)-Ebene plazierte ideale Uhren hinzu, so würden diese einen typischerweise ungleichmässigen und in Abhängigkeit vom Orte variierenden Zeitverlauf anzeigen.
N.B. Eine stillschweigende Annahme, die sicherlich jeder Betrachter einer solchen 2D-Animation intuitiv macht, ist die, dass dabei z = const. gilt und die Animation den zeitlichen Verlauf eines Geschehens getreu darstellt, d.h., der Zeitverlauf der animierten Darstellung ist proportional zur Koordinatenzeit des Dargestellten. (Dies sei nur festgestellt, um allfällige Missverständnisse oder Pathologien möglichst auszuschliessen.)
Vielleicht war’s nicht eindeutig genug formuliert.
Angenommen, Sie bekommen eine Animation gezeigt wie meinen periodisch deformierten Teilchenkreis, und Sie bekommen als einzige Zusatzinformation, dass sich alle dort dargestellten Teilchen geodätisch bewegen, dass die räumlichen Abstände in der Animation “proper distance” entsprechen, dass wir uns im lokal flachen System des zentralen dargestellten Teilchens befinden und dass wir in eine Ebene z=const. schauen.
(Sprich, Sie wissen zunächst nichts darüber, ob das irgendetwas mit TT frame, Wellen oder was sonst auch immer zu tun hat. Es geht nur darum, was Sie direkt aus der Animation und den angegebenen wenigen Zusatzinformationen ableiten können.)
Können Sie aus der Animation auf das Vorliegen oder die Abwesenheit von Raumzeitkrümmung schließen? Wenn ja, mit welchem Ergebnis?
Markus Pössel / 19. Juni 2016 10:33
Die Animation lässt sich schwerlich noch aus dem GW Kontext herausdenken, in dem sie hier präsentiert wird. Aber der Sachverhalt lässt sich auch etwas allgemeiner formulieren.
Wenn alle Koordinatenabstände in der gegebenen Darstellung der Ebene “proper distance” entsprechen, impliziert dies notwendig, dass die Geometrie dieser Ebene flach ist. Und das ist dann keine lokale Aussage, die Ebene ist immer und überall flach.
Wenn nun in dieser Ebene eine beschleunigte Bewegung gezeigt wird, dann lässt sich dies zunächst durch eine beschleunigende Kraft beschreiben. Nun sagen Sie, die Bewegung sei in dieser Darstellung geodätisch zu deuten. (Wobei genaugenommen noch zu sagen wäre, dass dies wirklich im Sinne der GR zu verstehen ist, was ich jetzt einfach mal unterstelle.) Das sagt mir dann, dass ich die Kraft als Zwangskraft behandeln und somit aus der Darstellung eliminieren kann und soll, wodurch sie als Krümmung der Raumzeit geometrisiert wird, ohne dabei jedoch die flache Geometrie der dargestellten Ebene zu verbiegen.
@Markus Pössel, Frank Wappler
Es scheint angebracht, die Transf. auf “proper distance” Koordinaten hier wenigstens prinzipell soweit zu skizzieren, dass wir noch wissen, wovon wir reden. Dazu ist es zunächst komfortabel, die Lichtkoordinaten
u = (ct − z)/√2, v = (ct + z)/√2
einzuführen. Damit ist
η = 2 du dv − dx² − dy²,
und eine ebene, in positive z-Richtung laufende GW werde beschrieben durch die Metrik
g = 2 du dv − (a(u))² dx² − (b(u))² dy².
Vermöge der Transformation
u = u*, v = v*, x = x*/a(u*), y = y*/b(u*)
hat der metrische Tensor in den neuen (und bequemerweise gleich wieder umbenannten) Variablen die Darstellung
g* = η + 2[A(u) x du dx + B(u) y du dy] − [(A(u) x)² + (B(u) y)²] du²
mit A(u)x = a'(u)/a(u) und B(u) = b'(u)/b(u), wobei ‘ die Ableitung symbolisiere.
In der Darstellung g* geben nun die Koordinaten x und y “proper distance” an. Die Variablen (t,z) lassen sich aus (u,v) wieder zurückgewinnen, und es lässt sich dann beispielsweise fragen, welchen lokalen Wert die Lichtgeschw. in der “proper distance” Darstellung an einem Punkt auf der x-Achse (y = 0, z = 0 und daher u = ct/√2) in positive resp. negative x-Richtung hat, nämlich
[(A(u) x)/√2 ± 1] c
Die Lichtkegel schwanken jetzt also bedrohlich in x-Richtung hin und her, und entsprechendes ergibt sich dann auch für die y-Achse. Folglich kann insbesondere bei einer Animation, die bewegte Lichtpunkte in x- und y-Richtung zeigt und auf diese Darstellung bezogen werden soll, die Geschwindigkeit dieser Lichtpunkte dem Betrage nach nicht konstant sein.
Erratum: A(u) = a'(u)/a(u)
Chrys schrieb (24. Juni 2016 12:10):
> […] dass wir noch wissen, wovon wir reden.
Im Hinblick insbesondere auf die erste Animation des obigen SciLog-Artikels, sowie die entsprechenden aus „Teil 1“, möchte ich deshalb nochmals rekapitulieren, wovon dabei die Rede ist, soweit ich davon angesprochen bin:
Die Rede ist von 33 unterscheidbaren, identifizierbaren Beteiligten, von denen nur genau einer (der „in der Mitte“, „M“) stets koinzidente Pings bezüglich jeweils vier anderen Beteiligten findet (wobei sieben solche Quadrupel von Beteiligten dargestellt sind), sowie jeweils paarweise koinzidente Pings bezüglich den zwei verbleichenden Paaren von Beteiligten.
Außerdem nimmt M diese neun Gruppen von jeweils koinzidenten Pings (als Echos zu je einer Signalanzeige) in bestimmter, wiederholt wechselnder Reihenfolge wahr:
– zuerst die Pings des einen Paares, dann nach und nach die Pings der sieben Quadrupel, und schließlich die Pings des anderen Paares,
– oder genau umgekehrt (hinsichtlich der Identifikation der Paare sowie der Identifikation der sieben Quadrupel),
– oder alle 32 Pings in Koinzidenz.
Unter den oben identifizierten sieben Quadrupeln von Beteiligten ist genau nur eines (die vier „auffallend ruhigen“), von denen jeder M stets als „Mitte zwischen“ sich selbst und einem weiteren Mitglied dieses Quadrupels identifiziert (d.h. insbesondere, zwei aufeinanderfolgende Pings bzgl. M koinzident mit einem Ping bzgl. des Gegenübers findet), sowie stets koinzidente Pings bzgl. der beiden anderen Mitglieder des Quadrupels.
(Die eventuellen Koinzidenzfeststellungen der anderen Beteiligten sind weniger erwähnenswert.)
Die genannten Animationen betrachte ich als Ausdruck und Gedankenstütze für diese Koinzidenzfeststellungen; ganz unabhängig von eventuellen Koordinatenzuordnungen.
Ich fände es aber jedenfalls interessant, diesen qualitativen Feststellungen von Koinzidenz, Reihenfolge bzw. Identitäten auch entsprechende quantitative Angaben über Ping-Dauer-Verhältnisse hinzuzufügen.
> […] Geschwindigkeit dieser Lichtpunkte […]
Wir verstehen uns doch hoffentlich dahingehend, dass die Angabe eines bestimmten Wertes von Durchschnittsgeschwindigkeit einen bestimmten Wert der Distanz von Startblock und Zielband gegenüber einander voraussetzt, sowie einen bestimmten Wert der Dauer der Belegung der Rennbahn; und dass ein Geschwindigkeitswert ggf. als Grenzwert von Durchschnittsgeschwindigkeits-Werten über immer kleinere Dauern zu gewinnen wäre …
Und unabhängig von der Möglichkeit einer solchen Bewertung im Einzelfalle ist dabei ja sicherlich stets von
Signalfront die Rede.
@Frank Wappler / 24. Juni 2016 14:59
Aufschlussreicher als die erste Animation des obigen SciLog-Artikels ist diese Animation mit den bewegten Spiegeln und wandernden Lichtpunkten. Gezeigt ist erneut die intrinsisch flache (x,y)-Ebene, doch die Art und Weise, wie die Lichtpunkte darin wandern, sagt einem, wie man sich hierbei die Lichtkegel vorzustellen hat. Die Kenntnis der Lichtkegel wiederum erlaubt einen Rückschluss darauf, ob sich das Gezeigte auf eine gekrümmte oder eine flache Raumzeit-Geometrie beziehen lässt. Und eine dem Betrage nach konstante Geschwindigkeit, mit der nach meiner Wahrnehmung alle Lichtpunkte dort wandern, kann ich nur mit einer flachen Raumzeit-Geometrie in Einklang bringen.
In dieser Animation wandern die Lichtpunkte nicht mit konstanter Geschwindigkeit; das sieht man vermutlich am einfachsten daran, dass sich die Abstände zwischen aufeinanderfolgenden Lichtpunkten ändern, je nach Streck- oder Stauchungszustand.
Ich habe die letzten Tage nicht alle Kommentare in diesem Thread jeweils gleich gelesen; aus meiner Sicht bleibt meine derzeitige zentrale Frage an Sie, warum Sie den Umstand, dass sich die Eigenabstände zwischen geodätisch bewegten Teilchen mit der Zeit beschleunigt ändern (wie in der Animation klar zu sehen; dass es sich um geodätische Bewegung handelt, ist Zusatzinformation, die der Text liefern muss), nicht auch schon als klares Zeichen für Raumzeitkrümmung werten. Dieser Umstand entspricht doch gerade der Definition von Krümmung: Geodäten werden (in der Raumzeit) aufeinander zu und voneinander weg gebogen. Ganz anders als in flacher Raumzeit, wo Geodäten Raumzeit-Geraden sind und dieses Verhalten gar nicht zeigen können.
@Markus Pössel / 25. Juni 2016 10:11
»In dieser Animation wandern die Lichtpunkte nicht mit konstanter Geschwindigkeit; das sieht man vermutlich am einfachsten daran, dass sich die Abstände zwischen aufeinanderfolgenden Lichtpunkten ändern, je nach Streck- oder Stauchungszustand.«
Daran sieht man nur, dass die Lichtwellenlänge gestreckt oder gestaucht wird, und so funktioniert im Prinzip ein Doppler Radar. Das funktioniert aber schliesslich auch in der SR, wo an der Konstanz der Lichtgeschw. schwerlich irgendwelche Zweifel bestehen dürften. In Ihrer Animation mit den bewegten Spiegeln wandern die Lichtpunkte genauso mit einer konstanten Geschwindigkeit wie in der Animation mit den unbewegten Spiegeln, die davor gezeigt ist.
Zu Ihrer Frage. Eine Metrik, die in einer flachen (x,y)-Ebene (mit “proper distance”-Koordinaten) die in Rede stehende Bewegung geodätisch hervorbringt, habe ich mit dem g* oben (24. Juni 2016 12:10) skizziert; die Anwendung auf die Beispiel-GW werde ich aber nicht auch noch vorzuführen versuchen. Nur verhält sich diese (überhaupt nicht relativ einfache) Metrik hinsichtlich der Variablen t und z, wenn man sich diese wieder zurückholt, dann anders, als es in den Animationen erscheint. Das betrifft nicht nur Geschw. der wandernden Lichtpunkte in x- und y-Richtung, sondern auch die wandernden Wellenfronten in z-Richtung bei den animierten 3D-Impressionen.
Was Sie in Hinblick auf die Erstellung der Animationen tun wollten, kann ich schon nachvollziehen, nämlich “proper distance” in der (x,y)-Ebene einführen, wobei mit t und z alles so belassen wird, wie es auch ohne Welle war. Die Animationen passen dann allerdings zu etwas anderem, nämlich “proper distance”-Koordinaten in der (x,y)-Ebene, wobei mit dt und dz alles so belassen wird, wie es auch ohne Welle war. Damit ist man jedoch im total Flachen gelandet und hat sich die GW als ein Gravitationsfeld über einem flachen raumzeitlichen Hintergrund zu denken, das auf Testmassen eine Kraft ausübt, so ähnlich wie ein EM-Feld eine Kraft auf Testladungen ausübt.
Chrys schrieb (25. Juni 2016 9:10):
> […] diese Animation mit den bewegten Spiegeln und wandernden [Signalfronten].
Gezeigt ist erneut die intrinsisch flache (x,y)-Ebene
Die Animation zeigt natürlich eine Sequenz von Einzelbildern.
Für jedes einzelne davon hatte Markus Pössel im Kommentar 18. Mai 2016 15:50 „Abstände Δ l“ als Funktion von Koordinatendefferenzen (Δ x, Δ y) angegeben, deren Cayley-Menger-Determinante für je vier Koordinatenpaare tatsächlich verschwindet.
Ob diese „(Momentan-)Abstände Δ l“ allerdings Verhältnisse von Koordinaten-unabhängigen gegenseitigen Pingdauern abbilden (sollen), oder in wie fern nicht, hat sich mir noch nicht erschlossen.
Entsprechend kann ich allein aus der Abbildung weder folgern, dass die gezeigten beteiligten Spiegel (zusammen mit geeigneten weiteren Beteiligten) durchwegs intrinsisch-chronometrisch flach sein sollten (aber periodisch wackelten), noch dass sie (zumindest periodisch veränderlich) intrinsisch-gekrümmt sein sollten.
> die Art und Weise, wie die [Signalfronten] darin wandern […]
eine dem Betrage nach konstante Geschwindigkeit, mit der nach meiner Wahrnehmung alle [Signalfronten] dort wandern
Entweder solche eventuellen Feinheiten und Unterscheidbarkeiten laufen ausdrücklich und nachvollziehbar auf Feststellungen von Koinzidenz (Reihenfolge, Identitäten der jeweiligen Beteiligten) hinaus, wie z.B. in meinem Illustrationsvorschlag angedeutet; oder sie sind als bloße Abbildungsartefakte aufzufassen und entsprechend zu ignorieren.
> wie man sich hierbei die Lichtkegel vorzustellen hat.
Als Darstellung der gedankenexperimentellen Beschreibung, dass bestimmte Signalfronten von bestimmten Beteiligten als koinzident wahrgenommen wurden, und dass die Ereignisse, die solche Wahrnehmungsanzeigen enthalten, wiederum (durch andere Beteiligte) wahrnehmbar sind. Ganz unabhängig von der Zuordnung irgendwelcher Koordinaten.
Markus Pössel schrieb (25. Juni 2016 10:11):
> Krümmung: Geodäten werden (in der Raumzeit) aufeinander zu und voneinander weg gebogen.
Dieser Zusammenhang besteht, falls geeignete Definitionen für die dabei auftretenden Begriffe („Krümmung“, „Geodäte“ und „Biegung gegenüber einander“) zugrundegelegt sind; Stichwort Cayley-Menger-Determinanten (wobei sich „Krümmung“ als auch „Biegung von Geodäten gegenüber einander“ dadurch definiert, dass die entsprechenden Cayley-Menger-Determinanten von Null verschiedene Werte haben.)
> Ganz anders als in flacher Raumzeit,
Stimmt: in diesem Fall haben die entsprechenden Cayley-Menger-Determinanten den Wert Null.
> wo Geodäten Raumzeit-Geraden sind
Geodäten verstehen sich aber in jedem Falle als (zumindest stückweise) intrinsisch gerade im Sinne von Herons Formel (die sich natürlich als einfacher Fall einer Cayley-Menger-Determinante auffassen lässt); also sowohl in flacher als auch in gekrümmter Raumzeit; jede zeitartige Geodäte insbesondere als (zumindest stückweise) intrinsisch gerade hinsichtlich Werten der sogenannten Lorentzschen Distanz zwischen je drei Ereignissen, durch die sie lief.
Es ist trotz der intrinsischen Geradheit von Geodäten möglich, dass zwei verschiedene „gegenüber einander gebogen“ sind, also dass die Cayley-Menger-Determinante z.B. für fünf Ereignisse nicht verschwindet, von denen zwei nur auf der einen Geodäte liegen, zwei weitere nur auf der anderen, und die Geodäten sich im verbleibenden Ereignis kreuzten.
@Frank Wappler / 24. Juni 2016 14:59
Apropos Signalfronten, gutes Stichwort. Markus Pössel schreibt oben im Blogtext: »Mein Beispiel war ein Kreis frei im All schwebender Teilchen; läuft eine Gravitationswelle senkrecht von hinten durch das Bild auf den Betrachter zu, ändern sich die Teilchenabstände wie in dieser Animation dargestellt: [1. Animation]«
Das heisst, die z-Richtung, in der die lineare Beispiel-GW wandert, ist hierbei orthogonal zur (x,y)-Bildebene {z = const.} zu denken, sodass die Animation den Eindruck von ebenen Signalfronten vermittelt, welche die Bildebene im rechten Winkel durchqueren. Zudem verwendet die Darstellung “proper distance”-Koordianten in der (x,y)-Ebene und soll sich auf eine insgesamt gekrümmte Raumzeit beziehen. Der metrische Tensor g*, den ich oben (24. Juni 2016 12:10) hingeschrieben hatte, genügt dieser letztgenannten Bedingung, allerdings wirkt sich die Krümmung der Raumzeit dann dahingehend aus, dass die z-Richtungsvektoren nicht mehr orthogonal zur (x,y)-Ebene stehen, denn es gilt (mit ∂x := ∂/∂x etc.):
g*(∂x,∂z) = −√2 A(u) x, g*(∂y,∂z) = −√2 B(u) y,
und diese Ausdrücke sind für die Beispiel-GW bei konstantem z mit generischen t-, x-, und y-Werten ungleich null.
Man kann eben nicht alles zugleich haben; “proper distance”-Koordinaten x und y zusammen mit der Forderung nach Orthogonalität in z-Richtung lässt sich nur in einer flachen Raumzeit erfüllen.
Chrys schrieb (29. Juni 2016 10:48):
> Signalfronten, gutes Stichwort. Markus Pössel schreibt oben im Blogtext: […]
Markus Pössel schrieb dazu (auch) im obigen Kommentar 12. Mai 2016 9:48:
Die „Schnappschüsse“ der genannten Animation (mit den 33 „identifizierbaren Beteiligten“) sind also offenbar „Flächen gleicher Phase φ“, und diese sind in einem bestimmten (aber für mich leider ziemlich obskuren) Sinn auch eben.
> die z-Richtung, in der die lineare Beispiel-GW wandert, ist hierbei orthogonal zur (x,y)-Bildebene {z = const.} zu denken, sodass die Animation den Eindruck von ebenen Signalfronten vermittelt, welche die Bildebene im rechten Winkel durchqueren.
Jedenfalls sind die einzelnen „Schnappschüsse“ in bestimmter Weise als Animation zusammengestapelt, so dass (mir) 5 der 33 Beteiligten als gegenüber einander starr auffallen.
In einer gekrümmten Region mit „Winkeln“ argumentieren zu wollen, werden wir uns aber hoffentlich sparen können; und Koordinaten eigentlich sowieso.
Es wäre aber jedenfalls interessant, Entfernungswerte „Δ l“ (bzw. zumindest deren Verhältnisse) zwischen (i.A.) verschiedenen Beteiligten mit Anzeigen von (i.A.) ungleicher „Phase φ“ zu erfahren
(meinetwegen auch in Bezug auf Koordinaten, wie ich hier schon 10. Juni 2016 15:28 angefragt hatte).
Frank Wappler / 30. Juni 2016 11:15
Vorab wieder ein Erratum: Ich hatte bei meinen Pseudo-Skalarprodukten einen Faktor 1/2 verschludert, besser ist g*(∂x,∂z) = −(A(u) x)/√2 sowie g*(∂y,∂z) = −(B(u) y)/√2.
Wenn physikalisch tönende Aussagen über Richtung, Geschw., Transversalität, oder Polarisation linearer GWs gemacht werden, so ist zu bedenken, dass sich dies nur in Hinblick auf die TT Eichung überhaupt mit einem Sinn verbinden lässt. Und adäquat dargestellt werden diese Sachverhalte dann im TT Frame, wo im übrigen, bezogen auf die Beispiel-GW, die (t,z)-Koordinaten “proper” sind. Für Animationen gibt der TT Frame allerdings nicht viel her, denn die gedachten Testmassen werden nicht von der GW geschubst, sodass man leider auf diese Weise von der Welle nichts sieht. Daher meint Markus Pössel womöglich, proper-(x,y) sei besser als proper-(t,z), denn damit kommt etwas Schwung in die Sache. Mit einer entsprechenden Transformation wird jedoch ganz beiläufig auch die TT Eichung zerschossen; die transformierte Metrik hatte ich ja praktisch in der Form g* = η + h* hingeschrieben, wobei dann das h* recht offensichtlich nicht TT ist.
Bei den Animationen werden nun Aussagen über ebene, senkrecht zur Ausbreitungsrichtung stehende Wellenfronten, die sich ausschliesslich auf die TT Eichung beziehen lassen, kombiniert mit Visualisierungen, die in gewissem Sinne das genaue Gegenteil der TT Eichung darstellen, oder zumindest darstellen sollen. Das kann so nicht gut funktionieren, und wie sich zeigt, wenn man es rechnet, funktioniert es auch nicht.
Das stimmt doch wieder hinten und vorne nicht.
Setzt man in der Metrik, die Maggiore als (1.87) hinschreibt, den hier behandelten Spezialfall ein und vernachlässigt wie üblich alles ab Ordnung h^2, dann ist der gesamte Raumanteil (alles ohne dt darin) flach. Damit ist die z-Ebene nach wie vor orthogonal zur x- und zur y-Ebene. Wo bekommen Sie da zusätzliche metrische Koeffizienten, die nicht mit h^2 oder höher gehen?
Deswegen bleibt die “Action” ebenfalls in der x-y-Ebene. Und proper distances haben nunmal den Vorteil, einigermaßen physikalisch sein (konventionsabhängigkeit nur über den Gleichzeitigkeitsbegriff, aber der ist im angenähert klassisch-flachen Bild ja recht alltagsnah).
Und ja, die Visualisierung zeigt zwar nicht die Koordinatenabstände der TT-Eichung (da steckt ja in der Tat keine aufregende Information drin), aber sie zeigt die in der TT-Eichung enthaltenen proper distance-Änderungen, beurteilt von einem zentralen Testteilchen aus. Also genau das, was man wissen möchte, wenn man anschließend darangehen will, Licht zur Abstandsmessung zwischen den beteiligten Testteilchen hin- und herzuschicken.
Dass die Visualisierung “in gewissem Sinne das genaue Gegenteil der TT Eichung darstellen” ist daher genau am physikalischen Verständnis vorbei argumentiert. Denn genau das, was auch in der TT-Eichung mit das Interessanteste an der Gravitationswellenwirkung ist, stellt die Visualisierung schließlich dar.
Und ja, selbstverständlich ist proper (x,y) ungleich aussagekräftiger als proper (t,z). Ganz elementar physikalisch einsehbar: Bei einer transversalen Welle ist die Wirkung nunmal transversal zur Ausbreitungssrichtung (bzw. im Raumzeitbild: transversal zu räumlicher Ausbreitungsrichtung und Zeitrichtung). Was passiert welche Abstandsänderung der Wellendurchgang bewirkt, sieht man daher in der Tat in der x,y-Ebene.
@Markus Pössel / 30. Juni 2016 19:35
Die seit geraumer Zeit hier in Rede stehende Koord.transformation hatte ich doch inzwischen (24. Juni 2016 12:10) immerhin soweit dargelegt zu haben gehofft, dass für einen Physiker grundsätzlich nachvollziehbar sein sollte, wie ich zu dem Schluss gelange, dass die z-Richtungsvektoren bezüglich der transformierten Metrik g* nicht mehr orthogonal zu den (x,y)-Ebenen stehen. Damit widerspreche ich Ihnen offenbar in einem wesentlichen Punkt, denn das hat schliesslich Konsequenzen für die Interpretation dessen, was in den Bildern überhaupt erkennbar ist.
Mindestens einer von uns muss etwas falsch transformiert haben, und es wäre schön, wenn sich dies aufklären liesse. Meine Vorgaben habe ich gebracht, und wenn Sie meinen, dass es nicht stimmt, müssten Sie mir das allerdings mit einer konkreten Bezugnahme darauf begründen, sonst wird das nichts. Da ich in meinen Kalkulationen keinen essentiellen Fehler finde, muss ich einstweilen weiter davon ausgehen, dass die fragliche Animation, wenn sie, wie im begleitenden Text erläutert, zusammen mit einer senkrecht zur Bildebene vorgestellten Ausbreitung der Welle gedacht wird, sich nur auf ein total flaches Ambiente beziehen kann. Mit anderen Worten, Sie sind mit Ihrer Darstellung bei Maggiore schon längst da, wo der schreibt:
Die GW ist dann als ein Gravitationsfeld und die Beschleunigung der Testmassen infolge einer hierdurch bedingten Kraft zu denken. Die dabei hintergründig angestrebte Analogie zu einer Beschleunigung von Testladungen in einem EM-Feld wird allerdings dadurch schief, dass diese GW-Kraft nur eine recht spukhafte “Gezeitenkraft” ist, mit der sich gar keine lokale Wechselwirkung verbinden lässt — was zu den weiteren, mir in der Tat schier unbegreiflichen Rätseln der GW-Theorie gehört.
Dann schauen wir doch noch einmal kleinschrittig, wo wir da auseinandergehen.
Sind wir uns zumindest noch einig, dass die (oder zumindest: eine) koordinatentransformierte Metrik, die man bekommt, wenn man ein frei fallendes System rund um den Nullpunkt wählt und x- und y-Koordinaten abstandsecht (im Sinne von “proper distance”) wählt, diejenige ist, die Maggiore in (1.87) hinschreibt?
@Markus Pössel / 2. Juli 2016 13:47
Maggiore beschreibt den Proper Detector Frame gleichsam aus der Sicht eines Experimenters, indem er zunächst ein Laborsystem konstruiert, wo sämtliche Abstände mit rigid rulers gemessen werden sollen, und in welchem das Erscheinen einer GW daran festzustellen wäre, dass frei bewegliche Gegenstände im Labor hin- und herbewegt würden. Mit dieser Sicht wird aber bereits ausgeschlossen, dass diese GW Einfluss auf die flache “rigid ruler”-Geometrie des Laborsystems hat — diese liefert dabei gerade den statischen Rahmen zur Darstellung der mit einer GW assoziierten Bewegung von Objekten.
Zudem soll das Laborsystem als frei fallend in einem schwach nichtlinearen Schwerefeld gedacht werden können, etwa dem Erdschwerefeld. Auch ganz ohne Welle nötigt dessen Nichtlinearität Maggiore dazu, die Konstruktion seines Laborsystems vermittels einer lokalen Linearisierung bei einem Punkt der Raumzeit vorzunehmen, sodass dann, hinreichend nahe bei diesem Punkt, die nichtlinearen Effekte für die Geometrie des Laborsystems als vernachlässigbar gelten können. Und die Gl. (1.87) repräsentiert die Geometrie eines so konstruierten Laborsystems.
Die Konstruktion eines Detektor-Labors erfolgt naturgemäss gänzlich ohne Einbezug allfälliger Wellen, die da anschliessend hindurchlaufen und detektiert werden sollen. In (1.87) stecken also überhaupt keine Beiträge von einer GW. In der Anwendung auf das Beispiel wäre das Laborsystem schlicht ein Inertialsystem im Minkowskischen Raum, mit der wie üblich durch η bezeichneten Geometrie. Und ganz egal ob mit oder ohne Welle, gemessen wird im Labor in jedem Fall mit den als starr betrachteten rulers des η-Laborsystems.
Sie schreiben, in (1.87) “stecken also überhaupt keine Beiträge von einer GW” und in Anwendung auf unseren Fall käme schlicht ein Minkowski-Raum heraus.
Aber in (1.87) ist ja im Gegenteil mit Bedacht so entwickelt worden, dass auch Terme zweiter Ordnung mitgenommen werden. Auch diese Terme enthalten Informationen.
Insbesondere haben wir als Teil von g_00 den Term R_0i0j, von dem Maggiore in (1.94) zeigt, dass er für unseren Fall gerade proportional ist zur zweiten Zeitableitung von h(t).
Sprich: Angewendet auf unseren Fall kommt da keineswegs ein Minkowski-Raum heraus, sondern in genau diesem Term (und dem einzigen gemischten Term, bei dt dz) stecken die Beiträge von der Gravitationswelle.
(Schreibt Maggiore ja auch in einem Kommentar unterhalb von (1.88): “the terms proportional to the Riemann tensor contain both the effect of slowly varying gravitational backgrounds and the effect of GWs.”)
@Markus Pössel / 4. Juli 2016 15:18
Die Krümmungskomponenten in (1.87) und (1.94) stehen ja nicht für dasselbe. Der Ausdruck in (1.87) ist zunächst völlig unspezifisch hinsichtlich des Vorhandenseins einer GW, und evaluiert wird der Krümmungstensor am Punkt der Linearisierung. Formal ist daraus nicht ersichtlich, ob eine Welle da ist oder vielleicht nur das Erdschwerefeld. Meine Formulierung, “enthält überhaupt keine Beiträge von einer GW”, ist allerdings unglücklich, eine zufällig vorhandene GW würde insgesamt natürlich schon zur Krümmung an diesem Punkt beitragen.
Die Krümmungskomponenten in (1.94) sind hingegen die einer linearen GW, und für eine in pos. z-Richtung laufende Welle wären das dann Funktionen von u = (ct − z)/√2. Wenn man aber, wie im Beispiel, eine solche GW schon vorausgesetzt und das Erdschwerefeld o.ä. ohnehin weggelassen hat, kann man sich den ganzen Zirkus mit (1.87) sowie dem Riemann Tensor ersparen und den Blick auf das Wesentliche richten.
Die Formel für die Beschleunigung (1.95) lässt sich dann auch direkt aus der gegebenen GW-Metrik herleiten, sofern man “rigid rulers” für x und y einführt. Die transformierte Metrik g* = η* + h* hat rigid rulers für x und y, nicht aber für ct und z, während η* rigid rulers für alle Koordinaten hat (Proper Detector Frame). Der * bei η* soll einfach zusätzlich darauf hinweisen, dass hier dieselben transformierten Koordinaten verwendet werden wie bei g*, im Unterschied zu g = η + h beim TT Frame. Die Beziehung (1.95) gilt sowohl für g* wie auch für η*, in den (x,y)-Ebenen induzieren beide schliesslich dieselbe Geometrie. Die Interpretation ist in beiden Fällen jedoch eine andere; im Proper Detector Frame lässt sich das beispielsweise ja nicht mehr durch Geometrie begründen.
Die transformierte Metrik g* ist keineswegs besser geeignet für irgendwelche physikal. Deutungen als der TT Frame, ganz im Gegenteil. Etwa die Konstatierung, die GW bewege sich mit Lichtgeschw. c in pos. z-Richtung wäre geometrisch so auszudrücken, dass der Tangentialvektor ∂u = (∂t/c − ∂z)/√2 stets lichtartig ist. Das trifft dann sowohl im TT Frame wie im Proper Detector Frame auch zu, nicht aber in g*. Hier macht sich die Krümmung nun bei t und longitudinal in z-Richtung bemerkbar, und gerade letzteres ist gewiss nicht das, was man bei einer als transversal behaupteten Welle sehen will.
Chrys schrieb (5. Juli 2016 22:44):
> […] sofern man “rigid rulers” für x und y einführt.
Lässt sich in einer Region “mit GW” überhaupt eine geeignet große Anzahl von Beteiligten finden, die (alle, paarweise) gegenüber einander “rigid” wären, also insbesondere chronometrisch starr, d.h. mit (hinsichtlich jedes einzelnen solchen Beteiligten, gegenüber jeweils einem bestimmten andern) konstanter Pingdauer
?
@Frank Wappler / 6. Juli 2016 8:50
Grob gesagt sind die “rigid rulers” für x und y die gedachten “Meterstäbe zur Messung von proper distance” in einer Ebene, die senkrecht zur (konsequenterweise dann durch z bezeichneten) Ausbreitungsrichtung einer ebenen GW zu denken ist.
Aus relativistischer Sicht und mit physikal. Anspruch betrachtet wäre diese GW jedenfalls etwas, das eine Raumzeit krümmt, indem nämlich die (x,y)-Ebenen intrinsisch quadrupolar deformiert werden, und zwar inclusive jeglicher rulers, die man in x- oder y-Ausrichtung irgendwo plaziert hat. Starre x- oder y-rulers kann es da physikalisch gar nicht geben. Wo argumentiert wird, das Vorhandensein einer GW sei durch eine mit starren x- oder y-Meterstäben messbare Abstandsänderung zwischen was auch immer feststellbar, wurde der begrifflichen Kontext der GR (nicht aber jener der SR) nach meinem Verständnis bereits verlassen.
Herr Pössel,
die Frage nach der Eichkurve hat sich erledigt, denn Professor Danzmann hat zugegeben, dass es diese Kurve nicht gibt. Zwar sollte sie gemäß diesem Satz in der Phys. Rev. Veröffentlichung PRL 116, 061102 (2016): “The detector output is calibrated in strain by measuring its response to test mass motion induced by photon pressure from a modulated calibration laser beam [63].” zu erstellen sein, doch die Intensitäten reichen bei Verschiebungen der Größenordnung 10^(-18) m nicht aus, um direkt gemessen zu werden. Damit ist es auch nicht möglich, ein zufällig hereingeschneites Gravitationswellensignal der gleichen Größe direkt zu messen, schon gar nicht mit einem s/n Verhältnis von 24. Das veröffentlichte Signal muss auf anderem Weg in das System geraten sein.
Frau Lopez dokumentiert die Korrespondenz mit dem Einstein-Institut fortlaufend unter dem link: http://www.kritik-relativitaetstheorie.de/Anhaenge/Anfrage%20LIGO-Experiment.pdf, wo weitere Einzelheiten nachgelesen werden können.
Wie gesagt: Sie setzen zwei Dinge gleich, die nicht gleich sind.
Die Eichkurve für die Kalibration der elektrostatischen Aktuatoren per Strahlungsdruck wird in dem betreffenden Artikel sehr wohl gezeigt; siehe meine ausführliche Schilderung in meiner Antwort an Sie vom 29. Mai. Damit ist dieser Teil der Schlusskette für den Nachweis durch die durchgeführten Messungen gut abgesichert.
Was Sie Eichkurve nennen, wenn Sie davon reden, ein künstliches Signal mit einer “ähnliche[n] Wellenform und Amplitude wie GW150914 […] [zu] erzeug[en] und gleichzeitig interferometrisch [zu m]essen” ist etwas anderes. Das hat man als Konsistenzcheck auch gemacht, nur eben nicht über den Strahlungsdruck, sondern über die elektrostatischen Aktuatoren. Die älteren Daten dazu (soweit ich weiß bis einschließlich Science Run S6) sind auch sämtlich veröffentlicht. Die Dokumentation ist für LIGO deutlich besser als für so gut wie alle Experimente, die ich kenne: Sie können mit den Informationen im LIGO Open Science Center selbst nachrechnen, was da passiert. Hier wird Schritt für Schritt beschrieben, wie man ein solches Injektions-Signal aus den Daten wieder herausfiltert. Das Beispiel ist genau die Inspiral-Wellenform, um die es bei GW150914 geht.
Insofern ist alles wichtige da: Die Kalibrationskurven für die elektrostatischen Aktuatoren mithilfe von Strahlungsdruck ist da, und die Daten zu den künstlich erzeugten und dann interferometrisch ausgelesenen Signalen sind da.
Was es in der Tat meines Wissens nach nicht gibt, ist eine direkte hardware injection mithilfe des Lasers, der für die Strahlungsdruck-Kalibration genutzt wird. Aber ob die künstliche Erzeugung der Signale elektrostatisch oder mit Strahlungsdruck erfolgt, sollte für die Art von Kontrolle Input-Output, die Sie sehen wollen, keinen grundlegenden Unterschied machen.
Dr. Engelhardt,
Sie beherrschen die Kunst der Zitatverschwurbelung perfekt und
spielen Aussagen gegeneinander aus – das ist Ihre Diffamierungsstrategie,
nur Ihr schwächelnder Wissensstand ist seidt 50 Jahren iwie eingefroren.
Die Fehlalarmquote ist 1:200.000 – nix Zufall: 2 Detektoren haben gleiche Signale.
Akzeptieren Sie keine unabhängigen Meßergebnisse? Der Nachweis ist wasserdicht!
Es ist ja nicht so, dass ich die Frustration nicht nachvollziehen könnte, aber: Könnten Sie sich bitte bei Ihren Antworten an Herrn Engelhardt auch auf das sachliche Beschränken und sich anwertende Formulierungen (schwächelnd etc.) verkneifen? Danke!
Herr Pössel,
Wenn ich mich kurz als Physiklaiin naiv einmischen darf:
Nach meinem bescheidenen Verständnis dieser hochfachlichen Disput fehlt der Nachweis, dass die LIGO-Detektoren in der Lage gewesen sind, die reale Verschiebung eines 40 kg-schweren Spiegels um 10^(-18) m durch Ausübung einer realen physikalischen Kraft zu registrieren. Wobei es in der Tat völlig irrelevant ist, das sehe ich ein, was diese reale physikalische Kraft überhaupt war: Strahlungsdruck, elektrostatisch oder sonst etwas – meinetwegen könnte man auch theoretisch dem Spiegel einen Fußtritt verpassen, um ihn zu verschieben, ist doch egal, Kraft ist Kraft, oder? 😉
So wie ich es jedoch bis jetzt verstanden habe, steht nirgendwo in der Veröffentlichung, dass die LIGO-Detektoren eine reale Verschiebung des 40 kg-Spiegels um diese winzige Größenordnung registriert haben bzw. überhaupt registrieren können, weder durch Strahlungsdruck noch elektrostatisch.
So wie ich es bis jetzt verstanden habe, wurde einzig durch künstliche „Fake-Signale“ (Injektions-Signale) diese Präzision am Computer eingespeist und ausgelesen, also durch keine reale Messung, sondern durch eine Computer-Simulation.
Viele Grüße
Jocelyne Lopez
Das ist falsch – die Hardware-Injektionen (siehe meine letzten Antworten an Herrn Engelhardt hier, hier, hier) verschieben die LIGO-Spiegel mithilfe elektrostatischer Abstoßung, und dann wird geschaut, was sich von diesem Prüfsignal am Interferometerausgang nachweisen lässt.
Wir sind uns offenbar einig (huch!), dass es egal ist, ob die Verschiebung elektrostatisch oder über Strahlungsdruck erfolgt. Daher eben meine Verwunderung, dass Herr Engelhardt auf Strahlungsdruck besteht und auf meine wiederholten Aussagen zu realen, künstlich erzeugten Spiegelverschiebungen auf elektrostatischem Wege bislang gar nicht eingegangen ist.
Die künstlichen Signale, die man da zu Testzwecken eingespeist hat, sind zum Teil ähnlich groß wie das Gravitationswellensignal GW150914, zum Teil sogar noch kleiner. Solche direkten Demonstrationen, dass LIGO derart winzige Spiegelverschiebungen nachweisen kann, gibt es eine ganze Reihe, und für die früheren Detektorläufe (Science Run 5 und 6) sind die alle im LIGO Open Science Center dokumentiert (siehe meine letzte Antwort an Herrn Engelhardt hier). Was das zur-Verfügung-stellen von Daten und Informationen angeht, ist die LIGO-Collaboration wirklich vorbildlich.
In den Artikeln, mit denen die LIGO-Betreiber ihren Detektor für die Fachwelt dokumentiert haben, werden diese Hardware-Injektionen auch erwähnt – und beim Inbetriebnehmen des Detektors hat man damit demonstriert, dass man in der Tat versteht, was in den LIGO-Detektoren vorgeht und wie man ihre Daten analysiert. Googeln oder ADS-Suche nach “LIGO [hardware] injections” fördert da rasch entsprechende Artikel zutage: z.B. hier, hier, hier.
Lopez schrieb: “So wie ich es bis jetzt verstanden habe, …” – sehen sie, da ist das Problem, sie haben es eben nicht verstanden, gar nicht. Aber Sie und Engelhardt wollen ja auch gar nicht wirklich was verstehen, sie werden nun mit einer falschen aus dem Zusammenhang gerissenen Aussage spazieren gehen und behaupten, da hätte wer zugegeben, dass eine echte Messung so gar nicht möglich war, und alles andere wie üblich unterschlagen.
Es ist verständlich, dass ihnen beiden normal kaum noch wer antwortet.
Wie gesagt, ich verstehe die Frustration, aber solange Herr Engelhardt und Frau Lopez hier Fragen/Aussagen zur Sache vorbringen, sich abfällige Bemerkungen verkneifen und sich die Diskussion dabei nicht im Kreise dreht, werde ich auch sachliche Antworten geben und die beiden nicht sperren.
Bitte tragen Sie Ihren Teil dazu bei, dass die Diskussion hier sachlich bleibt – ein Kommentar wie der obige trägt dazu nicht bei, im Gegenteil.
Herr Pössel,
ich empfinde Ihre Moderation des fachlich unqualifizierten Teilnehmers Manuel Krüger alias “Herr Senf” als äußerst lasch, der nichts fachlich zu diesem komplexen Thema beitragen kann und sich wiederholt nicht nur unsachlich, sondern unzumutbar mit ad hominem Schmähungen als notorischer “cranks-Jäger” über Dr. Engelhardt und mich einlässt.
Dass Sie dabei seine “Frustration” (?) verstehen, finde ich wiederum befremdlich, sowie auch Ihre Überlegungen “die beiden zu sperren”. Herr Pössel, “die beiden” haben sich zu keinem Zeitpunkt zu keinen ad hominem Äußerungen eingelassen, und zwar zu keinem einzigen Beteiligten dieser Diskussion, so daß Ihre wiederholte, unterschwellige Drohung jemanden zu sperren in die völlig falsche Richtung ausgeht, mit Verlaub. Das finde ich unzumutbar und nicht gerade dazu geeignet, eine wissenschaftliche Disput zu ermöglichen.
mfg
Jocelyne Lopez
Keine Metadiskussion bitte. Zur Sache hatte ich Ihnen ja oben schon geantwortet.
Ich gehe jetzt wieder dazu über, Kommentare, die nichts zur Sachdiskussion beitragen, zu löschen.
Herr Pössel,
ich beziehe mich auf Ihren Kommentar vom 2.6., 12:05, wo Sie genau wie Herr Danzmann bestätigen, dass es die Eichkurve “interferometrische Messung der Auslenkung, die durch Strahlungsdruck auf die Spiegel erfolgt” entgegen der Ankündigung in PRL 116, 061102 (2016) nicht existiert. Der Satz “The detector output is calibrated in strain by measuring its response to test mass motion induced by photon pressure from a modulated calibration laser beam [63].” ist also schlicht nicht wahr und stellt eine Täuschung der wissenschaftlichen Öffentlichkeit dar, zumal in der unveröffentlichten Referenz 63 zwar eine einschlägige Formel (10) geboten wird, diese aber nicht mit Messdaten unterlegt ist.
Von elektrostatischen Aktuatoren ist in PRL 116, 061102 (2016) nicht die Rede, sie können also bei der Frage, ob in dieser Veröffentlichung der Nachweis für die Existenz von Gravitationswellen erbracht wurde oder nicht, gänzlich außer Betracht bleiben. Die Wirkung elektrostatischer Aktuatoren kann nicht verlässlich berechnet werden, sondern muss selbst über den Strahlungsdruck von Hilfslasern geeicht werden, was Sie auch so beschreiben. Es bleibt deshalb dabei, dass eine verlässliche Eichung des Interferometer-outputs nur über den exakt berechenbaren Strahlungsdruck und das direkt ausgelesene Interferometersignal erfolgen kann.
Warum hat man diese Eichung nicht vorgenommen, obwohl sie angekündigt war und methodisch auf der Hand liegt? Darüber kann man nur Vermutungen anstellen, doch geben meine Fragen zur grundsätzlichen Machbarkeit, die noch nicht beantwortet wurden, einige Hinweise. Im Interferometer müssen 100 kW Lichtleistung zirkulieren, damit man Auslenkungen der Größenordnung 10^(-18) m überhaupt messen kann. Damit ist der stationäre Lichtdruck auf die Spiegel um 12 Größenordnungen größer, als die mit ca. 150 Hz oszillierende Lichtleistung, die man zur Simulation der Verschiebung, welche eine GW bewirken würde, benötigt. Es ist zweifelhaft, ob man eine Stabilität der Laserleistung mit einer Genauigkeit von 10^(-12) erreichen kann, jedenfalls wird dies weder erwähnt noch belegt. Wenn die Laserleistung nur äußerst geringfügig schwankt, werden sich die Spiegel bewegen und eine Auslesung des gewünschten Signals unmöglich machen.
Weiterhin wurde nicht belegt, dass die Amplituden der interferierenden Strahlen exakt (bis auf 10^(-12)) gleich waren, um ein ideales Dunkelfeld, d.h. perfekte Auslöschung zu ermöglichen. Und ob das Falschlicht um 24 Größenordnungen unterdrückt werden konnte, wissen wir auch nicht. Die Einhaltung der letzteren Bedingung wäre für eine stationäre Messung erforderlich, was auch Herr Danzmann für aussichtslos hält. Darum betont er, dass ja nur Änderungen im Signal gemessen werden mussten. Diese treten jedoch auch bei Schwankungen der Laserleistung im untersuchten Frequenzbereich auf.
Wegen praktischer Nichterfüllung der genannten grundsätzlichen Voraussetzungen war es wohl nicht möglich, die angekündigten Eichmessungen durchzuführen, so dass man mit einem ungeeichten Apparat arbeiten musste. Alle Aussagen über angebliche Gravitationswellen-Messungen hängen damit unbelegt in der Luft, denn die tatsächlichen Messungen mussten ja in der gleichen Weise wie die Eichmessungen direkt vorgenommen werden, doch dies erwies sich offenbar als unmöglich.
Im Übrigen möchte ich darauf hinweisen, dass der Titel der offiziellen, belastbaren Veröffentlichung “Observation of Gravitational Waves from a Binary Black Hole Merger“ lautet. Es ist daher nur zu prüfen, ob diese Beobachtung stattgefunden hat, oder nicht. Mit einem System, von dem ein unmittelbar Beteiligter sagt, dass es die versprochene Eichung nicht gibt, war diese „Observation“ sicher nicht möglich.
Dr. Engelhardt,
hilft Ihnen die Amplitudenstabilität des 180-W-Lasers mit 1 : 10^9
bei den Betrachtungen auf’s erste weiter?
Herr Engelhardt,
Sie unterscheiden nach wie vor nicht richtig zwischen mehreren durchaus verschiedenen Eichkurven, über die wir hier diskutieren: Kalibration der elektrostatischen Aktuatoren mittels Strahlungsdruckvariationen (Kalibrationslaser) einerseits, Simulation von Gravitationswellen durch aktive Spiegelverschiebung (Hardware-Injektion) andererseits.
Selbstverständlich ist der Satz “The detector output is calibrated in strain by measuring its response to test mass motion induced by photon pressure from a modulated calibration laser beam [63]” zutreffend:
Der Detektoroutput (estimated strain) ergibt sich als Kombination des Outputs der Photodiode und des Signals, das den zur Längenkorrektur mitlaufenden elektrostatischen Aktuators ansteuert (arXiv:1602.03845v1 Gleichung 2). Kalibrieren heißt zu modellieren, wie der auf diese Weise ausgelesene Strain mit Längenänderungen der Interferometerarme bekannter Größe zusammenhängt. Das macht man, wie ich schon in dieser Antwort an Sie beschrieben hatte, indem man den Strahlungsdruck-Kalibrationslaser und entsprechende elektrostatische Aktuatoren gleichzeitig leicht frequenzversetzt laufen lässt. Dabei überlagern sich das in-Bewegung-setzen der Testmasse durch den Strahlungsdruck-Kalibrator (test mass motion induced by photon pressure) und die dem üblichen Feedback-Loop entsprechende (aber eben leicht frequenzversetzte) Reaktion des elektrostatischen Aktuators auf die Änderungen (response to test mass motion).
An den Ergebnissen (Abbildungen 5,6,7 in arXiv:1602.03845v1) kann man ablesen, dass sich das System bei den künstlich eingespeisten Bewegungen (hervorgerufen durch den Strahlungsdruck-Kalibrationslaser) genau wie vorhergesehen verhält. Das ist ein überzeugendes Argument dafür, dass sich mit dem über solche Messungen abgeleiteten Modell für die Abschätzung des Strains aus Aktuator-Kontrollsignal und Restlicht am Photonendetektor auch die differentiellen Längenänderungen, die eine Gravitationswelle hervorruft, richtig messen lassen. Eine Kalibration eben, und zwar genau wie in PRL 116, 061102 (2016) angekündigt.
Was nicht Teil dieser Kalibration ist (und darauf bezieht sich meine und Herrn Danzmanns Aussage), war eine “ähnliche Wellenform und Amplitude wie GW150914 […] [zu] erzeug[en] und gleichzeitig interferometrisch [zu m]essen”. Zum einen, weil der Detektor eben nicht so funktioniert (es wird, im Gegensatz zum vereinfachten Modell oben in meinem Blogtext, nicht nur interferometrisch gemessen, sondern im Gegenteil steckt wohl die meiste Information im Aktuator-Kontrollsignal), zum anderen, weil man eine im Frequenzraum definierte Funktion wie jene, die die Detektorreaktion auf Spiegelverschiebungen modelliert (also gerade jene Funktion, die kalibriert werden soll) am besten messen kann, wenn man tatsächlich die Frequenzabhängigkeit durchmisst – anstatt die im Nachhinein aus einem komplizierteren Signal zu rekonstruieren.
Hardware-Injektionen, also die direkte Einspeisung von Spiegelbewegungen, wie sie durch Gravitationswellen zu erwarten gibt, hat es, wie erwähnt, auch gegeben, und zwar tausende davon – Standardverfahren ist, dass man dafür direkt die elektrostatischen Aktuatoren benutzt. Die hat man zum einen genutzt, um realistische Vorlagen für die Erprobung der Datenanalyse zu liefern, zum anderen um auf diese (in der Tat naheliegende) Weise zu überprüfen, ob man das Detektorverhalten richtig versteht und richtig modelliert hat. Den Hinweis auf das Datenarchiv, das viele dieser Testsignale enthält, hatte ich Ihnen ja bereits hier gegeben; Verweise auf Artikel, in denen solche Tests beschrieben werden, in dieser Antwort an Frau Lopez.
Zusammengefasst haben wir, soweit ich sehen kann, mindestens drei Eichkurven in der Diskussion:
(A) Eine Eichkurve, wo man nur mit dem Laser per Strahlungsdruck ein Signal simuliert und rein interferometrisch ausliest.
(B) Die Eichkurve(n) mit denen geprüft/gezeigt wurde, dass der Detektor auf differenzielle Längenänderungen so reagiert wie beim Nachweis von Gravitationswellen angenommen; die differenziellen Längenänderungen wurden für diese Kalibration per Kalibrations-Laser über Strahlungsdruck herbeigeführt, also in einer Situation, in der aus einfachen und grundlegenden physikalischen Gesetzen folgt, welche differenzielle Längenänderung man da gerade erzeugt.
(C) Eichkurven bzw. besser Testkurven die zeigen, wie künstlich eingespeiste, realistisch der Wirkung von Gravitationswellen nachgebildete
Herr Engelhardt,
Ihre Kritik beruht nach wie vor auf einem Missverständnis. Man kann in Bezug auf ein Experiment wie LIGO viele mögliche und tatsächliche Eichkurven definieren, aber Sie reden von einer anderen Eichkurve als die LIGO-Autoren – und zwar von einer Eichkurve, die nicht der Art und Weise entspricht, wie Gravitationswellensignale in Advanced LIGO wirklich nachgewiesen werden.
Im PRL-Artikel angekündigt und in [63] samt Daten veröffentlicht sind die Eichkurve(n) mit denen geprüft/gezeigt wurde, dass die LIGO-Detektoren auf differenzielle Längenänderungen so reagieren wie beim Nachweis von Gravitationswellen angenommen; die differenziellen Längenänderungen wurden für diese Kalibration per Kalibrations-Laser über Strahlungsdruck herbeigeführt, also in einer Situation, in der aus einfachen und grundlegenden physikalischen Gesetzen folgt, welche differenzielle Längenänderung man da gerade erzeugt (genaue Beschreibung: mein Kommentar hier). Kalibration bezieht sich auf den Vergleich des ausgelesenen Signals (Interferometerausgang plus Kontrollsignal für die elektrostatischen Aktuatoren!) mit dem, was der Strahlungsdruck-Kalibrationslaser liefert.
Sie fordern stattdessen eine Eichkurve, bei welcher das Interferometersignal direkt ausgelesen wird (ich verstehe das als: direkt nachgeschaut wird, was am Photodetektor am Ausgang ankommt). Aber so funktioniert Advanced LIGO nicht. Der Strain muss dort immer als Kombination des Kontrollsignals für den elektrostatischen Aktuator, der im Feedback-Loop die Längendifferenz ausgleicht, und des Restsignals am Photodetektor rekonstruiert werden. Der Feedback-Loop ist ja gerade so konstruiert, dass im Idealfall sogar alle Strain-Daten im Kontrollsignal enthalten wären! Sprich: Die alternative “Eichkurve”, die Sie fordern, enthält im Idealfall Null Information über Gravitationswellen!
Und noch einmal die Bitte: Solange wir die Sache mit der Kalibrationskurve nicht geklärt haben bitte keine weiteren Themen anschneiden. Sie werfen in Ihrem letzten Kommentar gleich wieder eine Reihe weiterer Fragen auf; ich hatte schon damals darum gebeten und bitte wieder darum: Lassen Sie uns eine Frage nach der anderen diskutieren. Das ist, wie die Diskussion um die Kalibration zeigt, kompliziert genug.
@ Herr Pössel:
Prof. Danzmann beschreibt zwei voneinander unabhängigen Methoden zur Eichung der Meßanlage beim LIGO-Experiment, die „auf wenige Prozent genau funktionieren“, siehe seine E-Mail vom 31.05.16 – Dokument 13 in der Zusammenstellung der Korrespondenz:: http://www.kritik-relativitaetstheorie.de/Anhaenge/Anfrage%20LIGO-Experiment.pdf
“Das Schöne ist, dass die Eichung tatsächlich am Ende auf wenige Prozent genau funktioniert, und zwar mit zwei voneinander unabhängigen Methoden: Einmal durch Strahlungsdruckvariation, aber auch durch Anlegen einer variablen Spannung an die elektrostatischen Aktuatoren zur Spiegelbewegung.“
Die Eichungsmethode durch kontrollierten Strahlungsdruck auf den 40 kg-Spiegel wird auch in der LIGO-Publikation erwähnt und beschrieben, so daß man verbindlich voraussetzen darf, dass dieses Testverfahren auch tatsächlich durchgeführt wurde. Leider sind keine Meßdaten in der Publikation hinterlegt. Man kann schwerlich prüfen, ob die zwei Eichungsverfahren „am Ende auf wenige Prozent funktionieren“, wenn die Daten von einem der zwei Verfahren nicht zur Verfügung stehen. Vielleicht ist es ein Versehen bei der Vorbereitung der Publikation? Man kann es aber nachträglich korrigieren: Es ist bestimmt möglich, die Experimentatoren in den USA darauf aufmerksam zu machen, dass bei der Publikation leider keine Daten für die Durchführung dieses Eichungsverfahren mitveröffentlicht wurden, und dass sie bitte die Publikation noch entsprechend ergänzen möchten. So eine nachträgliche Ergänzung einer Publikation ist wohl im wissenschaftlichen Betrieb möglich, oder?
Frau Lopez,
was meinen Sie mit “die LIGO-Publikation”, singular? Zu Advanced LIGO allgemein sind zahlreiche Publikationen erschienen, und allein zu den verschiedenen Aspekten des ersten Gravitationswellennachweises gibt es neben dem PRL-Kurzbericht ein Dutzend Begleitartikel, in denen die verschiedenen relevanten Aspekte des Nachweises, von den Rauscheigenschaften während der Messung bis zu den astrophysikalischen Konsequenzen, sorgsam dokumentiert sind.
Zu den Begleitartikeln zählt auch das hier von Herrn Engelhardt und mir mehrfach zitierte Kalibrationspapier arXiv:1602.03845v1. Dort finden Sie die Daten der Vergleiche der drei verschiedenen Eichverfahren im Anhang A; die Datenpunkte für den Vergleich der insgesamt mehr als 60 für den Vergleich durchgeführten Kalibrationen zeigen Abbildungen 9 und 10.
Dass die Daten für diesen Vergleich, bzw. für eines der Verfahren nicht zur Verfügung stünden, ist demnach schlicht nicht wahr.
Und jetzt bin ich ehrlich gespannt, ob von Ihnen bei so eindeutiger Beweislage dann doch einmal so etwas wie “Oh, da habe ich mich dann wohl geirrt”, oder “OK, dann nehme ich meinen Einwand zurück” kommt, oder ob Sie diesen Umstand komplett ignorieren und kommentarlos zum nächsten Einwand übergehen.
P.S.: Bitte bleiben Sie, und das gilt für die anderen natürlich genauso, direkt bei dem Fachthema, das wir hier diskutieren. Schnell mal 12 weitere Fragen und Behauptungen in die Runde zu werfen ist einer direkten Diskussion hier so abträglich, dass ich Ihren entsprechenden Kommentar gelöscht habe.
@ Herr Pössel,
wie es in dieser Diskussion und auch in der Bürgeranfrage wiederholt von Dr. Engelhardt angeführt wurde, geht es um die Publikation in der Phys. Rev. Veröffentlichung PRL 116, 061102 (2016) mit dem Satz: “The detector output is calibrated in strain by measuring its response to test mass motion induced by photon pressure from a modulated calibration laser beam [63].”, die die Eichung per Strahlungsdruck auf den 40-kg-Spiegel beschreibt, mit Figuren und Formel, jedoch ohne Meßdaten. Wenn die Tests nach dieser Eichungsmethode durchgeführt wurden, sind zwangsläufig Meßdaten vorhanden, womit zwangsläufig eine Eichkurve zu erstellen ist, um die durchgeführte Tests zu dokumentieren.
Hallo Herr Pössel,
steht mir fern Ihnen in die Handhabung Ihres Blogs zu reden, verzeihen Sie mir bitte, wenn es so klang, war mehr allgemein gemeint. Ich ging davon aus, und halte es auch für richtig, dass auch mein Beitrag gelöscht wurde, er war ja Teil der Metadiskussion. Jedoch finde ich es nicht ganz irrelevant, wie Personen sich an anderen Orten äußern und verhalten, vor allem wenn es hierhin einen Bezug gibt. Eine Diskussion sollte schon redliche geführt werden ohne versteckte Ziele, aber nun gut, ich belasse es bei diesen beiden Sätzen dazu, zurück zum Thema.
Ich habe da wohl etwas von Ihnen verpasst, wo haben Sie hier geschrieben, “dass die von LIGO versprochene Eichmessung nicht existiert”, – und welche soll das sein, welche wurde denn da vom LIGO wo versprochen? Ebenso sehe ich keinen Grund zu behaupten, das LIGO-Experiment ist ungültig: Die Messanlage wurde nicht geeicht! – Vielmehr düngt es mich, dass hier etwas an der Eichung der Anlage falsch, oder eben noch nicht richtig, verstanden wurde.
Für einen Menschen, der nicht Physik studiert hat, und sei es auch im Eigenstudium, und sich dann entsprechend viel Zeit nimmt, die Veröffentlichungen zu dem Experiment genau nachzuvollziehen, scheint es mir kaum möglich, die Eichung der Anlage im Detail nachzuvollziehen und richtig zu verstehen. Was ich bisher hier so mitbekommen habe zeigt mir, dass da wirklich sehr sorgfältig gearbeitet wurde um bei einer Messung auch sicher sein zu können. Ich bin sehr auf weitere Messungen und Ergebnisse gespannt.
Wünsche allen hier ein schönes Wochenende
@ Herr Pössel,
Da Sie weiter oben heute um 10:44 Uhr auf den Punkt der nicht-Veröffentlichung einer Eichkurve nach der wiederholten Nachfrage von Dr. Engelhardt schon geantwortet haben, komme ich selbst auf meine gleiche Nachfrage zurück – unsere beiden Nachfragen haben sich chronologisch gekreuzt:
Prof. Danzmann schreibt unmissverständlich, auch allgemeinverständlich wie es angebracht ist, dass beim LIGO-Experiment zwei voneinander unabhängige Eichungsmethoden angewandt werden, die man am Ende vergleicht und wo man feststellt, dass sie „auf wenige Prozent genau“ übereinstimmen, siehe noch einmal seine Aussage in seiner E-Mail vom 31.05.16 – Dokument 13 in der Zusammenstellung der Korrespondenz:: http://www.kritik-relativitaetstheorie.de/Anhaenge/Anfrage%20LIGO-Experiment.pdf
“Das Schöne ist, dass die Eichung tatsächlich am Ende auf wenige Prozent genau funktioniert, und zwar mit zwei voneinander unabhängigen Methoden: Einmal durch Strahlungsdruckvariation, aber auch durch Anlegen einer variablen Spannung an die elektrostatischen Aktuatoren zur Spiegelbewegung.“
Dies setzt voraus, dass die Eichungsmethode durch Strahlungsdruck auf den 40-kg-Spiegel effektiv durchgeführt wird und Meßdaten gesammelt werden, die völlig unabhängig von der anderen Methode ausgewertet werden. Dies setzt voraus, dass eine eigene Eichkurve mit diesen Meßdaten zu erstellen ist, völlig unabhängig von der anderen Eichungsmethoden. Nur so kann man logischerweise die Ergebnisse der zwei Eichungsverfahren vergleichen und feststellen, dass sie „auf wenige Prozent genau“ identische Kurven liefern.
Die Aussage von Prof. Danzmann in seiner o.g. E-Mail „So eine einfache Eichkurve, wie Sie sie sich vorstellen, gibt es nicht, weil der Prozess der Eichung viel komplizierter ist“ lässt daher aus meiner Sicht nur zwei Vermutungen zu:
1. Man kann keine Eichkurve für diese Eichungsmethode per Strahlungsdruck auf dem 40-kg-Spiegel liefern, weil sie nicht durchgeführt wurde,
oder
2. Man kann keine Eichkurve für diese Eichungsmethode per Strahlungsdruck auf dem 40-kg-Spiegel liefern, weil die Daten nicht auswertbar sind.
Mfg
Jocelyne Lopez
Sie übersehen, dass sich Herrn Danzmanns Begriff “so eine einfache Eichkurve” auf eine ganz spezifische Beschreibung von Herrn Engelhardt bezieht, nämlich auf einen wie ein Gravitationswellensignal geformtes (“ähnliches”) künstliches Signal, erzeugt mit dem kontrollierten Strahlungsdruck und als Zeitsignal dargestellt. (So Herr Engelhardt in Ihrem Dokument 12; in einigen Versionen schreibt Herr Engelhardt zusätzlich noch vom “Interferometer-output”, auf den sich die Kalibration beziehe.)
So wird die Kalibration / Eichung bei LIGO schlicht nicht durchgeführt, und zu einem nicht durchgeführten Verfahren gibt es, wen wundert es, auch keine entsprechende Kalibrationskurve. (Man hat ähnliche Versuche zum Testen von LIGO durchgeführt, aber nicht zur Kalibration; einige Artikel über solche Tests hatte ich Ihnen ja bereits hier genannt.)
Die Kalibration, die tatsächlich durchgeführt wurde, und die ich hier beschrieben hatte, misst stattdessen zuerst Kalibrations-Strahlungsdruck-Laser und elektrostatischen Aktuator im Fast-Gleichtakt (Sinuswellen bei verschiedenen Frequenzen, keine nachgebildeten Signalformen), im zweiten Schritt dann den Effekt des Kalibrations-Strahlungsdruck-Lasers auf das Gesamtsystem (Interferometer-output plus, eigentlich wichtiger, Korrektursignal für den Ausgleichs-Aktuator). Das ist die Art und Weise, wie LIGO kalibriert wurde, beschrieben in dem nun schon mehrfach zitierten Artikel arXiv:1602.03845. Ich hatte Herrn Engelhardt und auch auch Sie persönlich bereits darauf hingewiesen, wo die entsprechenden Diagramme mit den Datenpunkten zu finden sind.
Also: Für das im LIGO-Artikel behauptete, in arXiv:1602.03845 näher beschriebene, zur Kalibration verwendete Kalibrationsverfahren gibt es selbstverständlich die entsprechenden Kalibrationskurven, Vergleiche alternativer Kalibrationsverfahren etc.
Für das von Herrn Engelhardt beschriebene, nie zur LIGO-Kalibration (aber in anderer Konfiguration zum Testen von LIGO!) verwendete Verfahren, das sich aufgrund des Messprinzips von LIGO auch nicht gut zur Kalibration eignen würde, gibt es ganz selbstverständlich keine Kalibrationskurve (und darauf bezieht sich offenbar auch die Aussage von Herrn Danzmann).
Herr Pössel,
damit wir uns richtig verstehen, sollten wir zunächst einmal Einigkeit erzielen, worin die experimentelle Entdeckung einer GW besteht, die in Fig. 1 von PRL 116, 061102 (2016) demonstriert wird. Beschränken wir uns auf „H1 observed“ so ist dort die oszillierende Bewegung einer Testmasse (Spiegel) relativ zur Messstrecke, also der „strain“ als Funktion der Zeit gezeigt. Aus diesen Daten ergibt sich eine Auslenkungsamplitude von ca. 10^(-18) m. OK?
Der Nachweis einer so kleinen Bewegung ist eine Großtat, denn multipliziert man den strain mit 10^(13), so hat man die Verschiebung um die Breite eines Haares in Relation zur Entfernung bis zum nächsten Fixstern nachgewiesen. Dies übertrifft die relative Mößbauer-Genauigkeit um den Faktor10^(6). OK?
Behauptet man, dies Unwahrscheinliche sei gelungen, so ist man den Nachweis in derselben Veröffentlichung schuldig, damit es nicht bei einer bloßen Behauptung bleibt. Man muss also experimentell zeigen, dass eine so kleine Spiegelbewegung tatsächlich ein Signal der gezeigten Größe erzeugt. Dies nennt man Eichung, auf Englisch Calibration, welche hier allerdings nicht in derselben Veröffentlichung ausgeführt wird, sondern in einem unveröffentlichten internen Report [63]. An sich ist das nach wissenschaftlichen Gebräuchen nicht akzeptabel, es sei denn Ref. [63] ist selbst bereits als offizielle Veröffentlichung nach einem peer review Verfahren erschienen, was hier jedoch nicht der Fall ist. OK?
Die Ankündigung dieser Eichung lautet in meiner Übersetzung auf Deutsch: „Das Detektor-Signal wird in dimensionslosen Einheiten von „strain“ geeicht, indem man die Reaktion des Signals auf eine Massenbewegung misst, welche durch den Photonendruck eines modulierten Eichlaser-Strahls bewirkt wird. (The detector output is calibrated in strain by measuring its response to test mass motion induced by photon pressure from a modulated calibration laser beam) OK?
Es versteht sich von selbst, dass die Intensität des Eichlasers so gewählt wird, dass die Reaktion des Detektors in etwa der durch die GW ausgelösten entspricht. Trägt man Detektor-Signal gegen den Photonendruck auf, so erhält man eine Eichkurve, denn der Zusammenhang zwischen Photonendruck und Spiegelbewegung ist exakt berechenbar. OK?
Soweit mein Verständnis der Mitteilungen in PRL 116, 061102 (2016). Bitte teilen Sie mit, ob Sie ein anderes Verständnis haben, und wenn ja, warum. Sobald wir hierin Einigkeit erzielt haben, können wir weiter gehen.
Dr. Engelhardt, mir kommt da so ein vorläufiger Gedanke:
verwechseln Sie möglicherweise “accurat” und “sensitiv”?
Das aLIGO ist auf 10 % “accurat”, und genau das wurde kalibriert.
Die Empfindlichkeit kommt aber auf 10^-23. Extra dafür wurde mit optischen Mods
die Kohärenzlänge des Lasers auf 10^10 m “getrimmt”. Das reicht, um gelassen
eine Phasendifferenz von 10^-17 der halben Laser-Wellenlänge zu detektieren.
Man muß das nur noch ausreichenden Photonen und den Detektoren beibringen.
Die Michelson-Anordnung mißt nur die Wegdifferenz, die hier – das ist das gelöste
technische Problem – um Größenordnung kleiner als die Wellenlänge ist.
Die Testmassen sind reibungsfrei aufgehängt und folgen dieser Wegdifferenz mit
der Graviwelle, was soll man da nochmal kalibrieren – man mißt keine Kräfte?
Herr Engelhardt,
danke für den konstruktiven Beitrag; so sollten wir hoffentlich in der Tat weiterkommen.
Beim Begriff der Genauigkeit muss ich dem Kommentar von Herrn Senf zustimmen: Genauigkeit ist im üblichen physikalischen Sprachgebrauch etwas anderes. Wenn LIGO einen Strain von 3 mal 10^-18 auf 10% genau gemessen hat, dann beträgt die Genauigkeit 10%. Dass 10^-18 eine sehr kleine Größe ist, ist dagegen Ausdruck der Empfindlichkeit von LIGO (sensitivity). Die ist in der Tat beeindruckend.
Dass man einen Nachweis “in derselben Veröffentlichung” belegen muss ist keineswegs Usus. Es würde ja auch dem zentralen Prinzip widersprechen, dass wissenschaftliche Veröffentlichungen auf einander aufbauen.
Zur Veröffentlichungspraxis: Die auf der Detection Papers-Seite aufgelisteten Begleitartikel sind keineswegs “interne Reports”, sondern (soweit ich weiß: sämtlich) Artikel, die am 11. Februar bei entsprechenden Fachzeitschriften zur Veröffentlichung eingereicht wurden. Drei davon sind inzwischen auch in einer entsprechenden Fachzeitschrift erschienen. Öffentlich zugänglich waren sie alle. Dass ein besonders wichtiges Resultat erst vergleichsweise kurz als “Letter” veröffentlicht wird und dass in solch einem Letter auf einen zukünftigen ausführlicheren Bericht verwiesen wird, ist ebenfalls nicht ungewöhnlich. Genau zu diesem Zweck wurde die “Letter”-Kategorie eingeführt. Ungewöhnlich, aber löblich, ist dass die ausführlicheren Berichte gleich so ausführlich sind wie bei LIGO (und entsprechend in multiplen Artikeln erscheinen), und dass diese Artikel bei Erscheinen des Letters schon direkt als E-Print öffentlich zugänglich sind ist natürlich auch ein moderneres Vorgehen. Ursprünglich musste man nach Erscheinen des Letters erst noch auf den längeren Bericht warten. Heutzutage kann man ihn gleich selbst einsehen.
Und nicht zuletzt gibt es zum Funktionsprinzip, Tests und Kalibration von Advanced LIGO allgemein eine ganze Reihe früherer, in Zeitschriften mit peer review erschienenen Artikeln. Es ist ja bei weitem nicht so, als seien die LIGO-Leute mit ihrem Detektor erst am 11. Februar ganz neu an die wissenschaftliche Öffentlichkeit getreten.
Eichung, hat mein Physiklehrer uns immer eingebleut, darf nur das Eichamt, aber ich verstehe natürlich was sie meinen, und Herr Danzmann verwendet den Begriff auch; aber sagen wir doch lieber, wie die LIGO-Autoren: Kalibration (Kalibrierung?). Kalibration ist zunächst einmal der Vorgang, bei dem man ein Messgerät mit anderen Messgeräten oder Normalen abgleicht. Das heißt zunächst noch nicht, dass die Messung auch das tut, was sie soll; triviales Beispiel: Ich kann mein Lineal kalibrieren, indem ich es mit einem geeichten Längenmaß vergleiche, aber dass heißt noch lange nicht, dass ich bei der anschließenden Messung alles richtig mache (gerade anlegen, ohne Parallaxe ablesen etc.).
Bei den LIGO-Detektoren besteht die Kalibration darin, den Zusammenhang zwischen Spiegelverschiebung und Detektor-Ausgangssignal (interferometrisches Signal aus dem Photodetektor und Kontrollsignal des Ausgleichs-Aktuators) zu ermitteln. Dabei wird das Messgerät LIGO (bestimmt strain aus interferometrischem und Kontrollsignal) mit dem Normal “Kalibrationslaser” (lenkt Spiegel in einer kontrollierbaren Weise aus, die einfachen physikalischen Gesetzen gehorcht) abgeglichen.
Der zweite Teil des Kalibration (sensing function) leistet in der Tat mehr als nur Kalibration sondern zeigt, da dort in der Tat der gesamte Messvorgang reproduziert wird, auch jenseits der Kalibration, dass das Messinstrument funktioniert wie es soll.
Das reicht den Physikern aber noch nicht, sondern LIGO hat zu Recht noch weitere Detektortests nachgeliefert: Zum einen, ganz wichtig, die Rauschkurve, denn wenn das Rauschen sehr viel größer wäre als das Signal, dann würde man den Nachweis in der Tat nicht anerkennen. Zum zweiten die Simulationstests, also die “hardware injections”, bei denen (in der Regel mit einem der elektrostatischen Aktuatoren) simulierte Spiegelverschiebungen eingespeist und im normalen Messbetrieb ausgelesen und ausgewertet wurden. Zum dritten bis n-ten eine Batterie von weiteren Tests, Charakterisierungen etc. die zeigen sollen, dass die Komponenten des Detektors jeweils so funktionieren, wie behauptet.
All diese Tests zusammen, plus die erwähnte Kalibration, liefern die Informationen, die man braucht um zu beurteilen, ob die LIGO-Messungen solide (oder auch nur: plausibel) sind.
“Trägt man Detektor-Signal gegen den Photonendruck auf,” – im Prinzip ja, aber ich würde zwei Dinge hinzufügen: [Da die Übertragungskurve, die zur Auswertung sowohl der Kalibrationsmessungen als dann im Ernstfall der Gravitationswellensignale, im Frequenzraum definiert ist, ist es auch am einfachsten, sie im Frequenzraum (sprich: bei verschiedenen festen Frequenzen) zu messen; da man bei der Kalibration möglichst wenig Störeinfluss haben möchte, bekommt man die besten Ergebnisse, wenn man die Bestandteile der Übertragungskurve (sensing function und actuation function) auf die Weise getrennt kalibriert, wie in [63] beschrieben – dann erfahren Kalibrationslaser-Einfluss und Aktuator-Einfluss nämlich bei der Kalibration der actuation function gerade die gleichen zeitlich abhängigen Störungen, und das Abgleichen wird genauer. (Abschnitt in eckigen Klammern war weggefallen, nachgetragen 6.6.16 13:40)]
Und, ganz wichtig weil ich glaube, dass dort noch Verwirrung besteht: Was meinen Sie in Ihrem vorletzten Absatz mit “Detektor-Signal”? In Ihrem vorigen Kommentar nutzen Sie austauschbar dazu den Begriff “Interferometer-Signal”. Das ist missverständlich, denn das Detektorsignal, das in [63] kalibriert wird, ist ausdrücklich eine Kombination aus dem eigentlichen Interferometer-Signal (darunter verstehe ich das, was der Photodetektor am Interferometerausgang nachweist) und dem Kontrollsignal des Ausgleichs-Aktuators. Bei einem idealen Detektor (mit ultraschnellem Aktuator) wäre sogar die gesamte Gravitationswelleninformation im Kontrollsignal.
Eine “Eichkurve” (Ihr Begriff), die das Kalibrationslaser-Inputsignal mit dem interferometrischen Output (Photodetektor) gibt es, wie gesagt, nicht. Kann es mit dem Messprinzip, nach dem die Detektoren auslesen (interferometrischer Output und Kontrollsignal), ja auch nicht geben.
Herr Pössel,
lassen Sie mich der Reihe nach auf Ihre Punkte eingehen.
„strain“ enthält bereits eine relative Genauigkeit, nämlich Spiegelauslenkung/Messstrecke. Wenn man 10^(-18)m Auslenkung in Relation zu 4 km Messstrecke messen kann (und diese Messstrecke auch benötigt), dann ist man in der Lage, eine Verschiebung um Haaresbreite in Relation zu 4 Lichtjahren Messstrecke zu messen. Nachdem dies eine noch nie erreichte Leistung ist, auf der die gegenwärtige Entdeckung von GW beruht, ist man verpflichtet, diese Leistung experimentell nachzuweisen, was man auch ohne GW jederzeit tun kann und was LIGO mit Ref. 63 auch verspricht. Allerdings hat Ref. 63 den Status eines internen Reports und könnte im peer review Verfahren durchfallen oder verändert werden. Aus diesem Grund hat das „discovery paper“ den Status einer bloßen Behauptung. Natürlich muss der Nachweis jener extremen experimentellen Genauigkeit nicht in derselben Veröffentlichung erfolgen, wenn er bereits anderweitig veröffentlicht wurde, so dass man „darauf aufbauen“ kann. Im Fall von Ref. 63 trifft das jedoch nicht zu.
Zur Veröffentlichungspraxis von Phys. Rev. Lett. möchte ich mich nicht äußern, weil das Sache des Editorial Board ist. Natürlich hätten die Referees oder die Editoren erkennen müssen, dass es zum Nachweis von GW mindestens erforderlich ist, dass die angekündigte „calibration“ veröffentlicht wurde. Aber noch nicht einmal im Report Ref. 63 findet man einschlägige Daten, sondern nur Formel (10).
„Eichung“ verwende ich wie die LIGO-Autoren im Sinne von „calibration“. Darüber gibt es wohl keinen Disput. Ich denke, dass ich diesen Satz „The detector output is calibrated in strain by measuring its response to test mass motion induced by photon pressure from a modulated calibration laser beam.” auch in Ihrem Sinne korrekt übersetzt habe. Die Methode der Kalibration wird mit diesem Satz hinreichend genau beschrieben, „actuators“ kommen weder hier noch sonst wo im Papier vor. Wenn die „sensing function“ zeigt, dass das Instrument funktioniert wie es soll, dann ist das schön, hat aber keinen Einfluss auf das quantitative Messergebnis.
Dieser Satz: „All diese Tests zusammen, plus die erwähnte Kalibration, liefern die Informationen, die man braucht um zu beurteilen, ob die LIGO-Messungen solide (oder auch nur: plausibel) sind.“ ist unpräzise, denn man kann die Kalibration nicht in einenTopf mit Funktionstests werfen. Die Kalibration liefert den Zusammenhang zwischen „detector output“ und „test mass motion“, und weitere Tests prüfen, ob die Messung verlässlich ist.
Ihr drittletzter Absatz kommt bei mir verstümmelt an und kann nicht kommentiert werden.
„Interferometer-Signal“ und „Detektor-Signal“ habe ich synonym für „detector output“ verwendet. Darüber sollte es keine Missverständnisse geben.
Ihre Behauptung, man könne einen detector output – als „strain“ geeicht – zwar dann als Funktion der Zeit auftragen, wenn er durch eine GW erzeugt wird (Fig. 1), nicht aber, wenn man ihn durch eine mit Hilfe von Strahlungsdruck bewirkte Spiegelauslenkung vergleichbarer Amplitude und Frequenz erzeugt, kann ich nicht nachvollziehen. Wenn dem so ist (und Herr Danzmann gibt Ihnen in diesem Punkt Recht), wurde das Instrument nicht so kalibriert, wie in der discovery publication beschrieben. Der Nachweis, dass es überhaupt Auslenkungen von 10^(-18) m in Relation zu 4 km Armlänge messen könne, wurde nicht erbracht und, natürlich, von einem experimentellen Nachweis von GW kann keine Rede sein.
Herr Engelhardt,
dass Ihre Argumentation mit der im strain enthaltenen Genauigkeit nicht stimmt, kann man vielleicht am einfachsten so sehen: Nehmen Sie ein herkömmliches Michelson-Interferometer als einfachen Laborversuch auf der optischen Bank. Ich ändere mit einer Stellschraube den Abstand des einen Spiegels vom Strahlteiler ein wenig und bestimme am Photodetektor per Interferenzmuster, dass sich die Phase der beiden Lichtkomponenten um pi/2 gegeneinander verschoben hat. Ich schließe daraus, dass sich der Spiegel um die winzige Strecke von pi/4 mal Lichtwellenlänge verschoben hat, sagen wir: um 60 Nanometer. Niemand würde ob dieses Ergebnisses behaupten, es wäre mir gelungen, die Gesamt-Lichtlaufstrecke mit einer Genauigkeit von einigen Dutzend Nanometern auszumessen. Ebenso bei LIGO: Gemessen wird vom Prinzip her ΔL, und daraus und in Kenntnis von L kann man den Strain als ΔL/L abschätzen. Das heißt aber nicht, dass L dort irgendwie vermessen worden wäre, schon gar nicht mit Genauigkeit ΔL/L.
Zu “Letters”: Zumindest ich bezog mich nicht auf die konkrete PRL-Handhabung sondern auf auf eine ganz allgemeine Funktion der wissenschaftlichen Textgattung “Letter”. Letter sind Kurzberichte, und nicht selten werden dort nicht einzeln aufgeführte Details dann erst in späteren, längeren Veröffentlichungen vorgestellt. Das ist durchaus übliche Praxis.
[63] ist kein interner Report, sondern ein als E-Print veröffentlichter und in einer Fachzeitschrift zur Veröffentlichung eingereichter Artikel. Interne Reports sind nicht notwendigerweise öffentlich, richten sich an eine begrenzte Zielgruppe und nicht an die wissenschaftliche Öffentlichkeit und setzen typischerweise interne Vorkenntnisse voraus. All das trifft auf [63] nicht zu; Ihre Bezeichnung ist einfach irreführend und redet [63] kleiner, als es ist.
Die gewählte Methode wird mit dem kurzen PRL-Satz zur Kalibration keineswegs genau beschrieben. Was Sie nicht zuletzt daraus sehen, dass dieser Satz ebenso auf Ihr vereinfachtes (aber praktisch nicht gangbares) Verfahren und auf das tatsächliche Verfahren (das ich ja hier beschrieben hatte) zutrifft. Aktuatoren sind Teil des Messprinzips von LIGO; dass sie in dem kurzen Verweis-Satz nicht vorkommen, hat nichts zu sagen. Wer dem Verweis folgt und [63] liest, bekommt die Details schließlich dort erzählt.
Ich wollte Kalibration und weitere Tests nicht in einen Topf werfen, sondern nur darauf hinweisen, dass man für das, was wir hier eigentlich klären wollen, nämlich ob die LIGO-Detektoren so wie behauptet funktionieren, beides braucht.
Den obigen drittletzten Abschnitt habe ich gerade korrigiert; da war wohl etwas verschwunden, sorry.
Danke für die Auskunft, dass Sie “Interferometer-Signal” und “Detektor-Signal” synonym verwenden. Das ist zwar potenziell missverständlich, da das Interferometersignal im engeren Sinne (Licht, das beim Photodetektor am Ende ankommt) bei der verwendeten Messanordnung im Idealfall keine Informationen mehr über die Gravitationswelle enthält, aber solange Sie Ihren Sprachgebrauch klarstellen, sollte das hoffentlich niemanden hier verwirren.
Selbstverständlich kann man im Prinzip per zusätzlichem Strahlungsdruck eine Spiegelauslenkung bewirken und dann als Funktion der Zeit auftragen, was hinten am Detektor herauskommt. Aber beim wirklich verwendeten Kalibrationsverfahren ist man eben anders vorgegangen (zwei Gründe stehen im jetzt restaurierten Abschnitt meiner letzten Mail).
@ Herr Pössel:
Sie schreiben: “Sie übersehen, dass sich Herrn Danzmanns Begriff “so eine einfache Eichkurve” auf eine ganz spezifische Beschreibung von Herrn Engelhardt bezieht, nämlich auf einen wie ein Gravitationswellensignal geformtes (“ähnliches”) künstliches Signal, erzeugt mit dem kontrollierten Strahlungsdruck und als Zeitsignal dargestellt.“
Ich habe es gar nicht übersehen, sondern ganz im Gegenteil Herrn Danzmann richtig verstanden: Die Aussage von Herr Danzmann bezieht sich unmissverständlich auf die eine Eichungsmethode Strahlungsdruck auf dem 40 kg-Spiegel des Interferometers, wovon auch die ganze Zeit Dr. Engelhardt spricht und wofür er die Meßdaten vermisst. Es gibt kein Missverständnis oder Verwechselung meinerseits über den Bezug der Aussage von Herrn Danzmann.
Sie schreiben weiter: “Für das von Herrn Engelhardt beschriebene, nie zur LIGO-Kalibration (aber in anderer Konfiguration zum Testen von LIGO!) verwendete Verfahren, das sich aufgrund des Messprinzips von LIGO auch nicht gut zur Kalibration eignen würde, gibt es ganz selbstverständlich keine Kalibrationskurve (und darauf bezieht sich offenbar auch die Aussage von Herrn Danzmann).“
Mir erschließt es sich ehrlich gesagt nicht, warum diese Kalibrationsmethode durch Strahlungsdruck auf den 40-kg-Spiegel sich „nicht gut zur Kalibration eignen“ sollte. Ich würde sogar intuitiv als Laiin sagen, dass es ganz im Gegenteil die entscheidende Kalibration ist: Der Interferometer selbst mit seinem 40-kg-Spiegel ist ja das Meßapparat und es gilt das Messapparat zu kalibrieren! Und nicht „Aktuatore“, was das immer sein sollte… Schließlich werden sozusagen im „Ernstfall“ eventuelle Gravitationswellen vom Interferometer selbst mit seinem 40 kg-Spiegel direkt registriert. Es ist also aus meiner Sicht entscheidend zu messen, welche kontrollierte Verschiebungen des 40-kg-Spiegels welche meßbare Signale im Ausgang des Interferometers bewirken.
Nicht umsonst hat man wohl einen 40 kg-Spiegel vorgesehen, um messbare Verschiebungen zu bewirken, gehe ich davon aus. Auch Prof. Nicolai hat mir in seiner Antwort vom 05.04.16 darüber aufgeklärt, dass der 40-kg-Spiegel eine wichtige Rolle zur Genauigkeit der Messung beim Design der Messanlage spielt, siehe Dokument Nr. 2 in der Zusammenstellung der Korrespondenz: http://www.kritik-relativitaetstheorie.de/Anhaenge/Anfrage%20LIGO-Experiment.pdf
“Ob der Spiegel also 40 Gramm oder 40 Kilogramm wiegt, ist unerheblich, weil die Raumzeit selbst durch die Gravitationswellen verformt wird und die darin befindlichen Objekte mitgenommen werden. Eine hohe Spiegelmasse verringert jedoch im Detektor entstehende Rauschquellen, die die Messgenauigkeit beeinflussen.“
Es ist also für mich nicht nachvollziehbar, warum die Kalibration durch Strahlungsdruck auf den 40 kg-Spiegel sich nach Ihrer Aussage „nicht gut zur Kalibration eignen würde“. :(
Mfg
Jocelyne Lopez
Nein, die Signale werden eben nicht vom Interferometer selbst, im Sinne von: direkt abgegriffen am Photodetektor am Ausgang, “direkt registriert”. Der Ausgleichsaktuator (Element, das einen der Spiegel elektrostatisch verschiebt) ist selbst Teil des Messprozesses, auch bei der Messung der Gravitationswellensignale. Tatsächlich steckt die meiste Information über die Gravitationswelle im Kontrollsignal dieses Aktuators. Ich hatte das Grundprinzip in einem früheren Kommentar hier kurz umrissen.
Dementsprechend muss der Aktuator mitgeeicht werden, und das wird er auch.
Wir haben es daher zumindest in unserer Diskussion doch mit zwei verschiedenen Kalibrationsverfahren, die aber beide mit “Strahlungsdruck auf den 40-kg-Spiegel” funktionieren.
Erstes Kalibrationsverfahren (Herr Engelhardt): Mit dem Strahlungsdruck in Amplitude und Frequenz einem Gravitationswellensignal ähnliche Verschiebungen erzeugen und diesen Input direkt mit dem Detektor-Output (sprich: was der Detektor für den strain gemessen hat) als gegen die Zeit aufgetragenes Signal (h als Funktion der Zeit) vergleichen.
Zweites Kalibrationsverfahren (bei LIGO wirklich angewandt): Mit dem Strahlungsdruck entsprechende Verschiebungen bei jeweils konstanter Frequenz fast im Gegentakt mit dem Ausgleichsaktuator laufen lassen (das reduziert Störungen) und so die Aktuatorwirkung kalibrieren; anschließend mit den Ergebnissen jeweils bei konstanter Frequenz und einer wie bei den eigentlichen Messungen eingestellten Aktuatorwirkung den Rest des Messprozesses (sensing function) kalibrieren.
Zum ersten Kalibrationsverfahren gibt es, da aus guten Gründen nicht angewandt (konzeptuell einfacher, aber es vernachlässigt, wie tatsächlich gemessen wird) auch keine Kurve, wie Herr Danzmann schreibt.
Zum zweiten Kalibrationsverfahren, also dem bei LIGO tatsächlich angewandten, sind die entsprechenden Messdaten zu den beiden Kalibrationsschritten in arXiv:1602.03845 wiedergegeben (wie ich in dieser Diskussion sicher schon fünf, sechs Male geschrieben habe).
Lopez: “Ich habe es gar nicht übersehen, sondern ganz im Gegenteil Herrn Danzmann richtig verstanden: Die Aussage von Herr Danzmann bezieht sich unmissverständlich auf die eine Eichungsmethode Strahlungsdruck auf dem 40 kg-Spiegel des Interferometers, wovon auch die ganze Zeit Dr. Engelhardt spricht und wofür er die Meßdaten vermisst. Es gibt kein Missverständnis oder Verwechselung meinerseits über den Bezug der Aussage von Herrn Danzmann.”
Es wurde doch nun ganz deutlich erklärt, dass Engelhardt von einer Methode spricht, die nicht für die Eichung verwendet wurde, da es dafür bessere gibt. Da kann es dann auch keine Messdaten zu geben.
Lopez: “Mir erschließt es sich ehrlich gesagt nicht, warum diese Kalibrationsmethode durch Strahlungsdruck auf den 40-kg-Spiegel sich „nicht gut zur Kalibration eignen“ sollte. … Es ist also für mich nicht nachvollziehbar, warum die Kalibration durch Strahlungsdruck auf den 40 kg-Spiegel sich nach Ihrer Aussage „nicht gut zur Kalibration eignen würde“.”
Kommt vor, dafür gibt es eben Experten, die es nachvollziehen können und denen es sich erschließt, warum die eine Methode besser als eine andere geeignet ist. Die haben aber auch einige Jahre Physik studiert. Ähnliches kann es in der Medizin geben, auch da erschließt sich dem Laien nicht immer, warum eine bestimmte Methode zur Behandlung einer Erkrankung besser geeignet ist, als zum Beispiel homöopathische Mittel.
Wie dem auch nun immer sei, die Anlage wurde geeicht und/oder kalibriert, wie ist öffentlich nachzulesen, es wird nichts verschwiegen, es gibt also keine Täuschung der Öffentlichkeit, man könnte hier den Punkt abhaken und mit dem Thema selber fortfahren.
@ Herr Pössel:
Sie schreiben (zur Eichungsmethode, die von Dr. Engelhardt angeführt und unter Papier [63] beschrieben wird: “Zum ersten Kalibrationsverfahren gibt es, da aus guten Gründen nicht angewandt (konzeptuell einfacher, aber es vernachlässigt, wie tatsächlich gemessen wird) auch keine Kurve, wie Herr Danzmann schreibt.“
Herr Danzmann schreibt aber, dass beide Eichungsmethoden (die bisher herkömmliche konzeptuell einfache Eichungsmethode in der Interferometrie und die neue, komplizierte Eichungsmethode des LIGO-Experiments) bei der praktischen Durchführung quasi identische Eichkurven liefern: Zitat: “Das Schöne ist, dass die Eichung tatsächlich am Ende auf wenige Prozent genau funktioniert, und zwar mit zwei voneinander unabhängigen Methoden: Einmal durch Strahlungsdruckvariation, aber auch durch Anlegen einer variablen Spannung an die elektrostatischen Aktuatoren zur Spiegelbewegung.“
Konzeptuell komplizierter heißt also hier nicht besser und „aus guten Gründen nicht angewandt“ … 😉
Und wenn mit einer neuen, komplizierten Eichungsmethode, deren Meßergebnisse sich nur auf wenige Prozent von der herkömmlichen Eichungsmethode unterscheiden, die Leistung eines herkömmlichen Interferometers einen sensationellen Sprung in der Genauigkeit auf einmal schafft, die um eine Million die Mößbauer-Genauigkeit übersteigt, dann darf man sich berechtigt fragen, ob es nicht etwa auf einen unverhofften, revolutionären Fortschritt der herkömmlichen Interferometrie zurückzuführen ist, sondern eher auf ein unbemerktes Artefakt. So etwas kann passieren in der Experimentalphysik, zum Beispiel wenn man das Design einer Meßanlage gezielt für die gezielte Messung von bestimmten physikalischen Ereignissen konzipiert, oder? Ich habe zum Beispiel schon von hartnäckigen wissenschaftlichen Disputen gelesen, wo der Einwand vorgebracht wurde, dass das Design eines Teilchenbeschleunigers speziell konzipiert wurde, um die Unüberschreitbarkeit der Lichtgeschwindigkeit zu „beweisen“.
mfg
Jocelyne Lopez
Frau Lopez,
was Sie schreiben stimmt an (mindestens) einer entscheidenden Stelle nicht.
Die beiden Kalibrationsverfahren, von denen Herr Danzmann spricht, nutzen beide das LIGO-Messverfahren samt aktivem Ausgleichsaktuator – keines der beiden Verfahren ist das Verfahren, von dem Herr Engelhardt spricht. Eines der von Herrn Danzmann genannten Kalibrationsverfahren nutzt als Vergleichsgröße (Normal) den Strahlungsdruck, das andere zwei leicht frequenzverschobene Laser, nach deren Schwingung je einer der der Aktuatoren an jedem Armende mit variabler Spannung betrieben, also rhythmisch verschoben wird.
Auf die Quellen, in denen die beiden Verfahren (und noch ein drittes) sowie der Vergleich beschrieben werden, hatte ich Sie in diesem Kommentar bereits hingewiesen. Und meine dortige Vorhersage zu Ihrem Verhalten, das wirklich nicht zum Stil konstruktiver Diskussionen passt, hat sich ja auch bewahrheitet. 🙂
Insofern: Doch, das Engelhardt’sche Verfahren ist und bleibt zur Kalibration ungeeignet und wurde dementsprechend bei LIGO auch nicht angewandt. Aus guten Gründen, die ich zuletzt hier skizziert hatte.
Dass und warum Herrn Engelhardts Behauptung riesiger Genauigkeit, die Sie in Ihrem letzten Kommentar wiederholen, die Situation nicht richtig beschreibt, hatte ich zuletzt hier ausgeführt. Es wurde direkt eine (in der Tat sehr kleine) Längenänderung mit rund 10% Genauigkeit gemessen, nicht mehr und nicht weniger.
Ist zwar offtopic, aber trotzdem
heute gab es eine PK der ESA http://livestream.com/ESA/events/5502160
eLISA ist 100x besser geworden, als vorgegeben war und erwartet wurde! Die Sonde konnte 10^-15 m genau auf ihrer “Weltlinie” gehalten werden.
Diese Empfindlichkeit reicht aus, daß eLISA alleine sehr starke niederfrequente Gravitationswellen spüren könnte.
Die Technik ist perfekt, so daß dem Bau von LISA nichts im Wege steht.
Die Korrekturtriebwerke, die die Lage halten, funktionieren ja praktisch wie Aktuatoren.
Grüße Senf
Herr Senf schrieb (7. Juni 2016 12:57):
> heute gab es eine PK der ESA […]
> eLISA ist 100x besser geworden, als vorgegeben war und erwartet wurde! Die Sonde konnte 10^-15 m genau auf ihrer “Weltlinie” gehalten werden.
Selten so gelacht! …
Im Übrigen ist im begleitenden Dokument PRL 116, 231101 (2016) zwar viel von „free fall“ und „local inertial frames“ die Rede,
aber (für mich) nicht erkennbar, ob und wie denn gemessen worden wäre, dass bzw. in wie fern die betreffenden „test masses“ dabei (tatsächlich, einzeln) „frei“ gewesen wären, anstatt (nur) gegenüber einander „starr“.
(Also ganz ähnlich dem Mangel, der LIGO betrifft und der oben schon erläutert wurde.)
@ Herr Pössel:
Sie schreiben: Doch, das Engelhardt’sche Verfahren ist und bleibt zur Kalibration ungeeignet und wurde dementsprechend bei LIGO auch nicht angewandt.“
Soll das bedeuten, dass die Eichungsmethode durch Strahlungsdruck auf dem Spiegel, die herkömmlich in der Interferometrie seit Jahrzehnten angewandt wird und die auch im LIGO-Kalibrationspapier [63] beschrieben jedoch nicht durchgeführt wurde (wie wir es mühsam erfahren haben), nicht nur „konzeptuell einfach“, sondern grundsätzlich ungeeignet ist, die Leistung eines Interferometers richtig zu testen? Es wäre aber Zeit, dass man es merkt, seit Interferometer gebaut und damit Experimente durchgeführt werden, oder?
Und soll man davon ausgehen, falls die herkömmliche Eichmethode mit Strahlungsdruck auf dem Spiegel angewandt gewesen wäre und falls man sie mit der neuen LIGO-Eichmethode durch Strahlungsdruck über die Aktuatoren vergleichen könnte, dass die Eichkurven überhaupt nicht übereinstimmen würden? Dass also die Genauigkeit eines Interferometers von der Eichmethode abhängt?
Sie schreiben: “Es wurde direkt eine (in der Tat sehr kleine) Längenänderung mit rund 10% Genauigkeit gemessen, nicht mehr und nicht weniger.“
Der Physiker und Redaktionsleiter der Neue Zürcher Zeitung, Christian
Speicher, den ich in meiner Bürgeranfrage zitiert habe, hat hochskaliert zum Abstand zwischen Erde und Mond eine Verschiegung um weniger als den
Durchmesser eines Wasserstoffatoms gerechnet. Man kann auch hochskaliert berechnen, dass die LIGO-Detektore mit rund 10% Genauigkeit registriert haben, dass eine Verschiebung des Spiegels um eine Haarbreite durch Gravitationswellen aus 4 Lichtjahren Entfernung verursacht wurde. Das finde ich aber schwach von LIGO, es gibt ja feine und dicke Haare, geht es nicht ein bisschen genauer für den Preis? – Satire ist erlaubt, oder? 🙂
Ich hab mal was von Sockenpuppen gelesen?
Was issen das ? Ganz nach dem Motto:
“Man muß keine Ahnung haben, aber dagegen sein.”
Frau Lopez:
Nein, das soll es nicht heißen.
LIGO ist mithilfe von Strahlungsdruck kalibriert worden – wie dabei vorgegangen wurde wird in [63] genau beschrieben und ich hatte es kurz hier zusammengefasst. Der Artikel [63] (hier zum Teil zitiert als arXiv:1602.03845v1) liefert alle wesentlichen Informationen, die nötig sind, um die Kalibration richtig einzuschätzen: Die Kalibrationsfunktion ebenso wie Diagramme mit den Daten, außerdem einen Vergleich mit der von Herrn Danzmann erwähnten zweiten und sogar noch einer dritten Kalibrationsmethode (die Quellen hatte ich Ihnen hier genannt).
Damit ist alles in Ordnung: Kalibration durchgeführt, Kalibration erfolgreich (erreichte Genauigkeit schränkt die Genauigkeit der Messung nicht wesentlich ein), Kalibration konsistent mit Alternativverfahren, Kalibration dokumentiert.
Herr Engelhardt ist allerdings offenbar der Auffassung, die Kalibration mit Strahlungsdruck hätte man prinzipiell anders durchführen sollen, als es die LIGO-Leute gemacht haben. Soweit ich verstanden habe: Nicht bei festen Frequenzen sondern mit simuliertem Signal, und ausgelesen als Zeitkurve, nicht im Frequenzraum. (Von Mal zu Mal etwas unterschiedlich formuliert finden sich bei Herrn Engelhardt auch Aussagen, die auf noch weitere Abweichungen hindeuten.)
Die Gründe, warum die Engelhardt-Variation keine sinnvolle Kalibrationsmethode ist, hatte ich zuletzt hier kurz geschildert. (Und nein, es handelt sich definitiv nicht um eine “herkömmliche” Methode.)
Insofern bekommt Herr Engelhardt sowohl hier von mir als auch von Herrn Danzmann sinngemäß, in leichten Variationen, und zumindest in meinem Falle auch wiederholt, zu hören: “Doch, LIGO wurde (mit Strahlungsdruck) kalibriert, aber nicht in der (ungeeigneten) Art und Weise, die Sie vorschlagen.”
Wenn Sie behaupten LIGO sei nicht mit Strahlungsdruck kalibriert worden, oder sogar LIGO sei gar nicht kalibriert worden, ist das daher schlicht die Unwahrheit.
P.S.: Satire ist erlaubt, wirkt aber, wie in diesem Falle, peinlich, wenn daraus deutlich wird, dass der- oder diejenige nicht wirklich versteht, worüber er/sie sich lustig macht. Bleiben wir doch nicht zuletzt deswegen hier in dieser Diskussion bitte bei den Sachfragen.
@ Herr Senf:
Beschimpfen Sie hier die von mir namentlich zitierten Physiker Dr. Christian Speicher und Dr. Wolfgang Engelhardt als „Sockenpuppe“, die „keine Ahnung haben, aber dagegen sind“? Wenn man solche Schmähungen in einem wissenschaftlicher Disput ausspricht, sollte man zumindest den Mut und den Rest Anstand besitzen, es nicht anonym unter einem Pseudonym “Herr Senf“ zu tun, sondern dafür gerade stehen und es unter Klarnamen tun.
Jocelyne Lopez
Ich sehe nicht, an welcher Stelle der Physiker und Redaktionsleiter der Neuen Zürcher Zeitung, Dr. Christian Speicher, beschimpft worden wäre – er wurde lediglich von Ihnen zitiert und niemand hat diesem Zitat widersprochen.
Lopez: “Wenn man solche Schmähungen in einem wissenschaftlicher Disput ausspricht, sollte man zumindest den Mut und den Rest Anstand besitzen, es nicht anonym unter einem Pseudonym “Herr Senf“ zu tun, sondern dafür gerade stehen und es unter Klarnamen tun.”
Unterstellt haben sie mir, ich würde hier als “Herr Senf” schreiben:
Lopez: “ich empfinde Ihre Moderation des fachlich unqualifizierten Teilnehmers Manuel Krüger alias “Herr Senf …” ”
was gelogen und eine freche unbelegte Unterstellung ist, und da unwahr, auch nie belegt werden kann. Und meine fachliche Qualifikation sollten sie ganz sicher mir nicht absprechen, vor allem in Anbetracht all des Unfugs, denn sie und Engelhardt so schon über die Physik öffentlich behauptet haben.
Die Krönung ist ja nun mal wieder die Beschwerde über Professor Danzmann von ihnen bei Herrn Nicolai in der sie weitere Unwahrheiten aufzählen, soll das auch Satire sein?
@Herr Pössel,
ich hoffe die Farce hier findet bald ein Ende, Physik erklären können Sie nur erfolgreich, wenn der Gegenüber bereit ist dazuzulernen und offen, seinen Irrtum zumindest sich selber gegenüber, einzugestehen und nicht schon eine betonierte Meinung zu den Dingen hat.
Wirkt hier langsam wie im Zirkus, die Fakten sind doch nun wirklich klar, LIGO wurde kalibriert, es wurde nichts verschwiegen, wie kalibriert wurde ist auch öffentlich nachzulesen, alles ist transparent. Sie selber haben hier nun mehrfach erklärt wie und wo man alles nachlesen kann, und hat es geholfen?
Eine Frage wie man “Erfolg” definiert, noch immer werden Lügen zu dem Experiment, der Kalibrierung und der Messung verbreitet.
ich würde nun gerne mal da weiter lesen, wo hier der Stand war, bevor Engelhardt und Lopez mit dem “Trollen” begonnen haben.
Ihre Nachsicht und Ihr Verständnis ehrt Sie, beachtenswert, wohl aber dennoch vergeblich, bleibt zu hoffen, dass die anderen Leser hier, sich aus Ihren Erklärungen zur Kalibrierung dennoch was ziehen konnten.
Mit freundlichem Grüßen
Manuel Krüger
Wie schon geschrieben: Bitte überlassen Sie diese Entscheidung mir. Und bitte tragen Sie im positiven Sinne bei, indem Sie nicht über jedes Stöckchen springen, das Frau Lopez Ihnen oder anderen hinhält. Mit Ihrem Beitrag hat Frau Lopez jetzt sofort einen Anlass jenseits der Kalibrationsdiskussion, um auf die Meta-Ebene zu gehen.
Ich finde die Diskussion über die Kalibration in der jetzigen Form nach wie vor interessant; wenn sie sich zu sehr im Kreis dreht, werde ich sie in der Tat abbrechen.
Herr Pössel,
ich denke wir können nun die Diskussion der Eichmethode beenden. Sie wird im „discovery paper“ beschrieben, aber so offenbar nicht angewandt. Der „e-print“ (Ref.63, keine reguläre Veröffentlichung!) liefert keine Daten eines „detector output“ in „response to test mass motion induced by photon pressure“. Diese Daten existieren nach Danzmann nicht und können auch nachträglich nicht rekonstruiert werden, obwohl man sie täglich neu erzeugen könnte.
Hingegen existiert ein „detector output in strain“ als Funktion der Zeit, der durch eine Spiegelauslenkung aufgrund einer GW am 14.9.2015 einmalig erzeugt wurde. Warum diese Aufzeichnung möglich war, was durch gezielte Spiegelauslenkung per Strahlungsdruck niemals funktioniert hat, haben Sie versucht zu erklären, sind aber bei mir und anderen auf taube Ohren gestoßen. Dabei wird es auch bleiben, denn ich müsste an meinem Verstand zweifeln, wenn ich einen Unterschied zwischen Spiegelverschiebung per Gravitationswelle und Spiegelverschiebung per Strahlungsdruck machte. Verschiebung ist bei mir gleich Verschiebung. Bei Ihnen ist das offenbar anders, aber ich sehe, dass es aussichtslos ist, Sie von Ihrer Meinung abzubringen.
Wegen der fehlenden Eichkurve, welche meine ersten drei Fragen an das Einstein Institut beantwortet hätte, müssen wir uns nun doch den grundsätzlichen Fragen an die Machbarkeit der Messung zuwenden, womit Sie bereits begonnen haben. In Ihrem Kommentar vom 6. Juni, 13:49 sagen Sie, dass eine Spiegelverschiebung um ΔL auf die Wellenlänge des Lichts bezogen werden muss. Genau dies war die Basis meiner Abschätzungen und führte auf eine Phasenänderung von 2 pi 10^(-6)/10^(-18). Dieser Faktor mal die Amplitude im Hellfeld ergibt die Aufhellung des Dunkelfelds durch die Spiegelverschiebung. Voraussetzung allerdings ist, dass das Dunkelfeld wirklich schwarz ist (Falschlicht um 24 Größenordnungen unterdrückt, exakte Gleichheit (auf 10^(-12)) der interferierenden Strahlen). Weiterhin Konstanz der Laserleistung auf 10^(-12), damit die Spiegel nicht per Strahlungsdruck bei kleinsten Schwankungen ins Wackeln geraten. Sie werden diese Fragen voraussichtlich nicht beantworten können, weil Sie am Experiment nicht teilgenommen haben. Vielleicht können Sie aber einen Ihrer ehemaligen Kollegen am Einstein-Institut dazu bewegen, sich zu äußern, nachdem die Direktoren zu diesen Fragen bisher schweigen.
Noch ein Wort zur „Genauigkeit“ Haaresbreite zu 4 Lichtjahren. Herr Speicher hat in der NZZ das Verhältnis Spiegelauslenkung/Armlänge um den Faktor 10^5 hoch skaliert und kam auf weniger als einen Atomdurchmesser im Vergleich zur Entfernung Erde-Mond. Dies messen zu können, erschien Frau Lopez wie ein „Wunder“ und hat ihre Anfrage beim Einstein Institut ausgelöst. Sie wurde von Herrn Nicolai belehrt: „Bei dieser hochpräzisen Messung handelt es sich jedoch nicht um ein „unbegreifliches Wunder” sondern um das Ergebnis von vielen Jahrzehnten Grundlagenforschung auf höchstem Niveau…“ Kein Wort davon, dass die Hochskalierung bedeutungslos sei und, meiner Kenntnis nach, bei der NZZ keine Klarstellung. Meine Hochskalierung um 10^(13) sollte dann auch akzeptiert werden, denn man fragt sich ja, warum es überhaupt einer so großen Armlänge bedarf, um eine so kleine Verschiebung zu messen. Hier könnten Sie gewiss noch einige Aufklärungsarbeit leisten.
Herr Engelhardt,
ganz so schnell möchte ich eigentlich nicht aufgeben. Allerdings sind unsere letzten Antworten jeweils recht länglich geworden; ich schränke mich daher ein und gehe nicht auf alle Aussagen ein, die ich in Ihrer Antwort für falsch/missverständlich halte. Stattdessen würde ich gerne ausprobieren, ob wir in kleinen Schritten weiterkommen.
Stellen Sie sich vor, wir beide wären für die LIGO-Kalibration verantwortlich, also dafür, eine Funktion anzugeben, welches Detektor-Outputsignal durch gegebene Spiegelverschiebungen erzeugt wird.
Wenn ich Sie richtig verstehe, schlagen Sie vor, wir könnten dazu doch einfach einen der Endspiegel kontrolliert durch Strahlungsdruck so verschieben, wie es bei einem Gravitationswellensignal zu erwarten wäre (ähnliche Amplitude, ähnliches Frequenzspektrum bzw. zeitliche Änderung des Frequenzspektrums) und als Funktion der Zeit aufzeichnen, was bei diesem künstlichen Input als Detektor-Output-Signal herauskommt.
Verstehe ich Sie soweit richtig? Einfaches ja würde genügen, andernfalls korrigieren Sie mich bitte.
Corrigendum:
Es muss natürlich
“Phasenänderung von 2 pi 10^(-18)/10^(-6) = 2pi 10^(-12)”
heißen.
@ Herr Pössel:
Sie schreiben: „Damit ist alles in Ordnung: Kalibration durchgeführt, Kalibration erfolgreich (erreichte Genauigkeit schränkt die Genauigkeit der Messung nicht wesentlich ein), Kalibration konsistent mit Alternativverfahren, Kalibration dokumentiert.
Sie haben meine Grundüberlegung nicht verstanden. Ich versuche sie noch einmal darzulegen – das kann ich mir wohl als Laiin erlauben, wenn sogar Prof. Nicolai als Gründungsdirektor des AEI zugibt, dass er selbst von der Interferometrie nicht viel versteht und mich auf Ihren Blog hingewiesen hat:
1. Es gibt eine Kalibrationsmethode in der Interferometrie, die offensichtlich so gängig ist, dass sie sogar im Kalibrationspapier von LIGO [63] beschrieben wurde, und zwar durch kontrollierten Strahlungsdruck auf den Spiegel selbst, und womit man zum Dokumentieren der gesammelten Daten eine Eichkurve als Funktion der Zeit erstellt. Diese in der Interferometrie offensichtlich gängige Methode haben Sie grundsätzlich als Kalibrationsmethode als ungeeignet bezeichnet: “ Doch, das Engelhardt’sche Verfahren ist und bleibt zur Kalibration ungeeignet und wurde dementsprechend bei LIGO auch nicht angewandt.“
2. Stattdessen wurde eine neu Kalibrationsmethode für LIGO angewandt, und zwar durch kontrollierten Strahlungsdruck auf den Aktuatoren (die andere Kalibrationsmethode, wovon Prof. Danzmann spricht, und zwar durch Anlegen von variablen elektrostatischen Spannungen, lasse ich der Übersichtlichkeit halber hier außen vor, da Herr Danzmann ausgesagt hat, dass man die Eichkurven von diesen zwei von LIGO angewandten Kalibrationsmethoden verglichen habe und dass sie unter sich „auf wenige Prozent“ übereinstimmen).
Jetzt noch einmal meine Überlegung, die sie offensichtlich leider nicht verstanden haben:
Wenn man die Kalibrationsmethode durch kontrollierte Strahlungsdruck auf den Spiegel selbst (meine o.g. Nr. 1) durchgeführt hätte, ist es davon auszugehen, da Sie sie als ungeeignet bezeichnen, dass man ganz andere Daten gesammelt und eine ganz andere Eichkurve erstellt hätte, als für die angewandten LIGO-Kalibrationmethode durch Strahlungsdruck auf die Aktuatoren (meine o.g. Nr. 2)? Ist davon auszugehen, dass die beiden Kalibrationsmethoden nicht konsistent gewesen wären, falls sie beide durchgeführt gewesen wären und wenn man sie hätten vergleichen können?
Aus meiner Sicht verstehen Sie nicht, worum es geht, aus Ihrer Sicht verstehe ich Sie falsch.
Um weiterzukommen, schauen wir doch bitte, ob wir uns wenigstens über ein paar einfache Tatsachen einigen können:
Wo im LIGO-Kalibrationspapier wird eine “Kalibrationsmethode in der Interferometrie” beschrieben, “durch kontrollierten Strahlungsdruck auf den Spiegel selbst, und womit man zum Dokumentieren der gesammelten Daten eine Eichkurve als Funktion der Zeit erstellt”, wie Sie schreiben?
Meines Wissens nach steht das aus gutem Grund nirgends im Kalibrationspapier. Sie behaupten, es stehe dort. Das sollte einfach zu überprüfen sein. Wir haben beide Zugriff auf das Kalibrationspapier. Zeigen/sagen Sie mir doch bitte einfach, wo das steht.
@ Herr Pössel,
Sie schreiben: „Meines Wissens nach steht das aus gutem Grund nirgends im Kalibrationspapier. Sie behaupten, es stehe dort. Das sollte einfach zu überprüfen sein. Wir haben beide Zugriff auf das Kalibrationspapier. Zeigen/sagen Sie mir doch bitte einfach, wo das steht.
Herr Pössel, Sie können sich sparen, mich mit Links und Hinweise auf Papiere über das LIGO-Experiment die ganze Zeit zu überschütten, Sie sollten sich eigentlich denken, wie jeder es logischerweise denkt, dass ich nichts damit anfangen kann und sie auch deswegen überhaupt nicht lese. Das ist auch für Nicht-Fachleute (woraus die Öffentlichkeit mit massiver Mehrheit besteht) nicht zumutbar, das haben sogar Prof. Nicolai und Prof. Danzmann einsichtigerweise erkannt und betont. Ich beteilige mich also an der Diskussion als Laiin, mit meinen eigenen Worten und meine eigenen Überlegungen, und ich glaube nicht, dass man nicht verstehen kann, was ich meine – vorausgesetzt man gibt sich die Mühe zu verstehen, was ich meine, natürlich.
Also noch einmal:
Herr Engelhardt moniert seit Anfang an, dass die Eichkurve für die Kalibrationsmethode, die im Papier [63] beschrieben wurde, nicht veröffentlicht wurde (dieses Verfahren haben Sie sogar kürzlich als “Engelhardt’sche Verfahren” genannt, so oft hat er davon gesprochen, dass es keine Missverständnis geben kann). Herr Engelhardt vermisst seit Anfang an die Meßdaten für dieses Verfahren: Die Meßdaten sind nicht hinterlegt, es gibt nur Figuren und eine Formel. Nach endlosen hin- und- her wurde schließlich erst einmal von Prof. Danzmann sowie gleich anschließend von Ihnen ausgesagt, dass die Daten für dieses Eichungsverfahren nicht hinterlegt werden können, aus dem guten Grund, weil dieses Eichungsverfahren bei LIGO nicht durchgeführt wurde!
Also noch einmal meine Frage:
Falls man dieses Kalibrationsverfahren, welches Sie “Engelhardt’sche Verfahren” genannt haben, durchgeführt hätte, ist es davon auszugehen, dass man ganz andere Meßdaten gesammelt und eine ganz andere Eichkurve erstellt hätte, als für die angewandten LIGO-Kalibrationmethode? Ist davon auszugehen, dass die beiden Kalibrationsmethoden nicht konsistent gewesen wären, falls sie beide durchgeführt gewesen wären und wenn man sie hätten vergleichen können?
Hallo Frau Lopez,
ich war tatsächlich davon ausgegangen, dass Sie zumindest auf dem Level einfachen Leseverständnisses nachvollzogen hätten, worum es geht. Ob z.B. eine bestimmte Wortkombination in einem Artikel auftritt oder nicht ist schließlich auch für Laien nachvollziehbar, die sich für das Thema interessieren. Insofern wäre hilfreich gewesen, wenn Sie Aussagen, die Sie lediglich ungeprüft von Herrn Engelhardt übernommen haben, sinngemäß mit einem “Herr Engelhardt sagt:” eingeleitet hätten.
Wenn, wie Sie sagen, die Grundlage Ihrer Einwände die Behauptungen von Herrn Engelhardt sind, dann lassen Sie doch jetzt bitte erst einmal ihn und mich weiterdiskutieren; da gibt es aus meiner Sicht nämlich noch einigen Klärungsbedarf und einige Missverständnisse.
@ Pössel:
Herr Engelhardt, obwohl er wahrscheinlich nicht didaktisch ausgebildet wurde, kann jedoch einem Laien sehr wohl durch einen sehr klaren allgemeinverständlichen Schreibstil, sowie durch Veranschaulichungen bzw. Vereinfachungen Grundprinzipien seines Handwerks als Experimentalphysiker vermitteln. So hat mich zum Beispiel seine Veranschaulichung, man behauptet gemessen zu haben, dass Gravitationswellen aus 4 Lichtjahren Entfernung einen 40 Kg-Spiegel um eine Haarbreite verschoben haben, völlig verdutzt, wie auch die Veranschaulichung des Physikers Christian Speicher. Das alles scheint mir gar nicht “sensationell”, sondern vielmehr völlig irreal, geradezu esoterisch – und ich habe keinen Hang zu Esoterik. Ich hätte diese “Messung” sonst möglicherweise ohne irgendetwas zu verstehen und auch ohne zu zucken geschluckt, wie die überwiegende Mehrheit der Physiklaien in der Bevölkerung, wenn Herr Engelhardt mir das nicht für Laien erklärt hätte.
Wie denn auch sei: Sie dürfen sich gerne weiter allein mit Herrn Engelhardt austauschen, wenn er dazu bereit ist, kein Problem, jedoch hätte ich noch gerne ganz kurz die Beantwortung meiner Frage, vielleicht mit ja oder nein:
Falls man das Kalibrationsverfahren, welches Sie “Engelhardt’sche Verfahren” genannt haben und im LIGO-Kalibrationspapier [63] beschrieben wurde, durchgeführt hätte, ist es davon auszugehen, dass man ganz andere Meßdaten gesammelt und eine ganz andere Eichkurve erstellt hätte, als für die effektiv angewandten LIGO-Kalibrationmethode? Ist davon auszugehen, dass die beiden Kalibrationsmethoden nicht konsistent gewesen wären, falls sie beide durchgeführt gewesen wären und wenn man sie hätten vergleichen können?
Danke für Ihr Verständnis. Wie Sie in Unkenntnis der näheren Umstände und der Hintergründe auf bestimmte Veranschaulichungen reagieren, ist natürlich nicht besonders aussagekräftig.
Zu Ihrer Frage: Die Antwort hängt davon ab, wie Herr Engelhardt es anstellen würde, aus dem von ihm geforderten Grundprinzip (gravitationswellenähnliche Signale einspeisen; Input und Output als Funktionen der Zeit behandeln) die Kalibrationsfunktion abzuleiten. Mir ist spontan nicht klar, wie das laufen sollte. Wenn es gehen sollte, dann würden für diese Kalibration zwar ganz andersartige Messdaten gesammelt worden sein bei der tatsächlichen LIGO-Kalibration (man misst eben unterschiedliche Größen). Aber sobald die Antwort-Kurve des Detektors bestimmt wäre, sollten die Rekonstruktionen empfangener oder künstlicher Signale aus dem Detektor-Output im Rahmen der Fehlergrenzen in der Tat konsistent sein. Aber das sind sehr hypothetische Überlegungen. Ich sehe keinen Grund, warum man es sich so kompliziert machen und einen anderen als den messtechnisch einfachen und weitgehend störungsfreien Weg wählen sollte, den die LIGO-Leute gegangen sind.
“Sie können sich sparen, mich mit Links und Hinweise auf Papiere über das LIGO-Experiment die ganze Zeit zu überschütten, Sie sollten sich eigentlich denken, wie jeder es logischerweise denkt, dass ich nichts damit anfangen kann und sie auch deswegen überhaupt nicht lese.”
Gut, somit bestätigen Sie also Herrn Dr. Pössels Aussage, dass von dieser Methode nichts im Kalibrationspapier steht.
Damit kann man sich der nächsten Fragestellung widmen.
Herr Pössel,
was Sie hier beschreiben, ist nicht „mein“ Vorschlag, sondern das, was im discovery paper mit dem Satz ausgedrückt wird: “The detector output is calibrated in strain by measuring its response to test mass motion induced by photon pressure from a modulated calibration laser beam.” Ich gehe davon aus, dass dies nicht nur gesagt, sondern auch gemacht wurde. Allerdings finde ich dazu keine Daten und Herr Danzmann sagt, dass es auch keine gibt. Hieraus ergibt sich meine Antwort auf Ihre heutige Frage um 16 Uhr.
Hinzufügen möchte ich noch, dass man die Spiegelverschiebung auch nachträglich per Strahlungsdruck durchführen und messen sollte, nachdem man die Eigenschaften des GW-Signals genau kennt und mit dem Eichlaser simulieren kann.
Herr Engelhardt,
in dem von Ihnen zitierten Satz aus dem Discovery Paper und auch im Calibration paper [63] steht weder etwas von im Frequenzverlauf nachgebildeter Gravitationswellensignale noch etwas von der Aufzeichnung des Zeitverlaufes.
Beides sind Eigenschaften der Kalibration und der dabei erhobenen Daten, die Sie in Ihrem Kommentaren und auch von Herrn Danzmann gefordert haben.
Beides sind Eigenschaften, welche die tatsächlich durchgeführte Kalibration nicht hat – und zwar aus guten Gründen.
Beides sind Eigenschaften, die Sie – ich weiß nicht, aus welchen Gründen – in den oben zitierten Satz “The detector output is calibrated in strain by measuring its response to test mass motion induced by photon pressure from a modulated calibration laser beam” hineinlesen, aber eben fälschlich hineinlesen. Auf diesem falschen Verständnis baut dann Ihre Kritik auf.
Ich biete noch einmal an: Wir könnten gerne Schritt für Schritt, angefangen mit meiner obigen Zusammenfassung, durchsprechen, wie Sie sich die Kalibration vorstellen, die da gelaufen sein soll oder sollte. Ich denke, wir würden vergleichsweise schnell darauf kommen, wo der Haken ist – und warum LIGO anders vorgegangen ist.
Herr Pössel,
wir sind schon alle Schritte durchgegangen. LIGO hat (auf irgendeine Weise) einen strain von 10^(-21) gemessen, was einer Spiegelverschiebung von 10^(-18) m entspricht, die angeblich von einer GW erzeugt wurde. LIGO ist verpflichtet (und hat das im e-print Ref.63 auch anerkannt), die zugehörige – und bisher unerreichte – Empfindlichkeit nachzuweisen, bevor von einer GW gesprochen werden kann. Es muss also gezeigt werden, dass eine kontrollierte Verschiebung von 10^(-18) m tatsächlich einen messbaren strain von 10^(-21) erzeugt. Dies zu leisten wurde im discovery paper auch angekündigt, aber offenbar nicht durchgeführt, denn es sind keine einschlägigen Daten vorhanden. Damit ist der „Nachweis von Gravitationswellen“ nicht erbracht, also hinfällig.
Ich danke Ihnen, dass Sie mir Gelegenheit geben, diesen Sachverhalt nicht nur intern mit dem Einstein Institut zu diskutieren, aus dem leider außer Verbalinjurien keine Antworten geäußert werden, sondern auch gegenüber einer breiteren, interessierten Öffentlichkeit darzustellen.
Herr Engelhardt,
wir sind kaum etwas durchgegangen. Wir haben nicht darüber gesprochen, wie Sie mit Ihrem Verfahren überhaupt die Response-Funktion bestimmen wollen. Welche Funktionsbasis wollen Sie wählen? Vernünftigerweise wählt man eine Fourier-Basis – und dann liegt wiederum nahe, als Testsignale reine Sinussignale zu nehmen. Und die von LIGO angewandte Zweiteilung der Kalibration zu wählen, um noch weitere Störungen zu unterdrücken. Und schon sind wir weg von der übermäßig vereinfachten Vorstellung der als Funktion der Zeit produzierten und aufgezeichneten Signale und bei dem, was LIGO tatsächlich gemacht hat und wozu in [63] die Messkurven veröffentlicht sind.
Insofern reflektiert eine Reihe der Behauptungen, die Sie hier getätigt haben, leider nur Missverständnisse darüber, was bei LIGO tatsächlich passiert ist: Über die Kalibration, darüber dass LIGO mit Hardware-Injektionen seine Empfindlichkeit (unabhängig von der Kalibration) auch direkt gezeigt hat, über elementare Unterschiede wie jene zwischen der gemessenen Größe und deren Unsicherheit (sprich: der Genauigkeit).
Ich finde es schade, dass Sie an dieser Stelle abbrechen, denn mich hätte schon interessiert, ob wir, wenn wir nur kleinschrittig genug vorgehen und so die Gefahr, aneinander vorbeizureden, verringern, die Missverständnisse hätten ausräumen können.
So bleibt mir nur der Schluss, dass Ihre derzeitige harsche Kritik an LIGO leider auf einer Reihe von Missverständnissen beruht, Sie die Diskussion, die dies hätte zeigen können (bzw. hoffentlich zum Teil für eine Reihe der Mitleser hier bereits gezeigt hat) aber jetzt nicht fortsetzen möchten. (Was natürlich Ihr gutes Recht ist.)
Herr Pössel,
wieso unterstellen Sie mir immer wieder, dass ich das Eichverfahren, welches LIGO im discovery paper ankündigt und in Ref. 63, Sec. IV detailliert beschreibt, vorgeschlagen hätte?
Ihre Frage nach der Bestimmung der Response-Funktion ist leicht zu beantworten: Sie muss natürlich genauso gemessen werden, wie sie am 14.9.15 bestimmt wurde, als die Spiegelauslenkung durch eine Gravitationswelle erfolgte. Der „Response“ wurde als „strain“ in Fig. 1 des discovery letters veröffentlicht.
In Sec. IV von Ref. 63 wird der „photon calibrator“ beschrieben, welcher erlaubt, die Spiegel in gewünschter Weise per Strahlungsdruck zu bewegen: „Power modulation is accomplished via an acousto-optic modulator that is part of an optical follower servo that ensures that the power modulation follows the requested waveform [14].“ Das „displacement“ des Spiegels ist dann durch Formel (10) gegeben, zu der aber keine Messdaten veröffentlicht werden. Es wird nicht gesagt, dass man ca. 10^(-7) W modulierte Hilfslaserleistung benötigt, um eine Auslenkung von 10^(-18) m zu bewirken. Erst wenn diese Daten, die in (10) eingehen, z.B. in Form einer Eichkurve dokumentiert sind, ist der Nachweis für die angebliche Empfindlichkeit der Apparatur erbracht. Es heißt sogar, dass diese Messungen mehrfach wiederholt wurden: “Measurements made during and after the observation period revealed that the estimate of x^(PC)_T includes systematic errors delta_x^(PC)_T , resulting in frequency-independent correction factors of 1.013 and 1.002 for H1 and L1, respectively”. Nur, wo sind die Daten? Herr Danzmann sagt, es gibt sie nicht.
Man kann nur spekulieren, warum diese Daten nicht zu erhalten waren. Vermutlich erzeugte eine modulierte Zusatzleistung von 10^(-7) W zur stationären Laserleistung von 100 kW keinen messbaren „response“ und da hat man eben etwas anderes gemacht als in Sec. IV beschrieben. Einen experimentellen Nachweis für die behauptete Empfindlichkeit der Apparatur hat man aber nicht erhalten, denn man hätte ja zumindest nachträglich den gemessenen strain gegen die modulierte Laserleistung auftragen und so eine Eichkurve erzeugen können. Aber auch das scheint nicht zu gehen, weil man offenbar nicht weiß, welche Auswirkung eine mit einer Frequenz von ca. 150 Hz modulierte Laserleistung mit einer Amplitude von 10^(-7) W auf die Position der Spiegel hat. Dann allerdings kann man auch nicht von einem gemessenen Response auf eine Spiegelauslenkung von 10^(-18) m zurückschließen. Mit anderen Worten: Es gibt (bisher) keinen experimentellen Nachweis für eine Gravitationswelle.
Es ist natürlich Ihr gutes Recht, den LIGO-Leuten und dem auf Fragen schweigenden Einstein-Institut zu glauben, was immer dort behauptet wird. Ich für mein Teil befasse mich in diesem Zusammenhang nicht mit Glauben, sondern mit Physik. In Herrn Danzmann habe ich genügend Vertrauen um ihm abzunehmen, dass es weder eine Eichkurve gibt, noch dass eine solche aus den vorhandenen Daten rekonstruiert werden könnte. Warum sollte er an dieser Stelle lügen?
Herr Engelhardt,
ich unterstelle Ihnen keineswegs, dass Sie das Eichverfahren, welches LIGO im discovery paper ankündigt und in Ref. 63, Sec. IV detailliert beschreibt, vorgeschlagen hätten.
Im Gegenteil: Das Problem beginnt dort, wo Ihre Forderungen aus mir unerfindlichen Gründen über das dort detailliert beschriebene Verfahren hinausgehen. Sie argumentieren mit einem anderen Eichverfahren als dem dort vorgeschlagenen.
Sie fordern eine einfache Kurve “Eichsignal als Funktion der Zeit versus Detektor-Output als Funktion der Zeit” obwohl so eine Kurve ja nun wirklich nicht geeignet ist das zweistufige, im Frequenzraum durchgeführte Eichverfahren aus Ref. 63 zu dokumentieren.
Ich denke, wenn wir uns, wie ich vorschlug, Schritt für Schritt durch das LIGO-Eichverfahren durchgearbeitet hätten, wäre das recht schnell deutlich geworden.
Herr Pössel,
Sie missverstehen mich noch immer. Keineswegs stelle ich eine Forderung, die über Ref. 63 Sec. IV hinausgeht. Ich möchte lediglich, dass in Formel (10) Daten eingesetzt und diese veröffentlicht werden. Also: P(f) steuert man mit dem modulierten Hilfslaser, rechnet mit (10) das displacement aus, welches von der Größenordnung 10^(-18) m sein sollte. Mit dem Interferometer misst man gleichzeitig dieses displacement und liest es am detector output aus. Diese Schritte muss man ohnehin gemacht haben, wenn man den Apparat nach Sec. IV geeicht hat. Statt unter Formel (10) auf die Skizze Fig. 2 zu verweisen, verweist man auf eine Figur, in der die Daten tatsächlich gegeneinander aufgetragen werden.
Unbegreiflich, dass Herr Danzmann sagt, die beschriebene Darstellung ginge nicht. Wenn das so ist, hat man eben den Apparat nicht geeicht. Jedenfalls nicht bei einer relevanten Laserleistung, die nur von der Größenordnung 10^(-7) W sein darf, weil sonst die Bewegung der Spiegel nicht vergleichbar mit der durch die gemessene GW erzeugten wäre. Freilich müssen diese 10(-7) W auf einem Level von 100 kW eingespeist werden, was voraussetzt, dass die Laserleistung im Interferometer extrem stabil ist.
Sie schrieben ursprünglich, die Lücke bestehe darin, “dass das Messsignal, nämlich der ‘strain’ zwischen beiden Interferometerarmen, als Funktion der Zeit präsentiert wird, während ein ebenso großer strain, der durch kontrollierbaren Strahlungsdruck in ähnlicher Wellenform erzeugt wird, dem Leser als Funktion der Zeit vorenthalten wird. Mir ist es trotz Googelns nicht gelungen, ein solches Eichsignal zu finden. Umso mehr bin ich auf Ihre Eichsignale als Funktion der Zeit gespannt, die Sie den einschlägigen Publikationen angeblich entnehmen können.”
Nun findet aber die Eichung weitgehend im Frequenzraum statt (Fourier-transformiert), die Signalanalyse dann ja später auch. Die Ergebnisse der Eichung sind dementsprechend (ich verwies wiederholt auf die Abbildungen) auch im Frequenzraum angegeben.
Diese Ihre oben und an anderer Stelle nachlesbare Forderung, es müsse aber ein vom Zeitverlauf und Frequenzspektrum realistisches Eichsignal (“ähnliche[r] Wellenform”) erzeugt und als “Funktion der Zeit” wiedergegeben werden, meine ich, wenn ich sage: Sie stellen Forderungen, die über Ref. 63 und das dort beschriebene Verfahren hinausgehen.
Wenn Sie jetzt sagen, Sie würden/wollten gar nicht über das in Ref 63. beschriebene Verfahren hinausgehen: Warum sind Ihnen offenbar die Messungen bei konstanter Frequenz (natürliche Basis im Frequenzraum) und deren Ergebnisse zu wenig? Warum fordern Sie stattdessen für die Eichung eine komplexere Wellenform (für spätere Konsistenzchecks gibt es das, wie schon erwähnt)? Wieso sollte eine komplexere Wellenform überhaupt Teil der Eichung sein, in der man sich ja tunlichst ein möglichst einfaches Funktionensystem wählt, um die Übertragungsfunktion überhaupt berechnen zu können?
Warum, wenn Sie nicht über das in Ref. 63 beschriebene Verfahren mit seiner Messung von Funktionen der Frequenz hinausgehen wollen, fordern Sie eine explizite Darstellung als Funktion der Zeit? Und sehen es als schwerwiegenden Fehler an, wenn Sie eine solche Darstellung nicht bekommen? Natürlich kann man die Ergebnisse nachträglich irgendwie Fourier-transformieren, aber was wäre denn bei dem in Ref. 63 beschriebenen Verfahren, das im Frequenzraum arbeitet, in solch einer Darstellung enthalten, das nicht im Frequenzraum viel deutlicher wäre – und näher am Messprinzip der Eichung?
Wenn Sie Ihre expliziten Forderungen zurücknehmen, bei der Eichung müssten aber komplexe Wellenformen direkt erzeugt werden, und das Ergebnis müsse als Funktion der Zeit dargestellt werden, dann könnten wir ja noch darüber reden, was Sie an Verfahren und Darstellung aus Ref. 63 stört. Aber solange Sie diese Forderungen stellen, gilt eben, was ich schrieb: Ihre Forderungen gehen über das hinaus, was Ref. 63 verspricht (und hält). Sie argumentieren dann implizit mit einem anderen Eichverfahren als dem dort vorgeschlagenen.
Herr Pössel,
ich hoffte, es klar ausgedrückt zu haben, dass ich nichts weiter sehen möchte als die Daten, die man in die rechte Seite von (10) zecks Eichung hineingesteckt hat, welche dann zu einer Auslenkung (linke Seite) von 10(-18) m geführt haben. Dazu sollte die Power-Oszillation des Hilfslasers ca. 150 Hz betragen und etwa 10 Schwingungen liefern. Nach meiner Abschätzung müsste die Leistungsamplitude etwa 10^(-7) Watt betragen. Auf diese Weise würde die Wirkung des GW-Signals auf die Spiegel einigermaßen gut simuliert. Natürlich kann man auch noch andere Frequenzen und Amplituden wählen. Am realistischsten würde die Eichung, wenn man die “requested waveform” der GW genau anpasst, wie in Sec. 4 beschrieben. Letzteres kann man natürlich nur nachträglich machen, aber solche Messungen wurden ja auch durchgeführt. All dies muss man beim Einsatz des PC zwecks Eichung so oder so ähnlich gemacht haben. Leider wurden jedoch die einschlägigen Daten nicht veröffentlicht. Insbesondere die Leistung des Hilfslasers P(f) kann man Ref. 63 nicht entnehmen.
Kennt man die Daten, die in die rechte Seite von (10) einzusetzen sind, so ergibt sich aus der linken Seite die resultierende Auslenkung, welche mit Hilfe des hochempfindlichen Interferometers gemessen wird und mit der Rechnung verglichen werden kann. Besteht hinreichende Übereinstimmung, so hat man dokumentiert, dass es tatsächlich möglich ist, mit LIGO Spiegelauslenkungen von 10^(-18) m zu messen, was alles andere als selbstverständlich ist. Erst wenn dies hinreichend belegt und veröffentlicht ist, kann man evt. vermuten, dass GW150914 durch eine GW erzeugt worden sein könnte. Besser wäre es natürlich, wenn man mehrere solcher Ereignisse abwartete und dokumentierte. Es soll ja ca. 10 davon pro Jahr geben, die man allerdings noch nicht gesehen hat.
Um es noch einmal ganz deutlich zu sagen: Man hat doch den Hilfslaser, das Interferometer und Formel (10) zwecks Eichung benützt, oder? Warum veröffentlicht man dann nicht die hineingesteckten und die resultierenden Daten?
Herr Engelhardt,
so wie Sie es jetzt schreiben, habe ich es hoffentlich verstanden. Mit zahlreichen Ihrer vorigen Aussagen kann ich Ihre jetzige Nachfrage nicht wirklich in Einklang bringen; ich vermute, Herrn Danzmann ging es genau so. Aber sei’s drum; es sieht so aus, als hätten wir zur gegenseitigen Frustration aneinander vorbeigeredet.
Direkt zu Ihrer Frage: Aus meiner Sicht ist es wichtig, zwischen Kalibration und dem Nachweis der Linearität des Detektors zu unterscheiden.
Sind wir uns in dieser Aussage einig? Ich frage nach, weil sich ein Großteil Ihrer Nachfrage auf die Linearität zu beziehen scheint, Sie selbst das aber mit dem Begriff Kalibration bzw. Eichung belegen.
Ich befürchte weiteres aneinander-vorbei-reden, wenn wir an dieser Stelle nicht vorsichtig sind und unseren Gebrauch dieser beiden Begriffe klären (Kalibration vs. Linearitätsprüfung).
Herr Pössel,
eine „Linearitätsprüfung“ ist zweitrangig, denn der Zusammenhang zwischen Auslenkung und Laserpower nach (10) ist lineare Proportionalität. Die Richtigkeit von (10) ist gut gesichert und Voraussetzung dafür, dass man bei gegebenem Strahlungsdruck (Laserpower) die zugehörige Auslenkung berechnen kann. Darauf beruht ja die Eichmethode von LIGO.
Der Zusammenhang zwischen Aufhellung des Dunkelfelds und Phasenverschiebung der interferierenden Strahlen im Interferometer ist A_D = A_H sin (Δφ) = A_H Δφ für Δφ = 2 π d/λ «1, also auch linear abhängig von der Auslenkung d. (A_D,H Amplituden im Dunkel- bzw. Hellfeld.)
Wichtiger ist es nachzuweisen, dass man eine Auslenkung von 10^(-18) m, die man gemäß (10) per Strahlungsdruck erzeugt hat, tatsächlich messen kann. Bis jetzt liegen dazu keine Daten vor.
Herr Engelhardt,
ich bin anderer Ansicht, und zwar aus dem folgenden Grund:
Vereinfacht angenommen, der Zusammenhang zwischen Messgröße X und Detektor-Output D wäre linear (was man durch eine entsprechende Linearitätsprüfung nachweisen muss), in anderen Worten:
D = α· X,
mit einer Konstante α. Kalibration heißt in diesem Zusammenhang, den Wert der Konstanten α in einer geeigneten Einheit zu bestimmen. Dazu reicht es dank der Linearität, einen beliebigen bekannten Wert der Messgröße mit dem entsprechenden Detektor-Output zu vergleichen. Sobald man das getan hat, liegt α fest. Sobald α festliegt, kann man im Prinzip kalibrierte Messungen über den gesamten Linearitätsbereich hinweg durchführen.
Sprich: Sobald Linearität über den gewünschten Messbereich hinweg nachgewiesen ist, macht es keinen Sinn mehr zu fordern, die Kalibration (Bestimmung von α) müsse aber in einem ganz bestimmten Teil des Messbereichs vorgenommen werden. Aufgrund der Linearität kann die Kalibration im Prinzip mit einem beliebigen Messwert X vorgenommen werden, solange dieser Messwert bekannt ist.
Herr Pössel,
im Prinzip haben Sie Recht, nur praktisch sind die Dinge komplizierter. Die Beziehung A_D = A_H Δφ enthält noch einen Störterm A_D = A_H Δφ + A_S, der vom Falschlicht und von der mangelnden Amplitudenungleichheit der interferierenden Strahlen herrührt. Nach dessen Größe bzw. Beherrschung hatte ich gefragt, doch vom AEI keine Auskunft bekommen. Wenn A_S » A_H Δφ geht das zu messende Signal evt. im Rauschen unter. Desgleichen geht in Formel (10) nicht nur P(f), sondern auch der „stationäre“ Strahlungsdruck des Haupt-Lasers ein, der 12 Größenordnungen stärker ist. Schwankt er nur geringfügig, so wird dadurch die zeitliche Spiegelauslenkung bestimmt und man kann den Einfluss des Eichlasers nicht mehr messen. Auch hierzu keine Auskunft des AEI.
Wegen all dieser Unsicherheiten muss man den Zusammenhang zwischen detector output und Strahlungsleistung des Hilfslasers im relevanten Bereich messen, also bei resultierenden, kontrollierten Auslenkungen von 10^(-18) m. Ob dieser Zusammenhang in diesem Bereich dann linear ist oder nicht, ist ziemlich unwichtig, denn man kennt ja nun den tatsächlichen Zusammenhang, d.h. man besitzt eine experimentelle Eichkurve. Solange man die nicht gewonnen hat, ist das Gerät nicht als geeicht anzusehen und die „Entdeckung“ nicht nachgewiesen.
Herr Engelhardt,
natürlich sind die Dinge praktisch komplizierter. Ich würde nur nie auf die Idee kommen, die Frage nach den Störeinflüssen und dem Rauschen als Teil der Kalibration zu sehen.
Das sind konzeptuell getrennte Untersuchungen (die aber sämtlich durchgeführt wurden; ich hatte das ja hier bereits recht früh beschrieben):
(a) man testet die Linearität des Detektors (und wie Sie bereits schrieben: die kommt nicht unerwartet, da es jeweils um kleine Abweichungen, also um die linearen Terme von Taylor-Entwicklungen geht). Ergebnis: Detektor in der Tat linear.
(b) man kalibriert den Auslesemechanismus, und das heißt dank der Linearität: im Prinzip kann man diesen Schritt bei beliebigen Auslenkungen machen. Was das “im Prinzip” angeht sind wir uns jetzt einig, entnehme ich Ihrem letzten Kommentar – korrekt?
Anschließend kommt dann aber, wie Sie richtig bemerken, noch die Frage des Rauschens. Die hat aus meiner Sicht nichts mit der Kalibration (=funktionaler Zusammenhang Spiegelverschiebung und Detektor-Output) zu tun, sondern ist eine gesonderte Frage: Bis zu welcher Amplitude geht ein Signal im Rauschen unter? Wie groß ist das Rauschen überhaupt?
Der erste Schritt besteht darin,
(c) in einer Situation völlig ohne signifikantes Gravitationswellen-Signal (und das ist meistens!) direkt das Rauschen zu messen und auszuwerten. Amplitudenschwankungen, Frequenzinstabilitäten, Elektronikrauschen treten schließlich auch ganz ohne Signal auf, und da (bzw. soweit) das System linear ist, kann man sie auch ohne zusätzliches Signal vermessen. Einfach schauen, wie groß das Rauschen überhaupt bei den unterschiedlichen Frequenzen ist.
Das tut LIGO fortwährend, und die dabei entstehenden Rauschkurven sind mit das wichtigste, was die LIGO-Forscher in den letzten Jahrzehnten erstellt, analysiert, verbessert haben und anhand dessen sie die Empfindlichkeit ihrer Detektoren definieren.
Zusätzlich zu den von Ihnen genannten sind da ja durchaus noch weitere Rauschquellen: Brown’sche Bewegung der Spiegeloberflächen, Schrotrauschen auf den Spiegeln, Gravitations- und seismische Einflüsse insbesondere in den niedrigen Frequenzbereichen.
Deswegen ist die Rauschkurve, anhand derer man die Detektor-Empfindlichkeit beurteilen kann, auch im PRL-Paper prominent platziert: als Abbildung 3 (b), direkt Teil der grundlegenden Beschreibung des Detektors.
Das LIGO-Team hat speziell zu diesem zentralen Thema noch eigene Ergänzungen herausgebracht: hier ist die Charakterisierung des Detektors und seines Rauschverhaltens mit Verweisen auf entsprechende vorige Studien (in PRL veröffentlicht), und hier (bislang nur zur Veröffentlichung eingereicht) ist dem Thema möglicher vorübergehender Störungen (die eine nur-Rausch-Kurve nicht notwendigerweise erfasst) ein eigener Artikel gewidmet.
Wenn Elektronikrauschen, Dunkelstrom, Falschlicht etc., die ja nun wirklich immer auftreten wenn der Detektor in Betrieb ist, ein Problem wären, würde man das in den in veröffentlichten Rauschkurven direkt sehen. Diese Einflüsse sind Teil des Rauschens, das man vermessen hat.
Wenn man all das charakterisiert hat, kann man zur Sicherheit und als Konsistenz-Test natürlich immer noch das machen, was Sie ja auch mehrfach gefordert haben: künstliche Signale erzeugen, in den Detektor einspeisen und schauen, was am Ende (Nachweis plus Rauschen, analysiert wie man ein GW-Signal analysieren würde) herauskommt. Das bringt uns zu
(d) Hardware-Injektionen, bei denen man genau das gemacht hat, und zwar soweit ich sehen kann tausendfach, mit vielen verschiedenen möglichen, aber auch unrealistischen, nur zu Testzwecken eingespeisten Wellenformen. Auf entsprechende Artikel hatte ich in einer früheren Antwort an Frau Lopez hier verwiesen, auf das LIGO Open Science Center, wo sie die Daten solcher Signale selbst einsehen können, in dieser Antwort.
Allerdings hat man diese künstlichen Signale (zumindest in den Fällen, die ich gefunden habe) nicht direkt mit Strahlungsdruck erzeugt, sondern mithilfe von elektrostatischen Aktuatoren. Aber am Grundprinzip ändert das nichts: die Aktuatoren sind, siehe oben, kalibriert, und ihre künstlichen Signale zeigen, dass man Gravitationswellensignale der jetzt tatsächlich gemessenen Größe, und sogar noch einige schwächere Signale, mit den LIGO-Detektoren trotz des Rauschens tatsächlich nachweisen kann.
Na wer sagt’s denn, funktioniert doch prima:
Heute gibt es über AAS um 19:15 eine PK https://iframe.dacast.com/b/59062/c/316974
zur 3. Gravitationswelle GW151226, die über 5σ lag.
Die 2. LVT151012 hatte es ja nur bis 2σ geschafft.
Grüße Senf
Herr Senf schrieb (15. Juni 2016 13:46):
> Na wer sagt’s denn […] Heute gibt es über AAS um 19:15 eine PK […]
Man darf immerhin gespannt sein, ob denn (wenigstens) diesmal Ergebnisse Modell-unabhängiger Messungen vorgelegt würden, die besagten, dass die Passage einer Gravitationswelle wahrgenommen worden wäre, und nicht auch, oder stattdessen nur, korreliertes Wackeln gewisser Spiegel.
Sie erwarten doch nicht von 8 Spiegeln korreliertes Wackeln ohne “äußere” GW?,
die alle Spiegel gleichsam triff, gleichzeitig 4 und nach 10ms die anderen 4.
Herr Senf schrieb (15. Juni 2016 15:34):
> Sie erwarten doch nicht […]
Anspruch, Können und Stolz von Experimentatoren liegen eher darin, sich jeglicher Erwartungen hinsichtlich der Versuch für Versuch zu gewinnenden Messwerte zu enthalten. (Leider wird dieses Ideal aber bisweilen durch Wünsche nach „Ertrag“ kompromittiert.)
Entsprechend habe ich kein ausgeprägtes und/oder gepflegtes Talent zum „Model Building“.
Allerdings …
> von 8 Spiegeln korreliertes Wackeln ohne “äußere” GW?,
die alle Spiegel gleichsam triff, gleichzeitig 4 und nach 10ms die anderen 4.
… habe ich ja immerhin schon im Februar mal halb aus Spaß amd Kontrarianismus und halb aus Hoffnung aus Ertrag vom Kontrarianismus zum Beispiel Neutrino-gestoßene Wackeleien angesprochen. (Meinentwegen gern auch wegen astronomischen Quellen, die entsprechende Neutrinos geeignet kleckerweise abgegeben hatten.)
Sorry, aber die werden ihr Nachweisprinzip nicht grundlegend geändert haben. Aber eigentlich sollte natürlich jeder, der abfällig vom korrelierten Wackeln spricht, eine plausible Alternativerklärung dafür haben, warum das Wackeln so exakt die charakteristische Wellenform für eines der erwarteten Gravitationswellensignale nachmacht.
Markus Pössel schrieb (15. Juni 2016 15:36):
> eigentlich sollte natürlich jeder, der abfällig vom korrelierten Wackeln spricht, eine plausible Alternativerklärung dafür haben, warum […]
Mich interessiert Ausbildungs- und Beruf(ung)sgemäß allein, was gemessen bzw. was durch Messung ausgeschlossen wurde. Eine eventuelle Abfälligkeit meiner damit verbundenen Äußerungen ist allein eine Reaktion auf eventuelle Abfälligkeit(en) gegenüber dieser Einstellung.
Herr Pössel,
es freut mich, dass Sie nun genau verstanden haben, und dass es keinen Dissens mehr über das gibt, was ich im Einklang sowohl mit dem discovery paper als auch mit dem e-print Ref. 63 gefordert habe. Sie beschreiben dies mit den Worten: „…kann man zur Sicherheit und als Konsistenz-Test natürlich immer noch das machen, was Sie ja auch mehrfach gefordert haben: künstliche Signale erzeugen, in den Detektor einspeisen und schauen, was am Ende (Nachweis plus Rauschen, analysiert wie man ein GW-Signal analysieren würde) herauskommt.“ Nur handelt es sich hier nicht um einen “Konsistenz-Test”, sondern um die primäre Eichmethode per Strahlungsdruck, die LIGO mit den Worten beschreibt: „The detector output is calibrated in strain by measuring its response to test mass motion induced by photon pressure from a modulated calibration laser beam.” In Ref. 63 wird sie unter Bezugnahme auf Formel (10) noch genauer ausgeführt, jedoch werden dort keine experimentellen Daten mitgeteilt.
Auch Ihnen ist nun aufgefallen, worum es in dieser Diskussion die ganze Zeit geht: „Allerdings hat man diese künstlichen Signale (zumindest in den Fällen, die ich gefunden habe) nicht direkt mit Strahlungsdruck erzeugt, sondern mithilfe von elektrostatischen Aktuatoren“. Von Aktuatoren ist im discovery paper nicht die Rede, sie können also bestenfalls eine Hilfsfunktion haben, aber nicht die primäre Eichmethode per Strahlungsdruck ersetzen. Gegenüber Frau Lopez wurden Sie am 5.6. noch expliziter: „So [wie Herr Engelhardt die Eichung beschreibt] wird die Kalibration / Eichung bei LIGO schlicht nicht durchgeführt, und zu einem nicht durchgeführten Verfahren gibt es, wen wundert es, auch keine entsprechende Kalibrationskurve“. Und schließlich wurden Sie durch Herrn Danzmann bestätigt, als er mir schrieb: „So eine einfache Eichkurve, wie Sie sie sich vorstellen, gibt es nicht, weil der Prozess der Eichung viel komplizierter ist.“ Wohlgemerkt: Ich hatte mir den Eichprozess genauso vorgestellt, wie er von LIGO einschließlich der entscheidenden Formel (10) beschrieben wurde, der bei Durchführung natürlich zu besagter Eichkurve hätte führen können und müssen.
Wir können damit diese Diskussion beenden, denn Sie können zur nicht durchgeführten Eichung per Strahlungsdruck unter Verwendung von Formel (10) keine weiteren Informationen geben, weil Sie am Experiment nicht beteiligt waren. Im Nachgang zu seinem Kolloquium im IPP Garching hat Herr Allen, der detaillierte Fragen zur Eichung auch nicht beantworten konnte, auf Herrn Evan Goetz verwiesen, der mit dem PC-Calibrator vertraut sei. Herr Evans hat bereits seine Bereitschaft ausgedrückt, jede einschlägige Frage zu beantworten.
Herr Engelhard,
Ihre Antwort zeigt jedenfalls sehr klar, was hier vorgeht und wo nach wie vor Dissens zwischen uns besteht.
Erstens: Wenn Sie von Eichung/Kalibration reden, meinen Sie das, was ich in meiner letzten Antwort an Sie Schritt (d) genannt habe.
Ich, Herr Danzmann, die beiden weiteren AEI-Mitarbeiter mit denen ich über diesen Aspekt von LIGO gesprochen habe, meinen mit Kalibration/Eichung stattdessen das, was in meiner letzten Antwort Schritt (b) hieß. Auch der von Ihnen zitierte Satz (“The detector output is calibrated…”) bezieht sich auf Schritt (b). Und Paper [63] enthält alle zum Nachvollziehen von Schritt (b) nötigen Diagramme/Datenpunkte. Kann jeder nachlesen, der den Text über die von Ihnen angeführte Formel (10) hinaus weiterliest und sich sagen lässt, was mit dem in Formel (10) beschriebenen Prozess dann für die Kalibration eigentlich spezifisch gemessen wurde.
Dass Ihre Forderungen, was für das bzw. im Paper [63] versprochen, aber nicht gehalten werde, an der Sache vorbeigehen, ergibt sich genau aus diesem Ihren Missverständnis.
Ich bin sicher: wenn Sie mit Evan Goetz diskutieren und nicht darauf achten, dass er mit Kalibration etwas anderes meint als Sie, werden auch Sie beide aneinander vorbeireden.
Zweitens: Wenn man Sie darauf hinweist, dass genau das, was Sie hier abweichend vom Sprachgebrauch der anderen als Eichung bezeichnen, ebenfalls durchgeführt wurde, nur dass es anders heißt (hardware injection) und der Mechanismus ein anderer war (elektrostatische Aktuatoren), dann – ja, was?
Eigentlich könnte man dann sagen: Na gut, ist ja egal welches Wort dafür verwendet wird, wichtig ist die Physik, zeigen Sie mir doch bitte die entsprechenden Veröffentlichungen oder Daten: welche Signale wurden eingespeist, und was kam am Detektor-Output heraus?
Sie schränken Ihre Bedingungen dann stattdessen aber noch einmal künstlich ein: Auf einmal reicht nicht der generelle Nachweis, dass der Detektor auf ein künstlich erzeugtes Signal so reagiert wie erwartet, sondern es muss ein ganz spezifisches künstliches Signal sein, nämlich eines, das mit dem Photonenkalibrator erzeugt wurde.
Warum? Zur Demonstration des Funktionsprinzips und für den Nachweis, dass künstlich erzeugte Signale der richtigen Amplitude und Wellenform tatsächlich nachgewiesen werden können, ist es doch egal, mit welche Mechanismus die kontrollierte Spiegelverschiebung verursacht wird.
Wenn Ihre Antwort lautet “aber dieser Mechanismus wird doch im Discovery-Paper versprochen”, dann kann ich darauf nur sagen: Nein, das ist dann eine weitere Wiederholung ihres ersten Missverständnisses. Was in dem entsprechenden Satz mit Verweis auf Referenz [63] versprochen wurde, ist Schritt (b), nicht Schritt (d).
Wenn Ihre Antwort dagegen lautet “aber von Aktuatoren ist im Discovery-Paper nicht die Rede!”, kann ich nur sagen: das Discovery-Paper ist eine vergleichsweise kurze Zusammenfassung. Die Aktuatoren gehören untrennbar zum Messprinzip des Detektors. Das steht in Referenz [63] beschrieben und in jedem Artikel, der die Funktionsweise genauer beschreibt.
Zusammengefasst: Ihre Kritik beruht auf einer unguten Kombination eines Missverständnisses (Schritt b versus Schritt d), das sich durch alle Diskussionen zwischen Ihnen und mir bzw. Herrn Danzmann zieht, mit übermäßig spezifischen Forderungen.
@ Markus Pössel
Engelhardt scheint bedient, egal, was haben Sie von der neuen Messung gehört?
http://www.n-tv.de/wissen/Gravitationswellen-im-All-gemessen-article17945646.html
Selber was gefunden:
http://www.aei.mpg.de/1897744/gw151226
Warum in die Ferne schweifen, … ?
https://scilogs.spektrum.de/relativ-einfach/gravitationswellen-neues-von-ligo/
Ich wiederhole hier meinen Beitrag von soeben, der chronologisch ganz oben irgendwo in der Diskussion gelandet ist:
Herr Pössel:
Ob nach der Befindlichkeit des Teilnehmers Manuel Krüger „Engelhardt bedient zu sein scheint“ ist ein erneuter unsachlicher und hetzender Einwurf dieses notorischen Stalkers in der Diskussion – sowie übrigens in früheren Diskussionen in Ihrem Blog. Sie hätten schon genug Anläße, diesen Ihre „Hilfsmoderator“ längst zu sperren, auch aus Ihrer Blog-Reihe „Einstein verstehen“, anstatt diese Drohung gegenüber Herrn Engelhardt und mir auszusprechen.
Ich bitte Sie ausdrücklich, die unsachlichen und herabsetzenden ad hominem Einwürfe dieses Teilnehmers konsequent zu moderieren, er ist nicht zu belehren und wird sein Verhalten nicht ändern, er kann es auch nicht, das ist eine langjährige Zwangshandlung.
Ihre äußerst lasche Moderation halte ich für unvertretbar und unzumutbar, vor allem jetzt, wo Dr. Engelhardt und ich angekündigt haben, dass wir uns von Ihrer Blog-Diskussion, die sich quasi vom Anfang an im Kreise dreht, sinnvolller Weise fern halten wollen.
Jocelyne Lopez
Frau Lopez,
“bedient” ist zwar salopp, aber doch nicht hetzend. Ihren “notorische[r] Stalker” gegen Manuel Krüger dagegen kann man als Bezichtigung einer Straftat werten. Wie war das doch gleich mit dem Splitter im Auge des Nächsten und dem Balken im eigenen Auge? Ich bitte um Sachlichkeit!
Und dass in Ihrem Kommentar null zur Sachdiskussion beigetragen, sondern nur die Metadiskussion weitergetrieben wird, ist auch direkter Gegensatz zu Herrn Krügers insgesamt kurzem und im Großteil einem neuen Sachaspekt gewidmeten Kommentar.
Insofern: Reißen Sie sich bitte zusammen. Ich werde hier weiterhin Beiträge wegmoderieren – Ihre oder Herrn Krügers oder sonstwessen – die hier eine Metadiskussion vom Zaun brechen wollen. Das stört die Sachdiskussion.
Ich fände es schade, wenn sich Herr Engelhardt jetzt hier ganz herausziehen würde. Genügend Missverständnisse zu Kalibration vs. hardware injection gibt es bei ihm ja offenbar leider nach wie vor. Mein Angebot, ruhig auch Schritt für Schritt durchzugehen, wie die Kalibration tatsächlich ablief, steht nach wie vor. Aber es ist natürlich nur ein Angebot; wenn Herr Engelhardt das nicht annehmen möchte, ist das seine Entscheidung.
Herr Pössel,
was Sie seltsamerweise „Metadiskussionen“ nennen, sind meine Proteste und Meldungen gegen ad hominen Angriffe von Teilnehmern. Dass Sie als verantwortliche Betreiber eines Blogs nur gegen solche Angriffe reagieren, wenn ich protestiere und mir dann vorwerfen, eine störende „Metadiskussion“ auszulösen, ist nur Zeugnis ihres Mangels an Objektivität und Ihrer eigenen Aversion gegen die „cranks“, wie Sie seit vielen Jahren selbst die Kritiker der Relativitätstheorie herabsetzend genannt haben, bevor Sie die lächerliche Wortkombination „unorthodoxe Kritiker“ als Ersatz für den Umgang mit solchen Leuten fabriziert haben. Wenn es unorthodoxe Kritiker gibt, wo sind dann die orthodoxen Kritiker, wenn ich fragen darf? Kritiker Ihrer Lieblingstheorie sind grundsätzlich bei Ihnen nicht erwünscht, Ihre Lieblingstheorie darf nicht kritisiert werden, ist sie ja über jede Kritik erhaben, darüber belehren Sie uns seit Jahren, sie ist hier nur „Schritt für Schritt“ endlos als absolute Wahrheit aufzunehmen, zum Mitschreiben, sonst nichts.
Ich habe von einer kontroversen Diskussion über die erneute sensationelle Bestätigung der seit einem Jahrhundert bestens bestätigte Theorie in Ihrem Blog ohnehin von vornherein nichts erwartet, wollte ich trotzdem nicht den Hinweis von Prof. Nicolai unbeachtet lassen. Jetzt habe ich aber genug von Ihrer „Gastfreundschaft“, danke.
Jocelyne Lopez
Frau Lopez,
sorry, aber ich springe nicht über jedes Stöckchen, dass Sie mir hinhalten.
Wie ich mit sachlicher Kritik umgehe, sehen Sie an meinen Sachantworten an Herrn Engelhardt und bei entsprechender Gelegenheit auch an Sie: mit Geduld und dem Bemühen, Missverständnisse aufzuklären.
Von Ihrer sachlich unbegründeten Meckereien aus geringfügigstem Anlass habe ich jetzt aber in der Tat genug. Insofern begrüße ich es sehr, dass Sie sich jetzt verabschieden. Die meisten Mitleser hier dürften das ähnlich sehen.
Das gilt ausdrücklich nicht für Herrn Engelhardt, der sich während unserer Sachdiskussion hier weitgehend polemischer Äußerungen enthalten hat und mit dem ich hier, wenn er noch Fragen hat, gerne weiter diskutiere.
Wenn Ihnen statt “unorthodoxe Kritiker” eine bessere Bezeichnung einfällt, bin ich für Vorschläge offen. Bereits jenen Begriff hatte ich ja ausdrücklich gewählt, um eine einigermaßen neutrale Bezeichnung für Menschen zu haben, die nicht Teil des regulären Wissenschaftsbetriebs für ein bestimmtes Forschungsgebiets sind, aber von außen (teils heftige) Kritik daran üben (Details in dem verlinkten Artikel). Dass Sie mir wie in Ihrem letzten Kommentar selbst jenen Versuch, guten Willen zu zeigen, klatschend um die Ohren hauen, ist ja leider typisch für Ihre extreme Einstellung, die es praktisch unmöglich macht, vernünftig mit Ihnen zu diskutieren.
Aber damit Schluss mit der Meta-Diskussion. Ich arbeite gerade an weiteren Blogbeiträgen, in denen die technische Seite von LIGO näher beleuchtet wird. Dazu hat die Diskussion mit Herrn Engelhardt ja einige schöne Anregungen geliefert.
Lieber Herr Pössel,
teilen Sie bitte Ihrer Leserschaft mit, dass die “Entdeckung von Gravitationswellen” (GW150914 und GW151226) nicht unumstritten ist. Siehe diese Briefe an das Nobelkomitee:
https://www.researchgate.net/publication/304581873_Open_Letter_to_the_Nobel_Committee_for_Physics_2016?ev=prf_pub
https://www.researchgate.net/publication/304623546_Letter_to_the_Nobel_Committee_on_LIGO_claims_for_gravitational_waves_detections_GW150914_and_GW151226
Leider setzen sich das Einstein Institut und die von ihm benannten Experten nicht mit der in diesen Briefen angesprochenen Problematik auseinander.
Mit besten Grüßen
Wolfgang Engelhardt
PS: Es wäre gut, wenn Sie mal Herrn Senf beispringen könnten. Er schafft es nämlich nicht, aus Ihrem Ausdruck für eine GW: (x02-x01)(1+A sin (kz-ωt)) den zugehörigen Energiefluss F= {(c³ IaI² ω²) / (64 π G)} * I cosθ I herzuleiten.
Herr Pössel,
Sie haben die Diskussion weitergeführt, obwohl ich sie für beendet erklärt habe, weil inzwischen ein kompetenter Gesprächspartner vom Einstein-Institut benannt wurde. Sie selbst sind weder Autor noch waren Sie bei den Experimenten anwesend. Deshalb können Sie keine belastbare Antwort geben, warum LIGO nicht die Messungen durchgeführt hat, die in PRL 116, 061102 (2016) angekündigt wurden. Warten wir ab, was Herr Goetz dazu sagen kann. Spekulationen über seine Antworten sind hier unangebracht.
Herr Pössel,
ich habe mal eine konkrete Frage, ich hab leider die Quelle verloren, war meiner Meinung nach aber auch wo hier im scilogs Blog bei wem. Die Frage ist, krümmt die Gravitationswelle selber nur den Raum oder auch die Zeit, konkret war die Aussage, Uhren würden nicht kurz schneller und langsamer gehen, wenn eine Welle durch sie läuft, nur der Raum selber würde gestaucht und gestreckt. Und wo ich schon dabei bin, Gravitationswellen tragen doch normal Energie durch die Raumzeit, und nicht nur “potenzielle Energie”?
Auch mich würde interessieren, wie man die Energie berechnet, die in einer Gravitationswelle steckt. Bei elektromagnetischen Wellen ist es klar: Sowohl das E-Feld als auch das B-Feld gehorchen der em Wellengleichung. Aus ExB berechnet man dann den Energiefluss.
Oben hat Herr Pössel die (linearisierte) Wellengleichung für eine Gravitationswelle bestätigt:
c^2 (@^2 G) / @z^2 = (@^2 G) / @t^2, welcher die Größe G = (x02-x01)(1+A sin (kz-ωt)) genügt. Wie berechnet man hieraus den Energiefluss, der durch diese Welle bei großem Abstand zur Quelle transportiert wird?
Formel 3 aus http://arxiv.org/abs/1606.07437
dazu noch http://arxiv.org/abs/1606.07644
Meine Frage war, wie man aus der Größe G = (x02-x01)(1+A sin (kz-ωt)), welche proportional zu einem frei wählbaren Abstand ist und die Dimension einer Länge hat, einen Energiefluss analog zum Poyntingvektor konstruiert. Herr Pössel kann das sicher beantworten.
reicht der Energiefluß in der Form
F= {(c³ IaI² ω²) / (64 π G)} * I cosθ I
a – komplexe Amplitude
ω – Frequenz der Graviwelle
θ – Einfallswinkel
ist aber eher interessant für die Randabsorption
an elastischen Resonanzdetektoren
Der Energiefluss F geht also gegen unendlich, wenn der Abstand von zwei Massen – und damit G – gegen Null geht? Welche Dimension hat a? Was ist “Randabsorption”? Ist LIGO ein “Resonanzdetektor”?
Entschuldigung, ich dachte die Konstanten c und G wären klar.
Buchstaben reichen halt nicht für alles, ist hier nicht “Ihr” G.
Wie also berechnet man den Energiefluss, der zu Pössels Größe G = (x02-x01)(1+A sin (kz-ωt)), welche die homogene Wellengleichung befriedigt, und offenbar eine Gravitationswelle modellieren soll?
corrigendum:
Wie also berechnet man den Energiefluss, der zu Pössels Größe G = (x02-x01)(1+A sin (kz-ωt)), welche die homogene Wellengleichung befriedigt, gehört, wobei G offenbar eine Gravitationswelle modellieren soll?
Aus “Ihrer Gleichung für G_x” nimmt man die gemessenen Werte für Amplitude und Frequenz und setze sie in die Formel für den Energiefluß F am Detektor ein.
Welche physikalische Größe symbolisiert der Buchstabe G in der Formel für den Energiefluss einer Gravitationswelle F= {(c³ IaI² ω²) / (64 π G)} * I cosθ I ? Diese Größe muss die Dimension [G ]= [m^7 / (s^5 Watt)] haben. Aus Herrn Pössels Ausdruck für eine Gravitationswelle (x02-x01)(1+A sin (kz-ωt)) kann Ihre Größe G nicht erschlossen werden.
Hallo Dr. Engelhardt,
Sie meinen [G] = m^5 / kg*s²
ich nehme: [G] = m^3 / kg*s²
liegt vlt am IaI² mit [a²] = m²/m² und [F] = W/m²
Lieber Herr Pössel,
teilen Sie bitte Ihrer Leserschaft mit, dass die “Entdeckung von Gravitationswellen” (GW150914 und GW151226) nicht unumstritten ist. Siehe diese Briefe an das Nobelkomitee:
https://www.researchgate.net/publication/304581873_Open_Letter_to_the_Nobel_Committee_for_Physics_2016?ev=prf_pub
https://www.researchgate.net/publication/304623546_Letter_to_the_Nobel_Committee_on_LIGO_claims_for_gravitational_waves_detections_GW150914_and_GW151226
Leider setzen sich das Einstein Institut und die von ihm benannten Experten nicht mit der in diesen Briefen angesprochenen Problematik auseinander.
Mit besten Grüßen
Wolfgang Engelhardt
PS: Es wäre gut, wenn Sie mal Herrn Senf beispringen könnten. Er schafft es nämlich nicht, aus Ihrem Ausdruck für eine GW: (x02-x01)(1+A sin (kz-ωt)) den zugehörigen Energiefluss F= {(c³ IaI² ω²) / (64 π G)} * I cosθ I herzuleiten.
Engelhardt, nur weil sie und Lopez neben ein paar anderen “Kritikern” der Physik diese Dinge nicht verstehen können und/oder wollen, bricht die Welt nicht auseinander.
Würde man so einen Maßstab anlegen, dann gibt es nichts, das nicht von wem bestritten würde, demnach ist alles wo nicht unumstritten.
Hier spielt dann die Qualität der Kritik eine wichtige Rolle, wie kompetent ist jener der da zweifelt, was treibt ihn, was ist seine wahre Motivation.
Und es ist verständlich, dass sie beide nun einfach dort ignoriert werden, die Personen haben schon viel zu viel Zeit mit ihnen sinnlos verbrannt.
Was machen sie hier eigentlich wieder, sie hatten doch schon die Segel gestrichen, ist ihnen langweilig, wenn so gar keiner Notiz von ihnen nimmt?
Chrys schrieb (7. Juli 2016):
> Grob gesagt sind die „rigid rulers“ für x und y die gedachten „Meterstäbe zur Messung von proper distance“
Also (genauer) jeweils ein Paar von Beteiligten (“Enden”), deren “proper distance” gegenüber einander konstant ist.
Diese ansonsten ganz abstrakten, geheimnisvollen Werte von “proper distance” hängen nun offenbar mit (aus physikalisch-relativistischer Sicht relevanten, messbaren) Pingdauern zusammen; wie es z.B. Maggiore, S. 19, einigermaßen unbeholfen ausdrückt:
(Sofern die schon oft erwähnte SI-“Meter”-Definition ebenfalls auf der Bestimmung von Pingdauern beruht, auch wenn diese dabei leider nicht ausdrücklich erwähnt werden, erschließt sich auch der obige Hinweis auf “Meterstäbe“.)
> wäre diese GW jedenfalls etwas, das eine Raumzeit krümmt, indem nämlich die [Flächen gleicher Phase, senkrecht zur Ausbreitungsrichtung] intrinsisch quadrupolar deformiert werden
Hinsichtlich “proper distance” sind diese Flächen allerdings flach (sofern ich die Ausdrücke “Δ l” aus Markus Pössels entsprechendem Kommentar richtig verstanden bzw. interpretiert habe.
Der Zusammenhang zwischen “proper distances” und Pingdauern ist aber wohl nicht ganz einfach, so dass die genannten Flächen hinsichtlich der Pingdauer-Verhältnisse zwischen ihren Bestandteilen doch (wiederholt veränderlich) gekrümmt sind; und deshalb auch nicht unbedingt “Ebenen” genannt werden sollten.
> Starre x- oder y-rulers kann es da physikalisch gar nicht geben.
Doch: offenbar diejenigen, deren Enden in der Abbildung als die o.g. “fünf auffallend geraden/ruhigen” Beteiligten gezeigt sind; denn für konstante “proper distances” ist der Zusammenhang zu (konstanten) Pingdauern doch wohl sehr einfach. (Aber das sind nur die wenigsten Paare; insbesondere nur 10 von 528 der obigen Abbildung.)
> der begrifflichen Kontext der GR (nicht aber jener der SR) nach meinem Verständnis bereits verlassen.
– die Feststellbarkeit von Koinzidenzen (oder Reihenfolgen); insbesondere von Ping-Koinzidenzen (oder Ping-Reihenfolgen) je eines bestimmten Beteiligten gegenüber zwei unterscheidbaren anderen,
– die Feststellbarkeit von (permanenten) Ping-Koinzidenz-Gittern zwischen zahlreichen Beteiligten,
– die (eventuelle) Feststellbarkeit von (permanent) flachen, d.h. insbesondere von tetrahedral-oktahedrale, Ping-Koinzidenz-Gittern zwischen geeigneten Beteiligten …
p.s.
Test der möglicherweise kürzlich implementierten Kommentarvorschau:
$latex \LaTeX$,
\( \LaTeX \),
\[ \LaTeX \],
$$ \LaTeX $$.
@Frank Wappler / 11. Juli 2016 @ 22:20
Zunächst erneut eine Korrektur. Meine obige Aussage, dass durch eine ebene, in pos. z-Richtung laufende GW wie im Beispiel »die (x,y)-Ebenen intrinsisch quadrupolar deformiert werden,« nehme ich ganz entschieden zurück, denn das ist völliger Quatsch. Die Krümmungsformen zu einer solchen GW enthalten keine Terme mit dx ∧ dy, die Geometrie einer jeder einzelnen (x,y)-Ebene mit konstanten Werten für (t,z) ist stets flach. Die Krümmung der GW-Raumzeit kommt einzig durch die Art und Weise zustande, wie diese (t,z)-Familie flacher (x,y)-Ebenen dann in Abhängigkeit von u = (ct − z)/√2 zusammenhängt.
Die GW-Metrik besagt folglich auch nicht, dass ein in x- oder y-Ausrichtung plazierter, nach klass. Begriffen starrer Meterstab durch die Welle irgendwie “im Raume” deformiert würde. Hingegen besagt sie, dass sich eine mittels Pingdauer bestimmte “chronometrische Länge” eines solchen Meterstabes in Abhängigkeit von u ändert — es gibt da also keine, wenn man das so nennen kann, “chronometrisch starren” x- oder y-Meterstäbe. Die Krümmung der GW-Raumzeit macht sich gerade daran bemerkbar, dass man in x- wie in y-Richtung keine konstante Lichtgeschw. hat, die variiert hier abhängig von u. Infolgedessen wird die Pingdauer eines Lichtsignals bei seinem round trip von einem Ende des Meterstabs zum anderen und wieder zurück i.a. nicht stets dieselbe sein. Dieselbe Erkenntnis liesse sich dann prinzipiell auch durch interferometrisch festgestellte Phasenverschiebung erlangen.
Die Länge eines (im klass. Sinne) starren Meterstabes müsste sich demzufolge durch eine GW genauso verändern wie der Abstand zweier (ebenfalls in klass. Sinne) “freier Teilchen”, die man koinzident mit den Enden dieses Meterstabes positioniert hätte. Diese Koinzidenz bleibe trotz GW bestehen. Beim Proper Detector Frame geht man jedoch davon aus, dass man sich starre Meterstäbe verschaffen kann, die sich dazu verwenden lassen, eine Abstandsänderung der freien Teilchen infolge der GW festzustellen. Die Koinzidenz zwischen den freien Teilchen und den Enden eines solchen Meterstabes bliebe dann nicht bestehen. Was sogleich die Frage aufwirft: Welche Version sollen wir nun eigentlich glauben?
Da sind wir doch schonmal einen Schritt weiter.
Die verbleibenden Probleme ergeben sich aber wiederum daraus, dass Sie der ART Aussagen zuordnen, die dort einfach nicht zutreffen.
Nirgends steht geschrieben, dass die Länge eines (idealisiert, angenähert) starren Meterstabs gleich der mit Radarmethode ermittelten Länge sein muss. Und nirgends steht beschrieben, dass an den Meterstabenden platzierte freie Teilchen mit den Meterstabenden koinzident bleiben müssen.
Was die freien Teilchen in meiner Animation machen, kann man ganz direkt aus der Geodätengleichung ableiten (verbleibender nicht-Minkowski tt-Teil der Metrik): die bewegen sich relativ zu den Enden starren Meterstäben, sprich: ändern ihre proper distance zueinander. Das wird ja schließlich in der Animation dargestellt.
Chrys schrieb (13. Juli 2016 @ 23:27):
> es gibt da also keine, wenn man das so nennen kann, „chronometrisch starren“ x- oder y-Meterstäbe.
Selbstverständlich gibt es auch in einer Region mit GW “rundherum” Paare von Beteiligten, die gegenüber einander chronometrisch (in welchem nachvollziehbaren Sinne denn sonst??) starr blieben (also mit jeweils konstanter Pingdauer des einen bzgl. des anderen);
und in den hier betrachteten Fällen vermutlich (“aus Symmetriegründen”) sogar mit gegenseitig gleichen Pingdauern, sodass der Wert
1 / (2 * 299792453) (m / s) Pingdauer
durchaus im Sinne der SI-“Meter”-Definition als deren jeweilige(konstante) “Länge, in Metern” gelten kann,
sodass also wirklich von “Meterstäben” die Rede sein kann.
Schließlich betrachten wir ja wohl Beteiligte, für deren (Kausal-)Beziehungen untereinander Rindler-Horizonte o.Ä. keine Rolle spielen;
von denen also jeder Pings “rundherum” wahrnehmen konnte, zu jeder Anzeige diejenigen “rundherum” identifizieren und sortieren konnte, deren entsprechende Echos jeweils in Koinzidenz wahrgenommen wurden, und schließlich auch “rundherum” Beteiligte finden und sortieren würde, hinsichtlich denen die Pingdauer jeweils konstant blieb.
Vermutlich werden solche zueinander (chronometrisch) starren Paare aber nicht unbedingt mit jeweils konstanten Koordinaten-Tupeln “(x, y, z)” im Sinne von o.g. Koordinaten-“Frames” bestreußelt.
Und vermutlich sind die beiden Beteiligten, die ein solches (chronometrisch) starres Paar in einer Region mit GW bilden, nicht unbedingt beide “frei” (im nachvollziehbaren, relativistischen Sinne).
> die Pingdauer eines Lichtsignals bei seinem round trip von einem Ende des Meterstabs zum anderen und wieder zurück
???
Die Pingdauer eines Endes des Meterstabs bzgl. des anderen.
(Dem “Signal an sich” ist allenfalls Reise-Dauer Null zuzuschreiben.)
> i.a. nicht stets dieselbe sein.
Falls die Pingdauern eines Beteiligten bzgl. eines anderen nicht gleich blieben, waren sie im betreffenden Versuch offenbar nicht “Enden eines (des selben) Meterstabes” im Sinne der SI-“Meter”-Definition.
> […] Abstandsänderung der freien Teilchen infolge der GW festzustellen
Sofern die freien Teilchen nicht als gegenüber einander (chronometrisch) starr charakterisiert sind, sollte man nicht von “ihrem Abstand voneinander” sprechen, sondern von ihren (i.A. veränderlichen) Entfernungen bzw. konkret von ihren (i.A. veränderlichen) gegenseitigen Pingdauern.
Und sofern die genannten “Abstands“-Werte doch eigentlich Paare von Beteiligten charakterisieren, die gegenüber einander (chronometrisch) starr waren und blieben (nämlich den Enden bestimmter “Meterstäbe“),
ist es improper, damit (auch) irgendwelche transienten Paare charakterisieren zu wollen (also z.B. bestimmte Paare von freien Teilchen, die die Enden der “Meterstäbe” passierten).
> Die Koinzidenz zwischen den freien Teilchen und den Enden eines solchen Meterstabes bliebe dann nicht bestehen.
Ganz recht; natürlich abgesehen von gewissen Ausnahmen, die in der ersten Abbildung des obigen SciLogs-Beitrags ziemlich prominent erscheinen.
Der Zusammenhang ergibt sich als Theorem aus den (Mess-)Definitionen der Begriffe “GW”, “Meterstab” und “frei”.
Leihen wir uns gedankenexperimentell doch einmal einen starren Meterstab von Maggiores Proper Detector Frame aus, legen den e.g. in x-Ausrichtung hin, passend zur nachfolgend erwartenten Welle — etwa so, wie Einstein einen Meterstab längs des Bahndamms hinlegelegt haben würde — und positionieren noch je eine frei bewegliche Testmasse koinzident mit dessen durch ‘links’ und ‘rechts’ gekennzeichnete Enden. In einem Inertialsystem und noch ohne Welle liesse sich so etwas leicht bewerkstelligen. Anschliessend lassen wir die Pösselsche Beispiel-GW in z-Richtung durch das ganze Ensemble rauschen und schauen, was passiert.
Das Teilchen links berichtet dann: „Ich kann hier bei mir keinerlei Beschleunigung feststellen und bleibe koinzident mit meinem Ende des Meterstabes. Ergo kann nur mein Partner am anderen Stabende von der Welle herumgeschubst werden.” Der Partner am rechten Ende reportiert allerdings genau das gleiche und erlebt sich selbst ebenfalls in permanenter Koinzidenz mit seinem Ende des Meterstabes.
Eine physikal. Bestimmung zeiträumlicher Koinzidenzen kann freilich nicht davon abhängen, wohin dabei der Ursprung eines Koordinatensystems gelegt wurde. Doch genau dies handelt man sich ein bei dem Versuch, als vermeintlich physikalischen Effekt einer GW eine auf “rigid rulers” bezogene “proper motion” freier Teilchen hinzustellen.
Es kommt sogar noch schlimmer. Für eine solche angedachte “proper motion” existiert kein “proper speed limit” — ganz egal ob diese Bewegung nun als geodätisch oder, im Proper Detector Frame, als durch eine Newtonsche Kraft bedingt deklariert wird. Zu jeder noch so irrsinnigen Geschwindigkeit lassen sich auch Teilchen angeben, die beim unterstellten Hin- und Herwackeln diese Geschwindigkeit mühelos überschreiten würden. Wer sich so etwas dann widerspruchslos als eine ordinäre Bewegung von Testmassen im Raume aufschwatzen lässt, muss auch akzeptieren, für einigermassen ignorant gehalten zu werden.
Der entscheidende Fehler an Ihrer Betrachtung ist, dass man starre Körper selbst in der klassischen Physik nicht so behandelt (und behandeln kann), dass man einen beliebigen Punkt auf dem Körper als freies Teilchen betrachtet. Diese Beschreibung funktioniert nur, wenn man die Schwerpunktsbewegung des starren Körpers betrachtet (plus eine etwaige Drehung, die hier aber keine Rolle spielt). Bei freier Bewegung ist es der Schwerpunkt eines starren Körpers, der sich wie ein freies Teilchen bewegt – für die anderen Punkte gilt das nicht unbedingt.
Berücksichtigt man diesen Umstand, dann funktioniert alles, wie es soll: Aus Sicht des Teilchens am einen Ende ist der Schwerpunkt des starren Meterstabs halb soweit entfernt wie das Teilchen am anderen Ende. Da die Verschiebung durch die Gravitationswelle proportional zur Entfernung ist (wie bei Gezeitenkräften üblich/erwartet), wird der Schwerpunkt halb soweit auf das Beobachterteilchen zugerückt wie das freie Teilchen am Meterstabende.
Aus Sicht des Meterstabsmittelpunkts werden dagegen beide freien Teilchen an den Enden gleichweit nach innen gerückt, entsprechend der Verschiebung für den ursprünglichen Abstand von einem halben Meter.
Aus Sicht des Teilchens am anderen Ende ist die Argumentation die gleiche wie für das erste Teilchen.
Das Ergebnis ist also in allen drei Fällen das gleiche – Ihre Aussage, das Ergebnis sei vom Bezugspunkt abhängig, ist falsch. Das gleiche Ergebnis kommt auch bei Maggiore heraus (Ableitung mit geodesic deviation), oder wenn man die Geodätengleichung löst. Und genau dieses Ergebnis ist auch auf meiner Animation zu sehen. Insofern: alles so, wie erwartet, alles konsistent. Die angeblich erhalten bleibenden Koinzidenzen basieren schlicht auf einer (bereits in der klassischen Physik) unsinnigen Modellierung eines starren Körpers.
Ihre weiteren Absätze zum “unterstellte[m] Hin- und Herwackeln” oder angeblich irrsinnigen Geschwindigkeiten halte ich ebenfalls für unsinnig/falsch; falls die sich durch die obige Korrektur nicht bereits erledigt haben, kann ich aber gerne auch darauf noch eingehen. Vorausgesetzt, Sie untermauern diese Behauptungen und stellen sie nicht einfach so in den Raum.
Chrys schrieb (15. Juli 2016 @ 14:10):
> Leihen wir uns gedankenexperimentell doch einmal einen starren Meterstab von Maggiores Proper Detector Frame aus
Im oben verlinkten “Chapter 1: The geometric approach to GWs” of Maggiore wird der Begriff “rigid ruler” lediglich in der “Randnotiz 11” (p. 19) behandelt, die im wesentlichen besagt:
.
Was auch immer Maggiore unter “rigid ruler” (oder “bar“) verstanden haben will (falls überhaupt irgendetwas Nachvollziehbares) entspricht folglich nicht einem “(chronometrisch) starren Meterstab“.
(Übrigens tritt das Wort “duration” im genannten “chap. 1” offenbar überhaupt nicht auf. Ich allerdings demnächst mal versuchen herauszufinden, ob und wie Synge versucht hat, den Begriff “GW” nachvollziehbar zu machen.)
> und positionieren noch je eine frei bewegliche Testmasse koinzident mit dessen durch ‚links‘ und ‚rechts‘ gekennzeichnete Enden. In einem Inertialsystem und noch ohne Welle liesse sich so etwas leicht bewerkstelligen.
Vorausgesetzt, das bezieht sich außerdem auf geeignete nachvollziehbare (auf Koinzidenzfeststellungen rückführbare) Begriffe von “frei beweglich” und “Inertialsystem“. (Wobei mir jedenfalls auch nicht erkennbar ist, dass Magiore darüber verfügt.)
> Anschliessend lassen wir die Pösselsche Beispiel-GW in z-Richtung durch das ganze Ensemble rauschen und schauen, was passiert. Das Teilchen links berichtet dann: „Ich kann hier bei mir keinerlei Beschleunigung feststellen […] ”
Ich unterstelle wiederum eine nachvollziehbare, auf Koinzidenzfesttellungen rückführbare, geometrische Definition des Begrffes “keinerlei Beschleunigung“; also insbesondere die Feststellung des genannten Teilchens, zusammen mit geeigneten anderen Mitglied eines tetrahedral-oktahedralen Ping-Koinzidenz-Gitters zu sein.
Zur besonderen Beachtung: Pingdauern über die Gesamt-Ausdehnung eines solchen Ping-Koinzidenz-Gitters, dass das genannte Teilchen einschließt, wären zwangsläuig wesentlich geringer als die Pingdauern der Enden von “Meterstäben“, die sich zur Feststellung von eventuell variabler Krümmung der Gesamtregion eignen.
> „ […] und bleibe koinzident mit meinem Ende des Meterstabes.
Nein; das widerspräche der Vorgabe “GW (mit Amplitude entlang der Richtung zwischen den beiden betrachteten Enden des Meterstabes)”.
> Es kommt sogar noch schlimmer. Für eine solche angedachte „proper motion“ existiert kein „proper speed limit“ […]
Das entlarvt wohl eher diese Begriffe als unphysikalisch, die hier (von Maggiore) ausgerechnet als “proper” bezeichnet werden.
Sofern ein Teilchen als identifizierbar gedacht wird (und eventuell sogar identifizierbar ist), ist es dadurch/deshalb auch Signalträger;
und Signalfrontgeschwindigkeit ist und bleibt nun mal der (endliche) Grenzwert von jeglicher Signalgeschwindigkeit.
(Das galt schon, bevor OPERA ihr Steckerproblem aufklärte; und selbstverständlich auch weiterhin.)
Chrys schrieb (15. Juli 2016 @ 14:10):
> Leihen wir uns gedankenexperimentell doch einmal einen starren Meterstab von Maggiores Proper Detector Frame aus
Im oben verlinkten “Chapter 1: The geometric approach to GWs” of Maggiore wird der Begriff “rigid ruler” lediglich in der “Randnotiz 11” (p. 19) behandelt, die im wesentlichen besagt:
.
Was auch immer Maggiore unter “rigid ruler” (oder “bar“) verstanden haben will (falls überhaupt irgendetwas Nachvollziehbares) entspricht folglich nicht einem “(chronometrisch) starren Meterstab“.
(Übrigens tritt das Wort “duration” im genannten “chap. 1” offenbar überhaupt nicht auf. Ich möchte allerdings demnächst mal versuchen herauszufinden, ob und wie Synge versucht hat, den Begriff “GW” nachvollziehbar zu machen.)
> und positionieren noch je eine frei bewegliche Testmasse koinzident mit dessen durch ‚links‘ und ‚rechts‘ gekennzeichnete Enden. In einem Inertialsystem und noch ohne Welle liesse sich so etwas leicht bewerkstelligen.
Vorausgesetzt, das bezieht sich außerdem auf geeignete nachvollziehbare (auf Koinzidenzfeststellungen rückführbare) Begriffe von “frei beweglich” und “Inertialsystem“. (Wobei mir jedenfalls auch nicht erkennbar ist, dass Magiore darüber verfügt.)
> Anschliessend lassen wir die Pösselsche Beispiel-GW in z-Richtung durch das ganze Ensemble rauschen und schauen, was passiert. Das Teilchen links berichtet dann: „Ich kann hier bei mir keinerlei Beschleunigung feststellen […]”
Ich unterstelle wiederum eine nachvollziehbare, auf Koinzidenzfeststellungen rückführbare, geometrische Definition des Begrffes “keinerlei Beschleunigung“; also insbesondere die Feststellung des genannten Teilchens, zusammen mit geeigneten anderen Mitglied eines tetrahedral-oktahedralen Ping-Koinzidenz-Gitters zu sein.
Zur besonderen Beachtung: Pingdauern über die Gesamt-Ausdehnung eines solchen Ping-Koinzidenz-Gitters, dass das genannte Teilchen einschließt, wären zwangsläuig wesentlich geringer als die Pingdauern der Enden von “Meterstäben“, die sich zur Feststellung von eventuell variabler Krümmung der Gesamtregion eignen.
> „[…] und bleibe koinzident mit meinem Ende des Meterstabes.“
Nein; das widerspräche der Vorgabe “GW (mit Amplitude entlang der Richtung zwischen den beiden betrachteten Enden des Meterstabes)”.
> Es kommt sogar noch schlimmer. Für eine solche angedachte „proper motion“ existiert kein „proper speed limit“ […]
Das entlarvt wohl eher diese Begriffe als unphysikalisch, die hier (von Maggiore) ausgerechnet als “proper” bezeichnet werden.
Sofern ein Teilchen als identifizierbar gedacht wird (und eventuell sogar identifizierbar ist), ist es dadurch/deshalb auch Signalträger;
und Signalfrontgeschwindigkeit ist und bleibt nun mal der (endliche) Grenzwert von jeglicher Signalgeschwindigkeit.
(Das galt schon, bevor OPERA ihr Steckerproblem aufklärte; und selbstverständlich auch weiterhin.)
p.s.
Frank Wappler schrieb (17. Juli 2016 @ 09:17):
> Pingdauern über die Gesamt-Ausdehnung eines solchen Ping-Koinzidenz-Gitters, dass das genannte Teilchen einschließt, […]
Sollte natürlich sein:
Pingdauern über die Gesamt-Ausdehnung eines solchen Ping-Koinzidenz-Gitters, das das genannte Teilchen einschließt, wären zwangsläuig wesentlich geringer als die Pingdauern der Enden von Meterstäben gegenüber einander, die sich zur Feststellung von eventuell variabler Krümmung der Gesamtregion eignen.
p.p.s.
Mir fällt erst jetzt auf, dass die bisher bestehenden Formatiermöglichkeiten mit
“<i> Kursivtext </i>”
bzw.
“<f> Fetttext </f>”
z.Z. abgestellt sind;
und (um so schlimmer!) nach wie vor keine Vorschaumöglichkeit besteht, um nach anderen Formatiermöglichkeiten zu suchen.
Hoffentlich bitte uns wenigstens jemand für den dadurch verursachten Mehraufwand um Entschuldigung.
Frank Wappler schrieb (17. Juli 2016 @ 09:29):
> Chrys schrieb (15. Juli 2016 @ 14:10):
> > „ […] und bleibe koinzident mit meinem Ende des Meterstabes.“
> Nein; das widerspräche der Vorgabe […]
Das war leider zu kurz gefasst; stattdessen:
Von den zwei Enden eines (chronometrisch starren) Meterstabes, in einer Region mit (chronometrisch definierter) “GW mit Amplitude zwischen diesen Enden” kann höchstens **nur eines** (chronometrisch) frei gewesen sein.
Der Widerspruch ergibt sich folglich durch die (zuletzt genannte) Forderung
> > Der Partner […] reportiert allerdings genau das gleiche
.
@Markus Pössel, Frank Wappler
Die Darstellungen der GW in den diversen Frames sind allesamt covariant gegenüber Translationen in x- oder y-Richtung. Das heisst, man kann den Ursprung der (x,y)-Koordinaten nach Belieben dorthin verschieben, wo man ihn haben will, ohne dass die Form oder die Geltung der in Betracht gezogenen Gleichungen hiervon betroffen wäre. Insbesondere auch dann, wenn die x- und y-Koord. mit rigid rulers bestimmt werden, was nachfolgend angenommen sei.
Dem Teilchen am linken Ende des besagten Meterstabes lassen sich also die Koordinaten x = 0 und y = 0 zuschreiben, und dann erfährt es durch die GW keine Beschleunigung, es bleibt mithin koinzident mit seinem Ende des Meterstabes. Nun verschieben wir den Ursprung der (x,y)-Ebene zum rechten Ende des Meterstabes und studieren in den verschobenen Koordinaten erneut die geodätische Bewegung des Teilchens am linken Ende. Diese lässt jetzt eine Beschleunigung in x-Richtung erkennen, und das Teilchen bleibt demzufolge nicht koinzident mit seinem Stabende.
Es lässt sich also hier durch eine simple Verschiebung des Koord.ursprungs ein unbeschleunigte Bewegung in eine beschleunigte verwandeln. Und das ist sehr nachteilhaft für die Bestimmung zeiträumlicher Koinzidenzen, auf die, wie mir Herr Wappler gewiss zugeben wird, unsere zeiträumlichen Konstatierungen stets hinauslaufen (sollten).
Die Frage, welche Geschwindigkeiten die dergestalt beschleunigten Teilchen denn so erreichen, scheint mir doch ganz allgemein recht interessant zu sein, allein schon in Hinblick auf die Animationen. Mit welchen Geschwindigkeiten passieren die beschleunigten Teilchen im Teilchenkreis ihre Mittellage, und wie hängt das dann vom Kreisradius ab? Ich lass’ das einfach mal so als Frage stehen; für den Proper Detector Frame hat Maggiore die Bewegungsgl. ja schon hingeschrieben, sodass es eigentlich nicht wirklich schwierig ist.
Chrys schrieb (17. Juli 2016 @ 13:24):
> Die Darstellungen der GW in den diversen Frames sind allesamt covariant
Und natürlich auch die Feststellungen bzw. Darstellungen, welche Beteiligte “frei/unbeschleunigt” waren, und welche Beteiligte jeweils paarweise “Enden des selben Meterstabes” waren.
(Die Versuchsanordnung insgesamt soll garantieren, dass solche Beteiligte im chronometrischen Sinne gedacht, und eventuell sogar aufgefunden werden können.)
Konsequenter Weise lässt sich jegliche Erwähnung irgendwelcher Koordinaten vermeiden, zumindest soweit sich Betrachtungen auf Physik beschränken. Aber leider scheint das manchen schwer zu fallen …
> wenn die x- und y-Koord. mit rigid rulers bestimmt werden, was nachfolgend angenommen sei. Dem Teilchen am linken Ende des besagten Meterstabes lassen sich also die Koordinaten x = 0 und y = 0 zuschreiben,
(… whatever …)
> […] es bleibt mithin koinzident mit seinem Ende des Meterstabes.
Das ist eine eindeutige, sowieso Koordinaten-unabhängige Anordnung.
> und dann erfährt es durch die GW keine Beschleunigung,
Das **kann** sein, aber **muss nicht**.
Und natürlich darf man Beschleunigung (im chronometrischen Sinne, also dass die Reisedauer des betreffenden Teilnehmers zwischen je zwei bestimmten Ereignissen das Supremum der Reisedauern aller Teilnehmer an diesen beiden Ereignissen ist) nicht mit **Koordinaten**-Beschleunigung verwechseln (die offenbar zwangsläufig “Null” wäre).
> Nun verschieben wir den Ursprung der (x,y)-Ebene zum rechten Ende des Meterstabes und studieren in den verschobenen Koordinaten erneut die geodätische Bewegung des Teilchens am linken Ende.
Unabhängig von dieser Koordinatentransformation bleibt die obige Anordnung von ständiger Koinzidenz zwischen dem genannten Teilchen und dem “linken Ende des Meterstabs” gültig;
und ebenso die chronometrische Feststellung, ob dieses Teilchen dabei beschleunigt, oder ansonsten frei blieb.
Irgendwelches “Studium in Koordinaten” ist dafür nicht erforderlich (aber für die entsprechende **Koordinaten**-Beschleunigung ergäbe sich offenbar ebenfalls der Wert “Null”).
> Diese lässt jetzt eine Beschleunigung in x-Richtung erkennen,
Ich erkenne das jedenfalls nicht.
> Die Frage, welche Geschwindigkeiten die dergestalt beschleunigten Teilchen denn so erreichen, scheint mir doch ganz allgemein recht interessant zu sein, allein schon in Hinblick auf die Animationen.
Es kommt mir vor, als hätte ich diese Frage schon vor einigen Monaten kommentiert; und vielleicht sogar wir darüber diskutiert. (Nur leider konnte ich im Moment keinen entsprechenden Kommentar in der einschlägigigen SciLogs-Beiträgen finden.)
Das ist sicherlich ein Problem der (Interpretation der) oben gezeigten Abbildungen; aber nicht “eigentlich”/chronometrisch/physikalisch, denn Signalgeschwindigkeit (sofern diese gemessen wird) ist zwangsläufig durch Signal**front**geschwindigkeit (“c_0”) beschränkt.
@Frank Wappler / 17. Juli 2016 23:22
Verzeih’ bitte, wenn ich darauf jetzt nicht en détail eingehe, aber soll mir das zu einer Einsicht verhelfen, wie sich zwei an den Enden eines starren Meterstabes plazierte freie Teilchen beim Eintreffen einer ebenen GW verhalten, und falls ja, zu welcher?
Die Sache mit dem Meterstab ist doch eigentlich ein idealisiertes LPF Modell. Man nimmt sich einen starren Frame her, bezogen auf den sich dann die Orte von zwei frei beweglichen Testmassen beschreiben lassen, von denen gesagt wird, die würden zumindest im Prinzip unter dem Einfluss einer GW in Bewegung geraten. Wenn das noch Physik sein soll, dann muss diese Bewegung auch auf eine konsistente Weise beschrieben werden können. Und natürlich braucht es dazu Koordinaten — wie denn sonst sollen die jeweiligen Positionen der Teilchen in eine Beziehung zum Frame gesetzt werden können?
N.B. In einem Test hatte das <em>…</em> tag noch funktioniert, um kursiven Text zu setzen.
Chrys schrieb (19. Juli 2016 @ 11:06):
> soll mir das zu einer Einsicht verhelfen, wie sich zwei an den Enden eines starren Meterstabes plazierte freie Teilchen beim Eintreffen einer ebenen GW verhalten, und falls ja, zu welcher?
Na: zumindest eine Einsicht dahingehend, wie das LIGO-Experiment interpretiert werden kann.
Dabei habe ich den Begriff des “Meterstabes” zwar nicht zuerst in die Diskussion eingeführt (sondern das war offenbar ein gewisser Chris in einem Kommentar von 26. Mai 2016 @ 17:26);
aber ich habe diesen Begriff gern aufgenommen, und dabei natürlich im chronometrischen Sinne (entsprechend der SI-Definition) zu verstehen versucht,
weil chronometrische Starrheit (bzw. Abweichung davon) ganz eng mit interferometrischen Starrheit (bzw. Abweichung davon) verbunden ist,
zumindest in Regionen mit Brechungsindex n = 1,
die wiederum unmittelbar die in den LIGO-Versuchen gesammelten Beobachtungsdaten betrfft.
Und der Begriff der “freien Teilchen” tritt ja schon im vorliegenden SciLogs-Artikel auf, und ist im Zusammenhang mit (den Interpretationen) der LIGO-Versuchsanordnung als auch der obigen Abbildungen zweifellos relevant.
(Das könnte allerdings auch mit der konkreteren Einsicht verbunden werden, die Frage zu stellen, ob und wie denn überhaupt gemessen wurde, dass oder in wie fern gewisse Bestandteile der LIGO-Versuchanordnung(en) sich “frei bewegt” hätten; insbesondere während die o.g. Abweichungen von interferometrischer Starrheit dieser Bestandteile untereinander auftraten.)
> Man nimmt sich einen starren Frame her, […]
Ich bezweifle sehr, dass sich eine (3 + 1) dimensionale Region mit GW überhaupt mit Beteiligten gefüllt denken ließe, die gegenübereinander insgesamt chronometrisch starr wären.
Oben (14. Juli 2016 @ 11:43) hatte ich ja argumentiert, dass sich (sofern Horizonte keine Rolle spielen) zu jedem Beteiligten “rundherum” chronometrisch starre Partner finden lassen. Aber diese sind wiederum **nicht alle gegenübereinander** chronometrisch starr.
Das kommt auch insbesondere in meinem Vorschlag zur Abbildung einer GW zum Ausdruck.
Aber es lassen sich wohl (zum Zweck dieser Diskussion, als “Frames“) wohl “Kongruenzen” von geeigneten Beteiligten finden/charakterisieren/hernehmen, die nicht alle gegenüber allen chronometrisch starr wären.
> bezogen auf den sich dann die Orte von zwei frei beweglichen Testmassen beschreiben lassen
Sicher: es ließe sich für jede solche “Testmasse” angeben, welche (unterscheidbaren) Mitglieder des “Frames” sie traf/passierte;
in welcher Reihenfolge;
und “wie” diese Koinzidenzen wiederum von allen Mitgliedern wahrgenommen und (hinsichtlich Koinzidenz bzw. Reihenfolge bzgl. Wahrnehmungen von Pings) bewertet würden.
Das ist manifest unabhängig von irgendwelchen Koordinaten. Es ist dazu nicht erforderlich, die unterscheidbaren Mitglieder des in Betracht gezogenen “Frames” mit Tupeln reeller Zahlen zu bennen; es ist allenfalls erforderlich, diesen unterscheidbaren Mitgliedern überhaupt **irgendwelche** verschiedene Namen zuzuordnen.
@Frank Wappler / 19. Juli 2016 23:43
Die fraglichen “rigid rulers” für Distanzen in x- und y-Richtung kommen implizit schon mit der Transformation auf “proper distance”-Koordinaten für x und y herein. Denn in dieser Darstellung sind die (x,y)-Ebenen der GW-Raumzeit identifizierbar mit jenen des Minkowski Hintergrundes, und die x- und y-Meterstäbe lassen sich dann in Gestalt der orthonomierten Basisvektoren ∂x und ∂y eines Lorentz Frames aus der Minkowski Geometrie übernehmen. Chronometrische Fragen zu diesen “Meterstäben” wären so auf die SR zurückführbar. Und es gilt scghliesslich auch, mit den früher verwendeten Bezeichnungen und g* = η* + h*,
g*(∂x,∂x) = η*(∂x,∂x) = g*(∂y,∂y) = η*(∂y,∂y) = −1.
Man könnte also meinen, dass diese rulers mit Bezug auf die GW-Metrik g* im selben Sinne starr sind wie mit Bezug auf die Minkowskische Metrik η*, denn augenscheinlich lassen die sich beliebig irgendwohin verschieben, ohne dass dabei ihre Pseudo-Länge verändert würde. Doch etwas an diesem Argument ist faul… was stimmt damit nicht?
Chrys schrieb (21. Juli 2016 @ 17:15):
> […] Doch etwas an diesem Argument ist faul …
Dazu kann ich nur nochmal kurz zusammenfassen, was ich oben schon ausführlicher festgestellt habe:
Sofern das fragliche Argument mit Physik (bzw. “physikalischer Geometrie”) zu tun hat, sind Koordinaten bzw. Koordinatentransformationen zweitrangig bis irrelevant;
sondern es gilt, sich mit den eigentlichen (Koordinaten-freien, nachvollziehbaren, auf Feststellungen von Identitäten und Koinzidenzen beruhenden, und abgeleitet davon insbesondere auh chronometrischen) Definitionen der Begriffe bzw. Messgrößen zu beschäftigen, um die es “in echt” bzw. in den Abbildungen geht.
Mir ist allerdings noch etwas Konkretes aufgefallen, das kommentierbar bis korrigierbar erscheint, und das vielleicht den Groschen endlich zum Fallen bringt:
> die (x,y)-Ebenen der GW-Raumzeit identifizierbar mit jenen des Minkowski Hintergrundes […]
Wenn man einen Unterraum einer “3+1”-dimensionalen “Raumzeit”-Region betrachtet, für die man zur Angabe ihrer Dimension das “+”-Zeichen nicht benötigt, dann nennt man diesen Unterraum (in der Regel) “Riemannsch”, bzw. eventuell “Euklidisch”. In solchen Unterräumen lassen sich die genannten physikalisch-chronometrischen Definition gar nicht zur Entfaltung bringen; sie sind “bloß Abbildung” bzw. “bloß Mathematik”.
@Frank Wappler / 22. Juli 2016 00:01
Für alle praktischen Fragen zum observationellen Nachweis von GWs (Konstruktion von Detektoren etc.) ist eine GW gemäss Einsteins linearisierter GR als Störung einer gegebenen Hintergrund-Geometrie anzusehen, auf die allein man sich dann bei Beobachtungen beziehen kann. Niemand will ernsthaft eine GW-Geometrie chronometrisch ausloten, ganz bestimmt jedenfalls nicht die Leute, die erwarten, dass eine typische GW in 0.2 Sekunden vorbeihuscht und danach wieder weg ist.
Die Anwesenheit einer GW wäre nur dadurch bemerkbar, dass gewisse charakterist. Abweichungen gegenüber dem als bekannt vorauszusetzenden Hintergrund festgestellt werden, wozu freilich einige theoret. Betrachtungen darüber anzustellen sind, was überhaupt als charakterist. Indiz für eine GW gelten kann. Dass man sich zur Messung dann interferometrischer Methoden bedient, ist grundsätzlich schlüssig und nachvollziehbar. Dass man aber eine mutmasslich durch eine GW hervorgerufene Interferenz als Doppler-Effekt zu deuten hat, weil nämlich die GW angeblich irgendwelche Dinge im Raume herumschubst, lässt sich gar nicht zwingend theoretisch begründen, sondern scheint mir so etwas wie eine paradigmatische Zwangsvorstellung zu sein, die letztlich daher kommt, dass man Gravitation unbedingt in eine Analogie zur EM-Strahlung setzen will. Diese Deutung führt offensichtlich zu absurd tönenden Behauptungen, und die EM-Analogie hinkt ohnehin beträchtlich, denn EM-Strahlung übermittelt schliesslich keine gespenstische “Gezeitenkraft”.
In der linearisierten Theorie besagt der “koordinatenfreie” Ausdruck g = η + h eigentlich noch überhaupt nichts, denn eine Zerlegung in Hintergrund η und Störung h ist keineswegs eindeutig. Wesentlich ist dabei die Wahl der Eichung, und die wird dann nur bei der Wahl adaptierter Koordinaten reflektiert und dargestellt. Die Wahl der Eichung ist wiederum entscheidend dafür, was sich überhaupt mit physikal. Anspruch über eine GW aussagen lässt, sodass die Beschwerden über Koordinaten wohl kaum irgendwo so deplaziert wirken wie gerade hier. Die Koord.transf., die ausgehend vom TT Frame “proper distance”-Koordinaten für x und y einführt, bedeutet primär einen Wechsel der Eichung, und in der so erhaltenen Zerlegung g* = η* + h* ist die Störung h* weder transversal noch spurfrei. Insbesondere sind dann jedoch auch η und η* nur modulo Eichung miteinander vergleichbar, und man darf sie nicht einfach für identisch halten, auch wenn es jedesmal Minkowski ist. In der Tat sind die für η starren rulers nicht starr für η* und umgekehrt, sodass sich die Starrheit von Meterstäben als eine Frage der Eichung erweist!
Und was hierbei die aus physikal. Sicht einzig akzeptable Wahl der Eichung ist, sollte eigentlich auch schon seit fast 100 Jahren durch Einstein und Eddington geklärt sein.
Chrys schrieb (24. Juli 2016 @ 17:51):
> Niemand will ernsthaft eine GW-Geometrie chronometrisch ausloten […]
Aber gewiss doch alle, die Synges Auffassung der (A)RT für an sich nachvollziehbar halten;
oder wenigstens (wie ich) für in so fern zielführend,
als Feststellungen von Koinzidenz (oder Reihenfolge) dabei schon recht deutlich zu Tage treten.
Auch wenn meine langjährige wiederholte Bitte, den Begriff der “Lichtuhr” (und natürlich auch Beziehungen zwischen zahlreichen “Lichtuhren” im Verbund) in diesem SciLog ausdrücklich eingehender zu diskutieren, bisher vergeblich war,
hat sich das Thema anhand der LIGO-Intereferenz-Methodik offenbar doch durch die Hintertüre hineingeschlichen.
(Übrigens hatte ich mal Gelegenheit, Synges Artikel in einer Bibliothek in gebundener Form anzuschauen und durch den Kopierer zu jagen; vielleicht find ich diese Blätter ja noch irgendwo auf dem Speicher …)
> […] gegenüber dem als bekannt vorauszusetzenden Hintergrund
Es ist natürlich ein allgemeines Prinzip der (Experimental-)Physik, Werte oder Beziehungen nur in so fern vorauszusetzen, als diese zumindest im Prinzip als Messwerte gewonnen werden könnten.
Von Interesse ist also die Messung von “Geometrie” (geometrischen Beziehungen zwischen identifizierbaren Beteiligten) in jedem Falle; “mit GW” genauso wie “(nur) Hintergrund”.
> […] Insbesondere sind dann jedoch auch η und η* nur modulo Eichung miteinander vergleichbar, und man darf sie nicht einfach für identisch halten, auch wenn es jedesmal Minkowski ist.
Dahingehend sind die “mathematischen Objekte” η, g, h, usw. eben grundsätzlich Koordinaten-behaftet und für Physik bzw. physi(kali)sche Geometrie betreffende Betrachtungen grundsätzlich entbehrlich bis indiskutabel.
> In der Tat sind die für η starren rulers nicht starr für η* und umgekehrt, sodass sich die Starrheit von Meterstäben als eine Frage der Eichung erweist!
Ist hier “Starrheit” etwa (nur) im Sinne von “Koordinaten-Starrheit” gemeint (also dass manchen Beteiligten bestimmte Koordinaten-Tupel-Werte konstant zugeordnet wurde);
und nicht im Sinne von “chronometrischer Starrheit” (also dass bestimmte Paare von Beteiligten gegenseitig konstante Pingdauern fanden),
oder (sogar) im Sinne von “SI-Meter-Starrheit” (dass bestimmte Paare von Beteiligten gegenseitig konstante und sogar gleiche Pingdauern fanden),
oder (worum es grundlegend geht) von “Koinzidenz-Starrheit”
(die aus Ping-Beobachtungen von zahlreichen Beteiligten untereinander zu folgern wäre, Stichwort “Null lattice”),
oder (wenigstens) “Bornscher Starrheit” (mit bekannter improperer Definition)
?
Anders gefragt:
Wären für je zwei Ereignisse, “€” und “£”
deren “Interval s^2[ €, £ ]”
oder deren “Weltfunktion σ[ €, £ ]”
oder deren “Lorentzsche Distanz ℓ[ €, £ ]”
ebenfalls “eine Frage der Eichung”
??
@Frank Wappler Wenn Koordinaten für Sie ganz entbehrlich sind, dann schreiben Sie doch einfach mal eine Gravitationswellenlösung, oder die Schwarzschildlösung, hin, ohne die implizite Erweiterung des konkreten Koinzidenzbegriffs, die man bei der Wahl eines Koordinatensystems vornimmt. Von Differentialgleichungen wie Einstein-Gleichung und Geodätengleichung in einer Form, in der man Lösungen finden kann, ganz zu schweigen. Wenn man konkret werden will, muss man sich auf bestimmte Koordinaten festlegen. Dass es immer unendlich viele gleichwertige Koordinaten gibt, liegt in der Natur der Sache.
Zur Flachheit: Die lokale Flachheit mithilfe geeigneter Koordinaten auszudrücken, ist nicht signifikant weniger willkürlich, als das zu wählen, was sie ein “zugrundeliegendes System” nennen. Ersteres als “Schwafeln” zu bezeichnen dürfte weniger mit Physik zu tun haben als mit einer von der Sache gänzlich unabhängigen Motivation, den Gesprächspartner durch überzogene Formulierungen vor den Kopf zu stoßen.
Markus Pössel schrieb (8. August 2016 @ 18:19):
> Da stehen sie also, das rho und die Karlhede-Invariante.
(Dabei hat sich im vorausgegangenen Kommentar,
8. August 2016 @ 16:27, vor lauter Knappheit ein gewissen Fehler zumindest in die erste, allgemeinere Lösungsformel eingeschlichen. Falls das jemandem auffällt — Chrys würde ich das z.B. zutrauen — und mit einer entsprechend konkreten Nachfrage verbunden wird, würde ich das noch korrigieren.)
> Wie rechnen Sie mit der so ausgedrückten Schwarzschild-Lösung, und ohne Benutzung von Koordinaten, z.B. aus, welche Lichtablenkung von der Erde aus gesehen das Licht eines fernen Sterns am Sonnenrand erfährt?
Dazu mehrere Bemerkungen:
Erstens hatte ich “die Geometrie” als gegeben angenommen (als “kugelsymmetrisch”); da eine gewisse Lösung gesucht wurde, muss ja auch etwas Bestimmtes gegeben sein.
Zweitens bezieht sich der Begriff “Rand (einer Kugel)” auf einen “geometrischen Ort”, den man sicherlich definieren können sollte, wenn man (wie ich oben) “Kugelsymmetrie” voraussetzen will;
dessen Definition allerdings nicht ganz einfach ist und nicht (allein) durch Werte der genannten Karlhede-Invarinate geleistet wird. (Das hängt mit meinem o.g. Fehler zusammen; die betreffenden Werte entsprechen i.A. eher jeweils “Paaren von Rändern”.)
Es wäre also schön bis notwendig, eine andere Invariante zu kennen bzw. zu definieren, deren Werte sich in der betreffenden Geometrie direkt und unzweideutig als “Kugel-Rand“-Parameter nutzen ließen.
(Leider kenne ich mich aber nicht mal ausreichend in Geometrie/Kinematik aus, um eine solche Invariante bennen zu können; ich kann nur annehmen, dass es eine gibt, und sie schon einen googelierbaren Namen hat. Wen/Wo könnte man nur danach fragen? …)
Drittens ist der Begriff “Lichtablenkung” äußerst fragwürdig; schließlich geht es um Null-Intervalle bzw. Nullwerte der Syngeschen Weltfunktion bzw. Nullwerte der Lorentzschen Distanz (direkt angrenzend an Ereignispaare, deren Lorentzsche Distanz voneinander verschieden von Null ist). Es geht wohl eher um eine weitere Charakterisierung von Krümmung. Vielleicht springt ja doch endlich mal ein entsprechender Gast-Beitrag für mich heraus …
> mich würde interessieren, wie Sie da vorgehen – welche Gleichungen stellen Sie auf? Welche lösen Sie? Und wie, im Prinzip?)
Kurz: Um aus gegebenen geometrischen Messwerten wie schon beschrieben die (wahrscheinlichste) Verteilung von “Masse-Energie-Impuls-Stress” als Lösung zu ermitteln, löst man die Euler-Lagrange-Gleichung(en) des entsprechenden Variationsproblems nach den gesuchten Größen auf.
> Zu den besonders geeigneten Koordinaten: […] wie die üblichen Koordinaten in der Speziellen Relativitätstheorie (kartesische Raumkoordinaten, Einstein-Synchronisation ruhender Uhren)
Da stehen nun also zumindest andeutungsweise die Systemeigenschaften, die Koordinaten-frei (letzlich durch Koinzidenzfeststellungen) zu definieren und zu messen sind:
– dass bestimmte Beteiligte (“Uhren“) denkbar und evtl. sogar auffindbar sein sollen, die gegenüber einander ruhen (d.h. auch: nicht nur einzeln “ruhig/unbeschleunigt/frei” sein sollen, und sich nie auch nur paarweise treffen sollen); und (nicht unbedingt ganz unabhängig davon)
– dass bestimmte Beteiligte (bzw. die Region, in der sie während eines Versuchs enthalten waren) “speziell-relativistisch/flach” gegenüber einander waren.
Sofern es sich versteht, dass “Flachheit” (einer geeigneten Menge von Beteiligten, bzw. der Region, die sie enthielt) durch das Verschwinden der Cayley-Menger-Determinante(n) der Abstände (d.h. der konstanten Entfernungen) zwischen diesen Beteiligten definiert ist, dann ist leicht erkennbar dass/warum ausgerechnet die “kartesische” Koordinatenzuordnung zusammen mit der Pythagoräisch/Euklidischen Norm geeignet ist (und ggf. historisch üblich wurde).
Die Verallgemeinerung zur Definition flacher (Mengen von Ereignissen in) Raumzeit-Regionen durch as Verschwinden der Cayley-Menger-Determinante(n) der (in diesem Falle auch “Intervalle” genannten) Werte von Syngeschen Weltfunktionen zwischen diesen Ereignissen sollte offensichtlich sein; und die dadurch begründete Eignung der “kartesische” Koordinatenzuordnung zusammen mit der pseudo-Euklidisch/Lorentzsch/Minkowskischen Norm folgt leicht.
Man kann aber genauso gut mit den Abständen bzw. Intervallen an sich rechnen, die sowieso von vornherein gegeben bzw. gemessen sein mussten.
(Damit ist zwar noch nicht erklärt, wie Abstände bzw Intervalle oder wenigstens Abstands- bzw. Intervallverhältnisse an sich gemessen werden sollten, und wie die evtl. noch grundlegendere Messung gegenseitiger Ruhe erfolgen, also aus Koinzidenz-Feststellungen konstruiert werden sollte. Dahingehend erneut der Hinweis — nicht zuletzt an Chrys — auf Ping-Koinzidenz-Gitter; und in punkto “Äquivalenzprinzip” zur Beachtung deren gemeinsame konsistente/kommensurable Einbettung in eine flache Region.)
Chrys schrieb ( 24. August 2016 @ 00:33):
> […] Die fraglichen Ereignismengen wären wohl das, was in der GR gemeinhin „Raumzeit“ genannt wird,
… oder stattdessen natürlich auch irgendwelche Teilmengen dieser „Raumzeit“ …
> und es ist dann eine Annahme seitens der Theorie, dass diese durch Mannigfaltigkeiten zu modellieren sind, also durch Mengen mit einer zusätzlichen Struktur
Dieses Beispiel ist natürlich sowieso naheliegend, und auch konkret genug, um die Debatte nicht mit Selbstverständlichkeiten aufzuhalten/aufzuweichen.
Die geforderte zusätzliche Struktur (d.h. über die bloße Unterscheidbarkeit einzelner Ereignisse hinaus) ist dabei, dass die (gegebene, betrachtete) Ereignismenge außerdem durch eine Topologie charakterisiert sein soll, die ziemlich speziellen Eigenschaften hat (nämlich gerade den Eigenschaften der intrinsischen/natürlichen/standard Topologie der Menge(n) reeller Tupel, (𝒯 ℝ)^k ).
In der (Experimental-)Physik gilt dabei aber der (in diesem SciLog nicht zufällig schon mehrfach zitierte) Einsteinsche Grundsatz:
Jeder ist also aufgefordert, festzulegen (und ggf. unmissverständlich mitzuteilen), durch welche zumindest Gedanken-experimentelle Methode ggf. die konkrete Topologie einer konkreten Ereignismenge ℰ festzustellen ist.
Ein Mathematiker (bzw. der Strohmann, von dem ich mich abzugrenzen wünsche) kann sich das sicher sehr einfach machen:
Man sauge sich eine eins-zu-eins Funktion „x : ℰ → ℝ^k“ aus den Fingern, die (sinnvoller Weise) Menge ℰ genau auf eine nicht-leere offene Menge des ℝ^k (also z.B. auf ℝ^k insgesamt) abbildet, die aber ansonsten völlig beliebig ist;
und weise der Menge ℰ dann gerade diejenige Topologie 𝒯 zu, die dadurch induziert wird:
S ∈ 𝒯 ⇔
∃ P ∈ (𝒯 ℝ)^k : A ∈ S ⇔ x[ A ] ∈ P.
(Die Vorgabe, dass es sich bei der Menge : ℰ ausgerechnet um (eine Teilmenge) von „Raumzeit“, und bei deren Elementen ausgerechnet um Ereignisse handeln sollte, spielt dabei offenbar gar keine Rolle; es reicht aus, dass die Elemente der Menge ℰ überhaupt unterscheidbar benannt sind.)
(Experimental-)Physikern ist dagegen bekanntlich auferlegt, Methoden aus Feststellungen von Koinzidenz (und Identität) zu konstruieren. Sie sollen sich deshalb mit dem entsprechenden wahrnehmbaren Inhalt der in Betracht stehenden Ereignisse auseinandersetzen (Wer nahm an welchen Ereignissen teil?, Wer nahm was koinzident wahr?), und eventuelle topologische Bewertungen daraus, intrinsisch gewinnen.
(Die Einzelheiten einer/der entsprechenden Messmethodik mögen ja durchaus garantieren, dass dadurch zwangsläufig eine Mannigfaltikeit gefunden würde, falls überhaupt eine Topologie. Aber an Koordinaten, und welche Koordinatenfunktionen ggf. Homöomorphismen bzgl. der Standardtopologie reeller Tupel darstellen, wäre allenfalls im Nachhinein zu denken.)
> Was spricht also gegen Karten?
Es spricht gar nichts gegen solche Karten, die etwas Bestimmtes abbilden sollen (das intrinsisch gegeben bzw. schon ermittelt war).
Aber Karten, die einen solchen Bezug nicht von vornherein hatten, sondern lediglich noch induzieren können, sind bloß Füllstoff für Borges‘ Bibliothek (Grafik-Abteilung).
> Für Krümmung von Raumzeit existiert schliesslich keine Messoperation
???
Spätestens seit Kokkendorff’s o.g. Beitrag doch.
Was natürlich nicht ausschließt, dass diese Erfindung auch schon vorher gemacht worden wäre, oder erneut unabhängig gemacht werden könnte.
@Chrys: Sie machen immer noch den gleichen Fehler, auf den ich schon in der vorigen Mail hingewiesen hatte.
Klar kann ich das Teilchen am linken Ende des Meterstabes in meinen Nullpunkt legen. Aber das heißt eben nicht, dass es koinzident mit seinem Ende des Meterstabs bleibt, denn der Schwerpunkt des Meterstabes (der ja in diesem Bild nicht im Nullpunkt liegt) wird, Stichwort Gezeitenbeschleunigungen, auf das Teilchen im Nullpunkt zu beschleunigt.
Damit ist alles konsistent. Nachweisbar sind in solch einer Situation allein die relativen Beschleunigungen, und die sind gleich, egal wohin ich meinen Nullpunkt lege. Der angebliche Widerspruch koinzident vs. nicht koinzident ergibt sich nur, weil Sie mit dem starren Körper des Meterstabs falsch rechnen.
Markus Pössel schrieb (20. Juli 2016 @ 23:56):
> […] der Schwerpunkt des Meterstabes
Mal ganz abgesehen von Betrachtungen zur Dynamik (und den
wahrscheinlichsten Verteilungen von Massen, Ladungen, Feldern …
die aus gegebenen geometrischen Beziehungen zu folgern wären):
Dass zwei betrachtete Enden einen “Meterstab” bildeten,
also (im Sinne der Si-“Meter”-Definition) jeweils konstante und gegenseitig gleiche Pingdauern untereinander fanden,
garantiert keineswegs, dass sich dazu auch (mindestens) ein weiterer Beteiligter finden ließ,
gegenüber dem jedes der beiden Enden die halbe Pingdauer gefunden
hätte,
und der wiederum gegenüber diesen beiden Enden koinzidente Pings
gefunden hätte;
der also als (chronometrische) “Mitte zwischen” diesen beiden Enden identifizierbar wäre.
(Die Existenz eines solchen, als “Mitte zwischen” den beiden Enden identifizierbaren Beteiligten wird in der Si-“Meter”-Definition ja offenbar auch nicht gefordert.)
> […] Nachweisbar sind in solch einer Situation allein die relativen Beschleunigungen
Eventuelle Beschleunigungen, also insbesondere eventuelle
Abweichungen von “Freiheit”, sind für jeden einzelnen Beteiligten
(d.h. “absolut”) definierbar (und entsprechend nachweisbar);
konkret anhand der (Verhältnisse zwischen) Werte(n) von “Lorentzscher Distanz” zwischen den Ereignissen, an denen er teilnahm.
@Frank Wappler: “Garantiert” ist auch ein ziemlich hoher Anspruch. Allerdings wäre jede Einheitendefinition sinnbefreit, wenn die Physik keine geeigneten Unterteilungen und Vielfachen zuließe.
Für das praktische Verständnis, was hier vorgeht, sollte aber klar sein, dass sich die Vorstellungen der klassischen Physik recht gut auf das übertragen lassen, was wir hier untersuchen (diese Näherung wird bei Maggiore, hier schon oft zitiert, ja auch hergeleitet). Dass ein Meterstab einen hinreichend gut definierten Mittelpunkt hat, können wir an dieser Stelle mit gutem Gewissen voraussetzen.
Und: Nein, die Gezeitenbeschleunigungen (“aufeinander zu gebogene Geodäten”) lassen sich von einem frei fallenden Beobachter lokal nicht nachweisen, siehe Äquivalenzprinzip.
Markus Pössel schrieb (21. Juli 2016 @ 11:20):
> Dass ein Meterstab einen hinreichend gut definierten Mittelpunkt hat, können wir an dieser Stelle mit gutem Gewissen voraussetzen.
Wer gewissenhaft genug ist, sich dabei um die konkrete Definition zu kümmern, kann Versuch für Versuch bewerten, ob die Forderung exakt gut erfüllt war, oder ansonsten quantifizieren in wie fern nicht.
> Allerdings wäre jede Einheitendefinition sinnbefreit, wenn die Physik keine geeigneten Unterteilungen und Vielfachen zuließe.
Selbstverständlich.
Der Befund, dass z.B. die Beteiligten A und B einen Meter (chronometrischen) Abstand voneinander hatten und behielten,
und sich dabei aber kein Beteiligter denken (oder sogar auffinden) ließ, der sowohl einen halben Meter (chronometrischen) Abstand von A als auch einem halben Meter (chronometrischen) Abstand von B hatte,
schließt ja keineswegs aus,
dass sich zahlreiche Beteiligte denken (und eventuell sogar finden) lassen, die jeweils einen halben Meter (chronometrischen) Abstand von A hatten, aber nicht von B;
als auch zahlreiche Beteiligte, die jeweils einen halben Meter (chronometrischen) Abstand von B hatten, aber nicht von A.
> Gezeitenbeschleunigungen („aufeinander zu gebogene Geodäten“) lassen sich von einem frei fallenden Beobachter lokal nicht nachweisen, siehe Äquivalenzprinzip.
Selbstverständlich lassen sich Pingdauern jedes einzelnen Beteiligten bzgl. jedes (identifizierbaren) einzelnen Beteiligten beschreiben;
und genauso selbstverständlich sind zum Vergleich von Dauern miteinander zahlreiche geeignete, voneinander getrennt Beteiligte erforderlich (d.h. ganze Ping-Koinzidenz-Gitter; in der einschlägigen Literatur wohl auch “Null lattices” genannt).
Und worum es in meinem vorausgegangenen Kommentar insbesondere ging:
selbstverständlich bezieht sich die Charakterisierung,
sich “frei/geodätisch/Reisedauer-maximierend bewegt” zu haben (oder ansonsten: nicht),
jeweils auf einen einzelnen identifizierbaren Beteiligten.
Und ja, das Äquivalenzprinzip besagt, dass diese Charakterisierung sowohl im Flachen als auch im Krummen anwendbar ist.
@Markus Pössel / 20. Juli 2016 23:56
Sie können sich gerne eine komplette x-Koordinatenlinie mit unendlich vielen Kopien eines x-Meterstabes dicht an dicht vollgepflastert denken — dann sind Sie den Massenmittelpunkt los und alles andere bleibt wie gehabt. Der “starre Körper” gehört gar nicht hierher — das wäre ein Kategorienfehler.
Haben Sie mittlerweile die Geschwindigkeiten der freien Teilchen gemäss Ihrer Beispiel-GW bestimmt? Falls ja, mit welchem Ergebnis? Falls nein, warum nicht?
Im Gegenteil; die Situation, die Sie ursprünglich beschrieben (und dann die falschen Schlüsse zogen), mit einem einzigen Meterstab und den zwei freien Teilchen an den Enden, war sehr gut geeignet, zu zeigen (a) was da vorgeht und (b) was die Animation (korrekt!) wiedergibt. Eine unendliche Kette von physischen Meterstäben ist unphysikalisch und ich sehe nicht, was uns solch eine problematische Konstruktion an Erkenntnissen bringen soll. Oder warum Sie jetzt, wo ich Sie auf Ihren Fehler hinweise, die vorige Modellsituation, die ich recht instruktiv fand und finde, verwerfen.
Zu Geschwindigkeiten hatte ich noch nichts gerechnet, weil ich bislang nicht gesehen habe, was das mit unserem ursprünglichen Thema (Angemessenheit der Animation) zu tun hat; Sie hatten es ja auch eher beiläufig in den Raum gestellt. Verraten Sie doch einfach, worauf Sie da hinauswollen – ist es etwas analoges zur Kosmologie? Scheinbare Überlichtgeschwindigkeiten und so wenn man zu extrem großen Entfernungen geht (für die die hier vorgestellte lokale Näherung nun einmal sowieso nicht geeignet ist)?
@Markus Pössel / 24. Juli 2016 20:56
Ein x-Meterstab verhält sich zu x-Koordinatenlinie wie Einsteins Meterstab zu Bahndamm, und der Meterstab im Kontext geometr. Modellierung ist immer nur eine abstrakte Idealisierung ohne physische Eigenschaften. Repräsentiert wäre so ein x-Meterstab hier durch einen Richtungsvektor ∂x, den man sich, ganz wie in der SR, als x-Basisvektor eines Lorentz Frames verschaffen kann, und mehr war damit nicht gemeint.
Der Störungsansatz g = η + h impliziert, dass zu einer Koord.darstellung der GW-Metrik stets die Koordinaten — und mithin die Meterstäbe — der Hintergrundmetrik verwendet werden; das sind Mittel der gewählten Darstellung, die nur von dieser und keinesfalls von der Störung abhängen. Speziell für die TT Darstellung einer linearen ebenen GW in z-Richtung heisst das, dass auch die x- und y-Meterstäbe sowie x- und y-Koordinatenwerte des Hintergrundes bei Hinzunahme der Störung h unverändert übernommen und gleichsam von η an g vererbt werden. Der Umstand, dass die g- und die η-Pseudonorm des Meterstabs ∂x ganz verschiedene Werte haben, bedeutet nicht, dass sich ∂x als geometr. Objekt durch h irgendwie verändern würde, oder dass zwei Punkte P und Q = P + ∂x durch die Störung relativ zueinander in Bewegung gekommen wären. Hingegen sagen die Koeffizienten in der quadratischen Form
g = 2 du dv − a(u)² dx² − b(u)² dy²
etwas aus über die Lichtgeschwindigkeit, die dann (mit Orientierung) in x-Richtung ±c/a(u) und in y-Richtung ±c/b(u) beträgt. Die Störung hat den geometr. Effekt, dass die Lichtkegel auf eine ganz bestimmte Weise deformiert werden, und das liesse sich interferometrisch im Prinzip auch nachweisen.
Man könnte naiv meinen, dass eine Koord.transf. x* = ax und y* = by eine konstante Lichtgeschw. in x- und y-Richtung restauriert, womit sich Interferenzmuster als ein durch physische Bewegung im Raum hervorgerufener Doppler-Effekt deuten liessen. Das trügt jedoch, denn durch die Transf. kommen die Lichtkegel nur zusätzlich dramatisch ins Schwanken. Anstatt eine physische Bewegung zu offenbaren, wird durch die Transf. eine Illusion von Bewegung erzeugt, indem jetzt nämlich x- und y-Abstände durch die transformierten Meterstäbe ∂x* = ∂x/a(u) und ∂y* = ∂y/b(u) ausgedrückt werden, die gegenüber den alten Meterstäben zeitabhängig gedehnt und gestaucht sind.
Anders gewendet, wenn eine GW tatsächlich eine physische Bewegung im Raume bewirken soll, dann muss die GW-Kraft proportional mit dem Abstand vom Betrachter wachsen. Und das ist schlichtweg absurd.
Chrys schrieb (26. Juli 2016 @ 18:23):
> Ein x-Meterstab verhält sich zu x-Koordinatenlinie wie Einsteins Meterstab zu Bahndamm, und der Meterstab im Kontext geometr. Modellierung ist immer nur eine abstrakte Idealisierung ohne physische Eigenschaften.
Um dem Eindruck entgegenzutreten, dass die von Einstein im Rahmen von gedankenexperimentellen Anordnungen genannten „Maßstäbe“, „Meterstäbe“, „Referenzkörper“ bzw. „Bahndämme“ nicht durch physische, auf Feststellungen von Koinzidenz hinauslaufende Eigenschaften charakterisiert wären, seien hier insbesondere diejenigen Eigenschaften aufgelistet, die im Zusammenhang mit Einsteins Gleichzeitigkeitsdefinition von 1917, sowie vorausgehenden Betrachtungen über Synchronismus, von 1905
gefordert bzw. idealisiert zugrundegelegt werden:
Zwei unterscheidbare Beteiligte (A und B) sind geeignete „Enden eines Stabes“ bzw. „Konstituenten eines Referenzkörpers“ falls
(1): A und B nicht koinzident waren,
(2): A und B einander beobachteten (also insbesondere nicht durch einen Rindler-Horizont voneinander getrennt waren),
(3): sich ein weiterer Beteiligter (M) als „Mitte zwischen“ A und B denken bzw. eventuell sogar auffinden lässt, d.h. insbesondere so dass
– M Pings gegenüber A und Pings gegenüber B stets koinzident wahrnahm,
– A zwei aufeinanderfolgende Pings gegenüber M koinzident zum entsprechenden einen Ping gegenüber B wahrnahm,
– B zwei aufeinanderfolgende Pings gegenüber M koinzident zum entsprechenden einen Ping gegenüber A wahrnahm.
(Es lassen sich weitere auf Feststellungen von Koinzidenz hinauslaufende physisch-geometrische Eigenschaften
formulieren, anhand derer darüberhinaus zu unterscheiden wäre, ob A und B dabei gegenüber einander ruhten oder sich z.B. beide in die selbe Richtung gleichmäßig/hyperbolisch beschleunigt bewegten.)
Inwiefern Paare von Beteiligten, die die genannten Eigenschaften nicht erfüllten, dennoch die „Enden eines starren Stabes“, die „Enden eines Maßstabes“ bzw. sogar die „Enden eines Meterstabes“ zu nennen sind, kann im Rahmen der (von Einstein zwar angedeuteten, aber erst von Synge ausdrücklich formulierten) Chronometrie definiert werden, und läuft dabei ebenfalls auf Feststellungen von Koinzidenz hinaus.
@Markus Pössel
Da es hier passt, sei noch einmal speziell auf Ihre Ausführungen vom 18. Mai 2016 @ 15:50 Bezug genommen, wo dann auch Herr Wappler im Anschluss verschiedentlich nachgefragt hatte. Dort exemplifizieren Sie zunächst eine GW in TT Darstellung:
»Betrachten wir eine Ebene senkrecht zur Ausbreitungsrichtung der Gravitationswelle; konkret: die x-y-Ebene, während z die Ausbreitungsrichtung der Welle ist. … Dann gilt bei Durchgang der (einfachen, linearen, geeignet ausgerichteten) Gravitationswelle, dass sich die x- und y-Koordinaten eines solchen [in der Ebene ruhenden] freien Teilchens, dargestellt im üblichen abstandstreuen kartesischen Koordinatensystem, mit der Zeit wie folgt ändern: …«
Die Geodätengl. liefert allerdings die Einsicht, dass sich die x- und y-Koordinaten der besagten Teilchen durch die GW bei dieser Darstellung nicht ändern, die Teilchen bleiben auch bei Durchgang der GW ortsfest. Der Abstand zwischen zwei solcher Teilchen im Raume ist demnach stets der Abstand zwischen den Orten, wo die Teilchen ruhen, und die lassen sich dort auch festgenagelt denken. Sie fahren dann erläuternd fort:
»(2) Aus der Theorie folgen nicht direkt diese Koordinatenänderungen, sondern es folgen Abstandsänderungen, nämlich Änderungen der Metrik. Konkret ist der Abstand Δ l zweier Punkte, … Wählt man eines der freien Teilchen als Raumnullpunkt, kann man die Abstandsänderungen in die oben genannten Koordinatenänderungen umschreiben.«
Wenn sich nun Koordinatenabstände von Teilchenorten mit der GW ändern sollen, dann ist sind solche Koordinaten erst geeignet einzuführen. Dadurch geraten aber nicht die Teilchen im Bewegung, die sind noch immer ortsfest. Bestimmen wir zwei Teilchenorte als P und Q = P + [x(Q) − x(P)]∂x, etwa wie zwei fest markierte Stellen am Bahndamm, und noch bevor überhaupt eine GW hindurchläuft, dann gilt mit den neu eingeführten x*-Koordinaten:
Q − P = [x(Q) − x(P)]∂x = a(u)[x(Q) − x(P)]∂x* = [x*(Q) − x*(P)]∂x*.
Wenn P als Raumnullpunkt gewählt wird, variiert die x*-Koordinate von Q, also x*(Q) = a(u)x(Q), im zeitlichen Verlauf, wodurch der Teilchenort Q mitsamt dort befindlichem Teilchen jetzt bewegt erscheint. Eine genuine Bewegung eines bei Q positionierten freien Teilchens läge indessen vor, wenn sich die x-Koordinate des Teilchens ändert, während der Wert x(Q) konstant bleibt, das Teilchen also infolge der GW nicht am Ort Q verbleibt.
Nein, das ist wieder eine Mischung aus falschen und verkürzten Aussagen über die Allgemeine Relativitätstheorie.
Wir haben in der ART einerseits die völlige Freiheit, Koordinaten zu wählen. Damit haben Aussagen alleine über koordinatenabhängige Größen im allgemeinen keine direkte physikalische Bedeutung. Von Positionsänderungen, Geschwindigkeiten etc. zu reden wenn damit lediglich allgemeine Koordinatenänderungen, Änderungsraten der Koordinatenänderungen gemeint sind, ist daher missverständlich. Und der
Umso wichtiger ist es daher, diejenigen Größen zu betrachten, in denen tatsächlich Physik steckt. Das sind zum einen Messungen z.B. von Lichteigenschaften (Lichtlaufzeiten, Frequenzverschiebungen), aber andererseits auch über das Äquivalenzprinzip näherungsweise die Messungen, die ein Beobachter in einem lokal flachen Koordinatensystem ausführt (das per Äquivalenzprinzip zumindest näherungsweise den Systemen der klassischen Physik, deren Eigenschaften und Mechanik nahekommt).
Aus dem gleichen Grunde halte ich es für irreführend, einen bloßen Koordinatenvektor als Meterstab zu setzen. Wenn ich von einem starren Meterstab rede, dann steckt da immer ein Rückbezug auf ein lokal flaches Koordinatensystem drin (woraus bereits folgt, dass meine Meterstäbe nicht zu groß sein dürfen) und das, was auch in der klassischen Physik einen Meterstab ausmacht: Ein gebundenes System, so starr wie möglich wie mit den Regeln der SRT vereinbar; hat im entsprechenden lokal flachen Koordinatensystem in sehr guter Näherung eine konstante proper distance (bzgl. der Zeitkoordinate des Systems) zwischen den Endpunkten.
Damit folgt dann das, was meine Animation zeigt: Wenn ich einen oder mehrere solcher starren Meterstab im Raum schweben lasse oder noch besser: den mit ihnen zusammenhängenden, unseren Alltagsvorstellungen nahen Distanzbegriff gleich als Basis des Animations-Raumkoordinatensystems wähle, dann verändern sich die gegenseitigen Abstände (proper distances im lokal flachen System) bei Durchgang so, wie in meiner Animation gezeigt. Darin liegt der Wert der Animation: diese systematischen Änderungen sichtbar zu machen.
Dass sich dabei auch die lokale Lichtgeschwindigkeit ändert, zeigt ja auch meine entsprechende Animation oben. Insofern alles physikalisch korrekt, und so nahe wie möglich an unsere Alltagsvorstellungen von Abstand gerückt.
Dass Gezeitenbeschleunigungen proportional zum Abstand der betrachteten, relativ zueinander beschleunigten Objekte sind, ist keineswegs “absurd” (traditionell ja sowieso ein Wort, was oft dann fällt, wenn bessere Argumente fehlen), sondern schon in der Newton’schen Gravitationstheorie bei herkömmlichen Gezeitenkräften so (siehe Ebbe und Flut). Bei Gravitationswellen (oder, analog, bei der kosmischen Expansion) ist es genauso.
Ihre Aussage, “dass sich die x- und y-Koordinaten der besagten Teilchen durch die GW bei dieser Darstellung”, nämlich beim abstandstreuen Koordinatensystem, nicht ändern, ist schlicht falsch.
Und zum Begriff der Bewegung scheinen Sie Vorstellungen zu haben, die ich beim besten Willen nicht nachvollziehen kann und die auch nicht recht zur ART passen. Was soll denn bitte “genuine Bewegung” sein, und warum machen Sie die scheinbar an Koordinatenbewegung in einem bestimmten System fest – koordinatenabhängige Größen ohne direkte physikalische Bedeutung sind im Rahmen der ART mit ihrer großen Koordinatenwahlfreiheit das am wenigsten genuine, sprich: das noch am ehesten willkürliche, was man sich in diesem Zusammenhang vorstellen kann?
Alles in allem ein aus meiner Sicht durchaus verqueres Gemisch von einigen richtigen, einer gehörigen Zahl ganz falscher und vielen (die Ambiguität der Alltgagssprache im Vergleich zur Mathematik lässt Grüßen) missverständlichen Aussagen zur ART. Alles andere als eine solide Basis für Ihre Kritik an meiner Animation.
@Markus Pössel / 30. Juli 2016 @ 10:50
Dass Sie in Ihren an Herrn Engelhardt gerichteten Erklärungen vom 18. Mai 2016 kein Argument dafür angegeben haben, warum freie Teilchen durch eine GW physisch im Raum bewegt werden sollten, kann ich Ihnen gerne nochmals zusammenfassen. Vielleicht möchten Sie sich dann ja doch noch einmal konkret zum Sachverhalt äussern?
Also erneut zu Ihrem Beispiel: Es seien dort freie Teilchen an festen, identifizierbaren Orten im Raum ruhend plaziert, noch ohne GW, wobei wir uns Teilchen wie Orte als Punkte vorstellen. Bezogen auf das von Ihnen beschriebenen Inertialsystem lässt sich zwischen einem festen Ort und einem dort befindlichen freien Teilchen nur dadurch unterscheiden, dass die Weltinie eines Ortes eine t-Koordinatenlinie repräsentiert, was sich auch nachfolgend mit GW nicht ändert, während die Weltlinie des freien Teilchens eine zeitartige Geodäte ist.
Die Behauptung, das freie Teilchen werde durch die GW im Raume bewegt, bedeutet geometrisch, dass diese beiden Kurven, die ohne die GW-Störung geometrisch zusammenfallen, dann bei Hinzunahme der Störung h voneinander abweichen. Und Sie haben noch kein einziges Argument geliefert, warum das so sein sollte. Sie haben damit auch keine Rechtfertigung genannt, warum eine GW freie Teilchen denn anders behandeln sollte als feste Orte. Warum zum Kuckuck soll Ihnen also jemand glauben, dass Ihre Animationen etwas anderes zeigen als bewegte Koordinaten? Dass hätten Sie stichhaltig und nachvollziehbar zu begründen. Und mein Wort darauf — das wird Ihnen nicht gelingen.
Chrys schrieb (31. Juli 2016 @ 12:44):
> […] freie Teilchen an festen, identifizierbaren Orten im Raum ruhend plaziert
Die (Einsteins) wesentliche Einsicht (von 1916), dass
Chrys schrieb (31. Juli 2016 @ 12:44):
> […] freie Teilchen an festen, identifizierbaren Orten im Raum ruhend plaziert
Die (Einsteins) wesentliche Einsicht (von 1916), dass
ist insbesondere damit verbunden, die Phrase “identifizierbarer Ort im Raum” als nicht-relativistisches Phantom zurückzuweisen und an dessen Stelle “ein bestimmter identifizierbarer/materieller Beteiligter” zu setzen bzw. zu denken;
ganz so wie wir (seit 1905)
.
Es sind also (jeweils) zwei identifizierbare, unterscheidbare Beteiligte entweder ständig koinzident, oder nicht.
(Und ob sie dabei koinzident zusammen, oder ansonsten evtl. einzeln, “ruhend/unbeschleunigt” waren und blieben, oder in wie fern nicht, stellt eine separate Messaufgabe dar, die aber hier und im Folgenden auch relevant ist.)
> […] dass diese beiden Kurven, die ohne die GW-Störung geometrisch zusammenfallen
Welche unterscheidbaren Beteiligten ohne die GW-Störung (also “im Flachen”) ohne Weiteres ständig koinzident sein können, sind (mit einigen der Bezeichnungen aus der obigen Abbildung
– ein (als ständig frei/ruhend charakterisierter) Beteiligter “Sp1” und ein Beteiligter “A”, der dadurch charakterisiert war und blieb, dass A ständig chronometrisch starr bzgl. des (als ständig frei/ruhend charakterisierten) Beteiligten “T” war;
und ebenso
– ein (als ständig frei/ruhend charakterisierter) Beteiligter T und ein Beteiligter “Q”, der dadurch charakterisiert war und blieb, dass Q ständig chronometrisch starr bzgl. des (als ständig frei/ruhend charakterisierten) Beteiligten Sp1 war;
usw.
> dann bei Hinzunahme der Störung h voneinander abweichen.
Richtig; und das wird anhand des interferometrischen LIGO-Prinzips unmittelbar deutlich:
Bei (geeignet orientierter) GW-Störung ist der als ständig frei/ruhend charakterisierte Beteiligter Sp1 gerade nicht ständig chronometrisch starr bzgl. des (als ständig frei/ruhend charakterisierten) Beteiligten T,
also Sp1 nicht (mehr ständig) koinzident mit dem entsprechend charakterisierten Beteiligten A.
(Ebenso auch für den geometrisch-physischen Zusammenhang zwischen den Beteiligten “Sp2”, “B”, und T.)
(Eine zusätzliche Komplikation der Beschreibung ergibt sich natürlich dadurch, dass einige LIGO-Bestandteile piezo-elektrisch justiert werden, und die Charakterisierung durch “Freiheit/Ruhe” deshalb nur schematisch zutrifft. Aber das ist hoffentlich Thema eines anderen Diskussionsstrangs …)
Im Übrigen erwarte ich, dass auch Markus Pössel diese Begründung liefern könnte, falls er sich nur endlich vom bisherigen Koordinatengeschwafel trennen würde.
@Frank Wappler / 1. August 2016 @ 10:44
Der Schluss von einer (wie auch immer gearteten) Abstandsbestimmung im Raume auf eine allfällige Bewegung im Raume hat eine notwendige Bedingung zur Voraussetzung: Falls dabei keine Bewegung im Raume stattfindet oder zwischenzeitlich stattgefunden hat, muss die auf stets gleiche Weise vorgenommene Abstandsbestimmung auch stets das gleiche Ergebnis liefern, egal zu welchem Zeitpunkt sie vorgenommen wird.
In nicht-statischen Raumzeiten ist diese notwendige Bedingung jedoch nicht erfüllt — a metrologist’s nightmare…
Die LIGO-Leute wollen “proper distance”, und etwa in x-Richtung wird dabei nichts anderes als die g-Pseudonorm eines festen Tangentenvektors ∂x bestimmt, was über die metrische Störung h von u = (ct − z)/√2 als Parameter abhängt. Für konstantes z ist der erhaltene Wert dann eine Funktion der Zeit t, mit dem immer gleichen und in jeglicher Hinsicht unbewegten Vektor ∂x.
Die “proper distance” ist meines Wissens eine kosmologische Wortschöpfung, und in der Kosmologie dient bisweilen das Argument mit der Einführung von “proper distance”-Koordinaten zur Erklärung von expandierendem Universum. Die Kosmologen versuchen aber gar nicht erst, ihre kosmische Expansion als eine Bewegung im Raume auszugeben und weisen eine solche Deutung auch entschieden zurück.
Chrys schrieb (2. August 2016 @ 13:08):
> Der Schluss von einer (wie auch immer gearteten) Abstandsbestimmung im Raume auf eine allfällige Bewegung im Raume
Es geht (besonders im Folgenden) aber nicht um irgendwelche “wie auch immer gearteten” Bestimmungen,
sondern um nachvollziehbare, auf Feststellungen von Koinzidenzen (und deshalb zunächst auch: von Identitäten der Beteiligten) hinauslaufende Bestimmungen;
und es geht nicht (nur) um eventuelle Bestimmung von Abstand (je zweier, gegenüber einander durchwegs starrer nicht-koinzidenter Beteiligter gegenüber einander),
sondern um Bestimmung von eventuell Versuch zu Versuch variabler Entfernung (je zweier, insbesondere nicht-koinzidenter Beteiligter gegenüber einander),
und deshalb einschließlich der Bestimmung, ob mehrere bestimmte in Betracht gezogene Beteiligte überhaupt gegenüber einander starr waren und blieben, oder nicht.
Außerdem bezieht sich die Formulierung bzw. Einschränkung “im Raume” auf genau solche Entfernungsbestimmungen: von unterscheidbaren Beteiligten gegenüber einander;
im Unterschied zu “(unmittelbar) zeitlicher” Entfernungsbestimmung, also Bestimmung von Dauer, durch die jeweils ein Paar von Anzeigen nur eines bestimmten Beteiligten charakterisiert ist,
und die der Bestimmung zugrundeliegt, ob jeweils ein einzelner Beteiligter frei war, oder nicht.
Die Feststellung von Freiheit (bzw. Inertialität; oder ansonsten: Unfreiheit/Zwang/Nicht-Inertialität) eines Einzelnen und die Feststellung gegenseitiger Starrheit (oder ansonsten: gegenseitiger/räumlicher Bewegung/Mobilität) sind weitgehend unabhängige, kompatible Messoperationen.
(Erstere mag auch eher eine “lokale Bestimmung” genannt werden, und letztere eine “globale”.)
> eine notwendige Bedingung […] Falls dabei keine Bewegung im Raume stattfindet oder zwischenzeitlich stattgefunden hat, muss die auf stets gleiche Weise vorgenommene [Entfernungs]bestimmung auch stets das gleiche Ergebnis liefern
(Ein solcher Ergebniswert wird dann/deshalb “Abstand” genannt.)
Richtig.
Das ist schlich und einfach die Definition von “gegenseitiger Bewegung” bestimmter Beteiligter als Messgröße;
und die ist weitgehend unabhängig von (kompatibel mit) eventuellen Bestimmungen hinsichtlich einzelner Freiheit oder Unfreiheit dieser beiden Beteiligten.
> In nicht-statischen Raumzeiten ist diese notwendige Bedingung jedoch nicht erfüllt
Doch.
(Abgesehen vielleicht von besonders schlimm/pathologischen Fällen, die wir nicht betrachten wollen.)
Auch in nicht-statischen Regionen lassen sich (sogar “rundherum”) Paare finden, die gegenüber einander chronometrisch starr waren und blieben.
Aber: die beiden einzelnen Beteiligten, die ein solches gegenüber einander starres Paar bildeten, waren dabei nicht (bzw. nicht unbedingt) beide einzeln frei.
(Und natürlich bestehen Zusammenhänge zum Begriff “Geodäte”, den Markus Pössel hier mehrfach erwähnte; sowie letztlich zu “Krümmung”.)
> Die LIGO-Leute wollen „proper distance“ […]
Bei LIGO geht’s offensichtlich um Interferometrie, also ziemlich unmittelbar um Feststellungen von Koinzidenz oder Nicht-Koinzidenz (bzw. Reihenfolge) bestimmter Echos.
Allerdings eben nicht zwischen allen/beliebigen/irgendwelchen Beteiligten, sondern (zumindest vermeintlich) nur zwischen besonders ausgewählten. (Wobei allerdings die Nachvollziehbarkeit der Auswahl fraglich ist.)
> Die „proper distance“ ist meines Wissens eine kosmologische Wortschöpfung […]
Falls diese Wortschöpfung mit einem Messoperator verbunden wäre, der auf Feststellungen von Koinzidenz hinausläuft (oder mittelbar wenigstens auf Chronometrie), träte sie (auch) in der Physik auf.
@Frank Wappler / 4. August 2016 @ 15:09
Die mit dem Begriff Bewegung verbundene Idee ist grundsätzlich die einer Zustandsänderung, nicht die einer Abstandsänderung. Das heisst, modelliert wird so etwas durch einen Zustandsraum U zusammen mit einer Dynamik, durch die jedem Punkt von U ein Orbit in U zugeordnet wird. In physikal. Anwendungen geschieht das üblicherweise durch die Lösungen einer Bewegungsgleichung, und diese Bezeichnung spricht ja schon für sich. Eine Abstandsfunktion ist dazu nicht erforderlich.
Ein recht einfaches Beispiel für Abstandsänderung ohne Bewegung wäre das flache Friedmann Universum mit U = ℝ³. Die zugehörige Raumzeit hat bekanntlich die Form I × U mit einem metr. Tensor g = dt² − R(t)²〈·,·〉, wobei die spitzen Klammern für das Euklid. Skalarprodukt in U stehen. Es lässt sich dann danach fragen, wie sich die Punkte in U unter dem Einfluss der Gravitation gemäss der Einsteinschen Feldgl. in U bewegen. Sie bewegen sich nicht, jeder Punkt ist ein Fixpunkt der gefundenen Dynamik. Gleichwohl ändern sich sowohl für “proper distance” wie auch für Radarabstand die Abstandswerte je zweier ins Auge gefassten Punkte in U mit der kosmolog. Zeit t. In populärer Sprechweise gerät das dann zu “Der Raum dehnt sich aus,” oder so ähnlich, was Experten wie Laien tief beeindruckt.
Das Beispiel lässt auch prinzipielle Beschränkungen von Radarabstand erkennen, der kann hier leicht ins Unendliche wachsen. John Synge greift übrigens bei diesem Thema auf das astronom. Abstandsmass “luminosity distance” zurück, was jedoch gewiss kein chonometrisches Konzept ist.
@Chrys: Auweia, dass Sie jetzt schon Ihr Wort und damit einen Gesichtsverlust daran knüpfen, dass es mir nicht gelingen wird, eine bestimmte Begründung zu liefern, klingt für mich eher so, als ginge es jetzt nicht mehr um Sachargumente.
Aber vielleicht gibt es hier ja noch Mitleser, die Sachargumenten offen gegenüber stehen.
Ihre Beschreibung meines Beispiels lässt jedenfalls zentrale Elemente weg: Wir sind im freien Fall (können also auf kleinen Skalen mit dem Äquivalenzprinzip argumentieren), wählen unser Koordinatensystem in erster Ordnung flach (wie man das im freien Fall tun kann) und betrachten (a) Punkte mit konstanter proper distance und (b) Punkte, die wir an freie Teilchen heften.
In der Animation bilden die Punkte (a) den Bezugsrahmen der Darstellung, in dem dann die jeweils aktuelle Position der Punkte (b) dargestellt ist. Wir können die Punkte (a) aber auch mithilfe eines näherungsweise starren Meterstabs “verkörpern”. Daran sieht man, wie ja schon in früheren Beiträgen erklärt, wie die Verschiebung relativ zueinander zustandekommt: Auf genügend kleinen Skalen bewegt sich der Schwerpunkt des starren Stabs wie ein freies Teilchen. Dort, wo die mit der Gravitationswelle assoziierte Krümmung (entspricht einer Gezeitenbeschleunigung) freie Teilchen differenziell aufeinander zu beschleunigt, wandern zwei freie Teilchen, die zunächst an den Enden eines Meterstabs schweben, aufgrund dieser Beschleunigung auf den Meterstab-Schwerpunkt und aufeinander zu.
Was Sie unter “physisch” im Raum bewegt verstehen, habe ich noch nicht recht verstanden – ist das mehr als eine Worthülse? Ihre weitere Beschreibung im Kommentar von 5.8. 14:27 scheint mir jedenfalls komplett zu unterschlagen, dass es auch in der nicht-relativistischen Physik durchaus kinematische Bewegungen gibt, die nicht aus den Bewegungsgleichungen folgen, sondern dort als Anfangsbedingungen eingang finden. Eine Bewegungsgleichung führt ja gerade nicht zu einer eindeutigen Bewegung, sondern muss durch Anfangsbedingungen ergänzt werden, um zu einer eindeutigen Lösung zu gelangen.
@Frank Wappler: Koordinaten sind leider unumgänglich, wenn man konkrete Lösungen hinschreiben und konkrete Situationen modellieren will. Letztlich ist jedes Koordinatensystem ein Rahmen, in dem sich Vorhersagen über messbare Größen (womit wir wieder bei diversen Sorten von Koinzidenzen wären) treffen lassen, aber ein hilfreicher Rahmen, weil eine geeignete Koordinatenwahl unzählige Aussagen über prinzipiell messbare Koinzidenzen kompakt zusammenfasst. So etwas als “Koordinatengeschwafel” zu bezeichnen, wie Sie es tun, und darauf zu bestehen, man möge bitte alle Aussagen auf dem Level elementarer Koinzidenzen formulieren, kommt mir ähnlich sinnlos vor, als würde ein puristischer Mathematiker darauf bestehen, jegliche Arithmetik mit natürlichen Zahlen im Geiste Peanos mit expliziter “Nachfolger von (Nachfolger von (Nachfolger von (… )))”-Angabe durchzuführen.
Vielleicht ist Ihnen ja auch schon einmal aufgefallen, dass Einstein zwar zurecht auf die elementare Rolle von Raumzeit-Koinzidenzen hingewiesen hat; gerechnet hat er dann aber mit Koordinaten. Dass am Ende messbare Vorhersagen stehen müssen (in meinem obigen Haupttext sind es die Phasenunterschiede der Lichtwellen an ein und demselben Ort, nämlich am Photodetektor) versteht sich von selbst. Dass man auf dem Weg dorthin Koordinaten verwendet – einige davon reine Hilfsgrößen, andere wie im obigen Beispiel über Hilfsvorstellungen wie starre Längenmaße, näherungsweise flache Koordinatensysteme etc. mit Konzepten verknüpft, die über die spezifische Situation hinaus Bedeutung haben und auf diese Weise zum Verständnis beitragen – ist aber durchaus legitim.
Chrys schrieb (5. August 2016 @ 14:27):
> Die mit dem Begriff Bewegung verbundene Idee ist grundsätzlich die einer Zustandsänderung […] einen Zustandsraum U zusammen mit einer Dynamik, durch die jedem Punkt von U ein Orbit in U zugeordnet wird.
Im vorausgegangenen Kommentar (2. August 2016 @ 13:08) war ja (noch schlicht) von “allfällige[r] Bewegung im Raume” die Rede, was man (und ich selbst sowieso) im ganz ursprünglichen und üblichen Sinne auf Geometrie und Kinematik beziehen kann.
Aber sicher lässt sich der “Raum“-Begriff auch verallgemeinert denken; und zusammen mit dem schon oben erwähnten “+”-Zeichen (“Plus”-Zeichen) auch der entsprechend verallgemeinerte “Bewegungs“-Begriff.
(Im meinen vorausgehenden Kommentar habe ich dieses Wort vorsichtshalber gar nicht selbst eingesetzt; und ich würde ggf. auch von “Zustandsgleichungen” sprechen.)
Jedenfalls, wie schon öfters bemerkt, halte ich es für empfehlenswert, von Dynamik (Variationsrechnung, konjugierten Größen) die Finger zu lassen, bevor man Geometrie und Kinematik verstanden bzw. deren grundlegende Messgrößen definiert hat.
> […] Radarabstand […]
Das Wort “Radar” (wie auch schon mehrfach weiter oben erwähnt) hat im verbreiteten Verständnis doch immer ein Geschmäckle nach Koordinaten. Physiker dürften das Wort “Pingdauer” vorziehen. Und (worauf ich unermüdlich hinweise) natürlich sollte man von einem “Abstands“-Wert zwischen zwei Beteiligten nur sprechen, falls deren gegenseitige Ping-Dauern konstant und gleich waren; bei Ungleichheit ggf. von “Quasi-Abständen”, und bei Variabilität schlicht von “Entfernungen”.
> kann hier leicht ins Unendliche wachsen. John Synge greift übrigens bei diesem Thema auf das astronom. Abstandsmass „luminosity distance“ zurück, was jedoch gewiss kein chonometrisches Konzept ist.
Keiner ist vollkommen. Synge griff ja immerhin auch zur World Function, die allerdings den (nicht an sich nachvollziehbaren) Begriff “convex normal neighborhood” erfordert. (Daher mein gelegentlicher “Griff” zur (vermutlich moderneren) “Lorentzian Distance Function”.)
Markus Pössel schrieb (6. August 2016 @ 10:34):
> Koordinaten sind leider unumgänglich, wenn man konkrete Lösungen hinschreiben und konkrete Situationen modellieren will.
Die Beschreibungen des vorausgehenden Kommentars (6. August 2016 @ 10:21) erscheinen als Beispiel dafür, dass Koordinaten im Gegenteil ganz entbehrlich sind:
–
–
–
–
Zugegegebenermaßen ist im genannten Kommentar ein (einziges) Mal auch von Koordinaten die Rede:
— aber das (eineindeutige) Besprenkeln der Ereignisse einer (in erster Ordnung) flachen Raumzeit-Region mit irgendwelchen reellen Zahlentupeln erscheint ohne Konsequenz für die oben genannten koordinatenfreien Beschreibungen.
> Letztlich ist jedes Koordinatensystem ein Rahmen, in dem […]
Von Bedeutung (als “Rahmen“) ist lediglich das System von identifizierbaren Bestandteilen (hier insbesondere von Beteiligten und deren einzelnen Anzeigen; oder auch von Ereignissen) und deren (messbare) geometrisch-kinematische Beziehungen untereinander.
Das Besprenkeln dieser Bestandteile mit reellen Zahlentupeln erzeugt bestenfalls einen Abklatsch, der
– die Topologie der Bestandteile (soweit messbar) “homöomorph” abbildet (oder ansonsten: nicht mal das); oder
– die metrischen Beziehungen der Bestandteile untereinander (auch geeignet verallgemeinert, soweit messbar) “(skaliert) isometrisch” oder “glatt” oder “n-fach differenzierbar” oder (wenigstens) “stetig” abbildet (oder ansonsten: nicht mal das).
> gerechnet hat er [Einstein] dann aber mit Koordinaten.
Mit Messwerten, also den Eigenwerten nachvollziehbarer Messoperatoren, lässt sich ebenso rechnen wie mit reellen Zahlen bzw. wie mit Booleschen Werten.
(Bei der Beschäftigung mit dem “Lochargument” (“point coincidence principle”) dürfte Einstein zumindest darüber nachgedacht haben, womit zu rechnen ist.)
> näherungsweise flache Koordinatensysteme
“Flachheit” (oder jede andere nachvollziehbare Quantifizierung von “Krümmung”) ist unabhängig von Koordinaten;
sondern ggf. eine Eigenschaft des zugrundeliegenden Systems an sich (nämlich: dass die Cayley-Menger-Determinanten der Abstände geeigneter Bestandteile des Systems untereinander verschwinden; bzw. näherungsweise verschwinden).
Von “näherungsweise flachen Koordinatensystemen” zu schreiben, anstatt sich auf “näherungsweise flache Systeme” zu konzentrieren, verwischt sowohl die Bedeutung des Messwertes “flach” als auch die Definition des zugrundeliegenden Messoperators; und verdient deshalb zumindest im Rahmen der Physik die Charakterisierung als
(jawohl!): Schwafeln.
@Markus Pössel / 6. August 2016 @ 10:21
Da sich einer GW keine andere Art von Interaktion mit freien Teilchen zuschreiben lässt als die einer Gezeitenkraft ohne jegliche lokale Wechselwirkung, wird ein an einem Ort im Raum ruhend plaziertes freies Teilchen auch infolge einer GW nicht beschleunigt und verbleibt daher an diesem Ort. Im Gegensatz etwa zu einer dort ruhend plazierten Testladung, die durch eine EM-Welle beschleunigt und somit in Bewegung versetzt werden kann. Der GW-Formalismus unterscheidet nicht zwischen festen Orten im Raum und dort ruhend plazierten freien Teilchen. Die “proper distance” zwischen zwei festen Punkten P und Q = P + λ∂x im hierbei zugrundegelegten affinen Punktraum ergibt sich ja auch wieder nur durch die g-Pseudonorm des Vektors λ∂x, die dann mit der Zeit t variiert. Die GW-Metrik g produziert zeitlich variierende Massbestimmungen, was gerade ihren nicht-statischen Charakter ausmacht, doch sie verändert oder bewegt dabei keinesfalls die geometrischen Objekte, deren Mass durch g bestimmt wird.
Wenn sich also Koordinaten ändern, wie Sie es am 18. Mai beschrieben hatten, dann ist der Grund dafür nicht die GW schlechthin, sondern nur die Koord.transformation, bei der die variablen Massstäbe der GW-Metrik als Einheitsmass festgesetzt werden. Wer die Höhe des Eiffelturms mit einem zeitlich variablen Urmeterstab als festgesetzter Einheit misst, erhält als Ergebnis heute vielleicht 310 Meter, morgen nur 294 Meter usw., was sicherlich einige öffentliche Aufmerksamkeit erregen könnte, wenn es nur hinreichend spektakulär präsentiert wird.
Apropos Äquivalenzprinzip, womit hier vermutlich die “infinitesimale Version” gemeint ist, die besagt, dass sich längs einer Geodäten Riemannsche Normalkoordinaten einführen lassen. Dazu zwei Anmerkungen:
Für TT Wellen sind die t-Koordinatenlinien Geodäten, und es zeigt sich bei genauerer Inspektion, dass diese in der Tat unbeschleunigt sind. Allerdings verschwinden hier längs einer solchen Linie weder sämtliche Christoffel Symbole noch die Krümmungsformen. Dasselbe gilt im übrigen für exakte Plane Wave Metriken in Normalform, was für eine lineare GW gerade dem TT Frame entspricht. Was damit zum Ausdruck kommt, ist eine Symmetrie, die bei ebenen GWs generell gegeben ist, und die sich freilich durch die Wahl von Koordinaten, die nicht an diese Symmetrie adaptiert sind, auch verschleiern lässt.
Ein eher historischer Aspekt dieser “infinitesimalen Version des Äquivalenzprinzips” ist, dass sie von Schlick und Pauli in die Welt gesetzt wurde, wohingegen Einstein das nicht mit seinem Verständnis von Äquivalenzprinzip in Verbindung gebracht wissen wollte. Herr Wappler wird sich möglicherweise daran erinnern, dass diese Affaire hier irgendwo schon einmal diskutiert worden war.
An einem einzigen freien Teilchen lässt sich wenig festmachen – das ist aber ganz allgemein so. Daher ist in meiner Argumentation immer von mehreren Teilchen die Rede, daher redet Maggiore von differenziellen Abständen, darum zeigt meine Animation mehrere Teilchen. (Erkennen Sie den Trend?)
Ihre Aussage, dass beim Durchgang der GW keine Teilchen “verändert” oder “bewegt” werden, halte ich nach wie vor für inhaltsleer, und Sie sind ja bislang auch noch nicht überzeugend darauf eingegangen, wie Sie “wahre Bewegung” definieren wollen. (In Ihrem letzten Versuch hatten Sie ja mal eben die gesamte Kinematik über Bord geworfen; so gelangt man zu keiner vernünftigen Bewegungs-Definition.)
Die Größen, die ich in meiner vorigen Antwort an Sie miteinander verglichen und in der einfachen Animation dargestellt hatte, sind jedenfalls keine Koordinaten-Artefakte, sondern etwas, das der im Mittelpunkt der Animation befindliche, frei fallende Beobachter direkt mit seinem starren Meterstab messen kann. In der späteren Animation (Haupttext oben) sieht man ja anhand des hin- und hergeschickten Effekts, dass die Beeinflussung kein Koordinateneffekt ist, sondern etwas durchaus messbares. Ob und wie Wellenberg- und Täler am Nullpunkt aufeinandertreffen ist ja nun ganz direkt eine Frage von raumzeitlichen Koinzidenzen.
Markus Pössel schrieb (7. August 2016 @ 09:57):
> Wenn Koordinaten für Sie ganz entbehrlich sind, dann schreiben Sie doch einfach mal eine Gravitationswellenlösung, oder die Schwarzschildlösung, hin, ohne […]
Wenn die hier besonders naheliegende und absehbare Aufforderung gestellt wird, einfach mal bestimmte mathematische Ausdrücke hinzuschreiben, dann wäre natürlich die Möglichkeit sehr nutzlich (gewesen), diese hier durch LaTeX-Befehle auszudrücken; und am besten zusammen mit einer Kommentarvorschau, die dafür brauchbar wäre sicherzustellen, dass das, was man durch (möglicherweise nur vermeintliche) LaTeX-Befehle auszudrücken versucht, auch so ansehnlich dargestellt wird, wie beabsichtigt.
Mangels dessen, und weil ich mich mit Dynamik sowieso (noch) nicht auskenne, darum nur knapp:
Als Gravitationswellenlösung (d.h. als wahrscheinlichste Verteilung von “Masse-Energie-Impuls-Stress”, die aus der gegebenen Wellengeometrie durch Variationsrechnung folgt):
Masse-Energiedichte ρ_m = 0 (überall),
sodass ggf. Energiefluss und Impuls nur mit einem Stress-Signal verbunden sind.
Als Schwarzschildlösung (d.h. als wahrscheinlichste Verteilung von “Masse-Energie-Impuls-Stress”, die aus gegebener kugelsymmetrischer Geometrie folgt):
ρ_m = ρ_m[ K ],
wobei “K” die Karlhede-Invariante bezeichnet.
(Von besonderem Interesse ist wohl die spezielle Geometrie und entsprechende Lösung, für die
K ≥ 0
⇒
ρ_m[ K ] = 0,
wobei ich mich nicht festlegen möchte, ob die Karlhede-Invariante K ansonsten negativ oder imaginär wäre, sofern sie nicht Null ist.)
> […] die implizite Erweiterung des konkreten Koinzidenzbegriffs, die man bei der Wahl eines Koordinatensystems vornimmt.
Versteh ich nicht; bitte mal erklären.
Wenn man den unterscheidbaren Bestandteile eines (gegebenen) Systems Koordinaten, also reelle Zahlentupel, zuordnet, um dadurch ein Koordinatensystem zu erhalten, dann “eins-zu-eins” (ansonsten spräche man wohl von einer “Projektion”).
Die betreffenden Bestandteile sind dadurch nicht mehr und nicht weniger unterscheidbar, als ohne Koordinatenzuordnung; und irgendwelche Systemeigenschaften sind dadurch nicht bekannt bzw. abgebildet (abgesehen von der reinen Anzahl bzw. Mächtigkeit seiner gegebenen unterscheidbaren Bestandteile).
> Zur Flachheit: Die lokale Flachheit mithilfe geeigneter Koordinaten auszudrücken […]
Ahh: Worin bestünde denn die “Eignung“ bestimmter reeller Zahlentupel, Flachheit auszudrücken (bzw. meinetwegen mit der Einschränkung “lokale Flachheit”)??
Solche “Eignung“ bezieht sich sicherlich/zwangsläufig auf eine Charakterisierung von Systemen als “flach” (oder meinetwegen “lokal flach”), die ohne irgendwelche (geeigneten oder ungeeigneten) Koordinaten angegeben werden kann (und die am besten auf Koinzidenzfeststellungen hinausläuft).
Markus Pössel schrieb (7. August 2016 @ 17:56):
> […] etwas, das der im Mittelpunkt der Animation befindliche, frei fallende Beobachter direkt mit seinem starren Meterstab messen kann.
Eine (die!) Schwäche dieser betreffenden ersten obigen Animation (bzw. des damit zusammenhängenden Versuches, eine Graviationswelle schematisch abzubilden und zu erklären; bzw. des damit zusammenhängenden Versuches durch LIGO, Gravitationswellen experimentell nachzuweisen)
bleibt jedenfalls, dass nicht nur der Beteiligte im Zentrum der Animation als “frei fallend” verstanden und erkennbar sein soll, sondern alle 33 abgebildeten Beteiligten (obwohl man das wenigstens 28 davon gewohnheitsmäßig nicht unbedingt “ansieht”).
Es wäre aber sicher hilfreich, wenn (z.B. farblich) hervorgehoben würde, welche (von den schon abgebildeten) Beteiligten (falls überhaupt irgendwelche) jeweils (paarweise) zusammen mit dem im Zentrum befindlichen die Enden eines “starren Meter- bzw. Maßstabs” sein sollten;
welche (falls irgendwelche) davon gleiche Abstände zwischen den betreffenden Enden hätten;
oder sogar alle relevanten (ca. 32, einschl. evtl. mehrfach abgebildeten) Beteiligten, die jeweils (paarweise) zusammen mit dem im Zentrum befindlichen die Enden von gleichen “starren Maßstäben” sein sollten.
> […] ganz direkt eine Frage von raumzeitlichen Koinzidenzen.
Das trifft jedenfalls auf die Ping-Koinzidenzen bzw. -Nichtkoinzidenzen (Reihenfolgen) zu, die der Beteiligte im Zentrum bzgl. der anderen (32, oder wie oben vorgeschlagen evtl. sogar mehr) Beteiligten beurteilen kann.
Die Bestimmung von “Freiheit” (oder dem Gegenteil bzw. dem Rest des Wertebereichs) erfolgt dagegen wohl etwas weniger direkt (Stichwort: tetrahedral-oktahedrale Ping-Koinzidenz-Gitter).
@Frank Wappler: Da stehen sie also, das rho und die Karlhede-Invariante.
Wie rechnen Sie mit der so ausgedrückten Schwarzschild-Lösung, und ohne Benutzung von Koordinaten, z.B. aus, welche Lichtablenkung von der Erde aus gesehen das Licht eines fernen Sterns am Sonnenrand erfährt? (Sie müssen es nicht explizit rechnen, aber mich würde interessieren, wie Sie da vorgehen – welche Gleichungen stellen Sie auf? Welche lösen Sie? Und wie, im Prinzip?)
Zu den besonders geeigneten Koordinaten: Das sind solche, die bis zur linearen Ordnung genau so aussehen, die gleiche Metrik und in entsprechender Näherung die gleiche Interpretation haben wie die üblichen Koordinaten in der Speziellen Relativitätstheorie (kartesische Raumkoordinaten, Einstein-Synchronisation ruhender Uhren). Die ermöglichen lokal den Anschluss an alles, was man sonst noch son in der SRT berechnen kann.
@Markus Pössel / 7. August 2016 @ 17:56
Denken wir uns die Bahn, die ein freies, zur Zeit t = 0 am Ort P ruhend plaziertes Teilchen im Raum durchläuft, dargestellt durch eine Kurve q(t,P). Dann lässt sich sagen, das Teilchen habe sich im Raume aus seiner ursprünglichen Ruheposition bewegt, wenn irgendwann der Fall q(t,P) ≠ P eintritt. Wenn wir noch eine (gegebenenfalls explizit zeitabhängige) Abstandsfunktion, dist[t](·,·), auf diesem Ortsraum festlegen, lässt sich eine solche Bewegung des Teilchens auch daran festmachen, ob dist[t](q(t,P),P) > 0 für irgendein t > 0 gilt. Sehen wir zudem noch grosszügig über Herrn Wapplers Bedenken hinsichtlich der prinzipiellen Identifizierbarkeit von Orten hinweg, so dürfte schwerlich zu bezweifeln sein, dass sich für eine freie, anfänglich ruhend plazierte Testladung unter dem nachfolgenden Einfluss einer EM-Welle eine solche Bewegung im Raume konstatieren lassen wird. Doch dies wird freilich auch nicht mit Gezeitenkraft begründet.
Doch zurück zur GW. Hier wird nun Gezeitenkraft als Begründung für vermeintliche Bewegung angeführt, in Verbindung mit “proper distance” als einer zeitabhängigen Abstandsfunktion. Dabei bleibt jedoch dist[t](q(t,P),P) = 0 für alle Zeiten t > 0, das heisst, ein freies Teilchen verbleibt an dem Ort P, wo es anfänglich ruhend plaziert wurde. Wenn das Teilchen dennoch bewegt erscheinen soll, muss folglich auch sein Ort P bewegt erscheinen. Dies lässt sich dadurch erreichen, dass die zeitlich variierende “proper distance” zum Eichmass für räumlichen Abstand erhoben wird, und so machen es auch Kosmologen bei ihrer Modellierung expandierender Universen. Aber die Kosmologen sagen dann zumindest, “Der Raum expandiert,” und keiner von denen behauptet, diese Expansion habe etwas mit einer physischen Bewegung im Raum zu tun, die vermittels einer Kraft auf “galaktische Teilchen” zu erklären wäre, wozu eine sogenannte Gezeitenkraft schon vom Prinzip her völlig ungeeignet wäre. Mehr als ein ominöses “Raum bewegt sich” ist da nicht herauszuholen, denn mehr wurde nicht hineingesteckt.
Aber halt, lässt sich nicht doch noch mehr herausholen? Da sich eine GW nur durch einen phase shift am Interferometer verraten würde und einem phase shift nicht anzusehen ist, wie er zustandekommt, lässt er sich immer auch als klass. Doppler-Effekt verstehen, bei dem sich, wie jedem einleuchtet, etwas bewegt haben muss. Und damit muss dann auch jedem einleuchten, dass eine GW die LIGO-Spiegel bewegen kann. Dabei kommt es natürlich sehr gelegen, dass sich das Gewackel der Spiegel etliche Grössenordnungen unterhalb der Grenzen jeder praktischen Observabilität ereignet haben soll, das kann keine Sau jemals direkt nachprüfen.
Markus Pössel schrieb (8. August 2016 @ 18:19):
> Da stehen sie also, das rho und die Karlhede-Invariante.
(Dabei hat sich im vorausgegangenen Kommentar,
8. August 2016 @ 16:27, vor lauter Knappheit ein gewissen Fehler zumindest in die erste, allgemeinere Lösungsformel eingeschlichen. Falls das jemandem auffällt — Chrys würde ich das z.B. zutrauen — und mit einer entsprechend konkreten Nachfrage verbunden wird, würde ich das noch korrigieren.)
> Wie rechnen Sie mit der so ausgedrückten Schwarzschild-Lösung, und ohne Benutzung von Koordinaten, z.B. aus, welche Lichtablenkung von der Erde aus gesehen das Licht eines fernen Sterns am Sonnenrand erfährt?
Dazu mehrere Bemerkungen:
Erstens hatte ich “die Geometrie” als gegeben angenommen (als “kugelsymmetrisch”); da eine gewisse Lösung gesucht wurde, muss ja auch etwas Bestimmtes gegeben sein.
Zweitens bezieht sich der Begriff “Rand (einer Kugel)” auf einen “geometrischen Ort”, den man sicherlich definieren können sollte, wenn man (wie ich oben) “Kugelsymmetrie” voraussetzen will;
dessen Definition allerdings nicht ganz einfach ist und nicht (allein) durch Werte der genannten Karlhede-Invarinate geleistet wird. (Das hängt mit meinem o.g. Fehler zusammen; die betreffenden Werte entsprechen i.A. eher jeweils “Paaren von Rändern”.)
Es wäre also schön bis notwendig, eine andere Invariante zu kennen bzw. zu definieren, deren Werte sich in der betreffenden Geometrie direkt und unzweideutig als “Kugel-Rand“-Parameter nutzen ließen.
(Leider kenne ich mich aber nicht mal ausreichend in Geometrie/Kinematik aus, um eine solche Invariante bennen zu können; ich kann nur annehmen, dass es eine gibt, und sie schon einen googelierbaren Namen hat. Wen/Wo könnte man nur danach fragen? …)
Drittens ist der Begriff “Lichtablenkung” äußerst fragwürdig; schließlich geht es um Null-Intervalle bzw. Nullwerte der Syngeschen Weltfunktion bzw. Nullwerte der Lorentzschen Distanz (direkt angrenzend an Ereignispaare, deren Lorentzsche Distanz voneinander verschieden von Null ist). Es geht wohl eher um eine weitere Charakterisierung von Krümmung. Vielleicht springt ja doch endlich mal ein entsprechender Gast-Beitrag für mich heraus …
> mich würde interessieren, wie Sie da vorgehen – welche Gleichungen stellen Sie auf? Welche lösen Sie? Und wie, im Prinzip?)
Kurz: Um aus gegebenen geometrischen Messwerten wie schon beschrieben die (wahrscheinlichste) Verteilung von “Masse-Energie-Impuls-Stress” als Lösung zu ermitteln, löst man die Euler-Lagrange-Gleichung(en) des entsprechenden Variationsproblems nach den gesuchten Größen auf.
> Zu den besonders geeigneten Koordinaten: […] wie die üblichen Koordinaten in der Speziellen Relativitätstheorie (kartesische Raumkoordinaten, Einstein-Synchronisation ruhender Uhren)
Da stehen nun also zumindest andeutungsweise die Systemeigenschaften, die Koordinaten-frei (letzlich durch Koinzidenzfeststellungen) zu definieren und zu messen sind:
– dass bestimmte Beteiligte (“Uhren“) denkbar und evtl. sogar auffindbar sein sollen, die gegenüber einander ruhen (d.h. auch: nicht nur einzeln “ruhig/unbeschleunigt/frei” sein sollen, und sich nie auch nur paarweise treffen sollen); und (nicht unbedingt ganz unabhängig davon)
– dass bestimmte Beteiligte (bzw. die Region, in der sie während eines Versuchs enthalten waren) “speziell-relativistisch/flach” gegenüber einander waren.
Sofern es sich versteht, dass “Flachheit” (einer geeigneten Menge von Beteiligten, bzw. der Region, die sie enthielt) durch das Verschwinden der Cayley-Menger-Determinante(n) der Abstände (d.h. der konstanten Entfernungen) zwischen diesen Beteiligten definiert ist, dann ist leicht erkennbar dass/warum ausgerechnet die “Kartesische” Koordinatenzuordnung zusammen mit der Pythagoräisch/Euklidischen Norm geeignet ist (und ggf. historisch gelegentlich üblich wurde).
Die Verallgemeinerung zur Definition flacher (Mengen von Ereignissen in) Raumzeit-Regionen durch as Verschwinden der Cayley-Menger-Determinante(n) der (in diesem Falle auch “Intervalle” genannten) Werte von Syngeschen Weltfunktionen zwischen diesen Ereignissen sollte offensichtlich sein; und die dadurch begründete Eignung der “Kartesischen” Koordinatenzuordnung zusammen mit der pseudo-Euklidisch/Lorentzsch/Minkowskischen Norm folgt leicht.
Man kann aber genauso gut mit den Abständen bzw. Intervallen an sich rechnen, die sowieso von vornherein gegeben bzw. gemessen sein mussten.
(Damit ist zwar noch nicht erklärt, wie Abstände bzw Intervalle oder wenigstens Abstands- bzw. Intervallverhältnisse an sich gemessen werden sollten, und wie die evtl. noch grundlegendere Messung gegenseitiger Ruhe erfolgen, also aus Koinzidenz-Feststellungen konstruiert werden sollte. Dahingehend erneut der Hinweis — nicht zuletzt an Chrys — auf Ping-Koinzidenz-Gitter; und in punkto “Äquivalenzprinzip” zur Beachtung deren gemeinsame konsistente/kommensurable Einbettung in eine flache Region.)
@Frank Wappler
Gerade in der linearisierten GR lässt sich doch speziell hinsichtlich der Zerlegung in Hintergrund und Störung ohne eine Darstellung in Koordinaten praktisch noch gar nichts sagen. Zerlegungen der Form g = η + h sind nicht kanonisch, und die Eigenschaft einer Störung h, Lösung der linearis. Feldgl. zu sein, bleibt bei einem Wechsel der Darstellung nicht generell erhalten. Also sag nicht, das ist Physik und muss daher unabhängig von der gewählten Darstellung gelten, sonst würden Physiker sich nicht damit befassen, sonden schau, was sich darüber unabhängig von Darstellungen konstatieren und folglich mit einem physikal. Anspruch verteten lässt.
Die pp-waves wären noch eine Klasse ebener GWs, die irgendwas im Raum bewegen könnten. Die pp-waves haben die Form g = η + H du² und zudem die interessante Eigenschaft, dass sie Ric = 0 genau dann erfüllen, wenn H die linearis. Feldgl. für das Vakuum löst. Auch die Beispiel-GW liesse sich auf diese Form bringen, indem die früher skizzierte Koord.transf. noch zusätzlich so modifiziert wird, dass die Kreuzterme (mit du dx und du dy) verschwinden, was problemlos möglich ist. Jeoch gilt in diesem Fall Ric ≠ 0, die Beipiel-GW ist also keine pp-wave. Ohne Rückgriff auf Koordinaten liesse sich das aber kaum vermitteln. Mir fällt jetzt zumindest nichts dazu ein, wie das gehen sollte.
@Chrys An den Problemen mit der Identifizierbarkeit von Orten kommt man in der Situation, die Sie beschreiben, allerdings nicht vorbei. Schon in der klassischen Physik ist das so: Relativ zu einem Bezugssystem mag ein Teilchen in Bewegung sein, in einem anderen kann dasselbe Teilchen ruhen.
Wirft Ihr Definitionsversuch z.B. jegliche Bewegung mit konstanter Geschwindigkeit aus dem Fenster? Das wäre dann doch ein sehr, sehr enger Bewegungsbegriff – ein Privatvergnügen von Ihnen, das in entscheidender Hinsicht vom Sprachgebrauch der Physik abweicht. Wenn nein, wie modifizieren Sie Ihre Definition, die dann ja offenbar zu kurz greift?
@Frank Wappler Um direkt zu dem zu kommen, was aus meiner Sicht an Ihren durchaus voluminösen Ausführungen der Knackpunkt ist: Sie schreiben leichthin, man würde eine Verteilung ermitteln, Euler-Lagrange-Gleichungen lösen und so weiter – wie machen Sie das in einem konkreten Falle ohne Koordinaten?
Der Wikipedia-Artikel, auf den Sie verlinkten, schreibt ganz selbstverständlich von Zeitkoordinaten, Differenzierbarkeit, Funktionen der Koordinaten, Ableitungen nach bestimmten Koordinaten. Aber das war für Sie alles nur Geschwafel, um Ihre freundlich-sachliche Wortwahl aufzugreifen – was machen Sie stattdessen?
Chrys schrieb (13. August 2016 @ 13:38):
> Gerade in der linearisierten GR lässt sich doch speziell hinsichtlich der Zerlegung in Hintergrund und Störung ohne eine Darstellung in Koordinaten praktisch noch gar nichts sagen.
Es ist mir nach wie vor unbegreiflich, was (eine Teilmenge von) ℝ^(3+1) an sich über die geometrische Struktur des einen oder anderen Systems zu sagen hätte, auf dessen Bestandteile diese Zahlentupel (eins-zu-eins, aber ansonsten völlig beliebig) als Koordinaten gestäubt würden.
Zum konkreten Thema der Zerlegung (der geometrischen Beziehungen zwischen identifizierbaren Beteiligten/”materiellen Punkten”, in einer Region mit Gravitationswelle) “in Hintergrund und Störung” habe ich mich bisher zwar nicht geäußert.
Mein gelegentlich schon erwähnter Vorschlag zur (selbstverständlich Koordinaten-freien) Abbildung einer GW scheint mir aber dafür gut geeignet:
Wie beschrieben sind dazu jeweils Grüppchen von 5 Beteiligten zu betrachten, also insgesamt 10 Paare, von denen 9 Paare gegenüber einander chronometrisch starr bleiben (also jeweils konstante Entfernungen, d.h. Abstände, finden) und all diese 9 Paare gleiche chronometrische Abstände voneinander haben, während das verbleibende 10. Paar aber eventuell veränderliche chronometrische (Quasi-)Entfernung(en) findet.
Falls die variable Entfernung (jeweils innerhalb eines Fünfer-Grüppchens) eine ausgeprägte Fourier-Komponente (von maximaler Frequenz) hat, mag man diesen Anteil der Veränderlichkeit als “Störung” ansprechen; und den Rest des Spektrums als “Hintergrund“.
(Es versteht sich, dass auch zu beachten bzw. zu fordern ist, dass Grüppchen-Konfigurationen gleicher Phase eine Familie von Flächen bilden, die sich wie Signalfronten fortschreiten.)
> […] die Form g = η + H du^2
Vermutlich ist “u” dabei eine bestimmte Koordinaten-Variable.
Was bedeutet da “d” ??,
Was bedeuten da “η” und “g” ?? …
Markus Pössel schrieb (14. August 2016 @ 21:30):
> Euler-Lagrange-Gleichungen lösen und so weiter – wie machen Sie das in einem konkreten Falle ohne Koordinaten?
Indem man das entsprechende Variationsproblem Koordinaten-frei durch geometrische (Mess-)Größen als Variable ausdrückt; insbesondere durch Dauer (bzw. Lorentzian Distance) als “primärem Argument” der Lagrangefunktion ℒ, und Distanzen (eines metrischen Raumes) als “sekundären” und Geschwindigkeiten als “tertiären Argumenten”; entsprechend der (konventionellen) Argumenten-Reihenfolge, die im bereits oben verlinkten Wikipedia-Artikel angesetzt wird.
> Der Wikipedia-Artikel, auf den Sie verlinkten, schreibt ganz selbstverständlich von Zeitkoordinaten, Differenzierbarkeit, Funktionen der Koordinaten, Ableitungen nach bestimmten Koordinaten.
Im betreffenden Artikel (aktuelle Version) tritt das Wort “Koordinate” offenbar gar nicht auf …
In den angegebenen Beispielen sind die relevanten Größen aber unbestreitbar als Koordinaten gemeint: eine reelle “Zeitkoordinate t” als primäres Argument, reelle “Raum-Koordinaten” als sekundäre und “Koordinaten-Geschwindigkeiten” als tertiäre Argumente.
Ber Ansatz von (geometrischen) Größen anstatt von Koordinaten geht tatsächlich mit einer geeigneten Anpassung (oder wenn man so will: Verallgemeinerung) des “Ableitungs“-Begriffs einher; bekannt insbesondere aus der Gegenüberstellung von
– Koordinatengeschwindigkeit (Betrag der “Komponente in x-Richtung”):
xdot
“an der Stelle mit Koordinaten (t_0, x[ t_0 ])” :=
lim_{ epsilon –> 0 } ((x[ t_0 + epsilon ] – x[ t_0 ]) / epsilon)
und andererseits
– Geschwindigkeit (Betrag “am Start A”):
v := lim_{
Dauer der Belegung der Reisestrecke zwischen Start A und (dem als variabel aufzufassenden Durchgangspunkt) Б
/
Dauer der Belegung der Reisestrecke zwischen Start A und Ziel Z
–> 0
} (Distanz zwischen A und Б / Dauer der Belegung der Reisestrecke zwischen A und Б)
.
Der wesentliche Unterschied kommt formal dadurch zum Ausdruck, dass in der Definition der Koordinatengeschwindigkeit ein Minuszeichen auftritt; in der Geschwindigkeitsdefinition aber nicht.
Die Herleitung der Euler-Lagrange-Gleichung für geometrische Größen erfolgt mit dieser Anpassung analog zur Koordinaten-Variante im verlinkten Wikipedia-Artikel.
@Frank Wappler: Auch wenn Sie das Wort krampfhaft vermeiden, gilt doch wohl: was Sie da einführen, sind ganz bestimmte Koordinaten.
Die Frage ist also offenbar nicht mehr, ob Sie ganz ohne Koordinaten auskommen, sondern ob Sie mit Koordinaten auskommen, die konkrete geometrische Bedeutung (Längen/Dauern) haben.
Aber da macht Ihnen per Definition die Krümmung einen Strich durch die Rechnung. Krümmung ist ja gerade diejenige Eigenschaft des Raums, der uns davon abhält, den Raum mit abstandstreuen Koordinaten zu überziehen.
@Markus Pössel / 14. August 2016 @ 21:24
Jedes klassische Hamiltonsche System hat einen Begriff von identifizierbaren Orten zur Voraussetzung, denn sein Phasenraum ist nichts anderes als das Cotangentialbündel über einem als Ortsraum gedachten und bezeichneten Basisraum. Ein ruhend plaziertes Teilchen ist ein solches, das zu einer Anfangszeit, sagen wir t = 0, irgendwo im Nullschnitt positioniert wird. Unter dem Hamiltonschen Fluss folgt das Teilchen einer Trajektorie im Phasenraum, und seine Bewegung im Ortsraum wird beschrieben durch die Projektion dieser Kurve auf den Basisraum. Können Sie mir anhand dessen bitte erläutern, was Sie dabei mit “Privatvergnügen” meinen?
»Wirft Ihr Definitionsversuch z.B. jegliche Bewegung mit konstanter Geschwindigkeit aus dem Fenster?«
Die Bedingung des anfänglichen Ruhens von Teilchen hatten Sie in Ihrem Erklärungsversuch vom 18. Mai hier selbst explizit eingebracht; ich sah lediglich keinerlei Veranlassung, daran etwas zu ändern. Ob Sie dabei etwas aus dem Fenster geworfen haben, sollten dann auch Sie selbst beantworten können.
Zur eigentlich spannenden Frage haben Sie wieder nichts gesagt, nämlich wie Sie und die LIGO-Leute auf im Raume bewegte Teilchen kommen wollen, wenn Sie bestenfalls so etwas wie “Raum bewegt sich” behaupten können.
Markus Pössel schrieb (16. August 2016 @ 10:29):
> was Sie da einführen, sind ganz bestimmte Koordinaten.
Bitte mal ganz konkret zitieren, was aus meinem vorausgegangenen Kommentar (oder auch anderen) als „ ganz bestimmte Koordinaten“ aufzufassen wäre.
Schließlich benutze ich verschiedene Worte (wie „Koordinaten“, im Gegensatz insbesondere zu „Dauer“ bzw. „Distanz“) in dem Bemühen, die Unterscheidbarkeit der damit benannten Begriffe zu betonen und dafür auszunutzen, mich verständlich zu machen.
> […] Koordinaten […], die konkrete geometrische Bedeutung (Längen/Dauern) haben.
> […] abstandstreue Koordinaten
Koordinaten, also konkrete reelle Zahlen oder konkrete Elemente (Tupel) der Mengen ℝ^4 bzw. ℝ^(3+1) besitzen in Beziehung untereinander bestenfalls gewisse topologische Bedeutung (aufgrund der „natürlichen/intrinsischer Reihenfolge“ der reellen Zahlen); aber keine (geo-)metrische Bedeutung an sich.
Eine bestimmte Zuordnung
f : S \rarr ℝ^n
von Koordinaten zu Bestandteilen eines Systems S ist nicht an sich „abstandstreu</em“ (isometrisch, oder wenigstens „skaliert isometrisch“, oder ansonsten „nicht mal das“) hinsichtlich eines gegebenen metrischen Raumes (S, d_system);
sondern für diese Bewertung bedarf es zusätzlich der Festlegung einer bestimmten auf der Koordinatenmenge definierten Abstandsfunktion d_sekundär, z.B. der „Euklidischen Metrik“, oder einer bestimmten „Riemannschen Metrik“ etc.
Der Knackpunkt ist:
Die Einführung von Koordinaten (durch irgendeine bestimmte Zuordnung f) und die Einführung/Berechnung einer auf der Koordinatenmenge definierten Abstandsfunktion (d_sekundär, z.B. insbesondere so, dass die Zuordnung f Abstandstreue/Isometrie gewährleistet), sagt nichts über die geometrische Charakterisierung des Systems S durch die (Mess-)Größen d_system, das nicht schon von vornherein bekannt und gegeben war.
Man kann sich das also sparen.
Nicht zuletzt, um sich stattdessen darauf zu konzentrieren, wie denn die primäre Charakterisierung des Systems S durch die (Mess-)Größen d_system überhaupt zu gewinnen wäre.
> Krümmung ist ja gerade diejenige Eigenschaft des Raums, der uns davon abhält, den Raum mit abstandstreuen Koordinaten zu überziehen.
Riemannsche Abstandsfunktionen sind Beispiele dafür, dass sich auch für gekrümmte Räume Koordinaten(-Zuordnungen) finden lassen, die Abstandstreue/Isometrie gewährleisten.
Und Krümmung eines Systems (also das Nicht-Verschwinden von bestimmten Cayley-Menger-Determinanten der Größen d_system) hält uns davon ab, für alle Paare von Koordinatentupeln die Euklidischen Abstandsfunktion anzusetzen (für die alle relevanten Cayley-Menger-Determinanten nämlich verschwinden), falls wir Koordinatenzuordnungen suchen, die Abstandstreue/Isometrie gewährleisten.
Markus Pössel schrieb (16. August 2016 @ 10:29):
> was Sie da einführen, sind ganz bestimmte Koordinaten.
Bitte mal ganz konkret zitieren, was aus meinem vorausgegangenen Kommentar (oder auch anderen) als „ ganz bestimmte Koordinaten“ aufzufassen wäre.
Schließlich benutze ich verschiedene Worte (wie „Koordinaten“, im Gegensatz insbesondere zu „Dauer“ bzw. „Distanz“) in dem Bemühen, die Unterscheidbarkeit der damit benannten Begriffe zu betonen und dafür auszunutzen, mich verständlich zu machen.
> […] Koordinaten […], die konkrete geometrische Bedeutung (Längen/Dauern) haben.
> […] abstandstreue Koordinaten
Koordinaten, also konkrete reelle Zahlen oder konkrete Elemente (Tupel) der Mengen ℝ^4 bzw. ℝ^(3+1) besitzen in Beziehung untereinander bestenfalls gewisse topologische Bedeutung (aufgrund der „natürlichen/intrinsischer Reihenfolge“ der reellen Zahlen); aber keine (geo-)metrische Bedeutung an sich.
Eine bestimmte Zuordnung
f : S → ℝ^n
von Koordinaten zu Bestandteilen eines Systems S ist nicht an sich „abstandstreu“ (isometrisch, oder wenigstens „skaliert isometrisch“, oder ansonsten „nicht mal das“) hinsichtlich eines gegebenen metrischen Raumes (S, d_system);
sondern für diese Bewertung bedarf es zusätzlich der Festlegung einer bestimmten auf der Koordinatenmenge definierten Abstandsfunktion d_sekundär, z.B. der „Euklidischen Metrik“, oder einer bestimmten „Riemannschen Metrik“ etc.
Der Knackpunkt ist:
Die Einführung von Koordinaten (durch irgendeine bestimmte Zuordnung f) und die Einführung/Berechnung einer auf der Koordinatenmenge definierten Abstandsfunktion (d_sekundär, z.B. insbesondere so, dass die Zuordnung f Abstandstreue/Isometrie gewährleistet), sagt nichts über die geometrische Charakterisierung des Systems S durch die (Mess-)Größen d_system, das nicht schon von vornherein bekannt und gegeben war.
Man kann sich das also sparen.
Nicht zuletzt, um sich stattdessen darauf zu konzentrieren, wie denn die primäre Charakterisierung des Systems S durch die (Mess-)Größen d_system überhaupt zu gewinnen wäre.
> Krümmung ist ja gerade diejenige Eigenschaft des Raums, der uns davon abhält, den Raum mit abstandstreuen Koordinaten zu überziehen.
Riemannsche Abstandsfunktionen sind Beispiele dafür, dass sich auch für gekrümmte Räume Koordinaten(-Zuordnungen) finden lassen, die Abstandstreue/Isometrie gewährleisten.
Und Krümmung eines Systems (also das Nicht-Verschwinden von bestimmten Cayley-Menger-Determinanten der Größen d_system) hält uns davon ab, für alle Paare von Koordinatentupeln die Euklidischen Abstandsfunktion anzusetzen (für die alle relevanten Cayley-Menger-Determinanten nämlich verschwinden), falls wir Koordinatenzuordnungen suchen, die Abstandstreue/Isometrie gewährleisten.
@Frank Wappler / 15. August 2016 @ 21:54
»Mein gelegentlich schon erwähnter Vorschlag zur (selbstverständlich Koordinaten-freien) Abbildung einer GW …«
Wie wäre denn ganz ohne jeglichen Bezug auf Koordinaten zunächst überhaupt festzulegen, was eine Gravitationswelle genannt werden soll und was nicht, und zwar a) in der GR und b) in der linearisierten GR? Da argwöhne ich schon gewisse Schwierigkeiten…
Chrys schrieb ( 17. August 2016 @ 18:50):
> Wie wäre denn ganz ohne jeglichen Bezug auf Koordinaten zunächst überhaupt festzulegen, was eine _Gravitationswelle_ genannt werden soll und was nicht, und zwar a) in der GR
Na mit den Koordinaten-freien begrifflichen Mitteln der GR; kurz gesagt:
durch Invarianten, und durch kovariante Beziehungen zwischen Invarianten
(deren Definitionen natürlich wiederum auf Feststellungen von Koinzidenz usw. gegeben sein sollen).
Die grundlegenden Invarianten betreffen dabei sicherlich metrische Verhältnisse (bzw. deren Verallgemeinerungen), also die (schon öfters erwähnten) Lorentzschen Distanzen bzw. (mit definitionsbedingten Einschränkungen) Werte der Syngesche Weltfunktion
(zumindest jeweils Verhältnisse).
Daraus lassen sich (vermutlich; sicherlich) weitere Invarianten definieren, und entsprechend deren Werte ermitteln; insbesondere Krümmungsinvarianten.
(Allerdings habe ich bisher ziemliche Schwierigkeiten damit, Werte dieser Invarianten ganz allgemein explizit durch gegebene metrische Verhältniswerte auszudrücken; also die vermuteten Definitionen explizit anzugeben.
Mein erwähnter Abbildungsvorschlag, und auch der zugrundeliegende Five-Point Curvature Detector von Synge sind eben nur Prinzipskizzen bzw. Beispielfälle.
Die einschlägige Literatur scheint sich meist mit irgendwelchen Koordinaten-Streußeleien aufzuhalten …
Als eine der wenigen löblichen Ausnahmen ist mir S.L. Kokkendorff, Gram Matrix Analysis of Finite Distance Spaces in Constant Curvature aufgefallen.)
Um zumindest anzudeuten, wie damit konkret festzulegen wäre, sein hier die (kovariante) Gleichung
I = K
als eine vermutlich geeignete „(homogene/quellenfreie) Wellengleichung“ angeführt, deren (nichttriviale) Lösungen (über eine geeignet ausgedehnte Region) ggf. _Gravitationswellen_ genannt werden sollten;
wobei I die Karlhede- und K die Kretschmann-Invariante bezeichnen soll.
> und b) in der linearisierten GR?
Wie wäre denn ganz ohne jeglichen Bezug auf Koordinaten zunächst überhaupt festzulegen, was „linearisierte GR“ bedeuten soll?
Falls schlicht und Koordinaten-frei gemeint sein sollte, dass nur Lösungen in Betracht gezogen werden sollten, für die der minimale Krümmungsradius viel größer ist, als der (maximale) Durchmesser der betrachteten Region, dann: wie oben beschrieben, aber unter Nichtbeachtung aller anderen Lösungen.
@Frank Wappler / 18. August 2016 @ 11:23
Doch was sind Invarianten? Befragen wir dazu einmal einen Klassiker: Luther P. Eisenhart, Riemannian Geometry, PUP, Sixth Printing 1966, Sec. I.3:
So einfach entkommt man den coördinates offensichtlich nicht.
Mich würde übrigens interessieren, ob sich Einstein nach der Affaire von 1936 überhaupt noch einmal zitierfähig über GWs geäussert hat. Dazu wüsste ich jetzt keine Quelle.
Chrys schrieb (21. August 2016 @ 09:36):
> @Frank Wappler / 18. August 2016 @ 11:23
> Doch was sind Invarianten?
Gemeint waren Messgrößen,
deren Wert jeweils (wie bei skalaren Krümmungsinvarianten) einem bestimmten Ereignis zugeschrieben wird,
oder jeweils (wie bei Lorentzschen Distanzen, oder bei der Syngeschen Weltfunktion) einem bestimmten Paar von Ereignissen,
oder jeweils (wie Masse oder Ladung) einem bestimmten Beteiligten,
oder jeweils (wie Entfernung oder Abstand) einem bestimmten Paar von Beteiligten;
jedenfalls ohne Abhängigkeit von irgendwelchen Tupeln reeller Zahlen, die den betrachteten Ereignissen oder Beteiligten zusätzlich als Koordinaten zugeordnet worden sein mögen.
> If a function f of the x’s and a function f‘ of the x’’s are such that they are reducible to one another by the equations of the transformations of the variables, they are said to define an invariant.
Explizit schreibt sich diese Invariante als die Funktionskomposition
f ∘ x‘ =
f‘ ∘ x‘‘,
für die beiden spezifisch betrachteten Koordinatenfunktionen (z.B.)
x‘ : ℰ → ℝ^k‘ und
x‘‘ : ℰ → ℝ^k‘‘;
woraus ersichtlich ist, dass die Invariante den Definitionsbereich (z.B. eine bestimmte Menge ℰ von Ereignissen) unmittelbar und Koordinaten-unabhängig in den Wertebereich abbildet; und als solche auch von vornherein Koordinaten-frei definiert werden kann.
(Die Verallgemeinerung zu Funktionen mit mehreren Argumenten im Definitionsbereich dürfte offensichtlich sein.)
p.s.
Mich würde übrigens interessieren, ob und ggf. wie sich Einstein zu A. A. Robbs Darstellung der (S)RT geäußert hat …
Chrys schrieb (21. August 2016 @ 09:36):
> @Frank Wappler / 18. August 2016 @ 11:23
> Doch was sind Invarianten?
Gemeint waren Messgrößen,
deren Wert jeweils (wie bei skalaren Krümmungsinvarianten) einem bestimmten Ereignis zugeschrieben wird,
oder jeweils (wie bei Lorentzschen Distanzen, oder bei der Syngeschen Weltfunktion) einem bestimmten Paar von Ereignissen,
oder jeweils (wie Masse oder Ladung) einem bestimmten Beteiligten,
oder jeweils (wie Entfernung oder Abstand) einem bestimmten Paar von Beteiligten;
jedenfalls ohne Abhängigkeit von irgendwelchen Tupeln reeller Zahlen, die den betrachteten Ereignissen oder Beteiligten zusätzlich als Koordinaten zugeordnet worden sein mögen.
> If a function f of the x’s and a function f‘ of the x’’s are such that they are reducible to one another by the equations of the transformations of the variables, they are said to define an invariant.
Explizit schreibt sich diese Invariante als die Funktionskomposition
f ∘ x‘ =
f‘∘ x‘‘,
für die beiden spezifisch betrachteten Koordinatenfunktionen (z.B.)
x‘ : ℰ → ℝ ^k‘ und
x‘‘ : ℰ → ℝ ^k‘‘;
woraus ersichtlich ist, dass die Invariante den Definitionsbereich (z.B. eine bestimmte Menge ℰ von Ereignissen) unmittelbar und Koordinaten-unabhängig in den Wertebereich abbildet; und als solche auch von vornherein Koordinaten-frei definiert werden kann.
(Die Verallgemeinerung zu Funktionen mit mehreren Argumenten im Definitionsbereich dürfte offensichtlich sein.)
p.s.
Mich würde übrigens interessieren, ob und ggf. wie sich Einstein zu A. A. Robbs Darstellung der (S)RT geäußert hat …
@Frank Wappler / 22. August 2016 @ 13:39
»… woraus ersichtlich ist, dass die Invariante den Definitionsbereich (z.B. eine bestimmte Menge ℰ von Ereignissen) unmittelbar und Koordinaten-unabhängig in den Wertebereich abbildet; und als solche auch von vornherein Koordinaten-frei definiert werden kann.«
Darin liegt ein Kurzschluss: Eine Wahl von Koordinaten bedeutet, grob gesagt, die spezielle Auswahl einer zulässigen Darstellung (im Rahmen einer Theoretisierung) von “Points” durch “Pointers”. Wenn dann von einer Aussage festgestellt wird, sie gelte unabhängig von der speziell gewählten Darstellung, ist damit längst nicht gesagt, dass sie darstellungsfrei formulierbar wäre, d.h., ohne dabei Bezug auf überhaupt irgendeine zulässige Darstellung zu nehmen.
Die fraglichen Ereignismengen wären wohl das, was in der GR gemeinhin “Raumzeit” genannt wird, und es ist dann eine Annahme seitens der Theorie, dass diese durch Mannigfaltigkeiten zu modellieren sind, also durch Mengen mit einer zusätzlichen Struktur, für die per definitionem die Existenz von Karten (lokalen Koord.) zu den konstitutiven Voraussetzungen zählt. Was spricht also gegen Karten? Wäre aus Dir versehentlich ein Geograph geworden, dann gewiss ein solcher, der den Gebrauch von Karten entschieden ablehnt und sich ausschliesslich daran zu orientieren versucht, was irgendwo in der Landschaft vorgefunden wird.
»Gemeint waren Messgrößen, …«
Messgrössen gehören für meinen Geschmack grundsätzlich zum Experimentellen, im Gegensatz etwa zu Krümmungsinvarianten, die Bestandteil einer abstrakten Modellierung sind. Für Krümmung von Raumzeit existiert schliesslich keine Messoperation, und das ist keinesfalls etwas, das in der Landschaft vorgefunden wird.
Lieber Herr Pössel,
anstatt Krügers substanzlose Polemik hier zu veröffentlichen, sollten Sie endlich Herrn Senf erklären, wie man aus Ihrem Ausdruck für eine Gravitationswelle (x02-x01)(1+A sin (kz-ωt)) den zugehörigen Energiefluss F= {(c³ IaI² ω²) / (64 π G)} * I cosθ I herleitet.
Auch mich würde interessieren, wie man das macht. Durch Integration über die gesamte Kugel von 1.3 Milliarden Lichtjahren Radius und über die Zeit von ca. 0.2 s sollte dann aus GW150914 die Energie von drei Sonnenmassen folgen. Vermutlich muss man noch eine realistische Emissionskeule berücksichtigen, weil es sich um eine Quadrupolstrahlung handelt. Das Problem, warum die schwarzen Löcher die Abstrahlung von Gravitationsstrahlung nicht genauso verhindern wie die Abstrahlung elektromagnetischer Energie wollen wir mal dahingestellt sein lassen.
Mit besten Grüßen
Wolfgang Engelhardt
Hallo Dr. Engelhardt,
der Energiefluß wird z.B. so hergeleitet
http://arxiv.org/pdf/1607.04202.pdf von Le Teic und Novak
dort auf S. 37 die Gl. 92 und Gl. 93 mit F ~ (c³ h² f²) / (32 π G) ohne cos
Grüße Senf
PS: übrigens finden Sie die Nachweisgrenze h=dL/L für ein Laserinterferometer
im Fließbach ART (2006) auf Seite 217 Gleichung 37.9
Hallo Herr Pössel,
das neue Layout sieht recht gut aus, besser als das Vorherige auf jeden Fall.
Engelhardt, was sie da wieder glauben lesen zu können, mein Betrag enthält keine Polemik.
Herr Pössel, ich hab da mal mehr allgemeine Fragen, in den Berichten wird von Masse Schwarzen Löcher geschrieben, das eine habe 29 das andere 36 und in Summe gab es aber nur 62 und nicht 65 Sonnenmassen.
Was für Massen sind hier gemeint? Normal wird mit Masse doch die Ruhemasse eines Objektes oder Körpers benannt, von dynamischer Masse spricht man so doch gar nicht mehr und wenn, dann macht man dieses explizit deutlich.
So könnte man vermuten, mit den 29 und den 36 Sonnenmassen sind Ruhemassen gemeint, also die Ruhemasse der Schwarzen Löcher. Auf der anderen Seite müsste dann real Ruhemasse der Löcher selber in Form von Energie abgestrahlt worden sein.
Handelt es sich da nicht doch mehr um Energie aus den Rotationen, also Energie, die noch nicht hinter dem Ereignishorizont zu finden war? Konkret gefragt, wird hier einfach die Rotationsenergie der Löcher mit zu deren Masse gerechnet und man hat es nicht mit deren Ruhemasse zu tun, wenn hier von 29 oder 36 Sonnenmassen geschrieben wird?
In vielen Beschreibungen der interferometrischen Gravitationswellendetektoren wird meiner Meinung die Rolle der als Pendel aufgehängten Spiegel zu wenig hervorgehoben.
Die als Pendel aufgehängten Spiegel bei LIGO stellen ein kraftfreies Bezugssystem dar. Auf der Erde funktioniert die kraftfreie Aufhängung natürlich nur für die beiden horizontalen Richtungen. Im Weltraum, bei LISA, wird das für alle drei Richtungen mit vollständig frei schwebenden Gold-Platin-Würfeln realisiert. Die kräftefrei aufgehängten Spiegel bei LIGO, bzw. die frei schwebenden Metallwürfel bei LISA, stellen ein kräftefreies Bezugssystem, ein Inertialsystem, also einen ebenen Tangentialraum dar. Mittels Laserinterferometrie wird der Abstand zu einem festen Bezugssystem gemessen. Bei LIGO verbunden mit der Erde, bei LISA „verbunden“ mit einem Lagrange-Punkt. Die kräftefrei aufgehängten Spiegel, bzw. die frei schwebenden Würfel, stellen auch beim Durchgang einer Gravitationswelle, ein Inertialsystem dar, sie bleiben kräftefrei. Der Abstand zwischen Spiegel, bzw. Würfel, zum festen, also der Gravitationsschwankung ausgesetzten Bezugspunkt, wird gemessen. Die Messung des Abstands zwischen den beiden verschiedenen Bezugssystemen, einerseits dem Inertialsystem, also dem kräftefreien von Gravitationsschwankungen isolierten Bezugssystem und andererseits dem der Gravitationsschwankung ausgesetzten Bezugssystem, stellt meiner Meinung nach den wichtigen Kern der Messung dar.
Siegfried Heiss schrieb (12. August 2016 @ 18:17):
> Die als Pendel aufgehängten Spiegel bei LIGO stellen ein kraftfreies Bezugssystem dar. Auf der Erde funktioniert die kraftfreie Aufhängung natürlich nur für die beiden horizontalen Richtungen.
Wurde denn gemessen, dass die wesentlichen Bestandteile von LIGO [1] horizontal (oder zumindest: jeweils in Interferometerarm-Richtung) einzeln hinreichend „kraftfrei“ (inertial, unbeschleunigt, ruhend) gewesen und geblieben wären;
insbesondere während (wie im obigen SciLogs-Beitrag beschrieben) der LIGO-Lichtdetektor ein (erwähnenswertes) Signal aufgezeichnete
??
Oder ist das etwa nur eine Modellannahme ? …
> Die Messung des Abstands zwischen den beiden verschiedenen Bezugssystemen,
Abstand (oder, sofern es um eine variable Größe geht, Entfernung) charakterisiert wohl eher jeweils ein Paar von bestimmten Beteiligten (z.B. die beiden Spiegeln eines optischen Resonators);
und nicht eine Beziehung zwischen ganzen Systemen.
> einerseits […] dem kräftefreien von Gravitationsschwankungen isolierten Bezugssystem […]
LIGO und der Beschreibung im obigen SciLogs-Artikel liegt aber offenbar zugrunde, dass sich in einer Region mit Gravitationwelle die chronometrischen Entfernungen zwischen (geeignet ausgewählten) einzeln „kräftefreien“ (inertialen, unbeschleunigten, ruhenden) Beteiligten dennoch periodisch veränderlich sind.
(Entsprechend ist die Gesamtheit dieser Beteiligten in solchen Versuchen wohl gerade nicht das, was unter einem „Inertialsystem“ verstanden wird.)
Allerdings lässt sich eine einer Region mit Gravitationwelle auch durch Entfernungsverhältnisse zwischen Beteiligten charakterisieren, von denen keiner unbedingt „kraftfrei“ (inertial, unbeschleunigt, ruhend) sein müsste (Stichwort: „Five PoInt Curvature Detector“ nach J. L. Synge). Man darf ja wohl hoffen, dass dieses, durch seine Modell-Unabhängigkeit ausgezeichnete Messprinzip demnächst angewandt wird …
Siegfried Heiss schrieb (12. August 2016 @ 18:17):
> Die als Pendel aufgehängten Spiegel bei LIGO stellen ein kraftfreies Bezugssystem dar. Auf der Erde funktioniert die kraftfreie Aufhängung natürlich nur für die beiden horizontalen Richtungen.
Wurde denn gemessen, dass die wesentlichen Bestandteile von LIGO [1] horizontal (oder zumindest: jeweils in Interferometerarm-Richtung) einzeln hinreichend „kraftfrei“ (inertial, unbeschleunigt, ruhend) gewesen und geblieben wären;
insbesondere während (wie im obigen SciLogs-Beitrag beschrieben) der LIGO-Lichtdetektor ein (erwähnenswertes) Signal aufgezeichnete
??
Oder ist das etwa nur eine Modellannahme ? …
> Die Messung des Abstands zwischen den beiden verschiedenen Bezugssystemen,
Abstand (oder, sofern es um eine variable Größe geht, Entfernung) charakterisiert wohl eher jeweils ein Paar von bestimmten Beteiligten (z.B. die beiden Spiegeln eines optischen Resonators);
und nicht eine Beziehung zwischen ganzen Systemen.
> einerseits […] dem kräftefreien von Gravitationsschwankungen isolierten Bezugssystem […]
LIGO und der Beschreibung im obigen SciLogs-Artikel liegt aber offenbar zugrunde, dass in einer Region mit Gravitationwelle die chronometrischen Entfernungen zwischen (geeignet ausgewählten) einzeln „kräftefreien“ (inertialen, unbeschleunigten, ruhenden) Beteiligten dennoch periodisch veränderlich sind.
(Entsprechend ist die Gesamtheit dieser Beteiligten in solchen Versuchen wohl gerade nicht das, was unter einem „Inertialsystem“ verstanden wird.)
Allerdings lässt sich eine Region mit Gravitationwelle auch durch Entfernungsverhältnisse zwischen Beteiligten charakterisieren, von denen keiner unbedingt „kraftfrei“ (inertial, unbeschleunigt, ruhend) sein müsste (Stichwort: „Five Point Curvature Detector“ nach J. L. Synge). Man darf ja wohl hoffen, dass dieses, durch seine Modell-Unabhängigkeit ausgezeichnete Messprinzip demnächst angewandt wird …
[1] D.h. abgesehen davon, dass (zur Optimierung der Sensitivität) zumindest einige LIGO-Spiegel mit Aktuatoren verbunden sind.
Wollte nur was Prinzipielles schreiben, damit ich es endlich selbst verstehe…
Die Erde mit den LIGO-Armen ist starr, diese werden durch die Gravitationswelle elastisch verformt, Spiegel und Detektor werden kraftfrei aufgehängt und bilden immer ein Inertialsystem in Richtung des Detektorarms. Der Laserstrahl dient als Maßstab im Erde-LIGO-Bezugssystem, von diesem Bezugssystem aus gesehen ändern die kraftfrei aufgehängten Spiegel beim Durchgang der GW ihre Abstände und diese Abstandsänderung wird detektiert. Ich wollte nur zum Ausdruck bringen, dass es in manchen Beschreibungen (irreführend) heißt, die Interferometerarme werden durch die GW in einer Richtung verkürzt und senkrecht dazu verlängert und diese Änderung wird gemessen. Würden aber die Spiegel fest mit den Interferometerarmen verbunden sein, würde man nichts messen, da die Lichtgeschwindigkeit in jedem Bezugsystem konstant bleibt und daher die Laufzeiten und Phasenbeziehungen beim Durchgang der GW immer gleich wären, der Laserstrahl bildet einen starren Maßstab der auch von der GW wie die starre Materie verändert wird. Die Pendelspiegelaufhängung soll nicht nur die Übertragung von mechanischen Schwankungen verhindern, sondern ermöglicht erst das Prinzip der GW-Messung.
Beim LISA-Experiment werden die Abstände zwischen frei fallenden (schwebenden) Massen bestimmt, dort bilden die Testmassen also tatsächlich Inertialsysteme in allen Richtungen. Das starre von der GW beeinflusste Bezugssystem sind die Satelliten (mit dem Sonnensystem) am Lagrange-Punkt.
Der frei fallende Aufzug im Gravitationsfeld ist kraftfrei, schwerelos, also ein Inertialsystem – Äquivalentsprinzip.
Siegfried Heiss schrieb (17. August 2016 @ 21:53):
> Die Erde mit den LIGO-Armen ist starr, diese werden durch die Gravitationswelle elastisch verformt, […]
Als „starr“ werden allerdings üblicherweise gerade solche Systeme (Paare von Enden, etc.) bezeichnet, die sich nicht verformen; deren Entfernungsverhältnisse untereinander sich nicht verändern (und gerade deshalb insgesamt „ihre Form“ behalten); und sogar: deren (paarweise) Entfernungen voneinander sich überhaupt nicht ändern (weswegen diese Entfernungen in diesem Falle auch „Abstand“ genannt werden).
Ja stimmt, „starr und von GW elastisch verformt“, klingt etwas widersprüchlich. Allerdings verformt sich die Materie mit dem metrischen Feld und das metrische Feld ist ziemlich das Starrste was man sich vorstellen kann, Elastizitätsmodul um ca. 30 Zehnerpotenzen höher als Stahl. Die Materie wird daher praktisch phasengleich ihre Abmessungen mit dem metrischen Feld mitändern. In unserem Bezugssystem können wir aber diese Änderung nicht feststellen, da alle „starren“ Maßstäbe und auch die Laserstrahlen aufgrund der Konstanz der Lichtgeschwindigkeit mit dem metrischen Feld „mitverformt“ werden. Unter Zuhilfenahme der Spiegel-Detektor-Inertialsysteme können aber die Distanzänderungen gemessen werden. Vom Erde-LIGO-Bezugssystem aus gesehen ändern sich die Spiegel-Detektor-Abstände, die LIGO-Arme bleiben von uns aus gesehen starr. Die Änderung der Raumkrümmung nur im eigenen Bezugsystem zu messen geht nach Gauß und Riemann auch, allerdings wird das experimentell schwierig, vielleicht irgendwann mit Satelliten über große Distanzen, Abweichung vom Pythagoras, die GW’s sind ja praktisch ebene Wellen und ändern daher die Metrik nicht nur lokal, sondern über große Distanzen. Mathematisch exakt gelingt es z.B.: nach Weyl relativ anschaulich durch Parallelentransport entlang von Dreiecken oder Parallelogrammen alle Komponenten des Riemannschen Krümmungstensors im Bezugssystem selbst zu bestimmen, experimentell wird das aber nicht so einfach realisierbar…
Siegfried Heiss schrieb (18. August 2016 @ 13:54):
> Allerdings verformt sich die Materie mit dem metrischen Feld […]
Was wäre denn mit „metrischem Feld“ anderes gemeint, als die Gesamtheit der (konstanten) Abstands- bzw. (evtl. variablen) Entfernungsverhältnisse aller (denkbaren, und evtl. sogar auffindbaren) materiellen Beteiligten untereinander??
„Form“ bzw. „Verformung“ ist jedenfalls ein intrinsisches Charakteristikum einer geeigneten Menge bestimmter materieller Beteiligter.
> […] da[ss] alle „starren“ Maßstäbe und auch die Laserstrahlen aufgrund der Konstanz der Lichtgeschwindigkeit mit dem metrischen Feld „mitverformt“ werden.
Natürlich gibt es allerlei historisch begründbare Begriffe von „Starrheit“, die z.B. an (nicht strikt geometrisch-kinematische) „Materialeigenschaften“, „Ausbreitung von Wirkungen“ oder Ähnliches, nicht unbedingt Nachvollziehbares appellieren. Nicht umsonst war in meinen vorausgehenden Kommentar aber ausdrücklich von chronometrischer Starrheit (bzw. ansonsten: Abweichungen von chronometrischer Starrheit) die Rede; also schlicht davon, ob bestimmte Paare von betrachteten Beteiligten (wie z.B. „Sp1“ und „T“ in der obigen Skizze) untereinander jeweils konstante Pingdauern finden (und evtl. sogar gegenseitig gleiche Pingdauern finden), oder nicht.
> Abweichung vom Pythagoras
Die genauere, wesentliche, weniger missverständlich formulierte Bewertung besteht darin, ob Cayley-Menger-Determinanten (der Abstands- bzw. Entfernungsverhältnisse von geeignet vielen, d.h. typischerweise fünf Beteiligten untereinander) verschwinden, oder nicht.
> […] nach Weyl relativ anschaulich durch Parallelentransport entlang von Dreiecken oder Parallelogrammen alle Komponenten des Riemannschen Krümmungstensors im Bezugssystem selbst zu bestimmen
Welchen (Paaren von) „Objekten“ sollte denn „Parallelität“ (oder Abweichung davon) überhaupt zugeschrieben werden? Und wie wäre deren eventuelle „Parallelität“ zumindest im Prinzip zu messen?? …
(Die Grundlage der RT als einem Gebiet der (Experimental-)Physik ist laut Einstein jedenfalls, dass „alle unsere zeiträumlichen Konstatierungen stets auf die Bestimmung zeiträumlicher Koinzidenzen hinauslaufen“.)
Das Metrische Feld ist fundamentaler als die Entfernungsverhältnisse aller materiellen Beteiligten, auch in der Abwesenheit von (unserer bekannten) Materie gibt es das Metrische Feld. Materie krümmt (komprimiert) das Metrische Feld, erzeugt es aber nicht, ändert dessen Energiezustand, auch in den ausgedehnten Leerräumen des Universums existiert das Metrische Feld, hat auch dort einen Energieinhalt, durch Ausdehnung verringert es seine Krümmung… In der ART wird das Gravitationspotential direkt mit dem Metrischen Feld in Verbindung gebracht und damit geometrisch vorstellbar, allerdings ohne die Natur des Metrischen Feldes genauer zu fassen, sicher steckt aber noch mehr drinnen. Der Wert der Vakuumlichtgeschwindigkeit ist eine direkte Eigenschaft des Metrischen Felds, warum sollte diese sonst in unserem Maßsystem gerade 299792458 m/s betragen? Diese invariante Maximalgeschwindigkeit jeder Form der Energie- bzw. Signalübertragung, auch der GW‘s, ist sicher die grundlegendste Naturkonstante.
„Abweichung vom Pythagoras“ sollte einfach heißen, „Abweichung vom euklidischen Raum“, kann man natürlich mathematisch exakter mit dem Tensorkalkül beschreiben, experimentell messen kann man aber Abstände und eventuell noch Winkel, daher habe ich mich auf „Pythagoras“ bezogen.
Aber das kann man in kurzen Zeilen sicher nicht exakt und unmissverständlich formulieren…
Strikte, instantane, „Starrheit“ eines Körpers gibt es schon aus relativistischen Gründen nicht, stößt man ein Ende eines Stabes an, so breitet sich diese Information maximal mit Lichtgeschwindigkeit zum anderen Ende hin aus. „Starr“ war in dem Sinne gemeint, dass der Körper mit der Metrik verbunden ist und mit dieser beim Durchgang der GW mitverformt wird.
Mein ursprünglicher Beitrag zum LIGO-Experiment, bzw. zu dessen Verständnis, ging in die Richtung:
Spiegel und Strahlteiler sind kraftfrei aufgehängt und daher „freifallend“, bilden ein lokales Inertialsystem, werden daher von der GW nicht beeinflusst, träge Masse ist gleich schwerer Masse, auch eine plötzliche Änderung der Gravitation lässt sich im freifallenden Aufzug nicht spüren. Der freifallende Aufzug bildet zu jedem Zeitpunkt ein lokales Inertialsystem.
In der Beschreibung von Markus Pössel heißt es:
„Spiegel und Strahlteiler betrachten wir als freie Teilchen, deren Abstände von der Gravitationswelle beeinflusst werden. Der Lauf der Lichtpulse wird, ähnlich wie oben, natürlich auch beeinflusst.“
Wenn man dann noch hört oder liest, dass die GW die gesamte Erde mit den LIGO-Armen verformt, was ja auch tatsächlich der Fall ist, kommt es oft zu Missverständnissen.
Ich finde, exakter müsste es heißen: „Die Erde und die LIGO-Arme werden beim Durchlauf der GW gestaucht und gedehnt, die Spiegel und Strahlteiler als lokale Inertialsysteme bleiben von der GW unbeeinflusst. Vom LIGO-Bezugssystem aus gemessen ändert sich natürlich der Spiegel-Strahlteiler-Abstand beim Durchgang der GW. Gemessen wird vom LIGO-Ruhesystem aus, daher gibt es Auslenkungen an den Spiegeln und Strahlteilern. Aufgrund des Äquivalenzprinzips ist das aber nichts anderes als die Schwankung des Gravitationsfeldes beim Durchgang der GW. Wird die Metrik in der einen Richtung senkrecht zur Ausbreitungsrichtung der GW gestaucht, verkürzt sich der LIGO-Arm in dieser Richtung, Spiegel und Strahlteiler bleiben unbeeinflusst, d.h. der Spiegel-Strahlteiler-Abstand vom (gestauchten) LIGO-Bezugssystem aus gemessen hat sich vergrößert.
Siegfried Heiss schrieb ( 22. August 2016 @ 21:42):
> stößt man ein Ende eines Stabes an, so breitet sich diese Information maximal mit Lichtgeschwindigkeit zum anderen Ende hin aus
Ganz recht … (Stichwort: Signalfront.)
> „Starrheit“ eines Körpers gibt es schon aus relativistischen Gründen nicht
Kommt ganz darauf an, was mit „Starrheit“ bzw. „Stab“ jeweils gemeint ist.
Der leicht vorstellbare und evtl. sogar experimentell vorliegende Befund, dass ein Ende das entsprechende Pingecho des anderen Endes jeweils erst deutlich nach dem Anstoß-Signal wahrnnahm (und nicht etwa koinzident damit, oder gar vorher),
bedeutet eben nicht zwingend,
dass die entsprechenden Pingdauern des einen Endes (gegenüber dem anderen) nicht konstant gewesen wären,
oder dass die Pingdauern des anderen Endes (gegenüber dem erstgenannten) nicht konstant gewesen wären,
oder auch nur, dass diese jeweils konstanten Pingdauern nicht gegenseitig gleich gewesen wären.
Im Übrigen tritt das Wort „starr“ ausgerechnet in den Grundlagen des relativistischen Gedankengutes recht prominent auf; vgl. http://einsteinpapers.press.princeton.edu/vol2-doc/473?highlightText=starr
Es scheint allerdings immer noch umstritten, ob damit die oben beschriebene „chronometrische Starrheit“ gemeint ist, oder (dieser zugrundeliegend) „Ping-Koinzidenz-Starrheit“, oder überhaupt irgendeine nachvollziehbare Definition …
@Frank Wappler / 24. August 2016 @ 13:59
Um noch halbwegs eine Übersicht bei der Abfolge von Kommentaren zu behalten, vermeide ich hier mal die Reply-Funktion.
Einsteins Begriff von Gleichzeitigkeit ist, wie er ja selbst in seinem populären Büchlein ausführt, eine nach freiem Ermessen getroffene Festsetzung, die gar keine physikal. Voraussetzungen oder Hypothesen enthält. Etwas formaler betrachtet, führt er mit diesem Begriff ein zweistelliges Prädikat P auf eine Variablenmenge M ein und fordert dabei von P nur, was die Logik gebietet, nämlich dass für alle x,y ∈ M entscheidbar ist, ob Pxy wahr ist oder nicht, wobei Pxy mit “x ist simultan zu y” zu übersetzen wäre. Was ich bei Einstein hingegen nicht herauslesen kann, sind Verhaltensregeln wie etwa diese:
»(Experimental-)Physikern ist dagegen bekanntlich auferlegt, Methoden aus Feststellungen von Koinzidenz (und Identität) zu konstruieren.«
Und Einstein scheint zeiträumliche Koordinaten doch für ein grandioses Mittel zur Darstellung zeiträumlicher Koinzidenzen gehalten zu haben; andernfalls hätte er schwerlich so ausgiebig Gebrauch davon gemacht.
Sich bei seiner GR des Formalismus der Riemannschen Geometrie zu bedienen, ist letztlich ebenfalls eine nach eigenem Ermessen getroffene Entscheidung Einsteins. Wie frei er seinerzeit in dieser Entscheidung war, sei mal dahingestellt, aber gewiss ist, dass wir nicht mehr frei sind zu entscheiden, was unter GR zu verstehen ist und was nicht.
Eine Karte ist nicht eine Bijektion und ansonsten beliebig, und eine (Pseudo-)Riemannsche Struktur ist auch nicht eine topologische Struktur. Lies’ doch beispielsweise einfach mal weiter bei dem eigenen Wiki-Link zu Mannigfaltigkeiten, dann sollte die Bedeutung von Karten für die Riemannsche Struktur doch ersichtlich werden.
»???
Spätestens seit Kokkendorff’s o.g. Beitrag doch.«
Spätestens seit Einstein mit dem Teleparallelismus herauskam, sollte eigentlich klar sein, dass seine Gravitation auch ohne Krümmung funktioniert.
Chrys schrieb (28. August 2016 @ 16:10):
> Eine Karte ist nicht eine Bijektion und ansonsten beliebig [sondern wie im Wikipedia-Link zu Mannigfaltigkeiten beschrieben]
Eben.
Genau deshalb die Enttäuschung über bloße Beschwichtigungen:
und nicht zu vergessen
während sich doch die Frage aufdrängt:
.
Und nicht zu vergessen:
Kann diese Frage beantwortet werden, ohne dabei bestimmte Bijektionen zwischen Teilmengen von ℰ und (Teilmengen von) ℰ einzusetzen?;
von denen man nämlich vor Beantwortung dieser Frage noch nicht wissen kann, ob sie Karten im o.g. Sinne wären, oder doch “nur beliebig”.
(Der Rest ist hierzu “p.s.”; dazu komme ich vermutlich erst heute abend.)
Chrys schrieb (28. August 2016 @ 16:10):
> Eine Karte ist nicht eine Bijektion und ansonsten beliebig [sondern wie im Wikipedia-Link zu Mannigfaltigkeiten beschrieben]
Eben.
Genau deshalb die Enttäuschung über bloße Beschwichtigungen:
und nicht zu vergessen
während sich doch die Frage aufdrängt:
.
Und nicht zu vergessen:
Kann diese Frage beantwortet werden, ohne dabei bestimmte Bijektionen zwischen Teilmengen von ℰ und (Teilmengen von) ℝ^k zu benutzen?;
von denen man nämlich vor Beantwortung dieser Frage noch nicht wissen kann, ob sie Karten im o.g. Sinne wären, oder doch “nur beliebig”.
(Der Rest ist hierzu “p.s.”; dazu komme ich vermutlich erst heute abend.)
p.s.
Chrys schrieb (28. August 2016 @ 16:10):
> Einsteins Begriff von Gleichzeitigkeit ist, wie er ja selbst in seinem populären Büchlein ausführt, eine nach freiem Ermessen getroffene Festsetzung
… das entspricht wirklich ziemlich genau dem, was da steht …
> die gar keine physikal. Voraussetzungen oder Hypothesen enthält.
Nein: nicht in uneingeschränkter Allgemeinheit; sondern:
.
Zu den ganz expliziten Voraussetzungen zählt die Möglichkeit eines (geeigneten) Beobachters zu beurteilen,
.
(Zugegeben: Einstein benutzte an dieser Stelle die Formulierung “zusammen wahrnehmen” leider nicht; und leider auch nicht die Formulierung “koinzident wahrnehmen” …)
> Und Einstein scheint zeiträumliche Koordinaten doch für ein grandioses Mittel zur Darstellung zeiträumlicher Koinzidenzen gehalten zu haben
Wenn es Einstein (oder denjenigen, die Einstein in Richtung Differentialgeometrie geführt haben) um Mittel allein für die “Darstellung zeiträumlicher Koinzidenzen” im schlichten Sinne gegangen wäre, dass unterscheidbare (Koinzidenz-)Ereignisse mit verschiedenen Namen benannt werden sollten,
wofür sich Mengen von reellen Zahlen(-Tupeln) durchaus grandios eignen dürften,
dann wären dafür jegliche Bijektion geeignet;
es wäre ganz unerheblich, ob solche Namensgebungen “homöomorph” gegenüber der Ereignismenge (oder gegenüber einander) wären; oder sogar “diffeomorph”, oder “isometrisch” bzw. “gut”.
Aber nein: bei der “Darstellung” es geht üblicherweise um mehr;
und also geht es (mir) vorrangig darum, wie denn die “darzustellende Struktur” zunächst intrinsisch/endogen/invariant aus der (gegebenen) Ereignismenge an sich zu ermitteln ist.
> (Pseudo-)Riemannsche Struktur ist auch nicht eine topologische Struktur
(Das habe ich auch nicht bestritten; die Redundanz von Koordinatendarstellungen und insbesondere von Karten lässt sich aber offensichtlich und für meine Argumentation am einfachsten anhand von “topologischer Struktur” erläutern.)
Riemanns entsprechende Antrittsvorlesung “Über die Hypothesen, welche der Geometrie zu Grunde liegen” weist offenbar “Längen von Linien” (bzw. deren Verhältnisse) als die wesentliche Struktur aus.
Also drängt die Frage:
Wie misst man das (oder die entsprechende pseudo-Riemannsche Verallgemeinerung) in der ART??
> Spätestens seit Einstein mit dem Teleparallelismus herauskam, sollte eigentlich klar sein, dass seine Gravitation auch ohne Krümmung funktioniert.
Sofern das (nur) darauf anspielt, dass “Torsion” von “Krümmung” zu unterscheiden wären, fällt mir eine Unterscheidung tatsächlich schwer;
vorrangig und wesentlich/Koordinaten-unabhängig geht es doch (nach Kokkendorff) jedenfalls um das Aufstellen und Nullsetzen der relevanten Gram-Determinanten, bzw. ggf. Cayley-Menger-Determinanten.
Die dafür erforderlichen Messwerte von Abstands- (bzw. zumindest Entfernungs-)verhältnissen, also von Pingdauerverhältnissen, sind natürlich aus Koinzidenzfeststellungen zu gewinnen; gemäß Einsteins (Kretschmanns, Comstocks, …) Forderung, dass
.
p.p.s.
Wir haben oben natürlich nur eine von (mindestens) zwei geläufigen Bedeutungen des Wortes “Invariante” diskutiert …
p.p.p.s.
> Um noch halbwegs eine Übersicht bei der Abfolge von Kommentaren zu behalten […]
Seufz …
Man muss ja fast schon dankbar dafür sein, dass wenigstens immer noch die letzten fünf Kommentare zum jeweiligen SciLog angezeigt werden (geschweige denn Wikipedia-artig: alle).
Und danke übrigens für den Formatierungshinweis (“<em> … </em>”) neulich …
Frank Wappler / 29. August 2016 @ 08:56 p.s. …
Für (Pseudo-)Riemannsche Mannigfaltigkeiten ist schliesslich etwas mehr gefordert:
Um überhaupt einen Tangentialraum an jedem Punkt zu haben, braucht es eine differenzierbare Struktur auf einer solchen Mannigf., und diese Struktur wird durch geeignete Karten dort eingeführt. Speziell für eine Raumzeit in der GR wird jeder Tangentialraum durch das Pseudo-Skalarprodukt mit der Minkowskischen Geometrie ausgestattet, wodurch die SR hier als tangentiale Näherung an die GR herauskommt. Was wiederum für Einsteins Idee von der allg. Covarianz von Belang ist, indem physikal. Gesetze, die Lorentz-covariant in der SR formulierbar sind, sich dann auch in die GR übertragen lassen (via “comma to semicolon“), wozu allerdings im konkreten Fall erneut lokale Darstellungen durch Karten heranzuziehen sind.
Zwischen GR (Krümmung) und TP (Torsion) lässt sich durch Observationen nicht unterscheiden oder entscheiden, in dieser Hinsicht sind beide Theorien gleichwertig. Vergleichbar damit, wie wir es in der QM ja auch mit ganz unterschiedlichen Deutungen zu tun haben, von denen sich dann keine rein observationell gesondert bevorzugen lässt.
Chrys schrieb (1. September 2016 @ 18:49):
> eine differenzierbare Struktur auf einer solchen Mannigf. […] wird durch geeignete Karten dort eingeführt.
Der Knackpunkt ist und bleibt, dass man im Rahmen der Physik „Struktur“ durch Messwerte gewinnt (die aus tatsächlichen oder ggf. auch aus simulierten Beobachtungsdaten zu ermitteln sind);
und nicht durch beliebiges Bestreuen einer Ereignismenge mit reellen Tupeln, die alleine deshalb „geeignete Karten“ zu nennen wären, weil solches willkürliches Vorgehen im selben Atemzug „Einführung (von topologischer bzw. differenzierbarer Struktur)“ genannt würde.
In der Physik kommt die endogene Struktur (insbesondere von Ereignismengen) zuerst;
und nur im Bezug darauf und im Nachhinein ist zu entscheiden, welche Abbildungen durch reelle Tupel „geeignet/gut“ sind (sofern nämlich die gegebene topologische oder metrische Struktur durch die entsprechende „natürliche“ Struktur reeller Tupel homöomorph oder sogar differenzierbar oder sogar (skaliert) isometrisch abgebildet und dargestellt würde), und welche nicht, sofern das über die sowieso gegebene Struktur hinaus überhaupt von Interesse sein mag.
> […] gefordert: Eine Riemannsche Metrik (auch Metrischer Tensor genannt) definiert im Tangentialraum jedes Punktes der Mannigfaltigkeit ein Skalarprodukt.
Dieser Forderung, die mathematisch zweifellos möglich ist (wenn auch offenbar nicht zwangsläufig), lassen sich Forderungen entgegensetzen, deren Erfüllung strikt in Auswertung der durch Messung vorgegebenen Struktur
beurteilt werden kann; also in direkten Bezug auf die oben erwähnten, von Riemann in Betracht gezogenen „Längen von Linien“ (bzw. zumindest den reell-wertigen Verhältnissen solcher „Längen von Linien“):
– einer bestimmten „Linie“ wird allein aufgrund der Elemente, die sie enthält, ein bestimmter „Längen“-Wert (zumindest im Verhältnis zu anderen) zugeordnet (d.h. „Durchlaufrichtung“ spielt keine Rolle; Symmetrie).
– „Linien“ von endlicher „Länge“ haben entweder zwei verschiedene Elemente als „Enden“, oder sie sind geschlossen.
– zu je zwei verschiedenen Elementen hat das Infimum der „Längen“-Werte aller „Linien“, die diese beiden Elemente als „Enden“ haben, einen von Null verschiedenen Wert; genannt „Distanz“ dieser beiden Elemente. (Damit zusammenhängend: die Dreiecksungleichung für Distanzen.)
– für jedes Element konvergiert der (maximale) Krümmungsparameter κ (durch den die entsprechende Gram-Determinante n + 1ter Ordnung Null wird) im Grenzübergang immer kleinerer Distanzen einer bestimmten Anzahl n ≥ 3 weiterer Elemente bzgl. des erstgenannten Elementes, als auch untereinander. (Damit zusammenhängend: die Dimension n – 1 der Riemannschen Mannigfaltigkeit.)
In Teilmengen, für die die reelle Zahl κ MaxAbstand ≪ 1 sind die Werte aller Cayley-Menger-Determinanten n + 1ter Ordnung dann entsprechend nahe an Null. Darauf aufbauend kann der Begriff „gegenüber einander tangentialer Linien“ („die sich in einem bestimmten Element berühren, aber nicht schneiden“) sowie das Maß „Winkel“ („zwischen Linien die sich in einem bestimmten Element schneiden“, bzw. zwischen den entsprechenden Äquivalenzklassen tangentialer Linien) aus den Distanzverhältnissen definiert werden.
Damit ist in jedem Element ein Skalarprodukt ermittelt, das Distanz- und Winkelverhältnisse zusammenfasst; zumindest in beliebig guter Näherung, auf einer Teilmenge mit entsprechend kleinen maximalen Distanzen.
(Wer’s nicht lassen kann, mag ja immer noch Koordinatentupel so darüber stäuben, dass Werte dieses Skalarprodukts als Bilinearform aus „ Metrischem Tensor“ und Koordinatendifferenzen ausgedrückt würden.)
> Speziell für eine Raumzeit in der GR wird jeder Tangentialraum durch das Pseudo-Skalarprodukt mit der Minkowskischen Geometrie ausgestattet, wodurch die SR hier als tangentiale Näherung an die GR herauskommt.
Wahrlich keine Physik-bezogene Auffassung von „Geometrie“.
Dem entgegenzusetzen ist der Aufbau geometrischer Begriffe aus dem (Einsteinschen) Koinzidenzbegriff, über Ping-Koinzidenz-Gitter (einschl. der Beurteilung, ob diese bei immer feinerer Auflösung immer genauer
konformal flach sind,
daraus die Definition geeignet verallgemeinerter metrischer Begriffe bzw. Maße (insbesondere von „Dauer“ und „Lorentzscher Distanz“, die die umgekehrte Dreiecksungleichung erfüllt),
und ziemlich analog zu oben bis zum Skalarprodukt;
immer hübsch Koordinaten-frei.
> Zwischen GR (Krümmung) und TP (Torsion) lässt sich durch Observationen nicht unterscheiden
Soweit
das entsprechende Wikipedia-Bild verständlich ist, geht es dabei schlicht um (die Messung von) Ebenheit/Planarität bzw. von Abweichung davon; also um Gram- bzw. Cayley-Menger-Determinanten der Ordnung 4; in Unterscheidung (aber natürlich auch in engem Zusammenhang) zu entsprechenden Determinanten der Ordnung 5 bzw. 6, die sich mit Krümmung (oder ansonsten: Flachheit) im Drei- bzw. Vierdimensionalen beschäftigen.
@Frank Wappler / 2. September 2016 @ 15:46
Hinsichtlich empirischer Untersuchungen hat Einstein immerhin zwischen deren logisch-formalen Mitteln einerseits und ihren phänomenalen Gegenständen andererseits kategoriell zu unterscheiden gewusst. Und seine Auffassung davon, in welcher Beziehung diese Kategorien zueinander stehen, hat er nicht zuletzt in seinem Vortrag Geometrie und Erfahrung dargelegt.
Ein Begriff wie `Krümmung der Raumzeit’ bezeichnet keine Naturerscheinung. `Raumzeit’ und `Krümmung’ gehören zu den logisch-formalen Mitteln, deren Wahl eine vom menschlichen Verstand vorzunehmende Festsetzung ist. Observabel sind immer nur Erscheinungsformen von `Gravitation’. Aus Beobachtungsdaten ist jedoch beispielsweise keine `Krümmung’ deduktiv zu gewinnen, und Einsteins Feldgleichungen lassen sich nicht einfach irgendwie aus Messwerten herauslesen,
Krümmung kommt nicht unmittelbar mit einem metrischen Tensor herein, denn die Metrik lässt einem noch immer die Freiheit der Wahl eines mit ihr verträglichen affinen Zusammenhanges. Für die GR wird der affine Zus.hang als torsionsfrei gefordert und ist erst durch diese zusätzliche Forderung eindeutig festgelegt. Im TP wird indessen der affine Zus.hang gerade als krümmungsfrei gefordert. GR und TP sind also gleichsam zwei zueinander duale Betrachtungs- oder Beschreibungsweisen. Die Wahl einer Betrachtungsweise ist aber etwas, das im Ermessen des Betrachters liegt, die wird ihm nicht durch den Gegenstand seiner Betrachtung aufgezwungen. Und letzteres gilt in den empirischen Wissenschaften ganz grundsätzlich — weshalb dann auch immer wieder so fruchtlos gestritten wird, wenn jeder meint, die eigene Betrachtungsweise sei die einzig wahre.
Chris schreibt: “Aus Beobachtungsdaten ist jedoch beispielsweise keine `Krümmung‘ deduktiv zu gewinnen, und Einsteins Feldgleichungen lassen sich nicht einfach irgendwie aus Messwerten herauslesen, ….”
Licht ist unser universales „Messinstrument“. Gerade die Messung der Lichtablenkung kann direkt mit der Raumzeit-Krümmung korreliert werden, Lichtablenkung, Periheldrehung lässt sich quantitativ aus den Einstein’schen Feldgleichungen ermitteln, transversaler Dopplereffekt, Mössbauereffekt, usw. sind alles Effekte die mit der ART quantitativ erklärt werden können. Das relativistische Konzept des Lorentz-kovarianten Energie-Impulstensors und des Elektromagnetsichen-Feldtensors sind alles direkt nachmessbare Konzepte der SRT. Das Magnetfeld selbst ist ein relativistischer Effekt von bewegten elektrischen Ladungen! Daher kann man auch einen logischen Weg von den Maxwellgleichungen zur SRT nachzeichnen.
Ich finde man sollte bei der Betrachtung der mathematischen Werkzeuge die physikalischen Zusammenhänge nicht vergessen, schließlich sind die mathematischen Werkzeuge Mittel zum Zweck und nicht Selbstzweck.
Chrys schrieb (4. September 2016 @ 11:01):
> […] zu den logisch-formalen Mitteln, deren Wahl eine vom menschlichen Verstand vorzunehmende Festsetzung ist.
Das schließt konkret ein:
Die Definitionen von Messgrößen durch nachvollziehbare Operatoren;
als Konstruktion basierend auf (jeweils) einer Festsetzung, was dabei überhaupt als gegebene Beobachtungsdaten aufzufassen ist, worauf die konstruierten und ausgewählten Messoperatoren dann ggf. anzuwenden sind, um Messwerte zu ermitteln.
> Die Wahl einer Betrachtungsweise ist aber etwas, das im Ermessen des Betrachters liegt
Das bedeutet aber keineswegs Beliebigkeit.
Was als “Festsetzung” gemeint ist, muss haltbar sein:
.
Diese Forderung bedeutet konsequenter Weise, ausschließlich diejenigen logisch-formalen Mittel (Begriffe) bei anderen vorauszusetzen und selbst einzusetzen, über die man sowieso verfügt haben muss, um diese Forderung zu begreifen, selbst zu stellen, und einschätzen zu können, ob sie erfüllt ist.
Nur Begriffe, von denen man allein durch das Stellen der Frage “Was bedeutet dieser Begriff?” kundtut, dass man Verständnis des entsprechenden Begriffes bereits besitzt, und allenfalls noch eine Übersetzung der entsprechenden sprachlichen Ausdrucksformen dafür benötigt;
nur selbstverständliche, nachvollziehbare Begriffe.
Konkret:
;
(die geometrisch-zeit-räumlichen recht unmittelbar; und darauf basierend das, was mit weiteren Erwartungen zu tun hat, per Variationsrechnung).
Dass Einstein das wohl formuliert und punktuell vorgeführt, aber vielleicht trotzdem nicht gründlich verstanden und verinnerlicht hatte, ist allerdings tragisch und beeinträchtigt die Physikdidaktik offenbar immer noch.
> Aus Beobachtungsdaten ist jedoch beispielsweise keine `Krümmung‘ deduktiv zu gewinnen
Was macht eigentlich ein (in diesem SciLog schon öfters erwähnter) “Five-Point Curvature Detector” nach Synge ? …
@Siegfried Heiss / 5. September 2016 @ 09:46
»Gerade die Messung der Lichtablenkung kann direkt mit der Raumzeit-Krümmung korreliert werden, …«
Wer Lichtablenkung im Schwerefeld veranschaulichen will, zeichnet sich einen “Lichtstrahl” als gekrümmte Linie auf eine flache Zeichenebene und demonstriert damit, was sich der Mensch ganz naiv so unter `Krümmung’ vorstellt. Unmittelbar wahrgenommen wird `Krümmung’ nur in Gestalt gekrümmter Linien oder Flächen in Relation zu einem ungekrümmten Bezugsrahmen. Für intrinsische Krümmung von Raum — geschweige denn Raumzeit — haben wir keine eingebaute Antenne, keine direkte Intuition, und es ist eine Denkleistung des menschl. Verstandes, dennoch mit solchen Begriffen sinnvoll umgehen zu können.
Wenn also Lichtablenkung im Schwerefeld gemessen wird, dann wird eben genau das als Phänomen gemessen, und für den Messvorgang ist es unerheblich, ob Gravitation als Krümmung konzipiert wird oder nicht. Physiker sollten sich der Erfordrnis einer sauberen Trennung zwischen phänomenal Observiertem und theoriebezogen Interpretiertem grundsätzlich bewusst sein. Wo das unterbleibt, kann man leicht die Orientierung verlieren und sich einer Illusion von Wissen hingeben, mit der man dann sich selbst und womöglich andere nur in die Irre führt.
Chrys schreibt:
Wer Lichtablenkung im Schwerefeld veranschaulichen will, zeichnet sich einen „Lichtstrahl“ als gekrümmte Linie auf eine flache Zeichenebene …
Wenn sich jemand die Raum-Zeit-Krümmung durch gekrümmte Lichtstrahlen auf einer flachen Zeichenebene vorstellt, oder wie es oft demonstriert wird, mit Kugeln die eine Gummimembran verformen, so sind das nur sehr vereinfachte Modelle die keine tiefere Erkenntnis bringen. Um eine Vorstellung von der Raumzeitkrümmung zu bekommen, reicht nicht die natürliche Intuition unter Zuhilfenahme eines ebenen Einbettungsraums. Die Intuition hat ja auch zuerst zur Galilei-Transformation geführt und erst über einen Umweg über die Elektrodynamik zur Lorentz-Transformation. Eine direkte Intuition kann man nur entwickeln, wenn man den mühseligen Weg nicht scheut den mathematischen Apparat zu erfassen und sich mit vielen praktischen Beispielen und Gedankenexperimenten das Raumzeit-Kontinuum vertraut macht.
Es geht bei der Lichtablenkung im Schwerefeld auch nicht nur darum, dass das Phänomen in der ART grundsätzlich auftritt, sondern, dass der gemessene Wert genau mit den Feldgleichungen der ART errechnet werden kann. Die Basis der ART ist das einfach intuitiv erfassbare Äquivalenzprinzip zwischen Beschleunigung und Gravitation(sbeschleunigung), aber zur ART ist es dann noch ein weiter Weg. Für die Formulierung der Feldgleichungen hat Einstein 10 Jahre gebraucht, da ihm der Tensorkalkül erst durch Grossmann nahegebracht wurde. Wenn man den vorgezeigten Weg heute nachgeht, geht’s natürlich schneller, mühsam ist es trotzdem. Riemann, Ricci und Levi-Civita hatten das mathematische Werkzeug längst entwickelt, für Hilbert war die erforderliche Mathematik auch klar, die Einbindung in das physikalische Weltbild hat aber nur Einstein geschafft.
Chrys schreibt:“ Physiker sollten sich der Erfordernis einer sauberen Trennung zwischen phänomenal Observiertem und theoriebezogen Interpretiertem grundsätzlich bewusst sein. Wo das unterbleibt, kann man leicht die Orientierung verlieren und sich einer Illusion von Wissen hingeben, mit der man dann sich selbst und womöglich andere nur in die Irre führt.“
Die Leistung von großen Physikern ist ja gerade das Auffinden von Zusammenhängen und die Entwicklung von Modellvorstellungen die eine möglichst genaue Berechnung der gemessenen Phänomene erlaubt. Die Erklärung des Phänomens an sich wird damit nicht erreicht, ist auch nicht das vordergründige Ziel. Die genaue mathematische Beschreibung von Zusammenhängen, meistens mittels Differentialgleichungen, bei der Elektrodynamik zum Glück durch lineare, bei der ART leider durch nichtlineare, führt zu fortschreitender Erkenntnis.
Der Erfolg der mathematischen Beschreibung in der Quantentheorie ist die Basis für unseren Fortschritt im Bereich der Elektronik in den letzten Jahrzehnten, trotzdem gibt es keine „direkte Intuition“ für das Verständnis von Zustandsfunktion und verschränkten Zuständen. Populärwissenschaftlich lässt sich daher auch nicht über den Quantencomputer berichten. Frei nach Feynman „wer sagt, er hat die Quantentheorie verstanden, der hat sie nicht verstanden“
@Frank Wappler / 5. September 2016 @ 11:24
»We must be able to communicate what we have done and what we have found«
C’est vrai.
»… nur selbstverständliche, nachvollziehbare Begriffe.«
Nachvollziehbar — ja, selbstverständlich — nein. Ohne hier tiefer in die Semantik abdriften zu wollen, ist es an dieser Stelle angebracht, zwischen Objekt- und Metasprache zu unterscheiden. Die Festlegung der Bedeutung von Begriffen einer Objektsprache mit wissenschftl. Anspruch ist grundsätzlich Aufgabe einer zugehörigen Metasprache. Auch wenn sich dieses Schema letztlich vielleicht nur für formale Sprachen strikt durchhalten lässt, ist wissenschaftl. Sprache in dieser Hinsicht viel strengeren Regeln zu unterwerfen als Umgangssprache. Und eine solche Regel wäre, dass in einer Objektsprache kein Platz für `selbstverständlich’ ist: entweder man kann das Intendierte hier intersubjektiv nachvollziehbar formulieren oder man kann es nicht. Wenn man es nicht kann, hat man auf alle Fälle ein Problem, das sich nicht mit `selbstverständlich’ wegreden lässt.
»Was macht eigentlich ein (in diesem SciLog schon öfters erwähnter) „Five-Point Curvature Detector“ nach Synge ? …«
Es ist für die GR eine axiomatisch getroffene Festsetzung, dass Gravitation dort durch Krümmung von Raumzeit repräsentiert wird, und Synges Buch, wo das auftritt, behandelt schliesslich die GR. Wenn er hier eine Beobachtung im Sinne von Krümmung deutet, ist das eine theoriebezogene Interpretation, und das ist auch in Ordnung, denn der Kontext ist ja offenkundig. Aber die Betonung liegt schon auf theoriebezogen, denn wir können auch anders. Bei dieser Gelegenheit bietet sich eigentlich noch ein Link zu einem neueren Überschtsartikel an:
Maluf, J. W. (2013). The teleparallel equivalent of general relativity. Ann. Phys., 525(5), 339-357. arXiv:1303.3897 [gr-qc]
Chrys schrieb (7. September 2016 @ 13:18):
> […] — ja, […] — nein.
> […] zu unterscheiden.
> […] als […]
> entweder […] oder […].
Das sind doch Ausdrucksformen des Begriffskomplexes, den ich oben als “selbstverständlich” zu motivieren versuchte:
den man verstanden haben muss, um (andere, als auch sich selbst) nach der Bedeutung von Begriffen fragen zu können;
dessen Verständnis man bei anderen voraussetzt, um sich mitzuteilen.
Dazu gehört (oder darauf baut direkt auf) der Begriff, der mit dem Wort “intersubjektiv” gemeint sein dürfte (nämlich: betreffend nicht Ein-und-den-Selben, sondern Verschiedene, Unterscheidbare, in Beziehung zueinander);
zusammen mit dem Verständnis von “Subjekt” (“man selbst” bzw “andere”) und von “Wahrnehmung”.
Und schließlich auch: “zusammen wahrnehmen (anstatt einzeln, voneinander getrennt)”; d.h. “koinzident”.
> Es ist für die GR eine axiomatisch getroffene Festsetzung, dass Gravitation dort durch Krümmung von Raumzeit repräsentiert wird, und Synges Buch, wo das auftritt, behandelt schliesslich die GR
Es geht beim “Five-Point Curvature Detector” aber rein um Geometrie, (noch) nicht um Dynamik.
> Wenn er hier eine Beobachtung im Sinne von Krümmung deutet, ist das eine theoriebezogene Interpretation
Natürlich benötigt jede Messgröße eine Definition, bevor man bestimmte Zahlen als (deren) Messwerte gewinnen oder auffassen kann. Aber was gäbe es an Cayley-Menger-Determinanten als Indikator von Krümmung denn groß zu interpretieren?
Drei (gegenüber einander starre) Beteiligte werden nun mal “gegenüber einander gerade (und nicht: ungerade, krumm)” genannt, wenn sich zwei ihrer Abstände untereinander genau zum dritten summieren;
und das drückt die Herons-Formel unmittelbar aus.
Und da sich die Formel eine Cayley-Menger-Determinante erster Ordnung darstellt, lässt sich dieser Krümmungsindikator ohne Weiteres auch für höheren Ordnungen benutzen, um auszudrücken bzw. Fall für Fall konkret herauszufinden
– ob vier (gegenüber einander starre) Beteiligte “gegenüber einander eben (und nicht: uneben, verdreht)”,
– ob fünf (gegenüber einander starre) Beteiligte “gegenüber einander flach (und nicht: krumm)”,
– ob sechs Ereignisse (mit gegebenen, geeignet verallgemeinerten metrischen Beziehungen untereinander) “gegenüber einander flach (und nicht: krumm)” wären.
Mir dämmert aber, worum es mit der erwähnten “Interpretation” gehen soll: Das Aufpfropfen von “Parallelitäts”-Mutmaßungen (oder doch nicht etwa Messungen??) auf die oben erwähnten Äquivalenzklassen.
Auch das noch! …
Einfach „Der Absolute Differentialkalkül und seine Anwendungen in Geometrie und Physik
von Tullio Levi-Civita und Aldabert Duschek,“ oder Hermann Weyl‘s „Raum, Zeit, Materie“ nachlesen. Liest man diese Bücher aus der Anfangszeit der ART, so kann man die damaligen Umwälzungen und Einflüsse auf die Physik am besten verstehen. Aus populärwissenschaftlichen Darstellungen wird man nie ein fundiertes Wissen erlangen. Man muss sich die Arbeit machen, die mathematischen Grundlagen der physikalischen Modelle zu erarbeiten, sonst ist man nicht in der Lage die Folgerungen aus diesen Modellen, das Zurückführen von komplizierten Zusammenhängen auf fundamentale Grundgesetze, zu begreifen.
Siegfried Heiss schrieb (9. September 2016 @ 10:00):
> Einfach „Der Absolute Differentialkalkül und seine Anwendungen in Geometrie und Physik
von Tullio Levi-Civita und Aldabert Duschek,“ oder Hermann Weyl‘s „Raum, Zeit, Materie“ nachlesen. […] Man muss sich die Arbeit machen, die mathematischen Grundlagen der physikalischen Modelle zu erarbeiten
Sicher kein schlechter Rat.
Betrachtungen wie beispielsweise zum „Lochproblem“ geben darüberhinaus einen Eindruck, wie viel Mühe es macht, aus allerlei mathematischen Grundlagen diejenigen zu destillieren, die physikalisch relevant sind (also auf Koinzidenzfeststellungen hinauslaufen).
@Frank Wappler / 9. September 2016 @ 08:10
Die Cayley-Menger Determinanten betreffend geht es um die Frage nach metrischen Bedingungen für kongruente Einbettung eines beliebigen semimetrischen Raumes in einen Euklidischen Raum. Ein Begriff von Krümmung ist für allgemeine semimetrische Räume jedoch nicht definert, und in den Fällen, wo eine solche Einbettung nicht möglich ist, kann man die metrische Obstruktion, die dem entgegensteht, auch nicht einfach `Krümmung’ nennen.
Eine Bedeutung von `Krümmung’ ist eben auch jeweils kontextuell zu spezifizieren, und abhängig vom Kontext werden mit diesem Wort recht unterscheidliche Konzepte verknüpft. Die Menger curvature wäre ein Beispiel dafür, dass Krümmung zwar in einem rein metrischen Kontext begrifflich vorkommen kann, bedeutet dann aber auch nicht dasselbe wie etwa bei Riemann.
Die Größe der massenabhängigen Raumkrümmung, kann man sich durch den Exzessradius veranschaulichen. Feynman betrachtet dazu eine Massekugel mit näherungsweise homogener Dichte. Man vermisst die Oberfläche der Kugel und bestimmt unter Verwendung der Kugeloberflächenformel den Radius R1. Anschließend misst man den Radius der Kugel, mit dem lokal gültigen Maßstab. Der direkt gemessene Radius R2 ist aufgrund der Raumkontraktion um den Exzessradius größer als R1. Der Durchmesser des kugelförmigen Raums, der die Erde enthält, wird aufgrund der darin enthaltenen Masse um ca. 3mm komprimiert, d.h. der Kugeldurchmesser der Erde weicht um 3mm gegenüber dem Kugeldurchmesser im euklidischen Raum ab. Das metrische Feld wird also durch die Masse verdichtet, man könnte statt einer Raumkrümmung in der Umgebung einer Masse auch von einer „Verdichtung“ des Raumes (der Metrik des Raumes, bzw. des metrischen Feldes) durch die Masse sprechen. Diese „Verdichtung“ des metrischen Feldes krümmt einen tangential zur Erdoberfläche verlaufenden Lichtstrahl, der Krümmungsradius beträgt ca. 9×10^12 km also ca. 1 Lichtjahr, bei einer größeren Massenansammlung, z.B.: der Sonne ist der Krümmungsradius kleiner ca. 3 x10^11 km…
Jede Masse wird in Richtung der verdichteten Metrik gezogen, die Metrik führt direkt zum Gravitationspotential. Man kann dies in Verbindung mit der nötigen Mathematik sicher exakter formulieren… Ähnlich hat Riemann schon 60 Jahre vor Einstein erwähnt, dass auf einer Fläche mit konstanter Krümmung Figuren, welche bestimmte Bereiche dieser Fläche überdecken, ohne Dehnung und Stauchung bewegt werden können. Figuren sind auf Flächen mit lokal unterschiedlicher Krümmung nicht frei beweglich.
Auf jeden Fall die nötige Mathematik durcharbeiten und man ist nicht mehr der Lakai fremder Gedanken…
Siegfried Heiss schrieb (10. September 2016 @ 22:14):
> Man vermisst die Oberfläche der Kugel
Sofern die entsprechenden Abständsverhältnisse in der Oberfläche (d.h. im Falle einer Kugeloberfläche die Verhältnisse der Großkreisabstände) zwischen ihren Bestandteilen bekannt sind, ist das sicher nicht schwer:
Man betrachte vier Bestandteile dieser Oberfläche („A“, „B“, „P“, „Q“), die nicht alle vier gegenüber einander gerade sind (d.h. nicht alle vier auf dem selben halben Großkreissegment liegen), aber ansonsten beliebig;
und man ermittle den (größten) Wert der Zahl „ρ“ als Lösung der Gleichung
0 =
Det[ {
{ 1, Cos[ 1/ρ ], Cos[ 1/ρ (AP / AB) ], Cos[ 1/ρ (AQ / AB) ] },
{ Cos[ 1/ρ ], 1, Cos[ 1/ρ (BP / AB) ], Cos[ 1/ρ (BQ / AB) ] },
{ Cos[ 1/ρ (AP / AB) ], Cos[ 1/ρ (BP / AB) ], 1, Cos[ 1/ρ (PQ / AB) ] },
{ Cos[ 1/ρ (AQ / AB) ], Cos[ 1/ρ (BQ / AB) ], Cos[ 1/ρ (pQ / AB) ], 1 }
} ],
wobei “(AP / AB)” den (Großkreis-)Abstandsverhältniswert zwischen A und P und zwischen A und B bezeichnet, usw.
(Falls für verschieden ausgewählte Bestandteile auf diese Weise ungleiche Werte „ρ“ ermittelt würden, dann wäre die betrachtete Oberfläche nicht die einer Kugel gewesen.)
Dann berechne als Maß dieser Kugeloberfläche (zumindest formal) als
4 π ρ^2 AB^2.
> und bestimmt unter Verwendung der Kugeloberflächenformel den Radius R1
Dann wohl unmittelbar aus der obigen Lösung R1 = ρ AB.
> Anschließend misst man den Radius der Kugel, mit dem lokal gültigen Maßstab.
Sofern ein Beteiligter überhaupt als „Mittelpunkt der Kugel, M“ beobachtbar ist bzw. existiert (der insbesondere dadurch identifizierbar wäre, dass er koinzidente Pings bzgl. allen Bestandteilen der betrachteten Kugeloberfläche findet) lassen sich M und z.B. A sicherlich als „die beiden gegenüber einander (chronometrisch) starren Enden eines Maßstabs“ auffassen;
und A mag z.B. seine Pingverhältnisse bzgl. B und bzgl. M feststellen.
Wieso man allerdings dieses oder überhaupt irgend ein Paar von gegenüber einander (chronometrisch) starren Enden „ lokal gültig“ nennen sollte ?? …
Ansonsten lassen sich z.B. mehrere zwiebelartig angeordnete Kugeloberflächen in Betracht ziehen (und deren jeweilige „Radien R1“ wie beschrieben ermitteln, und miteinander vergleichen), und sich die Abstände dieser Schalen untereinander (jeweils als geringste Abstände zwischen Bestandteilen der einen, und Bestandteilen der anderen) vergleichen.
> dass auf einer Fläche mit konstanter Krümmung Figuren, welche bestimmte Bereiche dieser Fläche überdecken, ohne Dehnung und Stauchung bewegt werden können.
So wie „Figuren“ durch Abstandsverhältnisse ihrer (hinreichend vielen) Bestandteile beschrieben werden, und „Bewegung“ im hier benutzten Sinne sogar durch jeweils gleiche Abstände für „Urbild“ und „Abbild“,
so ist auch (wie oben skizziert) die Geometrie einer Fläche (oder allgemeinerer „Räume“) qualitativ durch die Abstandsverhältnisse zwischen ihren (gegenseitig starren) Bestandteilen bestimmt und ermittelbar;
und quantitativ (z.B. der Wert des Krümmungsradius „R1“) dann in Referenz zu einem konkreten geeigneten „Maßstab“ (z.B. den beiden Enden A und B).
Siegfried Heiss schrieb (10. September 2016 @ 22:14):
> Man vermisst die Oberfläche der Kugel
Sofern die entsprechenden Abstandsverhältnisse in der Oberfläche (d.h. im Falle einer Kugeloberfläche die Verhältnisse der Großkreisabstände) zwischen ihren Bestandteilen bekannt sind, ist das sicher nicht schwer:
Man betrachte vier Bestandteile dieser Oberfläche („A“, „B“, „P“, „Q“), die nicht alle vier gegenüber einander gerade sind (d.h. nicht alle vier auf dem selben halben Großkreissegment liegen), aber ansonsten beliebig;
und man ermittle den (größten) Wert der Zahl „ρ“ als Lösung der Gleichung
0 =
Det[ {
{ 1, Cos[ 1/ρ ], Cos[ 1/ρ (AP / AB) ], Cos[ 1/ρ (AQ / AB) ] },
{ Cos[ 1/ρ ], 1, Cos[ 1/ρ (BP / AB) ], Cos[ 1/ρ (BQ / AB) ] },
{ Cos[ 1/ρ (AP / AB) ], Cos[ 1/ρ (BP / AB) ], 1, Cos[ 1/ρ (PQ / AB) ] },
{ Cos[ 1/ρ (AQ / AB) ], Cos[ 1/ρ (BQ / AB) ], Cos[ 1/ρ (pQ / AB) ], 1 }
} ],
wobei “(AP / AB)” den (Großkreis-)Abstandsverhältniswert zwischen A und P und zwischen A und B bezeichnet, usw.
(Falls für verschieden ausgewählte Bestandteile auf diese Weise ungleiche Werte „ρ“ ermittelt würden, dann wäre die betrachtete Oberfläche nicht die einer Kugel gewesen.)
Dann berechne als Maß dieser Kugeloberfläche (zumindest formal) als
4 π ρ^2 AB^2.
> und bestimmt unter Verwendung der Kugeloberflächenformel den Radius R1
Dann wohl unmittelbar aus der obigen Lösung R1 = ρ AB.
> Anschließend misst man den Radius der Kugel, mit dem lokal gültigen Maßstab.
Sofern ein Beteiligter überhaupt als „Mittelpunkt der Kugel, M“ beobachtbar ist bzw. existiert (der insbesondere dadurch identifizierbar wäre, dass er koinzidente Pings bzgl. allen Bestandteilen der betrachteten Kugeloberfläche findet) lassen sich M und z.B. A sicherlich als „die beiden gegenüber einander (chronometrisch) starren Enden eines Maßstabs“ auffassen;
und A mag z.B. seine Pingverhältnisse bzgl. B und bzgl. M feststellen.
Wieso man allerdings dieses oder überhaupt irgend ein Paar von gegenüber einander (chronometrisch) starren Enden „ lokal gültig“ nennen sollte ?? …
Ansonsten lassen sich z.B. mehrere zwiebelartig angeordnete Kugeloberflächen in Betracht ziehen (und deren jeweilige „Radien R1“ wie beschrieben ermitteln, und miteinander vergleichen), und sich die Abstände dieser Schalen untereinander (jeweils als geringste Abstände zwischen Bestandteilen der einen, und Bestandteilen der anderen) vergleichen.
> dass auf einer Fläche mit konstanter Krümmung Figuren, welche bestimmte Bereiche dieser Fläche überdecken, ohne Dehnung und Stauchung bewegt werden können.
So wie „Figuren“ durch Abstandsverhältnisse ihrer (hinreichend vielen) Bestandteile beschrieben werden, und „Bewegung“ im hier benutzten Sinne sogar durch jeweils gleiche Abstände für „Urbild“ und „Abbild“,
so ist auch (wie oben skizziert) die Geometrie einer Fläche (oder allgemeinerer „Räume“) qualitativ durch die Abstandsverhältnisse zwischen ihren (gegenseitig starren) Bestandteilen bestimmt und ermittelbar;
und quantitativ (z.B. der Wert des Krümmungsradius „R1“) dann in Referenz zu einem konkreten geeigneten „Maßstab“ (z.B. den beiden Enden A und B).
War das jetzt so wichtig, daß es zweimal geschrieben werden mußte?
Herr Senf schrieb (13. September 2016 @ 11:56):
> War das jetzt so wichtig, daß es zweimal geschrieben werden mußte?
Wem Formatierungsfehler und deren Korrektur nicht egal sind, mag auch den Inhalt ernstnehmen.
Im Übrigen halte ich das schon oft beklagte, fortgesetzte Fehlen einer SciLogs-Kommentar-Vorschaufunktion für eine hartnäckige Missachtung der SciLogs-Leserschaft;
und die Limitierungen der Kommentaranzeigen (auf nach wie vor nur fünf in den einzelnen SciLogs, und deren vollständige Abschaffung von der Homepage) erst recht.
Chrys schrieb (10. September 2016 @ 10:33):
> Die Cayley-Menger Determinanten betreffend geht es um die Frage nach metrischen Bedingungen für kongruente Einbettung eines beliebigen semimetrischen Raumes in einen Euklidischen Raum.
Es geht damit nicht zuletzt um einen ausschließlich metrischen Zugang (auch unter eventueller Abschwächung der Definition von “Metrischem Raum” im engsten Sinne) zu einem Begriff von Geradheit/Ebenheit/Flachheit.
Und es besteht nun mal ein direkter Zusammenhang zur kongruenten Einbettung von (ggf. geeignet verallgemeinerten) metrischen Räumen in “Räume konstanter Krümmung” (vgl. Kokkendorff);
so dass ein ausschließlich metrischer Zugang dazu gegeben ist, was überhaupt mit “Krümmung eines Raumes (bzw. einer Fläche)” gemeint sein kann.
Diese Charakterisierungen (einschl. der erwähnten “Menger curvature“, also des Krümmungsradius eines … Bogens) sind offensichtlich alle “intrinsisch”, d.h. allein aus gegebenen/vorausgesetzten metrischen Beziehungen zwischen den zu charakterisierenden Mengen von Beteiligten/Elementen/Punkten zu ermitteln.
Mich interessiert dann natürlich die weitere Verallgemeinerung/Abschwächung, von metrischen Beziehungen zu bloßen (mehr oder weniger symmetrischen) Ping-Koinzidenz-Beziehungen;
daher der Zusammenhang zur LIGO/LISA-Methodik,
und die Hervorhebung von “endogenen” Krümmungsmaßen (z.B. dem Auffinden beliebig grober und feiner tetrahedral-oktagonaler Ping-Koinzidenz-Gitter).
> Eine Bedeutung von `Krümmung‘ ist eben auch jeweils kontextuell zu spezifizieren
Stimmt erstmal.
(Ach, wenn man konkrete Spezifizierungen doch enzyklopädisch verfassen und sogar Fall zu Fall geeignet ver(wiki)linken könnte! … &)
> […] kann man die metrische Obstruktion […] auch nicht einfach `Krümmung‘ nennen.
Ein Beispiel wäre hier von Interesse.
Ansonsten gilt schlicht:
Man soll Unterscheidbares nicht beim selben Namen, und nicht Unterscheidbares nicht bei verschiedenen Namen nennen.
> […] bedeutet dann aber auch nicht dasselbe wie etwa bei Riemann.
Dazu fällt (u.a.) auf, dass in Riemanns Habilitationsschrift wohl von
“Krümmungsmaß” die Rede ist, aber nicht (für mich erkennbar) von “Parallelität” …
Die Einbettung ist doch zum Verständnis der Raumzeitkrümmung nicht erforderlich. Die intrinsischen Eigenschaften können alleine durch die Maßbeziehungen vollständig beschrieben werden. Gauß hat gezeigt, dass eine gekrümmte Fläche nur durch Vermessung von Punkten auf dieser Fläche vollständig beschrieben werden kann. Riemann hat seine Untersuchungen auf mehrfach ausgedehnte, stetige, differenzierbare Mannigfaltigkeiten mit lokal nichtlinearer Krümmung erweitert. Lokal nichtlineare Geometrieverhältnisse werden durch lineare infinitesimale Abstandsänderungen beschrieben. Diese Linearisierung im Infinitesimalen wurde mittels Differentialkalkül von Christoffel, Ricci, Levi-Civita und anderen in eine mathematisch vollständige Form gebracht. Die koordinatenunabhängige Beschreibung der Raumzeitkrümmung durch den Krümmungstensor wurde für die Formulierung der ART aufgegriffen. Die Lichtausbreitung hat in der SRT und der ART eine zentrale Rolle. Die Lichtausbreitung erfolgt entlang von Geodäten. Der Verlauf von geodätischen Ebenen kann auch als Raumkrümmung bezeichnet werden. Der Raumzeitabstand zweier Ereignisse stellt die Differenz zur Lichtsignallaufzeit, multipliziert mit der Vakuumlichtgeschwindigkeit, dar. Lichtsignallaufzeiten sind daher unsere universellen Messinstrumente und damit kommt man auch wieder zu LIGO und LISA. Ähnlich wie intelligente 2D-Wesen ihre Weltkrümmung genau vermessen können ohne von der dritten Dimension Gebrauch zu machen, können wir auch unsere 4-dimensionale gekrümmte Raumzeit vollständig vermessen.
@Siegfried Heiss / 10. September 2016 @ 22:14
»Die Größe der massenabhängigen Raumkrümmung …«
Mit Hinblick auf die GR ist Krümmung der Raumzeit (ganz zu schweigen von Raumkrümmung) kein Gegenstand empirischer Untersuchung, sondern ein Mittel modellhafter Beschreibung im Rahmen einer Theorie von Gravitation.
Hierbei hat `Krümmung’ eine klar spezifizierte Bedeutung, nämlich als äussere covariante Ableitung eines Zusammenhangs, was sich dann kurz und (speziell für Herrn Wappler) koordinatenfrei ausdrücken lässt durch Ω = Dω. Ein affiner Zushg ω auf einem (Pseudo-)Riemannschen Raum wird (u.a.) Riemannsch genannt, wenn er torsionsfrei ist. Die Einsicht, dass sich dann ein mit der metrischen Struktur verträglicher Zushg auch nicht-Riemannsch und insbesondere so wählen lässt, dass er nicht torsions- sondern krümmungsfrei ist, wurde erst ab den 1920ern erlangt, im wesentlichen dank É. Cartan. Einsteins TP unterscheidet sich von der GR nicht in ihrer metrischen, sondern hinsichtlich ihrer affinen Struktur.
Und jenen Physikern, die ganz anders als Feynman tatsächlich etwas zu observablen Gravitationseffekten messen, kann dieser Unterschied auch weitestgehend egal sein, denn davon bemerken sie schliesslich nichts, wenn sie messen.
@Frank Wappler / 12. September 2016 @ 11:46
»Man soll Unterscheidbares nicht beim selben Namen, und nicht Unterscheidbares nicht bei verschiedenen Namen nennen.«
Dann wäre allerdings auch mit Bezug auf gekrümmte Kurven die Bezeichnung `intrinsisch’ sorgsam zu vermeiden. Denn diff.geometrisch gibt die innere Geometrie einer Kurve keine Krümmung her, dazu braucht es mindestens zwei Dimensionen.
»Ein Beispiel wäre hier von Interesse.«
Beispielsweise ist der flache 3-Torus ℝ³/ℤ³ so, wie er heisst, nämlich flach. Dass er sich nicht als Ganzes kongruent in den Euklid. 3-Raum einbetten lässt, liegt jetzt nicht an irgendeiner Art von Krümmung.
Wenn ich weiter oben schrieb, »Es ist für die GR eine axiomatisch getroffene Festsetzung, dass Gravitation dort durch Krümmung von Raumzeit repräsentiert wird,« so ist dies allerdings gewiss nicht Einsteins eigene Auffassung. Dazu sei einmal mehr an J. Nortons Analyse [1] erinnert. Einstein zufolge ist Gravitation durch den metrischen Tensor und nicht durch den Krümmungstensor repräsentiert. Die letztgenannte Sichtweise, bekanntlich prominent von Synge vertreten, steht in Konflikt zum Äquivalenzprinzip, wie Einstein es verstanden hat, und konsequenterweise hielt Synge das dann auch für obsolet. Einstein sah das freilich ganz anders; Krümmung allein reicht ihm nicht hin zum Verständnis von Gravitation.
[1] Norton, J. (1985). What was Einstein’s principle of equivalence? Stud. Hist. Phil. Sci., 16(3), 203-246. [PDF]
Chrys schrieb (14. September 2016 @ 17:35):
> […] mit Bezug auf gekrümmte Kurven die Bezeichnung `intrinsisch‘ sorgsam zu vermeiden.
Um Missverständnissen vorzubeugen sei wiederholt (vgl. mein Kommentar 12. September 2016 @ 11:46), dass es um “Kurven” im Sinne von “Bögen” gehen soll.
Der/Jeder (im strikten Sinne) metrische (und vollständige) Raum “(ℳ, d)”, der für jegliche vier verschiedene Bestandteile A, B, P, Q ∈ ℳ
2 + 2 (d[ B, P ] / d[ A, B ])^2 + 2 (d[ B, P ] / d[ A, P ])^2 – (d[ A, B ] / d[ A, P ])^2 – (d[ A, P ] / d[ A, B ])^2 – (d[ B, P ] / d[ A, B ])^2 (d[ B, P ] / d[ A, P ])^2
=
(d[ B, P ] / d[ B, Q ])^2
(
2 + 2 (d[ B, Q ] / d[ A, B ])^2 + 2 (d[ B, Q ] / d[ A, Q ])^2 – (d[ A, B ] / d[ A, Q ])^2 – (d[ A, Q ] / d[ A, B ])^2 – (d[ B, Q ] / d[ A, B ])^2 (d[ B, Q ] / d[ A, P ])^2
)
> 0
erfüllt,
ist ein Bogen mit von Null verschiedener konstanter Menger curvature.
(Mit “=” anstatt “>” definiert die Bedingung einen/jeden Bogen mit Menger curvature konstant Null.)
Was auch immer nicht Bestandteil der (jeweiligen) Menge ℳ wäre, ist dafür jedenfalls nicht unmittelbar von Belang; d.h. sofern die Distanzwerte “d” (bzw. zumindest die erforderlichen Distanzverhältnisse) für die Bestandteile der Menge ℳ selbst gegeben sind.
In genau diesem Sinne nenne ich diese Krümmung “intrinsisch”.
> [Ein Beispiel …] ist der flache 3-Torus ℝ³/ℤ³ so, wie er heisst, nämlich flach.
Es wäre natürlich hilfreich, wenn die Distanzverhältnisse zwischen den Bestandteilen eines/jedes solchen “flachen 3-Torus” explizit(er) beschrieben wären …
Gehe ich recht in der Annahme, dass sich darin fünf (!) verschiedene Bestandteile finden lassen, deren 10 paarweise Distanzen gegenüber einander alle gleich sind? Krümmer (Im Sinne von Cayley-Menger/Gram-Kokkendorff) geht’s ja kaum …
Chrys schrieb (14. September 2016 @ 17:31):
> äussere covariante Ableitung eines Zusammenhangs, was sich dann kurz und (speziell für Herrn Wappler) koordinatenfrei ausdrücken lässt
Dass die geläufige Forderung nach Koordinaten-Freiheit/Unabhängigkeit auch die Unabhängigkeit von Vorgaben irgeneines bestimmten sogenannten “Zusammenhangs” einschließt,
ist mir im Laufe unserer Korrespondenz immer deutlicher geworden (dahingehend: vielen Dank!) und lässt sich in Bezug auf die sogenannte Motivation begründen:
.
Da aber Koordinaten an sich völlig irrelevant sind, sofern man sich mit Physik beschäftigt, ist auch die zweite (oder jede andere) Ableitung (der Bogenlänge eines betrachteten Bogens) nach irgendwelchen Koordinaten ebenso irrelevant.
Das (angebliche) Problem, dass durch Betrachtung solcher “Zusammenhänge” gelöst werden soll, besteht in der Physik gar nicht.
> Mit Hinblick auf die GR ist Krümmung der Raumzeit […] kein Gegenstand empirischer Untersuchung
Dieser Auffassung ist wie gewohnt der Einsteinsche Imperativ entgegenzusetzen:
.
p.s.
> Äquivalenzprinzip
Ein durchaus interessantes und wichtiges Thema; und nicht erst im Hinblick auf Dynamik, sondern schon Geometrie/Kinematik betreffend:
in einer Region mit (beliebig feinen und groben) tetrahedral-octahedralen Ping-Koinzidenz-Gitter lassen sich auch (zumindest endliche) Ping-Koinzidenz-Gitter finden, die nicht tetrahedral-octahedralen sind (sondern intrinsisch und sogar endogen “beschleunigt”); zum “Vergleichen” im Sinne Alexandrovs.
Frank Wappler schrieb (14. September 2016 @ 23:00):
> Der/Jeder (im strikten Sinne) metrische (und vollständige) Raum „(ℳ, d)“, der für jegliche vier verschiedene Bestandteile A, B, P, Q ∈ ℳ […] erfüllt, ist ein Bogen mit von Null verschiedener konstanter Menger curvature.
Die angegebene Formel ist folgendermaßen zu berichtigen (ich hatte im allerletzten Term übersehen, „P“ durch „Q“ zu ersetzen):
2 + 2 (d[ B, P ] / d[ A, B ])^2 + 2 (d[ B, P ] / d[ A, P ])^2 – (d[ A, B ] / d[ A, P ])^2 – (d[ A, P ] / d[ A, B ])^2 – (d[ B, P ] / d[ A, B ])^2 (d[ B, P ] / d[ A, P ])^2
=
(d[ B, P ] / d[ B, Q ])^2
(
2 + 2 (d[ B, Q ] / d[ A, B ])^2 + 2 (d[ B, Q ] / d[ A, Q ])^2 – (d[ A, B ] / d[ A, Q ])^2 – (d[ A, Q ] / d[ A, B ])^2 – (d[ B, Q ] / d[ A, B ])^2 (d[ B, Q ] / d[ A, Q ])^2
)
> 0.
Und mit „<“ anstatt „>“ definiert diese Bedingung (natürlich) ebenfalls Bögen
mit von Null verschiedener konstanter Menger curvature.
> Dass die geläufige Forderung nach Koordinaten-Freiheit/Unabhängigkeit auch die Unabhängigkeit von Vorgaben irgeneines bestimmten sogenannten „Zusammenhangs“ einschließt […]
… lässt sich doch nicht ganz so (einfach) begründen, wie oben dargestellt:
Schließlich stellt die Auswertung der zweiten Ableitung (falls sie überhaupt existiert) der Bogenlänge eines betrachteten Bogens nach irgendwelchen Koordinaten nicht an sich ein mathematisches Problem dar;
vielmehr geht es um das Problem des Zuordnens (als „zueinander parallel“) der o.g. Äquivalenzklassen (von Bögen, die sich berühren, aber nicht schneiden) zwischen verschiedenen Punkten.
(Was nicht unbedingt und vordergründig mit Koordinaten zu tun haben muss.)
Fest steht:
Sofern solch eine Zuordnung ganz beliebig und willkürlich gemacht wird, ist sie nicht physikalisch relevant;
und sofern solche eine Zuordnung nicht beliebig ist, sondern in bestimmter Weise induziert, ist sie redundant.
(Genau so lässt sich sagen:
Sofern Koordinaten ganz beliebig und willkürlich dahingestreußelt werden, sind sie nicht physikalisch relevant;
und sofern Koordinaten nicht ganz beliebig sind, sondern in bestimmter Weise induziert, sind sie redundant.)
Fehlt (mir) nur noch ein Begriff, der beides einschließt …
@Frank Wappler / 15. September 2016 @ 11:29
Speziell zu Krümmungsinvarianten von GWs hilft ja vielleicht dies noch irgendwie weiter: H.-J. Schmidt (1994). Why do all the curvature invariants of a gravitational wave vanish?
Apropos verschwindende Krümmung. Seit mindestens 2007 sind Anmerkungen dazu publiziert worden, dass das Standardargument zur Begründung der GW-Gezeitenkraft dubios und eigentlich so ähnlich ist wie, sagen wir mal, ein Zylinderhut, aus dem ein Kaninchen hervorgezaubert wird. Was ich hingegen nicht gefunden habe ist, dass seitens der GW Proponenten darauf auch nur der Versuch einer Klarstellung unternommen worden wäre. Ein flüchtiger Blick auf den fraglichen Sachverhalt:
Gesucht ist die geodätische Abweichung der Weltlinien von anfänglich ruhenden freien Testmassen unter den Einfluss einer ebenen GW, wobei diese Weltlinien im TT Frame durch t-Koordinatenlinien als zeitartige Geodäten repräsentiert sind. Beispielsweise für eine ebene GW in z-Richtung sind dann ∂x und ∂y Jacobi Vektorfelder längs einer solchen Geodäten γ(t) mit γ'(t) = ∂t, und wenn dann L die zuvor (noch ohne GW) bestimmte Länge eines Detektorarms etwa in x-Richtung symbolisiert, bedeutet dies, dass L∂x die Jacobi Gleichung längs γ erfüllt, dass dort also gilt
(1) D²(L∂x)/dt² = R(∂t,L∂x)∂t.
Das Standardargument geht dann sinngemäss wie folgt: Man betrachte die Gl. (1) in Normalkoordinaten längs γ. Dort wird dann links die covariante Ableitung zu einer gewöhnliche Ableitung, und rechts lässt sich für lineare GWs der Krümmungstensor R einfach invariant aus dem TT Frame übernehmen. Das liefert dann die Gleichung für GW-Gezeitenkraft (in x-Richtung) formal in der Gestalt
(2) L” = ½ h” L.
Praktisch ein umgekrempeltes `comma-to-semicolon’-Argument, das offenbar sehr überzeugend wirkt. Übersehen wird dabei jedoch, dass für eine ebene GW die Krümmung faktisch gar nicht in die Gl. (1) eingeht, was im übrigen ganz entsprechend auch für exakte ebene GWs gilt. Tatsächlich steht der Term auf rechten Seite implizit schon als Summand auf der linken Seite, und das hebt sich weg. Der Übergang zu Normalkoordinaten lässt dann allenfalls noch verbliebene Eichterme verschwinden, und es bleibt anstelle von (2) nur die schnöde Gleichung L” = 0. Also keine Gezeitenkraft.
Je tiefer man da gräbt, desto mehr lässt sich der Eindruck gewinnen, dass der vorgebliche GW-Nachweis durch LIGO der unglaubwürdigste Vorgang in der Physik mindestens seit der vermeintlichen Entdeckung der N-Strahlen ist.
Chrys schrieb (21. September 2016 @ 18:45):
> Speziell zu Krümmungsinvarianten von GWs hilft ja vielleicht dies noch irgendwie weiter: H.-J. Schmidt (1994). Why do all the curvature invariants of a gravitational wave vanish?
Danke. (Der angegebene Artikel verweist auf ein Buch von H. Stephani; das lässt sich ja wohl früher oder später auftreiben …)
Damit drängt sich die grundsätzliche Frage wieder in den Vordergrund, wie der „Gehalt an Gravitationswellen“ in einer gegebenen Region denn überhaupt definiert bzw. zu messen wäre,
wenn nicht vermittels ((der Verteilung von) Werten von) Krümmungsinvarianten.
D.h. (meiner Auffassung nach):
wie sich der (vermeintliche?) Unterschied zwischen einer „Region mit (signifikanter) Gravitationswelle“ und einer „ohne“ denn überhaupt konkret aus Feststellungen von Koinzidenz (etc.) definieren und sich insbesondere durch Unterschiede der „Gestalt“ von Ping-Koinzidenz-Gittern in den betreffenden Regionen äußern würde bzw. ermitteln ließe,
wenn alle damit zusammenhängenden, für jedes Ereignis aus der „Gestalt“ der jeweils umgebenden Ping-Koinzidenz-Gitter zu ermittelnden Werte von Krümmungsinvarianten dabei nicht unterscheidbar sein sollen.
( Mein oben mehrfach erwähnter Vorschlag zu Definition/Illustration/Messung von „Gravitationswellen“ erscheint mir jedenfalls unvereinbar mit dieser Forderung nach „Unabhängigkeit von Krümmungsinvarianten“.)
Und natürlich stellt sich auch (wieder mal) die Frage, welche Messgrößen sich anhand der von LIGO zweifellos gesammelten (spezifischen, unterscheidbaren) Beobachtungsdaten denn überhaupt auswerten lassen.
> […] Länge eines Detektorarms
Ich frage erneut, ob damit eine Koordinaten-unabhängige Messgröße gemeint ist
(ansonsten erscheint sie aus Physik-Sicht egal);
und falls so, was deren konkrete, zumindest letztlich auf Koinzidenzfeststellungen hinauslaufende operative Definition ist.
Konkret:
Ist „Länge“ (zweier beteiligter Detektorbestandteile, gegenüber einander) hier chronometrisch gemeint?,
d.h. als die (konventionell genau halbe) Pingdauer jeweils eines dieser beiden Detektorbestandteile gegenüber dem anderen,
unter der Bedingung dass diese (einzeln festgestellten) Pingdauern zumindest im Verlaufe einiger aufeinanderfolgender Pings (nahezu) konstant blieben, und gegenseitig gleich waren,
wobei (zur formalen Unterscheidung von anderen Dauern) ein bestimmter symbolischer, von Null verschiedener Faktor „c_0“ angefügt wurde?
Oder wie oder was sonst ??
p.s.
Frank Wappler schrieb (15. September 2016 @ 11:29):
> […] Die angegebene Formel ist folgendermaßen zu berichtigen […]
Es ergibt sich daraus (offensichtlich! &) eine noch symmetrischere Formel:
2 + 2 (d[ A, B ] / d[ A, P ])^2 + 2 (d[ A, B ] / d[ B, P ])^2 – (d[ A, P ] / d[ B, P ])^2 – (d[ B, P ] / d[ A, P ])^2 – (d[ A, B ] / d[ A, P ])^2 (d[ A, B ] / d[ B, P ])^2
=
2 + 2 (d[ A, B ] / d[ A, Q ])^2 + 2 (d[ A, B ] / d[ B, Q ])^2 – (d[ A, Q ] / d[ B, Q ])^2 – (d[ B, Q ] / d[ A, Q ])^2 – (d[ A, B ] / d[ A, Q ])^2 (d[ A, B ] / d[ B, Q ])^2
> 0;
und auch diese definiert mit „<“ anstatt „>“ ebenfalls Bögen
mit von Null verschiedener konstanter Menger curvature.
Nach 2x LIGO warten wir doch einfach noch auf 1x VIRGO, was die sehen.
Dann müßten per VT schon drei mit Tarnkappe millisekundengenau rumlaufen.
Wow, in den Wochen, in denen ich in Urlaub, auf Sommerschule und auf dem HLF war, hat sich ja beachtliches an steilen Thesen angesammelt.
Hier in Kürze einige Kommentare meinerseits:
Solange man im Hamilton-Formalismus z.B. für freie Teilchen (klassisches Relativitätsprinzip) nicht unterscheiden kann, ob sich ein freies Teilchen im gegebenen Bezugssystem bewegt oder nicht, ist der entsprechende Flow kein gutes Kriterium für Bewegung. Und im Gegensatz zu dem, was Chrys da behauptet, ist “Raum expandiert, keinerlei Bewegung” keineswegs Konsens unter den Kosmologen. Was nicht zuletzt daran liegt, dass es kein allgemein anerkanntes Kriterium für “Bewegung durch den Raum” gibt. Wie so oft, wenn man von althergebrachten Begriffen extrapoliert und die Extrapolation nicht eindeutig ist.
Zur Wirkung von Gravitationswellen: Zumindest die Ableitungen die ich kenne, gehen anders: Man betrachtet zwei Geodäten (Testmassen) und schaut, wie deren Abstand sich ändert. Das entspricht direkt einer der Definitionen von Krümmung; für Gravitationswellen ergibt sich der entsprechende Zusammenhang von L und er Beschleunigung der Änderung von L. So wird es ja auch in dem von Chrys angeführten Kapitel von Maggiore gemacht. Wenn man ganz sicher gehen will, dann rechnet man sowieso aus, wie sich Licht in solch einer Raumzeit zwischen den Endpunkten bewegt; dabei kommen dann bei der Rückkehr am Strahlteiler die Koinzidenzen oder eben Phasenverschiebungen heraus, die man letztlich misst. Nicht zuletzt ist das ja zentraler Inhalt der Gravitationswellen-Detektor-Animation, die da irgendwo kilometerweit weiter oben im Haupttext des Blogbeitrags vor sich hin schwingt.
Zur Frage von Koordinaten und koordinatenfreien Darstellungen: Dazu mache ich in Zukunft mal einen gesonderten Blogbeitrag; das ist ein allgemeineres Thema.
Ansonsten werde ich die Kommentare hier recht bald abschließen. Vom ursprünglichen Blogbeitrag haben wir uns weit entfernt; Herr Engelhardt hat sich der Diskussion ja schon entzogen; Chrys hat jedes Zugeben eines Fehlers seinerseits so eng an Gesichtsverlust geknüpft, dass die Grundlage für ergebnisoffene Diskussionen im wesentlichen weg ist, und 99% der Leser dürften von der Fachausdruckdichte in den Kommentaren mittlerweile sowieso abgeschreckt sein.