Einstein verstehen VII: Bezugssystemwechsel in der klassischen Mechanik
BLOG: RELATIV EINFACH

Dies ist Teil VII einer Online-Einführung in die Spezielle Relativitätstheorie, die hier im Blog einen “Testlauf” absolviert und später – u.a. durch Feedback der Blogleser verbessert – ein Teil des Webportals Einstein Online werden soll. Nähere Informationen zu den Hintergründen finden sich in Einstein verstehen: Ein Blogexperiment, Teil I.
[Derzeit sind online: Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7]
Bislang geht es in der Einleitung um Vorarbeiten, nämlich um diejenigen Konzepte aus der klassischen Physik (also der Physik vor Relativitätstheorie und Quantentheorie) die man kennen muss, um zu verstehen, vor welchem Hintergrund und auf welcher Grundlage Einstein die Spezielle Relativitätstheorie einführte.
Im vorangehenden Teil VI hatte ich in allgemeiner Form den Übergang von einem Bezugssystem in ein anderes diskutiert. In diesem Teil soll es um konkrete Beispiele für den Bezugssystemwechsel gehen, nämlich um diejenigen Transformationen, die in der klassischen Mechanik möglich sind. Bei der Ableitung der Transformationsformeln gehe ich dementsprechend von Zusatzannahmen aus, die in der klassischen Mechanik getroffen werden: dass Strecken die gleiche Länge und Zeitintervalle die gleiche Dauer haben, egal von welchem Bezugssystem aus man sie bestimmt, und dass die Zeitkoordinaten aller Bezugssysteme sich allenfalls durch die Wahl des Zeitnullpunkts unterscheiden.
Transformationen der Zeit
Nehmen wir an, in zwei Bezugssystemen S und S’ werde in gleicher Weise eine Zeitkoordinate t bzw. t’ definiert. “In gleicher Weise” soll dabei heißen, dass baugleiche Uhren verwendet werden und dass die Vorschriften, wie Gleichzeitigkeit zu definieren sei, analog sind: Wäre beispielsweise Gleichzeitigkeit in S darüber definiert, dass eine Uhr in S relativ zu diesem Bezugssystem in bestimmter Weise von einem Ort zum anderen transportiert wird, dann soll die Gleichzeitigkeit in S’ ganz analog definiert sein – allerdings heißt “analog”, dass sich die Angaben dazu, wie die Uhr zu transportieren sei, jetzt auf das Bezugssstem S’ beziehen.
Auch die Zeiteinheiten wählen wir in S und S’ analog. Wäre die Zeiteinheit in S beispielsweise über bestimmte Eigenschaften einer in S ruhenden Referenzuhr definiert, dann würden wir in S’ die Zeiteinheit ebenfalls auf eine nach exakt dem gleichen Muster, mit gleichen Materialien auf gleiche Weise konstruierte, aber diesmal in S’ ruhende Referenzuhr bestimmen. (Darüber, wie solche Definitionen getroffen werden, hatte ich in Eine Sekunde bitte Teil 2 geschrieben.)
Unter solchen Voraussetzungen nimmt die klassische Mechanik an, dass die Zeitkoordinaten der beiden Systeme sich allenfalls durch unterschiedliche Wahl des Zeitnullpunkts unterscheiden können. Schaut man etwas genauer hin, so liegt dem Annahme zugrunde, dass die Uhren in den beiden Systemen, auf welche Weise man sie auch vergleichen mag, gleich schnell ticken, und dass auch Gleichzeitigkeit in beliebigen Systemen gleich definiert ist – wenn zwei Ereignisse E und F in einem System gleichzeitig stattfinden, dann auch bezüglich der Zeitkoordinate eines beliebigen anderen Systems.
(Diese Annahme wird in den meisten Darstellungen der klassischen Mechanik nicht ausdrücklich getroffen. Überhaupt wurde ja, dies wurde bereits erwähnt, der Gleichzeitigkeitsbegriff in der klassischen Mechanik lange Zeit nicht näher hinterfragt. Die Annahme ergibt sich aber implizit aus den in der klassischen Mechanik als zulässig postulierten Koordinatensystemwechseln.)
Damit bleibt für die Zeitkoordinaten nur noch eine mögliche Änderung übrig, und zwar ein Zusammenhang der Form
![]()
a0 ist dabei ein konstanter Wert mit derselben physikalischen Einheit wie die Zeitkoordinate t.
Wie in Teil VI ausgeführt, sind Gleichungen wie diese hier und im folgenden immer so zu lesen, dass sie sich auf ein und dasselbe Punktereignis beziehen: “Ist dem Ereignis E im Bezugssystem S der Zeitkoordinatenwert t zugeordnet, dann ist ihm im Bezugssysstem S der Zeitkoordinatenwert t’ = t + a0 zugeordnet”.
Eine solche Transformation heißt “Verschiebung des Zeitnullpunktes” oder auch “Translation der Zeitkoordinate”, denn schließlich ist a0 in diesem Falle genau der t’-Koordinatenwert des Zeitnullpunkts im System S, der schließlich durch den Zeitkoordinatenwert t=0 beschrieben wird.
Dieser Zeitkoordinaten-Unterschied entspricht genau der Festlegung unterschiedlicher Zeitnullpunkte für die verschiedenen Zeitzonen auf unserem Globus. Um von einer Zeitkoordinate zur anderen zu kommen, muss man also lediglich eine charakteristische Konstante addieren, meist eine ganzzahlige Anzahl von Stunden. Auf genau diese Weise komme ich (kleine Komplikationen bei Sommer- vs. Winterzeit außen vor gelassen) von der hier in Deutschland herrschenden Zeit zur US-amerikanischen Ostküstenzeit, indem ich 6 Stunden von der Anzeige meiner Uhr abziehe. Mit genau so einem Koordinatenwechsel haben wir es hier zu tun.
Die Umkehrtransformation lautet
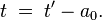
Dass a0 dabei mit anderem Vorzeichen auftritt, sorgt dafür, dass diese Transformation die in Teil VI erwähnte Hin-und-Zurück-Eigenschaft erfüllt: Berechnen wir für einen bestimmten t-Wert mit Hilfe der Transformation den zugehörigen t’-Wert und setzen das Ergebnis in die Rücktransformation von S’ nach S ein, dann ist das Ergebnis der ursprüngliche t-Wert,
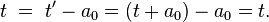
Führt man zwei Transformationen dieser Art hintereinander aus, etwa um vom System S mit Zeitkoordinate t zum System S’ mit Zeitkoordinate t’ und anschließend von dort zum System S” mit Zeitkoordinate t” zu kommen, dann ist das Resultat eine Transformation, welche die gleiche Form hat wie die Teiltransformationen: Gelangt man von S zu S’ mit
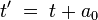
und von S’ zu S” mit
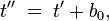
dann hat die Transformation von S zu S” die gleiche Form, nämlich
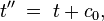
und es gilt c0 = a0 + b0.
Längenmessungen und Maßstäbe
Als nächstes schauen wir uns die Raumkoordinaten unterschiedlicher Bezugssysteme an. Ebenso wie bei der Zeit setzen wir auch hier voraus, dass die betrachteten Systeme für Längenmessungen dieselbe Einheit verwenden.
Dafür, wie die Gleichheit der Längeneinheit sichergestellt werden kann, gibt es mehrere Möglichkeiten. Wird die Maßeinheit durch eine Experimentiervorschrift aus den zugrundeliegenden Naturgesetzen abgeleitet, dann kann man dasselbe Experiment in jedem der betreffenden Bezugssysteme durchführen. Zwischenzeitlich war ja z.B. die SI-Längeneinheit Meter als 1.650.763,73faches der Wellenlänge des Lichts definiert, das bei einem bestimmten, genau identifizierbaren atomaren Übergangs von Krypton-86 ausgesandt wird. Experimente, die solche Atomübergänge untersuchen und die gesuchte Wellenlänge identifizieren, lassen sich im Prinzip in jedem Bezugssystem ausführen. (Die Vorteile der Definition von Maßeinheiten über Naturgesetze hatte ich in diesem Beitrag hier dargelegt.)
In der klassischen Mechanik ist auch die direkte Weitergabe eines Bezugs-Maßstabs möglich: Angenommen, ich verwende im System S einen ganz bestimmten Längenmaßstab. Das kann z.B. ein Referenzobjekt sein, das festlegt, wie lang ein Meter ist. In der klassischen Mechanik ist es ohne Probleme möglich, diesen Maßstab so zu beschleunigen, dass er anschließend im System S’ ruht, welches sich relativ zu S bewegt. Mit dem solchermaßen “transplantierten” Maßstab kann man dann im System S’ festlegen, wie lang ein Meter ist.
Bei näherem Nachdenken über diese Einheiten-Übertragungen wird man feststellen, dass sie von einer Eigenschaft der physikalischen Gesetze abhängen. Ist das Ergebnis eines die Längeneinheit definierenden Experiments beispielsweise in allen Bezugssystemen sinnvoll durchführbar, dann legt das eine allgemeinere Übertragbarkeit der dem Experiment zugrundeliegenden physikalischen Gesetze von einem System ins andere nahe. Solch eine Übertragbarkeit wird uns später, Stichwort Relativitätsprinzip, noch näher beschäftigen. An dieser Stelle halten wir nur fest, dass es in der klassischen Physik ohne große Probleme möglich ist, dafür zu sorgen, dass die unterschiedlichen Bezugssysteme die gleiche Längeneinheit benutzen. Damit nun zu eigentlichen Überlegungen dazu, wie sich klassische Bezugssysteme bezüglich der Art und Weise, wie sie den Raum kartieren, unterscheiden können.
Feste Translationen im Raum
Der einfachste Unterschied zwischen den Raumkoordinaten zweier Bezugssysteme besteht darin, dass der Nullpunkt des einen Systems S gegen den Nullpunkt des zweiten Systems S’ verschoben ist. Nehmen wir zunächst einmal an, dass sich diese Verschiebung mit der Zeit nicht ändert, dass also die beiden Raumnullpunkte relativ zueinander ruhen (sprich: dass sich die Raumkoordinaten, die jedem der beiden Raumnullpunkte im jeweils anderen System zugeordnet werden, mit der Zeit nicht ändern).
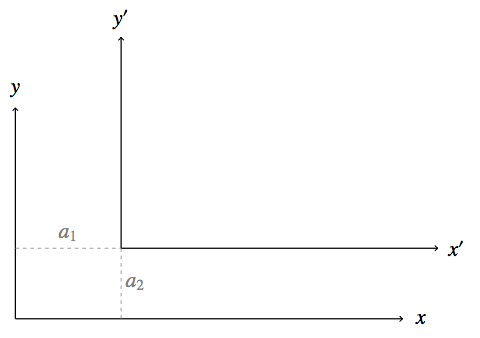
Am einfachsten sieht man die Zusammenhänge, die sich in dieser Situation ergeben, wenn man sich auf zwei Raumdimensionen beschränkt und z.B. nur die xy-Ebene betrachtet, wie hier dargestellt:
Zu sehen sind die Achsen x und y des Bezugssystems S (der Einfachheit halber ist nur der positive Teil angedeutet, x>0 und y>0), sowie die Achsen x’ und y’ des Bezugssystems S’ (ebenfalls nur die positiven Anteile).
In der Ebene gelten die üblichen Gesetze der euklidischen Geometrie. Wichtig wird an dieser Stelle, dass Abstandsmessungen im Bezugssystem S und im Bezugssystem S’ genau gleichwertig sind. Jede Operation, die wir vom Bezugssystem S zur direkten Bestimmung von Abständen zwischen zwei Raumpunkten vornehmen – das Anlegen eines Maßstabs; dazu gleichwertige Messungen; geometrische Konstruktionen – ist auch vom Bezugssystem S’ aus zur Abstandsbestimmung zulässig. Bei solchen Operationen spielen diejenigen Eigenschaften, in denen sich S und S’ unterscheiden, also die Positionen der Achsen im Raum, nämlich gar keine Rolle. Insbesondere gilt damit: Misst ein Beobachter in S für zwei gegebene Raumpunkte einen bestimmten Abstand d, so ist dies der gleiche Wert, den auch ein Beobachter in S’ für die gleichen Raumpunkte erhält.
Unterschiedliche Aussagen ergeben sich von S bzw. von S’ aus erst, wenn Koordinatenwerte bestimmt werden. Dann beziehen sich die Koordinatenwerte in S auf andere Achsen als die in S’, und ergeben dementsprechend für ein und denselben Raumpunkt unterschiedliche Werte.
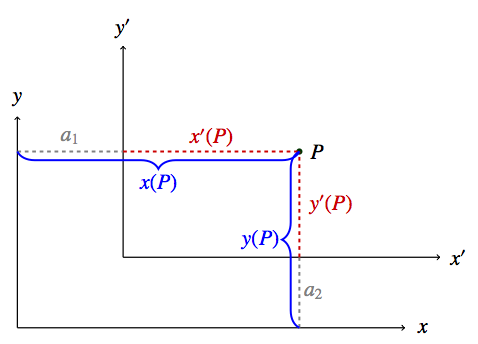
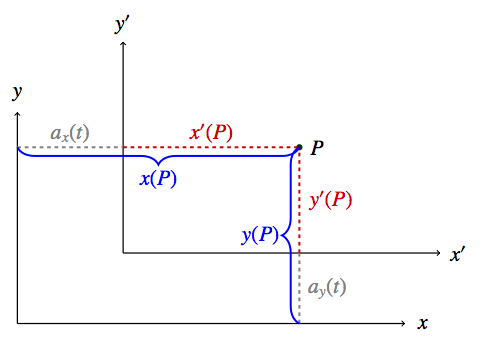
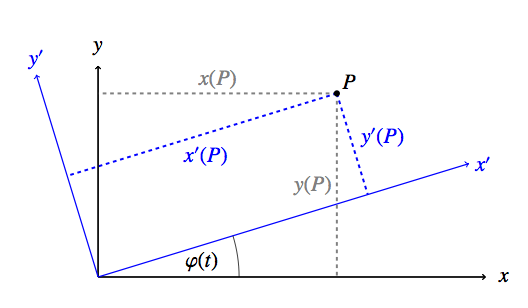
Da Abstandsmessungen von S und von S’ aus zum gleichen Ergebnis führen, kann man in der oben gezeigten Skizze direkt Abstände eintragen, ohne sich darüber Gedanken machen zu müssen, von welchem der Beobachter sie bestimmt wurden. Hier sind die für die Bestimmung von x’-, y’-, x- und y-Koordinatenwerten eines Punktes P nötigen Strecken eingezeichnet:
a1 ist dabei, wie gehabt, die Verschiebung der y’-Achse gegen die y-Achse in die x-Richtung, a2 die Verschiebund der x’-Achse gegenüber der x-Achse in y-Richtung. x(P), die x-Koordinate des Punktes P, ist der Abstand von P zur y-Achse, gemessen parallel zur x-Achse. y(P), die y-Koordinate des Punktes P, ist der Abstand von P zur x-Achse, gemessen parallel zur y-Achse. x'(P) und y'(P) sind analog für das gestrichene Koordinatensystem definiert.
Man sieht direkt, dass die Koordinatenwerte wie folgt zusammenhängen:
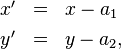
bzw. in die Gegenrichtung
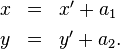
(Wie immer geht es um die Koordinatenwerte ein und desselben Ereignisses, bzw. in diesem Falle: desselben Punkts im Raum; vgl. die entsprechenden Ausführungen in Teil VI – ich werde das ab jetzt nicht mehr explizit dazu sagen.)
Genau wie bei den Zeit-Translationen kann man durch direktes Einsetzen zeigen, dass das Hintereinanderausführen der Transformation und der Umkehrtransformation einen beliebigen Punkt in sich selbst überführt.
Die Verallgemeinerung auf drei Dimensionen gelingt ohne Probleme: Auch eine Verschiebung in z-Richtung hat die hier gezeigte Form; zu den zwei Gleichungen für x’ und y’ tritt also noch
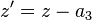
hinzu. Eine Transformation, bei der x,y,z und x’,y’,z’ in dieser Weise paarweise durch Addition einer Konstanten zusammenhängen heißt (räumliche) Translation oder Raumtranslation. Wie man an den Formeln direkt ablesen kann, entsprechen a1, a2, a3 gerade den x-, y- bzw. z-Koordinatenwerten des Raumnullpunkts des Bezugssystems S’, ausgedrückt im Bezugssystem S. (Dazu setzt man in die Transformationsformeln, welche die x-, y-, und z-Koordinatenwerte liefern, schlicht die Raumkoordinaten des Raumnullpunkts des Bezugssystems S’ in eben diesem System S’ ein, nämlich x=0, y=0, z=0.)
Rotation um einen festen Winkel
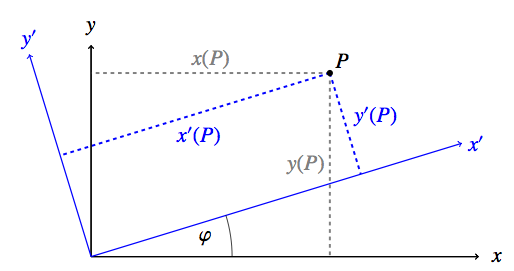
Als nächstes betrachten wir den Fall, dass zwar die Raumnullpunkte der beiden Systeme zusammenfallen, aber die räumlichen Achsen von S gegenüber jenen von S’ um einen konstanten Winkel φ verdreht sind. Der Einfachheit halber möge die Drehung zunächst in der x-y-Ebene stattfinden, mit der z-Achse als Drehachse. Hier ist eine Skizze der Situation zu sehen:
Die Rechnung ist hier etwas komplizierter als im Falle der Translation, erfordert aber über die Definitionen von Sinus und Kosinus und den Umgang mit rechtwinkligen Dreiecken hinaus keine höhere Mathematik. Ich habe die Details hier näher ausgeführt.
Das Ergebnis ist
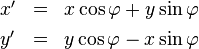
bzw. in die Gegenrichtung
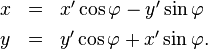
Die z-Koordinate ist in beiden Systemen die gleiche,
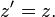
Wieder kann man sich durch direkte Rechnung überzeugen, dass die Hintereinanderausführung der Transformation und ihrer Umkehrung einen zum Ausgangspunkt zurückbringt, genau wie es sein muss.
Wendet man dieselbe Herleitung auf Drehungen um die x- oder die y-Achse an, so erhält man ganz analoge Formeln. Bei einer Drehung um die gemeinsame x-Achse beispielsweise ist die x-Koordinate in beiden Systemen gleich, und y und z sind in der oben angegebenen Weise über Sinus- bzw. Kosinusfunktion verknüpft. Bei einer Drehung um die gemeinsame y-Achse sind die y-Koordinaten gleich, und x und z über die Sinus-/Kosinusformeln verknüpft.
Kombinationen der Verknüpfungen
Mit den räumlichen und zeitlichen Translationen haben wir bereits alle Möglichkeiten erschöpft, wie Raumnullpunkte und Zeitnullpunkte zweier Bezugssysteme gegeneinander verschoben sein können.
Mit den drei hier vorgestellten Rotationen – um die z-Achse explizit hingeschrieben, um die x- bzw. y-Achse mit ganz analogen Formeln, die sich durch einfache Ersetzungen ergeben – haben wir dagegen zunächst nur drei Spezialfälle beschrieben. Tatsächlich kann man auf diese Art beliebige Verdrehungen zweier Bezugssysteme relativ zueinander beschreiben. Das sieht man am einfachsten, indem man sich überlegt, wie man die Achsen verdrehen muss, um von einem räumlichen Bezugssystem zum anderen zu kommen.
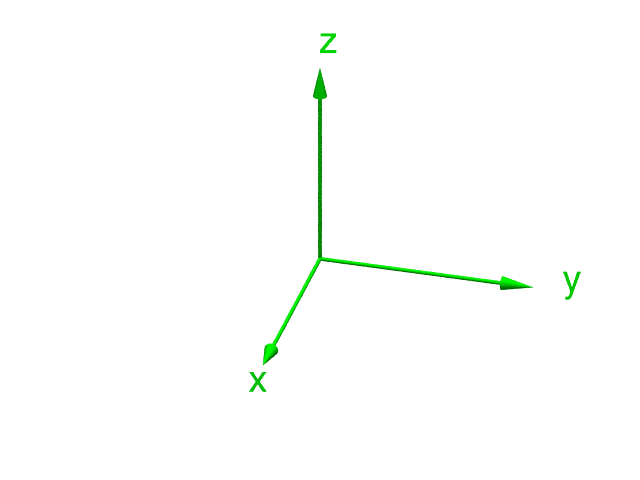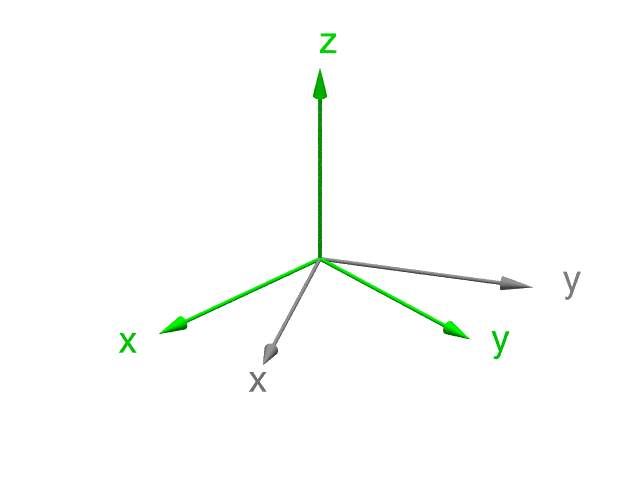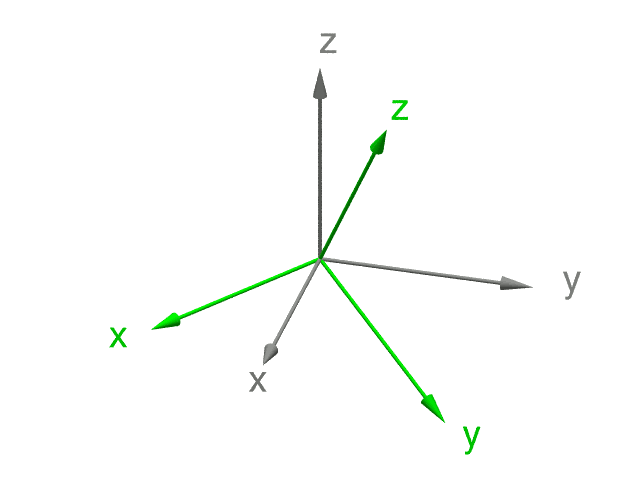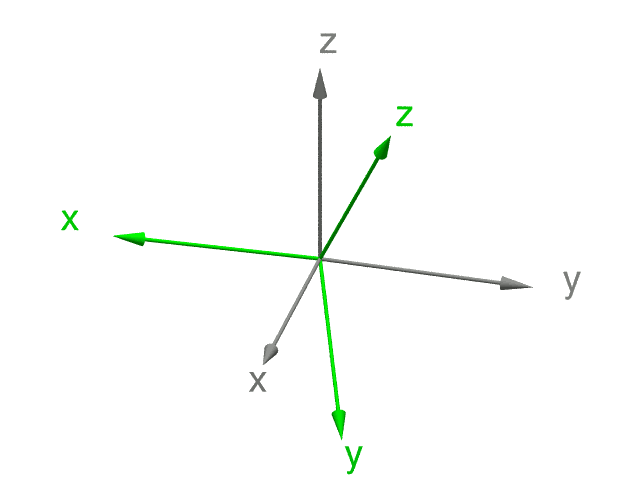
Die folgende Darstellung zeigt, wie solches Verdrehen vor sich gehen kann. Am Anfang fallen das grüne und das graue Bezugssystem zusammen. Anschließend verdrehen wir das grüne System dreimal hintereinander jeweils um eine seiner Achsen (denn für solche Verdrehung direkt um eine Achse hatten wir ja Formeln abgeleitet):
Vollzieht man diese Drehungen vor seinem geistigen Auge – oder mit materiellen Hilfsmitteln – nach, dann kann man sich klar machen, dass sich auf diese Weise tatsächlich jede mögliche Orientierung erreichen lässt. Die erste Drehung findet um die z-Achse statt; mit ihrer Hilfe kann man offenbar jede mögliche Ausrichtung der x- und y-Achsen bei festgehaltener z-Achse erreichen. Zusammen mit der zweiten Drehung um die (grüne, also bereits einmal verdrehte) x-Achse kann man die z-Achse mit diesen ersten beiden Drehungen in jede beliebige Richtung zeigen lassen.
Wie man am Zwischenergebnis sieht, ist das genau analog zur Wahl von geographischer Länge und Breite auf der Erdoberfläche: Die erste Drehung legt durch die Position der grünen y-Achse die geographische Länge des Endpunktes der grünen z-Achse fest, die zweite Drehung die geographische Breite. Und ebenso wie man durch Wahl der geographischen Länge und Breite jeden Ort auf der Erdkugel erreichen kann, kann man durch die ersten beiden Drehungen jede beliebige Richtung für die grüne z-Achse erreichen.
Ist die Ausrichtung der z-Achse einmal festgelegt, dann gibt es nur noch eine Variationsmöglichkeit, nämlich die Ausrichtung von x- und y-Achse in der Ebene senkrecht zur z-Achse. Mit der dritten Drehung, nämlich um die z-Achse in ihrer neuen Ausrichtung, lassen sich demnach alle möglichen Ausrichtungen von x- bzw. y-Achse erreichen – zumindest für die rechtshändigen Koordinatensysteme, auf die wir uns bislang beschränkt haben; ließe man auch linkshändige Systeme zu, dann müsste man zusätzlich noch die Möglichkeit zulassen, das Koordinatensystem an einer beliebigen Ebene zu spiegeln. (Zur Händigkeit von Systemen siehe kartesische Koordinaten im Teil I).
Die Transformationsformel, die alle drei Winkel berücksichtigt, kann man hinschreiben, indem man erst die Formel für die erste Drehung um die z-Achse hinschreibt, dann auf der rechten Seite die x-, y- und z-Werte durch diejenigen eines um den zweiten Winkel um die x-Achse gedrehten Systems ersetzt, und als letztes die darin vorkommenden x-, y- und z-Werte durch die eines um den dritten Winkel um die z-Achse gedrehten Systems. Nähere Informationen findet man in der Literatur unter dem Stichwort Eulersche Winkel.
Solange wir uns auf diejenigen Unterschiede zwischen zwei Bezugssystemen beschränken, die sich mit der Zeit nicht ändern, haben wir jetzt alle in der klassischen Mechanik zulässigen Möglichkeiten ausgeschöpft. Wie kann sich ein Raumkoordinatensystem von einem zweiten unterscheiden? Zum einen durch die Wahl des Raumnullpunkts. Diesbezüglich haben wir aber mit den oben definierten festen Translationen, den Verschiebungen in x-, y- und z-Richtung jeweils um eine konstante Strecke, alle irgend möglichen Unterschiede berücksichtigt. Ist der Raumnullpunkt festgelegt, können sich die Systeme noch durch die Orientierung der drei Raumachsen unterscheiden. Was jene angeht haben wir aber, wie gesagt, durch die Kombinations-Rotation alle Möglichkeiten erfasst, eine Orientierung in eine andere zu überführen. Und da bei der Zeit, wie erwähnt, nur Nullpunktsverschiebungen zugelassen sind, haben wir mit den oben definierten Zeitnullpunktsverschiebungen auch in dieser Hinsicht alle möglichen Unterschiede berücksichtigt.
Damit blieben noch jene Situationen, in der sich die Unterschiede zwischen zwei Bezugssystemen mit der Zeit ändern.
Zeitabhängige Zeittranslation?
Können wir den Ausdruck für die Zeittranslation (die Verschiebung des Zeitnullpunkts)
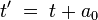
abändern, indem wir die Konstante a0 durch einen zeitabhängigen Ausdruck a(t) ersetzen, also
als Transformation haben? In der klassischen Mechanik wird gefordert – wie erwähnt: lange Zeit implizit, ohne diese Forderung näher zu durchdenken – dass Zeitintervalle zwischen zwei Ereignissen E und F in jedem Bezugssystem gleich lang sind, dass also demnach
gilt, wo wir die Transformationsformel bereits eingesetzt haben. Aus der linken und ganz rechten Seite dieser Gleichung folgt nun aber
Weil dies für beliebige Ereignisse E und F der Fall ist, so dass auch t(E) und t(F) jeweils beliebigen Zeitkoordinatenwerten entsprechen können, kann diese Gleichung nur erfüllt sein, wenn a(t) gar nicht von seinem Argument t abhängt, sondern zeitunabhängig ist, konstant.
Diesen Spezialfall haben wir aber bereits mit der konstanten Nullpunktverschiebung erfasst. Allgemeinere Transformationen sind mit den Annahmen der klassischen Mechanik offenbar nicht vereinbar. Erst im Rahmen der speziellen Relativitätstheorie werden wir Transformationen kennenlernen, welche die Zeitkoordinate in weitergehender Weise beeinflussen. Dann wird allerdings auch das Zeitintervall, das zwischen zwei Ereignissen E und F vergeht, vom Bezugssystem abhängen.
Zeitabhängige Translationen im Raum
Anders sieht die Situation bei den räumlichen Translationen aus. Dort hatten wir bislang nur konstante Translationen
berücksichtigt, mit konstanten Verschiebungen ax, ay, az der Nullpunkte gegeneinander. Setzen wir dort anstatt der Konstanten zeitlich veränderliche Ausdrücke ax(t), ay(t), az(t) ein, dann haben wir im Rahmen der klassischen Mechanik jenen Fall beschrieben, in dem sich der Raumkoordinatennullpunkt des gestrichenen Systems S’ vom ungestrichenen System S aus betrachtet auf der Bahn ax(t), ay(t), az(t) bewegt.
Die Annahmen der klassischen Mechanik über die Zeit- und Längenmessungen in verschiedenen Bezugssystemen machen es uns einfach, diese Situation zu beschreiben. Dass die Zeitkoordinate in S und S’ dieselbe ist – von einer etwaigen Verschiebung des Zeitnullpunkts einmal abgesehen – bedeutet, dass wir zu jedem Zeitpunkt in S einen Momentaufnahme der Situation aufzeichnen können, und dass diese Momentaufnahme außerdem auch eine Momentaufnahme im System S’ ist. Schließlich bedeutet
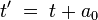
nicht zuletzt, dass alle Ereignisse mit dem gleichen t-Koordinatenwert (nur solche Ereignisse erscheinen für einen bestimmten, festen Wert von t auf einer Momentaufnahme im System S für den betreffenden Zeitpunkt) auch den gleichen t’-Koordinatenwert haben (und daher auf einer entsprechenden Momentaufnahme erscheinen, die im System S’ angefertigt wurde).
Die klassische Mechanik geht außerdem davon aus, dass Längenmessungen für ein und dieselbe Strecke in verschiedenen Bezugssystemen denselben Wert ergeben, insbesondere auch in den von uns betrachteten Bezugssystemen S und S’. Auf einer Momentaufnahme können wir demnach die Längen bestimmter Strecken bestimmen und davon ausgehen, dass das Ergebnis sowohl vom System S aus gemessenen Längen als auch vom System S’ gemessenen Längen entspricht.
Aus diesen beiden Gründen können wir für den Fall, dass sich der Raumnullpunkt auf der Bahn ax(t), ay(t), az(t) bewegt, für jeden Zeitpunkt t die gleiche Skizze malen wie für die konstante Verschiebung, die wir bereits oben behandelt haben, nämlich die folgende (wobei wir die dritte Raumdimension der Einfachheit halber unterdrücken):
Daraus ergeben sich Transformationsformeln ganz analog zum Falle der konstanten Verschiebung der Raumnullpunkte zueinander, nämlich
(Spezielle) Galilei-Transformationen
Ein interessanter Sonderfall liegt vor, wenn sich der Raumnullpunkt des Systems S vom S’-System aus beurteilt mit konstanter Geschwindigkeit entlang einer Geraden bewegt. Das ist die geradlinig-gleichförmige Bewegung, die wir bereits in Teil IV kennengelernt hatten,
Die jeweils letzten Summanden in jeder Gleichung, nämlich die konstanten ax, ay, az, sind nichts anderes als die uns nun schon sattsam bekannte feste (konstante) Translation im Raum. Neu sind dagegen die zu t proportionalen Terme. Beschränken wir uns einmal auf den Fall, in dem ax, ay, az sämtlich Null sind. Dann haben wir es mit der Transformation
zu tun, die (spezielle) Galilei-Transformation genannt wird. Sie zeigt, wie die Raumkoordinaten eines Bezugssystems S und eines relativ zum ersten mit konstanter Geschwindigkeit geradlinig bewegten Bezugssystems S’ zusammenhängen. Der einfachste Fall liegt vor, wenn der Zeitnullpunkt so gewählt ist, dass der Zeitpunkt, zu dem die Raumnullpunkte der beiden Systeme zusammenfallen, gerade der Zeitnullpunkt beider Systeme ist; dann sind ax, ay, az in der Tat sämtlich Null und ergänzend zu den obigen drei Gleichungen für die Raumkoordinaten kommt noch die Gleichung
hinzu.
Die Umkehrung der speziellen Galilei-Transformation lässt sich direkt ablesen: Es gilt
Das ist dieselbe Form wie für die Transformation von S nach S’. Der einzige Unterschied liegt darin, dass die Geschwindigkeitskomponenten bei der Rück-Transformation das umgekehrte Vorzeichen haben als bei der Hin-Transformation. Das entspricht unserer Erwartung: Für zwei Systeme, die genau gleich orientiert sind (x-Achse parallel zur x’-Achse, y-Achse parallel zur y’-Achse, z-Achse parallel zur z’-Achse) gilt: Bewegt sich der Nullpunkt von S’ vom System S aus gesehen in positive x-Richtung, so bewegt sich der Nullpunkt von S im System S’ in negative x-Richtung. Allgemeiner: Bewegt sich der Nullpunkt von S’ vom System S aus gesehen in eine bestimmte Richtung, so bewegt sich der Nullpunkt von S im System S’ in die Gegenrichtung.
Zeitabhängige Drehungen
Als letztes können wir uns noch den Fall der gegeneinander verdrehten Koordinatensysteme anschauen und uns fragen, was passiert, wenn eine solche Verdrehung sich mit der Zeit verändert.
Der Einfachheit halber betrachten wie oben lediglich die Drehung um eine der Achsen; ich hatte dort ja zumindest per Animation vorgeführt, dass sich aus der Zusammensetzung, nämlich der Hintereinanderausführung solcher Drehungen alle möglichen relativen Verdrehungen zweier Raumkoordinatensysteme ergeben.
Für diesen Fall gilt wie im Falle der zeitabhängigen Verschiebungen im Raum, die ich im vorangehenden Abschnitt behandelt hatte: Dadurch, dass in beiden Bezugssystemen S und S’ der gleiche Gleichzeitigkeitsbegriff gilt, können wir die Skizze, aus der wir die geometrischen Beziehungen für die Koordinatenwerte für in der x-y-Ebene gegeneinander verdrehten Systeme abgeleitet hatten, auch für den allgemeineren Fall nutzen. Zu einer festen Zeit t (entspricht einer zugehörigen festen Zeit t’) sieht eine Momentaufnahme der Achsen der beiden Systeme genau so aus wie bei unserer Verdrehung um einen konstanten Winkel:
In genau der gleichen Weise, wie hier für den Fall konstanten Drehwinkels abgeleitet, lassen sich in dieser Momentaufnahme, und in den Momentaufnahmen für jeden anderen Zeitpunkt t, die Dreiecksrechnungen durchführen, die uns auf die Transformationsformeln für den Übergang vom einen System zum anderen führen. Das Ergebnis ist analog zu der Transformation mit konstantem Drehwinkel – nur, dass der Drehwinkel jetzt eben von der Zeit abhängt:
Der einfachste Fall ist wiederum der, in dem sich der Drehwinkel linear ändert, also direkt proportional zu t ist. Der Proportionalitätsfaktor ω wird Winkelgeschwindigkeit genannt, und die Transformationsformeln sind dann
Mit Hilfe entsprechender Transformationsformeln lässt sich beispielsweise in guter Näherung der Übergang zwischen einem Bezugssystem beschreiben, das mit der Erde zusammen rotiert, und einem, welches die Erdrotation nicht mitmacht. Ich werde auf die Konsequenzen eines solchen rotierenden Bezugssystems später, in Teil IX, noch näher eingehen.
Allgemeinere Drehungen erhält man wiederum durch die Kombination von ingesamt drei geeigneten Einzeldrehungen – nur, dass die drei Drehwinkel im allgemeinen alle von der Zeit abhängen.
Fazit
Mit den hier angegebenen Bezugssystemübergängen haben wir alle Möglichkeiten ausgeschöpft, wie man in der klassischen Mechanik unterschiedliche Bezugssysteme wählen kann – zumindest solche Systeme, in denen die gleichen physikalischen Einheiten zur Zeit- und Längenmessung definiert sind.
Wir können alle Arten und Weisen beschreiben, wie sich die Raumnullpunkte zweier Systeme relativ zueinander bewegen, alle Arten und Weisen, wie die Achsen zweier Systeme ihre relative Orientierung mit der Zeit ändern und die konstante Verschiebung der Zeitnullpunkte zweier Systeme gegeneinander ausdrücken, und wir können (für allgemeine Drehungen im Prinzip, für die anderen Fälle explizit) angeben, welche Koordinatentransformationen je zwei solcher Systeme zueinander in Beziehung setzen.
Im allgemeinen Falle werden wir mehrere dieser Transformationen hintereinander anwenden müssen, um von einem gegebenen Bezugssystem S zu einem zweiten System S’ zu kommen: zuerst eine (im allgemeinen zeitabhängige) Translation, um vom Bezugssystem S zu einem Hilfssystem S’A zu kommen, dessen Raumnullpunkt sich jederzeit dort befindet, wo sich auch der Raumnullpunkt von S’ befindet. Anschließend eine (im allgemeinen ebenfalls zeitabhängige) Rotation, um die Achsen von S’A mit denen von S’ in Deckung zu bringen (wobei wir gesehen haben, dass wir für eine allgemeine Rotation mehrere Rotationen um die Achsen x, y, z des Ausgangssystems S’A kombinieren müssen).
Im nachfolgenden Teil VIII schauen wir uns genauer an, wie die Bewegungen freier Teilchen von unterschiedlichen Bezugssystemen aus beschrieben werden.
Soweit der Entwurf des siebten Teiltextes. Wie für die vorangehenden Teile von “Einstein verstehen” gilt auch für diesen hier, dass ich Veränderungen, die sich aus der hier geführten Diskussion ergeben, direkt umsetzen werde. Die Originalfassung habe ich zum Vergleich hier als PDF eingestellt. Die Zusatz-Textteile, in denen einige der Erklärungen aus dem Haupttext näher ausgeführt werden, befinden sich auf Seite 2 dieses Blogbeitrags.
Meinen Umgang mit Kommentaren in diesem Blog habe ich in diesem Blogbeitrag erläutert. Inbesondere gilt: Der obige Text stellt den siebten Schritt einer systematischen Einführung in die Spezielle Relativitätstheorie dar. Die Diskussion sollte auf den hier behandelten Themenbereich beschränken und insbesondere nicht auf das vorgreifen, was erst in den nachfolgenden Teilen der Einführung angesprochen wird. Ich behalte mir vor, Diskussionsbeiträge, die dem Leser keinen Mehrwert bieten, sondern die Diskussion stören, zu löschen.
Die Kommentare können zwischenzeitlich moderiert sein und werden dann von mir jeweils erst freigeschaltet. Daher bitte Geduld, wenn Sie einen Kommentar eingestellt haben, dieser aber nicht gleich unten auf dieser Seite erscheint!


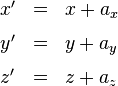
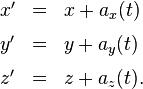
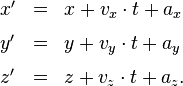
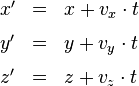
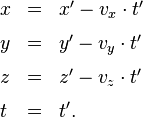
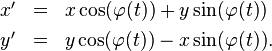
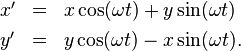
Sehr geehrter Herr Pössel,
ich finde Ihren Beitrag sehr lesenwert und finde die Systematik und Genauigkeit ihrer Beschreibung unübertrefflich. So zu schreiben erfordert viel Disziplin und Geduld.
Aber die wird auch vom Leser abverlangt. Der sehnt sich vielleicht zwischen durch nach Zusammenhängen. Dazu ein paar konstruktive Hinweise:
Sie erwähnen den Begriff “Isotropie des Raumes” nicht. Mit Absicht ? Sie setzen voraus, dass es einen Raum gibt, mit unendlich vielen Raumpunkten, zwischen denen ein geometrischer Abstand definiert werden kann. Reicht diese Voraussetzung aus, um die beschriebenen Transformationen zu erklären ? Oder müssen Sie nicht auch eine bestimmte Metrik voraussetzen. Oder wollten Sie nur die Existenz von Koordinatensystemen voraussetzen, die geeignet zu definieren wären. Bei dieser Definition brauchen Sie aber auch wieder den Begriff des Raumes und seiner Metrik. Es ist vielleicht nicht verkehrt, den Gedanken, dass ein Raum ohne Metrik nicht gedacht werden kann, frühzeitig einzuführen und zu verankern, und nicht erst, wenn es um komplizierte Raumgeometrien geht. Sie wollen ja beschreiben, wie Einsteins Gedanken zu verstehen sind, und dann wird die rein formale (mathematische) Betrachtung, die hunderfach in Lehrbüchern nachzulesen ist, ein unbefriedigtes Gefühl zurücklassen. Kurze Überlegungen zum Begriff der Metrik (Hinweise genügen) könnten gut auf eine „Metaphysik“ des Raumes vorbereiten, ohne die Sie später nicht auskommen.
Darüber hinaus wäre es vielleicht auch sinnvoll, etwas über die Anwendung der beschriebenen Transformationen zu erfahren, nämlich bei bewegten Bildern im Computer. Diese Grafiken entstehen, so glaube ich, indem eine Software Leuchtpunkte auf dem Bildschirm verschiebt – eben nach diesen einfachen Formeln, aber 100 Millionen mal pro Sekunde – diese einfachen Regeln machen ein bewegtes Bild – das finde ich ganz toll ?
Zuletzt überlege ich, ob in der nicht-relativistischen Betrachtung eine Translation in der Zeit „gleichwertig“ ist zu einer im Raum. Die Formeln haben die gleiche Struktur. Muss man daraus zwingend ableiten, dass eine gedachte Gerade das „gleiche“ ist, wie ein gedachtes „Fortschreiten“ der Zeit ? Auch nur strukturell gleichwertig ? Ich glaube das so ohne weiteres nicht. Auf einer Geraden können Sie nämlich Abstände von einem Nullpunkt aus in zwei Richtungen definieren, auf der Zeitachse von einem Nullpunkt aus nicht. Die Zeit „läuft“ nicht „zurück“. Nicht wegen irgendwelcher zeitsymmetrischer physikalischen Gesetze, sondern wegen des Wesens der Zeit: bei einer gedachten eindimensionalen geometrischen Schwingung wechseln die geometrischen Abstände das Vorzeichen, aber die zeitlichen Abstände nicht. Diese r geometrische Variation zeigt, dass da ein Symmetriebruch vorhanden ist, der in den Transformationen, die Sie beschrieben haben, irgendwie nicht zum Ausdruck kommt.
Es stellt sich natürlich die Frage, ob man solche fundamentalen Fragen über die Metrik von Raum und Zeit in dem beschriebenen Zusammenhang herein stellen soll. Aber irgendwann müssen Sie vielleicht darauf kommen. Ein HInweis darauf vielleicht vertieft das Interesse des Lesers und macht ihn gespannt auf das was dann später kommt.
Grüsse
Fossilium
Danke für den Kommentar!
Längenmessungen und den euklidischen Raum und dessen Geometrie hatte ich direkt in Teil I eingeführt.
Computergrafik ist eine schöne Anwendung. Da finden in der Tat viele der hier eingeführten Konzepte eine schöne Aufgabe.
Zu den Translationen: Mathematisch gesehen haben die in der Tat die gleiche Struktur. Und doch, auch auf einer Zeitachse kann ich Abstände in die Vergangenheit und in die Zukunft von einem gegebenen Nullpunkt definieren. Der Unterschied kommt erst ins Spiel wenn, wie Sie schreiben, es um die Bewegung von Teilchen geht. In der klassischen Mechanik ist das noch weniger gut definiert (da theoretisch erst einmal nichts gegen beliebig hohe Geschwindigkeiten spricht); in der Speziellen Relativitätstheorie ist die Struktur dann klar festgelegt.
Die Metrik werde ich vermutlich noch etwas außen vor lassen und erst später einführen, wenn die relativistischen Effekte bereits bekannt sind.
Sehr geehrter Herr Pössel,
ich möchte mich für die Mühe bedanken, die Sie da auf sich genommen haben und dem Wunsch und der Hoffnung Ausdruck geben, dass Sie den geneigten Leser (damit meine ich u.a. mich) denn auch wie vorgesehen weiter führen werden – und die nötige Zeit und Muße dazu finden.
Kurz: Bitte machen Sie so weiter. Ich bin begierig darauf weiter zu lesen und zu lernen.
Michael
Bezugssystemwechsel in der klassischen Mechanik
Etwas müde der Teil VII von Einstein verstehen. Nicht der Inhalt dieses Teils. Wie immer sorgfältig auf Korrektheit bedacht wird der Leser unmerklich auf einen Weg gebracht der mehr vom Wesentlichen ablenkt als den Fokus auf das bringt, was wirklich schmerzt. Mit Mathematik und Koordinatendarstellungen wird verschleiert was es tatsächlich bedeutet ein Wechsel der Bezugssysteme vorzunehmen. Von den bisherigen 3 Kommentaren kann man ableiten, dass der Zweck dieses Blogs zu 100% erfüllt ist. War der Informationszug zur Klärung der Relativitätstheorie flott gestartet aber schon bald danach haben die Bremsen dieser Beiträge angezogen und mit diesem Teil wurden sie blockiert. Da dieser Info-Zug nun steht muss man diesen ja nicht unbedingt wieder in Fahrt bringen. Für wen denn? Etwa für die die kritisch sind und Fragen haben? Auch ich bin versucht, nicht weiter in einer Wunde zu stacheln die schon Resistent gegen Schmerz ist. Wenn da bloß nicht die Scheiß verdammten Fragen wären.
Fragen wie: „ Welche Bezugssysteme zum Teufel noch eins sind da gemeint?“
S oder S‘? S der Bahnsteig, S‘ ein Zug? S und S‘, Variable die für Gott wer was stehen können. Wieso hat jedes Bezugssystem eine andere Zeit? Wieso wird der praktische Aspekt von Bezugsystemwechsel außen vorgelassen?
Das Gedankenexperiment mit dem Bahnsteig und dem durchrauschenden Zug eignet sich gut um verständlich zu machen was ein Bezugssystemwechsel bedeutet. Dazu bemühe ich nicht die Mathematik die theoretischer Natur ist sondern versuche praktisch hinter das Geheimnis des Bezugssystemwechsels zu kommen. Da der Bahnsteig und Zug für Menschen gemacht ist um ein Wechsel des Bezugssystems vorzunehmen muss man diese Systeme auch nutzen können. Ich stehe auf dem Bahnsteig und steige in den durchrauschenden Zug ein. Falls ich es noch kann bedanke ich mich bei Mutter Physik die mir Bezugssystemwechsel in der Bewegung gestattet. Danke. Bezugssysteme die zueinander ruhen gestatten die Möglichkeit des unfallfreien Wechsels. Bei Bezugssystemen die sich zueinander in Bewegung befinden ist ein spontaner Wechsel eine gefährliche Sache. Um den Wechsel gefahrlos zu vollziehen ist in der Praxis zuerst eine Annäherung der Geschwindigkeit der Objekte einzuplanen. Erst wenn die Geschwindigkeit der Bewegung beider Objekte gleich ist kann der Wechsel gefahrlos vollzogen werden. Wovon ich hier spreche ist schon Routine in der Raumfahrt wenn ein Versorgungsmodul an der ISS andockt.
Die Theorie in Teil VII und die Praxis die übergangen wird, passen nicht zusammen.
Der Verfasser beruft sich in diesem Teil immer wieder auf bereits erschienene Teile wie Teil I, II, IV, VI und verschiedene ergänzende Teile, aber niemals auf Kommentare die als Gegenargumente gewichtig genug sind um Erwähnung zu finden.
Ein Schelm, der Böses dabei denkt.
Mir ist bewusst, dass dieser Teil (und der davor, und vermutlich noch die zwei danach) technischer sind als die anderen. Aber ohne diese Basis für diejenigen, die den Aspekt Trägheitskräfte ganz genau verstehen wollen, kommt man eben nicht zu Inertialsystemen. Ich hatte allerdings bereits überlegt, ob ich am Ende der klassischen Vorarbeiten noch eine vergleichsweise kurze Zusammenfassung derselben biete – die wäre dann der normale Einstieg zu “Einstein verstehen”, und nur wer es genauer wissen will geht noch eine Stufe weiter in die Tiefe, zu den Teilen I bis VIIff.
Übrigens ist dem heutigen Sprachgebrauch nach die bessere Übersetzung “Ein Schuft, wer Böses dabei denkt”. Und wirklich ist es ja alles andere als konstruktiv, und durchaus schäbig, dem Gegenüber vorschnell üble Absichten zu unterstellen.
Mir ist es auch ein Bedürfnis die RT von Grund auf zu verstehen egal wie technisch sie ist. Aber kann man nicht an Hand kurzer praktischer Beispiele aufzeigen wie die Vorhersagen der Theorie funktionieren. Muss unbedingt die Mathematik immer dafür herhalten? Mathematik ist nicht die Physik. Eine gute Basis, der Ausgangspunkt für diejenigen die verstehen wollen, bietet nicht allein die Mathematik. Mit dem Inertialsystem, welches Sie anführen, möchte ich nicht auf zukünftige Teile vorgreifen, sondern nur darauf hinweisen, dass Inertialsysteme gewissermaßen ein Spezialfall der Bezugssysteme sind. Wikipedia schreibt: „In einem Inertialsystem wird keine Drehung des Fixsternhimmels beobachtet.“ Fixsternhimmel ist ein Teil des unendlichen Universums welches sich in Bewegung befindet. Alles bewegt und dreht sich in alle möglichen Richtungen mit unterschiedlichen Drehungen. Wo kann ich ein Inertialsystem antreffen? (Es ist ein Fehler vom Fixsternhimmel zu sprechen, nur weil wir die Bewegungen der Sterne nicht sofort wahrnehmen.)
Herr Dr. Pössel, mir ist der Schelm in der Redensart „Ein Schelm, wer Böses dabei denkt“ lieber, denn der Schelm ist ein lustiger Geselle und nicht so böse wie ein Schuft. Die Redensart ist auch heute noch in Gebrauch, aber es gibt mehrere Abwandlungen davon. Mich als schäbig zu bezeichnen kann ich Ihnen nicht verbieten aber mir unterstellen, dass ich Ihnen üble Absichten unterstelle ist mehr als vorschnell. Trotzdem halte ich Ihnen und dem Blog die Treue.
Guten Tag Herr Dr. Pössel,
wie sieht es mit Teil VIII aus?
mit freundlichem Gruß
Klaus Badke
Durch Einsteins-Jubiläumsbeiträge, Vorlesungsvorbereitung und Buchprojekt etwas in den Hintergrund gedrängt. Wenn alles gut geht, komme ich in den Weihnachtsferien dazu!
Markus Pössel schrieb (18. Juli 2015):
> […] allgemeinere Übertragbarkeit der dem Experiment zugrundeliegenden physikalischen Gesetze von einem System ins andere
Vor der (eventuellen) „Übertragbarkeit von physikalischen Gesetzen“, die wohl bisher gewonnene Messwerte und mögliche Erwartungen hinsichtlich noch zu gewinnender Messwerte zusammenfassen (sollen),
steht selbstverständlich die Nachvollziehbarkeit der betreffenden Messgrößen und der dazu eingesetzten Begriffe;
also konkret die Anerkennung und konstruktive Anwendung des Einsteinschen (Selbst-)Verständnisses, dass
> Solch eine Übertragbarkeit wird uns später, Stichwort Relativitätsprinzip, noch näher beschäftigen.
Es bleibt zu hoffen, dass sich in dieser Blogreihe dann endlich die von Einstein vorgeschlagenen „ Feststellungen zeit-räumlicher Koinzidenzen“ (also
– „wer wen zusammen traf“; und im Zusammenhang damit gewiss auch
– „wer wen in welcher Reihenfolge traf“,
– „wer die Treffen welcher Beteiligter zusammen wahrnahm“, und
– „wer die Treffen welcher Beteiligter in welcher Reihenfolge wahrnahm)
aufgegriffen werden,
und dargestellt wird, wie allein daraus Messmethoden zu konstruieren („an die Hand zu geben“) sind, durch deren Anwendung Versuch für Versuch zu entscheiden wäre
– ob eine gegebene Uhr „gut“ war, also z.B. insbesondere „mit einer bestimmten (Eigen-)Frequenz tickte“, oder in wie fern nicht,
– ob zwei gegebene Uhren, die im betrachteten Versuch einzeln „gut“ waren, dabei gleiche „Raten“ bzw. insbesondere gleiche (Eigen-)Frequenzen hatte, oder in wie fern nicht,
– ob zwei gegebene Kr86-Atome gegenüber einander „ungestört“ gewesen wären,
– usw. usf.
Bis dieser Knoten endlich platzt, insbesondere auch im Zusammenhang mit der schon sehr lange versprochenen Behandlung der Messmethodik „Lichtuhr“, bleiben die Bemühungen zum „Einstein verstehen“ leider alles andere als konstruktiv und zufriedenstellend, und laden sogar zur Vermutung anderer Absichten ein.
Moin Markus,
leider gehen die Links oben aktuell nicht …
OK, muss ich mir in den nächsten Tagen mal anschauen. Das müsste dann ja noch vom letzten Umzug der SciLogs übrig sein…