Was ist eine gute Maßeinheit?
BLOG: RELATIV EINFACH

 Ich habe bei meiner Schritt-für-Schritt-Einführung in die Spezielle Relativitätstheorie, “Einstein verstehen” (bislang erschienen: Teil 1, Teil 2) zwar bereits sehr elementar angefangen – mit Absicht, denn diese Einführung soll ja auch Leser mitnehmen, die nicht über weitergehendes physikalisches Vorwissen verfügen. In den Kommentaren kamen dann allerdings Fragen auf, die noch eine Ebene tiefer liegen und sich folgendermaßen zusammenfassen lassen: Was ist eigentlich eine gute Definition für eine Maßeinheit? Da ich das Thema spannend finde und es sich, wenn schon nicht als Hauptbeitrag, so doch als nützlicher Ergänzungstext für “Einstein verstehen” eignet, will ich der Frage hier nachgehen.
Ich habe bei meiner Schritt-für-Schritt-Einführung in die Spezielle Relativitätstheorie, “Einstein verstehen” (bislang erschienen: Teil 1, Teil 2) zwar bereits sehr elementar angefangen – mit Absicht, denn diese Einführung soll ja auch Leser mitnehmen, die nicht über weitergehendes physikalisches Vorwissen verfügen. In den Kommentaren kamen dann allerdings Fragen auf, die noch eine Ebene tiefer liegen und sich folgendermaßen zusammenfassen lassen: Was ist eigentlich eine gute Definition für eine Maßeinheit? Da ich das Thema spannend finde und es sich, wenn schon nicht als Hauptbeitrag, so doch als nützlicher Ergänzungstext für “Einstein verstehen” eignet, will ich der Frage hier nachgehen.
Einheiten
Vielleicht die wichtigste Eigenschaft der Naturwissenschaften ist, dass so viele ihrer Aussagen quantitativ formuliert werden können. Quantitative Beschreibungen sind (mit wenigen Ausnahmen) Vergleiche mit Hilfe von Zahlen, etwa die Aussage, dass Usain Bolt 2009 bei den Weltmeisterschaften in Berlin für seinen 100-Meter-Lauf nur 0,987 Mal soviel Zeit gebraucht hat wie Tyson Gay. Allerdings sind solche Vergleiche recht speziell. Der Faktor 0,987 sagt mir noch nichts darüber, wie schnell Bolt im Vergleich zu Tyson Gays Leistung bei den Weltmeisterschaften 2007 in Osaka gelaufen ist. Um möglichst weitgehende Vergleichbarkeit solcher quantitativen Aussagen zu ermöglichen, ist es sinnvoll, sich auf Maßeinheiten zu einigen.
Tatsächlich bedeutet messen im technischen Sprachgebrauch, mit einer Einheit zu vergleichen. Dass Usain Bolt 2009 in Berlin die 100 Meter in 9,58 Sekunden gelaufen ist, bedeutet, dass die Dauer seines Sprints das 9,58fache der im Internationalen Einheitensystem (Système International d’unités, daher abgekürzt zu SI) definierten Einheit “Sekunde” betrug. Da das Ergebnis in Tyson Gays Lauf 2007 in der gleichen Einheit ermittelt wurde (9,85 Sekunden), ist es einfach, diese zwei ganz unterschiedlichen 100-Meter-Läufe zueinander in Beziehung zu setzen.
Aber was ist eine “gute Maßeinheit”? Was heißt in diesem Zusammenhang “gut” oder, anders ausgedrückt: Welche Eigenschaften sind bei einer Einheitendefinition wünschenswert? Das ist die Schlüsselfrage der Metrologie, der Wissenschaft vom Messen und von den Maßeinheiten.
Konstanz und Reproduzierbarkeit
Entscheidende Eigenschaft einer Einheit ist, dass sie bezüglich der zu messenden physikalischen Größe konstant ist: Eine Längeneinheit muss eine konstante Länge haben, eine Zeiteinheit eine konstante Zeitdauer, eine Masseeinheit eine konstante Masse, und so weiter. Wenn wir nicht davon ausgehen könnten, dass die zur Messung herangezogene Sekunde beim 100-Meter-Lauf in Osaka die gleiche Sekunde war wie in Berlin, dann wäre die allgemeine Vergleichbarkeit, die doch gerade den entscheidenden Nutzen von Maßeinheiten ausmacht, futsch.
Auf den ersten Blick könnte man denken, die Konstanz einer Einheit stelle sich automatisch ein, sobald man die Definition einmal getroffen hat. Schließlich ist die Einheit das Bezugsmaß, mit dem die betreffende Größe überhaupt erst gemessen wird. Ein Meter ist trivialerweise zu jedem Zeitpunkt einen Meter lang. Spätestens auf den zweiten Blick wird dagegen klar, dass es um etwas anderes geht.
Nehmen wir als Beispiel die letzte Maßeinheit des Internationalen Systems (SI), die noch durch ein bestimmtes Objekt, in der Sprache der Metrologie eine “Maßverkörperung” bzw. einen “Referenzkörper”, definiert wird: das Kilogramm. Die Masse “1 Kilogramm” ist die Masse des im Internationalen Büro für Maß und Gewicht in Paris aufbewahrten Urkilogramms, eines Zylinders aus einer Platin-Iridium-Legierung.
Verändert sich die Masse des Urkilogramms mit der Zeit? Logischerweise hat das Urkilogramm zu jedem Zeitpunkt genau so viel Masse wie es selbst, in diesem Sinne also: eine Masse von einem Kilogramm. Doch die Frage danach, ob sich die Masse des Urkilogramms verändert, ist ja eine etwas andere: Wenn wir das Urkilogramm jetzt und das Urkilogramm, wie es vor einem Jahr war, zusammen auf die Waage legen könnten, würde sich dann ein Unterschied zeigen? Direkt können wir diese Frage nicht beantworten – wir können schließlich schwerlich eine Zeitreise machen, um das Urkilogramm zu einem direkten Vergleich mit einer früheren oder einer zukünftigen Version seiner selbst heran zu holen.
Wir können allerdings ausnutzen, dass es Zwillinge des Urkilogramms gibt, zum einen solche, die genau so konstruiert sind wie das Urkilogramm, zum anderen solche, die aus anderen Materialien bestehen bzw. eine andere Form haben, aber ebenfalls konstante Masse besitzen sollten. Viele Nationen besitzen eigene Kilogramm-Exemplare als Grundlage der Massenbestimmung im eigenen Land; diese nationalen Exemplare reisen in unregelmäßigen Abständen nach Paris, um mit dem Urkilogramm verglichen zu werden. Sowohl das internationale Büro in Paris wie auch die nationalen Metrologie-Institute besitzen Sammlungen weiterer 1-Kilogramm-Objekte. (Soweit ich weiss, werden die Kilogrammkopien nicht nachträglich verändert; nach einer Vergleichsmessung wird lediglich notiert, um wieviele Bruchteile der Vergleichskörper vom Urkilogramm abweicht; kennt man diesen Zahlenwert, dann lässt sich aus dem Kilogramm-Objekt die genaue Masse “1 kg” rekonstruieren.)
Die Massen des Urkilogramms und seiner diversen Kopien kann man mit Hilfe von Präzisionswaagen miteinander vergleichen. Die beste Prototypwaage der Physikalisch-Technischen Bundesanstalt – des nationalen Metrologie-Instituts für Deutschland – kann Kilogrammmassen mit einer Genauigkeit von weniger als 0,2 Millionstel Gramm vergleichen. Das entspricht einer relativen Genauigkeit von stolzen 0,2 Milliardsteln!
Zeigen sich bei diesen Vergleichsmessungen Abweichungen, dann könnte es natürlich im Prinzip sein, dass das Urkilogramm vollkommen unverändert geblieben ist, aber die verschiedenen Kopien z.B. ein paar Atome verloren oder dazugewonnen haben. Andererseits: Die physikalischen Eigenschaften eines Metallzylinders werden sich kaum ändern, nur weil er per internationalem Dekret zum Urkilogramm erklärt wurde. Man muss daher davon ausgehen, dass das Urkilogramm genau so Masse verliert oder gewinnt wie baugleiche Objekte, die unter vergleichbaren Bedingungen aufbewahrt werden.
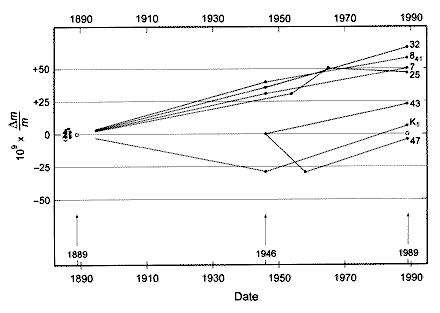
In der folgenden Grafik sind Massenänderungen verschiedener Urkilogramm-Kopien relativ zum Urkilogramm aufgetragen, die sich bei verschiedenen Vergleichsmessungen seit 1889 ergeben haben und von denen die Forscher bislang noch nicht wissen, wie sie zustandekommen:
 [Bild: BIPM-Webportal, Seite Verifications, abgerufen am 27.5.2011.]
[Bild: BIPM-Webportal, Seite Verifications, abgerufen am 27.5.2011.]
Vorsichtiger Weise sollte man davon ausgehen, dass sich die Masse des Urkilogramms mit der Zeit mindestens um einen Betrag verändert, der von derselben Größenordnung ist wie die Abweichungen, die sich beim Vergleich der Vergleichsobjekte untereinander und mit dem Urkilogramm zeigen. Aus solchen Vergleichsmessungen, im Fachjargon auch “Typ A-Messungen” genannt, lässt sich die Größenordnung der Veränderungen, mit denen man für das Urkilogramm rechnen sollte, abschätzen.
Bei Maßeinheiten, die nicht über einen künstlichen Referenzkörper definiert sind, kann man analog vorgehen. Bei einer früheren Definition der Sekunde mit Hilfe der Erdrotation beispielsweise nutzten die Astronomen die periodische Bewegung des Mondes um die Erde und der Planeten um die Sonne zu Vergleichsmessungen – und erhielten so tatsächlich Hinweise darauf, dass es ihrer gewählten Einheitendefinition an Konstanz mangelte!
Moderne Maßeinheiten wie Sekunde und Meter sind über die Eigenschaften von Licht definiert, das bei genau definierten Prozessen von bestimmten Atomsorten ausgesandt wird; eine Ergänzung, wie die Definition in die Praxis umzusetzen ist (ein “mise en pratique”) legt alle relevanten näheren Umstände des Experiments fest. So kann jedes hinreichend gut ausgerüstete Labor mit Hilfe geeigneter Experimente die Länge der Sekunde und des Meters rekonstruieren.
An die Stelle der Vergleiche verschiedener Referenzkörper tritt in diesem Falle der Vergleich unterschiedlicher Versionen des zur Definition verwandten Experiments, sei es innerhalb eines Labors, sei es zwischen verschiedenen Laboren: die genaue Reproduzierbarkeit der Maßeinheit.
Verstehbarkeit, Kontrollierbarkeit, Erforschbarkeit
Die erwähnten Vergleichsmessungen eines Referenzkörpers wie des Urkilogramms und seiner Kopien erlauben Rückschlüsse darauf, dass sich solche Körper ändern. Je nach Art der Änderung kann es allerdings durchaus sein, dass Vergleichsmessungen nur einen kleinen Teil der Änderungen anzeigen, die dort tatsächlich stattfinden. Angenommen, es handle sich um einen systematischen Prozess, in dem die betreffenden Kilogrammkörper sämtlich Masse verlieren, und zwar einige etwas schneller, andere etwas langsamer. Dann könnte die Vergleichsmessung lediglich nachweisen, dass der Masseverlust bei einigen der Körper etwas schneller, bei anderen etwas langsamer vor sich geht. Wieviel Masse diese Körper insgesamt verlören, bliebe den Vergleichen dagegen verborgen.
Anders gesagt: Wenn das Urkilogramm und seine Kopien alle pro Jahrzehnt jeweils 10 Tausendstel Gramm an Materie verlören (eine komplett fiktives Zahlenbeispiel), dann könnte kein Vergleich dieser Körper untereinander diesen Umstand nachweisen. Der Vergleich würde immer nur zeigen, dass jeder der Körper nach wie vor die gleiche Masse hätte wie die anderen.
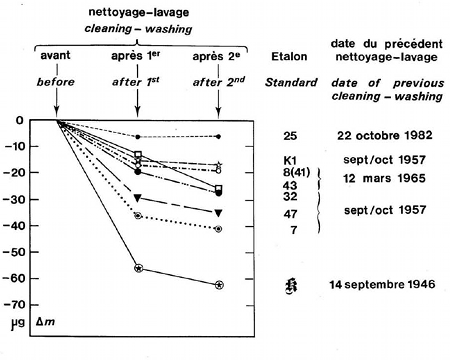
Weitergehende Aussagen können wir nur machen, wenn wir verstehen, was da vorgeht. Bereits ein ungefähres Verständnis kann weiterhelfen – ein Beispiel sind Verunreinigungen, die sich trotz aller Vorsichtsmaßnahmen auf dem Urkilogramm und seinen Kopien ansetzen und deren Masse vergrößern. Was da vorgeht, lässt sich verstehen, wenn man das Gewicht von Urkilogrammkopien vor und nach einer bestimmten Reinigungsprozedur vergleicht:
 [Bild: Abb. 15 aus G. Girard, The Washing and Cleaning of Kilogram Prototypes at the BIPM, BIMP 1990]
[Bild: Abb. 15 aus G. Girard, The Washing and Cleaning of Kilogram Prototypes at the BIPM, BIMP 1990]
Jede Kurve steht dabei für einen Urkilogramm-Zwilling; die Objekte sind rechts am Rand identifiziert (25, K1 usw.). Angegeben ist jeweils der Massenverlust in Millionstel Gramm (Mikrogramm, µg) nach dem ersten und dem zweiten Reinigungsschritt. Die Reinigungen wurden zu Beginn des dritten Abgleichs des Urkilogramms mit den nationalen Referenzkopien vorgenommen (der Abgleich fand von 1989 bis 1992 statt). Ganz rechts steht für jeden der Körper, wann er zuvor das letzte Mal gereinigt worden war.
Offenbar verlieren die Kilogrammkopien beim Reinigen an Masse; wie zu erwarten im ersten Reinigungsschritt mehr als im zweiten. Außerdem ist der Masseverlust umso größer, je mehr Zeit seit der letzten Reinigung vergangen ist. Am meisten Masse hat beim Reinigen das Urkilogramm (Frakturbuchstabe k) verloren, das zuletzt beim vorangehenden derartigen internationalen Vergleich 1946 gereinigt worden war.
Diese Zusammenhänge zeigen an, was dort vor sich geht: An den Kilogramm-Körpern lagern sich Verunreinigungen ab; die Ablagerungsraten kann man aus der obigen Grafik abschätzen. Durch Reinigen lassen sich die Ablagerungen weitgehend entfernen. Ist der Effekt einigermaßen verstanden, kann man ihn berücksichtigen, in diesem Falle: Sollen Abweichungen von weniger als einigen Dutzend Mikrogramm ausgeschlossen werden, dann reinigen die Metrologen die Kilogrammkörper vor dem Vergleichen, einer genau festgelegten Prozedur folgend.
Das Beispiel zeigt eine weitere Eigenschaft guter Maßeinheiten: Sie sollten so definiert sein, dass die betreffenden Wissenschaftler die so definierte Einheit und mögliche Störeinflüsse möglichst genau verstehen. Das Beispiel zeigt allerdings auch, dass ein konkretes Referenzobjekt es erschwert, Störeinflüsse und Variationen gezielt und systematisch zu erforschen. Das Objekt soll ja so ungestört und unbeeinflusst aufbewahrt werden wie möglich. Unter diesen Bedingungen ist es noch nicht einmal möglich, eine winzige Materialprobe zu nehmen und zu untersuchen!
Sind die Störeinflüsse bekannt, dann wird man selbstverständlich alles so einzurichten versuchen, dass die Einheitendefinition davon so weit wie irgend möglich unbeeinflusst bleibt.
Beim Prototyp für die (inzwischen veraltete) Definition des Meters beispielsweise, dem Urmeter, wurde der Querschnitt so gewählt, dass sich der Stab beim Messvorgang möglichst wenig in sich verdrehen kann; die Legierung, 90% Platin und 10% Iridium, wurde nach den Kriterien hoher Härte und Korrosionsbeständigkeit und geringer Elastizität gewählt. (Das Ausdehnungsverhalten bei verschiedenen Temperaturen spielte bei der Materialwahl keine wichtige Rolle; stattdessen hat man eine Ablesetemperatur festgeelgt: 0 Grad Celsius.)
Die Definitionen von Maßeinheiten mit Hilfe von Laborexperimenten und die ergänzenden Durchführungsbestimmungen “mise en pratique” werden ebenfalls so gewählt, dass alle bekannten Störeinflüsse so weit wie möglich unterdrückt werden; gibt es an irgendeiner Stelle Auswahlmöglichkeiten, wie eine bestimmte Messung durchgeführt werden kann, wird man immer dasjenige Verfahren empfehlen, das am wenigsten anfällig gegenüber Störungen ist und die genaueste Reproduzierbarkeit verspricht.
Verfügbarkeit
Maßeinheiten sind nur dann nützlich, wenn sie möglichst allgemein zugänglich sind. Sie sollen ja gerade Vergleichbarkeit sicherstellen – die Physiker in Hamburg sollen Ergebnisse Ihrer Experimente, die sie mit Hilfe von Maßeinheiten ausgedrückt haben, ohne Schwierigkeit mit den Ergebnissen der Kollegen in Boston vergleichen können, und ein über Maßeinheiten festgelegter Standard soll dazu führen, dass die CD-Spieler-Hersteller in China CD-Spieler herstellen können, auf denen sich in Japan gebrannte CDs abspielen lassen.
Frühe Längeneinheiten waren zumindest näherungsweise so definiert, dass jedermann sie ohne großen Aufwand nachvollziehen konnte: die Elle, definiert über die Länge eines Unterarms, ist zumindest grob für jeden Menschen anhand seines eigenen Körpers nachvollziehbar; gleiches gilt für die (Hand-)Spanne oder den Fuss.
Allerdings war das natürlich keine sehr genaue Definition, da Körpermaße von Mensch zu Mensch gehörig variieren; beim Zoll wurde stattdessen versucht, die Definition zu präzisieren als die durch drei hintereinander gelegte Gersternkörner definierte Länge, wobei jedes der Gerstenkörner rund und trocken zu sein habe. Immer mehr setzten sich dann allerdings konkrete Referenzkörper durch; Kopien davon konnte man hinreichend allgemein zugänglich machen, indem man sie beispielsweise an öffentlichen Orten aufhing:

[Bild: M. Schweiss. Gefunden auf Wikimedia Commons]
Mit Vereinheitlichung der Maße wurden die Referenzkörper allerdings immer weniger gut zugänglich, denn zumindest das Original ist ja jeweils nur an einem einzigen Ort untergebracht. Ist es aus irgendwelchen Gründen nicht zugänglich, so haben die Metrologen ein Problem. Beispielsweise kam einem der internationalen Vergleiche des Urkilogramms mit seinen Kopien der II. Weltkrieg in die Quere.
Definitionen, die auf Naturgesetzen und Naturkonstanten beruhen, etwa die erwähnten Definitionen von Meter und Sekunde mit Hilfe der Eigenschaften von Licht, vereinen hohe Verfügbarkeit mit hoher Präzision. Sie sind für jedes hinreichend gut ausgestattete Physiklabor direkt reproduzierbar – ein weiterer großer Vorteil dieser Art von Definition.
Beständigkeit
Sicher, es ist sehr unwahrscheinlich, dass ein Flugzeug auf das Internationale Büro für Maße und Gewichte stürzt, oder dass eine andere Katastrophe das Urkilogramm beschädigt. Und selbst wenn, dann sollte es gelingen, diese Masse mit Hilfe der existierenden Kopien ungefähr zu rekonstruieren. Dennoch dürfte den meisten Metrologen auch im Hinblick auf die Robustheit und Beständigkeit nicht ganz wohl dabei sein, eine Maßeinheit an ein bestimmtes Objekt zu binden.
Hier können Definitionen, die auf Naturgesetzen und Naturkonstanten beruhen, einmal mehr punkten. Solange unsere wissenschaftliche Tradition nicht durch eine weltweite Katastrophe komplett unterbrochen wird, werden uns Maßeinheiten, die jedes hinreichend ausgerüstete Laboratorium reproduzieren kann, erhalten bleiben.
Technische Anforderungen
 Allein schon aus Gründen grundlagenforscherischen Ehrgeizes streben Metrologen nach immer höherer Präzision. Doch auch bei technischen Anwendungen geht der Trend hin zu immer höherer Genauigkeit. Dass Satellitennavigationssysteme heute auf Genauigkeiten von einigen Milliardstel Sekunden angewiesen sind, oder dass industrielle Standards für in jedem Haushalt verfügbare Massenware wie CDs für bestimmte Größen Genauigkeiten von Zehnmillionstel Metern vorgeben werden (z.B. 11.3 im ECMA-Standard 130) dürfte sich vor hundert Jahren noch niemand träumen gelassen haben. Klar ist, dass jede Einheit mindestens so genau definiert sein muss, wie es die Anwendungen in Alltag, Industrie und Handel (vgl. z.B. den Kaarls-Report) erfordern. Und die erwähnten Beispiele GPS und CD/DVD zeigen, dass es sich lohnen kann, die Präzision vorausschauend noch merklich höher zu wählen.
Allein schon aus Gründen grundlagenforscherischen Ehrgeizes streben Metrologen nach immer höherer Präzision. Doch auch bei technischen Anwendungen geht der Trend hin zu immer höherer Genauigkeit. Dass Satellitennavigationssysteme heute auf Genauigkeiten von einigen Milliardstel Sekunden angewiesen sind, oder dass industrielle Standards für in jedem Haushalt verfügbare Massenware wie CDs für bestimmte Größen Genauigkeiten von Zehnmillionstel Metern vorgeben werden (z.B. 11.3 im ECMA-Standard 130) dürfte sich vor hundert Jahren noch niemand träumen gelassen haben. Klar ist, dass jede Einheit mindestens so genau definiert sein muss, wie es die Anwendungen in Alltag, Industrie und Handel (vgl. z.B. den Kaarls-Report) erfordern. Und die erwähnten Beispiele GPS und CD/DVD zeigen, dass es sich lohnen kann, die Präzision vorausschauend noch merklich höher zu wählen.
Einfache Messpraxis
Bei allen Anforderungen an die Präzision gilt: Je weniger aufwändig es ist, mit Hilfe der Maßeinheit konkrete Messungen durchzuführen, umso günstiger. Bei der von 1956 bis 1967 gültigen Definition der Sekunde, die die Mondbewegung als natürliche Uhr heranzog, dauerte es rund fünf Jahre, um die Maßeinheit Sekunde alleine aufgrund von Beobachtungen des Mondes mit hinreichender Genauigkeit zu rekonstruieren. Die moderne Definition der Sekunde anhand von Laborexperimenten erreicht binnen Minuten eine größere Genauigkeit.
Dass die Messung durch Fachleute mit entsprechender Ausrüstung durchgeführt werden muss, dürfte, wenn es um Präzisionsmessungen gibt, unvermeidlich sein; nur sollte man es zumindest diesen Fachleuten so einfach wie möglich machen.
Definitionen mit Hilfe von Naturgesetzen und Naturkonstanten
All diese Anforderungen zusammen haben in den letzte Jahrzehnten zu einem eindeutigen Trend bei der Definition von Maßeinheiten geführt. Möglichst einfache Situationen herzustellen, möglichst einfache Systeme zu präparieren, deren grundlegende Eigenschaften möglichst vollständig zu beschreiben und alle Störeinflüsse soweit wie möglich auszuschließen – das ist die Arbeitsweise der Experimentalphysik (und anderer experimenteller Wissenschaften).
Aus entsprechenden Experimenten und ihrer theoretischen Beschreibung hat sich das moderne physikalische Bild der Welt entwickelt, mit grundlegenden Naturgesetzen, die sich in der Sprache der Mathematik formulieren lassen. Vielleicht die wichtigste physikalische Erkenntnis ist, dass die Materie, mit der wir es hier auf der Erde zu tun haben, die wir im Alltag und in der Industrie verwenden, ebenso wie die Materie, deren Licht wir aus den Tiefen des Alls auffangen, aus Atomen besteht. Die Atome wiederum bestehen aus Elementarteilchen: ihre Kerne aus Neutronen und Protonen, ihre Hüllen aus Elektronen. Atome, Atomsysteme und ihre Eigenschaften sind in unzähligen Experimenten hochpräzise erforscht worden – von der Grundlagenforschung bis hin zu vielfältigen Anwendungen wie Transistoren und Laser.
Die Erforschung der grundlegenden Eigenschaften der Materie hat auch gezeigt, welche einfachen Materiesysteme für die genaue Definition von Maßeinheiten besonders geeignet sind. Die Wellenlängen eng definierter Frequenz beispielsweise, die Atome bei so genannten Spektrallinien aussenden, werden direkt durch einfache Eigenschaften des Atoms bestimmt – die Anzahl von Neutronen, Protonen und Elektronen, aus denen das Atom besteht –, wie sie von äußeren Umständen (z.B. äußeren Magnetfeldern) abhängen, ist gut erforscht, die äußeren Umstände sind gut kontrollierbar, und es sind hochpräzise Verfahren bekannt, diese Wellenlängen zu messen.
Ein Prototyp aus Metall ist im Vergleich mit einfachen Atomsystemen ein hochkomplexes Gebilde: Eine Legierung, also Gemisch aus einer Vielzahl von Atomen, wobei nicht exakt bekannt ist, in welcher Zahl welche Isotope (sprich: welche Atome mit einer bestimmten Neutronen- und Protonenzahl im Atomkern) darin vertreten sind; die Atome sind typischer Weise zu kleinen Kristallen zusammengesetzt, die sich wiederum in unübersichtlicher Weise zum eigentlichen Festkörper verbinden; zusätzlich können noch weitere Moleküle, z.B. von Gasen, im Festkörper eingeschlossen sein. All das macht z.B. das Urkilogramm zu einem nur schwer kontrollierbaren Objekt. Könnte es sein, dass darin eingeschlossene Gase mit der Zeit aus dem Festkörper entkommen? Rührt von solchen oder ähnlichen Effekten die relativ zu den meisten Urkilogramm-Kopien schrumpfende Masse (s.o.) her?
Konstanz bzw. Reproduzierbarkeit, daraus abgeleitete Kriterien wie Verstehbarkeit und Kontrollierbarkeit, um Störeinflüsse einschätzen und vermeiden zu können, Verfügbarkeit, Robustheit, den technischen Anforderungen genügbare Genauigkeit und dabei doch möglichst einfache Messpraxis – das haben wir als Wunschzettel für eine gute Einheitendefinition herausgearbeitet, und an diesen Kriterien orientiert hat die für die Definition von Maßeinheiten zuständige internationale Konferenz, die Generalkonferenz für Maß und Gewicht, mittlerweile so gut wie alle Definitionen des internationalen Einheitensystems an einfache physikalische Systeme geknüpft, deren Eigenschaften idealerweise nur von den Naturgesetzen und Naturkonstanten abhängen.
Jedem Wechsel von einer alten zu einer neuen Definition sind dabei jahrelange Tests vorausgegangen; eine neue Definition wurde jeweils nur eingeführt, wenn sichergestellt war, dass sie im Rahmen der mit der alten Definition erreichbaren Genauigkeit mit der alten Definition übereinstimmte. Wie schon erwähnt ist die letzte Definition, die noch an ein konkretes Objekt gebunden ist, das Kilogramm. Aber es ist zu erwarten, dass sich auch das in naher Zukunft ändert: Noch 2011 tagt die nächste Generalkonferenz, und es ist zu erwarten, dass sie die eine neue Definition des Kilogramms einführt, die dann ebenso nur noch von Naturgesetzen und Naturkonstanten abhängt.
Wie die Entwicklung der Definitionen für die grundlegenden Einheiten verlaufen ist, ist eine Geschichte für sich; die verdient dann aber einen eigenen Blogbeitrag.
Wie bei den Hauptkapiteln von “Einstein verstehen” soll auch für diesen Beitrag gelten: Veränderungen dieses Texts, die sich im Laufe der Zeit z.B. aus der hier geführten Diskussion ergeben, werde ich direkt umsetzen; der originale Entwurf bleibt zum Vergleich auf einer zu diesem Blogeintrag gehörigen Hintergrundseite erhalten.


Handle nur nach derjenigen Maxime …
Markus Pössel schrieb (30. Mai 2011, 22:30):
> Vielleicht die wichtigste Eigenschaft der Naturwissenschaften ist, dass so viele ihrer Aussagen quantitativ formuliert werden können.
Ja, das ist wichtig.
(Viele wichtige Messoperatoren haben reelle Zahlen als Eigenwerte.)
Ebenfalls wichtig sind natürlich qualitative Aussagen.
(Viele wichtige Messoperstoren haben Boolesche Werte als Eigenwerte.)
> Dazu benötigt man gut definierte Einheiten
Nein: quantitative Aussagen oder Feststellungen sind invariant bezüglich der Auswahl irgendwelcher Einheiten.
> Dass Usain Bolt 2009 in Berlin die 100 Meter in 9,58 Sekunden gelaufen ist, bedeutet, dass die Dauer seines Sprints das 9,58fache der im Internationalen Einheitensystem (Système International d’unités, daher abgekürzt zu SI) definierten Einheit “Sekunde” betrug.
Richtig
(so weit z.B. auch
http://www.associatedcontent.com/…rd_at_958.html
weiß;
und wobei sich natürlich versteht, dass dabei nicht Usain Bolts eigenliche Dauer seines Sprints betrachtet wird,
sondern die Dauer der Zieluhr von ihrer Anzeige gleichzeitig zur Startanzeige des Startblocks bis zu ihrer Anzeige des Zieldurchlaufes).
Nicht weniger quantitativ und richtig sind die Aussagen, dass die Dauer (im beschriebenen Sinne) von Usain Bolts Sprint das
9,58 / 9,71 =~= 0,987 -fache
der Dauer von Tyson Gays Sprint (beim selben Rennen) war, oder das
9,58 / 9,84 =~= 0,974 -fache
der Dauer von Tyson Gays Sprint (beim selben Rennen), oder das
9,58 / (2,197 D-6) =~= 436000 -fache der mittleren Lebensdauer von Myonen, oder …
> messen heißt, mit einer Einheit zu vergleichen.
Nein: Messen heißt, quantitativ oder qualitativ bewerten
(durch Anwendung eines Messoperators auf gegebene Beobachtungsdaten).
Um auch mal einige besonders wichtige Messgrößen mit Booleschem Wertebereich zu nennen:
– gegenseitige Ruhe (entsprechend dem Messoprator, durch dessen Anwendung z.B. festgestellt werden kann, ob ein gegebener Startblock und eine gegebene Zieluhr zueinder ruhten, oder nicht), und
– Gleichzeitigkeit (entsprechend dem Messoprator, durch dessen Anwendung z.B. festgestellt werden kann, ob eine bestimmte gegebene Anzeige einer gegebenen Zieluhr gleichzeitig zur Startanzeige eines gegebenen Startblocks war, oder nicht).
> Verstehbarkeit, Kontrollierbarkeit, Erforschbarkeit
> […] einer genau festgelegten Prozedur folgend.
Das ist entscheidend:
eine genau und nachvollziehbar festgelegte Prozedur bzw. Messoperation kann kopiert werden;
man kann entscheiden, in welchen (gültigen) Versuchen sie wiederholt gleich durchgeführt bzw. angewandt wurde, und in welchen (ungültigen) nicht.
Je zwei gegebene unterscheidbare “Referenzobjekte“, “Körper“, “Prototypen” oder Artefakte welcher Art auch immer sind a priori verschieden;
man mag allenfalls (Versuch für Versuch) messen, ob oder in wie fern sie einander gleich waren.
Antwort von MP: Vielleicht mal die offizielle Definition von “messen” nachlesen? Z.B. hier paraphrasiert. Streng nach Norm: DIN 1319.
Wie würde denn ein Vergleich der Laufzeiten zweier hundert-Meter-Läufer praktisch aussehen, ohne Umweg über eine Messeinheit? Beim Vergleich zweier Längen kann ich mir noch physikalische Umsetzungen von geometrischen Konstrukten vorstellen, auch wenn die wahrscheinlich wieder der ad-hoc-Konstruktion einer Einheit entspräche, aber wie sieht es bei den Laufzeiten aus?
Nachtrag von MP: Ich habe den entsprechenden Absatz jetzt noch etwas angepasst. Danke für die hilfreichen Anregungen, auch wenn ich einer Reihe Ihrer Aussagen nicht zustimmen kann!
p.s.
> […] dass die Dauer (im beschriebenen Sinne) von Usain Bolts Sprint das
> 9,58 / 9,71 =~= 0,987 -fache
> der Dauer von Tyson Gays Sprint (beim selben Rennen) war, oder das
> 9,58 / 9,84 =~= 0,974 -fache
> der Dauer von Tyson Gays Sprint (beim selben Rennen) war
Sollte sein:
[…] das
9,58 / 9,84 =~= 0,974 -fache
der Dauer von Asafa Powells Sprint (beim selben Rennen)
.
… was ist mit den Planckeinheiten?
Vielen Dank für den sehr erhellenden Artikel.
Ich hätte eine wahrscheinlich dumme, mit Sicherheit aber höchst laienhafte Frage: Warum benutzt man als Grundlage der gängigen Maßeinheiten nicht gleich die Planck-Einheiten, die doch gewissermaßen “von der Natur vorgegeben” sind, indem man zum Beispiel definiert ein Meter sei x Planck-Längen. Hätte dies nicht den Vorteil, dass zumindest die grundlegenden Einheiten frei von Willkür sind? Ist es vielleicht deshalb nicht möglich, weil Messungen in planckschen Maßstäben derzeit technisch nicht durchführbar sind, oder wäre eine solche Konstruktion der Maßeinheiten auf Grundlage der Planck-Einheiten prinzipiell unmöglich (etwa weil das Operieren mit den Planck-Einheiten selbst vorher definierter Einheiten bedarf)?
Antwort von MP: Die Frage ist weder dumm noch laienhaft – aus Sicht der theoretischen Physik sind solche Einheiten tatsächlich eine sehr natürliche Wahl. Das Hauptproblem ist in der Tat die technische Durchführbarkeit. Die Metrologen prüfen bei neuen Definitionen, die auf Naturgesetzen oder -konstanten beruhen, sehr gründlich, wie präzise sich die entsprechenden Messungen durchführen lassen. Das beste Beispiel ist vielleicht die anstehende Neudefinition des Kilogramms: Für die allermeisten theoretischen Physiker dürfte lange schon eingeleuchtet haben, dass eine Definition über das n-fache der Masse von Atomen eines bestimmten Isotops der Definition über einen einzigartigen großen Festkörper wie das Urkilogramm überlegen ist. Aber für die praktische Umsetzung fehlte eben bisher (das ändert sich ja gerade) der Nachweis, dass man soviele Atome auch in der Praxis genau genug abzählen kann.
@Markus Pössel
Oh, oh, wenn Frau Lopez das liest:
Ruhelänge oder nicht? Relativistisch sind bei einer Längenmessung gewisse Umstände der Messung schon relevant, denn bei einem Wechsel des Bezugssystems sind die jeweils gemessenen Werte über eine Lorentz Transformation miteinander zu vergleichen, die i.a. den Messwert nicht erhält. Die gegebene Formulierung könnte sich womöglich als ein Assist für Ihre ganz spezielle Freundin erweisen…
Antwort von MP: Noch allgemeiner; da müssen wir gar nicht relativistische Größen bemühen. Die Länge, die da gemessen wird, kann sich ja durchaus verlängern oder verkürzen, z.B. weil sich da eine Feder dehnt oder staucht. Aber ich sehe das potenzielle Missverständnis und schaue, ob ich mich da noch klarer ausdrücken kann.
Nachtrag von MP: Ich habe jetzt das Thema “100-Meter-Lauf” noch weiter durchgezogen und hoffe, dass jetzt klarer ist, worum es bei der Konstanz der Einheit geht. Danke für den Hinweis!
We must be able to tell our friends …
MP schrieb (nach 31.05.2011 | 04:58):
> [Frank Wappler schrieb: Messen heißt, quantitativ oder qualitativ bewerten
(durch Anwendung eines Messoperators auf gegebene Beobachtungsdaten).]
> Vielleicht mal die offizielle Definition von “messen” nachlesen? […] DIN 1319.
Na gut: in der normgerechten deutschen Industrie laufen die qualitativen Bewertung (durch Anwendung von Operatoren mit Booleschem Wertebereich) unter dem Begriff “Prüfen”.
Ansonsten wäre hier wohl eine pfiffig-schneidige Bemerkung von John A. Wheeler angebracht, mit besonderer Würdigung von “which way measurements” …
> Wie würde denn ein Vergleich der Laufzeiten [Dauern] zweier hundert-Meter-Läufer praktisch aussehen, ohne Umweg über eine Messeinheit?
Etwa so, wie ein Vergleich der Dauer eines Laufes mit der Dauer einer bestimmten Anzahl (sagen wir: 10^11) von Perioden irgendeines bestimmten Oszillators praktisch “aussieht” …
Sofern die Praxis so weit geht, dass der richtige reelle Verhältniswert dieser Dauern gar nicht strikt gemessen wird (durch Anwendung des definitionsgemäßen Messoperators der RT), sondern nur (“irgendwie anders”) abgeschätzt wird, dann gehört dazu auch die Bewertung des systematischen Vertrauensbereiches;
was natürlich trotzdem erfordert, die Definition des Messoperators festzulegen und zu berücksichtigen, auch wenn er nicht ausdrücklich zur Ermittlung des Messwertes eingesetzt wurde.
In der Praxis der Leichtathletik wird ja z.B. kaum gemessen, dass die Startanzeige des Startblocks gleichzeitig zur “Zeit-läuft”-Anzeige der Zieluhr gewesen wäre.
> […] ad-hoc-Konstruktion einer Einheit
Bei einem gemessenen reellwertigen Verhältnis zweier Dauern ist es vollkommen gleichgültig, ob die eine oder die andere als “Einheit” gewählt würde; wenn überhaupt.
> Danke für die hilfreichen Anregungen, auch wenn ich einer Reihe Ihrer Aussagen nicht zustimmen kann!
Danke für die Gelegenheit Anregungen geben zu können, bis Einvernehmen in denjenigen Aussagen hergestellt ist, in denen vernünftige Physiker (und solche, die es werden wollen) nicht differieren sollten.
p.s.
Wie kommt denn die Kommentar-Vorschau-Funktion voran? …
An das Wesentliche vorbei?
@ Dr. Markus Pössel
Ihre Ausführungen über eine gute Maßeinheit gehen meiner Meinung nach schon im ersten, einleitenden Absatz Ihres Blogtextes an das Wesentliche vorbei bzw. sind missverständlich und irreführend:
“Was ist eigentlich eine gute Definition für eine Maßeinheit?“
Eine Maßeinheit braucht keine Definition.
Eine Maßeinheit ist völlig willkürlich gewählt, ursprünglich hat man irgendeinen Gegenstand ausgewählt und als Maßeinheit erklärt, zum Beispiel einen Stock, einen Knochen, drei hintereinandergelegte Gerstenkörner oder auch einen Daum, einen Fuß, eine Elle, die breite einer gespreizter Hand, den Abstand zwischen den ausgestreckten Armen usw. Während der französischen Revolution haben französische Wissenschaftler den „Meter“ erfunden und als Maßeinheit festgesetzt. Das war ein Holzbalken und seine Länge sollte 1/40 Millionste des Erdumfangs darstellen. Ich sage die Definition auf Französisch, weil sie sprachlich so gut auswendig zu lernen ist und so wunderschön wissenschaftlich klingt, dass man es wohl nie vergisst: „la dix millionième partie du quart du méridien terrestre“.
Natürlich hat dieser Holzbalken nie und niemals genau das 1/40 millionste des Erdumfangs betragen, man hätte sich das Auswendiglernen und das Gefühl des wissenschaftlichen Wissens gerne sparen können. Kein Mensch hat je mit diesem Holzbalken den genauen Erdumfang gemessen, das ist auch nicht möglich, den Umfang der Erde auf ein Meter genau zu messen. Diesen Holzbalken hat ein Zimmermann angefertigt, er wurde „Meter“ genannt und er wurde als Maßeinheit der Länge erklärt. Punkt, fertig, mehr kann man darüber nicht sagen. Und mehr wäre auch nicht notwendig gewesen zu sagen, die Sache mit dem Erdumfang hätte man sich ruhig sparen können. Inzwischen wurde die Länge des Meters mehrmals geändert (zuletzt 1983, wo er verkürzt wurde), sowie seine Definition auch mehrmals geändert – was man sich genauso hätte sparen können wie mit dem Erdumfang.
Eine Maßeinheit braucht keine Definition, sie definiert sich selbst als Unikum mit ihrer physischen Ausdehnung, ihre physische Ausdehnung muß nur per Konvention als Maßeinheit erklärt und von allen anerkannt werden. Man könnte auch die Länge einer Cola-Dose „Meter“ nennen und sie als Maßeinheit erklären, das würde genauso gut funktionieren.
Das ist genauso für die Lichtgeschwindigkeit als Maßeinheit. Zum ersten Mal in der Geschichte der Maßeinheit „Meter“ wurde die Länge immateriell durch eine Relation festgesetzt, durch eine Geschwindigkeit, was zu vielen Verwirrungen geführt hat. Die Lichtgeschwindigkeit als Maßeinheit muß auch nicht eine richtige, gemessene Geschwindigkeit des Lichts entsprechen (man kann auch nicht eine Maßeinheit messen…), sie könnte genauso gut völlig erfunden werden, ihr Wert spielt hier gar keine Rolle, Hauptsache, sie wird per Konvention als Maßeinheit von allen anerkannt und dient durch Vergleich zur Quantifizierung von noch unbekannten Längen. Man hätte auch c=600.000.000 km/s als Maßeinheit festsetzen können, das würde genauso gut funktionieren – nur die Länge des Meters wäre halb so lang, man müsste eine Zeit lang umdenken, um unsere Umgebung räumlich abzuschätzen.
Die Lichtgeschwidigkeit als Maßeinheit muss nicht die richtige Geschwindigkeit des Lichts in der Natur sein, die willkürlich gewählte Geschwindigkeit bestimmt nur die physische Ausdehnung des Meters, mehr nicht.
Und bei der Bestimmung der physischen Ausdehnung des Meters ist das Bestreben sinnlos, die Maßeinheit mit einer Definition zu versehen, die die irrige Vorstellung suggeriert, man könne die Länge eines Objektes bis in seine molekulare oder atomare Struktur hinein messen. Das kann man nicht, auch wenn die Definition es mathematisch erlaubt. Diese Exaktheit ist eine Illusion, das ist lediglich eine trügerische mathematische Exaktheit und sie ist konkret bei einer Messung nicht realisierbar. Man degradiert dabei das Messen, das das Fundament der Physik darstellt, zu Mathematismus.
Auf diese aus meiner Sicht wichtige Problematik, die ich schon im „Blogteil I Einstein verstehen“ ausführlich und mehrfach angesprochen habe, sind Sie bis jetzt nicht eingegangen, auch in diesem separaten Blogtext über Maßeinheiten nicht, siehe meine Beiträge im Teil I:
Beiträge vom 20.05.11:
http://www.wissenslogs.de/…/page/6#comment-27065
http://www.wissenslogs.de/…/page/6#comment-27109
Beitrag vom 21.05.11:
http://www.wissenslogs.de/…/page/6#comment-27139
Könnten Sie hier in diesem speziell für Maßeinheiten eingerichteten Blog auf diese Problematik eingehen?
Viele Grüße
Jocelyne Lopez
Antwort von MP: Selbstverständlich braucht
eine Maßeinheit eine Definition. Auch das Auswählen eines
Gegenstandes, das Sie gleich darauf beschreiben, ist eine Definition;
irgendwie müssen Sie ja sagen (also definieren) worum es sich bei der
von Ihnen gewählten Maßeinheit handelt. Oder sind wir schon wieder bei
der Sprachklauberei gelandet, und Definition bedeutet für Sie etwas
ganz anderes als in diesem Zusammenhang allgemein üblich?
Warum es für die gewünschten Anwendungen in Technik und Physik
gute und weniger gute Definitionen gibt, lege ich im Blogbeitrag dann
ja ausführlich dar. Und beantworte nebenbei einige Fragen, die Sie in
früheren Kommentaren aufgeworfen hatten. Wenn Sie da anderer Ansicht
sind und das auch begründen können, dann könnten Sie ja mal auf das
eingehen, was ich da schreibe… nur mal so eine Idee. Bislang
jedenfalls scheinen Sie die vielen guten Gründe für den Übergang zur
neuen Meterdefinition von 1960 (die sich auch auf die Definition von
1983 übertragen lassen) schlichtweg zu ignorieren.
Darauf, dass Sie sich beim Material des Vor-Meters irren und dass der
Bezug auf die Erdausmaße durchaus politisch geschickt war, sind ja
schon andere Kommentatoren hier eingegangen. Zur angeblich
übertriebenen Genauigkeit: Die schon zitierte Genauigkeitsgrenze des
Platin-Iridium-Urmeters ist durchaus ungenauer als die Genauigkeit,
mit der z.B. die Standards bei der Fertigung von CDs definiert
sind. Und Physiker, die ja durchaus nicht nur die Längen materieller
Objekte messen wollen, sondern durchaus auch z.B. die Wellenlängen von
Licht, können durchaus auch mit genaueren Definitionen etwas
anfangen.
@Jocelyne Lopez
Auf Ihren Einwand, nach dem geltenden SI Standard würde mit unbegrenzter Genauigkeit gemessen, war am 21.05. auch eine Entgegnung erfolgt, falls Sie das meinen.
Die Länge des Meters wurde 1983 nicht verkürzt, woher haben Sie das denn?
“Eine Maßeinheit braucht keine Definition.” Wenn Sie das so sehen, dann macht das BIPM Ihrer Einschätzung nach doch etwas falsch, wenn dort beispielsweise von “la définition du mètre” die Rede ist. Dafür können Sie Dr. Pössel ausnahmsweise nicht verantwortlich machen, der Meter wurde ja aus Frankreich importiert.
Offenbar ist es Frau Lopez auch hier wieder nur daran gelegen, möglichst viel demagogischen Krawall zu veranstalten, mit dem Nebenziel, Herrn Dr. Pössel Zitate für ihre persönliche Hasskampagne gegen die SRT, Einstein und die moderne Wissenschaft allgemein zu entlocken.
Wäre ihr Ziel wirklich Erkenntnis, so hätte sie den Text dieses Blogeintrages gelesen. Ihr Kommentar zeugt vom kompletten Gegenteil, denn genau die Notwendigkeit einer Definition wird sehr schön herausgearbeitet.
Man misst nicht mit einer Definition
@ Chrys
“Eine Maßeinheit braucht keine Definition.” Wenn Sie das so sehen, dann macht das BIPM Ihrer Einschätzung nach doch etwas falsch, wenn dort beispielsweise von “la définition du mètre” die Rede ist. Dafür können Sie Dr. Pössel ausnahmsweise nicht verantwortlich machen, der Meter wurde ja aus Frankreich importiert.“
Damit sollte gezeigt werden, dass die Definition einer Maßeinheit keine Bedeutung für eine konkrete Messung hat, sondern einzig die physische Ausdehnung des Urmaßstabes als ausgewähltes Unikum eine Bedeutung für eine konkrete Messung hat.
Wenn ich damals als Schülerin im Unterricht gefragt wurde „Was ist ein Meter?“ kann ich mir gut vorstellen, dass ich brav geantwortet habe: „Un mètre est la dix-millionième partie du quart du méridien terrestre“, ein Meter ist 1/40 Millionste des Erdumfangs, und ich kann mir auch gut vorstellen, dass ich als Beurteilung der Lehrerin gehört habe: „Très bien“, Sehr gut. Die richtige Antwort wäre aber gewesen: “Ein Meter ist die Länge eines Holzbalkens, der im Bureau International des Poids et Mesures als Urmaßstab aufbewahrt wird“.
Zitat Chrys:
“Die Länge des Meters wurde 1983 nicht verkürzt, woher haben Sie das denn?“
Der Wert der Lichtgeschwindigkeit, der als Maßstab gewählt wurde, wurde 1983 aus mehreren Messungen der Lichtgeschwindigkeit gemittelt und ergab 299 792 458,6, was abgerundet wurde um nicht unendlich viele Dezimalstellen zu schleppen – was ohnehin schon der Fall ist. Diese Abrundung bedeutet eine rechnerische Verkürzung des Meters, jedoch sie hat wiederum absolut keine Relevanz in der Realität: es handelt sich bei Dezimalstellen um eine rein mathematische Genauigkeit, die wie alle Dezimalstellen davor bei einer konkreten Messung sowieso physisch nicht realisierbar ist (siehe mein vorheriger Beitrag). Ein Gymnasialphysiklehrer hat mir jedoch in einem Forum erklärt, dass die Wissenschaftler, die mit Hochgenauigkeitsmessungen arbeiten, nicht erfreut über diese Verkürzung waren und dass sie sie beim Vergleich von Hochgenauigkeitsmessungen vor und nach 1983 umrechnen und berücksichtigen müssen. Ich weiß nicht ob das stimmt, dass diese Verkürzung bei Vergleichen berücksichtigt wird, sie ist wie gesagt sowieso völlig irrelevant für die Physik, sie ist nur trügerisch, mathematisch exakt.
Viele Grüße
Jocelyne Lopez
@Jocelyne Lopez
Welch vielfältige Überlegungen zur Praktikabilität bei der Festsetzung einer Einheit zu berücksichtigen sind, das ist am Beispiel des Kilogramms im Blogtext doch ausführlich dargelegt. Wenn es nach Ihnen ginge, dann könnte man einen beliebigen handlichen Stein irgendwo einsacken, beim BIPM ins Archiv legen, und fertig ist das Kilogramm. So läuft der Hase aber nicht.
Die revolutionären Franzosen hatten in den 1790er Jahren eher ganz andere Sorgen. Der Meter sollte nicht nur für Frankreich akzeptabel sein, sondern symbolisch gegeben durch die Erde selbst und nicht durch die Willkür einer nationalen Autorität. Diese Symbolik wirkt weiter fort bis in den Schulunterricht. Das darf man nicht separiert vom zeitgeschichtlichen Hintergrund sehen. — Der Urmeter von 1799 war übrigens aus Platin und nicht aus Holz.
Mit dem von Ihnen genannten Wert von 299 792 458,6 m/s wäre doch
1 Lichtsekunde = 299792458 Meter(1983) = 299792458.6 Meter(1960)
also, gerundet, 1 Meter(1983) ≈ 1.00000000200138457119 Meter(1960). Der neue Meter wäre dann sogar länger als der alte. Das macht aber faktisch nichts, denn der Meter(1960) war auf eine Genauigkeit von 0.01 μm/m begrenzt, d.h., alle weiteren Dezimalen sind unterhalb der Fehlerschranken und damit nicht signifikant. Der Meter(1983) gilt folglich nach dem Standard von 1960 offiziell als “1 Meter lang“, mit Stempel und Unterschrift vom Eichamt. Keine Verkürzung, keine Verlängerung. Die Metrologen rechnen schon nicht sinnlos mit irrelevanten Dezimalstellen herum, da können Sie völlig unbesorgt sein.
Man lügt sich in die eigene Tasche…
@ Chrys:
“Welch vielfältige Überlegungen zur Praktikabilität bei der Festsetzung einer Einheit zu berücksichtigen sind, das ist am Beispiel des Kilogramms im Blogtext doch ausführlich dargelegt. Wenn es nach Ihnen ginge, dann könnte man einen beliebigen handlichen Stein irgendwo einsacken, beim BIPM ins Archiv legen, und fertig ist das Kilogramm. So läuft der Hase aber nicht.“
Doch, so läuft der Hase bei dem Prinzip der Festlegung von Maßeinheiten, doch, doch. Und diesem Prinzip verdankt die Wissenschaft alle ihrer bisherigen technologischen Errungenschaften, und sie sind fantastisch.
Zitat Chrys:
“Mit dem von Ihnen genannten Wert von 299 792 458,6 m/s wäre doch
1 Lichtsekunde = 299792458 Meter(1983) = 299792458.6 Meter(1960)
also, gerundet, 1 Meter(1983) ≈ 1.00000000200138457119 Meter(1960). Der neue Meter wäre dann sogar länger als der alte. Das macht aber faktisch nichts, denn der Meter(1960) war auf eine Genauigkeit von 0.01 μm/m begrenzt, d.h., alle weiteren Dezimalen sind unterhalb der Fehlerschranken und damit nicht signifikant.“
Eine Geschwindigkeit ist eine mathematische Relation zwischen Länge und Zeitdauer. Es nützt absolut nichts, eine extrem feine Unterteilung der Zeitdauer durch die Wahl der Maßeinheit Zeit meßtechnisch und mathematisch zu ermöglichen, wenn diese extrem feine Unterteilung bei einer konkreten Messung von Längen nicht physisch realisierbar ist, und zwar bei Weitem nicht. Die Maßeinheit Länge kann nunmal in der Realität die extrem feine Unterteilung der Maßeinheit Zeit nicht folgen: Man kann die Länge eines Objektes nicht bis in seine molekulare oder atomare Struktur hinhein konkret messen, auch mit dem Licht nicht, da hilft nichts. Man lügt sich also in die eigene Tasche, wenn man eine extrem feine Unterteilung der Maßeinheit Zeit meßtechnisch gewährleistet, wenn die entsprechende extrem feine Unterteilung der Maßeinheit Länge nicht praktikabel ist (außer mathematisch).
Viele Grüße
Jocelyne Lopez
Kommentar von MP: Das ist jetzt so ein
bisschen das Äquivalent von sich-die-Ohren-zuhalten-und-“Lalala, ich
kann Sie nicht hören, ich kann Sie nicht hören”-singen, oder?
Ich habe in dem Blogbeitrag ja nun wirklich genau beschrieben,
welche Kriterien bei der Wahl einer Einheitendefinition eine Rolle
spielen. Diese Gründe ignorieren Sie bislang standhaft, und
versteifen sich stattdessen auf einen ziemlich kuriosen
Nebenschauplatz. Ach ja, und ursprünglich hatten Sie ja noch eine
Lanze für den Pt-Ir-Urmeter gebrochen. Haben Sie sich denn jetzt
zumindest mit der Neudefinition von 1960 anfreunden können? Die ja
sehr wohl praktische Relevanz hat?
Freie Wahl nur im Rahmen einer Defini~40
Jocelyne Lopez schrieb (03.06.2011 | 09:09):
> Eine Maßeinheit ist völlig willkürlich gewählt […]
Zweifellos kann man sich in bestimmten (technischen oder naturgegebenen) Anwendungsfällen praktischere oder unpraktischere Maßeinheiten vorstellen.
Zweifellos ist aber auch jeder bestimmte Messwert, der aus reeller Maßzahl (evtl. mit Angabe eines Vertrauensbereiches) und Angabe einer Maßeinheit besteht, invariant bzgl. der Wahl irgendeiner bestimmten Maßeinheit. Genau so wie der Wert eines bestimmten “Inneren Produktes” zweier bestimmter Elemente eines Vektorraumes invariant bzgl. der Wahl irgendeiner bestimmten Basis dieses Vektorraumes ist.
> Eine Maßeinheit braucht keine Definition, sie definiert sich selbst als Unikum mit ihrer physischen Ausdehnung, ihre physische Ausdehnung muß nur per Konvention als Maßeinheit erklärt und von allen anerkannt werden.
Aber: der Begriff “physische Ausdehnung” muss als nachvollziehbare Messgröße an sich definiert sein.
Im konkreten Fall der Messgröße “Distanz (zwischen zwei zueinander ruhenden Enden)” muss definiert sein, durch welche Messoperation das eine gegebene Unikum (mit zwei bestimmten erkennbaren “Enden”) mit irgendwelchen anderen Artefakten zu vergleichen wäre.
Es steckt also “Know-how” in der Wahl einer bestimmten Maßeinheit:
zuerst (und m. E. vor allem) in der Definition der Messgröße bzw. Messoperation, für die die Maßeinheit einen Eigenwert repräsentieren soll; also “physische Ausdehnung” bzw. “Distanz (zwischen zwei zueinander ruhenden Enden)” z.B. irgendeines Prototyp-Unikums, und nicht z.B. dessen “Masse” oder “Ladung” usw.
Und erst nachgeordnet (und insbesondere bei einer Einführung in die Spezielle Relativitätstheorie zweitrangig) sind weitere Überlegungen zur Praktikabilität.
Wie Einstein eine Länge gemessen hat
@ Frank:
“Aber: der Begriff “physische Ausdehnung” muss als nachvollziehbare Messgröße an sich definiert sein. […] Im konkreten Fall der Messgröße “Distanz (zwischen zwei zueinander ruhenden Enden)” muss definiert sein, durch welche Messoperation das eine gegebene Unikum (mit zwei bestimmten erkennbaren “Enden”) mit irgendwelchen anderen Artefakten zu vergleichen wäre.“
Wie die physische Ausdehnung eines zu messenden Objekts zu verstehen ist und mit welcher Messoperation man sie bestimmt ist schon lange in der Physik definiert. Nehmen wir zum Beispiel die Messoperation, die Albert Einstein selbst in seiner SRT von 1905 Seiten 895-896 (wir sind ja in einem Neben-Blog „Einstein verstehen“ ) die physische Ausdehnung eines Objekts bestimmt:
“Es sei ein ruhender starrer Stab gegeben; derselbe besitze, mit einem ebenfalls ruhenden Maßstabe gemessen, die Länge l.“
Was ist in dieser Messoperation undefiniert oder nicht nachvollziehbar?
Viele Grüße
Jocelyne Lopez
Haben Sie überhaupt kapiert, was Thema des Blogeintrages war, Frau Lopez?
Wie Synge gegenseitige Starrheit …
… gemessen hat
Jocelyne Lopez schrieb (05.06.2011 | 13:22):
> Nehmen wir zum Beispiel die Messoperation, [mit der] Albert Einstein selbst selbst in seiner SRT von 1905 Seiten 895-896 […] die physische Ausdehnung eines Objekts bestimmt:
>
> Was ist in dieser Messoperation undefiniert oder nicht nachvollziehbar?
Im Wesentlichen:
Wie wäre zu messen, ob ein gegebenes Paar Enden ob ein gegebenes Paar Enden zueinander “starr” war, oder nicht?
(Bzw. entsprechend der moderneren Auffassung des “Distanz”-Begriffes in der RT, ob ein gegebenes Paar Enden zueinander “ruhte”, oder nicht; ganz abgesehen davon, ob sie dabei zueinander “starr” waren, oder nicht.)
Denn sicherlich sind auch Paare von Enden auffindbar (oder zumindest vorstellbar), die nicht zueinander “starr” wären
(bzw. die nicht zueinander und zu weiteren Beteiligten “ruhten”, selbst falls sie zueinander “starr” gewesen wären).
Einem Paar Enden, die zueinander ruhten, und solang sie zueinander ruhten, kann man offenbar einen einvernehmlichen (Eigen-)Wert “physischer Ausdehnung” zuschreiben (mit Variablennamen “l“).
Außerdem,
sofern (lediglich) zwei Enden, die zueinander ruhten, noch nicht wirklich das ausmachen, was man “Maßstab” nennt:
Wie wären Distanzverhältnisse zwischen mehreren Paaren von beteiligten Enden bzw. Markierungen zu messen, die alle zueinander ruhten?
Und damit letztlich,
was auf die besonders bekannte Messoperation der SRT führt
(Stichwort “Sqrt[ 1 – β² ]”):
Wie wären Distanzverhältnisse zu messen, falls die zu vergleichenden Paare (jeweils von Enden, die zueinander ruhten) nicht insgesamt zueinander ruhten;
oder falls von einem bestimmten Paar seine “physische Ausdehnung nachher gegenüber vorher” zu vergleichen wäre, wobei die Enden “zwischendurch” nicht zueinander ruhten?
Jedenfalls finde ich solche Fragen erheblich relevanter zum Thema “Einstein verstehen” (oder auch: “RT verstehen”, deren Entwicklung mit Einsteins Arbeit von 1905 erst begann), als ingenieurmäßig-praktische Erwägungen bei der Wahl von Maßeinheiten.
Wie Einstein eine Länge gemessen hat
@ Frank:
“Wie wäre zu messen, ob ein gegebenes Paar Enden ob ein gegebenes Paar Enden zueinander “starr” war, oder nicht?
(Bzw. entsprechend der moderneren Auffassung des “Distanz”-Begriffes in der RT, ob ein gegebenes Paar Enden zueinander “ruhte”, oder nicht; ganz abgesehen davon, ob sie dabei zueinander “starr” waren, oder nicht.)
Denn sicherlich sind auch Paare von Enden auffindbar (oder zumindest vorstellbar), die nicht zueinander “starr” wären (bzw. die nicht zueinander und zu weiteren Beteiligten “ruhten”, selbst falls sie zueinander “starr” gewesen wären).
Einem Paar Enden, die zueinander ruhten, und solang sie zueinander ruhten, kann man offenbar einen einvernehmlichen (Eigen-)Wert “physischer Ausdehnung” zuschreiben (mit Variablennamen “l”).“
Nun, unser Bestreben heißt „Einstein verstehen“ und nicht „Synge verstehen“ (kenne ich nicht, nie gehört). Und Einstein hat eine Theorie, die die Physik und unser Weltbild revolutioniert haben soll mit dem Messen eines Objektes wie folgt:
“Es sei ein ruhender starrer Stab gegeben; derselbe besitze, mit einem ebenfalls ruhenden Maßstabe gemessen, die Länge l.“
Und ich erkenne dabei nichts, was hier undefiniert oder nicht nachvollziehbar sein sollte. Ich kann es zumindest sehr gut nachvollziehen.
Viele Grüße
Jocelyne Lopez
Auch gut …
Jocelyne Lopez (05.06.2011 | 22:02):
> “Es sei ein […] starrer Stab gegeben […]“
> Und ich erkenne dabei nichts, was hier undefiniert oder nicht nachvollziehbar sein sollte. Ich kann es zumindest sehr gut nachvollziehen.
Geht diese Erkenntnis nicht so weit anzuerkennen, dass es auch Paare von Enden gibt (oder zumindest geben könnte), die nicht zueinander starr waren?
Und dass (nicht zuletzt deshalb) zu fragen wäre, wie zu entscheiden wäre, welche Paare als “starrer Stab gegeben” waren, und welche nicht?
Wo ein Problem nicht erkannt wird, kann das, was (hier von der RT) als Lösung angeboten wird, natürlich nicht auf Verständnis stoßen …
> Nun, unser Bestreben heißt „Einstein verstehen“ und nicht „Synge verstehen“ (kenne ich nicht, nie gehört).
Auch gut — wer sich einbildet, dass Einsteins Arbeiten aus sich heraus nachvollziehbar wären (und gar sein Artikel Ann. Phys. 17, 891, für sich), der muss sich nicht um J. Synge kümmern.
Im Übrigen fühle ich mich dadurch gegenüber M. Pössel bestätigt
(vgl.
http://www.wissenslogs.de/…eil-i/page/1#comments ):
Der Begriff “gegenseitiger Ruhe”, so kompliziert er (im Rahmen der RT) auch ist, gilt jenen, die die RT noch zu lernen haben, oft als selbstverständlich und unkontrovers (und auch als austauschbar zum Begriff “gegenseitiger Starrheit”).
Man misst nicht mit einer Definition…
@ Dr. Markus Pössel:
“Selbstverständlich braucht eine Maßeinheit eine Definition. Auch das Auswählen eines Gegenstandes, das Sie gleich darauf beschreiben, ist eine Definition; irgendwie müssen Sie ja sagen (also definieren) worum es sich bei der von Ihnen gewählten Maßeinheit handelt”
Ja, sicher, ich muß ja sagen, ob es sich bei der von mir gewählten Maßeinheit um Meter, oder um Zoll, oder um Inch, oder um Ellen, oder um Kilometer, ober um Meilen usw. handelt. Ich muß schon sagen, um welche von mir gewählte Maßeinheit es sich handelt, ist schon ganz klar, gar kein Thema.
Aber muß ich für eine konkrete Messung wissen, welche Definitionen historisch für diese Maßeinheiten gewählt wurden? Muss ich wissen, ob ein Inch durch die Breite des Daumes des Königs Sowieso III. oder eher des Königs Sowieso IX. definiert wurde? Muss ich wissen, ob der Urmeter ursprünglich aus Holz oder aus Platin war? Muss ich wissen, ob der Meter durch 1/40 Millionsten des Erdumfangs oder eher durch einen langen Schritt definiert wurde? Nein, ich muss das alles nicht wissen und kein bisschen berücksichtigen, wenn ich eine Messung durchführe. Sie haben wieder die von mir angesprochene Problematik nicht verstanden bzw. haben wieder daneben geantwortet. :- (
Man misst nicht mit einer Definition, Herr. Dr. Pössel, sondern mit einem Maßstab. Verwechseln Sie etwa den Begriff “Definition” mit dem Gegenstand “Maßstab”? Kurios… Oder ist das jetzt von Ihnen so ein bisschen das Äquivalent von sich-die-Ohren-zuhalten-und-“Lalala, ich kann Sie nicht hören, ich kann Sie nicht hören”-singen, oder?
Einstein beschreibt zum Beispiel die Messung der Länge eines Objektes in der wichtigsten Theorie der Geschwichte der Physik und alles Notwendiges wurde dabei beschrieben und definiert: Ein starres Objekt, ein materieller Maßstab, ein Beobachter, die alle drei im Zustand der gegenseitigen Ruhe zueinander während der Messung stehen:
“Es sei ein ruhender starrer Stab gegeben; derselbe besitze, mit einem ebenfalls ruhenden Maßstabe gemessen, die Länge l.“
Noch einmal: Wo gibt es bei diesem Meßvorgang etwas Undefiniertes oder Unverständliches?
Wie könnte man in dieser wichtigen Theorie die Länge l durch die Wahl einer besseren Definition der ausgewählten Maßeinheit genauer messen?
Wird die Länge dadurch genauer gemessen, wenn der Maßstab mit dem 1/40 millionste des Erdumfang definiert wird, oder durch die Länge des Fußes von König Sowieso III. oder lieber mit der Definition des Meters von 1960 oder lieber mit der von 1983? Welche Definition erlaubt Ihrer Meinung nach eine genauere Messung der Länge l des starren Stabes, wovon Einstein in seiner SRT spricht?
Viele Grüße
Jocelyne Lopez
Antwort von MP: Die Definition einer Maßeinheit umfasst genau die Informationen, die nötig sind, um die Maßeinheit festzulegen – nicht mehr, nicht weniger. Beim Meter also von 1889 bis 1960 Der vom CIPM gewählte Meter-Prototyp […] repräsentiert, beim Schmelzpunkt des Wassers gemessen, die Längeneinheit Meter bzw., ab 1960, Der Meter ist die Länge von 1 650 763,73 Wellenlängen der Strahlung des Übergangs zwischen den Energieniveaus 2p10 und 5p5 von Krypton-86-Atomen, und so weiter. Diese Minimalinformation muss in der Tat immer im Spiel sein, wenn Sie die betreffende Maßeinheit bei Messungen verwenden. Ohne einen Anschluss an die Definition keine Messung in der betreffenden Maßeinheit.
Was Sie zu historischen Hintergrundinformationen verschiedener Definitionen schreiben, geht deswegen schlicht am Thema vorbei. Ich hoffe, dass Sie dort, wo Sie Ihre Kommentare sonst noch im Internet verbreiten, immer schön auf den Originalbeitrag zurück verlinken? Nicht, dass jemand den falschen Eindruck bekommt, Ihre vehemente Kritik hätte irgendetwas mit dem zu tun, was ich dort geschrieben habe.
Zu Einsteins Aussage: Wenn dort eine ganz praktische, konkrete Messung
gemeint wäre (und nicht nur eine allgemeine Aussage zur physikalischen
Größe “Länge”), dann könnte man in der Tat mit den Meter-Definitionen von
1960 bzw. 1983 genauere Resultate erhalten als mit der vorher gültigen
Referenzkörper-Definition. Schlicht weil die Konstanz (erschlossen aus
Ensemble-Vergleichen, wie im Blogtext beschrieben) bei jeder der
Definitionen besser ist als bei den vorherigen, und das auf Größenskalen,
die bei Messungen an Festkörpern heutzutage durchaus praktische Bedeutung
haben.
Weiter
@ Dr. Markus Pössel
“Zu Einsteins Aussage: Wenn dort eine ganz praktische, konkrete Messung gemeint wäre (und nicht nur eine allgemeine Aussage zur physikalischen Größe “Länge”), dann könnte man in der Tat mit den Meter-Definitionen von 1960 bzw. 1983 genauere Resultate erhalten als mit der vorher gültigen Referenzkörper-Definition. Schlicht weil die Konstanz (erschlossen aus Ensemble-Vergleichen, wie im Blogtext beschrieben) bei jeder der Definitionen besser ist als bei den vorherigen, und das auf Größenskalen, die bei Messungen an Festkörpern heutzutage durchaus praktische Bedeutung haben.“
Tatsächlich? Eine bessere Definition der Maßeinheit erlaubt die genauere Messung der Länge eines Stabes?
Wie denn? Egal wie der Meter definiert wird, kann der Messende nur zwischen zwei materiellen Punkten des Objektes messen, und nicht darüber hinaus, auch wenn die Definition es mathematisch erlaubt, weil der Meter durch eine Geschwindigkeit definiert wird. Oder kann man mit einer besseren Definition des Meters einen starren Stab neuerdings bis in seine atomare Struktur hinein messen? Das Messen ist grundsätzlich durch die Berührung des Maßstabes mit der Materie des Objektes begrenzt, egal bei welcher Definition. Das Rechnen von Dezimalen bei einer mathematischen Relation wie eine Geschwindigkeit ist zwar unbegrenzt – aber ich hoffe, dass Sie den Unterschied zwischen Messen und Berechnen hier erkennen, darüber haben wir im anderen Blog schon diskutiert.
Aber ich merke schon, Sie halten sich da weiter die Ohren fest zu und singen “Lalala, ich kann Sie nicht hören, ich kann Sie nicht hören”. Ich lasse Sie dann mit Ihrer Illusion, dass das Schleppen von Dezimalen bei der Berechnung einer Geschwindigkeit einer genaueren Messung der Länge eines Objektes entspricht, Sie können wohl als Mathematiker nicht über Ihren eigenen Schatten springen. Und ausgerechnet bei der SRT halten Mathematiker die Theorie mit Mathematismus fest im Griff. 🙁
Viele Grüße
Jocelyne Lopez
Antwort von MP: Wieder einmal vollmundige Behauptungen, leider ohne konkrete Zahlenwerte, geschweige denn Belege.
Sagen Sie doch mal ganz konkret: Wo liegt denn Ihren Informationen nach die untere Grenze für genaue Längenmessungen an Festkörpern(*)? Mikrometer? Hundertstel Mikrometer? Nanometer? Nanometerbruchteile?
(*) Wenn wir uns mal auf die Festkörper beschränken und Wellenlängenmessungen außen vor lassen.
Paare und deren geometrische Beziehungen
Jocelyne Lopez schrieb (07.06.2011 | 11:35):
> @ Dr. Markus Pössel:
Es sei mir gestattet, die Diskussion auch weiterhin zu kommentieren, soweit sie mich interessiert; d.h. soweit sie nichts mit der Auswahl irgendwelcher bestimmter Maßeinheiten zu tun hat, sondern mit RT. Und insbesondere Themen betreffend, auf die M. Pössel zumindest hier nicht eingegangen ist; oder vielleicht überhaupt nirgendwo.
> Man misst nicht mit einer Definition, […] sondern mit einem Maßstab.
Auch in einem solchen Fall müsste definiert werden, wie unter allen (denkbaren) möglichen “Sachen” herauszufinden wäre, was “einen Maßstab” darstellte, und was nicht;
und wie (einschl. unter welchen Bedingungen) damit ein Messwert zu erlangen wäre.
Schlimmstenfalls hätte man das Fehlen irgendeiner nachvollziehbaren Definition zu konstatieren, und man könnte keine reellen, kommensurablen Messwerte erhalten.
> Noch einmal: Wo gibt es bei diesem Meßvorgang etwas Undefiniertes oder Unverständliches?
> Ein starres Objekt […]
Zuerst einmal:
Zwei “Enden” (Objekte, Beobachter) die zueinander starr sein (bzw. genauer: zueinander ruhen) sollten.
Aber es ruhten doch sicherlich nicht alle Paare von Enden von vornherein und ohne Weiteres zueinander, sondern es bedarf einer nachvollvollziehbaren Messdefinition um festzustellen,
welche Paare von Enden zueinander ruhten, und welche nicht.
(Noch ein kurzes Beispiel zu Unterscheidung von “gegenseitiger Starrheit” und “gegenseitiger Ruhe”:
eine Fahrradnabe und ein Fahrradschlauchventil waren i.A. stets starr zueinander;
aber sie ruhten höchstens dann zueinander, falls sich das Rad nicht drehte.)
> ein materieller Maßstab
Sicherlich ebenfalls mindestens ein Paar von Enden, sowie ggf. noch weitere Beteiligte (“Markierungen”) die alle zueinander ruhen sollten.
> ein Beobachter
Wieso noch ausdrücklich ein weiterer Beobachter? Vier verschiedene Enden sind doch sowieso schon mal vier …
> die alle […] im Zustand der gegenseitigen Ruhe zueinander während der Messung stehen
Zugegeben, das wirkt auf den ersten Blick nicht besonders spannend:
Wenn zwei Enden (“A” und “B”) eines “gegebenen Stabes” sowie
zwei Enden (“J” und “K”) eines “Maßstabes” alle zueinander ruhten,
und dabei sich z.B. A und J ständig trafen, und sich B und K ständig trafen,
dann schließt man eben ohne Weiteres, dass die Distanz von A und B zueinander
und die Distanz von J und K zueinander dabei gleich waren.
Erheblich interessanter ist natürlich der Fall, dass weitere zwei Enden (z.B. “P” und “Q”) ebenfalls zueinander ruhten, aber nicht gegenüber A, B, J und K;
und man dennoch die Distanz von P und Q zueinander mit der Distanz von A und B zueinander vergleichen will.
Das Problem dabei ist, und die obigen Betrachtungen sollen das verdeutlichen:
es wäre ein offenbar untauglicher Versuch, das Endenpaar J und K (“den Maßstab“, auch einschließlich weiterer Markierungen) “einfach schnappen” und “an P und Q halten” zu wollen,
denn J und K (usw.) kämen bei dieser Übung zwangsläufig zwischendurch “aus der Ruhe”;
und es ist genauso schwierig, die Distanz von J und K zueinander “vorher” mit “danach” zu vergleichen, wie die Distanz von A und B zueinander mit der Distanz von P und Q unmittelbar zu
vergleichen (d.h. während diese Paare nicht zueinander ruhten).
Die Lösung dieses Problems im Rahmen der RT kann man durchaus diskutieren (sozusagen als “RT-Kurs Track 1”) ohne sich allzu sehr darin vertiefen zu müssen, wie “gegenseitige Ruhe” überhaupt zu messen ist (“Track 2”).
Man sollte eben nur nicht vergessen: selbstverständlich ist das nicht.
Zeitverschwendung / @Jocelyne Lopez
Nur wer etwas lernen will. wird auch etwas lernen können. Und Sie wollen hier definitiv nichts lernen, das demonstrieren Sie sehr überzeugend dadurch, dass Sie jetzt wieder mit exakt den gleichen irrigen Parolen ankommen wie schon im April: “Das Messen ist grundsätzlich durch die Berührung des Maßstabes mit der Materie des Objektes begrenzt, egal bei welcher Definition.“
Sollten Sie jedoch tatsächlich glauben, dass in Wissenschaft und Technologie falsch gemessen wird, dann sind Ihre Kommentare hier völlig nutzlos. Stattdessen sollten Sie Ihre Beschwerden an die zuständige Stelle richten, und hier ist der passende Link. Da müssen Sie nur noch auf das Symbol neben “Contact form” clicken, dann können Sie sofort loslegen.
Sie sind doch sonst nicht so zurückhaltend mit Beschwerden bei offiziellen Institutionen. Also nur keine Hemmungen, allez hop! Wir sind sehr gespannt, was daraus wird.
Wurde die Lorentzkontraktion gemessen?
@ Dr. Markus Pössel:
“Sagen Sie doch mal ganz konkret: Wo liegt denn Ihren Informationen nach die untere Grenze für genaue Längenmessungen an Festkörpern(*)? Mikrometer? Hundertstel Mikrometer? Nanometer? Nanometerbruchteile?“
Ist zum Beispiel die Längenkontraktion von bewegten Objekten gemäß Lorentztransformation schon konkret gemessen worden? Bei welchen konkreten Messungen der Längen von bewegten Festkörpern? Wann? Bei welchen Experimenten?
Viele Grüße
Jocelyne Lopez
Antwort von MP: Jetzt bitte nicht ablenken. Von der Lorentzkontraktion ist weder in obigem Blogbeitrag die Rede noch in dem Kommentar, auf den sich meine Antwort bezieht.
Ihre Behauptung, nur zur Erinnerung: Die Meter-Neudefinitionen von 1960 bzw. 1983 erlaubten keine genauere Messung der Länge eines starren Stabes und seien daher unnötig bzw. “Mathematismus”.
Wenn das keine völlig aus der Luft gegriffene Aussage Ihrerseits ist, müssen Sie sich ja wohl überlegt haben (a) wie genau man die Länge eines Festkörpers messen kann und (b) wie sich das zum Genauigkeitsgewinn durch die beiden Meter-Neudefinitionen verhält.
Daher meine Frage, um diese Diskussion hier weiter voranzubringen, indem wir von vagen Behauptungen zu konkreteren Aussagen übergehen: Zu welchem Ergebnis sind Sie bei (a) gekommen? Wo liegt Ihren Informationen nach die untere Grenze für genaue Längenmessungen an Festkörpern?
Ich rede davon die ganze Zeit
@ Dr. Markus Pössel:
Jetzt bitte nicht ablenken. Von der Lorentzkontraktion ist weder in obigem Blogbeitrag die Rede noch in dem Kommentar, auf den sich meine Antwort bezieht.
Ihre Behauptung, nur zur Erinnerung: Die Meter-Neudefinitionen von 1960 bzw. 1983 erlaubten keine genauere Messung der Länge eines starren Stabes und seien daher unnötig bzw. “Mathematismus”.“
Ich lenke überhaupt nicht ab! Über die Problematik von konkret unmeßbaren Längen durch mathematische Berechnungen rede ich die ganze Zeit!!
Mit der Lorentztransformation, die die Lichtgeschwindigkeit als Maßeinheit zugrunde legt, werden Längen mathematisch berechnet, die in der Realität weit außerhalb des meßbaren Bereiches sich befinden! Was bedeutet, dass nicht mehr konkrete Messungen und nicht mehr Experimente die exakte Länge von Festkörpern bestimmen, sondern einzig die Mathematik.
Ich lenke überhaupt nicht ab, ich rede darüber die ganze Zeit, lesen Sie bitte noch einmal mein Eingangsbeitrag vom 03.06.11 in diesem Blog und meine anderen dort verlinkten Beiträge: http://www.wissenslogs.de/…/page/1#comment-27735 – zum Beispiel:
“Und bei der Bestimmung der physischen Ausdehnung des Meters ist das Bestreben sinnlos, die Maßeinheit mit einer Definition zu versehen, die die irrige Vorstellung suggeriert, man könne die Länge eines Objektes bis in seine molekulare oder atomare Struktur hinein messen. Das kann man nicht, auch wenn die Definition es mathematisch erlaubt. Diese Exaktheit ist eine Illusion, das ist lediglich eine trügerische mathematische Exaktheit und sie ist konkret bei einer Messung nicht realisierbar. Man degradiert dabei das Messen, das das Fundament der Physik darstellt, zu Mathematismus.“
Man baut also ganze Theorien, die eine universelle Gültigkeit haben sollen, mit Längen von Festkörpern auf, die man nie konkret gemessen hat und die auch nicht konkret meßbar sind, weil sie hoffnungslos außerhalb des meßbaren Bereichs liegen. Das Fundament der Physik als messende Wissenschaft ist das Messen, man entzieht der Physik ihr Fundament, wenn man die Natur mit Werten beschreibt, erforscht und deutet, die nicht gemessen wurden. Das ist keine Physik mehr, sondern eben Mathematismus. Ich lenke nicht ab, davon rede ich die ganze Zeit.
Viele Grüße
Jocelyne Lopez
Antwort von MP: Es geht nach wie vor um die Frage, ob die Meter-Neudefinitionen von 1960 und 1983 “Mathematismus” sind, wie Sie behaupten, oder ob es jeweils aufgrund der Genauigkeitsanforderungen von praktisch möglichen Messungen nötig war, die Definition des Meters zu verbessern. (Dazu gehören Messungen u.a. von Wellenlängen des Lichts, die wir hier beiseitegelassen haben, aber eben auch Messungen an Festkörpern, auf die Sie sich hier konzentriert haben.)
Um das zu beantworten, muss man wissen, welches denn nun die Genauigkeitsanforderungen von praktisch möglichen Messungen sind.
Sind die praktischen Genauigkeitsanforderungen höher, als es die Meterdefinition von vor 1960 leisten kann, dann war der Wechsel zur neuen Definition allein schon aus diesem Grund gerechtfertigt. Sind die praktischen Genauigkeitsanforderungen höher, als es die Meterdefinition von 1960 leisten kann, dann war der Wechsel zur neuen Definition allein schon aus diesem Grund gerechtfertigt.
Die Validität ihrer ganzen Argumentation hängt deswegen davon ab, was denn nun die praktischen Genauigkeitsanforderungen (meinetwegen, wie gesagt, zunächst auch nur für Längenmessungen an Festkörpern) sind.
Wenn Sie hier nicht völlig an den praktischen Erfordernissen vorbei argumentieren, und unter der Voraussetzung, dass es sich nicht um völlig aus der Luft gegriffene Aussagen Ihrerseits handelt, müssen Sie sich ja wohl überlegt haben (a) wie genau man die Länge eines Festkörpers messen kann und (b) wie sich das zum Genauigkeitsgewinn durch die beiden Meter-Neudefinitionen verhält.
Daher meine Frage, um diese Diskussion hier weiter voranzubringen, indem wir von vagen Behauptungen zu konkreteren Aussagen übergehen: Zu welchem Ergebnis sind Sie bei (a) gekommen? Wo liegt Ihren Informationen nach die untere Grenze für genaue Längenmessungen an Festkörpern?
Dann bitte nicht ablenken lassen! …
Jocelyne Lopez schrieb (09.06.2011 | 07:41):
> Das Fundament der Physik als messende Wissenschaft ist das Messen
Anders herum:
Das Fundament des Messens ist die Wissenschaft, die sich (u.a.) mit Messung (der Definition von bestimmten Messgrößen durch bestimmte nachvollziehbare Messoperatoren) beschäftigt — die Physik.
Entsprechend ist das Fundament der Physik wiederum: Nachvollziehbarkeit;
d.h. insbesondere, allen Beteiligten zumindest im Prinzip beobachterische Fähigkeiten zuzugestehen.
Welche konkrete Messungen?
@ Dr. Markus Pössel:
“Wenn Sie hier nicht völlig an den praktischen Erfordernissen vorbei argumentieren, und unter der Voraussetzung, dass es sich nicht um völlig aus der Luft gegriffene Aussagen Ihrerseits handelt, müssen Sie sich ja wohl überlegt haben (a) wie genau man die Länge eines Festkörpers messen kann und (b) wie sich das zum Genauigkeitsgewinn durch die beiden Meter-Neudefinitionen verhält.“
Ich argumentiere überhaupt nicht an den praktischen Erfordernissen vorbei, sondern ganz im Gegenteil, wenn ich frage, ob die Längenkontraktion von Objekten aus der Lorentztransformation meßbar ist und gemessen wurde, die als Maßstab die Lichtgeschwindigkeit zugrunde legt (also Maßeinheiten Meter und Sekunde). Ich bin voll im Thema.
Und ich argumentiere überhaupt nicht an den praktischen Erfordernissen vorbei, sondern ganz im Gegenteil, wenn ich frage, durch welche konkreten Messungen und durch welche Experimente die Längenkontraktion von bewegten Objekten mit dem Maßstab Lichtgeschwindigkeit gemessen wurde. Das interessiert mich nämlich sehr durch welche konkreten Messungen sie gemessen wurde und ob sie überhaupt mit dem Maßstab Lichtgeschwindigkeit (Meter/Sekunde) gemessen werden kann. Ich zitiere Sie aus unserer Korrespondenz aus dem Jahre 2008, aus Ihrer E-Mail vom 17.08.2008:
“Die gemessenen Laengenwerte sind selbstverstaendlich real – so real wie die Messungen von Relativgeschwindigkeiten. Es handelt sich nicht um optische Taeuschungen oder dergleichen, sondern um die Ergebnisse konkreter Messungen.“
Auch Ihr Kollege Dr. Peter Genath hat im Auftrag des Präsidenten der Deutschen Physikalischen Gesellschaft im selben Jahr 2008 als Antwort zu einer Anfrage von Herrn Ekkehard Friebe über das Experiment Hafele-Keating am 06.08.2008 von „tausenden von Hochpräzisions-Experimenten“ gesprochen:
“ Es gibt nicht den leisesten Zweifel, dass die Ergebnisse der Speziellen und Allgemeinen Relativitätstheorie falsch sein könnten. Zusammenfassend stellt der Fachverband damit fest: Die Spezielle und Allgemeine Relativitätstheorie ist in tausenden von Hochpräzisions-Experimenten immer besser bestätigt worden. Viele Technologien des täglichen Lebens funktionieren nur, weil die Spezielle und Allgemeine Relativitätstheorie richtig berücksichtigt wurde. Es kann keinen Zweifel an der Gültigkeit dieser Theorien im Rahmen der heutigen Messgenauigkeit geben.“
Ich argumentiere also nicht am Thema und an den praktischen Erfordernissen vorbei, wenn ich frage, mit welchen „konkreten Messungen“ bzw. „tausenden von Hochpräzisions-Experimenten“ die Längenkontraktion aus der Lorentztransformation mit dem Maßstab Lichtgeschwindigkeit gemessen wurde und ob sie überhaupt konkret meßbar sei, egal mit welcher Definition der Maßeinheiten.
Viele Grüße
Jocelyne Lopez
Antwort von MP: Sind Sie sicher, dass Sie den obigen Blogeintrag gelesen haben? Wo kommt denn da die Längenkontraktion vor? Da geht es um die Definition von Maßeinheiten!
Und auch in Ihren Kommentaren vom 3.6., 9:09, vom 4.6., 11:53, vom 5.6., 8:42, vom 7.6. um 11:35, vom 8.6. um 10:25, sprich: in den Kommentaren, die zu meiner Nachfrage geführt haben, geht es um Maßeinheiten.
Sie haben da zu den Maßeinheiten, nämlich zu den Meter-Neudefinitionen von 1960 und 1983, ziemlich vollmundig-kritische Behauptungen aufgestellt, mit dem Tenor: Die neuen Definitionen seien reiner “Mathematismus” und hätten nichts mehr mit praktischen Messungen zu tun.
Wer solche Behauptungen aufstellt, der muss natürlich wissen, wo denn nun die Genauigkeitsanforderungen von praktischen Messungen liegen. (Näher ausgeführt habe ich das z. B. in meiner Antwort auf Ihren Kommentar vom 9.6., 7:41). Andernfalls wären das Fantasiebehauptungen ohne Substanz – ohne zu wissen, wo die Genauigkeitsanforderungen von praktischen Messungen liegen, kann man nicht ernsthaft behaupten, eine bestimmte Genauigkeit liege jenseits dieser Anforderungen.
Deswegen hatte ich Ihnen (inzwischen drei Mal) die Frage gestellt: Wo liegt denn Ihren Informationen nach die untere Grenze für genaue Längenmessungen an Festkörpern?
Seit ich zum ersten Mal diese einfache und direkte Frage gestellt habe, lavieren Sie herum – da kommt, in diesem Teil der Diskussion erstmals, der Begriff “Lorentzkontraktion” ins Spiel, da ist, in diesem Teil der Diskussion erstmals, von Hochpräzisionsexperimenten zur SRT und ART die Rede, die in Ihren vorangehenden Ausführungen noch gar nicht vorkamen und mit meinem Blogeintrag nichts zu tun haben. Und Sie schreiben ellenlange Kommentare, warum Sie nicht ablenken und ausweichen und überhaupt ganz hundertprozentig beim Thema sind, aber versäumen es in dem ganzen Trubel dann irgendwie doch, auf meine einfache Frage zu antworten. Hm.
Dabei müsste es doch eigentlich einfach für Sie sein, mir eine direkte Antwort zu geben: Entweder einen Genauigkeitswert (1 Mikrometer, 100 Nanometer, 10 Nanometer,…), oder eben die Aussage, dass Sie schlicht nicht wissen, wo die Genauigkeitsanforderungen von praktischen Messungen liegen.
Von der Begrifflichkeit her – unklare Begrifflichkeiten wären ja in der Tat ein Grund, dass die Antwort länger ausfallen und man vorbereitend erst noch andere Fragen klären müsste – gibt es aus meiner Sicht auch keine Probleme.
Also, wie ist es? Geschätzter Zeitaufwand für Sie für die Beantwortung meiner Frage: nicht mehr als 15 Sekunden. Deutlich weniger Zeit, als Sie für Ihre letzte Nicht-Antwort auf meine Frage aufgewandt haben, würde ich meinen.
Kein Meßbarkeit = keine Meßgenauigkeit
@ Dr. Markus Pössel:
“Sind Sie sicher, dass Sie den obigen Blogeintrag gelesen haben? Wo kommt denn da die Längenkontraktion vor? Da geht es um die Definition von Maßeinheiten!
Herr Dr. Pössel, Maßeinheiten sind dafür da, dass man etwas messen kann, zum Beispiel die Länge eines Festkörpers. Die Länge eines bewegten Festkörpers ist auch eine Länge, die mit einem Maßstab gemessen wird, der einer Maßeinheit entspricht, die wiederum definiert wurde. Also bin ich voll beim Thema. Man kann Maßeinheiten, Definition von Maßeinheiten, Maßstäben, zu messenden Objekte, Messungen und Meßergebnissen doch nicht getrennt untersuchen, wie stellen Sie sich das vor? Es existiert einen Zusammenhang zwischen diesen Begriffen und bei der Handlung „Messen“, sie können nicht ohne Zusammenhang verwendet und verstanden werden, wie stellen Sie sich das denn vor? Soll man jetzt jedes Wort, das in der Physik gebraucht wird, getrennt und zusammenhanglos für sich allein in einem separaten Blog untersuchen? Wie können wir dann irgendwann dazu kommen, Einstein und seine Meßmethoden kennenzulernen und zu verstehen? Warum gehört die Längenkontraktion eines Objekts weder in der Rubrik “Messung von Längen”, noch in der Rubrik “Maßeinheiten” noch in der Rubrik “Definition von Maßeinheiten”? Oder sollen wir ewig wie Ping-Pong-Bälle von einem Blog zu dem anderen geschickt werden? In welchem Blog soll ich denn meine Frage stellen? In welchem Blog passt sie? Sie sind doch als Aufklärer derjenige, der Fragen beantworten soll, ich doch nicht. Gibt es überhaupt einen Blog, wo ich meine Frage stellen darf?
Sie behaupten, dass man durch eine gute Definition von Maßeinheit eine Länge genauer messen kann. Ich behaupte, dass man nicht mit einer Definition von Maßeinheit misst, weder genau noch ungenau, sondern nur mit einem Maßstab, sowie auch, dass man mit keinem Maßstab und folglich auch mit keiner Definition von Maßeinheiten zum Beispiel die Längenkontraktion eines bewegten Objektes im Rahmen der bestbewiesenen Theorie der modernen Physik je konkret gemessen hat, aus dem guten Grund, weil sie außerhalb des meßbaren Bereichs liegt. Weder 1 Mikrometer noch 100 Nanometer noch 10 Nanometer Meßgenauigkeit, gar nichts: Sie kann gar nicht konkret gemessen werden, keine Meßbarkeit bedeutet auch keine Meßgenauigkeit.
Sie behaupten im Gegenteil, dass man die Längenkontraktion durch konkrete Messungen gemessen habe. Dann sollten Sie mir bitte angeben, durch welche Meßmethoden, mit welchem Maßstab, mit welcher Maßeinheit und mit welcher Definition der Maßeinheit man die Längenkontraktion von bewegten Objekten gemessen hat. Wenn ich das erfahren darf, dann werde ich wohl gleich verstehen können, wie man mit der Wahl einer guten Definition genauer messen kann.
Viele Grüße
Jocelyne Lopez
Antwort von MP: Wow, netter
Ablenkungsversuch. Könnte bei Lesern, die nur diesen einen Kommentar
lesen und nichts von dem, was ihm vorangegangen ist, vielleicht sogar
verfangen.
Über die Längenkontraktion können wir gerne diskutieren, wenn die
Schritt-für-Schritt-Einführung von “Einstein
verstehen” bei diesem Punkt angekommen ist. In Diskussionen der
bisherigen Blogbeiträge von “Einstein verstehen” gehören Fragen der Längenkontraktion deswegen nicht,
weil wir bislang weder Bezugssysteme noch Bewegung noch die
Grundannahmen der Speziellen Relativitätstheorie eingeführt haben;
alles Voraussetzungen, ohne deren Kenntnis man nicht vernünftig über
die Längenkontraktion diskutieren kann. Sie hatten in einem früheren
Kommentar ja schon erklärt, sich an die Diskussionsregeln zu halten und
nicht vorgreifen zu wollen; ich fände es nett, wenn Sie diesem
Vorsatz weiterhin treu blieben.
Bei dem konkreten Blogbeitrag, den Sie
oben auf dieser Seite finden, ging es um die Güte
der Definition von Maßeinheiten. Dazu hatten Sie ja
durchaus auch etwas zu sagen gehabt – Sie hatten die
Meter-Neudefinitionen von 1960 und 1983 heftig kritisiert und
behauptet, es handle sich dabei um reinen “Mathematismus”, und der
Genauigkeitsgewinn bei der Definition hätte keine praktischen
Konsequenzen.
Auf diese Kritik von Ihnen bezog sich meine konkrete
Nachfrage, der Sie nun schon einige Textbeiträge lang
auszuweichen versuchen.
In Ihrem obigen Kommentar haben Sie mir wieder, wie Sie das leider
häufiger tun, Aussagen unterstellt; zur Klarstellung: Ich behaupte lediglich (übrigens im
Einklang mit den Metrologen), dass die Genauigkeit einer Messung, deren Ergebnis als
Vielfaches einer bestimmten Maßeinheit ausgedrückt werden soll, davon abhängt, wie konstant die Maßeinheit ist (was mit Konstanz
gemeint ist und wie man sie abschätzen kann, steht oben im
Blogeintrag).
Sehen Sie das anders? Könnte man Ihrer Meinung nach, selbst wenn
man damit rechnen müsste, dass eine Maßeinheit nur mit einer
Genauigkeit von einigen Prozent konstant ist, trotzdem in dieser
Maßeinheit ausgedrückte Messungen mit einer Genauigkeit im
Promillebereich ausführen?
Messmethoden misst man nicht
Jocelyne Lopez schrieb (09.06.2011 | 09:45):
> ich frage, mit welchen „konkreten Messungen“ […] die Längenkontraktion gemessen wurde und ob sie überhaupt konkret meßbar sei
Diese Frage ist abwegig; vergleichbar abwegig wie etwa zu fragen,
“ob jemals konkret gemessen wurde, dass derjenige Sprinter, der (in einem regulären Rennen) zuerst die Ziellinie überquert, das Rennen gewonnen hat”.
Das ist so per Definition (bzw. folgt unmittelbar aus der Definition); das ist der wesentliche Bestandteil der Messoperation, gemäß der zu entscheiden ist, wer ein Rennen gewonnen hat, und wer nicht.
So ist auch die Berücksichtigung des bekannten Faktors
“Sqrt[ 1 – β² ]” ein wesentlicher Bestandteil der Messoperation, gemäß der zu entscheiden ist, ob z.B. eine gegebene Garage länger als ein gegebenes Auto ist, oder nicht;
oder ob z.B. zwei gegebene Stichproben instabilier Teilchen gleiche mittlere Lebensdauern hatten, oder nicht.
Nicht weniger abwegig ist natürlich die Behauptung, “Längenkontraktion [sei … in Experimenten] bestätigt worden“.
> egal mit welcher Definition der Maßeinheiten.
Richtig: Messwerte von Distanzverhältnissen, oder von Verhältnissen mittlerer Lebesdauern, sind reelle Zahlen und invariant bzgl. der Wahl irgendwelcher Maßeinheiten.
> mit dem Maßstab Lichtgeschwindigkeit
Das bezieht sich wohl auf die chrono-geometrische Definition der Messgröße “Distanz”, die in der RT eingesetzt wird (worauf insbesondere J. L. Synge hingewiesen hat).
> aus der Lorentztransformation
Ohne der Herleitung des bekannten Faktors weiter vorgreifen zu wollen, als es in
http://www.wissenslogs.de/…eil-i/page/1#comments
(21.01.2011 | 16:55)
ohnehin schon geschehen ist:
diese Herleitung erfolgt direkt aus geometrischen Beziehungen, unabhängig von irgendwelchen Koordinaten und deren eventuellen Transformations-Beziehungen.
Warten auf die Längenkontraktion…
@ Dr. Markus Pössel:
“In Ihrem obigen Kommentar haben Sie mir wieder, wie Sie das leider häufiger tun, Aussagen unterstellt; zur Klarstellung: Ich behaupte lediglich (übrigens im Einklang mit den Metrologen), dass die Genauigkeit einer Messung, deren Ergebnis als Vielfaches einer bestimmten Maßeinheit ausgedrückt werden soll, davon abhängt, wie konstant die Maßeinheit ist (was mit Konstanz gemeint ist und wie man sie abschätzen kann, steht oben im Blogeintrag).“
Den Aspekt der Konstanz der Maßeinheit habe ich nicht angesprochen, sondern den Aspekt der historischen Definitionen von Maßeinheiten. Es ist klar, dass die Maßeinheit „konstant“ sein muss, sie ist es auch per Definition, egal ob sie als Erdumfang, als Elle, als Fuß oder als Inch historisch definiert wurde. Die meßtechnische Problematik der Konstanz betrifft also weder die Maßeinheit noch ihre Definition, sondern nur den Urmaßstab und seine Reproduktionen.
Der Urmaßstab ist allerdings auch per Konvention genau, er kann nicht ungenau sein, es gibt per Konvention nichts Genaueres als den Urmaßstab, er gilt per Konvention als konstant und genau: er stellt doch die per Konvention vereinbarte konstante Vergleichsgröße dar. Die Reproduktionen des Urmaßstabes dagegen müssen genau und konstant ihm gegenüber sein, sie sind nicht per Konvention genau oder konstant, das ist ein Problem der Reproduktion des Urmaßstabes und der industriellen Massenanfertigung der Reproduktionen. Hier zitiere ich wieder Helmut Hille in seiner Arbeit Messen als Erkenntnisakt:
“Das Meter oder Teile oder Vielfache von ihm ist, je nach Einsatzgebiet, die Vergleichsgröße mit der Dingen durch Messen ein uns Verständnis gebendes Meter-Maß zugeschrieben wird. Dagegen macht das Messen des Urmeters als Primärnormal durch ein anderes Meter, sei es ein Sekundär- oder Referenznormal oder ein Arbeitsmeßmittel, keinen Sinn, weil das Primärnormal immer dasjenige ist, was für jede Messung der Länge das Verständnis liefert. Würde man mir gestatten, einen Zollstock an das Urmeter anzulegen und ich würde feststellen, daß es 1,05 m lang ist, so würde diese Feststellung über das Urmeter überhaupt nichts besagen, sondern einzig eine Aussage über meinen Zollstock sein, der eine für mich vielleicht vorteil-, aber bestimmt unstatthafte Länge hat.“
@ Zitat Dr. Pössel:
“Sehen Sie das anders? Könnte man Ihrer Meinung nach, selbst wenn man damit rechnen müsste, dass eine Maßeinheit nur mit einer Genauigkeit von einigen Prozent konstant ist, trotzdem in dieser Maßeinheit ausgedrückte Messungen mit einer Genauigkeit im Promillebereich ausführen?
Nein, ich sehe nicht anders, dass eine Maßeinheit unveränderlich und konstant sein muss, und zwar völlig unabhängig von seiner historischen Definition. Ich habe nur das Problem der Machbarkeit in der Realität angesprochen, die die mathematische Exaktheit überhaupt nicht folgen kann.
Eine Maßeinheit kann man unendlich mathematisch fein unterteilen, ob es ein Meter ist, oder eine Elle, oder ein Fuß, oder ein Inch oder sonst etwas. Mathematisch kann man einen Maßstab unendlich unterteilen, es gibt keinen Grund sich auf Mikrometer oder Nanometer zu beschränken, man könnte einen Namen für alle mathematisch möglichen Unterteilungen erfinden. Die Mathematik kennt keine Grenze bei der Unterteilung eines Maßstabes bzw. einer Länge. Zahlen sind unendlich. Man darf nur seine Fantasie bei der Benennung der mathematischen Unterteilungen bemühen.
Die Realität kann aber diese mathematische, unendliche Unterteilung nicht folgen, beim Weiten nicht, das versteht sich meiner Meinung nach so von selbst, dass man eigentlich nicht darauf so lange einzugehen bräuchte. Immerhin wurde schon im I. Blogteil erwähnt, dass alleine die Dicke der Striche auf einem materiellen Maßstab eine unendliche Unterteilung bei der Messung der Länge eines Gegenstandes unmöglich macht und die Grenze der Genauigkeit gnadenlos setzt. Auch wurde erwähnt, dass allein die Dicke der Absteckungspfeiler eine Genauigkeit in dem Mikrometerbereich bei der Vermessung eines Grundstückes unmöglich macht. Die Länge eines Myons im Ruhezustand kann z.B. auch nicht gemessen werden, geschweige denn im Bewegungszustand, weder in Mikrometern noch in Nanometern, sondern überhaupt nicht. Ein GPS-Navigator bringt eine fantastische Leistung, wenn er die Position eines Autos auf 2 m oder 1 m genau bestimmt, eine Position auf 1 Mikrometer genau ist völlig realitätsfremd, ich wüsste nicht mal wo 1 Mikrometer oder 10 Nanometer auf der Straße unter den Vorderreifen meines Autos sich verstecken können, damit die Position so genau gemessen werden könnte, wie sie mathematisch bestimmbar ist.
Ich habe nur die technische Machbarkeit zur Diskussion gestellt, ich habe nie bestritten, dass eine Maßeinheit konstant und unveränderlich sein muß. Mich interessiert nämlich brennend seit ein paar Jahren, ob man in der Realität tatsächlich durch konkrete Messungen und durch Tausende von Hochgenauigkeits-Experimenten die Längenkontraktion von bewegten Objekten aus der Speziellen Relativitätstheorie gemessen habe. Gut, wir dürfen noch nicht über die konkrete Messung der Länge von bewegten Objekten sprechen, wir vertagen das also auf später, ich hoffe, dass wird noch was in diesem Jahr. 😉
Viele Grüße
Jocelyne Lopez
Antwort von MP: Danke für die Ausführungen zum Thema; jetzt geht es in der Tat in die Richtung, in die ich wollte, um Stellung zu Ihrer Kritik an den Meter-Neudefinitionen nehmen zu können.
Aber was sagen Sie denn dann zu den Argumenten im Abschnitt “Konstanz und Reproduzierbarkeit” des obigen Blogbeitrags? Sie können den Urmeter nicht mit einer früheren Version seiner selbst vergleichen. Aber geben Ihnen die Variationen zwischen Urmeter und exakten Kopien keine Hinweise auf eine mögliche zeitliche Veränderung des Urmeters?
Warten auf den Beobachter-Begriff
Markus Pössel schrieb (nach 09.06.2011 | 12:58):
> […] weil wir bislang weder Bezugssysteme noch Bewegung noch die Grundannahmen der Speziellen Relativitätstheorie eingeführt haben;
Ach so! (Na — besser ist das!)
Man hätte ja sonst fürchten müssen, dass sich die Einführung des Begriffes “Bezugssystem” mit den Bemerkungen aus
http://www.wissenslogs.de/…blogexperiment-teil-i
erledigt hätte
(etwa mit: “Ein solchermaßen in den wirklichen Raum eingebettetes Raumkoordinatensystem heißt Bezugssystem.” u. Ä.).
Dann besteht wohl noch Gelegenheit, zunächst einmal die Elemente solcher Systeme zu benennen und eingehender zu würdigen;
nicht zuletzt hinsichtlich ihres Auftretens in weiteren Begriffsdefinitionen (wie für “Bewegung“).
Markus Pössel schrieb (nach 09.06.2011 | 20:57):
> Sie können den Urmeter nicht mit einer früheren Version seiner selbst vergleichen.
(Warum eigentlich nicht? Und bzgl. welches Messoperators? Ist nicht insbesondere die Lösung solcher Probleme mit dem Begriff “Bezugssystem” verbunden? …)
> Aber geben Ihnen die Variationen zwischen Urmeter und exakten Kopien keine Hinweise auf eine mögliche zeitliche Veränderung des Urmeters?
Sofern der “Urmeter“-Artefakt schon nicht über mehrere Versuche hinweg mit sich selbst verglichen werden könnte (bzgl. eines geeigneten Messoperators), mit welcher Näherung sollte das denn für irgendwelche “Kopie“-Artefakte gelten, die nur in einzelnen Versuchen einmal mehr oder weniger “exakt” gewesen sein mögen??
Antwort von MP: OK, streng genommen habe ich ein Bezugssystem, das nur für statische Phänomene gilt, eingeführt. Aber Bewegung ist noch gar nicht definiert; das ist also ein sehr eingeschränktes Bezugssystem.
Zum Urmeter: Dann geben Sie doch mal ein praktisch durchführbares Verfahren an, wie man den Urmeter-Prototyp mit einer früheren Version seiner selbst (sprich: dem Zustand desselben Prototyps zu einer früheren Zeit) vergleichen kann.
Die Natur ist nie konstant, c’est la vie
@ Dr. Markus Pössel:
“ Aber was sagen Sie denn dann zu den Argumenten im Abschnitt “Konstanz und Reproduzierbarkeit” des obigen Blogbeitrags? Sie können den Urmeter nicht mit einer früheren Version seiner selbst vergleichen. Aber geben Ihnen die Variationen zwischen Urmeter und exakten Kopien keine Hinweise auf eine mögliche zeitliche Veränderung des Urmeters?“
Die Problematik der Veränderlichkeit eines Urmaßstabes in der Zeit wird immer existieren, damit muß man leben und sich abfinden, es gibt nichts, was sich in der Natur nicht verändert. Man kann zwar diese Veränderlichkeit begrenzen, indem man versucht, den Maßstab aus Materialen anzufertigen (ob Urmeter oder „Ur-Uhr“), die sich wenig verändern, aber man wird nie das Problem komplett aus der Welt schaffen, auch nicht durch Festsetzung von sogenannten Naturkonstanten: Naturkonstanten sind auch nicht konstant in der Zeit und sind auch nicht konstant in der Natur, nichts ist konstant, c’est la vie.
Das Problem der Veränderlichkeit eines Urmaßstabes mit sich selbst ist allerdings nicht von so gravierender Relevanz bei einer konkreten Messung, es ist nur relevant für Wissenschaftler, die alten Messungen mit neuen Messungen vergleichen wollen, also wohl eine marginale (historische) Bedeutung. Bei konkreten Messungen werden aktuelle Meßreihen unter sich verglichen und es wird per Konvention immer vorausgesetzt, dass die gegenwärtig gültige Maßeinheit invariant ist: Dafür wird per Konvention erklärt und es muß von allen akzeptiert werden, dass der Urmeter genau 1 Meter beträgt und dass 1 Meter nicht kürzer oder länger sein kann als der Urmeter, und dass die Ur-Uhr immer die richtige Dauer für eine Sekunde angibt, sie kann nie vorgehen noch nachgehen, sie gibt immer nur die richtige Zeit an. Ein Meter ist ein Meter und eine Sekunde ist eine Sekunde, immer und überall: das wird per Konvention erklärt und das muß von allen akzeptiert werden.
Von Bedeutung ist eher in der Tat die Reproduzierbarkeit der Urmaßstäbe, und zwar die Garantie, dass bei einer Messung im Labor oder in der Natur die Länge oder die Zeit genau den jeweiligen Ur-Maßstäben entspricht. Bei der Maßeinheit Lichtgeschwindigkeit nimmt man auch nur per Konvention an, dass den ausgewählten Wert als Maßeinheit in der Natur konstant ist, das ist sinnvoll und erlaubt auch die Bestimmung von Werten, die in Prozentzahl der Lichtgeschwindigkeit dargestellt werden können, also ist die Maßeinheit Lichtgeschwindigkeit wie alle Maßeinheiten unterteilbar (weniger als den konstanten festgelegten Wert) und vervielfachbar (mehr als den konstanten festgelegten Wert). Die konstante Lichtgeschwindigkeit als Maßeinheit darf jeder Zeit kleiner oder größer sein als den festgelegten Wert, was empirisch auch der Fall ist, sowohl im Labor als in der Natur – was aber bei manchen Theorien nicht der Fall sein darf. 😉
Viele Grüße
Jocelyne Lopez
Antwort von MP: Man kann die Veränderlichkeit nicht nur begrenzen, indem man den Maßstab aus Materialien zu fertigen versucht, die sich möglichst wenig verändern. Man kann, viel allgemeiner, die Festlegung in einer Weise treffen, die (Ensemblemessungen und ähnlichen Messungen zufolge) möglichst wenig Veränderung mit sich bringt. Exakt das haben die Metrologen mit der Meterdefinition von 1960 und der Neudefinition von 1983 getan. Bingo.
Die Aussage, dass die Veränderlichkeit nur “marginale Bedeutung” habe, ist schlicht falsch. Schauen Sie sich doch mal die Zahlenwerte im Blogbeitrag an, z.B. zur Veränderlichkeit der Kilgrammnormale. Innerhalb von 5 Jahren muss man da mit einer Änderung rechnen, die mehr als das Zehnfache der Messgenauigkeit beträgt! Außerdem sind 5, 10 oder sogar 20 Jahre für die Wissenschaft natürlich noch längst keine ferne Vergangenheit, die nur noch Wissenschaftshistoriker interessiert. Über solche (und zum Teil deutlich längere) Zeiträume hinweg müssen Wissenschaftler ihre Messergebnisse durchaus vergleichen. Dementsprechend wichtig ist die Veränderlichkeit des Urkilogramms (oder anderer Maßeinheiten) über solche Zeiträume hinweg; zu sehen ja nicht zuletzt daran, wieviel Zeit und Aufwand die Metrologen in den letzten Jahren investiert haben, um eine neue Definition zu finden.
Die Konstanz von Maßeinheiten wird übrigens keineswegs per Konvention festgesetzt – da dürfen Sie die physikalische Größe als Grundlage und die Maßeinheit als eine von unendlich vielen Wahlmöglichkeiten für eine einheitliche Bezugssgröße nicht durcheinanderbringen (wie Herr Wappler ganz am Anfang richtig kritisch angemerkt hatte: quantitativ Messen kann man auch ohne einheitliche Maßeinheit). Beim Urmeter war durch die Definition nur festgelegt, dass er zu jedem Zeitpunkt, trivialerweise, so lang ist wie der Urmeter. Das ist nicht das gleiche wie eine Festlegung, der Urmeter habe eine zeitlich konstante Länge. Im Gegenteil bemühen sich die Metrologen nach getroffener Festlegung mit vielen Messungen um Abschätzungen, ob die zentrale Eigenschaft der Konstanz gegeben ist, und wie groß etwaige Abweichungen sind.
(P.S.: Die Behauptung, dass die Natur nie konstant sei, ist in einer Situation wo eine ganze Reihe von Gesetzen und Größen im Rahmen der Messgenauigkeit tatsächlich konstant sind, nichts als gewagte Spekulation.)
@Jocelyne Lopez
Naturkonstanten gelten als konstant. Materielle Referenzkörper, die zur Festlegung einer SI Einheit dienten oder gegenwärtig noch immer dienen, werden aber keineswegs per definitionem als konstant angesehen. Dieses Missverständnis hätten Sie vermeiden können, wenn Sie den Blogtext aufmerksam gelesen hätten. Dann wüssten Sie beispielsweise, dass das Urkilogramm gerade nicht einfach so als unveränderlich gilt. Es geht beim BIPM immer nur darum, ideale Massstäbe mit aktuell bestmöglicher Genauigkeit anzunähern und entsprechende Standards für reale Messungen zu spezifizieren.
Der von Ihnen zitierte Herr Hille scheitert zwar spektakulär an den Uhren, am SI Meter von 1983 quengelt er im Gegensatz zu Ihnen aber nicht herum. In der unorthodoxen Kritikergemeinde besteht ganz offensichtlich keine Einigkeit darüber, was denn nun eigentlich alles kritisiert werden soll.
Keine Einigkeit bei den Orthodoxen…
@ Chrys
“Naturkonstanten gelten als konstant.“
Sagte ich doch… Auch die Lichtgeschwindigkeit, die wir als Maßeinheit ausgewählt haben, gilt als konstant und wird als Naturkonstant eingestuft, siehe: http://de.wikipedia.org/…Physikalische_Konstante
Man kann jedoch nicht davon ausgehen, dass eine Naturkonstante überall in der Natur gilt, wie ihr Name es vielleicht suggerieren könnte, sondern sie unterliegt einer gewissen Willkür und wurde vor allem aus der Empirie als Erfahrungswert festgesetzt.
Naturkonstanten sind sinnvoll und nützlich für die Wissenschaftler, vor allem für die Ingenieure und Techniker, weil sie bei technologischen Anwendungen brauchbare und zuverlässige Berechnungen innerhalb eines bestimmten Gültigkeitsbereiches ermöglichen. Das bedeutet aber keinesfalls, dass man sie unendlich extrapolieren darf, dass ihre Gültigkeit universell sei und dass sie außerhalb des Anwendungsbereiches gelten müssen.
Zitat von Chrys:
“Der von Ihnen zitierte Herr Hille scheitert zwar spektakulär an den Uhren, am SI Meter von 1983 quengelt er im Gegensatz zu Ihnen aber nicht herum. In der unorthodoxen Kritikergemeinde besteht ganz offensichtlich keine Einigkeit darüber, was denn nun eigentlich alles kritisiert werden soll.
Vielleicht liegt es daran, da die kritischen Ansätze so zahlreich und vielfältig sind, weil es an der Relativitätstheorie viel zu kritisieren gibt, oder? 😉 G.O. Mueller zum Beispiel listet ca. 130 Fehler in seiner Dokumentation, dem exhaustivsten Nachschlagewerk weltweit über die Kritik der Relativitätstheorie über eine Zeitspanne von 95 Jahren: Kapitel 2 – Fehlerkatalog zu beiden Relativitätstheorien
Und in der orthodoxen Relativitätstheoriegemeinde besteht ganz offensichtlich keine Einigkeit darüber, was denn nun eigentlich richtig sei oder nicht: Siehe zum Beispiel die Anfrage von Peter Ripota an Dr. Markus Pössel, worüber wir aber nur sprechen können, wenn wir über die Längenkontraktion sprechen dürfen. In der Zwischenzeit könnten Sie sich vielleicht auch eigene Gedanken darüber machen, warum in der orthodoxen Relativitätstheorie-Gemeinde keine Einigkeit darüber besteht, die Fragen aus der unorthodoxen Kritikergemeinde stehen auf jeden Fall schon seit Jahrzehnten ohne Beantwortung an:
Antwort von Dr. Markus Pössel an Peter Ripota
Viele Grüße
Jocelyne Lopez
Gewagte Spekulation
@ Dr. Markus Pössel:
“(P.S.: Die Behauptung, dass die Natur nie konstant sei, ist in einer Situation wo eine ganze Reihe von Gesetzen und Größen im Rahmen der Messgenauigkeit tatsächlich konstant sind, nichts als gewagte Spekulation.)“
Ja, das hat mir auch ein Teilnehmer in einer Forumdiskussion neulich auch erzählt, wie genau die Meßgenauigkeit von Naturkonstanten ist: “Die Naturkonstante c liegt nahe 300000km/s. Eine diskret genaue Bestimmung solcher Konstante ist praktisch schwierig. Zur Vereinheitlichung der wissenschaftlichen Forschung verwendet man einen einheitlich festgesetzten Wert, der dem Mittel der Messungen entspricht. Dabei muß man akzeptieren, daß physikalische Aussagen unter Verwendung dieses Wertes einen Fehler von 10 hoch -14 aufweisen können. 10 hoch -14 !!! Das ist ein relativer Fehler von 0,000000000000001“
Und ich antworte Ihnen, was ich auch diesem Teilnehmer geantwortet habe:
Über den Fehler von 10 hoch -14 bei der Festsetzung der Naturkonstante Lichtgeschwindigkeit können wir noch reden, wenn man z.B. die Lichtgeschwindigkeit auf 1 Mio Kilometer mal gemessen hat, anstatt auf ein paar Meter in einem Labor hin- und zurück. Und darüber können wir noch reden, wenn man zum Beispiel die Lichtgeschwindigkeit in einem Labor auf dem Pluton oder dem Jupiter gemessen hat. Machen Sie mal und dann reden wir noch darüber. Das wird aber wirklich nicht in diesem Jahr sein… Und mit hoher Wahrscheinlichkeit ist Ihre obige Einschätzung der Konstanz von Naturkonstanten, die wir einzig aus pragmatischen Gründen festgesetzt haben, nichts als eine naive Extrapolation und eine gewagte Spekulation. 😉
Viele Grüße
Jocelyne Lopez
Antwort von MP: Um nicht ein neues Thema anzuschneiden, bevor wir das alte abgeschlossen haben: Kann ich aus der Tatsache, dass sich Ihre Einwände nur noch auf das Postskriptum beziehen, und zudem nur Messungen auf Pluto oder sonstwo abseits der Erde betreffen, schließen, dass wir jetzt zumindest Einigkeit über die praktisch-irdische Überlegenheit der Meterdefinitionen von 1960 bzw. 1983 über ihre Vorgänger erzielt haben?
Nachtrag von MP: Und für die Leser, die doch gerne weiteres erfahren hätten, um sich entscheiden zu können, wer von uns beiden, Frau Lopez oder ich, sich hier in naiven und durch keinerlei Hintergrundinformationen getrübten Spekulationen ergeht, noch ein Buchtipp: John D. Barrow,
Das 1×1 des Universums. Neue Erkenntnisse über die Naturkonstanten. Campus, 2004. Da geht’s darum, wie sich die Konstanz der Naturkonstanten auch weit jenseits von Pluto noch messen lässt, ganz am Ende auch um Versuche, doch winzige Variationen mindestens einer Konstante über Milliarden Jahre hinweg nachzuweisen.
Unveränderlichkeit von Maßeinheiten
@ Dr. Markus Pössel
“Um nicht ein neues Thema anzuschneiden, bevor wir das alte abgeschlossen haben: Kann ich aus der Tatsache, dass sich Ihre Einwände nur noch auf das Postskriptum beziehen, und zudem nur Messungen auf Pluto oder sonstwo abseits der Erde betreffen, schließen, dass wir jetzt zumindest Einigkeit über die praktisch-irdische Überlegenheit der Meterdefinitionen von 1960 bzw. 1983 über ihre Vorgänger erzielt haben?“
Ich bleibe bei meiner Auffassung, dass man durch eine Definition der Längeneinheit Meter weder genauer noch besser reproduzierbar messen kann: Dies bleibt einzig von der gewährleisteten Unveränderlichkeit der Urmaßstäbe und ihrer Reproduktionen abhängig, sowie von den meßtechnischen Bedingungen. Noch einmal, man misst nicht mit einer Definition, sondern mit Gegenständen (mit Meßinstrumenten, Uhren, Lichtdetektoren), die Definition spielt keine Rolle sobald diese Objekte konkret zum Einsatz kommen, sondern einzig die Beschaffenheiten dieser materiellen Objekte sind maßgebend. Die Möglichkeit einer feineren Unterteilung der Maßeinheiten Meter und Sekunde bedeutet keine genauere Messung, das ist eben nur eine feinere Unterteilung, mehr nicht. Dabei bleibt ein Meter immer ein Meter und eine Sekunde immer eine Sekunde, sobald man die Urmaßstäbe gewählt hat, die ihre eigenen Maßen für alle Vergleiche mit anderen Objekten vorgeben. Man muss per Konvention voll akzeptieren, dass ein Meter immer ein Meter und eine Sekunde immer eine Sekunde ist, sobald sie von den materiellen Urmaßstäben vorgegeben sind, sonst stellt man das ganze Maßeinheitsystem in Frage. Das ist per Konvention zu akzeptieren, die Unveränderlichkeit von Maßeinheiten soll nicht in Frage gestellt werden. Man darf nie behaupten, das ist nicht zulässig, dass ein gemessener Meter in manchen Fällen anders ist als ein Meter und eine gemessene Sekunde anders ist als eine Sekunde, solange sie mit einer exakten Reproduktion (bzw. Synchronisation) der jeweiligen Urmaßstäbe gemessen wurden.
Aber unsere abweichenden Auffassungen über die Bedeutung der Definitionen von Maßeinheiten sollten uns nicht davon abbringen, weiter in die Einführung „Einstein verstehen“ fortzugehen.
Viele Grüße
Jocelyne Lopez
Antwort von MP: Sie schrieben, die Genauigkeit und Reproduzierbarkeit sei unter anderem “von der gewährleisteten Unveränderlichkeit der Urmaßstäbe und ihrer Reproduktionen abhängig”. Das ist exakt der Punkt. Legt man den Meter über materielle Urmaßstäbe fest, ist die Unveränderlichkeit dieser Einheit ungleich weniger gesichert als über die alternative Festlegung über die Lichtwellenlängen bestimmter Übergänge (1960) oder auf dem Umweg über die Zeiteinheit (1983). Das ist der Vorteil der neuen Festlegung, und es ist mir unerfindlich, wie Sie einerseits das Kriterium Unveränderlichkeit anerkennen und andererseits die direkte Schlussfolgerung daraus (durch direkte Messungen etablierte Überlegenheit der Festlegungen von 1960 bzw. 1983) verwerfen können.
Aber, wie Sie sagen, vom Kernthema von “Einstein verstehen” weichen wir mit diesen Fragestellungen in der Tat ab, und ich denke, die meisten Leser dieses Blogs haben an diesem Punkt der Diskussion genug Informationen um zu sehen, was Sache ist; belassen wir’s meinetwegen dabei.
SI Einheiten für Amateure und Profis
Hier ist ein Link zu einem Dokument “ABCs of Metrology” [PDF]. Table 1 auf p. 4 listet die aktuellen Definitionen der SI base units incl. deren Genauigkeiten. Diese letzteren Angaben fehlen meist in den wikis, aber immerhin findet sich hier eine Tabelle, an der für den Meter die Entwicklung der Genauigkeit in Abhängigkeit von der jeweiligen Definition deutlich wird. (Als Quelle wird dort auch P. Giacomo genannt, den ich bereits einmal zitiert hatte.)
Veränderlichkeit der Reproduktionen
@ Dr. Markus Pössel
“Sie schrieben, die Genauigkeit und Reproduzierbarkeit sei unter anderem “von der gewährleisteten Unveränderlichkeit der Urmaßstäbe und ihrer Reproduktionen abhängig”. Das ist exakt der Punkt. Legt man den Meter über materielle Urmaßstäbe fest, ist die Unveränderlichkeit dieser Einheit ungleich weniger gesichert als über die alternative Festlegung über die Lichtwellenlängen bestimmter Übergänge (1960) oder auf dem Umweg über die Zeiteinheit (1983). Das ist der Vorteil der neuen Festlegung, und es ist mir unerfindlich, wie Sie einerseits das Kriterium Unveränderlichkeit anerkennen und andererseits die direkte Schlussfolgerung daraus (durch direkte Messungen etablierte Überlegenheit der Festlegungen von 1960 bzw. 1983) verwerfen können.“
Es ist mir unerfindlich, warum Sie hier die Faktoren der Veränderlichkeit der Reproduktionen des Urmeters bei einer konkreten Messung mit der Lichtgeschwindigkeit partout ignorieren wollen, die ich als nachteilig gegenüber dem „so gut wie nicht veränderbaren materiellen Urmaßstab, auch bei Wechselnder Temperatur“ (wie Sie es selbst in Ihrem Blog-Text Teil I aussagen) ausführlich aufgeführt habe, zum Beispiel in folgenden Beiträgen:
http://www.wissenslogs.de/…/page/5#comment-26722
http://www.wissenslogs.de/…/page/5#comment-26836
http://www.wissenslogs.de/…/page/6#comment-26955
http://www.wissenslogs.de/…/page/6#comment-27019
http://www.wissenslogs.de/…/page/6#comment-27061
http://www.wissenslogs.de/…/page/6#comment-27065
Aber wir sollten es vielleicht hier doch lieber bei unseren abweichenden Meinungen belassen und ruhig mit der Einführung in „Einstein verstehen“ fortfahren, sonst treten wir ewig auf der Stelle. 🙁
Viele Grüße
Jocelyne Lopez
Antwort von MP: Ganz auf der Stelle treten wir noch nicht; insofern würde ich noch um ein wenig weitere Geduld bitten; ich bemühe auch, mich so kurz wie möglich zu fassen:
Störquellen gibt es bei allen drei Festlegungen (materieller Urmaßstab, Festlegung von 1960, und Festlegung von 1983). Bei allen drei Festlegungen bemüht man sich in Kenntnis dieser Störeinflüsse, die jeweiligen Störungen so gering wie möglich zu halten.
Entscheidend dafür, welche der drei Festlegungen in punkto Konstanz und Reproduzierbarkeit am zuverlässigsten ist, ist, zu welcher Gesamtunsicherheit sich die Störquellen bei Messungen unter Laborbedingungen addieren.
Stimmen Sie soweit noch mit mir überein?
@ Dr. Markus Pössel:
“Ganz auf der Stelle treten wir noch nicht; insofern würde ich noch um ein wenig weitere Geduld bitten; ich bemühe auch, mich so kurz wie möglich zu fassen:
Störquellen gibt es bei allen drei Festlegungen (materieller Urmaßstab, Festlegung von 1960, und Festlegung von 1983). Bei allen drei Festlegungen bemüht man sich in Kenntnis dieser Störeinflüsse, die jeweiligen Störungen so gering wie möglich zu halten.
Entscheidend dafür, welche der drei Festlegungen in punkto Konstanz und Reproduzierbarkeit am zuverlässigsten ist, ist, zu welcher Gesamtunsicherheit sich die Störquellen bei Messungen unter Laborbedingungen addieren.
Stimmen Sie soweit noch mit mir überein?“
Ja, damit kann ich leben.
Sie haben nur noch nicht die Addition der Störquellen und damit die Gesamtunsicherheit bei der Messung einer Länge mit der Lichtgeschwindigkeit analysiert, sowohl im Labor als auch in der Natur (wir wollen ja Längen in der Alltagsphysik oder in der Natur messen und nicht im Labor) und zwar bei 3 involvierten Gegenständen bei einer Zweiwegmessung anstatt bei einem: Uhr, Spiegel und Lichtdetektor:
Wikipedia:
„Die optische Abstandsmessung (auch: Laserentfernungsmessung) wird benutzt um die Distanz zwischen einem Abstandssensor und einem Objekt zu messen. Die Präzision hängt von verschiedenen Faktoren ab:
• von der Oberfläche der beiden Objekte (Material, Farbe)
• von der zu messenden Distanz
• von Umwelteinflüssen“
Ob die Bilanz der Gesamtunsicherheit hier zugunsten der Messung einer Länge mit der Lichtgeschwindigkeit anstatt mit konventionellen Methoden ausfällt? Das ist nicht direkt ersichtlich, die Störquellen scheinen sowohl quantitativ als auch qualitativ auf dem ersten Blick insgesamt bei 3 Gegenständen sogar größer. Das war nämlich der Anlaß meiner Nachfrage – und nicht um „rumzuquengeln“ wegen Messungen von Längen mit der Lichtgeschwindigkeit, die ohne Frage eine gute Idee und eine praktische Anwendung ist.
Viele Grüße
Jocelyne Lopez
Antwort von MP: Gut, dann sind wir ja wieder einen Schritt weiter. An einer Stelle möchte ich allerdings vorsorglich nachhaken, bevor ich einen weiteren Schritt gehe. Sie fordern eine Analyse der Störquellen “sowohl im Labor als auch in der Natur (wir wollen ja Längen in der Alltagsphysik oder in der Natur messen und nicht im Labor)”. Inwiefern sind nun aber die Störquellen “in der Natur” für die Festlegung der Maßeinheit relevant, um die es in meinem Blogbeitrag geht?
Für den Urmeter waren solche Störquellen doch auch nie relevant. Der blieb immer schön im Labor, unter kontrollierten Bedingungen, und wurde garantiert nie direkt für Messungen in der freien Natur verwendet.
Störquellen bei Messungen mit dem Licht
@ Dr. Markus Pössel:
“Sie fordern eine Analyse der Störquellen “sowohl im Labor als auch in der Natur (wir wollen ja Längen in der Alltagsphysik oder in der Natur messen und nicht im Labor)”. Inwiefern sind nun aber die Störquellen “in der Natur” für die Festlegung der Maßeinheit relevant, um die es in meinem Blogbeitrag geht?
Für den Urmeter waren solche Störquellen doch auch nie relevant. Der blieb immer schön im Labor, unter kontrollierten Bedingungen, und wurde garantiert nie direkt für Messungen in der freien Natur verwendet.“
Ja, sicher, der Urmeter blieb immer im Labor, aber seine industriellen Reproduktionen (die materiellen Maßstäbe) mit denen man konkret misst, waren ja immer in der Alltagsphysik oder in der Natur im Einsatz, da wo man sie eben zur Messung einer Länge braucht.
Die „Reproduktionen“ der Maßeinheit Lichtgeschwindigkeit, die auch im Labor unter kontrollierten Bedingungen bestimmt wurde, sind natürlich auch im Einsatz in der Alltagsphysik oder in der Natur, da wo man sie eben zur Messung einer Länge braucht: Die „Reproduktionen“ der Maßeinheit Lichtgeschwindigkeit sind die Messungen mit der Lichtgeschwindigkeit selbst!
Und die Reproduzierbarkeit der Lichtgeschwindigkeit, die im Labor bestimmt wurde, ist in der Alltagsphysik und in der Natur ziemlich beeinträchtigt, allein schon zum Beispiel wegen dem Faktor „Vakuum“: Die Lichtgeschwindigkeit wurde im Vakuum gemessen, jedoch wird in der Alltagsphysik oder in der Natur eine Länge nicht im Vakuum gemessen, sondern zum Beispiel in der Atmosphäre, wobei die auftretende Verlangsamung bei konkreten Messungen einer Länge nicht gemessen werden kann, sondern nur pauschal durch Erfahrungswerte geschätzt werden muss und jeweils immer bei jeder Messung individuell variiert (Dichte der Luft, Luftfeuchtigkeit, Luftverschmutzung). Alleine wegen der „Störquelle Medium“ ist also die Labor-Lichtgeschwindigkeit in punkto Konstanz und Reproduzierbarkeit prinzipiell benachteiligt, eine Gesamtunsicherheit ist schwierig abzuschätzen – schwieriger sogar als bei dem materiellen Urmeter, wo nur Material und Temperatur die Konstanz und Reproduzierbarkeit beeinträchtigt?
Viele Grüße
Jocelyne Lopez
Antwort von MP: Schon vor der Neudefinition von 1960, als der Urmeter noch ein konkretes Objekt in Paris war, gab es eine Vielzahl von Arten und Weisen, wie man vom Urmeter zu Alltags- und Labormessungen von Länge gelangen konnte. Es gab starre materielle Maßstäbe (inklusive Schublehren, Messkluppen und derlei Instrumente mehr), flexible Messbänder, es gab elektromagnetische Messungen wie Radarmessungen, es gab Messmethoden, die die mit Bezug auf den Urmeter festgelegte Wellenlänge bestimmter Arten von Licht nutzten, und so weiter.
Das Kalibrieren oder Eichen am Urmeter fand dabei in der Regel in mehreren Schritten statt: Der Urmeter wurde mit den nationalen Prototypen verglichen, die nationalen Prototypen mit “Hauptnormalen” oder ähnlichen Gebilden, die und ihre Abkömmlinge wurden wiederum zum Eichen diverser Arten Messgeräte genutzt, und so weiter – eine Kalibrationskette mit mehreren Kettengliedern, und das erste Kettenglied war der Urmeter in Paris.
Die Neudefinitionen von 1960 bzw. 1983 haben nichts an der Zulässigkeit der verschiedenen Messmethoden geändert. Es gibt nach wie vor materielle Maßstäbe, Schublehren, elektromagnetische Messmethoden, und sie alle sind nach wie vor gültige “Verkörperungen n-ter Hand” der Maßeinheit Meter. Niemand zwingt Sie, mit Lichtlaufzeiten zu messen, wenn das in der betreffenden Situation messtechnisch ungünstig ist.
Der einzige notwendige Unterschied zu vorher ist, dass am Anfang der Kalibrationskette nicht mehr der Pariser Urmeter steht, sondern eine bestimmte Art von Laborexperiment.
Gedankenexperimente-Verstehen durch Üben
Markus Pössel schrieb (nach 10.06.2011 | 08:23):
> streng genommen habe ich ein Bezugssystem, das nur für statische Phänomene gilt, eingeführt. [Beschreibung in http://www.wissenslogs.de/…blogexperiment-teil-i ]
Auf der angegebenen Webseite findet sich das Wort “statisch” insbesondere in den Formulierungen:
und
Meine obige Frage (10.06.2011 | 08:23), wie denn Elemente eines “(statischen) Bezugssystems” benannt werden sollen, hängt also offenbar mit der Frage zusammen (oder reduziert sich sogar darauf), wie die Elemente benannt werden sollen, aus denen der Definitionsbereich von “Abstands“-Messungen besteht.
Nennt man diese Elemente etwa “Phänomene“?? — Wohl kaum; die genannte Webseite benutzt stattdessen Formulierungen wie
.
Kann man nun insbesondere im Zusammenhang mit Gedankenexperimenten der RT jedes dieser (einzeln benannten) Elemente einschließlich jeweils eines (genauso benannten) Beobachters auffassen?
Also von einem “Abstand zwischen einem Paar von Beobachtern” sprechen,
und demnach sagen, dass ein “(statisches) Bezugssystem” ein “System von Beobachtern mit gemessenen, konstanten Abstandsverhältnissen untereinander” darstellt; oder ausdrücklich nicht?
> Aber Bewegung ist noch gar nicht definiert
(Was die angegebene Webseite offenbar nicht daran hindert, dieses Wort reichlich einzusetzen.)
> geben Sie doch mal ein praktisch durchführbares Verfahren an, wie man den Urmeter-Prototyp mit einer früheren Version seiner selbst (sprich: dem Zustand desselben Prototyps zu einer früheren Zeit) vergleichen kann.
Dafür wäre zunächst zu rekapitulieren, welche Messoperationen im Rahmen der Diskussion denn als “praktisch durchführbar” bzw. als axiomatisch gelten. Für die RT sicherlich:
– dass jeder beteiligte Beobachter Reihenfolge bzw. Koinzidenz der eigenen Wahrnehmungen beurteilen kann, und ein Gedächtnis seiner Anzeigenfolge hat, und
– dass jeder beteiligte Beobachter für jede seiner (Signal)-Anzeigen ggf. unterscheiden und wiedererkennen kann, wessen entsprechende Echo-Anzeigen er wahrnahm.
Um herauszufinden, welche Verfahren auf dieser Grundlage schon konstruiert wurden, durch die Begriffe wie “gegenseitige Starrheit” und “gegenseitige Ruhe” als Messgrößen definiert und ggf. durch bestimmte Beteiligte experimentell feststellt oder widerlegt werden könnten (z.B. von den beiden Enden bzw. Markierungen “des Urmeter-Prototyps“, u.a.), würde ich vor allem unter dem Stichwort “Null-Strut Calculus” recherchieren …
Antwort von MP: Irgendwie scheint Ihnen das
Grundkonzept dieser Einführung immer noch völlig fremd; ich war
ganz am Anfang bei Ihren ersten Kommentaren mehrmals darauf
eingegangen, hatte es dann ab einem gewissen Punkt allerdings
zugegebenermaßen schlicht aufgegeben.
Ich versuche die Leser relativ weit am Anfang abzuholen – bei den
“prä-physikalischen Alltagsvorstellungen”, wenn Sie so
wollen. Die Vorstellung, die die Leser von Phänomenen wie Bewegung
mitbringen, wird dabei Schritt für Schritt verfeinert.
Klar ist das etwas völlig anderes als die elegant-axiomatische
Entwicklung, die Ihnen offenbar als Ideal vorschwebt. Was nicht heißen
soll, dass nicht Elemente aus jener Entwicklung in späteren Folgen
dieser Blogbeitragsserie auftauchen werden, wenn die geeigneten
Grundlagen dafür gelegt sind.
“Phänomen” war schlicht mein Versuch, von Erscheinungen, sichtbaren
Dingen zu reden, ohne mich auf materielle Objekte
festzulegen. Abstände kann man ja zwischen allem messen, was in dem
zugrundeliegenden mathematischen Modell näherungsweise einem Punkt
entspricht.
Mit “praktisch durchführbar” meinte ich übrigens in der Tat, dass
das Verfahren in der Wirklichkeit umsetzbar sein sollte,
nicht nur als Gedankenexperiment im Rahmen eines bestimmten Axiomensystems. Ich kann mir zum Vergleich
vergangener Versionen des Urmaßstabs mit sich selbst nämlich momentan nur
nicht realisierbare Messungen vorstellen, bei denen man eine so große
Messanordnung aufbaut, dass Lichtlaufzeiten in der gewünschten
Größenordnung von Jahren oder Jahrzehnten auftauchen. Aber das ist
praktisch heute und in absehbarer Zukunft nicht realisierbar. Wenn Sie
anderes im Sinn hatten, wäre es nett, wenn Sie es zumindest kurz
skizzieren könnten.
Störquellen bei Messungen mit dem Licht
@ Dr. Markus Pössel
“Das Kalibrieren oder Eichen am Urmeter fand dabei in der Regel in mehreren Schritten statt: Der Urmeter wurde mit den nationalen Prototypen verglichen, die nationalen Prototypen mit “Hauptnormalen” oder ähnlichen Gebilden, die und ihre Abkömmlinge wurden wiederum zum Eichen diverser Arten Messgeräte genutzt, und so weiter – eine Kalibrationskette mit mehreren Kettengliedern, und das erste Kettenglied war der Urmeter in Paris.“
Und wieder gehen Sie nicht auf die Störquellen bei der Reproduzierbarkeit der Länge des Meters mit dem Licht ein. 🙁
Ich habe erst einmal zum Beispiel die Störquelle „Vakuum“ bzw. „Atmosphäre“ angesprochen.
1. Sehen Sie ein, dass die Reproduktion der Länge des Meters mit einer Messung mit dem Licht in der Atmosphäre anders ausfällt, als die Länge, die durch einer Messung der Lichtgeschwindigkeit im Vakuum als Maßeinheit ausgewählt und festgesetzt wurde?
2. Sehen Sie ein, dass die Länge des Meters, die durch eine Messung mit der Lichtgeschwindigkeit in der Atmosphäre bestimmt wird, in Paris, in Mexico, in London oder sonst woanders wegen Beschaffenheiten der Luft am Ort und zum Zeitpunkt der Messung (Luftdichte, Luftfeuchtigkeit, Luftverschmutzung) anders ausfallen wird?
3. Sehen Sie ein, dass allein diese Störquelle „Vakuum“ bzw. „Atmosphäre“ von vorneherein und methodologisch Variationen bei der Reproduktion der Länge des Meters mit dem Licht verursacht, die schon im Promille-Bereich anzusiedeln sind, also keine Lappalien im wissenschaftlichen Sinne?
Viele Grüße
Jocelyne Lopez
Antwort von MP: Aber inwieweit sind das denn Störquellen für das “erste Glied der Kalibrationskette”? Die findet doch, ob in Paris, Mexiko oder London, in der Tat im Labor statt, unter sorgfältigen Bedingungen, bei denen man Luftverschmutzung etc. außen vor lässt?
Noch einmal: Die Neufestlegungen von 1960 bzw. 1983 schreibt Ihnen nicht vor, wie Sie die Messung in der Natur und im Alltag vorzunehmen haben. Das einzige, was sich ändert, ist das erste Glied der Kalibrationskette, und dafür sind die Störungen, die Sie hier ansprechen, irrelevant.
Störquellen bei Messungen mit dem Licht
@ Dr. Markus Pössel
“Aber inwieweit sind das denn Störquellen für das “erste Glied der Kalibrationskette”? Die findet doch, ob in Paris, Mexiko oder London, in der Tat im Labor statt, unter sorgfältigen Bedingungen, bei denen man Luftverschmutzung etc. außen vor lässt?”
Herr Dr. Pössel, es geht mir hier nicht um Messungen der Lichtgeschwindigkeit im Vakuum im Labor, sondern es geht mir hier nur um die Reproduzierbarkeit der Länge des Meters durch eine Messung mit der Lichtgeschwindigkeit! Man sollte schon Messungen der Lichtgeschwindigkeit und Messungen mit der Lichtgeschwindigkeit auseinander halten.
Es geht darum, die Länge des Meters in Paris, Mexiko oder London durch eine Messung mit der Lichtgeschwindigkeit zu reproduzieren, als “letztes Glied der Kalibrationskette”, es geht doch nicht um die Messung der Lichtgeschwindigkeit im Vakuum in Paris, Mexiko oder London.
Und wie wollen Sie in Paris, Mexiko oder London die Atmosphäre und ihre örtlichen Beschaffenheiten außen vor lassen, wenn Sie dort die Länge des Meters mit dem Licht reproduzieren wollen, um zum Beispiel materielle Maßstäbe industriell anzufertigen?
Viele Grüße
Jocelyne Lopez
Antwort von MP: Um das erste Glied der Kalibrationskette geht es aber in dem Blogbeitrag, den wir hier kommentieren. Und um das erste Glied der Kalibrationskette geht es auch bei der Frage, ob es sinnvoll ist oder nicht, von der Verkörperung des Meters durch den Urmeter zu anderen Festlegungen, eben denen von 1960 oder 1983, überzugehen.
Sie hatten die Neufestlegungen von 1960 und 1983 vehement kritisiert. Diese neuen Festlegungen tun nichts anderes, als das erste Glied der Kalibrationskette zu ändern. Warum reden Sie hier auf einmal nur noch über das letzte Glied?
Zu Ihrem letzten Absatz: Wo die Luftverschmutzung stört, benutzt man Filter (Reinraumbedingungen); eine Reihe von Versuchsanordnungen in der Laseroptik sind sowieso zum Teil in Vakuumkammern untergebracht. Wo der Luftdruck eine Rolle spielt und man kein Vakuum braucht, gibt es geeignete Druckkammern.
@ Dr. Markus Pössel:
“Um das erste Glied der Kalibrationskette geht es aber in dem Blogbeitrag, den wir hier kommentieren. Und um das erste Glied der Kalibrationskette geht es auch bei der Frage, ob es sinnvoll ist oder nicht, von der Verkörperung des Meters durch den Urmeter zu anderen Festlegungen, eben denen von 1960 oder 1983, überzugehen. Sie hatten die Neufestlegungen von 1960 und 1983 vehement kritisiert. Diese neuen Festlegungen tun nichts anderes, als das erste Glied der Kalibrationskette zu ändern. Warum reden Sie hier auf einmal nur noch über das letzte Glied?
Ja, und das „erste Glied der Kalibrationskette“ bzw. die Wahl einer Definition für eine Maßeinheit hatte ich schon ganz am Anfang beim Einsteigen in die Blog-Diskussion nun mal kommentiert: Die Definition einer Maßeinheit spielt keine Rolle bei der Unveränderlichkeit und die Reproduzierbarkeit der Gegenstände, die die Länge des Meters darstellen: Hier sind einzig technische Bedingungen der Herstellung, Aufbewahrung und Reproduktionen des Urmeters und seiner Kopien von Belang. Alles andere sind Worte, man misst nicht mit Worten, man misst nicht mit einer Definition, sondern man misst am letzten Glied der Kalibrationskette mit Gegenständen!!
“Zu Ihrem letzten Absatz: Wo die Luftverschmutzung stört, benutzt man Filter (Reinraumbedingungen); eine Reihe von Versuchsanordnungen in der Laseroptik sind sowieso zum Teil in Vakuumkammern untergebracht. Wo der Luftdruck eine Rolle spielt und man kein Vakuum braucht, gibt es geeignete Druckkammern.“
Gut, alle Länder reproduzieren die Länge des Meters zur Herstellung ihrer eigenen Prototypen mit dem Licht in Vakuum- und Druckkammern. Ist es richtig? Warum sagten Sie mir es nicht gleich als ich das Thema Vakuum angesprochen habe, und warum sagen Sie es auch nicht in Ihrem Blog-Text? Das ist doch wichtig, andere Leser könnten dieselben Überlegungen wie ich anstellen, sogar 10-Klässler, oder? Das ist ja wichtiger als mit technischen Details überschüttet zu werden, die nur von Ingenieuren oder Experten der PTB verstanden und kommentiert werden können. 🙁
Bleiben jetzt Fehlerquellen bei Herstellung der Prototypen mit dem Licht die Fehlerquelle, die ich ein paar Mal schon seit meinem Einstieg gepostet habe:
“Die optische Abstandsmessung (auch: Laserentfernungsmessung) wird benutzt um die Distanz zwischen einem Abstandssensor und einem Objekt zu messen. Die Präzision hängt von verschiedenen Faktoren ab:
• von der Oberfläche der beiden Objekte (Material, Farbe)
• von der zu messenden Distanz“
Werden die in allen Ländern angefertigten Prototypen geeicht oder geht man blind davon aus, dass die jeweiligen Reproduktionen korrekt durchgeführt wurde und dass die reproduzierte Länge die Länge des pariser Urmeters darstellt?
Wie werden diese Fehlerquellen bei einer Messung mit dem Licht in allen Ländern ausgeschlossen? Wie werden z.B. die Fehlerquellen bei den anderen betroffenen Gegenständen Uhr, Spiegel, Lichtdetektor ausgeschlossen?
Und natürlich nicht zuletzt: Wie werden diese vielfältigen Fehlerquellen bei der Messung von Längen außerhalb der Labore ausgeschlossen? Ich möchte gern am Endeffekt beurteilen können, ob konventionelle Messungen von Längen genauer mit den festgesetzen Maßeinheiten übereinstimmen als Messungen mit dem Licht und ich möchte gerne beurteilen zu welcher Gesamtunsicherheit sich die Störquellen bei Messungen mit dem Licht in der Alltagsphysik und in der Natur addieren. Dabei interessieren mich die Definitionen von 1960 oder von 1983 genau so wenig, wie die Definition während der französischen Revolution mit 1/40 Millionsten des Erdumfangs mich jetzt interessiert. 😉
Viele Grüße
Jocelyne Lopez
Antwort von MP: Ich glaube, da liegt noch (mindestens) ein Missverständnis vor. Im Gegensatz zur Orientierung des ursprünglichen Meters am Erdumfang sind die neuen Definitionen tatsächlich die Festlegung der Maßeinheit.
Sprich: Es ist nicht so, dass man 1960 bzw. 1983 nach einer bestimmten Vorschrift aus atomphysikalischen Messungen einen neuen Urmeter als neues erstes Glied der Kalibrationskette geschaffen hätte, und dass dieser neue Urmeter von dort an maßgeblich war (so war es beim Erdumfang bei der französischen Revolution gewesen). Sondern die atomphysikalischen Messungen ersetzen den Urmeter. Niemand braucht, um die Maßeinheit “Meter” zu verwenden, Zugang zu einem Urmeter. Es gibt kein metrologisch maßgebliches Objekt “Urmeter” mehr. Jedes gut ausgerüstete Labor kann die entsprechenden atomphysikalischen Messungen selbst ausführen, und die daraus rekonstruierte Maßeinheit “Meter” als Grundlage für seine Längenmessungen verwenden.
Bei Ihren weiteren Fragen will ich, soweit sie den obigen Blogbeitrag betreffen, sehen, ob ich hie und da in der Tat noch ausführlicher werden kann. Ich will jetzt nicht über Zehntklässler spekulieren, aber auch so geben mir Ihre Kommentare ja durchaus Hinweise darauf, wo man noch etwas missverstehen kann.
Einige Ihrer Fragen passen allerdings nicht recht in den obigen Blogbeitrag – wahrscheinlich sollte ich direkt zum Meter noch einen eigenen Beitrag machen (wie ich es gerade für die Sekunde getan habe), und die verschiedenen Arten der Längenmessung sind, unabhängig von der zugrundeliegenden Einheit, sicher auch ein Thema für sich.
Für die praktische Realisierung des Meters im Laboratorium hat sich durch die Definition von 1983 weniger geändert, als man auf den ersten Blick meinen könnte. Dabei wird die Definition nämlich gar nicht direkt verwendet, sondern der Umweg über Wellenlängen genommen:
Quelle: http://en.wikipedia.org/wiki/Metre#Speed_of_light
Antwort von MP: Zulässig ist, soweit ich den “mise en pratique” erinnere, beides: Laufzeitmessungen und der Übergang von der Frequenz zur Wellenlänge. Der Grund für den Übergang ist wohl in der Tat gewesen, dass die spezielle 1960 ausgewählte Wellenlänge nicht mehr so genau genug gemessen werden konnte, wie es für die Praxis nötig war. Mit der neuen Definition gab es dann auf einen Schlag eine ganze Reihe von Wellenlängen, die sich mit hinreichender Genauigkeit messen lassen.
Keine gute Idee
@ Dr. Markus Pössel:
“Ich glaube, da liegt noch (mindestens) ein Missverständnis vor. Im Gegensatz zur Orientierung des ursprünglichen Meters am Erdumfang sind die neuen Definitionen tatsächlich die Festlegung der Maßeinheit.
Sprich: Es ist nicht so, dass man 1960 bzw. 1983 nach einer bestimmten Vorschrift aus atomphysikalischen Messungen einen neuen Urmeter als neues erstes Glied der Kalibrationskette geschaffen hätte, und dass dieser neue Urmeter von dort an maßgeblich war (so war es beim Erdumfang bei der französischen Revolution gewesen). Sondern die atomphysikalischen Messungen ersetzen den Urmeter. Niemand braucht, um die Maßeinheit “Meter” zu verwenden, Zugang zu einem Urmeter. Es gibt kein metrologisch maßgebliches Objekt “Urmeter” mehr. Jedes gut ausgerüstete Labor kann die entsprechenden atomphysikalischen Messungen selbst ausführen, und die daraus rekonstruierte Maßeinheit “Meter” als Grundlage für seine Längenmessungen verwenden.“
Sorry, aber bei mir lag auf jeden Fall dieses Missverständnis nicht vor: Ich habe ja schon am Anfang selbst hervorgehoben, dass zum ersten Mal in der Geschichte der Maßeinheit Meter eine Messung als Maßeinheit gewählt wurde, anstatt einem materiellen Urmaßstab, was zu vielen Verwirrungen und Missverständnissen geführt hat, siehe zum Beispiel hier: http://www.wissenslogs.de/…/page/6#comment-27061
Ich habe auch hervorgehoben, dass die Wahl einer Messung als Maßeinheit und als Maßstab aus meiner Sicht gar keine gute Idee war und habe zum Beispiel auch Helmut Hille zitiert (ich finde aber jetzt nicht mehr wo, man findet sich nicht mehr so ganz zurecht in diesen vielen zersplitterten Blogs):
Zitate Helmut Hille aus seiner Arbeit Messen als Erkenntnisakt:
“1. Maßstäbe werden nicht gemessen sondern gesetzt
Wie ich zeigen werde, haben wir heute eine Situation, in der sich niemand daran stößt, wenn zwischen dem Maß als Meßmittel und dem Gegenstand des Messens nicht klar unterschieden wird und wenn in Meßeuphorie geglaubt wird, auch Maße messen zu können.
[…]
Maßstäbe und ihre Einheiten sind keine Frage der Wahrheit sondern der Gültigkeit. Sie werden nicht durch Tatsachen sondern durch Normen bestimmt.
[…]
Und mit was will man überhaupt messen, wenn die Maßeinheiten selbst erst gemessen werden müßten???“
Ja, mit was wollen Sie zum Beispiel die Strecke bei einer Messung der Lichtgeschwindigkeit oder mit der Lichtgeschwindigkeit messen, die ausgerechnet die Länge des Meters als Meßergebnis bestimmt? Perfekter Zirkelschluß. 🙁
Und wozu braucht man eine Definition für eine Maßeinheit? Ob der Meter das 1/40 Millionsten des Erdumfanges darstellen sollte, oder das 1/25 Millionsten des Mondumfanges oder aber die Länge von einem in China umgekippten Sack Reis, ist es völlig egal: Ein Meter ist die Länge eines per Konvention ausgewählten Gegenstandes, das wir als Urmeter erklären, Punkt, fertig, aus.
Auch die Messung der Lichtgeschwindigkeit als Maßeinheit ist keine „Definition“, sie ist eine Entscheidung, sie ist eine Auswahl, genauso wie die Auswahl eines Gegenstandes als Urmaßstab: Man hat 1983 entschieden, dass ein Meter die Strecke ist, die das Licht im Vakuum in einer Zeit von 1/299.792.458 Sekunde zurücklegt. Einzig dieses Meßergebnis, und kein anderes, ist die Länge des Meters. Das Ergebnis dieser Messung (es war eigentlich ein gemitteltes Ergebnis aus mehreren Messungen) ist der Meter, und keine andere Messung der Lichtgeschwindigkeit oder mit der Lichtgeschwindigkeit, und kein anderes Ergebnis.
Und nein, das war und bleibt aus meiner Sicht keine gute Idee für die Wissenschaft 1983 das Ergebnis von gemittelten Messungen der Lichtgeschwindigkeit als Maßeinheit zu erklären, also die Maßeinheit gemessen zu haben: Eine Messung ist zwangsläufig mit Fehlern behaftet, das kann man nicht verhindern, vor allem eine so empfindliche und störanfällige Messung wie die Messung der Lichtgeschwindigkeit, die sich auch mit modernen Instrumenten am Rande der Meßbarkeit befindet – das können Sie ruhig für die 10-Klässler im Blog-Text erklären. Die Reproduzierbarkeit dieses einen ausgewählten Meßergebnisses ist von daher so gut wie nicht gewährleistet, sondern es ist meiner Meinung nach im Gegenteil 100%ig davon auszugehen, dass alle Länder eine andere Länge für den Meter bei der Messung ihrer Prototypen mit dem Licht bestimmen, zumal sie nicht mehr geeicht werden. Sie haben mich nicht überzeugt, dass es nicht der Fall sein kann. Das spielt zwar gar keine Rolle in der Praxis, weil die Variationen sowieso nur rein mathematisch als Dezimalstellen sich auswirken, die in der Praxis nicht realisierbar sind, aber das war keine gute Idee für die theoretische Physik und für die Interpretation der Experimente mit der Lichtgeschwindigkeit (Mathematismus in der theoretischen Physik).
Zitat Dr. Markus Pössel:
“Einige Ihrer Fragen passen allerdings nicht recht in den obigen Blogbeitrag – wahrscheinlich sollte ich direkt zum Meter noch einen eigenen Beitrag machen (wie ich es gerade für die Sekunde getan habe), und die verschiedenen Arten der Längenmessung sind, unabhängig von der zugrundeliegenden Einheit, sicher auch ein Thema für sich.“
Wann dürfen wir über die Spezielle Relativitätstheorie sprechen?
Viele Grüße
Jocelyne Lopez
Antwort von MP: Kurios. Erst führen Sie lang und breit aus, dass Sie dem genannten Missverständnis nicht unterliegen, und dann kommt ein Satz wie “Ein Meter ist die Länge eines per Konvention ausgewählten Gegenstandes, das wir als Urmeter erklären, Punkt, fertig, aus.” – nein, das ist der Meter eben gerade nicht mehr. Exakt darin besteht das Missverständnis, das ich meine. Es gibt seit 1960 keinen ausgewählten Gegenstand mehr. Nur noch eine Vorschrift, wie jedes entsprechend ausgerüstete Labor die Länge der Maßeinheit aus bestimmten atomphysikalischen Experimenten rekonstruieren kann. (Was das für Vorteile hat, wird ja im obigen Blogbeitrag ausführlich beschrieben.)
Dass Sie sich zum einen eifrig beschweren, sobald ich mal eine Ihrer Fragen zu den Maßeinheiten nicht gleich beantworte, und mir jetzt umgekehrt Vorwürfe machen, weil ich signalisiert habe, die zahlreichen Fragen in Ihrem letzten Kommentar zu beantworten und sich damit der Übergang zur Speziellen Relativitätstheorie verzögert, ist übrigens, zurückhaltend ausgedrückt, eine Frechheit. Aber es passt natürlich ins Schema; nur ja keine Möglichkeit für einen persönlichen Anwurf auslassen.
@ Dr. Markus Pössel
“Kurios. Erst führen Sie lang und breit aus, dass Sie dem genannten Missverständnis nicht unterliegen, und dann kommt ein Satz wie “Ein Meter ist die Länge eines per Konvention ausgewählten Gegenstandes, das wir als Urmeter erklären, Punkt, fertig, aus.” – nein, das ist der Meter eben gerade nicht mehr. Exakt darin besteht das Missverständnis, das ich meine. Es gibt seit 1960 keinen ausgewählten Gegenstand mehr. Nur noch eine Vorschrift, wie jedes entsprechend ausgerüstete Labor die Länge der Maßeinheit aus bestimmten atomphysikalischen Experimenten rekonstruieren kann. (Was das für Vorteile hat, wird ja im obigen Blogbeitrag ausführlich beschrieben.)“
Das Missverständnis haben Sie ja selbst in Ihrem Blog-Text eingeführt und gepflegt, indem Sie sich über die Reproduzierbarkeit des materiellen Urmaßstabes im Blog-Teil I ausgelassen, sogar mit Bild, und davon in der Gegenwart gesprochen haben – dafür aber kein Wort über die Reproduzierbarkeit des Maßstabes „Messung mit der Lichtgeschwindigkeit“ verloren haben:
02.12.2010 – Zitat Dr. Markus Pössel:
”Urtyp eines Längenmaßes ist ein Maßstab, also ein Festkörper mit gerader Kante, darauf zwei Markierungen, die Nullmarke und die Einsmarke, die unsere Längeneinheit definieren. Alle anderen Abstände und Längen wollen wir als Vielfache oder mit Hilfe von Bruchteilen des Abstands dieser beiden Marken angeben. Wenn wir in diesem Zusammenhang davon reden, der Abstand zweier Punkte habe den Wert 2, ist damit gemeint, dass die Verbindungsstrecke der Punkte gerade doppelt so lang ist wie unsere Längeneinheit. Der so gemessene Abstand soll, so unsere Zuordnung, dem euklidischen Abstand entsprechen.
Streben wir eine besonders hohe Genauigkeit an, müssen wir sicherstellen, dass sich unser Maßstab so wenig wie möglich verformt. Beim wohl bekanntesten Längenmaß, dem in Paris aufbewahrten Urmeter, und bei seinen Kopien, ist das durch einen besonders stabilen Querschnitt sichergestellt; hier eine entsprechende Ansicht der Urmeter-Kopie, die jetzt im deutschen Museum aufbewahrt wird: (Bild)
Außerdem müssen wir berücksichtigen, dass sich Festkörper je nach Temperatur ein wenig ausdehnen oder zusammenziehen können; wir können unseren Maßstab dazu aus einem Material herstellen, dessen Länge sich mit wechselnder Temperatur so gut wie nicht verändert (“Invar”), oder unsere Konstruktionen und Messungen sämtlich bei einer konstanten Temperatur durchführen, oder beides.“
Kurios. Wie sollen denn 10-Klässler daraus erkennen, dass das alles nicht mehr gilt? Woher sollen 10-Klässler wissen, wie es mit der Reproduzierbarkeit der Länge des Meters mit der Lichtgeschwindigkeit steht und welche Nachteile bei der Reproduzierbarkeit bestehen? Darüber haben Sie kein Wort in Ihrem Blog-Text verloren, das habe ich Ihnen nur mit Mühe und Not im Diskussionsteil aus der Nase ziehen müssen (zunächst seitenlang übrigens bei Ihrer großzügigen Duldung von persönlichen Angriffen gegen mich).
Zitat von Dr. Markus Pössel:
“Dass Sie sich zum einen eifrig beschweren, sobald ich mal eine Ihrer Fragen zu den Maßeinheiten nicht gleich beantworte, und mir jetzt umgekehrt Vorwürfe machen, weil ich signalisiert habe, die zahlreichen Fragen in Ihrem letzten Kommentar zu beantworten und sich damit der Übergang zur Speziellen Relativitätstheorie verzögert, ist übrigens, zurückhaltend ausgedrückt, eine Frechheit. Aber es passt natürlich ins Schema; nur ja keine Möglichkeit für einen persönlichen Anwurf auslassen.“
Dass Sie trotz eindeutigen und zahlreichen Anzeichen der Leser Ihrer Einführung „Einstein verstehen“ seit dem 02.12.2010, dass ein großes Gesprächsbedarf über die Spezielle Relativitätstheorie besteht und dass man auf das Thema übergehen sollte, langatmig und scheinbar endlos das Thema immer wieder auf später verlagern, ist aus meiner Sicht zurückhaltend ausgedrückt eine Frechheit. Die Frustration der Leser und engagierten Teilnehmer Ihrer Einführung bei Ihrem Gebot „nicht vorgreifen“ könnten Sie ruhig verstehen. Ich kann mir auch nicht vorstellen, dass 10-Klässler so viel Geduld und Lernwilligkeit mitbringen, eine so strukturierte Einführung in “Einstein verstehen” zu verfolgen – diese Kritik sollten Sie als Aufklärer verkraften können und nicht als „persönlichen Anwurf“ einsehen.
Viele Grüße
Jocelyne Lopez
Antwort von MP: (1) Ich vermute, dass
einigermaßen clevere Zehntklässler direkt den obigen Blogtext lesen, wo ja durchaus von der direkten Reproduktion einer Maßeinheit durch
Laborexperimente die Rede ist. Aber wie gesagt: Ich kann gerne
schauen, ob ich das noch deutlicher herausarbeiten kann.
(2) Ich verstehe die Frustration durchaus, aber ich sehe keine
Alternative. Denn dass chaotische Diskussionen, in denen die
gemeinsame Grundlage fehlt, auch kein gangbarer Weg sind, zeigen ja
nun wirklich viele Beispiele im Netz. Nicht zuletzt unsere eigene
E-Mail-Diskussion, wo ich alle Nase lang das Problem bekam,
elementares Vorwissen vorausgesetzt zu haben, das dann doch nicht vorhanden
war. Ich denke wirklich, dass es zu diesem
Schritt-für-Schritt-Vorgehen keine Alternative gibt.
Ausbremsen
@Jocelyne Lopez
Frau Lopez fragt: “Und wozu braucht man eine Definition für eine Maßeinheit?“
Herr Hille antwortet: “Als Bekanntes ist das Normal das in allem Messen Gleichbleibende mit dem verglichen wird. Daher muß die Wissenschaft der Messung, die Metrologie, durch geeignete Normale und Definitionen dafür sorgen, daß ihre Maßeinheiten möglichst unveränderlich sind und weltweit gelten. […] Erst wenn das Meter z. B. mit Hilfe des Lichtwegs definiert ist, kann das Urmeter oder seine Skalierung durch diesen Lichtweg in sinnvoller Weise gemessen werden, weil es dann ein neues aktuelleres Urmeter gibt.“
Das stammt aus dem von Ihnen verlinkten Text “Messen als Erkenntnisakt”, Hervohebungen von mir.
Zitieren Sie den Herrn Hille nun eigentlich als Zeugen der Anklage gegen Dr. Pössel oder als Zeugen zu seiner Verteidigung?
Eichung der Länge des Meters
@ Dr. Markus Pössel:
“(1) Ich vermute, dass einigermaßen clevere Zehntklässler direkt den obigen Blogtext lesen, wo ja durchaus von der direkten Reproduktion einer Maßeinheit durch Laborexperimente die Rede ist. Aber wie gesagt: Ich kann gerne schauen, ob ich das noch deutlicher herausarbeiten kann.“
Ich stellte bei einem Leser unseres letzten Austausches in einer anderen Diskussion fest (kein Zehntklässler), dass er die Vorstellung hat, die einzelnen Länder würden jetzt keinen eigenen materiellen Prototyp des Meters mit einer Labor-Messung mit der Lichtgeschwindigkeit anfertigen, also dass es materielle Prototypen des Meters jetzt nirgendwo mehr gibt – dementsprechend auch keine geeichte. Ich kann mir es dagegen nicht richtig vorstellen: Ich stelle mir vor, dass das jeweilige Eichamt im jeden Land einen Meter-Prototyp als Grundlage der industriellen Massenanfertigung von materiellen Maßstäben anfertigt (also geeicht). Wie läuft es wirklich bei der Eichung zur industriellen Massenanfertigung von materiellen Maßstäben?
Viele Grüße
Jocelyne Lopez
Antwort von MP: Nationale materielle Prototypen als Ausgangspunkt der Festlegung der Maßeinheit Meter in Deutschland gibt es in der Tat nicht mehr. Das erste Glied der Kalibrationskette ist auch auf nationaler Ebene das Laborexperiment nach den Vorschriften der offiziellen Definition und des “mise-en-pratique” des Meters.
Bei den zweiten oder dritten Gliedern der Kalibrationskette dürften in der Tat noch materielle Vergleichskörper (“Normale”) zum Einsatz kommen. Zumindest dort, wo die benötigte Genauigkeit nicht allzu hoch liegt. Für viele industrielle Anwendungen dürfte die Eichung mit solch einem Normal vollkommen ausreichen.
Tja — aber …
Markus Pössel schrieb (nach 15.06.2011 | 00:29):
> Irgendwie scheint Ihnen das Grundkonzept dieser Einführung immer noch völlig fremd
… ich war mir vor allem gar nicht sicher, ob der vorliegende Artikel als Bestandteil “dieser Einführung” (“Einstein verstehen …”) gedacht ist. Dann tu ich mal weiter so, als ob …
> Ich versuche die Leser relativ weit am Anfang abzuholen – bei den “prä-physikalischen Alltagsvorstellungen”, wenn Sie so wollen.
Das find ich ja prima; tja — aber …
> Die Vorstellung, die die Leser von Phänomenen wie Bewegung mitbringen, wird dabei Schritt für Schritt verfeinert.
… warum sollte man nicht ausdrücklich Leser einschließen, deren “prä-physikalischen Alltagsvorstellungen” lediglich in der Fähigkeit besteht, lesen zu können (Buchstaben wiedererkennen, die Reihenfolge der Wahrnehmungen von Buchstaben beurteilen)?
Mehr Vorstellungsvermögen und Verständnis ist zum “Einstein verstehen” doch sicher nicht erforderlich und vorauszusetzen. Genau das berechtigt doch zu dem Anspruch, “Einstein verständlich machen” zu können. (Einen Anspruch, den man bzgl. Aristoteles oder Galileo oder Newton oder Maxwell sicher nicht hat.)
Eine Einführung in die RT, die spezifischere Anforderungen stellt und entsprechende “tja — aber”-Einwände herausfordert, wird m. E. der RT nicht gerecht.
> Mit “praktisch durchführbar” meinte ich übrigens in der Tat, dass das Verfahren in der Wirklichkeit umsetzbar sein sollte, nicht nur als Gedankenexperiment im Rahmen eines bestimmten Axiomensystems. Ich kann mir zum Vergleich vergangener Versionen des Urmaßstabs mit sich selbst nämlich momentan nur nicht realisierbare Messungen vorstellen, bei denen man eine so große Messanordnung aufbaut, dass Lichtlaufzeiten in der gewünschten Größenordnung von Jahren oder Jahrzehnten auftauchen. Aber das ist praktisch heute und in absehbarer Zukunft nicht realisierbar.
Das halte ich erstens für pessimistisch — immerhin tauschten die Bestandteile “des Urmaßstabs” doch sicherlich über Jahrzehnte hinweg ganz praktisch Signale miteinander aus; sonst wäre zu erwarten, dass sich das gute Stück schon längst in Luft aufgelöst oder als Pfütze ausgebreitet hätte.
Zweitens ist schon allein unmissverständliche Vorstellbarkeit wertvoll, auch bei eingeschränkter Durchführung; nämlich um den systematischen Vertrauensbereich dessen zu bewerten, was aus dem praktisch und tatsächlich Durchgeführtem geschlussfolgert würde.
Wenn man sich nicht festlegt, wie zumindest im Prinzip zu messen wäre, ob und in welcher Hinsicht z.B. “der Urmaßstab” “gleich” blieb,
dann ist die Behauptung “der blieb gleich” genauso wertlos wie die Behauptung “der blieb nicht gleich”. Man könnte sich bestenfalls darauf verlassen, nach wie vor die selben Bestandteile “des Urmaßstabs” zu beobachten.
Antwort von MP: Zum Status als Ergänzungstext von “Einstein verstehen siehe den ersten Absatz des Blogbeitrags.
Zu den Voraussetzungen: Falls Sie für die von Ihnen vorgeschlagene Art der Einführung nicht völlig neue Begriffe für Konzepte wie Länge, relative Ruhe, Geschwindigkeit etc. verwenden wollen – und dann dürften Sie die meisten Leser ziemlich rasch verlieren – müssen Sie an die prä-physikalischen Vorstellungen irgendwie anknüpfen.
Zu den Lichtlaufzeiten: Ungestörte Lichtausbreitung bekommen Sie über diese Zeiträume hinweg sicher nicht. Dazu, das Gleichbleiben zumindest abzuschätzen, dienen die im Text erwähnten Ensemblemessungen; Gleichbleiben aller Ensemblemitglieder impliziert nun einmal, dass bei diesen Messungen immer das Gleiche herauskommt.
Reproduktionen der Länge des Meters
@ Dr. Markus Pössel:
“Zu Ihrem letzten Absatz: Wo die Luftverschmutzung stört, benutzt man Filter (Reinraumbedingungen); eine Reihe von Versuchsanordnungen in der Laseroptik sind sowieso zum Teil in Vakuumkammern untergebracht. Wo der Luftdruck eine Rolle spielt und man kein Vakuum braucht, gibt es geeignete Druckkammern.“
Hier habe ich drei Fragen:
1. Spielt der Luftdruck dann eine Rolle bei der Reproduktion der 1983 festgesetzten Länge des Meters mit der Strecke, die das Licht im Vakuum in 1 / 299.792.458 Sekunde zurücklegt? Bestimmt man dann eine andere Lichtgeschwindigkeit, sprich eine andere Länge des Meters, wenn die Eichämter der Länder die Länge des Meters z.B. in Genf, in Mexiko oder in London reproduzieren wollen? Bei welchem Luftdruck wurde dieser festgesetzte Wert bestimmt bzw. bei welchem Luftdruck ist die genaue Reproduktion der Länge des Meters gewährleistet?
2. Wikipedia spricht auch bei Messungen mit der Lichtgeschwindigkeit von Variationen in der Präzision je nach Distanzen, wie ich es zum Beispiel in meinem Beitrag http://www.wissenslogs.de/…/page/6#comment-26955 zitiert habe:
“Die optische Abstandsmessung (auch: Laserentfernungsmessung) wird benutzt um die Distanz zwischen einem Abstandssensor und einem Objekt zu messen. Die Präzision hängt von verschiedenen Faktoren ab:
• von der Oberfläche der beiden Objekte (Material, Farbe)
• von der zu messenden Distanz
• von Umwelteinflüssen“
Bei welcher Distanz wurde 1983 die festgesetzte Länge des Meters erzielt bzw. bei welcher Distanz wird die Reproduktion dieser Länge gewährleistet?
3. Wikipedia spricht auch von Variationen der Werte der Lichtgeschwindigkeit je nach Farbe, also je nach Frequenz.
Bei welcher Frequenz des Lichts wurde 1983 die festgesetzte Länge des Meters bestimmt bzw. bei welcher Frequenz ist die Reproduktion dieses Wertes gewährleistet?
Gibt es festgesetzte und verbindliche internationale Vorschriften, wonach die Länder die Reproduktion der Länge des Meters in ihren jeweiligen Laboren vorzunehmen haben? Wenn ja, wie wird die Einhaltung dieser Vorschriften durch die jeweiligen Länder kontrolliert?
Viele Grüße
Jocelyne Lopez
Alles was du anbringst bringt keine Pkte
Markus Pössel schrieb (nach 17.06.2011 | 00:35):
> Falls Sie für die von Ihnen vorgeschlagene Art der Einführung nicht völlig neue Begriffe für Konzepte wie Länge, relative Ruhe, Geschwindigkeit etc. verwenden wollen […]
Doch hoffentlich genau diejenigen, die man erreichen könnte, wenn irgendwelche “prä-phsikalische Vorstellung[en …] Schritt für Schritt verfeinert ” würden (entsprechend dem in diesem Blog vorgesehen Vorgehen, skizziert nach 15.06.2011 | 00:29).
Wenn man dabei irgendwelche prä-phsikalische Vorstellungen zunächst als nachvollziehbar erscheinen lässt, um danach doch zu versuchen sie wegzuschleifen, dürfte ein solches Vorgehen Leser wohl eher verprellen, als wenn von vornherein klargestellt wird, welche prä-phsikalische Vorstellungen durchweg als uneingeschränkt nachvollziehbar gelten, und man sich auf genau diese konzentriert.
> Zu den Lichtlaufzeiten: Ungestörte Lichtausbreitung bekommen Sie über diese Zeiträume hinweg sicher nicht.
Diese Erwartung stellt offenbar einen Vorgriff dar, weil Begriffe wie “gestörte Lichtausbreitung” und z.B. “Brechungsindex” erst noch als Messgrößen zu definieren wären.
Sicher: viele Gedankenexperimente der RT, und entsprechend erhaltene Messwerte, verstehen sich “vorbehaltlich eventueller weiterer Festsetzungen und Feststellung zum Brechungsindex in der beobachteten Region”.
(Ohne zu weit vorgreifen zu wollen: sind diese Festsetzungen im Rahmen von “Einstein verstehen” überhaupt vorgesehen?)
Genauso können bestimmte Messwerte vorbehaltlich weiterer Festsetzungen zur Definition der Messgröße “Temperatur” angegeben werden, um dann ggf. z.B. “auf 0 K bezogen” zu werden;
oder weiterer Festsetzungen zur Definition der Messgröße “el.-mag. Feld”, um dann ggf. “auf ein homogenes el.-mag. Feld bezogen” zu werden; usw.
> Dazu, das Gleichbleiben zumindest abzuschätzen, dienen die im Text erwähnten Ensemblemessungen;
Da war meine diesbezügliche Kritik …
(Je zwei gegebene unterscheidbare “Referenzobjekte”, “Körper”, “Prototypen” oder Artefakte welcher Art auch immer sind a priori verschieden;
man mag allenfalls (Versuch für Versuch) messen, ob oder in wie fern sie einander gleich waren. 31.05.2011 | 04:58)
… wohl noch nicht eindringlich genug.
> Gleichbleiben aller Ensemblemitglieder impliziert nun einmal, dass bei diesen Messungen immer das Gleiche herauskommt.
Eher: dass das gegebene bzw. betrachtete Ensemble nicht unbedingt alle Eventualitäten ausschöpft, die im Rahmen des Wertebereiches des zum Vergleichen eingesetzten Messoperators liegen.
PTB Realisierung des SI Meters
Zur Realisierung des Meters verwendet auch die PTB diverse Laser Wellenlängen. Mehr dazu findet sich z.B. hier
http://www.ptb.de/…ereinheiten/das-si/meter.html
und speziell hier
http://www.ptb.de/…serwellenlaengennormalen.html