Einstein verstehen V: Klassische Mechanik – Kräfte, starre Körper, verschiedene Anwendungen
BLOG: RELATIV EINFACH

Dies ist Teil V einer Online-Einführung in die Spezielle Relativitätstheorie, die hier im Blog einen “Testlauf” absolviert und später – u.a. durch Feedback der Blogleser verbessert – ein Teil des Webportals Einstein Online werden soll. Nähere Informationen zu den Hintergründen finden sich in Einstein verstehen: Ein Blogexperiment, Teil I.
[Derzeit sind online: Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7]
Bislang geht es in der Einleitung noch um die “Vorarbeiten”: um diejenigen Konzepte aus der klassischen Physik – der Physik vor Relativitätstheorie und Quantentheorie – die man kennen muss, um zu verstehen, vor welchem Hintergrund und auf welcher Grundlage Einstein die Spezielle Relativitätstheorie einführte. Dieser Teil schließt direkt an Teil 4 Klassische Mechanik – Massenpunkte, Newton’sche Gesetze, Impuls, an. Dort hatte ich einige grundlegende Konzepte und Gesetze der klassischen Mechanik vorgestellt – zuletzt den Impuls, in isolierten Systemen eine Erhaltungsgröße. Die zeitliche Änderung des Impulses eines Teilchens entsprach der auf das Teilchen wirkenden Kraft. Kraft ist bis dahin freilich nur ein allgemein definierter Begriff. Um physikalische Modelle formulieren zu können, müssen wir konkreter werden und spezifische Sorten von Kräften beschreiben. Zeit für einige einfache, aber vielfältig anwendbare Beispiele.
Kräfte I: Der harmonische (Feder-)Oszillator
Eine der einfachsten Kräfte führt zwei weitere idealisierte Gebilde ein, nämlich eine Feder (Gebilde 1), mit der ein Massenpunkt an einem unbeweglichen Objekt (Gebilde 2) befestigt ist. Die Feder hat eine Ruhelänge, nämlich ihre Länge in demjenigen Zustand, indem sie, einfach sich selbst überlassen und ohne äußere Einflüsse, in sich unbeweglich ruht.
Entspricht die Länge der Feder gerade ihrer Ruhelänge, dann macht die Feder keinerlei Anstalten, ihre Länge zu ändern, sondern bleibt so, wie sie ist. Dehnt man die Feder dagegen, so dass sie anschließend um Δl länger ist als ihre Ruhelänge (man stelle sich vor, dass man den Massenpunkt anfasst und etwas nach außen zieht), dann übt die Feder in diesem neuen Zustand auf den Massenpunkt eine Kraft mit dem Betrag
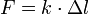
aus, wobei k Federkonstante der betreffenden Feder genannt wird. Je kräftiger die Feder, umso größer ist k. Die Kraft wirkt dabei so, dass sie versucht, die Feder zusammenzuziehen – also hin zu der Ruhelage, in der die Feder gerade ihre Ruhelänge besitzt.
Staucht man die Feder um Δl, dann wirkt eine Kraft gleicher Stärke wie bei der Dehnung um Δl, diesmal aber in die Gegenrichtung: die Kraft bemüht sich, die Feder zu verlängern und damit wieder hin zur Ruhelänge zu kommen.
Wir betrachten dabei nur Bewegung und Auslenkung in eine Richtung, parallel zur Feder. Kompliziertere Bewegungen, bei denen die Feder seitlich verbogen wird, lassen wir außer Acht. In der Praxis kann man z.B. durch eine Führungsschiene sicherstellen, dass sich der Massenpunkt tatsächlich nur entlang einer Raumrichtung hin oder zurück bewegen kann.
 Die Proportionalität von Auslenkung und Kraft heißt “Hooke’sches Gesetz”, nach Robert Hooke (1635-1703), einem Zeitgenossen und Widersacher Newtons, der dieses Gesetz anhand experimenteller Untersuchungen fand. Sein Versuchsaufbau, gleichzeitig Frontispiz seines Buches zum Thema, ist in dem Bild rechts dargestellt (danke, Wikimedia Commons).
Die Proportionalität von Auslenkung und Kraft heißt “Hooke’sches Gesetz”, nach Robert Hooke (1635-1703), einem Zeitgenossen und Widersacher Newtons, der dieses Gesetz anhand experimenteller Untersuchungen fand. Sein Versuchsaufbau, gleichzeitig Frontispiz seines Buches zum Thema, ist in dem Bild rechts dargestellt (danke, Wikimedia Commons).
Lenkt man die Feder aus, indem man an dem Massenpunkt zieht, und lässt dann los und überlässt Feder und Massenpunkt sich selbst, dann sieht man, warum solch ein System auch (eindimensionaler) harmonischer Oszillator genannt wird. Es beginnt nämlich zu schwingen, zu oszillieren: Die Feder zieht den Massenpunkt in Richtung Ruhelage; der Massenpunkt gewinnt dabei an Schwung (Impuls), der ihn über die Ruhelage hinausschnellen lässt; dadurch erfolgt als nächstes eine Stauchung der Feder, durch die sich eine Gegenkraft in der Feder aufbaut; diese Gegenkraft beschleunigt den Massenpunkt wieder in Richtung Ruhelage, der Massenpunkt gewinnt dabei Schwung, die Ruhelage wird wiederum überschossen, es kommt zu Dehnung, Überschießen, Stauchung, Überschießen usw. in unaufhörlicher Folge.
Das Adjektiv “harmonisch” zeigt an, dass die Auslenkung eines solchen Systems (zumindest in guter Näherung) einer Sinusfunktion
folgt, das einfachste Beispiel einer Klasse von Funktionen, die Mathematiker harmonisch nennen.
Das Adjektiv “eindimensional” zeigt schlicht an, dass wir nur Bewegungen in einer Richtung (hin und zurück) zulassen, nicht allgemein im Raum.
Der harmonische Oszillator ist eines der vielseitigsten Systeme der Physik. Jede Rückstellkraft, die auf eine Ruhelage hinstrebt, lässt sich näherungsweise (das heißt üblicherweise: für hinreichend kleine Auslenkungen) als harmonischer Oszillator beschreiben.
Dementsprechend vielfältig sind die Anwendungen für dieses einfache Modell und seine Abkömmlinge: Sind mehrere Massenpunkte mit solchen Federn verbunden, dann lassen sich Modelle für schwingende Festkörper formulieren (darauf kommen wir unten noch zurück). In der Quantenmechanik, der derzeit besten Theorie zur Beschreibung von Atomen, Molekülen und anderen winzig kleinen Dingen, ist der harmonische Oszillator ebenfalls ein Schlüsselmodell. In einer der Vorlesungen während meines Physikstudiums fiel sinngemäß der Satz, wer alle Anwendungen des harmonischen Oszillators verstünde, der habe 90% der gesamten Physik verstanden.
Kräfte II: Gravitation
Zumindest in der Nähe der Erdoberfläche ist die Schwerkraft, die Gravitation, eine Kraft mit sehr einfachen Eigenschaften. Die Schwerkraft der Erde, die in Oberflächennähe auf einen Massenpunkt der Masse m wirkt, hat den Betrag m·g, wobei g die sogenannte Schwerebeschleunigung ist, die überall auf der Erde ungefähr den gleichen Wert besitzt, nämlich g = 9,81 m/s2 (genauer: recht genauen Messungen zufolge dürfte das Maximum bei 9,83366, das Minimum bei 9,76392 m/s2 liegen). Die Schwerkraft ist zum Erdmittelpunkt hin gerichtet. Wir nennen diese Richtung im Alltag “unten”.
Die Schwerkraft m·g, die auf das Teilchen wirkt, heißt auch Gewicht des Teilchens. Mit dieser Kraft drückt das Teilchen nämlich z.B. auf die Wagschale einer Waage. Dass g überall auf der Erde ungefähr den gleichen Wert besitzt, so dass Gewicht und Masse von Objekten in guter Näherung proportional sind, hat zu der unscharfen Sprachgewohnheit geführt, für “das Gewicht des Körpers beträgt g mal 50 Kilogramm” verkürzt zu sagen “das Gewicht des Körpers beträgt 50 Kilogramm”. Physikalisch ist das falsch – Kilogramm ist eine Maßeinheit für Masse, nicht für Gewicht.
Bei genauerer Betrachtung, und wenn wir uns nur weit genug von der Erdoberfläche entfernen auch durchaus bei weniger genauer Betrachtung, hat die Schwerkraft andere, weniger einfache Eigenschaften. Wie das Newton’sche Gravitationsgesetz beschreibt, hat die Schwerkraft, die zwischen zwei Massenpunkten mit den Massen m1 und m2 wirkt, die Stärke
![]()
mit G der Gravitationskonstante und r dem Abstand der Massenpunkte voneinander. Die Konstante G ist universell: nicht situationsspezifisch, sondern für die Schwereanziehung zwischen beliebigen Körpern gültig.
Eine Kraft dieser Stärke wirkt sowohl auf den ersten als auch auf den zweiten Massenpunkt. Die Kräfte sind gerade so gerichtet, dass der erste Massenpunkt direkt in Richtung des zweiten Massenpunktes gezogen wird und umgekehrt. Der Wert der Gravitationskonstanten beträgt
![]()
Ein kleiner Vorgriff: Dieses Gesetz gilt nicht nur für Punktmassen, sondern auch für kugelsymmetrische Massen, und damit in guter Näherung für Planeten, Kometen, Mond und Sonne. Mit Hilfe dieses Gesetzes und den Grundgesetzen der Mechanik kann man Berechnung zur Bewegung dieser Himmelskörper – zur Himmelsmechanik – anstellen, die weit über das hinausgeht, was vor Newton möglich war.
Die Kepler’schen Gesetze, veröffentlicht von Johannes Kepler (1571-1630) in den Jahren 1609 (Astronomia Nova) und 1619 (Harmonice Mundi), beschreiben die Bewegungen der Planeten um die Sonne zwar besser als alle ihre Vorgänger. Aber strenggenommen geben sie lediglich die Bewegung jeweils eines einzelnen Himmelskörpers um eine ortsfeste Zentralmasse richtig wieder. Sobald der Schwerkrafteinfluss der Himmelskörper untereinander wichtig wird, oder sobald es z.B. um Kometen geht, die nicht um die Sonne umlaufen, sondern nach ihrer Reise durch dass innere Sonnensystem auf Nimmerwiedersehen in die Tiefen des Alls entschwinden, sind die Kepler’schen Gesetze nicht mehr anwendbar.
Mit Newtons Gravitationsgesetz und seinen Grundgesetzen der Mechanik lassen sich zum einen die Kepler’schen Gesetze ableiten. Zum anderen kann man so berechnen, was jenseits von Kepler liegt: der Schwerkrafteinfluss der Himmelskörper untereinander und offene Kometenbahnen.
Edmond Halley konnte auf diese Weise Anfang des 18. Jahrhunderts berechnen, wie Jupiter und Saturn die Umlaufbahnen von Kometen beeinflussen. Damit und mit Zugriff auf historische Beobachtungen konnte er die Rückkehr eines bereits im 16. und im 17. Jahrhundert beobachteten Kometen vorhersagen.

Heute heißt dieser Komet, oben zu sehen auf seiner Reise durch das innere Sonnensystem im Jahre 1986, zurecht Halleys Komet. Halleys Vorhersage war ein wichtiger Schritt hin zur allgemeinen Akzeptanz der Newton’schen Mechanik.
Kräfte IIa: Die Schwerkraft nahe der Erdoberfläche
Näherungsweise ist die Schwerkraft, die einen Körper an der Erdoberfläche zu Boden zieht, konstant. Der Term 1/r2 in dem obigen Ausdruck für die Schwerkraft ändert sich nicht allzusehr, wenn wir für r anstelle des Erdradius die Kombination “Radius der Erdoberfläche plus einige Meter (oder sogar Kilometer, oder Dutzende Kilometer, oder hunderte Kilometer)” einsetzen. Das sieht man in dieser Aufstellung hier; 6.370.000 ist dabei der Erdradius in Metern:
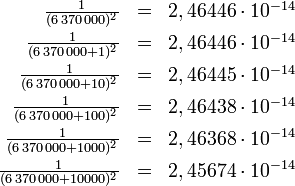
Selbst in 10 Kilometer Höhe über dem Erdboden unterscheidet sich der Ausdruck 1/r2 demnach um nur rund 0,3 Prozent von dem Wert auf Höhe des Meeresspiegels. In guter Näherung ist damit
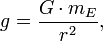
mit mE der Masse der Erde, überall auf der Erdoberfläche konstant. Die durch diese Formel definierte Größe g und ihren ungefähren Wert von 9,81 m/s2, der von Ort zu Ort nur etwas variiert, hatten wir bereits kennengelernt – ihre Größe damals aber noch nicht aus den Eigenschaften der Erde und der Gravitation ableiten können. Auf die hier gezeigte Weise ergibt sich aus der Newton’schen Formel für die Gravitationskraft die oben bereits getroffene Aussage, die Schwerkraft, die einen Körper in Nähe der Erdoberfläche zu Boden zieht, habe den Betrag F = mg mit konstantem g.
Starre Körper und der Begriff des Schwerpunkts
Für bestimmte Situationen liefert bereits die Beschreibung durch einzelne Massenpunkte gute Modelle. Ersetzt man beispielsweise Sonne, Planeten und Kometen durch Massenpunkte, dann erhält man bereits eine sehr genaue Beschreibung der verschiedenen Umlaufbahnen im Sonnensystem.
Die Festkörper, mit denen wir im Alltag umgehen, sind dagegen unserer Erfahrung nach nicht punktförmig, sondern besitzen eine räumliche Ausdehnung. Wo diese Ausdehnung eine Rolle spielt, bietet sich als einfachstes Modell der sogenannte starre Körper an. Ein solcher Körper besitzt eine Form, die sich im Raum geometrisch definieren lässt.
 Im einfachsten Falle könnte es sich um einen Würfel handeln, wie rechts dargestellt. Oder um eine Kugel, einen Quader, eine Pyramide. Oder aber um Formen, die aus solchen einfachen Grundformen zusammengesetzt sind – ebenso, wie man mit Lego komplexere Konstrukte aus einfachen Grundbausteinen bauen kann, können wir in Gedanken aus einfachen geometrischen Formen komplexere Gebilde zusammenbauen.
Im einfachsten Falle könnte es sich um einen Würfel handeln, wie rechts dargestellt. Oder um eine Kugel, einen Quader, eine Pyramide. Oder aber um Formen, die aus solchen einfachen Grundformen zusammengesetzt sind – ebenso, wie man mit Lego komplexere Konstrukte aus einfachen Grundbausteinen bauen kann, können wir in Gedanken aus einfachen geometrischen Formen komplexere Gebilde zusammenbauen.
Teil der Definition ist, dass der starre Körper seine Form nicht verändert: Er kann sich im Raum bewegen oder drehen, aber die Abstände zwischen je zwei charakteristischen Punkten seiner Form – etwa zwei bestimmten Eckpunkten, oder zwischen Markierungen auf der Körperoberfläche – ändern sich dabei nicht.
Zusätzlich zur Form des Körpers muss man festlegen, wie sich die Masse auf das Volumen des Körpers verteilt. Auch diese Verteilung ändert sich per Definition relativ zur Körperform nicht mit der Zeit. Die einfachste Massenverteilung ist komplette Homogenität, entsprechend einem Körper überall konstanter Dichte. Einen strukturlosen Körper aus einem einfachen Material wie Metall, Plastik, Glas oder Holz kann man in guter Näherung als homogenen Körper beschreiben.
Um aus den Grundgesetzen der Mechanik das Verhalten starrer Körper abzuleiten, zerlegen wir ihn gedanklich in winzig kleine Volumenabschnitte und behandeln jeden dieser Abschnitte wie einen Massenpunkt (mit genau definierter Position und Masse). Mit Hilfe der Infinitesimalrechnung lässt sich eine solche Zerlegung mathematisch stimmig und wohldefiniert durchführen.
Ein wichtiges Konzept ist dabei das des Schwerpunkts. Nummerieren wir die Volumenabschnitte, in die wir den Körper gedanklich zerlegt haben, von 1 bis n durch. Wir bezeichnen die Masse des Teilvolumens mit der Nummer i mit mi die Masse und die x-Koordinate des Teilvolumens mit xi (die Ortskoordinaten könnten wir beispielsweise über den geometrischen Mittelpunkt des Teilvolumens definieren). Dann ist die Größe
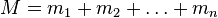
die Gesamtmasse des Körpers: Jedes Teilvolumen trägt seinen Teil der Masse zur Gesamtmasse bei. Die Summe über all die mi·xi für jedes der Teilchen, geteilt durch die Gesamtmasse M des Körpers, also
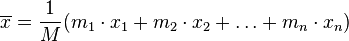
heißt x-Koordinate des Schwerpunkts des Körpers. Analog sind y- und z-Koordinate des Schwerpunkts definiert. Der Schwerpunkt ist der Ort, dem diese x-, y- und z-Koordinatenwerte zugeordnet sind.
Die Geschwindigkeit des Schwerpunktes, malgenommen mit der Gesamtmasse des Systems, entspricht dem Gesamtimpuls des Systems – der Summe der Einzelimpulse der vielen Volumenabschnitte, in die wir unseren Körper in Gedanken zerteilt haben. Das kann man wie folgt sehen: Die Geschwindigkeit des Schwerpunkts in x-Richtung ist die zeitliche Änderung der oben definierten x-Koordinate des Schwerpunkts, also auch die zeitliche Änderung der Summe, die in obiger Formel auf der rechten Seite steht.
Diese zeitliche Änderung wiederum erhält man, wenn man die zeitlichen Änderungen all der Summanden aufsummiert (das folgt direkt aus der in Teil IV gegebenen Definition der Änderungsrate; die Gesamtmasse M bleibt dabei unverändert). Die zeitliche Änderung von mi·xi ist, weil sich die Masse mi jedes der Teilvolumina nicht ändert, gerade gleich mi mal der zeitlichen Änderung von xi. Und die wiederum ist die x-Komponente der Geschwindigkeit des i-ten Teilvolumens, vix. Jene Größe, malgenommen mit mi, ist die x-Komponente des Impulses des i-ten Teilvolumens, pix. Endlich haben wir also
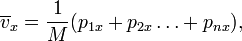
und damit ist die x-Komponente des Impulses des Schwerpunkts, nämlich
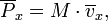
in der Tat die Summe all der Einzelimpulse der Teilvolumina. Der Schwerpunkt und seine Bewegung liefern damit eine ganz bestimmte zusammenfassende Information über den Körper.
Um die Bewegung des Körpers vollständig beschreiben zu können, bedarf es noch weiterer Informationen. Aber was können die einzelnen Teilvolumina eigentlich sonst noch tun? Ihre Abstände zueinander können sie per Definition nicht ändern; ihre Massen auch nicht. Ihren Abstand zum Schwerpunkt können sie demnach auch nicht ändern. Was sie aber können, ist gemeinsam um den Schwerpunkt zu rotieren. Die Bewegung des starren Körpers lässt sich also beschreiben, indem man zum einen angibt, wie sich sein Schwerpunkt bewegt, zum anderen, wie der Körper um den Schwerpunkt herum rotiert.
Zur Beschreibung der Rotation definiert man eine Reihe weiterer Größen, die ich am Ende von Teil IV in Bezug auf Punktteilchen schon kurz angesprochen hatte: die Rotations- oder Winkelgeschwindigkeit (analog zur Geschwindigkeit bei linearer Bewegung), proportional zur Winkelgeschwindigkeit den Drehimpuls (analog zum Impuls), das Drehmoment (analog zur Kraft), das den Drehimpuls ändert, und das Trägheitsmoment, dass bestimmt, wie sich die Winkelgeschwindigkeit ändert, wenn ein bestimmtes Drehmoment angreift (ungefähr analog zur Masse). Es ist sicher nicht schlecht, diese Begriffe einmal gehört zu haben; auf die Details werde ich an dieser Stelle aber nicht eingehen.
Massenkugeln und Massenschalen
Ein interessanter Spezialfall des starren Körpers ist die Massenkugel: ein kugelförmiger Körper, dessen Masse kugelsymmetrisch verteilt ist. Kugelsymmetrie bedeutet, dass sich die Massenverteilung nicht ändert, egal, wie wir die Kugel um ihren Mittelpunkt drehen. Einen solchen Körper kann man sich aus konzentrischen, in sich jeweils homogenen Schalen aufgebaut denken. Die Dichte kann dabei von Schale zu Schale durchaus variieren. Der Körper könnte beispielsweise immer dichter werden, je tiefer man Richtung Kugelmittelpunkt vordringt.
Auch einen solchen Körper kann man in Gedanken in Teilvolumina aufteilen, die Teilvolumina wie einzelne Massenpunkte behandeln und daraus berechnet, wie solch ein Körper vermittels der Schwerkraft auf andere Körper wirkt, oder wie die Schwerkraft anderer Körper auf ihn wirkt. Man findet in beiden Fällen, dass sich der Körper so verhält, als sei er ein Massenpunkt:
Ein außerhalb der Kugelfläche befindliches Punktteilchen wird von einer Massenkugel genau so angezogen, als befände sich statt der Kugel ein Punktteilchen mit der Gesamtmasse der Kugel am Ort des Kugelmittelpunkts. Dies ist genau der Grund, warum sich die Bewegung der (näherungsweise kugelförmigen) Planeten um die (näherungsweise kugelförmige) Sonne in guter Näherung durch die Bewegung von Punktmassen modellieren lässt.
Betrachtet man Massenschalen – Massenkugeln, um deren Mittelpunkt herum ein kugelförmiges Volumen ausgespart ist -, dann ergibt sich, dass eine solche Schale auf einen in ihrem Inneren befindlichen Körper gar keine Schwerkraft ausübt. Auf einen außerhalb befindlichen Körper wirkt dagegen auch eine Massenschale so, als sei ihre gesamte Masse in ihrem Mittelpunkt konzentriert, sprich: wie eine Punktmasse.
Kräfte III: Reibung
Eine weitere Sorte von Kräften, die für die Modellierung physikalischer Situationen wichtig ist, sind Reibungskräfte. Wir kennen aus dem Alltag hinreichend viele Beispiele: Der Stift, der über den Tisch rutscht und schließlich liegen bleibt, weil Reibungskräfte seine Bewegung hemmen. Der Fahrtwind, der uns beim Fahrrad- oder Autofahren entgegenbläst. Diese Kräfte zeichnen sich dadurch aus, dass sie die Bewegung des betroffenen Körpers (relativ zum Tisch, relativ zur Luft etc.) hemmen und verlangsamen, also entgegen der Bewegungsrichtung wirken. Die genaue Form der Reibungskräfte hängt von der Situation ab, die man modelliert.
Bestimmte Reibungskräfte, als Festkörperreibung bezeichnet, sind proportional zu jenem Anteil der Schwerkraft, die einen starren Körper auf eine ebene unterliegende Fläche drückt (“Normalkraft”). Zieht man den Körper über die Ebene, oder versucht man einen auf der Ebene ruhenden Körper in Bewegung zu setzen, dann wirkt eine Kraft entgegen der Bewegungsrichtung. Deren Stärke ergibt sich als Reibungskoeffizient mal dem erwähnten Schwerkraftanteil, der den Körper auf die Ebene drückt.

Heute verstehen wir diese Art von Reibung als Folge der winzigen Unebenheiten, die selbst scheinbar glatte Körper auf mikroskopischen Größenskalen aufweisen. Der Widerstand, der sich ergibt, wenn die unebenen Flächen “übereinanderrattern” und sich dabei immer wieder ein wenig ineinander verhaken bewirkt die Reibungskraft.
Ein Beispiel für diese Unebenheiten zeigt das Bild rechts: Eine glatte Metalloberfläche, hier eine Teilregion der Oberfläche einer Ein-Cent-Münze, sieht, mit einem Rastertunnelmikroskop betrachtet, gar nicht mehr so glatt aus, sondern zeigt eine Art Terrassenstruktur mit Absätzen und Vorsprüngen (hier habe ich weitere Bilder derselben Serie).
Wieder andere Reibungskräfte treten bei der Bewegung durch ein Medium wie Luft oder Wasser auf. Im einfachsten Falle sind sie proportional zur Geschwindigkeit, mit der sich der Körper durch das Medium bewegt (Stokessches Gesetz für kugelförmige Körper, die sich durch das Medium bewegen, ohne dass es zur Verwirbelungen kommt) oder zum Quadrat der Geschwindigkeit (Newton-Reibung, sobald die Geschwindigkeit so groß geworden ist, dass Verwirbelungen wichtig werden).
Zwei Beispiele für die Rolle von Reibungskräften im Alltag hatte ich bereits erwähnt. Andere Beispiele sind weniger offensichtlich. Wie wichtig die Reibung zwischen unseren Schuhsohlen oder Fußsohlen und dem Boden für unser Gehen ist, merken viele Menschen nur in jenen Ausnahmesituationen, wo diese Reibung drastisch reduziert ist – etwa auf spiegelglatter Eisfläche.  Und dass nur die Reibung die in unseren Kleidungsstücken verwebten oder eingestrickten Fädern und Fasern davon abhält, einen losen Haufen zu unseren Füßen zu bilden und uns unbekleidet zurückzulassen, ist den meisten Menschen gar nicht bewusst. Ohne Reibung würden die Fäden, aus denen Textilien bestehen – rechts eine Nahaufnahme von Kunstseide (Bild: Wikimedia Commons, gemeinfrei) – übereinandergleiten, auseinanderfallen, und sich in die elementaren Härchen auflösen, aus denen sie zusammengesponnen wurden.
Und dass nur die Reibung die in unseren Kleidungsstücken verwebten oder eingestrickten Fädern und Fasern davon abhält, einen losen Haufen zu unseren Füßen zu bilden und uns unbekleidet zurückzulassen, ist den meisten Menschen gar nicht bewusst. Ohne Reibung würden die Fäden, aus denen Textilien bestehen – rechts eine Nahaufnahme von Kunstseide (Bild: Wikimedia Commons, gemeinfrei) – übereinandergleiten, auseinanderfallen, und sich in die elementaren Härchen auflösen, aus denen sie zusammengesponnen wurden.
Für das Verständnis der Mechanik sind Reibungskräfte wichtig, da sie uns zeigen, wie die grundlegende Newton’sche Aussage “Körper, auf die keinerlei Kraft wirkt, bewegen sich mit konstanter Geschwindigkeit entlang gerader Bahnen” mit unserer Alltagserfahrung “Körper, die wir sich selbst überlassen, kommen nach einiger Zeit zur Ruhe” vereinbar ist. Selbst wenn wir einen Körper sich selbst überlassen, ihm also beispielsweise einen Schubs geben und ihn danach nicht weiter beeinflussen, sind da immer noch Reibungskräfte – Luftreibung, Rollreibung, Gleitreibung -, die den Körper abbremsen. Der Körper kommt nicht deswegen zur Ruhe, weil dies wie in der Aristotelischen Mechanik ein Grundgesetz für sich wäre, sondern weil Reibungskräfte auf ihn wirken.
Nicht-starre Körper
Starre Körper sind ein stark vereinfachtes Modell. Wir kennen zwar aus dem Alltag Körper, die in der Tat recht starr sind – eine dicke Eisenstange beispielsweise, einen Holzbalken, einen Stein. Aber unter den richtigen Bedingungen zeigt sich, dass dies nur eine Näherung ist. Eine lose aufgehängte Eisenstange, auf die man mit einer zweiten Eisenstange schlägt, gibt einen Ton von sich (man denke an ein/eine Triangel; z.B. in diesem YouTube-Video). Das ist ein deutliches Zeichen dafür, dass dieser auf den ersten Blick starre Körper unter geeigneten Umständen in sich schwingt, dabei seine Form etwas verändert und so die Luft um ihn herum ebenfalls zum Schwingen anregt. Becken sind ein Standardelement beim Schlagzeug (z.B. in diesem YouTube-Video). Auch beim Anschlagen eines Steins hinreichender Größe ergibt sich ein Ton (vgl. sogenannte Lithophone, z.B in diesem YouTube-Video).
Dass sich Eisenträger oder Holzbalken unter entsprechender Belastung durchbiegen, ist ein weiteres Zeichen dafür, dass es sich nicht um idealisierte Festkörper handelt. Die sogenannte elastische Verformung zeichnet sich dadurch aus, dass der Körper, wenn die Belastung aufhört, in seine Ausgangsform zurückkehrt. Ab einer gewissen Belastungsgrenze ist aber selbst für Metall ein Stadium erreicht, in dem der Körper sich unumkehrbar verformt und auch nach Ende der Belastung eine Verformung beibehält. Das wird plastische Verformung genannt.
Für all diese Situationen gibt es Modelle, die berücksichtigen, dass wirkliche Körper eben nicht perfekt starr, sondern verformbar sind. Ein mögliches Modell denkt sich den Körper aus Massenpunkten zusammengesetzt, die untereinander durch Federn verbunden sind, ähnlich denen, die ich im Zusammenhang mit dem harmonischen Oszillator erwähnt hatte. Hier ist ein solches Modell für den Fall einer Glocke schematisch dargestellt:
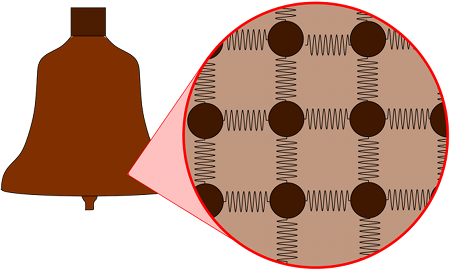
Der Ansatz der sogenannten Kontinuumsmechanik zerlegt den Körper gedanklich in winzige Teilvolumina, denen man jeweils eine Dichte zuschreiben kann; die Formen dieser Teilvolumina und ihre Positionen relativ zueinander können sich in diesem Modell mit der Zeit verändern – im Gegensatz zu den Verhältnissen beim starren Körper.
Wo beim starren Körper zusätzlich zur Schwerpunktbewegung nur die Rotation um den Schwerpunkt zu berücksichtigen war, kommt in diesen Modellen noch eine Beschreibung der Deformation hinzu. Dazu werden neue charakteristische Eigenschaften von Körpern eingeführt, wie die Poissonzahl (grob: wie beult der Körper nach außen aus, wenn man ihn in einer Richtung komprimiert?) und der Elastizitätsmodul (um welchen Betrag dehnt sich der Körper, wenn auf eine seiner Flächen eine äußere Kraft wirkt?).
Änderungen, die über die Trägheitsbewegung hinausgehen, werden, den Gesetzen der Newton’schen Mechanik folgend, durch Kräfte bewirkt. In der Kontinuumsmechanik sind das zum einen Volumenkräfte, die direkt auf jedes der Teilvolumina wirken, allen voran die Schwerkraft, die wir bereits kennengelernt haben. Darüber hinaus gibt es aber auch noch Flächenkräfte, die über die Oberflächen der Teilvolumumina übertragen werden. Ein einfaches Beispiel für solch eine Flächenkraft ist ein Körper, der auf einen anderen Körper Druck ausübt.
Die mit Hilfe dieser Modelle, entsprechender Annahmen über die Kräfte und der Gesetze der Newton’schen Mechanik gewonnenen Gesetze erlauben es beispielsweise zu beschreiben, wie sich eine Verformung durch einen langen Stahlträger fortplanzt, dem man an einem Ende entweder von der Schmalseite her (“longitudinal”) oder seitlich (“transversal”) einen plötzlichen Schlag versetzt. Dass die Verformungsgeschwindigkeit, die sogenannte Schallgeschwindigkeit in diesem Festkörper, fast 6000 Meter pro Sekunde (longitudinale Schallgeschwindigkeit) bzw. über 3000 Meter pro Sekunde (transversale Schallgeschwindigkeit) beträgt, erklärt, warum wir beispielsweise im Alltag nicht wahrnehmen, dass sich das andere Ende eines 6 Meter langen Stahlträgers, dem wir einen Schubs geben, erst eine Tausendstel Sekunde später in Bewegung setzt.
Übrigens gibt es auch eine Art von Reibungsart, die mit der Verformbarkeit von Körpern zusammenhängt: Die sogenannte Rollreibung, die die Rollbewegung eines Rades auf einer Oberfläche hemmt, kommt zustande, weil sich sowohl das Rad als auch die Oberfläche während des Rollens immer wieder ein wenig anders verformen.
Flüssigkeiten und Gase
Mit Hilfe der Teilvolumina, die komprimiert werden und sich gegeneinander bewegen können, kann man auf Grundlage der Newton’schen Mechanik auch die Dynamik von Flüssigkeiten und Gasen beschreiben. So gelangt man zum Teilgebiet der Fluiddynamik (mit Fluid als zusammenfassendem Begriff für Flüssigkeiten und Gase). Elemente des physikalischen Modellbaus sind dabei Eigenschaften wie Kompressibilität und Viskosität; auf die Flüssigkeit wirken ebenfalls die schon erwähnten Volumen- und Oberflächenkräfte. So entstehen Modelle etwa für Situationen, in denen ein Festkörper von Luft oder Wasser umströmt wird oder eine Flüssigkeit durch eine Rohranlage fließt.

Auf Grundlage solcher Modelle werden Flugzeuge, Schiffe, Tauchboote und Raumfahrzeuge ebenso entworfen wie Rohrsysteme, Zentrifugen oder Klimaanlagen. Auch für das Verständnis der Mechanik des menschlichen Körpers – wie fließt Blut durch das Herz? – liefert die Fluiddynamik wichtige Teilmodelle.
Oftmals muss man die Newton’sche Mechanik und Fluiddynamik dabei als Grundlage für Computermodelle verwenden, mit denen man die eigentlichen Rechnungen durchführen kann – realistische Situationen sind, wie überall in der Physik, in der Regel schlicht zu kompliziert, als dass man sie auf einem Blatt Papier direkt berechnen könnte. Das Bild rechts zeigt ein Beispiel für eine solche Simulation: Die Druckverhältnisse eine Minute nach dem Start eines Space Shuttles (lila und rot zeigen besonders hohen Druck an).
Nach diesem Ausflug in einige der Modelle, die man im Rahmen der klassischen Mechanik bauen kann, zurück zu den Grundlagen. Genauer: zu einer weiteren physikalischen Größe, die in der Mechanik eine wichtige Rolle spielt, nämlich der der Energie.
Kinetische und potenzielle Energie
Wir hatten mit dem Impuls bereits ein Beispiel für eine Erhaltungsgröße kennengelernt – anders gesagt: für eine Größe, deren Gesamtwert sich für ein gegebenes System von Teilchen oder Körpern nicht verändert, solange nicht äußere Einflüsse auf dieses System wirken.Eine zweite Erhaltungsgröße, die sich allerdings mit den hier bereits eingeführten Begriffen nicht ganz so einfach definieren lässt, ist die Energie. Fangen wir mit dem einfachsten Beispiel an.
Solange ein Massenpunkt unabhängig von jeglichen Einflüssen und ohne Einwirkung irgendwelcher Kräfte dahinfliegt, verändert die Größe
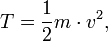
wobei m die Masse des Massenpunkts ist und v der Betrag seiner Geschwindigkeit, ihren Wert mit der Zeit nicht: sie ist konstant. In der Sprache der Physik handelt es sich damit um eine Erhaltungsgröße ähnlich wie die Komponenten des Impulses, von denen wir ja in Teil IV bereits gesehen haben, dass sie Erhaltungsgrößen sind.
Dass T erhalten bleibt ist in diesem einfachen Falle keine großartige Erkenntnis: Dem ersten Newton’schen Gesetz zufolge ist die Geschwindigkeit und damit der Geschwindigkeitsbetrag v des Massenpunkts konstant (denn per Definition wirken keine äußeren Kräfte), seine Masse per Definition auch; diese spezielle Kombination der beiden Größen ist damit, ebenso wie unendlich viele andere mögliche solcher Kombinationen, ebenfalls konstant.
Lassen wir zu, dass eine Kraft auf unseren Massenpunkt wirkt, dann erfährt der Massenpunkt eine Beschleunigung. Die Geschwindigkeit ändert sich dabei; ändert sich auch der Betrag der Geschwindigkeit, dann ändert sich auch die Größe T.
Auch wenn T für sich allein betrachtet in solchen Situationen damit keine Erhaltungsgröße mehr ist: In vielen Situationen gibt es eine Möglichkeit, zu T noch einen oder mehrere Ausdrücke hinzu zu addieren, so dass zumindest die Summe trotz des Wirkens äußerer Kräfte konstant bleibt.
Der einfachste Fall ist der eines Körpers in einem einfachen Schwerefeld mit konstanter Schwerebeschleunigung g. Wir hatten gesehen, dass dies ein nützliches Modell z.B. für fallende Gegenstände in der Nähe der Erdoberfläche ist. Für solch einen Körper kann man direkt ausrechnen, dass zwar nicht
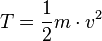
für sich genommen erhalten bleibt. Definiert man zusätzlich aber noch eine Größe
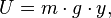
wobei die Gravitationsbeschleunigung in diesem Beispiel entgegen der y-Richtung (in Richtung auf kleinere y-Werte hin) wirken soll, dann kann man zeigen, dass die Größe T + U erhalten bleibt. Ich rechne das hier vor.
Das dürfte das einfachste Beispiel für die Erhaltung der Energie in Anwesenheit einer Kraft sein: T heißt Bewegungsenergie oder kinetische Energie des Teilchens. Die Größe T hängt, wie man an der Definition erkennt, in der Tat direkt mit der Bewegung zusammen, nämlich mit der Geschwindigkeit des Teilchens: hohe Geschwindigkeit entspricht große Bewegungsenergie. Der Ausdruck U ist ein Beispiel für potenzielle Energie oder Lageenergie des Teilchens; diese Energieform wird auch ganz allgemein häufig mit dem Symbol U bezeichnet, nicht nur in diesem speziellen Fall. Die hier definierte potenzielle Energie kommt dem Körper alleine deswegen zu, weil er sich in einem Gravitationsfeld befindet.
Fällt der Körper, dann nimmt seine potenzielle Energie ab, seine Bewegungsenergie zu. Anders gesagt: während der Körper beim Fallen immer schneller wird, wird die potenzielle Energie in Bewegungsenergie umgesetzt. Die kinetische Energie wächst genauso schnell an wie die potenzielle Energie abnimmt; dadurch bleibt die Gesamtenergie T + U konstant.
Die Energie als Erhaltungsgröße ist nicht nur als physikalisches Konzept von Interesse, sondern hat durchaus praktischen Nutzen: Will man anhand der Newton’schen Gesetze und konkreter Ausdrücke für die wirkenden Kräfte die Bewegung eines Körpers beschreiben, steht man jeweils vor der Aufgabe, aus Gleichungen für die Beschleunigung auf den Bewegungsverlauf schließen – im mathematischen Sprachgebrauch: eine Differentialgleichung zweiter Ordnung lösen – zu müssen. Mit Hilfe der Energie lassen sich zumindest einige Größen direkter und deutlich einfacher berechnen.
Betrachten wir als Beispiel einen Körper, den wir aus einer Höhe h0 nicht allzu hoch über dem Erdboden fallen lassen. Die Luftreibung soll dabei vernachlässigbar sein. Dann wirkt nur die (erdnahe) Gravitationskraft, und die Summe
![]()
bleibt während des gesamten Falls erhalten. In dem Moment, wo wir den Körper gerade bei der Höhe h0 loslassen, hat er noch die Geschwindigkeit Null. Entsprechend verschwindet seine Bewegungsenergie zu diesem Zeitpunkt, und wir haben dann also
![]()
Auf die Erde schlägt der Körper per Definition bei der Höhe-über-dem-Erdboden Null auf. Nennen wir die Aufschlaggeschwindigkeit va, dann ist direkt vor dem eigentlichen Aufprall und der damit einhergehenden Abbremsung des Körpers
![]()
Durch Gleichsetzung der beiden Ausdrücke auf der jeweils rechten Seite – beide geben schließlich T+U zu jeweils einem anderen Zeitpunkt an und müssen, weil die Gesamtenergie erhalten bleibt, gleich sein – erhält man auf einfachem Wege einen Ausdruck für die Aufschlaggeschwindigkeit, nämlich
![]()
Energie allgemein
Hatten wir einfach nur Glück, dass wir in dieser besonderen Situation einen Ausdruck U gefunden haben, der, zu T hinzu addiert, eine Erhaltungsgröße ergibt? Im Gegenteil: Wenn wir weitere physikalische Situationen betrachten, wird sich zeigen, dass es eine durchaus überschaubare Sammlung von Energiesorten gibt, die wir unserem Repertoire hinzufügen müssen, damit die Summe all dieser Teilenergien, also die Gesamtenergie, erhalten bleibt.
Berücksichtigen wir all diese Teilenergien, dann geht Energie in einem System nicht spontan verloren und erscheint nicht aus dem Nichts, sondern wenn sich die Gesamtsumme an Energie verändert, dann nur, weil dem System in nachvollziehbarer Weise Energie hinzugefügt oder entzogen wurde.
(Der Vollständigkeit halber: im Rahmen der Quantentheorie und der Allgemeinen Relativitätstheorie wird es mit der Energieerhaltung verzwickter. Hier in der klassischen Mechanik und danach bei der Speziellen Relativitätstheorie spielen die entsprechenden Effekte aber keine Rolle, und ich werde nicht weiter auf sie eingehen.)
Einige der neuen Energiesorten sind Spielarten der potenziellen Energie. Für Kräfte auf ein Teilchen, deren Wirkung nur vom Ort des Teilchens (z.B. relativ zu einer Masse, einer elektrischen Ladung, relativ zum Haltepunkt einer Sprungfeder) abhängt, aber z.B. nicht von der Teilchengeschwindigkeit (wie bei der Luftreibung), lässt sich aus der Formel für die Kraft ganz allgemein eine potenzielle Energie bestimmen. Solche Kräfte heißen konservative Kräfte – ganz unabhängig von der politischen Bedeutung des Wortes.
Hängt man beispielsweise einen Massepunkt der Masse m an eine Sprungfeder, die dem Hooke’schen Gesetz genügt (s.o.), dann kann man dem Massepunkt in Abhängigkeit von der Streckung der Feder (Abweichung von der Ruhelage) Δl eine potenzielle Energie U zuweisen,
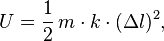
und T+U ist in Systemen, deren Verhalten sich allein durch das Hooke’sche Gesetz beschrieben lassen, wiederum eine Erhaltungsgröße. Das rechne ich hier vor.
Zur Newton’schen Gravitationskraft gibt es ebenfalls eine potenzielle Energie: Einem Massenpunkt der Masse m, der sich im Abstand r von einer großen Masse M befindet, kann man die potenzielle Energie
![]()
zuordnen. Das rechne ich hier vor.
Beschreibt man die Bewegung des Massenpunkts unter dem Einfluss der Gravitation der großen Masse – etwa einen Satelliten unter dem Einfluss der Erdschwerkraft -, dann kann man ausnutzen, dass die kinetische Energie T des Massenpunkts plus diese potenzielle Energie U dabei konstant bleiben. So lässt sich beispielsweise die Fluchtgeschwindigkeit ausrechnen, also die Geschwindigkeit, mit der man einen Körper von einer großen Massekugel aus senkrecht nach oben schießen muss, damit er gerade nicht mehr auf die Massekugel zurückfällt.
(Bei dieser Beschreibung vernachlässigt man, dass sich auch die große Masse M unter dem Schwereeinfluss des Massenpunkts m ein wenig bewegt; wo diese Bewegung der großen Masse wichtig wird, muss man natürlich auch für die große Masse kinetischen und potenzielle Energie hinzuzählen, um einen Ausdruck für die Gesamtenergie zu erhalten, der sich mit der Zeit nicht verändert.)
Energien, wie wir sie hier kennengelernt haben, sind nur bis auf eine Konstante definiert. Wenn T + U ein Ausdruck ist, der sich nicht mit der Zeit verändert, dann ist natürlich auch T + U + K, mit K einer Konstante mit der richtigen physikalischen Einheit, ein unveränderlicher Ausdruck. Bei der kinetischen Energie liegt es noch recht nahe, keine Konstante zu dem oben genannten Ausdruck zu addieren – keine Bewegung, also v=0, entspricht dann die Bewegungsenergie Null. Bei der potenziellen Energie ist die Lage weniger klar. Halten wir an dieser Stelle einfach fest, dass die Wahl des Energienullpunkts in der klassischen Mechanik nicht eindeutig ist.
Bindungsenergie, Wärme & Co.
Systemen, in denen mehrere Bestandteile durch Kräfte aneinander gebunden sind, kann man auf Grundlage der kraftspezifischen potenziellen Energie eine Bindungsenergie zuordnen. Sind die Bestandteile weit voneinander entfernt, und wirkt eine anziehende Kraft zwischen ihnen, dann ist die potenzielle Energie hoch; bringt man die entfernten Bestandteile zueinander, dann ist die potenzielle Energie des dabei entstehenden Zustands deutlich niedriger. Die Differenz, eben die Bindungsenergie, ist ein Maß für die Stärke der Bindung – sie drückt schließlich umgekehrt aus, dass man dem System Energie zuführen muss, um es wieder in seine Bestandteile zu zerlegen.
Wird ein Körper durch Reibung abgebremst, erwärmen sich Körper und Untergrund bzw. Medium. Das ist ein erstes Beispiel für die Notwendigkeit einer weiteren Energieform, nämlich der thermischen Energie oder Wärmeenergie EW. Zusammen mit dieser Wärmeenergie, der Bewegungsenergie T des Körpers und der potenziellen Energie U etwaiger dort wirkender konservativer Kräfte erhalten wir mit T + U + EW wiederum eine Erhaltungsgröße.
Wandelt man Verbindungen mit gegebener Bindungsenergie in andere Verbindungen mit größerer Bindungsenergie um, dann wird die Energiedifferenz üblicherweise in Form von Wärmeenergie freigesetzt. So funktionieren beispielsweise Verbrennungsprozesse.
Weitere Energiesorten sind mit elektromagnetischer Strahlung verknüpft; später in der Speziellen Relativitätstheorie kommt noch die sogenannte Ruheenergie von Elementarteilchen dazu. Insgesamt haben wir jetzt aber schon die wichtigsten Energiesorten aufgeführt. Ihre Summe ist tatsächlich eine Erhaltungsgröße.
Betrachtungen, wie sich die verschiedenen Formen der Energie ineinander umwandeln, sind oft der direkteste Weg, schnell Aussagen über ein System zu erhalten. Die Energieerhaltung – Energie kann nicht einfach verschwinden oder erzeugt werden; verändert sich der Energieinhalt eines Systems, dann weil ihm Energie zugeführt oder entzogen wird – ist ein wichtiger Bestandteil der physikalischen Modelle.
Thermodynamik und statistische Mechanik
Energie ist eine Größe, mit der man eine zusammenfassende Aussage über ein physikalisches System treffen kann – anstatt vieler Details nennt man den Wert einer zusammenfassenden Größe, eben der Energie, und hat damit eine wichtige Systemeigenschaft erfasst. Solche groben, zusammenfassenden Kennzahlen kennen wir aus dem Alltag noch in vielerlei anderer Form – die Einwohnerzahl eines Landkreises oder einer Stadt, das Bruttosozialprodukt eines Staates, Geburts- und Sterberaten, Wahlergebnisse und so weiter.
Auch in der Physik gibt es außer der Energie noch weitere zusammenfassenden Kennzahlen für Systeme. Die haben allerdings den Vorteil, dass man direkt mit ihnen rechnen und recht allgemein gültige Beziehungen zwischen ihnen ableiten kann. Damit beschäftigt sich das Teilgebiet der Physik namens Thermodynamik. Alleine aus Größen wie Gesamtenergie, Bindungsenergien für die verschiedenen Sorten von Stoff, Volumen, Temperatur und Entropie – letztere werden in der Thermodynamik als Grundgrößen definiert – können bereits sehr allgemeine Aussagen zum Systemverhalten getroffen werden.
Eine wichtige Erkenntnis der Thermodynamik ist, dass sich Wärmeenergie nicht vollständig in Energieformen umwandeln lässt, mit denen man beispielsweise Maschinen antreiben kann, kurz: in “nutzbare Energie”. Diese Erkenntnis erklärt auch, warum sich unsere Gesellschaft überhaupt um hinreichende Energieversorgung Gedanken macht. Nach dem in früheren Abschnitten hätte man ja denken können, wir müssten uns um die Energieversorgung überhaupt keine Sorgen machen: Energie als Erhaltungsgröße ginge schließlich nicht verloren, sondern es gebe immer genau gleich viel Energie wie zuvor.
Wenn von Energieversorgung, Energieproduktion, Energieverschwendung etc. die Rede ist, ist aber stets nutzbare Energie gemeint. Und auch wenn die Energie insgesamt gleich bleibt: Die Menge der nutzbaren Energie nimmt kontinuierlich ab.
In der Thermodynamik wird die Detailstruktur der beteiligten Systeme bewusst ausgeblendet. Temperatur und Wärme beispielsweise werden als fundamentale physikalische Größen behandelt. Die Brücke zwischen dieser allgemeinen Perspektive und dem, was in den beschriebenen Systemen im Einzelnen passiert, schlägt die statistische Mechanik. Sie zeigt beispielsweise, dass die Temperatur eines Gases der mittleren Bewegungsenergie der Gasteilchen entspricht.
Bei der gleichen Betrachtung stellt sich heraus, dass Wärmeenergie mikroskopische Bewegungsenergie ist: die Energie etwa, mit der sich die Teilchen der Luft ungeordnet durcheinander bewegen, oder die Energie, mit der die Atome eines Festkörpers im Kristall um ihre Ruhelage schwingen.
Die statistische Mechanik zeigt z.B. auch, dass der Druck eines in einem Behälter eingesperrten Gases auf die unzähligen Stöße der herumflitzenden Gasteilchen gegen die Behälterwände zurückzuführen ist. Die Begriffe, mit denen die Eigenschaften der Teilchen oder anderen grundlegenden Bestandteile (z.B. Modell eines Kristallgitters aus mit Federn verbundenen Massepunkten) beschrieben werden können, sind dabei die der Mechanik: Masse, Impuls, Bewegungsenergie und so weiter.
Zwischenbilanz
Unsere Beschreibung des “Modellbaukastens” der Mechanik ist jetzt bereits recht vollständig – von spezifischen Kräften bis hin zu Elementen wie idealisierten Federn, starren oder schwingenden Körpern, Flüssigkeiten und Gasen bis hin zum grundlegenden Konzept der Energie.
Aber für Modelle muss immer auch gesagt werden, wie sie sich durch Messungen überprüfen lassen – das erst schlägt die Brücke zum Experiment und ermöglicht es, die Modelle auf die Probe zu stellen oder, allgemeiner, für Vorhersagen oder zur Beschreibung realer Situationen zu verwenden. Da besteht freilich an entscheidender Stelle noch Nachholbedarf, nämlich was die Begriffe Masse und Kraft angeht.
Definition von Masse und Kraft
Ich hatte die Masse oben nur als Eigenschaft von Massenpunkten eingeführt und, davon abgeleitet, von Festkörpern und Flüssigkeitsmengen. Ich hatte aber noch keine Möglichkeit angegeben, wie diese Größe durch Messungen zu bestimmen sei. Das möchte ich an dieser Stelle nachholen. Definitionen der Masse nutzen den Zusammenhang zwischen Masse, Kraft und Beschleunigung aus, den wir als
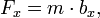
mit entsprechenden Beziehungen für Fy, Fz mit by, bz, kennengelernt hatten – das zweite Newton’sche Gesetz. Man muss dabei etwas aufpassen, da diese Formel in der Mechanik gleich mehrere Rollen spielen muss; ich gehe in diesem Zusatzabschnitt näher auf diesen Umstand ein.
Zur Definition der Masse greifen wir uns eine besonders einfache Kraft heraus, deren Eigenschaften wir im Labor gut unter Kontrolle haben. Historisch gesehen stand für die Physik die Gewichtskraft am Anfang – nicht zuletzt daher kommt der nach wie vor sehr enge Zusammenhang von Masse und Gewicht im Alltag. Die Gewichtskraft haben wir aber gerade nicht sehr gut unter Kontrolle. Sie ergibt sich schließlich als Schwereanziehung unseres Heimatplaneten im Ganzen, und wir haben keine Möglichkeit, ihren Wert zu ändern oder zum Vergleich ein zweites System herzustellen, das eine Kraft mit derselben Stärke und denselben Eigenschaften erzeugt.
Eine geeignetere Möglichkeit (so z.B. in dem Lehrbuch Arnol’d 1989) ist eine Feder, die dem Hooke’schen Gesetz genügt. In der oben formulierten Form, in der die Hooke’sche Rückstellkraft der Feder die Stärke
![]()
hat, können wir das Gesetz zwar nicht nachprüfen. Direkt messen können wir nur die Beschleunigung, die (wir nutzen F=mb) die Form
![]()
haben sollte. Die Beschleunigung lässt sich schließlich aus der Ortsbestimmung der Kugel zu verschiedenen Zeitpunkten ableiten.
(Durchaus plausible) Zusatzannahmen sind, dass k eine Eigenschaft der Feder ist, die unabhängig davon ist, welches Objekt man an der Feder anbringt, während m eine Eigenschaft des an die Feder angebrachten Objekts ist, die sich nicht ändert, solange man nicht das Objekt selbst verändert (wobei ändern hier vor allem heißt: Materie davon entfernt oder dazupackt). Diese Zusatzannahmen werden im Hintergrund stehen, wenn wir die physikalische Größe Masse unten über eine Messvorschrift definieren.
Zunächst zu unserem Versuchsaufbau: Kugel und Federn sind in dem folgenden Versuch waagerecht angebracht; die Kugel (oder ein anderes Objekt, dessen Masse wir bestimmen möchten) soll so reibungsfrei gelagert sein wie möglich. Die Kugel wird dann um eine kleine Distanz Δx ausgelenkt. Was passiert?
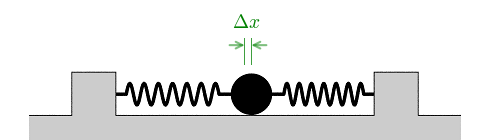
Dass die Feder tatsächlich dem oben angegebenen Hooke’schen Gesetz für die Beschleunigung genügt, lässt sich experimentell nachprüfen. Dazu spannen wir eine Kugel in unsere Apparatur ein, lenken sie in aufeinanderfolgenden Versuchen um verschiedene Werte für Δx aus und messen anschließend jeweils die Beschleunigung, welche die Kugel erfährt. Das Hooke’sche Gesetz sagt für diese Situation voraus, dass die Beschleunigung proportional zur Auslenkung sein sollte, mit einem bei Experimenten mit ein und derselben Kugel immer gleichen Proportionalitätsfaktor.
Solche Messreihen, in denen jeweils die Messwerte für Beschleunigung und Auslenkung festgehalten sind, können wir mit verschiedenen Kugeln verschiedener Größe und Zusammensetzung wiederholen. Für jede Kugel kann man separat zeigen: Ihre Beschleunigung ist proportional zur Auslenkung Δx. Das ist offenbar eine allgemeine Eigenschaft des Federsystems.
Im nächsten Schritt vergleichen wir bei gleicher Auslenkung Δx verschiedene Kugeln. Wir definieren dann die Masse eines Objekts durch die folgende Messvorschrift: Erfährt eine Kugel 1 bei Auslenkung Δx die Beschleunigung a1, und erfährt eine andere Kugel 2 bei gleichem Δx die Beschleunigung a2, dann sollen sich die Massen der beiden Kugeln per Definition verhalten wie
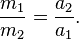
(Ist diese Definition getroffen, dann gilt das Hooke’sche Gesetz auch automatisch in der ursprünglich beschriebenen Form: dann ist nämlich die Rückstellkraft in der Tat gleich der Auslenkung mal der Federkonstante k.)
Günstigerweise für die Messpraxis ergibt sich aus der Proportionalität der Beschleunigung und der Auslenkung eine recht einfache Schwingungsgleichung. Lässt man die Masse bei der Auslenkung los, dann führt sie näherungsweise eine einfache Sinusschwingung aus, wie hier dargestellt:

Deren Schwingungsdauer ist eine deutlich einfacher messbare Größe als die Beschleunigung selbst; aus der Rechnung ergibt sich, dass das Massenverhältnis für zwei Objekte proportional zum Quadrat ihrer Schwingungsdauern ist,
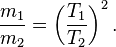
Hat man auf diese Weise Massenverhältnisse definiert, kann man einen Körper zum Referenzkörper (mit anderen Worten: zur verkörperten Masseneinheit) erklären und alle anderen Massen relativ zu ihm messen.
Auf Basis dieser Definition kann man anschließend nach äquivalenten Methoden suchen, Massen zu vergleichen. Das Wiegen, also der Vergleich der Gewichte von Objekten (sprich: der Stärke der Gravitationskraft, mit der die Erde sie nach unten zieht) ist zum einen historisch, zum anderen auch in der heutigen Praxis sicher das wichtigste solcher Verfahren.
Ist die Massenmessung über die Federkräfte erst einmal definiert, dann kann man
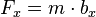
und die entsprechenden Gleichungen für die anderen Komponenten verwenden, um mit Objekten, deren Masse bereits bestimmt wurde, über die direkt gemessenen Beschleunigungen verschiedene Kraftwirkungen zu erkunden.
So kann man auf Formeln für die Kraftstärken kommen, wie ich sie oben für die Gravitationskraft hingeschrieben hatte, wie sie aber beispielsweise auch für elektrische, magnetische oder Reibungskräfte existieren.
Sind die Eigenschaften spezifischer Kräfte und die Massen der beteiligten Objekte bestimmt, kann man diese Erkenntnisse in neuen Situationen auf die Probe stellen – wobei das zweite Newton’sche Gesetz dann auch bei diesen Tests typischer Weise eine Schlüsselrolle spielen dürfte.
Damit ist der Dreifachnutzen des zweiten Newton’schen Gesetzes abgesteckt.
Es gibt eine Möglichkeit, die Grundgesetze der Mechanik zu definieren, bei der die Definitionen von Masse und Kraft klarer getrennt sind: An die Stelle der Newton’schen Gesetze tritt dann zum einen ein Erhaltungssatz für den Impuls (letzterer definiert als Masse mal Geschwindigkeit), zum anderen eine Aussage dazu, dass die weitere Bewegung eines Teilchens vollständig festgelegt ist, wenn Ort und Geschwindigkeit zu einem beliebigen (und frei wählbaren) Zeitpunkt bekannt sind. Aus diesen Setzungen die herkömmlichen Konzepte und Gesetze der Mechanik herzuleiten ist aber mathematisch deutlich anspruchsvoller, als es diese Einführung leisten kann.
Bemerkung zu Konventionen und Erhaltungsgrößen
Ich hatte gegen Ende von Teil I zwei Möglichkeiten aufgezeigt, welche Rolle Konventionen bei der Definition von Bezugssystemen spielen können. Erst einmal könnten sich die physikalischen Gesetze bei einer bestimmten Wahl z.B. des Koordinatennullpunkts als besonders einfach erweisen; dann würden diese Gesetze eine der Wahlmöglichkeiten vor allen anderen auszeichnen. Oder aber die physikalischen Gesetze wären unabhängig von der getroffenen Wahl dieselben.
Ich leite an dieser Stelle nicht ab, teile aber als interessantes Faktum mit, dass es den Newton’schen Gesetzen der Mechanik egal ist, wohin man seinen Koordinatennullpunkt legt. (Bei den Rechnungen im Anhang zu den verschiedenen Formen von potentieller Energie wird dieser Umstand an mehr als einer Stelle ausgenutzt.)
Gelten diese Gesetze in einem bestimmten Bezugssystem, dann gelten sie in exakt der gleichen Form auch in einem Bezugssystem, das sich vom ersten alleine durch eine feste Verschiebung des Koordinatennullpunkts unterscheidet; wählt man bei gleicher Achsenorientierung einen neuen Nullpunkt, bleiben die Gesetze die gleichen. Auch die Wahl des Zeitnullpunkts ist für die Newton’schen Gesetze der Mechanik in diesem Sinne egal, da die Zeitkoordinate darin nicht explizit auftaucht. Und schließlich ist es für diese Gesetze auch egal, wie man sein Bezugssystem orientiert: Gelten die Gesetze in einem bestimmten Bezugssystem, so gelten sie auch in einem System, das gegenüber dem ersten um bestimmte konstante Winkel verdreht ist.
Eines der elegantesten Resultate der Physik ist das Noether-Theorem, das Anfang des 20. Jahrhunderts von der genialen Mathematikerin Emmy Noether bewiesen wurde. Diesem Theorem zufolge (dessen Beweis den Rahmen dieser Einführung endgültig sprengen würde!) ergibt sich aus jeder “Konventionsunabhängigkeit” der Mechanik (die Physiker reden dabei von einer “Symmetrie”) die Existenz einer Erhaltungsgröße. Aus der Unabhängigkeit der mechanischen Gesetze gegenüber einer Verlegung des Nullpunkts (diese Verlegung heißt “Translation”; die entsprechende Unabhängigkeit “Translationsinvarianz”) folgt direkt die Impulserhaltung. Aus ihrer Unabhängigkeit gegenüber der Wahl des Zeitkoordinatennullpunkts folgt die Energieerhaltung; aus ihrer Unabhängigkeit gegenüber der Verdrehung um einen festen Winkel die Erhaltung des Drehimpulses.
Eines meiner bislang unerreichten Ziele in der Wissenschaftskommunikation ist es, eine gute und allgemein verständliche Herleitung des Noether-Theorems zu formulieren. An dieser Stelle jedenfalls konnte ich das Theorem nur beschreiben, aber nicht näher erklären.
Technische Mechanik
Die hier eingeführten Konzepte bilden die Grundlage der Technischen Mechanik (z.B. Magnus & Müller 1990), deren Aufgabe es ist, die Mechanik in Maschinenbau, Fertigungs- und Verfahrenstechnik, im Bauwesen und im Verkehrswesen anzuwenden. Anwenden heißt dabei: Zu einer gegebenen Fragestellung ein vereinfachtes Modell zu entwickeln, das die wesentlichen Eigenschaften der betrachteten realen Systeme wiedergibt; das vereinfachte Modell mit den Gesetzen der Physik zu beschreiben und die für die Fragestellung relevanten Eigenschaften herauszufinden, und diese Ergebnisse zurück in die wirkliche Welt zu übertragen.
Dabei kommen als Bausteine alle hier genannten einfachen Konzepte zum Einsatz: die Punktmassen ebenso sowie starre Körper (Stereo-Mechanik), elastische Körper, die vorübergehende Verformungen erfahren (Elasto-Mechanik), Körper, die plastische, also bleibende Verformungen erleiden können (Plasto-Mechanik) sowie flüssige und gasförmige Gebilde (Fluid-Mechanik). Elasto-, Plasto- und Fluid-Mechanik gehören weitgehend zur Kontinuums-Mechanik, in der die betrachteten Stoffe als im Prinzip unendlich fein unterteilbar angesehen werden.
Die Dimensionierung von Werkstücken für Maschinen, Lagern und Gelenken, die Statik von Fachwerken oder ganzen Gebäuden; die Reibungskräfte, die bei beweglichen Verbindungen, aber beispielsweise auch bei Schrauben auftreten; die inneren Spannungen und die Dehnungen von Objekten unter Zug oder Spannung; die Biegelehre und die Beschreibung von Knickung, die Eigenschaften von Schalen, die z.B. zur Beschreibung von Behältern oder Dachkonstruktionen nützlich sind; Fragen nach dem Druck in Flüssigkeiten, der Auftriebsstabilität von Schiffsrümpfen; die Wirkung von Drallrädern in Raumfahrzeugen, die gefederte Lagerung von Wellen; das Strömungsverhalten rund um Flugzeug- oder Schiffsrümpfe; die Stabilität und Verformbarkeit verschiedener Bodentypen; die Mechanik des Skeletts verschiedener Lebewesen samt daran angreifender Muskeln in der Biomechanik: Insgesamt dürfte die Mechanik derjenige Teilbereich der Physik mit den vielfältigsten und umfassendsten Alltagsanwendungen sein.
Und damit schließt sich in dem hier und in Teil IV gegebenen Überblick zumindest ein historischer Kreis, denn solche praktischen Überlegungen standen schließlich auch am Anfang der Mechanik als Wissenschaft. Hier zum Abschluss ein entsprechendes Bild aus Galileis Discorsi e Dimostrazioni Matematiche intorno a due nuove scienze, veröffentlicht 1636:
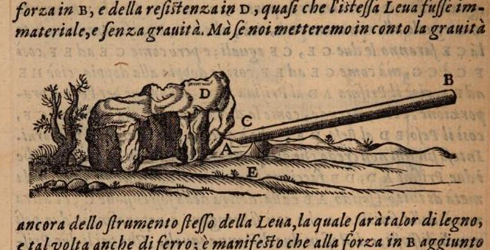
Im nächsten Teil wird es um die Frage gehen, wie man den Wechsel von einem Bezugssystem in ein anderes beschreiben kann. Noch später dann werden wir die in Teil VI entwickelten Beschreibungen benutzen, um uns genauer anzusehen, in welchen Bezugssystemen die klassische Mechanik in der hier vorgestellten Form gilt und in welchen nicht, und wie sich die verschiedenen Klassen von Bezugssystem identifizieren lassen.
Wie für die vorangehenden Teile von “Einstein verstehen” gilt auch für diesen hier, dass ich Veränderungen, die sich aus der hier geführten Diskussion ergeben, direkt umsetzen werde. Die Originalfassung habe ich zum Vergleich hier (Haupttext) und hier (Ergänzungen) als PDF eingestellt. Diejenigen Zusatztexte, in denen einige der Behauptungen oder Ableitungen des Haupttextes näher ausgeführt werden, habe ich auf die Seite 2 dieses Beitrags gestellt.
Meinen Umgang mit Kommentaren in diesem Blog habe ich in diesem Blogbeitrag erläutert. Inbesondere gilt: Der obige Text stellt den fünften Schritt einer Einführung in die Spezielle Relativitätstheorie dar; die Diskussion sollte auf den hier behandelten Themenbereich beschränken und insbesondere nicht auf das vorgreifen, was erst in den nachfolgenden Teilen der Einführung angesprochen wird. Ich behalte mir vor, Diskussionsbeiträge, die dem Leser keinen Mehrwert bieten, sondern die Diskussion stören, zu löschen.
Die Kommentare können zwischenzeitlich moderiert sein und werden dann von mir jeweils erst freigeschaltet. Daher bitte Geduld, wenn Sie einen Kommentar eingestellt haben, dieser aber nicht gleich unten auf dieser Seite erscheint!


Wäre es sinnvoll, in diesem Teil noch den Begriff der Zwangskraft zu erklären?
Ich sehe derzeit nicht, wo ich den später benötigen würde (im Kern ist all das, was ich hier mache, ja eine Vorbereitung auf die Spezielle Relativitätstheorie) – übersehe ich da etwas?
Uff da hatte man aber echt viel zu Lesen, doch bereuhen tuh ichs nicht! Ich konnte einfach nicht aufhören zu lesen. Es war echt super Gestaltet mittendrin mit Beispielen und anhand der Formeln belegt. Top! So habe sogar ich etwas verstehen und lernen können.
Danke und weiter so!
Grüße Yvonne
…dann ergibt sich, dass eine solche Schale auf einen in ihrem Inneren befindlichen Körper gar keine Schwerkraft ausübt. hhmmmm, gilt dies auch,wenn sich die Probe nicht genau im Zentrum befindet?hajo.
Ja, in der Tat – eines der schönsten Resultate der Newton’schen Gravitationstheorie, finde ich. Wenn man “Gravitationsfeld Kugelschale” googelt kommt man auf verschiedene Rechenwege dazu. Für diese Einführung hier fand ich die Rechnungen aber zu kompliziert (weil man dazu integrieren muss).
@Dr.Pössel,
es geht ganz kurz und ohne Integration, rein “geometrisch”, könnte man einbauen.
Man nimmt einen beliebigen Punkt im Kreis und zieht zwei Geraden durch.
Räumlich in der Kugel wären das dann Kegelschnitte mit den Flächen A und B.
Bzgl. der Abstände zu den Flächen gilt einfach A/B = a²/b² , ebenso für die Massen.
Das eingesetzt ins Gravigesetz gibt Fa=Fb, also Aufhebung der “Gegenflächen”.
Müßte man nur aufmalen und drei Zeilen “Schulformeln” schreiben.
Oder ein Scan an Sie aus dem Novikov 1982 S.16-21 per mail.
Freundliche Grüße – Senf
Dann hätte ich doch aber zunächst einmal nur zwei Teilabschnitte der Kugelschale, deren Einfluss sich aufhebt (in der Tat, trotz unterschiedlicher Abstände, das sieht man da natürlich bereits sehr schön). Aber dann muss ich doch noch zeigen, dass ich mit solchen Teilstücken die Kugelfläche “austapezieren” kann, ohne irgendeine Region doppelt zu zählen. Da kann man sicher mit der Winkelgröße der Regionen argumentieren, aber das scheint mir auch nicht so einfach zu sein. Dann kann ich mir schon vorstellen, dass man da mit Kreisringen in der Kugelfläche weiter kommt.
zum “Austapezieren”:
Die Serie soll ja “relativ einfach” eigentlich komplizierte Physik erklären.
Wenn man es anschaulich machen will, muß man wohl Abstriche in Mathe machen.
Novikov hat das ganz plausibel so formuliert “Da die Kräfte jedoch in entgegengesetzten Richtungen wirken, heben sie einander auf. Dasselbe läßt sich für beliebige andere Richtungen wiederholen. Damit heben sich alle entgegengesetzten Kräfte auf, und die resultierende Kraft, die auf m wirkt, ist gleich Null.”
Genauso einfach beschreibt er, wie auf einer gedachten Kugeloberfläche, nur die Kraft durch die Masse der Kugelmaterie bestimmt wird unabhängig von der (homogenen) Masse außerhalb dieses Volumens, das geht dann schon in Richtung Newton/ART.
Gut, die gleiche Winkelgröße der entgegengesetzt wirkenden Regionen muss man schon noch herausstellen, aber dann kann man so (oder eben mit den Ringen) wohl in der Tat so argumentieren, dass plausibel wird, was sich da aufhebt. Mal schauen, wenn nicht hier dann in einem anderen Beitrag. Danke!
Zum Starren Körper habe ich ich noch eine andere Ansicht.
Wenn ein solcher Körper dadurch gekennzeichnet ist, dass seine Massenpunkte einen festen
unveränderlichen Abstand zu einander haben – ein elastischer Körper aber nicht – dann genügt es doch, einen langezogenen elastischen Körper einfach an jedem Ende mit einer Feder vorzuspannen und seine Verlagerung in Längsrichtung durch die Längenvariation einer
Feder in Gang zu halten, dann müssen sich, zumindest in der Verschieberichtung, sämtliche
Massenpunkte ohne Veränderung ihres gegenseitigen Abstands mitschieben lassen – was
einen verschiebestarrren Körper entspricht.
Da dieser In der SRT nicht vorkommt, ist diese Theorie entweder falsch oder nur für elastische Körper verbindlich.
Darauf sollte man einmal deutlich hinweisen.
W.Schneider
Markus Pössel schrieb (15. Dezember 2013):
> […] bietet sich als einfachstes Modell der sogenannte starre Körper an. Ein solcher Körper besitzt eine Form, die sich im Raum geometrisch definieren lässt.
Welche konkrete, nachvollziehbare (Mess-)Definition käme denn für die Feststellung des eventuellen Besitzes von „Form“ in Frage (und wäre ggf. auch „im Sinne Einsteins“) ? —
Konstante Pingdauern jedes (unterscheidbaren) Bestandteils des zu untersuchenden Systems bzgl. jedes anderen, d.h. „τABA = constant“ ?
Oder (zumindest): konstante Pingdauer-Verhältnisse sowohl zwischen jeweils zwei Bestandteilen, also
„τABA / τBAB = constant“,
also auch von je drei Bestandteilen untereinander, d.h.
„τHJH / τHKH = constant“,
„τJHJ / τJKJ = constant“ und
„τKHK / τKJK = constant“ ? …