Einstein verstehen IV: Klassische Mechanik – Massenpunkte, Newton’sche Gesetze, Impuls
BLOG: RELATIV EINFACH

Auf dieser zweiten Seite habe ich die Zusatztexte versammelt, in denen einige der Behauptungen oder Ableitungen des Haupttextes näher ausgeführt werden. Im Prinzip sollten die Textteile hin und zurück verlinkt sein. Aber: neues System. Hoffentlich klappt’s.
Historischer Einschub 1: Zwei spezielle Sorten von Bezugssystem
Historisch gesehen standen die allgemeinen Überlegungen dazu, in welchen Bezugssystemen die klassische Mechanik gilt, ebenfalls nicht am Anfang der Entwicklung. Das dürfte vor allem daran liegen, dass es zwei spezielle, uns recht naheliegende Sorten von Bezugssystem gibt, in denen sich mit den Gesetzen der klassischen Mechanik in guter Näherung erfolgreiche Modelle formulieren lassen. In diesen beiden Sorten Bezugssystem wurden denn auch die meisten Experimente und Beobachtungen durchgeführt, mit denen sich die klassische Mechanik als erfolgreiche physikalische Theorie etablieren konnten. Grund genug, auf sie einzugehen.
Die erste historisch wichtige Klasse von Bezugssystemen sind erdfeste Systeme, bei denen man sich einen festen Ort auf der Erde als Nullpunkt sucht (sei es direkt auf dem Erdboden, sei es an einem Gebäude oder einer anderen feststehenden Struktur, sei es auf einem Labortisch); drei weitere solcher festen Bezugspunkte definieren dann die Richtungen der drei Raumachsen. Ein solches Bezugssystem entspricht unseren Alltagsbegriffen von Ruhe und Bewegung: Wir sagen, ein Auto beispielsweise sei in Ruhe, wenn es seine Position relativ zum Erdboden nicht verändert, und es bewege sich, wenn es sich relativ zum Erdboden bewegt. Häufige Konvention ist es, eine der Achsen senkrecht zur Erdoberfläche zu wählen. Wenn wir im Labor oder in der Schule ein mechanisches Experiment aufbauen – z.B. eine Luftkissenbahn für Stoßversuche – messen wir die Bewegungen der beteiligten Objekte relativ zu einem solchen System.
Ein weniger direkt zugängliches, aber nicht weniger wichtiges Bezugssystem legt seinen Nullpunkt in den Mittelpunkt der Sonne, bzw. in späteren Verfeinerungen in den (noch zu definierenden) Schwerpunkt des Sonnensystems. Die drei Raumachsen werden mit Bezug auf die Blickrichtungen zu fernen, aus unserer Sicht praktisch unbeweglichen Fixsternen festgelegt. Ein solches Bezugssystem ist exzellent geeignet, um die Bewegung der Planeten und anderer Himmelskörper um die Sonne zu beschreiben. Oft wählt man dabei zwei der Achsen in der sogenannten Ekliptik. Das ist, grob gesagt, die Ebene, in der die Planeten um die Sonne laufen. Die dritte Achse steht dann natürlich senkrecht zur Ekliptik.
Die Ableitung: mathematischer Ausdruck für die Änderungsrate
Betrachten wir eine Funktion y = f(x), manchmal schlicht geschrieben als y(x), also einen Ausdruck dafür, wie der Wert einer Größe y vom Wert einer anderen Größe x abhängt. Eine Funktion ist eine Zuordnungsvorschrift: gegeben ein bestimmter Wert von x gibt sie den zugehörigen Wert von y aus. In der Mathematik sind y und x meistens reelle Zahlen; in der Physik haben sie physikalische Bedeutung. So könnte eine Funktion T(E) ausdrücken, wie sich die Temperatur T eines Körpers ändert, dem man in bestimmter Weise Energie E zugeführt hat, oder wie sich der x-Koordinatenwert eines Teilchens in Abhängigkeit von der Zeit t ändert, x(t), oder wie ein Pendel mit der Zeit hin- und herschwingt und sein Aufhängungsseil dabei den zeitabhängigen Winkel φ(t) zur senkrechten bildet, und so weiter.
Wir können jeweils als erstes die Funktion selbst betrachten oder graphisch darstellen. So sehen wir direkt, wo sie welche Werte annimmt. Aber es gibt noch eine weitere interessante Eigenschaft der Funktion, nämlich wie schnell sie sich ändert. Anders ausgedrückt: Wenn ich von einer bestimmten Stelle x ein kleines Stückchen nach rechts gehe, also zu x + Δx, um wieviel nimmt die Funktion dann zu oder ab? Nur ganz wenig? Oder viel?
Schaut man sich die Funktionskurve an, dann ist diese Frage für ganz kleine Δx gleichbedeutend mit der Frage, wie steil der Kurvenverlauf an der Stelle x ist. Diese Steilheit kann man sichtbar machen, wenn man an die Kurve eine Gerade anschmiegt, und zwar so, dass sie am Punkte x soweit wie möglich in die gleiche Richtung (“tangential”) verläuft wie die Funktionskurve. Die Steilheit dieser angeschmiegten Gerade nennt man dann die Änderungsrate der Funktion an der betreffenden Stelle, oder auch die Ableitung (von f(x) nach x) an der betreffenden Stelle.
Auf Wikipedia gibt es eine schöne Animation, die für eine bestimmte, nicht allzu einfache Funktion Funktionskurve und angeschmiegte Geraden zeigt (Quelle hier; die Datei ist in der Public Domain):
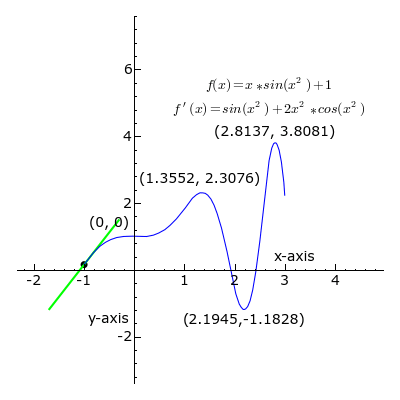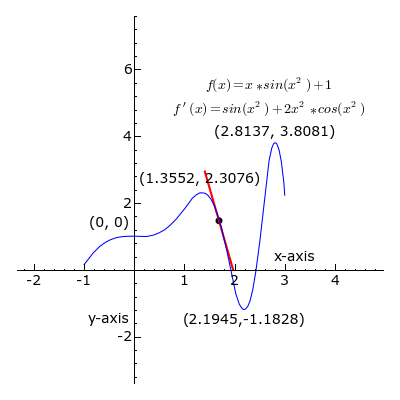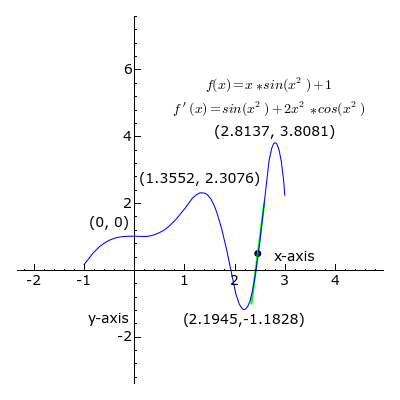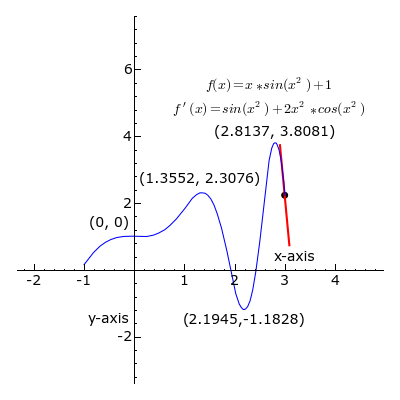
Der schwarze Punkt wandert dabei die Funktionskurve entlang. Die eingezeichnete Schmiegegerade an die Kurve zeigt, wie steil die Kurve jeweils an dem dickeren schwarzen Punkt verläuft. Ist die Gerade grün, dann wächst die Funktion, wenn man in Richtung größerer x-Werte weitergeht; ist sie schwarz, haben wir es mit einem lokalen Maximum oder Minimum zu tun, an dem die Schmiegegerade waagerecht ist; eine rote Gerade heißt, dass die Kurve dort zu noch größeren x-Werten hin abfällt.
An dieser Stelle können wir uns überlegen, wie man die Steigung der Kurve in einem bestimmten Punkt, also die Ableitung, berechnen kann.
Generell gilt: angenommen, eine Gerade y = ax + b ginge durch die zwei verschiedenen Punkte (x1, y1) und (x2, y2). Dabei sind a und b die beiden Parameter, welche die Gerade (vollständig) definieren: a gibt die Steigung der Gerade an (je größer a ist, umso mehr wächst y, wenn wir x ein wenig vergrößern) und b die Höhe ihres Durchgangs durch die y-Achse (für x=0 ist y=b).
Dass die Gerade durch die genannten Punkte geht, heißt, in die Geradengleichung eingesetzt, dass
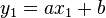
und
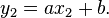
Das sind zwei Gleichungen für die zwei Unbekannten a und b. Es handelt sich sogar um die einfachste Sorte von Gleichungen, nämlich lineare Gleichungen. Man kann diese Gleichungen direkt nach a und b auflösen und erhält dann
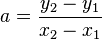
und
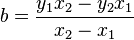 .
.
Vor diesem Hintergrund schauen wir uns jetzt die Funktion y=f(x) in der Nähe des Punktes x0 an. Durch den Funktionswert alleine, er ist an diesem Punkt y0 = f(x0), können wir noch nichts über die Steigung der Funktionskurve aussagen. Aber wenn wir jetzt etwas weiter nach rechts gehen, zu x0 + Δx, dann kennen wir bereits zwei Punkte, die auf der Kurve liegen: (x0, y0) und (x0 + Δx, f(x0 + Δx)). Hier ist die Situation aufgezeichnet – erst für ein etwas größeres Δx, dann für immer kleinere:
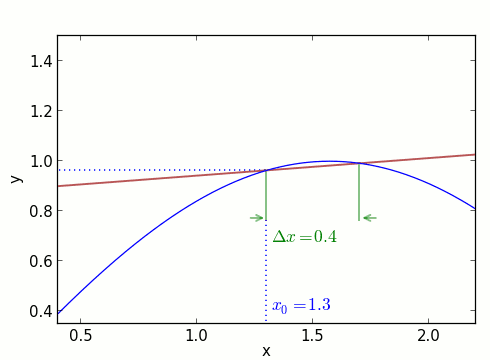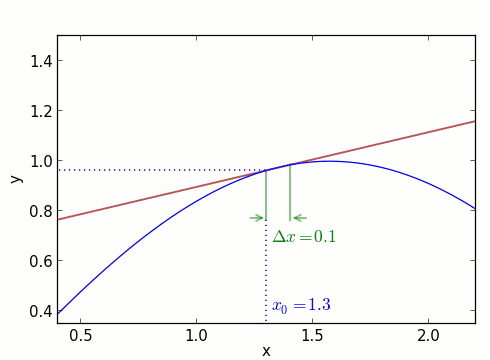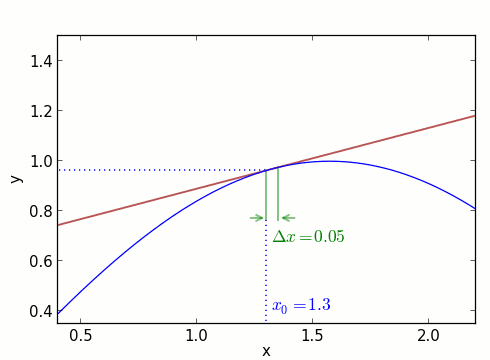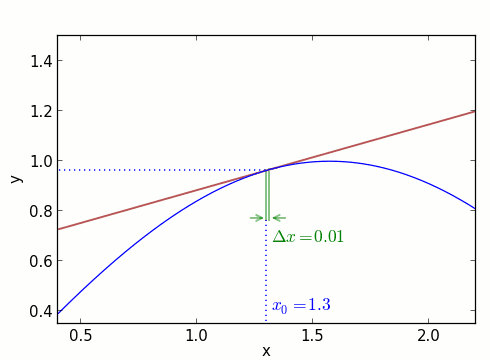
Mit den oben genannten Formeln können wir die (hier braun eingezeichnete) Gerade charakterisieren, die durch (x0, y0) und (x0 + Δx, f(x0 + Δx)) läuft. Wenn wir Δx sehr klein machen, dann nähert sich diese Gerade immer stärker der Verbindungskurve zwischen den beiden Punkten an. Ihre Steigung entspricht dann immer besser der Steigung der Kurve selbst im Punkt (x0, y0). Das sieht man auch in der obigen Animation: Bei Δx = 0.4 weichen die Steigungen von blauer Kurve und brauner Gerade noch deutlich voneinander ab. Für die immer kleineren Δx wird die Annäherung immer besser – die Gerade schmiegt sich immer dichter an die blaue Kurve.
Die Steigung der Gerade ist aber, siehe der obige Ausdruck für a, gleich
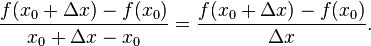
Definieren wir Δy = f(x+Δx) – f(x), so ist dies gerade der Differenzenkoeffizient Δy/Δx. Im Grenzfall immer kleinerer und kleinerer und schließlich ganz verschwindender Δx, Mathematiker sprechen vom “Grenzwert Δx gegen Null”, nähert sich dieser Ausdruck der Steigung der Kurve am Punkt x0 an. Diesen Grenzfall bezeichnet man als den Wert der Ableitung am Punkt x0, geschrieben als
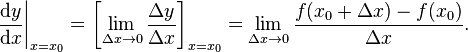
Bestimmt man die Ableitung einer Funktion, so ist auch davon die Rede, man differenziere die Funktion.
Der Grenzwert, mit dem man Δx gegen Null gehen lässt, so dass es zum “infinitesimalen” dx wird, bedarf mathematisch gesehen einiger Unterfütterung. In der Analysis, dem Teilbereich der Mathematik, der sich mit dieser Art von “Differenzialrechnung” beschäftigt, wird der Grenzwertbegriff deswegen mit großer Sorgfalt eingeführt – aber das geht nun wirklich darüber hinaus, was “Einstein verstehen” leistne kann und will.
In der Praxis stellt sich das obige Rezept denn auch zumeist auch ohne tieferes Verständnis von Grenzwerten als unproblematisch heraus. Ein Beispiel bietet im nächsten Abschnitt die Herleitung der Formel für die konstante Beschleunigung; was dort passiert, ist typisch: wenn man f(x0+Δx) – f(x0) hinschreibt, dann findet man – manchmal direkt, manchmal erst nach bestimmten Näherungen – dass es sich um einen Term handelt, in dem ein Summand proportional zu Δx ist und alle anderen proportional zu höheren Potenzen wie Δx2, Δx3 usw. sind. Beim Teilen durch Δx bleibt damit ein nicht von Δx abhängiger Term übrig plus weitere Terme, die proportional zu Δx oder höheren Potenzen von Δx sind. Die letzteren Terme werden null, wenn wir Δx gegen Null gehen lassen; der erste Term bleibt übrig.
Insbesondere bei Größen, die von der Zeit abhängen, wird die Ableitung bisweilen durch einen Punkt über der entsprechenden Größe ausgedrückt. Für eine Funktion x(t) wäre die Ableitung dann
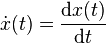
Herleitung der Formel für die konstante Beschleunigung
Für den Fall konstanter Beschleunigung hatte ich behauptet, dass
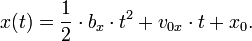
Nun betrachten wir den Ort des Teilchens eine kurze Zeit später, nämlich zur Zeit t+Δ t, mit Δ t einem sehr kleinen Zeitintervall. Er ist offenbar
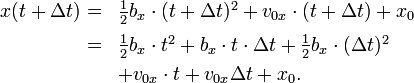
Die Strecke in x-Richtung, die das Teilchens während der Zeit Δ t zurückgelegt hat, ist demnach
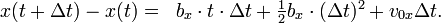
Diese Strecke, geteilt durch die Länge des Zeitintervalls, in der sie durchlaufen wird, nämlich Δ t, ergibt die Durchschnittsgeschwindigkeit des Körpers im Zeitintervall t bis t+Δ t:
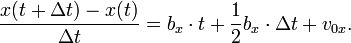
Nun lassen wir die Zeitdifferenz Δ t immer kleiner werden. Das Ergebnis ist dann nicht mehr eine Durchschnittsgeschwindigkeit, sondern so etwas wie eine momentane Geschwindigkeit in x-Richtung zur Zeit t. Die rechte Seite der obigen Gleichung ist, wenn wir Δ t gegen Null gehen lassen, wird zu
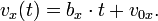
Das ist in der Tat die im Haupttext angegebene Formel. Die x-Komponente der Geschwindigkeit verändert sich linear mit der Zeit; der Proportionalitätsfaktor ist die (konstante) Beschleunigung bx, die ursprüngliche Geschwindigkeit zur Zeit t=0 ist v0x.
Ableitung der Impulserhaltung
Betrachten wir ein System von Teilchen. Das System möge isoliert sein, und das soll insbesondere heißen: Es wirken keine Kräfte von außen auf das System, sondern wann immer eine Kraft auf eines der Teilchen wirkt, rührt diese von einem anderen der Teilchen her.
Fangen wir der Einfachheit halber mit drei Teilchen an. Ich rechne hier und im folgenden nur mit den x-Komponenten der Impulse; die Rechnungen lassen sich aber genau analog für y- und z-Komponenten durchführen.
Die Summe der x-Komponenten der Impulse unserer drei Teilchen ist
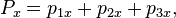
und die Änderung von Px ist die Summe der Änderungen der x-Komponenten der Impulse auf der rechten Seite, nämlich
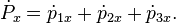
Das folgt direkt aus der Definition der Ableitung, die im vorigen Ergänzungsteil eingeführt wurde – wendet man das dort gegebene Rezept zur Berechnung der Änderungsrate auf eine Summe an, dann kann man die einzelnen Terme so rearrangieren, dass man die Summe der Änderungsraten erhält.
Für jedes der drei Teilchen gilt entsprechend dem zweiten Newton’schen Gesetz, dass die zeitliche Änderung der x-Komponente seines Impulses gerade die Summe der x-Komponente aller Kräfte ist, die auf dieses Teilchen wirken. Da wir vorausgesetzt hatten, dass es keine äußeren Kräfte gibt, bestimmt sich die auf das Teilchen 1 wirkende Kraft als Summe der vom Teilchen 2 und der vom Teilchen 3 ausgehenden Kräfte, und entsprechend für Teilchen 2 und 3.
Als Formel geschrieben: Für die x-Komponente F1x der Kräfte, die auf Teilchen 1 wirken, gilt
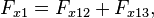
wobei Fx12 die Kraft bezeichnet, die vom Teilchen 2 auf das Teilchen 1 wirkt und Fx13 die Kraft, die vom Teilchen 3 auf das Teilchen 1 wirkt; für das Teilchen 2 gilt mit der gleichen Notation
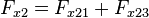
und für das Teilchen 3
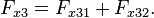
Die Änderung der x-Komponente der Impulssumme ist damit
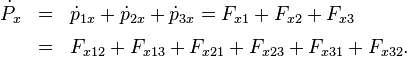
Nach dem dritten Newton’schen Gesetz ist die Kraft, die Teilchen 1 auf Teilchen 2 ausübt entgegengesetzt gleich der Kraft, die Teilchen 2 auf Teilchen 1 ausübt, in der hier gewählten Notation also
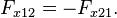
In der obigen Summe tauchen beide Terme auf und heben sich dementsprechend weg. Aber das dritte Newton’sche Gesetz gilt auch für das Teilchenpaar 1 und 3, und für das Paar 2 und 3, also
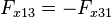
und
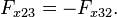
Auch diese Anteile heben sich in der Summe paarweise auf, und am Ende steht dort
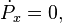
in Worten: Die x-Komponente der Impulssumme ändert sich mit der Zeit nicht. Die Impulssumme bleibt immer gleich. Der Impuls gleicht erhalten.
Was ich hier für drei Teilchen vorgeführt habe, lässt sich auf eine allgemeinere Anzahl von Teilchen verallgemeinern. Nummerieren wir die Teilchen mit den Nummern 1 bis n durch. Dann ist die Summe der x-Komponente der Teilchenimpulse
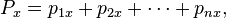
wobei auf der rechten Seite die x-Komponenten der Impulse aller n Teilchen aufsummiert werden: Die x-Komponente p1x des Impulses der ersten Teilchens, plus die des zweitens, und so weiter bis zur x-Komponente pnx des Impulses des letzten Teilchens unserer Zählung.
Die Änderung von Px mit der Zeit ist wieder die Summe der Änderungen der x-Komponenten der Impulse der einzelnen Teilchen,
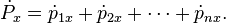
Für jedes der Teilchen gilt nach dem zweiten Newton’schen Gesetz wiederum, dass die zeitliche Änderung der x-Komponente seines Impulses gerade die Summe der x-Komponente aller Kräfte ist, die auf dieses Teilchen wirken. Wegen der Abwesenheit äußerer Kräfte ist die auf das Teilchen mit der Nummer i wirkende Kraft wieder
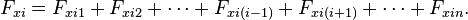
Dabei ist auf der rechten Seite Fxi1 die Kraft, die das erste Teilchen auf das i-te Teilchen ausübt, und entsprechend so weiter. Die Summe auf der rechten Seite soll ausdrücken, dass dort die Beiträge aller Teilchen berücksichtigt werden (außer dem i-ten Teilchen selbst, das auf sich selbst schließlich keine Kraft auswirkt). Streng genommen muss man für i=1, i=2 oder i=n eine etwas andere Summe hinschreiben. Da aber klar sein sollte, was mit der Summe rechts gemeint ist, schreibt man die Spezialfälle in der Regel nicht extra hin.
Die Änderung der x-Komponente des Gesamtimpulses ist
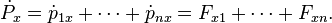
Jede der Teilkräfte Fxi auf der rechten Seite ist ihrerseits eine Summe wie in der Formel zuvor. Aber wie im Falle der drei Teilchen treten, wenn wir alle Teilkräfte-Summen zusammenfassen, jeweils paarweise Terme auf: für jeden Anteil Fxij, der die Kraft des j-ten Teilchens auf das i-te Teilchen beschreibt, ist da auch ein Term Fxji für die Kraft des i-ten Teilchens auf das j-te Teilchen. Aufgrund des dritten Newton’schen Gesetzes ist dabei jeweils
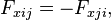
und die Terme heben sich sämtlich paarweise auf. Am Ende steht wieder
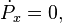
und das heißt, dass der Impuls auch in einem System mit n Teilchen erhalten bleibt.
Für kompliziertere Systeme kann man oft Modelle finden, die auf dem Zusammenspiel von Punktteilchen basieren; deswegen ist die hier gezeigte Ableitung recht allgemein anwendbar.


Markus Pössel schrieb (18. November 2013):
> Bislang geht es in der Einleitung noch um […] diejenigen Konzepte […] die man kennen
muss, um zu verstehen, vor welchem Hintergrund und auf welcher Grundlage Einstein die Spezielle Relativitätstheorie einführte.
Was die Grundlage der RT betrifft (wenn auch nicht unbedingt deren historischen Hintergrund), hat Einstein das zum Verständnis erforderliche gedanken-experimentelle Konzept recht deutlich
benannt:
[ “Die Grundlage der allgemeinen Relativitätstheorie”, §3;
http://www.physik.uni-augsburg.de/annalen/history/einstein-papers/1916_49_769-822.pdf ]
Also Feststellungen wie:
– A und A’ trafen und passierten einander,
– B und B’ trafen und passierten einander,
– M und M’ trafen und passierten einander,
– M sah das Treffen von A und A’ und das Treffen von B und B’ zusammen,
– M’ sah zuerst das Treffen von A und A’ und danach das Treffen von B und B’,
– A sah zusammen, dass B das Treffen von A und A’ gesehen hatte und dass C das Treffen von A
und A’ gesehen hatte,
usw.
(Beispiele entnommen aus weiteren Veröffentlichungen Einstein’s, die insbesondere der Einführung und dem Verständlichmachen der SRT gewidmet waren.)
Allerdings fehlen derartige Betrachtungen im vorliegenden SciLogs-Beitrag offenbar gänzlich, und sind auch in den verlinkten bisherigen Teilen von “Einstein verstehen” kaum auffindbar.
Mal sehen, ob sich das in eventuell folgenden Teilen noch ändert.
Klar kommen solche Aussagen noch. Aber momentan sind wir noch bei dem, was Einstein in dem angeführten Werk in §1 über die grundlegenden Eigenschaften der Speziellen Relativitätstheorie erzählt. Über die referiert Einstein da so verkürzt, wie man es für Physiker, die die Grundlagen von Newton’scher Mechanik, gleichförmigen Bewegungen, Koordinatentransformationen, euklidischem Raum etc. natürlich schon kennen, machen kann, in einer an allgemeineres Publikum gerichteten Einführung wie hier freilich nicht.
Markus Pössel schrieb (19. November 2013 18:20):
> […] was Einstein in dem angeführten Werk in §1 über die grundlegenden Eigenschaften der Speziellen Relativitätstheorie erzählt. Über die referiert Einstein da so verkürzt
Der Mangel dieses Referats liegt nicht unbedingt in seiner Kürze, sondern im Fehlen von ausdrücklichen Bezügen auf die von Einstein selbst wohl erst im Nachhinein so begriffene Grundlage von geometrisch/kinematischen Konstatierungen; also auf Urteile über Koinzidenz (oder ansonsten: Reihenfolge).
> Klar kommen solche Aussagen noch.
Wenn das Verständlichmachen (allerdings auch das Verstehen) mit dem Benennen und Benutzen von Grundlagen beginnt, dann sollten solche Aussagen zuerst kommen.
@Herr Wappler, man muß hierbei aber auch berücksichtigen daß andere Mitleser “anders” verstehen. Wenn es um “relativ einfach” erklären für eine breitere Leserschaft geht, sollte man beim “Normalsprech” bleiben, philosophieren verwirrt.
(a) Wer sagt denn, dass das ein Mangel des Einstein’schen Texts sei? Für die Zielgruppe des Textes ist die Kürze völlig angemessen. Hier im Blog wäre sie es nicht.
(b) “Wenn das Verständlichmachen (allerdings auch das Verstehen) mit dem Benennen und Benutzen von Grundlagen beginnt” – das tut es eben oftmals nicht. Diese Fehlvorstellung zieht sich durch viele der kritischen Kommentare, die Sie hier hinterlassen haben. Aber wenn ich Kindern das erste Mal das Zählen beibringe, beginne ich eben nicht mit den Peano-Axiomen. Und in der Biologie mit gutem Grunde nicht mit der DNA, ihrer Struktur und chemischen Zusammensetzung, obwohl das in der Tat die Grundlage von allem Leben ist, wie wir es kennen.
Analog eben auch bei der Speziellen Relativitätstheorie. Der einzelne Beobachter, der allein aus bei ihm ankommenden Signalen die Kinematik und Dynamik um ihn herum rekonstruiert, mag ja durchaus grundlegend sein. Aber um überhaupt zu verstehen, woher die Grundannahmen kommen, die man dabei bereits benutzt, warum sie durchaus gut motiviert sind (obwohl die Konstanz der Lichtgeschwindigkeit unserer direkt extrapolierten Alltagserfahrung ja nun widerspricht), was es mit den dabei auftauchenden verschiedenen Klassen von Beobachtern auf sich hat, wie man darauf gekommen ist, gerade jene und keine anderen Grundannahmen zu machen, und so weiter, muss man vieles an Vorwissen bereits haben. Dieses Vorwissen baue ich hier Stück für Stück auf.
Markus Pössel schrieb (21. November 2013 8:18):
> Aber wenn ich Kindern das erste Mal das Zählen beibringe […]
Aber wirklich das Zählen (an sich), nicht (nur) irgendwelche austauschbaren Zahlworte, -symbole oder -gesten; nicht wahr?
Falls so, dann ist das, was dabei gelernt/verstanden werden soll, durch die Peano-Axiome zumindest inhaltlich konkret und vollständig benannt. Verschiedene Kinder oder Pädagogen mögen allerdings verschiedene Formen finden bzw. bevorzugen, um sie auszudrücken, sich einzuprägen, und wiederum zu vermitteln.
> Analog eben auch bei der Speziellen Relativitätstheorie. […] Aber um überhaupt zu verstehen, woher die Grundannahmen kommen
Gute Frage! — Woher kommt denn die oben (19. November 2013 15:49) zitierte Grundannahme, dass “die Bestimmung zeiträumlicher Koinzidenzen” als selbstverständlich vorausgesetzt und gebraucht werden kann?
Ist denn irgendeine Zielgruppe vorstellbar, deren Mitgliedern man nicht zumindest soviel
Verständnis von vornherein zugestehen würde?
Kann man jemandem überhaupt irgendetwas verständlich machen, der nicht von selbst in der Lage
wäre, die Begriffe “zusammen” und “getrennt/nacheinander/verschieden” zu unterscheiden?
Ansonsten kann man diese Grundlage(n) als notwendig betrachten.
Und da nach Einsteins (1916 möglicherweise noch perspektivischem) Bekunden diese Grundlage
auch hinreichend ist, um “alle unsere zeiträumlichen Konstatierungen” verständlich zu machen, sind die Vorarbeiten zu den Grundlagen des Verstehens der (S)RT damit abgeschlossen.
Also ab an die eigentliche Arbeit!
Ach, kommen Sie – dass das nicht so einfach ist, wie Sie hier (mit durchaus missverständlich selektivem Zitieren aus meiner Antwort) behaupten, steht doch in meiner Antwort bereits.
Hier als leicht abgewandelte Wiederholung:
Die Bestimmung zeiträumlicher Koinzidenzen mögen ja durchaus grundlegend sein. Aber um überhaupt zu verstehen, woher die Grundannahmen kommen, die man bei deren Beschreibung und den sich daraus ergebenen Interpretationen (Kinematik, Dynamik) benutzt, warum das alles
gut motiviert ist (obwohl die Konstanz der Lichtgeschwindigkeit unserer direkt extrapolierten Alltagserfahrung ja nun widerspricht), was es mit den dabei auftauchenden verschiedenen Klassen von Beobachtern auf sich hat, wie man darauf gekommen ist, gerade die verwendeten und keine anderen Grundannahmen zu machen, und so weiter – dazu muss man vieles an Vorwissen bereits haben. Dieses Vorwissen baue ich hier Stück für Stück auf.
Markus Pössel schrieb (21. November 2013 12:58):
> […] muss man vieles an Vorwissen bereits haben. Dieses Vorwissen baue ich hier Stück für Stück auf.
Sofern die bisher vorgebrachten Stücke nicht (bzw. noch nicht erkennbar) auf der o.g. Grundlage der (S)RT beruhen, kann von “zielführendem aufbauen” (noch) keine Rede sein;
sondern allenfalls von “Baustelle”.
Aber zugegebenermaßen empfiehlt es sich, schon vor dem Losbauen einen Plan zu machen; um
(Auf-)Baufortschritte auch über den allerersten Schritt hinaus beurteilen zu können.
Hier nochmals zur gelegentlichen Ansicht:
[ “Über die spezielle und die allgemeine Relativitätstheorie (Gemeinverständlich)”, §8;
http://archive.org/stream/berdiespezielle00unkngoog/berdiespezielle00unkngoog_djvu.txt ]
Das ist doch jetzt wirklich Krittelei. Und ja: Natürlich ist es eine Baustelle. Die übrigens, wie ich beim nochmaligen Durchschauen des (leider nicht sehr schön digitalisierten) verlinkten Textes bestätigt finde, vom Aufbau her gar nicht so arg von dem Einstein-Text abweicht, den Sie hier, warum auch immer, anführen (mit wieder einmal missverständlich verkürztem Zitat).
Markus Pössel schrieb (23. November 2013 1:12):
> Das ist doch jetzt wirklich Krittelei.
Mein Hinweis auf
– Einsteins Forderung, dass Begriffe (zwangsläufig mit Ausnahme des Begriffs “Koinzidenz”) durch Messoperatoren definiert sein müssen, und
– Einsteins Bemerkung, dass im Rahmen der (S)RT derartige Definitionen ausschließlich unter Verwendung des “Koinzidenz”-Begriffs zu erstellen sind,
wäre eine “Krittelei” am vorliegenden Beitrag (und den oben verlinkten vorausgegangenen Teilen), worin derartige Definitionen auffallend fehlen?
Meine Absicht war es jedenfalls, damit massive, grundsätzliche Kritik daran auszudrücken, die vorliegenden Fragmente als geeignet zum “Einstein verstehen” auftischen zu wollen.
> eine Baustelle. Die übrigens […] vom Aufbau her gar nicht so arg von dem Einstein-Text abweicht
Offenbar zumindest abgesehen von Einsteins entscheidender (aber von manchen wohl stattdessen “belanglos” genannter) Aufforderung:
[ ibid. ]
(Jedenfalls hat Einstein selbst diese Aufforderung in Klammern gesetzt; und offenbar hat er sie umgekehrt selber — als Schreiber — nicht ernst genug genommen, um an dieser Stelle zunächst mit dem Schreiben innezuhalten und vorausgehende Texte anhand der geforderten Überzeugung selber kritisch zu prüfen.)
p.s.
> […] des (leider nicht sehr schön digitalisierten) verlinkten Textes
Stimmt erstmal: schön kann die verlinkte Version von “Über die spezielle und die allgemeine Relativitätstheorie (Gemeinverständlich)” wirklich nicht nennen.
Aber leider kenne ich (noch) keine schönere frei zugängliche deutsche Version, die auch durchsuchbar und “copy-‘n’-paste”-geeignet wäre.
Hoffentlich wird sich das bald ändern; insbesondere aus Anlass des bevorstehenden 100-jährigen Jubiläums der Erst-Veröffentlichung dieses entscheidenden (aber von manchen wohl stattdessen “belanglos” genannten) Werkes.
Schauen Sie sich doch noch einmal an, wie Einstein in dem von Ihnen zitierten Text vorgeht: Er beschreibt Ortsbestimmungen, kartesische Koordinatensysteme, Grundlagen der Zeitmessung (wobei er Komplikationen durch die endliche Fortpflanzungsgeschwindigkeit des Lichts erst einmal außen vor lässt und sagt, er käme später darauf zurück), beschreibt in Paragraph 4 kurz das Trägheitsgesetz.
Bis dahin laufen meine Blogserie Teil I-IV und Einsteins Darstellung ziemlich exakt parallel. Nur, dass meine Darstellung wesentlich ausführlicher ist (was überhaupt nicht wertend gemeint ist – für einige Leser wird meine Darstellung damit geeigneter sein als Einsteins, für andere wird es anders herum sein).
Das, was Sie als oh-so-große-Abweichung präsentieren (“Bevor du mir dies mit Überzeugung zugegeben hast…”) ist genau mein Teil III mit der Erklärung, warum Gleichzeitigkeit nicht vom Himmel fällt, sondern eben einer (operationalen) Definition bedarf.
Dass Sie den Einsteintext trotz dieser Parallelität als angeblichen Beleg dafür anführen, dass Einstein es ganz anders gemacht und gemeint hat, gewürzt mit Ausdrücken wie “Fragment”, ist aus meiner Sicht in der Tat kleinliche und ziemlich schiefe Kritik.
Wobei Sie, was ja nun schwerlich mehr in den Bereich redlichen Argumentierens fällt, nicht davor zurückschrecken, sich Einstein-Zitate zurecht zu biegen, um Einstein sagen zu lassen, was Sie gerne möchten, dass er sagt: Sie schreiben
– aber das ist, wenn man genauer hinschaut, gerade kein Beleg für Ihre allgemeine Behauptung, da gäbe es “Einsteins Forderung, dass Begriffe (zwangsläufig mit Ausnahme des Begriffs ‘Koinzidenz’) durch Messoperatoren definiert sein müssen”. Im Original heißt es nämlich stattdessen viel eingeschränkter und konkreter
Es geht hier also gar nicht um Begriffe allgemein, sondern (zumindest an dieser Stelle) lediglich ganz spezifisch um den Begriff der Gleichzeitigkeit. Und auf diesen Begriff bezogen wird ja auch bei mir, eben in Teil III, beschrieben, dass die Definition einer geeigneten Messmethode notwendig ist und wie solch eine Methode aussehen kann.
Insofern sieht es für mich so aus, als würden Sie sowohl meinen als auch Einsteins Text durch eine sehr subjektive Brille betrachten – und daran dann weitgehende, oft und gerne wiederholte, zum Teil falsche, zum Teil kleinliche, zum Teil auf missverständlich verkürzten Zitaten basierende Kritik aufhängen. Einen großartigen Mehrwert für die weiteren Mitleser hier kann ich an dieser Stelle nicht erkennen (das war bei Ihren früheren Beiträgen durchaus anders!), und möchte diese Diskussion deswegen jetzt hier zu einem Ende bringen.
Markus Pössel schrieb (23. November 2013 23:37):
> […] sich Einstein-Zitate zurecht zu biegen
Das fragliche Zitat (21. November 2013 17:39) diente der Darstellung von Einsteins Argumentation. Die Auslassungen (die die Anwendung der Argumentation auf den spezifischen Fall “Gleichzeitigkeit” betreffen) waren deutlich gekennzeichnet. Und offensichtlich kann man den kompletten Text u.a. in der angegebenen Quelle nachlesen.
> Es geht hier also gar nicht um Begriffe allgemein, sondern (zumindest an dieser Stelle) lediglich ganz spezifisch um den Begriff der Gleichzeitigkeit.
Wieso sollte Einsteins Argument davon abhängen, welcher spezifische Begriff die (im obigen Zitat absichtlich freigelassene) “Stelle” einnimmt ??
Wieso sollte Einstein das, was er sinnvoller Weise für den Begriff “Gleichzeitigkeit” fordert, nicht ebenso für andere Begriffe fordern, die mit “Ortsbestimmungen” oder “Zeitmessung” verbunden wären?
(Bzw. um anhand der angegebenen Quelle ganz konkret zu sein: u.a. für Begriffe wie “im Zustande der Ruhe verharren” oder “gleichförmig-geradlinigen Bewegung” oder “zwei an verschiedenen Stellen des Bezugskörpers ruhend angeordnete“.)
Ist das schon weiter oben (19. November 2013 15:49) in diesem Zusammenhang gezeigte Zitat (
)
etwa “zurechtgebogen” oder missverständlich ?!?
> Einen großartigen Mehrwert für die weiteren Mitleser hier kann ich an dieser Stelle nicht erkennen
Sind von der Mitleserschaft dieses SciLogs etwa solche Leser auszuschließen, die den (Einsteinschen) Begriff “zeiträumlicher Koinzidenzen” zwar schon verstehen (was man wohl jedem denkbaren Leser zugestehen kann), aber alle anderen Begriffe, die “zeiträumlichen Konstatierungen” betreffen, im Einsteinschen Sinne ausdrücklich durch eine Methode definiert haben möchten, die auf die Bestimmung zeiträumlicher Koinzidenzen hinausläuft?
Falls so, dann muss man sich als Physiker und Nutzer der RT hier eben ausgeschlossen betrachten; allerdings auch als entsprechend gewissenhafter Nichtphysiker.
Sie fragten
– weil Gleichzeitigkeit derjenige Begriff ist, der den Physikern beim Übergang von der Praxis der klassischen Mechanik (traditionellerweise machte sich da niemand groß Gedanken darüber, wie Gleichzeitigkeit gemessen wird) zur Speziellen Relativitätstheorie (Definition der Gleichzeitigkeit per Messmethode essentiell – Konsequenzen daraus, Relativität der Gleichzeitigkeit, durchaus ungewohnt) die größte Transformation erfährt. Weil Orte bestimmen, Längen messen, Uhrzeiten ablesen zu unseren (erweiterten) Alltagserfahrungen gehört, während die Gleichzeitigkeit üblicherweise einfach so hingenommen oder allenfalls durch Uhrentransport berücksichtigt wird.
Das war Einstein durchaus bewusst, was sich vor allem darin zeigt, dass er den Begriff der Gleichzeitigkeit und alles, was an Messungen damit zusammenhängt, besonders ausführlich und genau behandelt und beschreibt. Weswegen man also, wenn man schließen will, was Einstein besonders wichtig war, was er für grundlegend ansah, wo er auf operationale Definitionen besonderen Wert legt bzw. deren Wichtigkeit besonders betont, nicht einfach ein Zitat hernehmen und den Begriff “Gleichzeitigkeit” durch beliebige andere Begriffe ersetzen oder ganz weglassen kann.
Dass Sie sich am Ende gleich stellvertretend für alle Physiker und Nutzer der RT in Stellung bringen, die hier mitlesen, halte ich für ebenso überheblich wie irregeleitet. Ich bin nach wie vor der Meinung, dass Sie mit Ihrer kritischen Einschätzung der Systematik meiner Einführung ziemlich alleine stehen, und dass die allermeisten Physiker und Nutzer der RT, die hier mitlesen, sehr wohl sehen, worauf ich hinauswill, und warum ich welche Grundbegriffe in welcher Reihenfolge einführe. Weswegen ich, wie gesagt, denke, dass diese Diskussion – diese letzte Runde mit eingeschlossen – den meisten Mitlesern kaum Mehrwert bringt und ich sie deswegen hier beenden möchte.
Markus Pössel schrieb (25. November 2013 14:10):
> […] von der Praxis der klassischen Mechanik (traditionellerweise machte sich da niemand groß Gedanken darüber, wie Gleichzeitigkeit gemessen wird)
Ja — und hätte man sich wenigstens über alle möglichen anderen Begriffe Gedanken machen sollen (d.h. ggf. über die eventuellen diversen “ (erweiterten) Alltagserfahrungen” hinaus)?
Hat sich etwa irgendwer vor Einstein groß Gedanken darüber gemacht, wie z.B. “Längen” zumindest im Prinzip zu messen wären?? (Oder war das wirklich erst Synge? …)
Hätte sich wenigstens jemand Gedanken darüber machen sollen (oder gar gemacht), auf welcher Grundlage bzw. mit welchen begrifflichen Mitteln man sich groß Gedanken machen könnte, wie jeweils nachvollziehbar zu messen sei??
> diese Diskussion […] hier beenden
Na schön — wie schon eingangs (19. November 2013 15:49) abzusehen war:
Mal sehen, ob in eventuell folgenden Beiträgen “Bestimmungen von Koinzidenz (oder ansonsten: von Reihenfolge)” noch erwähnt werden, und inwiefern sich daraus die bisher fehlenden Begriffsdefinitionen ergeben; z.B. eine Methode, durch deren Anwendung im konkreten Fall herauszufinden wäre, ob “die Länge AM” und “die Länge MB” “einander gleich” gewesen wären, oder nicht.
p.s.
> Dass Sie sich am Ende gleich stellvertretend für alle Physiker und Nutzer der RT in Stellung bringen, die hier mitlesen
Ein geringerer Anspruch wäre als Physiker unehrlich, und unter Physikern abwegig. Únd Einstein gibt auch dafür die bekannte rhetorische Steilvorlage.
Bei den Längen und beim Bau einzelner Uhren gab es jahrhundertelange Messpraxis, und damit keinen Mangel an operationalen Definitionen. In dieser Hinsicht scheint die Gleichzeitigkeit tatsächlich etwas besonderes gewesen zu sein.
Zumindest um einige Aspekte von Koinzidenzen wird es in Teil VI gehen.
“Ein geringerer Anspruch wäre als Physiker unehrlich,” – ja, es sei denn, man zieht zumindest im Prinzip in Betracht, dass die eigene Interpretation und Auffassungsweise möglicherweise nicht allgemeingültig und damit allen vernünftigen Wesen verpflichtend sein könnte oder, schauder, dass die Möglichkeit eigenen Irrtums besteht.
Hallo Herr Pössel,
schön das es nun wieder weiter geht, hatte ja schon fast die Hoffnung verloren. Ich habe da eine kleine Bitte, es beginnen schon wieder diese nervigen Metadiskussionen, die alle nicht wirklich sachlich sind und mit dem Thema Relativitätstheorie direkt nichts zu tun haben. Können sie nicht gleich grundsätzlich Beiträge die „kritisch“ die Methode der Darstellung hier im Blog hinterfragen, ausgliedern?
Ziel sollte hier wirklich sein, Einstein und seine Theorie sachlich zu diskutieren um im Verständnis weiterzukommen. Wer die Theorie für falsch und einen ganz großen Betrug hält und nur das Ziel verfolgt die SRT zu bekämpfen und zu zerstören ist hier sicher falsch. Denn er ist ja schon überzeugt, sie sei falsch, er will sie also nicht mehr verstehen. Damit ist das einzige Ziel, dass dann verfolgt wird, hier die anderen beim Verstehen zu stören.
Lieben Gruß
P.S.: Was eine Vorschaufunktion ist, ist bekannt? Oder ist der Retro Look ein stilistisches Element?
Ich habe den Eindruck, dass Herr Wappler in die Kategorie “falsch und ganz großer Betrug” fällt, und die Frage, ob man axiomatischer anfangen sollte (Raumzeit-Koinzidenzen), finde ich auch nicht banal. Richtig ist allerdings, dass sich solche Diskussionen mit Herrn Wappler leider recht zäh und sicher auch länger als nötig hinziehen. Wenn nicht gerade große Flaute hier gewesen wäre, hätte ich sicher schneller den Stecker gezogen. Vielleicht schreibe ich auch noch einen Meta-Einstein-Verstehen-Beitrag, auf den man solche Diskussionen umlenken kann.
Zur Vorschaufunktion (bei Kommentaren): Ich bin schon sehr froh, wie es hier mit der Modernisierung vorangeht (sowohl hinter den Kulissen als auch z.B. direkt bei den Kommentaren die Möglichkeit, direkt zu antworten); vielleicht kommt die Vorschaufunktion ja auch bald…
Korrektur: “Ich habe nicht den Eindruck […]”. Oh Manno. Ich ändere das gleich noch; bitte nicht direkt auf diesen Kommentar hier antworten, den lösche ich nach der Änderung wieder.
Nur um meine Aussage zu begründen, ich habe alle Kommentare nun gelesen, und da geht es um langweilige Banalitäten, wirklich Sachliches zur RT ist in den Kommentaren nicht zu finden. Ist doch egal, wie Einstein zitierte, ob Texte bunt oder in schwarzweiß im Internet stehen. Geht es noch?
Ich finde es traurig, dass es hier so anfängt, wie es letzte Mal aufgehört hat.
Hallo Herr Pössel,
die bisherige Einführung in die SRT ist meines Erachtens gelungen. Allerdings sind mittlerweile 3 Jahre vergangen und und der Hauptteil der SRT steht noch aus. Ich kann dem Vorschlag von Herrn Krüger daher nur zusimmen. Wie sieht den überhaupt die weitere Zeitschiene aus?
mit freundlichem Gruß
Eine richtige Zeitschiene gibt es nicht nicht; ich arbeite (meist abends und am Wochenende) regelmäßig an “Einstein verstehen” weiter, und was fertig ist, wird ins Netz gestellt. Teile IV und V haben unter anderem deswegen länger gedauert, weil ich erst einen Überblick haben musste, wie es in den darauffolgenden Teilen weitergeht und welche Konzepte dort benötigt werden.
Markus Pössel schrieb (18. November 2013):
> […] ein Inertialsystem [ist] ein Bezugssystem, in dessen Raumkoordinaten […] und Zeitkoordinate ausgedrückt die Gesetze die hier vorgestellte Form haben. [… »Ein Massenpunkt, auf den keine Kraft wirkt, erfährt auch keine Beschleunigung.« …]
Dieser prä-relativistichen Auffassung lässt sich nach W. Rindler entgegensetzen:
Dabei versteht sich:
– dass die Beurteilung, ob (hinreichend viele) gegebene Beteiligte gegenübereinander ruhten, oder nicht, ausschließlich auf Bestimmungen zeit-räumlicher Koinzidenzen hinausläuft, wie von Einstein (1916) gefordert,
– wobei insbesondere je zwei Mitglieder eines bestimmten Inertialsystems nie koinzident waren (sich nie trafen/passierten),
– dass ein Inertialsystem hinsichtlich gegebenen gegenübereinander ruhenden Beteiligten maximal sein soll, d.h. auch alle weiteren Beteiligten beinhaltet, die sowohl untereinander als auch bzgl. den ersteren ruhten,
– dass je zwei Mitgliedern eines Inertialsystems eine bestimmte konstante Distanz voneinander zugeschrieben wird, und Messungen der Distanz-Verhältnisse zwischen Paaren von Mitgliedern des selben Inertialsystems wiederum ausschließlich auf Bestimmungen zeit-räumlicher Koinzidenzen hinauslaufen,
– dass, wie von Rindler betont, zwischen einem Inertialsystem und einem inertialen Koordinatensystem strikter Weise zu unterscheiden ist; wobei ein “inertiales Koordinatensystem” ein Inertialsystem zusammen mit einer bestimmten eindeutig-umkehrbaren Zuordnung von Koordinaten-Tupeln jeweils zu dessen Mitgliedern (bzw. als “t”-Koordinate jeweils zu deren Anzeigen) darstellt.
Anhand der messbaren Distanz-Verhältnisse lassen sich geometrische Beziehungen zwischen bestimmten Mitgliedern eines Inertialsystems feststellen; also z.B. ermitteln, welche davon “gegenüber einander gerade gelegen” hätten,
es lassen sich “Bewegungen” von Beteiligten, die nicht zum betreffenden Inertialsystem gehörten, bzgl. der Mitglieder dieses Inertialsystems beschreiben, usw.
Alternativ könnte man den Artikel von Rindler genauer lesen und sehen, dass das nichts mit “entgegensetzen” zu tun hat, sondern dass Rindler Inertialsystem, “inertial system”, so einführt, wie ich es auch tue (am Anfang dieses Abschnitts) und später eine mögliche, aber nicht zwingende Unterscheidung zwischen Inertialsystem (“inertial system”) und “inertial frame” einführt (letztere die hier von Herrn Wappler verfälschend als Rindlers allgemeine Inertialsystem-Definition präsentierte Punktwolke). Tatsächlich ist die Aussage zur Differenzierung mehr eine Nebenbemerkung, “We should, strictly speaking, differentiate…” und wird später, soweit ich sehen kann, nicht mehr aufgegriffen. Weil die entsprechenden Begriffe eben in der Praxis austauschbar sind. Herr Wappler muss Rindlers Text schon sehr seinen persönlichen Vorlieben entsprechend hinbiegen, um auf die ihm genehme, aber bei Rindler schlicht nicht vorhandene strenge Vorschrift, dass “zu unterscheiden” “ist” zu kommen. Und die sprachlichen Feinheiten zwischen “inertial system” und “inertial frame” muss er auch ignorieren; anders käme man halt darauf, dass der Unterschied letztlich für die Praxis so unwichtig ist, dass sich in den im deutschen Fachbüchern üblichen Sprachgebrauch neben dem “Inertialsystem” gar nicht erst eine allgemein so verstandene Entsprechung von “inertial frame” etabliert hat. Letztlich also wieder ein Sturm im Wasserglas, diesmal mit dem unangenehmen Beigeschmack verzerrender Zitate bzw. Behauptungen zu den Aussagen von Rindler.
Markus Pössel schrieb (11. Juni 2019 @ 13:53):
> […] sondern dass Rindler Inertialsystem, “inertial system”, so einführt
Sorgfältigen Lesern des betreffenden Scholarpedia-Artikels “Special relativity: kinematics” mag auffallen, dass die Wortgruppe “inertial system” darin gar nicht auftritt;
sondern “system” stets in Verbindung als “coordinate system”; und davon ein paar mal ausdrücklich als “inertial coordinate system” (erstmals im oben gezeigten Zitat) …
> wie ich es auch tue
Es ist zwar nicht zu bestreiten, dass (auch) Rindler den Begriff “free particle(s)” einstreut, als bedürfe der keiner Definition.
Hinsichtlich geometrisch-kinematischer Grundlagen ist allerdings die Einführung (bzw. “systematische Entwicklung von Definitionen und Konzepten“) beachtlich, die schon in “Einstein verstehen: Ein Blogexperiment, Teil I” gegeben ist;
man liest (u.a.) von
– “festen Punkten” (bzw. “festen Orten“),
– “Abstand der entsprechenden Punkte [paarweise voneinander]”, und schließlich:
– “Kartesische Koordinaten […] Jedem Punkt im Raum wird zur eindeutigen Identifikation ein Satz [Tupel] von drei [rellen] Zahlen (x,y,z) zugeordnet.”
Ist dort nicht zwischen “(jeweils einem bestimmten) (festem) Punkt” und “Koordinaten-Tupel, das diesem Punkt zugeordnet wurde” zu unterscheiden, sodass nämlich überhaupt vom “Zuordnen” die Rede sein kann ?
Kann man von einem “System bestimmter (gegenüber einander fester) Punkte, einschl. (der Verhältnisse) ihrer Abstände untereinander” sprechen, ohne dessen Bestandteilen irgendwelche Koordinaten zuzuordnen ?
Und konkret wie lautet die (dort zwar beworbene, mittlerweile aber offenbar dem “link rot” zum Opfer gefallene) “ausführliche Ableitung der Formel der dreidimensionalen Version des Satzes des Pythagoras [für Kartesische Koordinaten]“, anhand der sich womöglich unterscheiden ließe, ob Koordinaten “Kartesisch zugeordnet” worden wären, oder “anders” ??
…OK, bei Rindler in der Tat “inertial coordinate system” anstatt “inertial system” aber entscheidend ist: meist interchangeably mit “inertial frame” bzw. “inertial reference frame”. Was den Umstand, dass Sie system vs. frame bei Rindler in Ihrem vorigen Kommentar ganz unter den Tisch fallen ließen nicht weniger irreführend/irreleitend macht.
Ihre Fragen machen mir nicht den Eindruck, als hätten Sie den Blogteil eins vollständig gelesen. Was mit physikalischen Orten gemeint ist, wird dort schließlich ausführlich beschrieben; auf die Idealisierung wird explizit hingewiesen; dann folgt die Verallgemeinerung.
Zum angeblichen “link rot”: Das entsprechende Link führt mich ganz wie es soll auf die Hintergrundseite hier. Erhalten Sie stattdessen eine Fehlermeldung?
Markus Pössel schrieb (12. Juni 2019 @ 13:39):
> …OK, bei Rindler in der Tat “inertial coordinate system” anstatt “inertial system” aber entscheidend ist: meist interchangeably mit “inertial frame” bzw. “inertial reference frame”.
Entscheidend ?!?
Wohl kaum! — solche quantitativen Kontingenzen und Befunde (“meist“, oder “mehrheitlich”) interssieren allenfalls am Rande;
darin kommen lediglich individuelle Interessen oder Vorlieben für die eine oder andere Art von (oben erwähnter) “Praxis” zum Ausdruck.
Entscheidend ist vielmehr die strikte Anerkennung oder strikte Zurückweisung des Knallhart-Grundsätzlichen:
– Sind die jeweiligen “Sätze von drei Zahlen (x,y,z)” an sich die elementaren Bestandteile von geoemtrischen Figuren/Objekten/Systemen ?
Oder:
– Sind diese Zahlen-Tupel den eigentlichen “Gegenständen” der Geometrie bzw. Kinematik (“nur”) zugeordnet ?
(Punkt.)
Zwar ist die Antwort darauf doch offenbar selbstverständlich, sofern es z.B. um “den euklidischen Raum” und dessen Bestandteile geht: “Jedem Punkt im Raum wird zur eindeutigen Identifikation ein Satz von drei Zahlen (x,y,z) zugeordnet.“, und “Es gibt unendlich viele verschiedene Möglichkeiten [von Kartesischen Koordinaten-Zuordnungen] im Euklidischen Raum […]” … und zweifellos noch mehr nicht-Kartesischen.
Um so mehr wundert und beunruhigt es mich, dass es so verdammt kontrovers bis absurd sein sollte,
– ein “System von Punktteilchen, die gegenüber einander ruhen, einschl. ihrer Abstände untereinander” an sich in Betracht zu ziehen, und
– von “Zahlensätzen, die den Bestandteilen des genannten Systems zugeordnet wurden, einschl. der dadurch induzierten bzw. komponierten Abstandsfunktion” gedanklich und terminologisch zu unterscheiden.
> […] dass Sie system vs. frame bei Rindler in Ihrem vorigen Kommentar ganz unter den Tisch fallen ließen
Dieses “vs.” habe ich höchstens insofern unter den Tisch fallen lassen, als ich “Koordinaten” insgesamt, und folglich auch “coordinate systems”, konsequent unter den Tisch fallen lasse. Koordinaten interessieren mich, als Physiker, nur insofern, als sie vom physikalisch-geometrisch Eigentlichen unterscheidbar sind (“nur nachträglich zugeordnet” sind), und darüberhinaus ganz und gar nicht interessieren. Mich beschäftigen von allem Definition und Messung von geometrisch-kinematischen Beziehungen an sich, und möchte mich ggf. mit anderen Physik-Interessierten darüber austauschen; nicht über Definition oder “natürliche” Topologie oder intrinsische Metrik und Differentialstruktur der rellen Zahlen-Tupel.
> Ihre Fragen machen mir nicht den Eindruck, als hätten Sie den Blogteil eins vollständig gelesen. […]
Diese Reaktion macht mir nicht den Eindruck, als sei der bereits 24. September 2016 @ 10:56 in Aussicht gestellte “gesonderte [SciL]ogbeitrag zur Frage von Koordinaten und koordinatenfreien Darstellungen“ schon in Arbeit. (Ich stehe nach wie vor gerne zur Verfügung, um einen entsprechenden Gast-SciLog-Beitrag zu verfassen …)
p.s.
> Zum angeblichen “link rot”: Das entsprechende Link führt mich ganz wie es soll auf die Hintergrundseite
Stimmt ja!, Entschuldigung!, ich hatte vor lauter sattsam-nebensächlichen bunten Bildchen zunächst gar nicht bemerkt, dass ich auf einer separaten Webseite gelandet war.
Zum Inhaltlichen der dort gezeigten “ausführlichen Ableitung der Formel“: Insbesondere an dieser Stelle …
… wird “offenbar” etwas angenommen, das doch erst bewiesen werden sollte. Leslie Lamport hätte sicherlich seine (ironisch-sprichwörtliche) “helle Freude” dran. …
Da es hier wieder zu aus meiner Sicht eher nebensächlichen Dingen sehr länglich wird, verlasse ich mich einfach mal darauf, dass die meisten Mitleser*innen anhand der vorangehenden Kommentare selbst beurteilen können, was hier abläuft.
Der abfällige Seitenhieb auf die “sattsam-nebensächlichen bunten Bildchen”, mit der Sie entweder den Umstand, dass es zahlreiche Menschen gibt, für die solche Darstellungen hilfreich sind, als unwichtig beiseitewischen oder aber schlicht Ignoranz dieses Umstandes zum Ausdruck bringen, bestärkt mich jedenfalls darin, Ihnen erst einmal keine Gastbeitragsmöglichkeit hier in diesem Blog anzubieten.