MoFi – Experimente zur Vermessung der Erde

Wo bin ich auf der Erde? oder: Wo liegt eine bestimmte Stadt? Modern geben wir hierfür Koordinaten in geographischer Länge und Breite an. Doch stellen Sie sich vor, Sie sind irgendwo im Nirgendwo und wollen navigieren. Dann müssen Sie Ihre Position in Länge und Breite bestimmen und Sie sollten besser eine Karte dabei haben, auf der steht, wo die nächste Ortschaft ist – dann können Sie in Erfahrung bringen, wohin Sie gehen sollten. Doch wie kommen die Koordinaten in die Karte?

Die geographische Breite ist leicht bestimmt, weil man z.B. die Höhe des Polarsterns (bzw. früher des Himmelspols ohne Stern bzw. die Mittagsschattenlänge der Sonnenuhr) bestimmen kann. Die geographische Länge war allerdings höchst schwierig zu bestimmen. Ziemlich einfach ginge das mit einer Uhr, die man auf einen Nullmeridian eicht und mit sich herumträgt, aber solche Uhren und das auch noch reisetauglich, wurden erst im 18. Jahrhundert entwickelt. Wir haben das also erst seit ca. 200 Jahren zur Verfügung (*). Im Altertum, d.h. vor ca. 2000 Jahren, gab es allerdings auch schon Kartographen, die angeben wollten, wo welcher Ort auf der Erdkugel liegt. Sie schlugen vor, dass man Mondfinsternisse zur Vermessung der Erde benutzen könnte, genauer gesagt, zur Bestimmung der geographischen Länge von Orten.

Wie das?

Zwei Beobachter sehen die Mondfinsternis über verschiedenen Positionen ihres Horizontes. Für den einen steht sie westlich, für den anderen östlich. Da der Augenblick, in dem der Schattenrand den Mondrand berührt, ein absolutes Ereignis ist, also unabhängig vom Beobachter im Weltraum stattfindet, müssen Zeitunterschiede, die von Beobachtern gemessen werden, an der Beobachterposition auf der Erde liegen.

Für jeden Beobachter auf der Erde ist per Definitionem “Mittag” (seiner lokalen Ortszeit) genau dann, wenn die Sonne im Süden steht. Wir haben das quasi vergessen, da wir heutzutage die Erde in Zeitzonen aufgeteilt haben und Armbanduhren bzw. Handys nicht die Ortszeit anzeigen, sondern die Zeit der Zeitzone (also alle Uhren in Deutschland zeigen die Zeit von Görlitz an, egal, ob man sich in München, Köln oder Berlin befindet, wobei für die drei genannten Städte die lokale Zeit unterschiedlich stark davon abweicht: in Berlin sind es nur 4 min, in Köln schon fast eine halbe Stunde). Die Beobachter im Altertum wussten es aber und Navigatoren können es sich zu Nutze machen.

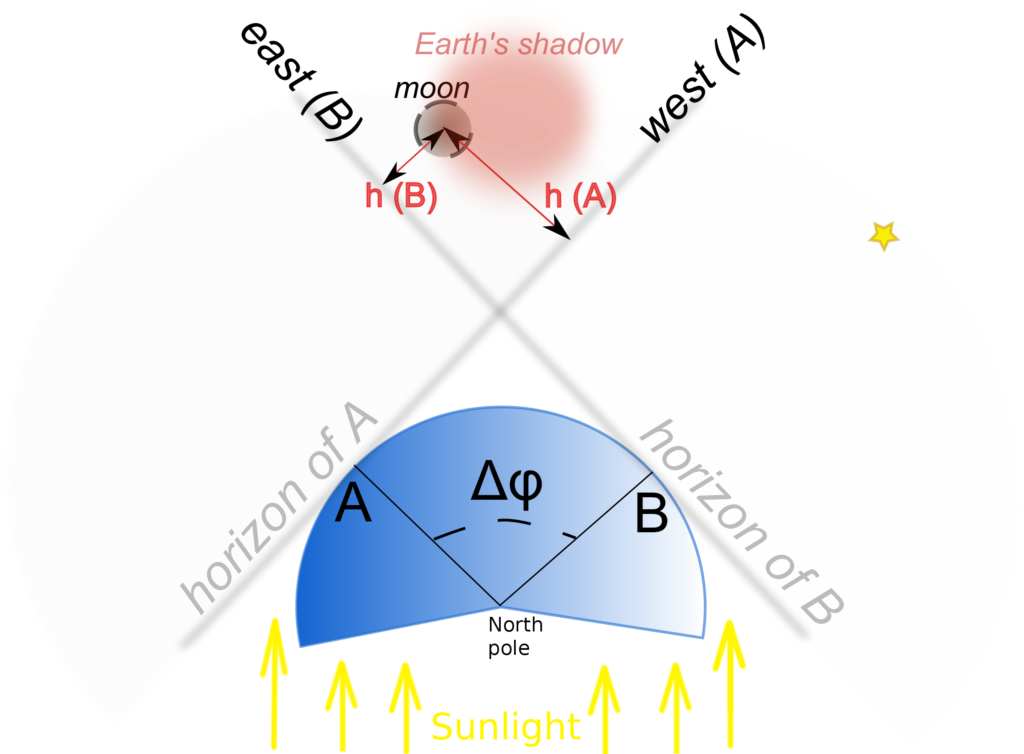
In der Graphik haben die Beobachter A und B einen sehr großen Unterschied in geo. Länge: IN dem Augenblick, wenn der Mondrand den Kernschattenrand berührt, steht er für A über dem westlichen Horizont und für B über dem östlichen. Nehmen wir idealerweise an, die beiden Orte A und B liegen auf dem gleichen Breitenkreis.

Wenn die beiden antiken Beobachter nun gleichzeitig auf ihre Uhr schauen, werden sie verschiedene (lokale!) Uhrzeiten feststellen. Im Altertum geschah diese Messung zwar etwas komplizierter durch Messung von Azimut oder Höhe des Mondes, aber was man letztlich vergleicht, ist der Lokalzeitunterschied zwischen den beiden Orten. Messen die beiden Beobachter einen Unterschied von einer Stunde, d.h. ist es für den einen gerade 22 Uhr und den anderen 21 Uhr, dann ist ihr Unterschied in geo. Länge 15°. Messen sie einen Unterschied von 7 Stunden, ist ihr Unterschied in geo. Länge 195°.

Ein historisches Rechenbeispiel

Wir finden diese Rechnung als Rechenbeispiel im Almagest von Ptolemaios aufgeschrieben, d.h. etwa 130 n.Chr. kompiliert und dann durchs arabische und durchs christliche Mittelalter konsequent abgeschrieben und als Schultext/ Rechenübung weiter verwendet. Alle Astronomen damals verwenden nur ein Beispiel:

Als Alexander der Große vor Babylon kampierte (kurz bevor er es in der Schlacht von Gaugamela im Jahr 331 v.Chr. eroberte) fand eine totale Mondfinsternis statt. Das überliefern die Chronisten des Alexanderzugs. Angeblich soll diese Mondfinsternis auch in Kartago beobachtet worden sein (von wem, wissen wir nicht) und zwar mit einem gewissen Zeitunterschied. Daraus leitete man in dem Beispiel den Längenunterschied zwischen Babylon und Kartago ab. – ABER: Der Zeitunterschied wird von Ptolemaios und Plinius d.Ä. verschieden angeben, weshalb wir (u.a.) nicht sicher sind, dass dieses Beispiel auf realen Beobachtungen beruht oder ob es sich vllt. nur eine “akademische” Konstruktion handelt, also eine theoretische Überlegung, die nie umgesetzt wurde. Ptolemaios beklagt im Almagest, dass zu wenig Leute die Mondfinsternisse entsprechend genau vermessen hätten und das, obwohl es seit der Erfindung dieses Messprinzips (vllt von Hipparch, also 260 Jahre vor Ptolemaios, aber das ist nicht genau überliefert) genug Zeit und Gelegenheiten gegeben hätte.

Islamische Gelehrte vermaßen die Welt

Der erste, von dem wir zu wissen glauben, dass er dieses Messprinzip wirklich angewandt hat, ist daher vermutlich kein antiker Gelehrter, sondern ein islamischer: der Universalgelehrte Al Biruni, der in Chiva in Choresme (Usbekistan) lebte. Zusammen mit seinem Freund Abu al’Wafa in Bagdad hat er die Mondfinsternis am 24. Mai 997 (J) beobachtet und sie haben damit den Längenunterschied zwischen Chiva und Bagdad bestimmt.

Mein Bachelorand hat’s nachgemacht

Deren Messprinzip haben wir letztes Jahr wiederholt:

• mein Student Akyas maß in Pemalang auf Java, Indonesien den Austritt des Mondes aus dem Kernschatten um 02:54 Ortszeit
• ich war damals gerade zwischen Auslandsaufenthalten kurz in Berlin und beobachtete ihn um 20:19 Uhr Ortszeit
• eine Beobachterin in Hattenhausen (Bayern) war meinem Aufruf ihre in kosmologs gefolgt und stellte den Austritt um 20:06 Uhr fest. VIELEN DANK!

Akyas hat optimistischerweise für jeden Beobachter 1 min Messunsicherheit angenommen und das Beispiel damit durchgerechnet:

• Ortszeitunterschied Pemalang-Berlin 395 min +/- 2min
• Ortszeitunterschied Pemalang-Hattenhausen 408 min +/- 2min
• Ortszeitunterschied Hattenhausen-Berlin 13 min +/- 2min

Damit ergeben sich Längenunterschiede

	gemessene Diff.	wahre Diff.	Kommentar
Pemalang-Berlin	98° 45′ +/-0.5°	96°	Fehler 2.75°, 3%
Pemalang-Hattenhausen	102° +/-0.5°	98°	Fehler 4°, 4 %
Hattenhausen-Berlin	3° 15′ +/-0.5°	2°	Fehler 1.25°, 62.5 %

Für Schulzwecke, also wenn man z.B. auf einer Klassenfahrt eine Mondfinsternis beobachtet, dann ist das eine ganz wunderschöne Übung – und vor allem kann man dabei auch ganz wunderschön die verschiedenen Messunsicherheiten kennenlernen, anwenden und sich ausprobieren.

gewidmet sei dieser Artikel Gerd Graßhoff,
als Dank für zahlreiche gute Ideen

(*) wunderschöner Buch- und Filmtipp:

• Buch: Dava Sobel: Longitude: The True Story of a Lone Genius Who Solved the Greatest Scientific Problem of His Time (2005)
• dessen Verfilmung: Der Längengrad – Longitude (2er DVD Set), 2008

Weitere Literatur

• How time served to measure the geographical position since Hellenism, in: Arias, E.F., Combrinck, L., Gabor, P., Hohenkerk, C., Seidelmann, P.K. (Eds.): The Science of Time 2016 – Time in Astronomy & Society, Past, Present and Future, Springer, 2017
• Bachelor-Arbeit meines Studenten Akyas Mohammed: “Dr. Susanne M. Hoffmann Discourse on Observing the Moon” an der Universität Walisongo Semarang, verteidigt im Februar 2018