Potenzreihen und Konvergenzkreise
BLOG: Heidelberg Laureate Forum

Nach längerer Pause will ich mich jetzt beeilen, dem Lobpreis der komplexen Zahlen und der holomorphen Funktionen das dritte wesentliche Teilstück hinzuzufügen: die Sache mit der unendlichfachen Differenzierbarkeit, mehr noch: der Entwickelbarkeit in eine Potenzreihe.
Diesmal geht es gewissermaßen tief in den Maschinenraum der Mathematik, da, wo man sich manchmal an den öligen Zahnrädern die Finger schmutzig macht – zum Beispiel an dem Begriff der Differenzierbarkeit, den Sie vielleicht noch aus der Schule kennen und sich nicht so recht mit ihm anfreunden konnten; er ist ja wirklich etwas sperrig. Wenn Sie sich mit Potenzreihen auskennen, werden Sie am Ende alte Bekannte wiedertreffen.
Wie war das? Differenzierbar ist, wenn die Kurve eine Tangente hat. Tangente ist, wenn sie sich an die Kurve so eng anschmiegt wie überhaupt möglich. Das ist schon richtig. Aber was heißt das genau?
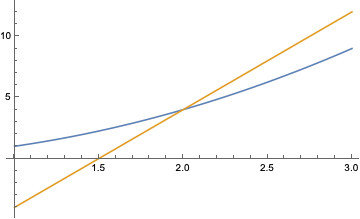
Hier Kurve, da Gerade. Kurve \(f(x)=x^2 \) und Gerade \(g(x)=8x-12\) treffen sich in einem Punkt, und zwar (2, 4). Wenn man mit \(x\) langsam auf den Punkt \(x=2\) zuwandert, geht die Differenz \(f(x)-g(x)\) gegen null. Kein Wunder, wenn die beiden sich in \(x=2\) treffen. Aber eine Tangente ist \(g\) offensichtlich nicht.
So sieht eine richtige Tangente aus:
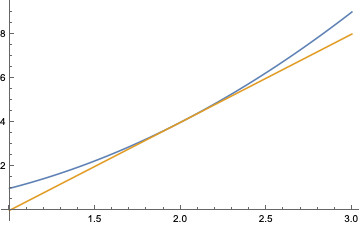
Die Idee ist, dass die Differenz \(f(x)-g(x)\) „schneller“ gegen null geht als die Differenz \(x-2\). Das wiederum wäre zu präzisieren zu der Aussage, dass \(f(x)-g(x)\) selbst dann noch gegen null geht, wenn man es durch \(x-2\) (was ja auch gegen null geht) dividiert. Mit ein bisschen Umrechnen kommt dann die übliche Definition heraus, nämlich dass \( (f(x)-f(2))/(x-2) \) einem endlichen Grenzwert zustrebt, den man dann die Ableitung von \(f\) an der Stelle 2 oder kurz \(f’(2)\) nennt.
Hier will ich auf einen anderen Aspekt hinaus: Die Tangente ist die beste Möglichkeit, die Kurve anzunähern, wenn man nur Geraden, sprich lineare Funktionen zur Auswahl hat. Die Annäherung ist richtig gut in der Nähe des speziell dafür ausgewählten Punktes, in unserem Beispiel \(x=2\), und wird mit zunehmender Entfernung schlechter – beliebig schlecht, um genau zu sein, denn die Tangente in dem speziellen Punkt hindert die Kurve nicht, weiter draußen die wildesten Sprünge zu vollführen.
Was heißt „in der Nähe“, und was heißt „weit draußen“? Das weiß man nie so genau. Die ganze Definition bleibt ja abstrakt und sagt erst einmal nichts darüber, wie viele Zentimeter lang die Näherung noch gut bleibt. (Wir wissen noch nicht einmal, ob die \(x\)-Werte überhaupt in Zentimeter gemessen werden!) Um dieses Problem präzise zu fassen, verwendet man die (gewöhnungsbedürftige) Epsilon-Delta-Definition, was hier nicht weiter vertieft werden soll.
Wie kann man die Näherung an die Funktion verbessern? Immer in der Nähe eines speziellen Punktes, der ab jetzt \(x_0\) heißen soll? Indem man das Sortiment der zur Näherung verwendbaren Funktionen vergrößert. Zum Beispiel indem man außer linearen auch quadratische Näherungsfunktionen zulässt. Die sind immerhin krumm und deswegen bereit, sich noch enger an eine krumme Funktion anzuschmiegen.
Oder man genehmigt sich nicht nur die erste und die zweite Potenz von \(x\), sondern die dritte; damit kommt man Funktionen bei, die sich mal linksherum und mal rechtsherum krümmen, die vierte, die noch größeres Gehampel mitmacht, die fünfte …
Mit jeder Potenz, die man hinzunimmt, wird die Näherung besser – kein Wunder, schlechter kann es ja nicht werden. Wenn die neu hinzugekommene Möglichkeit unter allen Umständen die Sache schlechter machen würde, könnte man sie ja mit dem Faktor null versehen und wäre wenigstens so gut wie zuvor.
Das wirklich Schöne an der ganzen Annäherei ist: Es gibt ein einfaches Kochrezept, um die jeweils optimale Menge an Zutaten zu bestimmen. Man nehme \(a_0\) Gramm von der konstanten Funktion \(f_0(x)=1\), \(a_1\) Gramm von der linearen Funktion \(f_1(x)=x-x_0\), \(a_2\) Gramm von der quadratischen Funktion \(f_2(x)=(x-x0)^2\) und so weiter, addiere die alle zusammen, und fertig ist die Näherung. Denn die Zutatenmengen („Koeffizienten“) \(a_0, a_1, a_2, \dots\) sind leicht auszurechnen: \(a_n = f^{(n)}(x_0) / n!\) Die \(n\)-te Zutat (die natürlich nicht in Gramm gemessen wird) ist gleich der \(n\)-ten Ableitung unserer Funktion \(f\) in dem Punkt \(x_0\), geteilt durch \(n!\) (\(n\)-Fakultät), das Produkt aller natürlichen Zahlen von 1 bis \(n\).
Diese Fakultätsfunktion wächst rasant an, schneller als jede Potenz von \(n\). Das heißt, die Zutatenmengen werden mit zunehmendem \(n\) sehr schnell immer kleiner – vorausgesetzt, die Werte der \(n\)-ten Ableitungen halten sich einigermaßen in Grenzen. Und natürlich vorausgesetzt, es gibt sie überhaupt. Schon die Differenzierbarkeit ist eine ziemlich spezielle Eigenschaft einer Funktion, und ob deren Ableitung ebenfalls differenzierbar ist, die Funktion also überhaupt eine zweite Ableitung hat, ist nicht von vornherein klar. Und so weiter. Zu jeder Bedingung, die man gerne erfüllt sehen würde, findet sich ein Gegenbeispiel.
Eigentlich sind also die Funktionen, deren erste, zweite, dritte … Ableitungen sämtlich existieren, geradezu exotische Ausnahmeerscheinungen. Aber in der mathematischen Praxis laufen sie einem die ganze Zeit über den Weg. Und zwar diejenigen, die nicht nur unendlich oft differenzierbar sind, sondern bei denen die nach obigem Rezept zubereitete Näherungsfunktion (sie heißt übrigens „Taylorpolynom“) auch tatsächlich funktioniert. Selbst dafür gibt es Gegenbeispiele.
Was genau heißt es, dass die Näherung durch ein Taylorpolynom optimal ist? Dass der Unterschied zwischen Funktion und Näherung schneller gegen null geht als die höchste Potenz von \(x-x_0\), die unter den Zutaten des Taylorpolynoms vorkommt. Und wenn das für jedes Taylorpolynom der Fall ist, dann darf man „unendlich viele Zutaten zusammenschütten“ und erhält nicht nur eine Näherung an die Funktion, sondern eine exakte Darstellung der ganzen Funktion.
Na ja. Wenn es unendlich viele Summanden zu addieren gibt, läuft das auf einen Grenzwert hinaus, dann will wieder bewiesen werden, dass er existiert, und um ihn auszurechnen, muss man manchmal erheblich um die Ecke denken. Aber zumindest der Existenzbeweis ist in diesem Fall nicht besonders problematisch. Unsere unendliche Summe (die „Taylorreihe“) lautet ausgeschrieben
\[ f(x)=\sum_{n=0}^\infty {f^{(n)}(x_0) (x-x_0)^n \over {n!} }\; ,\] und solche unendlichen Summen pflegen zu konvergieren – das heißt, es gibt einen endlichen Grenzwert, der als Wert der Summe gelten kann –, wenn die einzelnen Summanden hinreichend schnell klein werden. Zum Kleinwerden trägt einerseits die große Zahl \(n!\) im Nenner bei, andererseits der Faktor \( (x-x_0)^n\); denn wenn \(x\) nahe bei \(x_0\) liegt, also der Betrag von \(x-x_0\) klein ist, dann gehen seine Potenzen gegen null wie eine geometrische Folge. Das hilft bis zu einem gewissen Grad sogar, wenn die Ableitungswerte \(f^{(n)}(x_0)\) mit zunehmendem \(n\) gegen unendlich gehen.
Genauer: Es gibt für jede Taylorreihe einen Maximalabstand \(r\), den „Konvergenzradius“. Wenn der Betrag \(|x-x_0|\) kleiner als \(r\) ist, konvergiert sie; ist er größer als \(r\), konvergiert sie nicht, und wenn er gleich \(r\) ist, weiß man es nicht so genau.
Insbesondere darf der Konvergenzradius unendlich sein. Dann passiert etwas sehr Merkwürdiges: Das Verhalten der Funktion auf der ganzen reellen Achse ist bestimmt durch ihr Verhalten in einem einzigen Punkt \(x_0\)! In einer beliebig kleinen Umgebung dieses einzigen Punktes, um genau zu sein, denn es kommt auf den Wert der Funktion und aller ihrer Ableitungen in diesem Punkt an, und die Ableitungen sind ja Grenzwerte, in die Funktionswerte in der Nähe von \(x_0\) eingehen. Also muss man, um die Funktion vollständig zu kennen, das gedachte Fernrohr nicht nur auf den Punkt \(x_0\) richten, sondern muss sich eine beliebig kleine Umgebung von \(x_0\) mit anschauen.
Analytische Funktionen, das sind solche, deren Taylorreihe überall konvergiert, haben sozusagen einen starken inneren Zusammenhalt. Man kann nicht an einer Stelle ein bisschen wackeln, ohne die ganze restliche Funktion in Mitleidenschaft zu ziehen – wenn sie analytisch bleiben soll.
Auch wenn die Taylorreihe überall konvergiert, wird die Konvergenz typischerweise um so mühsamer, je weiter man sich von dem speziellen Punkt \(x_0\) entfernt. Das wird deutlich an Funktionen, die zwar analytisch sind wie die Sinusfunktion, aber sich vollkommen anders verhalten als jedes Polynom.
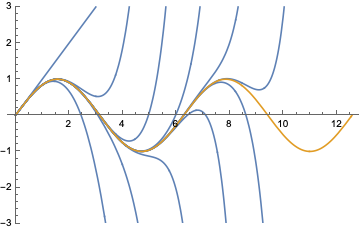
Die Sinusfunktion (braun im Bild) bewegt sich brav zwischen 1 und –1 und kreuzt dabei unendlich oft die \(x\)-Achse. Polynome dagegen haben das so an sich, dass sie für große Werte von \(x\) gegen unendlich gehen; und ein Polynom vom Grad \(n\) kann auch höchstens \(n\)-mal die \(x\)-Achse kreuzen. Entsprechend haben die ersten paar Taylorpolynome (blau im Bild) die größte Mühe, sich der Sinusfunktion anzupassen.
Und wenn eine Funktion an irgendeiner Stelle unendlich wird, kann es dort keine Konvergenz mehr geben. Nehmen wir \(f(x)=1/(1-x) \). An der Stelle \(x=1\) wird der Nenner null, der Funktionswert ist dort also nicht definiert, und in seiner Nähe geht es rasant gegen unendlich. Vielleicht kennen Sie die Potenzreihe dieser Funktion noch aus der Schule. Es gilt \(f(x) = 1 + x + x^2 + x^3 + \dots \), das folgt aus der Summenformel für die geometrische Reihe. Und die konvergiert bekanntlich nur, wenn \(|x|\), der Betrag von \(x\), kleiner als 1 ist.
Aber was ist mit einer Funktion wie \(f(x)=1/(1+x^2)\)?
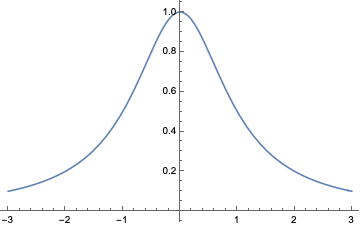
Die ist nun wirklich das Paradebeispiel eines Schlaffis. Ewig lang passiert nichts; einmal im Leben, in der Nähe von \(x=0\), rafft sie sich zu einer gewissen Aktivität auf, um dann alsbald wieder nachzulassen und in alle Ewigkeit monoton auf die Null zuzuschleichen. Von Unendlichkeitsstelle keine Spur. Da sollte doch die Taylorreihe kein Problem haben, dieses friedliche Wesen wiederzugeben, weniger jedenfalls als mit der Sinusfunktion. Aber weit gefehlt! Der Konvergenzradius ist 1, wie bei ihrer wilden Schwester \(1/(1-x)\).
Wieso? Hier hilft ein Blick auf die komplexen Zahlen. Ich habe zwar die ganze Zeit nur von reellen Funktionen geredet; aber das lässt sich alles ohne nennenswerte Änderungen auf komplexe Werte von \(x\) und \(f(x)\) übertragen. Dann ergibt auf einmal der Begriff „Konvergenzradius“ einen Sinn, denn in der komplexen Ebene ist es tatsächlich ein Kreis, in dem die Taylorreihe konvergiert.
Im Komplexen läuft unsere Schlaffifunktion zu großer Form auf; denn für \(x=\pm i\) wird \(x^2=-1\), der Nenner wird null, und unsere Funktion hat an diesen beiden Stellen Pole; so nennt man diese milde Form von Unendlichkeitsstelle. Der Konvergenzkreis mit Mittelpunkt null stößt bei \(\pm i\) sozusagen auf eine natürliche Grenze, über die hinaus er nicht wachsen kann.
Philosophische Schlussbemerkung: Selbstverständlich ist es legitim, sich ausschließlich mit reellen Funktionen zu beschäftigen und von komplexen Zahlen nichts wissen zu wollen, vor allem für einen Menschen, der die Mathematik auf reale Gegenstände anwenden will. Seltsamerweise bleiben dabei Fragen offen („Wieso ist der Konvergenzradius von \(1/(1+x^2)\) so klein?“).
Diese Fragen finden eine elegante Antwort, wenn man sich auf komplexe Zahlen einlässt. Eigentlich ist das Grund genug, sich ihnen zuzuwenden.


Christoph Pöppe schrieb (26. Jul 2023):
> […] Tangente [in einem bestimmten, geeigneten Punkt einer gegebenen Kurve] ist, wenn sie [eine Gerade, die den betreffenden Punkt mit der Kurve gemeinsam hat, dabei außerdem] sich an die Kurve so eng anschmiegt wie überhaupt möglich.
Das liest sich, als sei gemeint, dass sich (i.A.) mehrere verschiedene Geraden denken bzw. finden ließen, die alle den selben geeigneten Punkt einer gegebenen Kurve gemeinsam haben (den “Treffpunkt”), sich aber ungleich “eng” an die Kurve anschmiegen.
Das entspricht jedenfalls nicht der Bedeutung von “Tangente” als (ggf. eindeutig bestimmbare) “Schmiegegerade” der gegebenen Kurve;
die sich (gegenseitig) “im Treffpunkt berühren” (und dabei/drumherum ggf. auch “die Seiten wechseln”), aber einander nicht “(scharf) schneiden”.
> […] Aber eine Tangente ist […] offensichtlich nicht.
> So sieht eine richtige Tangente aus: […]
Sofern mit “sehen” u.Ä. hierbei nicht das ausdrückliche Auswerten “mathematisch-analytischer Ausdrücke” gemeint ist,
sondern das Einschätzen von “geometrischen Beziehungen” und insbesondere von “Distanz-Verhältnissen”
(das Menschen, die unter “irdisch-üblichen Umstanden” aufgewachsen bzw. trainiert sind, womöglich “intuitiv” bewältigen), geht es dabei vermutlich darum:
je einen Punkt “von entgegengesetzten Ästen (bzw. Strahlen)” zu wählen, und jeweils (“intuitiv”) einzuschätzen, aber auch (“definitiv”) zu messen bzw. zu berechnen,
ob der Umkreis des Dreiecks, den diese beiden Punkte zusammen mit dem Treffpunkt bilden,
– bei geeigneter Wahl der Punkte beliebig kleinen Radius haben kann (dann “schneiden” sich Gerade und Kurve); oder
– bei jeglicher Wahl der Punkte (aber wohlgemerkt “von entgegengesetzten Ästen”) einen Radius hat, der einen bestimmten, positiven minimalen Wert nicht unterschreitet (dann “schmiegen” sich Gerade und Kurve aneinander).
(In diesem Sinne ließe sich aber z.B. in jedem Punkt dieser aus abwechselnden Halbkreisen gebildeten Wellenlinie eine bestimmte Tangente (als “Schmiegegerade”) finden.
Mit “Analysis” hat das zugegebener Maßen nur mittelbar zu tun.)
p.s.
> […] Funktion wie […] \( 1/(1 + x^2) \)
> […] Im Komplexen […]
Eine denkbare Übertragung des o.g. Funktionsausdrucks wäre doch (auch, hier in ganz besonders ausführlicher Notation):
\[ \frac{1}{1 + (\mathfrak{Re}[ \, z \, ])^2 + (\mathfrak{Im}[ \, z \, ])^2}. \]
Ist die entsprechende (“extra-schlaffe”) Funktion des komplexen Arguments $z$ analytisch ?
Zu dumm, ich kann Ihrer Darstellung nicht folgen, weil nicht klar ist, was unter entgegengesetzten Ästen zu verstehen ist. Aber auf Ihre Schlussfrage gibt es eine klare Antwort: Nein, die Funktion \( f(z) = {1 \over 1 + |z|^2} = {1 \over 1 + z \bar z} \) ist nicht analytisch. Als Faustregel kann man sich merken, dass jedes Vorkommen der komplex-konjugierten Variable \( \bar z\) die Analytizität verdirbt.
Christoph Pöppe schrieb (26.07.2023, 23:47 o’clock):
> Zu dumm, ich kann Ihrer Darstellung nicht folgen, weil nicht klar ist, was unter entgegengesetzten Ästen zu verstehen ist.
Zugegeben: Es bedürfte gewisser Sympathie, in den ersten beiden Bildern des obigen SciLog-Beitrages jeweils vier einzelne Kurven-“Äste” zu “sehen”, die (jeweils alle vier) von einem gemeinsamen “Treffpunkt” ausgehen, und von denen jeweils ein “Ast” zwei anderen “Ästen” “entgegengesetzt” liegt (was gleichermaßen für alle vier “Äste” eines Bildes gilt). Ich komme weiter unten darauf zurück.
Bedenklicher ist, dass auf den Teil meines obigen Kommentars (26.07.2023, 18:32 o’clock), der der Erwähnung von “(Kurven)-Ästen” deutlich und abgegrenzt vorausging, gar keine Reaktion erfolgte.
Deshalb nochmals in Bezug auf die schon einmal zitierte Aussage (Christoph Pöppe 26. Jul 2023)
hier ganz direkt meine Aufforderung:
Bitte geben Sie ein Beispiel einer Kurve und eines bestimmten Punktes dieser Kurve, in dem sich zwei verschiedene Geraden ungleich eng an diese Kurve anschmiegen!
(Mindestens eine dieser Geraden wäre demnach im betreffenden Punkt nicht “so eng an die Kurve angeschmiegt wie überhaupt möglich”, und würde somit die zitierte Formulierung zur Definition bzw. Unterscheidung der “Tangente” rechtfertigen.)
Nun zu den “Ästen” von Kurven (das Wort “Kurvenast” tritt übrigens auch im deutsch-sprachigen Wikipedia-Fragment auf):
Neben der obigen “anschaulich-intuitiven”, “Sympathie erfordernden” Beschreibung wird sich ja auch eine Beschreibung “für alle Fälle” angeben lassen:
Es sei \(M, d\) ein gegebener metrischer Raum, und \(p \in M\) ein ausgezeichneter Punkt (im Sinne des o.g. “Treffpunktes”).
Zwei weitere, sowohl voneinander als auch von \(p\) verschiedene Punkte \(x, y \in M\) heißen dann “auf entgegengesetzten Ästen (der Menge \(M\)) bzgl. Punkt \(p\)”, im Sinne meines obigen Kommentars (26.07.2023, 18:32 o’clock), falls:
– ((d[ \, x, p \, ] \lt d[ \, x, y \, ]) \text{ und } (d[ \, y, p \, ] \lt d[ \, x, y \, ]))
und
– \(\forall \, j \in M : \)
\( \qquad ((d[ \, j, x \, ] \lt d[ \, x, p \, ]) \text{ und } (d[ \, j, p \, ] \lt d[ \, x, p \, ])) \implies \)
\( \qquad \qquad (d[ \, j, p \, ] \lt d[ \, j, y \, ]) \)
und
– \(\forall \, k \in M : \)
\( \qquad ((d[ \, k, y \, ] \lt d[ \, y, p \, ]) \text{ und } (d[ \, k, p \, ] \lt d[ \, y, p \, ])) \implies \)
\( \qquad \qquad (d[ \, k, p \, ] \lt d[ \, k, x \, ]) \).
(Im Übrigen ging es dann um die Radien von Umkreisen aller Dreiecke bestehend aus “dem Treffpunkt \(p\)” und jeweils einem Paar \((x, y)\) von “Punkten auf entgegengesetzten Ästen, bzgl. \(p\)”.)
p.s.
> Aber auf Ihre Schlussfrage gibt es eine klare Antwort: Nein […] Als Faustregel kann man sich merken, dass jedes Vorkommen der komplex-konjugierten Variable \(\bar z \) die Analytizität verdirbt.
Danke für die deutliche Antwort; diese Schlussfrage meines obigen Kommentars war doch recht Reflex-haft bzgl. der gewissermaßen provokanten “Schlaffheit” des Beispiels.
(Die genannte Faustregel war mir jedenfalls grundsätzlich nicht ganz unbekannt. Mit der Idee — um’s mal so zu nennen — dass eine entsprechende Reihenentwicklung hinsichtlich des “Radius
r” ja “nur ab Null” konvergieren müsste,kam ich bzw. kommt die Konvergenz dann doch nicht allzu weit (von Null weg).)
p.p.s. — Mangels zuverlässiger SciBlog-Kommentar-Vorschau: …
… Nochmals zu den “Ästen” von Kurven (das Wort “Kurvenast” tritt übrigens auch im deutsch-sprachigen Wikipedia-Fragment auf):
Neben der obigen “anschaulich-intuitiven”, “Sympathie erfordernden” Beschreibung wird sich ja auch eine Beschreibung “für alle Fälle” angeben lassen:
Es sei \((M, d)\) ein gegebener metrischer Raum, und \(p \in M\) ein ausgezeichneter Punkt (im Sinne des o.g. “Treffpunktes”).
Zwei weitere, sowohl voneinander als auch von \(p\) verschiedene Punkte \(x, y \in M\) heißen dann “auf entgegengesetzten Ästen (der Menge \(M\)) bzgl. Punkt \(p\)”, im Sinne meines obigen Kommentars (26.07.2023, 18:32 o’clock), falls:
– \( (d[ \, x, p \, ] \lt d[ \, x, y \, ]) \text{ und } (d[ \, y, p \, ] \lt d[ \, x, y \, ]) \)
und
– \(\forall \, j \in M : \)
\( \qquad ((d[ \, j, x \, ] \lt d[ \, x, p \, ]) \text{ und } (d[ \, j, p \, ] \lt d[ \, x, p \, ])) \Rightarrow \)
\( \qquad \qquad (d[ \, j, p \, ] \lt d[ \, j, y \, ]) \)
und
– \(\forall \, k \in M : \)
\( \qquad ((d[ \, k, y \, ] \lt d[ \, y, p \, ]) \text{ und } (d[ \, k, p \, ] \lt d[ \, y, p \, ])) \Rightarrow \)
\( \qquad \qquad (d[ \, k, p \, ] \lt d[ \, k, x \, ]) \).
(Im Übrigen ging es dann um die Radien von Umkreisen aller Dreiecke bestehend aus “dem Treffpunkt \(p\)” und jeweils einem Paar \((x, y)\) von “Punkten auf entgegengesetzten Ästen, bzgl. \(p\)”.)
Allmählich lichtet sich das Dunkel …
Ich hatte „schmiegen“ nicht im mathematischen Sinn gemeint (da ist es in der Tat ein anderes Wort für „tangential sein“), sondern im umgangssprachlichen. Aus meiner (vor allem im Kleinkindalter gewonnenen) Erfahrung weiß ich, dass man sich mehr oder weniger geschickt aneinander schmiegen kann; und wenn die Passung nicht perfekt ist, kann das trotzdem ganz kuschelig sein. Ja, das war ein Appell an die Anschauung. Eine Tangente sieht so aus, wie ich sie gezeichnet habe, und zu beweisen, dass es eine Tangente ist, ist etwas anderes.
Und Ihre vier Äste! Also gut: Wir haben eine Kurve und eine Gerade, die treffen sich in einem Punkt, nennen wir ihn \(x_0\). Dann gehen von diesem Treffpunkt vier Äste ab, ein gerader und ein krummer nach links, und ein gerader und ein krummer nach rechts. (Kann man auch mit Ihren metrischen Räumen ausdrücken, ist aber an dieser Stelle theoretischer Overkill.)
Jetzt wählen Sie drei Punkte, nämlich \(x_0\), einen Punkt auf einem linken Ast und einen auf einem rechten, und bestimmen den Kreis, der durch diese drei Punkte geht. Das lässt noch mehrere Möglichkeiten offen:
a) beide Äste gerade: Alle drei Punkte liegen auf einer Geraden, Kreisradius ∞, langweilig. Das hatten Sie offensichtlich nicht im Sinn.
b) beide Äste krumm: Der Kreise konvergiert gegen den Krümmungskreis an die Kurve im Punkt \(x_0\), also den Kreis, der sich in diesem Punkt am besten an die Kurve anschmiegt, im Allgemeinen besser als die Gerade. Die Krümmung (= 1 durch den Kreisradius) ist nicht ganz die zweite Ableitung der Funktion im Punkt \(x_0\), aber diese kommt vor. Wir sind also einen Schritt weiter als eigentlich vorgesehen; Thema war an dieser Stelle noch die einfache Differenzierbarkeit.
c) ein Ast gerade, der andere krumm: Mir ist nicht unmittelbar klar, was in diesem Fall passiert. Ich sehe mich auch nicht in der Lage Ihre Behauptung zu beweisen oder zu widerlegen. Wozu auch? Es ging ja darum, ob die Gerade eine Tangente ist. Und das ist auf die übliche Weise mühelos herauszukriegen. Wozu also der Umstand mit dem Kreis, den man sich zu allem Überfluss nicht so richtig vorstellen kann?
Christoph Pöppe schrieb (29.07.2023, 21:15 o’clock):
> […] umgangssprachlich […]
Bei solchen Mängeln hilft SciLog.
> [… wozu Kurvenäste + Dreiecksumkreise …]
Um überhaupt einen Zusammenhang zwischen “Tangente” und
\(f[ \, x_0 \,] + f'[ \, x_0 \, ] (x – x_0) \)
herzustellen.
Dass Newton und Leibniz mit Geometrie so gefremdelt hätten, ist schwer vorstellbar.
Als Nichtmathematiker kann ich nur vermuten, worum es hier geht. In der Schule lernt man, dass eine Tangente eine Gerade ist.
Jetzt erweitert man diesen Gedanken indem man eine Kurve sucht, die einer bestehenden Kurve, die sich vielleicht aus Werten einer Messreihe ergibt, sehr nahe kommt.
Ist das richtig gedacht ?
Fast richtig gedacht.
Die Kurven, um die es in diesem Beitrag geht, sind alles Kurven von überall definierten Funktionen. Eine Kurve, die sich aus den Werten einer Messreihe ergibt, hat ernstzunehmende Werte nur an den Messpunkten. Dazwischen unterliegt sie der Willkür desjenigen, der da (in der Regel) die Messwerte zu etwas Ansehnlichem verbinden will.
Was Sie ansprechen, ist eher ein Interpolationsproblem: Finde eine Funktion, die an den Messpunkten die gemessenen Werte annimmt. Das kann man mit den Polynomen machen. Für n Messwerte genügt ein Polynom vom Grad n–1.
In der Praxis spielt das Interpolationsproblem keine wesentliche Rolle. Man muss bei Messungen immer mit Messfehlern rechnen. Also kommt es nicht darauf an, dass die Kurve die Messpunkte genau trifft, sondern nur, dass sie ihnen nahekommt. Andere Aspekte sind dagegen wichtiger: Polynome gehen für große Werte von x stets gegen unendlich. Das ist vielleicht für die Funktion, die gemessen wird, absurd. Also muss man für eine gute Näherung weitere Eigenschaften der zu messenden Größe heranziehen, und dann sind wir in einer ganz anderen Ecke der Mathematik.
Es geht also um die Sinusfunktion und Potenzreihen. Vielleicht auch um mehr, das kann ich nicht überlicken.
Spontan erinnert mich das an ein Dreieck, wo ein Winkel größer wird, wenn der andere kleiner wird. Die Winkelsumme bleibt immer 180 Grad.
Die Sinusfunktion verhält sich wie eine “Gefangene”, die aus ihrem Käfig nicht ausbrechen kann. Die Potenzreihen sind auch solche Gefangenen.
Welche Rolle spielt jetzt der Konvergenzkreis ?
Es geht um Potenzreihen im Allgemeinen. Die Sinusfunktion ist eine der zahlreichen Funktionen, die durch eine Potenzreihe ausdrückbar sind.
Die Sinusfunktion sin(x) ist (für reelle Werte von x) in der Tat beschränkt. Für Potenzreihen im Allgemeinen gilt das nicht. Im Gegenteil. Eine komplex-analytische Funktion ist stets unbeschränkt, es sei denn, sie wäre eine Konstante.
Der Konvergenzkreis hat damit unmittelbar nichts zu tun.
Verständnisfrage an den werten hiesigen Inhaltegeber, Dr. Christoph Pöppe sein Name, und hier zu :
Sie sind so-o unterwegs :
-> https://de.wikipedia.org/wiki/Komplexe_Zahl (‘Der so konstruierte Zahlenbereich der komplexen Zahlen bildet einen Erweiterungskörper der reellen Zahlen und hat eine Reihe vorteilhafter Eigenschaften, die sich in vielen Bereichen der Natur- und Ingenieurwissenschaften als äußerst nützlich erwiesen haben.’)
..und sind als Mathematiker und Naturlehrer (eine vely gute Kombination, wie einige finden) in der Lage wie zitierte Nützlichkeit (derartiger numerischer Konstruktion oder Funktion) zu erkennen und anzuwenden?
Mit freundlichen Grüßen
Dr. Webbaer
Verständnisfrage. Was wollen Sie wissen?
Wo ich die Nützlichkeit komplexer Zahlen und Funktionen sehe? Das habe ich in den vergangenen drei Beiträgen ausgeführt.
Wie ich diese Nützlichkeit erkannt habe? Klassisches Mathematikstudium.
Irgendwie habe ich das Gefühl, dass das nicht Ihre Frage war.
Christoph Pöppe schrieb (29.07.2023, 21:15 o’clock):
> […] Also gut: Wir haben eine Kurve und eine Gerade, die treffen sich in einem Punkt, nennen wir ihn \(x0\). Dann gehen von diesem Treffpunkt vier Äste ab, ein gerader und ein krummer nach links, und ein gerader und ein krummer nach rechts. […]
Endlich habe ich die Gelegenheit (nämlich wieder ein ordentliches Key-Board zur Verfügung, anstatt — im Urlaub — nur ein Handy, und das auch nur minutenweise), hinreichend ausführlich zu zitieren und entsprechend deutlich zu antworten.
Zunächst einmal: in den ersten beiden Bildern des obigen SciLog-Beitrages (auf die ich 27.07.2023, 14:29 o’clock als Beispiel-haft hingewiesen hatte), sind offenbar jeweils alle vier “Äste” “krumm”; also keiner davon ein sogenannter “Strahl” (der vom gemeinsamen Schnittpunkt gerade wegführte); und erst recht zeigen diese beiden Bilder keine Gerade (die sich ggf. aus zwei Strahlen zusammensetzt). Eventuell Tangenten-Geraden ließen sich in diesen beiden Bildern allenfalls dazudenken.
Entsprechend sind die 29.07.2023, 21:15 o’clock genannten und im Folgenden zitierten Möglichkeiten wohl unter der oben nicht ausdrücklich genannten Annahme gemeint, dass zur jeweils gegebenen Kurve im “Punkt \(x_0\)” überhaupt eine Tangente existiert.
> Jetzt wählen Sie drei Punkte, nämlich \(x_0\), einen Punkt auf einem linken Ast
… der gegebenen, zu untersuchenden Kurve …
> und einen auf einem rechten, und bestimmen den Kreis, der durch diese drei Punkte geht.
Richtig; wobei ein gewisser Sonderfall bzw. eine naheliegende Konkretisierung gleich zu diskutieren ist:
> a) beide Äste gerade: Alle drei Punkte liegen auf einer Geraden, Kreisradius ∞, langweilig. Das hatten Sie offensichtlich nicht im Sinn.
In diesem Fall, dass die gegebene “Kurve” an sich eine Gerade ist, und demnach beliebig gewählte drei verschiedene Punkte (einschl. \(x_0\)) gegenüber einander gerade liegen, ist die eingangs (26.07.2023, 18:32 o’clock) vorgelegte “Tangenten”-Definition in extremer Weise erfüllt:
Der (“nominelle”) Radius-Wert ∞ des/jedes entsprechenden Dreiecks-Umkreises, sofern man davon überhaupt sprechen kann, unterschreitet gar keinen bestimmten, positiven endlichen Wert.
Folglich existiert eine Tangente an diese gegebene Gerade, sowohl im Punkt \(x_0\), als auch in jedem anderen Punkt; und die gegebene Gerade selbst ist diese Tangente.
Um auch die bloße Erwähnung von “∞” zu vermeiden, ließe sich natürlich vom entsprechenden Kehrwert (alias “Krümmung”) reden; insbesondere vom Kehrwert des Umkreisradius ausgedrückt durch die drei Seiten-Längen des betreffenden (ebenen) Dreiecks, also vermittels der entsprechenden [[Cayley-Menger-Determinante]] im Spezialfall von [[Satz des Heron]].
Ergänzend zum zitierten Fall a), nämlich gerade ohne von vornherein anzunehmen, dass eine Tangente an die gegebene Kurve existiert, ließe sich zwei (verschiedene) Strahlen betrachten, die nicht gemeinsam eine Gerade bilden.
Die Anwendung der o.g. eingangs (26.07.2023, 18:32 o’clock) vorgelegte “Tangenten”-Definition bzw. ihrer Kehrwert-Darstellung, nämlich, dass es dann keinen minimalen positiven (Radius-)Wert gibt, der für alle wählbare Dreiecke von deren Umkreis-radien nicht unterschritten würde, dürfte (auch hinsichtlich der noch folgenden “Möglichkeit c)”) dann besonders aufschlussreich und geradezu paradigmatisch sein. Nun weiter:
> b) beide Äste krumm: Der Kreise konvergiert
… [sic!] (?) …
> gegen den Krümmungskreis an die Kurve im Punkt \(x_0\), […]
Wieso sollte eine gegebene Kurve, die im Punkt \(x_0\) eine Tangente hat, deren von \(x_0\) ausgehende zwei Äste aber beide keine Strahlen sind, überhaupt einen (und insbesondere nur einen bestimmten) “Krümmungskreis an die Kurve im Punkt \(x_0\)” haben ??
> also den Kreis, der sich in diesem Punkt am besten an die Kurve anschmiegt, im Allgemeinen besser als die Gerade.
Bezüglich genau welcher mathematisch-unmissverständlicher Definition von “anschmiegen” ?!?
Bis auf Weiteres lassen sich dagegen jedenfalls Beispiele setzen — praktischer Weise hier natürlich als Funktionen \(y[ \, x \, ]\) mit “affin adaptierten” Koordinaten \((x, y)\) — in denen sich “der (vermeintliche) Krümmungskreis”
– entweder nicht eindeutig bestimmen lässt:
\[ \text{Cos}[ \, (2 \, \text{Floor}[ \, \text{Abs}[ \, x \, ] \, ] + 1) \, \pi \, x \, ] \]
im Punkt \(x_0 := 1\),
siehe hier
– oder sich gar nicht bestimmen lässt:
\[ x^3 \, \text{Sin}\left[ \, \frac{1}{x} \, \right] \]
im Punkt \(x_0 := 1\) (wo die betreffende Funktion natürlich auch stetig sein soll, also \(y[ \, 0 \, ] := 0).
> Die Krümmung (= 1 durch den Kreisradius) ist nicht ganz die zweite Ableitung der Funktion im Punkt \(x_0\),
… in Koordinaten-freier Grundlage also auch nicht ganz die Hälfte der Wurzel aus entsprechenden Cayley-Menger-Determinanten …
> aber diese kommt vor.
In meinen beiden Gegenbeispielen kommt “diese” [zweite Ableitung] aber nicht eindeutig bzw. gar nicht vor.
> c) ein Ast gerade, der andere krumm:
Wie betreffend die Fälle a) und b), wäre auch hinsichtlich c) die Möglichkeit zu kontrastieren, dass die Kurve im gemeinsamen (Start-)Punkt dieser beiden Äste keine Tangente hat.
p.s.
> […] auf die übliche Weise mühelos herauszukriegen.
Sofern diese sogenannte “übliche Weise” bestimmte Zuordnungen von Koordinaten voraussetzt, muss ich mir wohl gefallen lassen, dass Koordinaten-freie Betrachtungen von gewissen Mathematikern als “unüblich” tituliert würden.
Vorbehaltlich einer Einladung zum Administrieren eines SciLogs, oder wenigstens zur Gestaltung eines SciLog-Gastbeitrages, bleibt mir, wie anderen SciLog-Kommentatoren, immerhin, Schnittmengen meiner Interessen mit gegebenen SciLogs-Themen zu suchen und zu kommentieren.
Hä?
Verzeihung, aber die hellbraune Linie ist in beiden Grafiken gerade. So ist sie programmiert, und so sieht sie auch aus. Hat Ihr Bildschirm eine ungewöhnliche Krümmung?
Ja, es geht an dieser Stelle um Funktionen, die im Punkt x_0 differenzierbar sind, die zugehörige Kurve also dort eine Tangente hat.
Ihr erstes Beispiel Cos[(2Floor[Abs[𝑥]]+1)𝜋𝑥] ist an der Stelle x_0=1 in der Tat nicht differenzierbar. Da gibt es schon keine Tangente, und einen Krümmungskreis erst recht nicht. (Ja, es gibt einen Grenzwert des Differenzenquotienten von links und einen von rechts, aber die sind eben verschieden.)
Ihr zweites Beispiel x^3 sin(1/x) ist bei x_0 = 1 vollkommen harmlos: beliebig oft differenzierbar, insbesondere gibt es eine zweite Ableitung und damit auch einen Krümmungskreis. Meinten Sie x_0 = 0? Da ist die Funktion erstmal nicht definiert. Man kann sie stetig fortsetzen, und dann passieren bei x=0 möglicherweise interessante Dinge. Ohne es explizit durchzurechnen, schätze ich mal, dass die zweite Ableitung der ergänzten Funktion dort existiert und gleich 0 ist. Also Krümmungskreisradius unendlich.
Bezüglich der üblichen: Für x -> x_0 geht die Differenz zwischen Kurve und Krümmungskreis gegen 0 mit der Ordnung |x–x_0|^3.
Christoph Pöppe (14.08.2023, 22:05 o’clock):
> […] Hä? Verzeihung, aber die hellbraune Linie ist in beiden Grafiken gerade.
Oh, richtig!, das war mir zwischenzeitlich ganz entfallen — ich bitte um Entschuldigung dafür.
Entsprechend sind auch in beiden Bildern jeweils zwei der vier “Äste” “gegenüberliegende Strahlen”; und diese beiden Strahlen bilden jeweils eine Gerade.
Trotzdem, und wie die beiden Bilder doch ausdrücklich darstellen, bleibt es relevant zu unterscheiden und zu untersuchen, welche Geraden die blaue Kurve “(scharf) schneiden”, und welche eine Gerade stattdessen die eindeutig bestimmte Tangente wäre, die die blaue Kurve wörtlich “nur berührt”; falls überhaupt eine.
> […] erstes Beispiel
\[ \text{Cos}[ \, (2 \, \text{Floor}[ \, \text{Abs}[ \, x \, ] \, ] + 1) \, \pi \, x \, ] \]
> ist an der Stelle x_0=1 in der Tat nicht differenzierbar.
Diese Einschätzung überrascht mich; und ich widerspreche:
diese Funktion ist an der Stelle x_0 = 1 einmal differenzierbar;
aber nicht zweimal, oder gar mehrfach.
Hier nochmals der entsprechende Plot zur Ansicht.
An der Stelle x_0 = 1 hat die Funktion den Wert -1, und die erste Ableitung den Wert 0.
Es lassen sich auch die einseitigen Ableitungen “von links” (alias “von kleineren Werten her”) bzw. “von rechte” (alias “von größeren Werten her”) hin zur Stelle x_0 = 1 auswerten: die haben ebenfalls beide gleichermaßen den Wert 0.
Genau so, wie das für harmonische Funktionen
Cos[ k pi x ]für alle ganzen Werte
kan dieser Stelle x_0 = 1 gilt.> Da gibt es schon keine Tangente
Ich hoffe sehr, dass Sie sich nun vom Gegenteil überzeugt haben …
(Ansonsten wäre ich auf eine Erklärung sehr gespannt.)
> und einen Krümmungskreis erst recht nicht. (Ja, es gibt einen Grenzwert des Differenzenquotienten von links und einen von rechts, aber die sind eben verschieden.)
Das trifft auf die einsitigen zweiten Ableitungen zu!, usw.
Die Existenz oder Nicht-Existenz einer Tangente hängt in der Analysis aber insbesondere mit Existenz oder Nicht-Existenz der ersten Ableitung zusammen.
(Jedenfalls hatte ich das Beispiel mit dem Ziel konstruiert, diesen Unterschied zu illustrieren.)
> Ihr zweites Beispiel x^3 sin(1/x) ist bei x_0 = 1 vollkommen harmlos: beliebig oft differenzierbar,
Ach! — mein Schreibfehler! (Bitte nochmals um Entschuldigung.)
Gemeint war in meinem zweiten Beispiel stattdessen Differenzierung an der Stelle \(x_0 = 0\).
(“natürlich” — immerhin hatte ich 14.08.2023, 14:42 o’clock ja richtiger Weise darauf hingewiesen, dass diese Stelle
.)
> Meinten Sie x_0 = 0? Da ist die Funktion erstmal nicht definiert. Man kann sie stetig fortsetzen, und dann passieren bei x=0 möglicherweise interessante Dinge.
Eben/Genau.
> Ohne es explizit durchzurechnen, schätze ich mal, dass die zweite Ableitung der ergänzten Funktion dort existiert und gleich 0 ist.
Dann rechnen Sie doch bitte mal explizit durch;
zunächst die erste Ableitung, und ggf. anschließend die zweite Ableitung der (an der Stelle x_0 = 0 stetig ergänzten) Funktion
\[ x^3 \, \text{Sin}\left[ \, \frac{1}{x} \, \right] \]
Verbindlichsten Dank.
p.s. — und damit zu weniger Trivialem, sondern hoffentlich eher Aufschlussreichem:
> Bezüglich der üblichen: Für x -> x_0 geht die Differenz zwischen Kurve und Krümmungskreis gegen 0 mit der Ordnung |x–x_0|^3.
Hmm …
Das akzeptiere ich hier
– nachdem ich mir
Series[ a - Sqrt[ a^2 - x^2 ], { x, 0, 5 } ]habe ausrechnen lassen, und
– mit dem Vorbehalt, dass in einem »gesonderten [SciLog]beitrag [zur] Frage von Koordinaten und koordinatenfreien Darstellungen«, der uns 24.09.2016, 10:56 Uhr in Aussicht gestellt wurde (aber bisher nicht erschienen ist) zu fragen wäre, wie diversen “Stellen einer Kurve” überhaupt bestimmte reelle Zahlenwerte
xzuzuordnen wären (meinetwegen “bis auf globale affine” Festlegung).Es verbleibt mir ansonsten lediglich die Frage warum, bzw. die (dann doch ziemlich Korinthen-kackernde) Beanstandung, dass in diesem Zusammenhang überhaupt ausdrücklich von “Krümmungs-Kreisen” die Rede wäre, und nicht genauer von “Krümmungs-Parabeln“.
Frank Wappler schrieb (15.08.2023, 00:19 o’clock):
> Christoph Pöppe schrieb (14.08.2023, 22:05 o’clock):
> > […] Bezüglich der üblichen: Für x -> x_0 geht die Differenz zwischen Kurve und Krümmungskreis gegen 0 mit der Ordnung |x – x_0|^3.
> Hmm … Das akzeptiere ich hier […] Es verbleibt mir ansonsten lediglich […]
Jetzt kann ich doch noch ein Beispiel vorzeigen, um meine Zurückhaltung gegenüber der zitierten “analytischen” Definition von Krümmungskreisen zu illustrieren,
nämlich die (“Hauptzweig”-)Funktionskurve
\[ \text{ArcSin}[ \, 1 – x \, ] \]
zusammen mit dem Kreis von (Koordinaten-)Radius
1und Koordinaten-Mittelpunkt \(\left(1, \frac{\pi}{2} \right)\);siehe hier.
Diese Funktionskurve und dieser Kreis haben offensichtlich einen gemeinsamen Koordinaten-Punkt; nämlich (jeweils) “an der (Koordinaten-)Stelle” \(x_0 = 0\).
Einerseits weist diese “Plot-Konfiguration” nun geometrische Ähnlichkeit u.a. mit der hier skizzierten auf, die aus Funktionskurve
\[ 1 -\text{Sin}[ \, x \, ] \]
zusammen mit dem Kreis von (Koordinaten-)Radius
1und Koordinaten-Mittelpunkt \(\left(\frac{\pi}{2}, 1 \right)\) besteht;wobei der letztere (im zweiten Plot nur halb skizzierte) Kreis ja unbestritten der Krümmungskreis der Funktionskurve \(1 -\text{Sin}[ \, x \, ] \) an der (Koordinaten-)Stelle \(x_0 = \frac{\pi}{2}\) darstellt.
Aber:
Die Differenz zwischen Kurve \(\text{ArcSin}[ \, 1 – x \, ]\) und dem ersteren Kreis (und zwar sinnvoller Weise dem unteren, grün skizzierten Halbkreis im ersten Plot)
geht (“mit Annäherung an die in Frage kommende Stelle” \(x_0 = 0\)) (erheblich) “steiler” gegen 0 als mit der Ordnung |x – x_0|^3;
und zwar offenbar mit der Ordnung |x – x_0|^(3/2);
konkret:
Series[ Pi/2 - Sqrt[ 1 - (1 - x)^2 ] - ArcSin[ 1 - x ], { x, 0, 2 } ] :=(Sqrt[ 2 ] / 3) x^(3/2) + (Sqrt[ 2 ] / 20) x^(5/2) + ....In Anwendung der zitierten “analytischen” Definition wäre der (im ersten Plot gezeigte) Kreis von (Koordinaten-)Radius
1und Koordinaten-Mittelpunkt \(\left(1, \frac{\pi}{2} \right)\) also doch kein Krümmungskreis der Funktionskurve \(\text{ArcSin}[ \, 1 – x \, ]\) “an der Stelle” \(x_0 = 0\);und zwar trotz der erwähnten “geometrischen Änhlichkeit” zum zweiten Plot.
(Einzelheiten dieser “geometrischen Ähnlichkeit” hängen natürlich damit zusammen, ob und wie “angepasst” die \(x\) und \(y\)-Koordinaten bzw. -Funktionswerte gewissen Bildschirmpixeln zugeordnet wären …)
In dieser Hinsicht halte ich die zitierte “analytische” Definition von Krümmungskreisen für unbefriedigend, und ziehe eine rein geometrische Definition vor (insbesondere basierend auf den Umkreis-Radien gewisser Dreiecke, bzw. deren Reziproken, wie in vorausgegangenen Kommentaren angedeutet).
Ich bin überzeugt. Mein Fehler; ich hatte einen Knick gesehen. Aber den gibt’s erst in der Ableitung.
Wenn’s bloß um eine Funktion geht, die (z. B. an der Stelle x=0) einmal, aber nicht zweimal differenzierbar ist: Da bietet sich f(x)=x^2 für x≥0, 0 für x<0 als wesentlich einfacheres und übersichtlicheres Beispiel an.
Ja, OK, die 2. Ableitung wird ganz schön wild. Habe ich nicht gesehen.
Krümmungskreise waren nicht meine Idee! Krümmungsparabeln rechnen sich viel einfacher. Am Ende ist die Näherung in der Nähe von x_0 gleich der Taylorreihe, abgebrochen nach dem zweiten Glied.
Ich sag doch, ich stehe nicht so auf Krümmungskreise. An einem Punkt, an dem sowohl die erste als auch die zweite Ableitung gegen ∞ gehen, ist natürlich mit der analytischen Definition erstmal nichts zu machen. Vielleicht konvergiert der Krümmungsradius gegen etwas Vernünftiges, wenn Sie x_0 gegen 0 gehen lassen. Ob Sie mit Ihren drei Punkten und zugehörigem Grenzprozess besser zum Ziel kommen? Ich habe keine Lust, mir das zu überlegen.
Für den Fall, dass Sie’s wirklich wissen wollen (und nicht die arcsin-Funktion nur studieren, damit’s schwieriger ist), hier eine klassisch-geometrische Lösung. Der Graph von arcsin x ist gleich dem Graphen von sin x, gespiegelt an der Diagonale im Koordinatensystem (Vertauschung von x und y). Zeichnen Sie eine Sinuskurve plus den Krümmungskreis (z. B.) bei x=pi/2 und spiegeln Sie beides zusammen an der Diagonalen. Kreis bleibt Kreis beim Spiegeln, also …
Christoph Pöppe schrieb (17.08.2023, 22:53 o’clock):
> […] An einem Punkt, an dem sowohl die erste als auch die zweite Ableitung gegen ∞ gehen, ist natürlich mit der analytischen Definition erstmal nichts zu machen. Vielleicht konvergiert der Krümmungsradius gegen etwas Vernünftiges, wenn Sie x_0 gegen 0 gehen lassen.
Was käme denn dafür überhaupt als “etwas Vernünftiges” in Frage, wenn nicht der Wert (bzw. der entsprechende Kehrwert), auf den ich ständig (zuletzt oben 14.08.2023, 14:42 o’clock, unterlegt mit entsprechender Wikipedia-Verlinkung) hinweise …
??
> Ob Sie mit Ihren drei Punkten und zugehörigem Grenzprozess besser zum Ziel kommen? Ich habe keine Lust, mir das zu überlegen.
Gäbe es denn dahingehend überhaupt noch irgendwelche Fragen bzw. Zweifel, angesichts der angegeben Wikipedia-Enzyklopädischen Erwähnung und weitergehender Links bzw. Referenzen ?? …
“Isso” — Wer eben keine Lust hat, der/dem ist eben auch nicht unbedingt Lust zu machen.
Danke zumindest für diese SciLog-kommentarische Gelegenheit, mich öffentlich (auch) an jene zu wenden, die (hinreichend) Lust auf Geometrie haben.
p.s.
> Der Graph von arcsin x ist gleich dem Graphen von sin x, gespiegelt an der Diagonale im Koordinatensystem (Vertauschung von x und y).
Das gilt nur unter bestimmten Zuordnungen von Koordinatenwerten zu gegebenen (“Bildschirm”-)Elementen, von denen jeweils eine bestimmte Teilmenge einen “Graph” bildet;
und nur für bestimmte Maße (die natürlich vorab allgemein und nachvollziehbar definiert sein müssten).
In diesem Zusammenhang mahne ich hiermit erneut das bisherige Fehlen eines SciLogs-Beitrages an, der daran (Lust-voll) Interessierte zur Beschäftigung mit Fragen bzw. Zusammenhängen zwischen Koordinaten und Koordinaten-freien Darstellung einladen würde.
> Zeichnen Sie eine Sinuskurve plus den Krümmungskreis (z. B.) bei x=pi/2
… Mangels Dokumentation (oder sogar mangels Zur-Verfügung-Stellung überhaupt) der eventuellen Verfügbarkeit von \(\text{ps-tricks}\)-Mitteln zum Erstellen von Zeichnungen in SciLogs-Kommentaren verweise ich (erneut) auf den zweiten Link in meinem obigen Kommentar (16.08.2023, 10:26 o’clock):
.
> und spiegeln Sie beides zusammen an der Diagonalen.
Bitte definieren Sie die (womöglich geometrisch gemeinte) Operation “Spiegelung an der Diagonalen”.
(Jedenfalls steht ein derartiger Zeichen-Befehl in “Wolfram Alpha” wohl nicht ausdrücklich zur Verfügung.
Allerdings möchte ich dabei auch (und erneut) auf den ersten Link in meinem obigen Kommentar (16.08.2023, 10:26 o’clock) verweisen:
;
wobei ich leider nicht weiß, ob damit die maximal zulässige Anzahl von Links in einem SciLogs-Kommentar überschritten ist, weil diese Zahl leider immern noch nicht ausfindbar öffentlich dokumentiert ist. Ich muss mich überraschen lassen, wenn ich “Send” gedrückt habe. …
p.p.s.
Meine Kommentar-Einreichung 18.08.2023, 11:06 o’clock ging diesbezüglich offenbar daneben.
Ich versuche nun deshalb, die genannte Link im Memo dieses Kommentars unterzubringen.
)
p.p.p.s.
> Kreis bleibt Kreis beim Spiegeln
Das könnte (auch) einer der Vorzüge eines (“Krümmungs-“)Kreises gegenüber einer (“Krümmungs-“)Parabel sein.
So wie ein bestimmter (ebener) Kreis “im geometrisch-Wesentlichen” durch nur einen einzigen Parameter gekennzeichnet ist, nämlich: durch dessen “Radius” (bzw. damit direkt zusammenhängende Größen),
ist allerdings auch eine Parabel durch nur einen einzigen Parameter gekennzeichnet. (Dessen Bezeichnung, “latus rectum”, habe ich mir übrigens gerade erst angelesen. Im deutsch-sprachigen Wikipedia-Fragment ist davon zumindest im Zusammenhang mit Parabeln gar keine ausdrückliche Erwähnung zu finden …
Und zu analytischen Betrachtungen, ob und wie sich Parabeln “geeignet geneigt” jeweils mit ihrem Scheitelpunkt an bestimmte Punkte gegebener Kurven berührend anheften ließen, fehlt mir bei aller Lust gerade die Zeit.)
Habe ich oben gemacht. In Koordinaten ausgedrückt ist die Abbildung \( (x,y) \mapsto (y, x) \). Und wie in der Schulmathematik üblich, habe ich implizit vorausgesetzt, dass an der x- wie der y-Achse derselbe Maßstab gilt. So wird aus dem Graph einer Funktion der Graph der Umkehrfunktion. Ja, Mathematica (und in der Folge Wolfram Alpha) macht nicht automatisch gleiche Maßstäbe, weil die Macher etwas seltsame ästhetische Vorstellungen haben. Aber von solchen Mätzchen (oder Mängeln der Bildschirmdarstellung) darf man sich nicht abhängig machen.
Koordinatenfreie Darstellung der Sinusfunktion? WIe soll das gehen?
Ihre Liebe zum Krümmungskreis in Ehren; aber haben Sie schon mal ernsthaft versucht, mit ihm zu rechnen? Sie haben drei Punkte, nämlich die Punkte des Graphen der Funktion bei (zum Beispiel) \(x_0-h, x_0, x_0+h\). Jetzt wollen Sie den Kreis ausrechnen, der durch diese drei Punkte geht, was der Umkreis des Dreiecks aus den drei Punkten ist. Wie Sie dem zitierten Wikipedia-Artikel entnehmen können, sind die zugehörigen Formeln nicht wirklich benutzerfreundlich. Und nicht vergessen: Sie wollen \(h \to 0\) gehen lassen, und das h steht dann irgendwo im Nenner, unter der Wurzel oder beides. Da haben Sie alle Mühe, das umzuformen, so dass ein ordentlicher Grenzwert herauskommt.
Das funktioniert bestimmt; aber wozu dienet dieser Unrat? Was wollen Sie mit dem Krümmungskreis anstellen, was mit der (viel einfacher zu berechnenden) anschmiegsamsten Parabel nicht geht?
Christoph Pöppe schrieb (23.08.2023, 00:14 o’clock):
> [… die (womöglich geometrisch gemeinte) Operation “Spiegelung an der Diagonalen” …] In Koordinaten ausgedrückt ist die Abbildung \((x,y) \mapsto (y,x) \).
Damit ist eine bestimmte Koordinaten-Transformation beschrieben, durch die (auch, entsprechende Umkehrbarkeit vorausgesetzt) der Graph einer Funktion \(y[ \, x \, ]\) auf den Graphen der entsprechenden Umkehrfunktion \(x[ \, y \, ]\) abgebildet ist.
Geometrie kann jedoch nur dadurch “ins Spiel kommen”, dass geometrische Beziehungen (zwischen bestimmten Punkten bzw. zwischen bestimmten Punktmengen) an sich beschrieben werden. Zum Beispiel (vermutlich):
Die Punktmenge, die durch ihre (ursprüngliche, Definitionsbereichs-)Koordinatenzuordnung als \[ \{ \, (a, b) \in \mathcal X \times \mathcal Y \, | \, a = b \} \, \]
bezeichnet werden kann,
und die durch die angegebene Koordinatentransformation \((x,y) \mapsto (y,x) \) offenbar “auf sich selbst” abgebildet wird,
soll insgesamt eine Gerade bilden; genannt “die Diagonale”. Und (vermutlich):
Die minimale Distanz jedes Punktes \((j, k)\) zu den Punkten der Diagonale soll gleichder minimalen Distanz des “entsprechenden” Punktes \((k, j)\) zu den Punkten der Diagonale sein.
Insgesamt geht es darum, welchen Punkten eines gegebenen metrischen (oder allgemeineren) Raumes jeweils welche Koordinaten zugeordnet sind, und welche (zwangsläufig geometrische) Eigenschaften dieser gegebene Raum an sich von vornherein hat. Vermutlich soll ja die spezielle Wahl der Koordinaten-Bezeichnung mit “\(x\) und \(y\)” dazu gewisse “konventionelle” Hinweise geben, die mit anderen Koordinaten-Bezeichnungen wie z.B. “\(x\) und \(t\)” oder “\(r\) und \(\phi\)” oder “\(\theta\) und \(\phi\)” konventionell womöglich nicht gemeint wären.
> Koordinatenfreie Darstellung der Sinusfunktion? WIe soll das gehen?
Eine (die?) Koordinaten-freie Darstellung einer [[Kurve#die.Bildmenge.eines.{{Weg}}es.nennt.man.Kurve]], die in einer Ebene liegt und die unter gewissen bestimmeten Zuordnungen von [[Kartesischen Koordinaten# \((x,y)\)]] zu Punkten dieser Ebene den Graph der Funktionsgleichung \(y := \text{Sin}[ \, x \, ]\) darstellt ??
Das wäre tatsächlich ein ziemlich ambitioniertes, sicher nicht im Handumdrehen realisierbares Projekt …
… aber möglicherweise lohnend, denn nützlich dafür wäre insbesondere die Umkehrfunktion \(r^{(-1)}\) bzw. \(x[ \, r \, ]\) der monotonen, also umkehrbaren Funktion
\[r : \mathbb R_+ \rightarrow \mathbb R_+, x \mapsto r[ \, x \, ] := \sqrt{x^2 + (\text{Sin}[ \, x \, ])^2} \].
Die Koordinaten-freien Darstellungen, an denen ich vorrangig interessiert bin (und die wohl kaum komplizierter wären, als eine “Koordinatenfreie Darstellung der Sinusfunktion”), betreffen stattdessen
– “Geraden” (in Unterscheidung von anderen, “allgemeineren” Kurven),
– “Ebenen” (in Unterscheidung von anderen, “allgemeineren” Flächen), …
– “flache Raumzeit”, oder genauer wenigstens “konformal-flache Raumzeit(en)” (in Unterscheidung von anderen, “allgemeiner gekrümmten” Ereignismengen).
> Ihre Liebe zum Krümmungskreis in Ehren; aber haben Sie schon mal ernsthaft versucht, mit ihm zu rechnen?
Dreiecks-Umkreis-Radien jeweils ausdrücklich vermittels Auswertung der entsprechenden [[Cayley-Menger-Determinante]] ausrechnen ? — Na selbstverständlich; neulich erst, um den Radiuswert
1des Kreises auszurechnen, der (in einer Ebene mit Distanz-Verhältnissen angepassten Kartesischen Koordinaten) den Graphen der Funktion \[y := \text{ArcSin}[ \, 1 – x \, ]\]im Punkt \((x_0, y[ \, x_0 \, ] := (0, \pi / 2)\) berührt (nicht schneidet) und der in diesem Punkt (halb-seitig) genau so gekrümmt ist, wie der genannte Funktions-Graph.
> […] Wie Sie dem zitierten Wikipedia-Artikel entnehmen können, sind die zugehörigen Formeln nicht wirklich benutzerfreundlich.
Na, geht so. Für den gerade beschriebenen Kreis lässt sich dessen Radiuswert
1sogar (so gerade noch, in mehreren “Schritten”) vermittels Wolfram-Alpha ausrechnen. Gewisse, womöglich bekanntere analytische Formeleien, in denen die erste und die zweite Ableitung einer gegebenen Funktion auftritt, sind an solchen Punkten, in denen die zweite (oder gar die erste) Ableitung der Funktion gar nicht als endlicher Wert existiert, zwangsläufig ganz Benutzer-unfreundlich.> Da haben Sie alle Mühe, […] dass ein ordentlicher Grenzwert herauskommt.
Mir ist noch kein (Gegen-)Beispiel untergekommen, geschweige denn auf die Schnelle vorstellbar, in dem die geometrisch definierte “Krümmung einer Kurve, in einem bestimmten Punkt” nicht auch entsprechend als Grenzwert auswertbar wäre. (Wer Lust hat, möge bitte ein solches (Gegen-)Beispiel präsentieren! …)
> Das funktioniert bestimmt; aber wozu dienet dieser Unrat?
… Ich bitte um Mäßigung! …
> Was wollen Sie mit dem Krümmungskreis anstellen,
… Die Betrachtung von Umkreisen gewisser Dreiecke, und die Untersuchung, ob deren Radien eine positive untere Schranke haben, oder nicht, trat ja schon ganz oben (26.07.2023, 18:32 o’clock) auf, als es darum ging, nachvollziehbar zu unterscheiden, ob sich gegebene Kurven “schneiden” oder “(nur) berühren” alias “einander tangential sind”.
Das Thema “Krümmungskreise” ist zwar verwandt, aber doch ein anderes.
> was mit der (viel einfacher zu berechnenden) anschmiegsamsten Parabel nicht geht?
Bezogen auf das (mir vorrangigere) “Problem der Tangentialität” ließe sich entsprechend fragen (vgl. die “analytische Definition von Krümmungskreisen” im Kommentar 14.08.2023, 22:05 o’clock):
An dieser “analytischen Definition von Tangentialität” ist auszusetzen, dass Kurven, als Bilder von [[Weg]]en (z.B. in einem bestimmten metrischen Raum), von vorherein ohne irgendeine bestimmte Zuordnung von Koordinaten(-Tupeln) gegeben sind. Eine geometrische Bedeutung dieser Definition ließe sich bestenfalls nur daraus erschließen, wie (alias “wie angepasst” an gegebene Distanzverhältnisse) bestimmte Koordinaten den Punkten der Kurven zugeordnet würden.
Mathematikern mag das ja herzlich egal sein.
Physiker jedoch bevorzugen deshalb Definitionen, die unmittelbar durch die gegebenen geometrischen Begriffe formuliert sind (u.a. durch Distanzverhältnisse); die dadurch Koordinaten-frei formulierbar sind.
Frank Wappler schrieb (24.08.2023, 01:49 o’clock):
> […] “analytische Definition von Tangentialität”
Dieser skizzenhafte Vorschlag einer “analytische Definition von Tangentialität” bezieht sich implizit auf Kartesische Koordinaten.
Und mit dieser Festlegung wäre die folgende Ergänzung sinnvoll bzw. jedenfalls konventionell: