Was ist eigentlich Licht?
BLOG: RELATIV EINFACH

Was ist eigentlich Licht? Bei meiner Vorlesung Methoden der Astronomie für Nicht-Physiker am letzten Donnerstag ging es unter anderem auch um diese Frage. Redet man darüber redet, dass Astronomen das Licht ferner Objekte auffangen und analysieren, sollte man tunlichst wissen, was Licht ist, und welche Informationen Licht überhaupt tragen kann. Weil meine Vorlesung weitgehend ohne Formeln und mathematische Ableitungen auskommt, ist mir besonders wichtig, welches Bild und welche Vorstellungen wir uns von Licht machen. Mit den richtigen Vorstellungen von Licht im Hinterkopf kann man besser verstehen, wie astronomische Beobachtungen funktionieren.
Licht als Teilchen
Die erste korrekte Vorstellung von Licht ist die von Licht als Teilchen. Sich Licht anschaulich als kleine, kugelartige Gebilde vorzustellen, ist natürlich eine Vereinfachung. Aber sie vermittelt den folgenden richtigen Schluss: Trifft Licht auf einen Detektor, geschieht dies Teilchen für Teilchen, ein Teilchen nach dem anderen:  Jedes dieser Lichtteilchen transportiert eine bestimmte Menge an Energie. (Ich komme später darauf zurück, dass diese individuelle Lichtteilchen-Energie der Farbe des betreffenden Lichts entspricht; deswegen sind die Lichtteilchen in dem vereinfachten Bild farbig dargestellt.) Dokumentieren wir, wieviel Energie mit der Zeit in unserem Detektor nachgewiesen wird, dann sieht das Ergebnis schematisch aus wie in diesem Diagramm hier:
Jedes dieser Lichtteilchen transportiert eine bestimmte Menge an Energie. (Ich komme später darauf zurück, dass diese individuelle Lichtteilchen-Energie der Farbe des betreffenden Lichts entspricht; deswegen sind die Lichtteilchen in dem vereinfachten Bild farbig dargestellt.) Dokumentieren wir, wieviel Energie mit der Zeit in unserem Detektor nachgewiesen wird, dann sieht das Ergebnis schematisch aus wie in diesem Diagramm hier: 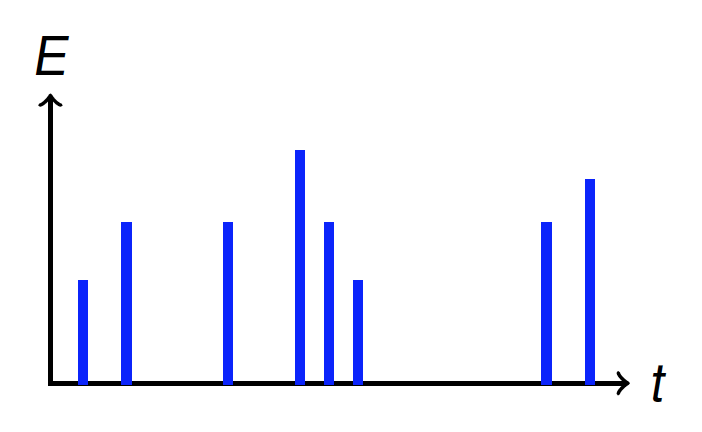 Jedes Mal, wenn eines der Lichtteilchen eintrifft, wird ganz plötzlich die von diesem Teilchen transportierte Menge Energie im Detektor deponiert. Je nach Teilchen trifft dabei unterschiedlich viel an Energie ein.
Jedes Mal, wenn eines der Lichtteilchen eintrifft, wird ganz plötzlich die von diesem Teilchen transportierte Menge Energie im Detektor deponiert. Je nach Teilchen trifft dabei unterschiedlich viel an Energie ein.
Im Vakuum bewegen sich Lichtteilchen geradlinig mit der üblichen (Vakuum-)Lichtgeschwindigkeit, c = 299 792 458 m/s.
Lichtteilchen nennt man in der Physik auch Photonen oder Lichtquanten. Der Ausdruck “Quanten” zeigt dabei bereits an, dass diese Art von Beschreibung von Licht Teil der Quantentheorie ist. Sie gehört damit in den Beschreibungsrahmen, in dem Physiker auch Atome, Moleküle, Elementarteilchen und allgemein die Welt des allerkleinsten und deren Eigenschaften und Konsequenzen beschreiben.
Licht als Welle
Andererseits ist Licht eine Welle. Das ist unter Physikern unumstritten, seit James Clerk Maxwell in den 1860er Jahren die allgemeinen Gleichungen für den Elektromagnetismus hinschrieb. Aus den Maxwell-Gleichungen folgt die Möglichkeit elektromagnetischer Wellen – und elektromagnetische Wellen in einem bestimmten Frequenzbereich sind das, was wir im Alltag als Licht bezeichnen. (Astronomen sind in ihrem Sprachgebrauch etwas allgemeiner und bezeichnen alle Arten von elektromagnetischen Wellen als Licht – Infrarotlicht beispielsweise, oder Röntgenlicht. Ist vom Alltagslicht die Rede, nennen Astronomen dies sichtbares Licht.)
Stellen wir die Frage, wie die Wellennatur mit den Teilcheneigenschaften zusammenpasst, erst einmal hintan und fragen stattdessen: Welche Eigenschaften sind denn überhaupt gemeint, wenn wir sagen, etwas sei eine Welle oder verhalte sich wie eine Welle?
Das einfachste Bild, das man vor Augen haben kann, wenn von einer Welle die Rede ist, ist das eines einfachen Sinusmusters: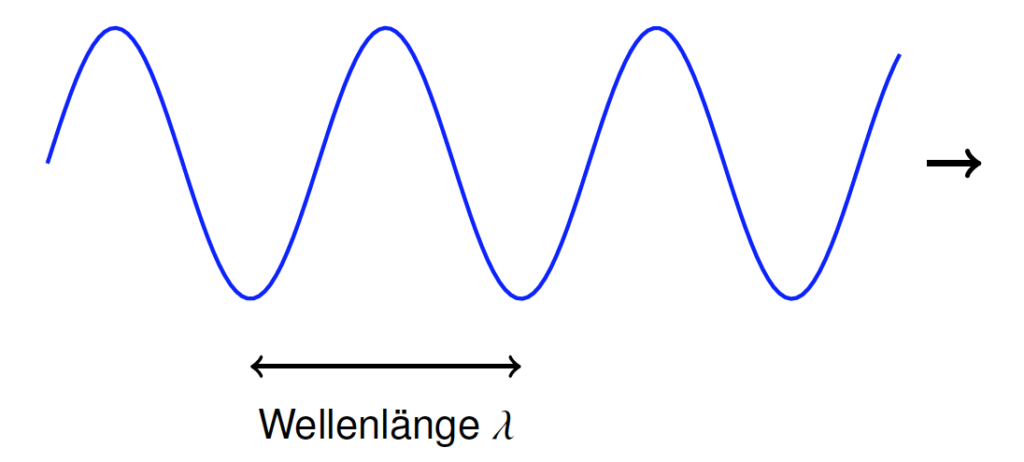
Die Größe, die da schwingt, ist von Welle zu Welle verschieden. Bei Oberflächenwellen auf dem Wasser ist es die Abweichung vom mittleren Wasserspiegel – Wellenberge liegen darüber, Wellentäler darunter. Bei Schallwellen ist es der Luftdruck: Wellenberge entsprechen höherem Druck, Wellentäler niedrigerem Druck. Das Muster wechselnden Drucks, das unser Ohr erreicht, nehmen wir als Geräusch, Ton oder Sprache wahr.
Elektromagnetische Wellen
Bei Lichtwellen sind es mehrere miteinander verbundene Größen, die da schwingen, nämlich elektrisches und magnetisches Feld. Mit deren Bedeutung wollen (und müssen) wir uns an dieser Stelle nicht auseinandersetzen; ich habe mich auf Einstein Online im Beitrag Von der Kraft zum Feld an einer einfachen Erklärung versucht. Bestimmte Eigenschaften haben alle diese im Detail verschiedenen Wellen gemeinsam, und um diese Eigenschaften soll es uns hier gehen.
Das Sinusmuster bewegt sich als ganzes durch den Raum (in der obigen Abbildung angedeutet durch den Pfeil). In dieser einfachen Variante ist die Abfolge von Wellenberg und Wellental absolut regelmäßig. Der Abstand zweier benachbarter Wellentäler ist die Wellenlänge, häufig mit einem kleinen Lambda bezeichnet: \(\lambda\).
Wellenlänge, Frequenz, Schwingungsdauer
Hier ist eine Animation, die zeigt, wie sich das Muster durch den Raum bewegt: 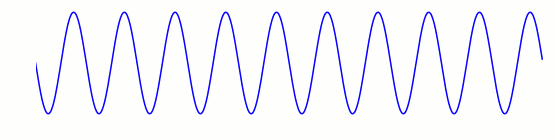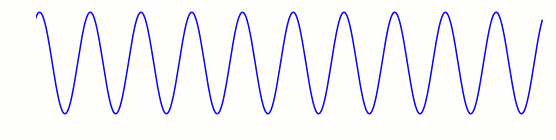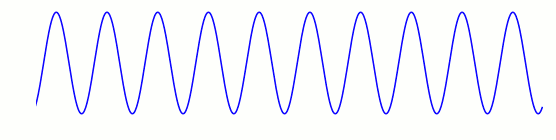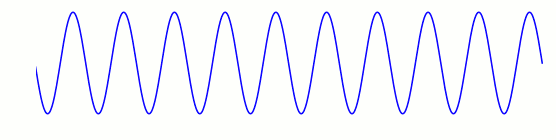 Die Darstellungsform verhindet, das Wellenmuster soweit nach links und rechts fortzusetzen, wie es realistisch wäre. Das Geschlängel am linken und rechten Rand solltn Sie daher bitte ignorieren. Einen guten Eindruck von der Ausbreitung des Musters bekommen Sie, wenn Sie sich auf die Mitte der Animation konzentrieren und verfolgen, wie dort Wellen und Täler ganz regelmäßig immer weiter nach rechts wandern, nämlich in regelmäßigem Abstand mit konstanter Geschwindigkeit durch den Raum laufen. Die Geschwindigkeit, mit der die verschiedenen Teile der Welle durch den Raum laufen – beispielsweise jeder der Wellenberge in dieser Animation nach rechts – heißt Geschwindigkeit der Welle, genauer: Phasengeschwindigkeit der Welle.
Die Darstellungsform verhindet, das Wellenmuster soweit nach links und rechts fortzusetzen, wie es realistisch wäre. Das Geschlängel am linken und rechten Rand solltn Sie daher bitte ignorieren. Einen guten Eindruck von der Ausbreitung des Musters bekommen Sie, wenn Sie sich auf die Mitte der Animation konzentrieren und verfolgen, wie dort Wellen und Täler ganz regelmäßig immer weiter nach rechts wandern, nämlich in regelmäßigem Abstand mit konstanter Geschwindigkeit durch den Raum laufen. Die Geschwindigkeit, mit der die verschiedenen Teile der Welle durch den Raum laufen – beispielsweise jeder der Wellenberge in dieser Animation nach rechts – heißt Geschwindigkeit der Welle, genauer: Phasengeschwindigkeit der Welle.
Setzen wir uns an einen festen Ort im Raum und messen, welche Werte die Wellengröße genau an diesem Ort hat, sieht das wie in der folgenden Animation aus; der rote Rahmen repräsentiert dabei den Ort auf dem Ausbreitungspfad der Welle, an dem wir unsere Messungen vornehmen: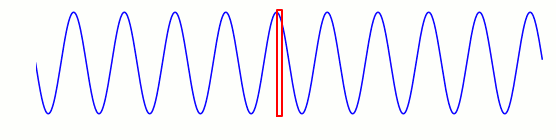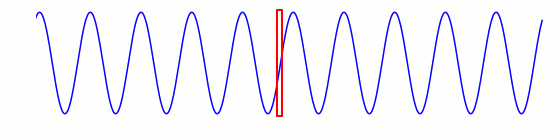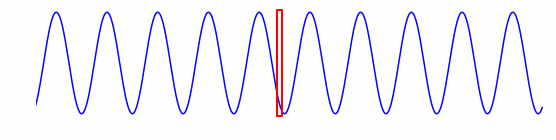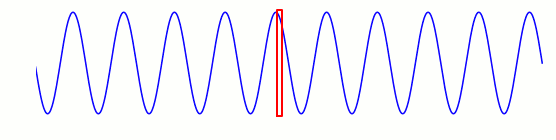 Noch deutlicher wird das Ergebnis der Messung, wenn wir alles außerhalb der roten Box ausblenden:
Noch deutlicher wird das Ergebnis der Messung, wenn wir alles außerhalb der roten Box ausblenden: Beschränkt man sich auf einen einzigen Ort, an dem eine Welle vorbeiläuft, dann misst man für die Wellengröße an jenem Ort offenbar eine regelmäßige Schwingung, auf und ab, auf und ab. Die Zeit, die zwischen einem Schwingungsmaximum und dem nächsten vergeht, heißt Schwingungszeit der Welle.
Beschränkt man sich auf einen einzigen Ort, an dem eine Welle vorbeiläuft, dann misst man für die Wellengröße an jenem Ort offenbar eine regelmäßige Schwingung, auf und ab, auf und ab. Die Zeit, die zwischen einem Schwingungsmaximum und dem nächsten vergeht, heißt Schwingungszeit der Welle.
Der Kehrwert der Schwingungszeit ist die Frequenz der Welle, \(f = 1/T\) (hier mit f, oft auch mit griechischem \(\nu\), “ny”, bezeichnet). Sie sagt, wieviel Schwingungen unsere Welle in einer gegebenen Zeit ausführt. Eine Frequenz von “1000 pro Sekunde”, anders ausgedrückt: von 1 kHz = 1000 Hz (ein Kilohertz, also 1000 Hertz) bedeutet, dass die Welle pro Sekunde 1000 Schwingungen ausführt.
Die Schwingungszeit \(T\) hängt mit der Wellenlänge \(\lambda\) und der Phasengeschwindigkeit \(c\) wie folgt zusammen. In der nachfolgenden Animation ist ein einziger Schwingungszyklus dargestellt, von der Zeit \(t=0\) bis zur Zeit \(t=T\). Am Anfang dieser Zeit befindet sich in unserem roten Messrahmen ein Schwingungsmaximum, am Ende der Zeit das nächste Schwingungsmaximum: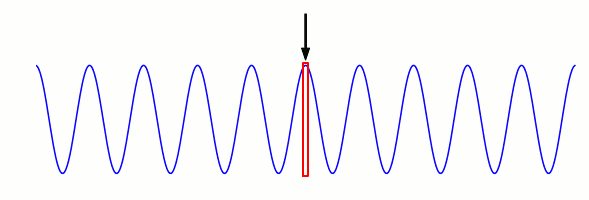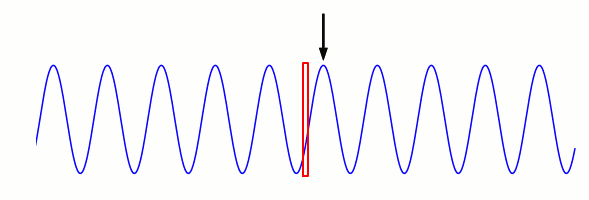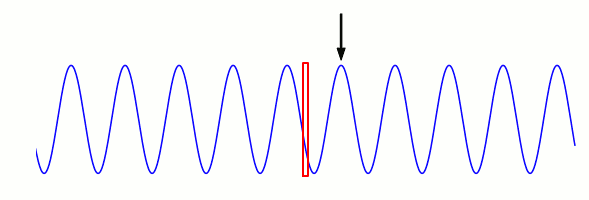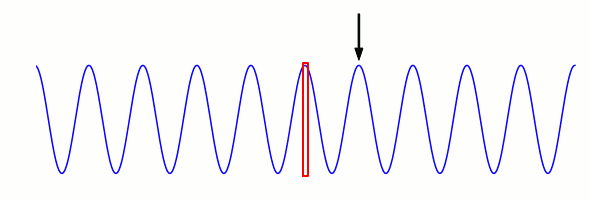
Der Schwingungszyklus insgesamt hat die Dauer \(T\). In diesem Zeitraum hat sich der ursprünglich gemessene Wellenberg (mit Pfeil markiert) gerade um eine Wellenlänge nach rechts bewegt. Eine Wellenlänge ist bei einer einfachen Welle schließlich der Abstand von einem Wellenberg zum nächsten, und am Anfang des Zyklus ist der eine Wellenberg in unserem roten Messrahmen, am Ende des Zyklus der nächste.
Die (Phasen-)Geschwindigkeit unserer Welle ist damit \(c=\lambda/T\). Schließlich hat unser Wellenberg in der Zeit \(T\) die Distanz \(\lambda\) zurückgelegt. Anders ausgedrückt:
\(c = \lambda\cdot f.\)
Da ist eine ganz zentrale Gleichung für einfache Sinuswellen. Bei Lichtwellen ist die Phasengeschwindigkeit im Vakuum gerade die Vakuum-Lichtgeschwindigkeit, wie oben bereits angegeben: c = 299 792 458 m/s
Überlagerung von Wellen
Charakteristisch für Wellen ist, dass sie sich überlagern können. Laufen zwei Teilwellen aufeinander zu, dann kommt es dort, wo die Wellen sich treffen, zu einer solchen Überlagerung. Qualitativ dürften die meisten Leser das schon einmal gesehen haben, etwa wenn sich Oberflächenwellen einer Flüssigkeit treffen. Hier ist es eine Pfützen-Oberfläche, mit kreisförmigen Wellen, die durch Regentropfen hervorgerufen werden. Die Wellen überlagern sich dort, wo sie aufeinandertreffen, und bilden einigermaßen komplexe Muster:

Die einfachsten Fälle solcher Überlagerung zeigen die beiden folgenden Grafiken. Dabei ist zur Anschauung nur ein Schnappschuss der beteiligten Wellen in einer Raumdimension dargestellt. In rot und blau sind die Teilwellen dargestellt, die sich da überlagern, in lila im untersten Feld, was bei der Überlagerung herauskommt: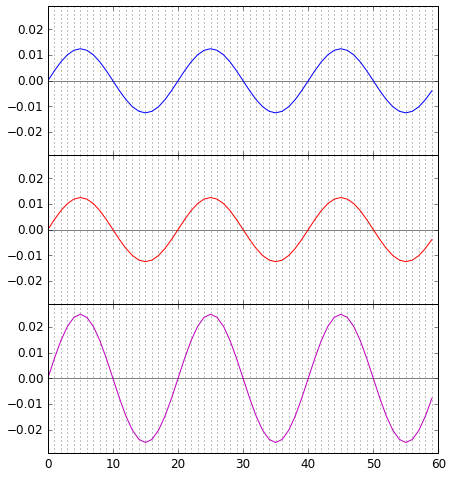 Die Überlagerung ist an jedem Punkt der waagerechten Achse eine einfache Addition: Ist beispielsweise bei Wasserwellen die eine Teilwelle an einem bestimmten Ort 1,3 cm höher als der mittlere Wasserspiegel und die andere Teilwelle ebenfalls 1,3 cm höher als der mittlere Wasserspiegel, dann ragt die überlagerte Welle an jener Stelle 1,3 + 1,3 = 2,6 cm über den mittleren Wasserspiegel hinaus. Dieser Fall, in dem sich die Wellen verstärken, heißt konstruktive Interferenz.
Die Überlagerung ist an jedem Punkt der waagerechten Achse eine einfache Addition: Ist beispielsweise bei Wasserwellen die eine Teilwelle an einem bestimmten Ort 1,3 cm höher als der mittlere Wasserspiegel und die andere Teilwelle ebenfalls 1,3 cm höher als der mittlere Wasserspiegel, dann ragt die überlagerte Welle an jener Stelle 1,3 + 1,3 = 2,6 cm über den mittleren Wasserspiegel hinaus. Dieser Fall, in dem sich die Wellen verstärken, heißt konstruktive Interferenz.
In der obigen Abbildung ist der Idealfall zu sehen, an dem zwei Wellen mit gleicher Wellenlänge sich so überlagern, dass sich jeder Wellenberg der einen Welle exakt am Ort des Wellenberges der anderen Welle befindet (und entsprechend für die Wellentäler). Das Ergebnis ist eine Überlagerung, die gerade die Summe der Wellengrößen der Teilwellen ist. Maximale konstruktive Interferenz.
Eine Welle plus eine Welle gleich – keine Welle?
Es kann allerdings auch ganz anders kommen. Hier sind zwei eigentlich gleich starke Wellen überlagert, und zwar so gegeneinander verschoben, dass jedes Wellental der einen gerade auf einen Wellenberg der anderen Welle trifft, und umgekehrt: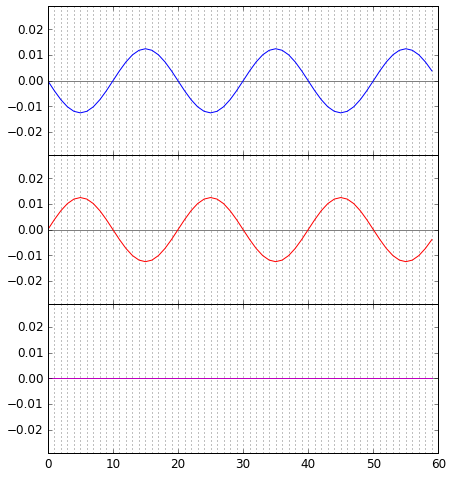 Wieder addieren sich die Wellen, nur eben in diesem Falle zu Null. Bei einer Wasserwelle würde z.B. gelten: Eine Teilwelle 1,5 cm über dem mittleren Meeresspiegel, die andere Teilwelle am gleichen Ort 1,5 cm darunter, addieren sich zu 1,5 + (-1,5) = 0 cm, also gerade zum mittleren Meeresspiegel. Wo sich Wellen in solcher Weise gegenseitig abschwächen, heißt das destruktive Interferenz.
Wieder addieren sich die Wellen, nur eben in diesem Falle zu Null. Bei einer Wasserwelle würde z.B. gelten: Eine Teilwelle 1,5 cm über dem mittleren Meeresspiegel, die andere Teilwelle am gleichen Ort 1,5 cm darunter, addieren sich zu 1,5 + (-1,5) = 0 cm, also gerade zum mittleren Meeresspiegel. Wo sich Wellen in solcher Weise gegenseitig abschwächen, heißt das destruktive Interferenz.
Ein Anwendungsbeispiel (mit Laserlicht) hatte ich in Gravitationswellen-Nachweistechnik: Michelson-Interferometer vorgestellt.
Apropos einfache Wellen: Wie sehen denn kompliziertere Wellen aus? Fast beliebig, dann jedes periodische Muster, das durch den Raum reist, lässt sich als Summe von einfachen Sinus- oder Kosinuswellen schreiben! Wie das geht und was das bedeutet hatte ich in Gravitationswellen-Nachweistechnik: Signale und Wellen näher ausgeführt. Dank der linearen Überlagerungseigenschaften gilt aber glücklicherweise: Versteht man das Verhalten der einfachen Sinus- oder Kosinuswellen, dann versteht man auch das Verhalten solcher Summenwellen.
Gerade die Möglichkeit destruktiver Interferenz ist übrigens ein gutes Kriterium, um Wellen und Teilchen auseinanderzuhalten. Für herkömmliche Teilchen gilt: Bringe ich eine Gruppe von Teilchen mit einer zweiten Gruppe von Teilchen zusammen, dann habe ich am Ende insgesamt die Summe beider Teilchen. Teilchen plus Teilchen gibt immer insgesamt mehr Teilchen, niemals weniger Teilchen. Die destruktive Interferenz zeigt, dass es bei Wellen anders sein kann: Welle plus Welle kann je nach den näheren Verhältnissen durchaus auch weniger Welle oder gar keine Welle ergeben.
Soweit zu den Grundeigenschaften von Wellen und teilchen. Wie kann Licht unter diesen Bedingungen Welleneigenschaften und Teilcheneigenschaften haben?
Licht als Welle und Teilchen
Die Eigenschaft, dass Licht plus Licht immer mehr Licht ergibt, hat Licht definitiv nicht. In dieser Hinsicht verhält es sich anders als normale Teilchen. Im Detektor kommt Licht dagegen immer in Form einzelner Teilchen, einzelner Energiepakete an. Das wiederum passt nicht zu einer herkömmlichen Welle, die ihre Energie allmählich an einen Detektor übertragen würde.
Insgesamt ist Licht eine Sammlung von Teilchen, deren Verteilung durch eine zugrundeliegende Welle bestimmt wird. Diese Welle wird auch Wellenfunktion genannt – eine grundlegende Größe der Quantentheorie, in deren Gefilden wir uns hier bereits bewegen.
Etwas vereinfacht (weil ich hier keine komplexen Zahlen einführen möchte): Wenn die zugrundeliegende Welle eine einfache Sinuswelle ist (wie dargestellt im oberen Teil der folgenden Abbildung), dann gibt das Quadrat der Welle (dargestellt im unteren Teil) so etwas wie die Aufenthaltswahrscheinlichkeit für Lichtteilchen an: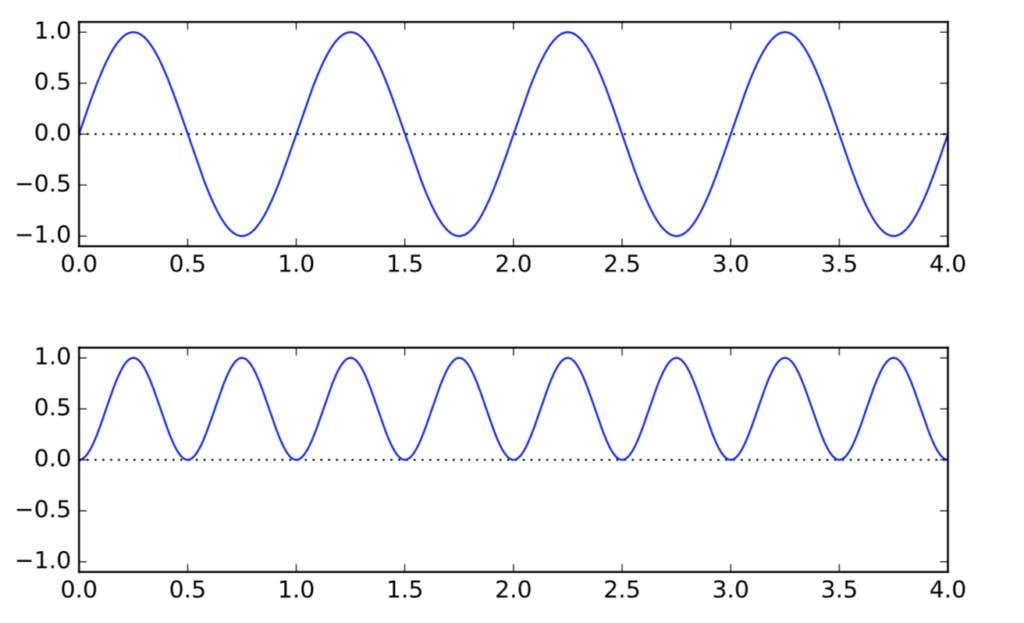 Anders gesagt: Je größer der Wert des Quadrats an einem bestimmten Ort ist, umso mehr Lichtteilchen sind dort anzutreffen. Wo die Welle ein Wellenberg oder einen Wellental besitzt, sind dementsprechend besonders viele Lichtteilchen anzutreffen, am Ort eines Nulldurchgangs (auf halbem Wege zwischen Berg und Tal) gar keine.
Anders gesagt: Je größer der Wert des Quadrats an einem bestimmten Ort ist, umso mehr Lichtteilchen sind dort anzutreffen. Wo die Welle ein Wellenberg oder einen Wellental besitzt, sind dementsprechend besonders viele Lichtteilchen anzutreffen, am Ort eines Nulldurchgangs (auf halbem Wege zwischen Berg und Tal) gar keine.
Die folgende Animation zeigt die drei Größen untereinander: oben die Wellengröße, darunter ihr Quadrat, und ganz unten eine Häufigkeitsverteilung von Photonen, die dem Quadrat der Wellengröße entspricht; alle drei Muster wandern nach rechts: 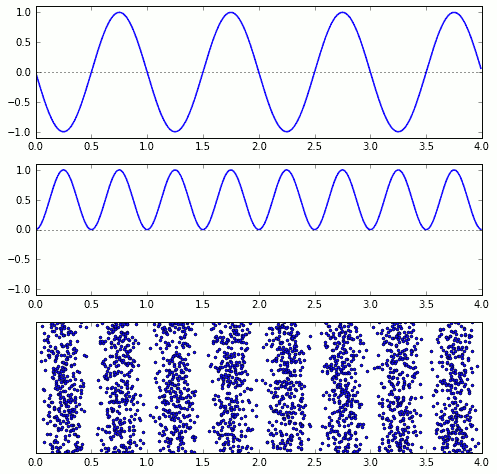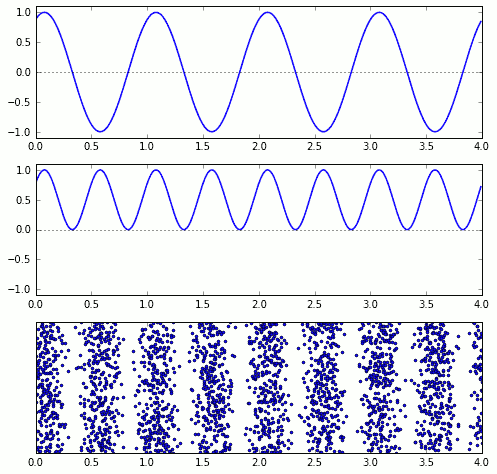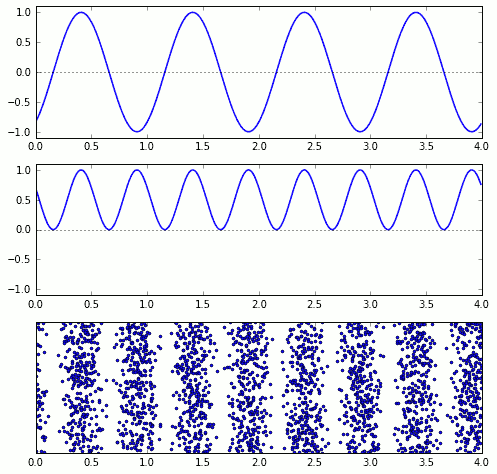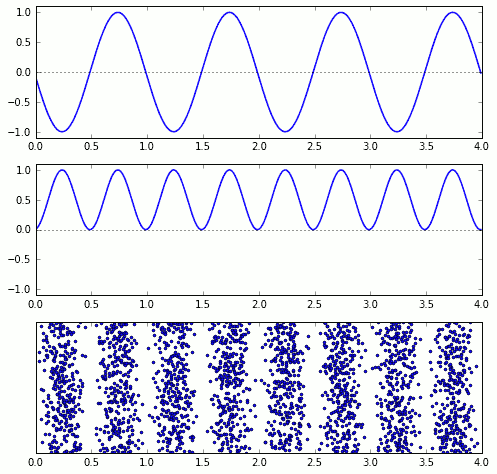
Alleine die Vorstellung, dass dort räumlich geordnete Gruppen von Photonen durch den Raum laufen, wird dem Wellencharakter allerdings noch nicht gerecht. Eine Häufung von Photonen kann schließlich entweder bei einem Wellenberg oder bei einem Wellental stattfinden. Und je nachdem ob es sich um einen Wellenberg oder ein Wellental handelt, kann das Ergebnis ein ganz anderes sein, wenn man diese spezielle Welle mit einer anderen Welle überlagert – im Extremfall kann dieser Unterschied der Unterschied zwischen völliger gegenseitiger Auslöschung und maximaler Verstärkung der Wellen sein.
Auch wenn man weiß, dass Lichtwellen so etwas wie Photonenhäufigkeiten bestimmen, sollte man das Berg-und-Tal-Bild der einfachen Welle noch im Hinterkopf behalten. Man wird es brauchen, sobald Überlagerungen und Interferenzen ins Spiel kommen.
Einen weiteren wichtigen Zusammenhang zwischen Teilchen- und Welleneigenschaften gibt es noch. Die Energie \(E\) eines Photons hängt direkt mit der Frequenz \(f\) (und damit auch mit der Wellenlänge \(\lambda\)) der zugehörigen einfachen Welle zusammen. Konkret gilt
\( E = hf = hc/\lambda.\)
Wellenlängen und Farben
Einfache Wellen mit konstanter Frequenz entsprechen je nach Frequenzwert unterschiedlichen elementaren Farben den Farben des Regenbogens, des Spektrums. Diese Farbfolge hat jeder schon einmal gesehen, der einen Regenbogen kennt:

In einem geeigneten Instrument, nämlich einem Spektroskop oder Spektrograf, kann das Licht noch deutlich feiner aufgespalten werden. Hier ein Beispiel eines Spektrums vom am Mond reflektierten Sonnenlicht. Dass das Spektrum dreimal untereinander in unterschiedlicher Helligkeit zu sehen ist, ist eine Folge des Aufbaus des verwendeten Instruments (für Kenner: drei unterschiedlich breite Spalte untereinander):  Dass der gelbe Bereich zwischen dem grünen und orange-roten Teil nicht so ausgeprägt ist, hat mit der verwendeten Kamera zu tun. Von solchen Artefakten abgesehen sind hier genau die Farben abgebildet, die einfachen Lichtwellen unterschiedlicher Wellenlängen entsprechen. Es fängt links bei lila-blau mit den kurzen Wellenlängen (höheren Frequenzen) an und geht von links nach rechts hin zu immer längeren Wellenlängen (niedrigeren Frequenzen) über türkis, grün, gelb, orange bis hin zu dem tiefroten Bereich der längsten Wellenlängen (niedrigsten Frequenzen) für sichtbares Licht.
Dass der gelbe Bereich zwischen dem grünen und orange-roten Teil nicht so ausgeprägt ist, hat mit der verwendeten Kamera zu tun. Von solchen Artefakten abgesehen sind hier genau die Farben abgebildet, die einfachen Lichtwellen unterschiedlicher Wellenlängen entsprechen. Es fängt links bei lila-blau mit den kurzen Wellenlängen (höheren Frequenzen) an und geht von links nach rechts hin zu immer längeren Wellenlängen (niedrigeren Frequenzen) über türkis, grün, gelb, orange bis hin zu dem tiefroten Bereich der längsten Wellenlängen (niedrigsten Frequenzen) für sichtbares Licht.
Jenseits des sichtbaren Spektrums geht es natürlich noch weiter. Weiter links vom blauesten hier dargestellten Bereich schließen sich bei noch kürzeren Wellenlängen erst UV-Strahlung, dann Röntgenstrahlung und schließlich Gammastrahlung an. Weiter rechts vom rötesten Bereich folgen Infrarotstrahlung, Mikrowellen, Submillimeter- und Millimeterwellen und das Reich der immer längerwelligen Radiowellen.
Zusammenfassung
Diese Ausführungen zeigen ungefähr, wie man sich Licht vorstellen sollte: Als Photonengemisch, dessen räumliche Struktur (die Verteilung der Photonen im Raum) durch eine zugrundeliegende Welle bestimmt wird, die Wellenfunktion. Teilcheneigenschaften zeigt das Licht, weil dort Photonen fliegen, die dann als Energiepakete einzeln an einem Detektor ankommen.
Welleneigenschaften zeigt das Licht, weil die zugrundeliegende Wellenfunktion Überlagerungen aufweisen kann und bei Licht daher konstruktive und destruktive Interferenz möglich sind. Nicht zuletzt hängen außerdem die einfachsten Wellen- und Teilchengrößen miteinander zusammen: die Energie E eines Photons ist proportional zur Frequenz der entsprechenden elementaren Welle, gemäß \(E=hf\).
Mit diesen Grundlagen wissen wir jetzt auch, was Astronomen prinzipiell, auf fundamentaler physikalischer Ebene, beobachten können: Sie können Photonen zählen, deren Energien bestimmen, und Phaseninformationen über die zugrundeliegenden Wellen erhalten. Wie das mit den üblichen Begriffen zusammenhängt, mit denen man astronomische Beobachtungen beschreibt, wird Inhalt eines weiteren Blogbeitrags sein.


Zitat:
Mit dieser Erkärung werden Lichtwellen auf das (quantenmechanische) Verhalten von Teilchen (Photonen) zurückgeführt. Richard Feynman hat das sehr detailliert in seinem für Laien geschriebenen Büchlein QED gemacht, wobei er aber nicht die Wellenfunktion bemüht, sondern das von ihm erfundene Äquivalent, das Pfadintegral, womit er dann optische Phänomene durch Photonen erklärt, die gleichzeitig alle möglichen Pfade durchlaufen. Jedes Photon – in seiner Erklärung für Laien – besitzt einen Pfeil (Arrow) , dessen Länge seine Aufenthaltswahrscheinlichkeit angibt. Die Pfeile aller Photonen, die einen bestimmten Punkt erreichen müssen vektoriell aufaddiert werden.
Mir scheint, diese Art der Erklärung gut geeignet um Quantenphänomene zu erklären und um Licht in das Phänomen zu bringen, dass Licht sich gelegentlich wie ein Teilchen und gelegentlich wie eine Welle verhält. Doch diese Art der Erklärung von Lichtwellen hat sehr wenig mit den elektromagnetischen Transversalwellen zu tun, die gemäss Maxwell das Licht beschreiben und mit denen sich viele Interaktionen von Licht mit Materie als Wirkungen des oszillierenden E-Feldes einer Lichtwelle auf Ladungen in der Materie beschreiben lassen. Mir scheint, die Erklärung von Licht als elektromagnetische Welle führt im allgemeinen zu einfacheren Modellen der Licht-Materie-Interaktion als die Erklärung von Licht als Ansammlung von sich wellenartig verhaltenden Lichtteilchen (Photonen).
Ergänzung: Licht als Ansammlung von Teilchen, also von Photonen, zu beschreiben scheint auf den ersten Blick intuitiv. Ein Lichtstrahl wäre dann eine Gruppe von Photonen, die mit Lichtgeschwindigkeit unterwegs sind. Doch scheinbar ist diese Vorstellung zu einfach (und somit nicht korrekt) wie die Suche in der Wikipedia für Kohärente Strahlung (Laserstrahlung) zeigt. Das Wellenbild für kohärente Strahlung wird duch elektromagneitsche Wellen gleicher Wellenlängen mit fester Phasenbeziehung beschrieben. Das Teilchenbild, welches als Kohärenter Zustand bezeichnet wird, aber ist intuitiv nur schwierig zu verstehen. Dazu liest man in der Wikipedia:
Ein Laserstrahl enthält also in Teilchenbetrachtung eine unbestimmte Anzahl von Photonen. Da versagt bei mir die Vorstellungskraft, denn wenn ich an Teilchen denken, denke ich an N Teilchen und nicht an eine unbestimmte Anzahl von Teilchen.
Drei Dinge versteh ich nicht so ganz. In dem Link * Gravitationswellen-Nachweistechnik: Signale und Wellen * steht:
* Auch der Unterschied zwischen Sinus und Kosinus ist ein einfacher Phasenunterschied: eine Sinuswelle erhält man aus einer Kosinuswelle, indem man die Kosinuswelle um ein Viertel der Wellenlänge nach rechts verschiebt. *
Damit ist wohl gemeint dass wenn man in diesem Bild * https://upload.wikimedia.org/wikipedia/commons/thumb/7/71/Sine_cosine_one_period.svg/600px-Sine_cosine_one_period.svg.png *
den Beginn der blauen Linie (bei y = 1) um zwei Quadrate nach rechts verschiebt die blaue Linie deckungsgleich mit der roten wird, also eine Sinuswelle. Inwiefern ist das nun in der/für die “Wellenpraxis” wichtig?
Und bei den beiden Diagrammen hier mit dem Wellenquadrat: Warum befindet sich die “quadratische” Welle ausschließlich oberhalb der mittleren Achse/dem mittleren Wasserspiegel? Und was genauer hat man sich unter einem Wellenquadrat vorzustellen? Eine Welle “hoch 2”?
Vgl. auch mit:
-> https://de.wikipedia.org/wiki/Welle-Teilchen-Dualismus#Interferenz_gr.C3.B6.C3.9Ferer_Molek.C3.BCle
Folgt daraus nicht, dass Materie, wie auch immer theoretisiert, Photonen gelten wohl physikalisch nicht als ‘Materie’, sogenannte Mutterstoffe sind gemeint, oder die Welt allgemein anders theoretisiert werden müsste, letztlich?
Irgendwie in der Art, dass Daten, also Messbares, vorliegen und auch derart gedacht werden darf, dass Messende eine Rolle bei der Bestimmung der Welt spielen könnten oder zu spielen haben?
Bspw. Zeilinger hat hierzu einiges gesagt (und wohl auch geschrieben – der Schreiber dieser Zeilen bleibt natürlich auch hier nur interessierter Laie, wenn auch nicht ganz blöde im physikalischen Verständnis).
MFG
Dr. Webbaer (der keine Reaktion erwartet, hier nur von Physikern (“Physiklehrern”) annimmt, dass alles schon so gefragt worden ist, wenn auch noch nicht von allen)
Vielleicht liesse sich Joachim Schulz ja zu einer erhellenden Reaktion bewegen, der hierzu schliesslich auch schon einiges in seinem Blog geschrieben hat. Einstweilen sei noch ein Zitat über ein Zitat eines relativ bekannten Physikers beigetragen:
As Einstein wrote a few years before he died: “All these fifty years of conscious brooding have brought me no nearer to the answer to the question ‘What are light quanta?’ Nowadays every Tom, Dick, and Harry thinks he knows it, but he is mistaken” (Einstein to Besso, December 12, 1951; quoted, e.g., in [Martin J.] Klein 1979, 138).
Zitiert nach The Cambridge Companion to Einstein (M. Janssen & C. Lehner, eds. CUP, 2014. p. 34).
Zitat:
Im ontologischen Materialismus wie er in Bunge&Mahner’s “Natur der Dinge” beschrieben ist, werden alle Elementarteilchen (und auch Felder) als materiell bezeichnen. Was Energie einthält ist nach Bunge&Mahner materiell und nur was materiell ist ist real.
In der deutschen Wikipedia dagegen wird weiterhin nur das als Materie bezeichnet, was massenbehaftet ist (Zitat):
Ob etwas massebehaftet ist oder nicht, macht aber keinen riesigen Unterschied. Vor kurzem betrachtete man Neutrinos noch als masselos, heute weiss man, dass sie massebehaftet sind. Für den ontologischen Materialismus ist diese Statusändern der Neutrinos bedeutungslos, denn beim ontologischen Materialismus geht es darum, was real ist und was nicht. Neutrinos sind real – ob nun massebehaftet oder nicht. Auch Photonen sind real.
Hi zusammen,
Jetzt sind wir 65 Jahre weiter, aber Einstein würde immer noch dasselbe behaupten, und dies zu Recht.
Einstein hat sich während des Studiums und auch danach viel mit Philosophie und Metaphysik befaßt. Er kannte daher den Unterschied zwischen dem realen Sein und einem Modell. Lichtquanten sind Modellobjekte. Und natürlich nicht real. Über das Reale des Lichts wissen wir gar nichts, null komma nichts.
Deshalb darf man nicht schreiben: Licht “ist” eine Welle. Was ist, ist eine metaphysische und keine physikalische Frage, Aber wegen der sehr schönen Darstellung des Lichts, wie man es im physkalisch modellhaften Kontext verstehen muß, ist Herrn Pössel das zu verzeihen. Wir wissen ja wie es gemeint ist.
Grüße
Fossilium
Licht ist real, weil es Energie entält und diese Energie an ein anderes Objekt abgeben kann. Lichtquanten sind möglicherweise Konstrukte, allerdings Konstrukte mit einem realen Hintergrund, denn ein Lichtquant ist mit einer Energiemenge korreliert.
Zitat:
. Sollte dieser Satz behaupten, es gäbe etwas Reales hinter dem Licht, das wir nur noch nicht kennen und das etwas anderes als ein Lichtquant oder eine Welle ist, so ist er wohl falsch. Vielmehr gilt: Licht ist etwa reales (physikalisch real und im Sinne der materialistischen Ontologie real), weil Licht mit anderen Objekten interagieren und dabei Energie austauschen kann. Die Beschreibung von Licht als Lichtquant oder Welle ist die beste Beschreibung, die es im Moment für Licht gibt und es gibt keinen Bedarf für eine noch bessere Beschreibung.
Hier etwas was zwar nicht direkt mit Licht zu tun hat, aber (u.a.) mit Wellen. Bei den Videos ist es nicht leicht dem Englisch zu folgen. Wenn man unterhalb (rot unterstrichen) Untertitel anklickt geht’s besser (und ggfls. das Video anhalten um den Text langsam zu lesen).
Dieses Video https://www.youtube.com/watch?v=WIyTZDHuarQ schaute ich mir gestern Abend an — i.V.m. diesem Artikel: http://nerdist.com/pilot-wave-theory-video-will-make-you-totally-rethink-quantum-mechanics/.
Heute Morgen dieses: https://www.youtube.com/watch?v=KJDEsAy9RyM — i.V.m. mit diesem Artikel: http://www.sciencealert.com/these-bouncing-droplets-behave-strangely-like-quantum-particles?
Und das (auch vorhin gelesen) passt ja irgendwie dazu: https://www.sciencenews.org/blog/context/why-quantum-mechanics-might-need-overhaul.
… Zu der Frage aus meinem post weiter oben was man sich unter einem Wellenquadrat vorzustellen hat ist wohl das https://de.wikipedia.org/wiki/Bornsche_Wahrscheinlichkeitsinterpretation eine Erläuterung.
Was ist eigentlich Licht?
31. Oktober 2016| Von Markus Pössel
Licht ist auch ein Grundsätzlicher Pfeiler in der Relativitätstheorie den die Astronomie nicht vernachlässigen darf.
Licht verkürzt den Raum.
In der Nähe großer Massen wird Licht abgelenkt.
Licht ist verräterisch.
Licht richtig angewandt und die RT schmilzt dahin wie Eis in der Sonne.
In der Lichtuhr spielt es eine sehr große Rolle.
Wann darf man mit einer Aufklärung über die Lichtuhr rechnen?
Reiner Bergner schrieb (20. November 2016 @ 18:57):
> […] In der Lichtuhr spielt es
… Licht; Signalaustausch, unter besonderer Berücksichtigung der Signalfront …
> eine sehr große Rolle. Wann darf man mit einer Aufklärung über die Lichtuhr rechnen?
In diesem SciLog wurde doch unter dem Stichwort „LIGO“ einigermaßen umfänglich von Beteiligten („Enden“, „Spiegeln“) berichtet, die ihre Anzeigen gegenseitig beobachteten und Feststellungen hinsichtlich der Koinzidenz bzw. Nicht-Koinzidenz der entsprechenden „Pings“ machten.
Es wurde insbesondere betrachtet (und in diversen Kommentaren aufgegriffen), dass solche zwischen (mindestens) drei (oder mehr) Beteiligten feststellbare „Ping-Koinzidenz“-Beziehungen veränderlich sein können.
Welche Art von „ Aufklärung über die Lichtuhr“ wäre denn darüber hinaus überhaupt vorstellbar??
Frank Wappler schrieb (5. Dezember 2016 @ 16:02):
„In diesem SciLog wurde doch unter dem Stichwort „LIGO“ einigermaßen umfänglich von Beteiligten („Enden“, „Spiegeln“) berichtet, die ihre Anzeigen gegenseitig beobachteten und Feststellungen hinsichtlich der Koinzidenz bzw. Nicht-Koinzidenz der entsprechenden „Pings“ machten.
Es wurde insbesondere betrachtet (und in diversen Kommentaren aufgegriffen), dass solche zwischen (mindestens) drei (oder mehr) Beteiligten feststellbare „Ping-Koinzidenz“-Beziehungen veränderlich sein können.“
Na dann, wenn LIGO auch die Lichtuhr erklärt ist die SRT ja bestens bestätigt. Endlich muss ich mir keine Kopfschmerzen mehr machen.
Frank schreibt weiterhin:
„Welche Art von „ Aufklärung über die Lichtuhr“ wäre denn darüber hinaus überhaupt vorstellbar??“
Lieber Frank, ich darf doch Frank sagen, über das Licht und die Lichtuhr gibt es noch sehr viel Aufklärungsbedarf. Ist wirklich schon alles gesagt und erörtert?
Wie funktioniert denn die berühmte Lichtuhr? Der Aufbau ist bekannt, zwei Spiegel und zwischen diesen eine Strecke die das Licht in einer Sekunde überwindet. Bewegt sich diese Lichtuhr mit hoher Geschwindigkeit entsteht dieses berühmte Dreieck, wenn das Licht wieder am unteren Spiegel ankommt. Soweit so gut. So die Theorie.
Lassen wir den immer im Dienst stehenden Beobachter beobachten. Das Experiment startet, das Licht geht nach oben – während dieser Zeit bewegt sich die Uhr nach rechts – das Licht kommt oben an und der Spiegel ist nicht mehr da, weil er sich nach rechts bewegt hat. Wie kommt nun das Dreieck zustande? Diese Grundlage zur Berechnung der Zeitdehnung ist schon mal nicht gegeben.
Nur ein Beispiel von weiteren die die Lichtuhr in einem anderen Licht erscheinen lassen.
Reiner Bergner schrieb (5. Dezember 2016 @ 19:02):
> […] Wie funktioniert denn die berühmte Lichtuhr?
Vor allem so wie jede/irgendeine Lichtuhr:
zwei unterscheidbare Beteiligte/Beobachter/Enden („A“ und „B“) sollen einander beobacht haben, wobei jeder der beiden die jeweiligen Ping-Echos des anderen wahrnahm;
d.h. hinsichtlich jeder bestimmten (Signal-)Anzeige, die von A dargestellt wurde, nahm A wahr, dass B diese (Signal-)Anzeige As wahrgenommen hatte.
Sofern hinsichtlich einer bestimmten (Signal-)Anzeige, die von A dargestellt wurde, eventuell mehrere verschiedene Wahrnehmungen As von eventuell mehreren verschiedenen Wahrnehmungen Bs dieser (Signal-)Anzeige As gesammelt wurden, geht es im Folgenden stets um die jeweils allererste; d.h. um Wahrnehmungen der Signalfront, um Pingechos.
Und natürlich können A und B ihren Anzeigen ganz beliebige Koordinatenwerte „t“ zuordnen. Um beide zusammen aber als eine (gemeinsame) Uhr aufzufassen, sollen A bzw. B insbesondere aufeinanderfolgenden Ping-Echos zählen (deren Werte zumindest eng miteinander zusammenhängen).
Womöglich ist „die berühmte“ Lichtuhr aber durch noch darüber hinausgehende Anforderungen gekennzeichnet, die noch aufzuklären bleiben:
> Der Aufbau ist bekannt, zwei Spiegel und zwischen diesen eine Strecke die das Licht in einer Sekunde überwindet.
Das soll wohl konkret bezogen auf eine Lichtuhr (entsprechend der obigen allgemeinen Beschreibung) bedeuten,
– dass As Pingdauern (d.h. bzgl. der Echos von B) alle gleich (also konstant) sein müssten;
nämlich „2 Sekunden“,
– dass Bs Pingdauern (d.h. bzgl. der Echos von A) alle gleich (also konstant) sein müssten;
nämlich „2 Sekunden“,
– dass As Pingdauern (d.h. bzgl. der Echos von B) und Bs Pingdauern (d.h. bzgl. der Echos von A) einander gleich sein müssten; nämlich „2 Sekunden“.
(Derartige Anforderungen, „chronometrische Starrheit“, setzen offenbar voraus, dass definiert wäre, wie Dauern überhaupt miteinander zu vergleichen sind; sowohl hinsichtlich jeweils eines Beteiligten, als auch von mehreren Beteiligten untereinander …)
> Bewegt sich diese Lichtuhr mit hoher Geschwindigkeit […]
(Nun geht es offenbar sogar um die Beziehungen zwischen mehreren geeigneten Systemen, jeweils bestehend aus hinreichend vielen Beteiligten/Beobachtern/Enden, die unter sich chronometrisch starr sein sollten …)
> entsteht dieses berühmte Dreieck, wenn das Licht wieder am unteren Spiegel ankommt. Soweit so gut.
Vgl. wohl etwa https://de.wikipedia.org/wiki/Zeitdilatation#Lichtuhr
> Lassen wir den immer im Dienst stehenden Beobachter beobachten.
Wieso nur „den (einen) Beobachter“ ??
Es ist doch wohl jedem der unterscheidbaren Beteiligten (sowohl den ausdrücklich genannten A und B, als auch den offenbar zahlreichen erforderlichen nicht ausdrücklich genannten) zuzugestehen zu beobachten; also Wahrnehmungen zu sammeln und sich zu merken, und diesbezüglich insbesondere Koinzidenzurteile zu fällen.
> Das Experiment startet, das Licht geht nach oben
Die Formulierung, dass „Licht geht“, weckt womöglich unzutreffende Assoziationen.
(Ebenso wie die Linien, die in den Skizzen der berühmten Dreiecke deren Ecken verbinden.)
Schließlich lässt sich hinsichtlich des (bloßen) Austauschs eines Signals nichts „beim Gehen beobachten“; grundsätzlich anders als ein Beteiligter/Beobachter/Lichtuhr-Spiegel, dessen Anzeigen durchwegsbeobachtbar sind.
Deshalb richtiger:
Das Experiment startet, A stellt die erste (Signal-)Anzeige dar;
A und/oder B werden von allerlei weiteren, nicht näher benannten Beteiligten passiert
(von denen wiederum jeder seinerseits feststellt: „A bzw. B hat mich passiert“).
Für das Folgende seien zwei bestimmte dieser „passierenden“ Beteiligten benannt und in ihren Beziehungen untereinander und gegenüber A bzw. B genauer festgelegt:
P und Q seien durchwegs chronometrisch starr gegenüber einander;
P passierte A genau zum Start des Experiments, d.h. so dass A_P (d.h. As Anzeige der Passage Ps) die erste (Signal-)Anzeige darstellte;
und Q passierte B so dass Q_B (d.h. Qs Anzeige der Passage Bs) und P_A (d.h. Ps Anzeige der Passage As) gleichzeitig waren.
(Das bezieht sich natürlich auf Einsteins Definition zur Feststellung von Gleichzeitigkeit oder Ungleichzeitigkeit von Anzeigen einzelner Beteiligter.)
> das Licht kommt oben an und der Spiegel ist nicht mehr da, weil er sich nach rechts bewegt hat.
Sicherlich kann auch Q die betreffende Anzeige A_P zum Start des Experiments wahrnehmen
(und in Koinzidenz damit auch die Anzeige P_A, also das Startereignis E_AP insgesamt);
nennen wir diese Anzeige Qs ausdrücklich Q_sah_AP.
Wesentlich ist: Qs Anzeigen Q_B und Q_sah_AP sind nicht die selbe, sondern verschiedene;
Q_B war vor Q_sah_AP.
(Das ist eine Konsequenz der beschriebenen Versuchsanordnung, unter Zugrundelegung der genannten Messdefinitionen.)
In anderen Worten: Ja, der Spiegel B war „da schon weg“.
> Wie kommt nun das Dreieck zustande?
Na: B kann und muss doch trotzdem die Anzeige A_P (und das Startereignis E_AP insgesamt) wahrgenommen haben.
Die Versuchsanordnung fordert doch insbesondere, dass A und B hinsichtlich des Starts des Experiments eine Lichtuhr bildeten; also ausdrücklich „dass A sah dass B sah dass A_P“.
> Diese Grundlage zur Berechnung der Zeitdehnung ist […]
Das ist ein leider immer noch verbreiteter Irrtum. Nein: dieses Gedankenexperiment verbunden mit der bekannten Berechnung eines Pythagoräischen (flachen, rechtwinkligen) Dreiecks ist stattdessen die Grundlage zum Vergleich von chronometrischen Distanzen „quer zur Achse“;
hier also zur konkreten Berechnung, dass die Distanz PQ gleich der Distanz AB ist.
(Dabei wird die bekannte Dilatationsbeziehung benutzt und vorausgesetzt; die ihrerseits zuerst „entlang der Achse“ herzuleiten ist.)
Frank Wappler
6. Dezember 2016 @ 15:33
Frank meint die Lichtuhr der RT funktioniert so wie jede/irgendeine Lichtuhr. Frank, es gibt nur eine einzige Lichtuhr nämlich die die aus einem Gedankenexperiment hervorgegangen ist und die plausibel die Zeitdehnung erklären soll. Frank ist der Meinung, dass Gedankenexperiment der Lichtuhr benötigt unbedingt zwei oder mehrere Beobachter, aber laut RT gibt es nur einen Beobachter der seine subjektive Eindrücke uns als wahres Geschehen verkaufen will.
Wohlgemerkt: Ein Gedankenexperiment und dazu noch subjektiv wird als Tatsache ausgelegt. Können wir uns auf nur einen Beobachter einigen?
Herr Pössel schreibt zur Lichtuhr:
„Lichtuhr:
Hypothetische Uhr, bei der hin- und herlaufendes Licht als Taktgeber dient. Die Konstanz der Lichtgeschwindigkeit stellt dabei sicher, dass solch eine Uhr gleichmäßig tickt.“ (http://www.einstein-online.info/lexikon/lichtuhr)
Weitere Anforderungen werden weder von Einstein noch anderen physikalischen Experten an die Lichtuhr gestellt.
Frank schreibt: „Das soll wohl konkret bezogen auf eine Lichtuhr (entsprechend der obigen allgemeinen Beschreibung) bedeuten.“
Allgemeine Beschreibung, mmm, Es geht um die spezielle Relativitätstheorie. Für das große Publikum ist die Aufklärung über die RT immer und in allen Varianten allgemein beschrieben.
Frank schreibt: „(Nun geht es offenbar sogar um die Beziehungen zwischen mehreren geeigneten Systemen, jeweils bestehend aus hinreichend vielen Beteiligten/Beobachtern/Enden, die unter sich chronometrisch starr sein sollten …)“
Die Rede ist von einer Lichtuhr.
Frank Schreibt: „Die Formulierung, dass „Licht geht“, weckt womöglich unzutreffende Assoziationen.“
Frank, ich halte mich in meiner Kritik immer an die Vorgaben der RT. Zitate entnehme ich nicht irgendwelchen Parallelwelten sondern siehe z.B. oben das Zitat vom Herrn Pössel.
Frank schreibt: „In anderen Worten: Ja, der Spiegel B war „da schon weg“.“
Frank, Ihre Bestätigung macht mir Hoffnung.
Frank Schreibt: „> Diese Grundlage zur Berechnung der Zeitdehnung ist […]
Das ist ein leider immer noch verbreiteter Irrtum. Nein: dieses Gedankenexperiment verbunden mit der bekannten Berechnung eines Pythagoräischen (flachen, rechtwinkligen) Dreiecks ist stattdessen die Grundlage zum Vergleich von chronometrischen Distanzen „quer zur Achse“;
hier also zur konkreten Berechnung, dass die Distanz PQ gleich der Distanz AB ist.“
Leider kein Irrtum, diverse Versuchserklärungen zur Lichtuhr behaupten immer die Seite b des Dreiecks ist länger als die naturgegebene Senkrechte die der Lichtimpuls beschreibt. Davon wird die Zeitdehnung abgeleitet.
Frank schreibt: „(Dabei wird die bekannte Dilatationsbeziehung benutzt und vorausgesetzt; die ihrerseits zuerst „entlang der Achse“ herzuleiten ist.)“
Die Zeitdehnung folgt aus den Gedankenexperimenten und ist nicht schon vorher da.
Reiner Bergner schrieb (7. Dezember 2016 @ 19:59):
> ich halte mich in meiner Kritik immer an die Vorgaben der RT.
Wissenschaft beinhaltet aber das Aneignen, Erarbeiten und Weitergeben von Wissen.
Es geht um das Nachvollziehbarmachen von Inhalten, nicht das bloße Nachplappern von Phrasen.
Daraus entspringt die Auseinandersetzung damit, was überhaupt damit gemeint sein soll „sich an die Vorgaben der RT zu halten“; ja auch darüber, was vorausgesetzt und begriffen sein müsste, um sich überhaupt „an etwas zu halten“.
> Zitate entnehme ich nicht irgendwelchen Parallelwelten […]
Übrigens findet sich das Wort „Lichtuhr“ in Einsteins eigenen Schriften offenbar nicht vor dem Jahre 1913 …
> Herr Pössel schreibt zur Lichtuhr: […]
(Ich würde es vorziehen, wenn Herr Pössel seine eventuellen Ansichten zum Thema „Lichtuhr“ selbst so zum Ausdruck bringen würde, dass sie sich öffentlich und ausfindbar kommentieren lassen; insbesondere in Form eines SciLog-Beitrags, da er offenbar das Privileg genießt, solche zu veröffentlichen. Aber, ach! … &)
Daran ist zu bemängeln, dass suggeriert wird, Lichtsignale würden („von einer Takt-Anzeige zur anderen“) beobachtbar laufen; etwa so wie eine angestoßene grellrote Billiardkugel über das Tischtuch laufen würde.
Und es ist fraglich, wieso die Forderung erhoben würde, dass „ solch eine Uhr gleichmäßig tickt“ (entsprechend einer bestimmten geeigneten Definition, wie die betreffende „Gleichmäßigkeit“ zu messen wäre); schließlich sind nicht alle Uhren zwangsläufig gute Uhren.
Und falls im diesem Zusammenhang zu lesen stünde: …
… würde ich zustimmen und hervorheben, dass sich das anhand des Lichtuhr-Gedankenexperiments zeigen lässt.
> […] Können wir uns auf nur einen Beobachter einigen?
Nein: eine Lichtuhr-Versuchsanordnung umfasst (mindestens) zwei unterscheidbare Beteiligte/Spiegel, und ich möchte keinem davon von vornherein alle beobachterischen Fähigkeiten gänzlich absprechen bzw. gegenüber irgendeinem die Fragestellung von vornherein ausschließen, was ich „an dessen gedankenexperimenteller Stelle“ wahrgenommen hätte.
Frank Wappler, (8. Dezember 2016 @ 11:55)
Frank schreibt: „Reiner Bergner schrieb (7. Dezember 2016 @ 19:59):
> ich halte mich in meiner Kritik immer an die Vorgaben der RT.
Wissenschaft beinhaltet aber das Aneignen, Erarbeiten und Weitergeben von Wissen.
Es geht um das Nachvollziehbarmachen von Inhalten, nicht das bloße Nachplappern von Phrasen.
Daraus entspringt die Auseinandersetzung damit, was überhaupt damit gemeint sein soll „sich an die Vorgaben der RT zu halten“; ja auch darüber, was vorausgesetzt und begriffen sein müsste, um sich überhaupt „an etwas zu halten“.“
Genau mein Anliegen. Kritik an der RT üben heißt doch nicht, dass ich z. B. die „Flache Erde Theorie“ studiere, aneigne, erarbeite und weitergebe. Von nachplappern kann schon gar keine Rede sein. Frank mir drängt sich eher der Verdacht auf, dass Sie nicht ganz über die RT informiert sind. Da spüre ich einen verzweifelten Versuch den Überblick über die z. B. vielen Beobachter usw. zu behalten.
Es geht auch nicht darum ob und wann Einstein die „Lichtuhr“ und andere Gedankenexperimente öffentlich machte sondern im Moment ganz allein um die Lichtuhr. Als Einstein sein großes epochales Werk in den „Annalen der Physik“ veröffentlichte wusste er noch nichts vom Zwillingsparadoxon und all den anderen Paradoxa.
Frank schreibt: „(Ich würde es vorziehen, wenn Herr Pössel seine eventuellen Ansichten zum Thema „Lichtuhr“ selbst so zum Ausdruck bringen würde, dass sie sich öffentlich und ausfindbar kommentieren lassen; insbesondere in Form eines SciLog-Beitrags, da er offenbar das Privileg genießt, solche zu veröffentlichen. Aber, ach! … &)“
Mein Zitat zur Lichtuhr ist die Ansicht von Herrn Pössel.
Frank schreibt: „…schließlich sind nicht alle Uhren zwangsläufig gute Uhren.“
Sämtliche Uhren einschließlich der einen Lichtuhr der RT sind sehr gute Uhren. Sie weisen eine hohe Ganggenauigkeit auf und sind bis in alle Ewigkeit verlässlich. Also brauchen wir uns nicht mit solchen Kleinigkeiten auseinander zu setzen.
Frank schreibt: „ Über Abstände senkrecht zur Bewegungsrichtung, so lässt sich zeigen, sind sich relativ zueinander bewegte Beobachter auch in der Speziellen Relativitätstheorie einig.“
Die Senkrechte zur Bewegungsrichtung spielt in der SRT keine Rolle.
Kommen wir noch einmal zum nachplappern: Sie, sowie alle Anhänger, Kritiker und Neutrale plappern alle nach, wenn die Lichtuhr überzeugend die Zeitdehnung darstellen soll. Statt das der Lichtimpuls senkrecht nach oben geht wird geglaubt, dass der Impuls nach rechts oben (Seite b des Dreiecks) dem Spiegel hinterher läuft obwohl der Spiegel längst weg ist. Niemand begreift aber, dass durch die hohe Bewegung die Grundlinie a des Dreiecks kleiner wird. Außer der Zeitdehnung die die Uhr nachweist und erfährt, entsteht auch eine Längenverkürzung. Wenn die Grundlinie a kürzer wird erfährt die Seite b auch eine Veränderung und wird dadurch kürzer in seiner Diagonale.
Und es wird nur ein Beobachter benötigt für dieses Gedankenexperiment. Er kann die Uhr in Ruhe genau studieren und für die sich bewegende Uhr genügt der eine Beobachter, wenn er fertig ist die ruhende Uhr zu studieren. Wenigstens werden dadurch die Personalkosten reduziert. Wissenschaft braucht auch Geld.
Reiner Bergner schrieb (8. Dezember 2016 @ 19:46):
> […] die Grundlinie a des Dreiecks
Es wäre wirklich sehr hilfreich, die Ecken dieses zu betrachtenden Dreiecks ausdrücklich und unterscheidbar zu benennen. (Etwa so: https://commons.wikimedia.org/wiki/Category:Triangles#/media/File:Angulo_Triangulo_Isosceles_Demonstra%C3%A7ao.svg )
Damit sind allein schon mindestens drei verschiedene Ecken/Enden/Beteiligte/Beobachter benannt (im verlinkten Bild „A“, „B“ und „C“);
es ist darin sogar ein bestimmter weiterer Beteiligter/Beobachter von Interesse („M“) benannt.
Diese vier Beteiligten/Beobachter sollen sicherlich gegenüber einander starr sein und bleiben (und sogar: gegenüber einander ruhen);
ihre Entfernungsverhältnisse untereinander sollen konstant bleiben
(deshalb kann man diese Entfernungsverhältnisse auch „Abstandsverhältnisse“ nennen);
und sie sind als System durch (fünf) Abstandsverhältnisse untereinander charakterisiert.
Und nun könnten wir und sogar noch weitere Beteiligte/Beobachter vorstellen; z.B. eine „Blitzlichtfotoapparat F“ und ein „Rundsichtradargerät G“, die untereinander starr sein sollen, aber nicht gegenüber A, B, C, M …
> Sämtliche Uhren einschließlich der einen Lichtuhr der RT sind sehr gute Uhren.
Ganz offensichtlich nicht:
eine Uhr, die „tickt“, aber nicht ausdrücklich „nicht gleichmäßig tickt“, ist trotzdem eine Uhr.
p.s.
Als Einstein sein großes epochales Werk in den „Annalen der Physik“ veröffentlichte wusste er noch nichts vom Zwillingsparadoxon
Aber ganz ausdrücklich von bestimmten „eigentümlichen Konsequenzen“.
Reiner Bergner schrieb (8. Dezember 2016 @ 19:46):
> […] die Grundlinie a des Dreiecks
Es wäre wirklich sehr hilfreich, die Ecken dieses zu betrachtenden Dreiecks ausdrücklich und unterscheidbar zu benennen. (Etwa so: https://commons.wikimedia.org/wiki/Category:Triangles#/media/File:Angulo_Triangulo_Isosceles_Demonstra%C3%A7ao.svg )
Damit sind allein schon mindestens drei verschiedene Ecken/Enden/Beteiligte/Beobachter benannt (im verlinkten Bild „A“, „B“ und „C“);
es ist darin sogar ein bestimmter weiterer Beteiligter/Beobachter von Interesse („M“) benannt.
Diese vier Beteiligten/Beobachter sollen sicherlich gegenüber einander starr sein und bleiben (und sogar: gegenüber einander ruhen);
ihre Entfernungsverhältnisse untereinander sollen konstant bleiben
(deshalb kann man diese Entfernungsverhältnisse auch „Abstandsverhältnisse“ nennen);
und sie sind als System durch (fünf) Abstandsverhältnisse untereinander charakterisiert.
Und nun könnten wir und sogar noch weitere Beteiligte/Beobachter vorstellen; z.B. eine „Blitzlichtfotoapparat F“ und ein „Rundsichtradargerät G“, die untereinander starr sein sollen, aber nicht gegenüber A, B, C, M …
> Sämtliche Uhren einschließlich der einen Lichtuhr der RT sind sehr gute Uhren.
Ganz offensichtlich nicht:
eine Uhr, die „tickt“, aber nicht ausdrücklich „nicht gleichmäßig tickt“, ist trotzdem eine Uhr.
p.s.
> Als Einstein sein großes epochales Werk in den „Annalen der Physik“ veröffentlichte wusste er noch nichts vom Zwillingsparadoxon
Aber ganz ausdrücklich von bestimmten „eigentümlichen Konsequenzen“.
Reiner Bergner schrieb (8. Dezember 2016 @ 19:46):
> […] die Grundlinie a des Dreiecks
Es wäre wirklich sehr hilfreich, die Ecken dieses zu betrachtenden Dreiecks ausdrücklich und unterscheidbar zu benennen. (Etwa so: https://commons.wikimedia.org/wiki/Category:Triangles#/media/File:Angulo_Triangulo_Isosceles_Demonstra%C3%A7ao.svg )
Damit sind allein schon mindestens drei verschiedene Ecken/Enden/Beteiligte/Beobachter benannt (im verlinkten Bild „A“, „B“ und „C“);
es ist darin sogar ein bestimmter weiterer Beteiligter/Beobachter von Interesse („M“) benannt.
Diese vier Beteiligten/Beobachter sollen sicherlich gegenüber einander starr sein und bleiben (und sogar: gegenüber einander ruhen);
ihre Entfernungsverhältnisse untereinander sollen konstant bleiben
(deshalb kann man diese Entfernungsverhältnisse auch „Abstandsverhältnisse“ nennen);
und sie sind als System durch (fünf) Abstandsverhältnisse untereinander charakterisiert.
Und nun könnten wir und sogar noch weitere Beteiligte/Beobachter vorstellen; z.B. eine „Blitzlichtfotoapparat F“ und ein „Rundsichtradargerät G“, die untereinander starr sein sollen, aber nicht gegenüber A, B, C, M …
> Sämtliche Uhren einschließlich der einen Lichtuhr der RT sind sehr gute Uhren.
Ganz offensichtlich nicht:
eine Uhr, die „tickt“, aber ausdrücklich „nicht gleichmäßig tickt“, ist trotzdem eine Uhr.
p.s.
> Als Einstein sein großes epochales Werk in den „Annalen der Physik“ veröffentlichte wusste er noch nichts vom Zwillingsparadoxon
Aber ganz ausdrücklich von bestimmten „eigentümlichen Konsequenzen“.
Frank Wappler, 9. Dezember 2016 @ 11:04
Frank schreibt: „> […] die Grundlinie a des Dreiecks
Es wäre wirklich sehr hilfreich, die Ecken dieses zu betrachtenden Dreiecks ausdrücklich und unterscheidbar zu benennen. (Etwa so: https://commons.wikimedia.org/wiki/Category:Triangles#/media/File:Angulo_Triangulo_Isosceles_Demonstra%C3%A7ao.svg )“
??? Ein Dreieck? – ist ein Dreieck spätestens bekannt seit Pythagoras und hat sich seitdem nicht mehr verändert. Es hat drei Ecken die beliebig bezeichnet werden dürfen, man hat sich im Lauf der Zeit auf die Ecken A – B – C geeinigt. Dementsprechend sind die gegenüberliegenden Seiten mit den Bezeichnungen a – b – c belegt worden. Drei Winkel bleiben übrig, aber kein mittlerer Buchstabe mehr, deshalb mussten die griechischen Buchstaben herhalten α – β – γ. Die Bezeichnungen der Ecken, Seiten und Winkel sind keine Beobachter sondern nur Punkte die beobachtet werden.
Frank schreibt: „…ihre Entfernungsverhältnisse untereinander sollen konstant bleiben“
Es gibt nur eine Konstante in der RT ohne die die RT nicht funktioniert.
Ich bleibe auch dabei, dass nur ein Beobachter für das jeweilige Gedankenexperiment nötig ist.
Frank, auch wenn Sie vehement bestreiten, dass die Uhren der RT keine sehr guten und präzisen Uhren sind, glaube ich kaum, dass Einstein in seinen Gedankenexperimenten sich mit defekten Uhren herum geschlagen hat.
Was ist nun mit der Seite c des Dreiecks? Verkürzt es sich oder?
Reiner Bergner schrieb (9. Dezember 2016 @ 19:20):
> Ein Dreieck? – […]
> Es hat drei Ecken […] Punkte die beobachtet werden.
Wer beobachtbar und sogar von anderen unterscheidbar, identifizierbar ist, dem spreche ich nicht von vornherein und grundsätzlich ab, wiederum selbst beobachten zu können.
In der (gedankenexperimentellen Darstellung der) RT (und darüber hinaus) spricht man von “identifizierbaren materiellen Punkten“,
Beteiligten “wie du und ich”,
in die man sich (natürlich einzeln, abwechselnd) “hineinversetzen kann”.
> Ich bleibe auch dabei, dass nur ein Beobachter für das jeweilige Gedankenexperiment nötig ist.
Damit fehlt eine unverzichtbare Voraussetzung zum Verständnis von Gedankenexperimenten im Allgemeinen, und des gedankenexperimentellen Zugangs zur RT insbesondere.
> Frank, auch wenn Sie vehement bestreiten, dass die Uhren der RT keine sehr guten und präzisen Uhren sind
Was ich vehement bestreite ist, dass “gute Uhren” (bzw. insbesondere “Tick”-Anzeigen eines Beteiligten die “gleichmäßig” wären) überhaupt von solchen unterschieden werden könnten, die es nicht sind, wenn nicht nachvollziehbar gemacht würde, wie diese Unterscheidung als Messung auszuführen wäre, und dass die dazu erforderlichen Beobachtungsdaten im betreffenden Versuch gesammelt werden können.
Um Einstein dahingehend nochmals ausführlich zu zitieren:
> glaube ich kaum, dass Einstein in seinen Gedankenexperimenten sich mit defekten Uhren herum geschlagen hat.
Ich halte es durchaus für möglich, dass Einstein seiner eigenen Anforderung nicht immer gerecht geworden ist;
besonders hinsichtlich darauf, womit sich Einstein herumschlug, bevor er diese Anforderung überhaupt erstmals ausdrückte.
Frank Wappler, 10. Dezember 2016 @ 10:08
schrieb: Dreieck – Floskel, Floskel
schrieb: Beobachter – Floskel, Floskel
schrieb: Gedankenexperiment – Floskel, Floskel
schrieb: Uhren – Floskel, Floskel
schrieb: nichts zu den angesprochenen Fakten die der Lichtuhr
widersprechen.
Frank Wappler, 5. Dezember 2016 @ 16:02
…“ Welche Art von „ Aufklärung über die Lichtuhr“ wäre denn darüber hinaus überhaupt vorstellbar??“
Frank, ich lese auch Ihre Beiträge in anderen Themen und bin immer wieder erstaunt über welches Wissen Sie verfügen. Die Mathematik bereitet Ihnen keine Schwierigkeiten. Alle Achtung. Ich ziehe den imaginären Hut vor Ihnen. Chapeau! Eigentlich kann ich Ihnen nicht das Wasser reichen. Trotzdem bin ich erstaunt wenn nicht gar erschrocken über Ihre obige Frage. Jeder denkt: ah, Lichtuhr, na gut! Schon ist das Thema beendet. Es wird nicht gefragt warum der senkrechte Lichtimpuls plötzlich diagonal geht. Es wird nicht gefragt wo das imaginäre Dreieck herkommt. Es wird nicht gefragt warum der Beobachter den Lichtimpuls schräg verlaufen sieht. Es wird nicht gefragt warum der Beobachter keine Uhr in der Hand hält um die Zeit zu messen wann der Lichtimpuls oben ankommt. Es wird nicht gefragt verkürzt sich das imaginäre Dreieck in Bewegungsrichtung.
Es gibt da noch eine wesentliche Frage die da lautet: „Warum gibt es eine Zeitdehnung nach oben, wenn es doch laut Relativitätstheorie gar keine Auswirkung in der Senkrechten haben dürfte, sondern nur in Bewegungsrichtung?“
Nur ein paar Striche salopp und gedankenlos hingeworfen und die Lichtuhr ist fertig. Eine Lichtuhr die die Zeitdehnung bekräftigen soll und Sie fragen welche Aufklärung vorstellbar ist. Sie sehen welcher Aufklärungsbedarf noch besteht nicht nur hinsichtlich der Lichtuhr.
Im Internet gefunden:
Zitat:
…Bewegte Objekte erweisen sich im Vergleich zum Ruhezustand in Bewegungsrichtung als verkürzt. Senkrecht zur Bewegungsrichtung tritt keine Verkürzung auf. (http://www.e13.physik.tu-muenchen.de/Muellerb/Uebung/work.pdf)
Wenn aber senkrecht zur Bewegungsrichtung keine Verkürzung auftritt, dann darf auch keine Verlängerung auftreten.