Gravitationswellen-Nachweistechnik: Michelson-Interferometer
BLOG: RELATIV EINFACH

Auch wenn der Physik-Nobelpreis dieses Jahr in die Quantenphysik der kondensierten Materie ging: Die Gravitationswellenastronomie hat spätestens mit dem am 15. Juni 2016 bekanntgegebenen zweiten Nachweis der Gravitationswellen verschmelzender Schwarzer Löcher begonnen, und ich hatte in einigen jüngeren Blogbeiträgen bereits eine Reihe von Aspekten des Nachweises von Gravitationswellen besprochen: die Störungen, welche durch Erschütterungen des Erdbodens, bestimmte Quanteneigenschaften des Lichts und den Umstand, dass alle Bauteile eines Gravitationswellendetektors thermische Schwingungen ausführen zustandekommen, und zuletzt die Techniken, mit denen man Gravitationswellensignale (aber auch, viel allgemeiner, andere Signale) als Summe von Kosinuswellen betrachten und so unterschiedliche Frequenzbereiche getrennt untersuchen kann. In diesem Beitrag soll es um das Funktionsprinzip für Michelson-Interferometer gehen – von dieser Art, wenn auch ordentlich modifiziert, sind Detektoren wie LIGO oder VIRGO.
Die grundlegende Funktionsweise von Detektoren wie LIGO hatte ich bereits in Gravitationswellendetektoren: wie sie funktionieren (GW Teil 2) zusammengefasst und mit Animationen gezeigt, wie die von einer Gravitationswelle erzeugten rhythmischen Verzerrungen des Raums einen Detektor wie LIGO beeinflussen. In diesem Beitrag soll es darum gehen, wieweit ein Detektor von der einfachen Interferometer-Form, die ich dort behandelt hatte, abweicht – und was das für Konsequenzen hat.
Michelson-Interferometer
Fangen wir damit an, uns LIGO vereinfacht als Interferometer vorzustellen. In Gravitationswellendetektoren: wie sie funktionieren war ich auf dieses Konzept kurz eingegangen. In diesem Video hier wird kurz vorgeführt, wie ein ganz einfaches Michelson-Interferometer funktioniert, dessen Artverwandte man in vielen Physik-Sammlungen finden kann:
Zumindest in denjenigen Fällen, in denen die Verweildauer des Lichts im Interferometer deutlich kleiner ist als die Schwingungsdauer der Gravitationswelle, deren Einfluss nachgewiesen werden soll, kann man sich die Wirkung der Gravitationswelle auf den Detektor in guter Näherung so vorstellen, dass die Welle systematisch die Abstände der beiden äußeren Spiegel vom Strahlteiler verkleinert und vergrößert – analog dazu, wie es im Video mit der Stellschraube demonstriert wird.
(In Gravitationswellendetektoren: wie sie funktionieren [GW Teil 2] gehe ich darauf ein, dass der allgemeine Fall komplizierter ist und dabei auch der direkte Einfluss der Gravitationswelle auf das Licht eine Rolle spielt. Bei Detektoren mit größerer Licht-Verweildauer, etwa bei dem geplanten weltraumgestützten Detektor LISA, wird dieser Umstand wichtig.)
Reisende Wellen im Michelson-Interferometer
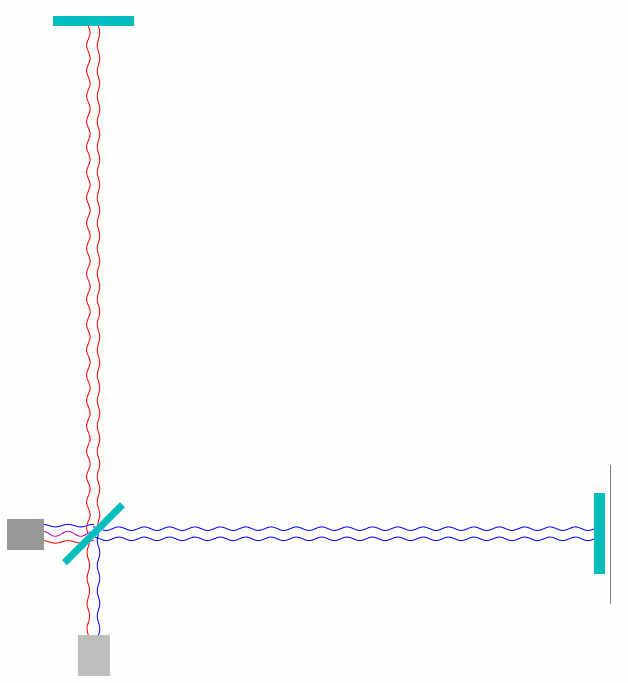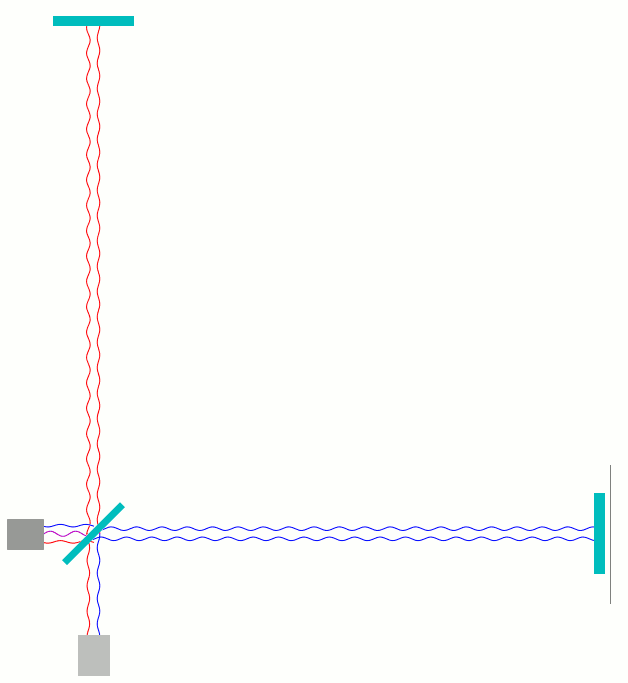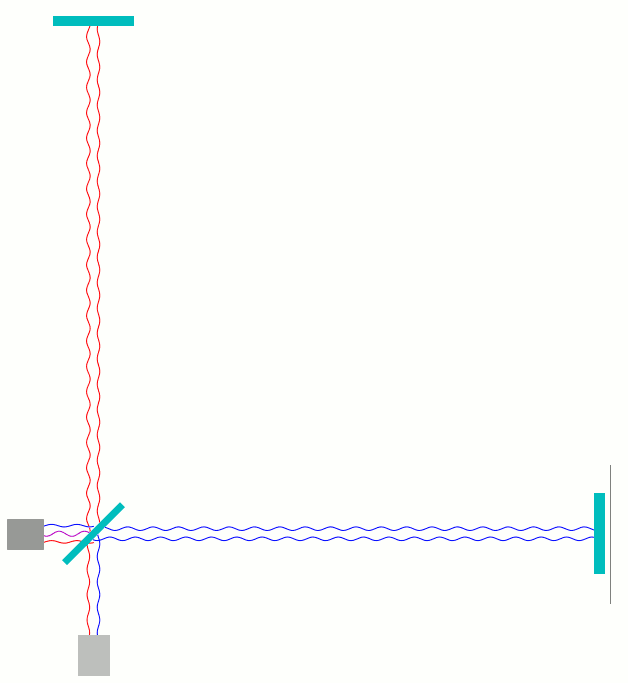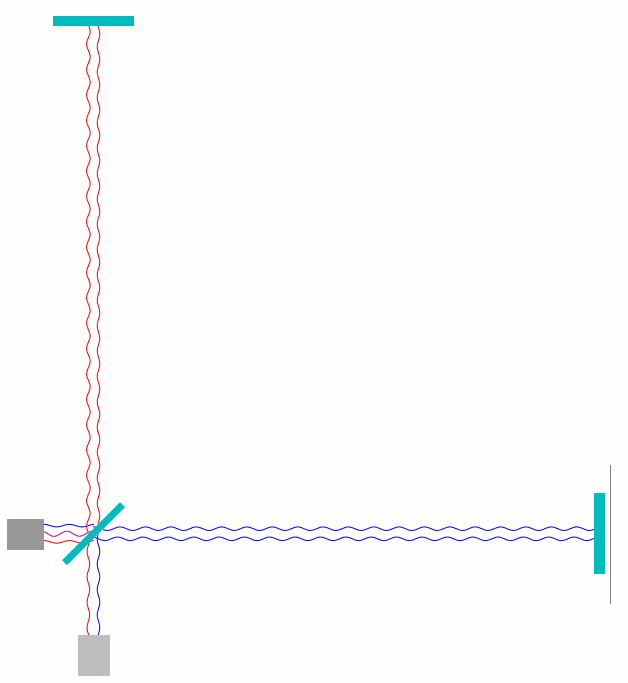
In den folgenden Animationen habe ich auf verschiedene Weisen dargestellt, was in einem solchen Michelson-Interferometer geschieht, wenn man einen der Spiegel näher zum Strahlteiler bewegt und anschließend wieder zurück. Die folgende Animation zeigt eine Beispielanordnung. Hier wie in den folgenden Animationen weiter unten gilt: ganz links als dunkelgraue Box dargestellt ist der Laser, der das Licht produziert; am Strahlteiler (schräggestellt, mittig) wird die Hälfte des Lichts zum oberen Spiegel gelenkt, die andere Hälfte geht ungestört weiter zum Spiegel rechts. Nach der Reflexion kommt das Licht wieder zum Strahlteiler. Ein Teil des Lichts läuft anschließend nach unten zum Photodetektor. Ein anderer Anteil läuft nach links zurück zum Laser: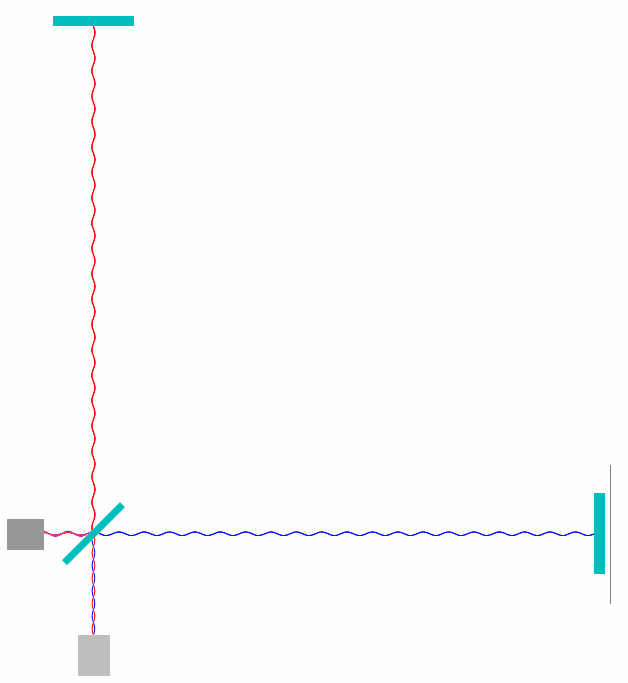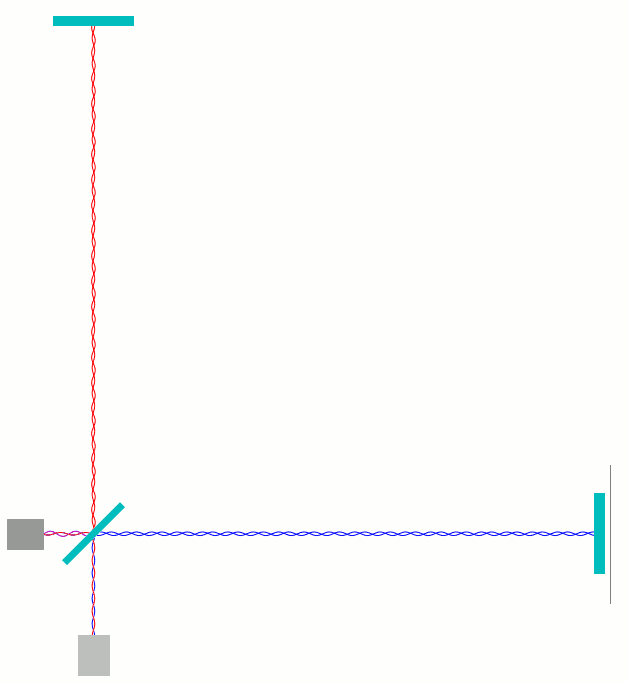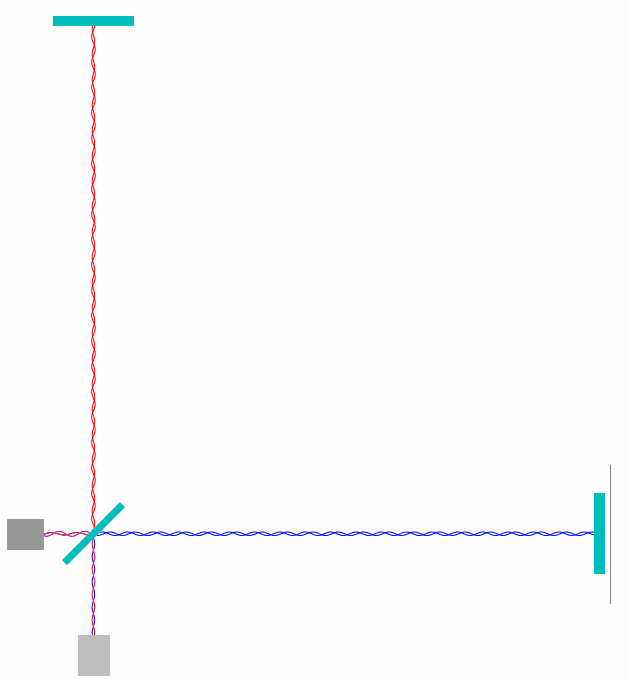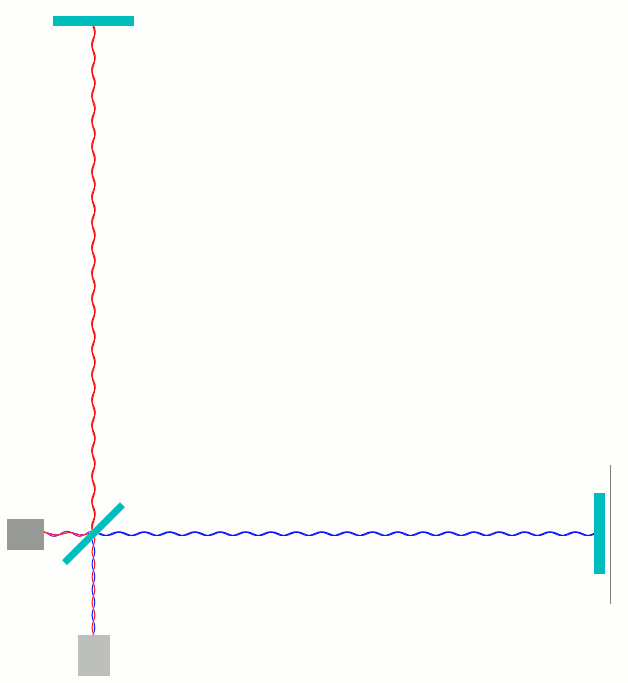
Was in dieser Animation und im folgenden am Photodetektor gemessen wird, ist übrigens nur der Mittelpunkt dessen, was in dem obigen MIT-Video die konzentrischen Ringe waren. Gravitationswellendetektoren sind extra so eingerichtet, dass nur jene Lichtanteile tatsächlich durch die Anordnung laufen, die der Phase in diesem Mittelpunkt entsprechen; die zusätzliche räumliche Struktur, die für die konzentrischen Ringe sorgt, entfällt in diesem Falle.
Einiges an meiner animierten Darstellung ist künstlich. Zum einen habe ich die Welle als Schwingung senkrecht zur Ausbreitungsrichtung dargestellt, mit Wellenbergen und -tälern. In Wirklichkeit ist die Welle, ist das, was da schwingt und sich als Schwingungsmuster ausbreitet, eine Eigenschaft des elektrischen (und des magnetischen) Felds entlang der eingezeichneten Lichtwege, keine Auslenkung einer “Wellenlinie” senkrecht zum Lichtweg. Meine Version dient lediglich der Illustration, wo sich jetzt gerade ein Wellenberg und wo sich ein Wellental befindet. Insbesondere direkt am Strahlteiler darf man diese Darstellung auch nicht allzu ernst nehmen; da ergeben sich durch das räumliche hin- und herschwingen einige unphysikalische Konfigurationen, die ich mithilfe des Strahlteiler-Rechtecks dezent verdeckt habe.
Ich habe die Wellenlinien außerdem unterschiedlich eingefärbt: Denjenigen Lichtanteil, der hinter dem Strahlteiler zunächst einmal nach rechts weiterläuft blau, den Anteil, der zum oberen Spiegel läuft, rot.
Um noch etwas deutlicher zu machen, wie die Wellenanteile hin- und herlaufen, habe ich die hin- und herlaufenden Anteile in der folgenden weiteren Animation künstlich (und wirklichkeitswidrig) jeweils etwas senkrecht zur Ausbreitungsrichtung gegeneinander verschoben:
Am und um den Strahlteiler ist diese Darstellung noch ungünstiger als die andere, aber zumindest auf dem Weg vom Strahlteiler zu den äußeren Elementen und hin zum Strahlteiler sieht man jetzt, welche Phase die Wellen haben, die da laufen. Insbesondere sieht man sehr deutlich, dass die roten und blauen Wellen, die vom Strahlteiler zum Photodetektor laufen, an jedem Ort entgegengesetzte Phasen haben – Wellenberg (hier: Auslenkung nach links) der einen Tei trifft auf Wellental (Auslenkung nach rechts) der anderen und umgekehrt.
Hier ist, etwas wirklichkeitsnäher, die Überlagerung der Signale vor und in den Armen dargestellt. Was jetzt noch an Auslenkungen zu sehen ist, zeigt, wieviel an Feld man in den betreffenden Regionen antrifft: 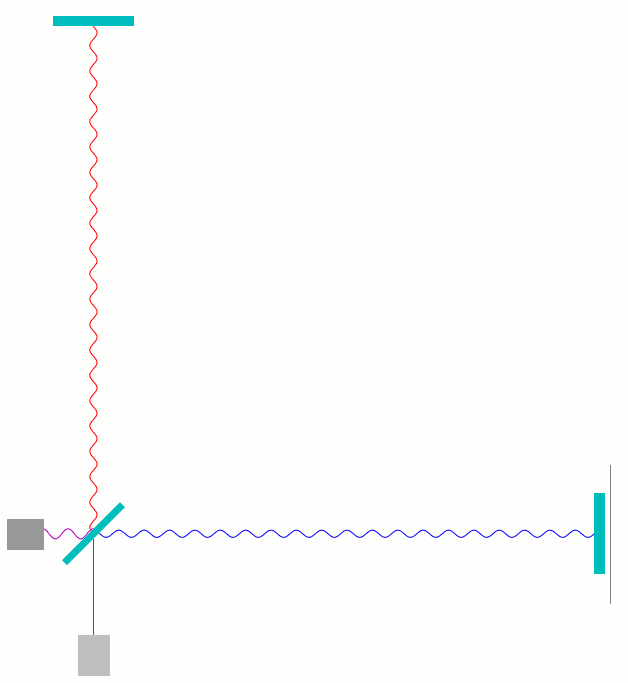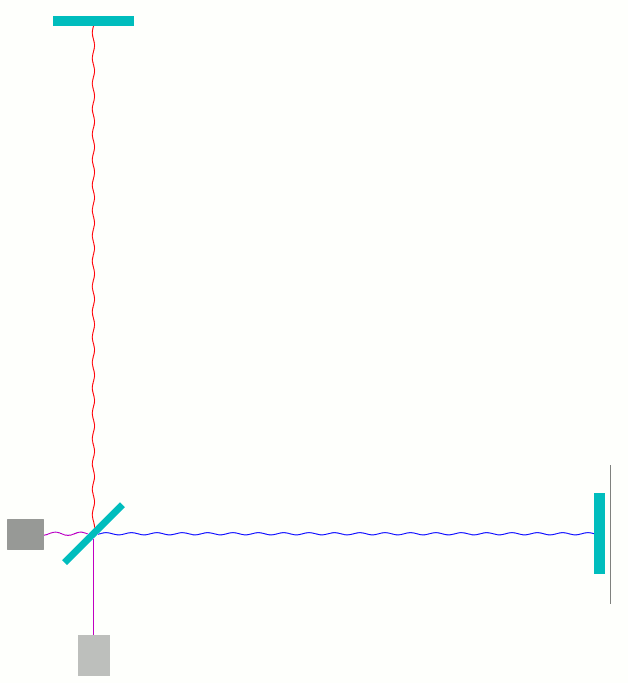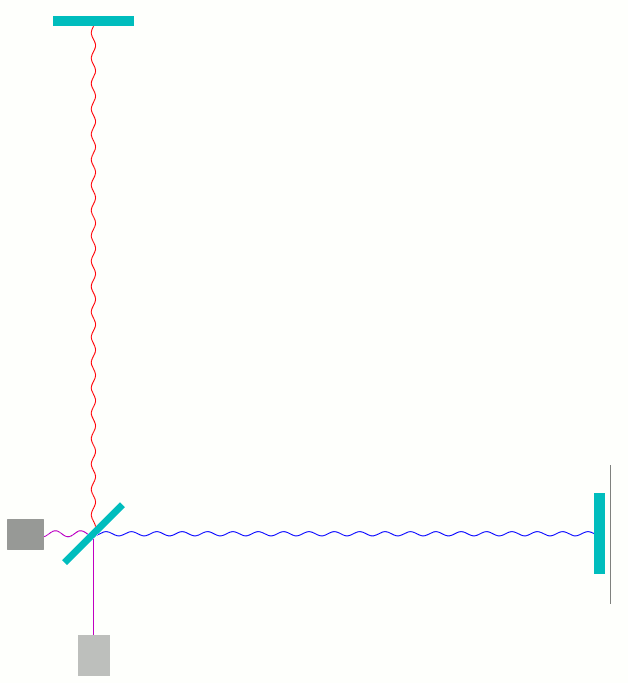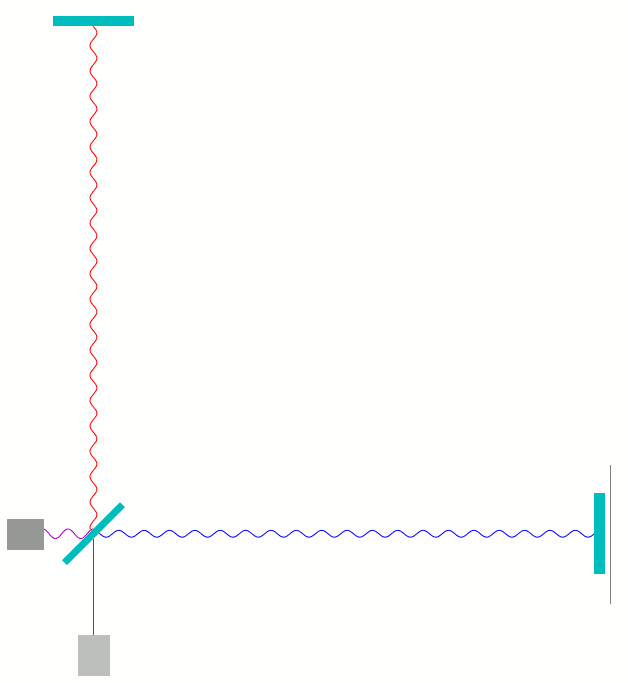
In diesem Falle ist die Länge des waagerechten Arms ein Viertel der Wellenlänge kürzer als die des senkrechten Arms. Da diese Länge zweimal durchlaufen wird, hat das Licht im waagerechten Arm eine halbe Wellenlänge weniger lang zu laufen als im senkrechten Arm. Wenn ein Wellenberg aus dem senkrechten Arm beim Strahlteiler ankommt, kommt dort gleichzeitig eine Wellenphase aus dem waagerechten Arm an, die eine halbe Wellenlänge weiter vorne liegt – also ein Wellental. Umgekehrt trifft ein Wellental aus dem senkrechten Arm auf einen Wellenberg aus dem waagerechten Arm. In der vorletzten Darstellung, wo in rot und blau die Einzelwellen zu sehen sind, war das gut zu erkennen: die rote Welle ist an jedem Ort gerade umgekehrt ausgelenkt wie die blaue Welle.
Wellenberg und Wellental löschen sich gegenseitig aus; deswegen kommt in diesem Falle bei der Überlagerung unten beim Detektor überhaupt nichts an: perfekte destruktive Interferenz.
Die Gesamtwelle ist die Summe beider Anteile. Die folgende grafische Darstellung zeigt, welche Wellenanteile (obere beide Grafiken) und welches Gesamtsignal aktuell (unterste Grafik) zu jedem Zeitpunkt am Photodetektor ankommen: 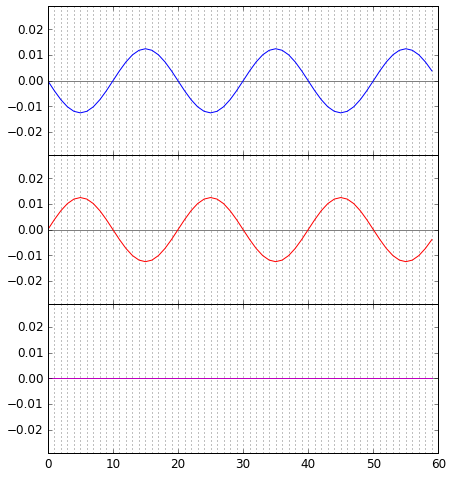 Wieder ist zu sehen: die Phasen der Welle, die den waagerechten Arm entlang gelaufen ist (blau) und der Welle, die den senkrechten Arm entlang gelaufen ist (rot) sind exakt entgegengesetzt; die Summe der Auslenkungen ist zu jedem Zeitpunkt null (lila Strich ganz unten).
Wieder ist zu sehen: die Phasen der Welle, die den waagerechten Arm entlang gelaufen ist (blau) und der Welle, die den senkrechten Arm entlang gelaufen ist (rot) sind exakt entgegengesetzt; die Summe der Auslenkungen ist zu jedem Zeitpunkt null (lila Strich ganz unten).
Konstruktive Interferenz im Michelson-Interferometer
Sobald wir einen der Spiegel im Vergleich zur vorigen Situation um eine viertel Wellenlänge des veränderten Laserlichts verschieben – bei der in LIGO und den anderen Gravitationswellendetektoren verwendeten Wellenlänge sind das weniger als 0,3 Millionstel Meter – ändert sich die Situation komplett. Schieben wir beispielsweise den rechten Spiegel um eine Viertel Wellenlänge vom Strahlteiler weg, dann ist die waagerechte Armlänge jetzt genauso lang wie die senkrechte Armlänge. Das Licht, das zum Photodetektor weiterläuft, hat dieselbe Phase, egal, ob es durch den senkrechten oder den waagerechten Arm gelaufen ist. Die Wellen addieren sich auf und verstärken sich. Hier ist dieses Szenario zunächst einmal in der Darstellung zu sehen, wo die Lichtwege etwas gegeneinander versetzt sind, so dass man hin- und heraufendes Licht besser unterscheiden kann:
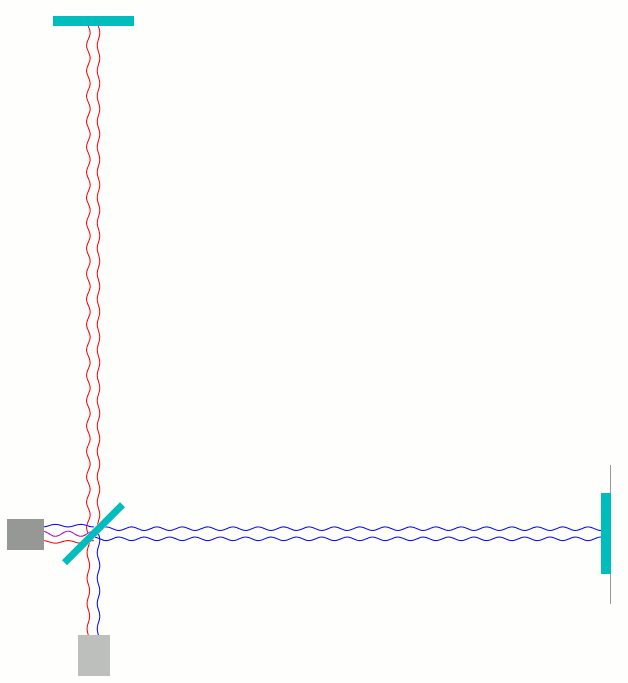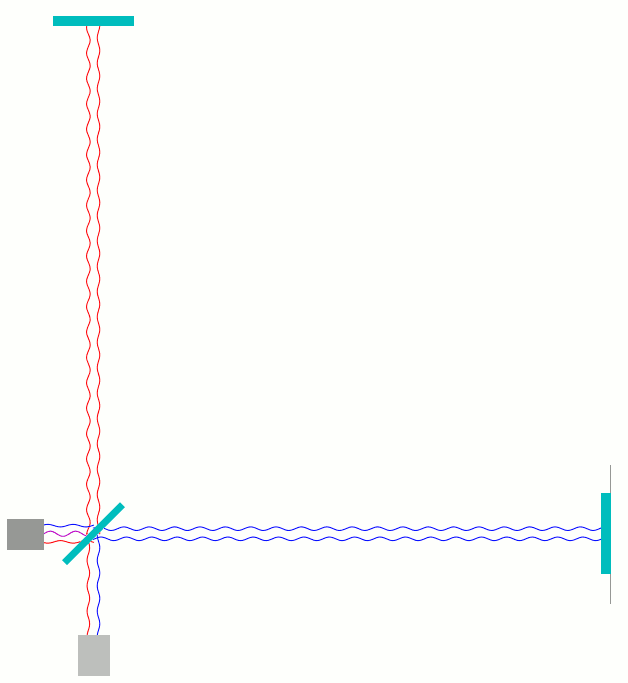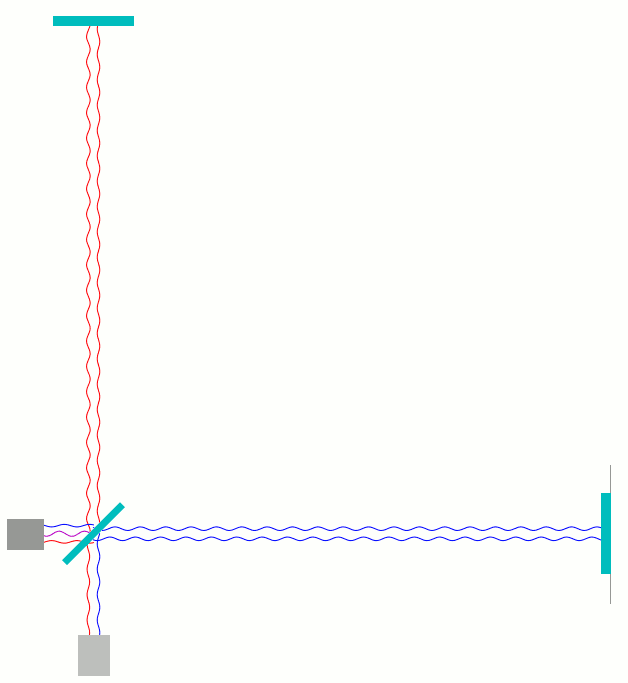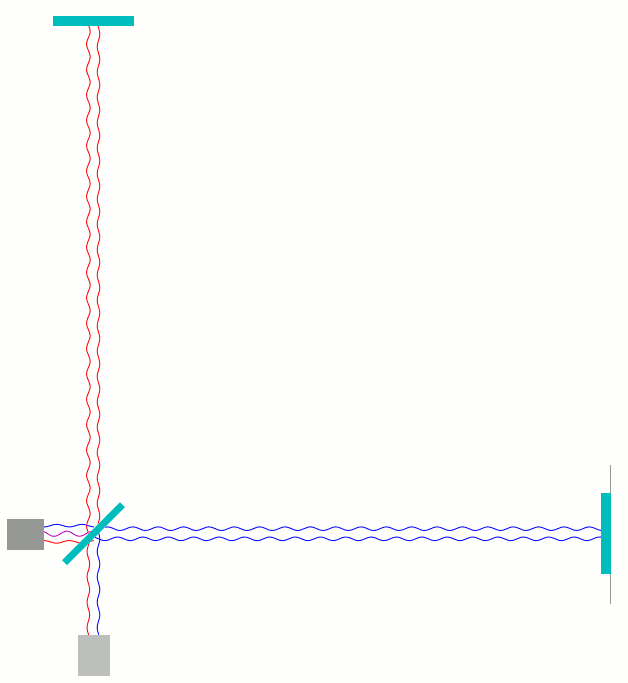 Unten am Photodetektor sieht man direkt, wie rote und blaue Welle in Phase ankommen, roter Wellenberg gleichzeitig mit blauem Wellenberg, rotes Wellental gleichzeitig mit blauem Wellentag. Bei der Überlagerung – die Trennung in dieser Darstellung ist, wie gesagt, nur künstlich – verstärken sich die Wellen entsprechend, wie in der nächsten Darstellung zu sehen:
Unten am Photodetektor sieht man direkt, wie rote und blaue Welle in Phase ankommen, roter Wellenberg gleichzeitig mit blauem Wellenberg, rotes Wellental gleichzeitig mit blauem Wellentag. Bei der Überlagerung – die Trennung in dieser Darstellung ist, wie gesagt, nur künstlich – verstärken sich die Wellen entsprechend, wie in der nächsten Darstellung zu sehen:
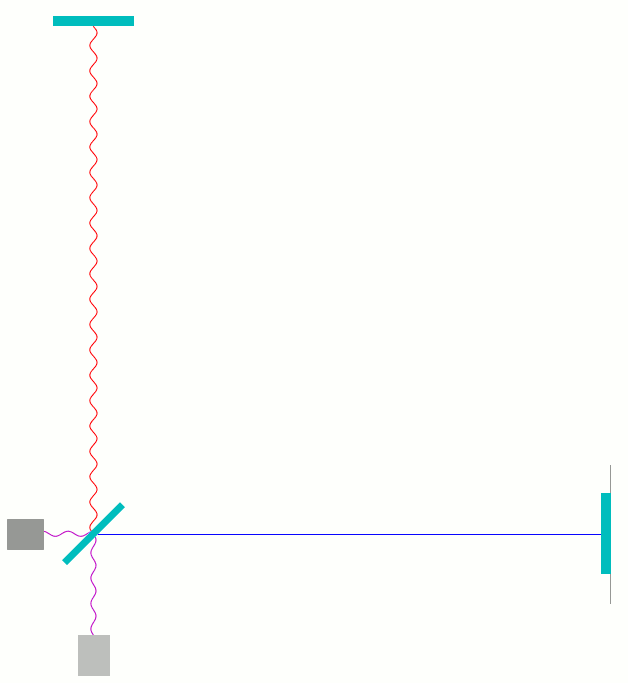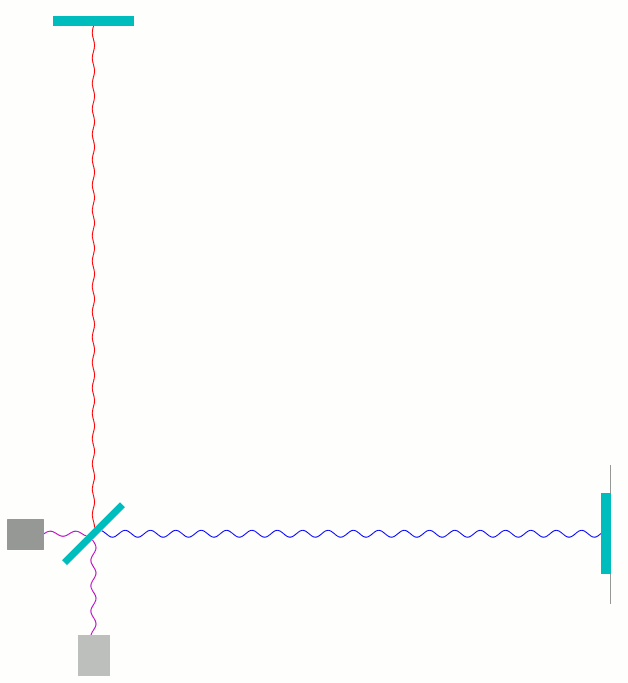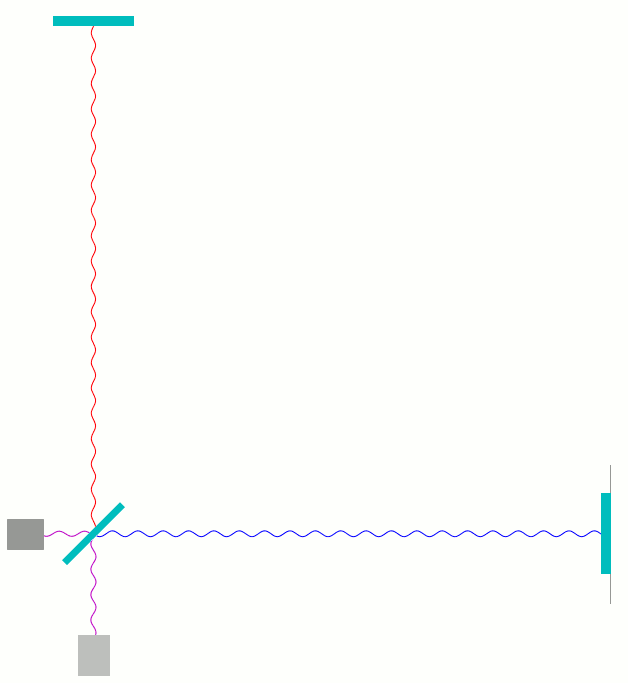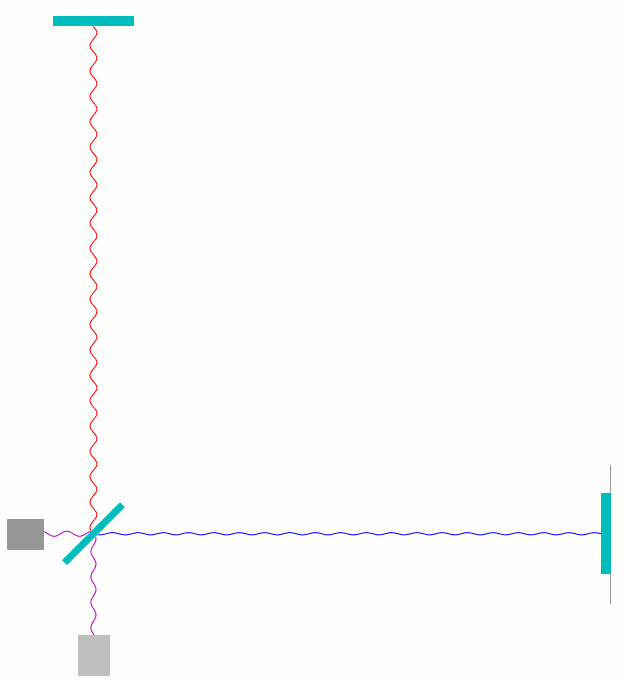 Im Vergleich zu vorher ist hier übrigens auch schön zu sehen, wie die Welle vom Laser (links) in den Detektor hereinläuft. Im Falle der destruktiven Interferenz lief ja zwangsweise genau so viel Licht links wieder hinaus, wie hineingelaufen war (schließlich kam kein Licht unten beim Photodetektor an und verließ die Anordnung aus diesem Wege), so dass dort im Gegensatz zu hier eine stehende Welle zu sehen war. In dieser Anordnung dagegen läuft alles Licht, was von links in den Detektor läuft, nach unten in Richtung Photodetektor wieder hinaus.
Im Vergleich zu vorher ist hier übrigens auch schön zu sehen, wie die Welle vom Laser (links) in den Detektor hereinläuft. Im Falle der destruktiven Interferenz lief ja zwangsweise genau so viel Licht links wieder hinaus, wie hineingelaufen war (schließlich kam kein Licht unten beim Photodetektor an und verließ die Anordnung aus diesem Wege), so dass dort im Gegensatz zu hier eine stehende Welle zu sehen war. In dieser Anordnung dagegen läuft alles Licht, was von links in den Detektor läuft, nach unten in Richtung Photodetektor wieder hinaus.
Hier ist das Diagramm, das für jeden Zeitpunkt zeigt, welche Phase der roten Welle (senkrechter Arm) und der blauen Welle (waagerechter Arm) am Photodetektor ankommen und wozu sich die Teilwellen addieren (lila):
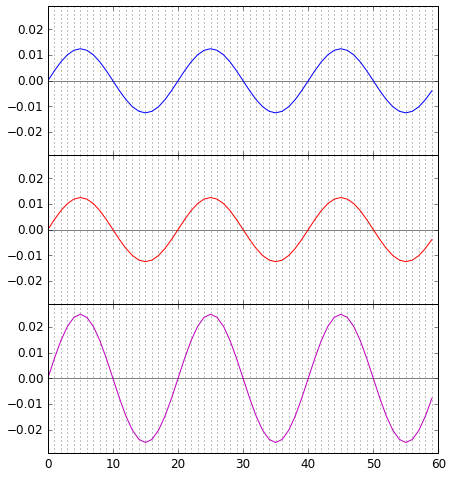 Wellenberg trifft auf Wellenberg, Wellental auf Wellental. Die Summe, unten dargestellt, ist eine Welle mit doppelt so großer Amplitude (Abstand zwischen Berg und Tal) wie bei den beiden Teilwellen. Das ist konstruktive Interferenz.
Wellenberg trifft auf Wellenberg, Wellental auf Wellental. Die Summe, unten dargestellt, ist eine Welle mit doppelt so großer Amplitude (Abstand zwischen Berg und Tal) wie bei den beiden Teilwellen. Das ist konstruktive Interferenz.
Der einzige Unterschied zwischen komplett destruktiver Interferenz (kein Signal am Photodetektor) und komplett konstruktiver Interferenz (maximales Signal) war die Verschiebung eines der Spiegel um eine Viertel Wellenlänge. Das zeigt bereits die Empfindlichkeit dieses Grundaufbaus eines Michelson-Interferometers. Gravitationswellendetektoren wie LIGO oder VIRGO (siehe mein Besuchsbericht hier) sind noch deutlich empfindlicher; in ihnen wird das Licht in den Armen zwischen Spiegelpaaren sozusagen gespeichert. Eine Armlängenverschiebung wirkt sich auf diese Weise einige hundert Male auf das Licht aus, bevor es zum Strahlteiler gelangt. Entsprechend größer sind die Auswirkungen. Darauf gehe ich in einem späteren Blogbeitrag noch näher ein.
Zeitabhängige Verschiebung
In der nächsten Animation ist ein Zeitverlauf zu sehen – der horizontale Arm wird etwas verkürzt und dann wieder auf seine alte Länge zurückgesetzt. Die ursprüngliche Länge entspricht gerade der destruktiven Interferenz, bei der am Photodetektor gar kein Licht nachweisbar ist. Durch die zwischenzeitliche Verkürzung wird dieser Zustand gestört. Hier wieder zuerst die künstlich entzerrte Darstellung, mit den Teilwellen, die künstlich senkrecht zur Ausbreitungsrichtung versetzt sind:
Hier ist mit der zugehörigen Überlagerung gezeigt, was dabei passiert:
 Deutlich ist zu sehen: Nachdem der rechte Spiegel sich etwas nach rechts verschoben hat, pflanzt sich im waagerechten Arm eine Phasenänderung in Richtung Strahlteiler fort; ist sie beim Strahlteiler angekommen, wird die destruktive Interferenz unterbrochen und ein Teil der Welle erreicht den Photodetektor. Nachdem sich der rechte Spiegel in die Ausgangsposition zurückgeschoben hat, pflanzt sich noch eine Phasenänderung von dort zum Strahlteiler fort; hat sie den Strahlteiler erreicht, ist die destruktive Interferenz wieder hergestellt.
Deutlich ist zu sehen: Nachdem der rechte Spiegel sich etwas nach rechts verschoben hat, pflanzt sich im waagerechten Arm eine Phasenänderung in Richtung Strahlteiler fort; ist sie beim Strahlteiler angekommen, wird die destruktive Interferenz unterbrochen und ein Teil der Welle erreicht den Photodetektor. Nachdem sich der rechte Spiegel in die Ausgangsposition zurückgeschoben hat, pflanzt sich noch eine Phasenänderung von dort zum Strahlteiler fort; hat sie den Strahlteiler erreicht, ist die destruktive Interferenz wieder hergestellt.
Hier ist, wie die letzten Male, die Zeitdarstellung derjenigen Teilwellen und kombinierten Welle, die zu jeder Zeit am Photodetektor ankommen:
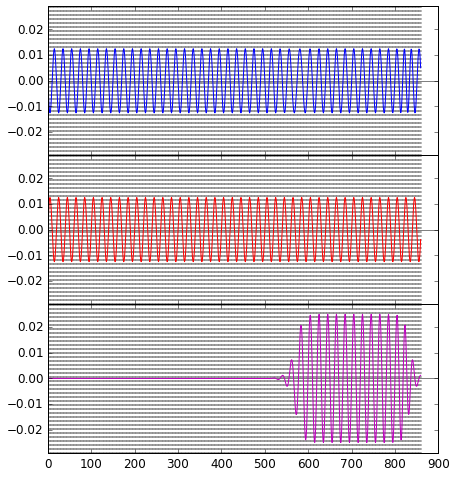 Am Anfang herrscht am Photodetektor wieder einmal Dunkelheit. Erst ab Zeitschritt 500, wo sich die Folgen der Spiegelverschiebung bis zum Photodetektor fortgeplanzt haben, schaltet das System auf maximale Wellenhöhe am Ausgang. Bei ca. Zeitschritt 860 ist der Spuk vorbei und das System wieder auf destruktiver Interferenz.
Am Anfang herrscht am Photodetektor wieder einmal Dunkelheit. Erst ab Zeitschritt 500, wo sich die Folgen der Spiegelverschiebung bis zum Photodetektor fortgeplanzt haben, schaltet das System auf maximale Wellenhöhe am Ausgang. Bei ca. Zeitschritt 860 ist der Spuk vorbei und das System wieder auf destruktiver Interferenz.
Gravitationswelle und Michelson-Interferometer
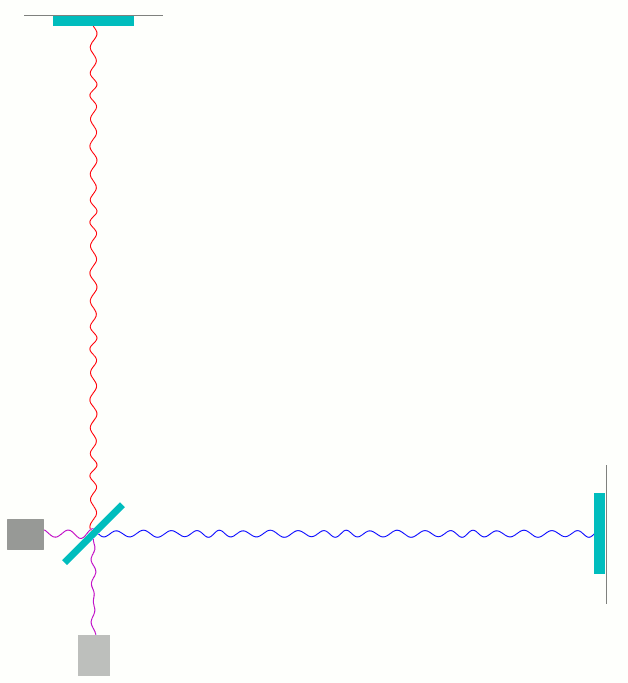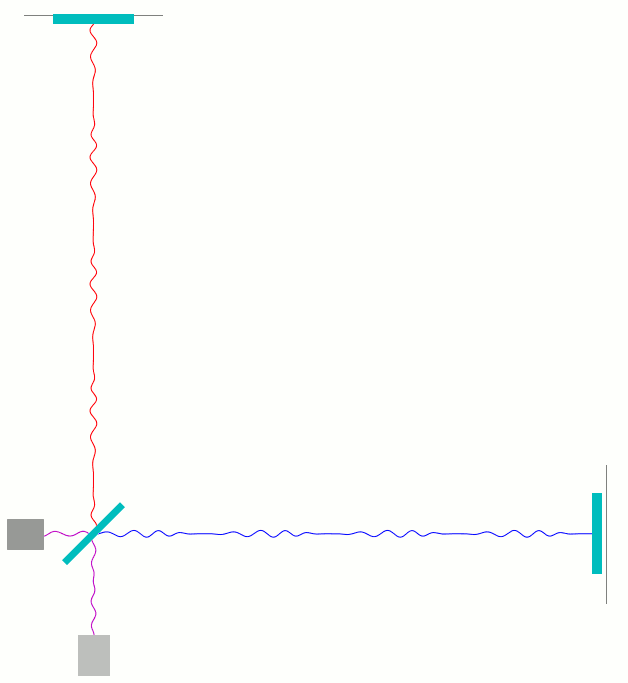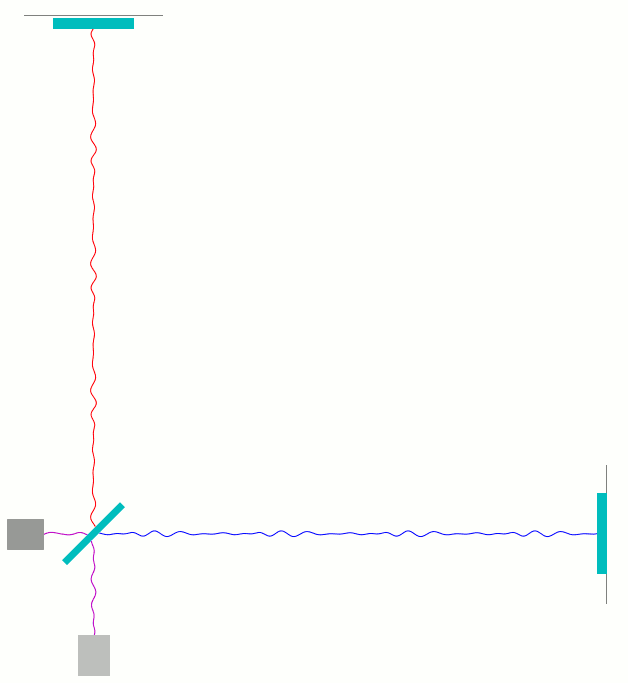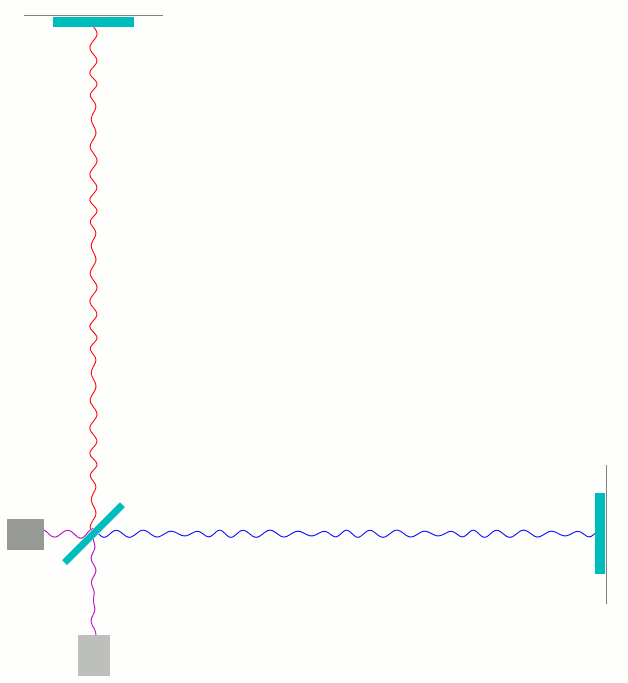
Als letztes zeige ich hier noch eine Animation zu dem Fall einer einfachen, geeignet polarisierten periodischen Gravitationswelle, die von hinten aus der Bildebene auf den Betrachter zu durch das in der Animation gezeigte Michelson-Interferometer läuft und dabei systematische Verschiebungen von einem Zehntel der Wellenlänge des Interferometerlichts verursacht.
Charakteristisch für die Gravitationswelle ist, dass sie im günstigste Falle, wie hier dargestellt, den senkrechten Arm verkürzt während sie gleichzeitig den waagerechten Arm gleichzeitig verlängert, und eine halbe Periode später umgekehrt. (Siehe hierzu meine früheren Beiträge Was sind eigentlich Gravitationswellen? [Teil 1] und Gravitationswellendetektoren: wie sie funktionieren [Teil 2].)
Hier ist zuerst wieder die Darstellung mit getrennt dargestellten hin- und herlaufenden Wellen:
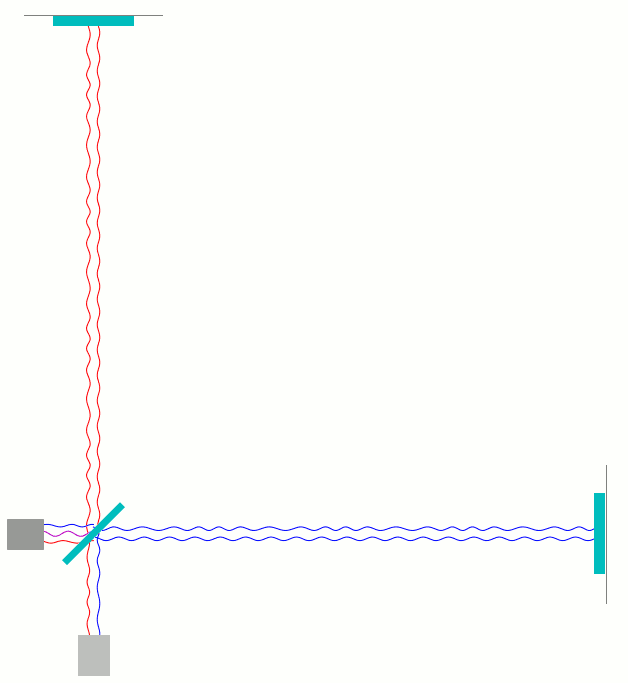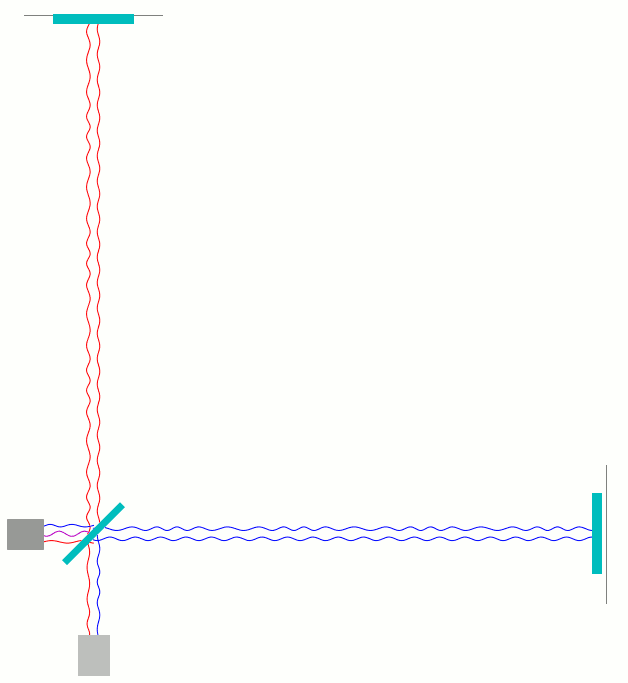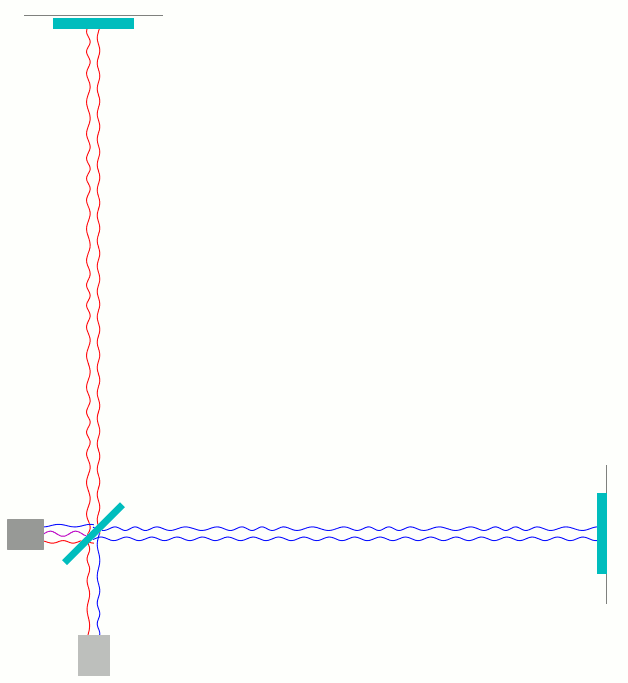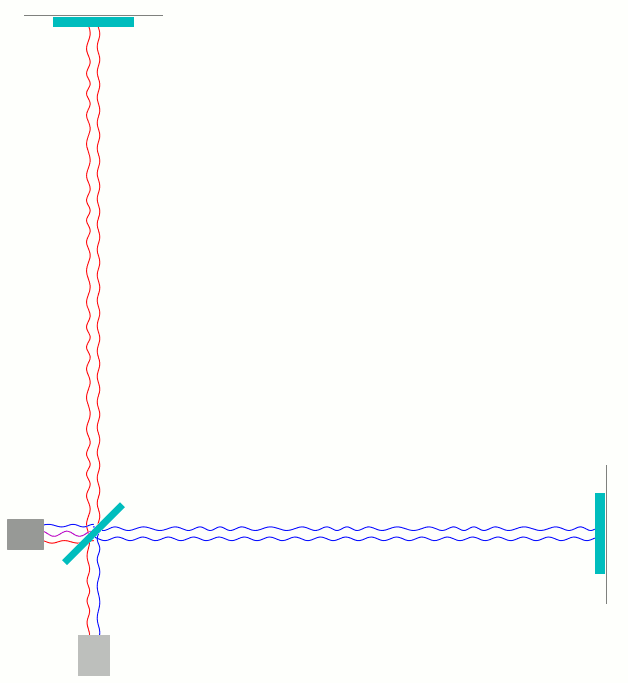 Bei genauem Hinsehen kann man direkt sehen, wie die Wellenberg- und Täler der beiden Teilwellen (rot und blau) sich kurz vor dem Photodetektor mit der Zeit etwas gegeneinander verschieben.
Bei genauem Hinsehen kann man direkt sehen, wie die Wellenberg- und Täler der beiden Teilwellen (rot und blau) sich kurz vor dem Photodetektor mit der Zeit etwas gegeneinander verschieben.
Hier ist die realistischere, überlagerte Darstellung:
 Die Abweichung vom Nullsignal am Photodetektor ist auch hier deutlich zu erkennen.
Die Abweichung vom Nullsignal am Photodetektor ist auch hier deutlich zu erkennen.
Hier ist für diesen Fall wieder das Signal am Photodetektor als Funktion der Zeit dargestellt. Wo der Photodetektor ohne Gravitationswelle bei destruktiver Interferenz wäre und am Photodetektor gar kein Signal ankäme, sorgt die Gravitationswelle für ein Signal ungleich Null:
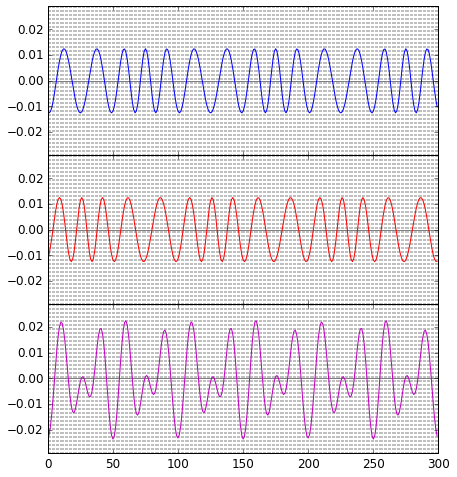 Man sieht deutlich, wie die Gravitationswelle die blaue und die roten Wellenberge einmal ein wenig eher, einmal ein wenig später ankommen lässt. Das ist das vereinfachte Grundprinzip des Nachweises von Gravitationswellen mit einem Michelson-Interferometer.
Man sieht deutlich, wie die Gravitationswelle die blaue und die roten Wellenberge einmal ein wenig eher, einmal ein wenig später ankommen lässt. Das ist das vereinfachte Grundprinzip des Nachweises von Gravitationswellen mit einem Michelson-Interferometer.
Die Summe liefert ein charakteristisches Muster. Ein tatsächlicher Gravitationswellendetektor wird allerdings nicht diesen Zeitverlauf zeigen, sondern einen zeitlichen Mittelwert des Quadrats des hier gezeigten Signals (entsprechend der Leistung des Lichts, das im Photodetektor landet), gemittelt über einige der Perioden des verwendeten Laserlichts.
In späteren Beiträgen wird der Detektoraufbau noch etwas komplizierter – und damit empfindlicher. Aber das Grundprinzip des Nachweises ist dasselbe wie bei einem einfachen Michelson-Interferometer wie in den hier gezeigten Animationen.


Kompliment für die vielen, viele Fälle abdeckenden Animationen von Lichtwegen im Interferometer.
Faszinierend finde ich, welche Messgenauigkeiten ein konzeptionell so grundlegendes, einfaches und “schönes” Instrument wie das Michelson-Interferometer erreichen kann. A.A.Michelson hat rückblickend betrachtet zurecht den Physiknobelpreis für die Erfindung dieses Instruments erhalten. Bei dieser Gelegenheit lässt sich auch sagen, dass der Nobelpreis für Physik wohl auch darum so viel Beachtung findet, weil das Nobelpreiskomitee meist eine glückliche Hand bei der Auwahl der Preisträger hat und hatte. Exemplarisch für diese glückliche Hand stehen die Nobelpreisträger welche für die Erforschung der Supraleitung vergeben wurden: Nicht nur Theoretiker wie Bardeen, Cooper und Schrieffers (BCS-Theorie) sondern gerade auch Praktiker wie Heike Kamerlingh Onnes (Erstentdeckung der Supraleitung) oder Bednarz und Müller (Entdeckung der Hochtemperatursupraleitung) erhielten Nobelpreise. Das Michelson-Interferometer gehört zu diesem praktischen Zweig der Physik. Messgeräte fast überirdischer Präzision wie die optischen Interferometer oder die praktische Erzeugung von exotischen Materiezustände wie dem Boson-Einstein Kondensat zeigen, dass sich das gedachte Ideale auch in der Praxis approximieren lässt.
Markus Pössel schrieb (4. Oktober 2016):
> Zumindest in denjenigen Fällen, in denen die Verweildauer des Lichts im Interferometer deutlich kleiner ist als die Schwingungsdauer der Gravitationswelle, deren Einfluss nachgewiesen werden soll, kann man sich die Wirkung der Gravitationswelle auf den Detektor in guter Näherung so vorstellen, dass die Welle systematisch die Abstände der beiden äußeren Spiegel vom Strahlteiler verkleinert und vergrößert
> Charakteristisch für die Gravitationswelle ist, dass sie im günstigste Falle, wie hier dargestellt, den [einen] Arm verkürzt während sie [den anderen, orthogonalen] Arm gleichzeitig verlängert, und eine halbe Periode später umgekehrt.
Der Umkehrschluss ist allerdings nicht zwingend:
Allein aus dem interferometrischen Befund, dass die (chronometrischen) Entfernungen jeweils zwischen (äußerem) Spiegel und dem Strahlteiler sich (systematisch, charakteristisch) periodisch und in entgegengesetzter Phase verändert hatten,
mit Periodendauer deutlich größer als die Verweildauer des Lichts im Interferometer,
folgt nicht unbedingt,
dass das Interferometer dabei von einer Gravitationswelle dieser Periodendauer betroffen gewesen wäre.