Die rauhen Welten des Martin Hairer – Teil 2
BLOG: Heidelberg Laureate Forum

In Teil 1 von “Die rauhen Welten des Martin Hairer” hatte ich einige Grundbegriffe Revue passieren lassen, die für Hairers Forschung zu stochastischen Differentialgleichungen wichtig sind – und damit auch zum Verständnis von Hairers Vortrag beim Heidelberg Laureate Forum am Dienstag Morgen.
Aber wofür sind diese sonderbaren Differentialgleichungen und die “rauhen Funktionen” denn nun eigentlich gut?
Wie man eine Grenzfläche wachsen lässt
Grenzflächen kennen wir aus dem Alltag: Sie trennen das Holz des Tisches von der umgebenden Luft, den Stein des Fußbodens von der Luft, den Boden der Badewanne von dem darin befindlichen Wasser. Wichtig ist: Dort treffen zwei unterschiedliche Stoffe aufeinander – oder auch zwei Aggregatzustände (Phasen), etwa an der Grenze zwischen Eiswürfel und dem Wasser, in dem der Würfel schwimmt.
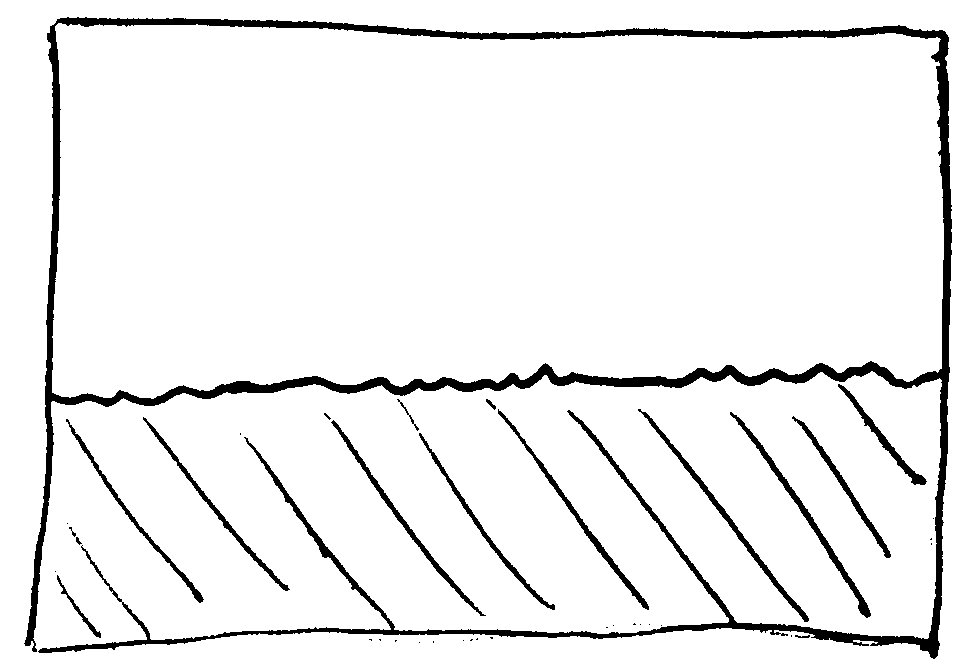
Von der Seite her betrachtet sieht eine Grenzfläche ungefähr so aus:
Die beiden Materialien sind Stoff A (freigelassen) oben, Stoff B (schraffiert) unten; die Grenzfläche (als Linie eingezeichnet) trennt die beiden.
Es gibt Situationen, in denen die Region B anwächst. Wenn A Wasser ist und B Eis, dann werden sich bei hinreichend niedriger Temperatur weitere Eiskristalle formen, so dass die Eisregion in das Wasser hineinwächst. Eine künstlichere Situation liegt vor, wenn Physiker einen Molekularstrahl auf eine Oberfläche richten, auf der mit der Zeit immer mehr Moleküle hängenbleiben, so dass das betreffende Materialstück immer weiter wächst.
Mit anderen Worten: Es gibt viele physikalisch interessante Situationen, in denen wachsende Grenzflächen eine Rolle spielen.
Betrachtet man solche wachsenden Grenzflächen wie in der Skizze oben, nämlich von der Seite, oder beschränkt man sich gleich auf ein vereinfachtes, zweidimensionales Modell, ist die Grenzfläche eine eindimensionale Linie. Für den vereinfachten, aber nicht unrealistischen Fall, dass diese Linie nicht zu sehr in sich selbst zurückgebogen ist, können wir die Linie als Funktionskurve darstellen: Die waagerechte Achse nehmen wir als x-Achse; die Linie entspricht dann dem Graphen einer Funktion h(x). Die Wahl des Buchstabens h suggeriert, dass wir so etwas wie die Höhe der Grenzfläche oberhalb der x-Achse erfassen wollen.
Aber was für eine Art von Kurve ist h(x)? Das hängt natürlich von den Details des Modells ab. Eine Klasse von Wachstumsmodel ist bekannt als ballistische Modelle. Teilchen aus dem Stoff B fallen in zufälliger Weise von oben auf die bestehende Oberfläche; sobald sie die Oberfläche erreichen, backen sie dort fest. (In einigen Modellen reicht es auch bereits, wenn sie einem anderen B-Teilchen genügend nahe kommen.)
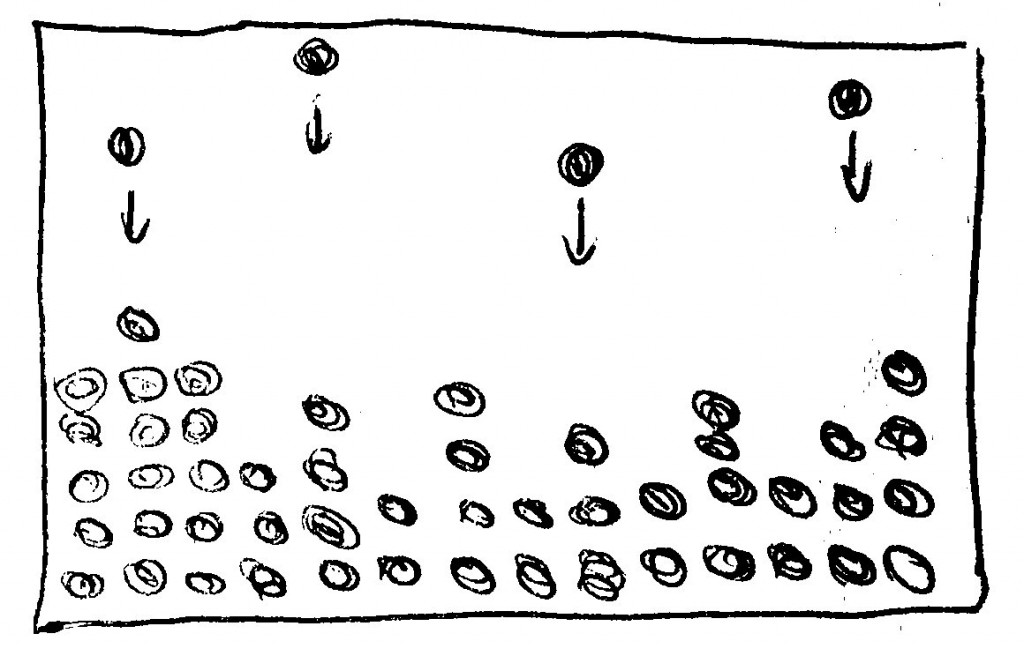
Die folgende Skizze soll das zeigen. Sie zeigt das Material B, das hier sozusagen spaltenweise aus Teilchen aufgebaut ist (ausgefüllte Kreise), und sie zeigt einige B-Teilchen, die von oben herabregnen. In welche Spalte das nächste Teilchen fallen wird, bestimmt der Zufall:
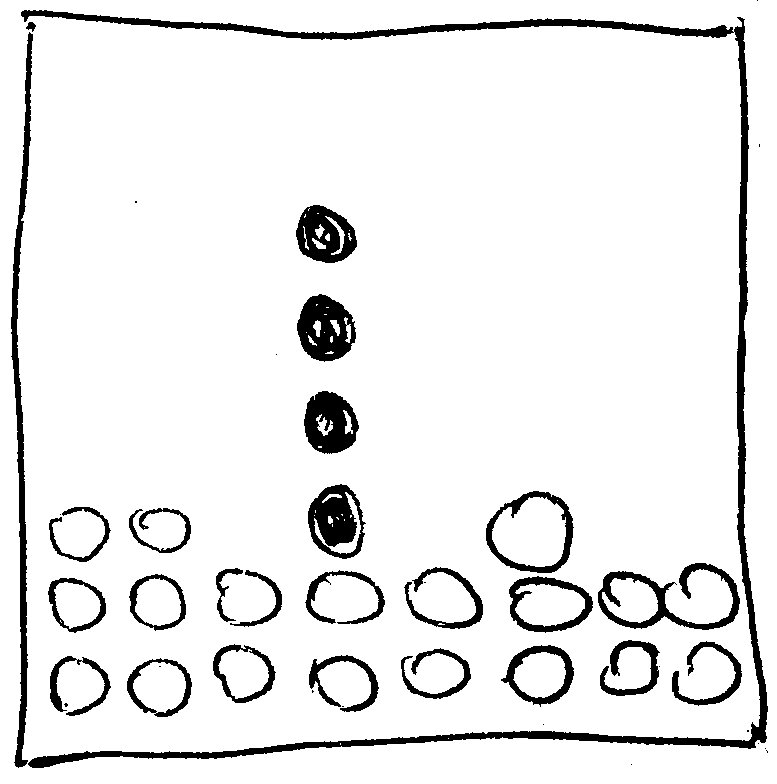
Einige der Eigenschaften dieses einfachen Modells, bei dem die Teilchen nur zufällig herunterregnen, sind unphysikalisch – sie dürften nicht geeignet sein, das Wachstum einer realen Oberfläche zu beschreiben. Zum Beispiel wird dieses Modell immer einmal wieder zu absurd dünnen, hohen Säulen führen, die senkrecht aus der Oberfläche hervorragen, wie hier skizziert (B-Teilchen in der Säule sind ausgefüllt dargestellt, die anderen B-Teilchen als leere Kreise):
In Wirklichkeit werden solche filigranen Strukturen nicht lange überleben. Deswegen ist es sinnvoll, in das Modell einen Mechanismus einzubauen, der solche hohen Türme etwas in sich zusammensacken lässt, so wie hier:
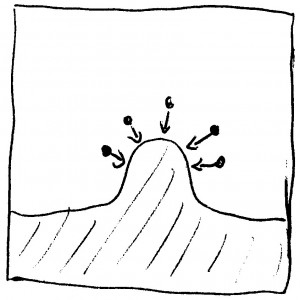
 Dass die Teilchen direkt von oben fallen, hat auch einen etwas unrealistischen Effekt. Angenommen, die Oberfläche hat sich schon etwas ausgebeult. Dann wäre in den meisten Fällen (z.B. Eisbildung) nicht zu erwarten, dass sich neue Teilchen nur direkt von oben anlagern, wie hier skizziert:
Dass die Teilchen direkt von oben fallen, hat auch einen etwas unrealistischen Effekt. Angenommen, die Oberfläche hat sich schon etwas ausgebeult. Dann wäre in den meisten Fällen (z.B. Eisbildung) nicht zu erwarten, dass sich neue Teilchen nur direkt von oben anlagern, wie hier skizziert:
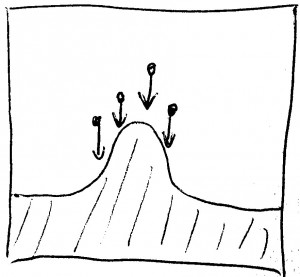
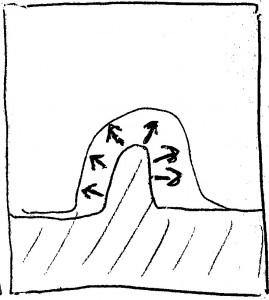
Stattdessen würden wir erwarten, dass sich die Teilchenanlagerung nach der bereits vorhandenen Oberflächenform richtet, sie also etwa so erfolgt wie in dieser Skizze hier:
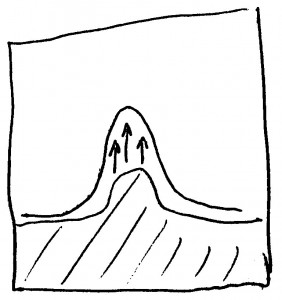
Mit anderen Worten: Die Grenzfläche sollte nicht direkt nach oben wachsen, wie hier…
…sondern eher von der bestehenden Form nach außen, wie hier:
Das KPZ-Modell
Ein Modell zufälligen Wachstums, das alle diese Eigenschaften hat, ist das KPZ model, benannt nach Mehran Kardar, Giorgio Parisi und Yi-Cheng Zhang.
Wenn wir, wie schon kurz erwähnt, die waagerechte Richtung in all diesen Skizzen als x-Richtung wählen, und die Funktion h(t,x) die Grenzkurve beschreiben lassen, die sich mit der Zeit t verändert, dann ist das KPZ-Modell definiert durch die Gleichung
Die linke Seite sagt uns, dass dies eine Gleichung dafür ist, wie sich h(t,x) mit der Zeit verändert.
Die Terme auf der rechten Seite berücksichtigen die Modelleigenschaften, die ich als wünschenswert beschrieben hatte: Die Funktion Eta beschreibt das Zufallswachstum, nämlich die Teilchen, die von oben herabregnen.
Die zweite Ableitung von h nach x ist der Diffusionsterm – er sorgt dafür, dass dünne, hohe Strukturen mit der Zeit etwas auseinanderfließen.
Das Quadrat der ersten Ableitung nach x ist für “laterales Wachstum” verantwortlich: dafür, dass Ausbuchtungen nicht direkt nach oben wachsen, sondern von der bereits existierenden Form nach außen.
Brown’sche Bewegung, KPZ und problematische Unendlichkeiten
So weit, so gut – aber ist das überhaupt eine vernünftige Gleichung? Bei näherer Betrachtung ergeben sich in der Tat einige Probleme.
Ausgehend von der linearisierten Form der Gleichung (ohne das Quadrat der x-Ableitung) kann man zeigen, dass zweiseitige Brown’sche Bewegung als Ausgangskurve auch zu späteren Zeiten Brown’sche Bewegung bleibt (freilich nach oben verschoben). Beim Übergang zu allgemeineren Fällen lässt sich zeigen, dass sich selbst eine ursprünglich vernünftige, glatte Kurve mit der Zeit so entwickelt, dass jeder Teil der Kurve zu einem Ausschnitt aus einer Kurve Brown’scher Bewegung wird. Die Lösungen dieser Gleichung sind sehr rauhe Kurven.
Das Problem? Wir haben gesehen, dass das Quadrat der Ableitung der Brown’schen Bewegung nicht sinnvoll definiert ist, sondern unendlich. Aber genau dieses Quadrat kommt in der KPZ-Gleichung vor. Hm.
Ähnliches Problem, ähnliche Lösung? Renormierung bei Elementarteilchen
Damit wären wir endlich beim Titel des Vortrags von Hairer, denn das sind genau die Unendlichkeiten, die gezähmt werden sollen. Hier schlagen wir die Brücke zu den Physikern, die mit einem ähnlichen Unendlichkeitsproblem zu kämpfen hatten – und es gelöst haben! – als sie begannen, Elementarteilchenreaktionen zu beschreiben.
Angenommen, ich will ausrechnen, wie zwei Elektronen, die ich im Teilchenbeschleuniger aufeinander zu schieße, miteinander reagieren. In der Quantenfeldtheorie – der physikalischen Theorie, die derartige Rechnungen beschreibt – gibt es unendlich viele Beiträge zu dem, was in solch einer Situation passiert. Glücklicherweise sind nicht alle davon gleich wichtig – je mehr unterschiedliche Teilchenreaktionen bei einer bestimmten Version der Situation stattfinden, umso kleiner der Beitrag zum Gesamtergebnis (das mir sagt, mit welcher Wahrscheinlichkeit die Geschwindigkeiten und Flugrichtungen der beiden Elektronen nach der Reaktion gegebene Werte annehmen).
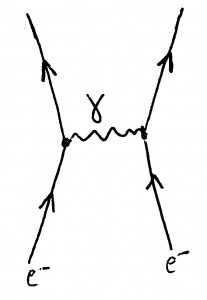
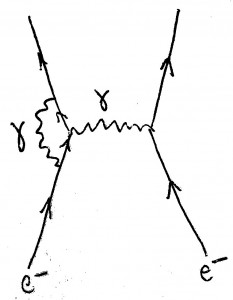
Der größte Beitrag zum Ergebnis kommt von einer Reaktion, wie sie in diesem Diagramm gezeigt wird; solche Diagramme heißen Feynman-Diagramme; in diesem Falle liest man das Diagramm von unten (Vergangenheit) nach oben (Zukunft):
Die zwei Linien, die von unten kommen, stellen die beiden Elektronen dar. Die Schlangenlinie entspricht einem Photon (“Lichtteilchen”), das zwischen den beiden Elektronen ausgetauscht wird. Dieser Beitrag ergibt dafür, wie sich die beiden Elektronen abstoßen, das gleiche Ergebnis wie die klassische Elektrodynamik.
Hier ist ein Beispiel für die nächst kompliziertere Art von Beitrag:
Diesmal werden zwei Photonen ausgetauscht – links in dem Diagramm findet sich eine zusätzliche Schlangenlinie. Ein Ereignis dieser Art ist deutlich seltener als das im ersten Diagramm dargestellte, und dementsprechend ergibt sich aus diesem Diagramm nur eine kleine Korrektur dazu, wie Geschwindigkeiten (inklusive Flugrichtungen) der Elektronen sich verändern.
Das ist zumindest das Endresultat; am Anfang sieht es so aus, als würden Diagramme dieser Art keine kleine Korrektur ergeben, sondern im Gegenteil die ganze Theorie ad absurdum führen. Bei einer naiven Rechnung ergibt sich sogar ein unendlich großer Beitrag eines solchen Diagramms, und das ist mit Sicherheit falsch. Insbesondere erhält man bei Beiträgen dieser Art unendliche Werte für Masse oder elektrische Ladung der beteiligten Teilchen.
Die Teilchenphysiker haben allerdings einen Weg gefunden, diese Unendlichkeiten zu vermeiden. Eine Möglichkeit zu verstehen, wie die Unendlichkeiten auftreten, ist die folgende: Die Rechnung summiert über alle Arten und Weisen, wie die Elektronen miteinander wechselwirken können – auch diejenigen, bei denen die Elektronen sich beliebig nahe kommen. Es gibt aber gute Gründe für die Annahme, dass die verwendeten Theorien gar nicht für beliebig kurze Abstände (das entspricht: beliebig hohen Energieskalen) gültig sind. Bei sehr, sehr hohen Energien dürfte neue Physik ins Spiel kommen.
Der Ausweg besteht denn auch darin, anzunehmen, dass die Theorie nur bis zu einer gewissen Energie-Obergrenze E gilt, die man zunächst per Hand einführt (dafür gibt es verschiedene Verfahren). Dank dieser Obergrenze bleibt das Ergebnis endlich, hängt nun allerdings von dem einigermaßen willkürlich gewählten Wert E ab. Das lässt sich ändern, wenn man die Parameter der Theorie geeignet umdefiniert – die Form der Gleichungen lässt das zu – und insbesondere neue Versionen der Parameter zur Beschreibung von Massen und Ladungen der Teilchen einführt.
Unter Benutzung dieser Parameter lassen sich dann diejenigen Größen ausrechnen, die sich in Experimenten tatsächlich beobachten lassen – die schon erwähnte Wahrscheinlichkeitsverteilung für die Elektronen nach der Reaktion. Bei der richtigen Rechnung kann man dann auch E wieder beliebig groß werden lassen, ohne dass sich das Ergebnis verändert. Parameter für Massen und Ladungen müssen dann noch experimentell bestimmt werden, aber sobald dies geschehen ist, sind Vorhersagen zu Teilchenreaktionen möglich, die zu den genauest bestätigten gehören, welche die Physik überhaupt zu bieten hat.
Die Prozedur, die Unendlichkeiten loszuwerden, funktionieren also am Ende sehr gut. Schaut man sich an, was man da eigentlich gemacht hat, sieht es aus, als hätte man in kontrollierter Art und Weise unendlich große Terme von dem ursprünglichen, nicht richtig definierten Ergebnis abgezogen, und als wäre dabei dann ein am Ende nur noch endlich großes Ergebnis herausgekommen (inklusive einiger freier Parameter, die man sich eingehandelt hat, aber was soll’s).
KPZ zähmen
Dieses Vorgehen, nämlich Counterterme (“Gegenterme”) einzuführen, funktioniert auch bei der KPZ-Gleichung: auch dort lässt sich auf kontrollierbare Art und Weise “eine Unendlichkeit abziehen”, so dass am Ende eine sinnvoll definierte Gleichung herauskommt, die sich untersuchen lässt.
Man kann das Vorgehen auch auf andere Art betrachten, die ich faszinierend fand. Hairer hat das wie folgt erklärt: Dass eine normale Funktion differenzierbar ist, bedeutet, dass man diese Funktion in jedem Punkt als Polynom (Taylorentwicklung!) auffassen kann. Der Koeffizient des linearen Terms ist der Wert der ersten Ableitung an dem betreffenden Punkt, der des quadratischen Terms die Hälfte der zweiten Ableitung, und so weiter.
Das Problem bei Lösungen der KPZ-Gleichung war die Zufalls-Eigenschaft desjenigen Terms, der die Beiträge der zufällig herunterfallenden Teilchen zum Wachstum der Grenzfläche beschreibt (und bei der Brown’schen Bewegung analog die Zufalls-Eigenschaft der Änderungen). So ergaben sich undefinierte Ableitungen (bzw. Quadrate davon). Bei der Brown’schen Bewegung war einsichtig, woher das Definitionsproblem kam – beim Hineinzoomen wird man aufgrund der Selbstähnlichkeit nie etwas sehen, das linear oder wie ein einfaches Polynom aussieht.
Hairer sprach die Möglichkeit an, solche Funktionen anders als Summe zu schreiben – nicht als Polynom, aber als Summe von Funktionen die ähnlich ungewöhnliche Eigenschaft haben wie die Brown’sche Bewegung (letztere wäre ein guter Kandidat für einen Teil der neuen Basis!).
Faszinierenderweise könnte man eine solche ungewöhnliche Basis so wählen, dass man fast alles damit machen könnte, was auch mit der Polynomentwicklung geht. Auch in der neuen Basis würden die Koeffizienten die Rolle von Werten der Ableitung spielen; auch dort könnte man die einzelnen Summanden nach ihrem Grad ordnen (wie die Monome) und die Funktion annähern, indem man die kleineren Beiträge höheren Grades erst einmal weglässt.
Auf bemerkenswerte Art und Weise bekäme man so eine ganze Reihe der Eigenschaften zurück, die Physiker an normalen, glatten Funktionen so schätzen – und die unwiederbringlich verloren gegangen zu sein schienen, sobald Zufallsterme ins Spiel kamen.
Schluss
Was ich hier beschrieben habe, ist noch längst nicht alles, was Hairer erzählt hat – an dieser Stelle folgten noch Vermutungen darüber, ob man beim “Herauszoomen” nicht nur bei der KPZ-Gleichung, sondern bei allen verwandten Modellen letztlich bei einer universellen, selbstähnlichen Lösung vom Typ Brown’sche Bewegung landet. Wer da noch etwas mehr wissen möchte, sollte sich direkt Hairers Folien anschauen.
Ich begnüge mich hier, einen Überblick über einige der Grundideen gegeben zu haben, die in Hairers Vortrag eine Rolle spielten – für mich ein Einblick in eine völlig fremde Welt, und damit ein Vortrag, wie er beim HLF glücklicherweise immer einmal wieder vorkommt.


Noch ein populRwissenschaftlicher Artikel über stochastische Differentialgleichungen und Hairers Theorie: http://images.math.cnrs.fr/Qu-est-ce-qu-une-Equation-aux.html