Wie kann bei der Mondlandung der Treibstoff ausgehen?

Am 25.4.2023 stürzte eine japanische Mondsonde beim Landeversuch ab, angeblich weil ihr “der Treibstoff ausgegangen” sei, wie der Presse zu entnehmen ist. Wie kann das sein?
Zuwenig Treibstoff im Tank?
Ein Laie könnte das so auffassen, als wäre da aufgrund eines Irrtums oder eines Rechenfehlers zuwenig Treibstoff in die Tanks gefüllt worden. Das zumindest halte ich aber für ausgeschlossen. In der Missionsplanung wird zunächst das gesamte Geschwindigkeitsinkrement (delta-v) genau berechnet. Es gehen dort alle deterministischen (also exakt berechenbaren) Manöver ein.
Wo erforderlich – ganz sicher ist das beim großen Bremsmanöver vor dem Aufsetzen so – kommen Gravitationsverluste hinzu. Dabei handelt es sich um die zwangsläufige Zunahme der Manövergröße durch die Tatsache, dass ein großes Manöver nicht auf einen Schlag am optimalen Punkt verabreicht werden kann, sondern sich über einen längeren Zeitraum hinzieht.
Bei einer Landung wird man oft auch eine Schwebephase vorsehen. Diese findet in geringer, aber noch sicherer Höhe über dem Boden statt, vielleicht so 100 Meter. Man kann an diesem “Hold Point” noch einmal kurz innehalten und schauen, ob es wirklich keine gefährlichen Dinge am Landepunkt gibt oder prüfen, ob die Horizontalgeschwindigkeit auch wirklich Null ist.
Das kostet natürlich noch einmal delta-v. Auf dem Mond kostet eine Minute Schweben ziemlich genau 100 m/s. Nicht ganz billig, aber schon eine sinnvolle Investition, meine ich. Zumal das delta-v-Budget bei einer Mondlandemission immer erheblich ist. Die Landung aus einer 100 km hohen Parkbahn kostet immer mindestens rund 1850 m/s an delta-v, was aber von verschiedenen Faktoren abhängt. Wie hoch ist der Triebwerksschub im Verhältnis zur Masse, wie gut lässt sich das Triebwerk regeln, hat man einen Haltepunkt und wie lange will man dort bleiben, usw..
Und dann muss man ja erst einmal in diese 100 km-Parkbahn kommen. Da fällt das mehr oder weniger große LOI (“Lunar Orbit Injection”) an (plus Gravitationsverluste), dann vielleicht noch weitere Manöver zur Zirkularisierung. Auch auf dem Transfer kann es weitere deterministische Manöver geben.
Aber es gibt nicht nur deterministische Manöver, sondern auch stochastische: die Navigationsmanöver, mit denen unvermeidliche Ungenauigkeiten in der Bahnbestimmung und Abweichungen bei der Ausführung vorangegangener Manöver korrigiert werden. Zur Missionsplanung gehört auch eine ausführliche Navigationsanalyse, an deren Ende der 3-Sigma-Wert des Navigationsbudgets steht.
Alle Einzelposten des delta-v-Budgets kommen in eine große Tabelle, und dann kommen zu jeden Wert noch “margins” hinzu, also Zuschläge, um die in der tatsächlichen Mission zu erwartenden Unsicherheiten verkraften zu können. Möglicherweise kommt noch ein weiterer Zuschlag für “Contingencies” drauf, bei Raumfahrtleuten auch als “____ happens-cost” bekannt. Meist wird der am Ende nicht gebraucht, weil die “margins” auf die einzelnen Budgetwerte ausreichten, aber wenn man ihn doch braucht, ist man froh, dass man ihn vorgesehen hatte.
Vom delta-v zum Treibstoff
Wenn man alles zusammenrechnet, kommt ein Gesamtwert für das delta-v heraus. Das ist aber erst einmal nur ein abstrakter Hilfswert. Was am Ende gebraucht wird, ist die erforderliche Menge an Treibstoff. Die Manöver werden nicht alle mit demselben Triebwerk absolviert. Für die großen gibt es das Haupttriebwerk, das hohen Schub und eine hohe Ausströmgeschwindigkeit bietet. Für kleine Manöver, auf jeden Fall für die Navigation, verwendet man eine Anzahl kleinerer Triebwerke, die das RCS (“Reaction Control System”) bilden. Üblich sind heute Triebwerke, die ein Gemisch aus Brennstoff und Oxidator verbrennen. Der Brennstoff ist meist Hydrazin, der Oxidator Distickstofftetroxid (beides in unterschiedlichen Varianten). Für die Umrechnung von delta-v zu Treibstoffverbrauch gibt es die Ziolkowskigleichung. Dabei muss aber auch die Trockenmasse des Raumfahrzeugs schon klar feststehen.
Am Ende hat man das gesamte delta-v Budget der Missionsanalyse in eine entsprechende Menge an Treibstoff umgerechnet. Jetzt kommt noch der Treibstoff drauf, der für die Lageregelung gebraucht wird. Man kann noch eine Sicherheitsmarge draufschlagen, und man wird noch mehr Treibstoff einfüllen, weil die Tanks nicht bis zum letzten Tropfen geleert werden können. Am Ende der Rechnung steht die Masse des für die Mission erforderlichen Treibstoffs.
Lange Rede, kurzer Sinn: Die Berechnung des delta-v-Budgets und die daraus folgende Berechnung der Masse an Treibstoff gehören zu den am genauesten überwachten Einzelfaktoren bei der Entwicklung eines Raumfahrzeugs. Jeder einzelne Punkt wird endlos diskutiert und verifiziert, alles durchläuft mehrfache “reviews”. Wahrscheinlich hat die für die Missionsanalyse verantwortliche Person sich im Lauf der Karriere Feinde gemacht, und diese werden versuchen, es ihm oder ihr heimzuzahlen, indem sie einen Fehler in den Berechnungen nachweisen und diesen laut heraustrompeten. Ein weiterer Anreiz für alle Beteiligten, ganz genau hinzuschauen.
Es fehlt mir jetzt wirklich die Fantasie, mir vorzustellen, dass trotz alledem am Ende tatsächlich ein grober Patzer unentdeckt durchrutscht.
OK, aber wie kann man dann mit zuwenig Treibstoff dastehen?
Ich lehne mich jetzt mit einer reinen Spekulation zum Fenster ‘raus, aber wenn man das ausdrücklich ankündigt, darf man das auch mal. Allemal im Rahmen eines Blog-Artikels.
Zunächst einmal stelle ich dar, wie so eine Landung überhaupt vor sich geht. Stellen wir uns vor, die Raumsonde ist in einer kreisförmigen Parkbahn mit einer Höhe von 100 km.
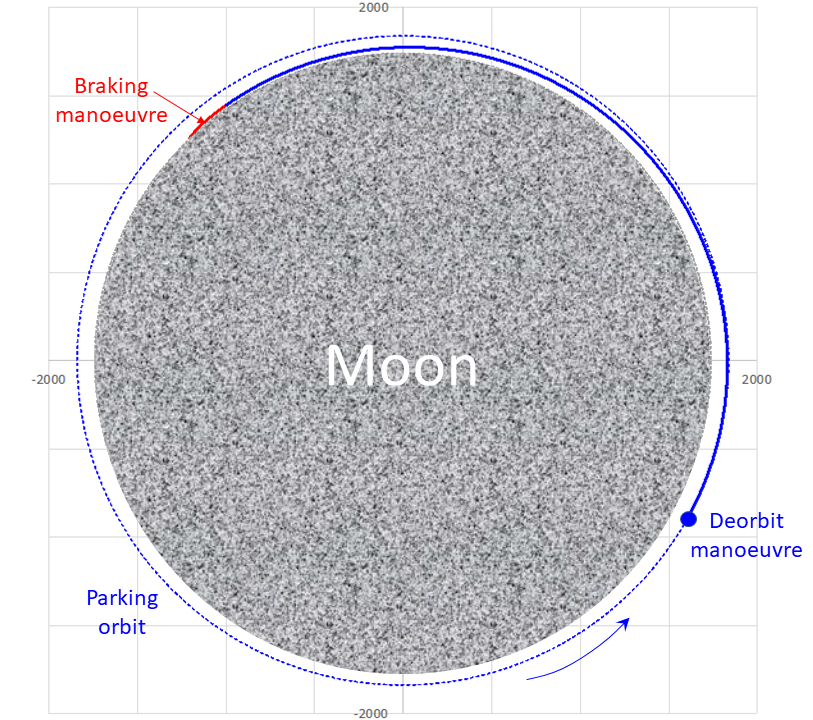
Das Diagramm ist zwar etwas vereinfacht, aber maßstabsgetreu. Man hat zunächst ein ziemlich kleines Manöver, das aus der kreisförmigen eine leicht exzentrische Bahn macht, sagen wir etwa 100 x 15 km. Dieses Manöver muss etwa einen halben Umlauf vor dem Erreichen des Landeorts durchgeführt werden. Die Kreisbahn hat eine Umlaufperiode von knapp 118 Minuten. Die elliptische Bahn hat eine Umlaufdauer von rund 114 Minuten.
Kurz vor Erreichen des niedrigsten Punkts auf der exzentrischen Bahn beginnt das große Bremsmanöver. Dabei muss die Lage der Sonde kontinuierlich verändert werden, sodass die Bremswirkung in die erforderliche optimale Richtung zeigt. Während des Großteils des Manövers ist die optimale Richtung die entgegen dem aktuellen Geschwindigkeitsvektor. Das wird auch als “gravity turn” bezeichnet; ich habe der Einfachheit halber angenommen, dass diese Bedingung während des gesamten Manövers gilt.
Ferner habe ich angenommen, dass am Ende des Bremsmanövers, wenn die Fluggeschwindigkeit bereits niedrig ist, der Schub reduziert wird. Das ist in der Realität immer so. Niemand fliegt mit Vollschub der Landung entgegen – es wäre viel zu schwierig, auf diese Weise annähernd eine Geschwindigkeit nahe Null bei Höhe nahe Null zu erreichen. Schauen wir uns jetzt den Verlauf der Bahnhöhe ab dem Deorbit-Manöver an.
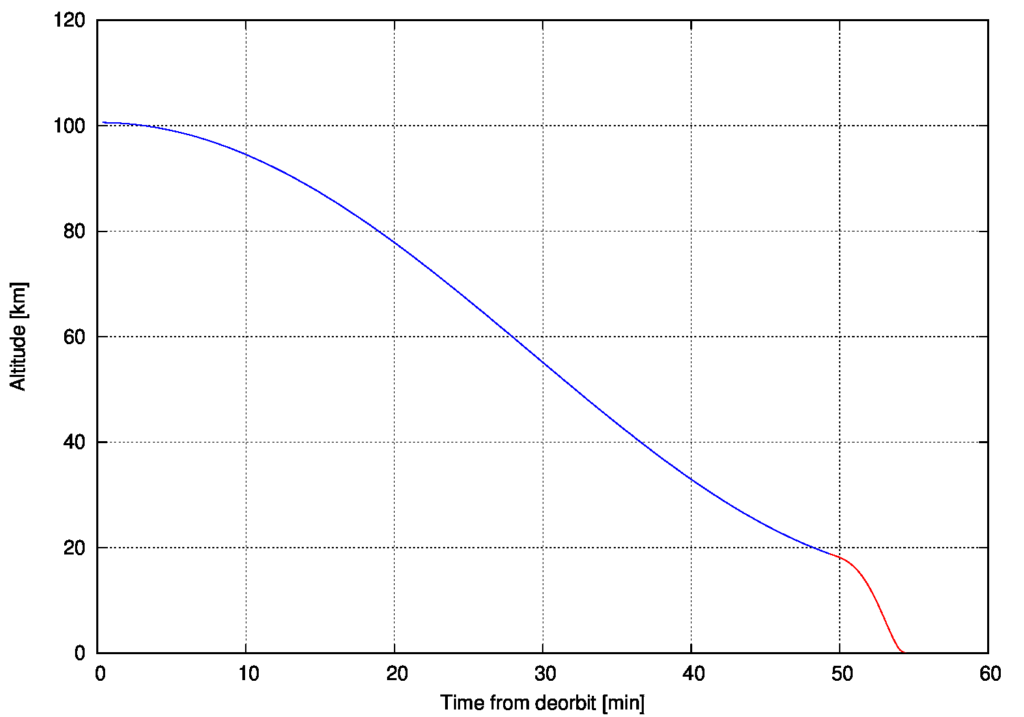
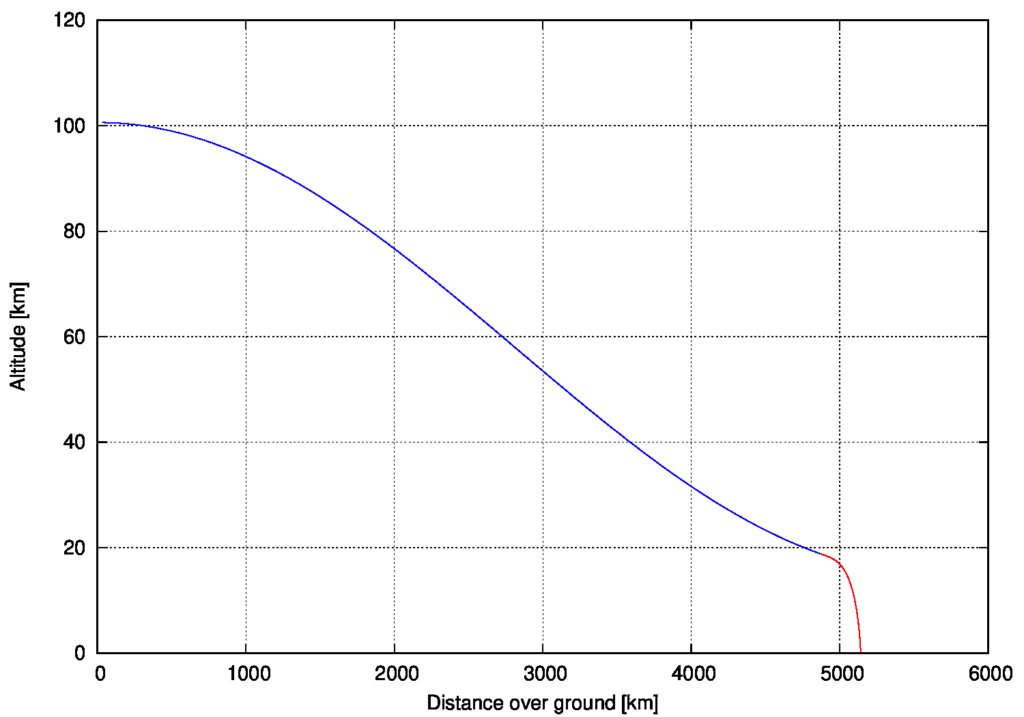
In der ersten Grafik ist die Höhe über der Zeit, in der zweiten über der zurückgelegten Strecke über Grund aufgetragen. Wie man sieht, ist die Zeit zwischen Deorbit und Aufsetzen nicht ganz die halbe Bahnperiode und die Strecke auch nicht ganz der halbe Mondumfang. Wie lange es genau dauert und wie weit die Sonde fliegt, das hängt von dem Eigenschaften des verwendeten Triebwerks und der Regelungsstrategie ab. Schauen wir uns jetzt noch die eigentliche Bremsphase am Ende an.
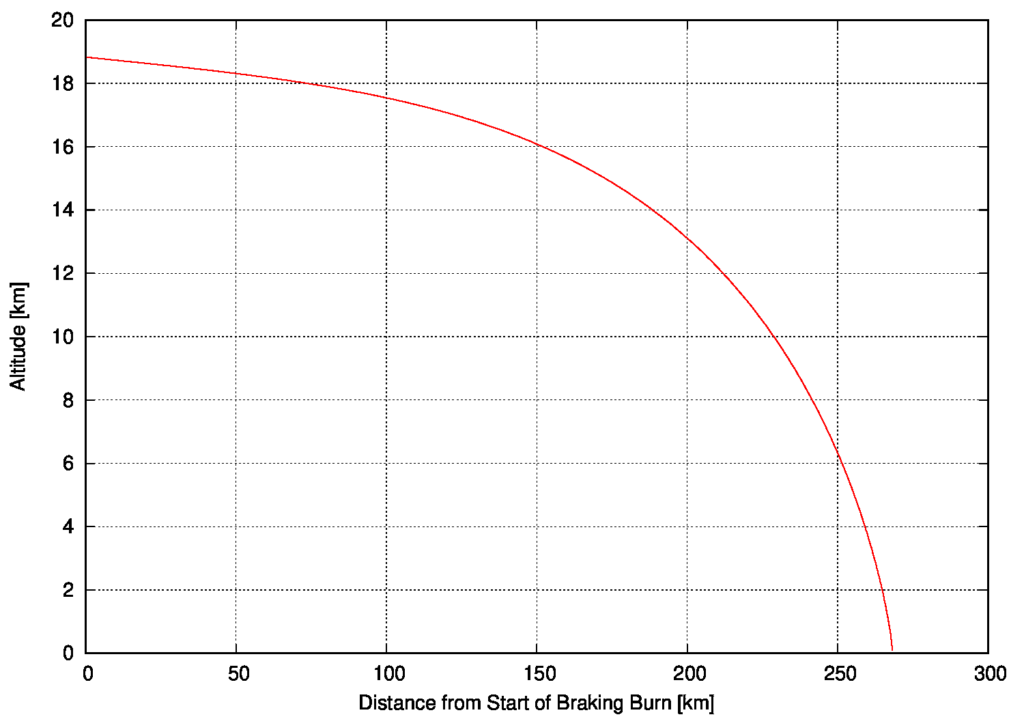
Da werden mehr als 250 km zurückgelegt und die Bahnhöhe wird von rund 19 auf 0 km verringert. Nochmals: die exakten Verläufe sind von Landesonde zu Landesonde verschieden. Das hier ist nur ein Beispiel, allerdings schon ein einigermaßen repräsentatives.
Mögliche Fehlerszenarien
Wie schon oben ausführlich dargelegt, eine Fehlberechnung des Treibstoff-Budgets erscheint mir nicht plausibel. Aber es kann schon Probleme geben, die dazu führen, dass es am Ende nicht zur sicheren Landung reicht.
Erster Hinweis: Wie man dem ersten Diagramm weiter oben im Artikel entnimmt, muss das Deorbit-Manöver schon rund einen halben Umlauf vor dem Landeort stattfinden. Das bedeutet aber auch: Wenn auf der erdzugewandten Seite des Mondes gelandet werden soll, muss das Deorbit-Manöver unvermeidlich über der erdabgewandten Seite durchgeführt werden. Das heißt, wahrscheinlich kann die Durchführung des Manövers nicht direkt überwacht werden, weil der Mond im Weg ist und keine Funkverbindung zur Sonde besteht.
Wenn nun das Manöver vergeigt wird – und dafür gibt es verschiedene Möglichkeiten – dann kriegt man es erst mit, wenn die Sonde wieder aus dem Funkschatten heraus kommt. Dann hat man aber sehr wenig Zeit, um die Situation zu analysieren, eine Go/No-Go-Entscheidung zu fällen und das entsprechende Telekommando an die Landesonde zu schicken, damit das Bremsmanöver nicht startet. Wenn dieses bereits begonnen hat, ist es wahrscheinlich zu spät für eine erfolgreiche Intervention.
Aus den anderen Diagrammen kann man ablesen, dass die Landung nur erfolgreich sein kann, wenn die Bahnhöhe bei Beginn des Bremsmanövers eine bestimmte Höhe hat. Wenn das Deorbit-Manöver zu hoch ausfiel, dann wird das Periselenium zu niedrig sein und die Sonde schafft die Abbremsung nicht mehr, bevor es kracht.
Wenn das Deorbit-Manöver aber zu gering ausfiel, dann ist das Periselenium noch zu hoch. Wenn nun das Bremsmanöver durchgeführt und erfolgreich absolviert wird, dann endet es mit Null-Geschwindigkeit in erheblicher Höhe, vielleicht einige km oder mehr, je nachdem, wie viel beim Deorbit gefehlt hat. So viel Treibstoff, um das jetzt noch zu retten, wird nicht an Bord sein. Irgendwann ist der Tank leer und die Sonde legt den Rest der Strecke im freien Fall zurück und schlägt hart auf … oder sehr hart. Der Mond hat zwar nur ein Sechstel der Anziehungskraft der Erde, aber beim freien Fall aus nur 1 km Höhe würde der Aufschlag trotzden mit mehr als 200 km/h erfolgen.
Wie kann das Deorbit-Manöver so weit daneben liegen? Dafür gäbe es diverse Möglichkeiten. Es könnte per Telekommando eine falsche Manövergröße vorgegeben worden sein oder aber die Ausrichtung der Sonde zum Manöverzeitpunkt war nicht korrekt, sodass das ansonsten korrekt ausgeführte Manöver nicht in die korrekte Richtung zeigte und deswegen nicht seine volle Wirkung entfaltete. Das für das Deorbit-Manöver verwendete kleine RCS-Triebwerk könnte zuwenig Schub geliefert haben, oder aber eine andere, nicht rechtzeitig erkannte Fehlfunktion verhinderte das Zünden dieses Triebwerks oder brach es mitten im Manöver ab. Raumsonden sind komplexe Maschinen.
Wenn das Manöver selbst nicht direkt beobachtet werden konnte, hängt alles daran, wie die Steuerung an Bord programmiert wurde. Die Ausführung des Manövers müsste durch die Trägheitsplattform (IMU=”Inertial Measurement Unit”) überwacht worden sein und das automatische Regelungssystem müsste die Autorität haben, das darauffolgende Bremsmanöver zu unterbinden. Wenn das nicht gegeben ist, dann erzeugt ein zunächst noch relativ kleiner Fehler in der Folge einen viel größeren, der zum Verlust der Landesonde führt.
Wenn es nun also keine Möglichkeit gibt, ein so kritisches Manöver direkt zu überwachen, dann könnte man wenigstens die Sequenz so auslegen, dass zunächst ein kompletter Umlauf auf der exzentrischen Bahn erfolgt, sodass die Leute im Kontrollzentrum die Chance haben, einen Fehler zu entdecken und einzugreifen.


Hört sich gerade nicht unkompliziert an, aber es war ein start-up-Versuch, der gerechnet hat 😉
Kompliziert ist eigentlich nur die Berechnung der Budgets für delta-v and Treibstoff. Allerdings muss man nur aufpassen, dass man nichts vergessen hat und alle Margins richtig anwendet. Eigentlich ist das nichts mehr als eine reine Fleißaufgabe.
Die wirkliche Take-Home-Message ist, dass man sich bei kritischen Manövern die Möglichkeit zur Überprüfung und des Eingreifens offenhalten sollte. Einfach, weil man gerade bei einem neuen, unerprobten System nicht davon ausgehen kann, dass man das Verhalten des Systems hinreichend genau kennt, um sich auf dessen korrektes Funktionieren verlassen zu können.
PS:, Ja, es ist ein Start-Up-Unternehmen, allerdings haben die ja auch ordentlich Kohle eingesammelt (300 M$ wurden genannt). Mit dem Kapital kommen gewisse Verpflichtungen. Auch ein kleines Start-Up-Unternehmen (ispace scheint gar nicht so klein zu sein) kann Consultancy einholen. Manche sogar ohne Kosten, beispielsweise zum Thema Minimierung der Risiken bei kritischen Operationen. Andere Start-Ups kommen ja auch mit ihren Fragen zu Raumfahrtagenturen; ich habe auch schon an mehreren Meetings teilgenommen, bei denen jeweils eine Start-Up sich zu bestimmten Fragenkomplexen beraten ließ.
Entscheidend scheint der Bahnpunkt zu sein an dem das Bremsmanöver, also die allerletzte Phase, beginnt, also ungefähr 20 Kilometer über Grund. Falls man dort mit falschen Werten/falscher Geschwindigkeit ankommt, dann braucht man sehr viel mehr Treibstoff um ohne Zerschellen unten anzukommen. Und diese kritische Phase bevor man zum Beginn des Bremsmanövers kommt, die liegt im Funkschatten. Das bedeutet, dass jede Abweichung vom korrekten Kurs des Deorbit-Manövers automatisch korrigiert werden muss. Und da es immer Abweichungen gibt, muss das System sehr „feinfühlig“ reagieren. Es könnten damit auch falsche Messwerte der IMU eine Rolle spielen. Oder die Steuerungssoftware war nicht ausgereift.
Ob es 20 km oder ein etwas anderer Zielwert sind, hängt an der Auslegung des Antriebssystems, aber ja, am Ende wird es in der Größenordnung sein.
Das Deorbit-Manöver muss eigentlich nur sicherstellen, dass die richtige Bahnhöhe im richtigen Abstand vor dem Ziel-Landeort erreicht wird, denn von Start des Bremsmanövers bis zur Landung werden immer noch rund mehrere Hundert km zurückgelegt. Auch das ist abhängig von der Auslegung des Antriebssystems. Eigentlich ist das keine besonders schwer zu erfüllende Zielsetzung. Man muss einfach nur zum richtigen Moment ein Manöver der richtigen Größe in Anti-Geschwindigkeitsrichtung absolvieren.
Wenn man den richtigen Zeitpunkt verfehlt, kommt der Lander an einer ganz anderen Stelle herunter als geplant, was nicht wünschenswert ist und wahrscheinlich das Risiko eines Fehlschlags erhöht, aber nicht unbedingt zum Scheitern führt.
Wenn man aber die Manövergröße oder -richtung nicht hinbekommt, ist man ganz schnell am Punkt, wo der Fehler nicht mehr abgefangen werden kann, sobald das Bremsmanöver begonnen hat. Deswegen sollte man kein solches Konzept wählen, das keine Möglichkeit zur Korrektur zulässt. Man sollte einfach noch eine Ehrenrunde auf dem exzentrischen Orbit drehen, wodurch das Kontrollzentrum Zeit zum Eingreifen gewinnt.
Das gilt auch dann noch, wenn die Ursache des Scheiterns im gegebenen Fall doch nichts mit einem nicht korrigierten Fehler beim Deorbit-Manöver zu tun haben sollte. Man sollte niemals grundlos ein Risiko eingehen. Ein falsches Deorbit-Manöver könnte weitgehend unkritisch sein, wenn man die Gelegenheit zur Nachkorrektur zulässt.
Übrigens behaupten die Leute der Amateurfunkerstation AMSAT in Bochum, sie hätten noch bis 18:45, also 5 Minuten nach dem geplanten Landezeitpunkt das Signal von Hakuto-R empfangen. Das ist zwar noch kein Beweis für das von mir skizzierte Fehlerszenario, aber vielleicht schon ein Hinweis.
Ich erinnere mich an die Anfangszeit der Computerspiele (“Pong” ) und daran, dass es damals auch ein Spiel “Mondlandung” gab:
Ein Lander flog mit Geschwindigkeit v auf den Mond zu ( vertikal ), man hatte eine Menge Treibstoff zur Verfügung und musste durch die Pfeiltasten den Bremschub so einrichten, dass man mit minimal Treibstoff=0 mit Geschwindigkeit v=0 auf der Höhe=0 ankam.
Meistens jedoch war noch Geschwindigkeit übrig, wenn der Treibstoff bereits verbraucht war …
Es gab auch die Fälle von Überbremsung, der Lander stieg dann mit dem Zuviel an Schub wieder etwas auf, dann war der Treibstoff verbraucht und es ging dann ungebremst abwärts.
Die häufige “Antwort” des Programms:
“Herzlichen Glückwunsch! Sie haben einen neuen Krater erzeugt, er hat einen Durchmesser von … “
Ich hatte als Student so ein Spiel auf meinem Computer, aber ich meine mich zu erinnern, dass es bei meinem auch eine zusätzliche Schikane mit Bergen gab, denen man durch seitliches Manövrieren ausweichen musste. Man wurde durch mehrfaches Versuchen immer besser, bald hatte ich kaum noch Abstürze.
Die Situation des Mondlanders mit dem Treibstoff und der Geschwindigkeit ist im Grunde der Lebenssituation eines Studenten nicht unähnlich. Beim Studenten war am Ende des Geldes manchmal noch sehr viel Monat übrig.
Anders als beim Studenten hätte es beim Mondlander jedoch möglicherweise einen relativ einfachen Weg gegeben, um trotz des anfänglichen Problems noch erfolgreich zum Ziel zu kommen.
In meiner Penne hatten wir einen Olivetti 6040 mit LED-Zeilendisplay (einzeilig, IIRC, also kein Bildschirm), an dem ich ein paar große Krater produziert habe (nur vertikale “Bewegung”, ausgedrückt als Werte von h und v).
Was ich hier sehr empfehlen kann, ist das Spiel Kerbal Space Program. Da kann man das mal realistischer ausprobieren, und zwar nicht nur die Landung sondern auch andere Flugphasen. Sogar Rendezvous-Manöver und Andocken gehen da.
Läuft übrigens auch unter Linux.
Urs Ganse hat bei einem CCC-Kongreß übrigens mal einen sehr interessanten Vortrag über das Fliegen von Raumschiffen gehalten. (Wobei es da generell um’s Fliegen ging und weniger um Landungen.)
Und hat sich dabei auch dieses Programms bedient um gewisse Dinge (wie z.B. den Hohmann-Transfer) zu veranschaulichen. Den Vortrag kann man noch nachschauen: https://www.youtube.com/watch?v=7cpdOR4nFRU
Ca. 5 Minuten dauert auf dem Mond der freie Fall aus ca. 70 km Höhe.
Hier wurde schon sehr viel über Sicherheitsmargen usw. geschrieben. Das ist sicher auch alles richtig. Ich würde aber doch zur Verteidigung der Missionsplaner anmerken, dass in der Raumfahrt eigentlich fast immer wenn jemand versucht das erste Mal auf etwas anderem zu landen am Ende ein mehr oder minder großer Schrotthaufen auf dem Himmelskörper ankommt. Und den Preis für den peinlichsten Absturzgrund wir noch auf lange Sicht der Mars Climate Orbiter halten…
Einspruch. Der Preis für den dümmsten Fehlschlag gebührt ganz ohne Zweifel Schiaparelli.
Der wirkliche Hintergrund des ungewollten Eintritts des MCO wurde von den wenigsten Leuten, die darüber reden, wirklich verstanden. Da wird meist etwas von “Meilen mit Kilometern verwechselt” erzählt, ohne wirkliches Verständnis der Hintergründe.
Sehe ich das richtig: es sind beim Livestream am Tag der versuchten Landung nie Daten gezeigt worden, die auf wirklicher Telemetrie basierten? Die dargestellte Höhe und Geschwindigkeit folgte nur aus einer Simulation, und ich vermute, das Radarsymbol, das suggerierte, dass das Bordradar die Höhe über dem Monden misst, war auch nur simuliert.
Mir kam das auch “komisch” vor, wie Zeichentrickfilm.
Ich hatte was Dolles erwartet, so mit Landekamera zum Zugucken.
Genau das, die Livekamera während der Landung, haben die Chinesen mit Chang’E-3 schon vor über 10 Jahren gebracht, und die hatten anders als Hakuto-R auch den Haltepunkt in ihrer Trajektorie. Und dann haben sie es auch auf Anhieb geschafft. Angesichts der vielen Sponsoren aus der japanischen Wirtschaft war die Show von ispace wirklich erstaunlich dürftig.
“Sehe ich das richtig, oder sind beim Livestream am Tag der versuchten Landung nie Daten gezeigt worden, die auf wirklicher Telemetrie basierten?” Der Startkommentator hatte zu Beginn des Webcasts davor gewarnt, den eingeblendeten Zahlen zu trauen – und sie müssen ja auch wirklich grob falsch gewesen sein, denn auf der Erde wurde das Funksignal noch bis 18:45:10 MESZ empfangen, volle 5 Minuten nach dem nominellen Landezeitpunkt (das wissen wir von den beteiligten Amateurfunkern in Europa, im iSpace-Stream erwähnten sie die Diskrepanz nicht). Dem Anschein im letzteren nach glaubten sie in der MC bis 18:39 MESZ oder so an einen nominellen Abstieg und staunten dann wohl sehr.
Auf einer Pressekonferenz einige Stunden später war dann von einem gestörten Höhenmesser die Rede, der an allem Schuld gewesen sei, aber eine detaillierte Darstellung des gesamten Abstiegs – und ab wann und wie er vom geplanten abwich – aufgrund der Radiobeobachtungen (im Auftrag von iSpace war übrigens eine Schüssel der ESA maßgeblich beteiligt) und einer ggf. nachträglich korrigierbaren Telemetrie habe ich noch nicht gesehen. Vor dem bitteren Ende gab sich iSpace in dem Webcast betont offen: Ich hoffe sehr, dass das auch bzgl. der Untersuchung des Fehlschlags (wieder) so sein wird, schließlich lernen dann auch die vielen andere Privatmondlander in der Warteschlage daraus.
Ich denke, das Auffangen des Signals von Hakuto-R ist ein gewichtiges Indiz, das man nicht ignorieren kann. Wahrscheinlich liegt dort der Schlüssel zur Suche nach der Ursache des Versagens. Das von mir skizzierte Szenario des zu geringen Deorbit-Manövers wäre mit der Beobachtung aus Bochum vereinbar.
hallo zusammen,
sicher ist das mit der *web-cam* vom mond nicht ganz einfach,
die telemetrie geht da an datenstrom sicher vor, aber würde die sendeleistung da heute nicht auch dafür ausreichen?.
kein vergleich: aber heute nacht startet wieder eine Falkon-Heavey, da gibt es immer bilder. von den zwillingsboostern die sicher wieder syncron landen, und mir immer noch jedesmal schleierhaft, das ganze auf einem schwankenden schiff auf dem weiten meer aufsetzen zu lassen.
man kann sagen was man will, aber das haben die spaceX’ler echt im griff
um halb 2 live: https://www.rocketlaunch.live/?filter=falcon-heavy
grüssle
Mar(ku)s
2 Fragen:
a) wäre es nicht sinnvoll, die Sonde auf dem Papier einen Faktor X schwerer zu machen, um die ganzen “margins” nicht seperat rechnen zu müssen? Masse ist Masse egal ob aus Folie oder Metall.
b) Wie kann man denn den Abstand zum Boden genau messen? Der Mond ist schließlich nicht flach. Welche “Margen” gibt es hier für den “Aufschlag”, wie schnell er sein darf um nicht schädlich zu sein.
Die Sicherheitsmargen sind nicht für alle Manöver gleich groß, sie hängen von Kritikalität, Triebwerkstyp, Manöverdauer und anderen Faktoren ab.
Am Ende ist es eine Frage der Erfahrung, wieviel man man wo ansetzt. Der eigentliche Rechenvorgang ist nicht das Problem, das kann man eben mal in der Tabellenkalkulation machen. Die Schwierigkeit liegt darin, die Manöver selbst zu berechnen, bzw. die ganze Strategie, um zum Ziel zu kommen. Aber das ist ein ganz anderes Thema und hat mit dem Blogartikel nicht mehr so viel zu tun.
Den Abstand zum Boden misst das Radar oder Lidar, und wenn der Boden so uneben ist, dass die Messung versagt, dann sollte man dort ohnehin keine Landung versuchen.
Wie schnell man maximal aufsetzen darf, bestimmen die Landebeine. Bevor man den Hersteller aussucht und das Modell wählt, muss man deren “specs”, die Auflistung der Spezifikationen lesen. Da steht genau drin, für welche Kombinationen aus Landermasse und Aufsetzgeschwindigkeit, bis zu welcher Schieflage etc. ein jeweiligen Produkt qualifiziert ist. Für alle zugekauften Bauteile gibt es solche “specs”. Die Entwicklungsingenieure verbringen viel Zeit mit dem Wälzen von Katalogen. Das ist aber wohl bei jeder technischen Entwicklung ähnlich.
Ich danke Kerbal Space Program dafür, dass ich in der Lage bin diesen Artikel zu verstehen und genießen.
Ich frage mich gerade, wie die Tanks einer Sonde im All funktionieren. Also, wie der Treibstoff in die Triebwerke kommt. Stehen die Tanks unter Druck? Wie wird dieser Druck produziert?
Die Schwerkraft kann es ja nicht.
Ja, Tanks stehen unter Druck durch ein Inertgas, das in einem Drucktank gespeichert wird. Wenn der Druck gegen Ende der Mission nachlässt, kann auch der Schub der Triebwerke nachlassen oder das Mischungsverhältnis zwischen Brennstoff und Oxidator sich ändern. Das erschwert die Vorhersage des Treibstoffverbrauchs und verringert die Ausführungsgenauigkeit der Manöver. Auch die Kenntnis der verbleibenden Treibstoffmenge wird zunehmend ungenauer. Ein Grund mehr für ausreichende “margins”.
Solange Schub geleistet wird, sammelt sich der Treibstoff ja “unten” im fast leeren Tank, aber sobald mal nicht gebremst wird, hilft auch kein Inertgas mehr, die schwebenden Flüssigkeitsblasen in die Kraftstoffleitungen hineinzubekommen. Wie löst man dieses Problem? Vielleicht mit einem kleinen Hilfsschub, den zu erzeugen, hätte aber auch das gleiche Problem…
Eine häufige Bauart bei Tanks hat eine flexible Membran im Inneren. Auf der einen Seite ist der Treibstoff, auf der anderen das Druckgas.