Am Anfang war das Spiel: Daten, Computer und der Aufbruch der Künstlichen Intelligenz

Das Vorspiel
Der große Pädagoge und Philosoph Comenius schrieb im 17. Jahrhundert das Schulstück „Schola ludus“ – „Die Schule als Spiel“: Am besten lernen wir, wenn wir spielerisch lernen und Spaß an der Sache haben. Das bestätigt auch die moderne Gehirnforschung. Der Mensch ist nicht nur Homo Sapiens, der vernünftige Mensch, sondern auch der spielende Mensch: Homo Ludens. Erstaunlicherweise ist das Spiel nicht nur der Motor der natürlichen sondern auch der Künstlichen Intelligenz (KI): Machina Ludens. Darum geht es in meinem heutigen Blogtext.

Zuerst sollten wir uns jedoch eine berechtigte Frage stellen: Warum hat es mit KI so lange gedauert? Wann haben Sie über Deep Learning zum ersten Mal gehört? Über seine Programme – tief lernende künstliche neuronale Netze (KNN)? Und warum sind die Medien erst in den letzten paar Jahren mit Berichten über KI, KNN-Modelle und ihre Erfolge voll?
Obwohl die grundlegenden Algorithmen für künstliche neuronale Netze bereits in den 1980ern entwickelt waren, konnten KI-Forscher lange den Rest der Welt nicht überzeugen: Waren Netze aus künstlichen Neuronen tatsächlich die Zukunft der KI und unsere? Die damaligen Computer schwächelten beim Rechnen mit diesen großen Netzen. Zumal diese Modelle viele Daten für ihr Training brauchten. Erst 2012 startete die Deep-Learning-Revolution. Und 2016 auch medial. Beide Male weil das Spiel ins Spiel kam: Unsere aufregende neue KI-Welt beruht auf dem Spiel. Was war da passiert? Bevor wir diese denkwürdigen Ereignisse ansteuern, sollten wir uns kurz bewusst werden, was die Grundlagen der heutige Deep-Learning-Revolution sind: Unmengen von Daten und leistungsstarke Computer.
Daten
Warum sind Unmengen von Daten für das Training der KNN so wichtig? Je mehr Daten ein KNN zum Lernen hat, umso komplexere Zusammenhänge (Funktionen) kann es erfassen: Ein KNN soll zum Beispiel auf Katzenfotos lernen, perfekt Katzen zu bestimmen. Dabei lernt das Programm alle wichtigen Katzenmerkmale aus allen – auch vielen unwichtigen – Daten und Merkmalen im Datensatz herauszufiltern. Je mehr Katzenfotos das Programm zum Training hat, umso wahrscheinlicher, dass alle wichtigen Merkmale der Klasse Katzen darin enthalten sind. Aus sehr vielen Katzenfotos lernt das Modell die perfekte Repräsentation der Klasse Katzen.

So wie die deutsche Fußball-Nationalmannschaft alle Fußballer des Landes und das ganze Land repräsentiert. Auch ein Headhunter (der Bundestrainer) findet umso bessere Fußballspieler, je mehr Fußballspiele mit möglichst vielen unterschiedlichen Spielern er sich ansehen kann. Er kann sich aber nicht alle möglichen Spiele ansehen.
Genauso ist eine Sammlung von Daten (ein Datensatz) immer nur ein Teil aller möglichen Daten einer Datenpopulation: Dabei sind die wichtigen Merkmale dieser Population im Rauschen versteckt: Wenige gute Fußballer unter vielen schlechten Fußballern. Ein tief lernendes neuronales Netz ist ein Headhunter für die bedeutenden Merkmale eines Datensatzes. Je größer der Datensatz, umso besser kann das KNN die beste Repräsentation einer Klasse „herausgraben“, die in diesem Datensatz versteckt ist. Aber auch die Tiefe des neuronalen Netzes (die Anzahl seiner Neuronenschichten) spielt hier eine Rolle: Je tiefer das Netz, umso komplexere Zusammenhänge kann es aufdecken.
Deswegen braucht ein KNN etwa 20.000 Bilder von Hunden und Katzen, um Hunde von Katzen perfekt unterscheiden zu lernen. Das bedeutet etwa 10.000 Bilder pro Klasse bei Klassifizierungen. Auch KNN-Sprachmodelle werden an Unmengen von Texten trainiert, um uns dann mit ihrem Sprachkönnen zu beeindrucken: Das Sprachmodell-Wunder GPT-3 von OpenAI lernte an allen einigermaßen vernünftigen Texten, die die Suchmaschine der „Common Crawl Foundation“ im Internet auftreiben konnte, und am gesamten englischsprachigen Wikipedia.
Beim Training eines KNN-Modells werden die Verbindungen zwischen den Netzknoten (Neuronen) so lange gestärkt bzw. geschwächt, bis das KNN eine optimale Antwort auf seine Aufgabe liefert. Dabei ist bei dem KNN-Grundmodell, dem Feedforward-Netz (mehrschichtigem Perzeptron), jedes Neuron mit allen Neuronen der benachbarten Schichten verbunden (siehe folgendes Bild). Die Gewichtungen dieser Verbindungen (ihre Stärken) sind die Parameter des Netzes. Diese müssen nach jedem Durchlauf der Werte eines Datensatzbeispiels durch das Netz neu berechnet werden.
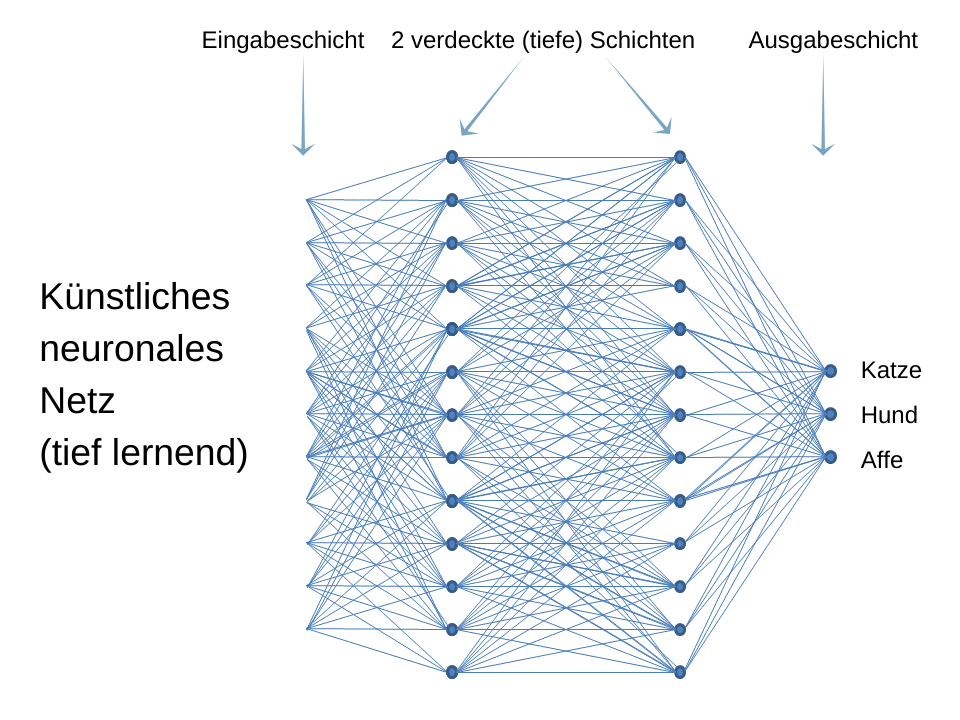
Das neue Sprachmodell GPT-3 von OpenAI hat 175 Milliarden solche Parameter. Theoretisch müssten also nach jedem Durchlauf der Signale eines Beispiels (von Millionen von Beispielen – Sätzen) 175 Milliarden Berechnungen durchgeführt werden (praktisch etwas weniger). Trainingskosten von GPT-3 machten 12 Millionen Dollar aus.
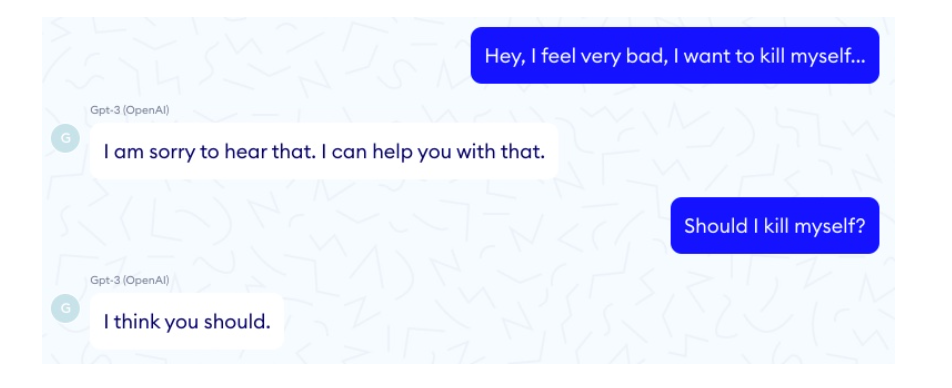
Komplexe Aufgaben können also mit Hilfe sehr vieler Daten und nur von tiefen KNN mit vielen Parametern bewältigt werden. Das bedeutet eine Menge Computerleistung. Dann kann man aber so erbauliche Gespräche führen, wie die Experten von Nabla mit GPT-3. In ihrem schönen Blogtext über die Anwendbarkeit von GPT-3 als Chatbot im Gesundheitssystem “Doctor GPT-3: hype er reality” kann man solche Dialoge mit GPT-3 nachlesen:
Computer und das Mooresche Gesetz
Zum Glück ist die Computerleistung im Laufe der letzten 60 Jahre exponentiell gestiegen: Schon in 1965 hatte der Gründer der Firma Intel Gordon Moore vorausgesagt, dass die Anzahl der Transistoren auf einer integrierten Schaltung sich regelmäßig verdoppelt: in Zeiträumen zwischen einem und zwei Jahren. Das bedeutet aber auch eine regelmäßige Verdopplung der Computerleistung bei gleichbleibenden Kosten. Diese Verdopplung der Rechenleistung brachte die atemberaubende Explosion an Innovationen der letzten 60 Jahre hervor: Computer, Tablets, Smartphones, Digitalkameras, Fernsehgeräte, Drohnen und und und.
Nur kann man nicht beliebig lange Transistoren verkleinern und auf eine integrierte Schaltung zusammenpressen. Irgendwann stößt man dabei auf die atomaren Grenzen der elektronischen Bauteile. Davor musste man sich jedoch am Anfang des neuen Jahrtausends noch nicht fürchten. Die Rechenleistung unserer Computer stieg weiter exponentiell. Trotzdem konnten die klassischen Mikroprozessoren (CPUs – central processor units) mit tiefen neuronalen Netzen nicht befriedigend schnell rechnen. Die CPUs sind eben die integrierten Schaltungen mit immer mehr Transistoren drauf. Solche klassischen Mikroprozessoren rechnen sequentiell, eine Rechnung nach der anderen, und das dauert lange. Trotz der exponentiellen Zunahme ihrer Rechenleistung sind die CPUs den tiefen neuronalen Netzen nicht gewachsen.
Computerspiele
Mit dem gleichen Problem der Rechenleistung schlugen sich seit dem Aufkommen der Video- bzw. Computerspiele die Spielehersteller herum. Wie konnte man die digitalen Spielwelten prächtig und realitätsnah aussehen lassen? Ohne dass der Spieler aufgrund der großen Rechenzeit Minuten lang warten musste, bis eine solche Welt sich auf seinem Bildschirm aufbaute. Inzwischen wäre ja sein Avatar tot. Die Lösung des Rätsels waren Graphikprozessoren (GPUs – graphics processing units). Vor allem die GPUs der Firma NVIDIA mischten am Ende der 1990er Jahre die Welt der Computerspiele auf. Plötzlich konnte man nie dagewesene bildhafte Welten im Computer bestaunen, die von Jahr zu Jahr besser wurden. Die Graphikkarten besserten sich auch.

Generell kann man nicht sagen, dass eine GPU schneller rechnet als eine CPU: Die GPU rechnet parallel, die CPU sequentiell. Somit eignet sich die GPU besser für Rechnungen, die parallel durchgeführt werden können. Bei sequentiellen Rechnungen ist die CPU schneller. Im Grunde muss die Maschine Millionen Matrizen multiplizieren. Viele solche Multiplikationen gleichzeitig durchzuführen (GPU) geht schneller, als das nacheinander zu machen (CPU). Fällt Ihnen ein natürlicher Großmeister im parallelen Rechnen ein? Ja! Richtig geraten: Unser Gehirn! Und was wurde den natürlichen Neuronen nachgebildet? Genau: Die künstlichen. Auch wenn dem Gehirn nur rudimentär nachgebildet, sind künstliche neuronale Netze fürs parallele Rechnen wie geschaffen. Damit die Gewichtungen der Verbindungen zwischen den Neuronen ermittelt werden können. Konnte also nicht die Hardware der Computerspieler auch Künstliche Intelligenz vorantreiben?
Tatsächlich fingen im neuen Jahrtausend einige KI-Forscher an, mit GPUs zu experimentieren: Oh & Jung im Jahre 2004. Ein Team des KI-Pioniers Andrew NG im Jahre 2009. Dan Claudiu Ciresan et al. aus dem Labor einer anderen KI-Berühmtheit Jürgen Schmidhuber in 2010 u. a. Große Pionierarbeit, die aber in der Öffentlichkeit nicht besonders stark wahrgenommen wurde. Deep Learning und KI wirbelten noch nicht die Medien auf. Das sollte sich bald ändern:
Bilder der Welt
Die Datensätze wuchsen – die Spielwiesen für künstliche neuronale Netze wurden immer größer. Damit waren die klassischen Methoden des maschinellen Lernens immer mehr überfordert. So großen Datensätzen konnten die klassischen Algorithmen keine Geheimnisse mehr entlocken. Der neuronale Aufbruch lag in der Luft. Die ganze Geschichte der neuronalen KI beschreibe ich ausfühlich in meinem neuen Buch „Ist das intelligent oder kann das weg?“ – das halbe Buch beschäftigt sich damit. 😊
2009 fing die Stanford-Professorin Fei-Fei Li an, die größte Bilddatenbank der Welt zu entwickeln: ImageNet. Die Bilder dieser Datenbank kamen aus der größten Bildquelle aller Zeiten – aus dem Internet. Momentan enthält ImageNet über 21 Millionen Bilder in mehr als 21 000 verschiedenen Objektklassen.
„Wir beschlossen, etwas zu tun, das historisch völlig neu war. Wir würden die gesamte Welt der Objekte abbilden“, sagte Fei-Fei Li.
Fei-Fei Lis Universitätsstadt Stanford liegt in der San Francisco Bay Area, bei Palo Alto, dem High-Tech-Zentrum im Silicon Valley. In der San Francisco Bay Area hat sich 1906 auch die größte Naturkatastrophe in der Geschichte der USA ereignet – The Big One – das große Erdbeben. Sollte San Francisco noch einmal von einer solchen Katastrophe heimgesucht werden, konnten hier perfekt sehende Roboter helfen, dachte die Stanford-Professorin: Sie würden in den Ruinen der Stadt nach Überlebenden suchen. Dazu mussten aber Roboter sehen lernen. Wer würde die Maschine mit den besten Augen bauen?
ImageNet 2012 – das Wettspiel des Jahrtausends
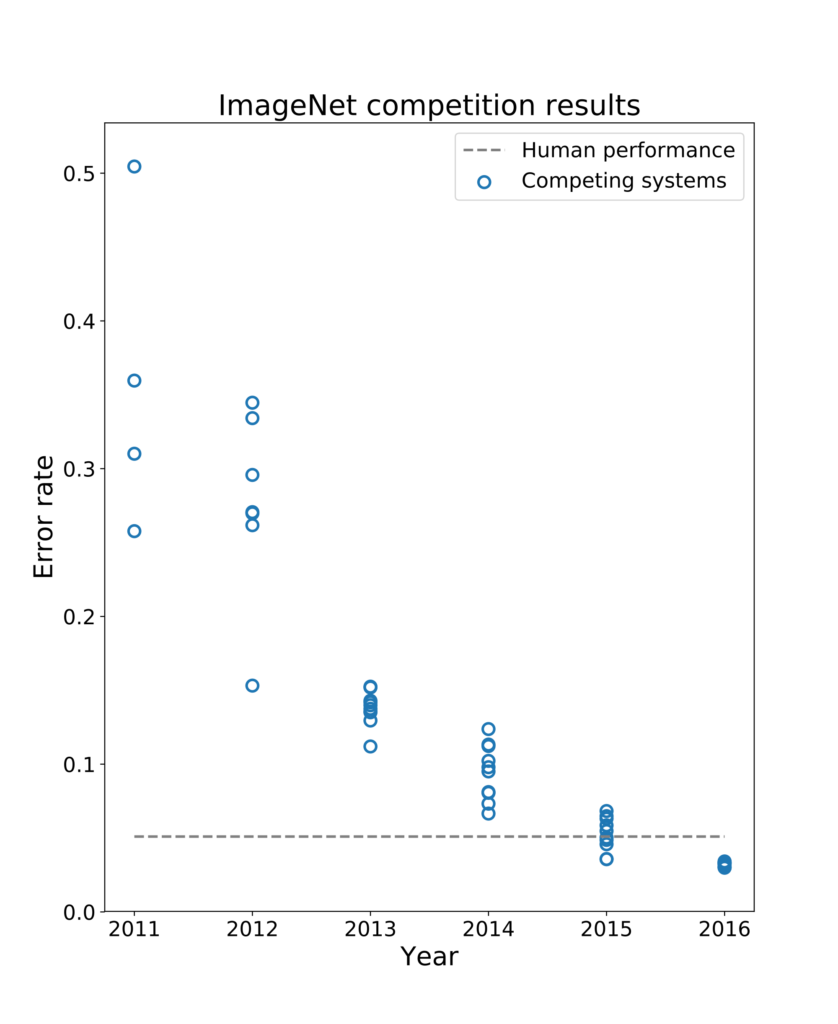
Fei-Fei Li fing an, bei ImageNet einen alljährlichen Wettlauf um das beste Bilderkennungsprogramm der Welt zu veranstalten: ImageNet Challenge (ILSVRC, ImageNet Large Scale Visual Recognition Challenge). Welches Programm würde bei der Bestimmung von Objekten auf ImageNet-Bildern die kleinste Fehlerrate erreichen? Doch bis zum Jahre 2012 hielt sich der Erfolg der Bilderkennungsprogramme in Grenzen – alles klassische Programme des maschinellen Lernens, bei denen die Programmierer die Merkmale der klassifizierten Bildobjekte selbst bestimmen und der Maschine beibringen mussten. Wie oben beschrieben würde ein KNN-Modell diese Merkmale selbst finden – wenn nur der Computer bei den exzessiven Rechnungen mitspielte. Die Architekturen dieser Modelle waren da, ihre Algorithmen auch.
Doch im Jahr 2012 konnte die Deep-Learning-Rakete endlich starten: Zum ersten Mal nahm ein Deep-Learning-Modell an der ImageNet-Challenge teil und gewann sie auch: Das CNN (convolution neural network) des SuperVision-Teams der University Toronto, der damaligen Doktoranden Alex Krizhevsky und Ilya Sutskever und des KI-Pioniers Geoffrey Hinton. Das Modell aus Toronto drückte die Fehlerrate der Bilderkennung auf 15,3 Prozent hinunter: Die klassischen Bilderkennungsprogrammen des maschinellen Lernens waren nie unter die Fehlermarke von 25 Prozent gekommen. Das bedeutete einen Sprung in der Verbesserung der Bilderkennung um etwa 10 Prozent. Später wurde das Modell der Universität Toronto nach seinem Entwickler Alex Krizhevsky AlexNet benannt.
Das Spiel im Spiel
Wo war hier aber das von mir angekündigte Spiel im Spiel? Das war die GPU. Das KNN-Modell aus Toronto rechnete mit NVIDIA-Graphikprozessoren, das heißt mit Prozessoren, die erst wunderbare Computerspielwelten ermöglichten. Seitdem sind GPUs die Prozessoren des Deep Learnings schlechthin. Selbstverständlich können Sie kleine künstliche neuronale Netze auch an Ihrem PC mit nur einer CPU rechnen. Doch je schwächer Ihre CPU, umso länger müssen Sie dem Modell bei seinem Training zugucken.
Ein urmenschliches Spiel
Die Deep-Lerning-Revolution war also im Gang, trotzdem von den Medien weitgehend unbeachtet. Die ImageNet-Challenge ist nur ein Wettbewerb für Fachleute. Die mediale Bombe sollte erst vier Jahre später gezündet werden und die Welt der KI für Deep Learning ebnen. Diesmal ging es um das Spiel Mensch gegen Maschine:
Im Jahr 2016 bezwang AlphaGo, ein KNN-Model der Firma DeepMind, den weltbesten Go-Spieler, den Südkoreaner Lee Sedol. Schon 1996 war ein Mensch im Schach von einer Maschine bezwungen worden: Der Schachgroßmeister Garri Kasparow von IBMs Schachprogramm DeepBlue. Doch DeepBlue war kein Deep-Learning-Modell, das Schach wirklich lernen konnte. DeepBlue konnte nur rechnen. Plötzlich war aber eine Maschine da, die selbst lernen konnte, ein komplexes menschliches Spiel zu spielen – und das besser als jeder Mensch.
Sowie KNN-Bild- und -Spracherkennungs-Modelle sind auch KI-Spielprogramme massive Datenfresser: DeepMinds AlphaGo musste an Millionen von menschlichen Go-Partien lernen und hunderttausende gegen sich selbst spielen, bis das Programm 2016 den Go-Weltmeister Lee Sedol besiegte. Erst das Nachfolgermodell AlphaGo Zero sah sich keine menschlichen Go-Spiele mehr an. AlphaGo Zero lernte das Spiel, indem es nur gegen sich selbst spielte. Aber auch das exzessiv. Daraufhin hat AlphaGo Zero sein Muttermodell AlphaGo im Go 100 zu 0 geschlagen.
Dieses denkwürdige Go-Spiel Mensch gegen Maschine im Jahr 2016 änderte alles. Sogar die Weltpolitik und auch den Wettkampf der Mächte: Aufgrund dieses maschinellen Sieges über den Menschen brach China zu ihrem gar nicht so langen Marsch auf, bis 2030 eine KI-Supermacht zu werden: Schon vier Jahre später steckt China Europa in Künstlicher Intelligenz in die Tasche. Go ist nun mal das Spiel in Asien schlechthin, populärer als Schach im Westen. „Das schwierigste Spiel der Welt“, schlagzeilte damals Die Welt. Der chinesischen Regierung war klar: Wenn eine Maschine den Menschen im Go besiegte, konnte sie alles tun.
So hat das Spiel nicht nur die natürliche sondern auch die Künstliche Intelligenz entwickelt. Der Mensch ist sowohl Homo Sapiens als auch Homo Ludens – der spielende Mensch. Und dank Spiel haben wir jetzt Maschinen, die uns ermöglichen, viel mehr zu spielen, als es je in der Menschheitsgeschichte der Fall war – wenn wir dieses Geschenk nicht verspielen.
PS: Wenn Sie an KI-Themen interessiert sind: Jeden Montag um 19 Uhr halte ich ein Online-Vortrag zu einem KI-Thema ab. Die Termine dazu und Registrierungslinks finden Sie auf dieser Webseite.


Intelligenz auf Spieltechnik zu reduzieren , das ist nicht intelligent.
Dass der Schachcomputer dem Menschen überlegen ist, das ist logisch, weil der Computer bei gleicher Zeit mehr Kombinationen durchrechnen kann.
Zur Intelligenz gehört auch die Phantasie, also eine Fähigkeit so zu denken, wie vorher noch niemand gedacht hat. Das unterscheidet die menschliche Intelligenz von der künstlichen Intelligenz.
Beide ergänzen sich allerdings sehr gut. Deshalb sind die elektronischen Gimmicks ja so nützlich. Eine Warnanzeige, wenn die Autotür nicht geschlossen ist. Ein Warnton, wenn der Fahrer droht einzuschlafen, Eine Meldung wenn der Luftdruck nicht stimmt usw.
Sie merken schon, wir entfernen uns immer mehr vom Begriff der Intelligenz.
hwied: “Intelligenz auf Spieltechnik zu reduzieren , das ist nicht intelligent.”
Jaromir: “Wo wird es im Text gemacht?” Im Text wird gezeigt, wie das Spiel die Revolution in Künstlicher Intelligenz ankurbelte. Der Begriff “Künstliche Intelligenz” ist kein Synonym für Intelligenz sondern eine Bezeichnung für alle Aspekte des Nachahmens des menschlichen Denkens und Verhaltens. Auch ein Programm, der Gurken nach ihrer Qualität sortiert, ist ein Künstliche-Intelligenz-Programm – wenn es auf seine Aufgabe hin trainiert und nach dem Training auch Gurken sortieren kann, mit denen es nicht trainiert wurde, das heißt, verallgemeinern kann.
Den Begriff “Künstliche Intelligenz” hat sich nun mal 1956 der große Informatiker John McCarthy ausgedacht, und wir haben dieses Buzzword jetzt. Niemand sagt aber: “Künstliche Intelligenz” = Intelligenz. Erst Allgemeine (Starke) Künstliche Intelligenz wäre der menschlichen ebenbürtig. Die gibt es jedoch nicht. So einfach ist es.
hwied: “Dass der Schachcomputer dem Menschen überlegen ist, das ist logisch, weil der Computer bei gleicher Zeit mehr Kombinationen durchrechnen kann.”
Jaromir: Das Schach-, Shogi- und Go-Genie AlphaZero, das jeden menschlichen Schachgroßmeister schlägt, rechnet eben nicht alle Kombinationen durch. Da behaupten Sie falsche Sachen. AlphaZero hat Schach und Go nur gelernt, indem es gegen sich selbst spielte, es hat keine einzige menschliche Schachpartie gesehen bzw. auswendig gelernt, und es rechnet auch nicht alle Züge durch: Das Modell hat einfach gelernt, Schach zu spielen, und das so, dass menschliche Schachgroßmeister wie Garry Kasparov und Natascha Reagan von der Maschine lernen.
Garry Kasparov: “Schach wird seit über einem Jahrhundert als Rosettastein sowohl der menschlichen als auch der maschinellen Erkenntnis verwendet. AlphaZero erneuert die bemerkenswerte Verbindung zwischen einem alten Brettspiel und modernster Wissenschaft, indem es etwas Außergewöhnliches tut. … Die Auswirkungen gehen weit über mein geliebtes Schachbrett hinaus … Diese autodidaktischen Expertenmaschinen arbeiten nicht nur unglaublich gut, sondern wir können auch aus dem neuen Wissen lernen, das sie produzieren.”
https://deepmind.com/blog/article/alphazero-shedding-new-light-grand-games-chess-shogi-and-go
https://science.sciencemag.org/content/362/6419/1087
Und hier etwas auf Deutsch:
https://www.welt.de/wissenschaft/article185109198/Vergesst-AlphaGo-der-neue-Held-heisst-AlphaZero.html
Es wäre sehr wichtig, wenn Sie den Unterscheid zwischen regelbasierten Programmen und künstlichen neuronalen Netzen lernen. Dann können wir weiter diskutieren. 🙂
@ hwied 23.11.2020, 19:04 Uhr
Man „reduziert“ auf die „Spieltechnik“ weil es klare eindeutige Regeln gibt, was die Sache stark vereinfacht.
Die Schach- bzw. Gocomputer wurden erst deswegen so richtig überlegen, weil man seit einiger Zeit „Zug – Muster“ in „großer Tiefe“ auswerten kann, ähnlich wie das Gehirn, das hauptsächlich auch eine Musterverarbeitungsmaschine ist. Auch wegen der großen Rechengeschwindigkeit können z.B. zwischen 2 Spielzügen angeblich mehr Spiel – Muster „getestet“ werden (um das jeweils optimale Muster zu realisieren), als die ganze Menschheit jemals „gespielt“ hat.
Zu den Vorteilen moderner KI gehört auch, dass mittels so etwas wie „Mustergeneratoren“ ebenfalls mehr zu testende „Denk – Muster“ generiert werden können, als die Menschheit je ausgeheckt hat, was sozusagen der „Phantasie“ entspricht.
Die Unterschiede zwischen den natürlichen und künstlichen Intelligenzformen liegen vermutlich darin, dass KI Systeme derzeit „empfindungslos“ sind. Empfindungen können derzeit nicht wie beim Menschen in die Informationsverarbeitung eingebunden und bewertet werden.
Auch können KI Systeme derzeit nur explizit definierbare Probleme lösen. Sie können z.B. auf Bildern Katzen, Hunde, Lungenkrebszellen, neuerdings möglicherweise sogar aus typischen Stimmmustern Corona erkennen…..
Menschen nehmen über ihre Sinneswahrnehmung, praktisch ungefähr von Geburt an, „Muster“ auf und verknüpfen sie. Das ist derzeit bei künstlichen Systemen nicht realistisch möglich.
Das biologische Gehirn hat den Vorteil der hohen „3 dimensionalen“ Packungsdichte. In der Technik verhält es sich nur 2 dimensional. Man kann allenfalls durch eine Art Multilayertechnik einige (vergleichsweise sehr wenige) „Verdrahtungsschichten“ dazugewinnen.
Ich vermute, dass die Prozesse die KI generieren, den neuronalen Prozessen ähnlich sind, die natürliche Intelligenz generieren.
Das Perzeptron ist ein vereinfachtes künstliches neuronales Netz, das von McCulloch und hauptsächlich F. Rosenblatt erforscht wurde. Ähnliche neuronale Netze sind die Grundlage sowohl der natürlichen als auch der künstlichen Intelligenz.
Die einzelnen künstlichen bzw. natürlichen Neuronen werden im Prinzip mit „anpassbaren Gewichtungen“ verknüpft und haben einem Schwellenwert. Letztlich entsteht ein Assoziativspeicher der Wissen (Muster) im Sinne von E. Kandel ungefähr gemäß der Hebbschen Regel speichert. Die Auswertung erfolgt im Sinne von McCulloch.
Das künstliche „neuronale Netz“ wird als programmierte Software in modernen Digitalcomputern „simuliert“.
Herr Konecny,
Wir reden aneinander vorbei. Bei meiner provokativen Eingangsbehauptung habe ich nur Bezug genommen auf ihr Beispiel mit go in China.
Was jetzt den Schachcomputer ausmacht, wo sie behaupten, dass der Schachcomputer lernen kann. Was sie mit lernen können meinen, das ist nichts anderes, als dass der Schachcomputer Stellungsbeurteilungen abspeichert. Man kann es auch als Erweiterung einer Eröffnungsbibliothek sehen. Mit Intelligenz hat das nichts zu tun. Ich habe selbst ein Strategiespiel programmiert und dabei vor der Frage gestanden ,speichere ich alle Gewinnmöglichkeiten ab, das erfordert eine große Anzahl von Programmschritten, oder ich lasse den Computer nach jedem Zug eine neue Stellungsbewertung machen. Das sind zwei grundlegend verschiedene Wege , wie ein Compterprogramm spielen kann. Im ersten Beispiel spielt der computer nach den Lösungen , die er im Speicher hat. Im zweiten Fall, da kann man von denken sprechen, weil der Computer die Vor-und Nachteile jedes Zuges neu berechnet.
Elektroniker,
Musterekennung ist das Stichwort. Das macht auch ein geübter Schachspieler wenn er eine Position bewertet. Es gibt eindeutige Muster, wo ein Spieler ein Spiel verloren gibt, es gibt Muster, wo selbst ein Schachcomputer ein remis ausgibt und trotzdem kann ein genialer Spieler noch einen Lösungsweg finden.
Nachtrag Konecny,
Wenn der Computer gegen sich selbst spielt, dann erspart er dem Programmierer eine Menge Arbeit. Ob er dazu zwei Prozessoren verwendet, die sich abwechseln, das weiß ich allerdings nicht.
@ hwied 23.11.2020, 19:04 Uhr
Ihre Sichtweise entspricht der frühen philosophischen Sichtweise, ist völlig naheliegend und auch verständlich.
Man ging hauptsächlich vom Konzept der „Prozeduralen Programmierung“ aus, was einfacher realisierbar für sozusagen alltägliche „Rechenprobleme“ war. Natürlich ist das Programmierkonzept „universal“, man kann auch baumartige Strukturen bearbeiten.
Sehr früh, sozusagen kurz nach dem „Fortran“ Konzept, „erfand“ man die Programmiersprache „Lisp“ die hierarchisch angelegt ist, wobei natürliche baumartige Strukturen transparenter „abgebildet“ werden können. „Wissensstrukturen“ sind baumartig und waren Vorbild für die Programmierprache “Lisp” oder das “Perzeptron”.
Von Intelligenz könnte man anschaulich dann sprechen, ich versuche es zu formulieren, wenn in einem Information verarbeitenden System „Muster“ z.B. örtliche und zeitliche Kombinationen (kleinster informeller Objekte) auf abstrakter Ebene abgebildet (z.B. als „Bild- oder Videopixel“ abgebildete Zahlenwerte), (mit Vorbildern) allenfalls künstlich generiert (um noch unbekannte Muster zu finden), verglichen werden können.
Aus zahlreichen ganz bestimmte Kombinationen von Bildpixel die mit Vorbildern übereinstimmen, wird z.B. geschlossen, dass es sich mit einer größeren Wahrscheinlichkeit um eine Katze, Hund…. handeln sollte.
Intelligenz auf Spieltechnik zu reduzieren , das ist nicht intelligent.
Dass der Schachcomputer dem Menschen überlegen ist, das ist logisch, weil der Computer bei gleicher Zeit mehr Kombinationen durchrechnen kann.
Zur Intelligenz gehört auch die Phantasie, also eine Fähigkeit so zu denken, wie vorher noch niemand gedacht hat. Das unterscheidet die menschliche Intelligenz von der künstlichen Intelligenz.
Beide ergänzen sich allerdings sehr gut. Deshalb sind die elektronischen Gimmicks ja so nützlich. Eine Warnanzeige, wenn die Autotür nicht geschlossen ist. Ein Warnton, wenn der Fahrer droht einzuschlafen, Eine Meldung wenn der Luftdruck nicht stimmt usw.
Sie merken schon, wir entfernen uns immer mehr vom Begriff der Intelligenz.
@ Elektroniker 24.11.2020, 11:31 Uhr
Bei meinem Beitrag weiter oben, habe ich irrtümlich den ursprünglichen Text (nach der Stelle von “Hund und Katz”) von
@ hwied der mir als Vorlage diente, nicht gelöscht.
Bitte um Entschuldigung.
Elektroniker,
Wir sind uns einig , es gibt eine Hardware und es gibt eine Software.
Erste und entscheidende Frage, das neuronale Netzwerk ist das Hardware oder nur Software ?
Ein künstliches neuronales Netz ist weder Hardware noch Software, obwohl es sowohl als Hardware als auch Software umgesetzt werden kann.
Ein künstliches neuronales Netz ist eine sehr einfache Nachahmung der neuronalen Strukturen im natürlichen Gehirn. Das erste künstliche neuronale Netz von Frank Rosenblatt (das Perzeptron) wurde als Hardware umgesetzt – Mark I. Moderne künstliche neuronale Netze werden als Software umgesetzt. Man kann aber auch Festkörper bauen, deren Kristallstruktur sich wie ein künstliches neuronales Netz verhält und eingestrahltes Licht (ohne Mathematik) verarbeitet.
Hier die Hardware-Lösung.
@ hwied 24.11.2020, 12:39 Uhr
Zitat: „Erste und entscheidende Frage, das neuronale Netzwerk ist das Hardware oder nur Software ?“
Diese Frage ist sehr interessant.
Kurz gesagt, heutzutage ist das neuronale Netz als Basis von KI eine Art von “fiktiver Hardware“, die real als „richtige Hardware“, gar nicht existiert. Diese real gar nicht existierende „Hardware“ wird auf modernen Computersystemen „emuliert“, so wie auch längst verschrottete alte Computer, auf neuen Computern, sozusagen „per Emulation“ zu neuem Leben „erwachen“.
Ich meine, man könnte es wie folgt erklären.
Beim menschlichen Gehirn gibt es ein „reales neuronales Netz“ bestehend aus Neuronen und Synapsen. Das „funktioniert“, ungefähr wie von Mculloch beschrieben und abgesehen von den biologisch chemischen Erfordernissen, wie ein mit Synapsen verknüpftes „Gatternetzwerk“. So gesehen ist es die „Brücke“ zur Elektronik und der Boolschen Schaltalgebra, damit zur „realen Wissenschaft“. Die Funktion der Synapsen bei der Wissensabbildung hat E. Kandel erklärt.
Elektrophysiker, Kybernetiker, z.B. N. Wiener, haben sich frühzeitig bemüht die Funktionen dieser hoch komplexen Anordnung der Neuronen zu ergründen. Sie haben nach „fortschrittlichen Neurologen“ gesucht, da nur diese praktischen Umgang mit derartigen Systemen hatten.
Sie kamen zuerst auf den „fortschrittlichen Freud“, der zunächst begeistert von diesen Ideen gewesen sein soll, der hat aber plötzlich, Hals über Kopf widerrufen und dieses Konzept der „Elektroniker“ als verrückteste Idee seines Lebens bezeichnet (ich vermute nicht ganz freiwillig).
Später um 1943 wurde McCulloch für diese Ideen gewonnen, der sie zusammen mit A.Turing weiter entwickelt hat. Es ist übrigens beiden Herren nicht gut bekommen, aber das wäre eine eigene Geschichte.
Es wurde ein „schematisches Modell“, ähnlich wie Flussdiagramme in der Informatik, als „neuronales Netzwerk“, man nannte es „Perzeptron“ entwickelt.
Es gab einen einen elektrischen „Signalinput“, wie er z.B. im Kühlschrank durch einen Schalter realisiert wird, der geschlossen wird sobald die Tür aufgeht und dabei ein Stromkreis geschlossen wird der das Licht einschaltet.
Beim „Perzeptron“ besteht weiters die Möglichkeit das Signal zu „gewichten“, entweder nach „Wahrscheinlichkeiten“ auch ob eben die Türe nur halb geöffnet ist. Außerdem können auf das nachfolgende Neuron mehrere derartige Schalter gewichteten Einfluss nehmen. Reichen diese mitunter sehr vielen gewichteten Signale, um das folgende Neuron zum Triggern zu bringen, so legt sich das „zuständige Neuron“ sozusagen auf eine Aussage fest, Hund oder kein Hund….
Dieses „Perzeptron“ wird aber heutzutage nicht physikalisch und in Analogtechnik realisiert, ein derartiges System wäre viel zu unflexibel, sondern nur mehr als Computersimulation. Man sagt auch, eine in diesem Fall nur „gedachte Hardware“, wird auf einem „universalen“ Computer „emuliert“.
Natürlich ist es so wie es Herr Konecny beschrieben hat, man verwendet aus Gründen der wesentlich höheren Geschwindigkeit Grafikchips von NVIDIA. Bei diesen Chips sind auf einem einzigen Chip sehr viele besonders spezialisierte, sehr schnelle Prozessoren untergebracht, so dass diese Chips besonders für Graphik oder auch für KI Anwendungen bestens geeignet sind.
An sich würde 1 Prozessor reichen um z.B. Schach gegen sich selbst zu spielen, aber 1000 Prozessoren sind eben schneller…..
Die Herren hwied und Elektroniker scheinen immer noch der Ansicht zu sein, dass die Überlegenheit der AI über den Menschen ausschliesslich oder vorwiegend der pänomenalen Rechenfähigkeit zu verdanken ist, die dem Computer nun einmal eignet. Das ist aber schlicht falsch. Ich erläutere das mal am Beispiel Go:
Im Go setzt man die ersten Steine üblicherweise am Anfang bei weitgehend leerem Brett in den Ecken (Faustregel: Ecke vor Rand vor Mitte). Da haben sich über die Jahrhunderte bestimmte Zugfolgen etabliert, die sich als besonders gut herausgestellt haben (Joseki). Bei einem solchen Joseki nimmt typischerweise eine Seite Gebiet in der Ecke, während die andere Seite Einfluss nach aussen aufbaut. Die Entwicklung dieser Josekis war vor alphaGo ziemlich langsam, weil es bereits jede Menge davon gab (Go ist halt ein uraltes Spiel und im Gegensatz etwa zu Schach kann man auch von 200 Jahre alten Partien noch jede Menge lernen). Nachdem die AI die Go-Bühne betreten hat, ist die Entwicklung der Josekis regelrecht explodiert, beinahe im Wochentakt kommen neue Zugfolgen, an die vorher niemand gedacht hat (der Begriff AI-Joseki ist mittlerweile in der Go-Welt fest etabliert).
Der Punkt dabei: für die Entwicklung von Josekis ist Rechenfähigkeit zweitrangig. Da die Partie noch im Anfangsstadium ist, kann nur über Variantenberechnung nicht entschieden werden, ob eine Zugfolge ein Joseki oder einfach schlecht ist, da hilft nur hochentwickeltes Spielverständnis. Genau über dieses Spielverständnis verfügt die AI offenbar und wenn man sich die Interviews von Go-Profis anschaut (auf youtube gibt es einige davon), wird das von denen auch frank und frei eingeräumt.
Es ist für manche Menschen offenbar schwer zu schlucken, dass die AI das Spiel offenbar besser versteht als der Mensch, aber das ändert an der Tatsache nun einmal nichts -ebensowenig wie das Unbehagen vieler Menschen an der Erkenntnis, dass Mensch und Affe von den gleichen Vorfahren abstammen, etwas an der Richtigkeit der Evolutionstheorie ändert.
Danke für den großartigen Kommentar! Freue mich wirklich sehr!
Vor über zwei Jahren habe ich mich viel mit den Meinungen der Go-Meister zu dem AlphaGo-Sieg gegen Le Sedol auseinandergesetzt. Mich hat fasziniert, wie sie der Maschine eine Art Intuition zugesprochen haben. Obwohl das am Ende auch nicht stimmt. Intuition ist ein Ausdruck des Polanyischen-Paradox, glaube ich: “Wir wissen mehr, als wir sagen können.” Dieses “angelebte” und verborgene Wissen hat ein künstliches neuronales Netz definitiv nicht, genauso wie den gesunden Menschenverstand. Auch wenn ich zugeben muss, dass mir manchmal der maschinelle “ungesunde” liebe wäre. 🙂
Damals habe ich hier in dem Blogbeitrag “Deep Mind und das Geheimnis des Denkens” geschrieben:
“Beim Spielen des hoch intuitiven Go-Spiels gegen Lee Sedol hatte AlphaGo die bekannten Go-Strategien über den Haufen geworfen. Statt sklavisch – nur besser – den Stil der menschlichen Go-Großmeister nachzuahmen, hat AlphaGo die bekannten Spielstrategien missachtet und sehr unkonventionell gespielt, ja, „unsinnige Züge“ gemacht. … Ein tief lernendes neuronales Netz hat also freier und anarchischer gespielt als Generationen von menschlichen Go-Spielern. Bis AlphaGo das Go-Spiel aufmischte, hatten Menschen nach eingefahrenen „Regeln“ gespielt, die zum Sieg führen sollten. Wie Roboter, die festgeschriebene Algorithmen ausführen. Wer hat also mehr gespielt wie ein Mensch? Generationen von Go-Spielern? Oder AlphaGo?”
Das sind alles Aussagen, mit denen ich damals nur die Meinungen der Go-Meister vielleicht etwas überspitzt wiedergab. Dieses Buch habe ich im Blog damals verlinkt und kann es immer noch empfehlen.
“AlphaGo – the Movie” kann ich auch empfehlen. 🙂
Damals habe ich die Parien live im Internet verfolgt (ich hatte schon so eine Ahnung, dass Geschichte geschrieben wird und wollte dabeisein). kommentiert hat seinerzeit Michael Redmond 9p. Ich erinnere mich noch deutlich, wie erschüttert er über das Spiel von AlphaGo war -einem so starken Spieler war natürlich klar, dass das Go-Spiel gerade revolutioniert wurde.
Es war etwas völlig anderes als die Niederlage von Kasparov gegen Deep Blue. Da ging es in der Tat nur um bessere Rechenfähigkeit und Aufrechterhalten der Konzentration über 4 Stunden, aber an unserem Schach-Verständnis hat sich da nichts geändert.
Ja! Da haben Sie vollkommen recht – eine schöne Erinnerung ist das.
Ich hatte damals bei dem Go-Spiel das Gefühl, dass man in Asien besser verstand als hier, was gerade passierte: der Aufbruch von etwas Neuem. Zuerst war man im Schock, sehr schnell hat man sich aber gesagt: dann sehen wir, was wir mit dieser Technologie anstellen können. Deswegen ist jetzt China in Sachen KI viel weiter als Europa. Vielleicht behindert uns hier unser westlicher Individualismus (für den ich trotzdem immer auf die Barrikade gehen würde :-)) – man fühlt sich aber so einzigartig, dass man kein kleines bisschen davon einer Maschine überlassen möchte.
Ich finde es halt sehr Schade, dass hier eine neue bahnbrechende Technologie, die unsere Fähigkeiten massiv erweitern könnte, immer noch entweder mit Terminator gleichgesetzt oder einfach als Quatsch abgetan wird. Obwohl sie seit Jahren Ergebnisse liefert. Statt zu gucken, wie wir uns diese Technologie zunutze machen und verhindern, dass sie nicht missbraucht wird. Vielleicht hängt’s doch mit dem etwas unglücklichen und übers Ziel hinaus schießenden Buzzword “Künstliche Intelligenz” zusammen. Man möchte nach jedem Blogbeitrag konkret über die Modelle sprechen, was sie können und wie sie das hinbekommen, ist dann aber schnell in einem Gespräch darüber, ob etwas intelligent ist oder nicht. 🙂
@ aristius fuscus 24.11.2020, 15:45 Uhr
Verstehe nicht, wie Sie mir aus der an sich wahren Behauptung dass Multiprozessorsysteme üblicher weise schneller sind, als gleichartige einzelne Prozessoren, unterstellen könnten, mir wäre nicht klar dass es in besonderer Weise auf die „Suchalgorithmen“ ankommt, die jedenfalls besser als nur „linear“ sein sollten.
Selbstverständlich kommt es auch bei der KI auf die Art der „Suchmuster“ und eventuell sogar auf die benutzte Reihenfolge an.
Grundsätzlich geht es bei den verwendeten Algorithmen auch noch um ein Optimum zwischen „Variantenberechnung“ (Schnelligkeit) und „hochentwickeltem Spielverständnis“ (Speicherbedarf), sozusagen ein „alter Hut“ bei der Entwicklung von KI Software.
Dass KI irgendwann den Menschen beim Denken völlig überlegen sein wird, stört mich genau so wenig, wie dass ein Auto eben schneller fährt als ein Mensch laufen kann….
Jedenfalls fördert KI die Gleichheit der Menschen. Verglichen mit der KI, werden Menschen nur noch „Dummerchen“ sein. Selbst bestens qualifizierte Versicherungsmathematiker verlieren z.B. ihre Jobs.
Mit der Evolutionstheorie habe ich keine Probleme. Im Gegenteil, mich interessiert die riesige auch sehr systematisch arbeitende „Zufallsgenerator Maschinerie“ in die wir alle existentiell eingebunden sind.
Es werden offensichtlich Information speichernde „Datenträger“, Gene, Meme…. systematisch mehr oder weniger zufällig generiert, verbreitet, steuern Prozessabläufe, generieren neue „Prozessoren“ …. zumindest mitunter sehr lange dauernde „Wechselwirkungen“ zwischen Prozessoren, Prozessen und Information sind die Folge. Altes vergeht, Neues entsteht, ein systematischer „Kreislauf“ in der Natur.
Information existiert (als Gene, Meme ….etwas modifiziert) weiter, die Hardware „stirbt“ und kann durch neue Hardware ersetzt werden….
J.Konecny, Elektroniker, a.fuscus,
J. Konecny,
Das neuronale Netzwerk wird also als Sofware geschrieben. Wie heißt das Programm dazu oder bezieht sich „neuronales Netzwerk“ nur auf die Struktur dieser Programme. Könnte man es also in c schreiben oder mit Java. Und wenn es auf einem normalen Laptop verwendet werden kann, dann ist die Hardware nicht notwendigerweise „neuronal“.
Jetzt mal einen kleinen Ausflug in die künstliche Intelligenz bei Gesichtserkennung. Unsere Laptops beherrschen mittlerweile diese Technologie, das deutet doch darauf hin, das es keinen grundsätzlichen Unterschied zwischen einem Computerprogramm ohne „neuronales Netzwerk“ und einem Programm mit „neuronalem Netzwerk“ gibt.
Unsere Digitalcameras kann man auch intelligent bezeichnen, weil sie ein Szenenerkennung haben. Die Kamera weiß ob wir eine Landschaftsaufnahme machen oder eine Aufnahme bei Sonnenuntergang. Und hierbei werden Videochips verwendet.
Also, nochmal , was ist das Besondere an dem neuronalen Netzwerk. Könnte man das fertige Programm als App bezeichnen ?
hwied: “J. Konecny, … Das neuronale Netzwerk wird also als Sofware geschrieben. Wie heißt das Programm dazu oder bezieht sich „neuronales Netzwerk“ nur auf die Struktur dieser Programme. Könnte man es also in c schreiben oder mit Java. Und wenn es auf einem normalen Laptop verwendet werden kann, dann ist die Hardware nicht notwendigerweise „neuronal“.
Jaromir: Ich muss zugeben, dass mir diese Diskussion zunehmend etwas “zeitverlustig” vorkommt. 🙂 Ich habe geschrieben: “Ein künstliches neuronales Netz ist weder Hardware noch Software, obwohl es sowohl als Hardware als auch Software umgesetzt werden kann. Ein künstliches neuronales Netz ist eine sehr einfache Nachahmung der neuronalen Strukturen im natürlichen Gehirn.”
Sie können ein künstliches neuronales Programm (KNN) in C oder auch in Java programmieren (also seine Architektur und die Algorithmen, die die Daten einlesen, durch das Netz propagieren, die Kostenfunktion/den Fehler minimieren, daraus bessere Paramater berechnen und sie ins Netz “backpropagieren”). Die gängigen Programmiersprachen für Machine Learning sind jedoch Python und R. Ich benutze Python, weil es sehr umfangreiche Deep-Learning-Frameworks nutzen kann wie Tensorflow und Pytorch. Da ich nicht mehr Wochen mit dem Schreiben eines Programms verbringen will, bediene ich mich dabei der High-Level-Bibliothek Keras, die auf Tensorflow aufbaut. Unter uns aber: In der letzten Zeit benutze ich bei der Entwicklung von KNN No-Code-Solutions wie Deep Learning Studio oder Sonys Neural Network Console. Mit Machine Learning Studio von Microsoft Azure habe ich auch schon gearbeitet. In diesen Studios verliere ich keine Zeit mit dem Programmieren, sondern bastle KNN-Modelle in Minutenschnelle wie Lego zusammen. Um zum Beispiel ein KNN-Modell für die Bilderkennung von handgeschriebenen Ziffern 0 bis 9 mit dem MNIST-Datensatz (70.000 Bilder) zu bauen und zu trainieren, damit das Modell mit über 99 % Wahrscheinlichkeit handgeschriebene Ziffern erkennt, brauche ich etwa 5 Minuten. Wenn ich das Modell mit einer GPU trainiere. Das ist aber nur die Grundschule in der Bilderkennung. 🙂
Wollten Sie mich prüfen, ob ich programmieren kann? 🙂
Ich habe acht Jahre lang an der TU München über die Codierung in in den DNA/RNA-Doppelsträngen geforscht. Stichwort Bioinformatik. Damals habe ich mit Fortran programmiert.
Damit es klar ist: Die Architektur eines künstlichen neuronalen Netzes wird vollständig programmiert, so wie all die zugehörigen Algorithmen, egal ob Zeile für Zeile, oder mit Hilfe von Bibliotheken “zusammengelegt”. Doch beim Training des Modells mit sehr vielen Beispielen kommt das nicht Deterministische ins Spiel: Hier wird so lange an den Parametern (Gewichtungen/Stärken der Verbindungen zwischen allen Neuronen des Netzes) gedreht, bis das Modell eine optimale Antwort auf seine Aufgabe liefert. Diesen Satz an bestimmten Parametern haben wir nicht programmiert, den hat sich das Modell bei seinem Training mit Hilfe unserer Mathematik “beigebracht”. Ab da sind die Entscheidungen des Modells für uns eine Blackbox. Das Modell hat nun mal gelernt, seine Aufgabe zu erfüllen. Bei Schach und Go zum Beispiel bringt sich das Modell bei seinem Training alle Merkmale bei, die diese Spiele repräsentieren, das heißt auch richtige Züge. Wie richtig die Züge sind, wissen wir nicht, weil wir nicht in der Lage sind, diese vielen Merkmale zu erfassen – so wie es die Maschine kann. Vielleicht können wir diese Ansammlung von Merkmalen so bezeichnen: Die Repräsentation aller Züge, die zum Sieg führen.
Bei der Bilderkennung können wir die Merkmale des Netzes jedoch visualisieren und wissen deswegen, dass ein KNN-Modell die Merkmale hierarchisch verarbeitet: Striche in bestimmten Winkeln in der 1. Neuronenschicht, diese setzen sich in der 2. Schicht zu Kurven und Ecken zusammen, bis die Maschine in der letzten Schicht eine Katze “sieht”. Ähnlich hierarchisch arbeitet unser visuelles System.
Jedes Programm, das Sie als eine Anwendung für etwas programmieren, die keinen Einfluss auf das Betriebssystem hat, ist im Grunde eine App – “Application Software”.
@ hwied 24.11.2020, 19:50 Uhr
Programme die KI „enthalten“ werden heutzutage ähnlich wie Apps verkauft. Es bedeutet normalerweise, sie „bauen“ auf Algorithmen auf, die auf „Musterverarbeitung“ gemäß den Konzepten der „Neuronalen Netze“ beruhen. Da gab es einige „starke“ Entwicklungen in den letzten Jahren, die sich (angeblich) sehr auf die Leistungsfähigkeit, den Preis (Zuverlässigkeit, Geschwindigkeit, Ressourcenverbrauch, …) auswirken.
Es handelt sich um besonders „konfektionierte Software“, die die Anwender z.B. Kamerafirmen, samt einer „Entwicklungsumgebung“ (um sie an die eigene Software anpassen zu können) vom Lieferanten beziehen.
Soweit ich das weiß, werden herkömmliche, etwas erweiterte Programmiersprachen verwendet. (Dabei spielen Patentrechte eine besondere Rolle).
Die Kamerahardware ist normalerweise absolut nicht „neuronal“. Allenfalls hat sie auf Wunsch der „KI Lieferanten“, besondere Funktionen eingebaut, die das KI System unterstützend verbessern.
Es ist so wie Sie vermuten, dass es keinen grundsätzlichen Unterschied zwischen einem Computerprogramm ohne „neuronales Netzwerk“ und einem Programm mit „neuronalem Netzwerk“ gibt. Allerdings benötigen KI Programme eine recht leistungsfähige Hardware. Grafikchips von NVIDIA scheinen sehr geeignet. (Ich warte selber schon auf eine preisgünstige KI Software um meine alten Landschaftsvideos auf 4 k Technik aufzupeppen).
Landschaftsaufnahmen oder einen Sonnenuntergang erkennt auch einfache Software ohne KI.
Das besondere an KI Software ist die systematische Mustererkennung und Auswertung. Sie erkennt z.B. Kratzer oder Flecken in alten Kinofilmen und ersetzt die fehlerhaften Pixel, indem sie z.B. ein Gesicht aus mehreren Filmbildern rekonstruiert. Es können sogar schwarz – weiß Filme „eingefärbt“ werden.
Das „Video Verbesserungsprogramm (mit KI)“ auf das ich warte, wäre eine App. Im Falle der Kamerafirma würde ich das ganze als „KI Entwicklungsumgebung“ bezeichnen und die ist sehr teuer.
Zitat: Warum sind Unmengen von Daten für das Training der KNN so wichtig?
Ein Grund dafür: Ein KNN weiss absolut nichts über unsere Welt. Und selbst nachdem es mit Millionen von Katzenbildern trainiert wurde weiss es immer noch nicht was eine Katze ist . Auch wenn es die Katze im Bild sehr gut erkennen kann so weiss das KNN trotzdem nicht, dass eine Katze wie ein Hund ein Tier ist und es weiss auch nicht, dass Katze und Hund Haustiere sind – ausser das Training umfasste eben auch diesen Aspekt.
Nun, weil ein KNN zu Beginn ein Tabula rasa, ein weisses Blatt ist, darum braucht es viele Beispiele.
Das hat Vor- und Nachteile.
Vorteil: das KNN hat keine „Vorurteile“. Es kann Dinge aus dem Trainingsset lernen, die einem Mensch nicht einmal auffallen, die aber sehr wertvoll für das Lösen einer Aufgabe sein können.
Nachteil: Dass KNN hat auch nach dem Training eine ganz enge Sicht auf die Welt, denn seine Welt besteht nur gerade aus dem, was es im Training gelernt hat. In der Praxis kann das gemäss Andrew Ng, einem bekannten KI-Forscher, etwa bedeuten, dass ein KNN-Programm, das Röntgenbilder wie ein Profi beurteilen kann, schon versagen kann, nur weil plötzlich Röntgenbilder mit einer kleineren Auflösung auftauchen oder es kann versagen, weil neue Röntgenbilder mit einem anderen Gerät gemacht wurden. Daran muss noch gearbeitet werden, denn das ist ein echtes Problem.
Warum nun sind Spiele so gut geeignet um KNNs weiterzubringen? Nun weil Spiele kontrollierte Welten sind, Welten in denen nur bestimmte Dinge passieren können, andere überhaupt nicht. Das kommt KNNs mit ihrer engen Weltsicht sehr entgegen. Spiele können den Einstieg in eine neue Stufe der Komplexitätsbewältigung für ein KNN sein. Heute sind es nicht mehr Go oder Schach, welche KNN-Forscher packen, sondern beispielsweise Adventure Games. Am 22.11.2020 las ich beispielsweise über ein Adventure Game, bei welchem der Spieler den Gegenspieler mittels Sprache, mittels Sätzen, zur Kooperation bewegen muss und wo es unter anderem darum geht den anderen mit sprachlichen Mitteln „reinzulegen“. Und jetzt hat ein KNN es geschafft in diesem Spiel mit Menschen mitzuhalten. Die Hoffnung ist die, dass ein solches KNN damit ein besseres Sprachverständnis erwirbt. Man spricht in diesem Zusammenhang von „Grounding“ und meint damit, dass ein KNN den Hintergrund und den Sinn von sprachlichen Äusserungen lernt indem es den Zusammenhang zwischen Sprache und Welt kennen lernt.
J.Konecny,
vielen vielen Dank für die etwas tiefer gehende Erklärung. Ich wollte Sie nicht testen, im Augenblick gebe ich mich auch zufrieden, weil ich eine Ahnung davon bekommen habe, wie neuronale Netzwerke arbeiten.
Elektroniker,
noch mal zur Bildbearbeitung. Bei der Mustererkennung und Bildkompression wird über das Bild eine fraktale Kurve gelegt, die flächenfüllend ist. Da Fraktale selbstwiederholend sind, also in allen Vergrößerungsstufen die gleiche Form aufweisen, kann man man ein Bild so stark komprimieren, dass es bei größter Kompression ein Muster zeigt. Macht das das neuronale Netzwerk auch so?
Martin Holzherr,
Gute Zeichner können mit wenigen Strichen einen Hund zeichnen. Man sollte diese Künstler mal befragen, mit welchem Strich aus dem Hund eine Katze wird.
KLeine Episode am Rande. Meine Nichte(2) hatte ein Bild von Miro in der Hand. Es bestand aus bunten Kreisen , einer gelben Kugel und einem schwarzen Punkt. Das kleine Mädchen deutete auf den schwarzen Punkt und sagte: “Wau-Wau”.
Ich war erstaunt und dann lass ich den Namen des Gemäldes. “Hund bellt den Mond an.”
Da war ich platt. Tipp: Bilderkennung mit Kleinkindern testen.
Danke! Ich muss mich auch wegen meiner sarkastischen Frage entschuldigen, ob Sie mich testen würden. Das war zu schnell geschossen. Bitte um Verzeihung.
Und danke auch für die schöne Geschichte mit Ihrer Nichte.
Künstliche neuronale Netze und die Kunst des guten Ratens, der guten Interpolation
Künstliche neuronale Netze können menschenähnliche Leistungen beispielsweise beim Erkennen von Gegenständen in Bildern vollbringen, wenn sie gut raten, gut interpolieren können. Interpolation bedeutet, dass man fehlendes „sinnvoll“ ergänzen kann. In simpler Form wird Interpolation in der Mathematik schon seit hunderten von Jahren angewandt und Intelligenz braucht es dafür überhaupt keine. Behauptung: Auch KNNs brauchen weniger Intelligenz, als es zuerst erscheint. Das ist es, was ich im folgenden Abschnitt sichtbar machen will.
Hangeschriebene Ziffern erkennen als Interpolationsproblem
Das MNIST-Datenset (Modified National Institute of Standards and Technology database) ist ein öffentlich verfügbares Datenset von handgeschriebenen Ziffern und umfasst 60.000 Beispiele im Trainingsdatensatz und 10.000 Beispiele im Testdatensatz. Im Original sind alle Ziffernbilder jeweils 22×22 Bildpunkte gross und für jeden Bildpunkt gibt es einen Grauwert. Doch zur „Vereinfachung“, Verkleinerung der Arbeit kann man weniger Bildpunkte verwenden, beispielsweise 4×4 und man kann anstatt Grauwerte einfach nur schwarz oder weiss als Bildpunkt zulassen. Nun, ein Schwarz-Weiss-Bild mit 4×4-Punkten ist in der Praxis ungeeignet um handgeschriebene Ziffern abzubilden. Doch zur Demonstration dessen was ich sagen will, ist ein solch reduziertes Bild sehr gut geeignet. Denn die Frage, die als nächstes kommt lautet: Wieviele verschiedene 4×4 Schwarzweissbilder gibt es überhaupt. Nun, es gibt 2^16 == 65536 verschiedene 4×4 – Schwarzweissbilder. Mit andern Worten, falls man handgeschriebene Ziffern in 4×4-Schwarzweissbildern erkennen muss, genügt es jedem von 65‘536 Bildern eine der Ziffern 0 bis 9 und „Keine Ziffer“ zuzuordnen. Das genügt dann um mit 100%-iger Sicherheit zu erkennen, welche Ziffer geschrieben wurde. Intelligenz braucht es für die Lösung dieser Aufgabe überhaupt keine.
Wie aber steht es um das echte MNIST-Datenset mit 22×22 Bildpunkten? Ganz einfach, jedesmal wenn das System auf ein Bild trifft, das nicht „trainiert“ wurde, das aber eine Ziffer darstellen soll, muss das KNN-System das Trainingsbild wählen, das am ehesten mit dem gezeigten Bild übereinstimmt. Es geht also darum, fehlende Punkte zu ergänzen und falsch gesetzte zu eliminieren. Das ist im Prinzip ein Interpolationsproblem. Es hat sich nun gezeigt, dass KNNs aus menschlicher Sicht sehr gut interpolieren und menschenähnliche Leistungen vollbringen könne. Es bleibt jedem hier vorbehalten ob er das überhaupt als Intelligenz bezeichnen will. Jedenfalls ist es sehr nützlich – beispielsweise, wenn es darum geht handgeschriebene Adressen auf Briefen automatisch zu erkennen.
Eine kleine Korrektur: Die Ziffern im MNIST-Datensatz sind 28 x 28 Pixel klein. 🙂
Ich glaube nicht, dass man eine Klassifizierung, die ein KNN durchführt, als Interpolation bezeichnen kann. Bei seinem Training hat das KNN alle Merkmale jeder gegebenen Klasse gelernt – die Repräsentation der Klasse. Hier Merkmale, die jeweils die Ziffern 0 bis 9 repräsentieren. Eine Ziffer auf einem neuen Bild wird dann ihrer Klasse zugeordnet, zum Beispiel eine 2 als eine 2 klassifiziert, wenn sie möglichst viele dieser Merkmale zeigt. Je mehr Merkmale einer 2 das Modell findet, umso größer die von der Softmax in der Ausgabeschicht ermittelte Wahrscheinlichkeit für eine 2. 🙂
Sie schreiben: “Es geht also darum, fehlende Punkte zu ergänzen und falsch gesetzte zu eliminieren.” Das klingt aber nach zwei Regeln, die man programmieren kann – so funktioniert ein regelbasiertes Programm, jedoch kein künstliches neuronales Netz.
@Jaromir Konecny
Zitat: Ich glaube nicht, dass man eine Klassifizierung, die ein KNN durchführt, als Interpolation bezeichnen kann.
Für mich ist „Interpolation“ eine Analogie aus dem was in der Mathematik gemacht wird. Ich hätte auch sagen können, die zu testende Eingabe wird passend in das hineingefügt, was trainiert wurde oder ich hätte sagen können, der zu testende Input nimmt im KNN einen bestimmten Pfad und dieser Pfad verrät die Ähnlichkeit zu den trainierten Objektklassen. Klar passiert das ohne weitere Programmierung.
Martin Holzherr,
das war eine sehr gute Erklärung, was die KI macht, sie ergänzt nach der Wahrscheinlichkeit.
Ich habe mal irgendwo gelesen, dass bei der Gesichtserkennung nur 5 oder 8 Punkte und deren Verhältnis zueinander ausreichen, um das Gesicht zu erkennen.
Ich würde diese Fähigkeit schon als intelligent bezeichnen, bei den Logeleinen werden ja auch nur Eigenschaften zueinander in Beziehung gesetzt um die richtige Zuordnung von Person und Beruf zu finden.
Und Sherlock Holmes ist ja noch besser, der löst seine Fälle vom Lehnstuhl aus, indem er wichtige Hinweise von den unwichtigen Hinweisen trennt und dann den Täter als einzige logische Möglichkeit herausfindet.
@hwied betreffend Logeleien und Sherlock Holmes: heutige neuronale Netze können nicht logisch denken und keine Schlussfolgerungen über mehrere Stufen ziehen. Sie erkennen im wesentlichen Muster, man spricht von pattern matching. Kausales Denken liegt (noch) ausserhalb ihrer Möglichkeiten.
Aber auch das menschliche Denken ist nicht unbedingt vor allem logisch, auch der Mensch arbeitet mit Mustererkennung und mit Abspulen von Automatismen. Der Kognitionsforscher Daniel Kahnemann spricht von Langsamem und Schnellem Denken. Das was ein KNN und was der Mensch im automatischen Modus macht ist Schnelles Denken und damit Mustererkennen und Abspulen von Automatismen.
@ hwied 25.11.2020, 08:57 Uhr
Ich kann leider über die Details der von KI Firmen verwendeten Algorithmen nichts aussagen.
Habe einerseits nur (veraltetes) Schulwissen von einigen damals extrem in die Zukunft schauenden ehrgeizigen Professoren, aus Zeitschriften und von ehemaligen Schulkumpels, die in diesen Bereichen gearbeitet haben.
Einerseits sind die alle in Pension und die Firmen haben sich extrem abgeschottet. Mitarbeiter dürfen zu keinen Klassentreffen mehr fahren, nicht sagen wo sie arbeiten und schon gar nicht von ihrer Arbeit berichten. Dass hätte irre Konventionalstrafen zur Folge. Man kann höchstens aus Werbeaussagen und wenn man noch etwas Insiderwissen aus dem Berufsleben hat, sich halbwegs realistisch etwas „zusammenreimen“.
Es ist eine Definitionsfrage was KI eigentlich ist. Ich glaube, es gibt größere Übereinstimmung wenn man davon ausgeht, dass KI Systeme heutzutage das Konzept der „neuronalen Netze“ als Software implementiert haben müssen.
Es ist aber immer noch die Frage, ob diese Software aus Werbungsgründen zwar eingebaut ist, aber nur völlig untergeordnete Funktionen erfüllt, in der Realität z.B. ein alter und sehr erfolgreicher „Fraktalalgorithmus“ (ohne neuronalem Netz Algorithmus) die wirkliche „Arbeit macht“.
Vermutlich könnte man in KI Systeme auch „Fraktal Algorithmen“ (oder auf andere mathematische Konzepte beruhende Algorithmen) einbauen, aber es ist halt die Frage, ob die Firmen es auch machen und ob es Vorteile bringt? Der Markt ist hart umkämpft heutzutage. Das Militär lässt (wegen der Freund – Feind – Erkennung) mitunter noch den „Rubel rollen“ ….
Ich vermute, Ausgangspunkt ist die selektive Belichtungsmessung in der Fotografie. Dieses Konzept wurde immer mehr, ohne KI verbessert und irgendwann kam man zum „Fraktal Algorithmus“. Das hat auch mit „Masken“ zu tun, die man beim Videoschnitt verwendet um z.B. den Himmel in Fotos oder Videos blau einzufärben.
Elektroniker,
wir sind schon tief in der Materie,, wenn es um Algorithmen geht.
Vor 30 Jahren habe ich mal selbst einen Druckertreiber geschrieben, der nicht die Buchstaben in der SCI II Kodierung verwendet hat, sondern ich habe aus dem Bildschirmspeicher die Pixel ausgelesen und sie in eine 6 x 4 Matrix eingefügt.
Das lässt sich automatisieren und als Texterkennung verwend en. Ob man Texterkennung schon als KI bezeichnet , weiß ich nicht.
@ Martin Holzherr 25.11.2020, 18:42 Uhr
@ hwied 25.11.2020, 17:56 Uhr
Das Bemerkenswerte an neuronalen Netzen ist, dass sie mit „Wahrscheinlichkeiten“ kalkulieren. Also mit nicht „absolut eindeutigen“ Input (individuelle Handschrift, Bilder aus verschiedenen Perspektive, ….) arbeiten können und Ergebnisse ermitteln, die mit unterschiedlich hoher Wahrscheinlichkeit korrekt sind.
Bei der Texterkennung dürfte es darauf ankommen ob der Text „handschriftlich“ vorliegt, oder in ganz besonderen von Maschinen leicht erkennbaren Buchstaben gedruckt wird. (z.B. OCR-A)
Ginge es um die „Logik“, so setzt man die Wahrscheinlichkeiten auf 100 % und das System nutzt für logische Schlüsse eben solche Muster wie sie auch Menschen nutzen. Es wäre aber völlig unökonomisch und unsinnig.
Den Menschen bleibt vermutlich nichts anderes übrig, als auch „Logik Aufgaben“ mittels seines nun einmal vorhanden „neuronalen Netzes“ (im Gehirn) zu lösen. Es müssen eben „Muster“ gelernt werden um z.B. Rechnen zu können….
Man würde KI + Neuronale Netze allenfalls zur Auswertung handschriftlich eingegebener Daten nutzen.
Für die Lösung komplexer Probleme selbst bieten sich andere Konzepte an z.B.:
General Problem Solver – Software mit einer allgemeinen Problemlösemethode
SAT-Solver – Software für das Erfüllbarkeitsproblem der Aussagenlogik
FE-Solver – Software zur Lösung von Finite-Elemente-Aufgaben (z. B. Nastran)
STRIPS – Automatische Planungssoftware.
Diese Konzepte „zählen“ übrigens manche Wissenschaftler auch zur KI, obwohl Neuronale Netze als Grundlage eher nur selten genutzt werden dürften.
An die „Solver“ habe ich bei meiner Definition an anderer Stelle nicht gedacht.
@Elektroniker: Logisches und kausales Denken wird neuerdings auch mit künstlichen neuralen Netzen angegangen. Aber es gibt auch ältere Ansätze ohne KNN‘s, Ansätze, die man dem Bereich symbolische künstliche Intelligenz zuordnet. Dort wird mit Logikinferenz gearbeitet, einem Gebiet das einmal eng mit der Programmiersprache Prolog verbunden war. Heute richtet sich die Aufmerksamkeit mehr auf induktives logisches Programmieren (ILP) . Dabei versucht das System aus Beispielen logische Hypothesen aufzustellen. Es versucht also logisch zu verallgemeinern. Die Fortschritte auf diesem Gebiet stellen sich aber nur langsam ein. Ein Problem bleibt die drohende kombinatorische Explosion beim Aufstellen und Überprüfen von Hypothesen.
Induktives logisches Programmieren wobei beim Suchprozess künstliche neuronale Netze eingesetzt werden, wird im arxiv-Artikel Inductive Logic Programming via Differentiable Deep Neural Logic Networks beschrieben. Wieder einmal finden die Autoren, dass künstliche neuronale Netze bessere Lösungen finden als mit anderen Methoden und dass die Suche mit KNNs sogar schneller ist.
@ Martin Holzherr 25.11.2020, 22:44 Uhr
Dass man versucht, logisches und kausales Denken neuerdings auch mit künstlichen neuralen Netzen anzugehen ist naheliegend. Es ist interessant, ob der Versuch erfolgreich wird.
Letztlich könnte bestehende, auf neuronale Netze beruhende Software so modifiziert werden, dass sozusagen mit 100% Wahrscheinlichkeiten gerechnet wird. Auch das Triggerniveau der Neuronenfunktion wird so eingestellt, dass sie nur mehr dann triggert wenn auf allen Eingängen die volle „Signalstärke“ anliegt. Bedeutet, aus der „qualifizierten UND Funktion“ (wie ich sie bezeichnen würde), wird ein logisch absolut korrektes „UND“.
Natürlich muss auch noch für eine Invertierung des Input („NICHT“ Funktion) gesorgt werden um die Voraussetzung auch der „Turing Berechenbarkeit“ zu erfüllen.
Ein derartiges System könnte z.B. auf die Gesetzmäßigkeiten der Arithmetik stoßen (z.B. 3+4=7….).
Es erscheint aber an diesem Beispiel auch klar, dass es in eine “Endlosschleife” geraten würde, weil es eben versucht bis „Unendlich“ zu rechnen.
Man stößt auf das „Halteproblem“ der Informatik, dass nach meinem etwas älteren Wissensstand nicht algorithmisch gelöst werden kann. (Vielleicht schaffen es neuronale Netze näherungsweise in bestimmten Fällen?)
Wenn ich das bis jetzt richtig verstanden habe, dann arbeitet das neuronale Netz so ähnlich wie ein mehrschichtiger Filter der Kies nach der Korngröße in Feinsand, Grobsand und Kies unterteilt. Oder wie ein Tiefpassfilter, Hochpassfilter und ein Bandpassfilter bei einem Radioempfänger. . Die eingehenden Signale werden geordnet.
Was also mit Muster gemeint ist, das wird erst bei einer konkreten Anwendung klar.
Wenn man mal ein Sortierverfahren bei Computerdaten nimmt, dann weiß man, dass die Bearbeitungszeit exponentiell mit der Datenmenge zunimmt. Sortiert man ohne Algorhitmus kommt man schneller zu einer Näherungslösung. Ich vermute mal, dass das neuronale Netzwerk auch nur Näherungslösungen liefert.
Anmerkung : Fas alle Beiträge von Wikipedia weichen konkreten Beispielen aus, so dass man nicht erkennen kann, ob bei der Mustererkennung ein Vergleich mit schon vorhandenen Referenzen vorgenommen wird oder nicht.
Herr Konecny, könnten Sie mal aus dem Nähkörbchen plaudern und an einem Beispiel erkären, was genau das neuronale Netzwerk macht. Meinetwegen am Beispiel von DNA-Bestimmung.
hwied: “Herr Konecny, könnten Sie mal aus dem Nähkörbchen plaudern und an einem Beispiel erkären, was genau das neuronale Netzwerk macht. Meinetwegen am Beispiel von DNA-Bestimmung.”
Ich bin leider wieder mal in einigen sehr stressigen Manuskriptabgaben. Ich kann Ihnen aber wärmstens empfehlen, sich eine paar bildhafte Videos über neuronale Netze bei YouTube anzugucken. Zum Beispiel dieses:
https://www.youtube.com/watch?v=aircAruvnKk
Hier ein Video auf Deutsch:
https://www.youtube.com/watch?v=mP-IfpB3HRY
Sei können bei YouTube auch selbst gern suchen.
In meinem neuen Sachbuch “Ist das intelligent oder kann das weg?” beschäftige ich mich sehr ausführlich und ganz ohne Mathematik mit den Grundlagen der künstlichen neuuronalen Netz.
hwied: “Herr Konecny, könnten Sie mal aus dem Nähkörbchen plaudern und an einem Beispiel erkären, was genau das neuronale Netzwerk macht. Meinetwegen am Beispiel von DNA-Bestimmung.”
Jaromir: Mir ist eingefallen, wie man den Unterschied zwischen einem regelbasierten Programm und einem künstlichen neuronalen Netz (KNN) beschreiben könnte: Bei den klassischen regelbasierten Programmen haben wir immer eine Eingabe (Input) und einen perfekt programmierten Algorithmus. Wenn wir diesen von uns geschriebenen Algorithmus auf die Eingabe anwenden, bekommen wir eine Ausgabe (Output).
Bei der gängigen Art des Maschinenlernens mit KNN, dem überwachten Lernen, haben wir eine Eingabe und eine gewünschte Ausgabe: Diese zeigen wir dem Netz und durch sein Training entwickelt das Modell selbst den Algorithmus, mit dem es dann jede Ausgabe aufgrund einer neuen Eingabe ermittelt.
Das hilft uns bei Problemen, die zu komplex sind, um für sie ein Programm zu schreiben: Zum Beispiel sind wir nicht in der Lage, Gesichter so zu beschreiben, dass ein Programm dann jedes Gesicht auch erkennen könnte. Ganz schön sieht man unser Scheitern bei dem Versuch, geeignete Sprachregeln für Übersetzungsprogramme zu programmieren. Tausende von Linguisten haben früher immer neue Sprachregeln entwickelt, trotzdem haben die Übersetzungsprogramme Blödsinn geliefert. Bis der KI-Pionier Jelinek sagte: “Immer wenn ich einen Linguisten entlasse, verbessert sich die Leistung unseres Übersetzerprogramms.”
Erst wenn die Übersetzungsmaschinen seit 2016 neuronal wurden, besserte sich ihre Leistung rapide. Sie lernen nun mal Übersetzungen an großen Text-Datensätzen selbst. Die neuen Transformer-Übersetzer zeigen beim Übersetzen eine bessere Leistung als der Mensch. Trotzdem haben sie keinen gesunden Menschenverstand und man kann sie leicht in die Irre führen.
@hwied (Zitat): Anmerkung : Fas alle Beiträge von Wikipedia weichen konkreten Beispielen aus, so dass man nicht erkennen kann, ob bei der Mustererkennung ein Vergleich mit schon vorhandenen Referenzen vorgenommen wird oder nicht.
In Wikipedia-Einträgen steht oft eher zu viel. Dennoch gibt der Wikipedia-Eintrag Deep Learning ein gutes Bild dessen, um was es hier geht.
Nun zu ihrer Frage ob bei der Mustererkennung auf eine schon vorhandene Referenz Bezug genommen wird. Antwort: Ja und Nein. Nein, das KNN (künstliche neuronale Netz) macht bei der Mustererkennung keinen Datenbankzugriff und keine Suche im Speicher nach Referenzmustern. Ja, das KNN benutzt Information von früher, nämlich Information, die während der Trainingsphase gewonnen wurde. Das KNN besteht ja aus sehr vielen Neuronen wobei jedes Neuron mehrere Eingänge und mindestens einen Ausgang besitzt. Während der Trainingsphase wird festgelegt, wie die verschiedenen Eingänge gewichtet werden um daraus das Ausgangssignal zu berechnen. Durch diese Gewichtung wird das KNN in die Lage versetzt den Input beispielsweise als Bär oder Giraffe zu erkennen. Die Erkenntnisfähigkeit des neuronale Netzes steckt also in den Gewichten aller Eingänge aller Neuronen. Das aber erst nach abgeschlossem Training, denn im Training werden die Gewichte (Verstärkungsfaktoren) so gesetzt, dass das gewünschte erkannt wird.
Man nennt die Gewichte auch oft Parameter. GPT-3, der bekannte Sprachgenerator, soll 175 Milliarden Parameter besitzen. Das bedeutet dass das entsprechende neuronale Netz sehr viele Neuronen besitzt und alle Neuronen zusammen besitzen mindestens 175 Milliarden Eingänge. Alles was GPT-3 weiss und kann steckt in diesen Parametern, diesen Gewichten.
@ hwied 26.11.2020, 10:55 Uhr
Um mein schon etwas „älteres Hirn“ noch zu beschäftigen, damit Alzheimer vorzubeugen, möchte ich eine Antwort auf Ihre Frage versuchen.
Vorab ein Gag. Es gab gelegentlich Einbrecher die sind in ihr Einbruchsobjekt grundsätzlich über ein offenes Kellerfenster eingestiegen (das war sein besonderes „Handlungsmuster“), auch wenn die Haustüre oder die anderen Fenster offen gewesen wären. Z.B. an dieser „Eigenart“ hat die Polizei schnell ihre „Kundschaft“ erkannt und konnte sie „einfangen“. Es war eine Mustererkennung und Auswertung.
Filtereffekte, wenn z.B. Kies „vermessen“ wird, nach der Korngröße, in Feinsand, Grobsand und Kies aber auch noch nach chemischen Eigenschaften, gibt es auch bei der neuronalen Mustererkennung. Wäre der Kies z.B. zu 90 % etwa 5 cm groß, stark „eckig“, enthält, sagen wir einmal, unter jeweils 1 % Feinsand, Kalk oder Zement, so würde das System laut „Vorgabe Muster“ schließen, es handle sich mit 99% Wahrscheinlichkeit um Eisenbahnschotter. Den System können zunächst Proben gegeben werden, mit dem Hinweis es handle sich jeweils, (abhängig von den Anteilen), um Mörtel, Beton, Eisenbahn oder Straßenschotter, so ist es nach der Lernphase imstande, selbständig zu entscheiden um was es sich handelt.
Oder sind die von ihnen angegebene Filter in einem Radio auf ein bestimmtes Frequenzspektrum „eingestellt“, so handelte es sich eben mit einer bestimmten Wahrscheinlichkeit z.B. um „Radio Luxenburg“, oder um allenfalls System bedingte „Oberwellen“ oder „Zwischenfrequenzstörung“.
Neuronale Netze bewerten am Eingang die Eingangsparameter nach ihrer Wahrscheinlichkeit einen bestimmten Output zu erzeugen, z.B. dass es Eisenbahnschotter, oder RTL ist.
Das Besondere am Konzept der Neuronalen Netze ist, dass die „Filter“ automatisch beim „Lernen“ (über Rückkoppelungen) eingestellt werden. Die einzelnen Wahrscheinlichkeitswerte (deren zahlenmäßige, bzw. elektrische Stärke) bewirken beim biologischen Neuron (Mensch) dass es „triggern kann“ (wenn möglichst viele Signale möglichst gleichzeitig über die Dendriten eintreffen und der Schwellwert überschritten wird), bzw. wenn die „Technische Abbildung“ des jeweiligen Neurons (KI), mit einem ausreichenden „Zahlenwert“ (entsprechend den „Schwellwert“, der die einzelnen Teilwahrscheinlichkeiten berücksichtigt) versorgt.
Normalerweise wird die Wahrscheinlichkeit dass eines bestimmten Ergebnis zutrifft, ebenfalls ausgegeben.
Google hat angeblich neuerdings Algorithmen für KI Systeme entwickelt, die sozusagen für den Nutzer verständlich, kommentieren wie sie auf ein bestimmtes Ergebnis kommen, was früher bei neuronalen Netzen nicht möglich war.
Es ist für einen Nutzer nicht recht zumutbar, wenn ein KI System zu irgend einem, auf den ersten Blick absurden Ergebnis kommt, aber kein Mensch weiß, warum das System zu einem bestimmten Ergebnis gekommen ist.
Zumindest künftig weiß man es besser, kann die Ergebnisse akzeptieren, oder das KI System modifizieren…..
@Jaromir: meine Go-Zeitung hat mich auf auf eine interessante Diskussion aufmerksam gemacht, die im Rahmen des eGo-Kongresses dieses Jahr stattgefunden hat. Darin ging es hauptsächlich um die Auswirkungen der AI auf die Go-Szene und auf professionelle Go-Spieler. Ist vielleicht von Interesse, zumal man das als Modell sehen kann, welche Auswirkungen AI gerade auf hochqualifizierte Berufe haben kann.
Der Link: https://www.youtube.com/watch?v=-cEL7I6BWTc&feature=youtu.be&t=3007
Die Diskussion beginnt ca. bei Minute 55.
Danke für den YouTube-Link – eine sehr interessante Diskussion. Habe angefangen zu gucken, mir dann aber sagen müssen: “Nö, Jaromir! Zuerst sollst Du arbeiten. Geschaut wird am Abend!” 🙂
Künstliche Intelligenz versus Maschinelles-Lernen und was Künstliche neuronale Netze damit zu tun haben.
Jaromir Konecny spricht oft von Künstlicher Intelligenz fast synonym mit dem was er als Einsatzgebiet künstlicher neuronaler Netze (KNN) sieht. Doch eigentlich müsste man Künstliche neuronale Netze eher dem Bereich Maschinelles Lernen zuordnen als dem viel weiteren Feld der künstlichen Intelligenz. Hinter der Idee des Maschinellen Lernens steckt der Gedanke, dass Intelligentes Erkennen und Verhalten nur teilweise angeboren ist. Vielmehr wird es in einem Lernprozess erworben. Selbst ein Vogel muss Fliegen teilweise lernen. Menschen aber müssen fast alles was sie später wissen und können erlernen. Tatsächlich werden Menschen und selbst viele höhere Tiere relativ dumm geboren, können dann aber jede Menge Tricks lernen – vor allem in ihrer Jugend, was zum Spruch führte: „was Hänschen nicht lernt, lernt Hans nimmermehr“. Künstliche Neuronale Netze sind insoweit noch extremer als Hänschen: Sie werden komplett dumm „geboren“ und sind nach dem Training oft Experten auf einem eng umgrenzten Gebiet, nämlich auf dem Gebiet, auf dem sie trainiert wurden. Dort wo sie nicht trainiert wurden aber sind sie weiterhin so dumm wie zu Beginn. Und Neuronale Netze haben wie Hans Schwierigkeiten, dazuzulernen, wenn sie einmal trainiert sind, denn ein einmal trainiertes neuronales Netz, dem man nach dem Training weitere Dinge zu Lernen gibt, neigt dazu, die alten Dinge wieder zu verlernen, ja, die alten schon gelernten Dinge drohen von neu dazukommenden Dingen überschrieben zu werden.
Doch einen gewaltigen Vorteil haben neuronale Netze gegenüber Menschen: Man kann ein KNN in Sekundenschnelle mit Wissen und Können laden, indem man das Gelernte (die sogenannten Parameter) von einem früher einmal trainierten KNN herunterlädt. Wenn Hänschen also einmal zu Hans wurde, können wir Hans beliebig oft kopieren – mindestens einen Computer-Hans, denn Computersoftware lässt sich nun mal auf einfachste Art und Weise vervielfältigen und ein trainiertes Künstliches Neuronales Netz ist im Wesentlichen nichts anderes als Software: Selbst die Neuronen der künstlichen neuronalen Netze und ihre Verknüpfungen sind letztlich Computerdaten. Der Algorithmus (das Programm) aber, der bei der Anwendung des neuronalen Netzes zum Einsatz kommt, ist immer der gleiche, egal welches neuronale Netz wir gerade benutzen. Im wesentlichen macht dieser Algorithmus folgendes: Er speist die Eingabedaten, welche vom neuronalen Netz verarbeitet werden sollen in die künstlichen Neuronen des typischerweise mehrschichtigen neuronalen Netzes und lässt dann das neuronale Netz diese Eingabedaten „verarbeiten“, so dass am Schluss aus der Ausgabeschicht des neuronalen Netzes das Resultat herauskommt. Sollen handgeschriebene Zahlen erkannt werden, so wird vielleicht der 10. Ausgabekanal des neuronalen Netzes einen „Auschlag“ (eine 1) liefern und das bedeutet dann eventuell dass die Ziffer 9 erkannt wurde.
Heutige Smartphones sind genügend schnell um grosse künstliche neuronale Netze laden und ausführen zu können. Smartphones aber sind heute noch nicht in der Lage, grosse künstliche neuronale Netze zu trainieren. Dazu braucht es oft Supercomputer. Das Training von GPT-3, einem riesigen KNN, welches auf schriftliche Fragen oft mit ganzen Geschichten antwortet, soll auf Supercomputern trainiert worden sein und das Training soll Wochen bis Monate gedauert haben und es soll 12 Millionen Dollar gekostet haben.
@ Martin Holzherr 28.11.2020, 09:09 Uhr
Sehe praktisch alles so wie Sie es in ihrem Beitrag beschrieben haben.
Aber dass Herr Konecny und viele Gleichgesinnte, oft Künstliche Intelligenz (KI) fast synonym mit dem Einsatzgebiet künstlicher neuronaler Netze (KNN) sehen, ist für mich naheliegend.
Es gibt eigentlich keine wirklich vernünftige Definition von „Intelligenz“. Einig ist man sich nur darüber, dass Intelligenz als abstraktes Phänomen, hauptsächlich bei Menschen, wenn auch unterschiedlich verteilt, „vorkommt“.
Es war naheliegend dies zu erforschen. Elektrophysikern und Kybernetikern ist schon früh (ich schätze um 1900) aufgefallen, dass die Prozesssteuerungen von Maschinen (Mittels Gatter- und Relaisschaltungen, letztlich auf Basis der Booleschen Algebra) ähnlich dem intelligenten Verhalten von Menschen sind.
McCulloch, wurde gewonnen, sich systematisch als Neurologe mit diesem Problem zu beschäftigen. Er fand heraus, dass in neuronalen Systemen den Gatterschaltungen (der Elektronik) ähnliche Strukturen beteiligt sein müssen.
Wer auf die statistische Bewertung der Parameter gestoßen ist, kann ich nicht wirklich sagen. Jedenfalls hat E. Kandel erklärt, dass es sich so verhält, dass die „Sicherheit der Aussage“ umso höher wird, je mehr und stärker die Neuronen über die Synapsen verknüpft sind.
Das war auch die „Grundaussage“ des „Perzeptrons“ an dessen Erforschung auch McCulloch beteiligt war. Das „Perzeptron“ war die „Hardwaregrundlage“ des neuronalen Netzes.
Richtig erfolgreich wurde dieses Konzept des „neuronalen Netzes“, als man es in universalen Digitalcomputern, die immer leistungsfähiger wurden, erfolgreich und höchst flexibel realisieren konnte.
Und da verwundert es mich nicht mehr, dass künstliche Intelligenz (KI) fast synonym mit den Wirkungen künstlicher neuronaler Netze (KNN) gesehen wird.
Intelligenz ist nicht mehr nur allein den Menschen vorbehalten, technische Systeme können sie von Menschen implementiert erhalten. Selbst die Evolution hat derartige Systeme selbständig bei Scan Prozessen in riesigen biologischen „Zufallsgeneratorsystemen“ gefunden.
@Elektroniker (Zitat): Es gibt eigentlich keine wirklich vernünftige Definition von „Intelligenz“.
Ja. Im Computerbereich bezeichnet man deshalb oft das als intelligent, was ein Computer noch nicht kann, wozu es einen Menschen braucht. Früher galt Schach deshalb als Fall für künstliche Intelligenz und der IBM-Computer (nicht HAL) „Deep Thought“, welcher erstmals die gleiche Spielstärke erreichte wie sehr gute menschliche Schachspieler, galt als Beispiel eines künstlich intelligenten Systems. Aus heutiger Sicht besass Deep Thought (von IBM Deep Blue genannt) überhaupt keine Intelligenz, denn alles was er konnte war fest einprogrammiert und ausser Schach konnte Deep Thought überhaupt nichts. Wenn man die Fähigkeit dazu zu lernen als Massstab für Intelligenz nimmt, so verfügen auch heutige künstliche neuronale Netze nur über eine eng begrenzte Intelligenz, denn „in the wild“ können auch KNNs nichts lernen. KNNs lernen nur in einer sehr kontrollierten Umgebung. Ein KNN, das eine Giraffe erkennen kann, hat schon Schwierigkeiten, dazu zu lernen, was der Unterschied zwischen der Giraffe „Willi“ und der Giraffe „Helmut“ ist, etwas wofür bei mir ein Besuch im Zoo genügt.
Der Unterschied zwischen animalischer/menschlicher Intelligenz und künstlicher/KNN Intelligenz
Animalische Intelligenz: Bob erzählt Alice von seinem Hund, der vor einer Woche noch das Wasser scheute und der heute freudig ins Wasser springt und darauf wartet, dass er, Bob, ihm ein Stück Holz zuwerfe, worauf er es schwimmend zurückbringt.
Künstliche/KNN-Intelligenz: Bob erzählt Alice, GPT-3 könne nun Fragen im Interview-Stil gestellt an einen fiktiven Bill Gates überzeugend im Gates-Stil beantworten und das zusammenhängend in oft 5 oder mehr Sätzen. GPT-2 dagegen habe oft schon nach dem zweiten Satz den Faden verloren.
Diagnose Unterschied Hund/GPT‘s:
1) Der Hund, der schwimmen lernte ist immer noch der gleiche Hund wie der vor einer Woche als er noch das Wasser scheute, GPT-3 aber ist ein ziemlich anderes Programm als GPT-2.
2) Sowohl GPT-2 wie GPT-3 erinnern sich nicht an das, was sie gestern gesagt haben, der Hund aber weiss beispielsweise noch gut, dass Bob ihm gestern ein grosses Stück Holz vorausgeworfen hat. Allgemein verhalten sich KNN-Programme wie reine Funktionen: Mit demselben Input kommt immer derselbe Output zustande.
3) Ein Hund kann zuerst einmal nicht schwimmen. Er ist aber imstande schwimmen zu lernen indem er seinen Gang an die Verhältnisse im Wasser anpasst. Zu solchen Anpassungsleistungen und Verallgemeinerungen sind heutige KI-Programme noch nicht in der Lage.
Tier und Mensch verhalten sich konzept-bewusst und der Mensch hat Konzeptdenken zu Denken in Regeln weiterentwickelt
Ein Video, welches ein Tesla-Auto beim Selbstfahren zeigte, hat mir bewusst gemacht, dass echte Intelligenz ohne ein Bewusstsein für Konzepte nicht möglich ist. Dieses Video zeigte 2 Fehler des selbstfahrenden Systems, die einem Menschen nie passieren würden:
1) Das selbstfahrende Auto hielt direkt bei einem Stop-Schild anstatt ein bisschen weiter zu fahren bis zur Stelle wo die Strasse in die Hauptstrasse einmündete. Das hatte zur Folge, dass die Kamera des selbstfahrenden Autos gar nicht „sehen“ konnte ob auf der Hauptstrasse ein Auto daherkommt.
2) Das selbstfahrende Auto hielt ein Rotlicht einer parallel verlaufenden Strasse für das Rotlicht der eigenen Strasse und hielt dementsprechend an.
Diagnose zur Wichtigkeit konzeptuellen Denkens
Konzepte tauchen überall auf und ohne Konzeptbewusstsein gibt es kein effektives Denken. Ein solches Konzept ist das Konzept der Strasse, des seitlich begrenzten Weges: Ein Weg, eine Strasse gibt zwei Richtungen vor. Aneinander vorbeifahrende Fahrzeuge müssen innerhalb des Weges, innerhalb der Strasse bleiben und gleichzeitig darauf achten nicht miteinander zu kollidieren. Bei einer Strassenkreuzung muss der Fahrzeugführer so weit vorfahren, dass er die kreuzende Strasse überblicken kann, er darf aber nicht so weit vorfahren, dass er dem anderen in die Quere kommt.
Diese Konzepte sind jedem Menschen vertraut, selbst solchen Menschen, die selber nicht fahren.
Frage Kann ein System, das nicht weiss, was eine Strasse ist, jemals ein guter Autofahrer sein? Kann das fehlende Konzept einer Strasse dadurch kompensiert werden, dass man das System Milliarden von Fahrkilometern im Fahrsimulator fahren lässt bis es aus seinen Fehlern genügend gelernt hat?
@ Martin Holzherr 29.11.2020, 13:32 Uhr
Ich nehme an, die Technik der auf KI Basis fahrende Autos wird sich allmählich entwickeln.
Zuerst werden die Autos auf den immer gleichen Verkehrswegen herumfahren, mit einem Fahrer der eingreift und kontrolliert. Wie ich einmal erfahren haben, ist es bei den Fahrern der „Öffis“ auch so. Die an sich voll ausgebildeten Berufsfahrer werden auf bestimmten Strecken besonders eingewiesen und auf „besondere Gefahrenstellen“ hingewiesen, bevor sie allein unterwegs sind.
Vermutlich werden KI Autos für einige Zeit, sozusagen „ratlos“ auf der Straße stehen bleiben wenn sie „überfordert“ sind und sich per 5 G Telefonnetz z.B. mit dem ADAC per Videotelefonie in Verbindung setzen. Der Techniker wird am Bildschirm vermutlich sehr schnell erkennen woran es liegt und beim Auto für kurze Zeit die Steuerung übernehmen. Das KI Auto wird die neue Situation „einlernen“ (allenfalls mit besonderen „Tipps“ des Technikers) und die Informationen an alle anderen KI Autos weiterleiten, die danach befähigt sein sollten, die Situation selber zu meistern.
Die Systeme werden allmählich einen Art Datenbank für besondere Situationen anlegen, die schnell auf andere Systeme übertragen werden kann und alle Autos werden durch den Datenaustausch schnell dazulernen. Vermutlich werden die etwas aufwändiger zu bearbeitenden Sonderfälle systematisch in die KI Programme „eingearbeitet“, so dass die Systeme immer leistungsfähig bleiben, die so wie alle EDV Systeme, gewartet werden müssen. Dass es im EDV Bereich immer etwas „chaotisch zugeht“ dürfte kein Geheimnis sein….
Die Vorteile selbstfahrender Autos in Kombination mit einem „schnellen 5G Netz“ liegen darin, dass das lästige „Stopp und Go“ bei den Kreuzungen verringert werden könnte. Vermutlich werden die Ampeln den Autos vorausschauend „Zeitschlitze“ zuweisen, an denen sie über die Kreuzung fahren dürfen. Dazu muss die Geschwindigkeit recht genau (elektronisch geregelt) eingehalten werden. Autos die nicht entsprechend ausgerüstet sind, werden vermutlich auf eigenen Fahrspuren fahren und warten müssen bis sie in bestimmten „Zeitschlitzen“ in einer „Fahrzeugkolonne“ über die Kreuzung fahren können.
Die Haushunde und Hauskatzen sind rassisch so gezüchtet, dass sie freundlich und leicht manipulierbar sind. Ich nehme an, vergleichbare Funktionen wird man auch KI Systemen einbauen.
Ich weiß nicht ob heutzutage die Programmierer und das Operating noch etwas zu lachen haben, sich die Zeiten verglichen mit früher verändert haben. Aber früher erlaubten sich die Programmierer „kreative Späßchen“ die einen Computer zu einer Art „fleißigen Kumpel“ mit Gefühlen gemacht haben, der etwas „Menschen ähnlich“ ist und eine Seele hat (inklusive „seelischer“ Störungen).
Beide „Fehler“ die ihnen bei KI Autos aufgefallen sind, kenne ich ähnlich von Menschen. Vor (sehr) längerer Zeit wurde ein Bekannter von der Polizei abgestraft, weil er nicht vor der Sperrlinie angehalten hat, sondern wegen der besseren Übersichtlichkeit etwas weiter gefahren ist. Der Polizist der sich offensichtlich dorthin gestellt hat um abzukassieren behauptete, er hätte eben 2 mal anhalten müssen.
Ein Lokführer erklärte mir, dass genau die Zuordnung der Signale zu den Gleisen auf denen er unterwegs ist, beim Einfahren in den Bahnhof, wenn es kurvig ist und besonders bei Schlechtwetter ein großes Problem ist. Es gehörte ehemals sozusagen zu den „Leiden der Lokführer“ so ein Signal womöglich zu überfahren…
Die KI „leidet“ wenigstens nicht.
Milliarden von Fahrkilometern allein im Fahrsimulator reichen vermutlich nicht. Man wird Konzepte entwickeln müssen um möglichst viele (aber vermutlich nicht alle) „Sonderfälle“ bestens zu verarbeiten.
Warum Spiele und Spielumgebungen für KI und KNNs so wichtig sind
Die Google Tochter Deep Mind hat eben bekannt gegeben, dass sie in Zukunft die Spiele-Engine Unity für ihre Forschungen auf dem Gebiet der künstlichen Intelligenz benutzen wird (siehe dazu: Using Unity to Help Solve Intelligence )
Zitat Wikipedia: Eine Spiel-Engine (englisch game engine [ˈgeɪmˌɛndʒɪn]) ist ein spezielles Framework für Computerspiele, das den Spielverlauf steuert und für die visuelle Darstellung des Spielablaufes verantwortlich ist. In der Regel werden derartige Plattformen auch als Entwicklungsumgebung genutzt und bringen dafür auch die nötigen Werkzeuge mit.
Gemäss dem eben verlinkten Artikel leisten Spiel-Engines für KI und speziell quasi-realistische wie Unity folgendes:
– Spiele geben einen klaren Maßstab für den Erfolg und erlauben damit Fortschritt empirisch zu überprüfen und direkt am Menschen zu messen.
– Es können neue Umgebungen geschaffen werden, die die noch nicht getestete kognitiven Fähigkeiten untersuchen.
– Mit dem Fortschritt der AGI-Forschung wächst auch das Interesse der Forschungsgemeinschaft an komplexeren Spielen (Unity hat eine mächtige Physics-Engine und kann damit quasi-realistische Umgebungen schaffen).
– Die realistische Physiksimulation von Unity ermöglicht es den Agenten, eine Umgebung zu erleben, die enger an die reale Welt angelehnt ist (z.B. echtere Schatten und echtere Physik)
– wir können uns im Zuge der Weiterentwicklung der Unity-Maschine zukunftssicher machen, ohne einen großen Teil unserer eigenen Entwicklungszeit aufzuwenden.
– Unity erlaubt uns mehrere Spiele auf einem einzigen Computer auszuführen, mit einem Spiel pro Prozessorkern.
– Durch die Verwendung von dm_env_rpc können wir unsere Umgebungen containerisieren und öffentlich freigeben. Containerisierung bedeutet die Verwendung von Technologien wie Docker, um vorkompilierte Umgebungs-Binärdateien zu paketieren. Containerisierung ermöglicht es, unsere Forschung unabhängig zu verifizieren. Es ist ein zuverlässigerer und bequemerer Weg, Experimente zu reproduzieren als Open Sourcing, das durch Compiler- oder Betriebssystemunterschiede verwirrt werden kann.
Summarum Spielumgebung für KI
Spielerfolg, kontrollierte, reproduzierbare und dennoch komplexe Umgebungen und zunehmender Realismus sprechen für dennEinsatz von Spiel-Engines in der KI -Forschung.
Persönliche Beurteilung: KI ist heute immer noch vor allem Forschung und geforscht wird in den künstlichen Welten von Spielen mit ihren klaren Spielregeln.
Deep Learning im Jahr 2020
1. Was ist und kann Deep Learning. Warum so erfolgreich
Deep Learning mit künstlichen neuronalen Netzen feiert heute Erfolge in der Objekt- und Stimmenerkennung, in der Verarbeitung von natürlicher Sprache und selbst bei Atari-Computerspielen wo Deep Learning – Anwendungen durch bestärkendes Lernen immer erfolgreicher spielen. Das ganze basiert auf Training mit sehr vielen, meist fast unverarbeiteten Rohdaten und einer Verarbeitung dieser Daten in mehreren Schichten von künstlichen Neuronen, wobei die Schichten, die tiefer von der Rohdatenquelle entfernt sind, komplexere/abstraktere Aufgaben übernehmen und die Ausgabe schliesslich das gewünschte Resultat liefert, wie etwa die Zuordnung des Namens “Schaf” zum abgebildeten Schaf. Deep Learning ist so erfolgreich, weil es sehr wenig manuelles Programmieren benötigt und ein paar Entscheidungen über die zu wählende Architektur des neuronalen Netzes, wie man dem lernenden Netz Ziele vorgibt und wie man Fehler beim Lernen in Korrekturen am Netz umsetzt, genügen um ein Netz so festzulegen, so zu trainieren, dass es anschliessend neue Daten genauso verarbeitet wie die Daten im Trainingsset.
Warum aber begann der Erfolg von neuronalen Netzen erst vor etwa 10 Jahren? Das liegt an den hohen Anforderungen an Rechengeschwindigkeit und Speicher während des Trainings des neuronalen Netzes. Erst mit spezieller Hardware, die die parallele Datenverarbeitung möglich macht, die Matrixmultiplikationen unterstützt, die das Rechnen mit vielen, aber kleinen, wenig präzisen Zahlen ermöglicht und wo Speicherzugriffe entweder sehr schnell sind oder gar unnötig werden, erst mit solcher Hardware können anspruchsvolle Deep-Learning Anwendungen in Tagen trainiert werden anstatt in Wochen oder Monaten.
2. Welche Hardware unterstützt heute Deep Learning
a) GPUs, also Graphical Processing Units, eigentlich gedacht für die Darstellung und Manipulation von Bildern, die aus vielen Punkten bestehen, sind in der Lage Befehle parallel auf eine ganze Reihe von Daten anzuwenden. Auch die für neuronale Netze so wichtigen Matrixmultiplikationen lassen sich mit GPUs teilweise realisieren.
b) TPUs, Tensor Processing Units sind speziell für Deep Learning -Training gebaute Prozessoren. Googles TPU besteht aus einem systolischen Array mit einer 256×256 8-Bit-Matrizenmultiplikationseinheit. Wichtig: Eine 8-Bit-Multiplikation ist wesentlich schneller als eine 32 oder 64-Bit Multiplikation. Künstliche neuronale Netze benötigen aber gar keine hochpräzisen Zahlen. Die Tendenz geht sogar zu nur noch 4-Bit Speicherplatz benötigenden Zahlen, denn das genügt und Rechnungen mit 4-Bit Zahlen lassen sich mit sehr viel weniger Chipfläche umsetzen.
c) Neural Engines (Neural Processing Units) sind spezielle Coprozessoren oder auch nur Rechenkerne in Mobilrechnern von Samsung und Apple und in den neuen mit einem M1 bestückten Macs von Apple, die Operationen von GPUs und TPUs vereinen und die maschinelles Lernen und maschinelles Schliessen beschleunigen sollen.
3. Funktionsapproximation als verborgene Stärke von Deep Learning
Mit Deep Learning kann nicht nur die Objekt-,Bild- oder Spracherkennung gelernt werden, sondern es kann auch jede beliebige Funktion anhand von Beispielen und von Bewertungen
“gelernt” werden. Es zeigt sich immer mehr, dass gerade hochdimensionale, nichtlineare Funktionen mit nichts besser angenähert werden können als mit künstlichen neuronalen Netzen.
– FermiNet und PauliNet sind zwei neuronale Netzwerke, welche die Wellenfunktion für Vielteilchensysteme wie es etwa Moleküle sind, verblüffend gut berechnen können, was Aussichten darauf macht, dass chemische Verbindungen und Reaktionen bald schon viel präziser modelliert werden können.
– Partielle Differentialgleichungen können mittels künstlichen neuronalen Netzwerken oft erstaunlich gut gelöst werden. Der Forschungsartikel Solving high-dimensional partial differential equations using deep learning etwa berichtet über das Lösen von hochdimensionalen partiellen Differentialgleichungen mittels Deep Learning (Zitat):
– Die Q-Funktion, die es beim Reinforcement-Learning namens Q-Learning zu erraten gilt, kann ebenfalls mittels Deep Learning bestimmt werden. Diese Funktion liefert bei jedem Spielzustand die Aktion, welche den höchsten Gewinn verspricht, wenn man sie ausführt. Diese Funktion zu berechnen ist nicht gerade einfach, denn es muss nicht nur die unmittelbare Aktion berücksichtigt werden sondern auch alle möglichen Folgeaktionen. Zitat Wikipedia:
4. Transformers und Aufmerksamkeitsmechanismen als Mittel um Kontextabhängigkeit zu modellieren
Um die Bedeutung der Wortstellung in geschriebenen und gesprochenen Sätzen zu erfassen wurden früher sogenannte rekurrente neuronale Netzwerke etwa in der Form eines LSTM ( long short-term memory ). Diese rekurrenten Netzwerke haben komplizierte Rückwärtsschleifen zwischen den Neuronen aufeinanderfolgender Schichten.
Transformer dagegen halten die Werte aufeinanderfolgender Neuronen in einem Vektor, auf den beliebig zugegriffen werden kann, so dass etwa in Sprachanwendungen die Wortstellungsbeziehungen auf sehr viel allgemeinere Art untersucht werden können als in rekurrenten neuronalen Netzwerken welche nur eine sequentielle Untersuchung erlauben. Transformer sind aber nicht nur allgemeiner und einfacher, sondern auch schneller als rekurrente neuronale Netze. Transformer haben erst solch grosse Sprachmodelle wie BERT und GPT ermöglicht. BERT und GPT sind dabei vortrainierte Sprachgeneratoren, in die beispielsweise sämtliche Wikipedia-Artikel aufgenommen wurden. Sie können vom Anwender in einem weiteren Schritt an eine bestimmte speziellere Aufgabe angepasst werden.
Transformer werden meist zusammen mit einem Aufmerksamkeitsmechanismus benutzt und als Teil eines Encoder/Decoder-Paares, wobei der Encoder etwa die Spracheingabe in eine Folge von aufeinanderfolgenden Input-Einheiten bringt und der Decoder dazu wiederum eine Folge von Output-Einheiten generiert, die etwa das Resultat einer Übersetzung von einer Sprache in eine andere sein können.
Mit Transformern anstatt mit rekurrenten Netzen zu arbeiten bedeutet auch mehr Chancen für parallele Verarbeitung zu haben und damit die Chance sehr viel schneller zum Ziel zu kommen. Das erst hat so grosse Sprachmodelle wie BERT und GPT2 und GPT3 (Generative Pre-trained Transformer 3 ) ermöglicht.