Galilei und die neue Wissenschaft: Experiment und Mathematik
BLOG: Die Natur der Naturwissenschaft

Die Erkenntnis, dass es in einem Meer von Mystik und Dialektik immerhin noch die Möglichkeit gibt, die Wahrheit von Aussagen auf eine andere Aussage zu übertragen, hat mich in meiner Jugend, als mir dieses so richtig bewusst geworden war, sehr umgetrieben.
Wozu konnte man das nicht alles benutzen! Man könnte ja so eine Art logischer Ordnung zwischen Aussagen herstellen, in der klar wird, welche Aussagen aus welchen anderen Aussagen jeweils folgen. Man könnte von wahren Aussagen starten und darauf ein ganzes Gedankengebäude errichten, das nur aus wahren Aussagen besteht. Aber – mit welchen Aussagen kann man anfangen? Das war die große Frage.
Die Organisation sicheren Wissens
Solche Gedanken liegen natürlich nahe. In der Tat hatten sie auch schon die antiken Griechen. Aristoteles hatte, wie schon einem früheren Blogbeitrag erwähnt, gezeigt, dass man von den Syllogismen der 1. Form ausgehend, alle anderen Syllogismen ableiten kann. Er hatte damit das Problem, wie man überhaupt zu wahren Aussagen kommt, in der Weise gelöst, dass er die Syllogismen der 1. Form als wahre Sätze betrachtete. Diese waren ja auch unmittelbar einleuchtend. Einige Jahrzehnte später hatte dann Euklid von Alexandria das damalige Wissen über geometrische Flächen und Körper logisch geordnet und damit das erste größere axiomatisch-deduktive Gedankengebäude erstellt. Auch hier musste er zu Beginn einige Sätze als wahr ansehen. Hier schienen diese aufgrund der Anschauung evident zu sein.
In der Begriffslogik und in der Geometrie war also schon ein Modell entwickelt worden, mit dem man die Erkenntnis, dass es einen sicheren Transport von Wahrheit gibt, verwerten konnte. Wie wir aber im letzten Blogbeitrag gesehen haben, hat man erst sehr viel später die logische Basis für die Schlussfolgerungen in der Mathematik verstanden. Vorher galten diese als „unmittelbar einleuchtend“. Man machte dabei etwas richtig, konnte es nur nicht genau begründen; ja, man wusste nicht einmal, dass es da etwas zu begründen gab. Erst später sollte es nicht mehr reichen, dass einem etwas „unmittelbar einleuchtet“.
So war damals die Mathematik das einzige Gebiet, in dem man mit sicherem Wissen umgehen und auch praktische Probleme lösen konnte. Im 20. Jahrhundert ist nun die mathematische Logik dazu gestoßen. Zunächst war diese nur für theoretische Fragen interessant wie z.B. für das Studium der Grundlagen der Mathematik. Heute ist sie aber auch Grundlage für viele Algorithmen, die für die Extraktion und Gewinnung von Wissen in Rahmen der „künstliche Intelligenz“ entwickelt werden.
Die Mathematik blieb also über all die früheren Jahrhunderte ein unerreichtes Vorbild für die Organisation sicheren Wissens. Man hatte durchaus versucht, eine ähnliche Strenge der Argumentation in Philosophie und Ethik einzuführen. Solche Ansätze waren aber alle im Sand verlaufen (siehe Wikipedia: Mathesis universalis). Waren es die falschen Gebiete für eine Strenge der Gedankenführung nach Art der Mathematisierung gewesen?
Heute sehen wir, wie viele Gebiete der empirischen Wissenschaften immer stärker mathematisiert werden. Galileo Galilei war es, der die ersten Schritte dazu in der Naturforschung machte. Er hat als erster ein Ergebnis eines physikalischen Experimentes in der Sprache der Mathematik beschrieben. Dabei erkannte er durchaus die Tragweite dieser Verknüpfung von Mathematik und Experiment, er sah sofort, welch eine Revolution eine Mathematisierung für das damalige Verständnis von Wissenschaft darstellt. So sprach er von einer „neuen Wissenschaft“, die er begründet habe. Sein Satz „Das Buch der Natur ist in der Sprache der Mathematik geschrieben“ zeugt davon genauso wie auch die Passage seines Briefes an den toskanischen Staatssekretär Vinta im Jahre 1610: „Daher erlaube ich mir, das eine neue Wissenschaft zu nennen, die von ihren Grundlagen angefangen von mir entdeckt worden ist.“
Galilei griff damit den Gedanken der Pythagoreer wieder auf, aber in einer ganz neuen Weise. Er sah auch, dass es eine Ordnung, also Regelmäßigkeiten in der Natur gibt, die sich in mathematischen Beziehungen ausdrücken lassen, und hatte auch durch sein Studium der Euklidschen Geometrie die Strenge der mathematischen Schlussfolgerungen kennen gelernt. Er erkannte aber auch, dass man die Natur durch Experimente „befragen“ muss, um diese Ordnung zu entdecken. Nicht Mathematik allein, nicht Empirie allein, sondern Experiment und Mathematik sind die Pfeiler seiner neuen, strengen Wissenschaft.
Wir kennen alle die Folgen dieser Entdeckung, ohne diese wäre unsere Welt heute eine völlig andere. Irgendwann aber musste wohl diese „neue Wissenschaft“ entdeckt werden; zu nahe stehen sich Natur und Mathematik – besser gesagt: Natur und Logik.
Wann ist eine Implikation wahr?
Warum spielt Empirie, warum spielen „Befragungen“ der Natur in Form von Experimenten eine solch bedeutsame Rolle, wenn man sich eine Theorie nach dem Vorbild der Euklidschen Geometrie, also als axiomatisch-deduktives System wünscht? Schauen wir uns deshalb den Modus ponens als Prototyp eines logischen Schlusses noch einmal an:
A, A → B ⊨ B.
Um auf eine Aussage schließen zu können, die unanfechtbar wahr ist, müssen die Prämissen A und A → B wahr sein. Es gibt eine Aussage, nämlich A, die in beiden Prämissen vorkommt. Die Implikation bildet die Brücke zu einer neuen Aussage, nämlich B, auf die dann geschlossen wird. Solche „Brücken“ muss es in jeder Schlussregel geben, denn aus Aussagen, die völlig unabhängig neben einander stehen, kann nichts geschlossen werden. Auch die Syllogismen besitzen ja jeweils einen Mittelbegriff, der in beiden Prämissen vorkommt.
Eine wahre Implikation A → B bedeutet, dass A hinreichend ist für B: Stets, wenn A, so B. Wo ist das der Fall?
Wir können wahre Implikationen finden, wenn wir die Natur befragen. Wir erhalten dann z.B. folgende Antworten: „Wenn ich einen Ball in die Luft werfe, dann fällt er zur Erde,“ oder „Wenn in einem Draht ein elektrischer Strom fließt, dann existiert ein Magnetfeld in seiner Umgebung.“ Die Experimentalphysiker sind also Lieferanten wahrer Implikationen, die wir dann auch als Naturgesetze formulieren.
Wahre Implikationen können wir auch finden, wenn wir z.B. die Aussage „Alle Griechen sind Menschen“ umformen in
„Wenn x ein Grieche ist, dann ist x ein Mensch“.
Hier haben wir die Begriffe „Griechen“ und „Menschen“ so gebildet, dass die Implikation wahr ist. Die Aussage wird also dadurch wahr, dass wir die Begriffe entsprechend bilden.
Dann sind wir aber schon am Ende. Für alle anderen Implikationen ist wohl der dialektische Schluss zuständig, d.h. hier gehört eine Implikation zu der Kategorie von Sätzen, über die Aristoteles gesagt hat:
Glaubwürdig sind Sätze, wenn sie von Allen, oder von den Meisten oder von den weisen Männern und zwar bei Letzteren von allen, oder von den meisten oder von den erfahrensten und glaubwürdigsten anerkannt werden.
Wir können noch hinzufügen: Und das, was von den „weisen Männern“ anerkannt wird, hängt auch noch von der Zeit ab. Denken wir nur an die Gesetze der Rechtwissenschaft, z.B. an das Gesetz §1356 des BGB, das bis 1977 noch lautete: „Die Frau führt den Haushalt in eigener Verantwortung. Sie ist berechtigt, erwerbstätig zu sein, soweit dies mit ihren Pflichten in Ehe und Familie vereinbar ist.“
Wenn es um Regelungen für das menschliche Zusammenleben geht, um Moral, Sitten und Gebräuche, ja, um alles, was uns die Natur nicht sagt, kann es keine allgemein akzeptierbaren wahren Implikationen geben. Wir sind auf den dialektischen Schluss verwiesen und damit auf ein Verhandeln darüber, welche Implikationen denn als wahr gesetzt werden sollen. Hier können wir also Wahrheit nur „setzen“, nicht finden.
Die Folge davon ist, dass die Aussagen der Naturwissenschaften universell gelten, es aber unzählige Religionen und Rechtssysteme gibt. In den Naturwissenschaften gibt es zwar auch eine Veränderung im Laufe der Zeit. Diese ist aber, wie wir in späteren Blogbeiträgen sehen werden, eine Art von Evolution, ein „Finden vom immer besseren“ Grundannahmen aufgrund von stets neuen Entdeckungen über das Verhalten der Natur.
Einige Zeit hat man geglaubt, dass sich Regeln für das menschliche Zusammenleben auch aus der Natur des Menschen ablesen ließen. Eine solche Naturrechtslehre kann für verschiedenste Ideologien nutzbar gemacht werden. Letztlich sind es immer die „weisen Männer“, welche die Sätze, welche eigentlich nur für einige glaubwürdig erscheinen, allgemein als wahr dekretieren. Die katholische Kirche hält heute noch an dieser Lehre fest. Seit Jahrhunderten spricht man aber von einem „naturalistischen Fehlschluss“, wenn man vom „Sein“ auf das „Sollen“ schließt. Eine Implikation, die Aussagen über das Sein mit einer Aussage über das Sollen verknüpft, ist aus der Natur nicht ablesbar. Wir verdanken dem Philosophen David Hume (1711 bis 1776) die erstmalige explizite Formulierung dieser Einsicht.
Die neue Wissenschaft des Galileo Galilei
Das „heiße“ Thema der Naturforschung zu Zeiten Galileis war die Bewegung. In seinem Werk „Discorsi“ heißt es:
Nichts ist älter als die Bewegung, und über dieselbe gibt es weder wenig noch geringe Schriften der Philosophen. Dennoch habe ich deren Eigentümlichkeiten in großer Menge, und darunter sehr wissenswerte in Erfahrung gebracht.
Die Bewegung war ja schon Thema bei den Vorsokratikern gewesen. Aristoteles hatte verschiedene Klassen von Bewegungen unterschieden und dabei für jede eine besondere Erklärung gefunden. Die Bewegung ist nun einmal das Phänomen, das uns am unmittelbarsten begegnet, das man aber auch am Himmel als Gang der Gestirne beobachten kann. Wenn man überhaupt etwas von der Natur lernen wollte, musste man wohl zunächst die Bewegung „verstehen“.
Was für ein Experiment war das nun, mit dem Galilei die Bewegung studierte, und welche Form von Mathematik wandte er zur Beschreibung der Ergebnisse an? Wie Galilei das Problem anging, ist bemerkenswert und symptomatisch für den Gang der modernen Wissenschaft. Er richtete nicht den Blick auf „das Ganze“ wie die Vorsokratiker es taten, suchte auch keine allgemeine Übersicht zu erstellen wie Aristoteles, sondern fing es „im Kleinen an“. Er ließ eine kleine, glatt polierte Kugel eine schiefe Ebene, d.h. ein schräg gestelltes schmales Holzbrett herunterrollen, in das er eine Rinne eingegraben war – ein Kinderspiel in heutigen Zeiten.
Allein diese Wendung des Blicks zeugt schon von der Unabhängigkeit seines Denkens, wie sie einem Genie eigen ist. Noch zu Goethes Zeiten galt es für Philosophen, über das nachzudenken, „was die Welt im Innersten zusammenhält“, und Faust hat nur Spott für Mephistopheles übrig, wenn er um die Menschen kämpft: „Du kannst im Großen nichts verrichten, und fängst es nun im Kleinen an“. Religionen kennen nur diese Frage nach „dem Großen“.
Eigentlich hat Galilei damit die Fährte von Xenophanes wieder aufgenommen. Wenn man darauf vertraut, dass es möglich sein wird, „suchend das Bessere zu finden“, schätzt man auch „kleine Erfolge“ bei der Suche nach Erkenntnissen; man sucht eine Vorlage, auf der man aufbauen kann. So funktioniert die moderne Wissenschaft, die moderne Technik. Deshalb gibt es Forschung und Entwicklung.
Galilei musste nun bei jedem Rollen der Kugel Zeiten und Wegstrecken messen. Wie er insbesondere eine Zeiteinheit festlegen konnte, in dem er sein Gespür für einen gleichmäßigen Takt bei einem Lied ausnutzte, ist ausführlich in (Fölsing, 1983, p. 177ff) beschrieben. In seinen Aufzeichnungen berichtet er: „ … bei wohl hundertfacher Wiederholung fanden wir stets, dass die Strecken sich verhielten wie die Quadrate der Zeiten, und dieses für jede Neigung der Ebene, das heißt der Rinne, in dem die Kugel lief.“(Discorsi, nach (Fölsing, 1983, p. 174)).
Galilei formulierte das Ergebnis in Form von Proportionen, Verhältnissen, wie es damals üblich war und wie man es anders noch nicht gelernt hatte. Zeitabschnitte und Wegstrecken waren ja Größen unterschiedlicher Dimension, und man hatte noch nicht verstanden, wie man solche Größen direkt in Beziehung setzen kann. Deshalb schrieb er sein Ergebnis nicht in der Form auf, in der die Wegstrecke proportional zum Quadrat der benötigten Zeit auf, sondern als Gleichheit der Verhältnisse von zwei Strecken und zwei Quadraten entsprechender Zeiten. In einem Graphen, in dem die Zeiten gegen die Wegstrecken aufgetragen sind, stellt sich das als eine Halbparabel dar, etwa so, wie man sie in der Tat im Dialogo Quarto des Discorsi Galileis bei der Diskussion geworfener Körper findet (Abb. 1).
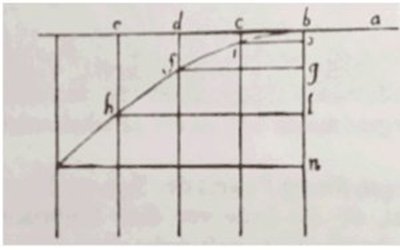
Hier muss man etwas zum Stand des mathematischen Wissens der Zeit Galileis sagen. Das kann nicht höher gewesen sein als dasjenige, was man aus der Spätantike kannte und wie es wohl auch an den Universitäten der Zeit an den Artistenfakultäten, den Fakultäten der „artes liberales“, der freien Künste“, gelehrt wurde. So dachte man in der Mathematik vorwiegend in geometrischen Begriffen, da ja die Geometrie in der Antike immer dominant gewesen war. Erst etwa zwei Generationen später sollte René Descartes eine „Analytische Geometrie“ entwickeln, in der man geometrische Beziehungen als arithmetische ausdrücken und man somit geometrische Probleme im Rahmen der Arithmetik analysieren konnte. Danach wurde die Mathematik im Wesentlichen zur Arithmetik und zur Algebra, der Lehre vom Umformen arithmetischer Beziehungen. Dass nun sich das Verhältnis von Zeiten zu Wegstrecken bei dem Fall auf der schiefen Ebene sich durch eine Parabel darstellen ließ, passte gut in die Welt, in der Mathematik zum größten Teil aus Geometrie bestand.
Galilei war zudem von einem Ingenieur und Geometer Ostilio Ricci in die Schönheit und Stringenz der “Geometrie” des Euklids eingeweiht worden. Er war damit auch schon von dem Gedanken „infiziert“, seine experimentellen Aussagen logisch ordnen zu müssen. Er suchte somit auch ein Prinzip, aus dem alle diese Aussagen herleitbar sind. Dabei geriet er allerdings auf eine falsche Fährte. Vier Jahre später konnte er diesen Irrtum korrigieren (Fölsing, 1983, p. 175ff). Eine solche „Theorie“ für eine Fallbewegung wäre ohnehin bald obsolet gewesen. Er konnte nicht ahnen, dass am Ende seines Jahrhunderts eine Theorie entstehen sollte, die alle Bewegungen am Himmel und auf der Erde von einigen wenigen Axiomen ausgehend erklären konnte. Seine Fallbewegung wurde darin zu einem kleinen Spezialfall.
Der englische Physiker und Mathematiker Isaac Newton stand bei der Entwicklung dieser Theorie gewissermaßen auf den Schultern Galileis. Das erste Axiom in dieser Theorie stützte sich nämlich auf eine Hypothese Galileis, auf die dieser bei seinen Fallexperimente geführt worden war. Es war die Hypothese, dass auf einer horizontalen Ebene die rollende Kugel ihre Geschwindigkeit „im Prinzip“ nicht ändert.
Eine solche Bewegung nennen wir heute geradlinig-gleichförmig, d.h. einer geraden Linie folgend und gleichbleibend in der Geschwindigkeit. Diese stellt nun einen Zustand der Kugel dar, bei dem nichts „erzwungen“ werden muss. Wenn man dieses Prinzip richtig verinnerlicht, kommt man vielleicht auf die Frage, wie sich denn diese Bewegung verändert, wenn man etwas „erzwingt“. Diese Hypothese Galileis muss also wohl eine Steilvorlage für Isaac Newton gewesen sein, und steht somit nicht ohne Grund am Anfang seiner Theorie. In der Praxis kommt die Kugel im Experiment Galileis natürlich zur Ruhe. Dafür sorgt die Reibung der Kugel an der Oberfläche.
Dieses Abebben der Bewegung durch die Reibung ist für Aristoteles in diesem Kontext die natürliche, eigentliche Bewegung, sie ist ein Prozess. Mit „Zwang“ kann sie aufrechterhalten werden. Die Ruhe ist für die Aristoteliker wie auch für die Vorsokratiker ein ganz besonderer Zustand, „wesensmäßig“ verschieden von einer Bewegung.
Bei Galilei ist in diesem Kontext die geradlinig-gleichförmige die natürliche, eigentliche Bewegung, sie ist ein Zustand. Durch äußere Umstände wie Reibung kann sie zur Ruhe kommen. Ruhe ist nur ein spezieller Zustand dieser Art, gewissermaßen das Nullelement der Klasse der geradlinig-gleichförmigen Bewegugen. Diese Einsicht steht am Anfang der modernen Physik.
Mit welchen Aussagen kann man bei der Formulierung eines axiomatisch-deduktiven Systems anfangen? Die Antwort auf diese Frage lag für eine Theorie der Bewegung, die Newton dann entwickelte, nahe: Die Einsicht Galileis musste wohl am Anfang einer Theorie der Bewegung stehen.
Schauen wir uns an, welche Aussagen in dieser Theorie, aber auch welche noch in weiteren physikalischen Theorien an den Anfang gestellt worden sind. Wir werden sehen, dass das auf höchst unterschiedliche Weise geschah. Verschaffen wir uns aber erst einmal im nächsten Blogbeitrag einen Überblick über diese Theorien.


Dem Experiment gehört die Krone. Als ich im Unterricht zum ersten Mal das Fallgesetz behandelte ließ ich vorher die Höhe des Klassenzimmers vom 3. Stock aus messen, indem wir ein Maßband zum Fenster hinauswarfen und ein Schüler unten die Höhe ablas und den Schülern die Höhe laut zurief.
Und jetzt wurde ich verwegen und behauptete, wir können die Fallzeit des Balles genau berechen und nachher mit der Stoppuhr überprüfen.
Wir berechneten die Fallzeit mit s = 1/2 g x t² und schrieben die Fallzeit mit zwei Nachkommastellenan die Tafel. Dann warf ein Schüler den Ball aus dem Fenster und beim Aufschlag des Balles stoppte ein anderer Schüler mit der Stoppuhr die Zeit auf die hunderstel Sekunde genau.
Und als der Schüler mit der Stoppuhr die Fallzeit laut nannte wurde es totenstill, sie stimmte auf die Hunderstel Sekunde mit der Zeit an der Tafel überein.
Das war auch für mich eine Sternstunde und seitdem ließ ich alle Ergebnisse nicht mehr runden, sondern mit mindestens zwei Nachkommastellen berechnen.
Die (Zitat) neue Wissenschaft des Galileo Galilei hat ihren Ursprung vielleicht nicht nur in den mathematischen und philosophischen Vorleistungen der alten Griechen. Auch die Handwerkskunst, die es zu Zeiten Galileis schon gab, könnte eine Rolle gespielt haben. Und das in mehrfacher Hinsicht:
1) empirisches Vorgehen und kontinuierliche Verbesserung durch Lernen aus Fehlern gibt es auch schon bei den spätmittelalerlichen Handwerkern und Handwerksgilden.
2) Galilei nahm selbst Handwerker für seine Projekte in Anspruch. Über die Zeit als Professor der Mathemaik in Padua etwa liest man in der Wikipedia: „Für die Fertigung dieses Vorläufers des Rechenschiebers, der Compasso genannt wurde und dessen Konstruktion er erheblich verbessert hatte, beschäftigte er einen eigenen Mechaniker. “
Ich denke, daß auch wie am Beispiel der Reibung noch ein anderer Aspekt dazukommt. Dies ist die Abstraktion der Bewegung von einer mit Reibung zu einer ohne Reibung. Vorher nahm man an, daß die Fallzeit von der Masse des fallen Körpers abhängt (Manche Zeitgenossen glauben das noch heute). Zu Mindestens gibt es die Erzählung, daß Galilei dies mit verschieden schweren Kugeln vorführte und die Leute nicht ihren Augen trauten.
Josef Honerkamp schrieb (12. Mai 2019):
> „Wenn ich einen Ball in die Luft werfe, dann fällt er zu Erde,“
„Wenn ich einen Ball in die Luft werfe, und er (noch) nicht zu[r] Erde fällt,
dann flieht er (noch) von der Erde; oder er (und/oder die Erde) wurde einzeln gefangen.“
> „Wenn in einem Draht ein elektrischer Strom fließt, dann existiert ein Magnetfeld in seiner Umgebung.“
„Wenn in einem Draht ein elektrischer Strom fließt, und in seiner Umgebung kein Magnetfeld existiert, dann fließt in seiner Umgebung ein kompensierender Strom.“
Frank Wappler,
übertreiben Sie nicht mit der Wortglauberei ?
Das Magnetfeld ist ein relativistischer Effekt einer bewegten Ladung.
Und wenn ein Ball in die Luft fliegt, beschreibt er eine Wurfparabel. Was gibt es da zu beckmessern?
Und die Gegner sterben nicht aus, die haben sicher auch Kinder.
Rudi Knoth
Galilei war sicher ein Genie.
bote19 schrieb (13. Mai 2019 @ 19:05):
> Das Magnetfeld ist ein relativistischer Effekt einer bewegten Ladung.
Das Magnetfeld hängt … (mal ganz abgesehen von “Retardierung”) … insgesamt mit _allen_ el.-mag. Strömen zusammen; nicht nur jeweils mit (dem Strom verbunden mit) einer einzigen Ladung; und nicht nur mit (den Strömen verbunden mit) Ladungen, die man erwartet hat bzw. von denen man schon von vornherein wusste.
> Und wenn ein Ball in die Luft fliegt, beschreibt er eine Wurfparabel. Was gibt es da zu beckmessern?
An Josef Honerkamps Formulierung eines entsprechenden “Naturgesetzes” aus dem obigen SciLogs-Artikel gibt es jedenfalls auszusetzen, dass ein Ball, der (bzgl. einer gleichförmig beschleunigten “Grundfläche” “hoch”-)geworfen wurde, dann nicht zwangsläufig und ausschließlich “durch die Luft” fliegt.
Und jedes System ist und bleibt geschlossen, außer, sofern es nicht so bleibt.
> Und die Gegner sterben nicht aus, die haben sicher auch Kinder.
Doch die Kinder können lernen, was zu lernen ist.
Gibt es einen grundsätzlichen Unterschied zwischen physikalischem Versuch und Anwendung?
Zitat:
Die Ruhe ist für die Aristoteliker wie auch für die Vorsokratiker ein ganz besonderer Zustand, „wesensmäßig“ verschieden von einer Bewegung.
Bei Galilei ist in diesem Kontext die geradlinig-gleichförmige die natürliche, eigentliche Bewegung, sie ist ein Zustand. Durch äußere Umstände wie Reibung kann sie zur Ruhe kommen. Ruhe ist nur ein spezieller Zustand dieser Art, gewissermaßen das Nullelement der Klasse der geradlinig-gleichförmigen Bewegugen. Diese Einsicht steht am Anfang der modernen Physik.
-> Na, wünschenswert wäre gewesen, wenn man die antike Betrachtung von Ruhe und Bewegung beibehalten hätte.
Das beträfe und änderte im Zweifel nicht die Physik oder Naturwissenschaft, aber es hat, wie es so dargestellt ist, sicher das Selbstverständnis der Menschen und ihr Tun verändert, dass man frei nach dieser Aussage, Gallilei hätte in Bewegung den Naturzustand gedeutet, anstatt in Ruhe.
Heute ist es ja so, das solche, die scheinbar nichts tun, wie Aussätzige gesehen und behandelt werden. Deswegen ist das Motto des modernen Menschen: Tu was, egal, ob es Sinn macht oder nicht. Hauptsache in “Bewegung”.
Bewegung sieht nach “Produktivität” aus. Ruhezustände nicht. Fertig ist die Weltsicht.
Eigendlich müsste man solche, die solcher Meinung sind, ihre Bürgerrechte entziehen, weil sie aus reiner Niedertracht oder/und Vorurteil ihre Mitmenschen an zweifelhaften Weißheiten messen.
Und seltsamerweise kehrt sich diese Ansicht bei psychiatrisch Diagnostizierten (weltsichlich diskreditierten) komplett um. Solche sollen lieber gar nichts tun. Die Praxis der Sedierung/Ruhigstellung sei hier beweisendes Indiz für die situative Zielsetzung.
Letztlich ist jede Diagnose, wie Zuschreibung politische Würdigung und anhand der Systeme erkennt man, wie weit es gediehen und verkommen ist, was man unter Menschenrechten und anderen “Gutmenschen-Idealen” so versteht.
Man muß nicht nur in Bewegung sein, nein, man muß das auch noch im Sinne einer scheinextistenten “Gesellschaft” tun…und sich dann auch noch, wie Hans im Glück fühlen – bei seiner selbstlosen Hyperaktivität.
Das auch dazu, was man im Sozialen oder im dynamischen Umgang miteinander für “Wahr” und anerkanntes Wissen hält.
Kommetatorfreund Dr.W.
Wenn man wissen möchte, wie tief ein Brunnen ist, wirft man einen Stein hinunter. Die praktische Anwendung wäre, wenn man zählt : einundzwanzig, zweiundzwanzig, dreiundzwanzig. Bei zweiundzwanzig, also nach 2 Sekunden, wäre die Tiefe etwa 20 m.
Beim Versuch würde man eine Stoppuhr benützen. Dann kann man tatsächlich ganz genau messen 4,9 x 2² Sekunden = 19.60 m.
Dr. Webbaer schrieb (14. Mai 2019 @ 14:10):
> Gibt es einen grundsätzlichen Unterschied zwischen physikalischem Versuch und Anwendung?
Eine “Anwendung” meint da sicherlich das Eintreten eines (physikalisch-experimentellen) Versuches begleitet von (mehr oder weniger bestimmten) Erwartungs-“Haltungen” (bzw. -“Befangenheiten”) der Anwender hinsichtlich des Versuchs-Ergebnisses; und womöglich sogar der Erfüllung solcher Erwartungen.
p.s.
Dr. Webbaer schrieb (10. Mai 2019 @ 13:33):
> Sog. Naturgesetze sind physikalische Theorien mit bestimmter, mit besonderer empirischer Dichte […]
Sauber!
Ob (und ggf. wie) sich anhand dieser Beschreibung wohl herleiten lässt, dass in den/allen derart Beschriebenen jene (im obigen SciLogs-Artikel und etlichen Kommentaren ach-so-inbrünstig-herbeigerufene) “Symmetrie” … wabert ?
p.s.
Zur Ausfechtung des alten, jüngst (8. Mai 2019 @ 09:48) von J. Schulz wieder losgetretenen, aber von Rudi Knoth (9. Mai 2019 @ 10:31) ganz anständig sekundierten Disputs wurde einstweilen
dort berichtet.
p.p.s.
Hinsichtlich des (häufig aber bisweilen nur flüchtig gebrauchten) Begriffs “Geschwindigkeit” noch ein Hinweis auf den allgemeinen (und offensichtlich Koordinaten-freien) Ausdruck für “β”:
(1 – (ℓ[ ϵ_AP, ϵ_AB ] / ℓ[ ϵ_BQ, ϵ_AB ])^2) /
(1 + (ℓ[ ϵ_AP, ϵ_AB ] / ℓ[ ϵ_BQ, ϵ_AB ])^2),
jeweils für zueinander lichtartige Paare von Ereignissen ϵ_AP und ϵ_BQ
(was natürlich insbesondere in einem bestimmten Grenzübergang bewertet werden kann, den ausdrücklich darzustellen ich mir aber hier vorerst verkneife).
@Dr. Webbaer 14. Mai 2019 @ 14:10
Nun ich verstehe den Unterschied so:
Versuch:
In einem Versuch wird überprüft, ob ein aus einer Theorie/Modell errechnete Vorhersage bezüglich von Messwerten im Rahmen der Messgenauigkeit zutrifft oder nicht. Trifft dies zu ist die Theorie (das Modell) vorerst bestätigt. Wenn nicht, ist sie (es) falsifiziert.
Anwendung:
Aufgrund einer von Versuchen bestätigten Theorien (Modellen) werden Apparaturen oder Verfahren entwickelt. Man verlässt sich also hier auf Versuche, mit denen die Gültigkeit der Theorien/Modelle bestätigt wurde.
PS:
@Frank Wappler:
Nun ja der Disput war ja vor einem Jahr. Wo wurde denn der Disput heuer weitergeführt?
Nachtrag zu meinem letzten Kommentar:
Der Disput wurde auf scilogs/quantenwelt weitergeführt,. Also alle klar. Und damit Verzeihung für die seltsame Frage.
Gruss
Rudi Knoth
Rudi Knoth schrieb (16. Mai 2019 @ 08:28):
> Frank Wappler [schrieb (15. Mai 2019 @ 12:00): »Dr. Webbaer schrieb (14. Mai 2019 @ 14:10):« …]
> Wo wurde denn der Disput heuer weitergeführt?
Wo der Disput, wie oben erwähnt, » jüngst (8. Mai 2019 @ 09:48) von J. Schulz wieder losgetreten« wurde ??
Mal schauen. — Das Internet vergisst doch (hoffentlich) nichts. …
Im Übrigen befeuert es diesen Disput, wenn von Versuchen und von Messwerten geschrieben wird, ohne nachvollziehbare Festsetzungen dafür in Betracht zu ziehen, wie das Auftreten “gültiger” Versuche festgestellt bzw. wie bestimmte Messwerte daraufhin ermittelt werden sollten; und/oder ohne das Wort “Theorie” konkret und ausschließlich für ein bestimmtes System solcher Festsetzungen zu verwenden.
Hallo Herr Honerkamp,
“Bei Galilei ist in diesem Kontext die geradlinig-gleichförmige die natürliche, eigentliche Bewegung, sie ist ein Zustand.”
Falls das stimmt, dann irrt Galilei hier gewaltig. Eine geradlinig-gleichförmige Bewegung kann es gar nicht geben. Sie kommt schichtweg nicht vor. Sie existiert nicht. Dies schon deshalb, weil sie empirisch nicht zu fassen wäre. Denn eine gleichförmige (unbeschleunigte) Bewegung ist nur möglich, wenn keine Wechselwirkung stattfindet. Ein nicht wechselwirkender Gegenstand ist aber nicht beobachtbar, weil Beobachtung Wechselwirkung voraussetzt.
Eine Idealisierung wird hier als “natürlich” beschrieben. Es ist genau das Gegenteil, nämlich im wahrsten Sinne des Wortes unnatürlich, weil sie wie schon gesagt in der Natur nicht vorkommt.
Man kann einen Gegenstand vom Rest des Universums nicht isolieren. Eine gleichförmig-geradlinige Bewegung ist kein Grundprinzip von Irgendwas, sondern eine schlichte Näherung, oder Vereinfachung, von dem was wirklich ist.
Grüße
Fossilium
Um noch mal das Verhältnis von Versuch und Anwendung zu beschreiben, nehme ich das Beispiel Funkwellen.
Versuch:
Heinrich Hertz
Er erzeugte in seinen Versuchen elektromagnetische Wellen mit Wellenlängen im Bereich von mehreren Dezimeter und wies sie auch nach.
Anwendung:
Später entwickelten das Leute wie Marconi Apparaturen, um mit diesen Wellen über grosse Entfernungen Nachrichten drahtlos zu übertragen. Sie wedetetn also die Ergebnisse der Versuche von Heinrich Hertz an.
@Rudi Knoth:
Schönes Beispiel. Man könnte auch sagen: Mit einem Experiment will man ein Naturgesetz erkunden, in einer Anwendung will man es nutzen.
@fossilium
Richtig. Aber das ist ja gerade das Neue bei Galilei, dass er von der Reibung absehen kann und ein idealisierte Modell für die Bewegung entwickelt. Physikalische Theorie sind immer Modelle der Wirklichkeit. Sonst könnten wir die Natur ja auch gar nicht mit der Mathematik beschreiben. Was wir in der Wirklichkeit beobachten, ist immer die “Summe” des idealisierten Phänomens und vieler anderer Einflüsse. Im Experiment, bei der Erkundung eines Naturgesetzes, versucht man so gut wie möglich diese anderen Einflüsse auszublenden oder zu minimieren. Die Formulierung der idealisierten Phänomens ist immmer ein geistiger Akt. All das ist ja gerade der “Witz” der Physik. Der Passus “natürliche, eigentliche Bewegung” ist in diesem Kontext zu verstehen.
“Im Experiment, bei der Erkundung eines Naturgesetzes, versucht man so gut wie möglich diese anderen Einflüsse auszublenden oder zu minimieren.”
Genau, schon die Vorsokratiker wussten: panta rhei.
Nichts und niemand in der Zeit ist identisch mit sich selbst, man ähnelt sich nur. Kein Experiment kann wiederholt werden, und niemals vom selben Forscher.
Trotzdem hat sich dieser Running Gag in die Experimentalwissenschaften eingeschlichen: ceteris paribus.
Hallo Herr Honerkamp,
genau so ist es: Theorien sind immer nur Modelle der Wirklichkeit, sie bilden im Modell die Wirklichkeit zwar anschaulich, aber eben nur näherungsweise ab.
Damit stellt sich die Frage: wie nah sind sie denn an der Wirklichkeit ? Was (oder wie viel(es) ) ist von den wirklich vorhandenen Eigenschaften weggelassen (wegreduziert) worden bei dieser näherungsweisen Beschreibung ? Wie sicher kann unser Wissen sein, wenn wir nicht wissen, wie weit unsere Beschreibung überhaupt zutrifft ? In den Theorien von Galilei und Newton bewegen sich Massenpunkte um einen zentralen Massenpunkt. Glücklicherweise ist beim Massepunkt offensichtlich, was alles an wirklichen Eigenschaften der agierenden Objekte weggelassen wurde – weil wir den weggelassenen Rest unmittelbar erkennen. Aber im Subatomaren ist das, was weggelassen wird, nicht offensichtlich. Wie können wir wissen, daß die Theorien und Modelle des Subatomaren nah an der Wirklichkeit sind ?
Vor allem weil leider auch die Mathematik nicht weiter hilft.
Auf was können wir denn bauen ? Was gibt uns Sicherheit ? Haben Sie dazu einen Vorschlag ?
Grüße Fossilium
Rudi Knoth schrieb (19. Mai 2019 @ 08:24):
> […] Versuch: Heinrich Hertz
> Er erzeugte in seinen Versuchen elektromagnetische Wellen mit Wellenlängen im Bereich von mehreren Dezimeter und wies sie auch nach.
Interessantes Beispiel.
Hinsichtlich der oben geäußerten Auffassung (Rudi Knoth, 16. Mai 2019 @ 08:28): »In einem Versuch wird überprüft, ob ein aus einer Theorie/Modell errechnete Vorhersage bezüglich von Messwerten im Rahmen der Messgenauigkeit zutrifft oder nicht.«:
Wurde denn die (wahrscheinlichste) Verteilung von “leitfähigem Material” bzw. (im Sinne meines obigen Kommentars 13. Mai 2019 @ 12:15) von “kompensierenden Strömen” bei den Hertzschen Versuchen im betreffenden Hörsaal der damaligen TH Karlsruhe,
nämlich im Wesentlichen: deren Fehlen,
von der Maxwell-Hertzschen Theorie über Erzeugung/Ausbreitung/Nachweis el.-mag. wellen vorhergesagt ?
Oder drückt dieser Verteilungswert (“lediglich”) einen experimentellen Befund aus, den Hertz in Anwendung dieser Theorie aus den o.g. Versuchen erhielt, und der vermutlich auch seinen diesbezüglichen Erwarten bzw. Modell-Vorstellungen (hinsichtlich dieses Hörsaals in diesen Versuchen) entsprach ?
Wer “Modell” (als “Beschreibung der Wirklichkeit, einschl. weiterer diesbezüglichen Erwartungen”) nicht strikt
von “Theorie” (als System der Festsetzungen, wie Messwerte bzw. “Wirklichkeit” jeweils überhaupt erst ermittelt werden soll) unterscheidet,
der gibt sich (wie mittlerweile bekannt sein dürfte) einer Täuschung hin, und täuscht womöglich sogar andere.
@Frank Wappler 20. Mai 2019 @ 15:33
Diese wurde wohl durch die Versuchsanordnung selber festgelegt. In der Theorie-(Vorlesung) wurde seine Lösung der Maxwellgleichungen als Hertzsche Lösung bezeichnet. Allerdings benutzte er nicht eine “kurze” Antenne sondern eine resonante Antenne, deren Länge die nahe der halben Wellenlänge ist. Seine Lösung ist dann auch eher als Modell anzusehen, das er dann experimentell realisierte.
Danke Jungs!, war eine gar nicht so dumme Frage, denn ein Versuch kann auch (gleichzeitig) eine Anwendung sein, so dass in diesem Fall die Anwendung auch ein Versuch wäre, bereits logischerweise, aber an sich (“per se” oder üblicherweise) basiert die (weltliche) Anwendung auf der Kombination physikalischer Versuchsleistungen, die zu Theorien führten.
Andersherum nicht n-lateral, denn (naturwissenschaftliche) Versuche sind punktuell isolierend, die zu überprüfenden Hypothesen / Modelle / Theorien meinend.
Hmm, hartes Brot für Dilettanten; womöglich führen sehr stabile Anwendungen aber schon zu mehr Vertrauen in (die viele) naturwissenschaftliche Theorie, auf der sie basieren.
MFG
Dr. Webbaer (der sich hierüber – ‘Theorien sind immer nur Modelle der Wirklichkeit, sie bilden im Modell die Wirklichkeit zwar anschaulich, aber eben nur näherungsweise ab.’ [Kommentatorenfreund ‘fossilium’] – noch teuflisch ärgern könnte, wegen der vielen Unklarheiten bzw. Fehler, dies an dieser Stelle, im Abgang begriffen, abär nicht tun wird)
Rudi Knoth schrieb (21. Mai 2019 @ 08:42):
> [… »die (wahrscheinlichste) Verteilung von “leitfähigem Material” bzw. von “kompensierenden Strömen” bei den Hertzschen Versuchen im betreffenden Hörsaal der damaligen TH Karlsruhe« …]
> Diese wurde wohl durch die Versuchsanordnung selber festgelegt. […]
Na — geht doch! …
Bei meinem anschließenden Versuch, diesen (auch von mir schon des Öfteren gebrauchten) Begriff “Versuchsanordnung” enzyklopädisch einzuordnen,
nicht zuletzt in der Absicht,
– “Anordnung” als Entwurf, Vorhaben, Anweisung (und dahingehend als mitteilbar bzw. nachvollziehbar)
von
– “Anordnung” als (eventuelle) Manifestation, Inkarnation, Realisierung (des oben Genannten)
zu unterscheiden
(um wiederum womöglich auf die Beurteilung der eventuellen “Gültigkeit” von Versuchs-“Versuchen” zu schließen),
bin ich gerade erstmals auf den Begriff [[Konstrukt]] gestoßen …
(Und [[construct]] gibt’s übrigens auch …)
Vielleicht ist ja dieses Wort (und das damit verbundene Vokabular) geeignet, um sich denjenigen gegenüber verständlich zu machen, die mit “(festgesetzter) [[Messgröße]]” und “[[Wahrer Wert]] (einer bestimmten Messgröße, in einem bestimmten Versuch)” offenbar wenig anfangen wollen.
p.s.
> In der Theorie-(Vorlesung) wurde seine Lösung der Maxwellgleichungen als Hertzsche Lösung bezeichnet. Allerdings benutzte er nicht eine “kurze” Antenne sondern eine resonante Antenne, deren Länge die nahe der halben Wellenlänge ist. Seine Lösung ist dann auch eher als Modell anzusehen
Vgl. “[[Der Hertz’sche Dipol als Modell]]“.
In wie fern ließe sich dieses konkrete Modell ggf. experimentell testen ? …
> das er dann experimentell realisierte.
Zumindest ließe sich wohl die Hypothese bzw. Erwartung bzw. Vorhersage testen, dass die im Hertzschen Hörsaal manifestierte Versuchsanordnung dem o.g. Modell “entsprach” (oder “davon abgebildet wurde”, oder “es realisierte”); zumindest “mit befriedigender/endlicher/quantifizierbarer Näherung”, und jedenfalls in Anwendung der relevanten Theorie (Festsetzungen von Messgrößen/”Konstrukten”).
@Dr. Webbaer 21. Mai 2019 @ 14:10
Zu mindestens kann man die Theorien dann nicht so einfach als “Hirngespinste” abtun. Andererseits kann es sehr lange dauern, bis aus einem Experiment eine technische Anwendung folgt. Beispiel ist hierfür die Kernfusion. Die Experimente sind schon vor dem 2. Weltkrieg gemacht worden, aber die Energieerzeugung ist noch nicht realisiert.
@Frank Wappler 22. Mai 2019 @ 01:39
Im Prinzip sind dies Antennen, die mit Endkapazitäten oder “Verlängerungsspulen” mechanisch wesentlich kürzer als die Wellenlänge sind, aber trotzdem “resonant” sind. Eine andere Möglichkeit sind “magnetische Antennen” die einen Schwingkreis mit einer grossen einzelnen Windung darstellen.