Die Vorsokratiker: Die Krise der Pythagoreer
BLOG: Die Natur der Naturwissenschaft

Nachdem wir im letzten Blogbeitrag die Mathematik der Pythagoreer und anderer griechischer Philosophen der damaligen Zeit studiert haben, müssen wir uns jetzt damit beschäftigen, welche Schlüsse die Pythagoreer aus Ergebnissen ihrer Studien gezogen haben. Dazu müssen wir uns vorher noch die Gemeinschaft der Pythagoreer etwas anschauen, um auch das weitere Schicksal der pythagoreischen Philosophie zu verstehen.
Die Gemeinschaft der Pythagoreer
Die Gruppe um Pythagoras bestand keineswegs aus vorwiegend weltfremden Philosophen, die allein Freude an mathematischen Problemen hatten. Aus späteren antiken Quellen (Iamblichos, 3./4. Jhdt) erfährt man, dass es bei den Pythagoreern später zwei Gruppen gab: „Mathematiker hießen jene, welche mehr in den besonderen, und im Hinblick auf Exaktheit gepflegten Lehre seiner Wissenschaft unterrichtet worden waren, Akusmatiker, jene, welche nur die kurzgefassten Vorschriften ohne exakte Begründung vernommen hatten.“ (Mansfeld & Primavesi, 2011, pp. 137, Nr.20).
Hier zeigte sich auch schon, wie soziale Trennungen entstehen: Für die Akusmatiker (ἄκουσμα = Akousma = auditive Wahrnehmung) waren die Mathematiker gar keine richtigen Pythagoreer. Andererseits verstanden sich die Mathematiker als eine Art „höherer“ Pythagoreer. Franz Schupp erwähnt in diesem Zusammenhang, dass es später bei den Gnostikern und frühen Christen auch eine ähnliche Unterscheidung gegeben habe: Es gab „Pistiker“, die einfachen Gläubigen, und „Gnostiker“, die eine höhere Einsicht haben oder solches nur behaupten (Schupp, 2003a, p. 67). In unserer Zeit sind es in den Religionen das „einfache Volk“ und auf der anderen Seite die Gruppe der Priester und Theologen.
Der Vergleich passt aber nicht in allen Aspekten. Man könnte es nämlich nicht unvernünftig nennen, wenn Pistiker oder Gläubige die Lehren der Gnostiker in Zweifel ziehen würden oder ganz vom Glauben abfielen. Sie wenden sich dann ja nur von den Setzungen bestimmter Autoritäten ab. Unvernünftig, also gegen die Vernunft handelnd, wäre es aber, wenn Akusmatiker mathematische Beweise grundsätzlich nicht anerkennen würden. Sie könnten sich höchstens so weit unterrichten lassen, dass sie fähig werden, die Beweise auf ihre Richtigkeit überprüfen zu können.
Beide Denkweisen, die dem Mythos wie die dem Logos nahestehende, gab es also in der Gemeinschaft und natürlich auch in einzelnen Köpfen. Und für spätere Zwecke ist es ratsam beim Mythos noch eine Unterscheidung zu treffen, nämlich in eine „rein philosophische“ Richtung, die eine Ähnlichkeit zwischen Strukturen der Natur und der Struktur mathematischer Begriffe, also zwischen den „Prinzipien des Mathematischen und die Prinzipien der seienden Dinge“ sahen, und in eine stark religiöse Richtung, die dieses Weltbild so weit interpretierte, dass man daraus strenge Regeln für das Leben und Zusammenleben folgern zu können glaubte. Zu dieser religiösen Richtung will ich auch die Seelenlehre zählen, die Zuordnung der Zahlen zu irgendwelchen Tugenden wie auch all die Vorschriften für das Leben, die man z.B. in der Liste von „Akusmata“ von Iamblichos findet (Mansfeld & Primavesi, 2011, pp. 193, Nr.102).
Was ich von der Seelenlehre gesagt habe, soll natürlich allgemein von der religiösen Richtung des pythagoreischen Denkens gelten. Dieses soll hier keine Rolle spielen.
Die Prinzipien des Mathematischen und die Prinzipien der seienden Dinge
Wenn man sich einen Überblick über die Mathematik der frühen Griechen verschaffen will, dann muss man sich die Mühe machen, die „Elemente“ des Euklid von Alexandria zu studieren. Euklid muss dieses Lehrbuch in den Jahren um -300 geschrieben haben, und nach Proklos Diadochos (412 bis 485) hat er dabei „vieles aus Eudoxos verwendet, vieles von Theaitetos Behandelte zum Abschluss gebracht, und was von Früheren nur oberflächlich dargestellt war, durch unanfechtbare Beweise gestützt“. Ob das gerecht geurteilt ist, wissen wir nicht.
Auf jeden Fall müssen wir feststellen, dass unter den Mathematikern, die später in irgendwelchen Listen frühgriechischer Mathematiker auftauchen, nicht allzu viele Pythagoreer gewesen sind. Aus den pythagoreischen Gemeinschaften bzw. Bünden sind uns aber auf jeden Fall zwei Gruppen bekannt, deren Führer Philolaos (-470 bis -399) und Architas von Tarent (-428 bis -347) berühmte Mathematiker waren, und deren mathematische Ergebnisse heute noch bemerkenswert sind.
Von Philolaos wissen wir über den Sammler antiker philosophischer Schriften Stobaios (5. Jhdt.), welches Weltbild die Pythagoreer aus ihren mathematischen Studien abgeleitet haben. In einem der Fragmente, die uns von ihm überliefert sind, heißt es:
„Und es ist wahrhaft alles, was man erkennen kann, Zahl, denn es ist nicht möglich, irgendetwas zu verstehen oder zu erkennen ohne diese“ (Mansfeld & Primavesi, 2011, pp. S. 147, Nr.28).
Der Begriff der Zahl ist danach also die Grundlage einer jeden Erkenntnis. Wenn man etwas erkennen will, muss es quantitativ formulierbar sein. Und in der quantitativ formulierbareren Erkenntnis entdeckt man die Ordnung und die Harmonie der Welt. In einem anderen Fragment heißt es:
„Es wäre jedoch ausgeschlossen, dass eines von den Seienden und von uns Menschen erkannten Dingen entstanden wäre, wenn es nicht auch schon das Wesen der Dinge gäbe, aus dem die Welt zusammengesetzt ist: Das Wesen der Begrenzenden und Unbegrenzten. Da aber diese Prinzipien […] nicht gleich sind, [..] muss es notwendig durch eine derartige Harmonie zusammengeschlossen sein, wenn es in der Weltordnung enthalten sein will.“ (Mansfeld & Primavesi, 2011, pp. 145, 27).
Mit dem Begriff der Zahl kommt auch das Unbegrenzte in den Blick. Aus der Tatsache, dass es die seienden Dinge gibt, muss man also folgern, dass dieses Unbegrenzte in Harmonie mit dem Begrenzten existiert. Es liegt nahe, dass es insbesondere die Entdeckung der rationalen Frequenzverhältnisse bei den Saiten z.B. des Tetrachords war, die hier die Verbindung von Zahlen mit einer Harmonie nahelegte. (Aristoteles, kein Datum) sagt dazu:
„Da sie nun auch darauf aufmerksam wurden, dass die Verhältnisse und Gesetze der musikalischen Harmonie sich in Zahlen darstellen lassen, und da auch alle anderen Erscheinungen eine natürliche Verwandtschaft mit den Zahlen zeigten, die Zahlen aber das erste in der gesamten Natur sind, so kamen sie zu der Vorstellung, die Elemente der Zahlen seien die Elemente alles Seienden und das gesamte Weltall sei eine Harmonie und eine Zahl.“
Wenn man einmal einen solchen Gedanken gefasst hat, sieht man in der Geometrie auch die Schönheit der regelmäßigen Polyeder durch die Beziehungen zwischen den dort vorliegenden Zahlen verursacht.
Die Pythagoreer gingen allerdings noch weiter. Aristoteles spottet darüber: „Was sich nur irgendwie an Übereinstimmungen zwischen den Zahlen und Harmonien einerseits und den Prozessen und Teilen des Himmelsgewölbes und dem gesamten Weltenbau andererseits auftreiben ließ, das sammelten sie und suchten einen Zusammenhang herzustellen; wo ihnen aber die Möglichkeit dazu entging, da scheuten sie sich auch nicht vor künstlichen Annahmen, um nur ihr systematisches Verfahren als streng einheitlich durchgeführt erscheinen zu lassen.“
Dazu führte er ein Beispiel an:
„Da sie die Zehn für die vollkommene Zahl halten und der Meinung sind, sie befasse die gesamte Natur der Zahlen in sich, so stellen sie die Behauptung auf, auch die Körper, die sich am Himmel umdrehen, seien zehn an der Zahl, und da uns nur neun in wirklicher Erfahrung bekannt sind, so erfinden sie sich einen zehnten in Gestalt der Gegenerde.“
Die Gegenerde hatte Philolaos erfunden. Man hatte auch ein Argument dafür parat, dass man diese nie sehen konnte: Sie sollte von der Erde aus gesehen immer genau hinter der Sonne stehen.
Man erinnert sich unwillkürlich an manche Hypothesen der Physik, z.B. an die Annahme Wolfgang Paulis, dass es ein bestimmtes Teilchen geben müsse, dass bei dem Zerfall eines Neutrons eine bestimmte Energie mit sich führt, so dass die Erhaltung der Energie auch hier bestätigt werden konnte. Der Unterschied ist aber ganz wesentlich: Zu Zeiten Paulis war die Hypothese ein Auftrag zur Nachprüfung, bei Philolaos war eine Überprüfung nicht denkbar. Es war also reine Metaphysik.
Die Krise: Inkommensurable Größen statt Zahlen
Aber nicht von diesen und anderen nicht überprüfbaren Aussagen drohte den Pythagoreer Unheil mit ihrer Philosophie. Dieses kam mit einer Entdeckung, die im Kern ihre Philosophie erschütterte. Um das zu verstehen, muss man ein wenig ausholen:
Die Pythagoreer kannten die natürlichen Zahlen {1,2,3,…} und die positiven rationalen Zahlen, also Verhältnisse von natürlichen Zahlen wie 3/4 oder 2/5. Da diese Zahlen die Beschaffenheit der Welt wiederspiegeln sollten, mussten auch alle Dinge ein Maß besitzen, das sich durch diese Zahlen ausdrücken lässt. Die Länge einer Strecke z.B. musste sich durch ein Vielfaches einer Einheitslänge ausdrücken lassen und für zwei Strecken musste es immer eine gemeinsame Einheitslänge geben. In Zahlen ausgedrückt: Es musste einen gemeinsamen Teiler g für zwei Zahlen geben, so dass die beiden Zahlen m und n als ganzzahliges Vielfaches von g darstellbar ist. Der größte dieser Teiler heißt dann sinnigerweise „größter gemeinsamer Teiler“ (GGT). Man denke an die Schulzeit. Für die Pythagoreer mussten also alle Strecken in diesem Sinne „kommensurabel“ sein, ja, alle Dinge der Welt mussten kommensurabel sein, also ein gemeinsames Maß haben. Denn die Zahlen regieren die Beschaffenheit der Welt.
Die antiken Griechen hatten sogar einen Algorithmus gefunden, mit dem sie leicht den größten gemeinsamen Teiler zweier natürlichen Zahlen ausrechnen konnten. In Abb. 1 wird dieser demonstriert:
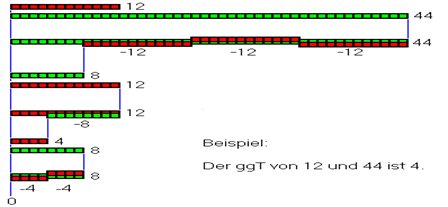
Abb. 1: Der Algorithmus der Wechselwegnahme zur Bestimmung des größten gemeinsamen Teilers von 44 und 12: Man zieht von der größeren Zahl, hier 44, so oft die kleinere Zahl , (hier 12), ab, bis der Rest kleiner n ist. Dann ist nun n (=12) die größere Zahl und man wiederholt das Spiel – solange bis sich dadurch Null ergibt. Die letzte Zahl, die man dafür abziehen muss, hier 4, ist der größte gemeinsame Teiler bzw. das gemeinsame Maß. common: https://de.wikipedia.org/wiki/Datei:Euklidischer_Algorithmus.png
Dieses Verfahren wird als „Wechselwegnahme“ bezeichnet und findet sich in Euklids „Elementen“; aber schon die Pythagoreer sollen diesen Algorithmus gekannt haben.
Nun kannten die Griechen aber auch, und die Pythagoreer schon gar, den so genannten Satz des Pythagoras. In einem Quadrat der Seitenlänge 1 hat die Diagonale eine Länge, deren Quadrat nach diesem Satz gleich 12 + 12 = 2 ist. Sie kannten aber keine Zahl, deren Quadrat gleich 2 ist. Seitenlänge und Diagonale können also nicht kommensurabel sein.
Wenn jemand noch an irgendeinen Ausweg sucht, kann man ihn mit einem strengen Beweis überzeugen:
Nennen wir die Größe, deren Quadrat gleich 2 ist, schon einmal $*latex \sqrt{2}$ , so wie wir es heute tun, und stellen die Behauptung auf, dass sich diese Größe als Zahl im Sinne der antiken Griechen, also als ein Verhältnis von natürlichen Zahlen darstellen lässt. Dann gilt also
\(\sqrt{2} = m/n\).
Die Zahlen m und n kann man ohne Beschränkung der Allgemeinheit so wählen, dass die Aussage
A:= „m und n sind teilerfremd“
wahr ist. Quadrieren der Gleichung ergibt
2 = m2/n2, also auch m2 = 2·n2
Darauf folgt, dass m eine gerade Zahl ist, dass man also m = 2·k schreiben kann, somit auch m2 = 4·k2 ist. Damit gilt mit Hilfe der vorherigen Gleichung auch 4·k2 = 2·n2, also n2 = 2·k2, was nun schließlich heißt, dass n wie n2 durch 2 teilbar ist. Also: m und auch n sind durch 2 teilbar.
Insgesamt kommen wir so zum Schluss, dass m und n nicht teilerfremd sind, d.h. die Aussage A ist falsch, obwohl sie als wahr angenommen wurde. Dann kann A nicht wahr sein. Denn aus einer wahren Aussage kann man nie logisch schließen, dass sie falsch ist. Das ist einleuchtend. In einem späteren Blogbeitrag werde ich diesen logischen Schluss streng formal im Rahmen einer so genannten Aussagenlogik zeigen.
Das Verhältnis \(\sqrt{2}\) : 1 lässt sich also nicht als ein Verhältnis natürlicher Zahlen m/n darstellen. Eine natürliche Zahl und eine Größe wie \(\sqrt{2}\) haben also kein gemeinsames Maß, sie sind inkommensurabel.
Die Größe \(\sqrt{2}\) wurde bis in die Neuzeit nicht als Zahl akzeptiert. Solche nicht-rationalen, als irrationalen Zahlen wurden höchstens als „unmögliche“ oder „eingebildete“ Zahlen gesehen. Man konnte zwar mit ihnen rechnen, ihr Quadrat war nun einmal gleich 2, aber man konnte diese Größen nie vollständig hinschreiben, wie es sich „für eine Zahl gehörte“. Erst Ende des 19.Jahrhunderts lernte man, den Zahlbegriff so zu definieren, dass auch irrationale Größen als eine besondere Klasse von Zahlen akzeptiert werden konnten.
Diese Entdeckung, dass es in der Natur Strecken geben kann, deren Länge sich nicht als eine rationale Zahl darstellen lässt, hat die Pythagoreer stark erschüttert. Dieses Wissen müsse geheim bleiben, so glaubte man. Iamblichos (245 bis 325) kolportiert in seinem Buch Über das pythagoreische Leben die Geschichte, dass jemand diese Entdeckung ausgeplaudert haben soll. Dieser sei dann aus dem gemeinsamen Kreis ausgeschlossen worden und später sei er gar im Meer umgekommen (Mansfeld & Primavesi, 2011, pp. 171, Nr.61,62). Wie alle Anekdoten aus dieser Zeit kann man auch diese zur Unterhaltung einstreuen. Glauben muss man sie nicht.
Das Erbe der Pythagoreer
Die antiken Griechen waren die Ersten, die aus dem mathematischen Wissen, das ihnen von früheren Völkern überliefert worden war, eine Wissenschaft machten. Sie fanden nicht nur interessante Beziehungen zwischen mehreren Zahlen sowie zwischen Zahlen und geometrischen Figuren, Körpern und Klängen. Noch viel bedeutsamer ist, dass sie eine Argumentation entdeckten, die unanfechtbar ist, also das darstellt, was wir heute einen mathematischen Beweis nennen.
Euklid von Alexandria hat dieses Wissen gesammelt und in eine logische Ordnung gebracht. In dieser Ordnung werden Definitionen und Axiome an den Anfang gestellt, und daraus wird das ganze Wissen in Form mathematischer Beweise abgeleitet. Ein „axiomatisch deduktives System“ wurde damit geschaffen. Damit war schon in der Zeit um -300 die Idee einer strengen Wissenschaft nicht nur geboren, sondern auch schon einmal realisiert worden ist. Diese Idee inspiriert bis heute alle, die sich Gedanken darüber machen, was eine Wissenschaft eigentlich ausmacht. In Die Idee einer Wissenschaft – Ihr Schicksal in Physik, Rechtwissenschaft und Theologie habe ich das weiter ausgeführt (Honerkamp, 2017).
Auch in den Jahren nach Euklid ist die Mathematik der Griechen weiter vorangeschritten. Mit Archimedes (ca. -287 bis -212) hat sie dann einen vorläufigen Höhepunkt erreicht. Aber Wissenschaftshistoriker sprechen von ersten Anzeichen des Schwindens kreativer Kräfte schon in den nächsten Jahrhunderten (Russo, 2005).
Pythagoras und die Pythagoreer gaben im antiken Griechenland den Anstoß zu dieser ersten Blüte einer Wissenschaft. Allerdings: Mit ihrer Lehre von der Harmonie übertrieben sie es, ihr religiöser Eifer einschließlich ihrer Vorschriften für den Lebenswandel wirkt heute auf uns höchst befremdlich, mitunter skurril. Mit ihrer Vorstellung von den Zahlen als Grundmuster für die Natur scheiterten sie.
Dennoch waren sie auf der richtigen Spur. Erst im zweiten Anlauf, 2.000 Jahr später, sollte sich eine Verbindung von Mathematik und Naturforschung ergeben, die dann aber zu einem Verständnis der Natur führte, aus dem heraus die Menschen höchst segens- wie auch schreckensreiche Instrumente entwickeln konnten.


Hallo Herr Honerkamp,
Sie schreiben: „Es gab „Pistiker“, die einfachen Gläubigen, und „Gnostiker“, die eine höhere Einsicht haben oder solches nur behaupten (Schupp, 2003a, p. 67). In unserer Zeit sind es in den Religionen das „einfache Volk“ und auf der anderen Seite die Gruppe der Priester und Theologen.“ – Das hört sich bezogen auf die Religion etwas abfällig an, in heutiger Zeit ist doch die Gruppe der Priester und Theologien nicht die einzige Personengruppe, die angeblich eine höhere Einsicht hat oder dies für sich beansprucht. Unter den Wissenschaftlern gibt es da auch viele Leuten, die glauben, sie hätten das bessere Wissen.
Sie schreiben auch: „Zu Zeiten Paulis war die Hypothese (zwei Teile statt eines) ein Auftrag zur Nachprüfung, bei Philolaos war eine Überprüfung nicht denkbar. Es war also reine Metaphysik.“ Das ist etwas seltsam formuliert. Das sieht so aus, als ob Sie der Meinung wären, die Metaphysik würde nicht-prüfbare Aussagen machen, im Gegensatz zur Physik, die nur prüfbare Aussagen macht. Die Metaphysik würden Sie dann aber sehr mißverstehen: die Metaphysik macht prüfbare und nicht-prüfbare Aussagen, und die Gültigkeit ihrer Aussagen speist sich aus vollkommen anderen Quellen als aus der Forderung nach Nachprüfbarkeit (eine Quelle zum Beispiel ist der Logos).
Dann sagen Sie auch: „Denn aus einer wahren Aussage kann man nie logisch schließen, dass sie falsch ist. Das ist einleuchtend. In einem späteren Blogbeitrag werde ich diesen logischen Schluss streng formal im Rahmen einer so genannten Aussagenlogik zeigen.“ Ich habe mich auch schon in den Kommentaren der Blogs Ihrer Kollegen immer gegen Behauptungen skeptisch gezeigt, die mit einer so großen Bestimmtheit daherkommen, daher möchte gegen diese Behauptung von Ihnen nun mal mit einem Gegenbeispiel antworten.
Wahre Behauptung: „Ein Stabmagnet ist von einem statischen Magnetfeld umgeben, wobei das Magnetfeld als Zuordnung von Zahlen an jedem Raumpunkt definiert ist.“ Das ist zwar ein langer Satz, aber er ist wahr im Sinne der Aussagenwahrheit physikalischer Aussagen. Die logische Schlussfolgerung, weist nun eindeutig nach dass der Satz falsch sein muss: „Ein Magnet kann nicht von einer Zuordnung von Zahlen umgeben sein.“ Es geht hier um die Logik physikalischer Begriffe. Diese lassen sich bei vielen Aussagen überhaupt nicht in irgendeine Logik bringen. Wenn Sie wollen vervielfältige ich die Beispiele. Ihre Aussage ist ebn nur richtig unter bestimmten Voraussetzungen, die Sie – wenn sie dies mit dieser Bestimmtheit behaupten – nennen müßten, was Sie aber nicht machen:
Wenn Sie schreiben, dass mit der Schaffung eines „axiomatisch deduktives Systems“ schon in der Zeit um -300 die Idee einer strengen Wissenschaft nicht nur geboren, sondern geschaffen wurde, dann mag man das so sehen, obschon man sich hier fragt, ob die Naturwissenschaften nicht eher induktiv als deduktiv schlußfolgern. Es sieht so aus, als würden Sie uns sagen wollen: seht her, mit der Entwicklung der Mathematik nahm die Naturwissenschaft ihren Anfang. Das ist so nicht richtig. Der Anfang war viel früher und wurzelt in der Philosophie. Denn auch die Mathematik, auf die die Naturwissenschaft gründet, gründet auf der Philosophie , sie baut auf begrifflichen Voraussetzungen auf, die sie selbst nicht hinterfragen kann. Das betrifft zum Beispiel die Frage nach der Identität eines Gegenstandes, nach dem numerischen Einen, nach dessen Bestimmtheit und allen Basisoperationen mit dieser Entität. Die Mathematik klärt diese Frage nicht, noch viel weniger die auf der Mathematik aufbauende Physik, und man muß hier fragen, welche Denkdisziplin die Frage nach der Entstehung des Einen als Voraussetzung der numerischen Eins und der darauf aufbauenden numerischen Bestimmtheiten beantwortet – und das ist eben die Metaphysik, die Philosophie, die genau dies bewerkstelligt, wenn dies überhaupt möglich ist. Ich weise auch nur deshalb darauf hin, um zu zeigen, daß jeder Versuch, die Naturwissenschaften als Erkenntnismethode sozusagen unabhängig oder im Gegensatz zur Philosophie entstehen zu lassen, zum Scheitern verurteilt ist. Ihr literarisches Werk würde in diesem Fall sich so angreifbar machen, was ich Ihnen nicht wünsche. Daher rate ich zur Vorsicht bei manchen Formulierungen, die so eine Art Abgrenzung zu allem Anderen darstellen.
Grüße
Fossilium
@Fossilium:
Bei den meisten stimmt das auch, wenn es um das Wissen ihres Faches geht. Das ist doch trivial. Mehr war auch nicht gemeint. Außerdem zahlt sich ein wissenschaftliches Studium auch meistens im Hinblick auf ein Argumentationsniveau aus.
Da wäre ich gespannt auf einige Beispiele für prüfbare Aussagen der Metaphysik.
Diese Aussage ist falsch. Sie unterschieden nicht zwischen dem realen Magnetfeld und der Beschreibung dieses Feldes in der Sprache der Mathematik.
Sie benutzen das Wort “Logik” im umgangssprachlichen Sinne. Das ist für dieses Niveau nicht brauchbar.
Das sage ich gar nicht. Mathematik ist die Sprache der Naturwissenschaft. Die moderne Naturwissenschaft ist entstanden, als Galilei die Bedeutung dieser Sprache für die Physik entdeckte.
Alle Wissenschaft baut auf Voraussetzungen auf (Begriffsbildungen und Aussagen(!)). Man kann sie auch hinterfragen, nur kommt man da selten weiter. (siehe aber: Newton -> Einstein).
Sie brauchen keineswegs die Philosphie zu verteidigen. In jeder Wissenschaft tauchen philosophische Fragen auf. Das sind aber welche, die man der analytischen Philosophie zurechnen muss.
Im Ganzen: Ich brauche etwas Zeit und noch viele Blogbeiträge, um alles “Logik”, “axiomatisch-deduktive Systeme usw.” zu erklären.
Alles ist Zahl (Pythagoreer), Alles ist Wasser (Thales), Alles ist Luft (Anaximenes) und Alles entspringt einem unbestimmten, unbegrenzten Urstoff (Anaximander) sind aus heutiger und vielleicht auch schon damaliger Sicht Versuche einer grossen Vereinheitlichung. Eine mythische/magische Aura lässt sich in diesen Konstrukten unschwer feststellen. Was aber ein Paradox ist, denn Pythagoras und die Milet-Scholasten wollten gerade wegkommen von der Mystik und dem nicht nachvollziehbaren.
Und wenn wir den grossen Bogen spannen zum heutigen Versuch der Teilchenphysiker die grosse Vereinheitlichung zu finden, dann findet sich vielleicht auch hier etwas Religiöses/Mystisches.
So langsam erahne ich den Sinn , der hinter dem Studium der Pythagoreer liegt.
Es sind die Denkweisen, die die Zeiten überdauern.
Die Zahlenmystik war damals sehr verbreitet, besonders bei den Juden, sie gibt es heute noch als Aberglaube, z.B. die 13 als Unglückszahl, die 3 und 7 als Glückszahl, die transzendenten Zahlen, in die man auch Geheimnisse hineininterpretiert.
Wenn man behauptet, alles sei Zahl , dann taucht dieser Gedanke in moderner Form auf als Quantenphysik wo sogar die Energie gequantelt ist, also gezählt werden kann.
Bei Einstein verwischt sich die Quantelung in den Grenzwerten der Relativitätstheorie .
Bei der Überlagerung des Lichtes muss man nach den Regeln der komplexen Zahlen rechnen. Hier versagt unsere anschauliche Logik, womit den Mathematikern unter den Pythagoreern eine späte Genugtuung widerfährt.
@Irrationale Zahlen
Ich wusste gar nicht, dass man die Irrationalen Zahlen erst Ende des 19. Jahrhunderts richtig eingeordnet hat. Die sind ja etwas unintuitiv. Und in der Praxis, z.B. in Computersimulationen, ignoriert man ihre Eigenschaften und rechnet eben mit Gleitkomma-Variablen. Die haben eine feste Anzahl an Nachkommastellen, und werden wie Rationale Zahlen verwendet. Meistens reicht das, weil die meisten Simulationen ohnehin mit ungenauen Messwerten und algorithmischen Vereinfachungen betrieben werden. Wenn man es doch genauer haben will, kann man auch die Anzahl der Nachkommastellen beliebig ausweiten, was dann programmiertechnisch nur etwas komplizierter wird.
Dass die Pythagoreer philosophische Probleme mit den Irrationalen Zahlen hatten, weil sie die Welt auf Zahlen reduzieren wollten, finde ich kurios. Wie kamen die auf die Idee, dass die Welt so einfach sein soll? Man kann ja praktische Geometrie mit irrationalen Hyphotenusen leicht so betreiben, dass man eben nur bis zu einer bestimmten Genauigkeit rechnet, und so alles hat, was man braucht.
Der Mythos scheint seine Attraktivität in seiner Einfachheit zu haben. So ist die vorchristliche Götterwelt komplizierter als der eine Gott des Christentums, und von daher ist das Christentum auf den ersten Blick einfacher, und allein deswegen schon attraktiver. Die weitere Reduzierung auf gar keinen Gott im modernen Atheismus, ist dann noch einfacher – aber nur, wenn man keine spirituellen Erfahrungen verarbeiten muss. Zu viel Reduktion macht es dann doch wieder komplizierter, wenn die Wirklichkeit da nicht mitmacht.
Man möchte ja gerne die Wirklichkeit so verstehen, dass man sich innere Bilder machen kann, die intuitiv sind, und gleichzeitig mathematisch konsequent sind. Aber die Wirklichkeit des Physikalischen nimmt da mitunter keine Rücksicht drauf. Ein einfaches Magnetfeld eines Stabmagneten reicht schon aus, dass die inneren Bilder an Grenzen stoßen.
Fossilium: „Ein Stabmagnet ist von einem statischen Magnetfeld umgeben, wobei das Magnetfeld als Zuordnung von Zahlen an jedem Raumpunkt definiert ist.“
Was ist das Magnetfeld jetzt wirklich? Die Zuordnung von Zahlen nach den hier geltenden physikalische Formeln ist kein Problem. Wenn man mit Kompassnadeln die Positionen rund um den Magneten ausmisst, sieht man, dass das so stimmt. Aber wie soll man sich das vorstellen? Herr Honerkamp, wie stellen Sie sich das vor?
@Tobias Jeckenburger:
Das ist eine gute Frage. Ich habe dazu früher schon mal etwas geschrieben:
https://scilogs.spektrum.de/die-natur-der-naturwissenschaft/was-ist-es-denn-nun-wirklich/
@https://scilogs.spektrum.de/die-natur-der-naturwissenschaft/was-ist-es-denn-nun-wirklich/
Danke für den Hinweis auf diesen Text. Meine Frage „Aber wie soll man sich das vorstellen?“ teilt sich auf verschiedene Beschreibungsebenen auf. Dann kann ich mir nur Bilder von je einer Beschreibungsebene machen, und diese sind dann auch mal unanschaulich. Weil die Alltagserfahrungswelt eben nicht auf allen Ebenen gut übertragbar ist.
Das Magnetfeld eines Stabmagneten ist also irgendwie komisch, und bleibt es auch, wie ich mich nun abmühe oder nicht, es bleibt unanschaulich. Ich kann mir nur immer wieder Beispiele von Feldlinien von Stabmagneten, Hufeisenmagneten, stromdurchflossenen Leitern, Spulen, Wirbelstrombremsen usw. anschauen, und hoffen, dass ich mit deren Geometrie vertraut werde. Diese Beschreibungsebene gibt eben mehr nicht her. Hab ich Sie so richtig verstanden?
Sie schreiben in dem Text im letzten Absatz: „Jeder von uns ist ständig mit verschiedensten Wirklichkeiten konfrontiert. In die meisten sind wir im Laufe des Lebens hinein gewachsen; wir haben uns an sie gewöhnt und uns damit eingerichtet. Das Gefühl der Geborgenheit und Sicherheit setzen wir dabei nicht so leicht aufs Spiel durch zu kritische Fragen nach deren Konsistenz.“
Deswegen meine Überlegungen, Platz für spirituelle Erfahrungen in der Physik des ganz Kleinen und des ganz Großen zu suchen. Der Konsistenz wegen, als Versuch spirituelle Erfahrungen jenseits von Halluzinationen erklären zu wollen. Wer kein spirituelle Erfahrungen hat, hat hier eher keinen Bedarf, diese einzuordnen. Der Bedarf ist eine Frage der persönlichen Erfahrung, die Wirklichkeit aber kann davon unabhängig sein.
@Tobias Jeckenburger
Ja, so sehe ich das auch. Die spirituelle Erfahrung spielt sich im Kopf ab, als Folge einer “Begabung” und als Folge vieler früherer Erlebnisse, die unsere Psyche geformt hat. Sie gehört zur Natur eines jeden Menschen, einer sehr komplexen Entwicklung der Natur. Die Natur “da draußen”, nicht annähernd so komplex, kennt so etwas nicht.
@Josef Honerkamp 25.02.19 11:15
„Die Natur “da draußen”, nicht annähernd so komplex, kennt so etwas nicht.“
Ich mein ja gerade, dass auch die Natur da draußen genauso viel mit (kosmischem) Bewusstsein zu tun haben kann wie ich selber. Wenn ich mein Bewusstsein als Synthese vom kosmischen Bewusstsein mit meinem lokalen Gehirn verstehe, ist die allgemeine Beseeltheit der Natur die Konsequenz daraus.
Offenbar kommt man aber auch klar, wenn man die Natur ohne Geist annimmt. Vor allem als Maschinenbauer, was wohl das Wesen der modernen Kultur und Wissenschaft zu sein scheint. Dafür reicht es, sich nur die Regelmäßigkeiten der Wirklichkeit anzuschauen.