Schattenriss eines Schwarzen Lochs: das Event Horizon Telescope
BLOG: RELATIV EINFACH

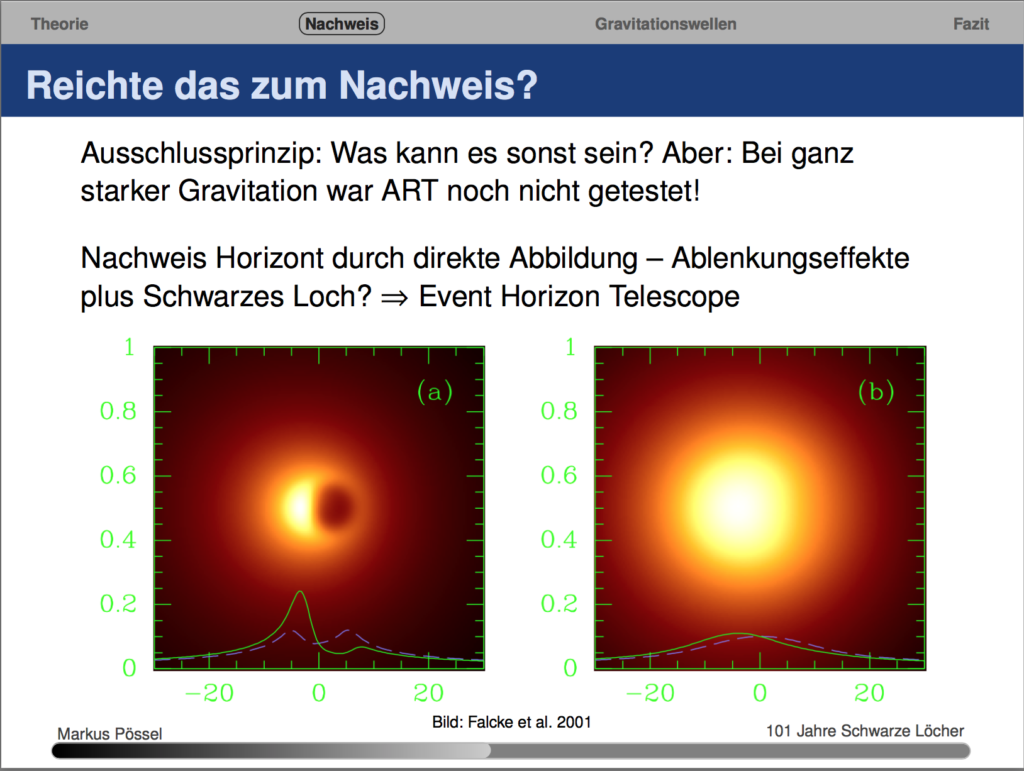
In allgemeinverständlichen Vorträgen über Schwarze Löcher bemühe ich mich vor allem herauszuarbeiten, wie sich der Status dieser Objekte mit der Zeit verändert hat. Seit Jahren habe ich dabei immer wieder diese Folie dabei, in der es um Forschungen des Event Horizon Telescope geht:
 Jetzt wird es nach langen Jahren mit diesen Beobachtungen ernst: zwischen dem 5. und 14. April 2017 wird das erste Mal ernsthaft daran gearbeitet, solche Aufnahmen tatsächlich anzufertigen.
Jetzt wird es nach langen Jahren mit diesen Beobachtungen ernst: zwischen dem 5. und 14. April 2017 wird das erste Mal ernsthaft daran gearbeitet, solche Aufnahmen tatsächlich anzufertigen.
Das Grundprinzip der Beobachtungen ist einfach. Die einfachste Vorstellung von einem Schwarzen Loch ist die einer kugelförmigen Region, in die Licht und Materie zwar von außen hineingelangen können, aus der sie, einmal im Inneren, aber nie wieder hinauskommen können. Dass uns daher aus der betreffenden Region kein Licht erreicht macht solche Gebilde tatsächlich im Alltagssinne schwarz – und zwar deutlich schwärzer als die meisten Objekte, die wir im Alltag schwarz nennen! Wie strukturlos ein tatsächlich schwarzes Objekt aussieht, kann man ja alle paar Jahre wieder sehen, wenn eine neue superschwarze Farbe entwickelt wird. Details, Konturen, jegliche Dreidimensionalität fehlen einem solchen Objekt:
Aber was man in dem obenstehenden Video sehr schön sieht: Selbst wenn man auf der beschichteten Maske selbst keine Details erkennen kann, kann man doch einiges von ihrer Struktur erschließen. Darüber, dass wir ihre Kontur vor dahinterliegenden Flächen sehen, deren Licht die Maske dann abschattet.
Ähnlich der Plan bei Schwarzen Löchern: Schieben die sich vor eine leuchtende Hintergrundquelle, schatten sie deren Licht ab. Und durch diesen Schatten verraten sie sich – und wenn man genau hinguckt auch Details über ihre Struktur. So direkt wie bei der beschichteten Maske ist die Angelegenheit dabei natürlich nicht. Insbesondere wirkt die Masse des Schwarzen Lochs ja auch als Gravitationslinse auf das Hintergrundlicht. (Schönes Anschauungsmaterial findet sich z.B. bei Ute Kraus auf Tempolimit Lichtgeschwindigkeit.) So kommt es zu Verzerrungen. Rotierende Schwarze Löcher lassen auch den Raum um sich herum in einem gewissen Sinne mitrotieren – das führt zu weiteren Effekten, an denen sich die Rotationsgeschwindigkeit des Schwarzen Lochs ablesen lässt.
Ich will an dieser Stelle gar nicht wiederholen, was z.B. bei Spektrum online, bei Florian Freistetter und bei Science schon sehr schön über die Hintergründe dieser Forschungen berichtet wurde, sondern nur ein paar Aspekte betonen. Auch die Pressemitteilung der Kollegen vom Max-Planck-Institut für Radioastronomie, antiquarisch zugänglich hier, ist nach wie vor lesenswert. Wer tiefer einsteigen will, kann das z.B. mit dem Artikel Falcke, Melia, Agol 2000 tun.
Warum das Zentrum der Milchstraße?
Das Event Horizon Telescope nimmt das Schwarze Loch im Zentrum unserer Milchstraße auf’s Korn. Als Lichtquelle, die das Schwarze Loch abschattet, soll eine weitgehend durchsichtige Gaswolke dienen, die das Schwarze Loch entsprechenden Messungen nach umgibt.
Aber Schwarze Löcher gibt es ja nicht nur in den Zentren von Galaxien. Warum peilt man keines der uns deutlich näheren stellaren Schwarzen Löcher an? Eine Abschätzung dafür geht wie folgt: Die Größe eines Schwarzen Lochs ergibt sich direkt aus seiner Masse. Im einfachsten Falle (ohne Rotation) kann man einem Schwarzen Loch als Längenskala den sogenannten Schwarzschildradius \({\cal R}\) zuordnen, definiert als
$${\cal R}\equiv \frac{2GM}{c^2} \approx 3\,\mbox{km}\;\frac{M}{M_{\odot}}$$
mit \(M\) der Masse des Schwarzen Lochs, \(G\) der Newtonschen Gravitationskonstante und \(c\) der Lichtgeschwindigkeit. Radiuswerte sind in der Allgemeinen Relativitätstheorie, mit ihrer großen Freiheit der Koordinatenwahl, immer erklärungsbedürftig; dieser hier ist über den Flächeninhalt der Kugelfläche definiert, die das Innere vom Äußeren des Schwarzen Lochs trennt. Er lässt sich aber auch geometrisch nutzen, um die Frage zu beantworten, die uns interessiert: Unter welchem Winkel würde uns ein Objekt von der Größe des Ereignishorizonts eines Schwarzen Lochs aus der Ferne erscheinen?
Wenn wir naiv mit den üblichen Schulformeln für die Winkelgröße rechnen, kommt heraus, dass uns ein Schwarzes Loch mit der Masse \(M\) aus einer Entfernung \(d\) unter einem Winkel von
$$\alpha = 0{,}1\,\mu\mbox{as}\cdot \frac{M}{M_{\odot}}\cdot \frac{1\;\mbox{Lj}}{d}$$
erscheinen würde. In Worten: Ein Schwarzes Loch mit einer Sonnenmasse würde aus der Entfernung von einem Lichtjahr nur ganze 0,1 Mikro-Bogensekunden groß sein, ein paar Zehnmilliardstel eines Winkelgrads.
Wenn wir auf der Wikipedia-Liste der uns nächsten Schwarzen Löcher nachschauen, kommen wir mit dieser Formel auf recht kleine Werte: 0,0005 Mikrobogensekunden für das uns nächste Schwarze Loch, A0620-00, und noch kleinere Werte für die anderen beiden Kandidaten. Stellare Schwarze Löcher, mit rund einem Dutzend Sonnenmassen, kann man auf diese Weise offenbar nicht erwischen.
Das Schwarze Loch im Zentrum unserer Milchstraße vereinigt rund 4 Millionen Sonnenmassen in sich, und ist rund 26.000 Lichtjahre von uns entfernt. Mit der obigen Formel ergibt das 20 Mikrobogensekunden. Eine genauere Rechnung kommt auf rund 30 Mikrobogensekunden (Falcke, Melia, Agol 2000). Von den Schwarzen Löchern, die wir kennen, ist das der bei weitem günstigste Kandidat.
Anforderungen an ein Event Horizon Telescope
20 Mikrobogensekunden sind aber alles andere als ein Klacks. Welche Details ein Teleskop noch auseinanderhalten kann ist nach einer klassischen Formel, hier gleich in Mikrobogensekunden umgerechnet, gegeben durch
$$\delta = 2{,}5\cdot 10^{11}\cdot\mu\mbox{as}\cdot\frac{\lambda}{D},$$
wobei \(\lambda\) die Wellenlänge des verwendeten Lichts ist und \(D\) der Durchmesser des verwendeten Teleskops. (Ich hatte die Hintergründe vor ein paar Monaten in Astronomische Beobachtungen: Wie funktionieren die eigentlich? erklärt.)
Der Winkel \(\delta\) ist dabei der Winkel zwischen zwei Strukturen, die ein solches Teleskop bei dieser Wellenlänge gerade noch auseinanderhalten kann. Das Event Horizon Telescope beobachtet bei Wellenlängen von der Größenordnung 1 mm. Setzen wir diese Wellenlänge und die Winkelgröße des Schwarzen Lochs im Zentrum der Milchstraße ein, dann muss das Teleskop mindestens 13 000 Kilometer Durchmesser haben, um zumindest grob festhalten zu können, was da passiert!
Immerhin hat unser Heimatplanet einen entsprechenden Durchmesser. Wir brauchen also nur ein Teleskop von der Größe der Erde. Dieses “nur” sollte man nicht geringschätzen: Wären die Verhältnisse nur etwas anders, nämlich die Masse des Schwarzen Lochs geringer oder seine Entfernung von uns größer, dann wären Beobachtungen dieser Art komplett unmöglich. Sie würden erst in den Bereich des Möglichen rücken, wenn man ein Millimeter-Weltraumteleskop in die Umlaufbahn schießen könnte – und für viele mögliche Parameterkombinationen nicht einmal dann!
So aber sind die entsprechenden Beobachtungen machbar: Radioteleskope, die in diesem Wellenlängenbereich beobachten, lassen sich mithilfe sogenannter Interferometrie über weite Distanzen “zusammenschalten” und agieren dann in punkto Detailschärfe wie ein deutlich größeres Teleskop. Der effektive Durchmesser entspricht dabei dem größten Abstand zwischen zweien der beteiligten Teleskope. Indem man in dieser Weise die Beobachtungen von Teleskopen kombiniert, die auf dem ganzen Erdball verteilt sind, kann man tatsächlich gerade so die nötige Genauigkeit erreichen. Ein Glücksfall!
Zeitskalen der Forschung
Zumindest kann man seit kurzem die nötige Genauigkeit erreichen: seit nämlich die Millimeterteleskope des ALMA-Observatoriums den Beobachtungsbetrieb aufgenommen haben. Mit ALMA haben das Auflösungsvermögen und die Empfindlichkeit von Submillimeter- und Millimeterbeobachtungen einen gigantischen Sprung gemacht. An meinem eigenen Institut, dem Max-Planck-Institut für Astronomie, zeigt sich das für mich als Öffentlichkeitsarbeiter insbesondere daran, wieviele Pressemitteilungen und damit Forschungsergebnisse bei uns in den letzten Jahren auf ALMA-Beobachtungen zurückgehen.
Empfindlichkeit ist auch für das Event Horizon Telescope wichtig. Nur mit entsprechend empfindlichen Beobachtungen lässt sich das Signal, also das, was man beobachten will, vom Rauschen trennen.
ALMA bringt uns zur Frage der Zeitskalen, denn das Event Horizon Telescope zeigt, wie geduldig man in der Wissenschaft bisweilen sein muss. Die ersten Artikel von Heino Falcke und Kollegen, ich hatte oben bereits Falcke, Melia, Agol 2000 und die zugehörige Pressemitteilung verlinkt, sind mittlerweile rund 17 Jahre alt. Was man würde tun müssen, um diese Beobachtungen durchzuführen, war damals im wesentlichen bekannt. Dass die beteiligten Wissenschaftler diese damals technisch nicht gangbare Idee konsequent weiterverfolgt haben, immer mit einem Auge auf den Fortschritt bei den Beobachtungsmöglichkeiten (z.B. anhand dieser Liste von Publikationen verfolgbar) und dass sie jetzt endlich die erste entsprechende Beobachtung durchführen können, zeugt für vorbildliche Ausdauer.
Unser Wissenschaftssystem ist ja leider in vieler Hinsicht auf kürzere Zeitskalen ausgelegt – bei Bewerbungen zählen oft die aktuellen Publikationen, die Produktivität aus jüngerer Zeit. Das Beispiel Event Horizon Telescope zeigt aber, was man verpassen würde, wenn man sich ganz auf schnell umsetzbare Projekte beschränkte.
Wie jetzt weiter?
Und wie sieht es mit den weiteren Zeitskalen aus? Die aktuellen Beobachtungen haben, wie gesagt, vor ein paar Tagen begonnen und laufen noch bis Mitte April. Wer live dabei sein möchte, sollte Heino Falcke (@hfalcke) auf Twitter folgen, der entsprechende Hashtag ist #EHT.
Bis erste Bilder und Ergebnisse zu sehen sind, wird es freilich noch dauern. Die vollständigen Daten werden die Forscher sowieso erst im November vorliegen haben. Die Datenmengen der einzelnen Teleskope sind so groß, dass sie nicht auf üblichem Wege übertragen werden können; zur Auswertung werden stattdessen Festplatten, auf denen die Daten gespeichert sind, an einem Ort zusammengeführt und die Daten direkt auf den Auswertungs-Computer übertragen. Eines der beteiligten Teleskope steht am Südpol, und die betreffende Festplatte wird erst dann zur Auswertung überführt werden können, wenn im November der Süd-Winter vorbei ist und der Flugbetrieb wieder aufgenommen wird.
Auch die Auswertung selbst wird einige Zeit in Anspruch nehmen. Schließlich besteht das Event Horizon Telescope aus einem Dutzend Observatorien, einige darum wieder mit mehr als einem Einzelteleskop. Die Daten dieser zum Teil sehr unterschiedlichen Teleskope zu kalibrieren und anschließend richtig miteinander zu kombinieren ist eine beachtliche Herausforderung.
Last but not least sind insgesamt rund 100 Wissenschaftler an der Kooperation beteiligt. Zur Auswertung und insbesondere zur anschließenden Interpretation der Daten muss es am Ende einen Konsens geben – und je nach dem, was herauskommt, kann auch das Erreichen eines Konsens eine Herausforderung sein. Klar: Falls alles besonders gut geht und das Ergebnis eindeutig ist, ist das alles ein Problem. Wenn das Ergebnis weniger klar ist, könnte es darum gehen, ob man anhand der Daten überhaupt sagen kann, den Ereignishorizont abgebildet zu haben – oder ob man eher von einem wichtigen Schritt hin auf die letztliche Abbildung redet.
Für die jetzigen Beobachtungen strebt das Event Horizon Telescope erst einmal eine Auflösung von bis zu 50 Mikrobogensekunden an (laut diesem BBC-Beitrag). Damit bekommt man selbst im günstigsten Falle einigermaßen verwischte Bilder des Schatten des Schwarzen Lochs; zum Vergleich eine ganz einfache Veranschaulichung direkt aus dem Grafikprogramm (Gimp): Wenn der schwarze Kreis links der Schatten in der Größe von 30 Mikrobogensekunden ist, ergibt sich bei einer Auflösung von 50 Mikrobogensekunden die Abbildung rechts (= linke Abbildung, verwischt mit Gaußfilter entsprechender Halbwertsbreite).
 Insofern dürfte es noch rund ein Jahr Dauern, bis wir ein erstes, etwas unscharfes Bild vom Ereignishorizont eines Schwarzen Loches sehen. Vielleicht auch noch länger. Und vielleicht ist diese Beobachtungskampagne auch noch gar nicht diejenige, an deren Ende wir ein Bild vom Ereignishorizont haben, sondern es sind noch weitere Beobachtungskampagnen nötig, bis es soweit ist – weitere Beobachtungen, die dann aber auf alle Fälle von den Erfahrungen mit den jetzigen Beobachtungen, nämlich von der ersten großen Kampagne des Event Horizon Telescopes profitieren werden.
Insofern dürfte es noch rund ein Jahr Dauern, bis wir ein erstes, etwas unscharfes Bild vom Ereignishorizont eines Schwarzen Loches sehen. Vielleicht auch noch länger. Und vielleicht ist diese Beobachtungskampagne auch noch gar nicht diejenige, an deren Ende wir ein Bild vom Ereignishorizont haben, sondern es sind noch weitere Beobachtungskampagnen nötig, bis es soweit ist – weitere Beobachtungen, die dann aber auf alle Fälle von den Erfahrungen mit den jetzigen Beobachtungen, nämlich von der ersten großen Kampagne des Event Horizon Telescopes profitieren werden.
Insofern: Es bleibt spannend. Und früher oder später sollten wir dann tatsächlich das erste Mal einen Schattenriss eines Schwarzen Lochs zu Gesicht bekommen.


Vermutlich werden die einzelnen Pixel des endgültigen Bildes so ähnlich erzeugt, wie bei der elektronischen Strahlschwenkung einer Phased-Array-Antenne.
Im Unterschied zur folgenden Animation handelt es sich aber um Empfänger, die sich auf einer rotierende Kugeloberfläche befinden.
Nur mit Hilfe von Atomuhren kann man dann die Phasenlagen der verschiedenen Empfänger auf eine ebene Fläche, die quer zu Zielrichtung steht, umrechnen.
https://upload.wikimedia.org/wikipedia/commons/4/4a/Phased_array_animation_with_arrow_10frames_371x400px_100ms.gif
Das zweite Bild ist nur eine grobe Vereinfachung.
http://members.chello.at/karl.bednarik/ANTISATE.PNG
Ja, man sollte ein Unternehmen wie das Event Horizon Telescope nicht gering schätzen. Nur schon der Nachweis eines Ereignishorizonts ist den Aufwand wert, denn anders als einige denken, halte ich es für nötig, alles auch wirklich nachzuweisen, was von den Theoretikern behauptet wird: Solange ein Ereignishorizont nicht nachgewiesen ist, ist er ein theoretisches Konstrukt selbst wenn dieses Konstrukt noch so plausibel ist.
Da sollte man allerdings nicht unterschätzen, welche Informationen in den Gravitationswellen-Signalen stecken. Bei den entsprechenden Wellenformen gehen die Eigenschaften von Horizonten, und zwar durchaus inklusive komplizierter Dinge wie der Dynamik, ganz massiv mit ein.
Markus Pössel schrieb (9. April 2017):
> Die Größe eines Schwarzen Lochs ergibt sich direkt aus seiner Masse.
> […] Im einfachsten Falle (ohne Rotation) […] den sogenannten Schwarzschildradius \( \mathcal R \)
> […] definiert als \( \mathcal R \equiv \frac{2 \, G \, M}{c^2} \) […]
Aber auch:
> dieser [Radiuswert] hier ist über den Flächeninhalt der Kugelfläche definiert, die das Innere vom Äußeren des Schwarzen Lochs trennt.
Wie lautet diese (letztere) Definition explizit ?
Und:
Ist demnach die “Masse” eines (nicht-rotierenden, statischen) Schwarzen Loches über den genannten bestimmten “Flächeninhalt” definiert ?
Oder ist umgekehrt dieser “Flächeninhalt” durch die genannte “Masse” definiert ?
Und:
Laufen diese Definitionen, so wie von Einstein offenbar gefordert, letztlich und explizit auf die Bestimmung “zeiträumlicher Koinzidenzen” hinaus ?
Frank Wappler schrieb (12. April 2017 @ 01:22):
> Laufen diese Definitionen, so wie von Einstein offenbar gefordert, letztlich und explizit auf die Bestimmung „zeiträumlicher Koinzidenzen“ hinaus ?
Eine der Konstatierungen, von denen recht deutlich erkennbar ist, dass sie auf Koinzidenzbestimmungen und insbesondere auf Bestimmungen von “(optischen) Ping”-Koinzidenz-Beziehungen hinauslaufen (können), besteht in der Feststellung, welche Beteiligte sich (gemeinsam und durchwegs) auf einer bestimmten sogenannten Photon-Sphäre aufhielten, innerhalb der die fragliche “Masse” enthalten wäre; und in wie fern diese “statisch” blieb.
Eine weitere ausdrücklich („als Maß für die Krümmung der Raumzeit“) geometrisch definierte Größe ist der Kretschmann-Skalar \( K \). Ausgewertet für Ereignisse an denen stets solche Beteiligte teilnahmen, die sich durchwegs auf der in Frage kommenden Photon-Sphäre aufgehalten hatten, besteht zumindest im einfachsten Fall offenbar die Beziehung $$ K[ \, \hbox{Photon-Sphäre} \, ] = \frac{256}{243} \, \frac{1}{\mathcal R^4} $$ zum o.g. “Schwarzschildradius \(R\)“.
Solang insbesondere der im obigen SciLogs-Artikel genannte Begriff “Flächeninhalt” nicht als Messgröße definiert ist, liegt es deshalb nahe, die Umkehrbeziehung als Definition des “Schwarzschildradius” aufzufassen:
$$ \mathcal R \equiv \left( \frac{256}{243} \, \frac{1}{K[ \, \hbox{Photon-Sphäre} \, ]} \right)^{(1/4)}.$$
Ich hoffe, die Leute vom EHT sind erfolgreich! Auf der Seite vom EHT steht etwas von erreichbaren 15 Mikrobogensekunden Auflösung. Aber wie will man bei einer derart flauen und verwischten Darstellung zwischen einem Ereignishorizont und zwischen einer zum Zentrum hin zunehmenden Rotverschiebung unterscheiden ?
Soweit ich weiß, ist 15 Mikrobogensekunden im ersten Durchgang noch nicht angepeilt – aber wer weiß, manchmal läuft es ja auch besser als gedacht! Zum Unterscheiden: Das wird darauf hinauslaufen, die Daten mit verschiedenen Modellen zu vergleichen; ich nehme an: durchaus auch mit exotischen Alternativen. Was unterscheidbar ist und was nicht entscheidet sich dann aus der Kombination von Modellen und Daten. Ich frage wegen beidem mal bei Heino Falcke nach.
Danke! Ich platze fast vor Spannung, was dabei herauskommen wird. Da ich selber vor 30 Jahren mal Bilder aufgearbeitet habe, weiß ich, wie schwierig es ist, aus derart verwaschenen Bildern den Inhalt vernünftig wieder hervorzuzaubern. Und man muß sehr vorsichtig sein, um keine Artefakte zu generieren!
Ein Eriegnishorizont wäre typischerweise prinzipiell inobservabel — danach lässt sich mit einem Teleskop nicht suchen, vgl. Visser (2014). Die bei Falcke et al. (2000) vorgefundene Behauptung, “The observation of this shadow […] would be the first direct evidence of the existence of an event horizon,” ist demnach unzutreffend und dient gewiss mehr der Werbung als der Wissenschaft.
Es ist doch völlig egal, welchen Horizont man darstellt, den Ereignishorizont (event horizon) den scheinbaren Horizont (apparent horizon) oder den closely related trapping horizon (ich kenne keine vernünftige deutsche Übersetzung und könnte es nur beschreiben) ! Für die Sache ist doch nur wichtig : Gibt es ihn überhaupt? Kann man ihn darstellen?
Passend zu solchen und verwandten Fragen ist soeben noch ein Review Paper erschienen. Insbesondere hinsichtlich EHT siehe dort den Abschnitt IV. The special case of Sgr A*.
Im Lexikon der Astronomie von Andreas Müller wird der Begriff Ereignishorizont und das Begriffsumfeld dazu vorgestellt.
Martin Holzherr schrieb (19. April 2017 @ 08:08):
> Im Lexikon der Astronomie von Andreas Müller wird der Begriff Ereignishorizont und das Begriffsumfeld dazu vorgestellt.
Nur eben leider nicht vollständig, gebrauchsfähig, nachvollziehbar.
Der auf angegebenen Seite gebrauchte Begriff “Metrik” (im Sinne von: “metrischer Tensor”)” verweist nämlich auf den Begriff “Linienelement”, von dem es wiederum heißt:
Was aber ist da mit “raumzeitlichem Abstand (zweier, insbesondere verschiedener Ereignisse voneinander)” gemeint?
Oder ansonsten:
Wie wäre (zunächst) zu entscheiden, welche Paare von Ereignissen “infinitesimalen, raumzeitlichen Abstand” voneinander hatten?
Und vor allem:
Entsprechend welcher Messdefinition liefe Ermittlung bzw. Vergleich von Werten solcher “raumzeitlichen Abstände” für die in Frage kommenden Ereignispaare, im Sinne Einsteins, …
??
@Martin Holzherr / 19. April 2017 @ 08:08
Recht so, fragen wir Andreas Müller. Der schreibt: “Falls Sie mich fragen, so teile ich die Position von Abramowicz und Kollegen.” Diese Position teilt er dann auch mit Bambi: “Bearing in mind the definition of a BH […] it is fundamentally impossible to test the existence of an event horizon.” Und Matt Visser sieht das genauso.
Ihre am 10. April 2017 @ 10:13 geäusserte Hoffnung auf observationellen Nachweis eines EHs wird vom EHT nicht erfüllt werden können, ganz egal welche Schattenrisse sich bei der Observation auch zeigen mögen.
Dass der Event Horizont nicht beobachtbar sei hab ich auch gelesen. Doch die Site Event Horizon Telescope ist da anderer Meinung. Man liest dort (von mir übersetzt):
Ein langgehegtes Ziel in der Astrophysik ist es, die unmittelbare Umgebung eines schwarzen Loches mit einer Winkelauflösung, die mit dem Ereignishorizont vergleichbar ist, direkt zu beobachten. Das Erkennen dieses Ziels würde ein neues Fenster auf das Studium der allgemeinen Relativitätstheorie im starken Feldregime, der Akkretions- und Abflussprozesse am Rande eines Schwarzen Lochs, der Existenz eines Ereignishorizonts und der grundlegenden Physik des Schwarzen Lochs eröffnen.
…
Der stärkste Hinweis darauf ist die jüngste Beobachtung bei 1.3 mm mittels Very Large Baseline Interferometry, welche eine Schwarzschild-Radius-Skalenstruktur in Sgr A* aufzeigte.
@Martin Holzherr
Ein Black Hole EH ist so definiert, dass die dort befindlichen Punkte gerade nicht in der kausalen Vergangenheit irgendeines externen Beobachters liegen. Terrestrische Betrachter können mit ihrem Teleskop von dort keine Licht- oder Partikelstrahlung empfangen, man schaut allenfalls in den umgebenden “Aussenraum”. Andreas Müller hat auch irgendwo einmal die Formulierung verwendet, die Black Holes mit ihren EHs existierten daher in unserer Zukunft, was zumindest aus meiner Sicht potentiell etwas missverständlich tönt. Korrekt ist jedoch, dass für uns hier auf der Erde mit unserer Beurteilung von Gleichzeitgkeit jetzt in diesem Moment bei Sgr A* ein EH im Sinne der relativist. Definition weder existiert noch jemals existiert hat. Was dann für alle mutmasslichen EHs irgendwo in den Tiefen des Kosmos ganz entsprechend gilt.
Die Phänomene in der “Umgebung” wären eigentlich schon interessant genug, um eine Observation zu rechtfertigen. Vor gut 40 Jahren schrieb der hinlänglich bekannte Rollifahrer aus Cambridge, “Black holes behave in a completely random and time-symmetric way and are indistinguishable, for an external observer, from white holes. The irreversibility that appears in the classical limit is merely a statistical effect.” Und schliesslich gibt’s dann ja noch die “Firewall” Hypothese. Eine direkte Observation könnte womöglich mehr Aufschlüsse bringen, was da eigentlich los ist.
Chrys schrieb (20. April 2017 @ 12:11):
> Ein Black Hole EH ist so definiert, dass […] ein EH im Sinne der relativist. Definition weder existiert noch jemals existiert hat.
Naja. …
> Die Phänomene in der „Umgebung“ wären eigentlich schon interessant genug
Zweifellos. Abgesehen von der (hier bereits erwähnten) Photon-Sphäre erscheint mir dabei besonders interessant, was innerhalb dieser außerdem noch beobachtbar und messbar existieren mag; insbesondere an weiteren “Sphären”, z.B. im Sinne von jeweils konstanten, endlichen, reellen Messwerten des Kretschmann-Skalars (die “zum Loch hin” weiter zunehmen).
Nachvollziehbarer Weise ausgehend von Ping-Koinzidenz-Gitter-Beziehungen zur näheren Untersuchung solcher denkbarer “Sphären” habe ich mein (unser?) diesbezügliches Interesse gerade in dieser Frage (“Can the strict triangle inequality hold in a length space?”, MSE/q/2244197) auszudrücken versucht …
Überaus faszinierend was möglich ist und wie schwarze Löcher das “mystische” verlieren und berechenbar werden. Ich wage zu behaupten, dass wir inzwischen über schwarze Löcher weitaus mehr Wissen haben, als über so machen Tier und Pflanzenarten in den Tiefen unserer Ozeane. Die Bilder, die wir aus den Weiten des Weltalls bekommen, empfinde ich als fantastisch. Es gibt kaum etwas Spannenderes als die Weiten zu erforschen und mehr Wissen zu bekommen, von dem was wir nach und nach besser kennenlernen und verstehen.