Astronomische Beobachtungen – wie funktionieren die eigentlich?
BLOG: RELATIV EINFACH

Physiker haben einen gewissen Drang, die Dinge auf’s Fundamentale zurückzuführen. Dem habe ich in meiner Vorlesung Methoden der Astronomie für Nicht-Physiker am Donnerstag vorletzter Woche nachgegeben und versucht, astronomische Beobachtungen auf die Grundlagen zurückzuführen: Was sind astronomische Beobachtungen eigentlich?
Licht untersuchen
Beschränken wir uns ruhig auf die klassische Form astronomischer Beobachtungen: Das Auffangen und Auswerten des Lichts oder anderer astronomischer Strahlung von fernen Himmelskörpern. Schaut man sich an, welche Eigenschaften Licht hat (siehe mein Blogbeitrag Was ist eigentlich Licht?), dann kommt man darauf: Was die Teleskope da aus dem Weltraum erreicht, ist ein Photonengemisch, dessen räumliche Struktur (die Verteilung der Photonen im Raum) durch eine zugrundeliegende Welle bestimmt wird.
An diesem Photonengemisch kann man im Prinzip drei Arten von Größen messen:
- Wieviele Photonen erreichen uns da überhaupt?
- Aus welcher Richtung erreicht uns das Licht?
- Welche Energien haben die Photonen, die uns da erreichen?

Man kann diese drei Auswertungs-Arbeiten auch konventioneller beschreiben, etwa anhand einer schönen astronomischen Abbildung wie dem her gezeigten Bild der Spiralgalaxie NGC 6814 im Sternbild Adler.
Dass wir winzigste Richtungsunterschiede für das Licht dokumentieren können, ist Voraussetzung dafür, dass wir überhaupt ein Bild der entsprechenden Himmelsregion erstellen können. Das obige Bild ist ein kleiner Ausschnitt der Himmelskugel, also der Gesamtheit aller Richtungen, aus denen uns Licht aus dem Weltraum erreichen kann. Dass wir darauf feine Details unterscheiden können – etwa die schönen Staubmuster auf den Spiralarmen – heißt, dass wir für das betreffende Licht selbst nahe beieinander liegende Einfallrichtungen zuverlässig unterscheiden können. Die Genauigkeit, Einfallsrichtungen von Lichtteilchen auseinander zu halten, ist damit ein direktes Maß für die Detailschärfe unserer Abbildungen. Astronomen sprechen dabei vom Auflösungsvermögen: Vom kleinsten Winkel zwischen zwei Licht-Einfallsrichtungen, die man bei der Beobachtung gerade noch auseinanderhalten kann.
Ob uns aus einer bestimmten Teilregion des Bildes in einem gegebenem Zeitraum mehr oder weniger Photonen erreichen, ist ein Maß für die Helligkeit der betreffenden Region. Schlüsselt man die Energien der Photonen auf, die uns aus jeder der Regionen erreichen, erhält man ein Spektrum für jede der Regionen.
Was zeichnet gute astronomische Beobachtungen aus?
Jetzt wo wir wissen, was wir da eigentlich beobachten bzw. messen, kann man fragen: Was zeichnet denn nun eigentlich gute astronomische Beobachtungen aus? Welche Voraussetzungen müssen erfüllt sein, damit wir unsere gesuchten Messgrößen möglichst genau bestimmen können?
Eine Schlüsselerkenntnis dazu hatte ich in meinem Beitrag Was Astronomie mit Münzwürfen zu tun hat: Photonenzählen und Fluktuationen besprochen: Photonen kommen in der Astronomie in guter Näherung zufällig am Teleskop an. Sie folgen dabei einer Zufallsverteilung namens Poisson-Verteilung. Eine Konsequenz daraus: Angenommen, aus einer bestimmten Himmelsregion erreichten uns im Mittel \(\bar{n}\) Photonen einer bestimmten Energie pro Sekunde; \(\bar{n}\) ist damit ein Maß für die Helligkeit der betreffenden Region. Wir belichten mit unserem Teleskop für die Dauer \(T\) und fangen in dieser Zeit \(N\) Photonen auf. Die Größe \(N/T\) ist unsere Abschätzung für die Helligkeit \(\bar{n}\). Allerdings müssen wir damit rechnen, dass der wahre Wert \(\bar{n}\) im Mittel um rund \(1/\sqrt{N}\) von unserem Schätzwert \(N\) abweicht – das folgt aus den Eigenschaften der Poisson-Statistik. Das heißt: Sollen unsere durch Photonenzählen ermittelten Helligkeits-Schätzungen möglichst genau werden, dann müssen wir jeweils möglichst viele Photonen zählen.
Himmels-Hintergründe
Bevor wir erkunden, was das für Konsequenzen hat, ist festzuhalten, dass nicht alle Photonen, die in ein (zumal bodengebundenes) Teleskop fallen, von astronomischen Beobachtungsobjekten stammen.
Da wäre als zusätzliche Quelle zunächst einmal das Nachthimmelsleuchten (ein Wort, das ich eben erst gelernt habe; ich kannte das Phänomen nur als englisch/denglischen Airglow): Chemische Prozesse, Ionisierung von Atomen durch Sonnenstrahlung bei Tage mit Rekombination bei Nacht und kosmische Strahlung regen Atome und Moleküle in unserer Atmosphäre ein klein wenig zum Leuchten an.
Außerdem gibt es das Zodiakallicht. Die Planeten unseres Sonnensystems laufen alle ungefähr in derselben Ebene um die Sonne. In dieser Ebene befinden sich außer den Planeten unzählige Staubpartikel. Diese Staubpartikel reflektieren ein wenig Sonnenlicht; kurz vor Sonnenauf- und kurz nach Sonnenuntergang ist es, einen ansonsten dunklen Himmel vorausgesetzt, als schwach leuchtende Region zu sehen. Ich habe das bislang nur einmal erlebt, bei einem Besuch am Standort Sutherland des Südafrikanischen Nationalobservatoriums:

Das Zodiakallicht im engeren Sinne ist der längliche Lichtschein, der von der Bildmitte nach links oben läuft. Aber ein wenig dieses Streulichts findet sich auch in den anderen Himmelsregionen – nur ist es dort bei weitem nicht so auffällig.
In höheren Breiten tragen zusätzlich noch Nord- und Südlichter zur Himmels-Aufhellung bei (die ich beide leider noch nie selbst gesehen habe). Und auch das Sternenlicht selbst wird in der Atmosphäre gestreut und trägt damit zum Himmelshintergrund bei.
(Bei Weltraumteleskopen bleibt von diesen Aufhellungs-Faktoren gerade mal das Zodiakallicht übrig – aber bereits das ist nicht zu unterschätzen.)
(Sprachlich unlogisch, aber üblich ist, all diese Beiträge in der Tat als Himmels-Hintergrund zu bezeichnen. In Wirklichkeit sind uns die erwähnten Lichtquellen und Streuquellen sämtlich näher als unsere Beobachtungsziele, die deutlich ferneren astronomischen Objekte.)
Bild und Hintergrund / Signal und Rauschen
Was bedeutet das alles für astronomische Bilder? Teilen wir eine uns interessierende Region am Himmel einmal in Quadrate auf (wie es letztlich auch eine astronomische Kamera mit ihren Pixeln tut). Hier eine Region, beschrieben mit einem sehr groben Raster. Je nachdem wieviel Licht uns aus der betreffenden Region erreicht sind die Quadrate heller oder dunkler ausgefüllt:  In welcher Region verbirgt sich beispielsweise ein Stern oder ein anderes helles, kleines Objekt? Im obigen Bild ist das eine deutlich hellere Quadrat zweifelsfrei auszumachen. Aber auch die anderen Quadrate sind nicht pechschwarz, sondern zeigen an, dass auch von dort Photonen angekommen sind, in einigen Quadraten mehr, in anderen weniger. Daran macht sich der Himmels-Hintergrund bemerkbar, den ich im vorigen Abschnitt beschrieb.
In welcher Region verbirgt sich beispielsweise ein Stern oder ein anderes helles, kleines Objekt? Im obigen Bild ist das eine deutlich hellere Quadrat zweifelsfrei auszumachen. Aber auch die anderen Quadrate sind nicht pechschwarz, sondern zeigen an, dass auch von dort Photonen angekommen sind, in einigen Quadraten mehr, in anderen weniger. Daran macht sich der Himmels-Hintergrund bemerkbar, den ich im vorigen Abschnitt beschrieb.
Wie sieht es aus, wenn sich uns kein so deutlich aufgehelltes Pixelquadrat zeigt? Ist beispielsweise in diesem Bild ein Objekt zu sehen oder nur noch Hintergrund?  Um das zu entscheiden, benötigen wir ein Maß dafür, wie viel (oder wenig) sich ein Pixel von dem unruhigen Hintergrund abhebt. Konkret haben wir es außer dem zu messenden Signal eben auch mit Störungen zu tun, die einige Pixel heller erscheinen lassen als es der Helligkeit eben jener Himmelsregion entspricht, andere dunkler. Fluktuationen des Lichts eines Beobachtungszieles lassen das Objekt andererseits manchmal etwas dunkler erscheinen als in Wirklichkeit, manchmal etwas heller. Auch das ist eine Störung. Die Störungen bezeichnet man in diesem Zusammenhang auch als Rauschen. Die entscheidende Größe dafür, wie zuverlässig eine gemessene Helligkeit ist, ist das Verhältnis zwischen Signal und Rauschen. Ist das Signal deutlich größer als alle Störeinflüsse, dann lässt es sich trotz jener Störungen nachweisen. Ist das Signal kleiner oder ähnlich groß wie das Rauschen, kann kein klarer Nachweis gelingen.
Um das zu entscheiden, benötigen wir ein Maß dafür, wie viel (oder wenig) sich ein Pixel von dem unruhigen Hintergrund abhebt. Konkret haben wir es außer dem zu messenden Signal eben auch mit Störungen zu tun, die einige Pixel heller erscheinen lassen als es der Helligkeit eben jener Himmelsregion entspricht, andere dunkler. Fluktuationen des Lichts eines Beobachtungszieles lassen das Objekt andererseits manchmal etwas dunkler erscheinen als in Wirklichkeit, manchmal etwas heller. Auch das ist eine Störung. Die Störungen bezeichnet man in diesem Zusammenhang auch als Rauschen. Die entscheidende Größe dafür, wie zuverlässig eine gemessene Helligkeit ist, ist das Verhältnis zwischen Signal und Rauschen. Ist das Signal deutlich größer als alle Störeinflüsse, dann lässt es sich trotz jener Störungen nachweisen. Ist das Signal kleiner oder ähnlich groß wie das Rauschen, kann kein klarer Nachweis gelingen.
Signal und Rauschen
Eine konkrete Zahl für dieses Signal-zu-Rauschen-Verhältnis (englisch Signal-to-Noise [ratio], Abkürzung daher oft SNR) ist für eine gegebene Beobachtungs-/Belichtungszeit
SNR = Anzahl der Signalphotonen / Anzahl der Rauschphotonen.
(Da Photonen, siehe mein Blogbeitrag Was ist eigentlich Licht?, Energie transportieren, entspricht dieses Verhältnis dem Verhältnis der während der Beobachtungszeit aufgefangenen vom Signal und vom Rauschen aufgefangenen Energie. Da die Energieströme, um die es hier geht, weitgehend zeitlich konstant sind, entspricht das SNR außerdem auch dem Verhältnis der durchschnittlichen Signalleistung zur durchschnittlichen Rausch-Leistung, also “Signalenergie pro Zeiteinheit” durch “Rausch-Energie pro Zeiteinheit”.)
Sowohl die Photonen der Lichtquelle (z.B. eines Sterns) als auch die Photonen des Himmelshintergrunds folgen der Poisson-Statistik. In einem festen Messzeitraum sind die jeweiligen Fluktuationen der Photonenzahl \(N\) daher, wie erwähnt, proportional zu \(\sqrt{N}\). Die gemessene Photonenzahl selbst hängt nicht nur von den Eigenschaften der jeweiligen Quelle, sondern auch von unserer Messvorrichtung ab: Je größer die Fläche \(F\) unseres Teleskops, umso mehr Photonen fängt es auf. Je länger die Belichtungszeit \(T\), umso mehr Photonen werden auf unserer Aufnahme erfasst.
Damit gilt für das Signal-zu-Rausch-Verhältnis – und zwar egal ob die Fluktuationen der Quelle selbst der dominante Beitrag sind oder die Fluktuationen des Hintergrunds dominieren –, dass
SNR \(\sim \sqrt{F\cdot T}\).
Je mehr Photonen wir sammeln, umso besser können wir die Signale, die wir eigentlich messen wollen – etwa die Helligkeit eines Sterns, oder eines Teils einer Galaxie oder eines Nebels – im Vergleich zum unvermeidlichen, störenden Rauschen identifizieren. Wiederum gilt, nur mithilfe des Signal-Rausch-Verhältnisses etwas anders ausgedrückt: Umso mehr Photonen wir sammeln, umso besser die Qualität unserer Beobachtung. Wieder gilt: Astronomen sollten tunlichst große Teleskope bauen, und ihre Aufnahmen möglichst lange belichten.
Richtungsinformationen für Licht
Außer den Informationen über Helligkeit (bzw. Helligkeitskontraste) interessiert uns, aus welcher Richtung die Photonen einfallen. Wie erwähnt: Aus solchen Richtungsinformationen setzen sich astronomische Bilder zusammen, und je feiner die Richtungen, die sich gerade noch unterscheiden lassen, desto feiner die im Bild erkennbaren Details.
Die Richtungsinformationen stecken in den Welleneigenschaften des Lichts, genauer: in den Informationen über die Phase – Wellenberg, Wellental oder an genau definierter Stelle dazwischen. Das ist in der folgenden Skizze dargestellt: 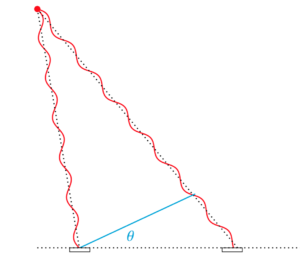 Links oben ist als rote Scheibe die Lichtquelle zu sehen, von der zwei phasengleiche Teilwellen abgehen (in Wirklichkeit eher: eine Kugelwelle in alle Richtungen). Unser Detektor hat zwei Elemente, dargestellt als Rechtecke unten im Bild. \(\theta\) ist der Richtungswinkel, der anzeigt, wo in der Bildebene sich die Quelle befindet. Am linken und rechten Detektorbaustein hat die Lichtwelle leicht unterschiedliche Phasen. Links hat sie gerade ein Wellental durchschritten und ist wieder bei Null angekommen, rechts ist sie kurz davor, ein Wellental zu erreichen.
Links oben ist als rote Scheibe die Lichtquelle zu sehen, von der zwei phasengleiche Teilwellen abgehen (in Wirklichkeit eher: eine Kugelwelle in alle Richtungen). Unser Detektor hat zwei Elemente, dargestellt als Rechtecke unten im Bild. \(\theta\) ist der Richtungswinkel, der anzeigt, wo in der Bildebene sich die Quelle befindet. Am linken und rechten Detektorbaustein hat die Lichtwelle leicht unterschiedliche Phasen. Links hat sie gerade ein Wellental durchschritten und ist wieder bei Null angekommen, rechts ist sie kurz davor, ein Wellental zu erreichen.
Die folgende Animation zeigt unterschiedliche Einfallswinkel und die dazugehörigen unterschiedlichen Phasen am rechten Detektorbauelement. Die Phase am linken Element habe ich der Einfachheit halber konstant gehalten.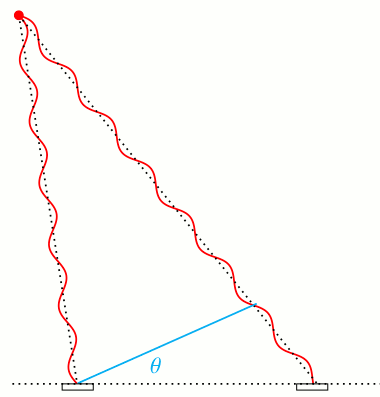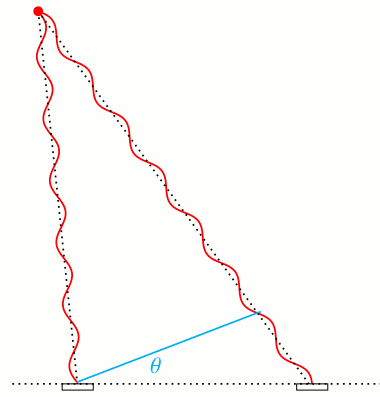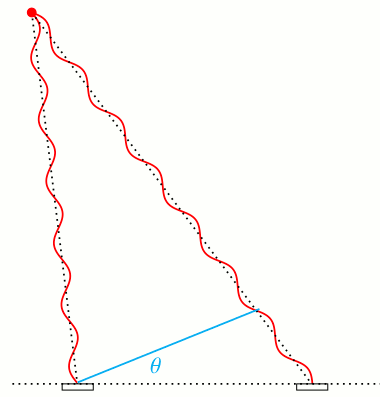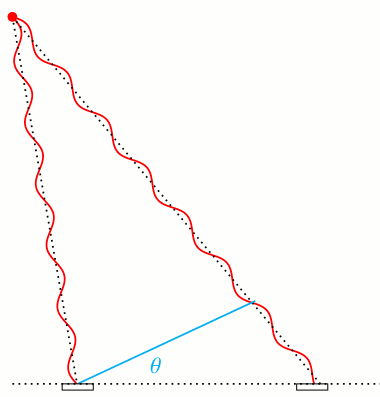
Das ist, von den physikalischen Grundlagen her, was Astronomen tun müssen, um Richtungsinformationen zu erhalten: Die Phasen der einfallenden Wellen bestimmen.
Was die Detektorgröße mit dem Auflösungsvermögen zu tun hat
Bereits diese einfachen Diagramme zeigen, dass dabei die Ausdehnung des Detektors, im einfachen Bild: der Abstand unserer Detektorelemente, eine Rolle spielt. Die Geometrie ist dabei die folgende: 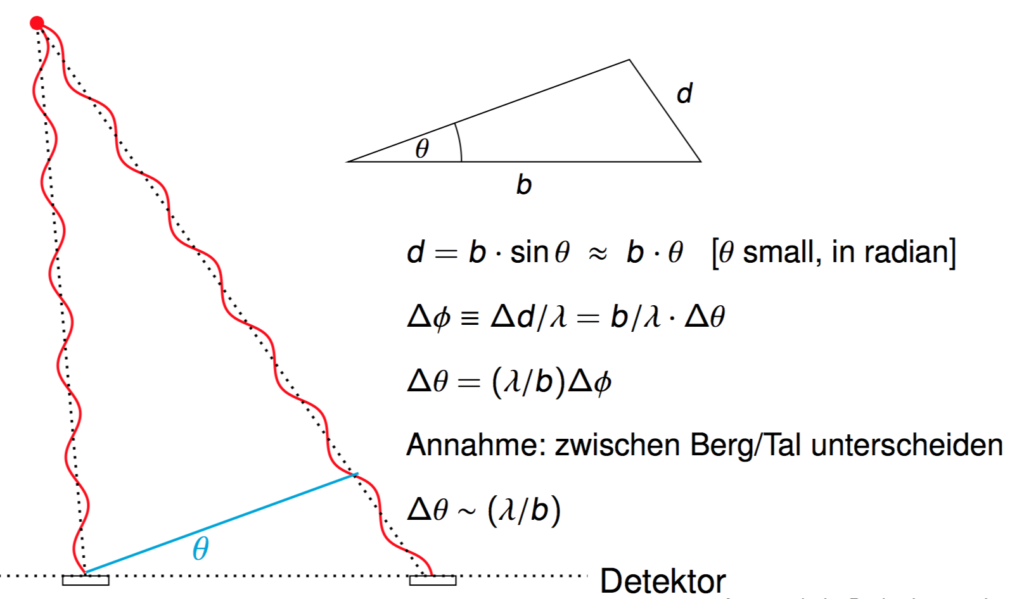 (Ich habe da einfach mal eine meiner Vorlesungsfolien abfotografiert.) Das Dreieck rechts oben zeigt, wie Detektorgröße b, Neigungswinkel \(\theta\) und die Länge des Wellenzugs d zusammenhängen, der für den Phasenunterschied sorgt. Ändert man die Länge des Wellenzugs um \(\Delta d\), dann ändert sich die Phase am rechten Detektorbaustein um \(\Delta\phi\) (Längenänderung geteilt durch Wellenlänge). Für kleine Winkel \(\theta\), gemessen in Radian, ist die Beziehung zwischen d und \(\theta\) näherungsweise linear. Kann man im Prinzip zwischen Wellenberg und -tal unterscheiden, dann kann man insbesondere feststellen, wann sich die Phase einmal komplett verschoben hat, etwa von einem Wellenberg zum nächsten. Bereits damit kann man Änderungen des Winkels nachweisen, die von der Größenordnung
(Ich habe da einfach mal eine meiner Vorlesungsfolien abfotografiert.) Das Dreieck rechts oben zeigt, wie Detektorgröße b, Neigungswinkel \(\theta\) und die Länge des Wellenzugs d zusammenhängen, der für den Phasenunterschied sorgt. Ändert man die Länge des Wellenzugs um \(\Delta d\), dann ändert sich die Phase am rechten Detektorbaustein um \(\Delta\phi\) (Längenänderung geteilt durch Wellenlänge). Für kleine Winkel \(\theta\), gemessen in Radian, ist die Beziehung zwischen d und \(\theta\) näherungsweise linear. Kann man im Prinzip zwischen Wellenberg und -tal unterscheiden, dann kann man insbesondere feststellen, wann sich die Phase einmal komplett verschoben hat, etwa von einem Wellenberg zum nächsten. Bereits damit kann man Änderungen des Winkels nachweisen, die von der Größenordnung
\(\Delta\theta \sim (\lambda/b)\)
sind. (Kann man Phasenänderungen genauer als das feststellen, dann steht rechts in dieser Formel noch ein entsprechend kleiner numerischer Faktor davor.)
Insbesondere ist das Unterscheidungsvermögen für unterschiedliche Richtungen von der Größe unseres Detektors abhängig, nämlich von b. Je größer b, umso kleiner \(\Delta\theta\), und umso genauer lassen sich Richtungen unterscheiden. Aber wie weist man Phasenunterschiede überhaupt nach?
Interferometer und Teleskope
Vom Konzept her am einfachsten wäre es, wenn jedes Detektorelement schlicht aufzeichnen würde, welche Phase die ankommende Welle zu jedem Zeitpunkt hat. Detektoren, die auf diese Weise funktionieren, gibt es in der Astronomie tatsächlich. Allerdings nicht für sichtbares Licht, denn dessen Schwingungszeiten liegen im Bereich von Femtosekunden (\(10^{-15}\;\mbox{s}\)); die Phasen wechseln damit viel zu schnell, als dass man sie in Echtzeit dokumentieren könnte.
Anders sieht das im Bereich der Radiowellen aus, mit Wellenlängen im Bereich von einem Meter oder mehr. Dann liegen die Schwingungszeiten nur noch im Bereich von Hundertmillionstel Sekunden oder länger. Für solche Wellen lassen sich Phaseninformationen, komplett mit Zeitangaben einer Atomuhr, aufzeichnen und anschließend auswerten.
LOFAR

Auf diese Weise funktioniert beispielsweise das LOFAR-Observatorium, das Radiowellen im Frequenzbereich 10–80 MHz und 110–240 MHz empfängt (entsprechend 3,7 bis 30 m Wellenlänge, bzw. 1,2 bis 2,7 m). Die Einzelantennen für den niedrigen Frequenzbereich (Bild oben rechts) sind recht einfach aufgebaut: Gekreuzte Dipolantennen, wahrscheinlich die einfachste physikalisch denkbare Art Radiowellen nachzuweisen.

Auf jeder LOFAR-Mess-Station (im Bild links die des Max-Planck-Instituts für Radioastronomie in Effelsberg bei Bad Münstereifel) stehen knapp 100 solcher Antennen (linker unterer Bildbereich) sowie die Antennen für die höheren Frequenzen (rechts oben im Bild). Insgesamt gehören knapp 50 Stationen zu LOFAR, die meisten davon in den Niederlanden.
Jede der LOFAR-Antennen dokumentiert die Phasen der dort ankommenden Radiowellen. Aus diesen Daten rechnet ein Supercomputer in Groningen die Richtungsinformationen aus. Beeindruckend an diesem Mess- und Auswerteverfahren ist, dass man sich zumindest im Prinzip gar nicht vorab entscheiden muss, welche Himmelsregion man beobachten möchte. Stattdessen kann der Computer den Radiowellen-Einfall aus allen beliebigen Richtungen (über dem Horizont) aus den Daten herauslesen, indem er die Signale der einzelnen Stationen in geeigneter Weise zueinander in Beziehung setzt.
Die Grenze der Leistungsfähigkeit ergibt sich lediglich aus dem Rechenaufwand und aus dem verfügbaren Speicherplatz. Pro Sekunde liefert LOFAR rund 300 GB an Daten; Speicherplatz steht in der Größe von 2 Petabyte zur Verfügung, sprich: für knapp 2 Stunden. Astronomische Beobachtungen mit einem solchen Interferometer können einige Stunden nach dem Zeitpunkt stattfinden, an dem das Licht nachgewiesen wurde!
Very Large Telescope Interferometer
Im Nahinfrarotbereich schwingt das Licht bereits zu schnell, als dass man die Phaseninformation an jedem Detektorelement getrennt aufzeichen könnte. Man kann allerdings folgendes machen: das an einem der Elemente ankommende Licht und das an einem der anderen Elemente ankommende Licht zusammenführen und die beiden Lichtwellen überlagern: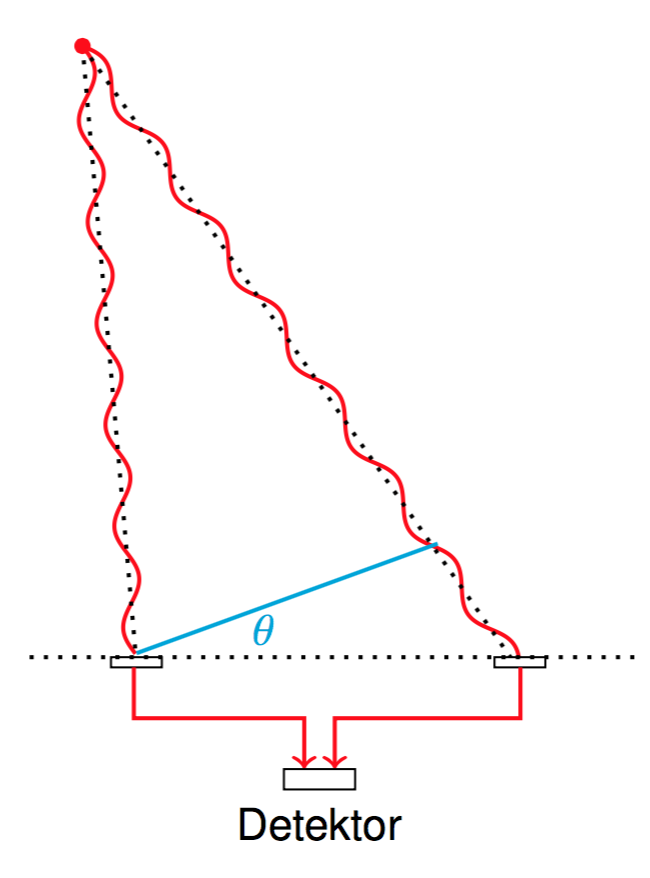 Bei der Überlagerung kommt es zur Interferenz. Die Eigenschaft der Summenwelle, deren Intensität man messen kann, gibt Aufschluss darüber, ob die beiden Teilwellen phasengleich angekommen sind (Wellenberg trifft auf Wellenberg, Wellental auf Wellental), oder um eine halbe Wellenlänge verschoben (Wellenberg trifft auf Wellental und umgekehrt), oder mit anderer Phasenverschiebung.
Bei der Überlagerung kommt es zur Interferenz. Die Eigenschaft der Summenwelle, deren Intensität man messen kann, gibt Aufschluss darüber, ob die beiden Teilwellen phasengleich angekommen sind (Wellenberg trifft auf Wellenberg, Wellental auf Wellental), oder um eine halbe Wellenlänge verschoben (Wellenberg trifft auf Wellental und umgekehrt), oder mit anderer Phasenverschiebung.
(Über Interferenz hatte ich bereits in anderem Zusammenhang im Blogbeitrag Gravitationswellen-Nachweistechnik: Michelson-Interferometer geschrieben.)
Durch geeignete Kombination des an verschiedenen Orten gesammelten Lichts kann man so etwas wie ein Bild einer bestimmten Himmelsregion rekonstruieren. Allerdings muss man sich entscheiden, wie man das Licht zur Überlagerung bringt, sprich: welche Region man beobachten möchte. Auf diese Weise funktionieren beispielsweise astronomische Beobachtungen mit den Keck-Teleskopen auf Hawaii, oder mit dem Very Large Telescope Interferometer (VLTI) der ESO auf dem Paranal, dessen Standort hier im Luftbild zu sehen ist:

Unterhalb des Plateaus sind Verbindungsgänge und Räume angelegt, in denen das Licht entweder mehrerer der Hauptteleskope (im Bild sind deren vier größere Kuppeln sichtbar) oder mehrerer der vier Hilfsteleskope (zwei davon mit charakteristischer Kugel-Kuppel sind im Bild zu sehen) oder einer Kombination dieser Teleskope zusammengeführt und im flachen Gebäude nahe der Bildmitte überlagert wird.
Auf diese Weise lassen sich ebenfalls astronomische Bilder rekonstruieren. SciLogs-Kollege Leonard Burtscher hat nebenan auf seinem Promotions-Blog ein paar Beobachtungen am VLTI beschrieben: hier und hier.
Teleskope
Rekonstruierte Bilder mithilfe von separaten Detektorelementen, deren Licht zur Interferenz gebracht wird, erfassen immer nur einen Teil dessen, was dort zu sehen ist. “Teil” ist dabei nicht im Sinne eines Ausschnitts gemeint, sondern bezieht sich auf die verschiedenen Größenskalen der Strukturen des Bildes. Manche solchermaßen rekonstruierten Bilder beispielsweise zeigen zwar kleinere Details, aber es fehlen größere Strukturen. (Wer sich das nicht vorstellen kann, aber mehr wissen möchte: Was da vor sich geht hat eine enge Beziehung zu den Fourier-Zerlegungen, die ich in Gravitationswellen-Nachweistechnik: Signale und Wellen beschreibe. An denen kann man zumindest sehen, wie Strukturen gegebener Größenskala getrennt vom Gesamtbild betrachtet werden können: Es sind die Kosinus-Wellen mit der entsprechenden Wellenlänge.)
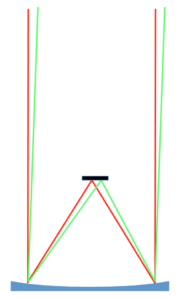 Es liegt daher nahe, möglichst viele Detektorelemente mit unterschiedlichen Abständen zueinander zu kombinieren. Im Idealfall hat man eine ganze Fläche voller Detektorelemente zur Verfügung, deren Licht dann zusammengeführt und zur Überlagerung gebracht wird. Am einfachsten gelingt das Zusammenführen, wenn man die Detektorelemente aus einem spiegelnden Material fertigt und so orientiert, dass sie das Licht in einer Ebene oberhalb der Fläche zusammenführen wie in der Grafik rechts zu sehen: der Brennebene. Licht aus leicht unterschiedlichen Richtungen, in der Grafik rot bzw. grün dargestellt, landet dabei an leicht unterschiedlichen Punkten in der Brennebene.
Es liegt daher nahe, möglichst viele Detektorelemente mit unterschiedlichen Abständen zueinander zu kombinieren. Im Idealfall hat man eine ganze Fläche voller Detektorelemente zur Verfügung, deren Licht dann zusammengeführt und zur Überlagerung gebracht wird. Am einfachsten gelingt das Zusammenführen, wenn man die Detektorelemente aus einem spiegelnden Material fertigt und so orientiert, dass sie das Licht in einer Ebene oberhalb der Fläche zusammenführen wie in der Grafik rechts zu sehen: der Brennebene. Licht aus leicht unterschiedlichen Richtungen, in der Grafik rot bzw. grün dargestellt, landet dabei an leicht unterschiedlichen Punkten in der Brennebene.
Tatsächlich ist dieser Fall in einiger Hinsicht anschaulicher als die Messungen der Interferometer. In der Brennebene entsteht ein Miniaturbild des beobachteten Himmelsausschnitts, den man mit einer Kamera festhalten kann. Das ist das Grundprinzip eines Spiegelteleskops.
Primär- und Sekundärspiegel
Bei den allermeisten Profiteleskopen ist der Aufbau komplizierter als das. Im einfachsten Falle ist noch ein weiterer Spiegel im Spiel, der Sekundärspiegel, der das Licht durch ein Loch im Hauptspiegel (Primärspiegel) zu einer dort befindlichen Kamera oder anderen Instrumenten umlenkt. Die sogenannte Cassegrain-Version dieses Aufbaus ist schematisch hier dargestellt:
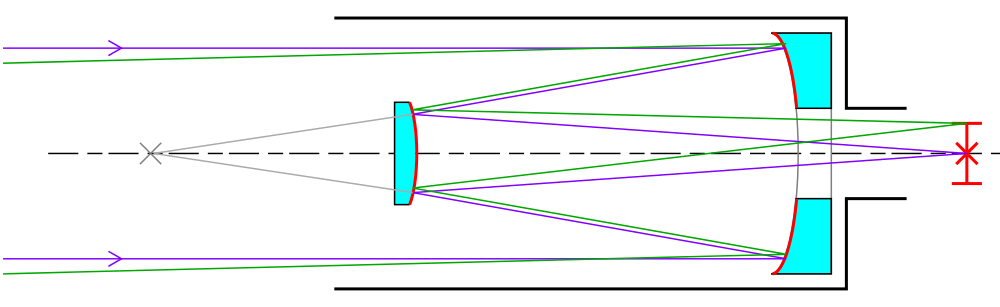

In diesem Bild des Durchmusterungsteleskops VISTA der Europäischen Südsternwarte (ESO) kann man die Halterung des Sekundärspiegels vorne gut sehen, dahinter den Primärspiegel. Die größten Spiegel der heutigen Arbeitsteleskope haben Durchmesser von rund 8 Metern. (Größere Spiegel werden aus einzelnen Segmenten aufgebaut.)
Begrenztes Auflösungsvermögen
Das Auflösungsvermögen eines solchen Teleskops ist allerdings wie im Falle eines Interferometers begrenzt: Richtungen, die um weniger als etwa \(\Delta\theta = D/\lambda\) auseinanderliegen, mit \(D\) dem Spiegeldurchmesser und \(\lambda\) wiederum der Wellenlänge, lassen sich nicht recht unterscheiden.
Das hat eine einfache Erklärung anhand von in der Brennebene aufgenommenen Bildern. Kleine Objekte, etwa Sterne, werden in der Brennebene größer abgebildet als es ihrer scheinbaren Größe am Himmel entspricht, nämlich als kleine Scheibchen (die Beugungsscheibchen heißen).
Hier ist ein Beispiel, das ich bereits im Beitrag Astronomische Trugbilder: Das hier ist nicht Proxima Centauri gezeigt hatte:

Das hier ist zwar einerseits ein Bild des Doppelsternsystems Alpha Centauri A und B, andererseits auch wieder nicht. Die Lichtpunkte entstanden aus dem Licht, das uns von Alpha Centauri A und B erreicht. Dieses Licht bestimmt auch die Gesamtfarbe der Scheibchen, die man da sieht. Der Abstand der Scheibchen-Mittelpunkte (Richtungsunterschiede, wieder einmal!) ist ein sinnvolles Maß für den Winkelabstand der beiden Sterne am Himmel. Aber alles andere, was in dem Bild zu sehen ist, die vier Zacken, die Größe und Struktur der Scheibchen selbst, ist keine Eigenschaft der angepeilten Himmelskörper, sondern des verwendeten Teleskops – in diesem Falle des Hubble-Weltraumteleskops.
Die Scheibchengröße limitiert das Auflösungsvermögen: Liegen zwei Objekte so nahe beieinander, dass ihre Scheibchen sich überlappen und nicht mehr zu unterscheiden sind, kann man diese Objekte auf einer Abbildung nicht mehr voneinander trennen. In dieser Weise “erbt” das Teleskop den Zusammenhang zwischen Größe und Auflösungsvermögen vom Interferometer.
Gut daran ist, dass Astronomen mit dem Bau großer Teleskope zwei Fliegen mit einer Klappe schlagen können: Große Teleskope ergeben sowohl größere Genauigkeit bei den Helligkeitsmessungen als auch ein größeres Auflösungsvermögen.
Spektroskopie: Energien unterscheiden
Auf den dritten Aspekt astronomischer Beobachtungen, das Erfassen unterschiedlicher Photonenenergien, will ich in einem gesonderten Blogbeitrag noch näher eingehen. Hier nur soviel: Wer hier eine gute Auflösung erreichen und Photonenenergien möglichst fein unterscheiden möchte, muss einen Kompromiss treffen. Für eine gute spektrale Auflösung müssen die Photonen in möglichst viele unterschiedliche “Energie-Schubladen” einsortiert werden. Je größer die Anzahl der Schubladen, desto geringer die mittlere Zahl der Photonen in jeder der Schubladen.
Geringere Photonenzahlen erlauben aber, siehe die Ausführungen zur Poissonstatistik oben, nur eine geringere Genauigkeit bei der Helligkeitsbestimmung. Damit wird auch die Messung des Spektrums – Helligkeit in jeder der “Energie-Schubladen” – ungenauer. Je nach wissenschaftlicher Fragestellung wird man daher unterschiedliche Kompromisse zwischen spektraler Auflösung und spektraler Helligkeits-Messgenauigkeit eingehen müssen. Anders als bei Helligkeitsmessungs-Genauigkeit und Auflösungsvermögen gibt es hier keine Möglichkeit, beide Kriterien gleichzeitig ins Extrem zu treiben.
Astronomische Beobachtungen: Fazit
Vom Photonenzählen zur Helligkeitsbestimmung, vom Phasen-Dokumentieren zur Einfallrichtung bzw. zum astronomischen Bild: Astronomische Beobachtungen ergeben sich direkt aus der zugrundeliegenden Physik. Auf diese Weise kommt man auch, in umgekehrter Reihenfolge als sonst, zu den hauptsächlichen Beobachtungsinstrumenten der Astronomen: Interferometern, bei denen die Phasen in jedem Element dokumentiert werden; Interferometern bei denen das Licht erst überlagert und dann gemessen wird, und schließlich herkömmlichen Teleskopen, die das Licht sammeln und in einer Brennebene eine verkleinerte, lichtstarke Abbildung des betreffenden Himmelsausschnitts erzeugen.
Aus der Physik folgt auch, warum Astronomen versuchen, immer noch größere Teleskope zu bauen (bessere Auflösung einerseits, genauere Helligkeitsmessungen andererseits) und lange zu belichten (genauere Helligkeitsmessungen).
Damit, wie diese Anforderungen praktisch umzusetzen sind, beschäftige ich mich dann noch in weiteren Blogbeiträgen.


Eine sehr gute Einführung und Übersicht über die physikalischen Fundamente von astronomischen Beobachtungsinstrumenten. Daran anschliessend ergäben sich viele praktische Fragen aus der Astronomie. Beispielsweise folgende Frage:
Ist eine Direkbeobachtung eines Exoplaneten nur dann möglich, wenn das Auflösungsvermögen des Teleskops den Stern und seinen Exoplaneten auseinanderhalten kann und in welcher Art stört der grosse Helligkeitsunterschied zwischen Stern und Exoplanet die Beobachtung.
Frage: Erhöht ein grosses Teleskop die Chance, dass man einzelne Photonen von sehr schwachen Quellen detektieren kann?
In einer reinen Photonenbetrachtung, in der man Photonen als Teilchen betrachtet wohl nicht, denn entweder trifft das Photon den Detektor oder eben nicht. Das Lichteinsammeln über den Spiegel sollte in der Photonen als Teilchen Betrachtung für Einzelphotonen keine Roöle spielen. Meine Vermutung ist aber, dass die Chancen ein einzelnes Photon zu entdecken mit einem grossen Spiegel dennoch grösser ist. Denn auch ein einzelnes Photonen hat Welleneigenschaften und diese Welle wird über den Spiegel fokussiert, je grösser der Spiegel ist umso besser.