Exomonde
BLOG: Uhura Uraniae

Exoplaneten findet man seit 1995 am laufenden Band (zur Betrachtung des Themas auf Schulniveau: akt. Heft Nr 126 von A+R i.U.) – doch bei der Suche nach der zweiten Erde stellen nur wenige die Frage, ob es vielleicht auch Monde um diese Begleiter geben könnte und ob wir diese finden. Ich habe mich vor ein paar Jahren in meiner ersten Diplomarbeit mit dieser Frage beschäftigt.
Eine der Teilfragen der Statistik der Astronomie ist auch, wie häufig Monde überhaupt in anderen Sonnensystemen vorkommen. Wieviele von den Exoplaneten, die man mit verschiedenen Methoden findet, haben Monde und wie kann man diese eventuell nachweisen?
 Laut der Greenbank-Formel stellt sich auf der Suche nach der zweiten, dritten und vierten Erde auch die Frage: Gibt es irgendwo ähnliche Lebensbedingungen wie auf unserem Planeten und wie “typisch” ist unser Sonnensystem im Vergleich zu anderen? Die ersten Funde von extrasolaren Planetensystemen schien zu eröffnen, dass unser SoSy was ziemlich besonderes ist. Allerdings ist das wohl nur ein “natürlicher Effekt” der Erstentdeckung von Exoten: Es ist, wie beim Blick in eine Menschenmenge: die besonders übergewichtigen oder besonders hochgewachsenen stechen heraus und fallen zuerst auf. Erst später nimmt man die ganzen “gewöhnlichen” Leute wahr. Inzwischen gab es mehrfach die Meldung von der Entdeckung erdähnlicher Planeten (siehe SuW, z.B: 2011).
Laut der Greenbank-Formel stellt sich auf der Suche nach der zweiten, dritten und vierten Erde auch die Frage: Gibt es irgendwo ähnliche Lebensbedingungen wie auf unserem Planeten und wie “typisch” ist unser Sonnensystem im Vergleich zu anderen? Die ersten Funde von extrasolaren Planetensystemen schien zu eröffnen, dass unser SoSy was ziemlich besonderes ist. Allerdings ist das wohl nur ein “natürlicher Effekt” der Erstentdeckung von Exoten: Es ist, wie beim Blick in eine Menschenmenge: die besonders übergewichtigen oder besonders hochgewachsenen stechen heraus und fallen zuerst auf. Erst später nimmt man die ganzen “gewöhnlichen” Leute wahr. Inzwischen gab es mehrfach die Meldung von der Entdeckung erdähnlicher Planeten (siehe SuW, z.B: 2011).
Manche wissenschaftlichen Thesen behaupten, dass die Erdachse insbesondere deshalb über Jahrmilliarden stabil ist, weil unser Mond die Erde umkreist. Vielleicht ist dies einer seiner tatsächlichen Beiträge für das Leben auf der Erde (nicht zu verwechseln mit den zahlreichen angedichteten Einflüsse)?
Was haben wir zum Finden von Planeten?
Gehen wir dazu die einzelnen Methoden kurz durch: Exoplaneten finden wir heute mit fünf verschiedenen Methoden. Pulsarplaneten stören die Regelmäßigkeit der Pulse jener kosmischen Taktgeber, die als Neutronensterne ihren Magnetpol gerade zufällig in unsere Richtung drehen. Hätte ein solch exotischer Planet einen Mond, dann könnte auch der Mond den Puls verkleinern oder aussetzen lassen, aber da der Mond naturgemäß immer nah am Planeten steht, würde auch der Planet allein denselben Effekt bewirken und der Mond nichts “aufmodulieren”. Wir würden den Mond nur registrieren, falls seine Bahnebene in exakt der Ebene der Pulse liegt und die Bahngeometrie des Mondes (Entfernung zum Pulsar und Durchmesser des Mondes) hinreicht, den Puls ebenfalls abzudecken oder seine Intensität merklich zu schwächen. Um dies vernünftig abzuschätzen, bräuchte man eine statistische Verteilung der Monde, die mindestens halb so groß sind wie ihr Planet. Zum Zeitpunkt meiner Diplomarbeit zählte Pluto-Charon noch als Doppelplanet und damit wäre die Häufigkeit eines solchen Falles in unserem SoSy = 1 bei etwa zehn Planeten und tausenden von Monden (Fehlerbalken der Astrophysik liegen ja oft im Exponenten). Betrachten wir nun aber noch, dass Pluto zu weit von der Sonne entfernt wäre, um bei seiner Mini-Größe einen Pulsar-Puls (Lichtkegel) zu stören, könnte es auch sein, dass wir Pluto und Charon, die um einen Pulsar kreisen, gar nicht finden.
Also, angenommen, alle Pulsarplaneten haben Monde. Dann ist die Chance, dass einer dieser Monde halb so groß ist wie sein Planet etwa 0,1 (mit der Stichprobenmenge von eins, die wir haben, nämlich unser SoSy). Kreist der Planet dicht am Pulsar, könnten er den Puls stören, kreist er in großer Entfernung stört er vielleicht nicht messbar. Die Chance für die Entdeckung von Pulsar-Monden liegt also im günstigsten Fall bei 0,1 mal der Anzahl der entdeckten Pulsar-Planeten, im ungünstigsten Fall bei 0. Bei deren geringer Häufigkeit und noch viel geringeren Relevanz für die Suche nach Leben im All ist dies jedoch wohl schlicht weg vernachlässigbar. 🙁
Ähnliches gilt für die astrometrische Planetenfinde-Methoden:
Weil im Gravitationsgesetz die Anziehungskräfte der beteiligten Massen gleichberechtigt eingehen, zieht jeder Planet auch seinen Stern an. Wir können entweder versuchen, die resultierende rhythmische Bewegung des Stern mit dem Planetenumlauf direkt zu messen, also als Verschiebung des Sternortes am Himmel, wenn der Stern an unserem Himmel quasi hin- und hertänzelt. Alternativ können wir versuchen, die Sternbewegung “auf uns zu” und “von uns weg” im Planetenrhythmus durch die Messung von Radialgeschwindigkeiten, also die Doppler-Verschiebung seines Spektrums zu bestimmen. In jedem Fall würde ein Mond um den Planeten kaum einen Effekt bewirken, weil er sich ungefähr am Ort des Planeten befindet. Die aufmodulierte Verschiebung des Sterns, die durch den Mond verursacht wird, ist derzeit mit astrometrischen Methoden gar nicht nachweisbar und auch bei der Doppler-Whobble-Methode wäre ich skeptisch, da sie ohnehin große Planeten (relativ zu ihrem Stern) auf engen Bahnen bevorzugt.
Es bleiben zwei Hauptverdächtige unter den Methoden, wie man Monde nachweisen kann: Die Transitmethode und die Gravitationslinsenmethode. In beiden Fällen handelt es sich um photometrische Methoden, bei denen wir also die Helligkeit eines Sterns messen. In den Veränderungen der Helligkeit eines per se kontinuierlichen Strahlers messen wir charakteristische Veränderungen, die auf Planeten schließen lassen.
Transitmethode
Bei der Transitmethode beobachten wir auf diese Art den Vorübergang eines Planeten vor seinem Mutterstern. Wir sehen also einen Helligkeitseinbruch in der Lichtkurve des Sterns, denn für die Dauer des Vorübergangs des Planeten vor seinem Mutterstern wird ein Teil der leuchtenden Sternoberfläche abgeschattet. Würde beim Planeten ein Mond stehen, könnte er in einer günstigen Konstellation die Symmetrie dieser Kurve brechen, denn er könnte z.B. beim Eintritt des Planeten vor die Sternscheibe “neben” dem Planeten stehen, so dass mehr Sternfläche abgedeckt wird als der Planet allein verdecken könnte. Andererseits könnte er bei Austritt oder spätestens beim nächsten Vorübergang desselben Planeten vor seinem Mutterstern eben nicht mehr “neben” dem Planeten stehen, so dass infolge der Rotation des Mondes um den Planeten, also seine Bindung an den Planeten die Sternhelligkeit jedes n-te Mal stärker zurückgeht als sonst – je nachdem, ob der Begleiter des Planeten gerade ebenfalls Sternlicht abschattet oder nicht.

Abb. 1: Im linken Bild gehen Planet und sein Mond “nebeneinander” an der Sternscheibe vorüber. Der Helligkeitsabfall ist die Summe aus den beiden einzelnen Helligkeitsabfällen. Im rechten Bild wäre der Mond nicht detektierbar, weil er sich in der Helligkeit des Sterns überhaupt nicht bemerkbar macht.
Natürlich ist der Effekt sehr klein und seine Messbarkeit fraglich. Der größte Mond unseres Sonnensystems, Ganymed, hat einen Durchmesser von 5262 km, also ein Dreihundertstel Sonnendurchmesser. Weil die Leuchtkraft aber mit dem Quadrat des Radius skaliert, kann man daraus grob abschätzen, dass Ganymed für einen Beobachter auf Alpha Centauri oder auf der Wega einen Helligkeitseinbruch von 0.7 Promille verursachen würde. Zum Vergleich: Jupiter hat ca 10 % des Sonnendurchmessers und verursacht mithin – grob geschätzt – einen Helligkeitsabfall von 1%.
Hätten wir also photometrische Genauigkeiten von 0.1 Promille, also Genauigkeiten, die einen Helligkeitsabfall um ein Hunderttausendstel registrieren können, dann könnten wir Ganymed und ähnlich große Monde in anderen Sonnensystemen mit der Transitmethode nachweisen. Meines Wissens hat das aber bisher noch niemand versucht. Selbstverständlich ist Ganymed wirklich einer der Giganten unter den Monden. Die meisten Monde – also “typische” Kandidaten – wären deutlich kleiner und erforderten eine Genauigkeit von 0.01 Promille und weniger. Wie mit jeder Art von Entdeckung wäre es aber wichtig, zunächst den prinzipiellen Nachweis zu bringen, dass die Methode funktioniert, also einen ersten Mond auf diese Art zu finden. Hinterher kann man dann auch die Messgenauigkeit verbessern und die Methoden verfeinern, damit einem auch die “kleinen Fische” ins Netz gehen (können).
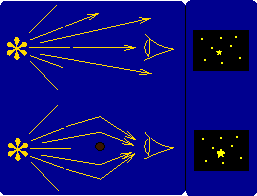
Abb. 2: Lichtablenkungen durch Gravitationslinsen: Der Mittelpunktstrahl kommt nicht an, stattdessen aber zahlreiche andere, die sonst an uns vorbei gehen würden. Wir sehen den Hintergrundstern heller.
Gravitationslinsenmethode
Die vielleicht raffinierteste und gleichzeitig brisanteste Methode der Planetensuche ist die Ausnutzung des Gravitationslinseneffektes. Mit ihr kann man erdähnliche Planeten sogar in gigantischen Entfernungen nachweisen, z.B. im Zentrum der Milchstraße. Wir beobachten dafür ferne Hintergrundsterne und messen deren Helligkeit. Falls wir Glück haben, zieht zwischen uns und diesen fernen Sternen eine andere Sonne mit ihren Planeten und Monden vorüber.
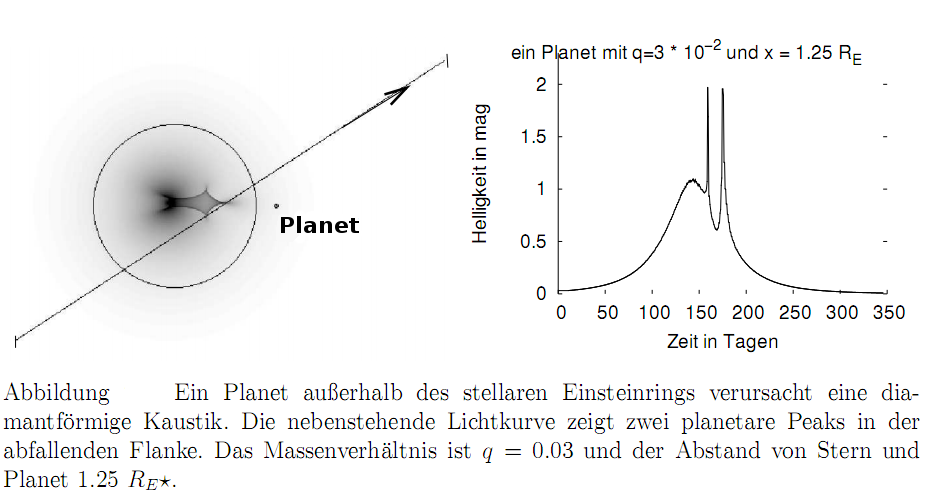
Diese Himmelskörper – egal, ob wir sie selbst sehen können oder ihre Helligkeit dafür nicht ausreicht – lenken das Licht des fernen Hintergrundsterns ab. Dieser Effekt, den wir aus der Allgemeinen Relativitätstheorie ableiten, führt bei großen Skalen (also Galaxien usw) zu Doppel- oder Mehrfachbildern des Hintergrundobjektes. Auf den hier betrachteten kleinen Skalen aber, wenn wir also nur von Sternen innerhalb unserer Milchstraße reden, können wir diese Mehrfachbilder nicht auflösen, sondern beobachten am Himmel “nur” eine Lichtverstärkung des Hintergrundobjektes. (siehe Abb.)
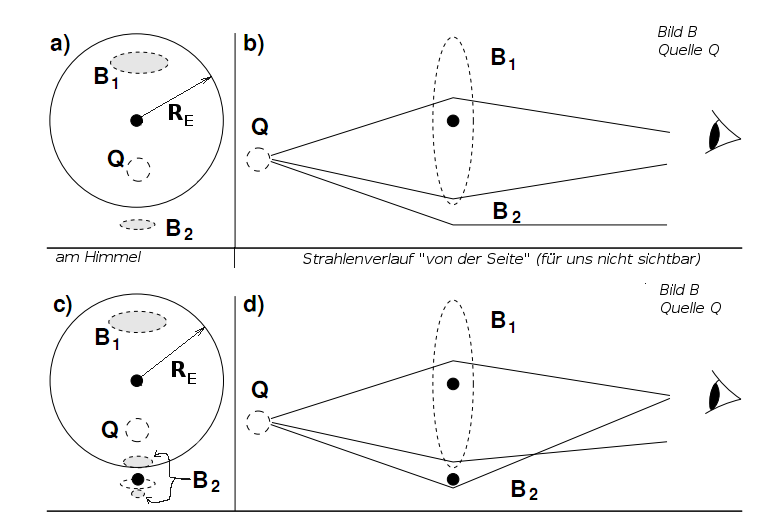
Abb. 4: Umwandert ein Mond den Planeten, dann wird das Muster der Lichtverstärkung komplizierter. Weil die Lichtstrahlen zwischen den Mikrolinsen Stern, Planet und Mond hindurch navigieren müssen, ist die Lichtverstärkung nicht eine einfach Addition der Einzellichtkkurven, sondern hängt empfindlich von der genauen Geometerie der Konstellation ab.
Das linke Teilbild zeigt ein Szenario in der Frontansicht (von uns aus gesehen). Eingezeichnet sind die projizierten Mehrfach-Abbilder B1, B2 einer Quelle Q in einem beliebigen System mit dem Einsteinradius RE um die Linse im Zentrum. Bei B1 und B2 würden wir die Bilder sehen, wenn wir sie auflösen könnten (in praxi auf diesen Skalen nicht gegeben). Das rechte Teilbild zeigt deren Zustandekommen in der Seitenansicht.
Hier wird natürlich kein Licht zusätzlich erzeugt und wir addieren auch nicht das Licht von verschiedenen Quellen. Man kann es sich vereinfacht so vorstellen: Der Hintergrundstern strahlt in alle Richtungen Licht ab, wovon uns das meiste natürlich nicht erreicht, weil er es nicht in unsere Richtung schickt. Steht nun aber eine Gravitationslinse zwischen uns und dem Stern, trifft uns der direkt auf uns gerichtete Lichtstrahl zwar nicht. Allerdings kommen ein paar Lichtstrahlen bei uns an, die ohne die Linse einfach “links und rechts” oder “oben und unten” an uns vorbei gehen würden – jene Lichtstrahlen also, die ohne Linse vielleicht ein Mond”bewohner” oder ein Mars”bewohner” sehen würde oder ein Beobachter auf dem Planeten um 51 Peg). Die Linse bewirkt also, dass von dem Hintergrundobjekt mehr Licht zu uns hingelenkt wird und bei uns ankommt, anstatt anderswo und wir sehen, wie der Hintergrundstern heller wird.
So sehen die Karten der Lichtverstärkung aus: Betrachten wir einen winzigen Bereich am Himmel um einen Hintergrundstern (unten links, weit außerhalb des Bildes: etwa die doppelte Kantenlänge der Bildhöhe), dann zeigen hier die (erdachten) Linien und Flächen an, wo es eine Verstärkung in der Lichtkurve des Hintergrundsterns gäbe, falls sich ein Planet bzw. Mond des Vordergrundsterns an dieser Himmels-Stelle befinden würde.

Abb. 5: Gravitationslinsenkaustiken wie diese entstehen als theoretische Simulationen des umgekehrten Lichtwegs. Sie geben sozusagen eine “Karte der Lichtverstärkung”. Weiß sind die Orte hoher Lichtverstärkung falls man nur einen jupiterähnlichen Planeten um einen Stern hätte. Dunkelgrau bis schwarz sind die Orte derselben Planet-Stern-Konstellation, wenn der Planet durch einen großen Mond begleitet wird. Der Mond verschiebt also auch den Ort der Lichtverstärkung für den Planeten. Natürlich wäre dieser Effekt nicht messbar, weil man den Mond ja nicht entfernen kann, aber für die theoretischen Simulationsrechnungen ist dieser Effekt sehr wichtig.
Problem der Größe von Hintergrundsternen
Auch Monde haben natürlich Massen und würden mithin eine solche Lichtablenkung bewirken. Da gerade die Linseneffekte bei einem solchen Dreipunktlinsen-System stark nichtlinear werden, kann man jedoch nicht einfach die Lichtkurven von zwei Sternbegleitern (einem großen, dem Planeten, und einem kleineren, dem Mond) addieren, wie es bei der Transitmethode möglich war. Stattdessen ergeben sich verschiedene Effekte in den Lichtkurven je nachdem, wie der Exoplanet, sein Mond und ihrer beider Mutterstern durch unser Gesichtsfeld vor der Hintergrundquelle vorüberwandern.
Monde können theoretisch auch einen Helligkeitsanstieg von einigen zehn oder sogar einigen hundert Millimagnituden bewirken, den wir heutzutage bereits detektieren könnten. Allerdings könnte sogar dieser relativ starke Effekt im Fall von großen Hintergrundsternen im Rauschen verschwinden: Hat nämlich ein Hintergrundstern einen größeren Durchmesser, dann wird seine Leuchtkraft stärker um eine (idealgedachte) Punktquelle verschmiert, als wenn er kleiner wäre. Selbst wenn also der ferne Riesenstern mehr Licht abstrahlt, als der ferne Hauptreihenstern, so trifft dennoch das meiste seines Lichts nicht in den Linsenbereich unserer Mikrogravitationslinse und wird folglich doch nicht zu uns irdischen Beobachtern umgelenkt. Das Licht, das von der Gravitationslinse zu uns hin abgelenkt werden kann, wird also eher weniger, wenn der ferne Strahler groß ist.
Eine Hoffnung ist allerdings, dass wir aufgrund der größeren Anzahl von kleinen und durchschnittlichen Sternen als von Riesen auch mehr von diesen kleineren beobachten als von den Riesensternen. Natürlich erfordert dieses Ziel sensible photometrische Messgeräte, denn die Riesen sind nunmal auch leuchtkräftiger als die Zwerge (weiter oben im HRD).
Eine andere – wenngleich sehr schwierige – Lösung dieses Dilemmas könnte sein, dass man gar nicht Sterne im Hintergrund beobachtet, sondern Quasare oder andere Objekte, die an sich Quasi-Punktquellen sind. Dann würden sich die Monde der Exoplaneten jedenfalls in den Lichtkurve zeigen. – Die Frage ist eher, ob es für ein derartiges Szenario eine sinnvolle Konstellation geben kann: Exoplaneten suchen wir bisher nur in unserer Milchstraße, der Galaxis, und wo sich die Sterne und die interstellare Materie der Galaxis befinden, können wir leider nicht ins ferne All schauen. Wo wir umgekehrt in die Ferne schauen können, da sind eben keine nahen Objekte im Weg, d.h. es ist sehr unwahrscheinlich (wenngleich nicht unmöglich), dass wir dort einem Freefloater begegnen, der vielleicht dann auch noch einen lunaren Begleiter mit sich führt.
| Stern | Ein Fusor, d.h. er generiert Energie durch Kernfusion. |
| Planet | Ein Nichtfusor, der (unmittelbar) um einen Fusor kreist. Ein Fusor erzeugt sein Licht durch Kernfusion selbst. |
| Mond | Ein Nichtfusor, der um einen Nichtfusor kreist. |
| Freefloater | Ein Objekt planetarer Masse, dass nicht um einen Fusor kreist, sondern sich zwischen den Sternen frei bewegt. |
Die charakteristische Form dieses Helligkeitsanstiegs lässt (nach unserem heutigen Wissen) eindeutig auf ein Linsenereignis schließen, auch wenn leider jedes Ereignis einzigartig und unwiederholbar ist. Jedoch verletzt diese Suchmethode daher ein ganz fundamentales Messprinzip der modernen Wissenschaften: Normalerweise fordern wir die Reproduzierbarkeit von Beobachtungen und das können wir in diesem Fall nicht garantieren: Im Gegensatz zur Transitmethode beobachten wir hier ja eine Helligkeitsänderung von einem unabhängigen Hintergrundstern und nicht eine Änderung bei der Muttersonne des Planeten. Wenn also der Mutterstern mit seinem Sonnensystem einmal den Hintergrundstern passiert hat, dann ist dieses Ereignis unwiederholbar vorbei. Man stützt also die Beobachtung eines solchen Events auf eine Mehrfachbeobachtung von unabhängigen Beobachtergruppen auf der Erde. Nur falls mehrere Gruppen gleichzeitig diese Beobachtung machen, gilt eine Lichtkurve als gesichert und wird akzeptiert.
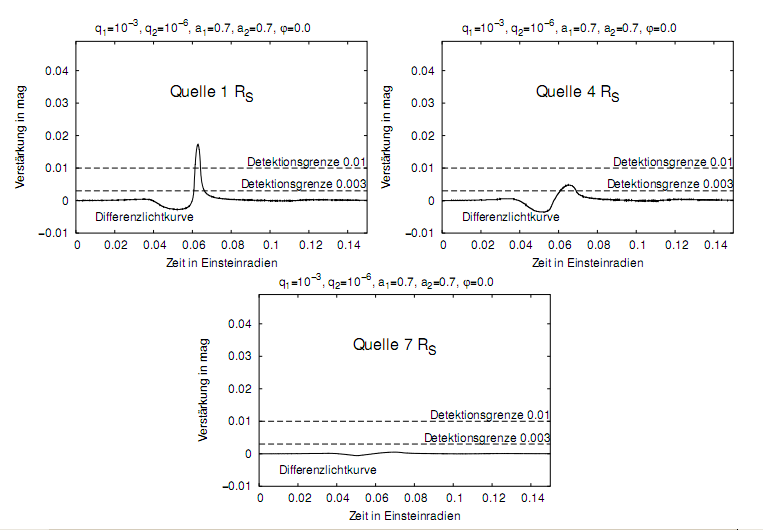
Abb. 6: Je größer der Hintergrundstern ist, desto weniger von seinem Licht steht der Linse für die Verstärkung zur Verfügung. Beobachten wir also unter den Hauptreihensternen eher größere von ca 4 Sonnenradien, dann kommt Effekt in für den hier simulierten Fall eines Doppelplaneten (Uranus umkreist Jupiter) gerade noch übers Detektionslimit. Doch falls dieselbe Konstellation an einem nur wenig größeren Riesenstern vorüberzieht, geht der Effekt des Mondes bereits im Rauschen unter. Man bedenke, dass typische Messdaten – im Gegensatz zur hier dargestellten Rechnung – keine kontinuierlichen Messkurven zeichnen könnten und die Punkte obendrein einer starken Streuung unterliegen würden.
Planeten und ihre Monde können also Lichtverstärkungen an Hintergrundsternen verursachen und die gute Nachricht ist: Sie können es sogar gleichermaßen intensiv. Ein Jupiter um die Wega könnte also die gleiche Höhe der Lichtverstärkung an einem (ideal punktförmig gedachten) Hintergrundobjekt bewirken, wie sein Mond Ganymed, weil die Höhe der Lichtverstärkung nicht von der Größe oder Masse der Linse abhängt, sondern nur von der Geometrie der Konstellation und der Größe des Hintergrundobjektes.
Dauer des Effekts
Überhaupt ist der Durchmesser der Linse von geringer Bedeutung, sondern als Einflussgröße benutzen Gravitationslinsenphysiker stets die Masse. Die Masse des linsenden Himmelskörpers hat eine andere Auswirkung auf die Beobachtung: sie reguliert nämlich die Dauer des Ereignisses! Ein durchschnittlicher Stern wie die Sonne würde z.B. als Gravitationslinse eine Helligkeitssteigerung beim Hintergrund bewirken, die einige Monate oder vielleicht ein Jahr andauert. Ein Planet hingegen hellt einen Hintergrund nur für einige Wochen auf, was aber noch immer bequem beobachtbar ist, solange es keine nachhaltigen globalen atmosphärischen Veränderungen gibt. Betrachten wir nun aber typische Mondmassen in unserem Sonnensystem, so müssen wir erkennen, dass ihre Mikrogravitationslinsenlichtkurven für sie nur von wenigen Stunden Dauer sein könnten. Monde sind also nur kurzfristig erhellend.
Diese Erkenntnis ist allerdings fatal für die Abschätzung der Beobachtbarkeit, denn dann könnte z.B. ein Teleskop in Zentralasien einen Exomond-Peak beobachten und während sich die Erde weiterdreht und binnen desselben Tages später, wenn es in Europa und Afrika oder den USA Nacht wird, der Exomond-Peak schon vorbei sein. Selbst wenn die Verstärkung sogar länger als einen Tag dauert und es dann in Zentralasien bewölkt ist, würde uns der Exomond durch die Lappen gehen, weil wir mit hoher Wahrscheinlichkeit diese eine Beobachtung niemals werden bestätigen können.
Plausibilität der Entdeckungswahrscheinlichkeit
Ein dritter Effekt kommt zum Tragen, den ich nicht unerwähnt lassen möchte: Die Unwissenheit des Beobachters. – Ich habe hier aus Sicht der theoretischen Astrophysik entwickelt, welche Effekte lunare Begleiter von Exoplaneten in deren Mikrogravitationslinsenlichtkurven überhaupt verursachen würden. Das Ergebnis ist, dass die Stärke des Effekts von Monden hauptsächlich vom Massenverhältnis Mond-Planet und der geometrischen Konstellation (Enge der Mondbahn und Lage, also Inklination in Bezug auf unser Beobachterbezugssystem) abhängen. Ich habe also kurzfristig aus der Perspektive des “allwissenden Gottes” nachgeschaut, wie stark der Effekt ist und ob der irdische Beobachter ihn bemerken könnte. Bei dieser deduktiven Methode ist es natürlich leicht zu behaupten, dass das doch mit Wahrscheinlichkeiten von einigen Prozent oder Promille eigentlich klappen könnte.
ABER Der Beobachter aber weiß ja in realitas nicht, ob ein Exoplanet einen Mond hat oder nicht. Wir haben gesehen, dass der Effekt photometrisch nahe am Rauschen ist, dass er von kurzer Dauer ist und dass er später auch nicht reproduzierbar sein wird.
ACHTUNG Es wäre also leicht, für einen Beobachter, diese Datenpunkte – selbst wenn er sie messen würde – als Messfehler zu deuten und gar nicht erst auf die Idee zu kommen, hier eine weitere Mikrolinse hinein zu interpretieren.
Bitte, liebe Beobachter, sucht trotzdem! 🙂
Es gibt mit dem neuen Exoplaneten-Suchprogramm auch für Amateure (SETI@home) wunderbare Möglichkeiten, sich in diesem Feld auszutoben! Lasen wir nicht kürzlich in SuW von Aufrufen zur Unterstützung der Kepler-Daten-Auswertung?
Ideen und Perspektiven
Im Grunde müssten also an jeder Beobachtungsstation auf der Erde mindestens zwei konkurrierende Gruppen stets gleichzeitig messen und sich gegenseitig bestätigen, um abzusichern, dass ein oder zwei Messpunkte, die man dann vielleicht nur hätte, tatsächlich real sind und weder technische Messfehler noch Fehlinterpretationen der Auswertung. Am besten wäre dafür sogar, die Erde mit einem feinmaschigen Netz aus (doppelten) Beobachtungsstationen zu umspannen, um eine Lichtkurve lückenlos und einwandfrei aufzuzeichnen. – Ob der einzelne Beobachter dann auf die Idee kommt, einen Ausreißer in seiner Lichtkurve tatsächlich mit einem Exomond in Verbindung zu bringen, ist trotzdem fraglich. Meine theoretischen Simulationen verschiedener Linsenszenarien und Betrachtungen, ob wir es schaffen werden, Exomonde auf diese Art zu finden, resümiere ich daher leider eher skeptisch.
Ich glaube, dass der Effekt der Monde an sich durchaus messbar wäre, wenngleich er mit einigen Prozent oder Promille recht klein erscheint: Beobachten wir aber einige hundert oder tausende von Sterne, die ein Sonnensystem mit Monden haben, dann wäre die Detektion von Monden realistisch. Die Chance jedoch, dass wir einen Mond tatsächlich als solchen erkennen, wenn er sich kurz bemerkbar macht, geht m.E. leider gegen Null. – Ich würde mich allerdings sehr freuen, wenn künftige Beobachtungen und Auswertungen diese derzeit ungünstige Abschätzung als zu pessimistisch herausstellen. Es bleibt also spannend in der Suche nach den Monden der “zweiten Erden”. 🙂
Good Luck!
 Endlich aufgeschrieben, was schon seit Jahren in meiner Schublade schlummert.
Endlich aufgeschrieben, was schon seit Jahren in meiner Schublade schlummert.


Transit Timing&Duration Variations
TDV and TTV scheinen es sogar zu ermöglichen mit Kepler Exomonde zu entdecken. Deshalb gibt es das HEK (
Hunt for Exomoons with Kepler Projekt.
Das Thema ist zeitgemäß –
gut und weist in die baldige Zukunft! Der Beitrag ist auch eine gute Zusammenfassung oder ein Einblick in die Aufgaben und Probleme.
So wie einst die Ozeane eine unendliche Wasserwüste waren, unser Sonnensystem die einzigen bekannten Planeten hatte – auch hier gab es mehrfach Entdeckerfreuden – so werden auch Monde in Zukunft in Massen entdeckt werden.
Und die Forschung geht weiter um auch zu beweisen, was der Universalgelehrte G. Bruno schon 1584 lehrte [SG]: „Die unzähligen Welten im Universum sind nicht schlechter und nicht weniger bewohnt als unsere Erde.“ F. Engels war der Meinung, dass das Universum ein gigantisches Reservoir von Leben sein muss – und Monde gehören einfach dazu.
Interessant war auch die Feststellung/Überraschung, dass einige Exoplaneten – so wie man sie gefunden hat – noch nicht erklärbar sind: Supererden machen Superprobleme:
Immer mehr Exoplanten widersprechen den gängigen Theorien zur Planetenentstehung
http://www.spektrum.de/…en-superprobleme/1137214
Das wird bei den Monden nicht viel anders werden. Wie Monde entstanden sein könnten/sind haben wir bei den Monden des Sonnensystems – speziell bei unserem Erdmond – ausführlich untersucht, und eine Variante aus den Überlieferungen noch nicht beachtet.
Gibt es Wasser auf dem Mond – das ging auch in der Entwicklung unserer Wissenschaft zwischen nein und ja (jetzt sicher), eine Zeit lang hin und her. Auch hier gibt es wissenschaftlich noch Neuland.
Wir können also gespannt sein, was uns mit der neuen Technik – manchmal auch im Nachhinein mit der älteren – noch präsentiert wird. Eine nicht nur wissenschaftlich faszinierende Zukunft!