Hat das Muon-(g–2)-Experiment neue Teilchenphysik entdeckt?

Auf Teilchenphysik-Twitter war die Vorfreude greifbar: Ob auf der Pressekonferenz des Muon-(g–2)-Experiments (gesprochen “Muon g minus 2) heute (7. April 2021) tatsächlich ein Hinweis auf neue Physik verkündet werden würde? Nach rund 50 Jahren mit einer Bestätigung des sogenannten Standardmodells der Elementarteilchenphysik nach der anderen Anzeichen für etwas, das die Teilchenphysiker*innen in fundamentaler Weise nicht verstehen?
Jetzt ist das Ergebnis da: Offenbar tatsächlich eine Abweichung des magnetischen Moments des Myons, engl. muon, – vereinfacht gesagt: wie ein massereicher Cousin des Elektrons als winziger Magnet wirkt, und damit z.B. auch auf äußere Magnetfelder reagiert – von den Vorhersagen des Standardmodells. Oder aber vielleicht doch nicht. Ich muss zugeben: Ich bin da derzeit eher skeptisch. Zum Teil aus physikalischen Gründen, zum Teil aus historischen.
Als ich noch Schüler war, fand ich sowohl Astronomie als auch Teilchenphysik äußerst spannend. In Hamburg, wo ich damals lebte, befand sich auch das DESY, dessen Forschungsschwerpunkt damals noch bei der Elementarteilchenphysik lag. Aus dem populärwissenschaftlichen Buch “Die Welt der kleinsten Teilchen” von Oskar Höfling und Pedro Waloschek lernte ich als unbedarfter Mittelstufenschüler erstmals etwas über die Suche nach den immer kleineren Konstituenten der Materie.
Abgekühlte Teilchenphysik-Liebe
Allerdings ist meine Liebe zu den kleinsten Teilchen, das muss ich zugeben, seither leider merklich abgeklungen. Ich habe mich dann im Studium noch mit der theoretischen Grundlage der Teilchenphysik, der Quantenfeldtheorie, auseinandergesetzt, und fand das anfangs auch sehr spannend, aber letztlich sprang der Funke nicht dauerhaft über. Für mich lief das auf durchaus komplexe Rechnungen hinaus, deren konzeptionelle Grundlage ich aber nicht recht verstand, und, so mein Eindruck, so ganz klar war die konzeptionelle Grundlage da auch letztlich gar nicht. Was erst einmal kein Manko sein muss; auch in der Quantentheorie selbst hat sich “shut up and calculate”, also in etwa “Mund halten und losrechnen” als durchaus erfolgreiche heuristische Strategie bewährt. Ich fand das im Falle der Teilchenphysik für meinen eigenen Anspruch, wie ich Dinge verstehen wollte, einen eher unbefriedigenden Zustand.
Hinzu kam, dass die Zeit der einfachen Entdeckungen auf dem Gebiet der Teilchenphysik in den 1990er Jahren bereits vorbei zu sein schien. In den 1970er Jahren hatte es ja offenbar jedes Jahr mindestens eine neue Entdeckung gegeben, ob auf theoretischer Seite oder an den Teilchenbeschleunigern: Schwache Wechselwirkungen ohne Ladungsaustausch. Starke Wechselwirkungen mit Gluonen als Wechselwirkungsteilchen. Und einer ungewöhnlichen Abstandsabhängigkeit (asymptotische Freiheit). Das J/psi-Teilchen, das seinen Doppelnamen dem Umstand verdankt, dass es gleich von zwei konkurrierenden Gruppen entdeckt wurde. Das Tauon. Das Bottom-Quark. Ein erster vergleichsweise direkter Nachweis der Gluon-Spuren.
Erstmal nichts Unerwartetes
Danach, ab den 1980er Jahren waren die Neuentdeckungen in der Teilchenphysik vor allem Bestätigungen, nämlich die Nachweise von Materieteilchen oder Wechselwirkungen, die Teil des sogenannten Standardmodells der Elementarteilchen waren, das die Physiker bis zu jenem Zeitpunkt aufgestellt hatten, um die bis dahin gemachten Messungen erklären zu können.
Erster Nachweis der W- und Z-Bosonen als Austauschteilchen der schwachen Kraft am CERN 1983: Klar, für die Konsistenz wichtig, aber eben die Bestätigung einer Beschreibung jener schwachen Kraft, ohne die man bereits die vorherigen Messungen nicht rechnerisch hatte beschreiben können. Messungen 1989 zur Zahl der (leichten) Neutrinos, und damit indirekt zur Zahl der Materieteilchen des Standardmodells insgesamt: Im wesentlichen die Bestätigung, dass es jenseits des Standardmodells, das seine Teilchen in ein Schema mit drei sogenannten “Generationen” ordnet, nicht so einfach eine vierte Generation geben kann.
1995, das war direkt während meines Physikstudiums, dann der Nachweis des Top-Quarks, samt Massenmessung, an den Experimenten D0 und CDF des Fermilab. Zu dem Zeitpunkt war klar: Dieses Quark musste es geben, wenn das Materieteilchen-Schema des Standardmodells so ist, wie erwartet. Dass das Top-Quark offenbar eine gigantische Masse besaß, mehr als 180 Mal soviel wie ein Proton, war übrigens das letzte, deutlichste Beispiel auf eine grundlegende Schwäche jenes Standardmodells. Zu einer ganzen Reihe von Teilcheneigenschaften, nämlich zur elektrischen Ladung und deren teilchenphysikalischen Verwandten, trifft das Standardmodell mathematisch sehr elegante Aussagen; all jene Eigenschaften ordnen sich dort in ein großes Schema ein.
Zu den Massen? Keine grundlegenden Vorhersagen. Massen sind dort freie Parameter, und erst wenn man sie (direkt oder indirekt) gemessen hat, weiß man, welche Werte sie haben.
Higgs-Euphorie 2012…
Als das CERN am 4. Juli 2012 bekanntgab, dass seine zwei Allround-Experimente ATLAS und CMS erstmals das letzte bis dahin noch nicht gemessene Teilchen des Standardmodells nachgewiesen hatten, nämlich das Higgs-Boson, war ich zufälligerweise gerade als Blogger auf dem Lindauer Nobelpreistreffen, wo dann nicht zufälligerweise eine ganze Reihe der Väter des Standardmodells herumliefen.

Die gaben dann natürlich auch gleich eine Pressekonferenz zum Thema, zusätzlich war für die Teilnehmer*innen des Treffens eine Diskussionsveranstaltung angesetzt. Die Stimmung war – gemischt. Einerseits war das natürlich eine beachtliche experimentelle Leistung, und der Higgs-Nachweis wäre ohne den Large Hadron Collider (LHC) am CERN als damals und immer noch größten Teilchenbeschleuniger auch nicht möglich gewesen. Aber andererseits war es zunächst einmal zumindest in jener Form wieder “nur” eine Bestätigung des Standardmodells.
…aber nichts direkt Unerwartetes vom LHC
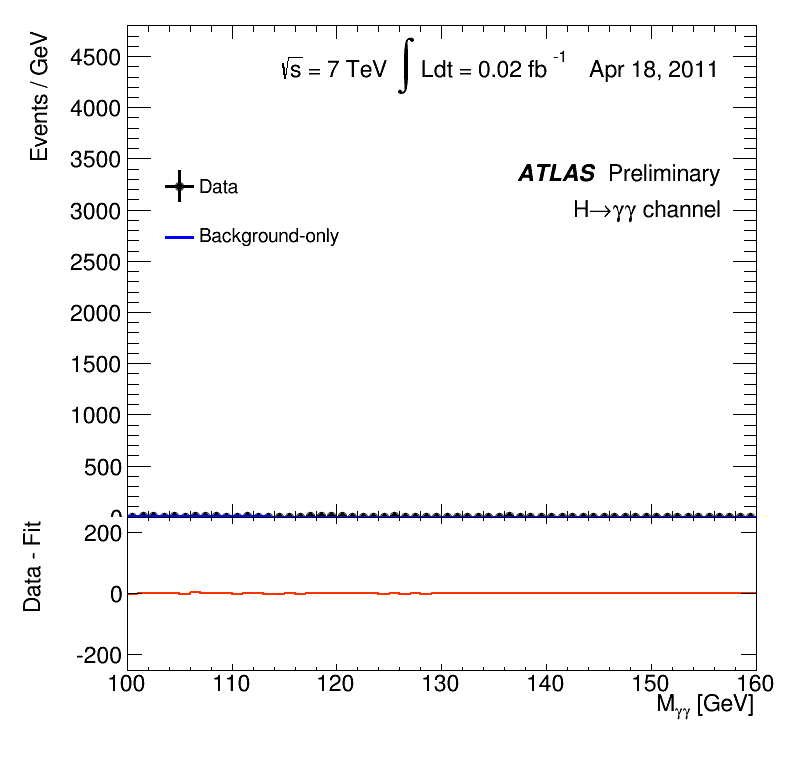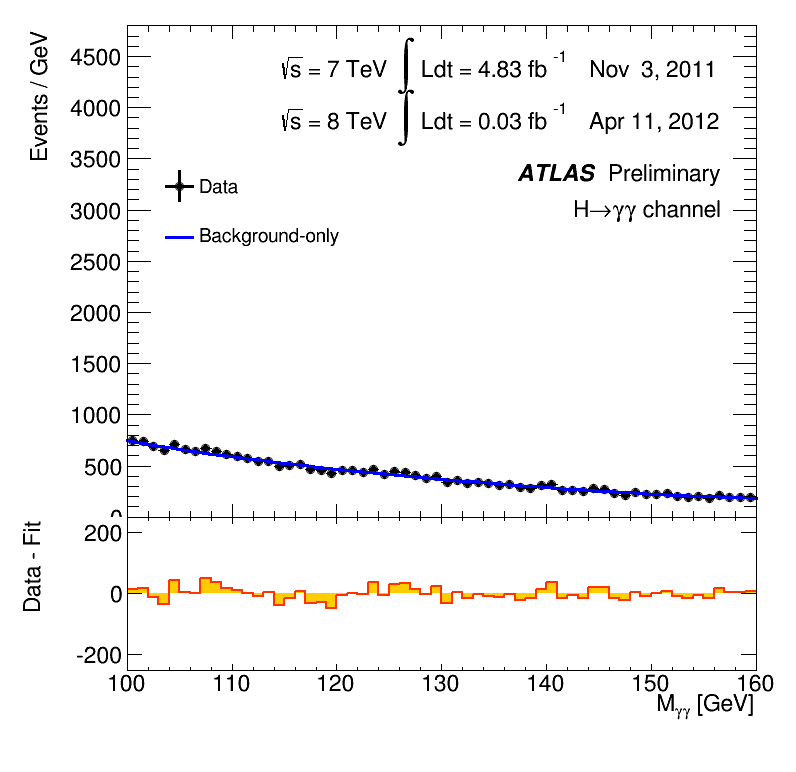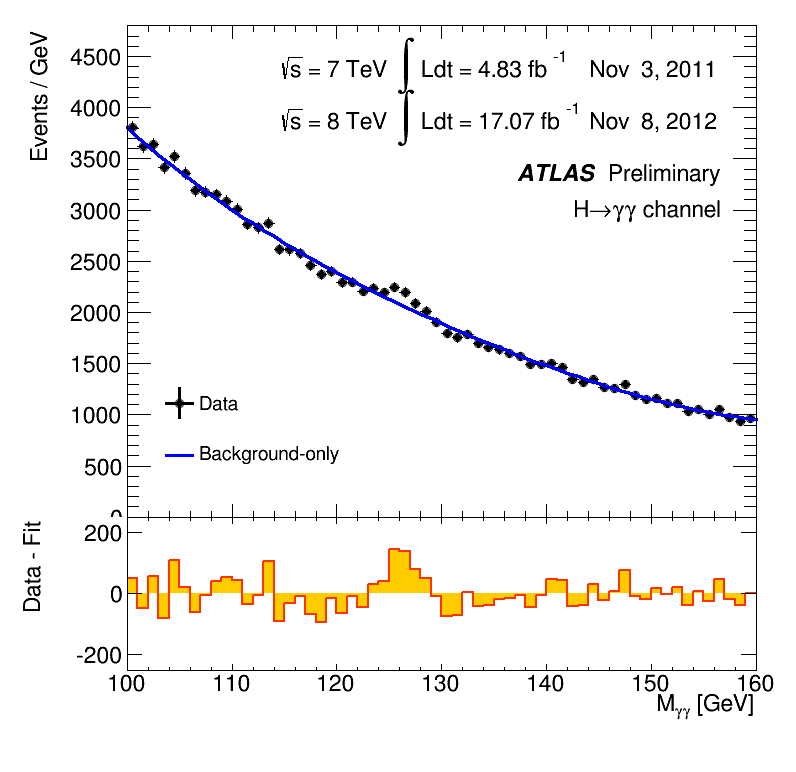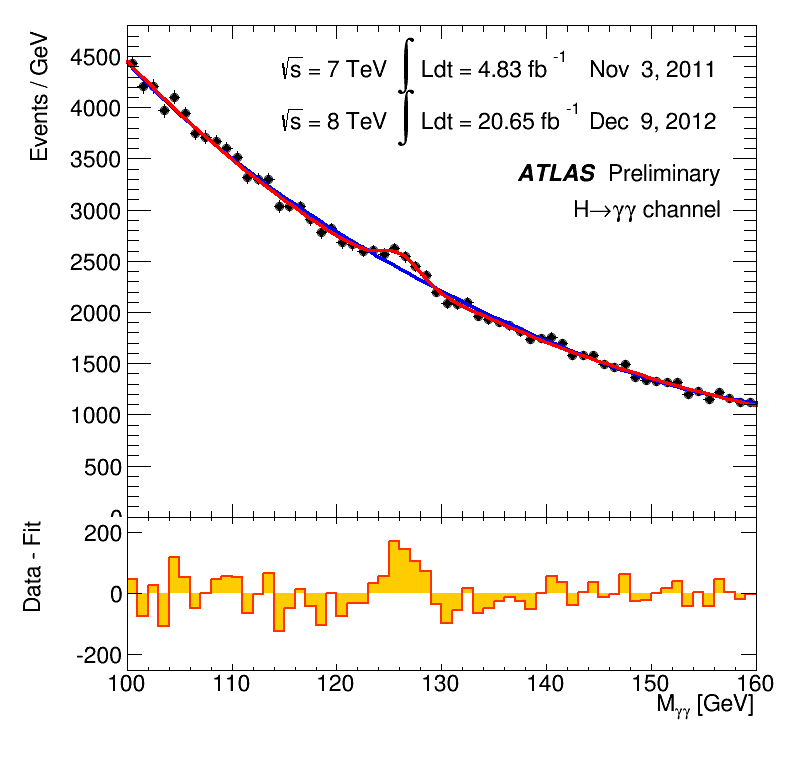
Dabei war der LHC eigentlich genau die Art von Maschine, von der man sich Neues erhoffen konnte. Ein Teilchenbeschleuniger mit deutlich höherer Energie als alle vorangehenden Teilchenbeschleuniger – das war zumindest in früheren Fällen oft der Auftakt für unerwartete Entdeckungen gewesen. Die Experimente an einem solchen Beschleuniger sind so ausgelegt, dass sie auch unerwartete Teilchen nachweisen können. Solche Teilchen machen sich typischerweise als unerwartete Buckel in einer Häufigkeitsverteilung von Teilchenreaktionen bemerkbar. Die Menschen vom ATLAS-Experiment haben das in diesem animierten GIF für die Entdeckung des Higgs-Teilchens schön dargestellt – dargestellt ist, wie sich die Verteilungskurve (Ereignisse in jedem Energiebereich dieser spezifischen Teilchenreaktion) mit zunehmender Messdauer bis Dezember 2012 immer deutlicher zeigt. Der Unterschied der blauen Kurve (Hintergrundreaktionen) und der roten Kurve (Reaktionen inklusive der Nachweisreaktionen für das Higgs-Teilchen) ist gerade der besagte Buckel:
Auf gleiche Weise könnte man an solch einem Teilchenbeschleuniger auch gänzlich unerwartete neue Teilchen nachweisen. Die Hoffnungen dafür waren hoch. Da war zum Beispiel die sogenannte Supersymmetrie, mit deren Hilfe man eine Klasse von Erweiterungen des Standardmodells beschreiben konnte, die was eine Reihe grundlegender theoretischer Eigenschaften anging eleganter waren als das herkömmliche Standardmodell. Im wesentlichen verdoppelt die Supersymmetrie den Teilcheninhalt des Standardmodells dabei auf einen Schlag – den herkömmlichen Teilchen wird dabei jeweils ein “Superpartner” mit ganz bestimmten Eigenschaften zur Seite gestellt. Hätte man solche Superpartner am LHC gefunden, und damit Hinweise auf eine supersymmetrische Version des Standardmodells, die Theoretiker*innen wären ekstatisch gewesen.
Und ob nun als Teil eines supersymmetrischen Modells oder in anderer Weise: Ein neuentdecktes Teilchen, das die richtigen Eigenschaften gehabt hätte, die in der Astronomie indirekt nachgewiesene Dunkle Materie zu erklären, wäre natürlich auch eine Sensation gewesen.
Oder aber ein ganz anderes Teilchen – why not?
Tatsächlich aber scheint dieser Brute-Force-Neuentdeckungs-Ansatz mit dem LHC bislang nicht gelungen zu sein. Wenn in dem betreffenden Energiebereich keine neuen, unbekannten Teilchen sind, kann man sie nun einmal auch nicht finden.
Teilchenphysik mit Präzision statt geballter Energie
Es gibt aber außer dem Brute-Force-Ansatz noch eine weitere Möglichkeit, neue Teilchen zu entdecken. Das hängt mit einer Besonderheit von Quantenfeldern zusammen: Bei komplexeren Teilchenreaktionen tragen in gewisser Weise alle Teilchen, die geeignete Eigenschaften aufweisen, zum Endergebnis bei – selbst wenn jene Teilchen gar nicht als Endprodukte der Reaktion auftauchen. Auch bei der Messung solcher Teilchenreaktionen kann man daher unerwartete neue Teilchen finden, dann nämlich, wenn das experimentell gemessene Ergebnis nur dadurch zu erklären ist, dass dort unbekannte Teilchen zur Reaktion beitragen.
Bereits um die Wechselwirkung eines Elementarteilchens mit Photonen, den Teilchen des elektromagnetischen Feldes, richtig beschreiben zu können, muss man solche komplexeren Teilchenreaktionen berücksichtigen. In den üblichen Einheiten ist das sogenannte magnetische Moment eines Elementarteilchens wie eines Elektrons oder seines schwereren Cousins, des Muons, dimensionslos und hat auf der einfachsten Beschreibungsebene (freie Teilchen, keine Wechselwirkungen) gerade den Wert 2. Nimmt man jene komplexeren Teilchenreaktionen hinzu, dann ergibt sich eine Abweichung des magnetischen Moments g vom Wert 2, sprich: g minus 2, g–2.
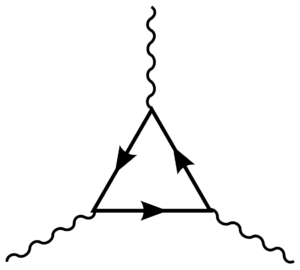
Strebt man eine entsprechende Genauigkeit an, dann sind die Rechnungen, die man durchführen muss um herauszubekommen, was das Standardmodell der Elementarteilchen denn nun für g–2 vorhersagt, nichts anderes als brutal. Selbst wenn man erst einmal nur elektromagnetische Wechselwirkungen mit einbezieht (Quantenelektrodynamik, QED) werden die Rechnungen rasch unübersichtlich. Für solche Rechnungen gibt es eine einfache graphische Notation, bei der die einzelnen Beiträge zu einer Reaktion mit Hilfe sogenannter Feynmandiagramme dargestellt werden, in denen Teilchen als Linien und Wechselwirkungen als Knotenpunkte repräsentiert werden. Hier ist ein immer noch recht einfaches Diagramm, für die Wechselwirkung von drei Photonen:
Für die Übersetzung eines solchen Diagramms in einen mathematischen Ausdruck, aus dem sich letztlich die Wahrscheinlichkeit einer bestimmten Teilchenreaktion berechnen lässt, gibt es feste Regeln. Die Feynman-Diagramme sind sozusagen die grafische Kurzform; die Rechnungen führt man dann aus, nachdem man ein Diagramm mithilfe der Regeln in eine mathematische Formel übersetzt hat.
Das wird immer komplizierter, je genauer man rechnet: In der ersten Genauigkeitsstufe für g–2 muss man nur ein einziges Diagramm berechnen. In der zweiten Genauigkeitsstufe (“zwei Loops”) sind es dann schon 9 Diagramme, bei Stufe drei (“drei Loops”) bereits 72, bei Stufe vier dann 891 Diagramme. Teilchenphysik-Theorie als Fleißarbeit. Von diesen Termen lassen sich dann leider auch nur noch wenige direkt berechnen. Für die anderen muss man numerische Näherungsrechnungen anstellen.
Und das war bislang nur die Quantenelektrodynamik (QED), also die Quantentheorie elektromagnetischer Wechselwirkungen. Will man auch die Reaktionen, an denen Quarks und aus ihnen zusammengesetzte Gebilde (“Hadronen”) beteiligt sind, einbeziehen – und das muss man für die angestrebte Genauigkeit! – dann wird es noch um einiges komplizierter.
Denn selbst die heroische Rechnung mit 891 Diagrammen war noch ein Näherungsverfahren, das als Störungsrechnung bezeichnet wird, und das man bei vergleichsweise schwachen Wechselwirkungen anwenden kann. Dabei geht man näherungsweise davon aus, dass die betreffenden Teilchen zwischen gelegentlichen Interaktionen (eben den Knoten der Linien) frei umherfliegen. Bei Quarks und der starken Kernkraft, über die sie wechselwirken, reicht diese Art von Näherung für die g–2-Rechnungen nicht aus. Da muss man das, was da vorgeht, dann tatsächlich so simulieren, dass auch gebundene Zustände berücksichtigt werden können. Dafür gibt es Elementarteilchen-Simulationen, in denen die Raumzeit nicht als Kontinuum, sondern als diskretes Gitter simuliert wird – ähnlich so, wie ein Schachbrett die Ebene in ein regelmäßiges Muster endlich großer Felder zerlegt. Solche Gitter-Rechnungen können Abschätzungen für die nötigen Reaktions-Beiträge liefern, aber das ist alles andere als einfach.
g–2 für Myonen: Resultat und Vergleiche von Theorie und Experiment
Das ist der Kontext der Resultate, die Fermilab heute (bzw. es ist jetzt schon recht spät geworden: gestern, am 7. April 2021) bekanntgegeben hat. Hier ist der formschöne Speicherring, an dem die Messungen stattfanden:
Die Vorgeschichte und Details kann man vermutlich spätestens morgen in der Tagespresse nachlesen. Mir geht es hier nur um die Grundlagen. Da kann man jetzt zunächst einmal sagen: OK, den Standards der Teilchenphysik nach war das jetzt noch keine echte Entdeckung einer Abweichung vom Standardmodell. Dafür haben sich die Teilchenphysiker*innen ein statistisches Kriterium namens “5 sigma” gegeben, vereinfacht gesagt: Die Wahrscheinlichkeit, dass das, was da als neues Ergebnis präsentiert wird, stattdessen auf zufällige Fluktuationen zurückgeht, muss unterhalb eines bestimmten Grenzwerts liegen. Diese Grenze ist bei den jetzt vorgestellten Ergebnissen noch nicht ganz erreicht (stattdessen 4.2 sigma, wenn man vorangehende ältere Messungen dazunimmt).
Nun gut, kann man sagen. Erstens misst das Experiment ja noch ein paar Jahre lang weiter. Seien wir mal optimistisch und nehmen wir an, dass die 5-sigma-Grenze dann überschritten wird.
Aber ist das dann auch ein Hinweis auf neue Physik? Dem Augenschein nach erst einmal ja – so wie das Ergebnis jetzt präsentiert wird, ist es eine klare Abweichung von den Vorhersagen der Standardmodell-Rechnungen. Und eine naheliegende Erklärung dafür wäre tatsächlich: Es gibt noch mehr Teilchen als die des Standardmodells. Noch unbekannte Teilchen, die bei den komplexen Teilchenreaktionen eine Rolle spielen und damit das Ergebnis verändern. Das wäre natürlich sehr spannend, denn damit wäre die lange Durststrecke, auf der das Standardmodell immer wieder bestätigt wird, aber es keine Anzeichen darauf gibt, was jenseits des Standardmodells liegen könnte, im besten Falle vorbei.
Allerdings ist ausgerechnet heute ein Artikel in der Zeitschrift Nature erschienen (und die zeitliche Übereinstimmung ist soweit ich weiß zufällig), der zeigt, wo eine deutlich weniger aufregende Lösung liegen könnte. (Ich bin auf den Artikel in diesem populärwissenschaftlichen Artikel von Natalie Wolchover zum g–2-Ergebnis aufmerksam geworden.) Dort wird genau für die vertrackten Gitter-Rechnungen für g–2 ein etwas anderer Ansatz gewählt, und das Ergebnis verschiebt sich damit deutlich in Richtung der vermeintlich anomalen Messergebnisse. Um tatsächlich eine Abweichung von theoretischer Vorhersage und experimenteller Messung festzustellen, muss man nun aber beides hinreichend sicher kennen. Die neuen theoretischen Rechnungen lassen zumindest Skepsis aufkommen, ob das bei diesem speziellen Vergleich bereits der Fall ist.
Vielleicht ist das neue Ergebnis also letztlich auch wieder nur eine Bestätigung des Standardmodells – zumindest sobald die Standardmodell-Rechungen hinreichend genau ausgeführt wurden. Komplett subjektiv halte ich das nach den eher enttäuschenden Teilchenphysik-Entwicklungen der letzten Jahrzehnte für durchaus wahrscheinlich. Aber in einer Ecke meines Gehirns ist vermutlich trotzdem noch eine kleine fahnenschwenkende Teilchenphysik-Fan-Region, die hofft, dass es diesmal anders ist. Dass es ausnahmsweise einmal keine Bestätigung gibt, sondern einen Hinweis auf neue, spannende Physik. Und ganz ausgeschlossen ist das beim jetzigen Stand ja in der Tat nicht.



Zitat obiger Beitrag:
Ja, wobei die Entdeckung einer Neutrinomasse ab 1998 eben keine Bestätigung, sondern eine unerwartete Neuentdeckung war. Die Neutrinooszillationen, die durch diese Masse möglich wurden erklärten aber die alte Entdeckung, dass es in den von der Sonne kommenden Neutrinos zuwenig Elektronneutrinos gab.
Fazit: Es ist äusserst relativ von Ereignislosigkeit in der jüngsten Teilchenphysik zu sprechen, wenn es noch nach 1998 Entdeckungen gab, die vom Standardmodell nicht vorausgesagt wurden. Klar sind 20 Jahre ohne Überraschungen in der Teilchenwelt eine relativ lange Zeit wenn man die Doktoranden-/Postdoktoranden -Zeitspanne von Physikern als Massstab nimmt. Es ist aber eine kurze Zeit, wenn man nur schon berücksichtigt was alles im Leben von heute noch lebenden, bekannten Physikern wie Steven Weinberg, Frank Wilczek oder Gerardus ’t Hooft in der Physik geschah.
Der Nature-Artikel Leading hadronic contribution to the muon magnetic moment from lattice QCD vom 7.April 2021 berichtet darüber, dass das jetzt gemessene magnetische Moment des Müons mit dem Standardmodell übereinstimmt. Dazu wurden mittels Lattice-QCD ab initio Berechnungen durchgeführt. In der Kurzzusammenfassung liest man (Zitat, übersetzt von DeepL):
Mit andern Worten: Das jetzt gemessene magnetische Moment des Müons entspricht genau den Erwartungen bei Anwendung des Standardmodells, wenn man nur „richtig“ rechnet. Die vorher verwendeten „dispersiven Methoden“ zur Berechnung des magnetischen Moments scheinen also irgendwo versagt zu haben.
Oder noch kürzer: Aufregung um nichts, wobei das Nichts wohl ein simpler Rechnungsfehler ist/war.
Das ist genau der Artikel, auf den ich im Haupttext eingehe; bei Ihnen klingt es so, als wäre das eine Zusatzinformation – warum? Und nein, simpel ist bei den entsprechenden Rechnungen nichts. Und auch das als “Rechnungsfehler” abzutun ist irreführend. Das sind wie beschrieben hochkomplexe Rechnungen, bei denen man bestimmte Zusatzannahmen machen muss, um überhaupt ein Ergebnis zu erhalten. Da bessere Methoden zu finden ist ganz einfach wissenschaftlicher Fortschritt; den vorigen Rechnungen zu unterstellen, sie hätten “versagt” ist unangebrachte Schwarzweißmalerei.
Warum? Ich wollte nur noch klarer herausstellen, dass nichts Neues entdeckt wurde, sondern es sich mehr um Theorie interne Probleme handelt,
Für mich lesen sich Ihre Kommentare oft in genau der hier vorliegenden Weise merkwürdig. Kein direkter Bezug auf den Hauptartikel, stattdessen mit extern verlinkter Quelle (nicht selten Wikipedia, hier andere populärwissenschaftliche Beiträge) Zusatzinformationen. Das hat für mich immer den Duktus einer Ergänzung, im Sinne von: das hier fehlte noch. Was dann eben befremdlich ist, wenn genau das scheinbar ergänzte eine der Hauptaussagen des Blogbeitrags selbst ist.
Der Quanta-Artikel ‘Last Hope’ Experiment Finds Evidence for Unknown Particles geht auf die unterschiedlichen Berechnungsresultate der beiden theoretischen Ansätze ein und besagt im Kern, dass die Theoriegruppe, welche zu einem abweichenden Wert kommt eigentlich mit etablierten Methoden arbeitet und nicht falsch liegen darf, denn wenn die Berechnung falsch wäre, würde das bedeuten, dass man etwas übersehen hat, was man eigentlich nicht übersehen kann.
Mir scheint der Titel des Quanta-Artikel jedoch so oder so irreführend, gibt es doch inzwischen Hinweise auf Verletzung der Leptonenuniversalität am LHCb-Experiment. Es gibt also noch weitere Hoffnung auf neue Physik.
Ich bin da optimistisch: Irgendwann findet man neue Physik. Sogar mit den existierenden Beschleunigern.
Markus Pössel schrieb (08. Apr 2021):
> […] In den üblichen Einheiten ist das sogenannte magnetische Moment eines Elementarteilchens wie eines Elektrons oder seines schwereren Cousins, des Muons, dimensionslos und hat gerade den Wert 2.
Dem ist entgegenzusetzen …
… dass der gyromagnetische Faktor des Spins eines Elementarteilchens,
g_s, oder im gegebenen Kontext kurzg, als das dimensionslose, reell-wertige, positive Verhältnis zwischen dem magnetischen Moment des Elementarteilchens “an sich” (das dem Elementarteilchen “aufgrund seines Spins” zugeschrieben wird), konventionell normalisiert mit (ins Verhältnis gesetzt zu) der Hälfte seiner elektromagnetischen Ladung,q / 2, und dem Spin (Eigendrehimpuls) des Elementarteilchens “an sich”, konventionell normalisiert mit seiner Massem, definiert ist;und dass dessen Wert sowohl für Elektronen als auch für Myonen zwar rund 2 beträgt, aber, wie 1946 entdeckt und mit zunehmender Genauigkeit gemessen wurde, sich doch (jeweils) signifikant von 2 unterscheidet (nämlich jeweils größer als 2 ist).
Soweit entsprechende Werte auch vom betreffenden Standardmodell zusammengefasst (“vorhergesagt”) sind, was allerdings anspruchsvolle Berechnungen und gewisse Unsicherheiten bei deren Bewältigung beinhaltet, stimmen diese jedenfalls “auf etliche Stellen nach dem Komma” mit den gemessenen Werten überein (und weichen jeweils mit großer Signifikanz von “genau 2” ab).
Unter bestimmten vereinfacht modellierenden Annahmen lässt sich jedoch der genaue Wert
g_s_vereinfacht = 2herleiten; deshalb ist …
> […] also vor allem die Abweichung des magnetischen Moments g vom Wert 2, sprich: g minus 2, g–2 [interessant].
> […] Selbst wenn man erst einmal nur elektromagnetische Wechselwirkungen mit einbezieht (Quantenelektrodynamik, QED) […] die einzelnen Beiträge zu einer Reaktion mit Hilfe sogenannter Feynmandiagramme dargestellt werden, in denen Teilchen als Linien und Wechselwirkungen als Knotenpunkte repräsentiert werden. Hier ist ein immer noch recht einfaches Diagramm, für die Wechselwirkung von drei Photonen: [ siehe Bild im obigen SciLogs-Beitrag ]
Das oben gezeigte Feynmandiagramm stellt jedoch ausgerechnet einen außerordentlich unbedeutenden Beitrag dar …
Was übrigens auch damit verbunden ist, dass die Berechnung der Beiträge einiger (QED-Feynman-)Diagramme, die sich entsprechend der dafür geltenden (QED-Feynmandiagramm-Repräsentations-)Regeln mit einer bestimmten Anzahl von Knoten und Linienstücken zeichnen lassen, jeweils ebenfalls so einfach ist, dass sie gar nicht ausdrücklich erwähnt und gezählt werden.
In der Tat, da habe ich offenbar einen nicht unwichtigen Teil des Satzes unterschlagen. Sollte jetzt klarer formuliert sein. Das gezeigte Feynmandiagramm soll nur zeigen, wie ein Feynmandiagramm im Prinzip aussieht. Ich behaupte entsprechend ja auch nirgends, dass es zu den hier beschriebenen komplexen Rechnungen beiträgt.
Markus Pössel schrieb (08.04.2021, 16:44 Uhr):
> In der Tat, da habe ich offenbar einen nicht unwichtigen Teil des Satzes unterschlagen.
Und sich von “den üblichen Einheiten” einschränken lassen, wo es doch physikalisch-universell “nur” um Messgrößen und deren Werte geht.
> Sollte jetzt klarer formuliert sein.
Jedenfalls hoffentlich nicht einfacher formuliert, als es der Klarheit bzw. der Nachvollziehbarkeit zuträglich wäre.
(Aber womöglich geht’s doch noch einfacher, wenn man “so einfach, wie der Klarheit bzw. der Nachvollziehbarkeit zuträglich” anstrebt.)
> Das gezeigte Feynmandiagramm soll nur zeigen, wie ein Feynmandiagramm im Prinzip aussieht.
Dieses Feynmandiagramm leistet das auch, wirkt dabei jedoch … noch bedeutender.
Wobei ich nicht behauptet habe, dass (anteiliges) “2-loop boson-by-boson scattering” ganz unbedeutend wäre —
(offenbar ausschließlich) außerhalb der QED; vgl. Diagramme (b) und (c) in Fig. 1 von [hep-ph:1306.5546].
p.s.
Jedenfalls danke für den obigen SciLogs-Beitrag, als Ablenkung von Spiegel-Schubsern, Panzer-Biegern und sonstigen Theorie-Testern …
Erstaunlich ist in diesem Zusammenhang der SPON-Artikel zum Muon-(g–2)-Experiment Neue Erkenntnisse in der Teilchenphysik Kundschafter ins Unbekannte.
Kein Wort von widersprüchlichen Messwertvorhersagen, sondern nur gerade die Aussage, es gebe – wie schon vor 20 Jahren – eine Abweichung vom erwarteten Wert beim g-Faktor des Müons und wenn diese jetzt genügend gross sei bedeute es einen Hinweis auf noch unentdeckte Teilchen. Nun, der SPON-Artikel erschien am 7.4.2021 und möglicherweise noch vor dem Artikel im Quanta-Magazin. Oder der Autor hat den Quanta-Artikel nicht gelesen oder er war informiert wollte aber den Artikel nicht mit Widersprüchlichkeiten „verderben“.
Klassischer Fall, ein vorausberechnetes Ergebnis stimmt nicht mit dem gemessenen Ergebnis überein. Die achte Nachkommstelle falsch,, das ist schon signifikant.
Spontan habe ich auf ein noch nicht entdecktes Teilchen getippt, das den Unterschied erklärt. Ich nenne es Delta-Teilchen. (wenn der Name noch nicht vergeben ist )
Insbesondere in Verbindung mit der „g=2 erzeugenden“ Dirac-Gleichung gibt es ein fundamentales „Näherungs-Problem“ erster Instanz für das Myon. In der Dirac-Gleichung wird zur Berechnung von g = 2 vorausgesetzt, daß das zu beobachtende „Dirac-Teilchen“ sich langsam bewegt, daß ist im Falle der experimentellen Bestimmung des magnetischen Moments des Myons, welches sich im Speicherring mit einer relativistischen Geschwindigkeit (Ekin ~ 30 · E0!) bewegt definitiv nicht der Fall. Aus diesem Grunde kann die Dirac-Gleichung formal logisch für das Myon gar kein Ergebnis für g liefern. Ohne g = 2 (Dirac-Gleichung) existiert aber kein „normales“ magnetisches Moment des Myons und folgerichtig ist das „anomale“ magnetische Moment des Myons ohne („normale“) Referenz gegenstandslos. Will man also mittels Dirac-Gleichung eine Aussage über das (normale) magnetische Moment des Myons machen, dann kommen nur Experimente in Frage, in denen sich das Myon „langsam“ bewegt.
Warum sollte es diese Begrenzung auf “langsame” Bewegung geben? Die Dirac-Gleichung ist doch im Gegenteil die speziell-relativistische Gleichung für freie Materieteilchen, die entsprechend alle Geschwindigkeitsbereiche v<c für solche Teilchen abdeckt. Korrekturen ergeben sich aus der Wechselwirkung jener Teilchen, nicht per se aus hoher Geschwindigkeit.
hwied schrieb (09.04.2021, 10:20 Uhr):
> [… Modell-]berechnetes Ergebnis stimmt nicht mit dem gemessenen Ergebnis
… also dem aus Beobachtungsdaten durch Anwendung des festgesetzten Messoperators (d.h. Auswertungs-Algorithmus) berechneten Ergebnis …
> überein. Die achte Nachkommstelle falsch,, das ist schon signifikant.
Jedenfalls sofern sogar mindestens auch noch die neunten Nachkommastellen beider Ergebnisse jeweils signifikant (und in diesem Sinne auch jeweils richtig berechnet) sind bzw, wären.
> Spontan habe ich auf ein noch nicht entdecktes Teilchen getippt, das den Unterschied erklärt. Ich nenne es Delta-Teilchen. (wenn der Name noch nicht vergeben ist )
Der ist allerdings schon vergeben; sogar mehrfach, und auch nicht unbedingt spontan und beliebig, sondern mit recht gut erkennbarem Grund.
Nachdem ich gerade gelernt habe, dass es sogar schon mal ein “iota particle” gab, fällt mir spontan aus dem griechischen Alphabet nur das “epsilon” als Symbol ein, das im Bedarfsfalle noch zu haben wäre. Auch gut: “das Errareon” …
p.s. — Markus Pössel schrieb (08. Apr 2021):
> […] Zu einer ganzen Reihe von Teilcheneigenschaften, nämlich zur elektrischen Ladung und deren teilchenphysikalischen Verwandten, trifft das Standardmodell mathematisch sehr elegante Aussagen; all jene Eigenschaften ordnen sich dort in ein großes Schema ein.
Übrigens schließt das “große Schema” des Standardmodells dabei auch Aussagen zur (geometrisch-kinematischen) Teilcheneigenschaft “Spin” ein; und (folglich) auch zu “Statistik”.
> Zu den Massen? Keine grundlegenden Vorhersagen. […] eine grundlegende Schwäche jenes Standardmodells.
Abgesehen von der grundlegenden Erwartung, dass die Massen (ggf. einschl. Zerfallsbreiten) aller jeweils durch die o.g. Eigenschaften identifizierten (Elementar-)Teilchen gleich sind — waren und bleiben; und zwar mit den (mittlerweile und immer noch zunehmend genau) gemessenen und tabulierten Werten.
(Das erlaubt, bestimmte “verfeinerte” Modelle aufzustellen; Stichwort “Koide”, z.B.; was wiederum nahelegen könnte, bestimmte weitergehende Messgrößen zu definieren.)
Weitermachen oder Abbrechen
Wenn das Standardmodell immer wieder bestätigt wird und nichts wirklich Neues herauskommt, dann könnte man folgern, dass die entsprechende Forschung aufgegeben werden soll. Tatsächlich spricht sich Sabine Hossenfelder gegen neue Teilchenbeschleuniger aus und sagt etwa im Video Particle Physicists Continue Empty Promises : „Today I want to tell you, how particle physicists are wasting your money“. Sie meint, Teilchenphysiker hätten keine überzeugenden Argumente mehr für neue Teilchenbeschleuniger, sie schalteten vielmehr als wissenschaftliche Arbeiten getarnte Anzeigen/Werbebotschaften für ihre geplanten neuen Riesenbeschleuniger.
Ich meine dazu: wenn neue Beschleuniger nur einfach grössere Maschinen wären und sie nichts garantiertes, nichts neues zu Wissenschaft und Technologie beitragen könnten, dann könnte man die Ausgaben dafür wohl nicht rechtfertigen. Doch das ist nicht der Fall. Schon der Bau des LHC bedeutete auch das Sammeln von Erfahrung mit dem Bau von supraleitenden Magneten und jetzt wird im CERN bereits die nächste Generation von Hochtemperatursupraleitern, die REBCO-Technologie erforscht und entwickelt. Überhaupt sind Teilchenphysiker offen für alle neuen Technologien, die ihnen etwas bringen. Machine Learning wird etwa für die Datenauswertung eingesetzt.
Im übrigen ist es nicht so, dass das Standardmodell mit Sicherheit in sich abgeschlossen ist. Vielmehr sprechen dunkle Materie und dunkle Energie dafür, dass es noch mehr Teilchen geben muss als die 17, welche das Standardmodell gegenwärtig vorsieht.
Allerdings müssen es nicht unbedingt Riesenbeschleuniger sein, welche uns bei der Erforschung dunkler Materie weiterbringen. Es sind allerdings nicht selten Teilchenphysiker, welche neue Methoden bei der Suche nach dunkler Materie vorschlagen. Der Artikel Sensitive qubit-based technique to accelerate search for dark matter etwa beschreibt eine neue Methode um mittels hypersensitiven quantenphysikalischen Methoden nach Axionen und dunklen Photonen zu suchen – zwei Kandidaten dunkler Materie. Und es sind Physiker des Fermi Lab, also eines Teilchenbeschleunigerstandorts, welche diese Methode entwickelt haben.
Mit andern Worten: Teilchenphysiker haben der Welt der Wissenschaft und Technologie noch viel mehr zu bieten als nur die Anwendung roher Beschleunigerkraft.
Sehr geehrter Herr Pössel,
so lautet der letzte Absatz Ihres Artikels:
Vielleicht ist das neue Ergebnis also letztlich auch wieder nur eine Bestätigung des Standardmodells – zumindest sobald die Standardmodell-Rechungen hinreichend genau ausgeführt wurden. Komplett subjektiv halte ich das nach den eher enttäuschenden Teilchenphysik-Entwicklungen der letzten Jahrzehnte für durchaus wahrscheinlich. Aber in einer Ecke meines Gehirns ist vermutlich trotzdem noch eine kleine fahnenschwenkende Teilchenphysik-Fan-Region, die hofft, dass es diesmal anders ist. Dass es ausnahmsweise einmal keine Bestätigung gibt, sondern einen Hinweis auf neue, spannende Physik. Und ganz ausgeschlossen ist das beim jetzigen Stand ja in der Tat nicht.
= = =
M. E. bedarf es wegen der Abweichung keine neue Physik, es müsste lediglich der g-Faktor
für das Elektron neu definiert werden.
Eine Berechnung dazu gibt es unter: http://www.4-e-inigkeit.info/Myon.html
Vonnöten wäre aber wohl eine Überarbeitung der Physik-Grundlagen.
M. f. G.
Neu definieren wäre ja gerade neue Physik. Wobei eine Ableitung, die da eine ernsthafte Lösung bieten kann, ja schon eng an das anschließen muss, was wir bereits wissen – eben an die Struktur des Standardmodelle mit seinen höchst genau bestätigten Aussagen zu Wirkungsquerschnitten.