Astronomisches Grundwissen 8: Kosmische Strahlung, Gravitationslinsen, großräumige Struktur
BLOG: RELATIV EINFACH

Dieser Blogbeitrag ist Teil einer zehnteiligen Serie, die astronomisches Grundwissen vermitteln soll. Alle Beiträge auf einen Blick:
- Nachthimmel, Lichtverschmutzung, Beobachtungen
- Bilder, Spektren, Einfluss der Atmosphäre, Entfernungen
- Unser Sonnensystem
- Die Sonne und andere Sterne
- Das Leben der Sterne
- Exoplaneten
- Die Milchstraße und andere Galaxien
- Kosmische Strahlung, Gravitationslinsen, großräumige Struktur
- Kosmische Expansion und Urknall
- Galaxienentwicklung, Dunkle Energie und Ausblick
Näheres zur Motivation der Serie und dazu, was ich unter astronomischem Grundwissen verstehe, findet sich hier in Teil 1.
Kosmische Teilchenstrahlung und kosmische Gammastrahlung
Aus dem Weltraum erreicht uns nicht nur elektromagnetische Strahlung, sondern auch Teilchenstrahlung, die sogenannte kosmische Strahlung. Überwiegend sind dies Protonen. Einige davon haben Energien, die weit (genauer: um Faktoren von z.B. deutlich mehr als einer Million) hinter sich lassen, was die irdischen Teilchenphysiker in ihren Beschleunigeranlagen erreichen können.
Einige kosmische Strahlungsquellen sind wohlbekannt, etwa Sonnenwind und Sonnenflares (dazu vgl. Teil 4). Bei den Teilchen, die uns aus größeren Entfernungen erreichen, zum Teil offenbar sogar von außerhalb unserer Heimatgalaxie, ist die Lage weniger klar. Schockfronten nahe Supernovae kommen in Frage; gerade zu diesem Thema gab es in den letzten Monaten einige Fortschritte zu vermelden (vgl. hier und hier). Für denjenigen Teil der Teilchen, die uns von außerhalb unserer Heimatgalaxie erreichen, sind außerdem noch Aktive Galaxienkerne oder Gammastrahlenausbrüche im Rennen. Insbesondere für die Teilchen mit den allerhöchsten Energien (die gesamte Energie eines schnell geworfenen Balls, konzentriert auf ein subatomares Teilchen) sind sowohl die Quellen als auch der Beschleunigungsmechanismus unklar. Möglicherweise ist hier sogar ganz neue Physik im Spiel: So könnten etwa exotische neue Elementarteilchen eine Rolle spielen.
Nachweisen kann man die Teilchen der kosmischen Strahlung, wenn sie mit Atomkernen aus der Erdatmosphäre kollidieren und dabei einen Schauer sogenannter sekundärer Teilchen erzeugen. Mit Teleskopen lässt sich dabei eine Art Nachglimmen beobachten (Fluoreszenz); mit Teilchendetektoren kann man die sekundären Teilchen direkt nachweisen. Die derzeit größte Anlage zum Nachweis kosmischer Strahlung, das Pierre-Auger-Observatorium in Argentinien, benutzt beide Techniken. Aus den kombinierten Daten seiner Teleskope und Detektoren lassen sich die Eigenschaften des ursprünglichen Teilchens recht genau rekonstruieren.
Bei hohen Energien hat auch elektromagnetische Strahlung deutliche Teilcheneigenschaften. Der Nachweis hochenergetischer Gammastrahlung, die auf die Erde trifft, ähnelt dem Teilchennachweis: Ein Mehrfach-Teleskop wie unten im Bild H.E.S.S. (Bild: Max-Planck-Institut für Kernphysik, zu sehen sind zwei von jetzt insgesamt fünf Teleskopen) weist Strahlung nach, die entsteht, weil sich die beim Aufprall von Gammastrahlung auf ein Atmosphären-Atom entstehenden sekundären Teilchen zum Teil schneller als das Licht durch die Luft bewegen (wohlgemerkt: nicht schneller als das Licht im Vakuum, sondern als Licht in Luft).

Die kosmische Gammastrahlung stammt ebenfalls von Supernovaüberresten, Aktiven Galaxienkernen und Gammastrahlenausbrüchen. Weitere Anteile stammen direkt aus der Umgebung von Pulsaren und aus dem Zentrum unserer Heimatgalaxie.
An dieser Stelle gilt es, einer Begriffsverwirrung vorzubeugen. Auch die elektromagnetische Strahlung, die uns aus dem Weltraum erreicht, ist natürlich im Wortsinne “kosmische Strahlung”. Ein bestimmter Teil der elektromagnetischen Strahlung, den wir später noch kennenlernen werden, heißt verwirrenderweise sogar “kosmische Hintergrundstrahlung”. Mit “kosmische Strahlung” ist aber in modernem Sprachgebrauch wirklich nur die Teilchenstrahlung gemeint, die uns aus dem Weltraum erreicht.
Gravitationslinsen
Einsteins Allgemeiner Relativitätstheorie zufolge wirkt die Gravitationsanziehung nicht nur auf Körper, sondern auch auf Licht. Licht, das an einer Masse vorbeifliegt, wird dabei ein wenig in Richtung der Masse abgelenkt.
Erstmals nachgewiesen wurde dieser Effekt durch zwei britische Expeditionen vor fast 100 Jahren. Die ablenkende Masse war hierbei die Sonne; das Licht stammte von weit hinter der Sonne liegenden Sternen. Aufgrund des Ablenkungseffekts schien es, als seien diese Sterne im Vergleich mit ihren eigentlichen Orten am Himmel etwas von der Sonne abgerückt. Dass es zweier Expeditionen und nicht einfach regulärer Beobachtungen bedurfte, lag daran, dass Sterne nahe dem Sonnenrand im Normalfalle vom Sonnenlicht überstrahlt werden. Die beiden Expeditionen führten an Orte, an denen zur Beobachtungszeit eine totale Sonnenfinsternis herrschte. Erst unter diesen seltenen Bedingungen war es möglich, die entsprechenden Sternörter zu bestimmen.
Die Lichtablenkung am Sonnenrand hatte zwar auf den Bekanntheitsgrad der Einsteinschen Relativitätstheorie einen großen Einfluss – damals begann der bis heute anhaltende Rummel um Einstein und seine Theorie. In der Astronomie blieb die Lichtablenkung eine exotische Randerscheinung. Das änderte sich erst in den frühen 1980er Jahren. Damals hielten die sogenannten Gravitationslinsen in die Astronomie Einzug, also Systeme, in denen das Licht eines Himmelsobjekts durch eine zwischen Objekt und Beobachter liegende Masse verzerrt wird.
Entscheidend dafür, wie häufig Gravitationslinsen bestimmten Typs beobachtet werden können, sind die geometrischen Verhältnisse. Sterne sind so klein und selbst innerhalb unserer Galaxie über ein so großes Volumen verteilt, dass es sehr unwahrscheinlich ist, dass zwei davon von der Erde aus gerade die richtige Anordnung haben, dass einer davon als Gravitationslinse für das Licht des anderen wirkt. Bei Galaxien sind die Zahlen-, Größen- und Abstandsverhältnisse im Vergleich dazu deutlich günstiger, so dass es deutlich häufiger zu Gravitationslinsen-Konstellationen kommt. Dementsprechend wurde das Phänomen auch erstmals an Galaxien beobachtet, genauer an einer Galaxie und einem Quasar.
Inzwischen gibt es gerade im Zusammenhang mit Galaxienhaufen Beobachtungen, in denen gleich eine ganze Anzahl von gelinsten Objekten sichtbar und zu interessanten Formen verzerrt sind. Das folgende Bild, aufgenommen mit dem Weltraumteleskop Hubble, zeigt ein schönes Beispiel (Bild: NASA/Andrew Fruchter und das ERO-Team [Sylvia Baggett (STScI), Richard Hook (ST-ECF), Zoltan Levay (STScI)]/STScI).

Im Vordergrund sieht man die Galaxien des Galaxienhaufens Abell 2218, dessen Licht mehr als 2 Milliarden Jahre braucht, um uns zu erreichen. Die länglichen, gebogenen Strukturen sind Bilder weit dahinterliegender Galaxien, deren Licht beim Durchgang durch den Haufen von der Masse der Vordergrundgalaxien verzerrt wurde. Der orangene Bogen oberhalb der Bildmitte ist ein Bild einer Galaxie, deren Licht mehr als 6 Milliarden Jahre zu uns unterwegs war; die bläulichen Bögen sind Bilder von Galaxien, deren Licht sogar knapp 8 Milliarden Jahre oder länger zu uns benötigt hat – einige davon sind mehrfache Bilder ein und derselben Galaxie, zu sehen an verschiedenen Stellen des Galaxienhaufens!
 Solche Gravitationslinsen können als eine Art natürlicher Teleskope wirken, dank derer Astronomen sonst nicht zugängliche Details ferner Galaxien kartieren können. Bei der geringen Wiedergabegröße des obigen Bildes sind sie zwar nicht zu sehen; auf dem vergrößerten Ausschnitt rechts dagegen schon (Bild: ESA, NASA, Richard Ellis [Caltech, USA] and Jean-Paul Kneib [Observatoire Midi-Pyrénées, France]): Zwei rötliche Bilder ein und derselben Ur-Galaxie, deren Licht 13,4 Milliarden Jahre benötigt hat, um uns zu erreichen. Ohne den Gravitationslinseneffekt wäre es unmöglich, diese Galaxie zu beobachten.
Solche Gravitationslinsen können als eine Art natürlicher Teleskope wirken, dank derer Astronomen sonst nicht zugängliche Details ferner Galaxien kartieren können. Bei der geringen Wiedergabegröße des obigen Bildes sind sie zwar nicht zu sehen; auf dem vergrößerten Ausschnitt rechts dagegen schon (Bild: ESA, NASA, Richard Ellis [Caltech, USA] and Jean-Paul Kneib [Observatoire Midi-Pyrénées, France]): Zwei rötliche Bilder ein und derselben Ur-Galaxie, deren Licht 13,4 Milliarden Jahre benötigt hat, um uns zu erreichen. Ohne den Gravitationslinseneffekt wäre es unmöglich, diese Galaxie zu beobachten.
Aus dem Gravitationslinseneffekt lassen sich außerdem Rückschlüsse auf die Massenverteilung ziehen, deren Einfluss das Licht ablenkt. Das ist als direkter Massennachweis sehr spannend, denn es erlaubt den Nachweis und die Kartierung der Dunklen Materie, die sich eben nur durch ihre Schwerkraft bemerkbar macht. Ein bekanntes Beispiel ist der Bullet Cluster, den die folgende Falschfarben-Abbildung zeigt (Bild: X-ray: NASA/CXC/CfA/M.Markevitch et al.; Optical: NASA/STScI; Magellan/U.Arizona/D.Clowe et al.; Lensing Map: NASA/STScI; ESO WFI; Magellan/U.Arizona/D.Clowe et al.).

In der herkömmlichen Interpretation (sprich: für alle außer den in Teil 7 erwähnten Astronomen, die anstelle Dunkler Materie lieber eine modifizierte Schwerkraft hätten) zeigt dieses Bild der Kollision zweier Galaxienhaufen folgendes: Während das Gas in jedem der beiden Haufen bei der Kollision zusammengeschoben wurde wie die Knautschzone zweier Autos (Röntgenlicht; in dieser Aufnahme rosarot) sind die Anteile Dunkler Materie der beiden Haufen, die ja außer über die Schwerkraft nicht miteinander wechselwirken, im wesentlichen ungestört durcheinander durchgerauscht (die Rekonstruktion ihrer Massenverteilung, im Bild lila-blau dargestellt, geschieht über den Gravitationslinseneffekt). Dies ist ein starkes Indiz dafür, dass da tatsächlich kaum wechselwirkende Materie ist, eben die Dunkle Materie.
Auf kleineren Skalen, nämlich innerhalb unserer Milchstraße, wird der sogenannte Mikrolinseneffekt interessant. Wenn ein Brauner Zwerg, ein Schwarzes Loch oder auch ein leuchtschwächerer Stern aus Sicht eines irdischen Beobachters vor einem fernen Stern vorbeiziehen, sieht man zwar keine Gravitationslinsen-Bögen, aber das Licht des fernen Sterns wird kurzzeitig gebündelt, und der Stern scheint derweil aufzuleuchten. So haben sich Astronomen z.B. auf die Suche nach nicht selbst leuchtenden Objekten in unserer Galaxie gemacht, Schwarzen Löchern etwa.
Auch insgesamt 18 Exoplaneten (Stand März 2013) sind auf diese Weise entdeckt worden – als kleines “Extra-Aufleuchten” neben dem viel stärkeren, durch die Masse ihres Muttersterns verursachten Mikrolinseneffekt. Im Vergleich mit anderen Nachweismethoden ist diese hier von den Eigenschaften des Planeten weitgehend unabhängig. Sie kann daher verwendet werden, um die Gesamtzahl an Exoplaneten abzuschätzen. Derzeitiger Stand ist, dass es in unserer Heimatgalaxie mehr Planeten geben dürfte als Sterne.
Nicht zuletzt ist inzwischen auch die Lichtablenkung durch die Masse der Sonne wieder aktuell – aber nicht mehr als Nachweis des Gravitationslinseneffekts, sondern als lästige Störung, die es zu berücksichtigen gilt: der ESA-Astrometriesatellit Gaia, der dieses Jahr startet, wird Sternpositionen so genau vermessen, dass der Ablenkungseffekt der Sonnenmasse dabei standardmäßig als Korrektur eingehen muss. Andernfalls würden die Sternpositionen zu ungenau – und das gilt auch, wenn die Sonne zu dem betreffenden Zeitpunkt in einer ganz anderen Himmelsregion steht als der Stern!
Die großräumige Struktur des Weltalls
Wie oben bereits erwähnt, treten Galaxien nicht einzeln im Kosmos verteilt auf, sondern gehören meist zu Galaxienhaufen, in denen sich tausende Galaxien (oder noch mehr) unter ihrer gegenseitigen Schwerkraft bedächtig umeinander bewegen. Der Coma-Haufen (knapp 1000 Galaxien), der Fornax-Haufen (mehr als 50 helle Galaxien) und der Virgo-Haufen (bis zu 2000 Galaxien) sind schöne Beispiele. Unsere eigene Lokale Gruppe, zu der die Milchstraße gehört, ist da eher mickrig – mit zwei großen Galaxien (der Milchstraße und der Andromedagalaxie) und rund 40 kleineren.
Auch die Galaxienhaufen sind nicht gleichmäßig verteilt, sondern bilden sogenannte Superhaufen. Unsere Milchstraße ist Teil des Virgo-Superhaufens, in dessen Zentrum der Virgo-Galaxienhaufen steht. Mit solchen Superhaufen sind wir auf Größenskalen von einigen hundert Millionen Lichtjahren angekommen. Zwischen den Superhaufen gibt es interessanter Weise noch längliche Strukturen, die Filamente genannt werden. Auf diesen Größenskalen ergibt sich damit ein fast schwammartiges Bild des Kosmos: Superhaufen, durch Filamente verbunden, dazwischen größere, weitgehend leere Hohlräume. Das ist in dem folgenden Bild schön zu sehen, in dem jeder der schwarzen Punkte für eine von mehr als 30.000 Galaxien steht, die in der 2dF-Durchmusterung erfasst wurden (Bild: 2dF Galaxy Redshift Survey Team):
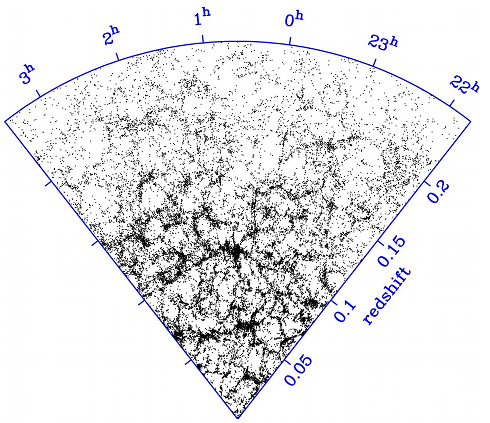
Unser Beobachtungsort – unsere Heimatgalaxie – liegt unten an der Spitze des Keils. Bei den näheren Galaxien, im unteren Teil, ist das schwammartige Muster besonders gut zu erkennen. Nach oben, zu den ferneren Galaxien hin, hat die Durchmusterung immer weniger der dort sicherlich auch vorhandenen Galaxien erfasst, einfach weil es schwieriger ist, leuchtschwache ferne Galaxien aufzunehmen. Dass das Muster nach oben hin verblasst, ist damit ein Artefakt der Beobachtungsdaten.
Warum bei der Entfernungsskala “redshift”, also “Rotverschiebung” steht, werden wir später noch genauer untersuchen.
Auf noch größeren Skalen setzt sich die Struktur dann allerdings nicht weiter fort. Betrachtet man Würfel mit einigen hundert Millionen Lichtjahren Seitenlänge, dann wird die mittlere Dichte in jedem solchen Würfel weitgehend dieselbe sein. Anders ausgedrückt: Auf so großen Skalen ist das Weltall homogen. Auf solchen Skalen können wir beginnen darüber nachzudenken, wie sich das Weltall als Ganzes beschreiben lässt. Mit anderen Worten: wir können beginnen, Kosmologie zu betreiben.
Weiter geht es mit Teil 9: Kosmische Expansion und Urknall
Ich danke meinen Kollegen Knud Jahnke, Carolin Liefke und Jakob Staude für hilfreiche Anmerkungen zu diesem Text.
Nachträglich geändert am 10.3.2013: Genauere Beschreibung von Abell 2218.


H.E.S.S.
Nur eine ganz kurze Anmerkung: Seit dem Sommer letzten Jahres besteht das HESS-Experiment aus 4 Teleskopen der oben gezeigten Größe sowie aus noch einem zusätzlichen und deutlich größeren Teleskop (Spiegelfläche: 600m² vs. 100m²).
@Thomas
Zu H.E.S.S.: In der Tat, und ich habe keine Ahnung, wie das durchgerutscht ist, denn das dachte ich eigentlich in einer früheren Fassung schon aktualisiert zu haben. Jedenfalls danke für den Hinweis!
Schwarze Löcher
Was mir bei diesen Schwarzen Löchern nicht in den Kopf will (und ich hoffe, hier ist die richtige Stelle, das zu fragen):
Eine Uhr, die in ein SL fällt, geht von außen betrachtet immer langsamer, am Ereignishorizont bleibt sie quasi stehen (was wir nicht sehen können, wegen Rotverschiebung unendlich).
Nun sagt aber Hawking, daß SL verdampfen. Extrem langsam zwar, aber aus Sicht der Uhr kurz vorm EH müssen doch selbst 10^40 Jahre wie ein kurzer Augenblick erscheinen.
Aus ihrer Sicht müßte der EH vor ihr zurückweichen, so wie sie sich ihm nähert, bis er am Ende ganz verschwindet, bevor sie die Singularität erreicht hat.
Nichts könnte je die Singularität erreichen.
Wo ist mein Denkfehler?
@H.M. Voynich
Das “immer langsamer gehen” bezieht sich nur auf einen äußeren, weit entfernten Beobachter, der Licht von der Uhr empfängt und daraus auf den Zeitablauf rückschließt.
Am Horizont gibt es aber in den Schwarzschild-Koordinaten, die als Zeitkoordinate die Zeit eines solchen Beobachters haben, eine Koordinatensingularität (kein Wunder – von hinter dem Horizont kommt nun einmal kein Licht heraus; dort lassen sich keine solchen “Radarkoordinaten” definieren).
Sprich: Diese Koordinaten sagen mehr darüber, was mit dem Licht passiert als was mit der Uhr passiert. Die Uhr, das kann man ausrechnen, fliegt nach recht kurzer (auf ihr selbst gemessener) Zeit durch den Ereignishorizont und erreicht dann etwas später die Schwarzloch-Singularität.
@Markus Pössel:
Vielen lieben Dank für die Antwort, auch wenn ich es noch nicht ganz – nein, eigentlich gar nicht – verstanden habe.
Das “kein Licht herauskommt” hängt doch auch damit zusammen, daß jede noch so kurze Wellenlänge spätestens am EH in die Unendlichkeit verschoben wird (das meinte ich mit Rotverschiebung, und Sie/Du vmtl. mit “was mit dem Licht passiert als was mit der Uhr passiert”?), sobald man – nein, nicht man, sondern die hypothetischer Uhr – sich dem EH hähert.
Habe ich das richtig verstanden?
“Man” hätte erstmal Probleme mit dem Gezeiteneffekt, wenn man Teil der Uhr wäre.
Aber angenommen, den übersteht man (er ist ja umso kleiner, je größer die Masse des SL ist, richtig? Also brauche ich ein richtig großes Loch).
In meinem Laienverständnis vermute ich, daß ich mir die GANZE Metrik anschauen muss, um dieses Problem zu verstehen, und nicht nur Annährungen von außen gesehen machen kann.
Aber wo genau der Schnitt, das deutlich andere Ergebnis liegen könnte, wenn ich es konsequent durchrechnen könnte, ist mir immer noch nicht ansatzweise klar.
p.s.
p.s.: hab ich schon mal erwähnt, wie toll ich es finde, daß ich hier selbst mitten in der Nacht Antworten auf blöde Fragen bekommen kann?
Danke.
Analogie
Ich bitte um Verzeihung, wenn ich jetzt etwas offtopic werde, aber vom didaktischen Standpunkt scheint mir meine Frage mit einer völlig anderen vergleichbar – eine Frage, die eigentlich ganz einfach sein sollte, aber von der mir alle sagen, daß man sie nur verstehen kann, wenn man die Mathematik macht.
EM ist Ladung. Partikel gleicher Ladung stoßen sich ab, entgegengesetzte Ladungen ziehen sich an; beide Ladungen multipliziert geteilt durch Abstandsquadrat, im Prinzip ganz einfach.
Aber wenn ich mir vorstelle (a la Feynman-Diagramm), wie ein Elektron ein Photon aussendet und daraufhin vom Proton im Atomkern angezogen wird, dann habe ich ein Problem, denn in meiner Vorstellung muß das emmitierende Elektron beim Aussenden seinen Impuls ändern, und zwar entweder nach vorn oder hinten, je nachdem, ob das Photon von einem Proton oder anderem Elektron absorbiert wird. Was ja noch gar nicht feststeht.
Vermutlich kann man das nur verstehen, wenn man vorher das Konzept virtueller Photonen begriffen hat.
Doch auch die haben eine begrenzte Reichweite, moderne Neodym-Magneten zeigen jedoch ihre Kräfte schon deutlich bei Abständen von 1 cm und größer!
Woher weiss bei diesen Abstaenden jedes Teilchen, ob es angezogen oder abgestossen sein soll, wenn das Photon keine Ladung enthaelt? Wo steckt die Info?
Mir wurde von verschiedenen Seiten gesagt, das kann man nicht verstehen, wenn man nicht die Analysis korrekt durchzieht.
Doch ich gebe die Hoffnung nicht auf, dass man auch einem Laien wie mir wenigstens zeigen kann, an welchen Stellen die Mathematik zu konterintuitiven Ergebnissen fuehrt.
Was will ich eigentlich sagen?
Ich muss wohl (und kann sehr gut) damit leben, dass ich nicht alles verstehe, was andere verstehen.
(Ach, sag bloss! – mich selbst ohrfeigend)
Eins der Dinge, die ich ueberaus liebe, ohne sie zu verstehen, ist die Didaktik.
Ich glaube, dass es fuer auch jede noch so komplizierte Berechnung eine Metapher gibt, die selbst Leute wie ich kapieren.
Man muss sie nur finden.
Didaktik
Es gibt in diesem Themenbereich sicherlich einige didaktische Schwierigkeiten.
Natürlich bedeuten didaktische Schwierigkeiten keineswegs, dass die Physik falsch ist.
Die didaktischen Schwierigkeiten bedeuten höchstens, dass die Didaktik falsch ist.
Einige Beipiele, nur zur Erheiterung:
1.) Es kann derzeit noch gar keine fertigen schwarzen Löcher geben, weil sie sich auf Grund der gravitativen Zeitdilatation nur unendlich langsam bilden können.
2.) Ein Photon fliegt von einem schwarzen Loch genau senkrecht nach oben.
Dabei bleibt es immer lichtschnell, aber es wird durch die gravitative Rotverschiebung immer energieärmer.
Irgendwann ist es ganz verschwunden, und kann daher auch nicht mehr in das schwarze Loch zurückfallen.
Wo ist seine Energie hingekommen?
3.) Wie kann der Austausch von elektrisch neutralen Teilchen mit positiver Masse, Energie oder Trägheit eine anziehende Kraft bewirken?
Eine abstossende Kraft lässt sich natürlich leicht erklären.
Noch viel schwieriger lassen sich die Querkräfte in den magnetischen Feldern erklären.
4.) Die folgende Berechnung der Reichweite virtueller Photonen scheint korrekt zu sein, aber sie passt leider überhaupt nicht zum Casimir-Effekt.
Wegen der vielen Sonderzeichen ist dieser Text als Bild dargestellt.
http://members.chello.at/….bednarik/VIRTPHOT.PNG
Karl Bednarik
(kann es ein, dass wir uns schon vor 15 Jahren begegnet sind, in einem Forum von Science, welches von einer gewisen J.L. damals im Alleingang getoetet wurde? Egal, tut nichts zur Sache 😉 )
Danke jedenfalls fuer die Antwort, auch wenn sie (auf den ersten Blick) nur der Erheiterung dienen soll.
Wie immer, ich glaube, dass Didaktik noch unentdeckte Tueren finden kann, komplizierte Sachverhalte anschaulich zu erklaeren. Und dass es sich lohnt, diese zu suchen. Bisher sind wir da noch bei fast Null.
Und so wie ich Sie (und ihre manchmal sehr lehrreichen gifs) kenne, sind wir da ganz beieinander.
Karl Bednarik
Beispiel 2 erscheint mir besonders produktiv, da man glaubt, eine Antwort finden koennen zu muessen, ohne auch je eine Schwarzschildmetrik berechnet zu haben (so wie ich).
Bei der Frage, wo die Energie hin ist, wuerde ich erstmal versuchen, das Problem in potentielle und kinetische Energie zu unterteilen; denn kinetische Energie ist ja immer Ansichtssache.
Naechste oder uebernaechste Woche kann ich Bescheid geben, ob mir das weiterhilft. 🙂
muss auch unfähig sein, sie aufzuspüren.
H.M.Voynich schrieb (04.08.2013, 22:04):
> Eine Uhr, die in ein SL fällt, geht von außen betrachtet immer langsamer, am […]
Das ist offenbar ein (“Denk“-)Fehler:
Im Deutschen werden regelmäßig gesteigerte Adjektive (im Komparativ) durch das Wort “als” zum Vergleichsobjekt verbunden.
Ein Folgefehler ist, keine nachvollziehbare Festlegung zu treffen bzw. zu beachten, wie ein derartiger Vergleich überhaupt zu erfolgen habe;
also wie im betrachteten Fall zumindest im Prinzip zu entscheiden wäre, ob zwei gegebene, voneinander getrennte Uhren “gleich gegangen” waren, oder zu quantifizieren, in wie fern nicht.
Daraus resultiert wiederum der Folgefehler, keine nachvollziehbare Festlegung zu treffen bzw. zu beachten, wie geometrische Beziehungen zwischen verschiedenen gegebenen Uhren überhaupt zu ermitteln seien, d.h. uber das voneinander getrennt Sein (anstatt ständig koinzident) hinaus;
im betrachteten Fall z.B. ob sich zwei gegebene, voneinander getrennte Uhren “auf der selben Seite eines Horizonts” aufhielten, oder nicht.