Fusionsforschung: Der Reaktionsparameter oder “Warum eigentlich Deuterium + Tritium ?”
BLOG: Formbar

Bei dem Rennen um den ersten Fusionsreaktor haben die meisten zugrundeliegenden Konzepte eines gemeinsam: sie basieren auf der Verschmelzung von Deuterium und Tritium als Energie-freisetzende Reaktion. Warum das so ist und was Vor- und Nachteile von alternativen Konzepten sind, werde ich hier versuchen darzustellen.
Die Energiegewinnung bei der Kernfusion basiert auf der Tatsache, dass bei der Verschmelzung leichter Atomkerne zu einem schweren Kern, letzterer weniger Masse hat als die Summe der beiden ursprünglichen. Aristoteles lag hier gewissermaßen falsch, das Ganze ist in diesem Fall nicht mehr als die Summe seiner Teile. Die fehlende Masse wird gemäß Einsteins relativ bekannter Formel E=mc² als Energie frei, welche auf die Fusionsprodukte verteilt wird.
Bei der Bildung von Atomkernen kann also Energie freigesetzt werden. Die Menge der Energie hängt von der Anzahl der Nukleonen im Kern ab, also von dem entstandenen Element und ist auch ein Maß für die Stabilität des Kerns: wurde bei der Bildung des Kerns viel Energie frei, muss man eben diese Energie auch wieder aufwenden, falls man ihn wieder kaputt machen möchte. Quantifizieren lässt sich das in der Bindungsenergie pro Nukleon, die in Abb. 1 dargestellt ist.
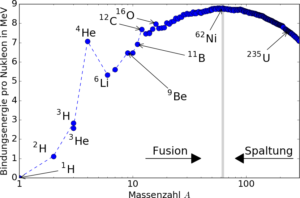
Man erkennt in dem Diagramm sehr schön zu einem den Bereich der Kernfusion, wo bei der Verschmelzung leichter Kerne Energie frei wird (die Bindungsenergie pro Nukleon steigt zu schweren Kernen hin an). Zum anderen ist der Bereich der Kernspaltung zu erkennen, wo bei der Spaltung eines schweren Kerns in leichtere Kerne Energie frei wird. Beide Prozesse treffen sich bei einer Gruppe von Fe- und Ni-Isotopen, welche somit die am stärksten gebundenen Kerne und die stabilsten Elemente darstellen (⁶²Ni liegt knapp vorne).
Okay, alles ganz einfach: leichte Atomkerne zusammen bringen so dass Fusion einsetzt und die freiwerdende Energie abschöpfen um Wasser heiß zu machen und so eine Turbine antreiben. Im Prinzip ja, das Problem besteht darin, dass Atomkerne (aufgrund der Protonen) positiv geladen sind und gleichnamige Ladungen sich abstoßen. Zumindest solange bis man die Protonen nah genug zusammenbringt und die starke Kernkraft wirkt. Das ist allerdings wirklich sehr nah (unterhalb von ca. 2 fm) und erfordert eine Menge Energie, anschaulich (und nicht maßstabsgetreu) in Abb. 2 dargestellt.
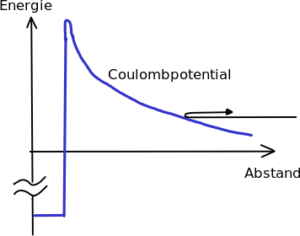
Zu erkennen ist der Potentialverlauf, den ein Atomkern spürt, wenn er sich einem anderen nähert: zunächst abstoßend und zwar umso mehr, je näher er kommt, bis er schließlich so nahe ist, dass von der starken Kernkraft angezogen wird und in den Potentialtopf fällt. Hat ein Kern nicht ausreichend Energie um über die Spitze zu kommen, wird er von der Coulombkraft reflektiert, so wie in der Skizze angedeutet. Man spricht daher auch vom Coulombwall. Berechnet man die Höhe der Spitze, die überwunden werden muss, für die auf der Sonne ablaufende Fusionsreaktion, kommt man auf eine Energie von 1,2 MeV, was einer Temperatur von ungefähr 14 Mrd. Kelvin entspricht. Das allerdings übersteigt die tatsächliche Temperatur im Sonnenzentrum um den Faktor 1000.
Kleiner Einschub: Die Energie der Teilchen wird in der Plasmaphysik üblicherweise in Elektronenvolt gemessen, wobei 1 eV die Energie ist, die ein Elektron beim Durchlaufen einer Spannungsdifferenz von 1 V erfährt. In Kelvin umgerechnet, entspricht 1 eV ungefähr 11600 Kelvin, 1 keV also ungefähr 11,6 Mio. Kelvin.
Wie löst mal nun das Problem der zu kalten Sonne? Hier helfen zwei physikalische Prinzipien: zum einen der Tunneleffekt, der das Durchtunneln durch den Coulombwall mit einer endlichen Wahrscheinlichkeit erlaubt. Dann ist das Konzept von Temperatur hier statistisch zu verstehen: es liegt eine Population der Teilchen vor, die eine Temperaturverteilung hat, typischerweise eine Maxwellverteilung. Eine solche Verteilung hat einen Mittelwert, meist ist das der Wert, den wir meinen, wenn wir von der Temperatur reden. Es gibt aber eben auch eine gewisse Wahrscheinlichkeit ein Teilchen mit einer höheren Temperatur anzutreffen. Zusammen reichen diese beiden Effekt aus, um bei “nur” 1,5 Mio. Kelvin eine endliche Fusionswahrscheinlichkeit in der Sonne zu erhalten.
Alles klar, machen wir es also einfach wie auf der Sonne? Nein, das ist keine gute Idee, denn der Fusionsprozess auf der Sonne, bei dem die Verschmelzung von zwei Protonen, also zwei Wasserstoffkernen, der erste Schritt ist, ist extrem unwahrscheinlich. So unwahrscheinlich, dass es ca. 10¹⁰ Jahre dauert, bis ein einzelnes Proton mit einem anderen fusioniert. Für die Sonne (bzw. für uns) ist das kein Problem, da die Sonne wirklich enorm groß ist und eine Menge Protonen hat. Auf der Erde müssen wir uns aber nach Alternativen umsehen. Dazu schaut man sich die Fusionsquerschnitte an, welche die Wahrscheinlichkeit für einen Fusionsprozess bei Aufeinandertreffen zweier Teilchen angibt. Diese wurden vor allem in den den Anfängen der Fusionsforschung detailliert vermessen. Geht man wieder von einer Maxwellverteilung der Geschwindigkeit der Teilchen im Plasma aus, kann man aus diesen Daten die Fusionsreaktivität, auch Reaktionsparameter genannt, abschätzen.
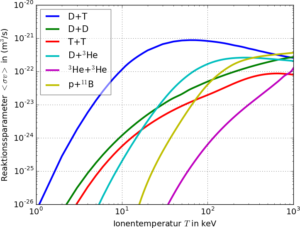
In Abb. 3 ist der Reaktionsparameter für verschiedene Fusionsprozesse als Funktion der mittleren Teilchenenergie (also der Temperatur) angegeben. In dem Diagramm erkennt man für fast den gesamten Bereich die größte Reaktivität für die blaue Kurve, und diese entspricht der Deuterium + Tritium Reaktion. Das ist der Grund, warum diese in den meisten Reaktorkonzepten favorisiert wird. Zudem wissen wir aus dem Bindungsenergie-Diagramm (Abb. 2), dass bei der Fusion von Deuterium und Tritium zu einem Heliumkern (und einem Neutron) eine Menge Energie frei wird. Die entsprechende Reaktion lautet: D + T → He (3,52 MeV) + n (14.06 MeV), wobei der Wert in der Klammer hinter den Fusionsprodukten, deren kinetische Energie angibt.
Wie Abb. 3 vermuten lässt, gibt es auch Alternativen, die vor allem durch die Nachteile der D+T Reaktion motiviert sind, wobei das hier im wesentlichen einen Nachteil meint, und zwar das freie Neutron. Aufgrund seiner nicht vorhandenen Ladung wird es nicht im Magnetfeldkäfig von Tokamak oder Stellarator eingefangen. So führt es zur Erhitzung der Wände des Experimentes und erlaubt damit die Energie aus dem Fusionsplasma abzuführen. Freie Neutronen haben allerdings den Nachteil, dass sie von Atomkernen eingefangen werden können und so ein eventuell radioaktives Isotop entsteht. Möchte man dies verhindern, so kann man entweder geeignete Wandmaterialien wählen oder auf Neutronen-freie Fusionsprozesse umsteigen. Mögliche Kandidaten hierfür sind auch in Abb. 3 eingetragen: D+³He, ³He+³He und p+¹¹B. Allen gemein ist allerdings die Tatsache, dass man wesentlich höhere Temperaturen benötigt um eine ähnliche Reaktivität wie für D+T zu bekommen. Zudem hat man mit ³He noch das Problem der Verfügbarkeit: ³He ist auf der Erde extrem selten, deswegen taucht in Science-Fiction Werken immer mal wieder das Szenario auf, in dem ³He auf dem Mond abgebaut wird um die Fusionsreaktoren auf der Erde zu befeuern (Beiträge dazu zum Beispiel hier oder hier). Deuterium hingegen ist ausreichend auf der Erde verfügbar. Tritium zwar nicht, da es mit einer Halbwertszeit von ca. 12 Jahren radioaktiv ist, allerdings kann es aus Lithium erbrütet werden (was auch in den Wandmaterialien von Fusionsreaktoren basierend auf der D+T Reaktion passieren soll).
Die Gründe für das Verwenden der Deuterium-Tritium Reaktion sind also zusammengefasst deren günstiger Reaktionsparameter sowie ihre Verfügbarkeit auf der Erde. Als Anmerkung zum Schluss sei noch darauf hingewiesen, dass ich unter der Überschrift “Fusionsforschung: …” künftig in loser Abfolge auf Grundlagen und wichtige Aspekte der Fusionsforschung eingehen werde. Angelehnt ist das ganze an eine Vorlesungsreihe, die auf dem deutschen Lehrbuch Plasmaphysik: Phänomene, Grundlagen, Anwendungen von Prof. Stroth beruht.


Bei der energetisch günstigen DT- Fusion scheint der Neutronenfluss durch die Tokamakwand ein Vielfaches des Neutronenflusses in einem AKW zu betragen – und schon dort (beim AKW) führt der ständige Neutronenfluss zur Aktivierung der Wand (es enstehen radioaktive Wandatome) und zur Schwächung/Versprödung der Wand. So gesehen ist die DT-Fusion nicht ideal.
Die neutronenlose (aneutronische) pB11-Fusion (Verschmelzung von Wasserstoffkernem mit Bor11-Kernen) dagegen wäre ideal wenn es darum geht zu verhindern, dass die Reaktorwand geschädigt wir und/oder radioaktive Atome entstehen. Zudem sind die nötigen Ausgangsstoffe der pB11-Fusion (Bor und Wasserstoffkerne) leicht beschaffbar. Die ersten Fusionsreaktoren werden aber wohl mit der DT-Fusion arbeiten, denn schon diese Fusion zu zünden ist alles andere als ein Kinderspiel.
Lieber Martin,
tatsächlich liegen die Neutronenflussdichten von Fusions- und Spaltungsreaktoren nicht weit auseinander, ganz grob ist man mit 10^13 Neutronen/(cm^2 s) über einen weiten Energiebereich dabei, erst bei hohen Energien übersteigt der Wert eines künftigen Fusionsreaktors (am Beispiel von DEMO) den eines Spaltungskraftwerkes.
Sie haben völlig recht, p-11B klingt verlockend, deswegen wird es beispielsweise von TriAlpha auch favorisiert. Allerdings muss man dort eben zu deutlich höheren Temperaturen kommen und, wie Sie schon sagen, probieren wir doch erstmal das naheliegende. ITER wird da in einigen Jahren interessante Experimente erlauben. Bis es soweit ist, können wir uns auf JET konzentrieren: zum Experimentierende ist dort noch einmal eine DT-Kampagne, vorbereitend für ITER, geplant.
Ich habe gelesen, dass die höhere Temperatur, die p-B11 benötigt, nur die Hälfte des Problems darstellt. Die Behauptung war, dass durch die Bremsstrahlung von dem relativ schweren Bor Kern extrem viel Leistung verloren ginge. Allein dieser Verlustprozess sollte dafür ausreichen, dass ein p-B11 Plasma nie auf die nötige Temperaturen kommen könnte – mal abgesehen von Turbulenz oder MHD Instabilitäten. Wie viel Wahrheit steckt in dieser Behauptung?
In der Tat sind die Bremsstrahlungsverluste enorm bei den hohen erforderlichen Temperaturen für die p-11B Fusion. Geht man von einem thermischen Plasma aus, bei dem Ionen und Elektronen dieselbe Temperatur haben, sogar zu hoch.
Eine Möglichkeit das zu umgehen, ist der Versuch ein nicht-thermisches Plasma zu erzeugen, bei dem zum einen die Elektronen deutlich “kälter” als die Ionen sind und zum anderen noch eine nicht-Maxwell-Verteilung mit einer ausgeprägten heißen Komponente der Ionen zu erzeugen.
@Chris: Die p-B11 – Fusion in einem Tokamak oder Stellerator ist – wie nicht nur sie sondern auch Alf Köhn ausgeführt haben -, schwierig.
Möglich, aber herausfordernd würden Fusionsforscher sagen, die an den magnetischen Einschluss glauben.
Möglich, aber einen völlig anderen Ansatz erfordernd, sagen dagegen die Forscher, welche das arxiv-Papier AV ALANCHE BORON FUSION BY LASER PICOSECOND BLOCK IGNITION WITH MAGNETIC TRAPPING FOR CLEAN AND ECONOMIC REACTOR publiziert haben.
Ihr Vorschlag beruht auf einer nicht mehr ganz neuen Idee, einer Idee, für deren Funktionieren sie aber Indizien gefunden haben. Die Idee ist folgende: Wenn man zwei Laserstrahlen von 30 Petawatt (3 Mal so viel Leistung wie bis heute maximal erreicht) für einige Picosekunden auf einen in einer Miniaturspule sich befindlichen Zylinder von Borwasserstoff (HB11) richtet, so erzeugt das elektromagnetische Lichtfeld kurzfristig extrem hohe Magnetfeldstärken. Dieses lokal extrem starke Magnetfed beschleunigt die Atome im HB11-Zylinder so stark, dass die resultierenden Atomkollisionen zur pB11-Fusion führen. Die pB11-Fusion erzeugt Alpha-Kerne, welche vom HB11-Zylinder in alle Richtungen wegfliegen.
Strom erzeugen kann man nun, indem man die wegfliegenden, positiv geladenen Alphapartikel in einem negativen elektrischen Feld von 1.4 Millionen Volt abbremst.
Nach der Theorie ist der Coulombwall das große Hindernis bei der Kernfusion. Nach de Daten würde er erstr bei ca. 1,5 Milliarden °C überwunden werden. Dass die Sonne trotzdem strahlt, führen Sie auf die Maxwellverteilung der Geschwindigkeit der Atome und den Tunneleffekt zurück, beides winzige Effekte, aber bei der riesigen Sonnenmasse ausreichend. Ergänzend möchte ich noch eine Effekt hinzufügen, den ich bei meiner Doktorarbeit 1969 mit Hilfe der 2H(d,p)3H – Reaktion mit polarisierten Deuteronen nachweisen konnte. Bei einer Energie von ca. 107 KeV gibt es eine hohe schmale Spitze der Fusionsreaktion. (Siehe im Internet “H.W. Franz 2H(d,p)3H”). Dieses Verhalten wurde in einer Vielzahl späterer Messungen bestätigt. Der damalige Stand der Theorie hatte dafür keine Erklärung, im Gegenteil. Man sprach später von einem “Resonanzverhalten”. Ich bin danach in die Industrie gegangen und war mit anderen Themen beschäftigt. Nach dem Lesen Ihres interessanten Artikels würde mich interessieren, ob dieser Effekt beim heutigen Stand der Theorie einen Beitrag zur Ausbeute bei der DT – Fusion leistet.
In der Tat ist die Tatsache, dass polarisierter “Brennstoff” zu einer Erhöhung der Fusionswahrscheinlichkeit führen kann seit rund 50 Jahren allgemein bekannt, da haben Sie völlig recht. Ein sehr spannendes Thema, wie ich finde, zu dem auch tatsächlich immer noch geforscht wird, es ist also noch immer nicht restlos geklärt, wie wir das in einem Fusionsreaktor im Detail umsetzen können.
Alf Köhn schrieb (4. Oktober 2016):
> […] Gruppe von Fe- und Ni-Isotopen, welche somit die am stärksten gebundenen Kerne und die stabilsten Elemente darstellen
Bei „Stärke der Bindung eines Kerns“ im Sinne der Bindungsenergie pro Nukleon, wie in Abb. 1 gezeigt einerseits,
und bei „Stabilität“ (bzgl. jeglicher Disintegration, die nicht äußerlich angeregt wurde), d.h. im Sinne des Maximums der jeweils für einen Kern eines bestimmten Elements geringsten Massendifferenz „alle (mindestens zwei) einzelnen Bruchstücke minus Ausgangskern“ andererseits,
handelt es sich offenbar um zwei verschieden definierte (Mess-)Größen.
> (62-Ni liegt knapp vorne).
In beiden Maßen?
Alf Köhn schrieb (4. Oktober 2016):
> […] Gruppe von Fe- und Ni-Isotopen, welche somit die am stärksten gebundenen Kerne und die stabilsten Elemente darstellen
Bei „Stärke der Bindung eines Kerns“ im Sinne der Bindungsenergie pro Nukleon, wie in Abb. 1 gezeigt einerseits,
und bei „Stabilität“ (bzgl. geeigneter „Anregung“, insbesondere gegenüber Photodisintegration), d.h. im Sinne des Maximums der jeweils für einen Kern eines bestimmten Elements geringsten Massendifferenz „alle (mindestens zwei) einzelnen Bruchstücke minus Ausgangskern“ andererseits,
handelt es sich offenbar um zwei verschieden definierte (Mess-)Größen.
> (62-Ni liegt knapp vorne).
In beiden Maßen?
Lieber Frank, ich bin mir nicht ganz sicher, ob ich Sie richtig verstehe: bezieht man sich auf die Stabilität des Kernes, dann “liegt 62-Ni knapp vorne”, geht es aber um die chemische Stabilität, also die Stabilität der Elektronenhülle, dann liegen wohl die Edelgase vorne, angeführt von Helium.
Da die Stabilität gegenüber Photodesintegration ja auch den Kern beinhaltet, müsste man sich anschauen, wieviel Energie das “Herausschlagen” eines Neutrons, Protons oder Alphateilchen benötigt. Nach ein bisschen Literaturrecherche, findet man Messreihen, die besagen, dass für He ein Wechselwirkungsmaximum bei einer Energie von 26 MeV liegt, für 62-Ni bei 22 MeV. Und dieses ist in der Tat eine andere Art der “Stabilität”, wo 62-Ni dann auch nicht vorne liegt.
Alf schrieb (6. Oktober 2016 @ 14:04):
> Da die Stabilität gegenüber Photodesintegration ja auch den Kern beinhaltet,
Ganz recht.
Und sofern nicht ausdrücklich auf mögliche andere Definitionen verwiesen würde, halte ich die „Stabilität gegenüber Photodesintegration“ sogar für die einzig naheliegende Definition von „Stabilität eines Atomkerns “;
abgesehen natürlich von den Isotopen, die radioaktiv sind („ganz von selbst zerfallen können“), und deren „Stabilität“ (bzw. wohl treffender: „Labilität“) stattdessen naheliegender Weise durch deren mittlere Lebensdauer (bzw. mittlere Zerfallsrate) definierbar/quantifizierbar wäre.
Jedenfalls ist die als Stabilität gegenüber Photodesintegration verstandene „Stabilität“ nicht definitionsgemäß/zwangsläufig das selbe Maß wie „Bindungsenergie pro Nukleon“ (worin 62-Ni „knapp führt“, wie Abb. 1 recht deutlich zeigt).
> müsste man sich anschauen, wieviel Energie das „Herausschlagen“ eines Neutrons, Protons oder Alphateilchen benötigt.
Ja, auch. Aber grundsätzlich: wieviel Energie (mindestens) für das Erreichen jedes denkbaren „Trümmerzustands“ mit der gleichen Anzahl von Protonen und Neutronen wie der Ausgangskern benötigt würde;
dann, für welchen solchen „Trümmerzustand“ eines bestimmten Kern die entsprechende “Mindest-Disintegrationsenergie” die geringste wäre;
und schließlich, für welche Kernart die so gefundene „minimale Disintegrationsenergie” wiederum den größten Wert hätte.
> dass für He ein Wechselwirkungsmaximum bei einer Energie von 26 MeV liegt
Stimmt: für 4-He lässt sich das sogar anhand von Abb. 1 recht gut überblicken,
insbesondere weil es dabei nur wenige mögliche „Trümmerzustände“ gibt; nämlich nur diese drei:
4-He + gamma ⇒ D + D,
4-He + gamma ⇒ T + p,
4-He + gamma ⇒ 3-He + n,
die offenbar alle etwa 26 MeV “Mindest-Disintegrationsenergie” brauchen.
> Nach ein bisschen Literaturrecherche findet man Messreihen, die besagen […] für 62-Ni bei 22 MeV.
(Um diesen Wert zu begründen/begreifen sind die Angaben aus Abb. 1 möglicher Weise nicht ganz ausreichend … Wo genau wäre die betreffende Messreihe zu finden, bitte?)
4-He ist demnach also eindeutig stabiler (in diesem Sinne) als 62-Ni;
und zwar egal, ob die betreffenden Messreihen sich „nur“ mit dem „(gamma-induzierten) Herausschlagen“ eines Neutrons, Protons oder Alphateilchen befassten, oder tatsächlich mit allen denkbaren „Trümmerzuständen“ von (hinreichend durch gamma angeregtem) 62-Ni.
Jedenfalls vielen Dank für die Recherche. Allerdings:
Ist 4-He tatsächlich der stabilste Kern (gegenüber Photodisintegration, wie beschrieben) überhaupt??
(Das mag zwar plausibel erscheinen, weil 4-He ja wie gezeigt sogar stabiler als 62-Ni ist;
aber letztlich überzeugend wären wohl nur ausführliche Vergleiche der “Mindest-Disintegrationsenergie” für alle denkbaren „Trümmerzustände“ aller Kerne …)
Die 62-Ni – Literaturstelle ist diese hier: http://iopscience.iop.org/article/10.1088/0370-1328/73/4/307/meta
Steckt zwar hinter einer paywall, aber im abstract ist dankenswerterweise die wichtigste Info drinnen.
Recherchiert man noch etwas mehr (was dank kostenfreiem WLAN im ICE auch jetzt gerade problemlos möglich ist, vielen Dank liebe Bahn 🙂 ), findet man einen Haufen Literaturstellen, die sich jeweils mit Photodesintegration für einzelne Elemente (jeweils aufwändige Experimente) befassen. Einen umfassenden Übersichtsartikel habe ich leider nicht gefunden, es gibt lediglich mehrere, die sich auf Gruppen von Elementen beziehen. Ich werde mich mal bei meinen Kollegen umhören, vielleicht fällt denen noch etwas dazu ein.
Alf schrieb (6. Oktober 2016 @ 20:23):
> Die 62-Ni – Literaturstelle ist diese hier: http://iopscience.iop.org/article/10.1088/0370-1328/73/4/307/meta
Nochmals vielen Dank für die Angabe
(und wie bedauerlich, dass sowas nicht einfach in Wikipedia erst-veröffentlicht oder zumindest routinemäßig eingepflegt wird).
> Steckt zwar hinter einer paywall, aber im abstract ist dankenswerterweise die wichtigste Info drinnen.
Man liest dort:
Die entsprechende “Mindest-Disintegrationsenergie” für diese Reaktion, als Abschätzung nach oben für die Stabilität von 62-Ni, wäre damit offenbar noch erheblich geringer als 22 MeV.
Frank Wappler schrieb (6. Oktober 2016 @ 17:22):
> [dass für He ein Wechselwirkungsmaximum bei einer Energie von 26 MeV liegt] Stimmt: für 4-He lässt sich das sogar anhand von Abb. 1 recht gut überblicken
Da habe ich mich leider getäuscht (und „Wechselwirkungsmaximum“ ist eben nicht „Mindest-Disintegrationsenergie“, um die es hinsichtlich Stäbilität eigentlich geht).
Für den Prozess
4-He + gamma ⇒ D + D
ergibt sich aus den Werten in Abb. 1 zwar etwa eine Mindest-Disintegrationsenergie (d.h. Mindestenergie des Photons) von rund:
4 * 7 MeV – 2 * (2 * 1 MeV) = 24 MeV,
aber für
4-He + gamma ⇒ T + p bzw.
4-He + gamma ⇒ 3-He + n
doch nur
4 * 7 MeV – 3 * 3 MeV – 0 MeV = 19 MeV.
D.h. es würden Photonen von mindestens ca. 19 MeV benötigt, um 4-He Kerne überhaupt zu zerbrechen; wenn auch sicherlich mit äußerst geringem Reaktionsquerschnitt.
Der Vergleichwert für 62-Ni ist (wie im vorausgehenden Kommentar 6. Oktober 2016 @ 23:04 argumentiert) allerdings sicherlich noch deutlich geringer; 4-He also doch stabiler als 62-Ni.