Mein Fitness-Center hatte mir zu meinem Geburtstag einen Gutschein über eine “Körperanalyse” geschenkt. Natürlich habe ich diesen bald eingelöst; ich war neugierig, was sich hinter solch einer Analyse verbirgt. Es war ernüchternd: Ich musste mich einfach auf eine metallische Plattform stellen und bekam in jede Hand eine Hantel, um in Kontakt mit zwei Elektroden zu kommen. Dann  wurde ein schwacher, für mich nicht merkbarer Wechselstrom durch meinen Körper geschickt, wobei die Frequenz über einen gewissen Bereich variiert wurde:  Schon war die Analyse geschehen. Nach ein paar Minuten kam ein Protokoll aus dem Drucker, in dem säuberlich und graphisch übersichtlich dargestellt das Gewicht meines Körpers aufgeteilt worden war in Anteile von Muskeln, Fett, Knochen – und das auch noch getrennt für Arme, Beine und Rumpf. 
Nun war ich amüsiert. Kannte ich diese Form einer Analyse nicht aus meiner Autowerkstatt? Da macht keiner mehr die Motorhaube auf, der Zustand des Motors und seiner elektronischen Schaltungen wird einfach über ein Messgerät ausgelesen und in einem Protokoll notiert. Aber diese Gedanken wurden bald vertrieben, als ich einen Blick auf das Protokoll warf und mein Betreuer begann, die Zahlen zu interpretieren.  Ich sah sofort, da konnte etwas nicht stimmen, und dieses Gefühl konnte nicht allein auf Eitelkeit beruhen. “Wie genau sind denn diese Parameter bestimmbar” fragte ich. “Oh, sehr genau”, hieß es, “in dem Gerät stecken drei hochwertige Prozessoren”. Da wurde mir wieder klar, wie schnell heute ein Endanwender eines High-Tech Produktes überfordert ist. Wenn man allerdings bedenkt, wie häufig in heutiger Zeit Daten in Diskussionen eine Rolle spielen und wie oft Interpretationen von Daten eine Grundlage für bedeutsame Entscheidungen werden, würde man sich wünschen, dass eine grobe Kenntnis über Wege der Datengewinnung und über eine sachgerechte Aufbereitung der Daten in der Bevölkerung vorhanden ist. 
Über Wikipedia konnte ich mich über die Grundsätze einer solchen “Körperanalyse” in Form einer bioelektrischen Impedanzanalyse informieren.  Der Körper wird als Zusammensetzung verschiedener Kompartimente gesehen, im einfachsten Fall sind das zwei: Körperfett und fettfreie Masse. Letztere kann wieder unterteilt werden in die Masse der Zellen und jener, die sich außerhalb der Zellen befindet und bei diesen kann man sich noch getrennt für den Wassergehalt interessieren. Jedes Kompartiment zeigt in Abhängigkeit von der Frequenz einen anderen Spannungsabfall und eine andere Phasenverschiebung beim Durchgang des Wechselstroms. Gemessen werden kann natürlich nur die Summe der Effekte, man erhält so den Spannungsabfall und die Phasenverschiebung in Abhängigkeit von der Frequenz.  Diese Kurven stellen also die Messdaten dar und aus diesen ist zu bestimmen, wie stark die einzelnen Kompartimente dazu beitragen, wie groß also der Anteil an Fett, Zellmasse usw. am Gewicht des Körpers ist.
Hier genau wird es interessant und schwierig: Man muss also aus Daten Schlüsse ziehen und man muss diese Schlüsse verlässlich begründen können. Wie kann eine solche Begründung denn überhaupt aussehen? Woher kommt eigentlich die Schwierigkeit? Kann man nicht einfach aus den Daten ausrechnen, was man wissen will?  Dann hätte der Betreuer im Fitness-Center mit seinem Hinweis auf die schnellen Prozessoren ja schon eine treffende Antwort gegeben.

Die Unsicherheit bei der Modellierung
Nein, von den Daten aus gibt es keinen direkten Weg zu einem Resultat, und zwar aus mehreren Gründen. Zunächst muss man natürlich fragen, ob die Modellierung unseres Körpers durch eine geringe Anzahl von verschiedenen Kompartimenten den Zweck hinreichend erfüllt. Man möchte wissen, wie viel der Masse des Körpers in Form von Muskeln, Fett, Wasser usw. vorliegt. Unter Anlegung eines Wechselstroms an Füßen und Händen verhält sich der Körper wie ein elektrisches Netzwerk aus Widerständen und Kondensatoren, wobei Muskeln, Fett und Wasser durch verschiedene Subnetzwerke dargestellt werden, die sich erfahrungsgemäß verschieden unter einem Wechselstrom verhalten. Die Frage ist also, wie gut solch ein Modell die wirklichen Verhältnisse wiedergibt, ja, wie man das überhaupt prüfen kann. Ehe wir das diskutieren, gehen wir aber zunächst einmal im folgenden davon aus, dass ein optimales Modell vorliegt. Dann stellt sich die Frage, wie man aus den vorliegenden Daten auf die Gewichtsanteile von Fett, Muskeln usw. schließen kann.

Die Unsicherheit der Daten
Zuerst  muss man erst einmal einsehen, dass Daten immer Zufallstreffer sind. Das klingt etwas drastisch, damit ist aber nicht gesagt, dass die Daten ganz beliebig sind. Tatsache ist aber, dass man bei jeder Wiederholung einer Messung immer einen etwas anderen Wert erhält. Offensichtlich gibt es immer äußere, immer andere nicht kontrollierbare Einflüsse auf die Messung. Bei unseren alltäglichen Messungen von Körpergröße oder Temperatur fällt uns das nicht auf; es reicht uns da ja auch ein relativ grober Wert.
Die häufige Wiederholung der Messung ergibt also eine Verteilung der Ergebnisse um einen mittleren Wert. Die meisten liegen in der Nähe dieses Mittelwertes, weiter davon entfernt immer weniger. Die Ausdehnung dieser Verteilung um den Mittelwert ist natürlich ein Maß für die Qualität der Messung. Je größer die Streuung der Messergebnisse, umso weniger vertrauenswürdig ist die Messung, umso weniger aussagekräftig die Angabe des Mittelwertes als Ergebnis der Messung. Deshalb reicht es nie, für eine Messergebnis nur eine Zahl anzugeben, man muss dazu auch noch eine Aussage über die Genauigkeit machen, indem man ein Maß für die Streuung bei wiederholten Messungen mitliefert.  So kommen Angaben wie z.B.  10.5 ± 0.4 zustande, wobei 10.5 hier der Lage des Mittelwerts entspricht und 0.4 die Streuung charakterisiert.  Mit Hilfe der Begriffe aus der mathematischen Statistik kann man diese Vorgehen noch mathematisch einwandfrei begründen und einsehen, dass dann der “wahre” Wert mit einer bestimmten Wahrscheinlichkeit innerhalb des Intervall [10.5 – 0.4, 10.5 + 0.4] liegen muss. Wie groß dieses Wahrscheinlichkeit ist, hängt davon ab, durch welche Wahrscheinlichkeitsverteilung man die Streuung beschreibt und wie man dann das Maß für die Streuung wählt. Das sind aber alles Feinheiten, die uns hier noch nicht interessieren müssen.
Wichtiger ist zunächst folgende Überlegung: Würde eine andere Gruppe von Wissenschaftlern eine ähnliche Messkampagne für die gleiche Größe machen, bekämen auch sie eine solche Verteilung der Ergebnisse, ähnlich der ersten, aber doch mit einem etwas anderen Mittelwert, und auch die Streuung hätte nun einen etwas anderen Wert. Sie gäben z.B. 10.8 ± 0.3 an und würden schließen, dass im Intervall [10.8 – 0.3, 10.8 + 0.3] der wahre Wert mit der oben genannten bestimmten Wahrscheinlichkeit liegt. Die beiden Ergebnisse kann man in einer Graphik wie in Abb.1 (links) darstellen. Man muss sich nun fragen, ob diese beiden Ergebnisse angesichts der Messfehler als verträglich angesehen werden können, und was man schließlich als Ergebnis denn nun ansehen will. Das alles kann man mit Methoden der Mathematischen Statistik eindeutig klären.
Eine Zahl als Messergebnis reicht also nie aus, man muss immer noch ein Maß für die Unsicherheit angeben, damit man überhaupt einschätzen kann, wie ernst man diese Zahl zu nehmen hat. Kann man dieses Maß nicht aus einer großen Anzahl von Messungen abschätzen, muss man eine mehr oder weniger plausible Annahme darüber machen und am Ende aller Überlegungen sich noch Rechenschaft darüber ablegen, wie sensitiv das Ergebnis des Schließens aus den Daten von dieser Annahme abhängt.

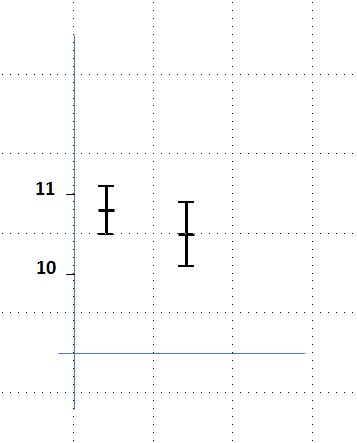
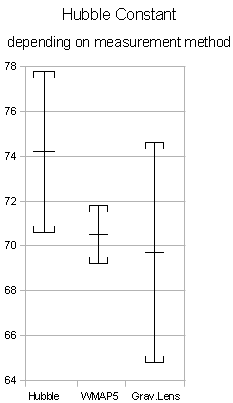
Abb.1: Graphische Darstellung von Messergebnissen. Links: Zwei Messergebnisse, die  als Beispiel im Text erwähnt sind. Man nennt die Strecken z.B. von 10.5 bis 10.9 oder von 10.1 bis 10.5 Fehlerbalken, die gesamte Strecke von 10.1 bis 10.9 Vertrauensintervall.  Rechts:  Messergebnisse für die Hubble-Konstante für drei verschiedene Messverfahren (Bild von Alexander.stohr (Eigenes Werk) [CC-BY-SA-3.0 (www.creativecommons.org/licenses/by-sa/3.0) oder GFDL (www.gnu.org/copyleft/fdl.html)], via Wikimedia Commons aus Wikipedia: Hubble-Konstante). Die Einheiten auf der Ordinate sind km/s pro Megaparsec, wobei ein Parsec einer Distanz von etwa 30ˑ 10 hoch 15 m entspricht.

Die Folgen der Unsicherheit der Daten für die Berechnung
Hat man so die Daten hinlänglich charakterisiert, indem man auch den Grad ihrer Vertrauenswürdigkeit abgeschätzt hat, kann man nun zum eigentlichen Problem kommen. In unserem Fall suchen wir hier ein paar Parameter, nämlich den Anteil der Massen von Muskeln, Fett, usw. . Es steht uns nun frei, für diese irgendwelche Werte anzunehmen und mit Hilfe des oben diskutierten Modells auszurechnen, welche Kurven sich dann für den Spannungsabfall und die Phasenverschiebung ergeben würden. Für jede Kombination von Parametern kann man ja die Modellergebnisse genau ausrechnen. Nun kommt die wichtige Überlegung: Wären diese Parameter genau die richtigen, so würden die berechneten Kurven genau zu den Kurven passen, die man misst. Die Frage ist allerdings, wie man diese Passung prüft – angesichts  der Unsicherheit der Daten, die sich jeweils in der Streuung ausdrückt.
Eine intuitiv verständliche Antwort auf diese Frage hat schon 1795 der große Mathematiker Carl Friedrich Gauß geliefert:  Man bilde eine geeignetes Maß für die Abweichung der Modellergebnisse von den Messergebnissen und richte die Parameter so ein, dass dieses Abweichung möglichst klein ist (s.a. Wikipedia: Methode der kleinsten Quadrate. Wobei die Leistung natürlich darin lag, das geeignete Maß zu finden). 
Wie dieses Maß für die Abweichung aussieht, soll hier nicht im einzelnen erklärt werden. Für den, der sich ein wenig in die Mathematische Statistik hinein gedacht hat, ist sie sehr plausibel und man kann dieses Maß auch noch durch einen anderen, noch näher liegenden Ansatz (Maximum- Likelihood-Methode) begründen. Wichtig ist aber noch zu bemerken, dass bei dem Maß für die Abweichung die Daten mit  einer größeren Streuung weniger zu Buche schlagen, so, wie es auch sein sollte. 
Die Bestimmung der Parameter läuft also auf eine Minimierung der Abweichung, einer Funktion mehrerer Parameter hinaus. Dafür für gibt es heute sehr schnelle Algorithmen, der Rechenaufwand hält sich also in Grenzen.

Die Unsicherheit in den Parametern
Mit der Bestimmung der Parameter ist es aber nicht getan. Wir hatten oben gesehen, dass z.B. eine zweite Gruppe von Wissenschaftlern bei ihren Messungen zu einem anderen Mittelwert und zu einer etwas anderen Streuung kommen würde. Diese gäben also bei gleichem Modell andere Daten in das Maß für die Abweichung ein und erhielten damit durch ihre Minimierung andere Parameter. Das heißt, auch die Parameter werden von Messkampagne zu Messkampagne streuen, auch für diese muss man also auch noch eine Streuung bestimmen, um einschätzen zu können, wie ernst man den erhaltenen Wert zu nehmen hat. Die Unsicherheit der Daten pflanzt sich also fort und zeigt sich auch in den Schlüssen aus den Daten. Wie sollte es auch anders sein. Das alles lässt sich mit den Methoden der mathematischen Stochastik einwandfrei verfolgen.
So wird man das Ergebnis der Bestimmung eines Parameters auch  in der Form z.B. 22.1 ± 2.4 angeben. Wann immer das nicht geschieht, also nur eine einzige Zahl als Ergebnis der Bestimmung eines Parameters genannt wird, muss man misstrauisch werden.  Kann es dann vielleicht in Wirklichkeit nicht auch 22 ± 20 heißen? Dann wäre das ganze Ergebnis so gut wie wertlos.

Bedeutung der Datenanalyse für das Testen von Modellen und Theorien
Bisher sind wir davon ausgegangen, dass das Modell, das wir bei der Datenanalyse unterstellt haben, die realen Verhältnisse widerspiegelt. Erst, wenn man weiß, wie man bei gegebenem Modell so verlässlich wie möglich Schlüsse aus den Daten ziehen, ist man in der Lage, zu prüfen, wie gut das Modell denn den Zweck erfüllt. 
Man hat also bei dem Schließen aus Daten immer mit zwei Fragen aus einander zu setzen: Wie gut begründet ist das Modell, das der Analyse der Daten zugrunde liegt und – wie schlägt sich die Ungenauigkeit der Daten in eine Unsicherheit bei den Schlussfolgerungen nieder?  Man spricht so immer von einem systematischen und von einem statistischen Fehler. Den statistischen Fehler hat man im Griff, indem den Zufallscharakter der Daten in Rechnung stellt und mit den Methoden einer Mathematischen Stochastik und Statistik bei allen Schlüssen aus den Daten berücksichtigt. Für die Behandlung eines systematischen Fehlers gibt es kein allgemeines Verfahren, da ist immer die Intuition und Kompetenz des Experimentators gefragt.
Welchen Nutzen habe ich aus der “Körperanalyse” ziehen können? Nun, immerhin hatte ich wieder ein Thema gefunden, über das es sich zu schreiben lohnt.