Von der Praxis in die Forschung und zurück

Für ihre Bewerbung um den KlarText-Preis für Wissenschaftskommunikation 2020 in der Kategorie Mathematik veranschaulichte Helene Krieg, was sie in ihrer Promotion erforscht hat.
Was es nützt, aus einer praktischen Frage ein abstraktes mathematisches Problem zu entwickeln.
Normalerweise geht Forschung anders herum: Zunächst werden die theoretischen Grundlagen einer Fragestellung untersucht, Experimente und Studien angestellt, bei denen das Wissen um ein Problem erweitert wird. Dann erst kommt es zur praktischen Verwertung durch neue Produktionsverfahren, Software oder Medikamente. Die Fraunhofer-Gesellschaft sieht sich als führende Forschungsorganisation für anwendungsorientierte Forschung in Europa. Kein Wunder also, dass man da als Wissenschaftler auch schon mal Forschung „entgegen der Fahrtrichtung“ betreibt. So ging es mir während meiner Promotion am Fraunhofer-Institut für Techno- und Wirtschaftsmathematik in Kaiserslautern.
Angefangen hat alles mit der Frage, wie ein Hersteller sein Angebot aus verschiedenen Transportpumpen am besten zusammenstellt. Solche Pumpen kommen überall dort zum Einsatz, wo Flüssigkeiten gefördert werden, und stellen unter anderem die Trinkwasserversorgung sicher. Die Anzahl der verschiedenen Pumpentypen bestimmt, wie viele Teile produziert werden müssen. Ideal ist natürlich, wenn die Anzahl begrenzt ist und die Vielfalt im Lager damit überschaubar bleibt. Allerdings steigt mit zunehmender Portfoliogröße auch seine Qualität. Denn dann können für einen größeren Kundenkreis solche Pumpen ausgewählt werden, die im Einsatz energieeffizient sind und einen geringen Verschleiß haben. Welche Größe hat nun ein nachhaltiges Pumpenportfolio? Und wie setzen sich die Pumpentypen darin zusammen? Ähnliche Fragen eröffnen sich auch Produzenten vieler anderer Maschinen und verlangen nach guten Entscheidungen.
Beim Stichwort „gute Entscheidung“ wurden wir als Optimierer unter den Mathematikern hellhörig. Zunächst ordneten wir das Problem des Pumpenherstellers der sogenannten Produktportfoliooptimierung zu. Die Fachrichtung hinter diesem sperrigen Wort entwickelt Strategien, ein Portfolio an Produkten so aus einer Variantenvielfalt zusammenzustellen, dass ein bestimmtes Ziel, wie der erwartete Gewinn, maximiert wird. Die untersuchten Anwendungen sind vielfältig und reichen vom optimalen Angebot an Tütensuppen oder Shampoos über Handys bis hin zu Platinen. Mathematisch ist ihnen eines gemeinsam: Für jedes Produkt stehen endlich viele verschiedene Komponenten zur Auswahl. Damit sind auch die Auswahlmöglichkeiten für das Portfolio, also die Kombination mehrerer Produkte, endlich. Das hört sich zunächst einfach an, wird aber schnell komplex. Wollten wir zum Beispiel ein Smartphone bauen, für das jeweils vier Varianten von Akku, Prozessor und Kamera zur Verfügung stünden, hätten wir bereits 4^3, also 64 verschiedene Möglichkeiten. Wenn wir uns dann für eine Serie aus drei Smartphones entscheiden sollten, mit denen wir die größten Verkaufszahlen erzielen würden, müssten wir 41664 Portfolios miteinander vergleichen, denn das entspricht allen Kombinationsmöglichkeiten, drei verschiedene Smartphones aus 64 zu wählen.
Bei den Pumpen ist die Situation sogar noch ein bisschen schwieriger. Pumpen werden über Größen, wie Abmessungen von Stutzen oder Förderrädern, und Einstellungen, zum Beispiel die Frequenz, definiert. Diese Parameter sind frei wählbar. Dadurch steigt die Variantenvielfalt ins Unendliche. Hier kommt man mit Kombinieren nicht weit. Geschickter wäre eine Problemformulierung, mit der sich verfolgen ließe, wie Änderungen der Parameter einzelner Pumpen die Eigenschaften des gesamten Portfolios beeinflussen. Die galt es aber zuerst zu finden.
Als dafür geeignetes Modell einer Pumpe stellte sich ihr sogenanntes Betriebsfenster heraus. Das Betriebsfenster umfasst alle Kombinationen von Menge und Druck, die eine bestimmte Pumpe dadurch liefern kann, in dem man Einstellungen wie beispielsweise die Drehzahl variiert. So ein Betriebsfenster existiert auch für andere Maschinen. Es umfasst alle Betriebspunkte, die eine Maschine leisten kann. Bei den Transportpumpen ist es eine scheibenwischerspur-ähnliche Form im zweidimensionalen Koordinatensystem von Fördermenge und Druck. Nicht jeder Betriebspunkt im Betriebsfenster einer Pumpe ist gleich gut. Je weiter ein Punkt von einem zentralen Bestpunkt entfernt ist, desto schlechter ist sein Wirkungsgrad. Das heißt, die Pumpe arbeitet dort weniger energieeffizient. Zudem treten verstärkt strömungsmechanische Effekte auf, die zu Verschleiß führen. Ändert man Pumpenparameter wie Abmessungen und erzeugt dadurch ein neues Gerät, verschiebt sich das Betriebsfenster und seine Form und Größe ändern sich.
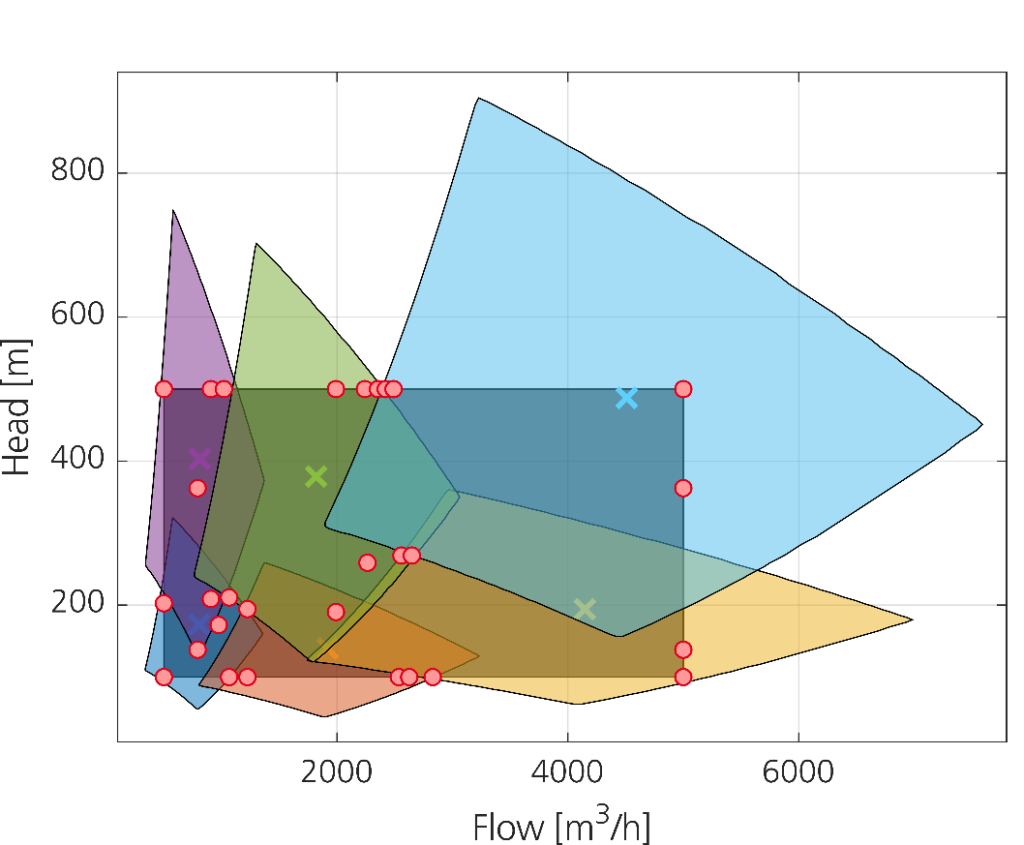
Der Hersteller möchte ein Portfolio, in dem möglichst viele Kunden eine passende Pumpe finden. Jeder Kunde gibt seine Anforderungen in Form eines Wunsch-Betriebspunktes an. Falls dieser in einem der Betriebsfenster der Pumpen aus dem Portfolio liegt, passt die Pumpe zu den Anforderungen. Viele Kunden können dann eine passende Pumpe erhalten, wenn die Betriebsfenster des Portfolios eine große Fläche abdecken. Das ist also eine Grundvoraussetzung. Der Konflikt der Portfolioauswahl äußert sich schließlich in der Art der Abdeckung: Sie kann einerseits durch wenige Pumpen mit großen Betriebsfenstern, und dementsprechend ressourcenschonender Produktion, erreicht werden. Diese halten dafür aber auch schlechtere Betriebspunkte für manche Kunden bereit. Alternativ kann man die Fläche auch mit vielen kleinen Betriebsfenstern abdecken und erhält somit eine gleichmäßig gute Qualität über alle Kundenanforderungen hinweg.
Das Problem, die beste Abdeckung der Menge an Kundenanforderungen durch Betriebsfenster zu finden, haben wir kontinuierliche Abdeckungsaufgabe genannt. Das Wort „kontinuierlich“ hat zwei Bedeutungen. Einerseits betrachten wir keine endliche Variantenvielfalt, sondern bewegen die Betriebsfenster der Pumpen über die freie Parameterauswahl „kontinuierlich“ im Diagramm. Andererseits spielt es auf die Menge, die abgedeckt werden soll, an. Diese enthält alle vom Hersteller als möglich erachteten Kundenanforderungen, und ist daher zusammenhängend und unendlich.
Das ist bei den bereits bekannten Abdeckungsproblemen, wie dem planaren Abdeckungsproblem, mit dem man zum Beispiel Standorte von Feuerwachen bestimmen kann, meist nicht so. Eine dem kontinuierlichen Abdeckungsproblem ähnliche Aufgabe ist das sogenannte Sprinklerproblem, bei dem Wassersprinkler so auf einem Feld platziert werden sollen, dass es komplett benetzt wird. Die Sprinkler sind aus mathematischer Sicht einfacher als die Betriebsfenster der Pumpen, denn beim Verschieben ändert sich weder ihre Größe noch ihre Form. Letzteres gilt auch für die Abdeckung eines Gebiets durch bewegliche, in der Größe veränderliche Rechtecke, ein Problem, was bei der Erkennung von Hindernissen in der Robotik aufkommt. All diese Probleme sind Spezialfälle des kontinuierlichen Abdeckungsproblems und können deshalb als solches aufgeschrieben werden. Für einige von ihnen wurden in verschiedenen Bereichen der Mathematik und Informatik clevere Lösungsverfahren entwickelt. Mit Hilfe unserer neuen allgemeineren Betrachtungsweise kann man nun untersuchen, ob sich eine für ein bestimmtes Problem entwickelte Technik auf ein anderes Problem übertragen lässt.
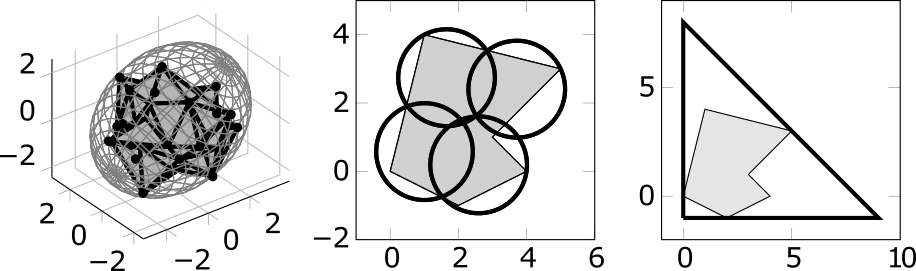
Langsam war es Zeit, die übliche Fahrtrichtung „von der Forschung in die Praxis“ einzuschlagen. Trotz der theoretischen Reichweite der kontinuierlichen Abdeckungsaufgabe, hätte sie nur dann einen Nutzen für unsere Ausgangsfrage, wenn wir das entstandene mathematische Optimierungsproblem auch lösen könnten. Naheliegend war es erstmal, bei den bekannten Lösungstechniken der Spezialfälle nachzuschauen. Leider fand sich dort nichts, was für die Optimierung des Produktportfolios geeignet war. Es hieß also weiter forschen.
Schließlich konnten wir die Abdeckungsaufgabe als semi-infinites Optimierungsproblem formulieren. „Halb unendlich“ bezieht sich bei dieser Art von Problemen darauf, dass man zwar nur endlich viele Forderungen unterschiedlicher Art, bei uns der Art „Abdeckung durch Betriebsfenster“, an seine Lösung stellt, diese aber in unendlich vielen Ausprägungen erfüllt sein müssen. Auch das ist bei unserem Problem der Fall: Jeder der unendlich vielen Punkte in der Menge möglicher Kundenanforderungen muss abgedeckt sein. Für semi-infinite Optimierungsprobleme gibt es bereits Lösungstechniken und für unser Abdeckungsproblem konnten wir aus diesen ein passendes Verfahren zusammenstellen.
Erste Testrechnungen haben es dann bestätigt: Mit einem realistischen Pumpenmodell findet das Verfahren schnell und praxistauglich ein optimales Portfolio. Wir sind also fast wieder zurück in der Praxis angekommen.
Ich hoffe, dieser Abriss aus meiner Forschungsarbeit gibt einen Eindruck davon, wie faszinierend vielschichtig „Mathematik machen“ sein kann. Ganz praktisch haben meine Kollegen und ich für die Optimierung eines Pumpenportfolios ein mathematisches Modell gefunden und ein praxistaugliches Lösungsverfahren entwickelt. Die Frage, mit der wir gestartet sind, können wir also beantworten. Indem wir uns von der Anwendung losgelöst haben, sind wir aber auch auf eine neue Problemklasse gestoßen. Ohne uns in diesem Moment um technische Details der Pumpen kümmern zu müssen, können wir über das kontinuierliche Abdeckungsproblem scheinbar völlig unterschiedliche Probleme miteinander vergleichen und vorhandenes Wissen über sie übertragen.
Helene Krieg hat an der Universität Konstanz Mathematik studiert. Bereits während ihrer Masterarbeit in der AG Umweltphysik stellte sie sich die Frage, wie Mathematik in anderen Forschungsdisziplinen Nutzen stiften könnte. Ihre Doktorarbeit schrieb sie an der TU Kaiserslautern in Kooperation mit dem Fraunhofer Institut für Techno- und Wirtschaftsmathematik. Unter dem Titel „Modeling and Solution of Continuous Set Covering Problems by Means of semi-infinite Optimization” entstand dabei ein mathematisches Verfahren mit dem ein Portfolio von Transportpumpen optimiert werden kann. Derzeit arbeitet sie als wissenschaftliche Mitarbeiterin am Fraunhofer Institut für Techno- und Wirtschaftsmathematik in Kaiserslautern.


