The Twelve Days of Christ-maths
BLOG: Heidelberg Laureate Forum

It’s the season for Christmas carols, and one of the most mathematically relevant is the Twelve Days of Christmas – it’s an anthem for generous gift-giving, as well as a great way to engage small children in learning to count. But is there any deeper mathematics behind this classic tune?
If you’re not familiar with the song, the lyrics tell the story of the increasingly generous gifts (although depending on who you ask, they might all actually just be types of bird) given to someone by their true love; each day, a new type of gift is added to the list, until eventually on the twelfth day the gifts are:

Twelve drummers drumming
Eleven pipers piping
Ten lords a-leaping
Nine ladies dancing
Eight maids a-milking
Seven swans a-swimming
Six geese a-laying
Five golden rings
Four calling birds
Three french hens
Two turtle doves, and
A partridge in a pear tree
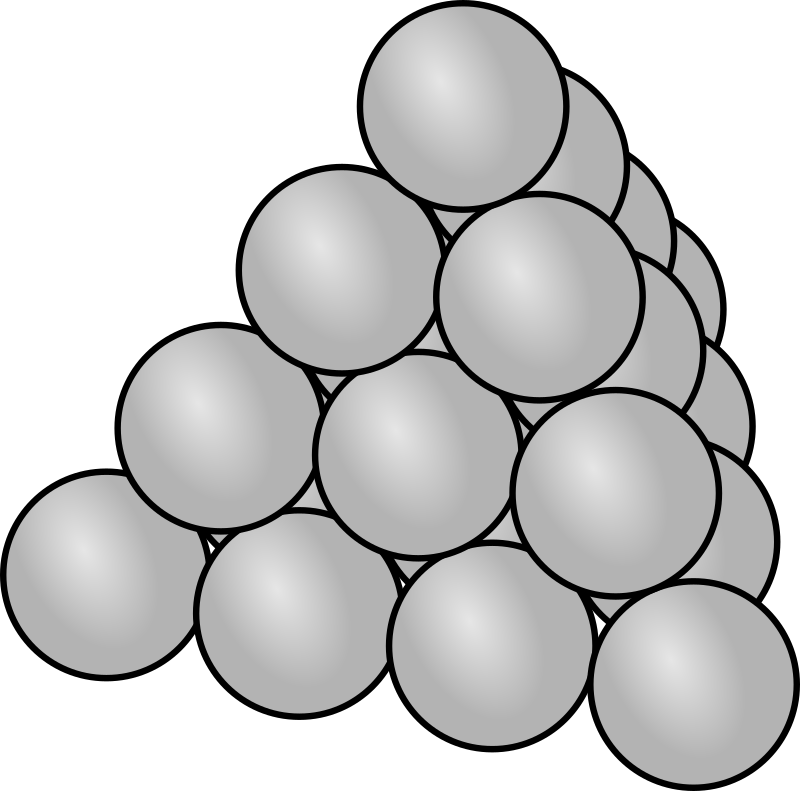
Mathematicians, on seeing a list of consecutive numbers added together like this, will immediately think of triangular numbers – the gifts could be arranged in a triangle, with a row of each type. These are sums which often crop up in different mathematical applications, and can be calculated using a simple formula:
\[ T_n = \sum_{i=1}^n i = \frac{n(n-1)}{2} \]
So in this case, we’d multiply \(11 \times 12\) and divide by \(2\), giving a total of 66 gifts. This formula has been studied historically by many different mathematicians, and there’s evidence that the followers of Pythagoras used to use stones laid out in triangular shapes to consider and understand the patterns. The formula was also known to Aryabhata (b. 476 CE), an Indian mathematician and astronomer, and Al-Karaji (d. 1019 CE) a mathematician and engineer based in Baghdad.
All I want for Christmas
However, mathematicians are known for their ability to interpret things literally. This holiday haul is actually even more generous than you might think – the song clearly states that one gift is given on the first day of Christmas, then on the second day, the gift includes the same gift from the first day plus an additional two gifts, and so on. So the total number of actual gifts is the sum of the first 12 triangular numbers.
Calculating sums of triangular numbers might seem intimidating – I could write a sum that uses the previous formula:
\[ \sum_{i=1}^n T_i = \sum_{i=1}^n \frac{i(i-1)}{2} \]
This isn’t particularly easy to use – and while I could probably wrangle this into something useful using algebra, I’m going to take the mathematicians’s route and think about this more geometrically. If I have a set of triangles increasing in size, I could stack them up into a pyramid – with the largest triangle at the bottom, and the smallest on top.
This would give me a tetrahedron – and tetrahedral numbers also have a general formula:
\[ \textrm{Te}_n = \sum_{i=1}^n T_i = \frac{n(n+1)(n+2)}{6} \]
This formula, given the value \(n=12\), returns 364 items – a truly generous gift. If you saw my ‘Twelve Facts of Christmas’ post from a few years ago, you might also recall that the tetrahedral numbers sit alongside the triangular numbers in the diagonals of Pascal’s triangle.
There are also other interesting questions to ask – on the first and eighth days of Christmas, the number of gifts are 1 and 36, which are both also square numbers. Square triangular numbers – those which are both square and triangular – also form a nice sequence to explore. You could ask yourself, when would the next square triangular occur – and how many gifts will my true love need to have given me by that day of Christmas? I’ll leave that one for you to calculate.
The true cost of Christmas
You might think that all this numerical and algebraic manipulation is too abstract for you, and you’d like a bit more real-world maths to think about. Well, the Twelve Days of Christmas has also made its way into the world of economics too, in the form of the Christmas Price Index.
Consumer price indexes are used by economists to measure inflation and and study economic performance – and many measures of this type involve calculating the price of a standard basket of consumer goods, including staples like bread and milk, clothing and medicine, as well as costs like rent and recreational activities. The variation in the cost of this standard set of purchases can be an indicator of how an economy is performing, and tracks the value of money.
In 1984, the chief economist at the U.S. bank PNC Wealth Management came up with the idea of the Christmas Price index, tracking how much it would cost to buy all of the items listed in the song, consulting local zoos, jewellers and performer’s unions to find out the going market rate of providing all the French hens, gold rings, and ladies dancing.
As well as calculating the Christmas Price Index (the total price of the gifts given on day 12 only), the bank also calculates the True Cost of Christmas, which includes the gifts given on all the other days (all 364 items). In 1984 the initial rates were $12,623.10 for the CPI, and $61,318.94 for the TCOC. Today (figures from 2021) you’d pay $41,205.58 (CPI) and $179,454.19 (TCOC) for the same items – maybe only a millionaire’s true love could benefit from such a gift.
Over the years, the index has been an interesting reflection of the growing service economy in the US – while prices for goods have fallen, the cost of labour has increased, and in this non-bird-based interpretation of the song, many of the higher-quantity gifts are in the form of people milking, dancing, or playing instruments (although critics complain that the cost of the eight maids-a-milking doesn’t also include the cost of a cow, bucket, or stool).
Whatever gifts you give or receive this Christmas, you can be glad you’re not the true love mentioned in the song – having committed to this excessive display of affection might leave you significantly out of pocket!


Katie Steckles wrote (14. Dec 2022):
> […] Mathematicians, on seeing a list of consecutive numbers added together like this, will immediately think of triangular numbers […] a simple formula
Indeed:
\[ T_n := \sum_{k = 1}^n \, k = \frac{n \, (n + 1)}{2}. \]
cmp. https://en.wikipedia.org/wiki/Triangular_number#Formula
This results in a total of
\[ T_{12} := \frac{12 \times 13}{2} = 78 \]
gifts being given in the course of \(12\) days;
not accounting for conceivable cutbacks due to inflation, recession, etc., of course.
p.s. — SciLogs comment sandbox:
Without having to engage in tedious considerations of diverse notions of “roundness” (touched upon in a prior SciLog article),
here — as a kind of gift — is a metric definition of a set \( \mathcal C \) having “a corner at” \( V \in \mathcal C \); namely if and only if:
\( 0 = \underset{(\tilde P, \tilde Q \in (\mathcal C \setminus \{ V \}), \tilde P \not\equiv \tilde Q)}{\text{Inf}} \left[ \frac{(V \tilde P)^2 \, (V \tilde Q)^2 \, (\tilde P \tilde Q)^2 }{ 2 \, (V \tilde P)^2 \, (V \tilde Q)^2 + 2 \, (V \tilde P)^2 \, (\tilde P \tilde Q)^2 + 2 \, (V \tilde Q)^2 \, (\tilde P \tilde Q)^2 – (V \tilde P)^4 – (V \tilde Q)^4 – (\tilde P \tilde Q)^4} \right] \).
It’s just a pity that there is no Big Bang version of the „Twelve Days of Christmas“