The Twelve Facts of Christmas: Pascal’s Triangle
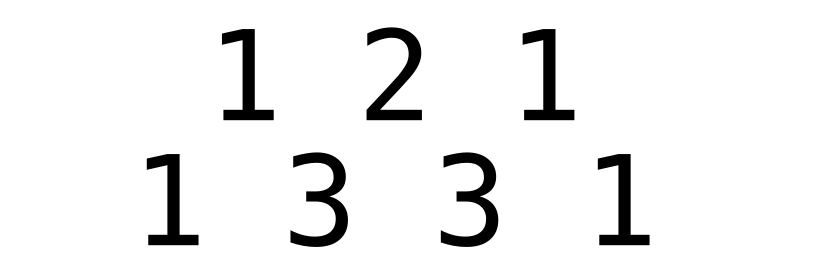
At this time of year, you’ll see a lot of decorations around and a lot of shapes – stars, trees, snowmen, and so on. One shape you might not see many of though, is the triangle, and I think that’s a shame. So I’m going to share with you my 12 facts of Christmas, about one of the greatest triangles in mathematics: Pascal’s triangle.
-
It can be created simply by adding numbers together
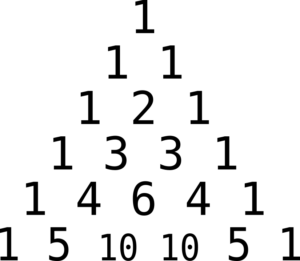
 To generate Pascal’s triangle, start with a one (the number of partridges in a pear tree) and imagine it’s sitting in an infinite row of zeroes going off to either side. Then you can generate the next row by writing the sum of each pair of numbers in the row in the gap underneath them.
To generate Pascal’s triangle, start with a one (the number of partridges in a pear tree) and imagine it’s sitting in an infinite row of zeroes going off to either side. Then you can generate the next row by writing the sum of each pair of numbers in the row in the gap underneath them.
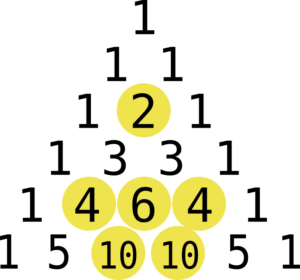
This will give you an infinite row of zeroes with two ones in the middle, then repeating again will give you that with 1, 2, 1 in the middle, and so on. The rest of the triangle is obtained by simply repeating this process for the rest of time.
-
It’s named after Blaise Pascal, but someone else discovered it first
Although Pascal’s triangle is named after mathematician Blaise Pascal, many other mathematicians knew about the triangle hundreds of years earlier. Chinese mathematician Jia Xian (c. 1050) supposedly “[used] the triangle to extract square and cube roots of numbers,” and Persian mathematician Omar Khayyam (c. 1048–1113) seemed to also have knowledge of the structure.
-
The numbers in the triangle are the coefficients of binomial expansions
If you have a bracket containing a sum, (a+b), and you want to raise that bracket to a power n, you will find that the different powers of a and b in the resulting expansions have different coefficients in front of them.
(a + b)2 = (1)a2 + 2ab + (1)b2
(a + b)3 = (1)a3 + 3a2b + 3ab2 + (1)b3
(a + b)4 = (1)a4 + 4a3b + 6a2b2 + 4ab3 + (1)b4
These coefficients are exactly the numbers in the nth row of Pascal’s triangle! (The first row of the triangle is called row 0, so when I say the nth row, I mean the one that starts ‘1, n’.)
This is connected to the fact that the triangle also encodes the ‘choose’ function in mathematics: If you have a pile of n things, and you want to choose k of them, the number of possible ways to do this will be the kth entry in the nth row of Pascal’s triangle (again starting from the 0th in rows and columns).
For example, if I have 5 gold rings, and I want to give one of them to each of my two true loves, the number of different ways to choose two rings from five is 10 – which can be found in the fifth row, second column.
-
The diagonals in the triangle are interesting number sequences
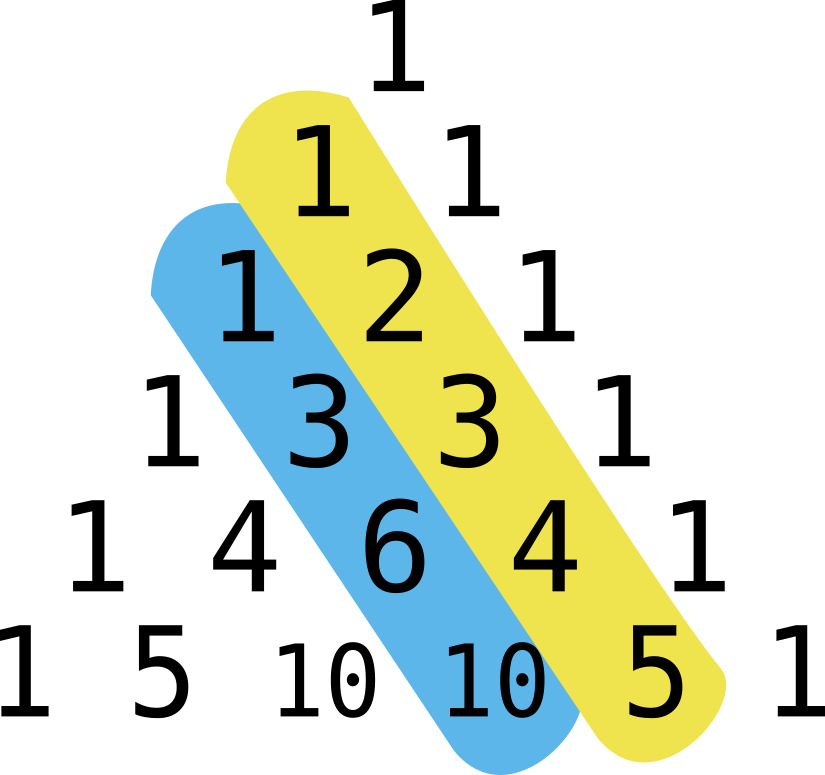 Apart from the outside edge, which is all made up of 1s, the other diagonals all have nice properties – the first stripe is just the whole numbers counting upwards; the next is the triangular numbers (sums like 1, 1+2, 1+2+3, 1+2+3+4 etc) – if you had a triangular number of Christmas puddings, you could arrange them into a triangle on the table.
Apart from the outside edge, which is all made up of 1s, the other diagonals all have nice properties – the first stripe is just the whole numbers counting upwards; the next is the triangular numbers (sums like 1, 1+2, 1+2+3, 1+2+3+4 etc) – if you had a triangular number of Christmas puddings, you could arrange them into a triangle on the table.
The next stripe is the 3D triangle numbers, or tetrahedral numbers: the number of spherical Christmas puddings you can stack in a triangular-based pyramid, and each such number is a sum of the first triangular numbers. In fact, this pattern continues – the next set is 4D tetrahedral numbers, called pentatope numbers, and so on.
-
It’s also got Fibonacci Numbers in there
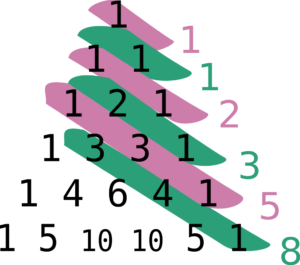
Taking a less steep diagonal slice through the triangle, and adding the resulting numbers, you’ll find they each sum to a Fibonacci number – each one is the sum of the previous two.
These numbers have many mysterious and deep connections in mathematics, and also occur in hypothetical rabbit population dynamics.
-
There’s a pattern in the sums of each row
If you add the numbers in each horizontal row together, you’ll find there’s an interesting pattern in the numbers you get. Bonus points if you can work out why!
-
The products of the rows also do something interesting
If you multiply together all the numbers in each row, that’ll give you a sequence of numbers. If you write Sn for the nth number in that sequence, then the following is true: This says that if you take the product of a row, multiply it by the product of the row two below that, and then divide that by the square of the product of the row in between, this value gets closer and closer to the exponential constant e (as your value for n gets bigger and bigger). It gets everywhere, the number e…
This says that if you take the product of a row, multiply it by the product of the row two below that, and then divide that by the square of the product of the row in between, this value gets closer and closer to the exponential constant e (as your value for n gets bigger and bigger). It gets everywhere, the number e…
-
It also gives you the number of paths in a grid
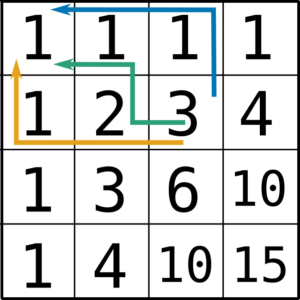 If you have a square grid, and are allowed to move from one box to another vertically or horizontally adjacent box, you can challenge yourself to find a route from anywhere in the grid to the top left square. If you write the numbers of Pascal’s triangle diagonally across a square grid, you’ll find that the number in each square gives the number of different routes you can take from that square to the top left square.
If you have a square grid, and are allowed to move from one box to another vertically or horizontally adjacent box, you can challenge yourself to find a route from anywhere in the grid to the top left square. If you write the numbers of Pascal’s triangle diagonally across a square grid, you’ll find that the number in each square gives the number of different routes you can take from that square to the top left square.
-
If you colour it in, you get a fractal
Colouring in the even numbers of Pascal’s triangle one colour, and the odd numbers another, results in an exact copy of Sierpinski’s triangle, the triangular fractal. The more rows you colour down the triangle, the more detailed a fractal you get (not much can be seen in this example, but this video shows the process nicely).
-
There are still open mathematical questions about it
Even though we know many things about the numbers in Pascal’s triangle, there are still mysteries to be solved. An open conjecture, called Singmaster’s Conjecture, muses on the question of how many times, at most, any given number N > 1 can occur in the triangle. The most frequently occurring number known is 3003, which is in there 8 times, but there’s no exact value known for a maximum, if one even exists. I wrote about it for The Aperiodical a few years ago, if you’d like to read more.
-
There’s a higher dimensional version called Pascal’s pyramid
The 3D triangle is a tetrahedron of numbers, and encodes trinomial coefficients – found when you raise a bracket of the form (a+b+c) to the nth power. The numbers on each layer of the tetrahedron are the sum of the three adjacent numbers in the layer above it. Makes you wonder what a 4D tetrahedron looks like, if you weren’t already from Fact 4.
-
There’s such a thing as the Christmas stocking identity, and it’s about Pascal’s triangle
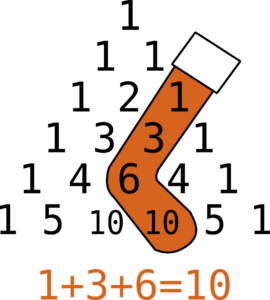 In case you were worried this post was veering away from being mildly Christmas-themed, don’t worry – if you draw the shape of a Christmas stocking and overlay it on Pascal’s triangle, there’s a nice pattern to be found there as well. Also called the hockey-stick identity, it states that the a sequence of numbers moving diagonally in towards the middle of the triangle will add up to the final number just off the diagonal at the bottom. Festive!
In case you were worried this post was veering away from being mildly Christmas-themed, don’t worry – if you draw the shape of a Christmas stocking and overlay it on Pascal’s triangle, there’s a nice pattern to be found there as well. Also called the hockey-stick identity, it states that the a sequence of numbers moving diagonally in towards the middle of the triangle will add up to the final number just off the diagonal at the bottom. Festive!




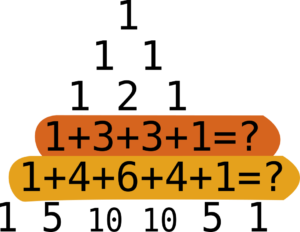
There is now available a most natural extension of Pascal Triangle called Newtonian Triangles or Binomial Triangles available on Google search engine which has been used to make some Diophantine Equations accessible
Are you sure about #7? (“The products of the rows also do something interesting”).
Yeah, they do something interesting, but the description is misleading, to say the least.
Actually, it is not the ratio between the products of adjacent rows. Its’s the ratio between neighbouring ratios! And it converges very very very slowly. Need long arithmetics to see what’s going on.
The bean machine, also known as the Galton Board:
https://en.wikipedia.org/wiki/Bean_machine
Pascal’s Marble Run – or the Deterministic Galton Board:
http://www.karlsims.com/marbles/
DearTeacher, where i’ll find the proof of the limit about #7?