The Mathematics of Distancing


Lately, we’ve all been made acutely aware of distances. Whether it’s two metres, one metre, six feet, or the UK government’s nebulous ‘one metre plus’, we’ve all been looking at the spaces between ourselves and those around us and trying to measure them. (Personally, I try to keep two metres’ distance, and an easy shorthand for this is to bear in mind that the average person is somewhere approaching two metres tall, so I always make sure there’s room for someone to fall over and land with their head at my feet).
In mathematics, the notion of distance has long been a point of discussion and study. We have various ways of measuring distance (called distance metrics), and not all of them work the way you’re used to. The standard way of measuring the distance between two points – in what’s called Euclidean geometry – is to draw a straight line between the two points and measure the length of that line. You might be thinking, “yes, that’s obviously what the word ‘distance’ means!”. But it’s not always that simple.
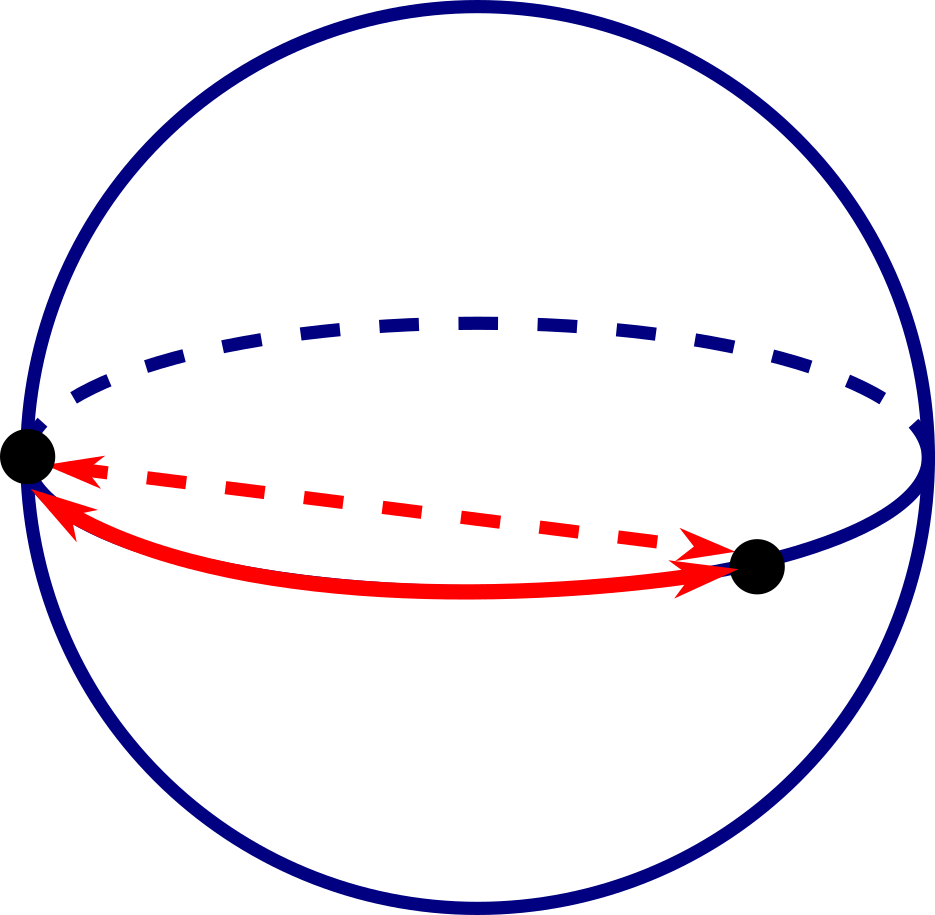
For example, if you’re comparing two points on the surface of a sphere, the distance between them isn’t defined in the same way. If you draw an actual straight line between two such points, it would go through the sphere itself, under the surface – and that’s not how you measure the distance between two cities on the surface of the earth!
In spherical geometry, a straight line is one running along the surface of the sphere; while it’s not in practice actually straight – it curves with the surface – it will be the shortest line that joins the two points, if you’re restricted to going along the surface. In fact, it will always be a section of a circle centred at the centre of the sphere, called a great circle. The length of this line is the definition of distance we use for cities on the planet or points on a sphere.
There are other notions of distance too. One which might be crushingly familiar if you live or work in a big city with blocks, like New York, is the taxicab distance metric – imagine two points at intersections of streets in a grid. Travelling between two points would involve going along the streets since you can’t cut through the buildings – so the shortest distance between two points is the number of blocks you need to go vertically and horizontally.
With a little checking, you can verify that this distance doesn’t change depending on the route you take (assuming you still go the sensible way and don’t go past the road you need to turn on to); if you have to go three blocks across and two blocks up, you’ll always move 5 units of distance to get there, regardless of whether you zig-zag or just go round the edge.
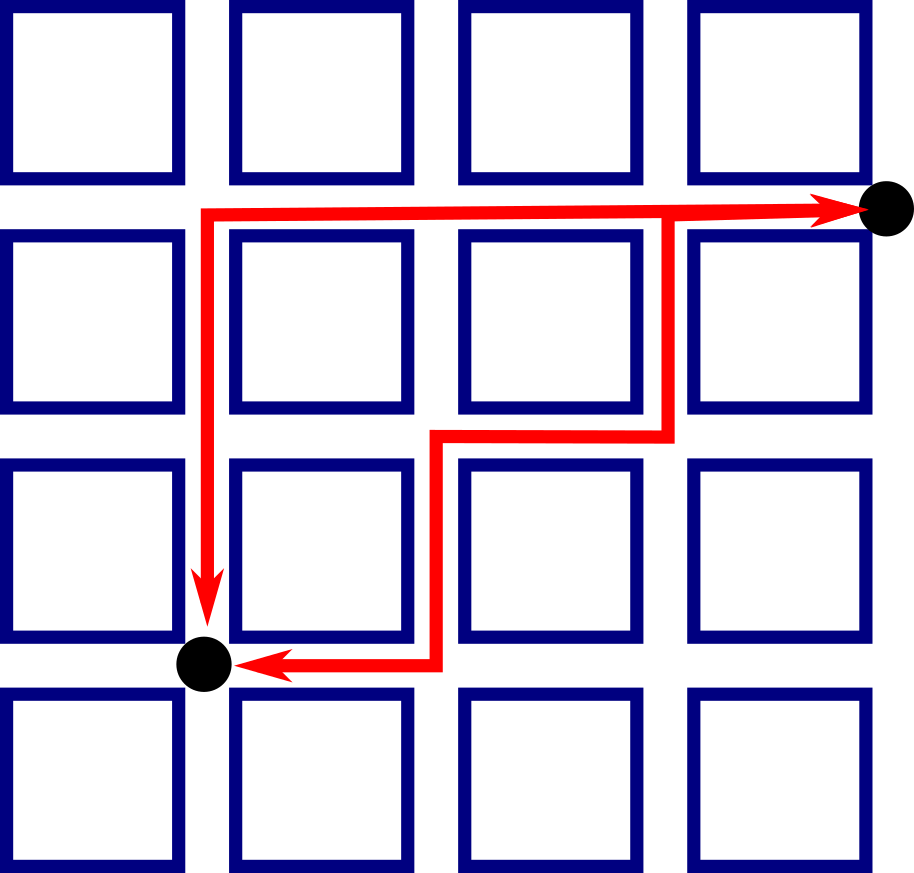
This is one of the important aspects of a distance metric – it has to make sense and be consistent. We say it’s well-defined. You need to have a way of defining it that gives a unique answer – so it’s usually something like ‘the shortest’ or ‘the fewest steps’.
We have some other rules too, which need to be true for something to be a valid metric. Firstly, the distance from A to B has to be the same as the distance from B to A – you should get the same answer whichever way you measure it. It’s also important that the distance from a point to itself should work out to be zero, and all other distances should be positive (greater than zero).
Finally, we also have a condition called the triangle inequality – this says that if you go from A to C via B, it should always be the same distance or longer than it would be to go directly from A to C. The name makes sense if you picture a triangle in the usual Euclidean metric – going via B will be the same distance if B is on a line between A and C, and longer if it isn’t, forming a triangle between the three points.
Not all metrics are physical distances between points – you can even define a metric on words, called Hamming distance. It’s defined as the number of places the words differ in. For example, the word ‘SONGS’ is one away from the word ‘SINGS’, but two away from the word ‘SNAGS’. This gives you a measure of how similar two strings of letters are – a ‘distance’ in the space of words of a given length – and it’s used in the theory of encoding.
I’ll leave you with a puzzle related to distances that might serve as a useful distraction if distancing in the real world gets all too much for you. Imagine your local rules about distancing are slightly strange – instead of having a specific distance you need to keep away from people, you’re only allowed to be one of two different distances away, but what those distances are is unspecified. (To be clear, we’re talking about the normal Euclidean definition of distance here). For example, if four people are meeting somewhere, they could stand in a square, as shown.
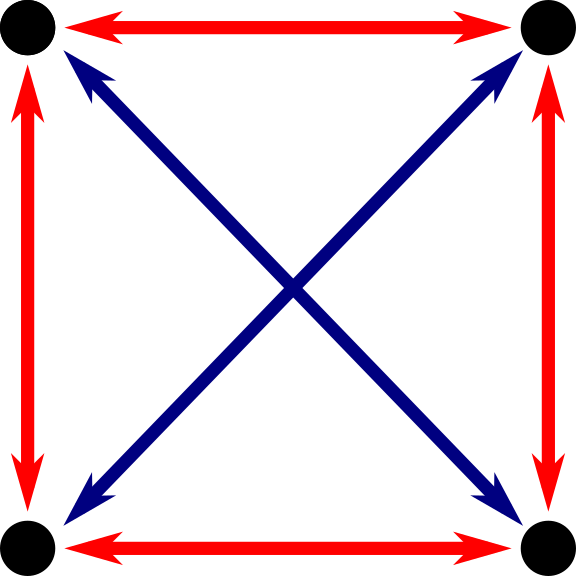
In this situation, there are two different distances involved: the four people are each the same distance away from the people next to them as you go around the square (since that’s the definition of a square – all four sides are the same length); the distance between the people who are diagonally opposite each other across the square is longer (√2 times the side of the square, to be exact). But for any of the six pairs of two people I could pick out, the distance between them is one of those two things.
This isn’t the only way to arrange four people so this works – there are a few other answers as well. I won’t tell you how many, but see how many different ones you can find. It’s called the Four Points, Two Distances problem, if you want to check whether you’ve found them all, and there are several good blog posts about it online. Can you see a way to prove you’ve got them all?


In Austria, the distance measure is a baby elephant. No joke.
Here a picture with Minister of Health Rudi Anschober, Federal Rescue Commander Gerry Foitik and Medical Association President Thomas Szekeres: https://images.derstandard.at/img/2020/06/02/IMG1807.jpg?w=1200&h=600&s=eb7c67ac
The Four Points Two Distances Proof of Colin Wright solves the problem by starting with a triangle ABC which has 2 short sides and one long side. Then he searches for all possible placements of point D so that Point D either has a short or long side with point A, a short or long side with point B and a short or long side with point C. These are 8 (2x2x2) possibilities. Two of them are geometrical impossible, so that we get 6 legal solutions.
Katie Steckles wrote (10. Aug 2020):
> […] In mathematics, […] The standard way of measuring the distance between two points – in what’s called Euclidean geometry – is to draw a straight line between the two points and measure the length of that line.
Then that’s apparently different (indeed quite the opposite) from the standard way of measuring the distance between two points (identifiable “material points”, “parts of objects” or “participants”) in physics and hence, in applied sciences.
There, distances (or at least: distance ratios) are determined first; and only subsequently, from these measured ratios, it is determined which points had been “(triplewise) straight” wrt. each other, and which had not, in the trial under consideration. For instance, points
H,JandKwould be called having been “straight” with respect to each other, in a particular trial, only if the values of their distance ratios among each other had been determined and it had been found in terms of these values that– either
(HJ / HK) + (JK / HK) = 1,– or
(HK / HJ) + (JK / HJ) = 1,– or
(HJ / JK) + (HK / JK) = 1.In spherical geometry, a straight line is one running along the surface of the sphere; while it’s not in practice actually straight – it curves with the surface – it will be the shortest line that joins the two points, if you’re restricted to going along the surface. In fact, it will always be a section of a circle centred at the centre of the sphere, called a great circle. The length of this line is the definition of distance we use for cities on the planet or points on a sphere.
> In spherical geometry, a straight line is one running along the surface of the sphere;
Or the other way around, with precedence given to measured distances (or at least distance ratios):
Given sufficiently many points with distance ratios such that between any arbitrary four among them (say
A,B,FandG) their distances obtained between each other are such that the corresponding Gram determinant vanishes for the same non-zero valueκ:0 = Det[ {{ 1 Cos[ √{κ} AB ] Cos[ √{κ} AF ] Cos[ √{κ} AG ]},
{Cos[ √{κ} BA ] 1 Cos[ √{κ} BF ] Cos[ √{κ} BG ]},
{Cos[ √{κ} FA ] Cos[ √{κ} FB ] 1 Cos[ √{κ} FG ]},
{Cos[ √{κ} GA ] Cos[ √{κ} GB ] Cos[ √{κ} GF ] 1 }
}
then these points would be called having “spherical configuration”, with “curvature radius
1 / √{κ}“. (Unless, of course, they also were all connected through overlapping straight segments.)> it curves with the surface – it will be the shortest line that joins the two points, if you’re restricted to going along the surface. […] a section of a circle centred at the centre of the sphere, called a great circle.
However, two points of a spherical configuration can be joint through (at least) two distinct great circle arcs; where generally one is longer than the other.
> The length of this line is the definition of distance we use for cities on the planet or points on a sphere.
If two points are joined through (at least one) line which is straight on overlapping segments, and if they lenght of the shortest such line equals the distance between these two points, then they are called “convex (wrt. each other)”.
p.s.
> […] a puzzle […] to arrange four people […] you’re only allowed […] one of two different distances away, but what those distances are is unspecified. (To be clear, we’re talking about the normal Euclidean definition of distance here).
The puzzling variant is apparently to restrict the arrangements to a plane (Euclidean) surface (cmp. link in comment Martin Holzherr, 10.08.2020, 16:59 o’clock);
in a flat (Euclidean) space “anything goes (within the bounds of the triangle inequality)”.
Man kann das Problem auch anders beschreiben.
Welches ist die zeitlich kürzeste Entfernung zwischen dem Ausgangspunkt A in der Wüste und den Wasserstellen B, C, D, von denen wir aber nicht wissen , welche Wasser hat. A,B,C,D bilden einen square und die Punkte sind jeweils 1 Stunde voneinander entfernt. Unterwegs bekommen wir eine Information, welche Oasis Wasser hat.
Laufen wir im Kreis, also A , B , D, also clockwise, dann beträgt die notwendige Zeit maximal 3 Stunden , wenn D mit Wasser gefüllt ist.
Geht es auch kürzer ?
Es geht kürzer, wenn wir einen Weg wählen, der in einem Bereich von 2 Punkten gleich weit entfernt ist und an einem Punkt sogar von allen 4 Punkten gleich weit entfernt ist.
Wie sieht der Weg aus. ?