Schnell, präzise und manchmal zickig: das Newton-Verfahren
BLOG: Heidelberg Laureate Forum

Im letzten Beitrag hatte ich Ihnen erzählt, welche Bedingungen ein Viereck erfüllen muss, damit es sich zusammen mit seinem Spiegelbild in insgesamt 72 Exemplaren zu einem speziellen „Monoeder“ fügen kann, einem geschlossenen Körper mit neunzähliger Symmetrie, der in der Tat nur von lauter kongruenten Polygonen begrenzt wird. Mit etwas klassischer Geometrie, vor allem dem Satz des Pythagoras, gelingt es, diese Bedingungen als Gleichungen zu formulieren, mit den Koordinaten der Eckpunkte des Vierecks als Unbekannten. Sieben Gleichungen mit sieben Unbekannten, um genau zu sein. Diesmal soll es darum gehen, wie man eine Lösung eines solchen Gleichungssystems findet.
Die Mathematik aus der Schule hilft da nicht wirklich weit. Das Höchste, was man uns in der Schule zumutete, waren drei Gleichungen mit drei Unbekannten, nennen wir sie x, y und z. Dann ging es darum, zum Beispiel eine der drei Gleichungen nach z aufzulösen, das heißt, z als einen Ausdruck darzustellen, der nur noch x und y sowie bekannte Größen enthält, und dann in den beiden anderen Gleichungen z durch diesen Ausdruck zu ersetzen. Damit hatte man es nur noch mit den beiden Unbekannten x und y zu tun. Das y wurde man auf dieselbe Weise los wie vorher das z, dann war x die einzige verbleibende Unbekannte, und mit der kam man klar.
Das Verfahren lässt sich sogar auf beliebig viele Gleichungen mit ebenso vielen Unbekannten verallgemeinern. Der Rechenaufwand gerät zwar sehr bald in Größenordnungen, die ein Schüler – mit oder ohne Taschenrechner – nicht mehr fehlerfrei bewältigen kann; aber das ist nicht das entscheidende Problem. Vielmehr funktioniert das Verfahren wirklich zuverlässig nur für eine sehr spezielle Sorte von Gleichungssystemen, die linearen. Alle Gleichungen müssen die Form haben: Konstante mal eine Unbekannte plus Konstante mal die nächste Unbekannte und so weiter plus noch eine Konstante gleich null.
Für lineare Gleichungssysteme gibt es eine erschöpfende Theorie. Entweder man findet mit ihrer Hilfe die eindeutige Lösung, oder es stellt sich heraus, dass es gar keine Lösung gibt – oder auch unendlich viele. In diesem Falle empfiehlt es sich nachzusehen, ob man von den Objekten, um die es eigentlich geht, in unserem Beispiel den Vierecken, zu viel oder auch zu wenig verlangt hat.
Zu dumm nur, dass unser Gleichungssystem nicht linear ist. Etliche der Gleichungen beschreiben nämlich die Forderung, dass gewisse Längen gleich sein müssen. Diese Längen drückt man mit Hilfe des Satzes des Pythagoras aus, Sie wissen schon: \(a^2+b^2=c^2\). Und schon kommen die Unbekannten im Quadrat vor.
Gleichungssysteme, die aus anderen Fragestellungen entstehen, haben ähnliche Probleme. Schwerkraft ist umgekehrt proportional dem Abstand zum Quadrat, ebenso die elektrostatischen Anziehungs- und Abstoßungskräfte. Chemische Reaktionsraten sind proportional dem Produkt der Konzentrationen der Reaktanden. Da steht vielleicht noch nicht einmal die kleine 2 oben an der Unbekannten, und trotzdem ist es nichtlinear, weil verschiedene Unbekannte miteinander multipliziert werden.
Die Fachleute pflegen zu lästern, dass ein Arbeitsgebiet „nichtlineare Probleme“ ungefähr so sinnvoll abgegrenzt ist wie in der Zoologie die Erforschung der Nicht-Elefanten. In der Tat: Die meisten Probleme sind von Natur aus nichtlinear, und die linearen unter ihnen sind eine ziemlich exotische Teilmenge mit dem einzigen herausstechenden Merkmal, dass es für sie eine vollständige Lösungstheorie gibt.
Da ist man als Anwender schon manchmal in der Versuchung, sein Problem so zu verbiegen, dass es linear wird. Manchmal funktioniert das sogar. Wenn es um kleine Abweichungen von einem bekannten Referenzzustand (dem „Arbeitspunkt“) geht, kann man so tun, als wären die Wirkungen der Unbekannten unabhängig voneinander und proportional der jeweiligen Ursache. Dann liefert das „linearisierte“ Problem Lösungen, die denen des echten Problems hinreichend nahe kommen.
Und was macht man, wenn das mit der Linearisierung nicht funktioniert, wie in unserem Geometrieproblem? Man linearisiert es trotzdem, gibt sich aber mit dem Ergebnis nicht gleich zufrieden. Vielmehr nimmt man es als Ausgangspunkt für einen weiteren Versuch, macht mit dessen Ergebnis dasselbe, und so weiter.
Genauer: Unser nichtlineares Gleichungssystem beschreibt eine „vektorwertige“ Funktion. Es macht nämlich aus n reellen Zahlen – den Unbekannten – n neue reelle Zahlen. Jede der n Gleichungen ist eine Anweisung, eine dieser n Zahlen zu berechnen. Und wenn alle diese Ergebnisse gleich null sind, haben wir das Gleichungssystem gelöst. Ein solches Ensemble von n Zahlen, seien es die Unbekannten oder die Zahlen, die bei der Auswertung der Gleichungen herauskommen, bezeichnet man als „Vektor“. Die Bezeichnung hat sich eingebürgert, obgleich sie das Wesentliche nicht trifft. Vielmehr ist es zweckmäßig, sich einen solchen Vektor als Punkt in einem n-dimensionalen Raum vorzustellen.
Vielleicht haben wir von der Lösung, also dem Vektor der Unbekannten, den unsere Funktion auf den Nullvektor abbildet, eine nebelhafte Vorstellung. Dann setzen wir diese vermuteten Werte in unsere Funktion ein – und bekommen natürlich nicht null heraus, wenn nicht gerade ein Wunder geschieht. Aber wenn wir ein bisschen an unseren Werten wackeln, verändert sich auch der Funktionswert. Wenn es wirklich nur ein bisschen ist, sind die Effekte des Wackelns an den einzelnen Werten voneinander unabhängig und proportional der Wackelweite, wenigstens fast. Und das heißt, das Problem ist so ungefähr linear. Wir ersetzen also unser echtes Problem durch ein lineares, und zwar dasjenige, das der Sache am nächsten kommt. In der Nähe unseres gegenwärtigen Probierpunkts, wohlgemerkt.
Wir lösen das lineare Ersatzproblem und erhalten eine neue Lösung. Die ist zwar immer noch falsch, aber – hoffentlich – weniger falsch als ihre Vorgängerin. An diesem Punkt linearisieren wir das Problem abermals; dabei kommt etwas anderes heraus als vorher, da die Linearisierung vom Arbeitspunkt abhängt. Wir lösen das neu linearisierte Problem, und so weiter, bis wir der Lösung des echten Problems beliebig nahe gekommen sind.
Das klingt jetzt alles eher nach Wischiwaschi als nach Mathematik. Man begnügt sich damit, dass die Dinge nicht exakt, sondern ein bisschen falsch sind. Wie falsch, darüber gibt es keine klare Aussage. Kann das überhaupt funktionieren? Ja. Unter der entscheidenden Voraussetzung, dass unsere Funktion differenzierbar ist. Das wiederum bedeutet nichts anderes, als dass es eine lineare Funktion gibt, die in der Nähe eines ausgewählten Punktes unserer Funktion richtig schön nahekommt. Was das genau heißt? Das will mit diesen Grenzwertbegriffen sorgfältig – und ziemlich umständlich – formuliert werden. Aber in dem Fall n=1, also eine einzige Gleichung mit einer Unbekannten, kann man sich sogar ein Bild davon machen.
Unsere Funktion wird dargestellt durch eine gewöhnliche Kurve, die gesuchte Lösung unserer Gleichung ist eine Nullstelle der Funktion, also eine Stelle, wo die Kurve die x-Achse schneidet, und die lineare Näherungsfunktion ist die Tangente an die Kurve in dem gewählten Punkt, der jetzt x0 heißen soll. Das sieht dann zum Beispiel so aus:
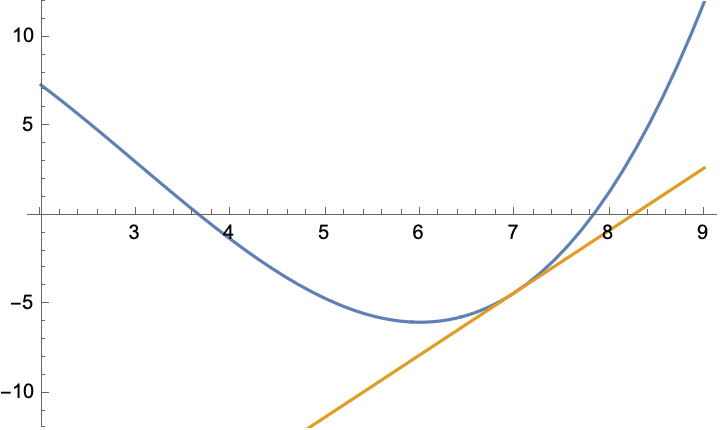
Der Graph der Funktion f(x)=x3/6 – (3/2)x2 +12 (blau) und die Tangente an diese Kurve (orange) im Punkt x0=7
Unsere Funktion hat also eine Nullstelle in der Nähe von 8. Nehmen wir an, wir hatten zunächst wenig Ahnung und vermuteten sie daher bei x0=7. Also legen wir an dieser Stelle die Tangente an die Kurve und nehmen statt der Nullstelle der Funktion, die wir suchen, vorläufig die Nullstelle der Tangente. Die ist nämlich mit einer einfachen Geradengleichung auszurechnen.
Na gut, die Tangente liegt wirklich schön eng angeschmiegt an die Kurve – in der Nähe von x0. Aber mit der Intimität ist es bald vorbei. Jedenfalls liegt die Nullstelle der Tangente immer noch ziemlich weit daneben. Aber jetzt nehmen wir den neuen Wert, nennen wir ihn x1, legen dort die Tangente an – und haben schon einen relativ ordentlichen Treffer gelandet! Man muss sich die Sache schon in der Ausschnittvergrößerung ansehen (rechts), um den verbleibenden Fehler richtig zu würdigen.
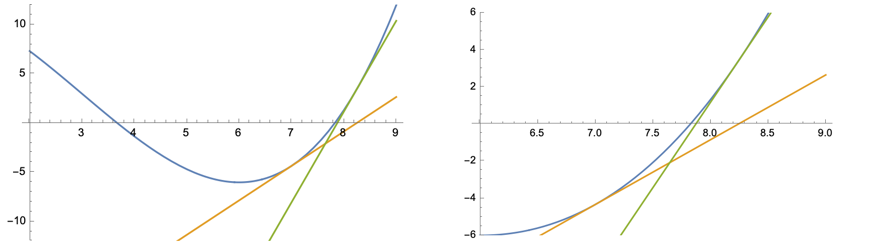
Wiederholt man das Spiel, so schießt sich das Verfahren mit atemberaubender Geschwindigkeit auf den richtigen Wert ein. Über den Daumen gepeilt verdoppelt sich mit jedem Schritt die Anzahl der richtigen Dezimalstellen.
Das Verfahren heißt Newton-Verfahren. Ob der große Meister Isaac Newton (1643–1727) als erster die Idee dazu hatte, ist umstritten.
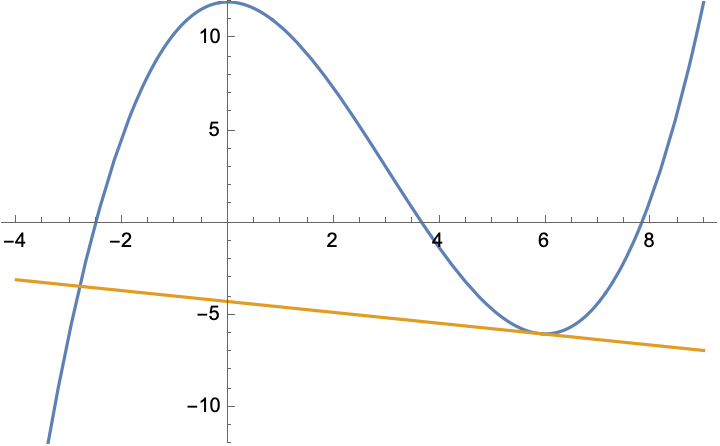
Die hohe Geschwindigkeit, mit der das Newton-Verfahren ein einmal erkanntes Ziel ansteuert, ist bis heute im Wesentlichen unübertroffen. Allerdings verhält sich das Verfahren unter Umständen sehr eigenwillig. Sehen wir uns von unserer Beispielfunktion einen etwas größeren Ausschnitt an und wählen einen anderen Ausgangspunkt x0:
Gut, die Funktion hat drei Nullstellen. Wie soll sich das arme Verfahren für eine von ihnen entscheiden? Die nächstgelegene (rechts) nimmt es jedenfalls nicht, die nur geringfügig weiter entfernte (Mitte) auch nicht. Vielmehr vollführt es einen wilden Sprung weit ins Negative, und dort könnte die Funktion die unglaublichsten Dinge anstellen (wenn ich sie nicht zu Demonstrationszwecken so schön einfach gewählt hätte). Und wenn der Ausgangspunkt nicht 5,9, sondern 6 ist, dann haben wir eine horizontale Tangente, die hat gar keine Nullstelle, und das Verfahren bricht zusammen, weil man durch null dividieren müsste.
Was kann man tun, um das Verfahren einigermaßen im Zaum zu halten? Man dämpft es, das heißt, man lässt es nicht den ganzen Schritt machen, sondern vielleicht nur ein Drittel. Dadurch bleibt es in der Tendenz eher in dem kuscheligen Bereich, wo die Kurve und die Tangente noch nicht ganz so weit auseinanderliegen. Nahe am Ziel muss man die Bremse wieder lösen, damit es hemmungslos seinen Geschwindigkeitsvorteil realisieren kann.
Der Ärger ist nur: Es gibt keinen Maßstab für Nähe. Alle Aussagen zur Differentialrechnung sind von der Gestalt „Es gibt eine Umgebung des Ausgangspunkts, in der der Unterschied zwischen Funktion und Tangente nur gering ist“, und dieser schwammige Spruch wird präzisiert dadurch, dass es eine Beziehung zwischen diesem Unterschied und der Größe der Umgebung gibt. Also kann man auch so etwas wie den Dämpfungsfaktor nicht zahlenmäßig festlegen, sondern muss ihn entsprechend den Eigenheiten des Problems steuern.
Zum Schluss noch eine gute Nachricht. Was ich hier für n=1 (eine Gleichung, eine Unbekannte) mit Kurven und Tangenten vorgezeigt habe, funktioniert genau so für größere n, also mehrere Gleichungen mit ebenso vielen Unbekannten. Nur ist jeder Versuch, das anschaulich zu machen, zum Scheitern verurteilt. Für n=1 kommt es in jedem Schritt im Wesentlichen auf eine einzige Zahl an, die Steigung der Tangente im aktuellen Punkt; und die kann man aus der Formel für die Funktion nach den Regeln fürs Differenzieren ausrechnen. Im allgemeinen Fall sind das n2 Zahlen, nämlich die Ableitungen jeder Gleichung nach jeder Variablen. Die bilden ein lineares Gleichungssystem, und dafür gibt es – siehe oben – ein erschöpfendes Verfahren. Wenn das versagt, also das lineare Gleichungssystem gar keine oder auch unendlich viele Lösungen hat, entspricht das dem Fall mit der horizontalen Tangente. Nur gibt es dafür bei n Gleichungen wesentlich mehr Möglichkeiten. Da man sich im n-dimensionalen Raum viel mehr verlaufen kann als auf der (eindimensionalen) reellen Achse, kommt es umso mehr auf geschicktes Dämpfen an.
Das Gleichungssystem für Hungerbühlers Gürteltier hatte übrigens etliche Lösungen mehr, als ich erwartet hatte. Die Gleichungen haben nämlich nichts dagegen, dass diese oder jene Seitenlänge gleich null ist und damit das Viereck zum Dreieck entartet. Zu einer der zugehörigen „falschen“ Nullstellen der Zielfunktion hüpfte das Lösungsverfahren denn auch bereitwillig hin. Es war nicht ganz einfach, einen Ausgangspunkt zu finden, von dem aus das Verfahren zu der interessanten Lösung fand.


Danke für die schöne Beschreibung zum Unterschied zwischen linearen und nicht linearen Gleichungen. Wie auch für den Blog. Liefert mir immer wieder Inspirationen.
Vielen Dank für diese Beschreibung eines nur scheinbar trivialen Problems praktischer Mathematik. Meine persönliche Schlussfolgerung:
1) entweder man findet einen völlig neuen Ansatz um die Nullstellen eines Polynoms oder gar einer beliebigen Gleichung zu finden
oder aber
2) man geht heuristisch vor und benutzt Newton‘s Verfahren im Zusammenhang mit anderen mehr heuristischen Verfahren.
Punkt 2) lässt heutzutage auch sofort an Verfahren der künstlichen Intelligenz denken, denn KI kann fast beliebig viele Methoden in Betracht ziehen und durch Training dann lernen, welche Kombination von Verfahren am schnellsten zum Ziel führt. Bestätigt werde ich in diesen Gedanken etwa durch den Artikel
A Neural Network-Based Approach for Approximating Arbitrary Roots of Polynomials †, wo man liest:
Fazit: KI scheint bis jetzt nicht besser zu sein als die simultane iterative Durand-Kerner-Methode (D-K).