Mathematik im Deutschen Museum
BLOG: Heidelberg Laureate Forum

„In diesem Haus darf jeder machen, was ich will.“ Mit diesem klassischen Spruch brachte Oskar von Miller, der Gründer und einflussreiche Gestalter des „Deutschen Museums von Meisterwerken der Naturwissenschaft und Technik“ in München bereits vor knapp 100 Jahren das „bildungsorientierte Mitmachprinzip“ auf den Punkt. Mitsamt seinen inneren Widersprüchen: Es ist ungeheuer hilfreich, wenn die Besucherinnen und Besucher an den Exponaten spielen können – aber natürlich nicht an den echten! Denn die klassische Aufgabe, historische Artefakte zu konservieren und für die Nachwelt zur Schau zu stellen, hat das Museum ja außerdem.
Nach sieben Jahren Bauzeit präsentiert sich das traditionsreiche Gemäuer seit dem 8. Juli 2022 zunächst zur Hälfte erneuert. Die Renovierung wurde in zwei Etappen aufgeteilt, damit zu jeder Zeit wenigstens eine Hälfte des Museums zugänglich ist; mit der anderen Hälfte wird die „Zukunftsinitiative“ („Zukini“ im internen Jargon) nun fortgesetzt. Unter den neu eröffneten Abteilungen sind „Bild Schrift Codes“ (einschließlich Drucktechnik und Kryptologie), „Foto und Film“, „Elektronik“ und „Mathematik“, die sich einen Flügel des Hauses teilen.
Und gerade die letztere hat in dem Spannungsfeld zwischen dem Mitmachen und dem Konservieren des Historischen eine extreme Position. Die Foto-und-Film-Leute haben eine eindrucksvolle Sammlung an alten Kameras und Bildaufbereitungszubehör anzubieten, bei der Drucktechnik gibt es historische Druckmaschinen, in der Elektronik-Abteilung kann man die Röhren, Transistoren, Kondensatoren und Widerstände noch leibhaftig besichtigen, deren moderne Äquivalente längst in der Anonymität eines langweiligen Mikrochips untergetaucht sind. (Ja, da kommen bei einem alten Mann nostalgische Gefühle für den Elektronikbaukasten seiner Jugendzeit hoch.) Und die Mathematik?
Dazu hatten die Münchner nicht viel in der Kiste. Kein Wunder: Eigentlich handelt diese Wissenschaft von abstrakten Gegenständen. Die kann man zwar manchmal durchaus in Modellen realisieren, was auch dem Verständnis sehr aufhilft; aber das sehen die Profis traditionell nicht als ihre Hauptaufgabe an. Es gab sogar eine Strömung, verbunden mit dem Namen Bourbaki, die der Reinheit zuliebe alle Anschauung aus der Mathematik verbannen wollte – gut, dass die sich einigermaßen totgelaufen hat. Immerhin: Gegen Ende des 19. Jahrhunderts kamen Modelle aus Gips, aus geschlitzten und ineinandergesteckten Papierscheiben oder auch aus gespannten Fäden in Mode, die spezielle Flächen im dreidimensionalen Raum eindrucksvoll ins Bild setzen. Und gerade für diese historischen Gegenstände kann sich die Kuratorin Katja Rasch sichtlich begeistern.
Spezielle Blenden vor einer Projektionslampe lassen (zum Beispiel) nur einen Lichtfächer austreten, der gänzlich in einer Ebene liegt. Dieser, auf einen aus Drähten modellierten Kegel gerichtet, macht spezielle Kurven sichtbar und erklärt, warum diese den Namen „Kegelschnitte“ tragen. Die Einzelteile dieses Exponats waren in den Depots verschiedener Abteilungen gelandet, weil niemand etwas mit ihnen anzufangen wusste, und haben erst aus Anlass der aktuellen Ausstellung wieder zusammengefunden.

Foto: Deutsches Museum
Flächen, die unter ihresgleichen einen minimalen Flächeninhalt haben, unter der Bedingung, dass eine gewisse Kurve im Raum (die „Randkurve“) zur Fläche gehört. Zur Visualisierung formt man üblicherweise die Randkurve aus Draht und taucht den in eine Seifenlösung. Beim vorsichtigen Herausziehen hängt in dem Drahtgestell dann eine Seifenhaut, und die hat die Gestalt einer Minimalfläche, weil minimaler Flächeninhalt auf ein Minimum der durch die Oberflächenspannung erzeugten Energie hinausläuft.

Foto: Deutsches Museum
Die Marburger Kristallografin Elke Koch und ihr Kollege Werner Fischer haben anstelle von Seife ein innovatives Material verwendet: Damenstrümpfe. Ja, auch deren Elastizität veranlasst sie, sich in eine möglichst energiearme Form zusammenzuziehen. Aber ob und unter welchen Umständen das tatsächlich exakt die Form einer Minimalfläche ist (sie sieht immerhin auf den ersten Blick so aus), konnten die anwesenden Fachleute auf die Schnelle nicht klären.
Und wie sieht es mit den aktuellen Objekten aus? Nun ja – wenn sie den Fingern des Publikums ausgesetzt sind, müssen sie unkaputtbar sein, was sich als äußerst restriktive Forderung erweist. Davon zeugen unter anderem die Holzklötze, mit denen sich die verschiedensten symmetrischen Muster legen lassen.

Die Linien auf den Klötzen sind so angeordnet, dass sie stets an die auf dem Nachbarklotz anschließen, einerlei wie die Klötze verdreht sind. Ein symmetrisches Muster bleibt symmetrisch, wenn auch vielleicht mit einer anderen Symmetrie, wenn man mit den Klötzen eine symmetrieerhaltende Operation vornimmt. Beispiel: in jeder zweiten Spalte alle Klötze um 90 Grad nach rechts drehen.
Eine neuere Entdeckung ist das Gömböc (ungarisch für „Dickerchen“). Es handelt sich um einen massiven, konvexen Körper, der wie ein Stehaufmännchen nur eine einzige stabile Gleichgewichtslage hat, aber nicht, weil in seinem Inneren ein Gewichtsstück verborgen wäre, das ihn in diese Position zwingt. Vielmehr ist die Massenverteilung vollkommen homogen. Bis vor wenigen Jahren war strittig, ob es einen solchen Körper überhaupt geben könnte. Nun ist er leibhaftig in der Ausstellung zu sehen – aber hinter Glas, man kann nicht an ihm wackeln, um sein Stehaufverhalten zu beobachten. Zu groß wäre die Gefahr, dass das gute Stück abhanden kommt.

Foto: Deutsches Museum
Kann es einen Körper geben, der in der einen Richtung einen Schatten wirft wie ein Dreieck, in der zweiten wie ein Quadrat und in der dritten wie ein Kreis? Eigentlich eine Standardaufgabe aus der darstellenden Geometrie; die Lösung ist bekannt und in der Ausstellung durch einen soliden Holzklotz realisiert, der gerade so durch drei Löcher mit den entsprechenden Formen passt. Dann stellt sich heraus: Es gibt sogar zwei wesentlich verschiedene Lösungen des Problems! Und schon grübeln die Profis, ob es noch mehr gibt, vielleicht sogar ein ganzes Kontinuum von Formen, die zwischen diesen beiden Lösungen interpolieren.

Den Holzklotz (rechts) kann man sich so entstanden denken: Auf der kreisförmigen Deckelfläche eines Zylinders, der so breit wie hoch ist, zieht man einen Durchmesser und führt einen Schnitt entlang einer Ebene, die durch diesen Durchmesser und einen Punkt auf der Bodenfläche des Zylinders geht, sowie einen gleichartigen Schnitt durch den Durchmesser und den gegenüberliegenden Punkt auf der Bodenfläche. Der 3-D-gedruckte schwarze Klotz dagegen ist ein etwas langgezogenes Tetraeder, an das vorn und hinten zwei halbe Kegel angefügt sind – keine Kreiskegel, sondern so geformt, dass die schräg zur Kegelachse geschnittene Bodenfläche einen kreisförmigen Rand hat.
Angesichts des mageren anfassbaren Materials (und des knappen Platzes) war an einen umfassenden Überblick über die Mathematik nicht zu denken. Stattdessen verlegten sich die Ausstellungsmacher auf „interessante Häppchen mit einem Schwerpunkt auf der Geometrie“. Und an dieser Stelle kommt die Wunderwaffe dieser Ausstellung ins Spiel: der Touchscreen mit dem richtigen Programm dahinter.
Man kann ja abstrakte Dinge – definitionsgemäß – nicht anfassen; aber was man mit den eigenen Fingern mit den Abbildungen dieser Dinge anstellen kann, kommt dem schon sehr nahe. Ein regelmäßiger geometrischer Körper erscheint auf dem Bildschirm; ich kann ihn nicht nur in alle Richtungen drehen, sondern ihm auch mit einem virtuellen Messer die Ecken abschneiden, mehr oder weniger radikal. Im Extremfall bleibt von jeder Kante nur noch ein Punkt übrig, und – zum Beispiel – ein Würfel hat sich in ein Oktaeder verwandelt oder auch umgekehrt. Ich kann das Messer nicht nur an die Ecken, sondern auch an die Kanten ansetzen und dadurch einen platonischen Körper allmählich in einen halbregelmäßigen (archimedischen) Körper übergehen lassen, und noch viel mehr.
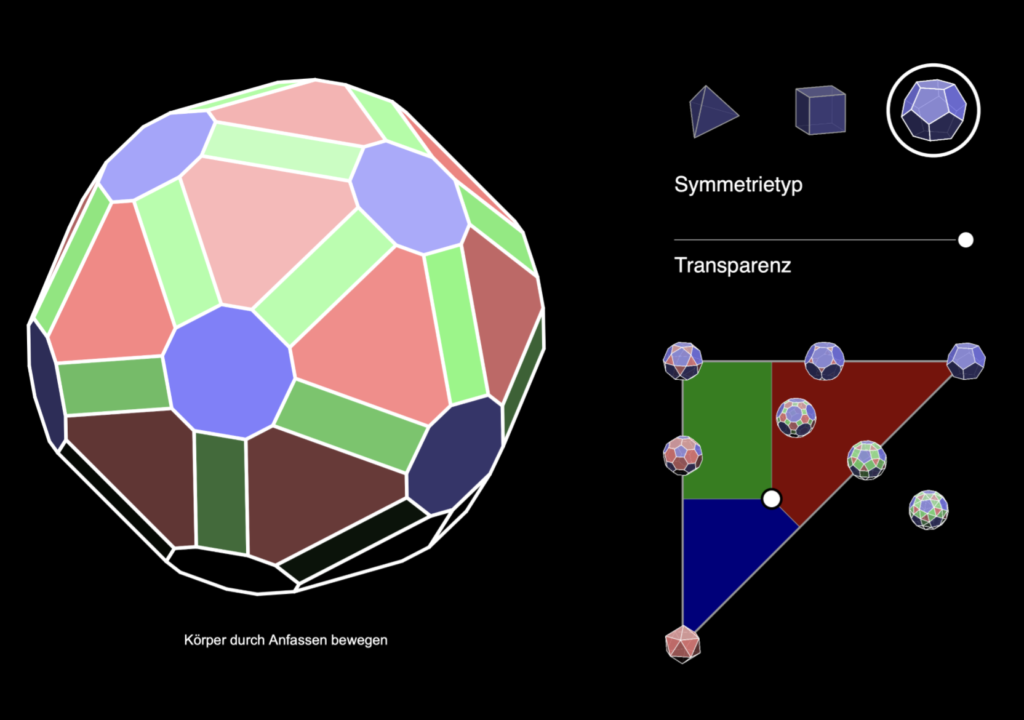
© Jürgen Richter-Gebert
Mein Finger verwandelt sich in einen virtuellen Pinsel (Farbe und Strichdicke einstellbar) und macht einen bescheidenen Strich auf den Touchscreen. Auf der Stelle erscheint nicht nur der Strich, sondern verschobene, gedrehte und gespiegelte Bilder desselben, so dass ein regelmäßiges Ornament entsteht, entsprechend einer Symmetriegruppe, die ich ebenfalls wählen kann. Das funktioniert nicht nur in der Ebene, sondern auch auf der Kugel – jawohl, man kann die Kugeloberfläche mit lauter kongruenten, leicht gewölbten Kacheln lückenlos bedecken. Die App iOrnament, die der aktuellen Entwicklung zu Grunde lag, bietet darüber hinaus auch Ornamente in der hyperbolischen Ebene. Das ist jenes Gebilde, in dem es zu einer Geraden durch einen gegebenen Punkt nicht nur eine Parallele gibt wie in der gewöhnlichen Ebene (das ist das berühmte euklidische Parallelenaxiom), sondern unendlich viele. In ihrer wahren Schönheit kann man sie nicht sehen, aber es gibt eine Verzerrung, die die ganze hyperbolische Ebene auf eine Kreisscheibe abbildet (die Poincaré-Abbildung). Und in dieser Form wirken die Muster äußerst dekorativ.

© Jürgen Richter-Gebert
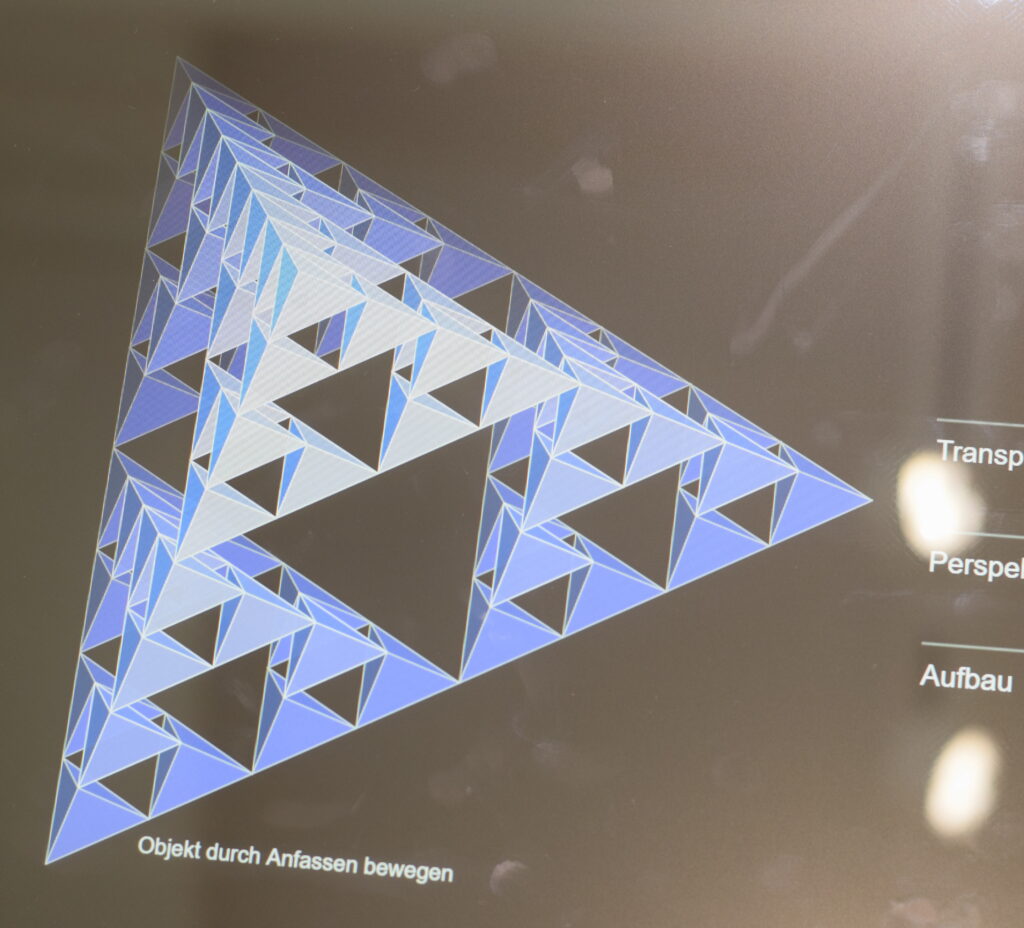
Ein abstraktes Objekt erlaubt den direkten Vergleich zwischen der leibhaftigen und der virtuellen Darstellung: das Sierpinski-Tetraeder. Man ersetze ein gewöhnliches (reguläres) Tetraeder durch vier seinesgleichen mit der halben Kantenlänge, die in dessen Ecken sitzen, oder was auf dasselbe hinausläuft, man schneide aus der Mitte des Tetraeders ein reguläres Oktaeder heraus, so dass die vier kleinen Tetraeder übrigbleiben. Man wiederhole diese Prozedur mit den kleinen Tetraedern, dann mit den 16 ganz kleinen Tetraedern, die dabei herauskommen, und so weiter ad infinitum. Das Ergebnis des Grenzprozesses ist ein Fraktal mit den merkwürdigsten Eigenschaften (Volumen null, Oberfläche endlich, Summe aller Kantenlängen unendlich); und natürlich kann keine Darstellung das wirklich erfassen. Ziemlich bald kommt sie wegen der Stabilität des Materials oder der Größe der Pixel auf dem Bildschirm an ihre Grenzen. Aber immerhin: An der Decke hängt eine Näherung an das Sierpinski-Tetraeder, im Glaskasten, damit den Besucherinnen und Besuchern nicht Stücke des empfindsamen Objekts auf den Kopf fallen, und auf dem Bildschirm kann man es auch bewundern.
(Foto links oben: Deutsches Museum) Das Sierpinski-Tetraeder leibhaftig (links) und virtuell. Wenn der Blick von der Mitte einer Kante genau zur Mitte der gegenüberliegenden Kante des Ur-Tetraeders gerichtet ist, dann ist das Sierpinski-Tetraeder ebenso wie jede seiner Näherungen blickdicht – einigermaßen erstaunlich für ein Objekt, das eigentlich nur noch aus einer Wolke von Punkten besteht.
Ich muss gestehen, das virtuelle Bild macht sich besser. Und das sagt jemand, der das Verfertigen leibhaftiger geometrischer Körper mit großer Intensität betreibt.
All diese Programme sind das Werk eines einzigen Menschen: Jürgen Richter-Gebert, Professor für Mathematik an der TU München und – nicht nur mit den Touchscreen-Programmen – maßgeblich an der Konzeption der Ausstellung beteiligt. Was die Ornamente angeht, hat seine rastlose Aktivität in der App iOrnament ihren Niederschlag gefunden. Weitere Projekte sind auf seiner Website science-to-touch zu finden.
Am Ende haben die Touchscreen-Exponate und die „hands-on“ Mitmachstationen als wesentliches Argument im Tauziehen um die Quadratmeter für die Mathematik gedient. „Da haben die Leute etwas zu spielen, und so viel Kindergarten muss das Museum haben, damit es attraktiv ist.“ Da mag die Nase rümpfen, wer in der Mathematik eine ernste Sache sieht, die keine Spielerei verträgt; aber wenn’s der Wahrheitsfindung dient …





Sehr guter Artikel.
Zum Thema fehlende Mathematik.
Zu Beginn des 20 . Jahhunderts waren Modelle aus Holz modern die mathematische Probleme lösen konnten. Bekannt ist nur noch der Weg des Handlungsreisenden, das Modell besteht aus einer Holzscheibe mit mehreren Löchern, die die Orte repräsentieren, die der Handlungsreisende aufsuchen muss.
Mit Schnüren und Gewichten lässt sich nun der optimal kürzeste Weg finden.
Es gab auch ein Modell für das Dreikörperproblem.
Und in einem sehr alten Buch waren noch mehrere solche Modelle aufgezeichnet. Ich habe trotz Recherche nicht herausfinden können, wie das Buch hieß.
Holzscheibe mit Löchern? Das klingt nicht nach dem Problem des Handlungsreisenden, sondern nach dem Problem des kürzesten aufspannenden Baums („Steiner-Baum“): Finde das Straßennetz mit der kürzesten Länge, das eine Anzahl von gegebenen Städten miteinander verbindet. Für drei Städte ist die Lösung: Von einem Punkt in der Mitte gehen Straßen zu jeder Stadt, und der Punkt ist der eindeutig bestimmte mit der Eigenschaft, dass alle drei Straßen sich unter einemWinkel von 120° treffen. Diesen Punkt findet der Holztisch mit den Löchern.
Modell für das Dreikörperproblem? Ich kann mir nicht vorstellen, wie das aussehen soll.
Mit dem sehr alten Buch meinen Sie wahrscheinlich „Mathematische Modelle“ von Gerd Fischer (Vieweg 1986), Bildband und Kommentarband.
Christoph Pöppe,
Sie haben Recht, das war das Modell für die kürzeste Straßenlänge.
Das gemeinte Buch habe ich schon um 1970 herum gelesen und es war sehr alt.
Aber Danke für den Hinweis.
Was das Dreikörperproblem betrifft, das macht es doch so spannend, man kann ja nicht ausschließen, dass solche Modelle einfach in Vergessenheit geraten sind.
Das war kein statisches Modell, es hatte zwei Hebelarme, mehr weiß ich nicht mehr. Wirklich schade.
Es gibt noch mehr Bücher, die ich kannte und kann sie nicht wiederfinden.
Wenn Sie einfachste Technik mögen “Katastrophenreparatur für Fahrräder”, nicht mehr auffindbar. Ein Beispiel, was macht man, wenn auf einem Waldweg der Lenker bricht ? Das Buch lieferte eine sehr einfache Lösung. Finden Sie sie !
Anhänger scheint diese Strömung noch in der Wikipedia zu haben, wenn man die Artikel so als Laie betrachtet.
Gilt das mit den (mindestens) zwei Lösungen für die Schatten im allgemeinen Fall, oder nur für den Spezielfall Dreieck/Quadrat/Kreis? Es gibt ja beispielsweise auch den Klotz, der je nach Richtung die Buchstaben G, E und B projiziert (auf dem Cover meiner Ausgabe von “Gödel Escher Bach”). Kann es da auch eine weitere Lösung geben, oder ist das Muster zu kompliziert dafür?