Magic in the Square
BLOG: Heidelberg Laureate Forum

Around this time of year, magic seems to be everywhere – the magic of Christmas, the beauty of falling snowflakes, and the wonder of coming together and sharing the darkest part of the year with gifts and delicious fare. But people sometimes forget about the most important kind of magic: that found in magic squares.
In maths, a magic square is defined as an arrangement of numbers in a grid which, if added along the rows, columns or diagonals, gives the same ‘magic’ total in each direction. For example, the three-by-three magic square made using the numbers 1 to 9 looks like this:
If you add up any row, column or major diagonal (one running from corner to corner) in this square, you should obtain the total 15. This pleasing symmetry is unique – this is the only possible way to arrange these numbers with this property, other than arrangements which are rotations or reflections of this one.
We call an n-by-n magic square like this – using the first n² whole numbers – a normal magic square. For such squares, the magic total is given by \(\frac{n(n^2+1)}{2}\). For normal magic squares of side length n = 3, 4, 5, 6, 7, and 8, the magic constants are 15, 34, 65, 111, 175, and 260 respectively.
The study of magic squares dates back a long way – ancient mathematics was fascinated with combinations of numbers with interesting properties, and magic squares date back to China in 190 BCE, with evidence of later study in Japan, India and Persia/Arabia before coming to Europe around 1315.
They have also been considered to have mystical properties and have made their way into wider culture and art – for example, in the 1514 artwork ‘Melancholia’, German painter Albrecht Dürer included a four-by-four magic square, as incidental background detail.
This one isn’t quite as unique as our three-by-three version – there are 880 possible normal four-by-four magic squares – and in fact Dürer was able to choose one perfect for his artwork, with the bottom row featuring ‘1514’ (the year of the painting) alongside a 1 and a 4, representing his initials AD.
In addition to the rows, columns and two main diagonals, this magic square also has a variety of other combinations that add up to 34 – including the four outside corners, the corners of any three-by-three subsquare of the grid, the four entries in two-by-two squares, and several other combinations. This is just a glimpse into the rabbit-hole of possible properties magic squares can have, and we can delve into some more impressive examples – but first, we need some terminology.
Types of Magic Square
We’ve already seen mathematicians up to their old tricks, coming up with terminology to denote magic squares with certain properties – like a normal magic square, which uses the first n² whole numbers. We call a semi-magic square one which just has the magic total in the rows and columns, and a simple magic square one which also has the two main diagonals.
A pandiagonal magic square is one that has the rows, columns, main diagonals and all the other diagonals – including ones that wrap around the square (sometimes called broken diagonals) having three squares in one off-diagonal and one in the opposite corner (labelled a & b in the diagram to the right), and sets of two pairs of two-square diagonals (labelled c) – all sum to the magic constant.
It’s possible to prove mathematically that there are no three-by-three pandiagonal magic squares (except for the trivial one, in which all nine squares contain the same number). Four-by-four examples exist, and have the pleasing property that they remain pandiagonal magic squares if a row or column is clipped off and reattached to the opposite face of the square.
Another interesting type of magic square is the most perfect magic square, which has to be a normal magic square with two additional properties. Firstly, each 2-by-2 subsquare of the n-by-n square must add to a total of \(2(n^2+1)\); and secondly, any pair of numbers which are \(\frac{n}{2}\) squares apart in the grid must sum to \(n^2+1\).
This seems like a difficult set of constraints to satisfy – but the image shows an example of a most-perfect magic square from the Parshvanath Jain temple in Khajuraho, dating back to the 12th century CE, and containing the numbers:

All most-perfect magic squares are also pandiagonal, and all are of side lengths that are a multiple of 4.
Kathleen Ollerenshaw

One of the leading mathematicians who investigated these properties of magic squares was Kathleen Ollerenshaw – originally from Manchester, Ollerenshaw had an incredible career working across mathematical research, politics and education, serving as Lord Mayor of Manchester and President of the Institute of Mathematics and its Applications, and publishing at least 26 mathematical research papers, including on algebraic structures called lattices. The most magical of her publications was, of course, “Most perfect pandiagonal magic squares: their construction and enumeration”.
Published with co-author David Bree, the topic is most perfect pandiagonal magic squares, and includes proofs of several of the properties and facts mentioned above, as well as methods for constructing such squares.
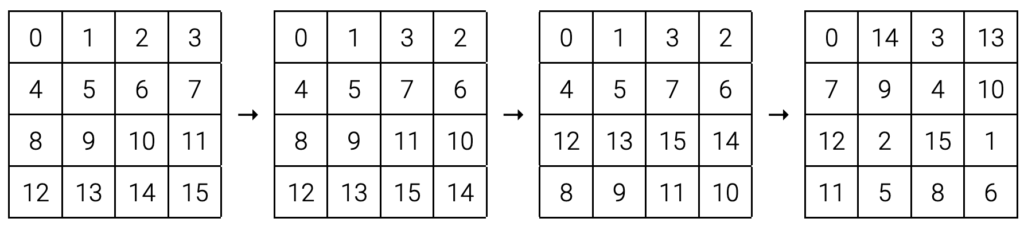
In the four-by-four case, there are 48 distinct possible most perfect pandiagonal magic squares, and one way to construct one is to start with a reversible square – not a type of magic square, but a grid of numbers with the property that any rectangle within the square has numbers in its opposite corners that add to the same total, and that reflecting the square horizontally or vertically and adding it to its own reflection gives a symmetrical result.
It’s trivial to construct a reversible square – simply writing the numbers 0 to 15 in rows will achieve this. Ollerenshaw & Bree showed how this can be transformed into a most-perfect magic square by interchanging two columns, then two rows, then applying a function to rearrange the elements (in this four-by-four case, moving the number in cell \((i,j)\) to \((i + 2j, 2i + 3j)\) modulo 4). An example is given below:
There’s plenty more to say about the theory of magic squares – Matt Parker, for instance, has certainly had a go – and if you’d like a way to impress your friends and relatives over the holiday season, I can recommend this method of producing a 4-by-4 magic square to any supplied total (sadly not a most-perfect one – although it’s got plenty of different sets that add up to the total in there).
Wishing you and yours a festive season as magical as these squares!