Dennis Sullivan, 2022 Abel Prize Laureate
BLOG: Heidelberg Laureate Forum

The Abel Prize for 2022 has been awarded to Dennis Sullivan, ‘for his groundbreaking contributions to topology in its broadest sense, and in particular its algebraic, geometric and dynamical aspects‘. I’m excited to hear this, as these are two topics quite close to my mathematical heart — and hoping that Dennis can soon join us at the HLF as a laureate.
Algebraic and Geometric
Topology, as many of the media outlets reporting on the prize have attempted to define, is ‘the study and classification of shapes’, and ‘the study of how surfaces deform’. Both of these are true, since in topology two shapes can be considered the same if one can be carefully deformed into the other — without tearing or gluing. It’s also very much all about classifying shapes by their fundamental properties — if you can deform something into something else, a lot of the properties the first shape had will be shared by the second.
One object of particular interest in topology is a manifold. To avoid a repeat of the 4-month-long comments debate that ensued the the last time I tried to define what a manifold is on this blog, I’ll steer clear and stick with Alex Bellos’ definition from the Abel Prize website: ‘a shape that is the same everywhere, meaning that it has no end points, edge points, crossing points or branching points’.
Many of the objects commonly studied by topologists — like one-dimensional circles, and two-dimensional spheres and toruses — are examples of manifolds. Two-dimensional manifolds are called surfaces, which provides a nice intuition for what they look like: each part of the manifold can be mapped to a piece of 2D space, as per Bellos’ ‘the same everywhere’.
Sullivan’s early work considered the classification of manifolds, particularly in higher-dimensional cases (5D and above). It might be hard to imagine what such an object looks like — simply saying ‘each part of it looks like a piece of 5D space’ doesn’t help much — but algebraic topology, Sullivan’s field, is filled with tools you can use to study shapes even if you can’t picture what they look like.
For example, the loop space of a manifold is the set of all types of closed loops you can draw on the surface of the shape. In the case of a sphere, there’s only one possible loop, since any closed curve you draw on the surface can be deformed — stretched, or squashed — into any other, all of which can be shrunk down to a single point.
On a torus, however, a loop passing through the hole in the middle (a), or one running around the edge of the torus (going around the hole (b)) are non-trivial loops. Both can’t be shrunk to a point without leaving the surface of the torus, so these loops are considered the ‘generators’ of the space of loops; any loop I can draw will be equivalent to some combination of these two loops in some order.
The fundamental group of a manifold — the space consisting of the categories of types of closed loops on a shape — is one of the tools that can be used to study it. A manifold made by sticking together two others will have a fundamental group that can be calculated from the fundamental groups of the shapes making it up. While this predates Sullivan’s work, it’s a nice example of what topologists call an invariant — a property of a topological space that can be used to classify and understand it.
Sullivan used algebraic structures to study topological objects, including commutative differential graded algebras, which are abstract structures defined based on the geometric structure of a given space. The algebra encodes the most important properties of the geometrical object, so that knowing the algebra is enough information to reconstruct the structure of the object. Algebraic objects are often useful invariants, as there are many tools and calculations that can be applied to them which couldn’t be applied to the original geometric structure.
Dynamical Aspects
As well as working in topology, Sullivan has also spent time working on problems from a very different area of maths, called dynamical systems. I’ve talked a little on the blog before about modelling systems that evolve over time, like the Lotka-Volterra predator-prey model, and generally, dynamical systems involve the study of such systems, where the state at each point in time depends on the previous state using a simple iterative step.
One important map in this field is called the Logistic Map, which is defined for an input value x so that the next step is ax(1-x). That is, given the value of the parameter a, if you put in the value x, the next value returned will be ax(1-x), a number which can then be put back into the function again, repeating until a pattern emerges in the values. This is actually a whole infinite family of maps corresponding to different values of a, and as you vary this parameter, different patterns can be seen.
For example, when a = 2, the map is 2x(1-x), or 2x – 2x². For this map, the sequence of x values stabilises to a particular value, or fixed point, regardless of your starting value. This graph shows what happens to various starting points when a = 2: they all converge to 0.5 within a few steps.
If we switch to a different value of a, such as a = 3.2, we might observe different behaviour; the graph below shows that the same set of starting points under this new map will follow a path which alternates between two values (and with enough steps, the values settle down to two specific points, at around 0.513 and 0.799) called a period two orbit.
One natural question is to ask how this behaviour changes for different values of a, and that’s also something we can plot on a graph: if we put values of a along the horizontal axis, and plot where these fixed points or periodic points are for each value, after approximately 100 iterations of the map, any stable points like this will be apparent.
This type of diagram is called a bifurcation diagram, as it helps to find the points where one single fixed point — as we have when a = 2 — splits, or bifurcates, into a period two orbit, like the one seen at a = 3.2.
For the logistic map, these bifurcations start slow but get much quicker: after the initial split at around a = 3, there is another bifurcation at the point 1 + √6 (around 3.44949) which splits two values into four that the value of x oscillates between. The period doubles again and again, and eventually descends into chaotic behaviour from a ≈ 3.56995 onwards. This type of behaviour is called a period-doubling cascade, and is observed in the behaviour of many families of parameterised functions like the logistic map.
The points where this doubling occurs are well-studied. The parameter values where bifurcations occur get closer together each time, and the ratio between the lengths of the intervals gets closer and closer to a fixed value: the Feigenbaum constant, δ ≈ 4.66920, named after the physicist Mitchell Feigenbaum.
This isn’t unique to the logistic map, either: Feigenbaum found that the same ratio occurs in period-doubling cascades for many other maps too, and Dennis Sullivan proved in 1988 that these limits are universal and underlie this type of behaviour more generally.
Crossing Fields
I was particularly interested to hear that Sullivan spent his career working on both topology and dynamical systems, mainly because the intersection of these two topics was the subject of my own PhD thesis and research paper.
Since my supervisor’s main work was in studying dynamical systems, and my interests lay in investigating topology, I was able to work on problems from dynamics and analyse them using topology. My main work was on choreographies: motions of particles in 2-dimensional space which follow a fixed path with a time delay, so the particles chase each other around a shape in an elaborate dance. Such patterns result when particles move under gravity from specific starting locations — each is attracted to the ones around it depending on the distance between them.
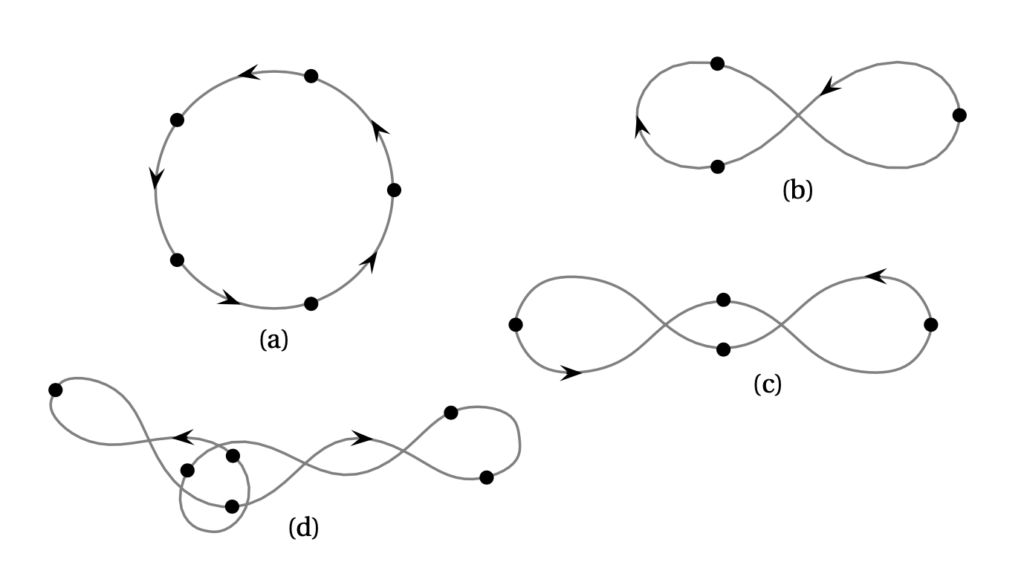
Some examples of planar choreographies: (a) circular, (b) the figure eight, (c) the super-eight and (d) a non-symmetric choreography.
As well as studying the dynamics of how these systems evolve over time, I was able to consider stable orbits, like the period 2 orbit in the logistic map — where given the right initial conditions, the particles will continue to move between the same set of points indefinitely — and their shape, symmetry and patterns. I also described spaces of loops using tools from algebraic topology, and categorised possible orbits into their main types.
My experience working across two different fields was a valuable insight into why people like Sullivan are important to mathematics and add so much to the discipline: studying more than one field allows you to see different sides of mathematics and appreciate how it all fits together. Sullivan was originally planning to study chemistry, but moved to a mathematics course later during college. Having a fixed idea of what you’re going to be interested in can hold you back from exploring new ideas, and Sullivan illustrates that whether you’re following your passion into mathematics, or discovering new areas to apply your skills to later in your career, having a flexible outlook can lead to some exciting discoveries.


Katie Steckles wrote (13. Apr 2022):
> […] One object of particular interest in topology is a manifold. […] Alex Bellos’ definition from the Abel Prize website [ https://abelprize.no/sites/default/files/2022-03/A%20glimpse_of%20the%20laureates%20work%20by%20AlexBellos.pdf ]:
> ‘a shape that is the same everywhere, meaning that it has no end points, edge points, crossing points or branching points’.
Interestingly, however, Alex Bellos’ article doesn’t refer to the quoted characterization explicitly as “(a) definition (of a manifold)” at all.
Perhaps it is merely meant to describe some, but not necessarily all, properties of a “(topological) manifold”.
p.s.
Since, apparently, there exist topological spaces of which some, but not all, points are »end points«, or »edge points«, or »crossing points« or »branching points«:
Are there topological spaces, too, of which all points are equally »end points«, or »edge points«, or »crossing points« or »branching points«, respectively ?