Wie Elektronen sich aus dem Weg gehen
BLOG: Hier wohnen Drachen

Elektronen sind extreme Individualisten: Das Pauli-Prinzip aus der Quantenmechanik sagt, dass nie zwei von ihnen genau dasselbe tun oder am selben Ort sein dürfen, oder, fachlich etwas sauberer ausgedrückt, dass nie zwei Elektronen im selben Zustand sein dürfen. Wie schaffen es die vielen Elektronen eines Atoms eigentlich, sich aus dem Weg zu gehen?
Atome und Orbitale
Das Pauli-Prinzip ist absolut essentiell für unsere Welt, ohne es gäbe es weder Atomkerne (da gilt es für die Protonen und Neutronen) noch Atome, wie wir sie kennen. Nehmen wir als Beispiel ein Atom. Wir haben also einen positiv geladenen Atomkern (beispielsweise den eines Kohlenstoff-Atoms mit 6 Protonen und 6 Neutronen), und weil die Protonen positiv geladen sind, brauchen wir 6 Elektronen, um das Atom elektrisch neutral zu machen.
Die Quantenmechanik sagt uns, dass Elektronen sich nicht irgendwie an Atomkerne binden können. Oft verwendet man ja zur Veranschaulichung von Atomen das Bohr-Modell, wo die Atome auf Kreis- (oder im verfeinerten Sommerfeldmodell auf Ellipsenbahnen) um den Atomkern kreisen:

Von LG UltraLink- Eigenes Werk, CC BY-SA 4.0, Link
Ein ikonisches Bild dieser Art durfte ja auch zumindest in den 60er und 70er Jahren auf keinem Cover eines Science-Fiction-Romans fehlen.
Anders als bei Planeten haben die Elektronen aber nicht irgendwelche Bahnen – Es gibt keinen physikalischen Grund, warum die Erde nicht auch 10 Millionen Kilometer dichter oder 5 Millionen Kilometer weiter weg von der Sonne unterwegs sein sollte. Elektronen können in diesem Modell nur auf ganz bestimmten Bahnen kreisen. Bohr hat das seinerzeit einfach ohne Begründung so postuliert (später wurde dann eins Erklärungansatz über Wellen gefunden), aber vor knapp 100 Jahren haben Schrödinger, Heisenberg et al. die Quantenmechanik im Detail entwickelt und für diese “quantisierten” Möglichkeiten der Elektronen eine klare physikalische Begründung gefunden. Heutzutage verwenden wir deshalb dieses Modell, bei dem die Elektronen durch “Orbitale” beschrieben werden:

Gemeinfrei, Link
In einem Atom gibt es also unterschiedliche Orbitale, angefangen beim sogenannten 1s-Orbital, dem Orbital mit der niedrigsten Energie, wo die Elektronen am dichtesten am Kern sind. Die Zahl am Orbital sagt etwas über die Energie (1=niedrigste, 2=zweitniedrigste usw), der Buchstabe sagt etwas über die Form des Orbitals aus, die ist heute aber nicht so wichtig. Wie die Orbitale genau funktionieren, schauen wir uns gleich an, erstmal gucken wir nochmal auf das Pauli-Prinzip. Stellen wir uns vor, wir hätten einen Atomkern eines Kohlenstoffatoms noch ohne Elektronen. Jetzt werfen wir ihm ein Elektron zu. Das Elektron wird vom Atomkern angezogen, verliert dabei Energie (die es als Licht oder Röntgenstrahlung abstrahlt) und landet schließlich im Grundzustand mit der niedrigsten Energie, also im 1s-Zustand.
Das Pauli-Prinzip und die Chemie
Werfen wir dem Atomkern noch ein Elektron zu, landet das ebenfalls im 1s-Zustand. Herr Pauli hat da deswegen nichts dagegen, weil die beiden Elektronen sich trotzdem unterscheiden – Elektronen haben eine etwas unanschauliche Eigenschaft, den Spin, der genau zwei Werte annehmen kann. Das eine Elektron hat also den einen Spin (meist kennzeichnet man die durch kleine Pfeile und spricht von “Spin rauf” und “Spin runter”), das andere Elektron den anderen Spin. Insofern können sie sich dasselbe 1s-Orbital teilen, ihre Individualität ist trotzdem gewährleistet. (Sehr sehr grob kann man sich den Spin als eine Art “Drehung” des Elektrons um seine Achse vorstellen, aber das ist nur sehr bedingt eine tragfähige Anschauung.)
Wenn wir jetzt aber ein drittes Elektron ins Spiel bringen, dann sieht die Sache anders aus. Egal wie es seinen Spin einstellt (rauf oder runter, ne dritte Möglichkeit gibt es leider nicht), der 1s-Zustand hat schon ein Elektron mit diesem Spin. Also bleibt dem dritten Elektron nichts anderes übrig als den nächstbesten Zustand zu besetzen, den 2s-Zustand. Da ist es nicht mehr so stark an den Kern gebunden (und die Elektronen im 1s-Zustand, die tendenziell dichter am Kern sind, schirmen das 2s-Elektron vom Kern ab und sorgen so zusätzlich für eine schwächere Bindung), hat also eine höhere Energie. Das vierte Elektron geht auch in den 2s-Zustand (mit entgegengesetztem Spin zum dritten), dann ist auch der voll und Elektron 5 und 6 müssen sich in einen der nächsten Zustande setzen, die 2p-Zustände (von denen gibt es 3, deshalb haben die Platz für 6 Elektronen.
Ihr seht schon, dass dieses sukzessive Auffüllen der Orbitale dafür sorgt, dass unterschiedliche Elemente unterschiedlich besetzte Orbitale haben, und die führen zu unterschiedlichen chemischen Eigenschaften. Vergleicht man, welche Orbitale es gibt, kann man so erklären, warum das Periodensystem der Elemente so aufgebaut ist, wie es ist: Erst werden die s-Orbitale besetzt, dann die p-Orbitale, später kommen dann noch d- und f-Orbitale hinzu, die sorgen für die Nebengruppenelemente und die Seltenen Erden.
Ohne Pauli-Prinzip gäbe es dagegen keinen wirklichen Grund, warum sich nicht alle Elektronen in 1s-Orbitalen tummeln sollten – Chemie wie wir sie kennen, gäbe es dann nicht. In Atomkernen ist das ähnlich – dort sitzen die Protonen und Neutronen auch in Orbitalen, Atomkerne mit sehr vielen Protonen und Neutronen haben deshalb Teilchen in hohen energetischen Zuständen, und die elektrische Abstoßung macht diese Kerne dann eher instabil. Deswegen sind Atomkerne von sehr schweren Elementen auch so oft radioaktiv.
So weit, so gut, und so steht das auch in so ziemlich jedem Buch zum Thema Atome, Chemie und Quantenmechanik.
Zwei Elektronen am selben Ort?
Schaut man aber etwas genauer hin, wird die Sache ein wenig seltsam: Der Einfachheit halber betrachte ich nur Elektronen mit ein und demselben Spin, beispielsweise Spin rauf, und schaue nur auf die 1s- und 2s-Orbitale. (Für die Spin-runter-Elektronen gilt dasselbe, aber Spin rauf und Spin runter sehen sich ja nicht, was das Pauli-Prinzip angeht.)
Erstmal müssen wir uns angucken, was diese Orbitale überhaupt bedeuten, dazu habe ich ja noch nichts gesagt (auch wenn die meisten von Euch es vermutlich wissen). Orbitale sind eine Veranschaulichung der berühmten “Wellenfunktion”, die die Elektronen beschreibt. Die Wellenfunktion für ein einzelnes Elektron (ψ(x) genannt, hat aber nichts mit dem Psi-Korps zu tun) gibt die “Wahrscheinlichkeitsamplitude an” – klingt komisch, heißt aber nur, dass ihr das Quadrat der Wellenfunktion an einem Ort berechnen könnt, und dann wisst ihr, wie wahrscheinlich es ist, das Elektron an diesem Ort zu finden. Weniger mathematisch ausgedrückt: Da wo die Wellenfunktion (bzw. ihr Betrag) groß ist, habt ihr eine hohe Wahrscheinlichkeit, das Elektron zu finden, da wo sie klein ist, ist die Wahrscheinlichkeit auch klein, mehr müssen wir eigentlich gar nicht wissen.
Wenn ihr nochmal auf die Bilder für die Orbitale schaut, seht ihr jetzt vielleicht schon ein Problem: Es gibt Orte, an denen hat sowohl das 1s-Orbital als auch das 2s-Orbital eine Wellenfunktion, die nicht Null ist, beispielsweise in der Mitte, da wo der Atomkern sitzt. (Tatsächlich sind die mathematisch fast überall beide nicht Null.) Wenn also ψ(x) die Wahrscheinlichkeit ist, das Elektron irgendwo zu finden, dann scheint es so zu sein, als gäbe es die Möglichkeit, beide Elektronen am selben Ort zu finden. Aber das verbietet das Pauli-Prinzip.
Müsste sich also das 2s-Orbital nicht vollkommen ändern, damit das Elektron darin dem Elektron im 1s-Orbital ausweichen kann?
Elektronen verschränken sich
Die Antwort lautet (vermutlich wenig überraschend): Nein. Die Elektronen behalten ihre Orbitale bei, schaffen es aber trotzdem, sich aus dem Weg zu gehen. Dazu nutzen sie die viel zitierte quantenmechanische Verschränkung.
Wenn wir in der klassischen Physik zwei Teilchen haben, dann ist deren Eigenschaft die Summe der Eigenschaften beider Teilchen – habe ich zwei Bälle, die jeweils einen Ort und eine Geschwindigkeit haben, dann weiß ich alles über die Bälle, wenn ich von jedem einzelnen den Ort und die Geschwindigkeit kenne.
In der Quantenmechanik ist das anders: Ein einzelnes Elektron hat seine Wellenfunktion ψ(x). Habe ich aber zwei Elektronen, habe ich nicht einfach zwei Funktionen ψ1(x) und ψ2(x), wie man es erwarten würde. Beide Elektronen werden zusammen durch eine einzige Wellenfunktion beschrieben: ψ(x1, x2).
Warum so eine gemeinsame Wellenfunktion einen Unterschied macht? Stellt euch der Einfachheit halber vor, ihr würdet eure Wellenfunktionen an endlich vielen punkten angucken, sagen wir an 2000 Punkten. Dann habt ihr mit zwei Wellenfunktionen 4000 Zahlenwerte, aber mit einer Wellenfunktion mit zwei Argumenten habt ihr 4000000 Zahlenwerte. Die verschränkte Wellenfunktion ist wie ein Bild mit 2000 mal 2000 Pixeln (4 Megapixel), die einzelnen Funktionen enthalten nur so viel Information wie die obersten zwei Zeilen eures Bildes.
Anschaulich kann man die gemeinsame Wellenfunktion so verstehen, dass der Wert für die Wahrscheinlichkeit, den wir für ein Elektron bekommen, davon abhängt, was das andere Elektron tut. Und genau das nutzen die Elektronen, um sich aus dem Weg zu gehen und trotzdem nichts an der Aufenthaltswahrscheinlichkeit ändern zu müssen.
(ExpertInnenhinweis: Mathematisch lässt sich das ziemlich einfach durch die sogenannte Slater-Determinante erledigen, die in den meisten Büchern zur QM erklärt wird. Es wird allerdings – jedenfalls in den Büchern, die ich angeguckt habe – nie explizit gezeigt, wie denn nun so eine gemeinsame Wellenfunktion tatsächlich aussieht.)
Leider ist das für Atome etwas schwierig darzustellen – die Wellenfunktion eines Elektrons ist eine Funktion im dreidimensionalen Raum, wenn ihr also eine gemeinsame Wellenfunktion für 2 Elektronen habt, ist das eine sechsdimensionale Funktion, die ist ein bisschen jenseits meiner Anschauungskraft. (MathematikerInnen machen es natürlich einfach so, dass sie sich einen n-dimensionalen Raum vorstellen und dann n=6 setzen, aber ich kann das nicht.)
Verschränkung im Kasten
Deswegen koche ich das alles jetzt auf eine einzige Dimension runter, dann kann man es sich leichter veranschaulichen. Statt eines Atoms betrachte ich einen eindimensionalen Kasten, also eine Linie, entlang derer ich die Elektronen einsperre, so dass, sie sich in einem endlichen Bereich aufhalten müssen.
In so einem Kasten tragen die Wellenfunktionen ihren Namen wirklich zu Recht, sie sind nämlich einfach Wellen, die am Rand des Kastens verschwinden. Der Grundzustand (violett) hat einen Wellenberg, der nächste Zustand (grün) zwei und so weiter. Je mehr Wellenberge, desto höher ist die Energie des Zustands. (Der Kasten hat hier genau eine Länge von pi, das habe ich gemacht, damit ich nicht so viele Vorfaktoren in meine Rechnungen einbauen muss.)
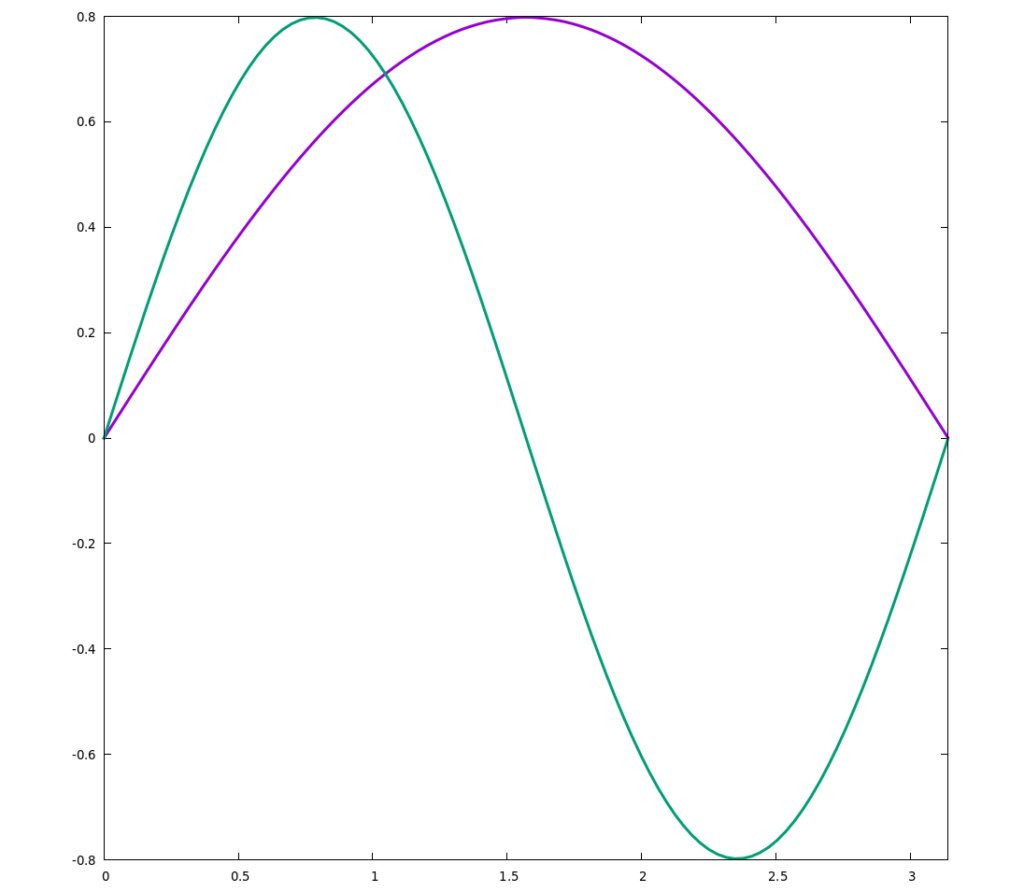
Ein Elektron im Grundzustand hat also eine hohe Wahrscheinlichkeit, sich in der Mitte aufzuhalten; zum Rand hin wird sie kleiner und da, wo der Kasten zu Ende ist, finden wir das Elektron auch nicht. Ein Elektron im ersten angeregten Zustand finden wir bevorzugt bei 1/4 und 3/4 der Kastenlänge, aber nicht am Rand rechts und links und auch nicht genau in der Mitte. (ExpertInnenhinweis: Mathematisch sorgt das dafür, dass die beiden Wellenfunktionen orthogonal sind.)
Analog zu dem beiden Elektronen im 1s- und 2s-Orbital packen wir jetzt also zwei Elektronen in den Grundzustand und den ersten angeregten Zustand, kurz Zustand 1 und Zustand 2 genannt. Wir können jetzt ausrechnen, wie groß die Wahrscheinlichkeit ist, ein Elektron an einem bestimmten Ort zu finden, wenn wir je ein Elektron in einem dieser Zustände haben:
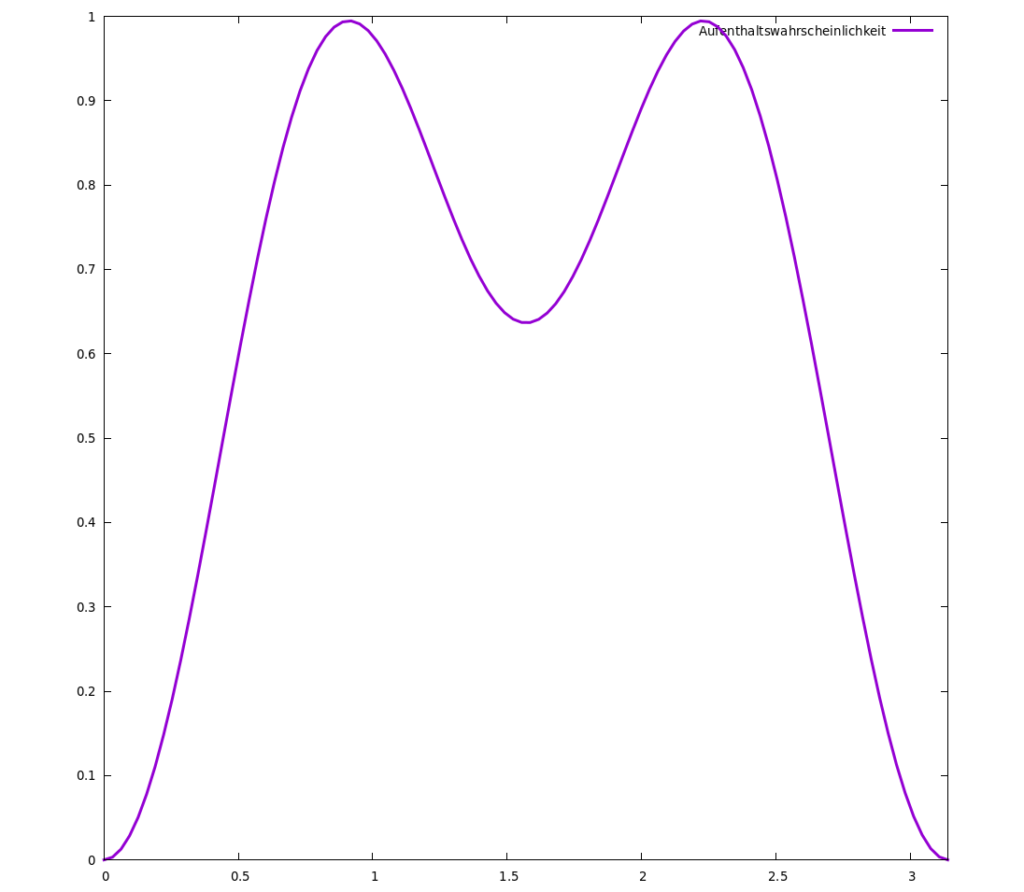
Die Funktion hat links und rechts ein Maximum, da, wo beide Wellenfunktionen große (absolute) Werte haben, in der Mitte ist der Wert etwas kleiner, weil da die zweite Wellenfunktion ja Null ist.
Allerdings dürfen die beiden Elektronen ja nicht einfach in diesen beiden Zuständen sein, dann hätten wir ja eine Wahrscheinlichkeit, beide zum Beispiel bei 1/4 der Kastenlänge zu finden, und das verbietet Pauli.
Wir müssen also für diese beiden Elektronen eine gemeinsame Wellenfunktion basteln (mathematisch mit Hilfe der Slater-Determinante), bei der nie beide Elektronen am selben Ort sind. So sieht diese Funktion aus:
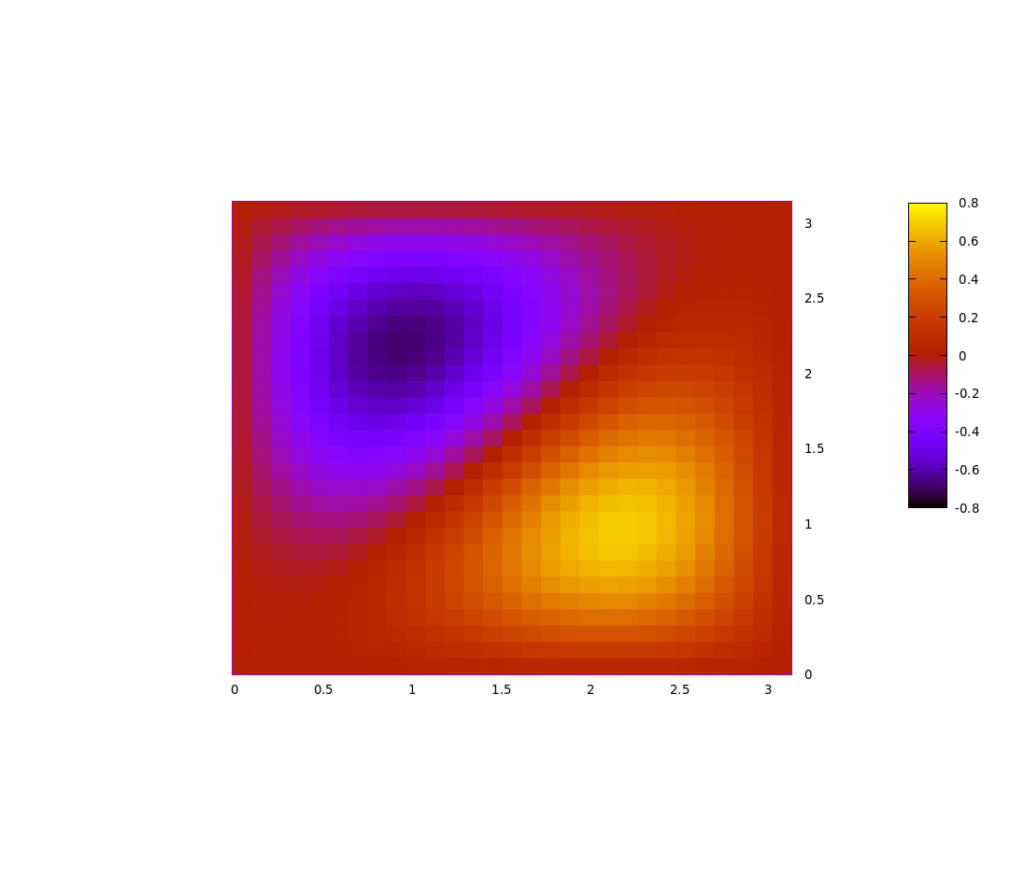
Der Wert der Funktion auf der Diagonale (wo also x1=x2 ist), ist immer Null, beide Elektronen sind nie am selben Ort.
Wenn wir jetzt gucken, wie wahrscheinlich es ist, ein Elektron an einem bestimmten Ort zu finden, dann bekommen wir

also genau dieselbe Funktion wie vorher.
(ExpertInnenhinweis: Das folgt letztlich natürlich schon daraus, dass die Ein-Teilchen-Wellenfunktionen orthogonal sind, gemischte Terme fallen beim Berechnen der Aufenthaltswahrscheinlichkeit also weg. Dass wir aber die Ein-Teilchen-Wellenfunktionen nehmen dürfen, ohne Ärger mit zwei Elektronen am selben Ort zu bekommen, das verdanken wir der Verschränkung und dem Trick mit der Slater-Determinante.)
Wir bekommen also dieselbe Wahrscheinlichkeit dafür, ein Elektron an einem Ort zu finden, wie wir sie hätten, wenn die beiden Elektronen nicht verschränkt wären. Die Wellenfunktion der beiden sieht aber ja ganz anders aus. Verhält sich also ein Atom mit so verschränkten Elektronen doch ganz anders als es das tun würde, wenn beide einfach ihre jeweilige Wellenfunktion hätten?
Die Antwort lautet: Nein. Quantenmechanische Systeme, die sich im Zustand mit niedrigster Energie befinden (so wie es Atome ja tun) haben eine sehr coole Eigenschaft: Alle ihre Eigenschaften sind festgelegt, wenn man die Aufenthaltswahrscheinlichkeit der Elektronen kennt. Es spielt keine Rolle, wie die sich aus der Wellenfunktion zusammensetzt, solange die Aufenthaltswahrscheinlichkeit zweier Systeme dieselbe ist, verhalten sie sich (im Grundzustand) identisch. Das ist das berühmte Hohenberg-Kohn-Theorem. Man nutzt dieses Theorem, um quantenmechanische Systeme zu berechnen, indem man sich Ersatzsysteme baut, die weniger kompliziert sind, aber (hoffentlich) dieselbe Aufenthaltswahrscheinlichkeit für die Elektronen haben. Das ist die Grundlage moderner Computersimulationen mit der Dichtefunktionaltheorie, über die ich auf meinem alten Blog auch mal geschrieben habe.
Also: Unsere verschränkten Elektronen haben trotzdem genau die Aufenthaltswahrscheinlichkeit, die man von zwei Elektronen erwarten würde, von denen das eine die eine und das andere die andere Wellenfunktion hat und damit sind auch die Eigenschaften unseres Systems dieselben. Und das erklärt schließlich, warum man so tun kann, als wären die Elektronen in unterschiedlichen Orbitalen, wo sie sich nicht gegenseitig stören.
(Noch ein ExpertInnenhinweis: Ich ignoriere hier, dass sich die Elektronen auch noch elektrisch abstoßen – diese Wechselwirkung würde dann tatsächlich zu einer Änderung der Orbitale führen, aber darum geht es heute ja nicht. Hier geht es ja nur darum, wie die Verschränkung der Wellenfunktionen funktioniert.)
Gekonnte Vermeidungsstrategie
Wir können auch gucken, was passiert, wenn wir wissen, wo eins der Elektronen ist. Wir könnten beispielsweise irgendwie einen Detektor bauen, der eins der Elektronen lokalisiert (welches ist egal, die sind ja ununterscheidbar.) Um das zu sehen, schauen wir entlang einer Linie auf unsere zweidimensionale Funktion. Das Ergebnis sieht dann beispielsweise so aus:
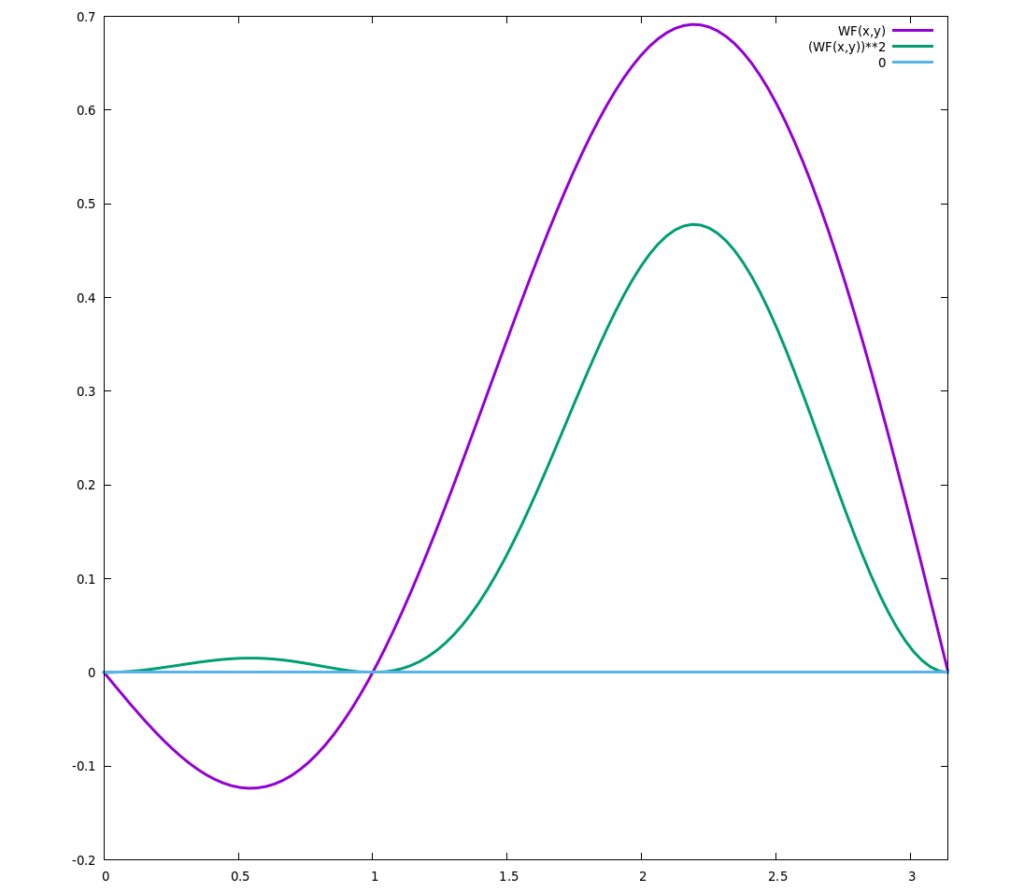
Hier ist das Elektron, dessen Ort wir kennen, bei x=1. Genau da hat das andere Elektron jetzt eine Aufenthaltswahrscheinichkeit von Null. (Die violette Kurve ist die Wellenfunktion, die grüne ihr Quadrat, also die Aufenthaltswahrscheinlichkeit. Achtung, ich war bei den Plots mit der Normierung etwas schlampig und garantiere nicht, dass die Funktionen korrekt 1 ergeben, wenn man alles integriert…) Wissen wir also, wo eins der Elektronen ist, dann ist das andere Elektron hier mit Sicherheit nicht, und es ist auch nur mit geringer Wahrscheinlichkeit in der direkten Umgebung dieses Ortes zu finden. (In der Fachsprache nennt man das ein “exchange hole” – ein “Austauschloch”.)
Fazit
Dass wir Elektronen in einem Atom mit Hilfe der einzelnen Orbitale beschreiben können, ist also gar nicht selbstverständlich. Eigentlich sind alle Elektronen miteinander verschränkt (und bei einem Atom wie Eisen mit 26 Elektronen haben wir also eine 78-dimensionale Wellenfunktion), um zu vermeiden, dass es möglich ist, zwei von ihnen am selben Ort zu finden. Die Verschränkung funktioniert aber so, dass genau dieselbe Aufenthaltswahrscheinlichkeit für die Elektronen herauskommt, als wären die beiden Elektronen unabhängig voneinander. Nur deshalb können wir so tun, als würden Elektronen in Atomen die einzelnen Orbitale (1s, 2s, 2p usw) der Reihe nach besetzen, obwohl das eigentlich nicht wirklich so ist, alle Elektronen sind auf komplizierte Weise miteinander verschränkt.
Wenn euch also mal wieder jemand erzählt, Verschränkung sei ein total subtiles Quantenphänomen, dessen Effekte man nur ganz selten bemerken kann – das ist falsch. Ohne Verschränkung würde kein Atom (außer Wasserstoff und Helium) sich so verhalten, wie wir es kennen, die gesamte Chemie wäre vollkommen anders. Die quantenmechanische Verschränkung ist einer der Grundpfeiler unseres Universums.
PS: Ich habe das so erklärt noch nie irgendwo gelesen – steht sowas in modernen Büchern zur QM drin? Ich finde es ja immer schade, dass Fachbücher nach einer Herleitung selten den Schritt zurück zur Anschauung machen und nochmal erklären, wie man sich das Ergebnis vorstellen und es interpretieren kann. Das bedeutet leider auch, dass ich mir das alles selbst überlegt habe – falls hier etwas falsches steht, kommentiert gern eine Korrektur.


Da haben die Chemiker also Glück gehabt. Glück, dass sich trotz Verschränkung der Elektronen in einem Atom Orbitale ergeben, deren Form nicht vom Füllungszustand der Orbitale abhängt. Wobei: So gross ist das Glück auch wieder nicht, denn dem Chemiker hilft das nur begrenzt beschäftigt er sich doch selten mit nur einem Atom. Es sind vielmehr Moleküle wie H2O oder O2. Und die haben dann Elektronenkonfigurationen, die sich mit Atom- Orbitalen nur noch wenig erklären lassen. Deshalb benötigen Chemiker also Programme für die Quantenchemie. Nun, so viel ich weiss gab es früher auch Heuristiken, die den Chemikern einiges erklären konnten.
Auch bei Molekülen bilden sich aber ja Orbitale, und in vielen Fällen kann man Moleküle auch dadurch beschreiben, dass man die Atomorbitale zusammenkombiniert (sogenannte LCAO-Methode).
Ein sehr guter Punkt! Konzeptionell können wir (kanonische) Atom- und Molekülorbitale auf noch fundamentalerer Ebene gleichsetzen: Beide sind Eigenfunktionen des Fock-Operators. Ob wir uns nun auf ein Atom oder Molekül beziehen, ändert nichts daran, dass wir über das Hartree-Fock-Verfahren für beide Arten von Elektronensystemen Orbitale berechnen können. Die LCAO ist dabei sogar eigentlich nebensächlich und nur ein effizienter und anschaulicher Ansatz, die Hartree-Fock- beziehungsweise Roothaan-Hall-Gleichungen für Moleküle zu lösen. Insofern gelten die Zusammenhänge, die Sie oben so anschaulich für Atome erklärt haben, natürlich auch für Moleküle.
Vielen Dank für den Artikel.
Es hat wirklich Spaß gemacht ihn zu lesen. Und auch wenn mein Wissen zu den beschrieben Dingen sehr klein ist, so ist mein Staunen beim Lesen um so größer geworden.
Ich bin überrascht wieviel ich dieses Mal (glaube ich) verstanden habe, bei Teilchen- und/oder Quantenphysik bin ich normalerweise raus.
Danke für die verständliche Erklärung!
Gruß
Aginor
Vielen Dank für den tollen Artikel!
So anschaulich und nachvollziehbar habe ich das noch nirgendwo gesehen.
Ich will mir gar nicht vorstellen wie viel Nachdenken, Arbeit und Zeit da hinter steckt.
Also nochmal: vielen Dank!
Ja, hat mich ne Weile gekostet, das zu verstehen, weil es in den Büchern immer nur ne Formel gibt und dann ist plötzlich von Austauschlöchern und so die Rede und ich brachte das Anschaulich nicht zusammen…
@Wellenfunktion
Was passiert denn jetzt, wenn wir eine chemische Reaktion haben? Der einfachste Fall wäre, wenn das Atom ein Lichtquant einfängt und die Elektronenhülle in einen angeregten Zustand übergeht.
Springt dann einfach die Konfiguration der einzelnen Orbitale in den neuen Zustand?
Und mit einer gewissen Halbwertszeit springt das Atom dann irgendwann zurück in den energieärmsten Zustand, und gibt die überschüssige Energie in Form eines Lichtquants wieder ab.
Kann man sich das so vorstellen, dass Atome und Moleküle eben immer nur eine Weile unverändert bleiben, und dann im Miteinander bei vielfältigen Kollisionen untereinander immer wieder in andere Zustände springen, eine Weile so verweilen, um nach und nach wieder in den energieärmsten Zustand zurück zu gelangen.
Also: Wenn wir von einem stabilen Zustand in einen anderen stabilen Zustand übergehen, dann ja, dann springt die gesamte Wellenfunktion der Elektronen vom einen Zustand in den neuen. (Theoretisch ist ein angeregter Zustand auch stabil, weil er eine wohldefinierte Energie hat; dass er es nicht ist, liegt soweit ich weiß letztlich an der Wechselwirkung mit dem Quantenfeld der Photonen – ist aber ewig her, dass ich darüber mal was gelesen habe, bin da nicht 100% sicher.)
Atome/Moleküle im Grundzustand bleiben da aber, solange man nicht so viel Energie zuführt, dass sie in einen anderen Zustand gehen.
Noch eine kleine Ergänzung zu Martins Antwort:
Die spontane Emission von Photonen, also das Zurückspringen von einem angeregten in den Grundzustand, kann man tatsächlich erst über die Quantenelektrodynamik erklären. In der reinen Quantenmechanik müsste ein einmal angeregtes Atom oder Molekül eigentlich in seinem angeregten Zustand verbleiben. In der Quantenelektrodynamik koppelt das System allerdings an quantisierte elektromagnetische Feldmoden – gewissermaßen die quantenmechanischen Zustände des Lichts selbst. Das ist auch dann der Fall, wenn gar kein Photon vor Ort ist, weil das Vakuum selbst als Grundzustand des elektromagnetischen Feldes verstanden werden kann. In dieser gekoppelten Beschreibung von Atom/Molekül und elektromagnetischem Feld ist der angeregte Zustand kein streng stationärer Eigenzustand mehr und kann mit einer gewissen Wahrscheinlichkeit zerfallen. Dabei springt das Atom/Molekül dann zurück in seinen Grundzustand, während das elektromagnetische Feld aus seinem Grundzustand in eine vorher unbesetzte Feldmode angeregt wird. Diese Anregung des quantisierten elektromagnetischen Feldes ist nichts anderes als die Emission eines Photons.
Dirac hat das in seinem epochemachenden Paper “Die Quantentheorie der Emission und Absorption von Strahlung” sehr schön beschrieben: “Das Licht-Quant hat die Eigenart, dass es zu existieren aufhört, wenn es in einem seiner stationären Zustände ist, namentlich der Null-Zustand, in dem sein Impuls, und daher auch seine Energie, null sind. Man kann es so verstehen, dass ein Licht-Quant, wenn es absorbiert wird, in diesen Null-Zustand springt, und, wenn eines emittiert wird, aus diesem Null-Zustand in einen Zustand springt, in dem es physikalisch existiert, sodass es so scheint, als wäre es erzeugt worden.”
Eine chemische Reaktion verläuft dabei noch ein bisschen anders. Hier verändern sich mit der Zeit die Positionen der Atomkerne, sei es, weil ein Molekül selbst nicht stabil ist, oder weil sich zwei oder mehr Moleküle aneinander annähern und stören. Wir können dabei zwischen Reaktionen im Grundzustand und photochemischen Reaktionen unterscheiden. Der erste Fall ist sozusagen der der “normalen” Chemie, die abläuft, wenn wir miteinander reagierende Substanzen zusammen bringen. Der zweite Fall ist der, dass sich das Molekül in ein anderes Molekül umwandelt, nachdem wir es mit Licht beschienen haben. In beiden Fällen führt die Veränderung der Position der Atomkerne nun dazu, dass sich auch die elektronische Wellenfunktion – und damit die Orbitale – verändern; und zwar so, dass die an der Reaktion beteiligten Moleküle am Ende eine niedrigere Energie haben als zum Zeitpunkt ihres Zusammentreffens beziehungsweise als unmittelbar nach der Lichtabsorption. Zu jedem Zeitpunkt während der chemischen Reaktion gelten aber die oben von Martin erläuterten Zusammenhänge. Elektronen weichen einander auch in Molekülen, die eine chemische Reaktion durchlaufen, immer aus.
Danke, sehr interessant.
Viel hab ich nicht verstanden, aber da scheint ein nicht zu viel zu sein.
Oh, danke.
Auf die Frage, warum das Pauli Prinzip gilt, also warum Teilchen mit halbzahligem Spin der Fermi-Statistik gehorchen und solche mit ganzzahligem Spin der Bose-Statistik, habe ich auch noch keine anschauliche Erklärung gefunden. Angeblich soll der Beweis ziemlich verwickelt sein.
Ich habe mal die Dirac memorial Lectures von Feynman gelesen, wo er das auf die angeblich einfachst mögliche Weise herleitet. Und “einfachst-möglich” hat in dem Fall wenig mit “einfach” zu tun.
Vielen Dank für diesen sehr anschaulichen und gut geschriebenen Beitrag! Es hat mir große Freude gemacht, ihn zu lesen. Auf eine ähnlich bildliche Darstellung bin ich tatsächlich auch noch nirgendwo gestoßen.
Ich möchte gern noch zum letzten ExpertInnenhinweis ergänzen, dass die Vorstellung, einzelne Elektronen befänden sich “in unterschiedlichen Orbitalen”, ganz wesentlich auf der angesprochenen Vernachlässigung dieser Abstoßung aufbaut. Wir können überhaupt erst so denken, wenn wir die explizite Korrelation zwischen den Elektronen ignorieren und davon ausgehen, dass die Wellenfunktion des Atoms durch eine einzelne Slater-Determinante beschrieben wird. Berücksichtigen wir die Abstoßung, ändern sich nicht bloß die Orbitale, die Wellenfunktion expandiert dann in mehreren Slater-Determinanten und das Bild der Orbitale beziehungsweise Einteilchen-Wellenfunktionen als physikalisch irgendwie eigenständige Objekte im Atom bricht zusammen. Insofern ist es meines Erachtens wichtig, bei aller Anschaulichkeit darauf hinzuweisen, dass wir uns hier im Rahmen einer Näherung bewegen. Orbitale sind extrem nützlich, aber für Mehrteilchensysteme keine tatsächlich physikalischen oder gar beobachtbaren Größen. Unter Chemie-Studierenden und selbst unter gestandenen WissenschaftlerInnen kommt es diesbezüglich leider immer wieder zu Missverständnissen und Verwirrung.
Um zu zeigen, dass Elektronen in einem Atom einander meiden, ist übrigens auch die Elektronen-Paarverteilungsfunktion recht anschaulich. Aus ihr kann man direkt ablesen, dass die Wahrscheinlichkeit, dass sich zwei Elektronen am exakt selben Ort zu finden, null beträgt. Und im Gegensatz zur Wellenfunktion ist die Paarverteilungsfunktion sogar experimentell zugänglich. Man kann sie im Grunde mit Röntgen- oder Elektronenstreuung messen.
Wie auch immer. Das sind natürlich alles nur ergänzende Feinheiten. Ich möchte mich abschließend noch einmal für den schönen Beitrag bedanken!
@Mats
Das ist natürlich alles richtig. Wobei Hohenberg+Kohn es dann wieder einfacher machen, weil sie es erlauben, dass man nicht wechselwirkende Orbitale konstruiert, die zumindest im Grundzustand zu denselben Eigenschaften führen, das ist ja auch der Kern aller numerischen Verfahren wie DFT. Auch die LCAO-Methode nutzt das ja.
Ich finde das übrigens wirklich in gewisser Weise verblüffend: Wer weiß, wie schwer es gewesen wäre, die QM sinnvoll zu verstehen, wenn es nicht so wäre und Ein-Elektron-Orbitale keine brauchbare Näherung für Moleküle wären.
@Martin
Deinem letzten Punkt stimme ich uneingeschränkt zu. Es ist in der Tat verblüffend, wie gut man das Verhalten der Elektronen in vielen Fällen bereits über Orbitale beschreiben kann. Die die Atom- und Molekülphysik wäre in den letzten 90 Jahren vermutlich nicht annähernd so erfolgreich gewesen, wenn die Näherung nicht funktioniert hätte. (In dem Zusammenhang staune ich auch immer wieder über Koopmans Theorem für die erste Ionisierungsenergie.)
Mit Hohenberg-Kohn wäre ich in diesem Zusammenhang aber wohl ein klein bisschen zurückhaltender. Orbitale treten in der Dichtefunktionaltheorie ja überhaupt bloß deswegen auf, weil wir das exakte Funktional nicht kennen. Wenn wir die Elektronendichte ohne Umwege direkt über das Funktional berechnen könnten, bräuchten wir die Orbitale gar nicht. (Den Punkt finde ich noch fast verblüffender.) Kohn-Sham-DFT ist so gewissermaßen selbst wieder eine Näherung. Und herkömmliche Kohn-Sham-DFT funktioniert ja auch nur dann wirklich gut, wenn die Korrelation im System hinreichend schwach ist, dass die exakte Wellenfunktion bereits gut durch eine einzelne Slater-Determinante beschrieben wird. Insofern unterstreicht der Punkt eigentlich nur noch einmal, dass das Bild einzelner Elektronen “in unterschiedlichen Orbtialen” bloß näherungsweise unter Vernachlässigung der expliziten Korrelation gilt, auch wenn diese Näherung in der Regel gut funktioniert und gerade für qualitative Veranschaulichungen extrem fruchtbar ist.
Dem stimme ich natürlich auch vollkommen zu – dass man mit den Ein-Teilchen-Orbitalen der DFT, obwohl sie eigentlich keine echte physikalische Bedeutung haben (können) trotzdem ganz sinnvolle Ergebnisse bekommt, ist ja auch eins dieser verblüffenden Dinge, die man nicht so recht versteht.
Absolut! Ich muss gestehen, dass ich wellenfunktionsbasierte Post-Hartree-Fock-Methoden diesbezüglich auch immer deutlich verständlicher fand als Kohn-Sham-DFT. Warum man eine bessere, stärker korrelierte Wellenfunktion bekommt, wenn man über verschiedene Slater-Determinanten expandiert, finde ich vergleichsweise einleuchtend. Warum Kohn-Sham-DFT überhaupt in der Lage ist, ausgehend von nur einer Slater-Determinanten und über ein genähertes Funktional deutlich bessere Ergebnisse zu liefen als Hartree-Fock, ist mir hingegen immer noch ein großes Rätsel. Da kann ich nicht viel mehr als staunen.
Ich glaube, dazu steht was im Buch von Koch/Holthausen
A Chemist’s Guide to Density Functional Theory
ist aber schon ne Weile her, dass ich mich damit so ganz intensiv befasst habe…
Vielen Dank für den interessanten Literaturhinweis! Das Buch kenne ich noch nicht. Ich habe mir ein Lesezeichen gesetzt und werde bei Gelegenheit sehen, ob ich darin etwas finde, was mich etwas mehr verstehen und nicht bloß staunen lässt.
Im Artikel wird ein wesentlicher “Vereinigungsaspekt” respektive “Transformationsaspekt” im Rahmen von Thermodynamik und Quantenmechanik nicht thematisiert…
Hintergrund:
Die Thermische De-Broglie Materiewelle λth stellt ein “einfaches Mittel” zur Abschätzung der Quantennatur eines System dar. Quanteneffekte beginnen eine Rolle zu spielen, wenn die Thermische De-Broglie Materiewelle λth mit anderen charakteristischen Längen des Systems, wie beispielsweise der mittleren freien Weglänge, vergleichbar werden. Quantenmechanisch steckt dahinter der theoretische Ansatz, dass man letztendlich durch Superposition der Wahrscheinlichkeits-Wellenfunktionen zu einer Gesamt-Wellenfunktion kommt.
Unterhalb einer kritischen Temperatur ist λth größer als der mittlere Teilchenabstand. Die Wellenfunktionen überlappen und bilden eine gemeinsame Grundzustandswellenfunktion, das Bose-Einstein-Kondensat.
Das liest sich erst einmal unspektakulär, ist es aber nicht.
Bedeutet: Das Bose-Einstein-Kondensat wird durch das Fermionen-Kondensat ergänzt, man geht zur Erklärung einfach davon aus, dass sich jeweils zwei Spin-1/2-Teilchen zu einem Spin-1-Teilchen zusammenschließen.
Zum Verständnis: Ein Fermionen-Kondensat (auch Fermi-Kondensat) ist ein durch Fermionen bedingter suprafluider Zustand bei Temperaturen nahe dem absoluten Nullpunkt und damit ein Aggregatzustand. Der Effekt beruht analog zum Bose-Einstein-Kondensat von Bosonen auf der Überlagerung der Wellenfunktionen der beteiligten Fermionen, woraufhin diese einen einheitlichen Quantenzustand annehmen.
Einfach ausgedrückt: Hier werden im Ergebnis aus Fermionen Bosonen. Das ist bemerkenswert.
Darüber hinaus vermisse ich zumindest den Hinweis, das Elektronen im Bild der Quantenmechanik respektive im Bild des Standardmodells der Elementarteilchenphysik (SM) als strukturlos angenommen werden. Das bedeutet: Es gibt zwar mathematisch formulierte Entitätseigenschaften und die Abstraktion der Wellenfunktion aber keine realphysikalisch phänomenologisch begründete Entität.
Von diesem Wikipedia-Artikel …
https://de.wikipedia.org/wiki/Higgs-Boson#Weblinks
… sind die beiden folgenden Blogartikel verlinkt:
http://scienceblogs.de/hier-wohnen-drachen/2011/12/17/wie-funktioniert-das-higgsteilchen/
http://www.scienceblogs.de/hier-wohnen-drachen/2011/12/22/das-higgs-und-das-nix-das-vakuum-ist-auch-nicht-mehr-was-es-mal-war
Das ist schön; mir ist aber nicht ganz klar, was mir das sagen soll…
“Das ist schön; mir ist aber nicht ganz klar, was mir das sagen soll…”
Ich dachte, das könnte vielleicht von Interesse sein. Mir war das nur aufgefallen, weil ich Scienceblogs kenne und weil in Wikipedia meistens Lehrbücher oder veröffentlichte wissenschaftliche Paper aufgeführt/verlinkt werden. Aber ein Link auf Scienceblogs ist ja auch hilfreich.
Ich glaube, an einigen Stellen sind Artikel von mir verlinkt, z.B. bei den Maxwell-Gleichungen.
Lustig ist, dass ich selbst mal versucht habe, eine Serie zur ART bei Wikipedia zu verlinken, aber da hat ein Moderator den Link sofort gelöscht, weil Wikipedia ja nicht auf Blogseiten verlinkt.
“PS: Ich habe das so erklärt noch nie irgendwo gelesen – steht sowas in modernen Büchern zur QM drin?”
Ich finde, dass das gut verständlich erklärt ist im Buch “Foundations of Modern Physics” von Steven Weinberg, erschienen im Jahr 2021. Dort im Kapitel “5.5 Bosons and Fermions”, Unterkapitel “Identical Particles”.
Das kenn ich gar nicht.
Im Buch “Foundations of Modern Physics” von Steven Weinberg steht im Kapitel “5.5 Bosons and Fermions”, Unterkapitel “Identical Particles”, dass die Wellenfunktion von zwei Fermionen antisymmetrisch bezüglich der Kennzeichnungen der Teilchen ist:
Ψ (x₂, σ₂ ; x₁, σ₁) = (-1) Ψ (x₁, σ₁ ; x₂, σ₂)
Dabei sind x₁ und x₂ die Orte und σ₁ und σ₂ die Spin 3-Komponenten der Teilchen 1 und 2.
Stimmt meine folgende Schlussfolgerung?
Wenn man das von Pauli ausgeschlossene Szenario einsetzt, d.h. x₁=x₂ und σ₁=σ₂, dann folgt:
Ψ = -Ψ
=>
Ψ²=0.
Im Buch ist das Pauli-Prinzip im weiteren Verlauf etwas aufwändiger erklärt.
@Anonym_2023
Ja, aus der Antisymmetrie der WF folgt, dass die 2-Teilchen-WF verschwindet, wenn Ort und Spin gleich sind, das stimmt.
Spannender Artikel!
Bei mir zeigt der allererste Plot als grüne Funktion eine sinusförmige Funktion und nicht eine mit zwei Maxima.
Zwei Extrema sind gemeint, also ein Maximum und ein Minimum.
Für die Wahrscheinlichkeit wird die WF ja quadriert, dann wird aus dem Minimum auch ein Maximum.