LISAMax: Der ultimative Gravitationswellendetektor

Der Weltraum-Gravitationswellendetektor LISA soll erst in den 30er Jahren gestartet werden, aber man denkt jetzt schon über seinen Nachfolger nach: LISAMax könnte LISA in den Dimensionen und auch der Empfindlichkeit um zwei Größenordnungen übertreffen.
Wie funktioniert LISA?
LISA steht für “Laser Interferometer Space Antenna“, was bereits die wesentlichen Eigenschaften beschreibt.
Sowohl LISA als auch LISAMax bestehen aus drei Raumsonden, die untereinander Laserverbindungen errichten und so ein gleichseitiges Dreieck im Weltraum aufspannen sollen. Die Bahnen der drei Raumsonden in beiden Systemen sind trickreich gewählt – Bei LISA sind alle Sonden in Bahnen, die der Bahn der Erde ähneln. Die Bahnen der drei Sonden unterscheidet sich jedoch leicht voneinander. Das Ergebnis ist, dass jede Sonde kontinuierlich einen Abstand von 2.5 Millionen km zu den beiden anderen Sonden hält.
Der Mittelpunkt dieses Dreiecks folgt der Erde auf ihrer Bahn im Winkelabstand von anfangs 20 Grad. Im Verlauf eines Jahres rotiert das Dreieck im seine Normalenachse, wobei diese von der Sonne weg, dabei aber noch 30 Grad nach oben aus der Ekliptikebene heraus zeigt. Das Dreieck scheint also geneigt über die Ekliptikebene zu rollen, wie die folgende Animation zeigt:
Schauen wir uns jetzt das rollende Dreieck genauer an, indem wir uns in den Mittelpunkt des Dreiecks setzen und mit ihm um die Sonne kreisen. Im Inertialsystem rotieren die Erde und die Sonne scheinbar um den Mittelpunkt des Dreiecks. Die Normale auf dem Dreieck vollführt ebenfalls eine komplette Drehung. Da er aber um 30 Grad nach oben aus der Ekliptik geneigt ist, zeichnet er dabei einen Kegel mit einem Öffnungswinkel von 2*60 Grad = 120 Grad.
Und wie kann LISA Gravitationswellen messen?
Jede der drei Sonden, die in den Ecken des rotierenden Dreiecks sitzen, hat zwei Teleskope an Bord, deren Blickrichtungen sich um 60 Grad unterscheiden. Jede Sonde sendet einen Laserstrahl zu den zwei anderen. Die Laserstrahlen werden dort von Teleskopen empfangen. Zudem enthält jede der Sonden in ihrem Inneren eine völlig frei schwebende Testmasse. Kleine Triebwerke wirken nicht-gravitationellen Störungen wie dem Solardruck entgegen. Der vollständige Ausgleich ist dann gegeben, wenn die Testmassen wirklich vollkommen frei schweben. Dann unterliegen die Bahnen der Sonden nur noch gravitationellen Störungen.
Die Änderungen der Entfernungen der Sonden voneinander können auf interferometrischem Wege hochgenau bestimmt werden. Nominal betragen die Entfernungen 2.5 Millionen km, aber aus bahnmechanischen Gründen ändern sich die Abstände leicht. Damit weichen auch die Eckwinkel etwas vom Nominalwert von 60 Grad ab. Das aufgespannte Dreieck ist also kein perfektes gleichseitiges Dreieck, wobei die Variationen großenteils zyklisch sind. Man kann sich das so vorstellen, dass das Dreieck leicht pulsiert oder “atmet”. Solange die Laser immer noch im Blickfeld der Teleskope bleiben, ist das kein Problem.
Gravitationswellen sind Wellen in der Raumzeit. Wenn eine solche Welle den Detektor passiert, dann führt dies zu einer Variation der gemessenen Abstände zwischen den Sonden. Terrestrische Gravitationswellendetektoren funktionieren nach demselben Prinzip, aber zwangsläufig bei viel geringeren Armlängen. LISA misst am genauesten solche Gravitationswellen, deren Ausbreitungsrichtung senkrecht zum Normalvektor auf dem aufgespannten Dreieck liegt. Da aber die Ausrichtung des Dreiecks einem stumpfen Kegel folgt, kann LISA über das Jahr hinweg das gesamte Himmelsgewölbe abtasten.
Und wie kann LISAMax das noch toppen?
LISA soll nicht an einem der stabilen Lagrangepunkte des Sonne-Erde-Systems positioniert werden (L4 eilt der Erde um 60 Grad voraus, L5 folgt der Erde in 60 Grad Winkelabstand), sondern in nur 20 Grad Winkelabstand von der Erde. Aufgrund von Bahnstörungen, vorwiegend durch die Erdanziehungskraft, entfernt sich jedoch die Konstellation langsam von der Erde. Der wachsende Abstand wird zunehmend die Kommunikation erschweren, bis das System nicht mehr funktioniert. Die Störungen führen auch zum “Atmen” der Dreieckskonstellation. Man kann das Dreieck deswegen nicht beliebig groß machen, denn ein größeres Dreieck unterliegt auch größeren Störungen, weil dann auch der Abstand von der Erde zu jeder einzelnen Sonde umso unterschiedlicher wird.
Ich habe mich mit einem Kollegen zusammengesetzt, um zu sehen, welche Maximalgröße eine stabile und leicht zu erreichende Dreieckskonstellation haben könnte. “Leicht zu erreichen” bedeutet immer erst einmal, dass man bei Bahnen bleibt, die der Erdbahn sehr ähnlich ist. Natürlich könnte man auch ganz andere Bahnen anvisieren, aber dann explodiert förmlich die Komplexität.
Theoretisch könnte man je eine Sonde in den Lagrangepunkten L3, L4 und L5 platzieren. Dann wäre die Seitenlänge des aufgespannten Dreiecks 259 Millionen km, also mehr als 100 Mal mehr als bei LISA!
Das wäre aber unvorteilhaft, weil dann die Sonde im L3-Punkt immer von der Erde aus gesehen hinter der Sonne wäre. Man könnte nur mit Schwierigkeiten m,it ihr kommunizieren, indem man die anderen Sonden als Relais verwendet.
Das Problem kann man aber umgehen, indem die ganze Konstellation um einige Grad gedreht wird, sodass die Elongation der problematischen Sonde gerade groß genug wird, um Kommunikation zuzulassen. Dann ist zwar keine der Sonden direkt in der stabilen Lokation, jedoch konnten wir zeigen, dass es auch so immer noch möglich ist, ein fast gleichseitiges Dreieck aufzuspannen und zu halten. Die Abweichung von der perfekt gleichseitigen Form und das “Atmen” der Eckwinkel sind sogar – auch ohne aktive Bahnregelung, deutlich geringer als bei LISA.
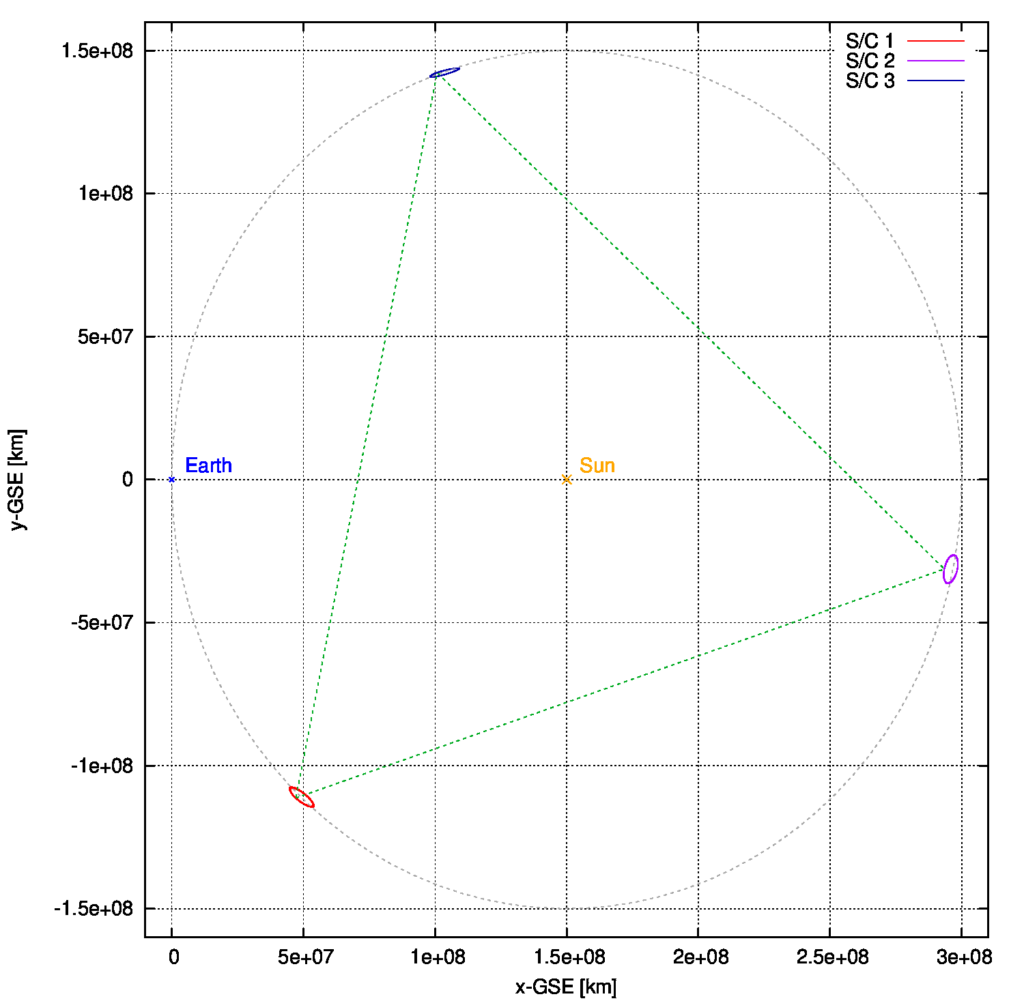
Die obige Grafik zeigt eine numerisch gefundene LISAMax-Konstellation, hier dargestellt im rotierenden System. Obwohl die jeweiligen Positionen erheblich variieren (in erster Linie aufgrund der Bahnexzentrizität), lassen sich die Bahnelemente und die Phase so wählen, dass über 10 Jahre hinweg die Eckwinkel nur um weniger als 0.1 Grad von 60 Grad abweichen. Bei LISA liegt diese Variation bei +/- 1 Grad. Auch die maximale Änderungsrate der Armlänge ist bei LISAMax viel kleiner: etwa +/- 2 m/s innerhalb von 10 Jahren gegenüber +/- 10 m/s für LISA.
Vor- und Nachteile von LISAMax
Es ist also bahnmechanisch möglich, eine solche LISAMax-Konstellation aufzubauen und stabil zu halten. Technische Herausforderungen gibt es natürlich zuhauf – die viel größeren Abstände erfordern stärkere Laser und größere Teleskope sowie größere Kommunikationsantennen an Bord der Sonden. Anders als bei LISA, wo alle drei Sonden mit derselben Rakete gestartet werden können, wird man bei LISAMax drei Starts brauchen. Die Kosten dürften also deutlich höher liegen.
Der wesentliche, prinzipbedingte Nachteil von LISAMax ist, dass das aufgespannte Dreieck fast genau in der Ekliptik liegt. Die Detektionsgenauigkeit nimmt für Gravitationswellen stark ab, deren Ausbreitungsrichtung eine hohe Deklination senkrecht zur Ekliptik aufweist. Daran lässt sich nicht viel ändern, wenn man nicht sehr viel mehr Komplexität in Kauf nehmen will.
Der Vorteil von LISAMax liegt in der 100fach größeren Armlänge gegenüber LISA, sodass der Messbereich um zwei Größenordnungen verschoben wird. LISA ist insbesondere im Frequenzbereich 10-2 bis 10-4 Hz empfindlich. Mit LISAMax würde man in den Bereich von Millionstel Hz vordringen.
Hier die erste öffentliche Präsentation des LISAMax-Konzepts durch meinen Kollegen Waldemar Martens. Dort wird auch eine erste Abschätzung der Sondengröße und der Instrumentenauslegung vorgenommen. Wir arbeiten parallel an einer Veröffentlichung in einem wissenschaftlichen Journal, aber das wird noch etwas dauern.


LISAMax arbeitet also im Mikrohertz-Frequenzbereich der Gravitationswellenastronomie und könnte somit Verschmelzungen (Merger) von supermassereichen schwarzen Loch-Binärpaaren in den späten Stadien des gegenseitigen Umkreisens nachweisen – also Tage bis Wochen bevor sie dann verschmelzen.
Allerdings gibt es auch Vorschläge Distanzmessungen Erde-Mond oder zwischen entsprechend präparierten Asteroiden (diese wären die Testmassen) zu nutzen um im Mikrohertz-Bereich zu messen. Ein solcher Vorschlag findet sich etwa im Artikel Asteroids for μHz gravitational-wave detection.
LISAMax wäre sicher viel sensitiver für Gravitationswellen im Mikrohertz-Bereich als ein Netzwerk von präparierten Asteroiden, allerdings ist LISAMax erst für die Zeit nach 2050 vorgesehen, was wohl auch mit der komplexeren Technologie und dem höheren Installierungsaufwand im Vergleich zu LISA zusammenhängt.
Ob LISAMax das richtige ist, hängt wohl sehr stark davon ab, was man im Mikrohertz-Gravitationswellenbereich alles zu finden hofft. Langfristig gesehen will die Menschheit aber wohl einen möglichst breiten Frequenzbereich der im All kursierenden Gravitationswellen beobachten und das mit der höchstmöglichen Sensitivität. LISAMax hat, falls es genügend sensitiv ist, also gute Chancen irgendwann realisiert zu werden.
Zumindest von wissenschaftlicher Seite aus scheint es ein erhebliches Interesse an Mikrohertz-Gravitationswellenastronomie zu geben. Allerdings konzentriert sich jetzt noch kaum jemand wirklich darauf – wer ernsthaft mit der Materie befasst ist, hat jetzt erst einmal mit LISA zu tun, das ja auch noch ziemlich weit in der Zukunft liegt. Wenn dann LISA erst einmal läuft, wird die Suche nach Nachfolgern an Fahrt gewinnen.
Den Vorschlag mit den präparierten Asteroiden sollte man nicht allzu ernst nehmen. Man müsste nicht nur die Asteroiden präparieren, sondern dann auch noch ihre Bahn anpassen. Ein ganz wesentlicher Parameter bei LISA ist die Limitieruing der “range rate”, also der Änderungsrate der Armlänge. Bei einer Raumsonde kann man die Bahnen der einzelnen Stationen so wählen, wie es optimal ist. Bei einem Asteroiden muss man entweder mit den Bahnen leben, die man hat, oder man muss diese Körper herumschieben.
Und selbst mit dieser gewaltigen Anstrengung würde ja der Frequenzbereich der maximalen Empfindlichkeit nur etwa 2.5 Mal unter dem von LISAMax liegen, also bei “few * 10^-7 Hz”. Das ergibt sich daraus, dass man das System im Haupt-Asteroidengürtel einrichten würde, also bei um die 2.5 AU (LISAMax: 1 AU) Der Sprung von LISA zu LISAMax ist dagegen zwei Größenordnungen. Ich halte es für wenig wahrscheinlich, dass diese Asteroidenidee jemals ernsthaft erwogen wird. Das Verhältnis von Aufwand zu Ertrag ist da nicht wirklich überzeugend.
Wenn man wirklich zu deutlich geringeren Frequenzen gehen will, also mindestens eine Größenordnung unter LISAMax, sollte man die Sonden mit den Teleskopen jenseits der Saturnbahn platzieren, erreichbar mit einem Swingby am Saturn. Das wäre dann aber wohl wirklich etwas für die zweite Hälfte dieses Jahrhunderts. Es wären sehr lange Transferdauern und sehr große Sonden. Bei Armlängen von mehr als 2.5 Milliarden km wären wohl sehr starke Laser und sehr große Teleskope auf den Raumsonden erforderlich.
Das Hauptproblem bei LISAMax sehe ich im späten Realisationstermin (nach 2050) und in den bis jetzt nicht dargestellten Alternativen. Ein solches, wohl einmaliges, kaum wiederholbares Projekt sollte nur realisiert werden, wenn alle denkbaren Alternativen schlechter abschneiden als das vorgeschlagene Projekt. Wobei schlechter abschneiden eine Gesamtbeurteilung einschliesst in die sowohl der wissenschaftliche Gewinn als auch die Kosten und die zu erwartenden Hindernisse eingehen.
Ein Problem bei LISAMax scheint mir noch die Orientierung des Sondendreiecks. Die Ausrichtung des Normalenvektors dieses Dreiecks bestimmt weitgehend die Richtungsabhängigkeit der Sensitivität. Ideal wäre wohl, wenn man gleichzeitig zwei (oder mehr) Sondendreiecke hätte, die senkrecht zueinander stehen.
Ich könnte mir vorstellen, dass die optimale räumliche Auflösung gerade im Mikrohertz-Frequenzbereich wichtig wird, denn es scheint, dass man in diesem Frequenzbereich nicht nur einzelne Ereignisse misst, sondern auch stunden- bis tagelang fortschreitende Gravitationswellenentwicklungen, beispielsweise verursacht durch sich umkreisende supermassereiche schwarze Löcher. Ich denke, es können sich mehrere solche Quellen von Gravitationswellen überlagern und die Apparatur, die diese Wellen aufzeichnet sollte deshalb über ein gutes örtliches Auflösungsvermögen verfügen. Mit einem einzelnen Sondendreieck erreicht man diese optimale örtliche Auflösung wahrscheinlich nicht. Technisch dürfte es allerdings schwierig sein, ein Sondendreieck einzurichten, dass nicht nahe an der Ekliptik liegt.
Nun vielleicht liegt die Lösung ja in einem Tetraeder von Sonden/Satelliten, denn es würde ein zusätzlicher Sondensatellit beispielsweise sehr sonnennah oder auch sehr sonnenfern genügen um aus einem Dreieck 4 Dreiecke zu machen.
Das mit der Realisierung “nach 2050” ist wohl ein Missverständnis Ihrerseits. Das Programm “Voyage 2050” sieht Missionen im Zeitraum 2035-2050 vor. Ich gehe davon aus, dass LISA innerhalb der 30er Jahre gestartet wird, hoffentlich nicht erst 2037. Die Entwicklung von LISAMax, falls das Projekt tatsächlich weiter verfolgt wird, sollte sich nahtlos anschließen – idealerweise – damit möglichst viele Synergien mit LISA genutzt werden können.
Es ist in der Tat so, dass eine Bewertung der Kosten und des wissenschaftlichen Ertrags stattfinden wird. Aber dabei geht es noch um viel mehr, was wahrscheinlich sogar für den schlussendlichen Erfolg wesentlicher ist: Politik und Proporz. Es gibt bei großen robotischen Forschungsmissionen immer die Blöcke 1.) “planetare Forschung”, 2.) “Astronomie” und 3.) “fundamental science” (in erster Linie Kosmologie). Mittlerweile ist auch noch der Block 4.) “Exoplaneten” hinzugekommen. Bei der Auswahl der aktuellen drei Großmissionen der ESA wurde die Blöcke 1.)-3.) exakt bedient: JUICE (1.), das Röntgenteleskop ATHENA (2.) und der Gravitationswellendetektor LISA (3.). Bei der kommenden Auswahlrund wird auf denselben Proporz geachtet werden, aber es wird sich zeigen, wie man den Block 4.) unterbringt.
Ob das am Ende die ESA macht oder eine andere Raumfahrtagentur oder mehrere oder gar keiner, wird sich zeigen. Der erste Schritt besteht darin, das Konzept auf den Tisch zu legen, damit es untersucht werden kann. Dabei helfen die Präsentation und die folgenden Papers. Es hilft auch, wenn das Missionskonzept Förderer in der Szene der Gravitationswellenforschung findet. Die Forschenden müssen das Missionskonzept vorschlagen. Wenn es nichts wird, dann ist es halt Pech, aber ich finde es trotzdem ziemlich cool, Co-Autor beim ersten Paper zu sein.
Das Problem mit dem feststehenden Normalenvektor habe ich ja bereits angesprochen. Das ist ein immanentes Problem, an dem sich realistischerweise wenig ändern lässt. Ich habe schon Vorschläge gesehen, wo eine zweite Konstellation senkrecht zur Ekliptik fliegt. Das kann man natürlich ganz einfach aufzeichnen, aber die Frage, wie man die Raumsonden dorthin bekommt, ist beliebig schwierig zu beantworten. Man sollte übrigens nicht den Fehler machen, dass man versucht, das ideale System zu definieren, das alles kann und alles löst. Es geht immer einen Schritt nach dem anderen.
Die wirkliche Konkurrenz für LISAMax sehe ich übrigens in einer erweiterten LISA, die mit deutlich vergrößerter Armlänge, vielleicht 5 Million km oder mehr, im Lagrange-Punkt L4 oder L5 zentriert ist. Dann hätte man immer noch eine kegelförmig rotierende Normalenrichtung, man hätte eine größere Armlänge bei geringeren Störungen, man hätte Sonden, die nicht gar so viel größer sind als die von LISA, aber man hätte eben auch nur eine Steigerung der Empfindlichkeit um etwa den Faktor 2, nicht 100.
Äußerst interessant diese Gravitationswellen. Beim Nachlesen im Internet stand, dass die Gravitationswellen eine Frequenz bis 150 Hz haben können. Also hörbar wären, wenn unsere Atmosphäre die Welle überträgt. die Fragen.
Gerät unsere Luft in Schwingung wenn die Gravitationswelle durch sie hindurchgeht.
Wie groß wäre die Amplitude , also die Lautstärke dieser Gravitationswelle.
LISAMax scheint mir wirklich erstrebenswert. Die hohe Sensitivität, die Stabilität der Satellitenkonfiguration und damit verbunden die potenziell lange Betriebsdauer und das Fehlen einer überzeugenden Alternative sprechen alle für LISAMax.
LISAMax ist aber für die ESA ein Grossprojekt, eines das wegen des hohen Aufwandes nicht schiefgehen darf. Hier könnte vielleicht eine Art Pathfinder-Mission ähnlich zu der LISA Pathfinder Mission mehr Sicherheit geben, dass der richtige Weg eingeschlagen und die richtige Technologie eingesetzt wird. Die LISA Pathfinder Mission war eine Proof-of-Concept-Mission, um die für den Erfolg von LISA erforderliche Technologie zu testen und zu beweisen, dass die gewünschte Präzision erreicht werden kann.
Wie könnte eine solche Pathfinder-Mission für LISAMax aussehen? Ein Aspekt, der getestet werden könnte ist die Stabilität der Satellitenkonfiguration. Drei Minisatelliten an den vorgesehenen Punkten in der Nähe von L3, L4 und L5 würden genügen um das zu testen. Diese Minisatelliten könnten sich selbst mit Ionenantrieben, gespiesen von Solarpaneln, zu den Punkten L3, L4 und L5 begeben. Somit würde ein einziger Raketenstart genügen um die Minisatelliten in eine höhere Umlaufbahn zu transferieren von der sie sich dann halbautonom auf den Weg zu ihren Zielen machen würden. Das wäre gerade auch eine Gelegenheit die Langlebigkeit von Ionenantrieben zu testen, denn die Reisen würde sich wohl über viele Monate hinziehen.
Ich sehe keine Notwendigkeit dafür, die bahndynamischen Aspekte vorher zu testen. Diese lassen sich exakt berechnen. Durch einen Test mit Raumsonden wird kein weiterer Erkenntnisgewinn erzielt.
Eine Pathfinder-Mission dient dazu, Technologien zu testen. Im Fall von LISA Pathfinder war das die Technik der durch Kleintriebwerke im Schwebezustand gehaltenen Testmasse, ohne die LISA nicht funktionieren kann. LPF war ein durchschlagender Erfolg. Dass aber LISA in bahnmechanischer Hinsicht funktionieren wird, steht nicht zur Debatte.
Der technische Herausforderung von LISAMax sehe ich in der Größe der Teleskope, bedingt durch den großen Satellitenabstand, der ja eine wesentliche Charakteristik des Systems wäre.
Michael Khan schrieb (03. Aug 2022):
> […] Sowohl LISA als auch LISAMax bestehen aus drei Raumsonden […] Zudem enthält jede der Sonden in ihrem Inneren eine […] Testmasse.
> Die Entfernungen der Sonden voneinander können auf interferometrischem Wege hochgenau bestimmt werden.
Durch Zwei-Arm-Interferometrie können immerhin Veränderungen von Entfernungsverhältnissen jeweils einer Sonde bzw. ihrer (verspiegelten) Testmasse bzgl. der beiden anderen bestimmt werden.
> […] wenn die Testmassen wirklich vollkommen frei schweben. Dann unterliegen die Bahnen der Sonden nur noch gravitationellen Störungen.
Falls die (drei) Testmassen wirklich und durchwegs vollkommen frei schweben, während sich ihre Entfernungsverhältnisse untereinander quasi-periodisch (insbesondere im Bereich μHz bis mHz) ändern, dann ist dieser Befund sicherlich eindeutig einer rein gravitationellen Störung und insbesondere der Passage einer Gravitationswelle zuzuschreiben.
Sonst: nicht.
> […] ultimative[r] Gravitationswellendetektor […]
Ausdrückliche und hinreichend genaue Messungen, ob eine gegebene Testmasse jeweils wirklich vollkommen frei geschwebt hätte, oder in wie fern nicht, können allerdings aufwändig sein, und für die relevante Größenordnung von Beschleunigung womöglich sogar jenseits der vorstellbaren technischen Realisierbarkeit.
In Frage kämen stattdessen eher Ausbaustufen der LISA- bzw. LISAMax-Antennen jeweils durch Hinzufügen einer vierten und einer fünften Testmasse (sowie der entsprechenden Auslese- und Nachführ-Infrastruktur für die dadurch gegebenen jeweils insgesamt 10 Interferometerarme), in Anlehnung an Five-Point Curvature Detectors (nach Synge).
Vorstellbar sind daraufhin natürlich (zunehmend ultimativere) Mehr-Arm-Interferometer-Systeme basierend auf immer noch mehr verspiegelten Testmassen …
p.s. — SciLogs-Kommentar-HTML-Test:
“10<sup>-4</sup> Hz” wird dargestellt als: “10-4 Hz”.
p.p.s.
Betreffend den Zusammenhang zwischen Krümmung und Gravitationswellen mögen sich aufmerksame SciLogs-Leser an den Hinweis (woanders) von Mitkommentator Chrys auf https://arxiv.org/abs/gr-qc/9404037 erinnern: “Why do all the curvature invariants of a gravitational wave vanish ?”, H.-J. Schmidt (1994).
Dort werden allerdings (nur) “generalized curvature invariants
I“ der DefinitionI[ g_ik, R_ijlm, ..., (R_ijlm;i1 ... ik) ]mit
I[ g_ik, 0, ..., 0 ] := 0in Betracht gezogen;
wobei Regionen, in denen Gravitationswellen vorhanden sind, offenbar (per Definition) in jedem Ereignis durch die Bedingungen
R_ijlm = 0, ..., (R_ijlm;i1 ... ik) = 0charakterisiert sind.
Wie ich mir erst recht kürzlich dazu (als ein denkbares “loophole”) überlegt habe, wäre deshalb aber womöglich trotzdem
g_iknicht unbedingt konstant,und für zumindest einige Paare von Ereignissen
(x, y)sogar∀ r ∈ ℜ : Exp[ r ] g_ik[ x ] ≠ g_ik[ y ](was den Begriff von “Krümmung” jedenfalls im Sinne Einsteins einschließt, gemäß dem
»[a]lle unsere zeiträumlichen Konstatierungen […] stets auf die Bestimmung zeiträumlicher Koinzidenzen hinaus[laufen]«).
Sehr interessantes (langes) Video der Zoom-Konferenz. Danke !