Kopfnüsse fürs Wochenende: Auflösung
BLOG: Die Sankore Schriften

Liebe Rätselfreunde, hier die Auflösung der Rätsel von Mai 2017.
Die Aussagenliste
Lösung
Falsch sind die Aussagen 1, 2, 3, 4, 5, 6, 7, 8, 10. Richtig ist die neunte Aussage.
Lösungsweg
Wenn die zehnte Aussage wahr ist, dann sind alle Aussagen der Liste, einschließlich der zehnten, falsch. Das ist ein Widerspruch, daher muss die 10. Aussage falsch sein. Wie wissen jetzt, dass mindestens eine Aussage der Liste falsch ist. Wie viele Aussagen der Liste können gleichzeitig wahr sein? Da sich die Aussagen gegenseitig ausschließen, kann höchstens eine Aussage wahr sein. Wenn eine Aussage wahr ist, müssen also neun Aussagen falsch sein.
Wasser predigen und Wein trinken
Lösung
In dem Weinfass waren zu Beginn vierzehneinhalb Gläser Wein.
Lösungsweg
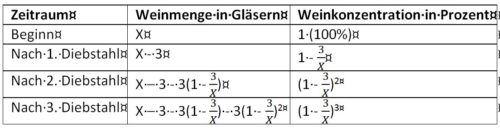
Nach dem dritten Diebstahl ist die Weinkonzentration 50%.
X ≈ 14,54
Eine Waschmaschine, die Socken frisst
Lösung
Der Statistiker hat 120 schwarze Socken und 106 weiße Socken. Eine weiße Socke ist in der Waschmaschine verlorengegangen.
Lösungsweg
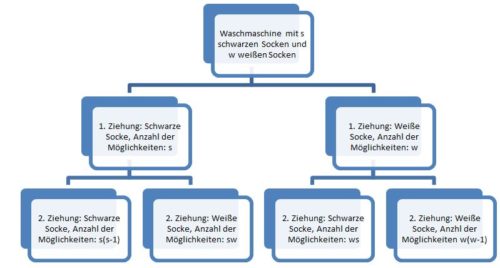
Die Möglichkeit zufällig ein gleichfarbiges Sockenpaar zu ziehen ist 50%. Das bedeutet die Möglichkeit zufällig ein ungleichfarbiges Sockenpaar zu ziehen ist auch 50%.
Daraus folgt: s(s – 1) + w(w – 1) (Möglichkeit zufällig gleichfarbige Socken zu ziehen) = sw + ws (Möglichkeit zufällig ungleichfarbige Socken zu ziehen)
Diese Gleichung lässt sich zu (s – w)2 = s + w vereinfachen
Wir erkennen das die Gesamtzahl der Socken (s + w) in der Waschmaschine eine Quadratzahl ist.
Wir wissen das die Gesamtzahl der Socken in der Waschmaschine größer als 200 und kleiner als 250 ist (200 < s + w < 250).
Das bedeutet, wir müssen nach einer Quadratzahl suchen, die zwischen 200 und 250 liegt.
Die Quadratzahl ist 225 = 152.
Das bedeutet, die Gesamtzahl der Socken in der Waschmaschine (s + w) ist 225.
Wir wissen (s – w)2 = 152 und das die Anzahl der schwarzen Socken größer als die der weißen Socken ist. Daraus folgt s – w = 15.
Wir erhalten nun ein lineares Gleichungssystem mit zwei Gleichungen und zwei Unbekannten.
s + w = 225
s – w = 15
Wir erhalten als Lösung s = 120, w = 105.
Wir wissen, dass der Statistiker Socken nur als gleichfarbige Paare kauft. Entweder ein schwarzes Paar oder ein weißes Paar. Das bedeutet, die Anzahl der schwarzen Socken ist gerade und die Anzahl der weißen Socken ist gerade. Da wir aber rausgefunden haben, dass die Anzahl der weißen Socken (105) in der Waschmaschine ungerade ist, muss die fehlende Socke weiß sein.


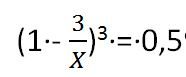
Howdy, Joe,
zum Glück lag Dr. Webbaer (auch) bei Problem Drei halbwegs richtig, eine statistische Fachkraft hat ja andere Lösung vorgeschlagen.
MFG + schönes Wochenende noch, gute Arbeit!
Dr. Webbaer
Ich war beim Rätseln nur so weit gekommen, daß ich zu dem Schluß kam, der Statistiker hat entweder einen Sockenfetisch oder sehr schlimme Schweißfüße, wenn er so viele Socken braucht. An der Frage, warum er die alle gleichzeitig wäscht, tüftele ich noch. ^^
Was wird sich als nächstes ändern, um die Entwicklung und Weiterentwicklung von zu verbessern cookie clicker 2 unblocked?