Von Mathematik und Genderpolitik – Emmy Noether: Wegbereiterin der abstrakten Algebra und der modernen theoretischen Physik
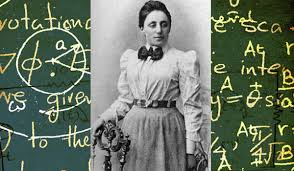
Wer die Geschichte der Mathematik betrachtet, erkennt schnell, dass hier offenbar ausschliesslich geniale Männern gewirkt haben müssen. Ob der „Mathematiker-Fürst“ („Princeps mathematicorum“) Carl Friedrich Gauß oder der Schweizer Leonhard Euler, ob Isaac Newton, Gottfried Wilhelm Leibniz oder David Hilbert, ob Pythagoras, Archimedes, Euklid, Fibonacci oder al-Chwarizmi, in der Riege grosser historischer Mathematik-Figuren finden wir kein einzige Frau. Bis zum 20. Jahrhundert ist die Liste von überlieferten Mathematikerinnen überhaupt sehr überschaubar. Aus der Antike überliefert ist nur Hypatia von Alexandria, von der allerdings keine Werke überliefert sind und die hauptsächlich wegen der spektakulären Umstände ihrer Ermordung in Erinnerung geblieben ist. Die frühe Aufklärungszeit kannte Émilie du Châtelet, die sich als mathematische Expertin der Physik Newtons auszeichnete, Bekanntheit aber eher als Partnerin Voltaires erlangte. Gewisse Ehren erwarb im 19. Jahrhundert Sophie Germain für den Beweis der Fermat’schen Vermutung (heute Satz) für eine bestimmte Gruppe von Primzahlen (die heute so genannten „Sophie-Germain-Primzahlen“), und 1889 erhielt Sofja Kowalewskaja als weltweit erste Frau einen Lehrstuhl für Mathematik. Kowalewskaja ist heute allerdings eher dafür bekannt, dass sich hartnäckig das – wohl falsche – Gerücht hält, es gebe keinen Nobelpreis für Mathematik, weil sie eine Liaison mit Alfred Nobel gehabt und ihn dann wegen eines anderen (Gösta Mittag-Leffler) verlassen habe. Erst in der zweiten Hälfte des 20. Jahrhunderts wird die Liste der Mathematikerinnen länger, aber auch daraus ragt kein Name hervor, mit einer einzigen Ausnahme, den ausserhalb der Mathematik (und theoretischen Physik) allerdings auch so gut wie niemand kennt: Emmy Noether. Und dass es bis zum Jahr 2014 dauerte, bis eine Frau die höchste Auszeichnung für Mathematik, die „Fields-Medaille“ zugesprochen erhielt (es handelt sich um die Iranerin Maryam Mirzakhani), gibt nicht weniger zu denken.
Die Suche nach Gründen für diese nahezu komplette Abwesenheit von Frauen auf der Liste grosser Mathematiker gleicht dem Stochern in einem Wespennest, mit der man sich heute nur allzu schnell auf eine Abschussliste manövrieren kann, wie dies beispielsweise Larry Summer, immerhin ehemaliger US-Finanzminister im zweiten Kabinett Bill Clintons, sehr gut weiss. Nach seiner törichten Aussage von einem Frauen möglicherweise fehlenden Gens für wissenschaftliches Talent und angeborenen Unterschieden zwischen Männern und Frauen, wenn es darum geht, Naturwissenschaften an den besten Unis zu praktizieren, war er 2005 gezwungen, von seiner Position als Präsident der renommierten Harvard-Universität zurückzutreten. Denn tatsächlich gibt es keine erstzunehmende akademische Referenz dafür, dass Frauen eine tiefere durchschnittliche mathematische Intelligenz besitzen als Männer, auch wenn es sowohl kognitive Aufgaben gibt, bei denen Männer im Durchschnitt besser abschneiden, als auch solche, bei denen Frauen überlegen sind. Zudem gibt es einige Hinweise dafür, dass die Varianz der Intelligenzverteilung bei Männern breiter ist als bei Frauen, mit anderen Worten, es gibt mehr äusserst dumme und äusserst intelligente Männer als Frauen. Aber auch diese Aussage ist nicht unumstritten. So tritt der Varianz-Unterschied nicht in allen Ländern auf und erscheint auch abhängig vom Mass der gesellschaftlichen Gleichstellung der Frauen. Ein einfacher Blick in die Geschichte der akademischen Einrichtungen gibt einen wesentlich deutlicheren Hinweis darauf, wo die Gründe für die augenfällige Unterrepräsentanz von Frauen in der Mathematik liegen: Bis weit ins 20. Jahrhundert war es Frauen schlicht verboten, an Universitäten Mathematik zu lehren. Unter diesen Umständen zu mathematischem Ruhm und Ehren kommen, war äusserst schwierig, wenn nicht gar unmöglich.
Nichtsdestotrotz ragte in der männlich dominierten Zunft der Mathematiker des frühen 20. Jahrhunderts eine Frau heraus, Emmy Noether. Doch auch sie hatte unter den Einschränkungen ihrer Zeit zu leiden. Denn man darf ohne weiteres davon ausgehen, dass wäre Noether ein Mann gewesen, dieser als einer der grössten Mathematiker (und theoretischen Physiker) des 20. Jahrhunderts gelten würde. Ihr Name sollte eigentlich auf einer Stufe mit denen von David Hilbert, Albert Einstein, Erwin Schrödinger oder Werner Heisenberg stehen. Doch hatte Emmy Noether zeit ihres Lebens noch nicht einmal eine feste Anstellung als ordentliche Professorin.
Emmy (Amalie) Noether wurde am 23. März 1882 in Erlangen als Tochter des Mathematikers Max Noether geboren. Der grosse David Hilbert lud sie ab dem Jahr 1909 regelmässig nach Göttingen ein, dem damals führenden mathematischen Zentrum der Welt, und ermutigte sie 1915, dort einen Antrag auf Habilitation zu stellen. Diesem folgten kontroverse Diskussionen in der Fakultät, in der sich viele grundsätzlich gegen eine Habilitation von Frauen aussprachen. Erst Hilberts Autorität und sein Ausspruch „eine Fakultät sei doch keine Badeanstalt“ brachten den erwünschten Erfolg unter den Göttinger Mathematikern. Doch wurde der entsprechende Antrag auf eine Sondergenehmigung (die Habilitation von Frauen war an preußischen Universitäten bis 1919 untersagt) vom zuständigen Minister mit der Begründung abgelehnt, dass „die Zulassung von Frauen zur Habilitation als Privatdozent in akademischen Kreisen nach wie vor erheblichen Bedenken begegnet“. Emmy Noether blieb nichts anderes übrig, als ihre Vorlesungen unter dem Namen Hilberts, als dessen Assistentin, anzukündigen – ohne dafür bezahlt zu werden. Erst als in der frühen Weimarer Republik die Habilitationsordnung geändert wurde, so dass auch Frauen eine mathematische Lehrbefugnis erhalten konnten, habilitierte sich Emmy Noether 1919 als erste Frau in Deutschland in Mathematik (der Anstoss dazu kam allerdings nicht von den Göttinger Mathematikern, sondern von Albert Einstein, der sie durch ihre Arbeiten zu Fragen der Relativitätstheorie kennen- und schätzen gelernt hatte) und erhielt die Lehrbefugnis – allerdings bei immer noch sehr geringer Bezahlung. Eine volle Professur wurde ihr vorenthalten, und selbst als international berühmte und verdiente Mathematikerin wurde ihre Beförderung in die Göttingen Gesellschaft der Wissenschaften 1930 abgelehnt.
Emmy Noether gilt als Begründerin der modernen abstrakten Algebra („Mutter der modernen Algebra“), eine der bedeutendsten Innovationen der Mathematik des 20. Jahrhunderts. Mitte der 1920er Jahre etablierte sich um sie eine eigene Schule, in der sich eine Reihe von hochbegabten Studenten aus aller Welt um sie scharten, die so genannten „Noether-Knaben“ (auch wenn unter ihren Doktoranden zwei Frauen waren). Viele ihrer akademischen Schüler wurden ihrerseits bedeutende Mathematiker (u. a. Grete Hermann, deren Rolle in der mathematischen Formulierung der Quantenmechanik von Historikern erst kürzlich erkannt wurde) und spielten eine bedeutende Rolle bei der Durchsetzung abstrakter algebraischer Methoden auf verschiedenen Gebiet der Mathematik. Nach Emmy Noether sind heute zahlreiche mathematische Strukturen und Sätze benannt (Noetherscher Ring, Noethersche Ordnung, Noetherscher Raum, Noetherscher Modul, u.a.).
Doch ihren wohl bekanntesten Beitrag leistete Emmy Noether in der theoretischen Physik mit ihrem Aufsatz Invariante Variationsprobleme aus dem Jahr 1918. Das darin formulierte und heute so genannte „Noether-Theorem“ entwickelte sich in der zweiten Hälfte des 20. Jahrhunderts zu einer der wichtigsten Grundlagen der modernen Physik. Auslöser ihrer Arbeit war ein Problem, das Hilbert in Einsteins Allgemeiner Relativitätstheorie wähnte: Das Prinzip der (lokalen) Energieerhaltung schien darin verletzt, so Hilbert. Noether löste die scheinbare Unvereinbarkeit der Einstein‘schen Theorie mit diesem Grundprinzip der Physik auf sehr elegante Weise auf und konnte dabei einen viel allgemeineren Zusammenhang entwickeln. Einstein war derart beindruckt von ihrer Arbeit, dass er schrieb: „Gestern erhielt ich von Fr. Noether eine sehr interessante Arbeit über Invariantenbildung. Es imponiert mir, dass man die Dinge von so allgemeinem Standpunkt übersehen kann. Es hätte den Göttinger Feldgrauen nichts geschadet, wenn sie zu Frl. Noether in die Schule geschickt worden wären!“
Das Noether Theorem besagt, dass jeder kontinuierlichen (mathematisch genauer: differenzierbaren) Symmetrie eines physikalischen Systems eine Erhaltungsgröße entspricht, und umgekehrt. Was bedeutet dies konkret? Mit „Symmetrie“ ist hier eine Transformation gemeint, die das Verhalten eines physikalischen Systems nicht ändert. So macht es beispielsweise keinen Unterschied, ob man ein Experiment heute, morgen oder in einem Jahr (oder in einer Milliarden Jahren) durchführt. Physiker sprechen auch von der „Homogenität der Zeit“. Analog dazu gibt es die „Homogenität des Raums“: Wo ich ein Experiment ausführe, spielt ebenso keine Rolle. Das Ergebnis sollte (bei identischen Randbedingungen, d.h. keine verschieden wirkende äusseren Kräfte) das gleiche sein. Das mag schnell einleuchten, aber die Konsequenzen daraus sind alles andere als trivial. Denn aus diesen Invarianzen ergeben sich direkt physikalische Erhaltungsgrössen. Der Homogenität der Zeit entspricht das wichtige physikalische Prinzip der Energieerhaltung: In jedem physikalischen System bleibt die Gesamtenergie erhalten. Analog entspricht der Homogenität des Raumes die Erhaltung des Impulses. Tatsächlich gilt ganz allgemein, dass immer dann, wenn sich in einem mathematischen Naturgesetz eine Symmetrie finden lässt, es eine dazu gehörige Erhaltungsgrösse geben muss. Ein erstaunlicher Zusammenhang, für die es die geniale Einsicht Emmy Noethers bedurfte (der grösste Mathematiker und der grösste Physiker des 20. Jahrhunderts hatten sich an diesem Problem die Zähne ausgebissen). Besonders in den modernen Quantenfeldtheorien, wo sehr viel abstraktere Symmetrien als räumliche oder zeitliche Homogenität bedeutende Rollen spielen (so genannte „Eichsymmetrien“, die beispielsweise der Erhaltung der elektrischen Ladung entsprechen), ergeben sich aus dem Noether-Theorem wichtige Hinweise auf die fundamentalen Eigenschaften der physikalischen Strukturen in unserer Welt, sowie nützliche Rechenmethoden und Hinweise für mögliche experimentelle Überprüfungen physikalischer Theorien.
Ihre mathematischen Eisichten machen Emmy Noether zu einem der wenigen Menschen überhaupt (wahrscheinlich der erste seit Isaac Newton), deren Arbeiten sowohl für die Physik als auch für die reine Mathematik derart bedeutend waren, dass sie wohl beide Auszeichnungen, den Physik-Nobelpreis und die Fields-Medaille der Mathematik verdient hätten (die Fields Medaille gibt es erst seit 1936 und hat eine Altersgrenze von 40 Jahren (was David Hilbert ausschliesst, Noether war bei Publikation ihres bekanntesten Aufsatzes 36), den Nobelpreis seit 1901).
Es ist zuletzt aber auch Emmy Noether zu verdanken, dass Frauen heute einen besseren Zugang zu mathematischer Ausbildung und akademischen Positionen haben. In den USA gibt es heute beispielsweise die „Noether Lectures“, eine jährliche Ehrung der Association for Woman in Mathematics für Frauen, die fundamentale und nachhaltige Beiträge zur Mathematik geleistet haben. Die Liste verdienter Mathematikerinnen hat seit der zweiten Hälfte des 20. Jahrhundert ein rasantes Wachstum hingelegt, was Aussagen eines Larry Summers als eine unbekömmliche Mischung aus Arroganz und Ignoranz entlarvt. Man muss nicht Feministin oder Feminist sein um zu mutmassen, dass unsere Nachkommen in 100 Jahren die zweite Hälfte des 20. Jahrhunderts vielleicht als den Zeitpunkt erkennen werden, an dem die Menschheit endlich einen lange brachgelegenen Teil ihres mathematischen und intellektuellen Kapitals freigesetzt hat. Emmy Noether könnte sich also auch in dieser Hinsicht letztlich als eine Pionierin erweisen.


Solche Blog-Einträge gehören für mich zu “lesenswerten” Arikeln. Interessant, informativ und vor allem, sie sind leicht zu lesen und zu verstehen.
schicke noch ein t nach…
ein Tippfehler: Mirzakhani’s Fieldsmedaille war 2014, nicht 2104.
Noch ein Tippfehler: Leonhard Euler, nicht Leonard.
Frau Noether ist wahrhaftig eine phänomenale Physikerin und Mathematikerin, und es tut gut zu sehen, daß sie mit diesem Beitrag gewürdigt wird, und auch die Voreingenommenheit ihrer männlichen Kollegen zur Sprache kommt. Diese Voreingenommenheit wäre ein eigener Beitrag wert gewesen, und die verdient es alle Male, ebenso ins Bewußtsein gehoben zu werden.
Frau Noether hat als Erste präzise ausformuliert, daß allgemeine statische Strukturmerkmale dieser Welt die dynamischen Prozesse, die in dieser Welt ablaufen, in gewissem Maße festlegen, was metaphysisch gesehen sofort einleuchtet. Symmetrien sind letztendlich sehr allgemeine Randbedingungen, die die Menge alle Möglichkeiten von physikalischen Prozesses einschränken, indem diejenigen (prinzipiell möglichen) Prozesse ausgeschlossen werden, bei denen sich alle Größen beliebig ändern, mit denen also eine Einschränkung auf eine gewisse Gesetzmäßigkeit überhaupt vorgenommen wird.
Was mir aber seltsam vorkommt ist, daß die Verschiebungs-Homogenität von Zeit und Raum zu Erhaltungsgrößen führen, die nicht lorenzinvariant sind (Energie und Impuls), aber die Richtungs-Homogenität des Raums zu einer ganz anderen Erhaltungsgröße führt – nämlich zur Erhaltung des Drehimpulses – welcher lorenzinvariant ist !
Was ich meine ist: es gibt zwei sehr ähnliche Raum-Homogenitäten: die Verschiebungs- und Rotationshomogenität – und beide führen zu vollkommen (wesenhaft) verschieden Erhaltungsgrößen.
Das finde ich sehr bemerkenswert. Warum ist die eine Erhaltungsgröße abhängig vom gewählten Inertialsystem und die andere nicht – obwohl beiden die Raumhomogenität als einheitliche Struktur zugrunde liegt.
Darauf hat Frau Noether keine Antwort gegeben. Mir ist jedenfalls keine bekannt. Würde sie noch leben, würde sie die Frage vielleicht beantworten können, ich traue es ihr zu. Von ihren Nachfolgern ist mir keine Antwort bekannt – sie hat der Nachwelt ein ungelöstes Rätsel hinterlassen. Keiner hat danach an sie herangereicht, das zeigt, wie überragend sie war.
Grüße Fossilium
fossilium schrieb (10. Juli 2017 @ 01:06):
> Warum ist die eine Erhaltungsgröße
… Impuls (eines bestimmten Beteiligten, B, gegenüber den Konstituenten eines bestimmten Inertialsystems, Σ),
p_Σ[ B ] …
> abhängig vom gewählten Inertialsystem
Das entspricht schlicht und einfach der Definition von “Impuls”, als Messgröße.
Genau so ist z.B. “(Durchschnitts-)Geschwindigkeit” eines bestimmten Beteiligten nicht “an sich” festzustellen,
sondern vorrangig durch zwei bestimmte geeignete (d.h. insbesondere gegenüber einander ruhende) Beteiligte (“Start” und “Ziel”);
sodass vollständig stets von der
“(Durchschnitts-)Geschwindigkeit des betreffenden Beteiligten gegenüber dem Inertialsystem, zu dem Start und Ziel gehörten”
die Rede sein sollte;
also von “v_Σ[ B ]”.
> […] und die andere [Drehimpuls] nicht
Offenbar doch:
auch “Drehimpuls” versteht sich vollständiger Weise als
“Drehimpuls eines bestimmten Beteiligten, B, gegenüber einem bestimmten geeigneten Konstituenten, K, eines Inertialsystems, Σ)”.
p.s.
> […] lorenzinvariant
Messgrößen sind (selbstverständlich) unabhängig von irgendwelchen Koordinaten-Zuordnungen,
und folglich invariant gegenüber jeglichen Transformationen zwischen bestimmten Koordinaten-Zuordnungen, wie etwa Lorentz-Transformationen.
Hallo Herr Wrappler,
in Fachtermini ausgedrückt heißt es:
Der Impuls ist nicht lorenzinvariant.
Der Drehimpuls ist lorenzenzinvariant.
So einfach ist das. Ist vielleicht beim vielfach angestimmten Loblied auf die allgemeinen Symmetriegesetze der Fachwelt noch nicht aufgefallen.
Aber ich frage warum ? Beide entstammen aus der gleichen allgemeinen Symmetrie des Raumes.
Grüße
Fossilium
fossilium schrieb (10. Juli 2017 @ 15:40):
> […] in Fachtermini ausgedrückt heißt es:
> Der Impuls ist nicht lorenzinvariant.
> Der Drehimpuls ist lorenzenzinvariant.
Dagegen behaupte ich:
Sowohl Impuls als auch Drehimpuls sind Lorentz-invariant.
(Die zugrundegelegten wesentlichen Definitionen und darauf aufbauenden Argumente habe ich oben bereits skizziert
Dass ich damit eventuell auch solchen Benutzern von Fachtermini widerspreche, die dazu tendieren, den Familiennamen von Hendrik Antoon Lorentz so zu schreiben, wie ich es gewohnt bin, nehme ich dabei natürlich billigend in Kauf;
und bin dankbar für die Gelegenheit.
> […] beim vielfach angestimmten Loblied auf die allgemeinen Symmetriegesetze
… sollte meines Erachtens die Stimme der Nachvollziehbarkeit (von Messgrößen) noch kräftiger erklingen.
Ada Lovelace (Augusta Ada Byron King, Countess of Lovelace) wäre vielleicht noch zu erwähnen.
Hi zusammen,
ich muß noch eins draufsetzen:
Impuls und Energie sind nicht einmal galileiinvariant – ihre Erhaltung auf Grund von Symmetrien gilt nur im aktuellen Bezugssystem. Bei Wechsel des Bezugssystems bricht die Erhaltung gnadenlos zusammen. Da greift keine Symmetrie mehr durch.
Der Drehimpuls aber bleibt erhalten. Da greift die Symmetrie. Das ist wirklich einmalig.
Der Drehimpuls ist auch ansonsten ziemlich besonders: Jede beliebige Bewegung, auch die geradlinig gleichförmige, hat einen Drehimpuls. Auch nicht so bekannt ist, daß die Plankschen Wirkungsquanten gar keine Energiequanten sind, sondern kleine Drehimpulse. Und was steht unter dem Integral der kleinsten Wirkung ? Nicht Energie – nein, der Drehimpuls. Und welche komplementären Größen sind wechselseitig unscharf ? die Im Produkt einen Drehimpuls bilden. Und was ist lorentzinvariant ? Der Drehimpuls (als einzige dynamische Größe). Sollte eigentlich Anlaß sein, den Drehimpuls mehr herauszustreichen in der Lehrphysik. Da ist aber komplette Fehlanzeige. Ein grandioses metaphysisches Defizit.
Offenbar gibt es solche und solche Erhaltungsgrößen. Und eine ist einzigartig: der Drehimpuls.
Nun ja, alle reden von Energie – ist auch nichts anderes als übertragbarer Drehimpuls. Kann jeder in einer Zeile nachrechnen. Wir brauchen den Energiebegriff im Prinzip gar nicht, kann man alles genauso gut mit dem Drehimpuls beschreiben. Ohne den Drehimpuls geht gar nichts !
Wieso erzeugt die räumliche Rotationssymmetrie so ein Ding ?
Weil wir darauf keine schnelle Antwort haben, können Symmetrien nicht strukturell die einzige Ursache von Gesetzmäßigkeiten sein. Es muß noch was dazu kommen. Ich hätte mich gerne mit Frau Nöther unterhalten. Es gibt eben nicht so viele Physiker, die in metaphyischen Kategorien denken Deshalb hat die gute Emmy Einstein so imponiert. Heute ist es eher schick, die metaphysische Seite der Physik zu mißachten, oder diletantisch damit herumzuspekulieren.
Diese heutige Voreingenommenheit hätte der Ersteller dieses Betrags auch mal thematisieren können.
Na gut, will ich nicht weiter unken.
Es grüßt alle
Fossilium
Und welche quantemechanische Größe ist mataphysisch am wenigsten verstanden ?
der Spin – ist auch ein Drehimpuls.
jetzt muß man aber mal wirklich aufwachen.
Grüße Fossilum
Fossilium schrieb (10. Juli 2017 @ 22:58):
> ich muß noch eins draufsetzen: […]
Dagegen kann ich mich z.B. auf “the world’s largest and most powerful” berufen …
> Impuls und Energie […] – ihre Erhaltung […] gilt nur im aktuellen Bezugssystem.
> Bei Wechsel des Bezugssystems bricht die Erhaltung gnadenlos zusammen.
Im (aktuellen) LHC Guide, Tabelle auf Seite 5, sind einige Werte von “kinetic energy and speed of a proton in the CERN machines angegeben.
(Leider fehlen darin die Einträge, die nominell den gegenwärtigen Betrieb beschreiben; also die insbesondere in der Tabelle auf Seite 30 genannte Protonenenergie im LHC von 6.5 TeV und der entsprechende Wert des Geschwindigkeits-Betrags dieser Protonen gegenüber dem LHC von ca. 99,9999990 Prozent der Lichtgeschwindigkeit. Aber das Prinzip dürfte trotzdem deutlich sein, zumal auf Seite 4 des Guides die zugrundeliegenden Formeln angegeben sind.)
Diese Werte sind und bleiben, wie sie sind (invariant, nachvollziehbar);
ganz egal in welchem Bezugssystem die geometrisch-kinematischen Beziehungen zwischen den genannten (beispielhaft betrachteten) Protonen und den “CERN machines” (d.h. all deren Konstituenten, die in praktischer Näherung gegenüber einander ruhen) ermittelt oder dargestellt würden.
Das gilt ebenso für den Impuls-Betrag der Protonen gegenüber diesen Konstituenten.
(Die Impuls-Richtung bzw. Geschwindigkeits-Richtung von Protonen bestimmter Energie gegenüber dem LHC ist natürlich i.A. veränderlich, da es sich beim LHC um einen Ring-Beschleuniger handelt.)
p.s.
> […] daß die Plankschen Wirkungsquanten gar keine Energiequanten sind,
… sondern Plancksche Wirkungsquanten.
Dass die Kommutatoren zueinander konjugierter (Mess-)Größen nicht nur grundsätzlich von Null verschieden sind, sondern alle den gleichen “Natur-konstanten” Wert zugeschrieben bekommen, ist allerdings der Gipfel. …
@fossilium, @Frank Wappler: Nach Noether folgt die Energieerhaltung daraus, dass Abläufe, die sich nur durch den Startzeitpunkt unterscheiden, sich nicht unterscheiden [dürfen]. @fossiliums Zurückführung der Energieerhaltung auf (Zitat)“Nun ja, alle reden von Energie – ist auch nichts anderes als übertragbarer Drehimpuls.” scheint mir zu restriktiv.
In einem Punkt hat er allerdings nicht völlig unrecht: Die Energieerhaltung gilt nicht unbedingt für das ganze Universums.
Martin Holzherr schrieb (11. Juli 2017 @ 16:13):
> […] dass Abläufe, die sich nur durch den Startzeitpunkt unterscheiden, sich nicht unterscheiden [dürfen].
Um einer derartigen Stilblüte nicht nur mit vollkommener Sprachlosigkeit zu begegnen:
Abläufe, die sich durchwegs zumindest abschnittsweise mit Durchschnittsgrößen bewerten lassen
(oder für die sogar durchwegs punktuelle Größen definierbar sind),
lassen sich dahingehend unterscheiden, ob die betreffenden Werte im jeweiligen Ablauf durchwegs gleich blieben, oder sich änderten.
> […] Energieerhaltung gilt nicht unbedingt für das ganze Universum
Es lässt sich von vornherein gar nicht unbedingt ein geeignetes Referenzsystem finden, hinsichtlich dem eine (andernfalls so zu bezeichnende) “Energie des gesamten Universums gegenüber diesem Referenzsystem” überhaupt definierbar wäre.
Zitat:“Um einer derartigen Stilblüte nicht nur mit vollkommener Sprachlosigkeit zu begegnen:” schreiben sie zu: “dass Abläufe, die sich nur durch den Startzeitpunkt unterscheiden, sich nicht unterscheiden [dürfen]”
Der entsprechende Satz aus Joachim’s Quantenwelt lautet:“Energieerhaltung liegt immer dann vor, wenn ein Vorgang bezüglich einer Verschiebung in der Zeit symmetrisch ist. Also wenn es unerheblich ist, wann der Vorgang startet. In dem Zimmer, in dem Sie sitzen ist die Energie wahrscheinlich erhalten.” Im Fahrstuhl sei das aber nicht der Fall liest man ein paar Sätze später.
Symmetrisch bezüglich der Verschiebung in der Zeit, bedeutet nach obiger Formulierung letzlich, dass man die bei Messungen von Vorgang1 gewonnen Daten durch Addition der Zeitverschiebung mit den Messungen von Vorgang2 zur Deckung bringen kann.
Martin Holzherr schrieb (12. Juli 2017 @ 11:55):
> […]
Für eine bei aller Kürze einigermaßen verständliche und akzeptable Formulierung halte ich:
Vor allem, weil darin gar nicht (ausdrücklich) von irgendwelchen Koordinaten die Rede ist
(im Zusammenhang mit quantitativer Bewertung von “zeitlicher Verschiebung” spräche man von “Dauer”);
und weil ausdrücklich von der “Wirkung” die Rede ist, die (z.B.) einem bestimmten “Vorgang” zugemessen wurde,
die sich als wesentlich invarianter/symmetrischer erweisen kann, als der betreffende “Vorgang” an sich; vgl. “hidden symmetry”
@Martin Holzherr / 11. Juli 2017 @ 16:13
»Die Energieerhaltung gilt nicht unbedingt für das ganze Universums.«
Das Energieprinzip ist in gängigen kosmolog. Modellen nicht verletzt, allerdings lässt sich dem Universum gar kein wohldefinierter globaler Wert an Energie zuweisen. Das ist so ungefähr die zentrale Aussage eines recht empfehlenswerten SciAm Artikels von Tamara Davis (2010), Is the universe leaking energy?
“Thus, the universe does not violate the conservation of energy; rather it lies outside that law’s jurisdiction.”
N.B. In deutscher Übersetzung erschien der Artikel dann auch irgendwann im Spektrum.
Wie dem auch sei, in diesem Zusammenhang, aus irgendwelchen, auch dem Schreiber dieser Zeilen unbekannten, unerkannten Gründen, war auch ihm weibliches Personal an entscheidender Stelle stets unerkannt; andere mögen diese Beobachtung meinend erste Steine werfen.
—
Ansonsten, bei erkennbarer Unterschiedlichkeit rät Dr. W an wie folgt einzuschätzen :
A) Es ist falsch zu behaupten, dass bestimmte Gruppen-Angehörige, im hier gemeinten Falle : womöglich Frauen, pauschal als diesbezüglich unbekömmlich einzuschätzen. – Eine derartige Einschätzung obliegt womöglich politisch konservativen (“rechten”) Kräften, sie ist falsch.
B) Es ist falsch zu behaupten, dass bestimmte Gruppen-Angehörige, im hier gemeinten Falle : womöglich Frauen, gesellschaftlich unterdrückt werden, so dass sich nur so die bekannte Beleglage ergibt. – Eine derartige Einschätzung ist gefährlich, wenn nicht angemessen belegt, sie wäre dann falsch und (gesellschaftlich) gefährlich, sie obliegt idR politisch linken Kräften.
C) Es ist richtig zu behaupten, in concreto aus liberaler Sicht, hier sozusagen agnostisch zu werden und dieser Aussage zu folgen:
—
Es handelt sich -in der diesbezüglichen Feststellung- letztlich um dreiwertige Logik, diese ist vergleichsweise lustig, aber auch durchgesetzt in allen dem Schreiber dieser Zeilen bekannten Datenverarbeitungssystemen, in relationalen Datenbanken und so.
Es ist nicht nur insofern cool sich zu bestimmten Fragen agnostisch zu stellen.
MFG + schönes Wochenende,
Dr. Webbaer
*
als diesbezüglich unbekömmlich einzuschätzen [sind]
(Opi W ist hier immer auch ein wenig “trumpy”, dieser Kollege, sofern nicht unumgebracht, wird “rocken”, so wie Dr. W abär noch mehr)
Zitat:“Und dass es bis zum Jahr 2014 dauerte, bis eine Frau die höchste Auszeichnung für Mathematik, die „Fields-Medaille“ zugesprochen erhielt (es handelt sich um die Iranerin Maryam Mirzakhani)” Mirzakhani starb am 15.07.2017. An der Preisverleihung (Fieldsmedaille) konnte sie wegen ihrer Krankheit bereits nicht mehr teilnehmen.
Hallo,
Ich besuche gerade die 11 Klasse und werde mit 2 meiner Klassenkameraden ein Referat über frauen in der Mathematik hakten. Ich habe mich für Emmy Noether entschieden und finde das Noether Theorem als Beispiel (also das mit der Symmetrie)interessant jedoch verstehe ich noch nicht den Gedanken dahinter. Ich habe versucht aus den Kommentaren schlau zu werden hat leider nicht geklappt. Ich wäre sehr dankbar falls jemand mir das Noether Theorem so unkompliziert wie möglich erklären könnte.
vielen Dank
Grüße Stella