Das Hirn und der rechte Winkel
BLOG: Anatomisches Allerlei

Die Behauptung, “dass die Natur keine rechten Winkel kenne”, ist natürlich Unsinn. Sie wird gerne den Anthroposophen unterstellt, schon wegen der Architektur ihres Hauptsitzes (erstes Goetheanum in Dornach, leider abgebrannt), aber noch nicht mal Rudolf Steiner kann so verbohrt gewesen sein, zum Beispiel so etwas,

(von hier)
einen Pyrit-Kristall, nicht zur Kenntnis zu nehmen. Rechte Winkel.
Allerdings muss man schon zugeben, dass in unserer mesokosmischen Alltagswelt, so im Massstab von ein paar Zenti- bis zu Kilometern, sich viele menschengemachte Artefakte durch ihre Rechtwinkligkeit leicht von den Naturgegenständen unterscheiden lassen – Pyrit hin oder her.
Was ist das eigentlich – ein rechter Winkel? Ein Winkel ist da, wo sich zwei Geraden schneiden, und das können die unter allen möglichen Winkeln tun. Eigentlich sind da sogar immer vier Winkel, denn die Geraden hören ja da, wo sie sich schneiden, nicht auf. Was zeichnet den “rechten”, den richtigen, vor allen anderen aus? Von dem Mathematiker Hilbert stammt die schöne Definition, dass der rechte Winkel im Geradenschnitt der einzige unter den unendlich vielen möglichen Winkeln ist, der genauso gross ist wie sein Nebenwinkel. Ich finde das eine sehr elegante Definition.
Wenn ich die Physiker und Mathematiker recht verstehe, zwingt uns niemand, den Raum partout mit den cartesischen Achsen (Höhe/Breite/Tiefe) zu durchmessen, den drei allbekannten Raumpfeilen also, die senkrecht, rechtwinklig, orthogonal aufeinander stehen. Ein System von drei “schiefen” Achsen täte es auch, Kugelkoordinaten, Zylinderkoordinaten – alles geht, mit allen kann man einen Punkt im Raum eindeutig bezeichnen. Die Koordinaten des Cartesius/Descartes liegen unserer Intuition halt am nächsten. Hätten wir tagtäglich den Eindruck, nicht auf einer vom Himmel überwölbten und der Hölle unterlagerten Scheibe, sondern auf einem Ball zu wohnen, dann hätten wir womöglich gleich zu den Kugelkoordinaten gegriffen.
Reine Willkür also. Statt: “Obacht! Da vorne, oben, links!” (das ist cartesisch gesprochen) könnte ich auch sagen “Achtung! Azimut 330 Grad, Polar 60, Radius 50 Meter!” (das sind Kugelkoordinaten). Das kapiert allerdings keiner, und wenn da von vorne oben links irgend etwas Verderbliches sich nähern sollte, dann ist es meinem Zuhörer auf den Kopf gefallen, bevor er die Koordinaten umgerechnet hat…
… aber: nicht-sprachlich arbeite ich doch mit Polarkoordinaten. Ich werde nämlich den Arm heben, und auf den bedrohlichen Gegenstand weisen. Und zwar nicht, indem ich den Arm erst vor-, dann nach links und dann nach oben schiebe, nein, ich werde ihn, wie den Pfeil einer Polarkoordinate, so aufklappen, dass mein Zeigefinger direkt auf den Punkt im Raume hinschiesst. Auf kürzestem Wege.
Wie navigiert die Natur selbst? Polar? Kartesisch?
Wenn man sich – so als Anatom – den Bau des menschlichen Leibes anschaut, sehen die Naturprodukte auf den ersten Blick ganz und gar nicht cartesisch, rechtwinklig aus. Decartes sagte: “Cogito, ergo sum”, aber alles, was ich da so “cogito”, ist krumm (“cogitare” hier im Sinne von: “erkennen”, um des Reimes willen). Kein rechter Winkel weit und breit, und der Anatom, der das “Os cuboideum” (das “Würfelbein”) so genannt hat, muss betrunken gewesen sein und alle rechten Winkel schief und alle schiefen Winkel recht gesehen haben. Das Ding (ein Fusswurzelknochen) ist kein Würfel, es ist noch nicht mal “würfelartig” (“cuboideus”). Es ist auch kein Polyeder, kein Vielflächner, denn es hat keine planen Flächen. Es besteht – wie so viele Knochen – aus lauter Vorsprüngen, Dellen, Knollen und Bollen. Eigentlich würde ich gerne den Terminus technicus “polyknollischer Knochen” dafür einführen, aber man wird mich nicht lassen.
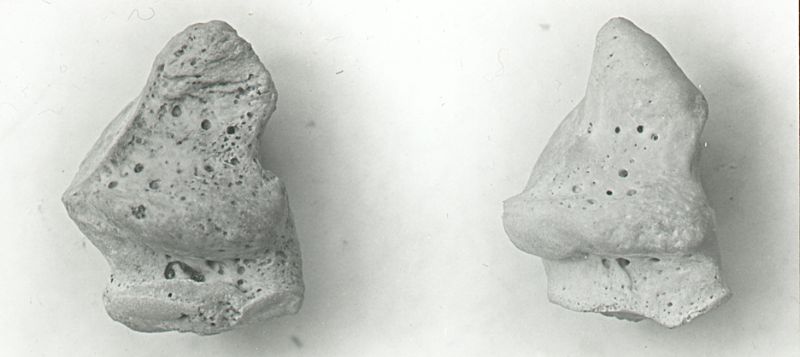
(Os cuboideum – von hier)
Im Nervensystem ist es nicht besser. Nicht auf den ersten Blick. Windungen des Grosshirnes – Bandnudelsalat. Innere Hohlräume des Hirns: bizzarste organische Architektur.
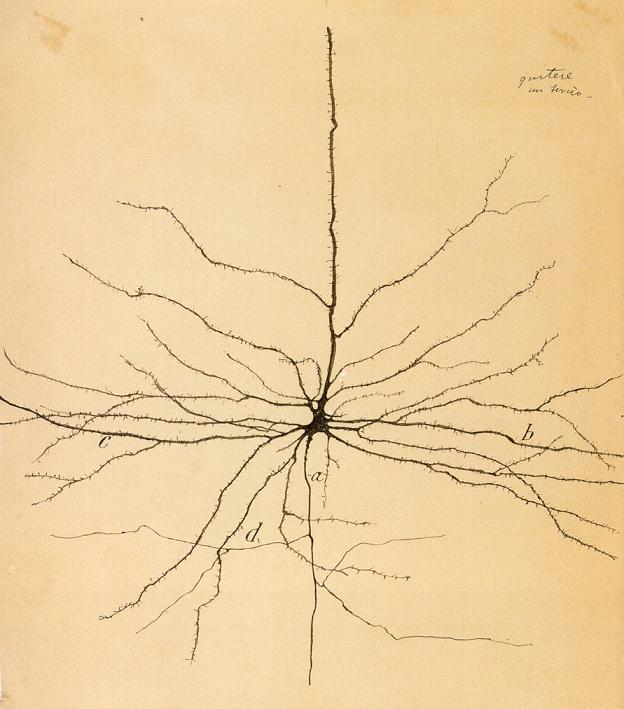
(von hier)
Auf den zweiten Blick wird es spannend. Das ist eine uralte Zeichung von Ramon y Cajal, um 1900. Sie zeigt eine Pyramidenzelle aus dem Cortex des Grosshirns. Der grosse Dendritenbaum (an seinen “moosigen” Spines erkenntlich) verzweigt sich organisch, wie die Äste eines Baumes eben. Das Axon (a) aber trägt einen Abzweiger (d), eine Kollaterale, die rechtwinklig abbiegt. Nun kann das natürlich alles auch ein Problem mit der Projektion sein. So ein Neuron ist ein dreidimensionales Gebilde, und wenn man seine Ausläufer auf 2D-Papier zeichnet, dann wird manch im Raume krummer Winkel gerade und manch gerader Winkel krumm. Allerdings ist auch schon seit Cajals Zeiten bekannt, dass auch anderswo im Nervensystem – im Cerebellum, bei den “Parallelfasern” und bei den Axonen der Hinterwurzelganglienzellen – rechtwinklige Aufzweigungen und Abbiegungen der Axone vorkommen.
Axone und ihre Kollateralen sind von Myelinscheiden umgeben. Das nennt man dann eine “Nervenfaser”. Nervenfasern legen sich zu Bündeln zusammen. Die Summe dieser Nervenfaserbündel nennt man die “weisse Substanz”.

Sie tut das, was dieser Herr da im Desy tut: die Rechner verkabeln. Selber rechnen tut sie meist nicht. Axo-axonale Interaktionen (Synapsen) sind selten. Der Herr verkabelt munter chaotisch. Kabelsalat. Das Hirn kabelt anders, und das kann man sich seit ein paar Jahren auch mit nicht-invasiven Methoden ansehen.
Diffusion magnetic resonance imaging. Ausnahmsweise guckt man dabei mal NICHT dem Gehirn beim Denken zu, misst also NICHT den lokalen Sauerstoffdurchsatz, sondern verfolgt die Diffusionsrichtungen von Wassermolekülen. Die können sich nämlich parallel zu den Faserbahnen des Gehirns (also “in Kabelrichtung”) rascher bewegen als quer dazu. Logisch: querbeet im Freien bin ich zu auch mühseliger unterwegs als entlang der Wege. Man kann, mit anderen Worten, Abbilder der Fasersysteme im Gehirn erzeugen, indem man die Pfade des Wassers verfolgt. Das Schicke daran: man kann nicht nur ein Faserbündel der weissen Substanz sichtbar machen, sondern alle. Zugleich – und sie dann, damit man nicht völlig die Übersicht verliert, wieder sortieren. Nach Richtungen zum Beispiel. Oder nach Kreuzungspunkten. Genau das haben die Autoren der hier verlinkten und unten(1) noch mal hochformal zitierten Arbeit getan. Sie haben irgendwelche Koordinaten, irgendein Volumen in der weissen Substanz ausgesucht, und sich dann alle Faserbündel zeigen lassen, die dies Volumen durchlaufen.
(aus der zitierten Publikation. Es kommt gar nicht auf die Details an, es geht um das Prinzip der rechtwinkligen Kreuzung der farbig dargestellten Faserbahnen)
Und die Ergebnisse können zu denken geben: lauter rechte Winkel. Wenn zwei Fasersysteme sich kreuzen oder durchdringen – dann tun sie das im rechten Winkel. Und wenn drei Bündel sich treffen, dann sieht es aus, wie am Ursprung des cartesischen Systems: orthogonal, rechte Winkel. Wenn Fasern von einem Bündel in das andere abzweigen – dann tun sie das im rechten Winkel.
(wie zuvor, grösserer Massstab, es sind ganze Grosshirnhemisphären zu sehen. Wiewohl die Faserbahnen geschwungen und gebogen verlaufen, kreuzen sie sich doch unter rechten Winkeln)
Es ist, als ob wir ein cartesisches Raumgitter im Kopfe hätten, wobei allerdings die “Gitterstäbe” krummen, gebogenen Linien folgen – ohne aber vom Prinzip der rechtwinkligen Kreuzung abzuweichen. Klar – die “Deformation” des Raumgitters ist dem differentiellen Wachstum in den verschiedenen Regionen, der Formbildung insgesamt geschuldet. An der prinzipiell cartesischen Natur der Sache ändert das nichts.
Ich bin mir jetzt nicht so ganz sicher, ob ich diese Einsicht trivial oder grossartig oder beides finden soll. Fast trivial ist sie natürlich insofern, als Lebewesen wie wir (“Bilateria”, d.i. so ziemlich alles was kreucht und fleucht und schwimmt und ein Vorder- und ein Hinterende hat) quasi natürlicherweise cartesisch verfasst sein müssen. Vorwärts, rückwärts, rauf, runter, rechts, links – die Anatomie muss dem Rechnung tragen. Die Beine gehören drunter. Der Schwanz dahinter. Sonst hat das keinen Sinn. Und wir wissen ja schon recht lange – allerspätestens seit der Entdeckung der Hox-Gene und des sonic-hedgehog-Systems – dass ein sich entwickelnder Embryo erst mal nichts Eiligeres zu tun hat, als ein orthogonales Koordinatensystem über sich zu werfen. Vermittels der Gradienten von Genprodukten, morphogenetischen Substanzen, die den Zellen feinsäuberlich signalisieren, ob sie jetzt Hirn oder Hintern machen sollen, Bauch oder Rücken, oder ob sie rechte oder linke Hand werden sollen (zwei linke Hände kommen nur im übertragenen Sinne und in der handwerklichen Praxis vor, meines Wissens gibt es das als Missbildung nicht).
Die Autoren der zitierten Studie führen natürlich genau dies Argument zur Erklärung ihrer Befunde an – ein in der Verkabelung des Hirns manifestes Überbleibsel des embryonalen Musterbildungssystems. Ausserdem – auch das ist ein eleganter Gedanke – dieses Gitter, einmal mit ein paar Nervenfasern früh angelegt, macht den später auswachsenden Axonen das Navigieren leichter. Es muss gar nicht dauernd nach dem rechten Weg zu Ziel gesucht werden – immer nur der Autobahn entlang, und nur an den Kreuzungen muss eine Entscheidung fallen. Und die geht auch nicht in alle möglichen Raumrichtungen, sondern nur in fünfe: geradeaus weiter, rechts, links, rauf, oder runter.
Einen dicken Nachteil hat die Sache freilich: die Strippen werden länger. Der Weg zum Ziel ist in diesem Raumgitter viel weiter, als er es auf den Pfaden eines Kugelkoordinatensystems wäre. Irgendwie kann man das mit Hilfe des Herrn Pythagoras wohl auch ausrechnen, ich weiss aber nicht wie.
Und endlich stellt sich natürlich die Frage, was die “Knotenpunkte” des Fasergitters zusammenhält, zumal unter den gewaltigen Deformationen, die dieses Gitter in der Entwicklung erleidet. Man bedenke: das Nervensystem beginnt als eine simple Platte von recht geringer Dicke. In der legen die Gradienten von Morphogenen fest, was vorn und hinten, oben und unten und die Flanken werden sollen. Die Platte formt sich zum (Neural-)Rohr um, und die ersten Fasern, die darin von den Nervenzellen auswachsen, bilden ein orthogonales 3D-Gitter. Das weiss man schon lange. Aber dann geht’s rund. Das Rohr wird deformiert, einige Regionen werden gewaltig aufgeblasen (Grosshirn), noch dazu verbogen, es wird ein- und ausgestülpt: Es ist ein wenig so, als ob man einen von diesen Luftballons aufbliese, die erst ganz harmlos als Gummiwürste anfangen, und die dann, genügend Druck und Knotungskunst vorausgesetzt, zu komplizierten Figuren werden.

(von hier)
Wieso übersteht das Nervenfasergitter diese Deformation? Wieso spannen sich die Nervenfasern nicht wie Gummibänder, um die kürzeren Wege zu finden? Die simpelste Erklärung ist wahrscheinlich, dass sie verwoben sind, wie Schuss- und Kettfasern eines Textils, allerdings in drei Dimensionen. Und ausserdem können sie an den Knotenpunkten ja auch noch die Richtung wechseln, so das sie sich umeinanderschlingen, so ähnlich, wie man einen Teppich knüpft. Und wenn ich dann an einem Knotenpunkt “ziehe” – dann muss alles mit, was da verknotet ist.
Erstaunlich und deshalb irgendwie grossartig erscheint mir dennoch, dass unter dieser Deformation vom Prinzip der Rechtwinkligkeit am Knotenpunkt nicht abgewichen wird. Wieso wird nicht – wie man das aus mechanischen Gründen erwarten würde – unter der Deformation mancher Winkel stumpf und manch anderer spitz, so wie es in einem elastischen Textil der Fall wäre, bei dem man an einem Knotenpunkt zieht? Woher dieses sture Festhalten an der cartesischen, orthogonalen Kreuzung?
Ich habe keine Ahnung. Vielleicht hat das Hirn Hilbert gelesen und findet den rechten Winkel einfach elegant. Ich werd’ mich mal auf die Suche machen, ob ich in der Anatomie irgendwo den goldenen Schnitt finde. Der ist auch schön.
—
(1) The Geometric Structure of the Brain Fiber Pathways.
J. van Wedeen, Douglas L. Rosene, Ruopeng Wang, Guangping Dai, Farzad Mortazavi,
Patric Hagmann, Jon H. Kaas, Wen-Yih I. Tseng
Science 335, 1628 (2012)
PS.: Dass dieser Artikel, in dem es um rechtwinklige Kreuz(ig)ungen geht, heute, an einem Karfreitag, in’s Netz gelangt, ist ein Zufall, der mir eben erst zu Bewusstsein kommt. No puns intended.
PPS.: “Joker” (siehe Kommentare) hat mich auf dieses Link
(http://www.youtube.com/watch?v=_oTEhFAAARE)
hingewiesen (Danke!). “There you have it from the horse’s mouth”, Herr van Wedeen persönlich. In den Animationen kommt die Rechtwinkligkeit noch besser zu Geltung.
Ich möcht’ aber noch zweierlei anmerken: die bunten “Strippen”, die man in den Bildern sieht, sind bei Gott keine einzelnen Nervenfasern. Es sind die graphischen Repräsentationen von tausenden, die allerdings die gleiche Richtung haben. Die Auflösung der diffusion-tensor-Methode in dieser Studie lag bei etwa 300x300x300 µm pro Voxel, eine einzelne Nervenfaser ist aber nur ein bis ein paar wenige µm dick. Mit anderen Worten: wenn man mit der Methode eine Kreuzung sieht, weiss man nicht, ob einige (oder alle?) Nervenfasern in der Kreuzung “abbiegen”, oder ob keine abbiegt. Auch über Kollateralen (s.o.) erfährt man nichts. Man muss also diese Faserarchitekturen aus dem Computer mit solchen, die man sich ganz klassich (invasiv) in “tracing-Studien” erarbeitet hat (die Einzelbündel und -fasern darstellen können) abgleichen. Das haben die Autoren auch getan – zumindest für die grösseren Bündel, die in der Tat so verlaufen, wie sie es darstellen.
Nachdem ich mir das Video und die Statements von Prof. van Wedeen angesehen habe, aber noch ein “Caveat”: Die “Simplizität” des Kabelapparates, die er immer wieder erwähnt, hat nichts (soweit ich jedenfalls sagen kann) mit irgendwelchen “geometrisierten Rechenoperationen” zu tun. Das ist kein “Rechengitter”, elektrisch tut sich an den Kreuzungspunkten nichts. “Gerechnet” (mit Synapsen) wird anderswo im Gehirn, im sog. “Neuropil” (den “Filz” aus Dendriten und axonalen Terminalien). Und dies Neuropil ist zwar nicht ungeordnet (mancherorts, im Cerebellum, gibt es sogar Dendriten und Axone, die stur rechtwinklig zueinander stehen), aber bei weitem nicht so “raumgitterartig” wie der Faserapparat der weissen Substanz. Eher ein Dickicht…


@Helmut Wicht
“Es ist, als ob wir ein cartesisches Raumgitter im Kopfe hätten.” Ja, dann könnte genau dies notwendig zur Idee der cartesischen Koordinaten (zurück-) geführt haben. Das Gehirn, wenn es nicht ein “Eigenleben” führt, ist konforme Abbildung seiner physkalischen Umwelt. Gibt es dort rechte Winkel (insb. das Vektorprodukt mit dem Sinus des Winkels), so wird es sie auch im Gehirn geben. Auf das Prinzip Rechtwinkligkeit kann die Natur nicht (irgendwo) verzichten, glaube ich, sie ist darauf aufgebaut, Lokalität als Relation abbilden zu können. Wenn ich an einer Kreuzung einen der möglichen Wegen gehe, so sorgt erst die Rechtwinkligkeit der Entscheidung dafür, daß auch wirklich nur dieser eine Weg “gemeint” ist. Natürlich sorgen schon die Myelinscheiden für eine Trennung der einzelnen Nervenfasern, aber erst (annähernd) rechte Winkel bei Verzweigungen gewährleisten eine Maximierung der räumlichen Trennung der Zielgebiete und der zu erwartenden funktionalen Antwort.
“… an den Kreuzungen muss eine Entscheidung fallen. Und die geht auch nicht in alle möglichen Raumrichtungen, sondern nur in fünfe: geradeaus weiter, rechts, links, rauf, oder runter.” Oder, als sechste mögliche Richtung: zurück – wenn wir uns verfahren haben? (Gibt es so etwas in nervösen Prozessen – eine Umkehr des Signals?)
@ schütze
“Oder, als sechste mögliche Richtung: zurück – wenn wir uns verfahren haben? (Gibt es so etwas in nervösen Prozessen – eine Umkehr des Signals?)”
Man kann – experimentell – Axone tatsächlich “antidrom”, also “falschrum”, zum Nervenzellkörper hin, stimulieren – das Aktionspotential läuft dann au den Zellkörper zu, nicht von ihm weg. Die (seltenen) axo-axonalen Synapsen könnten sowas auch in vivo bewirken, oder ein Aktionspotential “löschen” – aber das ist, soweit ich weiss, nicht erforscht.
Dass ein Axon irgendwo einfach “kehrt macht”, also einen 180 Grad-U-Turn veranstaltet – das kommt vor. Aber nicht schon während des Auswachsens selbst, sondern erst später – wenn sich das Axon (oder ein ganzer Nerv) um etwas herumgeschlungen hat, das dann sekundär verlagert und verschoben wird.
Der Nervus laryngeus recurrens (googeln) ist sicher das berühmteste Beispiel, im Hirn selbst wäre das innere Fazialisknie anzuführen.
Form und Funktion
“… erst später – wenn sich das Axon (oder ein ganzer Nerv) um etwas herumgeschlungen hat, das dann sekundär verlagert und verschoben wird.”
Das ist sehr faszinierend. Der Verlauf des Nervens erscheint passiv gebildet, aber in einer stets gleichen Richtung/Art/Verlauf als Folge des Deszensus’. Als sei dies verblüffend weitschauendes System, wäre ich geneigt zu sagen, wenn dies auch physiologische Konsequenzen hat, die ansonsten nicht zu erwarten wären.
Die kleinste Fläche
Die Axone haben alle eine bestimmte Dicke.
Wenn ein flaches Band aus vielen Axonen von 1 cm Breite ein zweites und gleichartiges im rechten Winkel kreuzt, dann benötigt das eine Fläche von 1 cm^2.
Bei allen anderen Winkeln wird eine grössere Fläche benötigt.
—
Technische Systeme, drei Bilder:
Die Lernmatrix von Karl Steinbuch:
http://ars.sciencedirect.com/content/image/1-s2.0-S0925231207003037-gr5.jpg
Kreuzschienenverteiler oder Koppelfeld:
http://de.wikipedia.org/w/index.php?title=Datei:Kreuzschienenverteilung002.png
Diodenmatrix:
http://www.internetarchaeology.org/www.geocities.com/Templarser/digital/CLK12.gif
—
Eine offene Frage gibt es noch:
Wenn es sich um eine Lernmatrix handelt, und wenn daher an den Kreuzungspunkten Synapsen wären, dann müsste ein Bündel aus Axonen ein Bündel aus Dendriten kreuzen.
—
Um 3 Ecken:
s = x + y + z
Raumdiagonale:
s = QWurzel( x^2 + y^2 + z^2 )
@ Bednarik
Es handelt sich sicher NICHT um eine “Lernmatrix”, denn die Kreuzungspunkte sind, nach allen was wir wissen, elektrisch untereinander so inert, wie es zwei isolierte, sich kreuzende Stromkabel sind.
Geokognition
Ein sehr schoener Artikel, der zu neuen Ideen inspiriert. Danke!
Space for growing 😉
Verschlungenes, um ein Wachstumsschub oder eine mechanische Einwirkung von außen flexibel bfangen zu können – kürzeste Verbindungen wären dabei “selbstmörderisch”?
Und eckig ist nicht kuschelig!
Eiereien heute passend…..
@Jörg Schütze: Konforme Abbildung
Können Sie genau benennen, was auf was abgebildet wird?
@ Ano Nym
“Können Sie genau benennen, was auf was abgebildet wird?”
Selbstverständlich nicht. Und mit diesem Eingeständnis löst sich meine Anmerkung “Das Gehirn […] ist konforme Abbildung seiner physkalischen Umwelt.” in Wärme auf, wenn Sie so argumentieren wollten.
Was hier allerdings fehlt, ist der […]-Zusatz: “wenn es nicht ein “Eigenleben” führt”. Was ich damit sagen will, sollte klar sein: Das Gehirn stellt keine grundsätzliche Ausnahme, kein Wunder dar, sondern eine zu erwartende Seltenheit, die gleichwohl nicht in Widerspruch zu den Regeln steht, nach denen es seine Umwelt erfährt; in diesem Sinne sei es konform.
@ Dramiga
Hast Du eine Idee, warum die RECHTwinkligkeit erhalten bleibt?
Danke.
@Jörg Schütze: Häuten des Kommentars
Schön, dass Sie einsichtig sind.
Ich bin zunächst davon ausgegangen, dass diese Bedingung nicht erfüllt ist. In diesem Falle wollen Sie nur warme Luft ausgestoßen haben. Dagegen habe ich nichts einzuwenden. Ihre Erläuterung
schafft allerdings mehr Unklarheit über das, was Sie sagen wollen. Ich weiß nicht, welches die von Ihnen betrachteten Grundgesamtheiten sind, in denen das Gehirn einerseits keine Ausnahme aber andererseits eine sogar (womöglich “vom Gehirn” selbst?) erwartbare Seltenheit sei. Welche “Regeln” Sie meinen ist mir nicht klar. Und den Sprachgebrauch, nachdem das Gehirn seine Umwelt “erfährt”, würde ich ablehnen.
Ach so: Konformität ist wohl ein mathematischer Fachbegriff:
http://en.wikipedia.org/wiki/Conformal_map
Baumstruktur
Hallo Helmut,
erinnern Sie sich noch an meinen Gedankengang, den ich einst in Ihrer Garage äußerte ?!
“Für mich sind die Verzweigungen des Blut- bzw. Nervensystems dem eines Baumes ähnlich.”
Damals haben Sie mich skeptisch beäugt und konnten meiner Theorie nicht viel abgewinnen. Schließlich haben die Äste des Baumes ein Ende, während das Gefäß- und Nervensystem anastomosieren würde.
Nun. Ich war freudig überrascht den Kommentar zu Ihrem dritten Bild lesen zu dürfen. Freilich weiß ich mittlerweile einen einzigen Dendritenbaum von einem Nervenplexus zu unterscheiden. Dennoch kam mir diese Darstellung in Hinblick auf mein eigenes Bild im Kopf sehr vertraut vor.
Und zum Thema “Kabelsalat”:
Der Herr auf dem vierten Bild verknüpft die Kontroller-Kabel zweckmäßig, so dass für den Laien hier ein *WirrWarr* vorherrschen mag, jedoch dem PC-Inneren diese Anordnung dienlich erscheint. Beachten Sie hierzu bitte die linke obere Ecke. Hier befindet sich ein Lüfter. Es wäre unpraktisch der Ordnung halber diesen zu verdecken. Ebenso musste der Zugang zum Inneren frei bleiben, wodurch augenscheinlich die Ordnung der Kabel verloren geht. Tut sie aber nicht. Der menschliche Organismus hatte es zumeist nicht nötig *Öffnungen* zu lassen, auf Kosten der geometrischen Anordnung. Ok ok. Sie werden mich nun eines besseren belehren und mir die segmentale Anordnung der Rückenmarksnerven, sowie gewisse Durchtrittstellen aufzählen. Zu recht. Aber ebenso bezweifle ich, dass unser Gehirn in sich *anders* verkabelt ist als dieser Rechner.
Würde man diesen Rechner *geometrisch korrekt* verkabeln wollen, so müsste man viele Zwischenstationen einbauen, so dass die Kabel von Punkt zu Punkt sauber gesetzt werden können. Da aber das PC-Innere nicht mit der Komplexität eines Gehirns zu vergleichen ist, erübrigt sich hier der weitere Gedankengang. Man bräuchte dann metergroße Mainboard´s, aber diese wäre dann dem PC entsprechend weniger dienlich.
Natürlich habe ich in meinem System eine höhere Ordnung. Alleine deshalb schon, damit ich eine ordentliche Kühlung meiner Komponenten gewährleisten kann. Aber an einigen Punkten wird sich immer ein Kabel(baum) querstellen ;).
Gleiches tut sich in meinem Gehirn. Manchmal ist da etwas falsch *verkabelt*.
Mit besten Grüßen
Florian Abram
_oTEhFAAARE
Es gibt auch ein entsprechendes Video von Van Wedeen auf youtube zu sehen, mit weiteren bunten Bildern, Animationen und natürlich Erläuterungen (ca. 3 min).
http://www.youtube.com/watch?v=_oTEhFAAARE
@ Joker
Danke für das Link!
Ich habe es angeschaut und oben eingebaut.
Weil mir, als ich Prof. van Weeden zuhörte, noch zwei Dinge auf- bzw. einfielen, die vielleicht von allgemeinerem Interesse sind, hab’ ich oben noch ein PPS an den Originalbeitrag angepappt.
Aber sind das wirklich “perfekte” rechte Winkel? Die Hypothenuse gegenüber eines rechten Winkels im Einheitsdreieck hat die länge Wurzel 2. Diese Seite hätte also soweit ich weiss unendlich viele Kommastellen. Allem Anschein nach sind aber Nervenfasern weder unendlich klein noch gross. Sicher handelt es sich hier nicht um Einheitsdreiecke. Aber auch in anderen rechtwinkligen Dreiecken kommen ja doch immer irgendwo irrationale Zahlen raus, die der Empirie zuwiderlaufen, sei es bei den Katheten oder den Winkeln, oder nicht?
@Ano Nym
“Ich weiß nicht, welches die von Ihnen betrachteten Grundgesamtheiten sind, in denen das Gehirn einerseits keine Ausnahme aber andererseits eine sogar (womöglich “vom Gehirn” selbst?) erwartbare Seltenheit sei.”
Nicht “aber” andererseits: “sondern” andererseits. Eine Seltenheit ist keine Ausnahme.
Wenn Sie auf etwas hinauswollen, schreiben Sie’s ruhig hin – wer weiß, vielleicht werde ich mich wundern, während Sie staunen.
@Jörg Schütze: Sprache
Nach meinem Dafürhalten sind Ausnahmen selten und Seltenheiten die Ausnahme. Sie schrieben:
Jedenfalls konnte ich Ihrer Ausführung nicht mehr entnehmen, als dass es Gehirne gibt.
konforme == winkeltreu
Ich lese hier nur oberflächlich mit und werfe in der Regel dann nichts ein, mache aber eine seltene Ausnahme:
Konforme Abbildungen sind winkeltreu.
Ich bin nicht sicher ob dies von irgendeinem Teilnehmer gemeint war.
rechte Winkel
Vorab hierzu:
Rechte Winkel sind Begriffe aus der Mathematik, die Mathematik ist anthropogen, nichts was vom Erkenntnissubjekt mathematisiert worden ist, existiert (nachgewiesenermaßen) in der Natur wie mathematisiert.
Die Regelmengen, denen die Welt (“Zustandsmengen”) unterworfen ist, sind vom Erkenntnissubjekt nicht mit letzter Sicherheit erfassbar. Insofern entzieht sich die Frage nach der Existenz rechter Winkel in der Natur oder Welt dem Beobachter.
Dasselbe gilt denn auch für Zahlen und was es da noch so gibt…
MFG
Dr. Webbaer (der hofft hier richtig verstanden zu werden, diese Nachricht war nicht wissenschaftskritisch, sondern das Gegenteil davon)
@Markus Dahlem
“… und werfe in der Regel dann nichts ein …”
Rightly so, in Anlehung eine Sprichworts: don’t take pills and derive.
“Konforme Abbildungen sind winkeltreu.” Und da hast Du natürlich recht. Ich hätte regelkonform schreiben sollen – im Sinne u.a. der globalen Implikation des angesprochenen Vektorpodukts.
Ich wollte …
… diesbezüglich auf potentielle Missverständnisse hinweisen.
Ich habe es aber auch als (regel)konform gelesen.
Gravitation und Erdoberfläche
Guten Tag,
der Artikel ist zwar nicht mehr ganz frisch, in Google trotzdem noch immer ganz oben gereiht und jedenfalls für mich sehr interessant – vielen Dank. Die Frage ist, ob ein Kommentar zum gegebenen Zeitpunkt noch viel Sinn macht. Mal sehen.
Jedenfalls: zum Verhältnis Mensch und rechter Winkel, sagen wir es einmal so: außerhalb des Körpers, gäbe es wohl noch einiges Mehr zu sagen. Was mir so auf anhieb einfällt und zum Thema vielleicht etwas beitragen kann, ist ein ganz elementares Vorkommen des rechten Winkels in der Natur. Eben das von Gravitation und Erdoberfläche. Ganz elementar und im menschlichen Schaffen bald umgesetzt: unsere Mauern stehen parallel zur Gravitation ganz gut da und ergeben mit dem Fussboden somit einen rechten Winkel. Und vieles andere in den von uns geschaffenen Räumen passt sich umso leichter an ihn an, wenn es ihn enthält.
Könnte man noch viel dazu denken und schreiben…
Mal wieder zurück zur Arbeit.
ArcSin[ 1/2 Sqrt[ 2 (AC/AB)^2 + 2 (AC/BC
Helmut Wicht schrieb (06. April 2012, 14:06):
> Was ist das eigentlich – ein rechter Winkel? […]
> Von dem Mathematiker Hilbert stammt die schöne Definition, dass der rechte Winkel im Geradenschnitt der einzige unter den unendlich vielen möglichen Winkeln ist, der genauso gross ist wie sein Nebenwinkel.
Und was ist das nun: eines Winkels “Größe“?
Nach welchem Urteil wär denn dies ( ABC) und jenes ( ABZ) gleich?
Ein Physiker gibt sich da keine Blöße —
nur Rechenknechte machen’s sich gern leicht.
)^2 + 2 – (AB/BC)^2 – (BC/AB)^2 – (AC/AB
Helmut Wicht schrieb (06. April 2012, 14:06):
> Was ist das eigentlich – ein rechter Winkel? […]
> Von dem Mathematiker Hilbert stammt die schöne Definition, dass der rechte Winkel im Geradenschnitt der einzige unter den unendlich vielen möglichen Winkeln ist, der genauso gross ist wie sein Nebenwinkel.
Und was ist das nun: eines Winkels “Größe“?
Wie urteilt man, ob dieses ( ABC) jenem ( ABZ) gleicht?
Ein Physiker gibt sich da keine Blöße —
vielleicht.
^2 (AC/BC)^2 ] ], juchhe!
… das misst den ABC.
Danke für diesen bemerkenswerten Artikel,
für mich als Bootsbauer ohne tiefere Kenntnisse der Neurologie war dieser Text nicht nur verständlich, informativ und erstaunlich sondern auch sehr unterhaltsam. Auch deshalb, da ich mich in sphärischen Strukturen häufig mit anderen als rechten Winkeln beschäftige.
Sollten Sie Ihre Vorlesungen ähnlich gestalten gehe ich davon aus das ein bemerkenswerter Teil Ihres Auditoriums mehr als gelegentlich von Ihrem smarten Kommunikationsbarrieren aufblickt und Ihren Ausführungen lauscht.
Ich wünsche Ihnen (vorwiegend aus Eigennutz) weiterhin Freude beim Schreiben!