Da fing die Erde sich noch einen Mond ….

Das Problem des gravitativen Einfangs am Beispiel des Kometen Shoemaker Levy 9 am Jupiter wurde kürzlich in den Kosmologs von Carolin Liefke erwähnt. Viele wissen vielleicht gar nicht, dass man gar nicht so weit hinausgehen muss, um ein Beispiel für einen gravitativen Einfang zu finden. Auch unsere Erde hat sich so etwas geleistet, und zwar vor gar nicht langer Zeit, und unter tatkräftiger Mithilfe der Sonne und des Monds Nr. 1, der wohl Gesellschaft brauchte.
 Dies liefert den Stoff für eine hübsche Geschichte, die auch noch den Vorteil hat, wahr zu sein und diverse interessante bahnmechanische Phänomene zu illustrieren. Man könnte direkt einen Film darüber drehen, zumindest eine Doku-Soap.
Dies liefert den Stoff für eine hübsche Geschichte, die auch noch den Vorteil hat, wahr zu sein und diverse interessante bahnmechanische Phänomene zu illustrieren. Man könnte direkt einen Film darüber drehen, zumindest eine Doku-Soap.
Im September 2002 entdeckte der Astronom Bill Yeung einen Asteroiden. Bei Vermessung der Bahn ergab sich, dass hier nicht, wie erwartet, ein Erdbahnkreuzer auf einer Bahn um die Sonne vorlag. Nein, das betreffende Objekt, man taufte es J002E3, war auf einer stark elliptischen Bahn um die Erde.
Damit hatte man allerdings ein Problem, denn solche hochexzentrischen Bahnen können nicht stabil sein. Ihr Apogäum ist so hoch, dass es in die Grenzregion schwacher Stabilität hineinragt, jenes gravitative Niemandsland, in dem sich ein Objekt nicht entscheiden kann, ob es nun die Erde oder doch lieber die Sonne umkreisen will.
Ferner kreuzt eine solche Bahn die Mondbahn und ist über kurz oder lang erheblichen gravitativen Störungen ausgesetzt, die entweder das Perigäum soweit absenken, dass das Objekt die Erde trifft oder es aber aus der Erdbahn herauskicken.
Woher auch immer J002E3 kam, lange konnte es nicht in dieser Bahn gewesen sein. Spektroskopische Untersuchungen lieferten weitere wichtige Hinweise. Die Oberfläche des Objekts musste weitgehend strahlend weiß und dazu aus Titandioxid sein. Dies ist ein bei natürlichen Objekten eher selten anzutreffender Zustand, aber typisch für die weiße Farbe, mit der Raketenstufen bemalt sind.
Es hatte aber niemand in oder kurz vor 2002 eine große Rakete in eine hochexzentrische Bahn gestartet, bei der der Verbleib der Oberstufe ungeklärt war. Die letzten solchen Missionen waren die des Apollo-Programms, und die lagen lange zurück.
 Die Oberstufe der Saturn-V-Rakete hieß S-IVB. Deren Größe und Farbe passte recht gut zu den Beobachtungen. Allerdings hatte man doch alle Saturn-V-Oberstufen ab Apollo 13 auf dem Mond einschlagen lassen und diese Einschläge auch mit den bei den vorangegangenen Missionen zurückgelassenen seismischen Messgeräten registriert.
Die Oberstufe der Saturn-V-Rakete hieß S-IVB. Deren Größe und Farbe passte recht gut zu den Beobachtungen. Allerdings hatte man doch alle Saturn-V-Oberstufen ab Apollo 13 auf dem Mond einschlagen lassen und diese Einschläge auch mit den bei den vorangegangenen Missionen zurückgelassenen seismischen Messgeräten registriert.
Also musste die Stufe von einer der vorangegangenen Missionen stammen. Die S-IVB-Stufen der Missionen Apollo 8, 10 und 11 waren in heliozentrische Bahnen eingeschossen worden. Dieses Manöver hatte sich bei der Mission Apollo 12 allerdings so verzögert, dass es nicht mehr zur Erdflucht ausreichte. Die S-IVB-Stufe der Mission Apollo 12 war am 14. November 1969 in einer hochexzentrischen Bahn um die Erde gestrandet.
Aber war es denkbar, dass die Stufe so lange in dieser instabilen Bahn durchgehalten hatte? Wohl kaum … man hatte sie zwar nach ihre Mondvorbeiflug am 18. November 1969 “verloren” (selbst das erdnahe Weltall ist immer noch sehr groß), aber numerische Nachrechnung ergab, dass die Stufe in der Folge der Erde entfleucht sein musste.
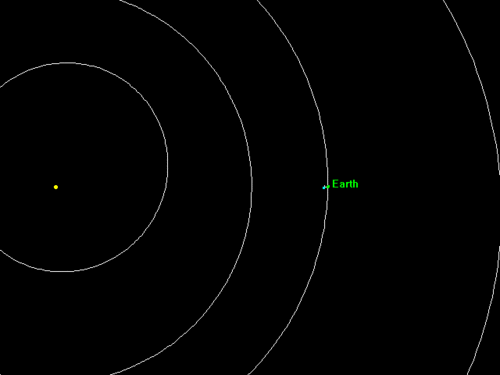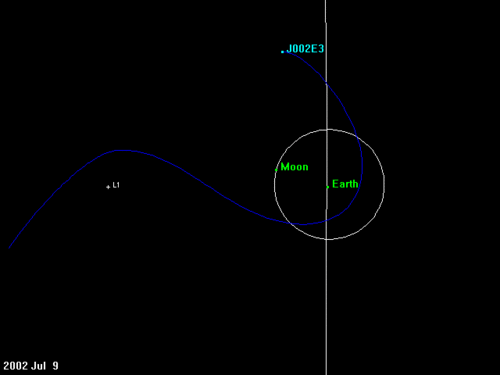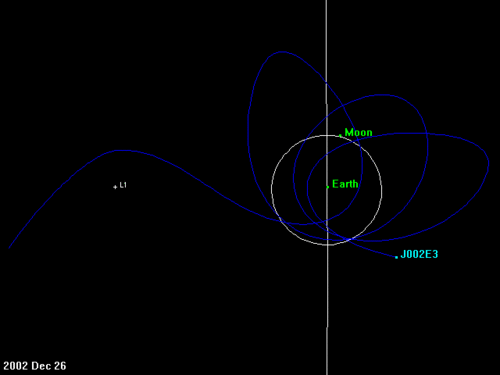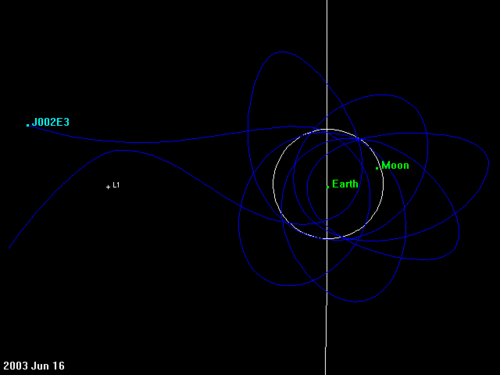
Weitere Rückwärtsrechnung der Bahn des 2002 beobachteten Objekts zeigte, dass J002E3 selbst erst im Mai des Jahres 2002, aus der Gegend des L1-Punkts, also von der Sonne her kommend, in eine weite Bahn um die Erde gefangen wurde. Die Animation stellt das Ergebnis der numerischen Simulation dar. Demnach war der Mond an diesem Einfang beteiligt (ca. 20. Juni 2002). Der zentrale Punkt bei der Betrachtung ist, dass die Erdflucht und auch der Wiedereinfang mit geringer Relativgeschwindigkeit erfolgten.
In der Folge vollführte J002E3 eine Reihe von Umläufen. Dass dabei scheinbar eine Blüte an den Himmel gezeichnet wurde, ist eine Folge des gewählten Koordinatensystems, in diesem Fall eins, das mit der Erde auf ihrer Bahn um die Sonne rotiert. In einem inertialen (nicht-rotierenden) System wäre die Ellipse mehr oder weniger raumfest. Allerdings wäre es da schwierig, den L1-Punkt und die Sonnenrichtung darzustellen.
Etwa ein Jahr nach dem Einfang verließ J002E3 wieder die Bahn um die Erde, auch diesmal wieder unter tatkräftiger Mitwirkung des Monds (ca. 1 Juni 2003), und wieder in Richtung von L1. Daraus ist zu schließen, dass die heliozentrische Bahn des Objekts eine der Erde vorauseilende Bahn sein muss. Das Objekt wird von der Erde angezogen. Dadurch wird seiner Bahn um die Sonne Energie entzogen, die Anziehungskraft der Erde ist wie eine dauernd wirkende Bremse.
Eine Bahn geringerer Energie ist aber niedriger, und das heißt schneller – das Objekt eilt somit mehr und mehr der Erde voraus und entzieht sich dadurch ihres Störeinflusses. Die Bahn ist immer noch der Erdbahn ähnlich, die Umlaufperiode ist allerdings geringer als ein Jahr … dies hat zur Folge, dass der Abstand sich zunächst weiter vergrößert, bis das Objekt den erdfernsten Punkt auf der gegenüberliegenden Seite der Sonne durchläuft und dann die Erde wieder von hinten einholt. (Eine solche vorauseilende Bahn wurde auch für eine der Sonden der NASA-Mission “STEREO” gewählt. Die andere “STEREO”-Sonde ist dagegen in einer nachzügelnden heliozentrischen Bahn, wie auch das IR-Teleskop “Spitzer”).
Dieser Prozess dauert rund dreißig Jahre. Es ist gut möglich, dass J002E3, wenn es sich um die S-IVB von Apollo 12 handelt, Anfang der 70er Jahre in eine solche vorauseilende heliozentrische Bahn geworfen wurde. 2002 wurde die Erde eingeholt, das Objekt eingefangen, und 2003 ging das Spiel von vorne los. Demnach wäre in den 2030er oder 2040er Jahren eine erneute Rückkehr möglich.
Ist doch nett, oder? Da demonstriert eine ausgebrannte Oberstufe alle komplizierten Sonderfälle der Vielkörperhimmelsmechanik und wird kurzfristig von Manchen sogar vorschnell für ein Alien-Raumschiff gehalten.
Weitere Information
Sammlung von Animationen der Bahnsimulation von J002E3 im NASA-NEO-Webauftritt


Und es geht doch mit dem Einfangen 🙂
Schöne Demonstration im Hinblick auf Karl Bednariks ursprünglichen Kommentar
Caro
Man koennte sogar sagen:
“Und sie fing ihn doch!”.
Ganz wesentlich ist in diesem Zusammenhang, ebenso wie bei SL-9, dass die hyperbolische Annaeherungsgeschwindigkeit niedrig war. Sonst funktioniert das naemlich nicht, weil es nicht moeglich ist, die Bahnenergie ausreichend zu veraendern, auch nicht mit einem relativ nahen Mondvorbeiflug.
Eine schwach hyperbolische und eine stark elliptische Bahn sind einander dagegen energetisch sehr aehnlich.
Ich habe hier das Beispiel J002E3 gebracht, weil es “close to home” ist. Gravitativer Einfang ist bei den Riesenplaneten aber, wie ich in der Diskussion zu Carolins Beitrag ausfuehrte, gar nichts seltenes.
Bahnänderungen
Bei den nicht eingefangenen erdnahen Asteroiden bereiten mir vor allem die ständigen Bahnänderungen Sorge.
Asteroid 2004 FH änderte zum Beispiel bei seinem nahen Vorbeiflug an der Erde seine Flugbahn um volle 15 Grad.
Seine Umlaufbahn um die Sonne muss doch jetzt völlig anders aussehen als vor dem Vorbeiflug.
Text und Bild dazu:
http://neo.jpl.nasa.gov/news/news142.html
Und ob!Es fliegen dauernd Asteroiden dicht an der Erde vorbei, manche sehr dicht, wie 99942/Apophis am 13. April 2029 im Abstand von unter 30,000 km.
Dabei wird die Asteroidenbahn natürlich und unvermeidlich gestoert, sogar in ganz erheblichem Umfang.
Die Kerle, die dieses auf der IAC 2007 vorgestellte Paper geschrieben haben, haben mal berechnet, wie sich die Bahn von 99942/Apophis durch den Vorbeiflug verändert (siehe Abb. 1 auf Seite 2). Die jetzige Bahn ist rot eingezeichnet, die neue hellblau. Das sagt schon alles, oder? Eine offensichtlich ganz andere Bahn mit ganz anderer Umlaufperiode und anderer Bahnebene.
Die Vorausberechnung von Asteroidenbahnen ist fundamental ein singuläres Problem. Liegen mehrere Vorbeiflüge im betrachteten Zeitraum, dann ist eine genaue Vorausberechnung nicht mehr moeglich.
Dies bedeutet, man muss die Asteroidenpopulation kontinuierlich beobachten und nachvermessen. Es ist keine besonders umfangreiche oder kostspielige Aufgabe, aber eine unerlässliche.