Tetraeder-Tetris: Noch ein Rekord, der im Sylvester-Knallen unterging
BLOG: MATHEMATIK IM ALLTAG

Wie dicht kann man gleich-große reguläre Tetraeder im Raum packen? Aristoteles soll behauptet haben, dass es eine perfekte Packung gibt, in der sie den Raum zu 100% ausfüllen. Der Irrtum hielt sich immerhin fast 1800 Jahre, bis Johannes Müller, genannt Regiomontanus (1436-1476), den Irrtum aufdeckte. Also sind 100% nicht zu erreichen, aber wie dicht kann man Tetraeder packen? Würfel lassen eine perfekte Packung zu (die man in Würfelzucker-Packungen bestaunen kann). Mit gleichgroßen Kugeln kann man den Raum nur zu 74,05% ausfüllen: die optimale Packung ist leicht zu konstruieren (Obsthändler verwenden sie auf dem Markt, um Orangen zu stapeln), aber der Beweis, dass die “offensichtliche” Packung optimal ist, war schwierig – das war die “Kepler-Vermutung”, von Johannes Kepler 1611 aufgestellt, und erst 1998 von Thomas Hales mit massiver Computerhilfe bewiesen. (Eine umkämpfte und umstrittene Lösung ….)
Aber reguläre Tetraeder? Wie dicht kann ein “Sand” sein, dessen Körnchen lauter gleich-große, regelmäßige Tetraeder sind?
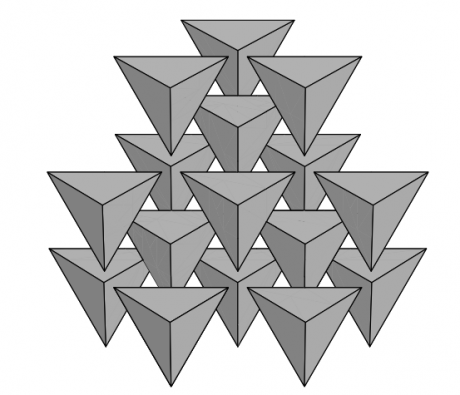
Das Problem ist noch recht einfach, wenn man annimmt, dass alle Tetraeder die gleiche Ausrichtung im Raum haben, und zudem gitterförmig angeordnet sind. Dann füllt die dichteste mögliche Packung lediglich 36,73% des Raums aus:
(Die dichteste Tetraeder-Gitterpackung: Abbildung aus Conway & Torquato, PNAS 2006.)
Wenn man auf die "Gitterstruktur" verzichtet, dann wird die Packung dichter, und komplizierter. Und wenn man auch noch erlaubt, die Tetraeder zu drehen, dann wird’s richtig kompliziert. Tetraeder-Tetris: man kann versuchen, geschickt zu drehen, um Lücken zu füllen. Aber wie dicht kann man den Raum dann ausfüllen?
Das Problem geriet erst vor kurzem ins Zentrum der Forschung – und wurde Gegenstand eines Wettrennens, an dem sich Wissenschaftler (und Wissenschaftlerinnen!) aus ganz unterschiedlichen Disziplinen beteiligt haben, und über das die New York Times kürzlich berichtet hat. (Dieser Bericht war auch der Ausgangspunkt für diesen Blog…) Startschuss: 2006 haben John H. Conway, ein legendärer Mathematiker aus Princeton, und Salvatore Torquato, ein Chemiker an derselben amerikanischen Eliteuniversität, des Problems angenommen, und ein bemerkenswert schlechtes Ergebnis erzielt und in den Proceedings of the National Academy of Sciences publiziert: Sie kamen über 72% des Raums nicht hinaus – schlechter als die optimale Kugelpackung.
Dies konnte Paul M. Chaikin nicht glauben, ein Physiker von der New York University: Er kaufte eine große Mengen von tetraederförmigen “Würfeln” (wie sie für das Brettspiel “Dungeons & Dragons” verwendet werden), und ließ Schüler damit experimentieren. Für Aquarien voller kleiner Tetraeder kamen sie (mit etwas Schütteln) deutlich über 72% hinaus. Aber das sind Experimente, die Mathematiker nicht als Beweis akzeptieren können – schon deshalb, weil die verwendeten Plastik-Tetraeder natürlich leicht abgerundete Ecken und Kanten haben, also keine mathematisch-idealen Tetraeder sein können.
Zur selben Zeit in Michigan … setzte der Mathematiker Jeff Lagarias (ein exzellenter und ausgesprochen vielseitiger Zahlentheoretiker und Geometer) seine Doktorandin Elisabeth Chen auf das Problem an: “Wenn Du Conway und Torquato übertreffen kannst, dann ist das sehr gut für Dich!” soll er ihr gesagt haben. Chen setzte sich ans Werk, analysierte viele verschiedene mögliche Konfigurationen, und kam im August 2009 schließlich auf immerhin 78% [arXiv:0908.1884] Und Lagarias wollte das gar nicht glauben!
Zur selben Zeit … an der selben Uni, aber in der Fakultät für Verfahrenstechnik (“Chemical Engineering”) interessierte sich Professor Sharon C. Glotzer für Tetraederpackungen: Sie und ihre Kollegen wollten sehen, ob sich Tetraeder in kristallinen Strukturen anordnen, wie sie das aus Flüssigkeitskristallen kannten. Dafür schrieben sie Computerprogramme, um das Schütteln und Anordnen von Tetraedern zu simulieren – und fanden eine regelmäßige (aber komplizierte Struktur), die aus Wiederholungen eines Grundmusters von 82 Tetraedern bestand. Kompliziert, aber dicht: 85,03%! Während die Ergebnisse zur Publikation in Nature vorbereitet wurden, kamen Konkurrenten aus der Deckung: Kallus, Elser & Gravel von der Eliteuniversität Cornell im Staat New York fanden eine viel einfachere Packung [arXiv:0910.5226], in der sich eine Konfiguration aus nur 4 Tetraedern wiederholt. (Nicht klar ist, warum dieses einfache Muster in den Simulationen von Sharon Glotzer nicht aufgetreten war.) Dichte: 85,47%.
Aber das Rennen ging weiter – kurz vor Weihnachten brachte es Salvatore Torquato mit seinem Doktoranden Yang Jiao auf 85,55%: die beiden hatten die Cornell-Lösung unter die Lupe genommen und leicht verbessert [arXiv:0912.4210]. War das nun das Ende der Fahnenstange?
Nein! Am 26. Dezember schlug Elisabeth Chen zurück: Ihr Preprint, kurz nach Sylvester im arXiv eingereicht [arXiv:1001.0586] (gemeinsame Arbeit mit der schon erwähnten Sharon Glotzer und Michael Engel aus dem Chemical Engineering Department) beschreibt eine weitere Verbesserung des Cornell-Kristalls, die durch systematische Optimierung gewonnen wurde.
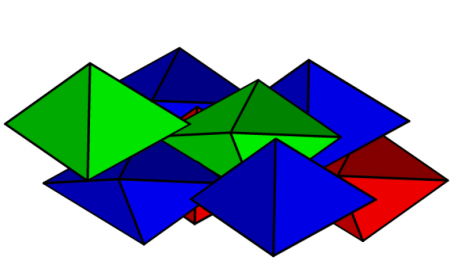
(Abbildung aus dem Aufsatz von Chen et al.: optimierte Konfiguration von N=16 Tetraedern, in der sich eine bestimmte Konfiguration von zwei Doppeltetraedern wiederholt.)
Dichte: 85,6347%. Und das ist der aktuelle Rekord – soweit ich weiß.
Wo liegt das Ende der Fahnenstange? Das weiß ich nicht, und offenbar gibt es überhaupt keine guten Abschätzungen, wie weit man vom Optimum entfernt sein könnte. Vielleicht sind die 85,6347% optimal, vielleicht geht es viel besser. Jetzt sind obere Schranken gefragt, und die sind nicht durch Konstruktionen zu gewinnen, sondern erfordern wohl ganz andere mathematische Methoden. Ich erwarte, dass jetzt ein Wettrennen vom anderen Ende her beginnt: Wer kann zeigen, dass mehr als 95% mit gleich-großen Tetraedern nicht zu erreichen sind?


Archimedes’ Irrtum
Was war den Archimedes’ Irrtum? Oder anders gefragt, was hat Johannes Müller bewiesen? Würde dies in die Richtung der anderen mathematische Methoden zur Bestimmung der obere Schranken weisen?
Guter Beitrag
Netter Beitrag, auch mal was für Mathematikinteressierte, die nicht sofort an der fragstellung schon scheitern. Weiter solche Themen.
Re: Archimedes’ Irrtum
Ich verweise auf einen wunderbaren und preisgekrönten Aufsatz von Majorie Senechal: “Which Tetrahedra Fill Space?”, Mathematics Magazine, 54 (1981), 227-243. Sie zitiert Archimedes so: “It is agreed that there exist only three plane figures that can fill a place, the triangle, the quadrilateral, and the hexagon, and only two solid bodies, the pyramid and the cube.”
Offenbar werden da nur reguläre Vielecke bzw. Körper betrachtet, und mit “pyramid” ist der Tetraeder gemeint. Was der Fehler war, ist daraus nicht herauszulesen – nur dass das als “bekannt” angenommen wurde (was die Fehlersuche ja behindern kann).
Das Manuskript von Regiomontanus gilt offenbar als verloren, also wissen wir auch nicht, was er wirklich beigetragen hat.
Der Fehler ist für uns heute (aus Winkelberechnungen) recht leicht nachzurechnen – aber viel schwieriger ist die Frage, wie man daraus obere Schranken gewinnen kann. Da kenne ich auch keinen guten Ansatz…
Archimedes Tetraeder
Wenn man mit Tetraedern den Raum füllen will, müssen sich insbesondere die Innenwinkel an jeder Kante zu 360 Grad aufaddieren.
Die Innenwinkel von 5 regulären Tetraedern addieren sich nur zu 353 Grad, die Innenwinkel von 6 regulären Tetraedern aber schon zu 423 Grad.
Wenn Archimedes wirklich gemeint hat, den Raum mit Tetraedern füllen zu können, dann hat er vermutlich den Innenwinkel eines regulären Tetraeders mit 60 Grad angenommen. (Das ist ja auch ein naheliegender Denk-Fehler. Heute könnte natürlich jeder Schüler mit Trigonometrie-Kenntnissen das richtige Ergebnis berechnen.)
Wenn man mit Tetraedern ….
….den Raum füllen will!
Bei Betrachtung der hier optisch gezeigten Lösungen kommt mir jede Möglichkeit der Form einer Kugel immer näher. Das würde der allgemeinen Regel folgen, welche die Kugel aus einem scheinbar natürlichen Zwang als letzte Form vor dem Ideal stünde. Wo also ist die Grenze zwischen Kugel und Tetraeder ? Es entbehrt doch dann den Sinn, wenn ich Tetraeder so zusammenpacke, dass es eine Form nahe einer Kugel annimmt. Da füll ich doch lieber gleich mit Kugeln.
Der nächste Schritt das Vorgangs könnte sich um die Ausübung von Druck handeln. Setze ich eine ungeordneten/unsortierten Anzahl dieser Tetraeder einen von allen Seiten gleichem Druck aus – welcher keine Rücksicht auf die Formen nähme, so entstünde wieder eine Kugel.
mich erinnert diese Strategie an Schillers Entgratung des Individuums – alles Abstehende abschlagen, bis die geschmeidige Fläche frei wird …
Es war Aristoteles, nicht Archimedes
… der antike Irrtum war von Aristoteles, nicht von Archimedes. Tut mir leid: ich hab’s mal im Blog-Artikel korrigiert, aber der Fehler zieht sich natürlich jetzt durch die Leserbriefe und meine Antworten darauf. Sorry!
Sehr schöner Beitrag. Der bringt genau meine Gedanken dazu auf den Punkt. Grüße aus Berlin. Micha
Sehr schöner Beitrag. Der bringt genau meine Gedanken dazu auf den Punkt. Grüße aus Berlin. Micha
Vielen Dank!
Vielen Dank für diesen interessanten Artikel!
Ich liebe die Mathematik und all die mit ihr verbunden Probleme 😀
Sehr interessant! Schön, aber vermutlich in weiter Ferne liegend wäre natürlich eine Verallgemeinerung auf beliebige Körper…
Verallgemeinerung auf “beliebige” Körper:
Das wird ein unerfüllbares Ziel bleiben, allein schon die Definition des Ausdrucks “beliebige Körper”.