Why A4? – The Mathematical Beauty of Paper Size
BLOG: Heidelberg Laureate Forum

Unless you have skipped a lot of school, or work, or both – or you live in the USA – you have probably used an A4 sheet of paper before now. Have you ever wondered why it is the shape or size it is? Time to dust off some high-school level maths to investigate.
Just in case you have never actually checked the size, I can tell you now it is precisely 210mm by 297mm. But don’t take my word for it. Go check. I’ll wait. If you haven’t got a piece of A4 within reach somewhere in your house then you have a much better tidying ethic than me. Conveniently, it is just short enough to be measured by that old 30cm ruler you also probably have lying nearby in a drawer somewhere. Nevertheless, the obvious question remains:
Why?
Sometimes this is closely followed by: “Seriously? 297mm? Why not 300mm?”. I know this is a genuine question because the words still echo in my memory from my school design classroom where one of my fellow students railed at the perversity of the world in that exact manner. My memory does not supply any detail about whether he received an answer, but I fear he was left to wallow alone in his own misery. Let us consider the rest of this piece as a response to this poor boy’s unresolved anguish.
It is true though – anyone who has ever wanted to mark half way across the long side of their paper has experienced the vague resentment that occurs when you realise you now need to measure 148.5mm and your ruler does not even have half millimetre divisions.
I invite you to take a rectangular piece of paper that is not A4 shaped. You can always just tear a bit off your A4 paper and then neaten it up to a rectangle. With your non-A4 rectangle, try folding it in half along the shortest line of symmetry. You will observe, in a spectacular anticlimax, that you now have a piece of paper half the size, and a different shape. Possibly, you started with a ‘squarey’ rectangle and now you have a ‘long-thin-rectangle’, or vice versa.
Now do it with an A4 sheet. You probably already know what happens. You get an A5 piece of paper. It is half the size (of course it is, you just folded in half). What’s more, it is the same shape. Technically a similar shape, of course, but the sides are in the same ratio. This is something of a shock, if you ponder it, because rectangles do not normally behave like this.
This is not an accident. It is possibly one of the greatest innovations of the 18th century. To take just one modern example: teachers have been using it to literally halve their photocopying budget for years. You want two copies on one page? Great – they fit exactly! Any other paper shape (say, ‘letter size’, or 8.5 by 11 inches, for all you North Americans out there) is sadly wasteful in comparison because your two half size copies leave an awkward gap on the original page.
The earliest recorded discussion of the idea comes from a 1786 letter from German academic Georg Christoph Lichtenberg to author Johann Beckmann1, but there is a suggestion it might have already been a problem used in a maths exam even earlier.2 However, it was not until the early 20th century that Germany – and then eventually most of the rest of the world – actually standardised the idea. It is now known as ISO 216, an international standard paper size.3
In fact, there is only one ratio of rectangle sides that will work, i.e., one that will give a similar shape when cut in half. Consider for yourself the question: Which ratio is it?4 Read on to see one possible method of settling this.
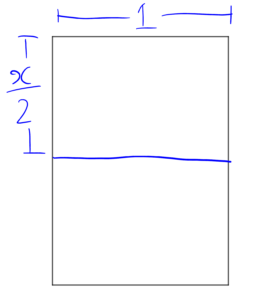
Draw a general rectangle, with sides in the ratio (long:short) \( x:1 \)
Now draw the half-way fold line, and consider the new rectangle which has a side ratio (long:short) of \(1:\frac{x}{2}\)
If we wish the two ratios to be the same for all the aforementioned goodness then we must have the fractions equal
\( \begin{array}& \frac{x}{1} &= & \frac{1}{\frac{x}{2}} \\ x^2 &= &2 \\ x &= &\sqrt{2} \end{array} \)
(or \( – \sqrt{2}\), but let’s discuss negative ratios another day)
So the only ratio that has this important property is the square root of 2, famously – and ironically in this case – not a ratio5. This is why the dimensions of the paper, whatever unit you use, are never going to be ones which most people would call ‘nice’. There just don’t exist a pair of integers that give you the ratio \(\sqrt{2}\), so we have to approximate.
We should (and did) therefore abandon the dream of having ‘nice’ side lengths, but that does not stop us from making ‘nice’ areas. In fact, the international A-size system now starts with A0 paper, with sides in the correct \(\sqrt{2}\) ratio, but with exactly 1m2 of area, or as near as you can get with whole millimetre side lengths (1189mm 841mm, to be precise). Then folding or cutting it a few times until it is conveniently desk/folder sized gets you to A4, hence the ‘4’ bit in the name.
By the way, if this is new to you but you do remember a bit of school maths, you might like another way of realising this: remember ‘area scale factors’ and ‘length scale factors’ are related in that the area scale factor is precisely the square of the length scale factor. Well, if you want the area scale factor to be \(2\) (or \(\frac{1}{2}\) ) then the length scale factor must be \(\sqrt{2}\) (or \(\frac{1}{\sqrt{2}}\) ). Of course.
It is somewhat sobering. Irrational numbers are useful, whether you like them or not (a lot of people do not, just check some of the myths that have grown up around what the Pythagoreans did to Hippasus when he suggested \(\sqrt{2}\) was not rational). But once we get over our fear of using these irrationals we can reap the benefits. In this case, paper weights are now easily calculated because weight is proportional to area: 80 gsm (grams per square metre) paper at A0 size weighs precisely 80g. A4 paper at that density therefore weighs 5g since it’s been halved 4 times.
Draughtsperson’s pens typically have widths that increase by factors of \(\sqrt{2}\approx 1.4\) so that the next pen in the series can have the correct width if used on a scaled up drawing on the next size of paper. It’s all nice and neat.
Some technical pens with their sizes marked (increasing by factor of approx 1.4 each time). Image Credits: Wikimedia Commons
What is our lesson from all this? We often have convenience now because someone did the maths before. Thanks to them, we can now safely forget that even some of the most basic aspects of our lives are governed by numbers and their properties. But they are, and we benefit greatly from the people that have reflected upon this.
I say we can safely forget all this, but I will end with a request: the next time you hear the cry “But WHY is it 297mm?” from a nearby anguished soul trying to measure halfway across their paper, bring it back to mind. Now you know.
[1] Lichtenberg is the same Lichtenberg who gives his name to the striking lightning burn patterns from high voltage incidents. Beckmann, for his part, was the very first person to coin the word ‘technology’. Now you know.
[2] https://www.cl.cam.ac.uk/~mgk25/lichtenberg-letter.html
[3] https://en.wikipedia.org/wiki/Paper_size
[4] No. It is not the Golden Ratio. That is a great ratio, but it is not this ratio.
[5] Not a ratio of integers. Look up a proof if you don’t believe me.



Ben Sparks wrote (24. Aug 2022):
> […] an A4 sheet of paper […] is precisely 210 mm by 297 mm. […]
Those exact values are (only) nominal.
The standards also specify size tolerances which in the A4 size range even exceed plus/minus 1 mm.
> I invite you to take a rectangular piece of paper that is not A4 sized. […]
But surely you mean that we take a piece of paper that is not even A4 shaped; especially not some A3 or A5 sized piece of paper.
> […] same shape […] similar shape […]
Arguably, within tolerances, all ISO standard pieces of paper have the same shape; and in a strict sense at least similar shape.
However, to say that an A4 piece of paper could be folded to half size with the same shape requires a sense of “shape” that is sufficienty tolerant to the number of layers (at least tolerant of having 2 layers instead of 1), and to the appearance of a fold.
And, Ben, as photographers know, √2 is the ratio of one f-stop to the next.
Huh – that’s a very good point – I’m a (clearly) amateur photographer, but did not know that. Presumably because f-stops are ratios, and using root 2 to scale would give you the ratio ‘halfway’ between doubling your exposure.
However, I think that my camera has 6 stops between a doubling of exposure (e.g. from f/2 to f/4)… so that implies it’s probably using the sixth root of 2 as a scaling. Which would give me (to 1dp) f/2.2 f/2.5 f/2.8 f/3.2 f/3.6 f/4
Does that seem right?
Annoyingly my camera does f/2.2 f/2.5 f/2.8 f/3.2 f/3.5 and f/4 and the 3.5 doesn’t make sense to me 🙁 Do you know why?
“But surely you mean that we take a piece of paper that is not even A4 shaped; especially not some A3 or A5 sized piece of paper.”
You’re quite right. Edited.
Sichtbereiche sind so beschreibenswert :
-> https://en.wikipedia.org/wiki/Angular_resolution
Die wie gemeinte Auflösung ist unterschiedlich, sog. Pixel meinend, auch die geübte Kopfbewegung der gemeinten Personen ist unterschiedlich.
Das Räumliche meinend.
Hängt auch mit individuellem Körperbau zusammen.
“A4” ist insofern ein <a href="https://en.wikipedia.org/wiki/Angular_resolution"<Standard, auf den sich geeinigt werden kann.
No probemo hier.
MFG
WB
Sozusagen mathematische A-Serie konkurrieren hier mit der Ergonomie.
Mehr ist nicht los.
Dr, W war in diesem Kommentariat bereits erklärend.
Der Rest ist sozusagen “Mathematicus”.
MFG
WB
—
Solly!
“A4” ist insofern ein Standard
Im ergonomischen Sinne, Dr. W will dieses Fachwort einmal herauskramen.
Ist auch gewohnheits-bedingt, einige mögen mehr von rechts nach links zu lesen, andere andersherum, es sind auch die wie hier gemeinten Größen unklar, Dr. W bspw. mag ca. 40 Buchstaben in einer Zeile und dann (Zeilen-)Abbruch.
Am wie hier gemeinten Größenverhältnis darf ebenfalls genagt werden.
Dr. W bspw. kann auch mit mehr als eimhundert Zeichen in einer Zeile auskommen.
Solly! – Die Textauszeichnung ist mal wieder verhunzt worden.
No problemo hier.
Last Try.
Mah.
🤔 …
Each A(n) rectangle can be constructed by folding an A(n+1) rectangle and vice versa, each A(n) rectangle can be formed by proper alignment of two A(n-1) rectangles. In addition, the area of an A0 rectangle is 1 m^2
The A(n) rectangular format contains a folding rule and an arbitrarily selected constant (here the area of A0).
I find this very useful because it avoids unnecessary complexity and unnecessary diversity. And it would be even more useful if such form standards had conquered construction and architecture. Why? Because it would be much easier to replace broken things and because it would be possible to build entire buildings or even cities only with standard shapes. That would make life easier.
And what is better in life than always choosing the catchiest solution provided it is also a good solution?
Martin Holzherr wrote (27.08.2022, 12:21 o’clock):
> Each A(n) rectangle can be constructed by folding an A(n+1) rectangle […]
Measure twice,
fold once.
Nice picture. Yes, it was the wrong direction.
Martin Holzherr wrote (31.08.2022, 12:34 o’clock):
> Nice picture.
Which one?, of the two pictures that I linked above (29.08.2022, 09:36 o’clock)?
> Yes, it was the wrong direction.
Glad that someone noticed.
p.s.
Too bad that SciLogs doesn’t support (yet) the generation, by SciLog commenters, of pictures from textual input, such as by means of
psfig.I beg your pardon, I rather meant
pstricks.M.Holzherr
you plead for prison architecture. Squares only are worse.
A better ratio would be 1 : 1,6, the golden ratio. think of beauty.
@fauv:A plea for a fractal architecture in which all parts fit together and something can always be added.
M.Holzherr
fractals are horrible. Wherever you go you see the same. Human houses must not be perfect.
The giant scyscrapers produce criminality. Our soul looks for a place that give us a „memento mori“
@fauv: FRACTAL PATTERN IN ARCHITECTURE is a good introduction to fractal architecture
@fauv(quote): „fractals are horrible. Wherever you go you see the same. “
Every tree has a fractal border. A fractal design has repetitive elements, but in a free, not strict order.
M. Holzherr
I agree to not strict order. Whether trees have a fractal border, on the first sight yes, on the second sight , no. On a closer look all parts are different from each other.
Nur ergänzend, statt auf der Schiene der “A Series” geht es auch so, vergleiche :
-> https://en.wikipedia.org/wiki/Letter_%28paper_size%29
-> https://history-computer.com/xerox-alto-guide/ (‘Bit-mapped black and white display sized 606 × 808 (the same dimensions as a regular (8.5″x11″) sheet of paper, aligned vertically)’ – vgl. auch mit WYSIWYG)
-> https://www.youtube.com/watch?v=q_Na1SJXSBg
Mit freundlichen Grüßen
Dr. Webbaer (der für den hiesigen Inhalt dankt und nur ergänzen wollte, auch folgen konnte)
This was a fun read, thanks—but I was hoping for a discussion of the geometrical idea of the ‘gnomon’, which I find fascinating. You were so close!
Gnomos wrote (02.09.2022, 17:23 o’clock):
> […] but I was hoping for a discussion of the geometrical idea of […]
I’d like to take this opportunity to express my hope that this SciLog, apparently as the very first SciLog, is going to offer a dedicated SciLog article to invite SciLog comments with public suggestions or requests of topics to be presented in forthcoming SciLog articles (not least for the purpose of inviting topical public discussion through subsequent SciLogs comments).
Dear Frank Wappler,
Topic suggestions are always welcome from our esteemed commenters. Feel free to send them to media@heidelberg-laureate-forum.org.
Nikolas Mariani wrote (05.09.2022, 18:37 o’clock):
> Topic suggestions are always welcome from our esteemed commenters.
Thank you, Nikolas Mariani, for responding to my suggestion (05.09.2022, 12:40 o’clock). I assume that your response also stands for that of Ben Sparks, who appears as the author and the ostensible administrative face of the above SciLogs article.
> Feel free to send them to […]
Of course, it’s disapointing to me that your answer to my suggestion is thus in the negative.
You as well as our fellow SciLogs commenters should be aware that there’s at least anecdotal evidence, such as this, for unsolicited (e_)mails and their senders being in poor regard with (selected) institutional scientists; and therefore presumably with authors of SciLog articles in general, too.
For myself, I much prefer to offer applicable suggestions publicly and archived, providing the opportunity of barrier-free public response or comment; as in this case, and following the example set above by Gnomos (02.09.2022, 17:23 o’clock).
I’m looking forward to requesting publicly, again in form of SciLog comments, one or the other SciLog article on mathematical topics I care about, at least if and when such opportunity might arise due to the contents of forthcoming articles of this SciLog.
Dear Frank Wappler,
my comment was on behalf of the HLFF, which runs this blog (hosted by Scilogs) and coordinates the various authors who contribute articles. Our authors are independent in their choices of article topics (within the parameters of the HLFF’s fields of interest: mathematics and computer science). That being said, we are happy to accept wishes for topics via email as stated above, and could happily share those ideas with our authors, should they be seeking inspiration for new topics to cover.
Not sure it’s been mentioned earlier, but the article explains the ratio, not the numbers themselves.
Which come from a rectangle with that exact height/width ratio *and* and area of 1 sqm (squared meter or m^2) before rounding. Which is the so-called A0 size.
Ref: https://en.wikipedia.org/wiki/ISO_216#A_series
Hi Vincent, we actually did mention this here:
Cool!
Good discussion. Now let’s look at photo’s. The A-series lends itself very well for the (this betrays my age) wet darkroom and how to make optimal use of the box of photo-sheets. However: anyone who ever developed a portrait will find that the A-shape is displeasing. The letter-format is often better suited for portraits. This is only a general finding: of course there are exceptions. But just look at series of portraits – what shape are they? Take the portrait of your wife/husband/child and cut it to A-shape, does it still look as good? Probably not.
Thanks for sharing this delightful knowledge 🙂 for an instance I still wasn’t satisfied with the Answer – why couldn’t they at least have the courtesy to round of one of the sides to either 20 or 30 cm?.
But then I realized the other side would end up like a literal mathematical disaster 🙂
Just did the calculation I shall take back my previous comment. If course 21 also doesn’t stay an integer after multiplying by the root of 2..
My question still remains 😊