Just over two months ago, the mathematical world celebrated a new discovery. And this was unlike any new discovery mathematics had seen for some time: as well as being a groundbreaking new piece of research in an active area of mathematics, it was also a simple enough discovery that it could be explained to others, arranged into beautiful images and printed on a t-shirt.

A team of mathematicians from all over the world had come together to write a research paper explaining an ingenious new family of shapes: one which solved a long-standing question that had stumped mathematicians for decades, while being pleasingly simple and elegant. The shapes, which were discovered by a retired print technician from Yorkshire, provide an answer to the question “Can there be an aperiodic monotile?”

Don’t Make Me Repeat Myself

When you mention tilings, most people will think of a regular repeating pattern of tiles on a wall. Mathematically, we consider tilings to be on an infinite plane, going on forever in all directions, and there is an important property of tilings that concerns whether a tiling repeats, called periodicity.

A periodic tiling is one which, if shifted across or down, gives the same pattern. For example, shifting a tiling by squares across or down by the side length of one square would give a tiling which matches up the outlines of the original set of tiles exactly.

If we wanted to break this, we could take an infinite tiling of squares and cut a random set of the tiles in half horizontally or vertically, giving two rectangles where there was previously a square. Assuming we picked our cuts randomly, this tiling could never be slid across or down to match itself again, and would be technically classed as a non-periodic tiling – it does not have a repeating pattern, or a translational symmetry.

It turns out that it is possible to design tiles, or sets of tiles, which are not just capable of non-periodic tilings, but in fact require them. Such a tile set is called aperiodic – it can only be used to produce a non-periodic tiling, and such tilings will contain as large a region as you like which has no repeats. Such tile sets produce beautiful non-repeating designs, but as you might imagine, they are a bit hard to find, and it is even harder to prove this aperiodic property.

Aperiodic tilings are of particular interest to physicists, as they are related to quasicrystals – structures found in certain minerals and chemical compounds, which exhibit this same non-periodic behaviour. Prior to this connection being found, work on aperiodic tilings was considered to be more recreational than proper research, and was often undertaken by amateur mathematicians such as Robert Ammann. But from the 1970s, physicists started to take an interest.

Penrose to the Occasion

The most famous type of aperiodic tiling is the Penrose tiles. Designed by physicist Roger Penrose, there are various versions of it out there but the most famous is a tiling by two rhombuses, one wide and one narrower. The particular dimensions of the rhombuses are related to the Golden ratio, and the angles at the corners are all related to pentagons. These tiles can be used to produce beautiful non-periodic tilings of the plane – but only if you use them correctly.

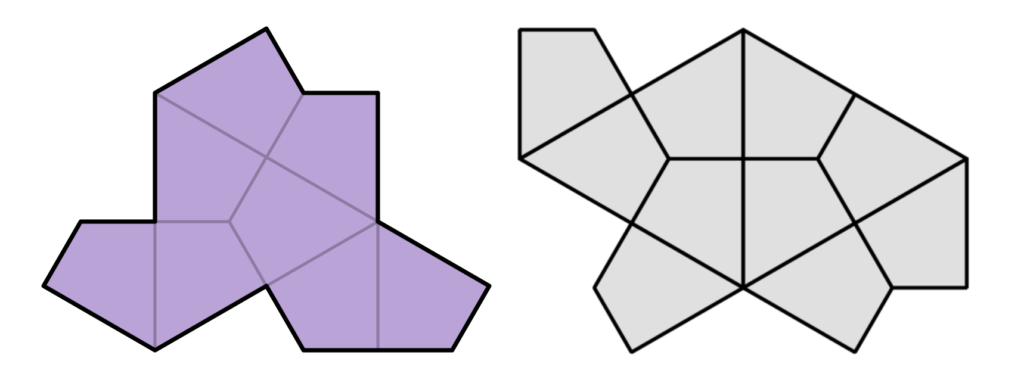
The Penrose rhombs themselves are fundamentally not aperiodic: if I wanted to, I could arrange the two rhombuses into a periodic tiling (below left). But if we apply certain rules to the way the rhombuses are allowed to combine – for example, we are not allowed to put two together so they form a parallelogram – we can force them to be aperiodic. The easiest way to do this in practice is to mark the tiles so they must be matched up correctly, or add notches to the sides so they fit together like jigsaw pieces in the right way.

This tiling is periodic.

Image CC BY-SA Geometry Guy on Wikipedia

This seems dissatisfying – and up until fairly recently, all the attempts at aperiodic tile sets were disappointing in some aspect. Several variations on Penrose tile sets exist, all of which need some kind of matching rules to prevent them tiling periodically. It is also annoying that you need more than one type of tile to cover the plane: a single tile with this property would be called a monotile, and while examples of aperiodic monotiles were known, they have so far been made up of multiple disconnected pieces that form one ‘tile’, like the Socolar-Taylor tile.

The One and Only

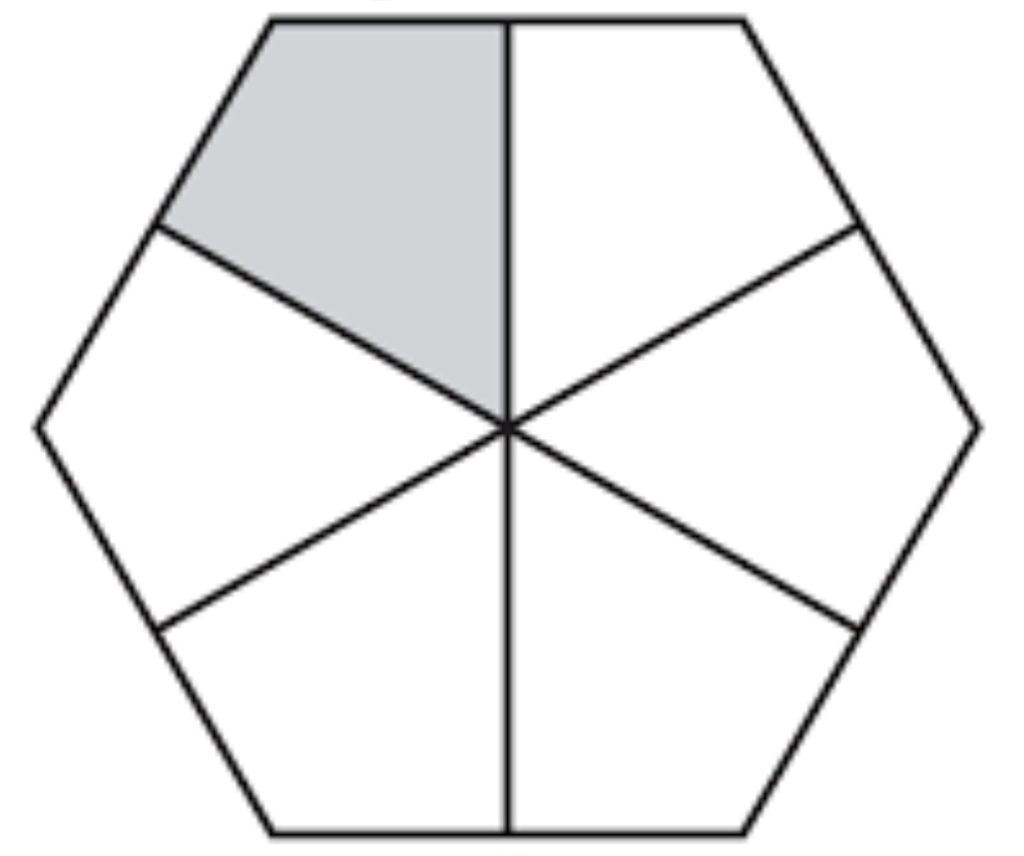
Enter maths enthusiast David Smith, who enjoys playing with tilings and patterns, and uses his computer to generate tilings with different shapes. He spent a lot of his spare time playing with tiles and trying to fill the screen, and one day he discovered an intriguing shape. Smith had split the whole plane into hexagons, then cut each hexagon along lines perpendicular to the centres of its faces to make six kites. These kite pieces could be joined together into tiles, and he found one particular combination that seemed to tile in a strange way.

Suspecting this might be an interesting discovery, Smith contacted his friend in Canada, research mathematician Craig Kaplan – they shared an interest in tilings and shapes, and Kaplan was able to take a look at this new tile to see if it was anything exciting. And it turned out, it was – Smith had discovered a single tile which tiles the whole plane non-periodically, and the non-periodicity is forced merely by the shape of the tile: not requiring any additional matching rules.

Kaplan and Smith pulled in some other mathematical friends, mathematician Chaim Goodman-Strauss and software developer Joseph Myers. Between them, they worked out a way to prove that this tile had the aperiodic property they were looking for. (If you would like more detail on this, Christian Lawson-Perfect has written a great explainer over at The Aperiodical). They wrote up the discovery and published it online – and the response was huge.

The breakthrough was unexpected and definitely new mathematics – making progress in an area where nobody had discovered anything in over 50 years – but it was also fairly simple to understand and explain. Plus, it involved a friendly-looking shape that makes pretty tilings that you can share and look at. This meant everyone was soon talking about it, creating their own tiles using laser cutters and 3D printers, and even sharing maths memes. Everyone was talking about it, with excellent write-ups in Quanta and The Guardian.

In fact, the researchers had discovered a whole infinite family of solutions, made by varying the two different lengths of edges of the shape, all of which provide monotiles. There are two members of this family which make particularly pleasing tiles, corresponding to length parameters of \((1, \sqrt{3})\) and \((\sqrt{3},1)\) and they have become known as ‘the hat’ and ‘the turtle’.

On reflection

Image CC BY-SA Cmglee on Wikipedia

As exciting as this discovery was, there was still one outstanding question, relating to one more slightly unsatisfying aspect of the discovery. The tilings produced by these shapes are non-periodic, but in order to fill the whole plane they need some of the pieces to be flipped over, or mirrored (the darkest pieces in the tiling above). Roughly one in six tiles – or less roughly if you prefer, one in ϕ⁴, where ϕ is the Golden ratio – needs to be facing the other way in order for it to work.

People immediately started wondering if this was as far as we could go, or whether someone would be able to find the elusive aperiodic monotile which does not need to be present in its flipped form in order to work. The team behind the first monotile discovery also wondered this, and continued working on the problem.

And less than two months later, they have announced that this problem is now also solved – and in fact, they had kind-of already solved it! One of the stages in the infinite family of solutions they had already seen – the half-way point in the video above, corresponding to edge lengths of \((1,1)\) – was previously discounted as an aperiodic tile, since the tiling it produces is periodic.

But on closer inspection it turns out that if you use this tile only in one orientation, this forces it to be a non-periodic tiling – if you are looking at examples including flipped versions, this must make it harder to see the aperiodicity. But it is there, and the authors have now produced a proof that this tile works, is aperiodic, and can tile the whole plane on its own when used without reflections.

Since using the tile in different mirror orientations can still lead to periodic tilings, we need to make one tweak to ensure it is aperiodic, and that is to change the straight lines making up the edges into some kind of curve – any curve will do, but just enough to force us to use the tile the right way round. The resulting slightly spooky-looking shape has caused this new tile to be christened ‘the spectre’ – and again, this means there is a whole infinite family of shapes we can create from it.

If you would like to hear more about these cool new shapes, we had the pleasure of chatting with Chaim Goodman-Strauss, one of the four paper authors, for my podcast Mathematical Objects. This chat took place between the first and second discoveries, so we mainly talk about the original monotile – but it comes across how excited the team were about this discovery, and I can understand why. This is a really cool, actually new piece of mathematics – and I can make myself a keyring from it.