A truly special occasion

Last week my husband and I celebrated our Golden Anniversary. No, not our 50th – we’re not quite that far along just yet. We celebrated ϕ years since our wedding – approximately 1.618 years, or 591 days – and since we’re both mathematicians, this was a completely logical milestone to celebrate (also, we spent our actual 1-year wedding anniversary at the Heidelberg Laureate Forum so this was a chance to do something with just us, and no famous mathematical Laureates). The number ϕ (phi), also called the Golden Ratio, or Golden Section, is a wonderful constant and we thought it was worth celebrating.

Imagine a taking a number and subtracting one from it. Then imagine starting with that same number, and finding its reciprocal (calculating the result of 1 divided by the number). Now imagine that if you do each of these things you get the same result. That would be quite a nice coincidence. In fact, there is a number that has this property, and it’s the Golden Ratio. The Golden ratio ϕ is an irrational number, as it contains √5. So it’s interesting that it’s called a ratio, since it’s… not an exact ratio of two things. But if you compare ϕ with 1, the ratio between the two numbers is what’s really Golden. Imagine you have a rectangle which has short side length 1 and long side length ϕ.
The Golden ratio ϕ is an irrational number, as it contains √5. So it’s interesting that it’s called a ratio, since it’s… not an exact ratio of two things. But if you compare ϕ with 1, the ratio between the two numbers is what’s really Golden. Imagine you have a rectangle which has short side length 1 and long side length ϕ.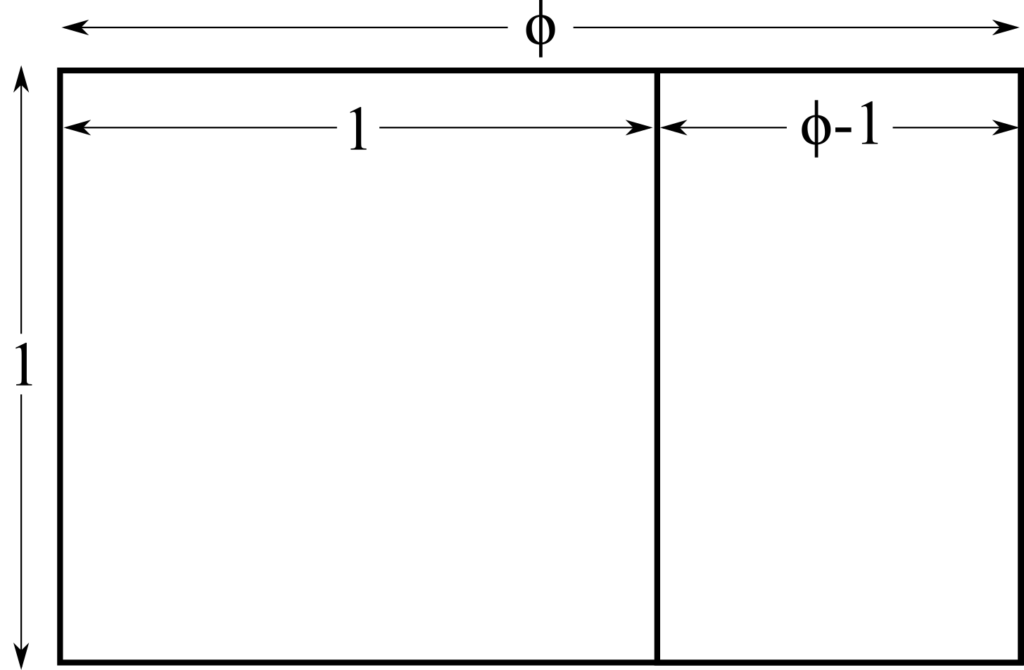
If you cut off a 1 by 1 square from this rectangle, the resulting rectangle will be (ϕ – 1) by 1, and given the fact above, this means the smaller rectangle is in the same ratio as the larger one – if you rotate it and scale it up in proportion, you’ll get back the original rectangle. There’s exactly one kind of rectangle for which this works – this one – and it’s called a Golden Rectangle.
Many people claim that this Golden Ratio is somehow a ‘perfect’ ratio – the ‘Divine Proportion’, symbolising perfect beauty and truth, or something. Claims are made about how art, nature and even the human body contain instances of this ratio. Unfortunately, some of these claims are mildly unfounded, and there’s no real evidence they are actually the Golden Ratio (and don’t get me started on Nautilus shells). It seems people just want to find it, and go looking for it in all kinds of places – and their enthusiasm carries them to draw Golden conclusions.

Artists, including Salvador Dali, have been known to employ the Golden Ratio in some famous works – but many others are also purported to have used it, when actually, there’s no evidence they did. If you draw a rectangle on the Mona Lisa enclosing only the subject’s face, you’ll get arrested and thrown out of the Louvre. Nobody seems able to produce proof that the Golden Rectangle is ‘the most visually appealing rectangle’, although it’s a claim that’s often made.
So, if this amazing sturdy fraction doesn’t crop up in nature and art as much as people say it does, why do mathematicians love it so much (and why did we have a celebration to mark ϕ years of marriage)? Read the following round-up of my top 5 places you’ll really actually find the Golden Ratio, and hopefully you’ll begin to understand.
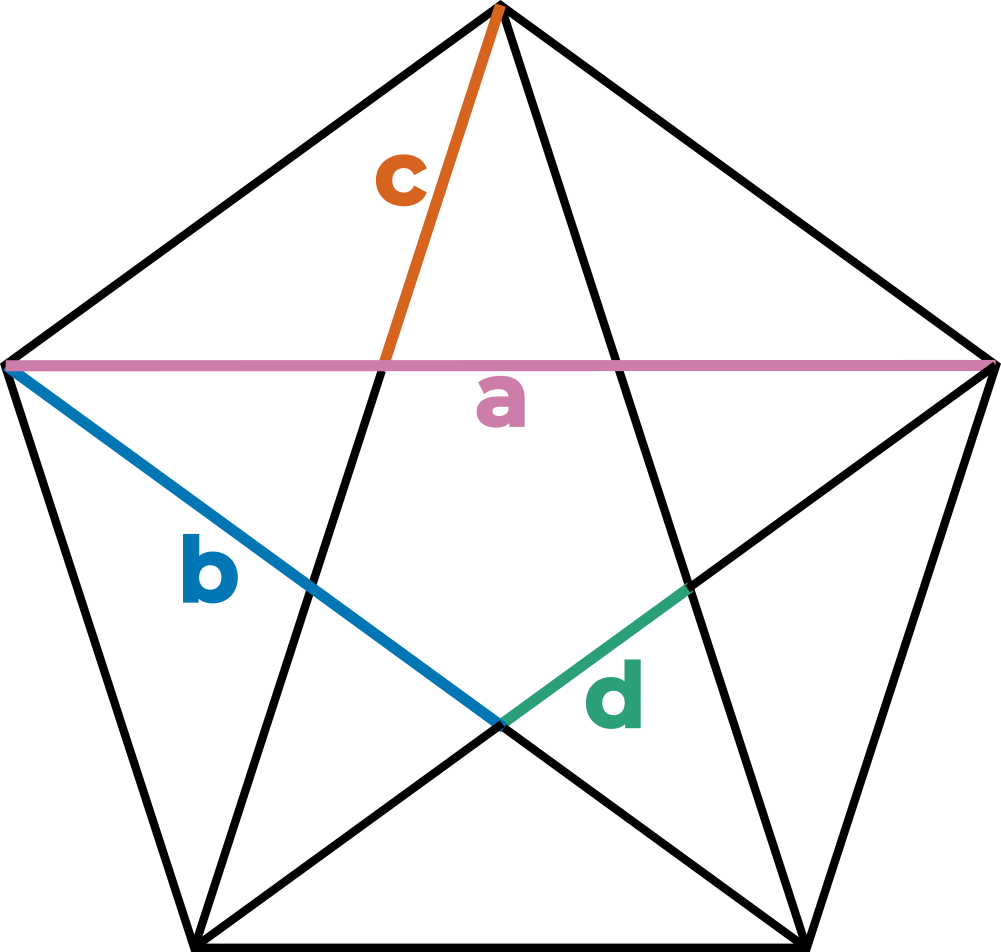
5. In a pentagram
This five-pointed star shape inscribed in a pentagon, sometimes also called a pentangle, has long-standing associations with religious imagery and symbolism across many cultures. But also maths! Pentagons – and by association, shapes made from pentagons, like the dodecahedron – are intricately linked to the Golden Ratio. The four distances marked in the diagram are in the Golden Ratio to each other – that is, a:b, b:c and c:d are all the Golden Ratio. If you knew this already, you win a gold star.
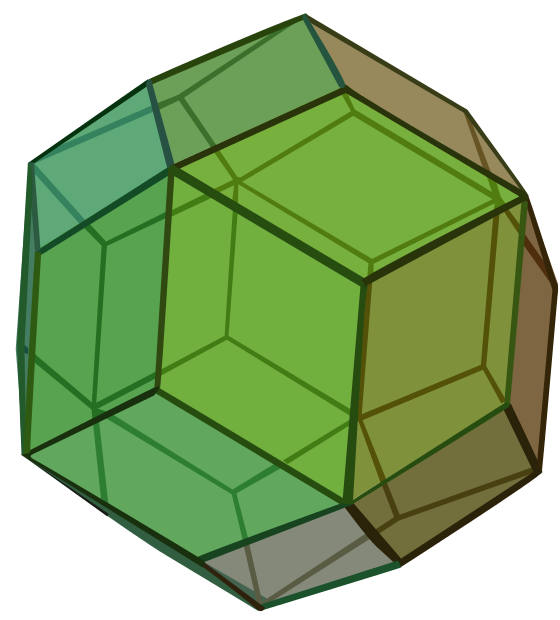
4. In a rhombic triacontahedron
While it’s not hugely well-known, it’s described by Wikipedia as ‘the most common thirty-faced polyhedron’, so if you’re attacked by a 3D shape and it has 30 sides, this is likely the culprit. The rhombuses making up the faces of the shape are called Golden Rhombuses – the ratio of the width to the height of the rhombus is the Golden Ratio, and that’s what makes them exactly the right shape to fit together in this way. If you’d like to build your own, here’s a net.
 3. In your wallet
3. In your wallet
Believe it or not, you’re almost certainly carrying a Golden Rectangle with you right now. Credit cards, and by extension most wallet-sized cards you might be carrying, are a pretty close Golden Rectangle. You can tell, by taking two cards from your wallet, and giving them to me… no, sorry, placing them on the table with one upright and one horizontal, with their edges touching. Another straight edge will allow you to verify that the line from the bottom left to the top right corner of the horizontal card will then run straight to the top right corner of the vertical card – showing that the small rectangle at the top is in the same ratio as the larger card. Even if you’re not rich enough for a Gold Card, it’s still Golden!
2. In the Fibonacci sequence
You might be familiar with the sequence of numbers starting with 1, 1 and then continuing to create each term by adding together the two numbers before it – so 1+1=2, then 1+2=3, then 2+3=5 and so on.
1,1,2,3,5,8,13,21,34,55,89,…
This sequence crops up in all kinds of interesting places – in rabbit population modelling, Sanskrit poetry, and in Pascal’s triangle. But if you take successive pairs of entries from this sequence and divide the larger by the smaller, the ratio will be somewhere between 1 and 2, and the further along the list you go, the closer and closer it gets to the Golden Ratio – that’s the limit of the ratios. Even as soon as 89/55, you already get three decimal places of accuracy.
It’s also, as a fun consequence, a handy way to convert between miles and kilometres – since the ratio between 1km and 1 mile is around ϕ, you can use the Fibonacci numbers as a rough conversion chart, by taking the distance in miles and going to the next Fibonacci number for the distance in km. So, 5 miles is around 8km, 13 miles is around 21km and so on.


