While I was listening to Sir Andrew Wiles speak, I saw the writer next to me had jotted three adjectives on his pad: “Calm. Elegant. Precise.”

Astute as those three words are, they miss the basic strangeness of Wiles’ life story. For all his calm, elegance, and precision, the guy is also a unicorn, a sasquatch, a one-of-a-kind creature from the pages of myth. He is, if you will, a walking oxymoron.

He is a celebrity mathematician.

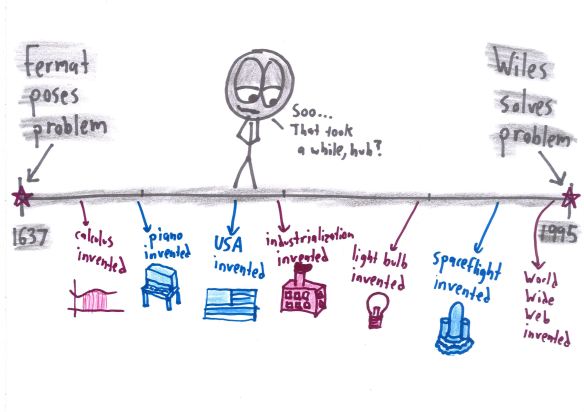
When he proved Fermat’s Last Theorem in 1994, it captured the public imagination in a way that few mathematical breakthroughs ever have. Usually, great mathematicians earn fame in their professional circles, but can walk down streets unnoticed. Wiles was different. He became the subject of bestselling books and primetime documentaries. He became “Sir.”

The difference, of course, was the problem he solved. Fermat’s Last Theorem can be explained to a high school student, but actually proving it took three centuries. It’s like the old board game commercial says: “a minute to learn, a lifetime to master.”

Or in this case, five lifetimes. Maybe more, if Wiles hadn’t come along.

Last autumn, Wiles spoke at the Heidelberg Laureate Forum in Germany—a conference putting young researchers in math and computer science into contact with living legends such as Wiles.

After describing the history of Fermat’s Last Theorem—and emphasizing its mathematical importance over the romantic tale of his work on it—Wiles answered their questions.

In the process, and without naming them as such, he articulated three clear and compelling rules for how—and whether—to tackle a famous problem.

Famously, Wiles hid his work on Fermat’s Last Theorem. He labored alone in an attic office, and covered his silence by discreetly releasing a trickle of research he’d saved up.

But this wasn’t what Wiles originally planned.

“I didn’t actually embark on it in secret,” Wiles says. “I did tell at least one or two people at the beginning.”

Wiles soon regretted that confidence. “It’s like issuing a weather forecast on the BBC. They wanted an update every hour and a half.”

That’s when Wiles went into intellectual hiding. “The secrecy was very much to give myself peace to work on it.”

For top researchers tackling famous problems, it’s the only way. “If you’re working on the Riemann hypothesis,” Wiles says of another famous problem, “there’s no point in telling people. They’ll just hound you.”

At his talk, an audience member asked Wiles about how to get started on a similar problem—such as proving that there are infinitely many perfect numbers.

“To be perfectly honest,” Wiles said, “I would say, ‘Don’t do that one.’”

Wiles’ reasoning relied on a key word: responsibility.

“I worked on Fermat[‘s Last Theorem] as a child, because I just loved the problem,” Wiles said. “But when I became a professional mathematician, I thought it was irresponsible.”

Glorious old problems like these are seductive. Prove a famous conjecture, and you might score not only a publication in the Annals of Mathematics but a profile in the New York Times or a BBC documentary: Wiles-level fame.

But in that seduction lies the danger. You can waste years chasing the pot of gold, and wind up empty-handed.

So why did Wiles return to Fermat’s Last Theorem as an adult? Because other researchers proved it was closely linked to a deep problem in algebraic number theory: the Taniyama-Shimura Conjecture.

“Then,” Wiles said, “I knew it was responsible to work on it. This was a problem that had to be solved, in the middle of mainstream mathematics, with lots of structure to it.”

That’s the other key word: structure. Deep connections to other ideas of value.

“Pick a problem that really appeals to you,” Wiles advises, “but pick one that has some structure—so even if you don’t succeed, you will prove other things.” Even if you never reach the pot of gold, you want to gather some coins along the way.

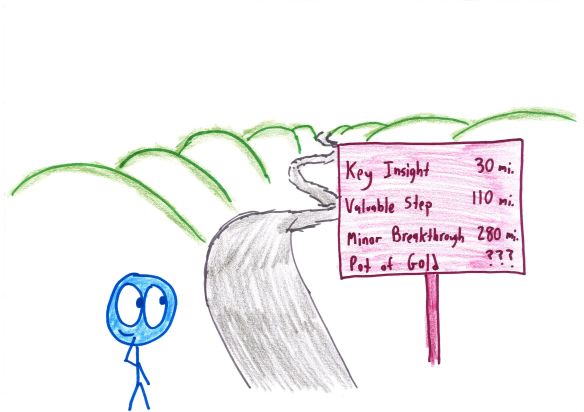
Perfect numbers don’t fit the bill. “Don’t be irresponsible and pick something where after two thousand years, there’s still no more structure to it [than when it was first stated].”

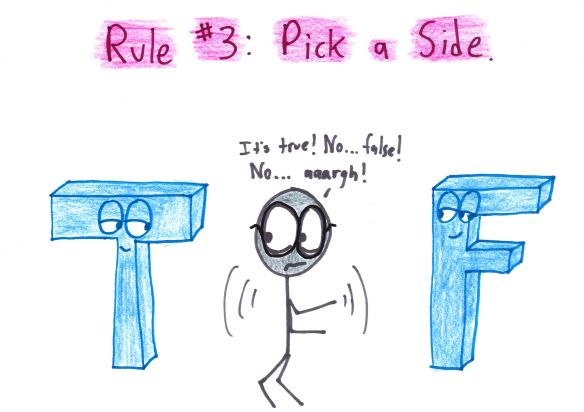
Finally, Wiles echoed the wisdom of a popular mathematical canard: Theorems are proved by believers.

“It’s a very odd thing in mathematics,” said Wiles, “that if you know something is true, it’s much easier to prove it.” There’s a mystery of human psychology here. “Having the choice between it being ‘true’ and ‘not true,’ you’d think, well, you spend half the time on each. But it doesn’t work that way.”

Researchers might try to prove a statement true for years—and then start looking for counterexamples, and find one quickly. Or they might spend ages searching for counterexamples—then, briefly supposing that it’s true, they’ll happen swiftly upon a proof.

Somehow it’s hard to entertain both thoughts at once.

Wiles, who has learned this lesson better than anyone, puts it succinctly: “You have to really believe.”

© Heidelberg Laureate Forum Foundation / Flemming­ – 2016