Strong Components via Depth-First Search
BLOG: Heidelberg Laureate Forum


Robert Tarjan at the 9th HLF. © Heidelberg Laureate Forum Foundation / Flemming
The laureates recognised at the Heidelberg Laureate Forum include very recent prize winners, and people who were awarded prizes for work some time ago. For our first laureate lecture this year, we were treated to a retrospective by Robert Tarjan, who was awarded the very first ever Nevanlinna prize for “outstanding contributions to mathematical aspects of information science.” The award was in recognition of work done in 1971 – over 50 years ago.
At the time, Bob Tarjan was a grad student at Stanford working with John Hopcroft, but the algorithm they devised has been praised for its elegance and utility, including by fellow laureate Donald Knuth, who has stated it is his favourite algorithm. It is simply called “Tarjan’s Strongly Connected Components Algorithm.”
Strongly Connected
Tarjan’s work concerns graphs – networks of nodes (points) and arcs (lines), which can be used to model the connections in computer networks, as well as many other real-world and abstract systems. In particular, Tarjan’s algorithm concerns directed graphs – ones where the connections between nodes are ‘one-way streets’, denoted by arrows pointing from one node to another, along which you can only travel in one direction.
Given a graph like this, a reasonable question you might want to answer is, which bits of the graph can I get to from which other bits? Generally, mathematicians consider graphs in terms of their connected components, which, as the name suggests, are regions of the graph that are connected to each other. Two unconnected sets of nodes can be considered part of the same graph: For example, if you’re modelling friendships within a school classroom, you might find two completely separate groups of people none of whom are friends with anyone in the other group.
When your graph has directed arcs, we can go one better and divide the graph into strongly connected components – even within a region of the graph with lines between the nodes, you might not be able to actually get to some of the nodes. For example, if there’s a node which only has an arrow coming out of it, you’ll never be able to get to there from anywhere else in the graph.
We consider the strongly connected components of a graph to be those subsets of the nodes in which all nodes can be reached from all others, by travelling along some set of arcs. We can divide a given graph up into its strongly connected components, which will be disjoint (not overlapping) and will cover the whole graph. For example, in the graph below, we have two strongly connected components, the left and right halves of the graph.
Knowing what the strongly connected components of a graph look like allows us to understand the behaviour of things moving on this network – the directed arcs could represent hyperlinks on the web, one-way streets on a city map, or wires in electronic circuits, and these components would have corresponding meanings depending on the context. We can even describe how the strongly connected components are connected to each other, in the form of a simpler graph showing the overall structure.
Searching by Algorithm
As Tarjan explained, it’s easy to look at ‘human-scale’ graphs like the one above and see the components visually; in ‘internet-scale’ examples, where you might have billions of nodes and trillions of arcs, you need a more thorough method to determine where each component lies – an algorithm, which given a graph will return the list of connected components.
It’s also often the case that graphs in this type of computation are defined implicitly – instead of having a picture of the whole graph we can look at all at once, we consider a single node and can just compute the arcs coming out of that node. This means an algorithm needs to work sequentially, starting from one node and asking simple questions each time.
Tarjan’s algorithm is based on a type of search called a depth-first search – given a starting point, you choose a path to take, and continue choosing an onward path from the node you visited most recently until you can’t go any further; only then are you allowed to take a step back and try out other paths branching off the one you chose.
Tarjan compared this to Ariadne’s golden thread from mythology – she gave it to Theseus in order to help him find his way through the maze where the Minotaur lived, and he paid the thread out on the way into the maze, allowing him to follow it back again. Tarjan’s algorithm involves numbering the nodes as you go along and placing them in a stack, allowing you to recall the order they were visited in, much like a piece of thread.
The algorithm is defined recursively – performing a depth first search from a particular starting point involves checking which of the adjacent nodes have already been visited, and if there’s one that’s unvisited, visiting it and then performing a depth first search from that node. It sounds like a never-ending loop, but once you’ve visited all the nodes in the graph, the search is complete and in the process it will have built up a description of the structure.
How it works
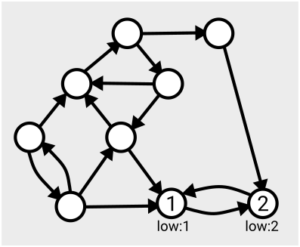
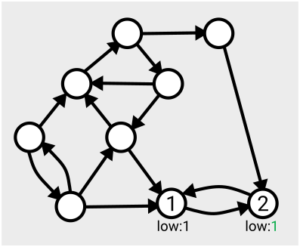
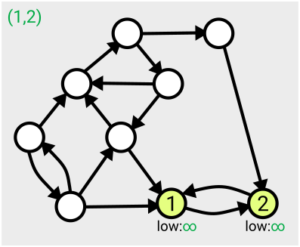
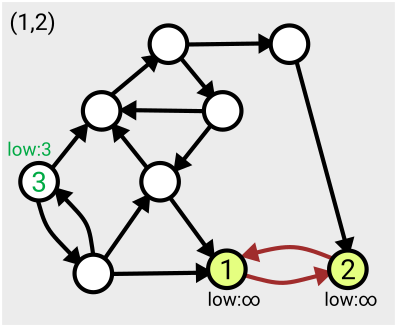
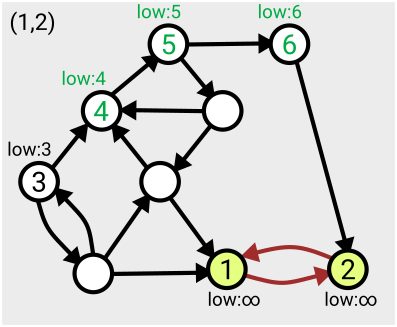
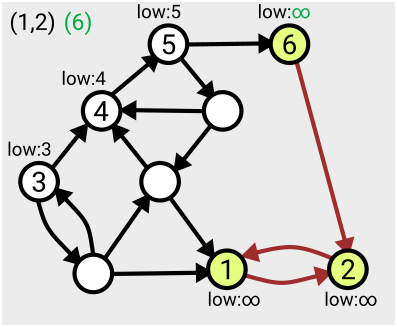
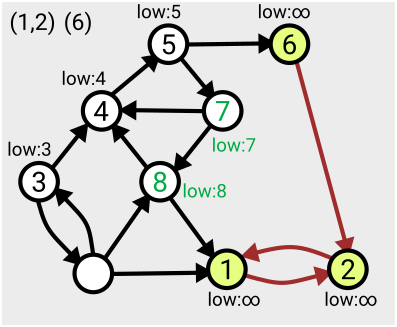
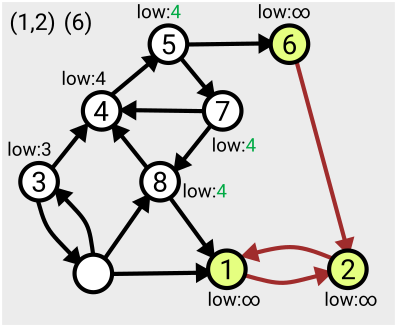
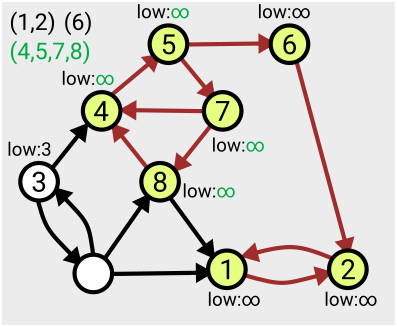
The algorithm can start from any point on the graph, and the first time each vertex is visited, it’s assigned a number in order from 1. As you search across the graph and find yourself within a particular strongly connected component, you’ll eventually find you’ve visited all the nodes within that component (since by definition, they’re all reachable from each other).
The algorithm makes use of a value denoted ‘low’ assigned to each node; this tracks the smallest ‘low’ value of an already-numbered node you can reach from that node. This value is initially set to be equal to the number of the node itself, and is updated for each node as the search proceeds and the layout of the graph becomes more apparent.
When you find that all nodes reachable from your current position have been assigned the same ‘low’ value, that means you’ve found the whole component – from each one you can roll back along the path to the point you entered the component (the lowest-numbered node), referred to as the ‘leader’.
This means you can then take that section off the stack, record it as one of your connected components, and then ‘remove’ it from the graph (by setting the ‘low’ values to some large number, effectively infinity, so it won’t be considered again).
Here’s an example of the first few steps of the algorithm in action, based on the one given in Tarjan’s slides:
The algorithm runs in linear time, which means the number of computations needed to complete the search is just a multiple of the size of the graph (measured as the number of nodes plus the number of arcs); so if your graph gets twice as big, it’ll take twice as long to run. Tarjan acknowledges that there’s an open problem to find ways to parallelise this work so it can be completed more quickly.
It was both refreshing and inspiring to hear someone talk about work they completed so long ago, and to know that this is an area people are still working on. Tarjan gave another example of an open problem: to find the largest set of arcs you can remove from a directed graph that’s strongly connected and have it remain strongly connected. An algorithm to compute this exists, but could be faster.
The Q&A for the session turned up some other sobering thoughts from the laureate. While he acknowledges it’s important to design algorithms well – with reference to Paul Erdős’ ‘Book of Mathematics in the Sky’, containing the perfect algorithms everyone is striving to obtain – he also emphasised the importance of keeping algorithms simple. While this does lead to a trade-off in efficiency, this isn’t so much of a problem if the network you’re searching is small – he recommends using the simplest algorithm that’s feasible for the context you’re working in.
Tarjan seems excited about the potential of modern computers, especially compared to the clunky ALGOL and punch card-based systems he was using when he originally came up with the algorithm – where mistakes were penalised with long waits to run the program again. In his own words, “The faster computers get, the more design space we have to play with these beautiful ideas.”


Quote from Robert Tarjan: “The faster computers get, the more design space we have to play with these beautiful ideas.”
My objection: Many algorithms were developed on paper alone and it even applies: just because an implementation of an algorithm provides the right results for some test examples does not yet mean that the implementation is correct. That an algorithm is correct must be proven, not calculated.
However, with faster computers that have complex memory hierarchies, something new comes into play: The runtime no longer depends solely on the logic of the algorithm, but also on how many memory accesses the algorithm requires and whether access is made to consecutive places in memory or to distant places in memory. Finally, the parallelizability of the algorithm is also becoming increasingly important, because today’s large and fast computers have many parallel computing units.
Overcoming the semantic gap
Any good C++ or Java programmer can implement and get the algorithm “Tarjan’s Strongly Connected Components Algorithm” described above by Katie Steckles in C++/Java and make it work. But today’s artificial intelligence programs can’t do that, because they only understand Katie Steckles’ text superficially. Today’s so-called language models can answer many questions they are asked about the text. But their understanding is not enough to implement the algorithm in a real programming language. By the way, the same applies to many less competent programmers who lack knowledge of data structures such as stacks, for example.
Real intelligence ultimately means the ability to establish connections between distant things. This requires knowledge, experience and logical thinking. Even the best AI programs are not yet close to a trained person in this respect .