New shape discovered – right under your nose

Mathematics is a very old discipline, and many of the techniques, ideas and theorems we use today were developed or discovered hundreds or even thousands of years ago. A nice example of this is that of 3D solids – the earliest regular solids were studied by the Pythagoreans in the 6th century BC (and it’s suggested they’ve been known of even longer than that), but over the centuries more and more shapes have been added to our knowledge, and many of them fit neatly into sensible categories.
Throwing shapes
The simplest and most regular type of solid is named after Plato – Platonic solids are convex 3D shapes consisting of one (regular) shape of face, and one type of vertex. That is to say, every face looks the same, and must be a regular polygon (with all its sides the same length and all its angles the same), and every corner where faces meet has the same number of faces joining there. This Numberphile video includes a proof that this set of restrictions only allows for five possible shapes – the tetrahedron, octahedron, icosahedron, cube and dodecahedron.
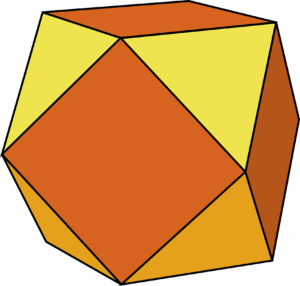
If we relax the condition that all the faces have to be the same shape, we can make Archimedean solids – these have faces which are all regular polygons, meeting at identical vertices, but include more than one type of face – for example, the cuboctahedron (right) has square and triangular faces, with two squares and two triangles around each corner.
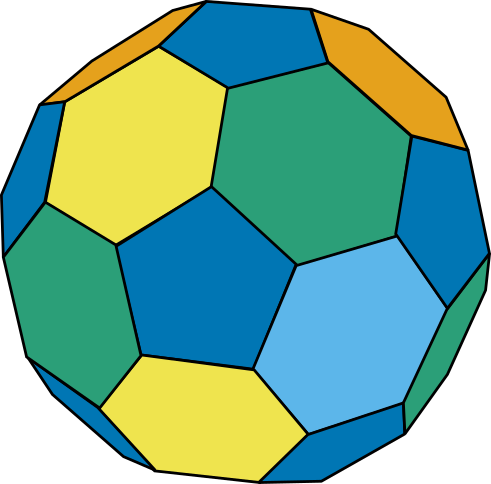
There are 13 solids which fit the strict definition of an Archimedean solid, including the truncated icosahedron (classic soccer ball shape, left). It consists of 12 pentagons and 20 hexagons, and is made by taking an icosahedron, and slicing off each of its corners (where three triangles meet) leaving a hexagon.
This is a nice way to discover new shapes – once you have basic shapes like the platonic solids, you can truncate them (cut bits off) or stellate them (add a pyramid to each face) to create new ones, and basically all of the Archimedean solids seem to be made by truncating something else.
If you further relax the requirement that all the vertices look the same (but still need it to be a convex shape with all sides regular polygons), you get the Johnson solids – there are 92 such shapes, including square-based pyramids, cuploae, and various shapes made by truncating bits off other known solids and then sticking cupolae on other bits.
The list of known shapes doesn’t stop there – it also includes prisms, whose long sides can be any length; solids which aren’t made up of regular polygons, and whose arrangement of faces isn’t uniform; and solids which aren’t convex, so they have parts where vertices point inwards, are all part of the rich tapestry of 3D shapes. Mathematicians have spent centuries enjoying cataloguing, sketching and building 3D models of them all – including Nat Alison, who’s made this brilliant polyhedron viewer, with 3D models and the ability to truncate, stellate and otherwise manipulate shapes to your heart’s content.
That’s about the shape of it… or is it?
But just when you thought it was safe to close the door of the glass cabinet containing your collection of 3D mathematical solids – think again! Despite the earliest 3D shapes being thousands of years old, it turns out we’re still discovering new ones today. Biologists studying the shapes of human epithelial cells (cells making up skin, and the linings of internal organs) have discovered a new type of prism, called a scutoid.

To define a scutoid, we can start with a regular old sensible prism – imagine two parallel faces, at the top and bottom, made of whatever shape you like, and then lines joining the two faces, running from the corners of the top shape to the equivalent corners on the bottom shape.
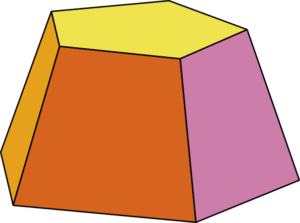
If we have both the shapes the same, and lined up directly above one another so all the lines run totally vertically and all the side faces are rectangles, this will make a boring old prism. If we let the shapes at the top and bottom differ in size, so the edges are no longer vertical, the shape is called a frustum – a general term for any solid made by cutting off some kind of pyramid leaving two parallel planes at the top and bottom.
Each of the faces of a frustum must be a trapezium, as there are the same number of corners on top and bottom to join with lines, but they’re just further apart at the bottom. If we allow the shapes on top and bottom a bit more freedom – rotating slightly, or being more irregular, so the sides are still quadrilaterals but can be trapeziums or parallelograms, we get a prismoid.
But if the number of corners on the top and bottom shapes is different, or if it’s rotated enough that a corner is now above an edge, we’ll need a way to deal with this. This puts us in the much broader category of prismatoid – in this case, it’s possible for one or more of the side faces not to be a quadrilateral, but be a triangle.
This category includes antiprisms, where the top and bottom faces are the same but oppositely oriented, so each corner is above a side and vice versa, and all the faces around the side are triangles; cupolae, where the faces round the side alternate between squares and triangles; and basically any other arrangement if the number of edges on the top and bottom shapes are different. The only real requirement is that all the vertices of the shape sit in one of the two parallel planes at the top and bottom.
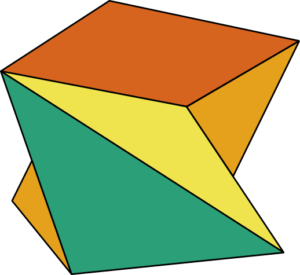
Scutoids
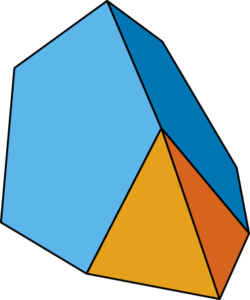
The new shape that the biologists discovered does have parallel faces at the top and bottom, but doesn’t require all the vertices to lie in those planes – you can have extra ones, part way up, making a Y-shape of edges. So, two points on the top shape can join together and form a single edge running down to the bottom. The number of possible such shapes is huge, and when packed together in groups, scutoids can fill 3D space.
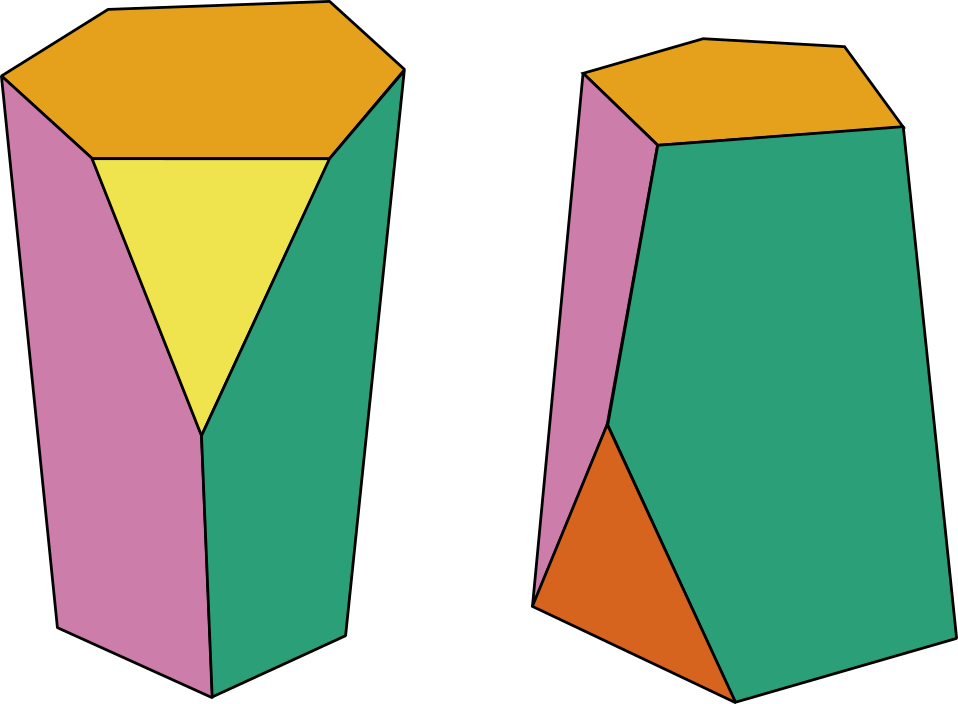 A research team based at the University of Seville in Spain found that when they tried to model what shape the cells in epithelial surfaces might be, standard prism shapes worked well for flat surfaces – but when the skin is curved (like literally all skin is) they would get a more efficient packing using scutoidal shapes packed together.
A research team based at the University of Seville in Spain found that when they tried to model what shape the cells in epithelial surfaces might be, standard prism shapes worked well for flat surfaces – but when the skin is curved (like literally all skin is) they would get a more efficient packing using scutoidal shapes packed together.
Having looked under a microsope, the team confirmed that cells found in fruit fly salivary glands and cells in zebrafish were actually scutoidal, and their theory was correct. The new shape, which hadn’t previously been given a name, was termed a scutoid as it resembles the scutellum of a beetle, which has a small triangular region near the top.
Their paper, published in Nature on 27th July, includes many diagrams of how such cells pack together, and describes how they discovered this ‘novel geometrical solid’.
Mathematician Matt Parker has made a video about it, setting himself the challenge of building his own scutoid from household materials, as well as chatting to one of the mathematicians involved in the project (and discovering some secret facts the press weren’t told about the origins of the shape’s name!). He’s also spoken to 3D printing expert and mathematician Laura Taalman, who’s made a 3D printable version of the scutoid you can download on Thingiverse.
It’s fantastic to see the way mathematics and biology can work together to describe and explore this kind of biological structure, and both reassuring and slightly scary to know that no matter how much work we do, there’ll still be new mathematics out there waiting for us.


Good post on shapes.
Katie
I’m impressed, great !
…was auch nicht verwundert, denn die Mathematik meint die (formalisierte) Fähigkeitslehre, sie ist Voraussetzung für die wissenschaftliche Arbeit, sie ist eine sehr früh aus der Philosophie herausgelöste Fachdisziplin.
Die Mathematik ist sozusagen direkt der Umgebung und dem Leben (vgl. mit ‘It’s fantastic to see the way mathematics and biology can work together (…)’) geschuldet.
Was abär auch bedeutet, dass andere Mathematiken denkbar und somit möglich sind, was an dieser Stelle aber nicht weiter interessieren muss.
MFG
Dr. Webbaer
Bonus-Kommentar hierzu :
Fairerweise ist die Topologie recht offen, in n-dimensionalen Räumen, und insofern ist Form insbesondere dann von Interesse, wenn ihre Bildung, die Formbildung, Nutzen zeigt, so dass auch eigene Begrifflichkeit zu bilden ist.
Womöglich ist aus unklaren Gründen beim Schreiber dieser Zeilen beim Geschilderten insofern keine Faszination entstanden, nicht hier und jetzt, im Sinne von “Muss ich haben!”.