Jack Dongarra – A Not So Simple Matter of Software
BLOG: Heidelberg Laureate Forum

Jack Dongarra is the recipient of – among many other prestigious prizes – the 2021 ACM A.M. Turing award, which he received “for pioneering concepts and methods which resulted in world-changing computations.” Hearing him talk about his work on high-performance computing and the developments he has been a part of over the years, it is easy to understand why he is so well-regarded.

Jack Dongarra. © Heidelberg Laureate Forum Foundation / Kreutzer
As part of his laureate lecture at this year’s HLF, Jack Dongarra gave a detailed history of high performance computing, starting from his first job working at a lab for the US Department of Energy in Argonne. He admits he was originally considering becoming a science teacher – and wasn’t even planning on further study – but the opportunity for a semester working in the lab set him on a different path in life: he found the experience “transformational.”
Getting to the point
The basic operation a computer performs – often called a floating point operation or FLOP – involves the addition or multiplication of two numbers. The term ‘floating point’ means the numbers are stored in a format where the decimal point can be in any place. So, using enough bits of information for 10 digits, I could store a large number like 8374455665000000000, or a very precise small number like 0.00000007482133221 or something moderately large and fairly precise like 2234.412253. As long as there’s only 10 non-zero digits, this format can store the whole number.
The ‘floating point’ means precision can be flexible depending on what’s needed. Using the same amount of computer storage space, we can record the distance between galaxies or the diameter of an atomic nucleus. In practice, the number is stored in standard form – a ‘significand’ which takes a value between 0 and 10 (like 8.374455665 in the first example above), and an exponent, indicating which power of 10 to multiply by to get the number (in the example, this would be 18).
Dongarra’s work at Argonne involved using computers to calculate the answers to scientific questions, and this required linear algebra: computations with vectors (lists of numbers) and matrices (rectangular grids of numbers). Basic computations might involve adding or multiplying two numbers together – but if you’re computing the outcomes of a complex system or model you need linear algebra – which involves multiplying or adding a lot of pairs of numbers.
Multiplying two numbers together uses a single operation. But if we have a vector of 10 numbers, and we want to multiply them all by another number, that’s 10 operations. If we have two vectors of 10 numbers and want to add them together, that’s also 10 operations – but if we want to know the product of each number in one vector with each one in the other vector, that’s 100 multiplication operations.
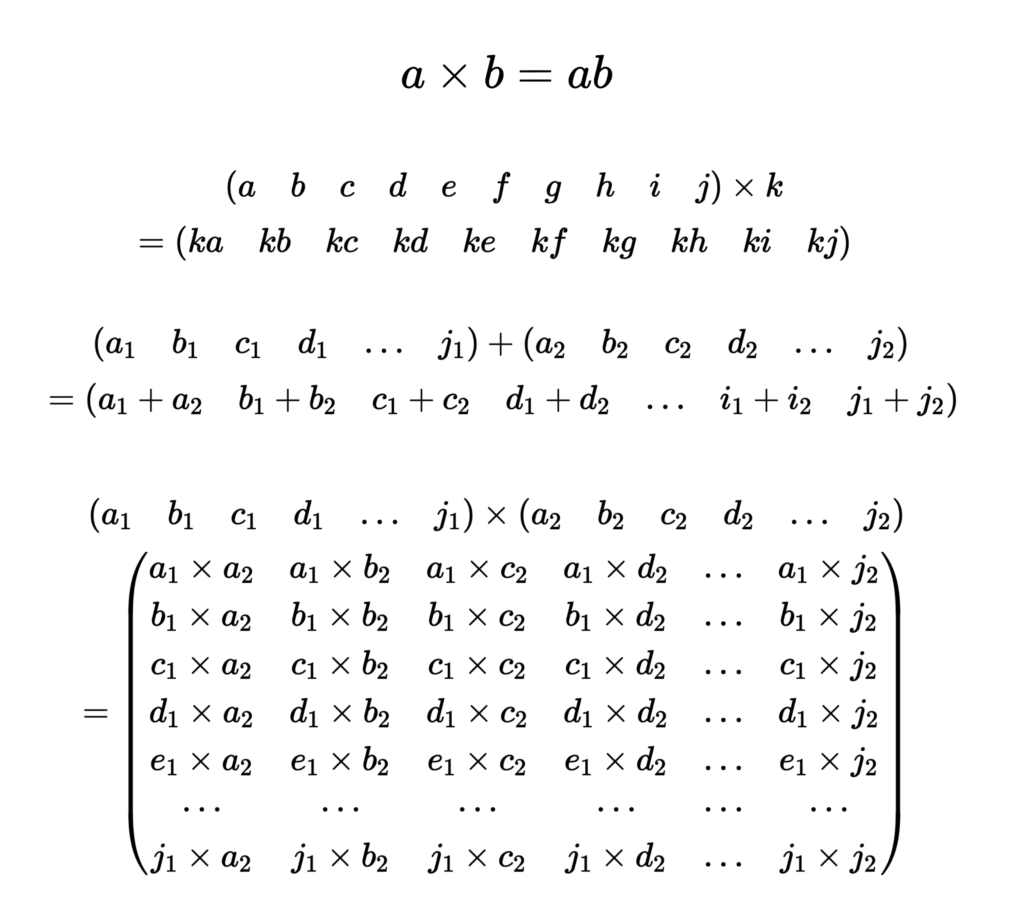
The number of calculations required to compute things is known as the computational complexity. If you have two matrices and want to multiply them together, this involves multiplying each entry in one row of the first matrix by an entry from one column of the other, and then adding them together. The resulting matrix has entries in each row and column made from the corresponding row of one matrix and column of the other. For two $n$ by $n$ matrices, this requires $n^3$ multiplications and $(n-1)n^2 additions.
But this is the maximum you might need to do this; more efficient algorithms have been developed that can multiply matrices together using fewer operations (depending on the size of the matrix), including the Strassen algorithm, and the Coppersmith-Winograd algorithm. It’s an active area of research, and as recently as 2020 a new algorithm by Josh Alman and Virginia Vassilevska Williams was published that uses even fewer operations.
The origins of LINPACK
Dongarra explained that his work involved such algorithms: for manipulating, multiplying and finding properties of matrices. He was part of the team that developed LINPACK, a software library written in the programming language FORTRAN and used for performing numerical linear algebra calculations, like these matrix operations.
He also worked on sophisticated architectures for pipelining overlapping operations, allowing complex calculations to be parallelised and made faster. Dongarra described ways to parallelise operations based on directed acyclic graphs – tree structures which allow different processes to proceed in ‘threads’, which split and merge as needed to complete the computation, improving overall efficiency.
But the efficiency of your algorithms and software is irrelevant if the machine you’re using it on isn’t fast enough to process it. Since the early 1970s computer hardware has changed tremendously. Dongarra treated us to a rundown of the history of computer architectures, from the CDC 7600 – which ‘fell over’ (crashed) four times a day – and early IBM models, through to today’s top-performing systems.
In the original manual for LINPACK, Dongarra included a section at the back listing 23 standard computers of the time and how long they’d take to perform a calculation – to allow users to determine how fast their machine was at performing operations.
The LINPACK Benchmark, as it was known, involved getting a computer to decompose a 100-by-100 matrix into two triangular grids of numbers which could be multiplied back together to get the original matrix. This uses a process called lower-upper decomposition, and it allows for the hundreds of simultaneous equations the matrix represents to be solved. The short list in the back of the manual allowed users to benchmark their own systems, by performing the same calculation and timing it.
But over time this grew into something larger: newer versions of the benchmark asking for larger matrix calculations – 300-by-300, or 1000-by-1000 – with more complicated computations, versions incorporating parallel operations, and eventually leading to High Performance LINPACK (HPL), which could be used for benchmarking real high-performance computers and testing them to their limit.
Top of the Flops
In the early 1990s, Dongarra was persuaded to join a new project developed at the University of Mannheim – called TOP500 – with the aim of creating a new definition of ‘supercomputer’. HPL became the benchmark used to track the top machines in the world, producing a biannual list of the 500 fastest computers in the world. Early list-toppers were operating in teraflops (trillions of operations per second).
This list continues to be produced today, and Jack Dongarra’s work is at the heart of it. It’s a goal for hardware manufacturers to strive for and has allowed us to track the increase in performance of top computers across the world. This cutting-edge technology has largely mirrored the predictions of Moore’s law (that computer performance will double roughly every 14 months) – the top machine in 2018 is roughly 1,432,513 times faster than the equivalent from 1993.
Dongarra admits this list isn’t a perfect measure. He acknowledges that they could have picked a smaller number than 500 as the number of machines to track – he estimates half of the performance of computers in the list is held by the top 10 machines, so a list of 50 or even 20 might have been easier to maintain and would tell us the same thing. But there’s another reason why this benchmark might not be telling us the whole story, and that is because the number of operations a computer can perform (FLOPS) isn’t the only important factor.
In order to perform a computation, he explains, as well as the actual processing of the computation, the system needs to move the pieces of data it’s processing into and out of the working memory of the computer, from the computer’s storage. The rate at which these ‘word movements’ can occur isn’t keeping pace with the processor, meaning it’s limiting the speed of computations.
Raw benchmarks like this also don’t take into account the different applications computations are needed for. Indeed, some industries build custom architecture for the applications they want, which works in a way specific to the types of calculations they’ll need to do, while the high-performance computing industry mainly uses commercialised processors and strives to meet the benchmarking tests, even though they may not be representative of what is needed for scientific computing.
Dongarra was also keen to point out that he’d be in favour of a more holistic approach to computer development generally. He described the process he had seen happen time and again over the years: the ‘hardware guys’ build something new and throw it ‘over the fence’ to the software developers. They then spend four or five years developing the software to make best use of the new hardware, by which time a new machine has been developed.
Something needs to change, said Dongarra. While he agrees that it’s exciting to see the development from teraflops and petaflops into the recently achieved exaflops – and potentially even zettaflops (a staggering 1021 operations per second), he also wants us to optimise better. How can we influence manufacturers not to just keep striving for better performance against benchmarks, and instead to co-design systems along with scientists and industry?
Scientific computing and high-level industrial applications are the main users of these extremely powerful machines. Dongarra hopes that by working together, we will be able to use this technology to keep doing incredible things.
Jack Dongarra’s lecture at the 9th HLF, as well as the entire scientific program, can be viewed on the HLF’s YouTube channel.


