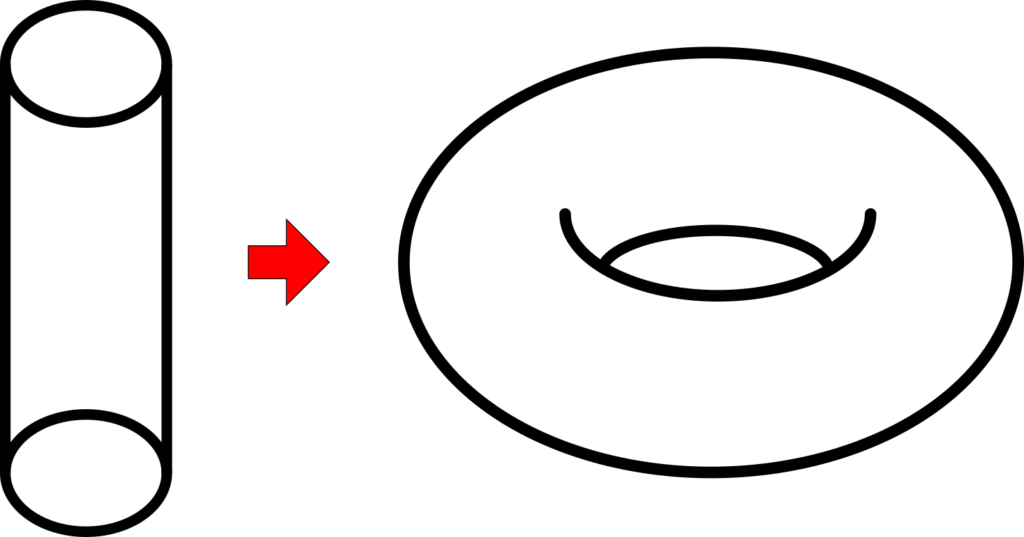
While it might seem like a boring shape, the humble square can be a source of many interesting mathematical structures. For example, if you bring the sides around and join them in the middle, you can form a cylinder. Considering it as a mathematical object, we have definitely created something new – the cylinder is obviously different to the square we started with.

It has a hole down the middle, and instead of having one open edge around the outside, it now has two separate open edges, one at the top and one at the bottom.

Continuing to modify the square in this way leads to several more interesting mathematical shapes.

Ringing the Changes

If we want to make things more interesting, we could consider what happens if we join the top and bottom of the square too – sticking the left and right edges first gives a cylinder, so then proceeding to stick the top and bottom edges is equivalent to glueing the two ends of the cylinder together. As I recently discussed in my post on Gaussian curvature, this would not necessarily be easy to do with a paper cylinder, since rolling it one way stops it curving the other way – but if it were a rubber square, we could bend it round and stick the ends of the tube together.

This would give us a new kind of surface – a donut shape, called a torus – which has no open edges at all, but has a different hole through its middle. Toruses are hugely important shapes in the mathematical field of topology, and any simple shape with one hole in it can be considered equivalent to the torus: this is the origin of the hilarious joke about how a mathematician cannot tell the difference between a donut and a coffee cup. Since explaining a joke always makes it funnier, I can clarify that this is because both have one hole: the hole in the torus, and the handle on the cup (the part you put the coffee in is not technically a hole – it is more of a large dent).

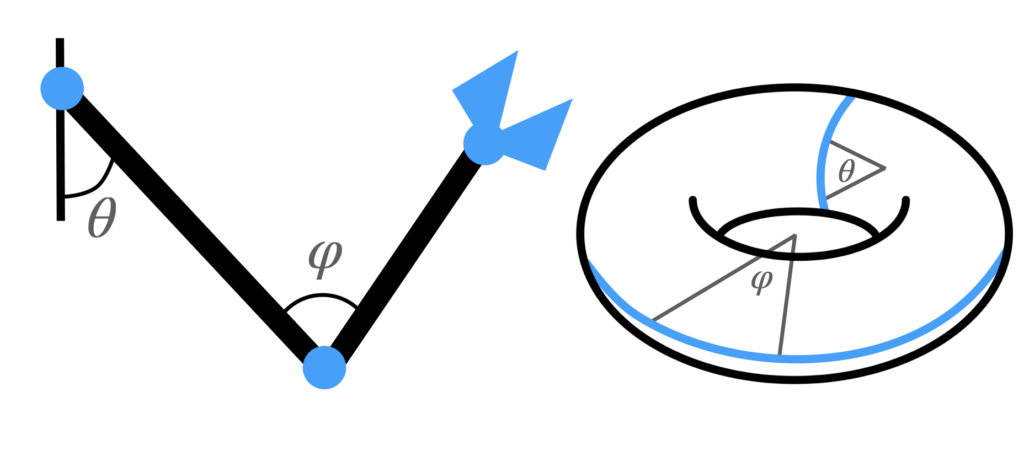
Since they are effectively a circle stretched out around a second circle, toruses can also be used to model two-dimensional spaces of possibilities: for example, a robot arm with two hinged elbows, moving in a 2D plane, has a range of possible positions it can be in, corresponding to the angles each of the two joints are set to. Each possibility corresponds to one point on the surface of the torus, given by one angle determining the distance around the torus, and the other the distance towards the centre hole.

Drawing Conclusions

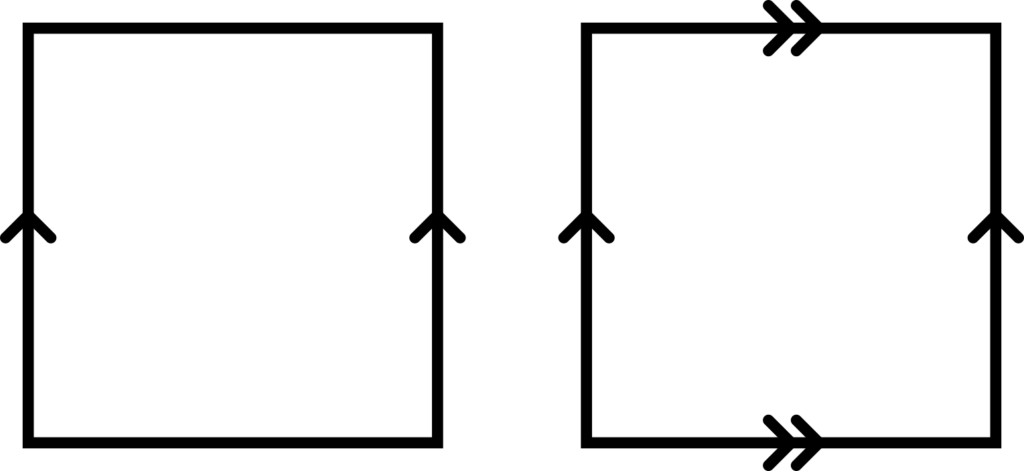
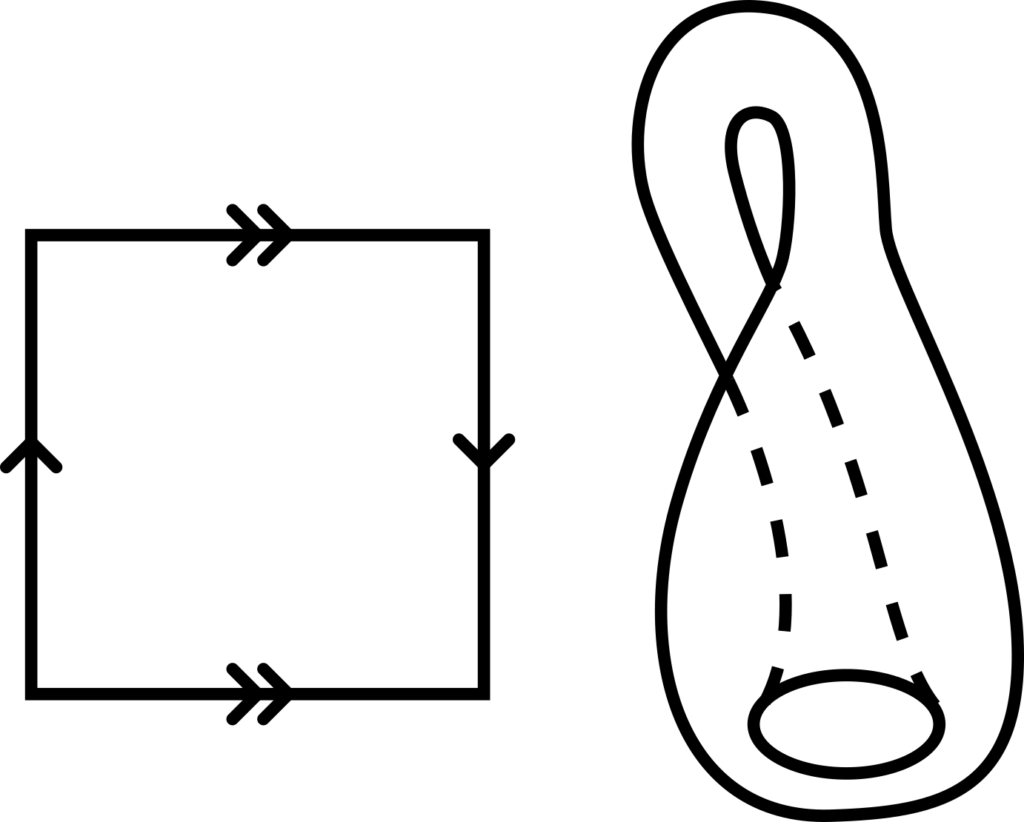
The mathematical way to represent these shapes is using an identification diagram – we say that the edges which have been glued are identified with each other, and we denote it using an arrow, or a pair of arrows (if we have a second pair of edges, to determine which pairs go together) to indicate the edges are stuck that way round. Below are the diagrams for a cylinder and a torus.

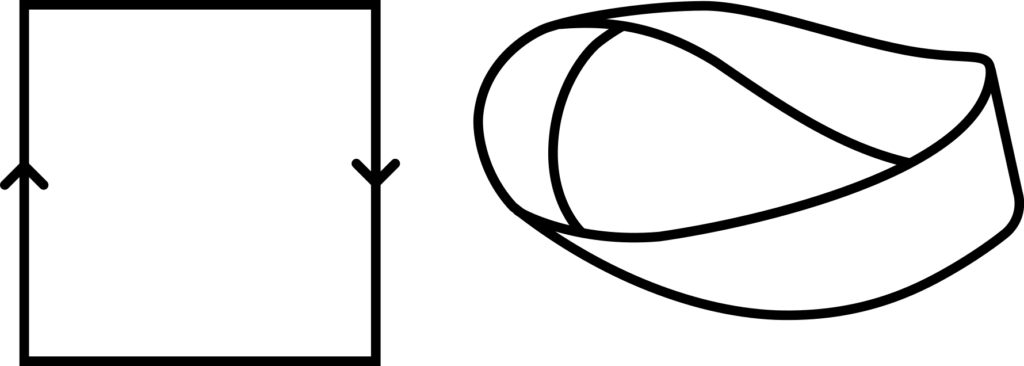
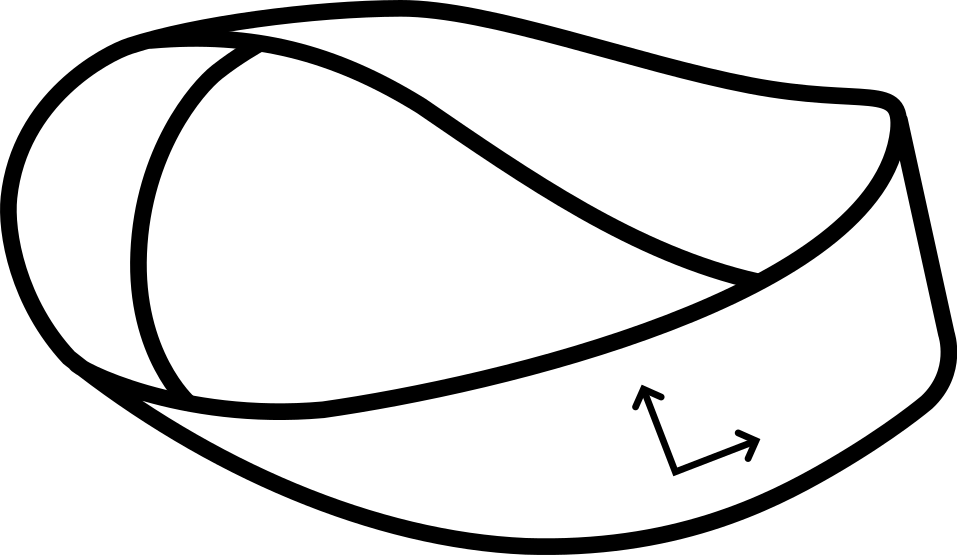
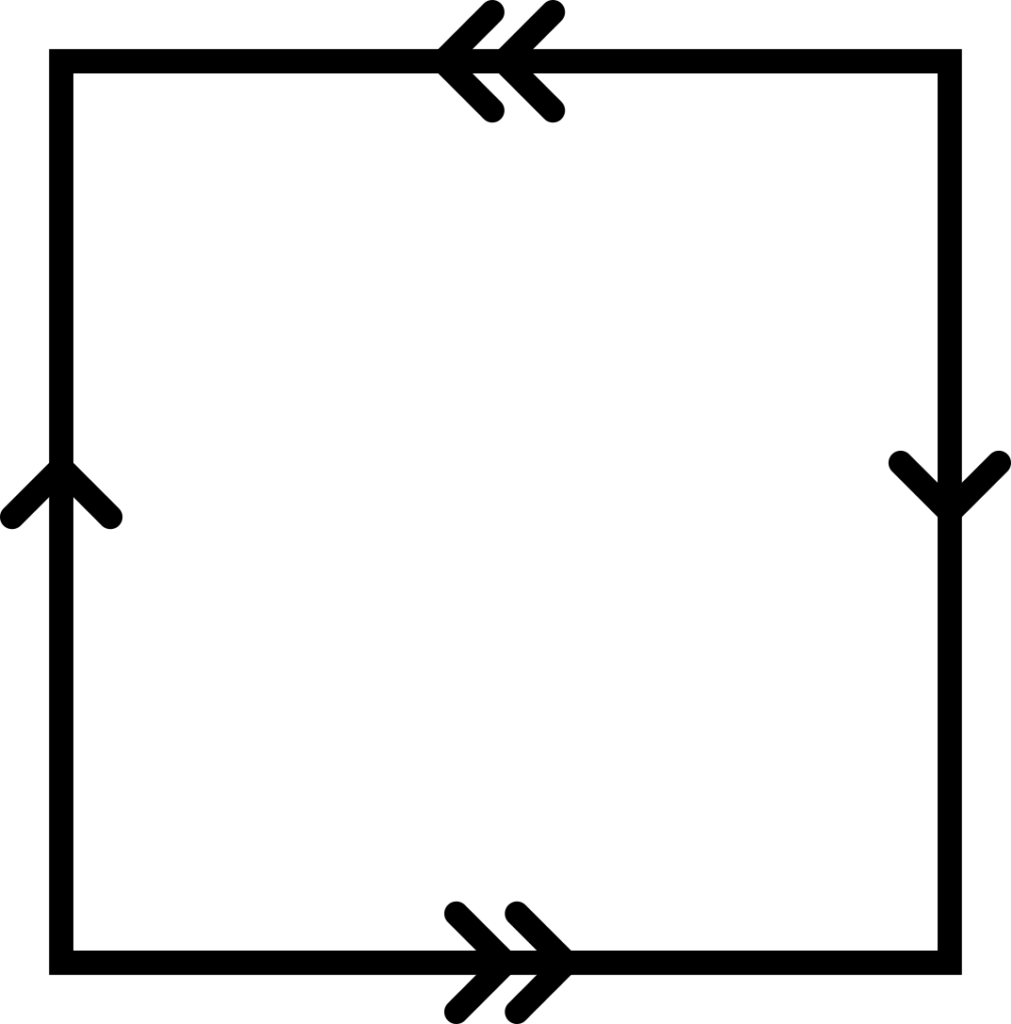
Presenting the shapes in this way presents an intriguing additional possibility: what if the arrows were not pointing in the same direction? Applying this to our cylinder gives us a shape with some very interesting topological properties: the Möbius band. This can be made from a simple square piece of paper (although in practice, you will need to stretch your square so it is much wider than it is tall) by joining the ends with a twist.

Named after the mathematician August Möbius, this shape has some curious properties, which can be easily explored if you have a paper one in front of you. For example, if you draw a line down the middle of the strip, it becomes apparent that it is possible to draw a line all the way along both sides of the paper without lifting off the pen. This makes sense if you consider that in adding the twist, we have joined the front of the paper to the back – so this shape has only one side.

The next twist (pun intended) comes when you try to cut the band in half along this line. Since most well-behaved objects, on being cut in half, obligingly become two separate pieces, it can be surprising to discover that the twist has also made the Möbius band have only one edge, meaning when cut in half it uncurls into one long loop, rather than splitting in two as you would expect. The resulting shape (which is actually a two-twist Möbius band) has two edges, one of which used to be the outside edge of your band, and the other of which was created by your cut.

There are plenty of other fun things to do with a Möbius band – some of which can be seen in this classic video by Stand-up Mathematician Matt Parker – but topologically it is a fascinating space. Mathematicians like to compare the local properties of a shape with the global ones; locally – looking at a small section of the strip – it is identical to a cylinder. It is only when considered as a whole that the twist becomes apparent.

Another nice property of the band is that it is non-orientable: if we tried to define a coordinate system on it, it would be inconsistent. Imagine drawing a pair of axes at right-angles to each other, then following one of the axes along the length of the strip. When you return to the point you started, your axes will be upside down, due to the twist – so it is impossible to define a consistent orientation.

Another Dimension

You might well be wondering what happens if we try to combine these two approaches: what would a Möbius torus look like? If we join two edges of the square, then try to join the other two edges with a twist, we find a slight problem: it is only possible to do this if we allow the shape to intersect itself and join on from the inside. Assuming this is permitted, we can create a shape called a Klein bottle: a tube which curves round, passes through itself and joins back on to the other end but from the inside.

Named after mathematician Felix Klein, this shape has similarly interesting properties to the Möbius band: it is non-orientable, and has only one surface. An ant standing on the outside of the shape could walk to the opening of the tube, crawl into the hole and follow the tube back out through the side, so they are walking on the inside of the part they were previously on the outside of. If you cut a Klein bottle in half, you get two Möbius bands, but if you cut one in half in a different direction, you get one Möbius band.

The self-intersection needed to make this shape work feels like cheating, but that is only true in 3 dimensions – if we are allowed to extend up into 4D the shape behaves itself perfectly, and connects up by just ‘going around’. In the same way that it is impossible to draw a 2D diagram of a knotted piece of string without a line crossing itself somewhere, it is impossible to perceive a 4D shape like a Klein bottle in 3D space without it intersecting itself.

There is one final combination we have not considered: putting a twist in both directions gives a shape called the Real Projective Plane. Also a 4D shape, it has to self-intersect to exist, and is incredibly hard to visualise. My favourite way of picturing it is to imagine a sphere with a hole in, and then glue a Möbius band’s edge (which it has only one of) along the edge of the hole.

If you’d like to try to picture this, here is an animation based on a video by Jos Leys, which shows the edge of a hole in a sphere being joined up Möbius-wise, intersecting itself in order to do so. This gives a shape known as a cross-cap, which is equivalent to the real projective plane and one possible way to embed it in 3D.

In fact, since this is topology and we are allowed to stretch things as long as we do not change their shape, we can consider even more possible presentations of the space. For example, if you were to take each point on the surface of a sphere and glue it to the point directly opposite, doing this for all the points simultaneously, the shape would need to intersect itself, and it would result in another object that is equivalent to the real projective plane. Notionally, this would be a space of points containing one point for each pair of opposite points on a sphere – we can think of it as having a point for each possible direction in 3D space, which is why it is useful for modelling rotations in 3D.

Starting from just a simple square, we can produce many interesting shapes with interesting and useful properties. Topologists love playing around with squares, and hopefully you can see why!