Building Blocks


A friend of mine recently kindly made me a present, using their 3D printer – a puzzle made up of 21 pieces, three each of seven different shapes. The statement of the puzzle is as follows:
“Can you arrange the pieces into seven groups of three so that for each possible pair of shapes, there is one group containing that pair?”
That is, I need to find a way to arrange the 21 pieces into 7 groups, so that if you name any two shapes, I can point to a group (and only one group) which contains those two pieces. The pieces are mounted on bases shaped like thirds of a circle, so groups of three fit together nicely, and we’ve had a lot of fun coming up with names for the seven shapes.
It’s an interesting puzzle, and it took me a few minutes to work out a solution – mostly by trial and error. I first noticed that it didn’t matter which three shapes I picked to put in the first group, since there are the same number of each shape, so they’re interchangeable. Then I tried some other groupings alongside that, and worked backwards whenever I reached a problem.
If you’d like to have a go at the puzzle, I’ve made a PDF of 21 pieces you can cut up, with three each of seven different shapes – you’ll need access to a 2D printer and a pair of scissors.
One way to extend this puzzle is to try it without paying attention to the colours first, then once you have a solution, try to rearrange the pieces so each group has one piece of each colour in it.
This kind of problem – looking at different ways to combine things so that they satisfy statements like ‘any two shapes occur in exactly one group’ is part of a branch of maths called combinatorics. I’ve mentioned it before in a previous blog post, as it also covers counting and enumerating combinations, but this kind of problem constitutes one particular branch – and solutions to them are called combinatorial block designs.
The term ‘block designs’ refers to the fact that it’s about ways of grouping things, in such a way that specific combinations occur. For example, a group of friends planning to play a series of games together might wish to work out a set of groupings they can arrange themselves in so that they all get to play against everyone else:
6 people want to play in three teams of two, for five different rounds of a game; each round, everyone would like to be on a team with someone they’ve not been on a team with before. How can they arrange themselves?
(One solution to this problem is given at the end of the post – but see if you can find one yourself!).
One very old problem in this area, which was originally stated in 1850 and appeared in several recreational mathematics books at the turn of the century, can be stated as follows:
Fifteen people wish to arrange themselves into groups of three, with a different arrangement each day for a week, so that no two people are in the same group on more than one day.
This problem can be solved (and solutions are given on the Wikipedia page) using a block design. This is a way of splitting up a set of things, call it X, into a collection of smaller sets – called blocks – with various constraints which can be applied depending on the desired properties – including:
- Uniformity – all the blocks are the same size (the most interesting and most often studied type)
- Any element of X is contained in a specific number of blocks – which may be one, or more than one if the sets can overlap
- Any set of elements from X of a given size is contained in a specific number of blocks
For example, in the 3D printed puzzle I was given, there are 7 blocks of size 3, any one shape is contained in exactly 3 blocks (as there are three pieces of each shape) and for any set of shapes of size 2, there is exactly one block which contains that set.
In the case of the 19th-century maths problem, there are 15 people who need to be arranged into groups across all seven days – so there are five groups of three each day, and each person is in exactly seven groups, one for each day.
Then the constraint is that no pair of people are in the same group more than once. This problem has the additional constraint that the seven groups each person is in all occur on different days – the groups form a partition of the people each day, but the groups themselves can be partitioned into seven days which contain each person once.
In cases where the design needs to have combinations of things occurring exactly once, such block designs are called Steiner Systems and are denoted S(t,k,n) where n is the total number of things, k is the size of each block, and t is the size of combination that has to occur exactly once. My puzzle is an S(2,3,7) system – and so is the diagram given here.
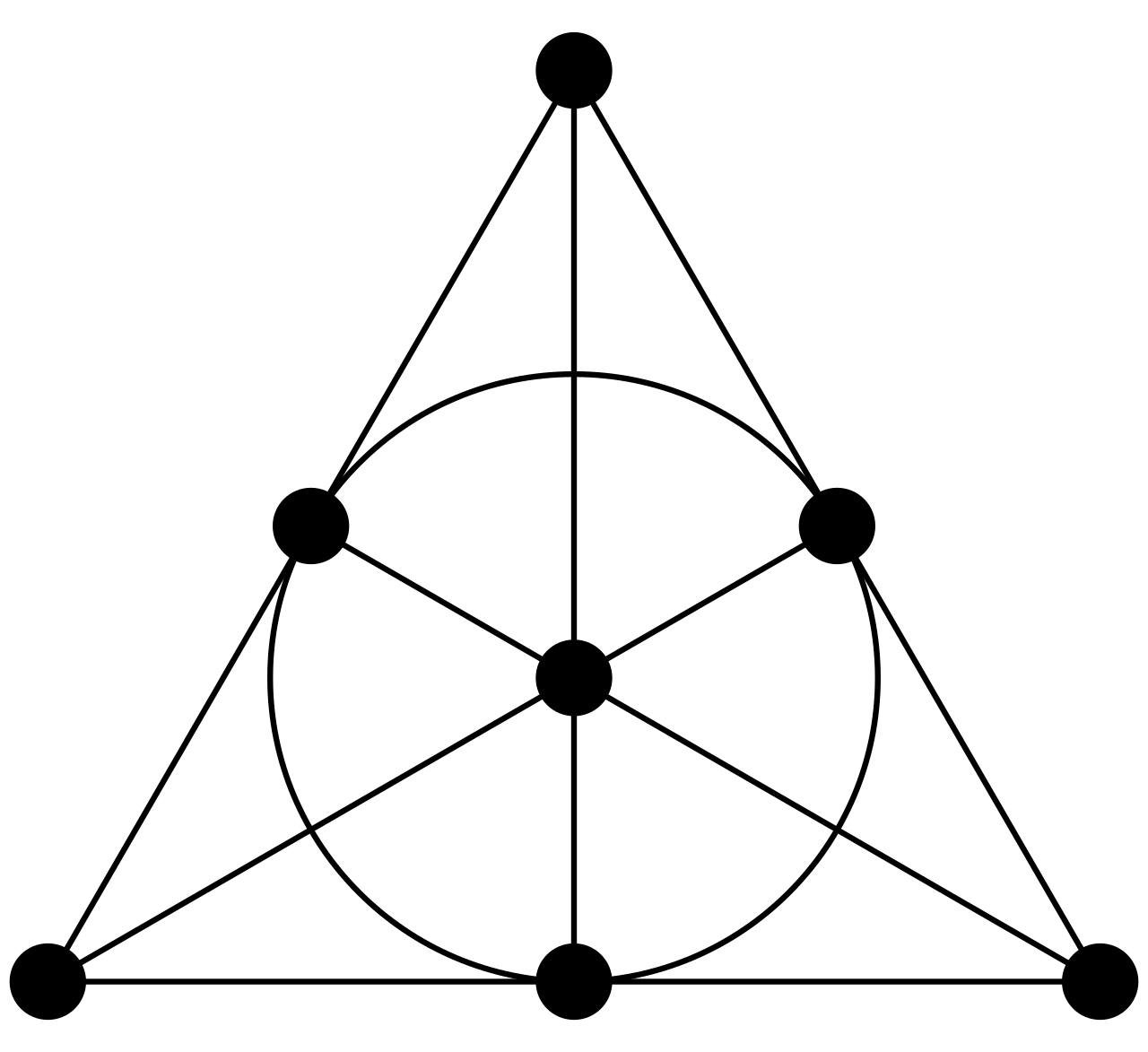
This shape is called the Fano plane, and is a visual representation of an S(2,3,7) system. It has seven points, which are arranged into lines – each of which passes through exactly three points, and any two points you can choose lie only on one line.
If you want an easy way to solve the seven shapes puzzle, or you’ve solved it and want to compare your solution to this structure, you could arrange each set of three shapes so it sits on one of the seven points – in such a way that each line has the three pieces of that shape sitting along it.
It’s possible to construct Steiner systems of the form S(2, q+1, q²+q+1) – the Fano plane is for the case q=2. There’s a chance you may also have encountered equivalent structures for other values of q – if you’re a fan of children’s card games.
Dobble (sold in some places as Spot-It!) is a simple picture-spotting game, which comes in a bright yellow and purple tin. It consists of a set of circular cards, each of which is covered in pictures of familiar objects (a car, a key, a turtle, etc.) – eight objects appear on each card, and there are various ways to play, but all involve comparing two cards and finding an object which appears on both cards.
Of course, if this game weren’t mathematically interesting, I wouldn’t be talking about it – and in fact, for any pair of cards in the game, there will always be a symbol, and exactly one symbol, which appears on both cards. In a way which has no impact whatsoever on children’s enjoyment of spotting and matching and shouting out the name of the symbol they’ve found in common, the game has a beautiful underlying mathematical structure.
Since there are 8 symbols on each card, and 57 symbols in total, it’s clear that this is an S(2,8,57) system (S(2, q+1, q²+q+1) where q=7). It also means that each symbol occurs on exactly 8 of the cards, and a quick rifle through the set I have confirms that there are only 8 cards with the turtle on.
There are various versions of the game available, including Beach Dobble – with waterproof cards, designed for use at the beach. Since this was clearly designed to be a portable version of the game, it’s got a smaller deck – but it’s still a Steiner system! Each card has 6 symbols on it, so we must have q=5; and indeed, there are 5²+5+1 = 31 different symbols, with each symbol appearing on 6 cards.
Since the whole thing is symmetrical, it’s also possible to construct 31 cards to go in this set – and in standard Dobble, there are 57 possible cards you could construct using the 57 symbols. However, for reasons unknown to mathematics, and presumably related to printing constraints, the makers of Dobble have decided to only include 55 cards in the game! Beach Dobble, with 31 possible cards, only includes 30.
This means there are two more combinations in standard Dobble, and one in Beach Dobble, which are missing from the set. Perhaps they wanted to give mathematicians the gift of an additional puzzle – to find which cards they are missing. If you’ll excuse me, I’m going to find count how many occurrences of each symbol there are on the cards, determine what the missing ones should be and design and print my own replacements. Hours of fun for all the family!
- Read Christian’s blog post about 3D printing the puzzle, including a link to 3D printing files you can use to print your own.
- One solution to the ‘six people, three pairs five ways’ puzzle from the top of the post: AB CD EF / AC BE DF / AD BF CE / AE BD CF / AF BC DE

