Abel Prize 2018 awarded to Robert Langlands

Last month it was announced that the Abel prize for 2018 will be awarded to Robert Langlands, a Canadian/American mathematician. The Abel prize recognizes contributions to the field of mathematics that are “of extraordinary depth and influence”, and is awarded annually by The Norwegian Academy of Science and Letters. The prize is accompanied by a cash award of 6 million NOK (around €625,000) and its laureates are among those invited along to the Heidelberg Laureate Forum each year – it’s widely considered to be the mathematics equivalent of a Nobel prize. So what did Langlands do that earned him this great honour?

Robert Langlands
Langlands was born in 1936 in New Westminster in Canada, and has had a long career in mathematics, working at US universities including Yale, Berkeley and Princeton, where he is now emeritus professor. His early mathematical work included studying automorphic forms – these can be thought of as a generalisation of the idea of a periodic function, one which repeats the same values (such as a sine curve). Langlands studied automorphic forms, and proved various results about them – including some on a particular class of automorphic forms called modular forms. These are a special case where the forms are defined on spaces of 2×2 matrices, and are interesting because while they’re defined and studied as part of the analysis of functions, they’re also connected with number theory.
Number theory is a branch of mathematics which deals with the whole numbers (integers). It includes investigating the properties of numbers, and particular types of numbers, such as prime numbers, or numbers that are made from integers, such as rational numbers (fractions). Number theory is quite often connected to the analysis of certain functions – a famous example is the Riemann Zeta function, which is defined on the complex plane but has deep connections with the distribution of prime numbers.
Langlands’ major contribution to mathematics was made in 1967, when he wrote a letter to French mathematician André Weil describing some of his recent insights on how to connect ideas in number theory to those in automorphic forms – called functoriality. While working at Princeton as an instructor, Langlands met Weil in a corridor on campus, and tried to explain his new ideas. Weil suggested that Langlands put some his thoughts down in writing. The letter was modest but thorough – Langlands expected Weil might readily just throw it in the bin – but it contained 17 pages of mathematical conjectures, generalisations and definitions.
This mathematics formed the basis of what became known as the Langlands Program – a collection of far-reaching and influential mathematical conjectures, relating many areas of maths from number theory to geometry. They have since formed the basis of decades of work by other mathematicians – Fields medals were awarded in 2002 and 2010 for proofs based on Langlands’ conjectures. In fact, the well-known proof of Fermat’s Last Theorem by Andrew Wiles hinged on mathematics laid out in Langlands’ original 17 handwritten pages.

Galois Theory
The Langlands program connects automorphic forms to the work of Galois. Évariste Galois (left) was a 19th-century French mathematician, who – in much the same way as Langlands – set down the basis for a whole area of mathematics, again in a single text, which in the case of Galois was written not long before he was killed in a duel. Galois’ work didn’t gain recognition until later, when others realised how much of a breakthrough it was.
Galois theory concerns the symmetry groups of polynomial equations. Given a polynomial – a sum of powers of a single variable, usually x – it’s sometimes possible to find solutions which you can substitute in for x and have the equation balance. Depending on how high the powers of x in the polynomial are, there might be different numbers of solutions possible. For example, a quadratic equation (one containing x²) might have two solutions, and a cubic equation (where the powers go up to x³) up to three solutions.
For quadratics, there’s a well-known formula which can be used to find the solutions – as every school student knows, the quadratic formula for a polynomial ax² + bx + c is given by: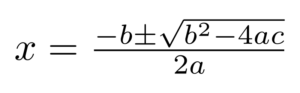 In the case of cubic equations, there exists a more complex but similar method to determine the roots. But for certain polynomials, it’s been proven that no such method exists – for example, it’s not possible to solve most quintics (polynomials containing powers up to x⁵) in this way.
In the case of cubic equations, there exists a more complex but similar method to determine the roots. But for certain polynomials, it’s been proven that no such method exists – for example, it’s not possible to solve most quintics (polynomials containing powers up to x⁵) in this way.
For polynomials in general, Galois groups are concerned with the way the polynomial’s solutions are related to each other. For example, consider the following equation:
x² – 4x + 1 = 0
This equation has two solutions: A = 2 + √3, and B = 2 – √3; either of these, substituted in for x, will satisfy the equation. The Galois group of the polynomial describes how these solutions relate to each other, and the ways you can add them together in different combinations – for example, in this case, A + B = 4 and A × B = 1, and in each of these, A and B can be swapped and the equation still holds. This is because A and B are roots which have a kind of symmetry, and the Galois group describes all the symmetries between the solutions.
Galois determined that certain types of Galois groups are possessed by polynomials that can be solved using a formula, like the quadratic equation. Galois called these groups solvable, and Galois theory proves that for all polynomials of degree 4 or lower, the Galois group is always solvable – and hence the polynomial’s roots can be found. For degree 5, some can and some can’t – but those which can are precisely those whose Galois group is solvable. In this way, the group structures are tied to the numerical equations, and Galois theory forms a connection between group theory and number theory. In a similar way, the Langlands program connects the structures of Galois theory to automorphic forms.
Langlands’ work can be seen as a bridge between two seemingly unrelated areas of maths – and increasingly many mathematical discoveries are of this nature. The fact that this kind of work can be so impactful underlines the extent to which mathematics is actually an intricate web of structures and concepts, all of which connect to each other in unexpected ways, and Langlands was a pioneer of this kind of thinking. His work in the 1960s laid the foundation for an entire field of study, and he deserves this recognition for his incredible insights.


Great ! Evariste Galois was a genius, but the best pass away first.
katie,
off topic
is it true, that many mathematician suffer from depressions?