Die Syllogismen des Aristoteles

Im letzten Blogbeitrag wurden mit den Worten von Nach Aristoteles gibt es drei Arten von Schlussfolgerungen. Der logische Schluss, der dialektische Schluss sowie den Fehlschluss. Jetzt müssen wir uns mit dem logischen Schluss genauer beschäftigen.

Dieser Schluss, in dem aus zwei wahren Prämissen eine wahre Konklusion ableitet wird, ist natürlich der wichtigste Schluss, denn hiermit wird ein sicherer „Transport von Wahrheit” von Aussagen gewährleistet. Dass es so etwas überhaupt gibt, ist die gute Nachricht, und man kann sie gar nicht überschätzen. Die „schlechte Nachricht“ wäre dann, dass dabei auf keine Weise Wahrheit gewonnen wird. Sie wird nur weitergegeben, denn die Prämissen müssen ja schon wahr sein. Die Frage, wie und wo man denn nun in der Praxis mit wahren Aussagen beginnen kann, wird uns später noch sehr beschäftigen.

Bei dem logischen Schluss kann man wiederum mehrere Arten unterscheiden. Diese unterscheiden sich in der Art der Prämissen und der Konklusion, welche sich durch ein „Zusammenrechnen“ der Voraussetzungen ergibt. „Zusammenrechnen“ heißt im Griechischen „συν-λογισμός“; man spricht also auch von einem Syllogismus; die Lehre von den Syllogismen heißt Syllogistik. 

Schauen wir uns erst einmal ein Beispiel eines Syllogismus an:

Alle Menschen sind sterblich
Alle Griechen sind Menschen
Also: Alle Griechen sind sterblich

Es gibt also drei Aussagen, zwei Vordersätze, von denen man ausgeht, und eine Konklusion, in der also die Vordersätze „zusammengerechnet“ werden.

Die Form der Sätze und ihre Darstellung

In diesem Beispiel sind alle Sätze von der Form „Alle A sind B“.  Der Satz „Alle A sind B“ kann aber auch so formuliert werden: „B kommt allen A zu.“  Diese Formulierung legt nahe, dass B ein Prädikat von allen A ist: B wird allen A zugesprochen (prädiziert). Sterblich zu sein, kommt jedem Menschen zu.

Die Formulierung ist auch diejenige, die dem griechischen Text am nächsten kommt, ist also die ursprünglichere Form. In der Scholastik wurde diese dann in „Alle A sind B“ umgeschrieben. Jedem A kommt das Prädikat B zu: Jeder Mensch ist also sterblich. 

Der obige Syllogismus lautet dann also in der ursprünglichen Form:

Sterblich zu sein, kommt jedem Menschen zu,
Mensch zu sein, kommt jedem Griechen zu,
Also: Sterblich zu sein, kommt jedem Griechen zu.

Darüber hinaus legt diese Formulierung auch eine Methode nahe, die erst viel später zur Veranschaulichung der Beziehung zwischen zwei Begriffen entdeckt worden ist. Man macht sich dabei zunutze, dass ein Begriff auch durch seinen Bedeutungsumfang beschrieben werden kann. Dann trifft jeder Begriff auf eine Menge von Entitäten zu: „Menschen“ können Griechen sein aber auch Ägypter, Thraker, Asiaten oder Europäer. Stellt man die Menge der Menschen durch einen Kreis oder irgendeine geschlossene Kurve dar, die Menge der Griechen ebenso, dann liegt der Kreis für die Griechen innerhalb des Kreises für die Menschen.

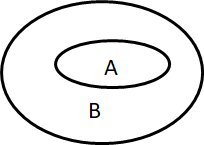
Abb. 1:  Die Menge der Griechen (A) ist eine Untermenge der Menschen (B). Ein Mensch zu sein (B), kommt allen/jedem Griechen (A) zu.

Man nennt solche Bilder Venn-Diagramme, nach dem Mathematiker John Venn (1834 bis 1923), der diese im Anschluss an Leonard Euler (1707 bis 1783) eingeführt hat. Eigentlich hat Gottfried Wilhelm Leibniz (1646 bis 1716) sie schon verwendet. Diese Venn-Diagramme veranschaulichen also allgemein Beziehungen zweier Mengen, egal, von welcher Art die Elemente sind. Im Rahmen einer Mengenlehre würden wir auch schreiben: A \(\subset \)  B, d.h. A ist Untermenge von B.

Dies ist aber nicht die einzige Form eines Satzes für eine Beziehung zwischen zwei Begriffen. Aristoteles verschaffte sich eine Übersicht über alle möglichen Formen der Sätze bzw. Aussagen. Dabei ergab sich: (Zitat nach (Höffe, 2009, p. 47)):

• Ein Satz ist nun eine Aussage, die etwas von etwas bejaht oder verneint;
• Eine solche Rede ist entweder allgemein oder partikulär oder unbestimmt.
• Allgemein nenne ich eine Aussage, die ein Jedem-Zukommen oder Keinem-Zukommen aussagt, 
• partikulär eine Aussage, die ein Irgendeinem-Zukommen, Irgendeinem Nicht-Zukommen oder Nicht-jedem-Zukommen aussagt.

Neben den allgemeinen Sätzen wie „Alle Griechen sind Menschen“ bzw. „Mensch zu sein, kommt jedem Griechen zu“ gibt es also noch die Negation (Kein-Zukommen) und die partikuläre Aussage (irgendeinem-Zukommen, aber nicht jedem).

Insgesamt erhält man damit folgende Typen von Sätzen:

B kommt jedem A zu,  (Alle A sind B),
B kommt keinem A zu, (Kein A ist B),
B kommt einigen A kommt zu, (Einige A sind B),
B kommt einigen A nicht zu, (Einige A sind nicht B).

Anschaulich können wir die weiteren Aussagetypen wie folgt darstellen:

In der Scholastik sind diese Formen abkürzend als ( A a B), (A e B), (A i B ) und (A o B) notiert. Dabei sollen die Buchstaben „a“ und „i“ an „affirmo“ erinnern, „e“ und „o“ an „nego“.

Die Struktur der Syllogismen

Zwei solcher Aussageformen bilden dann die Voraussetzungen, eine solche die Konklusion. Jeder Schluss kann also durch drei Buchstaben aus der Menge {a,e,i,o} charakterisiert werden und durch die Stellung der drei Buchstaben, die für die Begriffe in dem jeweiligen Satz stehen.

Einer von diesen Begriffen, der so genannte Mittelbegriff, muss in beiden Voraussetzungen vorkommen, er kann in diesen jeweils an erster oder an zweiter Stelle stehen, oder aber in einer Voraussetzung an erster, in der anderen an zweiter. Das ergibt vier verschiedene Formen bzw. Figuren. Die erste Figur ist folgende (vgl. obiges Beispiel)

C – B
B – A
C – A.

Nun sucht Aristoteles in allen Formen jene Kombination von jeweils zwei Aussageformen aus, die als Voraussetzungen notwendig zu einer Konklusion führen. Er sortiert dabei die Schlüsse, für die er ein Gegenbeispiel findet, einfach aus.

Die gültigen Schlüsse lassen sich dann jeweils durch die Form und eine bestimmte Kombinationen der Buchstaben a,e,i,o darstellen. Und um sich solche Kombinationen besser merken zu können, hat man sie in entsprechende Merkwörter eingebunden, z.B. merkt man sich z.B. die Kombination a a a mit dem Wort „Barbara“, und weiß noch dazu, dass hier die 1. Figur vorliegt. Dieser Schluss entspricht als genau dem obigen Beispiel.

Ein anderer wichtiger Schluss, auch von der 1.Form, wird auf diese Weise „Celarent“ genannt.

Aristoteles demonstrierte auf diese Weise, dass man systematisch ein System von Schlüssen formulieren konnte, bei denen aus der Wahrheit der Voraussetzungen notwendig die Wahrheit der Konklusion folgt.

Mit der Systematik eines Aristoteles hat man nun eine vollständige Übersicht über alle möglichen Schlussfolgerungen. Vorher hatte in der Syllogistik „die ganze Kunst darin bestanden, dass man mit großem Aufwand von Zeit und Mühe planlos herumsuchte“. So soll Aristoteles in seinen Sophistischen Widerlegungen geklagt haben (nach Schupp, I 275).

Wir haben mit dieser Aristotelischen Logik auch schon ein System vorliegen, das an die später noch einzuführende formale Prädikatenlogik erinnert. Man kann wie dort über die Prädikate „quantifizieren“, d.h. man kann mit Mengenangaben wie „alle“, „keine“ und „einige“ für die Prädikate operieren.

Am wichtigsten ist aber, dass Aristoteles hier die gültigen Schlussregeln „per Hand“ aus der Menge aller möglichen Kombinationen aussuchen muss, und zwar einfach, indem er solche, die er mit Hilfe eines Beispiels als ungültig erkennt, verwirft. Dieses „Erkennen“ ist ein intuitives, eines mit „gesundem Menschenverstand“. Man zweifelt nicht an der Richtigkeit der Schlussregel, aber für eine strenge Wissenschaft im heutigen Sinne reicht diese Art von Erkenntnis nicht aus.

Selbst wenn man heute Beziehungen der Begriffe mit Hilfe der Mengenlehre beschreibt, und damit die Schlussregeln im Rahmen der Mengenlehre begründet, ist die Erkenntnis eine mathematische. Damit wären die Schlussregeln nur indirekt logisch gerechtfertigt, denn die Mathematik nutzt auch nur, wie wir heute wissen, die Schlussregeln, die letztlich in der modernen Prädikatenlogik gewonnen werden.  Erst in dieser nämlich lassen sich die Schlussregeln streng begründen, indem man sie aus Tautologien ableitet. Wir werden das in einem späteren Blogbeitrag sehen. In der Prädikatenlogik also ist erst der Boden erreicht, auf dem man unanfechtbar aus wahren Sätzen wieder einen wahren Satz gewinnen kann. Diese Unanfechtbarkeit beruht nicht darauf, dass einem die Schlüsse jeweils „unmittelbar einleuchten“, sondern auf einer einzigen, viel grundlegenderen Annahme in der Prädikatenlogik, die uns noch viel „unmittelbarer“ einleuchtet.

Wir müssen noch die Bemerkung des Aristoteles zum dialektischen Schluss, also zu dem Schluss kommentieren, bei dem die Voraussetzungen nur wahrscheinlich wahr bzw. nur glaubwürdig sind. Dann könne die Konklusion auch nur wahrscheinlich wahr sein. Hier mehr zu sagen, war damals nicht möglich. Erst Anfang des 20. Jahrhunderts ist ja erst eine Wahrscheinlichkeitstheorie entstanden, mit der man in diesen Fall präziser werden kann. In einem späteren Blogbeitrag mit dem Thema „Über den Umgang mit unsicherem Wissen“ wird das genauer ausgeführt.

Die Syllogismen in einem axiomatisch-deduktiven System

Aristoteles hat uns mit seiner Logik aber nicht nur gezeigt, wie man sicheres Wissen sicher weitergeben kann. Er hat auch gezeigt, dass „man alle Schlüsse auf allgemeine Schlüsse der ersten Figur zurückführen“ kann, wie er in der Lehre vom Schluss, 1. Buch, 7. Kapitel schreibt. (Anon., kein Datum)

Damit haben wir also schon konkret ein axiomatisch-deduktives System vorliegen. Diese Struktur der Aussagen eines Wissensgebietes stellte für ihn das Ideal einer Wissenschaft dar. In der 2. Analytik, der Lehre vom Erkennen, 1. Buch, 3. Kapitel schreibt er:

• Ich behaupte dagegen, dass jede Wissenschaft zwar auf Beweisen beruhen muss, aber dass das Wissen der unvermittelten Grundsätze nicht beweisbar ist. Und dass dies notwendig so sein muss, ist klar. Denn da ein Wissen von den früheren Sätzen, aus welchen der Beweis geführt wird, notwendig ist, man aber einmal bei unvermittelten Sätzen anhält, so müssen diese notwendig unbeweisbar sein.
  Dieses ist meine Ansicht und ich behaupte, dass es nicht bloß Wissenschaften gibt, sondern auch oberste Grundsätze derselben, durch welche wir die Begriffe des Schlusses kennen lernen. (Anon., kein Datum).

Der Mathematiker Euklid von Alexandria wird in der Zeit um -300 die geometrischen Kenntnisse seiner Zeit in dieser Weise logisch ordnen. Die Organisation einer wissenschaftlichen Theorie als ein axiomatisch-deduktives System stellt bis heute ein Vorbild für jede Wissenschaft dar. Man versuchte in allen Jahrhunderten, diese Organisation eines Denkgebäudes nachzuahmen, also die Kenntnisse der Wissenschaften „more geometrico“, d.h. nach Art der Euklidischen Geometrie, zu ordnen. In Die Idee der Wissenschaft – Ihr Schicksal in Physik, Rechtswissenschaft und Theologie habe ich beschrieben, wie erfolgreich man bis heute war, diese Idee zu realisieren (Honerkamp, 2017).

Wer diese Idee als Erster gehabt hat, ist unklar. Der mathematische Beweis war ja schon den Pythagoreern bekannt. Wenn nun genügend durch Beweise gesicherte Aussagen in einem Gebiet vorhanden sind, wird man vermutlich sich auch irgendwann überlegen, welche Aussagen man als Axiome betrachten könnte. Damit stellt man sich der Frage: Welche Aussagen brauche ich als Vorgabe, um daraus alle anderen ableiten zu können? Also: Wie stelle ich eine logische Ordnung her? Solche Vorgaben werden dann immer besondere Aussagen sein, besondere Eigenschaften haben.

Diese Aussagen können unmittelbar einsichtig sein, also „durch sich selbst gewiss“, wie die Syllogismen der 1. Form oder wie allgemein in Theorien der Mathematik, aber auch höchst abstrakt und fern unserer Anschauung wie in Theorien der Physik. Auf jeden Fall hat man eine „logische Ordnung“ hergestellt, d.h. die Wahrheit einer großen Menge von Aussagen in unanfechtbarer Weise auf die Wahrheit einiger weniger Aussagen zurückgeführt. Genau das macht eine „strenge Wissenschaft“ aus.